Norwegian survival prediction model in trauma: modelling effects of anatomic injury, acute physiology, age, and co-morbidity

Abstract

Introduction

Anatomic injury, physiological derangement, age, and injury mechanism are well-founded predictors of trauma outcome. We aimed to develop and validate the first Scandinavian survival prediction model for trauma.

Methods

Eligible were patients admitted to Oslo University Hospital Ullevål within 24 h after injury with Injury Severity Score ≥ 10, proximal penetrating injuries or received by a trauma team. The derivation dataset comprised 5363 patients (August 2000 to July 2006); the validation dataset comprised 2517 patients (August 2006 to July 2008). Exclusion because of missing data was < 1%. Outcome was 30-day mortality. Logistic regression analysis incorporated fractional polynomial modelling and interaction effects. Model validation included a calibration plot, Hosmer–Lemeshow test and receiver operating characteristic (ROC) curves.

Results

The new survival prediction model included the anatomic New Injury Severity Score (NISS), Triage Revised Trauma Score (T-RTS, comprising Glascow Coma Scale score, respiratory rate, and systolic blood pressure), age, pre-injury co-morbidity scored according to the American Society of Anesthesiologists Physical Status Classification System (ASA-PS), and an interaction term. Fractional polynomial analysis supported treating NISS and T-RTS as linear functions and age as cubic. Model discrimination between survivors and non-survivors was excellent. Area (95% confidence interval) under the ROC curve was 0.966 (0.959–0.972) in the derivation and 0.946 (0.930–0.962) in the validation dataset. Overall, low mortality and skewed survival probability distribution invalidated model calibration using the Hosmer–Lemeshow test.

Conclusions

The Norwegian survival prediction model in trauma (NORMIT) is a promising alternative to existing prediction models. External validation of the model in other trauma populations is warranted.

Quality of care of trauma patients must be monitored continuously. Institutional performance data should therefore be analysed year-by-year and compared with previous data from the same institution as well as with data from other institutions or against a recognised standard.^1,2 A pre-requisite for performance analyses is a valid statistical model for prediction of outcome.

Outcome after hospitalisation is a function of patient characteristics on admission, quality of care, and random events.³ Comparison of crude mortality rates without adjusting for the risk profile of the patients is of limited value,⁴ as this approach will cause trauma centres treating high-risk patients to appear to have low performance compared with other centres. The rationale of risk adjustment is to remove sources of variation that are institution-independent, the goal being that the residual differences reflect actual differences in quality of care. Several prediction models for comparison of trauma care quality have been developed during the last 30 years.^5–7,* However, the external validity of such models may be limited by differences between trauma systems and imprecise data field definitions.^1,8–10

To obtain valid tools for intra- and inter-institutional comparisons, one must adjust for the extreme diversity of the trauma population with respect to anatomic injury, physiological derangement on admission, inherent reserve capacity because of age and pre-morbid conditions, and pre-hospital logistics. Further, outcome definitions must be unambiguous.¹¹ For more than 25 years, the Trauma Score – Injury Severity Score (TRISS) model has been the cornerstone in performance analysis in trauma worldwide,^1,5,12,13 although its shortcomings are well known.^14–16 TRISS was most recently updated with contemporary coefficients used to scale the relative importance of the various explanatory variables in 2005^† and 2009.¹⁷

TRISS employs the Injury Severity Score (ISS) as measure of anatomic severity.¹⁸ The same approach is taken by the UK Trauma Audit & Research Network (TARN) Ps04 and Ps12 survival prediction models.^6,* However, several authors have reported that the New Injury Severity Score (NISS) is a better predictor of mortality than the ISS.^7,19–22 The NISS has its advantage over the ISS in patients with several severe injuries in a single body compartment, e.g., penetrating injuries towards the torso, and in both blunt and penetrating traumatic brain injury.

In TRISS, physiology is documented according to the Revised Trauma Score (RTS),¹³ which is the sum of weighted coded values for Glasgow Coma Scale (GCS) score, respiratory rate (RR), and systolic blood pressure (SBP). According to TRISS convention, RTS is scored in the emergency department (ED).¹² This practice has considerable methodological implications as it results in missing RTS data for patients who have been sedated and tracheally intubated before ED arrival.^1,10 In the United States, patients with missing RTS data were previously excluded from survival prediction model development and use.¹² In contrast, several European and Australian prognostic models have used pre-hospital GCS, RR, and SBP scores when in-hospital values were unobtainable.^10,22,23 Recent studies on US trauma populations have demonstrated that patients excluded due to missing RTS data had more severe injuries and worse prognosis than patients with complete data and that such non-random exclusion will bias the conclusions drawn.^9,10,17,24 The most recent TRISS coefficients were therefore derived using multiple imputation of missing RTS values to avoid exclusion of this important patient group.¹⁷ The current TARN approach is to substitute the same single GCS coefficient for all patients intubated pre-hospitally, regardless of actual documented GCS.^*

Patient age is incorporated in the TRISS model in two separate ways. First, children < 15 years of age are given a separate set of coefficients. Additionally, all adults ≥ 55 years old are given a fixed penalty to account for increased risk of death because of age. A more complex approach is taken by TARN; their Ps04 and Ps12 survival prediction models incorporate age effects by applying eight different coefficients according to age group and an additional eight coefficients for interaction effects between age and gender.^* Although several studies have shown that the global medical condition of the trauma patient before injury affects outcome,^25–29 pre-injury co-morbidity is neither incorporated in the TRISS model nor in the TARN models.

Even outcome definitions vary among survival prediction models. In the TRISS model, survival is defined as status at end of acute care.¹² This end point is highly dependent on hospital discharge and transfer practices, and it is thus not readily transferable to other health-care systems. TARN uses survival status at 30 days post-injury, an end point that is used in many other fields of biomedical research. Differing definitions of mortality after trauma may greatly affect comparisons of institutional performance, and so will differing definitions of dead on arrival (DOA) and whether DOA patients are excluded from analyses.^11,18

In an attempt to remedy some of these sources of variability, we derived a trauma survival prediction model (Norwegian Prediction Model in Trauma – NORMIT). We strived to adhere to the definitions in the Utstein template for uniform reporting of data following major trauma.³⁰ Fractional polynomials (FPs) were utilised to optimally model numerical variables, and we evaluated whether anatomic injury is better represented by the NISS than the ISS. New coefficients were estimated for the individual RTS component scores as well as for their unweighted sum (Triage RTS; T-RTS) to evaluate how physiology best could be modelled. Finally, we assessed the performance of pre-injury American Society of Anesthesiologists Physical Status Classification System (ASA-PS) score^‡ as a predictor in the overall model. The resulting model showed very good discrimination between survivors and non-survivors when tested in a validation dataset.

Patients and methods

Population and study database

The study was based on data from the trauma registry at Oslo University Hospital, Ullevål (OUH-U). OUH-U is the major trauma hospital for 600,000 citizens, and the trauma referral centre for 2.7 million people. Presently, approximately 1800 patients, including nearly 190 children < 16 years old, are included in the registry per year. In the study period, the number of included patients per year increased from 843 in 2001 to 1328 in 2008. Regional pre-hospital triage protocols decide whether patients are transported to OUH-U, to local Level II trauma hospitals, or to local emergency medical centres. Consequently, approximately 40% of patients in the OUH-U Trauma Registry have severe injury defined as ISS > 15.¹² In accordance with the data validation protocol of the trauma registry, all information was thoroughly screened for inconsistencies and non-logical values before data extraction. The study was retrospective, non-interventional, and based on anonymised register data only. It was therefore considered exempt from patient consent requirements by the Oslo University Hospital Data Protection Officer, who in this matter acted on behalf of our Regional Committee for Medical and Health Research Ethics and the Norwegian Data Protection Authority.

Inclusion criteria

The study inclusion period at OUH-U was 1 August 2000 to 31 July 2008. Patients were included if they arrived within 24 h after injury, whether they were admitted directly or via a local hospital. Eligible were all patients admitted with trauma team activation (TTA), all patients with ISS ≥ 10, with head injuries scored as Abbreviated Injury Scale (AIS) ≥ 3, and/or with penetrating injuries towards the head, neck, torso, and/or proximal to elbow or knee irrespective of ISS.¹¹ Quarterly, hospital records were electronically searched for patients without TTA but with International Classification of Diseases 10th Edition (ICD-10) codes in Chapter XIX: Injury, poisoning and certain other consequences of external causes (S00–T98). Their records were checked and AIS coded by the registrars, and patients fulfilling the criteria above were included. Patients with an isolated single extremity fracture were excluded unless the trauma team was activated. Notably, patients classified as DOA were not excluded.

Coding

Anatomic injury was coded by two dedicated trauma registrars (nurse anaesthetists with broad trauma experience and Association for the Advancement of Automotive Medicine certification) according to AIS 1990 update 98 (AIS 98).³¹ Pre-injury co-morbidity was indexed by the registrars according to the ASA-PS score.^28‡ ASA-PS 1 represents no disease, ASA-PS 2 mild systemic disease, ASA-PS 3 severe systemic disease, ASA-PS 4 severe disease that is a constant threat to life, and ASA-PS 5 a moribund patient. Guidelines and examples were used to increase scoring accuracy.²⁸ Age was defined as the year the trauma occurred minus the patient’s birth year.

The backbone of the Norwegian pre-hospital emergency medical system (EMS) consists of ground ambulances with paramedics and emergency medical technicians. In addition, there is a nation-wide second-tier EMS using helicopters and rapid-response cars manned with specially trained anaesthesiologists. In a previous study from the OUH-U trauma registry, we found that 17.4% of included patients had been intubated prior to admission, either by pre-hospital services or in the ED of the local, referring hospital.¹⁰ For patients arriving at OUH-U intubated and in general anaesthesia, GCS and RR were scored based on values documented immediately prior to intubation. In cases of missing RTS data elements, all available information in the patient records was used to estimate pre-intubation RTS clinical category^13,30,32 (value 0–4, see Table 1). In order to avoid biasing data in our favour, the value closest to normal was used when in doubt, and normal values were used as final default.¹⁰

Table 1.

Categories for the three Revised Trauma Score (RTS) elements, with corresponding clinical signs

RTS category scale	Respiratory rate (breaths/min)		Systolic blood pressure (mmHg)		Glasgow Coma Scale score
4	10–29	Normal	≥ 90	Good radial pulse	13–15
3	> 29	Fast	76–89	Weak radial pulse	9–12
2	6–9	Slow	50–75	Femoral pulse palpable	6–8
1	1–5	Gasps	1–49	Carotid pulse only	4–5
0	0	No respiration	0	No carotid pulse	3

Triage RTS (T-RTS; range 0–12) is defined as the sum of the clinical category values of respiratory rate, systolic blood pressure and Glasgow Coma Scale.

Outcome

Outcome was defined as survival status (dead or alive) 30 days after injury. This information was obtained from patient records and the Norwegian Population Registry, where all Norwegian citizens and resident aliens can be traced via their social security number. Foreign citizens repatriated alive to their home country within 30 days after injury were defined as survivors.

Statistical methods

Prognostic variables deemed to be of interest were age, gender, pre-injury co-morbidity (ASA-PS score), dominant injury type (blunt/penetrating), intubated prior to admission, NISS, ISS, RTS clinical categories (0–4) of GCS, SBP and RR, and the T-RTS.¹³ T-RTS (range 0–12, see Table 1) is defined as the sum of the clinical category values of GCS, SBP, and RR.

Data analysis was undertaken using Intercooled Stata 9.0 (StataCorp LP, College Station, TX, USA) and Statistical Package for the Social Sciences (SPSS) release 17 (IBM Corporation, Armonk, NY, USA).

Model development

Eligible patients admitted at OUH-U between 1 August 2000 and 31 July 2006 formed the model derivation dataset. Univariate analyses were used to report mortality rates and unadjusted odds ratios (ORs) for categorical variables, and to explore the effect of grouped continuous variables on mortality (Tables 2 and 3). A logistic regression analysis examined joint relationships between prognostic variables of interest and 30-day mortality. The significance level was set to 0.05. The underlying principle was to derive a model that best represented the relationships between prognostic variables and mortality but also made sense from a clinical perspective.

Table 2.

Unadjusted mortality rates and odds ratios for death in the derivation dataset

Variable	Level or coded value	Deaths/Patients	Mortality (%)	Odds ratio (95% CI)
Gender	Male	289/3846	7.5	*
	Female	135/1517	8.9	1.20 (0.97–1.49)
ASA-PS	1	214/3987	5.4	*
	2	98/917	10.7	2.11 (1.64–2.71)
	3 or 4	112/459	24.4	5.69 (4.42–7.33)
Injury	Blunt	382/4874	7.8	*
mechanism	Penetrating	42/489	8.6	1.10 (0.79–1.54)
Intubated	No	184/4378	4.2	*
	Yes	240/985	24.4	7.34 (5.97–9.03)
SBP	4 (> 89)	300/5111	5.9	*
	3 (76–89)	21/93	22.6	4.68 (2.84–7.71)
	2 (50–75)	45/95	47.4	14.4 (9.49–22.0)
	0 or 1 (0–49)	58/64	90.6	155 (66.4–362)
RR	4 (10–29)	244/4872	5.0	*
	3 (> 29)	61/277	22.0	5.36 (3.92–7.32)
	1 or 2 (1–9)	56/144	38.9	12.1 (8.43–17.3)
	0 (0)	63/70	90.0	170 (77.4–377)
GCS score	4 (13–15)	89/4074	2.2	*
	3 (9–12)	39/421	9.3	4.57 (3.09–6.76)
	2 (6–8)	49/379	12.9	6.65 (4.61–9.59)
	1 (4–5)	63/191	33.0	22.0 (15.3–31.8)
	0 (3)	184/298	61.7	72.3 (52.8–98.9)

^*Reference categories.

Categorical and coded variables in the derivation dataset, comprising 5363 patients.

ASA-PS, pre-injury American Society of Anesthesiologists Physical Status Classification; Intubated, tracheal intubation performed prior to admission; SBP, systolic blood pressure (mmHg); RR, respiratory rate (breaths/min); GCS, Glascow Coma Scale.

Table 3.

Unadjusted mortality rates for grouped continuous variables in the derivation dataset

Variable	Range	Deaths/Patients	Mortality (%)
Age	0–4	6/157	3.8
	5–14	12/378	3.2
	15–24	63/1126	5.6
	25–34	50/1139	4.4
	35–44	43/825	5.2
	45–54	45/587	7.7
	55–64	43/464	9.3
	65–74	55/285	19.3
	75–84	69/293	23.5
	85+	38/109	34.9
ISS	0–8	7/1762	0.4
	9–15	17/1365	1.2
	16–24	48/1002	4.8
	25–34	168/781	21.5
	35–49	98/291	33.7
	50–75	86/162	53.1
NISS	0–8	6/1659	0.4
	9–15	13/961	1.4
	16–24	18/906	2.0
	25–34	63/970	6.5
	35–49	77/393	19.6
	50–75	247/474	52.1
T-RTS	0–3	66/71	93.0
	4–6	54/92	58.7
	7	35/74	47.3
	8	74/184	40.2
	9	43/199	21.6
	10	43/370	11.6
	11	42/492	8.5
	12	67/3881	1.7

Data from 5363 patients, forming the derivation dataset. Mortality increased with increasing age, ISS and NISS and decreased with T-RTS.

ISS, Injury Severity Score; NISS, New Injury Severity Score; T-RTS, Triage Revised Trauma Score.

The effects of continuous variables on mortality were explored using:

1. Defined categorical representations based on relationships observed in the study data and, for age, based on previously published categorisations.^5,6,33,34

2. First-degree (FP1) and second-degree (FP2) fractional polynomial transformations³⁵ to model any non-linearity. FP1s have the form β₁X^p, where power p is chosen from the set −2, −1, −0.5, 0, 0.5, 1, 2, and 3. These eight FP1s represent, respectively, reciprocal square, reciprocal, reciprocal square root, logarithmic, square root, linear, square, and cubic transformations. FP2s have the form 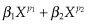, where p₁ and p₂ are chosen from the same set of eight powers, resulting in 28 FP2s with differing values of p₁ and p₂. When p₁ and p₂ are equal, the FP2s are defined as 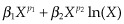, resulting in an additional eight FP2 functions. FP fitting in Stata of a continuous predictor X used an adjusted form that centred the FP transformation on the mean of the observed values, and age was increased by 1 to avoid the log of 0.

In the model-building procedure, we experienced that the best FP representation of a continuous variable varied according to which other covariates were also in the logistic regression model. The model building process was therefore carried out in the following order:

1. A forward stepwise procedure with a test for backward elimination of covariates to obtain a preliminary main effects model. The significance levels were set to 0.05 for entry into and 0.10 for elimination from the model.

2. Determination of the best FP representation for the continuous variables in the preliminary main effects model. The order in which these variables were investigated was according to their significance in this model. The best FP transformation for a variable was identified by comparing the best fitting FP1 with the best-fitting FP2 and choosing that which gave the most significant fit.

3. The FP transformations determined under 2 were verified by simultaneous FP modelling using backward elimination Stata routine mfp.³⁶

4. A forward stepwise procedure with a test for backward elimination of interaction effects, with particular attention to a previously found interaction between age and gender.⁶ The significance level for interaction effects was set to 0.01 to reduce the risk of including spurious effects in the model.

Model validation

Eligible patients admitted at OUH-U between 1 August 2006 and 31 July 2008 formed the dataset for temporal validation for the model.^8,37 The choice of relative size of the prediction dataset and the validation dataset were done according to the recommendation by Steyerberg.³⁸ Model calibration was first explored using a calibration plot. Second, a Hosmer–Lemeshow (H-L) goodness-of-fit test was performed. The H-L test divides the survival probabilities into 10 groups of approximately equal numerical size (termed deciles) and compares the observed and predicted number of survivors and non-survivors within each decile. Model discrimination denotes the model’s overall ability to correctly classify patients as survivors or non-survivors. Discrimination was assessed by the area under the receiver operating characteristic (ROC) curve and by presentation of median probability of survival (Ps) for survivors and non-survivors.

Results

Model development

A total of 5409 eligible patients were admitted between 1 August 2000 and 31 July 2006, of which 5363 (99.1%) had available information on all prognostic variables of interest and formed the derivation dataset. The number of deaths in the derivation dataset during the first 30 days following injury was 424 (7.9%). The dataset comprised 308 foreign citizens (5.7%) from 42 different nations. Within 30 days of injury, 112 of these (2.1% of the entire material) had been repatriated to a foreign somatic hospital, 18 (0.3%) transferred to another Norwegian hospital, and 163 (3.0%) discharged alive; 293 foreign citizens were thus defined as survivors. Fifteen foreign citizens (0.3%) were non-survivors.

The distribution of possible predictive variables in the derivation dataset is shown in Table 2. There were 3846 (71.7%) males, 4874 (90.9%) patients had blunt injuries, 3987 (74.3%) had no co-morbidity (pre-injury ASA-PS score 1), and 4378 (81.6%) were not intubated prior to admission. Normal physiology (i.e., RTS clinical category 4) was present in > 90% of patients for SBP and RR, and in 76.0% for GCS score. Median (interquartile range) for age was 33 (22–51), T-RTS 12 (11–12), ISS 10 (5–22; mean 15.2), and NISS 16 (5–29; mean 19.9).

There were only a small number of patients with pre-injury ASA-PS 4 (n = 23), SBP clinical category value 1 (n = 15), and RR clinical category value 1 (n = 37) (Table 1). For analysis purposes, these categories were therefore combined with an adjacent category having a similar mortality rate (see Table 2). The univariate analyses showed increased mortality for patients intubated prior to admission and increased mortality by decreasing category of SBP, RR, and GCS, and by increasing ASA-PS classification of co-morbidity (Table 2). An observed increased mortality for females and for penetrating injuries was not statistically significant. The effects of grouped continuous variables on mortality are summarised in Table 3.

Multivariable logistic regression analyses revealed that the effect of the NISS on mortality was greater than that of the ISS. The T-RTS had greater significance than any of the three individual RTS components (GCS, SBP, and RR). The variables gender, intubated prior to admission, and injury mechanism did not contribute significantly to the model. Therefore, we chose as preliminary main effects model one comprising NISS, T-RTS, age, and pre-injury ASA-PS.

FP analysis supported treating NISS and T-RTS as linear functions. A cubic function of age was found to best represent the gradual increase in mortality at younger ages followed by a steeper increase at older ages. It was confirmed that these FP transformations were significant and stronger predictors than categorical representations. There was a significant interaction effect between NISS and pre-injury ASA-PS, suggesting that in ASA-PS 3 and 4 patients, mortality was to a lesser degree predicted by NISS. Gender, evaluated together with an interaction between gender and age, did not contribute significantly.

Coefficients and ORs for predictors in the resultant NORMIT model are presented in Table 4. All variables in the model were highly significant (P < 0.001).

Table 4.

NORMIT coefficients for predicting survival and odds ratios of death

Predictors*	Coefficients for predicting survival (95% CI)	Odds ratio of death (95% CI)
T-RTS – 11.1889	0.5422 (0.48 to 0.61)	0.58 (0.54–0.62)
[(Age + 1)/100]3 − 0.0571	−5.1288 (−5.98 to −4.28)	169 (72.2–395)
ASA-PS
1	0
2	−1.4366 (−2.09 to −0.78)	4.21 (2.18–8.11)
3 and 4	−1.9210 (−2.56 to −1.28)	6.83 (3.59–13.0)
(NISS − 19.9303) by ASA-PS
1	−0.1027 (−0.12 to −0.09)	1.11 (1.09–1.12)
2	−0.0637 (−0.08 to −0.05)	1.07 (1.05–1.08)
3 and 4	−0.0535 (−0.07 to −0.04)	1.05 (1.04–1.07)
Constant	5.8034

^*For numerical variables, the statistical package Stata adjusts the variables by subtracting the sample mean before model coefficients are calculated.

T-RTS, Triage Revised Trauma Score (0–12); ASA-PS, pre-injury American Society of Anesthesiologists Physical Status Classification (1–4); NISS, New Injury Severity Score; CI, confidence interval.

The final NORMIT model equation is displayed in Fig. 1. Observed and predicted death rates by age, adjusted for other variables in the model, are depicted in Fig. 2.

Figure 1.

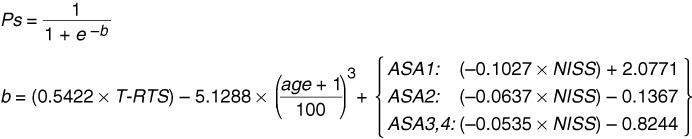
The NORMIT model equation. The model equation was derived from the more complex expressions shown in Table 4. Predicted probability of survival for an individual trauma victim is calculated by inserting the patient’s T-RTS value, age, and NISS value in the equation, selecting the adequate NISS expression depending on the patient’s pre-injury ASA-PS classification. Ps, Probability of survival; T-RTS, Triage Revised Trauma Score; age, years; ASA1, ASA2 and ASA3,4, individual pre-injury American Society of Anesthesiologists Physical Status Classification System (ASA-PS) categories; NISS, New Injury Severity Score.

Figure 2.

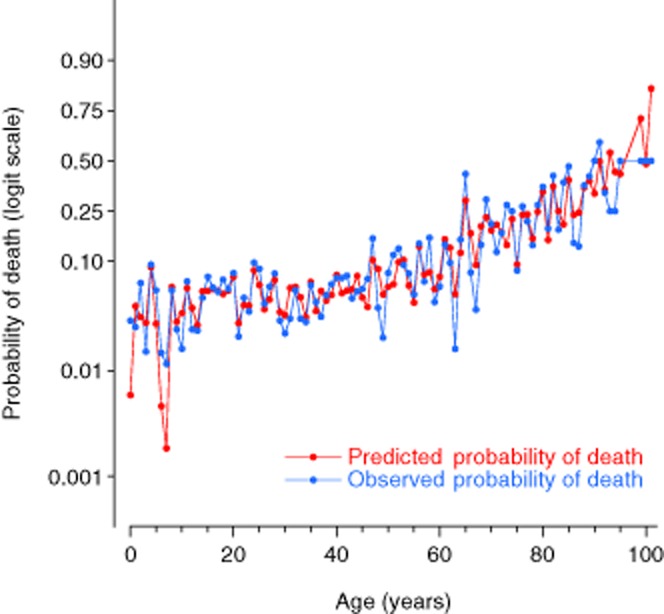
Observed and predicted (NORMIT) death rates by patient age. Data from the model derivation dataset. The displayed death rates are adjusted for the other variables in the model.

Model validation

A total of 2521 eligible patients were admitted between 1 August 2006 and 31 July 2008, of which 2517 (99.8%) had available information on all model predictors and formed the validation dataset. The number of deaths during the first 30 days following injury was 155 (6.2%), significantly less than the 7.9% mortality in the prediction dataset (P = 0.006). Median (interquartile range) for age was 34 (21–51), T-RTS 12 (12-12), ISS 10 (5–21; mean 14.3), and NISS 14 (5–29; mean 19.2). One thousand eight hundred seventy-four (74%) patients had pre-injury ASA-PS score 1.

Because of the highly skewed survival probability distribution, tabulation for the H-L test in 10 equally sized patient groups (deciles) resulted in six groups comprising Ps values greater than 0.99 (Table 5). Moreover, the small number of expected deaths among deciles 4–10 limited the validity and usefulness of applying the H-L test to either the figures presented in Table 5 or to a reduced table with deciles 4–10 combined to increase the size of the expected frequencies (not shown). An alternative approach utilising tabulation of observed and expected events by Ps intervals of 0.1 provided a more informative comparison (Table 6). We found similar numbers of observed and expected events at each Ps interval, with the exception of Ps between 0.2 and 0.4 for which there were more survivors in the validation dataset than predicted by the model. A calibration plot is shown in Fig. 3.

Table 5.

Hosmer–Lemeshow tabulation: survival probability in 10 patient deciles in the validation dataset

Decile	Probability of survival	Survivors (n)		Non-survivors (n)		Total
		Observed	Predicted	Observed	Predicted
1	< 0.7897	136	118.8	116	133.2	252
2	0.7897–	226	225.6	26	26.4	252
3	0.9517–	246	245.2	6	6.8	252
4	0.9852–	247	248.5	4	2.5	251
5	0.9938–	250	250.9	2	1.1	252
6	0.9970–	252	251.5	0	0.5	252
7	0.9986–	251	250.7	0	0.3	251
8	0.9993–	251	251.9	1	0.1	252
9	0.9996–	253	252.9	0	0.1	253
10	> 0.9997	250	249.9	0	0.1	250

Deciles were constructed by ranking all patients from lowest to highest probability of survival and then dividing the material in 10 equally sized groups. Overall mortality was low; only the two lowest deciles had probabilities of survival less than 95%. The skewed distribution invalidated the use of the Hosmer–Lemeshow statistical test.

Table 6.

Observed and predicted events by survival probability intervals of 0.1 in the validation dataset

Interval	Probability of survival	Survivors (n)		Non-survivors (n)		Total
		Observed	Predicted	Observed	Predicted
1	< 0.1	3	1.1	23	24.9	26
2	0.1–0.19	4	3.8	21	21.2	25
3	0.2–0.29	12	5.9	11	17.1	23
4	0.3–0.39	12	7.4	9	13.6	21
5	0.4–0.49	13	12.2	14	14.8	27
6	0.5–0.59	12	13.2	12	10.8	24
7	0.6–0.69	30	26.6	11	14.4	41
8	0.7–0.79	56	54.2	16	17.8	72
9	0.8–0.89	97	92.6	11	15.4	108
10	≥ 0.9	2123	2129.0	27	21.0	2150

Figure 3.

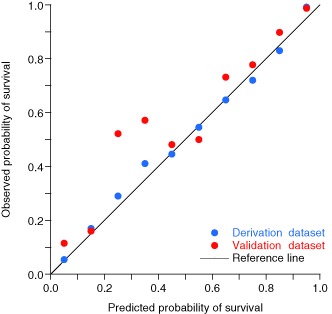
Calibration plot. Observed vs. predicted probability of survival in the derivation (blue markers) and validation (red markers) datasets. Note higher observed survival in the validation dataset for predicted survival probabilities between 0.2 and 0.4.

The area [95% confidence interval (CI)] under the ROC curve was 0.946 (0.930–0.962) in the validation dataset, indicating very good discrimination³⁹ between survivors and non-survivors. The median (interquartile range) for Ps was 0.998 (0.984–0.9995) for survivors and 0.496 (0.178–0.793) for non-survivors.

Discussion

An optimal modelling of predictors is crucial to achieve a clinically valid prediction model. The first trauma survival model, TRISS, was simple and interpretable but did not accurately represent complex relationships between risk and injury. Recent trauma models therefore have incorporated more variables and non-linear relationships. To our knowledge, NORMIT is the first published prediction model in trauma that explores fractional polynomial modelling of all continuous predictors, compares the effect of the NISS with the ISS, compares the effect of T-RTS with its three components, and also incorporates co-morbidity. In the present study, this model had outstanding discrimination between survivors and non-survivors.

Validation – strategy and findings

The performance of NORMIT was evaluated both by its discrimination abilities (how well the prediction model can discriminate between survivors and non-survivors) and its calibration (comparison of observed and predicted death and survival rates for patient groups in different risk strata).

As recommended by several authors, validation of NORMIT’s discrimination and calibration was performed in a separate dataset.^8,38 As expected, performance in the validation dataset was somewhat lower than in the derivation dataset on which the model was developed. The area (95% CI) under the ROC curve was 0.966 (0.959–0.972) in the derivation dataset and 0.946 (0.930–0.962) in the validation dataset. Temporal validation, i.e., evaluating the model on a more recent dataset, was chosen as strategy. This is considered as a stronger validation procedure than splitting a dataset into two random parts to obtain one derivation and one validation dataset, or performing a cross-validation procedure.^8,37 Temporal validation represents a prospective evaluation of a model, is independent of the original data, and may thus be considered an external validation in time.³⁷ However, we recognise that true external validation, using a separate dataset from another institution, would be a stronger and even better validation procedure. The internal consistency of the OUH-U Trauma Registry is probably high because data are entered by only two dedicated trauma registrars, who have access to all patient information. Increased variability in data quality would be expected if a number of smaller institutions were to supply data, and NORMIT’s prediction abilities should be tested also in the latter setting.

Model calibration using the H-L test was invalidated by the low overall mortality and consequent skewed survival probability distribution (Table 5). This problem has been pointed out also for the TRISS model, where several studies have shown that although overall discrimination was acceptable, calibration varied substantially across different strata of injury severity, and undue emphasis was placed on strata with minor injury because the majority of patients belonged there.^9,17

In NORMIT, although the derivation and validation datasets had similar distributions of model predictors, the significantly reduced mortality in the more recent validation dataset (6.2% vs. 7.9%) is likely to have confounded the comparison between observed and expected events. The number of observed survivors exceeded predicted for all but one probability interval, although this discrepancy was only marked for survival probability between 0.2 and 0.4 (Table 6 and Fig. 3). This is in line with the results from a recent study demonstrating a significant improvement in survival of critically injured patients in our trauma centre starting in 2005.² Our findings emphasise the need to update any model’s coefficients on a regular basis.

At present, at least two European trauma prediction models exist. The UK TARN Ps04 prediction model was launched by Bouamra et al. in 2006⁶ (coefficients recently revised, producing the Ps12 model^** ). The Ps04 model’s performance was compared with predictions based on the TRISS model with UK TARN revised coefficients. The area under the ROC curve using the Ps04 on the validation dataset was 0.952 (95% CI 0.946–0.957), while TRISS with customised UK coefficients yielded a value of 0.941 (95% CI 0.936–0.952). Bouamra et al. used a random split of the entire dataset to form one derivation dataset (70%) and one validation dataset (30%). A random split approach will tend to give optimistic results of model validation because the two datasets will be very similar.

The German Revised Injury Severity Classification score (RISC)⁷ was launched by Lefering in 2006. A random split of the dataset into a derivation and a validation dataset was used. Validation showed that the area under the ROC curve for the RISC model was 0.909 (95% CI 0.879–0.938). A temporal validation of the RISC model in a dataset obtained 1 year later from the same trauma registry yielded an area of 0.907 (95% CI 0.890–0.924).

As far as we know, neither the UK TARN nor the RISC model has been validated in an external dataset. To compare generalisability of different prediction models, the existing models should be benchmarked on the same, external dataset. Compared with the results of published internal validation of the UK TARN prediction model and the RISC model, we have found the temporal validation of the NORMIT model to be promising.

Patient inclusion in the model dataset

High-quality data from Norwegian trauma patients formed the basis for development of the NORMIT survival probability model. The derivation dataset comprised almost 40 deaths per prognostic variable of interest, satisfying the suggested minimum of 10 events per predictor.⁴⁰ The validation dataset fulfilled the recommendation of at least 100 events (deaths) and 100 non-events (survivors).³⁸ The relative sizes of the derivation and validation datasets were approximately 2 : 1, as recommended for temporal validation.³⁸

Missing covariates in a dataset will result in patient exclusion from model development, which may bias results. We normally scored RTS on ED admission, but when necessary, documentation of GCS and RR from pre-hospital services or the delivering hospital was used to obtain scores. This practice enabled Ps estimation in nearly all trauma patients. Our practice is especially advantageous in the most severely injured patients, for whom exact physiological measurements often are not recorded in the ED until one obtains therapeutic response or the patient dies.

The long-time practice of systematically excluding from studies trauma patients for whom RTS scoring was not possible in the ED represents a major limitation in the accumulated body of trauma research. We have previously shown that the exclusion rates in large US studies were unacceptably high, as well as being non-random with regard to patient prognosis.¹⁰ In an attempt to remedy this problem, Schluter et al. used a multistage multiple imputation technique to estimate values for missing data points in their 2009 revision of the TRISS coefficients.¹⁷ Schluter et al. reported large differences in results from analyses run on complete cases only and analyses run on the entire dataset with imputed values. In our trauma system, GCS and RR scores recorded before intubation could be systematically used to obtain precise data as well as optimal patient inclusion.

Anatomic injury – the best representation in the model

The model development process demonstrated that the NISS was a better predictor of mortality than the ISS. Moreover, FP modelling suggested that the effect of NISS could be best represented as a linear function. This contrasts with UK TARN’s highly complex FP transformation of ISS using both a logarithmic and a square root representation.⁶ Several studies have compared the performance of NISS and ISS in predicting outcome after trauma. The NISS should intuitively have its advantage over the ISS in patients with multiple serious injuries in a single body region, e.g., blunt or penetrating traumatic brain injury or penetrating injuries towards the torso. One study found NISS and ISS to have nearly equal performance in predicting overall mortality before trauma centre discharge or transfer,⁴¹ while several studies both in paediatric²¹ and adult trauma^20,22 have shown NISS to outperform ISS, with better calibration especially in the severely injured.

A study aiming at comparing NISS and ISS must be prospective in nature and designed for coding of all injuries. This has not always been the case. Coding of all injuries, including duplicate coding, e.g., in bilateral femoral fractures or multiple spine fractures, must be emphasised in the study period. If ISS is the only focus, the registrar may not necessarily give priority to coding of all injuries in each body region as only a single injury in each of up to three different body regions may be used for ISS calculation. Furthermore, instead of using dedicated trauma registrars, some registries use computer programs that automatically generate AIS codes from a patient’s ICD-9 codes. If the database has limitations in the number of ICD-9 codes that can be recorded – previously reported as a problem in European and US studies^20,42 – only the most severe injuries will be coded, and coding of duplicate injuries will probably not be prioritised. This would invalidate or at least severely bias comparative studies between ISS and NISS. In our database, every injury is always coded, including bilateral injuries and multiple injuries in the same body region. This may have contributed to our finding that the NISS was the strongest predictor of mortality of all variables evaluated in the model-building procedure.

Scoring of physiological derangement

Physiological scores measure the acute, dynamic component of injury. Since 1989, the RTS – based on measurements of GCS score, SBP, and RR¹³ – has been used worldwide. In the original TRISS model,⁵ separate weights were first calculated for each individual RTS element. Subsequently, the three weighted elements were summed, and a fourth coefficient was calculated to estimate the impact of the weighted RTS sum on survival. In contrast, in the 2009 revision by Schluter et al., each RTS element was assigned its own coefficient and implemented directly in the TRISS prediction model.¹⁷ In NORMIT, the variable best representing physiology was the T-RTS, i.e., the sum of the unweighted RTS elements (0–12, Table 1). Inclusion of a single, linear representation of T-RTS in a model may in itself represent an advantage over including one or more of GCS, SBP, and RR, as it maximises the clinical information introduced in the model while minimising the number of variables. A comparison of the model including a linear representation of T-RTS with one including the three RTS components as categorical variables showed that the latter model decreased deviance only modestly and increased R² only from 0.574 to 0.583 while containing more than twice as many variables (16 vs. 7). Face validity of the T-RTS is high. It is easy to convert raw data from GCS score, SBP, and RR into RTS clinical categories (Table 1), and T-RTS is simple to use both in the pre-hospital environment as a triage tool and in-hospital for prognostication. It is of educational value, both for paramedics and for trauma team members, that this instrument is in extensive use.⁴³ Moreover, using NORMIT, exclusion rates because of missing data can be reduced because pre-hospital data can be used for prognostication if ED data are missing.

Modelling patient age

We found that the effect of age could best be represented by a cubic function. This allows for the non-linear relationship generated by mortality rates increasing slowly at younger ages followed by a more rapid increase with increasing age (Fig. 2).

In all published trauma survival models we have seen, age has been treated as a categorical variable. In the TRISS model, age is dichotomised (< 54 years or ≥ 55 years).⁵ Generally, a recommendation in model building is not to dichotomise a continuous variable because valuable information could be lost. In the RISC model, age has four categories,⁷ and in the UK TARN Ps09 model, age has eight categories as well as eight categories for interactions between age and gender.⁶ The NORMIT approach, implementing age as a single cubic function in the model, is a much simpler and more intuitive representation that also was the most statistically significant.

Inclusion of a co-morbidity score

Although there is general agreement that physical status before trauma influences outcome, an overall quantification of the effect has been difficult to achieve because of major methodological differences concerning grading of disease. Accordingly, reported incidences of pre-existing disease in various trauma populations vary widely, from 5% to 19% in North America to 39% in the United Kingdom.²⁶ Several other authors have explored pre-injury co-morbidity as mortality predictor. The estimated effects obviously depend on which measures of co-morbidity were used and whether they were dichotomous^23,44,45 or ordinal categorical variables calculated from the number of pre-existing medical conditions.^26,29

We have previously shown that pre-injury co-morbidity measured as ASA-PS was an independent predictor of mortality after trauma²⁸ and a reliable score for classifying co-morbidity in trauma patients.⁴⁶ The revised Utstein template for uniform reporting of data following major trauma has included pre-injury ASA-PS as a core data variable.³⁰ Compared with patients with no documented co-morbidities (ASA-PS category 1) in the present study, unadjusted OR for death was 2.11 for ASA-PS category 2 patients and 5.69 for ASA-PS category 3 or 4 patients.

Interaction effects

A significant interaction effect between NISS and co-morbidity suggested that the effect of NISS on mortality was less marked for patients with documented pre-existing disease affecting everyday function (ASA-PS 3 or 4). This finding probably reflects that patients with, e.g. cardiac, respiratory, or renal conditions were more vulnerable to succumb even to lesser trauma. In contrast, for a previously healthy person, anatomic injury would be more deciding for outcome. We have not found other studies focusing on this subject.

The interaction effect between age and gender published elsewhere⁶,^§ was not replicated in this study. Unadjusted mortality rates by gender were very similar at all age groups in our material, with the exception of the 75+ group where mortality was 29% in males and 24% in females.

Conclusions

A statistical prediction model can be a powerful tool for evaluating trauma care, but inappropriately applied, it may result in misleading evaluations. Only if the prognostic model includes all variables significantly affecting outcome and if these are well defined and modelled appropriately can the model be used for performance evaluations. If, however, one or more important variables are not present in the model, a variation in case-mix between different centres could lead to perceived different performance. Given the typical spectrum of injury mechanisms in Scandinavia and the advanced pre-hospital EMS systems, there is a strong need for a Scandinavian survival prediction model. We found the NORMIT model to effectively predict trauma outcome in our South-East Norwegian population, and we recommend that it should be tested on datasets from other European trauma registries for external validation and further development.