Brain connectivity and novel network measures for Alzheimer’s disease classification

Abstract

We compare a variety of different anatomical connectivity measures, including several novel ones, that may help in distinguishing Alzheimer’s disease patients from controls. We studied diffusion-weighted MRI from 200 subjects scanned as part of the Alzheimer’s disease Neuroimaging Initiative (ADNI). We first evaluated measures derived from connectivity matrices based on whole-brain tractography; next, we studied additional network measures based on a novel flow-based measure of brain connectivity, computed on a dense 3D lattice. Based on these two kinds of connectivity matrices, we computed a variety of network measures. We evaluated the measures’ ability to discriminate disease with a repeated stratified 10-fold cross-validated classifier, using support vector machines (SVMs), a supervised learning algorithm. We tested the relative importance of different combinations of features based on the accuracy, sensitivity, specificity, and feature ranking of the classification of 200 people into normal healthy controls, and people with early- or late-stage mild cognitive impairment (MCI), or Alzheimer’s disease (AD).

1. Introduction

Current approaches used to classify Alzheimer’s disease (Kohannim et al., 2010; Klöppel et al., 2008) rely on features such as volumetric measures from anatomical regions in magnetic resonance imaging (MRI) images of the brain, CSF biomarkers, ApoE genotype, age, sex, body mass index, and, in some cases, clinical and cognitive tests. Here we attempted to improve our understanding of the best features for Alzheimer’s disease classification by studying the utility of a variety of brain connectivity measures derived from diffusion-weighted images (DWI) of the brain. Some of the features we chose came from standard tractography-based maps of fiber connectivity (Rubinov and Sporns, 2010) between brain regions; we supplemented these with more novel features derived from a flow-based connectivity method (Prasad et al., 2013a). We aimed to understand the information contained in the raw connectivity matrices versus network measures derived from them; we used all of the resulting features to differentiate diagnostic categories related to Alzheimer’s disease (e.g., MCI). To do this, we employed support vector machines (SVMs), a machine learning algorithm for classification, to learn from training data and then classify a separate test set.

Cui et al. (2012) used SVMs to classify amnestic mild cognitive impairment (aMCI) based on features indexing anatomical atrophy through segmentations of T1-weighted MRI and fraction anisotropy values from diffusion images using tract-based spatial statistics (TBSS). They ranked the features using Fisher scores, and selected the best performing subset using cross-validation. They achieved an accuracy of 71.09%, sensitivity of 51.96%, and specificity of 78.40% for the classification of aMCI. Our method differs in that we use only measures of connectivity from diffusion images for our feature set and the ranking is computed within a set of features we are interested in evaluating. Laplacian Regularized Least Squares was used to classify Alzheimer’s disease in (Zhang and Shen, 2011) where they tried to incorporate structural MRI, PET imaging data, and CSF biomarker features from MCI into an AD classifier, which achieved a performance of almost 95% accuracy. In our case, we explore classification of both MCI and AD and focus on the information contained in different types of connectivity features. Cortical thickness features from structural MRI were evaluated by Eskildsen et al. (2012) using classification though they focused on conversion from MCI to AD and achieved accuracies ranging from 70–76% depending on the time to conversion, in contrast we used classification as a means to understand the information captured in measures of connectivity. The emphasis in the current study is to explore and understand which diffusion based network measures are predictive of Alzheimer’s disease in contrast to the goal of optimizing the accuracy of classification in previous studies.

Our results and experiments seek to characterize the information contained in different features used to represent connectivity in the brain. This is related to the problem of feature selection methods (Guyon and Elisseeff, 2003), which rank features in a meaningful way to understand the ones that are important and those that can be discarded because they are redundant or irrelevant. One approach to select the best features (Peng et al., 2005) is to use mutual information to find the most relevant features for a target class. Another popular approach is the least absolute shrinkage and selection operator (Tibshirani, 1996) that uses a linear model and its regression coefficients to choose the best subset of features. De Martino et al., (2008) chose the most informative voxels in functional MR images using a recursive feature elimination approach that repeatedly trains an SVM model to remove features contributing a small amount to the training model. In our technique, we use the accuracy from classification to evaluate different types of brain connectivity features and to understand which ones may have an advantage to classifying MCI or AD. In addition, we used the SVMs to rank the features within the different feature sets to get a better description of what features were driving the classifier.

Our connectivity measure computation, classification framework, and ranking was applied to publicly available structural magnetic resonance imaging (MRI) and diffusion MRI from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (Mueller et al., 2005). We studied neuroimaging data from 200 subjects: 50 normal healthy controls, 38 people with late-stage mild cognitive impairment (L-MCI), 74 with early MCI (eMCI), and 38 AD patients.

We extracted measures of connectivity between 68 automatically parcellated regions of interest on the cortex using both fiber and flow connectivity methods and organized the information into connectivity matrices. From these connectivity matrices, we computed a variety of widely-used network measures. These features were then fed into a repeated stratified 10-fold cross-validation design, using SVMs to classify controls vs. AD, controls vs. eMCI, controls vs. L-MCI, and eMCI vs. L-MCI. Our results show a significant difference in the accuracy of various combinations of features that were used to distinguish between the various diagnostic groups.

2. Methods

2.1. Data

Our data was from 200 subjects scanned as part of ADNI-2, a continuation of the ADNI project in which diffusion imaging (among other scans) was added to the standard MRI protocol. The dataset included diffusion MRI data from 50 cognitively normal controls (C), 74 early- and 38 late-stage MCI subjects (eMCI, LMCI), and 38 people with Alzheimer’s disease (AD).

Subjects were scanned on 3-Tesla GE Medical Systems scanners, which collected both T1-weighted 3D anatomical spoiled gradient echo (SPGR) sequences (256 × 256 matrix; voxel size = 1.2 × 1.0 × 1.0 mm³; TI=400 ms; TR = 6.98 ms; TE = 2.85 ms; flip angle = 11°), and diffusion weighted images (DWI; 256 × 256 matrix; voxel size: 2.7 × 2.7 × 2.7 mm³; scan time = 9 min). Per subject, the DWIs consisted of 41 diffusion images with b = 1000 s/mm² and 5 T2-weighted b₀ images. This protocol was chosen after an effort to study trade-offs between spatial and angular resolution in a tolerable scan time (Jahanshad et al., 2011).

The groups were matched in both age and sex that we confirmed using two-sample t-tests and multiple comparison correction. Detailed demographic information for each subgroup of subjects is listed in Table 1.

Table 1.

We show the demographic details for our age and sex matched sample. The number of subjects (N), sex, and age are given for the full sample (All), normal elderly controls (NC), early- and late-stage mild cognitively impaired (eMCI, L-MCI) subcategories, and Alzheimer’s disease (AD) patients. We carried out two-sample t-tests comparing age and sex between all pairs of subcategories and found no significant differences that passed the multiple comparison threshold.

	All	NC	eMCI	L-MCI	AD
N	200	50	74	38	38
Sex	115 M/85 F	23 M/27 F	46 M/28 F	24 M/14 F	22 M/16 F
Age	73.1±7.5	72.4±6.2	72.5±8.0	72.6±5.6	75.8±9.1

2.1.1. Image Preprocessing

We processed the T1-weighted images to parcellate them into 68 cortical regions. We first automatically removed extra-cerebral tissues from the anatomical images using ROBEX (Iglesias et al., 2011a), a method that learned from manual segmentations of hundreds of healthy young adults. Skull-stripped brains were inhomogeneity corrected using the MNI N3 tool (Sled et al., 1998) and aligned to the Colin27 template (Holmes et al., 1998) with FSL Flirt (Jenkinson et al., 2002). The resulting images were segmented into 34 cortical regions (in each hemisphere) using FreeSurfer (Fischl et al., 2004) and are listed in Table 2. These segmentations were then dilated with an isotropic box kernel of 5 × 5 × 5 voxels to make sure they intersected with the white matter for subsequent connectivity analysis.

Table 2.

This is a list of the 34 regions that are segmented in the cortex by Freesurfer in each hemisphere, making a total of 64 regions. These regions represent the nodes in the connectivity network for both the fiber and flow connectivity methods. In the network each method calculated the connectivity strength between all pairs of regions. For fiber connectivity, this is computed as the number of tractography fibers that connect the two regions and for the flow connectivity it is computed using an approximate maximum flow algorithm between the regions.

Cortical Regions
1.	Banks of the superior temporal sulcus	18.	Pars orbitalis
2.	Caudal anterior cingulate	19.	Pars triangularis
3.	Caudal middle frontal	20.	Peri calcarine
4.	Cuneus	21.	Postcentral
5.	Entorhinal	22.	Posterior cingulate
6.	Fusiform	23.	Precentral
7.	Inferior parietal	24.	Precuneus
8.	Inferior temporal	25.	Rostral anterior cingulate
9.	Isthmus of the cingulate	26.	Rostral middle frontal
10.	Lateral occipital	27.	Superior frontal
11.	Lateral orbitofrontal	28.	Superior parietal
12.	Lingual	29.	Superior temporal
13.	Medial orbitofrontal	30.	Supra marginal
14.	Middle temporal	31.	Frontal pole
15.	Parahippocampal	32.	Temporal pole
16.	Paracentral	33.	Transverse temporal
17.	Pars opercularis	34.	Insula

We corrected head motion and eddy current distortion in each subject by aligning the DWI images to the average b₀ image with FSL’s eddy correct tool. The brain extraction tool (BET) (Smith, 2002) was then used to skull-strip the brains. We EPI-corrected these images with an elastic mutual information registration algorithm (Leow et al., 2007) that aligned the DWI images to the T1-weighted scans. Preprocessing steps are further detailed in (Nir et al., 2012).

We used a global probabilistic tractography method based on the Hough transform (Aganj et al., 2011). While ADNIs scans are not high angular resolution, due to the need for a fast scan, this method takes advantage of all the diffusion information provided at each voxel, parametrized by the orientation distribution function (ODF). The Hough method generates curves in the fiber space and scores them based on fractional anisotropy (FA) and the ODF at each point along the curve. FA was computed from the single-tensor model of diffusion (Basser and Pierpaoli, 1996). ODFs at each voxel were computed with a normalized, dimensionless estimator derived from Q-ball imaging (QBI) (Aganj et al., 2010). This model is more accurate and outperforms the previous QBI definition (Tuch, 2004), offering better detection of multiple fiber orientations (Aganj et al., 2010; Fritzsche et al., 2010) and additional information for the scoring function.

To generate close to 50,000 fibers per subject, we used an accelerated form of this tractography method (Prasad et al., 2013b). Our optimizations included an ODF lookup table and a randomized search of the parameter space, to generate fibers in less than 1/60 of the original time.

2.2. Connectivity Features

We used features derived from brain connectivity matrices that categorize connections between different regions of interest on the cortex. From these matrices, we computed a set of network measures that quantify different network characteristics. We chose different subsets of these features in our experiments. We used the classification accuracy as a metric to understand the utility of the connectivity information captured, in the context of diagnostic classification of Alzheimer’s disease.

2.2.1. Connectivity Matrix

We computed connectivity matrices using two methods. The first quantifies pairwise connectivity strength as the relative proportion of fibers connecting the two brain regions. The second is a novel method that computes the maximum flow between regions by interpreting the diffusion image as a network of pipes - or a flow graph (these terms are defined further below).

Our first method takes fibers computed using the accelerated Hough tractography method and computes the number that intersect pairs of regions from the 68 cortical areas. We used these frequencies to populate a 68 × 68 connectivity matrix (with no normalization).

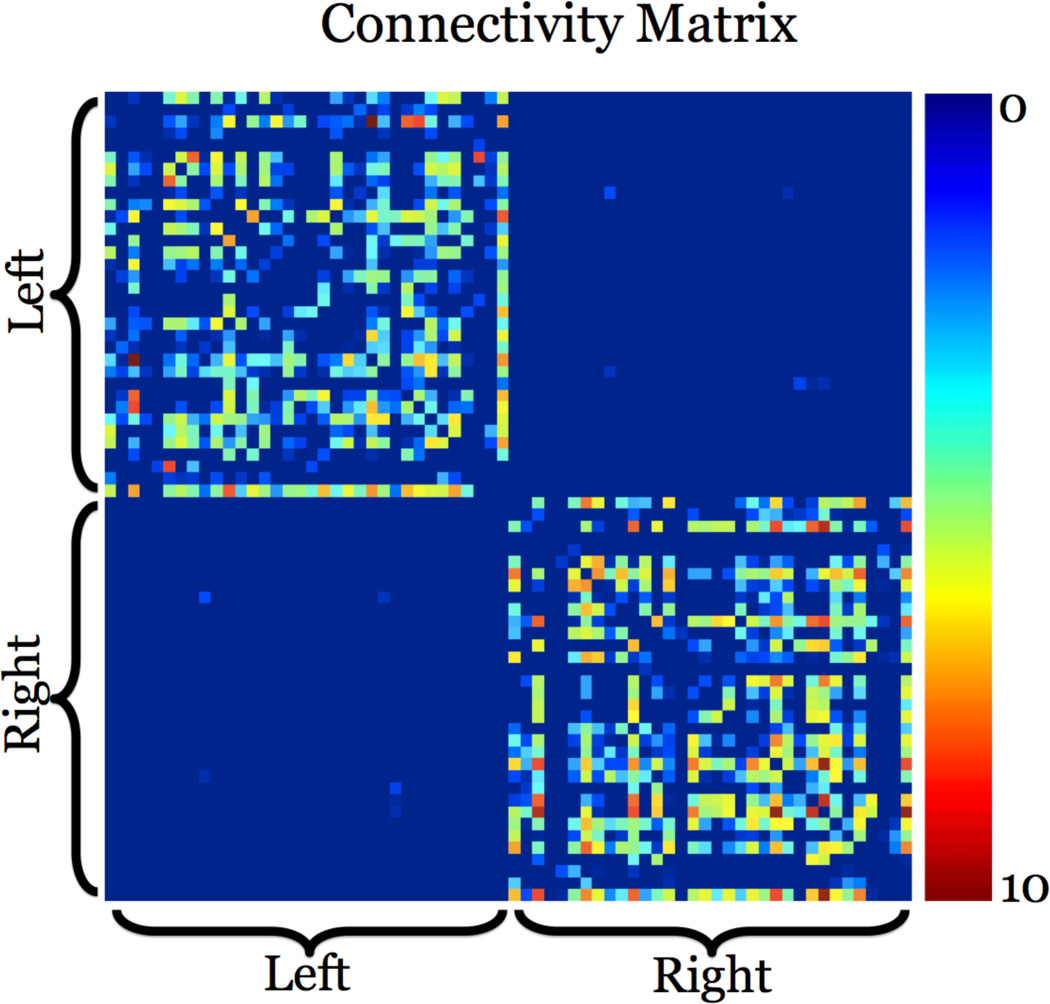
The second method we used is a flow-based measure of anatomical connectivity between all region pairs (Prasad et al., 2013a). In short, we first created a lattice network by connecting all lattice points (voxel centers) to all their immediate neighbors in 3D. Edge weights were based on the orientation density function (ODF) value in the direction of the edge. These edges were interpreted as pipes and their weight as the capacity of the pipe. In contrast to counting fibers between ROIs, we computed the maximum flow - or capacity - between each ROI pair, by following connecting tractography fibers projected onto the flow network edges. We used a modified maximum-flow algorithm that is robust to noise in the diffusion data, and guided by biologically viable pathways and structure of the brain. The resulting flow is used to create a distinct 68 × 68 flow connectivity matrix. Fig. 1 gives an example flow connectivity matrix using this method from our data. The lack of detected interhemispheric connections could be because most of them travel through the corpus callosum so it is difficult to detect fibers (for example) that connect frontal regions in the left hemisphere to the temporal regions in the right hemisphere. Additional research (Hagmann et al., 2008; Gong et al., 2009; Ingalhalikar et al., 2013) gives more examples of connectivity matrices that have a similar inter- and intrahemispheric distribution of connections.

Figure 1.

We present an example 68 × 68 flow connectivity matrix from our data. This matrix was derived using a flow connectivity method that computed the maximum amount of flow between pairs of regions of interest on the cortex. In this subject, the connections within each hemisphere are far more extensive than those across the hemispheres. A brighter color means there is a stronger connectivity (in the sense of greater normalized fiber counts) between the two areas. We use this matrix - along with the standard fiber connectivity matrix - to compute network topology measures. These are then used in a machine learning model to classify different disease states in our data.

2.2.2. Network Measures

We represent the two types of connectivity matrices with network measures described in (Rubinov and Sporns, 2010) and computed them with the Brain Connectivity Toolbox. We derived these measures from both weighted and binary connectivity matrices: global efficiency, transitivity, path length, modularity, small world, radius, diameter, participation, local efficiency, optimal community structure, eigenvector centrality, and eccentricity. In addition, we computed density, number of vertices, number of edges, subgraph centrality, assortativity, nodal flow coefficient, average flow coefficient, total flow across central node, degree, matching index, edge neighborhood overlap, node pairs degree, and connected component sizes from only binary matrices and strengths from only weighted matrices. As is standard, ten different thresholds were applied to each connectivity matrix, to preserve a fixed fraction of the weights ranging from 0.1 to 1, in intervals of 0.1.

In some cases a network measure was computed for each node in the connectivity network, this was the case for participation, local efficiency, and eigenvector centrality among others. This resulted in a vector of 68 values for a single network measure. For matching index or edge neighborhood overlap, the output was a 68 × 68 matrix of values. If a feature was multi-dimensional, we took the mean value in addition to its raw values. The results from each network measure were vectorized and the entire set contained 14,930 features per threshold, making a total of 149,300 network measures per connectivity method. In addition, there are 2,278 unique values from each connectivity matrix. These values represent the lower diagonal elements (not including the actual diagonal) and factoring in the ten thresholds make 22,780 connectivity matrix features per connectivity method. In total there are (149,300 network measure features + 22,780 connectivity matrix features) × (2 connectivity methods: fiber & flow) = 344,160 possible features per subject.

2.3. Classification

Support vector machines (SVMs) (Cortes and Vapnik, 1995) are supervised learning models that we used to classify our connectivity features, to differentiate between disease states. SVMs classify two-class data by training a model - or classification function - to find the best hyperplane between the two classes in the data. Let x_i ∈ ℝ^d represent the connectivity feature vectors, where d is the dimension of the feature set of interest, and y_i = ± be their label with −1 and 1 representing two different disease states that could include controls, eMCI, L-MCI, or AD. Our target hyperplane is

$$\langle w,x\rangle +b=0,$$

where w ∈ ℝ^d should separate as many data points as possible. We find it by solving the L2-norm problem

$$\underset{w,b,v}{\text{arg min}}(\frac{1}{2}\langle w,w\rangle +D\sum _i{v}_i^2)$$

such that

$$\begin{array}{cc}\hfill y_i(\langle w,x_i\rangle +b)& \ge 1-v_i\hfill \\ \hfill v_i& \ge 0,\hfill \end{array}$$

where v_i are slack variables and D is a penalty parameter. In many instances, a hyperplane cannot be found to completely separate the two classes of data, and the slack variables are added to create soft margins to separate most of the points.

Our classification design was to test the information provided by the connectivity features with repeated stratified 10-fold cross-validation as recommended by Kohavi, (1995). For the results in the cross-validation our performance metrics were accuracy (AC), sensitivity (SE), and specificity (SP). We repeated the cross-validation 30 times, which allows us to use paired sample t-tests to statistically compare different feature subsets based on their classification performance.

For each classifier we learned, the features were ranked by their relationship to the hyperplane (De Martino et al., 2008). The ranking was computed by sorting in decreasing order the |w| values from the hyperplane. Features with high values mean they contribute the most to the final boundary between the classes. In our experiments, we averaged the feature ranking across all folds within repeated cross-validation instances. These rankings will tell what network measure or what element of a connectivity matrix was most important to the classifier in the context of all other features in a feature set of interest.

2.4. Experiments

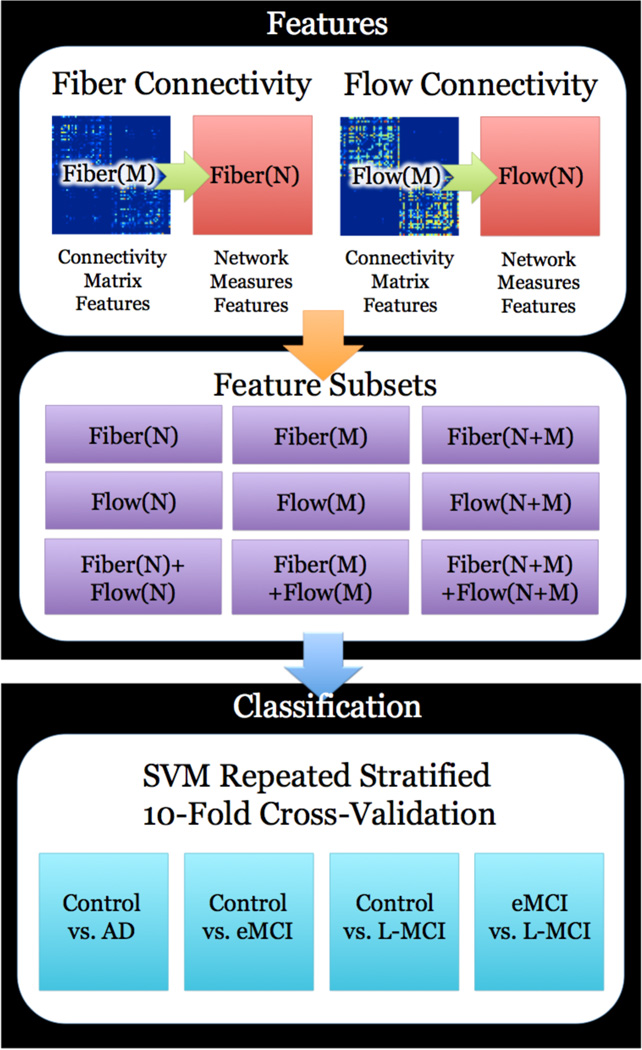
We designed experiments to test the utility of different subsets of features to identify differences between sets of two disease states from our data. Our metric was the accuracy, sensitivity, and specificity from stratified 10-fold cross-validation that was repeated 30 times comparing controls vs. AD, controls vs. early-MCI, controls vs. late-MCI, and early-MCI vs. late-MCI. In each of these classification problems we used nine different sets of features: the fiber connectivity matrix, (FI(M)), the flow connectivity matrix (FL(M)), the fiber network measures (FI(N)), the flow network measures (FL(M)), combinations of these sets as FI (N+M), FL(N+M), FI(N)+FL(N), FI(M)+FL(M), and FI(N+M)+FL(N+M). Each of these sets of features was organized into a matrix and then fed into the SVM algorithm using a repeated stratified 10-fold cross-validation design. A summary of our experimental design is in Fig. 2.

Figure 2.

A summary of how we select features of brain connectivity and classify them using support vector machines (SVMs). Our framework begins by computing hundreds of thousands of network measures from both fiber and flow connectivity matrices. We created nine different subsets of features that are combinations of the network measures and raw connectivity matrices from a fiber and flow based connectivity method. Each subset is evaluated by understanding their performance in classification problems based on the four different groups of subjects. These problems include control vs. Alzheimer’s disease, control vs. early-mild cognitive impairment (MCI), control vs. late-MCI, and early-MCI vs. late-MCI. For each problem we used a stratified 10-fold cross-validated support vector machine classifier to understand how well the feature subset was able to discriminate between the two classes. The metrics used to evaluate the classifier performance were accuracy, sensitivity, and specificity.

3. Results

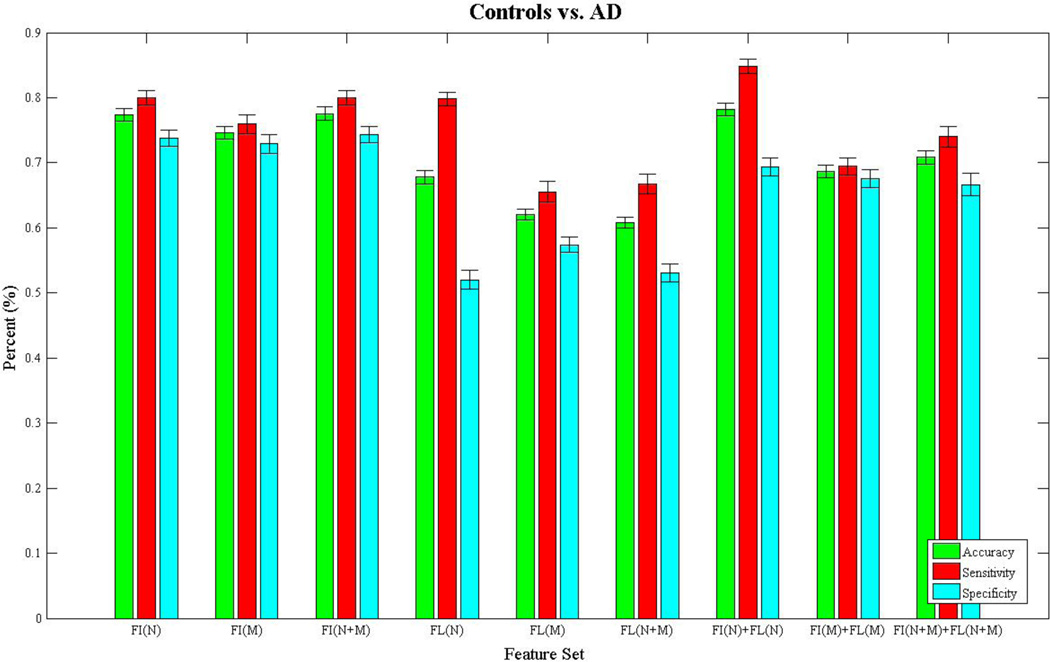
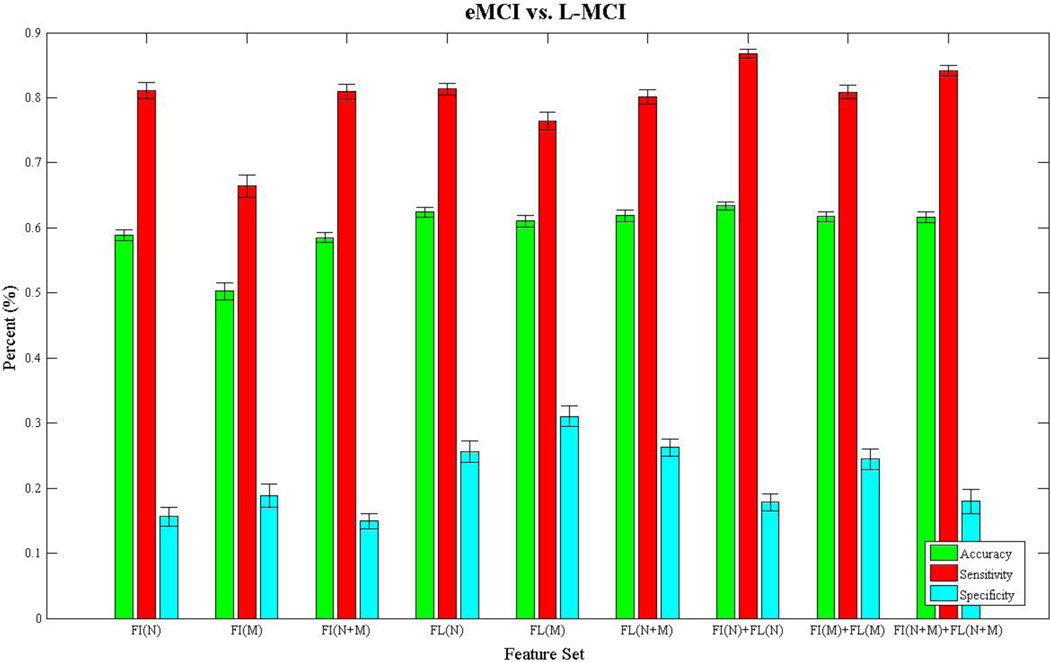
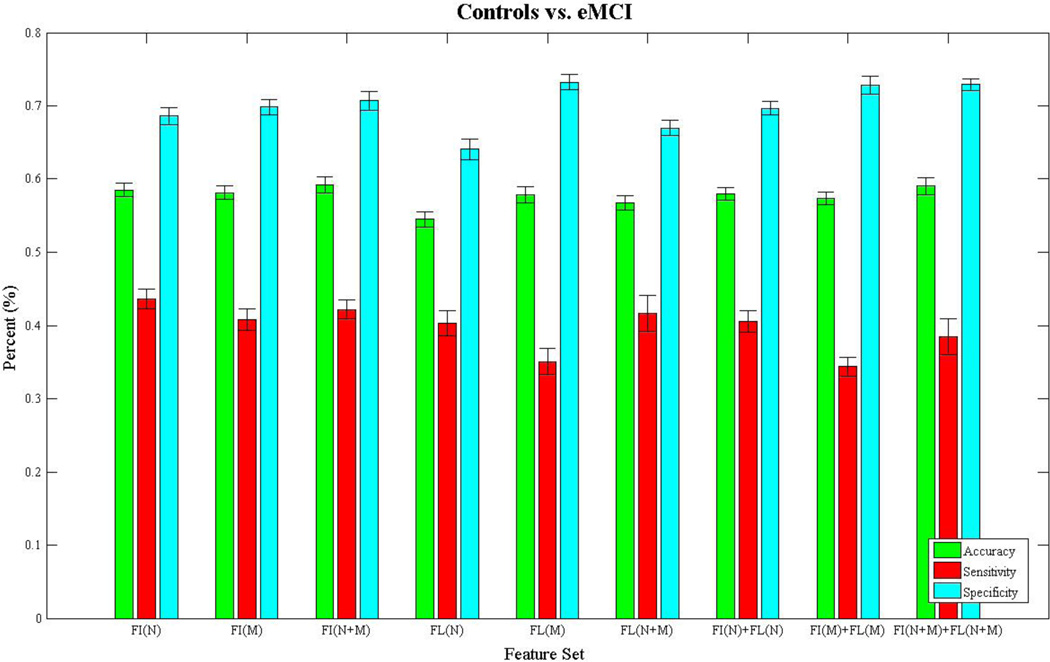
Figures 3–6 show bar charts of the results for each of our four classification problems using the nine different subsets of features. These include controls vs. AD (Fig. 3), controls vs. eMCI (Fig. 4), controls vs. L-MCI (Fig. 5), and eMCI vs. L-MCI (Fig. 6). It shows the accuracy, sensitivity, and specificity as percentages for each of the nine feature sets including FI(N), FI(M), FI(N+M), FL(N), FL(M), FL(N+M), FI(N)+FL(N), FI(M)+FI(M), and FI(N+M)+FL(N+M) along with their 95% confidence intervals over the stratified 10-fold cross-validated results that were repeated 30 times. For controls vs. AD we found feature set FI(N)+FL(N) had the highest accuracy of 78.2% and using paired-sample t-tests (p>0.05) we found it was not statistically different in performance from FI(N) and FI(N+M). FI(N+M) had the highest accuracy of 59.2% for the controls vs. eMCI classifier and was not significantly different in performance from FI(N+M)+FL(N+M). In the case of controls vs. L-MCI, FL(N) had the highest accuracy of 62.8% and was significantly better in performance than all other feature sets. eMCI vs. L-MCI performed best with FI(N)+FL(N) reaching an accuracy of 63.4% and was significantly different than all other feature sets.

Figure 3.

We present the results from the stratified 10-fold cross-validated (CV) support vector machine classification of controls vs. Alzheimer’s disease using nine subsets of connectivity features. These features come from both a fiber connectivity method (FI) and flow connectivity method (FL) and include a variety of graph based network measures (N) along with the raw connectivity matrices (M). We evaluated the performance of each subset’s ability to classify using accuracy, sensitivity, and specificity. The CV was repeated 30 times for each feature set using corresponding CV folds and we evaluated differences using paired-sample t-tests. The bar plot shows the mean accuracy, sensitivity, and specificity over the 30 CV results along with 95% confidence intervals. FI(N)+FL(N) had the highest accuracy of 78.2% and was not significantly different (p>0.05) in performance from FI(N) and FI(N+M).

Figure 6.

We present the results from the stratified 10-fold cross-validated (CV) support vector machine classification of early-mild cognitive impaired subjects vs. late-mild cognitive impaired subject using nine subsets of connectivity features. These features come from both a fiber connectivity method (FI) and flow connectivity method (FL) and include a variety of graph based network measures (N) along with the raw connectivity matrices (M). We evaluated the performance of each subset’s ability to classify using accuracy, sensitivity, and specificity. The CV was repeated 30 times for each feature set using corresponding CV folds and we evaluated differences using paired-sample t-tests. The bar plot shows the mean accuracy, sensitivity, and specificity over the 30 CV results along with 95% confidence intervals. FI(N)+FL(N) had the highest accuracy of 63.4% and was significantly different (p>0.05) in performance from all other subsets.

Figure 4.

We present the results from the stratified 10-fold cross-validated (CV) support vector machine classification of controls vs. early-mild cognitive impaired subject using nine subsets of connectivity features. These features come from both a fiber connectivity method (FI) and flow connectivity method (FL) and include a variety of graph based network measures (N) along with the raw connectivity matrices (M). We evaluated the performance of each subset’s ability to classify using accuracy, sensitivity, and specificity. The CV was repeated 30 times for each feature set using corresponding CV folds and we evaluated differences using paired-sample t-tests. The bar plot shows the mean accuracy, sensitivity, and specificity over the 30 CV results along with 95% confidence intervals. FI(N+M) had the highest accuracy of 59.2% and was not significantly different (p>0.05) in performance from FI(N+M)+FL (N+M).

Figure 5.

We present the results from the stratified 10-fold cross-validated (CV) support vector machine classification of controls vs. late-mild cognitive impaired subject using nine subsets of connectivity features. These features come from both a fiber connectivity method (FI) and flow connectivity method (FL) and include a variety of graph based network measures (N) along with the raw connectivity matrices (M). We evaluated the performance of each subset’s ability to classify using accuracy, sensitivity, and specificity. The CV was repeated 30 times for each feature set using corresponding CV folds and we evaluated differences using paired-sample t-tests. The bar plot shows the mean accuracy, sensitivity, and specificity over the 30 CV results along with 95% confidence intervals. FL(N) had the highest accuracy of 62.8% and was significantly different (p>0.05) in performance from all other subsets.

In addition to the bar charts we ranked the top five features for each classification problem and feature set in Tables 3–6. Each of the top features is also listed with its corresponding threshold value. A multi-dimensional feature such as edge neighborhood overlap may be listed multiple times at the same threshold for a single feature set and classification problem because the ranking is differentiating between parts of the feature vector for that single network measure. We also include the specific labels for elements in the connectivity matrices that were highly ranked, the symbol “<->” represents the undirected edge between the two regions on the cortex.

Table 3.

We show the top five ranked features from each of the 9 feature subsets in the controls vs. Alzheimer’s disease classification problem. The features were computed using a fiber connectivity (FI) and flow connectivity (FL) method using a variety of graph based network measures (N) and the raw connectivity matrices (M). The network measures were computed from binary and weighted connectivity matrices that were filtered using a proportional threshold ranking from 0.1 to 1.0 (meaning all edges are retained) at intervals of 0.1. The features are shown along with their corresponding threshold (Th.). The ranking is derived from the support vector machine classification boundary and is averaged over each of the 10 cross-validated folds and 30 repeat runs. In cases that use features including the raw connectivity matrices at different thresholds, the label includes the two regions from the Freesurfer segmentation that an edge connects. The symbol “<->” represents the undirected edge connecting the two regions in the connectivity network.

Controls vs. AD
Feature Set	Rank 1/Th.		Rank 2/Th.		Rank 3/Th.		Rank 4/Th.		Rank 5/Th.
FI(N)	Binary Nodal Betweenness Centrality	0.5	Binary Nodal Betweenness Centrality	0.6	Binary Nodal Betweenness Centrality	0.7	Binary Nodal Betweenness Centrality	0.8	Binary Nodal Betweenness Centrality	0.9
FI(M)	R-Entorhinal <->L-Pars opercularis	0.2	R-Fusiform <->L-Pars opercularis	0.2	R-Inferior parietal <->L-Pars opercularis	0.2	R-Inferior temporal <->L-Pars opercularis	0.2	R-Isthmus of the cingulate <->L-Pars opercularis	0.2
FI(N+M)	Binary Nodal Betweenness Centrality	0.5	Binary Nodal Betweenness Centrality	0.6	Binary Nodal Betweenness Centrality	0.7	Binary Nodal Betweenness Centrality	0.8	Binary Nodal Betweenness Centrality	0.9
FL(N)	Edge Neighborhood Overlap	0.2	Edge Neighborhood Overlap	0.2	Edge Neighborhood Overlap	0.3	Matching Index	0.2	Edge Neighborhood Overlap	0.3
FL(M)	R-Posterior cingulate <->L- Parahippocampal	0.3	R-Precentral <->L- Parahippocampal	0.3	R-Precuneus <->L- Parahippocampal	0.3	R-Rostral anterior cingulate <->L- Parahippocampal	0.3	R-Rostral middle frontal <->L- Parahippocampal	0.3
FL(N+M)	Edge Neighborhood Overlap	0.2	Edge Neighborhood Overlap	0.2	Matching Index	0.2	Edge Neighborhood Overlap	0.3	Edge Neighborhood Overlap	0.3
FI(N) +FL(N)	FL(N): Strengths	0.1	FL(N): Edge Neighborhood Overlap	0.3	FL(N): Edge Neighborhood Overlap	0.3	FI(N): Binary Nodal Betweenness Centrality	0.5	FI(N): Binary Nodal Betweenness Centrality	0.6
FI(M) +FL(M)	FL(M): R-Posterior cingulate <->L- Parahippocampal	0.3	FL(M): R- Precentral <->L- Parahippocampal	0.3	FL(M): R- Precuneus <->L- Parahippocampal	0.3	FL(M): R-Rostral anterior cingulate <->L- Parahippocampal	0.3	FL(M): R-Rostral middle frontal<- >L- Parahippocampal	0.3
FI(N+M) +FL(N+M)	FL(N): Strengths	0.1	FL(N): Edge Neighborhood Overlap	0.3	FL(N): Edge Neighborhood Overlap	0.3	FI(N): Binary Nodal Betweenness Centrality	0.5	FI(N): Binary Nodal Betweenness Centrality	0.6

Table 6.

We show the top five ranked features from each of the 9 feature subsets in the early-mild cognitive impairment (eMCI) vs. late-mild cognitive impairment (L-MCI) classification problem. The features were computed using a fiber connectivity (FI) and flow connectivity (FL) method using a variety of graph based network measures (N) and the raw connectivity matrices (M). The network measures were computed from binary and weighted connectivity matrices that were filtered using a proportional threshold ranking from 0.1 to 1.0 (meaning all edges are retained) at intervals of 0.1. The features are shown along with their corresponding threshold (Th.). The ranking is derived from the support vector machine classification boundary and is averaged over each of the 10 cross-validated folds and 30 repeat runs. In cases that use features including the raw connectivity matrices at different thresholds, the label includes the two regions from the Freesurfer segmentation that an edge connects. The symbol “<->” represents the undirected edge connecting the two regions in the connectivity network.

eMCI vs. L-MCI
Feature Set	Rank 1/Th.		Rank 2/Th.		Rank 3/Th.		Rank 4/Th.		Rank 5/Th.
FI(N)	Edge Neighborhood Overlap	0.3	Edge Neighborhood Overlap	0.3	Matching Index	0.1	Binary Edge Betweenness Centraily	0.4	Binary Edge Betweenness Centraily	0.4
FI(M)	L-Frontal pole <->L-Supra marginal	0.8	L-Temporal pole <->L-Supra marginal	0.8	L-Pars orbitalis <->L-Lateral occipital	0.3	L-Transverse temporal <->L-Supra marginal	0.8	L-Insula <->L-Supra marginal	0.8
FI(N+M)	Edge Neighborhood Overlap	0.3	Edge Neighborhood Overlap	0.3	Matching Index	0.1	R-Transverse temporal <->R-Lingual	0.8	Edge Neighborhood Overlap	0.4
FL(N)	Matching Index	0.1	Community Structure	0.3	Matching Index	0.1	Binary Nodal Betweenness Centrality	0.1	Community Structure	0.3
FL(M)	R-Parahippocampal <->R-Lingual	0.9	R-Cuneus <->L-Frontal pole	0.1	R-Paracentral <->R-Inferior parietal	0.1	R-Inferior parietal <->R-Entorhinal	0.3	R-Isthmus of the cingulate <->L-Superior temporal	0.6
FL(N+M)	Community Structure	0.3	Matching Index	0.1	Matching Index	0.1	Community Structure	0.3	Binary Nodal Betweenness Centrality	0.1
FI(N) +FL(N)	FL(N): Community Structure	0.3	FL(N): Community Structure	0.3	FL(N): Community Structure	0.3	FL(N): Community Structure	0.3	FL(N): Binary Community Structure	0.3
FI(M) +FL(M)	FL(M): R-Superior frontal <->L-Peri calcarine	0.1	FL(M): R-Superior parietal <->L-Peri calcarine	0.1	FL(M): R-Superior temporal <->L-Peri calcarine	0.1	FL(M): R-Supra marginal <->L-Peri calcarine	0.1	FL(M): R-Frontal pole <->L-Peri calcarine	0.1
FI(N+M) +FL(N+M)	FL(N): Community Structure	0.3	FL(N): Community Structure	0.3	FL(N): Community Structure	0.3	FL(N): Community Structure	0.3	FL(N): Community Structure	0.3

4. Discussion

For classification of normal elderly controls relative to people with AD, Table 1 shows FI(N)+FL(N) has the highest classification accuracy. Even so, when these features combined with additional features, the accuracy does go down in some instances. FI(N+M) was able to distinguish controls vs. eMCI the best, and FL(N) was the best for distinguishing healthy controls vs. L-MCI. In the eMCI vs. L-MCI classification experiments, we again saw a combination of network measures (FI(N)+FL(N)) produced the best results. The results show that when studying L-MCI, including flow based network measures can have an advantage in distinguishing class differences and may be useful for studying other aspects of L-MCI. In the case of eMCI and AD, the performance of classification could be optimal based on fiber measures alone, though the addition of flow in AD may have slightly higher accuracy.

In addition to offering a principled approach to select or rank the importance of connectivity features for this kind of classification problem, we provided a proof of concept and framework for using support vector machines as a metric for use with brain connectivity data. We recently used it to choose the architecture of the connectivity matrix by selecting the best nodes or regions of the cortex. This adaptive cortical parcellation was created based on a framework to evaluate different cortical parcellations by their accuracy from diagnostic classifiers, such as SVMs (Prasad et al., 2014).

Learning algorithms, such as SVM, Adaboost, or random forest classification can be sensitive to the feature set used. We note that other schemes may be used and their effects could also be useful to categorize this dataset and other related data or even filter out features in each of the feature sets we studied. Other classification techniques that may be effective include a variation of manifold learning used by Iglesias et al. (2011b) to classify Alzheimer’s disease using registration- and overlap-based similarity measures. Alternatively, we could organize the features into a tensor representation for multilinear subspace learning (Tao et al., 2007).

These other algorithms may be particularly adept at classification of AD because of how well they can build a model with the relatively limited number of subjects in these studies, by contrast with the large number of features for each subject. New subjects are continually being added to the ADNI dataset and more training data would give us a stronger and more secure understanding of these relationships. With larger datasets we can explore the absolute and relative performance of different features and biomarkers using deep learning (Hinton et al., 2006) or artificial neural networks that allow for a great deal of freedom and a richer model when there are multiple layers included (Bengio, 2009) and massive amounts of data available. Here we chose SVM as it works well with relatively small samples and a larger number of features without having to apply regularization (Hastie et al., 2001).

The feature ranking approach we used leveraged the hyperplane from the SVM and gives a ranking of a feature in the context of all other features in the set we are studying. Other approaches such as uni-variate ranking by using t-tests on a single feature (Chu et al., 2012) or by using regression on each feature (Polyn, 2005) give the importance of a single measure by itself but may miss cases when a feature by itself is weak but in the context of other features, the feature set becomes highly discriminatory. There is also a variety of multi-variate feature selection approaches being proposed in the literature. One method by Liu et al. (2013) addresses the geometric relationship of the target classes in Alzheimer’s disease structural MRI training data by using graph matching. Another approach combines uni-variate feature selection and multi-variate recursive feature selection by using correlation based ranking of single features. It then uses recursive and forward sequential feature selection to select a set of features that will include mostly the top ranked features (Fan et al., 2007). In (Cuingnet et al., 2011), the authors study ten algorithms that classify AD using T1-weighted MRI and conclude that different feature selection methods did not greatly affect performance. In our case, we used the feature selection to evaluate a classifier and its features without removing or selecting features based on training data.

Different sets of features may uncover detail in the connectivity structure of the brain that is better for representing important changes in networks across the various phases or stages of Alzheimer’s disease. We can extend the framework in the current study to use different features such as those from dynamic simulations of connectivity (Prasad et al., 2013c) or connectivity measures that summarize the fibers from tractography using maximum density paths (Prasad et al., 2011a) that are registered (Prasad et al., 2011b) into the same space. We can then use the subset of features that best predicts or classifies a category in our data that could include affects of aging, severity of the disorder, or even those that emphasize parts of the network that are associated with the effects of risk genes for Alzheimer’s disease.

Table 4.

We show the top five ranked features from each of the 9 feature subsets in the controls vs. early mild cognitive impairment classification problem. The features were computed using a fiber connectivity (FI) and flow connectivity (FL) method using a variety of graph based network measures (N) and the raw connectivity matrices (M). The network measures were computed from binary and weighted connectivity matrices that were filtered using a proportional threshold ranking from 0.1 to 1.0 (meaning all edges are retained) at intervals of 0.1. The features are shown along with their corresponding threshold (Th.). The ranking is derived from the support vector machine classification boundary and is averaged over each of the 10 cross-validated folds and 30 repeat runs. In cases that use features including the raw connectivity matrices at different thresholds, the label includes the two regions from the Freesurfer segmentation that an edge connects. The symbol “<->” represents the undirected edge connecting the two regions in the connectivity network.

Controls vs. eMCI
Feature Set	Rank 1/Th.		Rank 2/Th.		Rank 3/Th.		Rank 4/Th.		Rank 5/Th.
FI(N)	Binary Edge Betweenness Centrality	0.4	Binary Edge Betweenness Centrality	0.5	Binary Edge Betweenness Centrality	0.4	Binary Edge Betweenness Centrality	0.6	Binary Edge Betweenness Centrality	0.7
FI(M)	R-Transverse temporal <->R-Banks of the superior temporal sulcus	1.0	R-Inferior parietal <->L-Temporal pole	1.0	R-Inferior temporal <->L-Temporal pole	1.0	R-Isthmus of the cingulate <->L-Temporal pole	1.0	R-Lateral occipital <->L-Temporal pole	1.0
FI(N+M)	Binary Edge Betweenness Centrality	0.3	Binary Edge Betweenness Centrality	0.3	Edge Neighborhood Overlap	0.3	Edge Neighborhood Overlap	0.3	Binary Edge Betweenness Centrality	0.4
FL(N)	Community Structure	0.4	Matching Index	0.1	Binary Edge Betweenness Centrality	0.3	Binary Edge Betweenness Centrality	0.3	Edge Neighborhood Overlap	0.1
FL(M)	R-Peri calcarine <->L-Pars opercularis	0.5	R-Lateral orbitofrontal l<->L-Lateral orbitofrontal	1.0	R-Medial orbitofrontal <->L-Insula	0.8	R-Pars opercularis <->L-Lateral orbitofrontal	0.3	R-Pars orbitalis <->L-Lateral orbitofrontal	0.3
FL(N+M)	Binary Edge Betweenness Centrality	0.3	Binary Edge Betweenness Centrality	0.3	Matching Index	0.1	R-Transverse temporal <->R-Superior temporal	0.3	Community Structure	0.4
FI(N) +FL(N)	FL(N): Strengths	0.1	FI(N): Binary Edge Betweenness Centrality	0.4	FI(N): Binary Edge Betweenness Centrality	0.5	FI(N): Binary Edge Betweenness Centrality	0.6	FI(N): Binary Edge Betweenness Centrality	0.7
FI(M) +FL(M)	FL(M): R-Pars opercularis <->L-Lateral orbitofrontal	0.3	FL(M): R-Pars orbitalis <->L-Lateral orbitofrontal	0.3	FL(M): R-Pars triangularis <->L-Lateral orbitofrontal	0.3	FL(M): R-Peri calcarine <->L-Lateral orbitofrontal	0.3	FL(M): R- Postcentral <->L-Lateral orbitofrontal	0.3
FI(N+M) +FL(N+M)	FL(N): Strengths	0.1	FL(M): R-Pars opercularis <->L-Lateral orbitofrontal	0.3	FL(M): R-Pars orbitalis <->L-Lateral orbitofrontal	0.3	FL(M): R-Pars triangularis <->L-Lateral orbitofrontal	0.3	FL(M): R-Peri calcarine <->L-Lateral orbitofrontal	0.3

Table 5.

We show the top five ranked features from each of the 9 feature subsets in the controls vs. late mild cognitive impairment classification problem. The features were computed using a fiber connectivity (FI) and flow connectivity (FL) method using a variety of graph based network measures (N) and the raw connectivity matrices (M). The network measures were computed from binary and weighted connectivity matrices that were filtered using a proportional threshold ranking from 0.1 to 1.0 (meaning all edges are retained) at intervals of 0.1. The features are shown along with their corresponding threshold (Th.). The ranking is derived from the support vector machine classification boundary and is averaged over each of the 10 cross-validated folds and 30 repeat runs. In cases that use features including the raw connectivity matrices at different thresholds, the label includes the two regions from the Freesurfer segmentation that an edge connects. The symbol “<->” represents the undirected edge connecting the two regions in the connectivity network.

Controls vs. L-MCI
Feature Set	Rank 1/Th.		Rank 2/Th.		Rank 3/Th.		Rank 4/Th.		Rank 5/Th.
FI(N)	Matching Index	0.1	Matching Index	0.2	Binary Edge Betweenness Centrality	0.4	Binary Edge Betweenness Centrality	0.4	Binary Edge Betweenness Centrality	0.5
FI(M)	R-Inferior parietal <->L-Temporal pole	1.0	R-Inferior temporal <->L-Temporal pole	1.0	R-Isthmus of the cingulate <->L-Temporal pole	1.0	R-Lateral occipital<->L- Temporal pole	1.0	R-Lateral orbitofrontal <->L-Temporal pole	1.0
FI(N+M)	Binary Edge Betweenness Centrality	0.4	Matching Index	0.1	Binary Edge Betweenness Centrality	0.4	Binary Edge Betweenness Centrality	0.5	Binary Edge Betweenness Centrality	0.6
FL(N)	Binary Local Efficiency	0.2	Matching Index	0.1	Matching Index	0.1	Edge Neighborhood Overlap	0.4	Edge Neighborhood Overlap	0.4
FL(M)	R-Supra marginal <->L-Medial orbitofrontal	1.0	L-Pars opercularis <->L-Lingual	0.9	L-Supra marginal <->L-Inferior parietal	0.9	L-Frontal pole <->L-Inferior parietal	0.9	L-Temporal pole <->L-Inferior parietal	0.9
FL(N+M)	Binary Local Efficiency	0.2	Matching Index	0.1	Edge Neighborhood Overlap	0.4	Edge Neighborhood Overlap	0.4	Edge Neighborhood Overlap	0.5
FI(N) +FL(N)	FI(N): Edge Neighborhood Overlap	0.5	FI(N): Edge Neighborhood Overlap	0.6	FI(N): Edge Neighborhood Overlap	0.7	FI(N): Edge Neighborhood Overlap	0.8	FI(N): Edge Neighborhood Overlap	0.5
FI(M) +FL(M)	FL(M): R-Pars opercularis <->L-Banks of the superior temporal sulcus	0.4	FL(M): R-Pars orbitalis <->L-Banks of the superior temporal sulcus	0.4	FL(M): L-Supra marginal <->L-Inferior parietal	0.9	FL(M): R-Pars triangularis <->L-Banks of the superior temporal sulcus	0.4	FL(M): L-Frontal pole <->L-Inferior parietal	0.9
FI(N+M) +FL(N+M)	FI(N): Binary Edge Betweenness Centrality	0.5	FI(N): Binary Edge Betweenness Centrality	0.6	FI(N): Binary Edge Betweenness Centrality	0.7	FI(N): Binary Edge Betweenness Centrality	0.8	FI(N): Binary Edge Betweenness Centrality	0.9