Covariate Measurement Error Correction Methods in Mediation Analysis with Failure Time Data

Summary

Mediation analysis is important for understanding the mechanisms whereby one variable causes changes in another. Measurement error could obscure the ability of the potential mediator to explain such changes. This paper focuses on developing correction methods for measurement error in the mediator with failure time outcomes. We consider a broad definition of measurement error, including technical error and error associated with temporal variation. The underlying model with the ‘true’ mediator is assumed to be of the Cox proportional hazards model form. The induced hazard ratio for the observed mediator no longer has a simple form independent of the baseline hazard function, due to the conditioning event. We propose a mean-variance regression calibration approach and a follow-up time regression calibration approach, to approximate the partial likelihood for the induced hazard function. Both methods demonstrate value in assessing mediation effects in simulation studies. These methods are generalized to multiple biomarkers and to both case-cohort and nested case-control sampling design. We apply these correction methods to the Women's Health Initiative hormone therapy trials to understand the mediation effect of several serum sex hormone measures on the relationship between postmenopausal hormone therapy and breast cancer risk.

1 Introduction

Mediation analysis is important in biomedical and social sciences research to understand the mechanisms whereby one variable causes changes in another (MacKinnon, 2008). A classical mediation analysis compares coefficients of the independent variable Z in two linear models: one regresses the outcome Y on Z and other covariates C, while the other regresses Y on Z, C and the potential mediator X. There is evidence of X mediating the relationship between Z and Y , if the coefficient of Z in the second model is substantially closer to the null compared to that in the first. With failure time data, Lin et al. (1997) considered the mediation by comparing two Cox proportional hazards models, and they discussed conditions under which the two Cox models are approximately compatible. Lange and Hansen (2011) proposed a decomposition of the total treatment effect into ‘natural’ direct and indirect effects under the Aalen additive hazards model, assuming that X can be modeled by a linear regression on Z and C. In this paper, we extend the methods in Lin et al. (1997) to settings in which mediator measurement error needs to be taken into account.

Covariate measurement error methods have been investigated in failure time data settings. Hughes (1993) examined the naive approach, which replaces X with an observed error prone W in the Cox model, and found that the bias depends on true coefficient value, measurement error magnitude, censoring mechanism and others factors. Prentice (1982) considered the induced hazard function as

$$\lambda (t;W,Z,\mathit{C})=E\{\lambda (t;X,Z,\mathit{C})|\stackrel{\sim }{T}⩾t;W,Z,\mathit{C}\},$$

where T̃ denotes the failure time. It was noted that when λ(t; X, Z, C) follows a Cox model, the corresponding induced hazard ratio involves the baseline hazard function due to the conditioning event {T̃ ⩾ t}. However the induced hazard can typically be approximated in the rare disease setting by replacing X with E(X|W, Z, C), the so-called regression calibration approach. Wang et al. (1997) provided a suitable variance estimator for resulting regression parameter estimates. Xie et al. (2001) extended this method to risk set regression calibration, which recalibrates at each failure time. Zhou and Pepe (1995), Zhou and Wang (2000) and Carroll et al. (1995) investigated nonparametric approaches to estimate the model the induced hazard. Other measurement error correction approaches include a nonparametric corrected score approach proposed by (Huang and Wang 2000, 2006), and a full likelihood approach proposed by Hu et al. (1998). None of these methods has been investigated in the mediation analysis setting.

Here we propose two correction methods based on the induced partial likelihood in Section 2. We describe procedures to estimate parameters needed for the correction methods in Section 3. The performances of the proposed methods are demonstrated through simulation studies in Section 4. Section 5 applies our methods to the Women's Health Initiative (WHI) hormone therapy trials. We conclude with discussion in Section 6.

2 Calibration Approaches

2.1 Model Assumptions

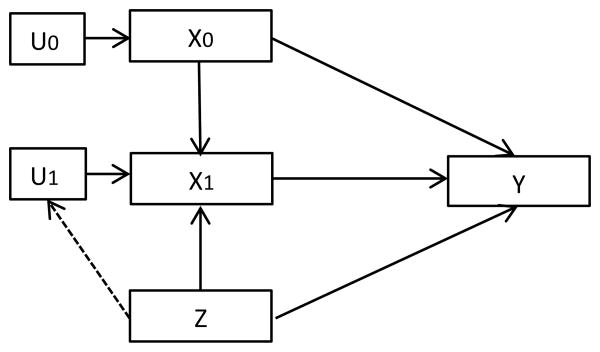
We assume an underlying causal diagram is as in Figure 1. The outcome Y = (T, δ) relates directly with pre- and post-randomization biomarker values X = (X₀, X₁) and with treatment assignment Z ∈ {0, 1}, where T = min(T̃, C) is the censored failure time, and T̃, C are the underlying failure and censoring times, δ is an non-censoring indicator. T̃ and C are assumed to be independent given (X, Z). In addition, the post-randomization biomarker value X₁ (or equivalently, the change due to treatment X₁‒X₀) may mediate the relationship between Z and Y. Thus treatment Z can have both a direct effect and an indirect effect through the biomarker change X₁ − X₀ on Y. For now, we do not consider other covariates C, but all the methods described can be extended readily to include covariates. To assess the mediation, we compare treatment effects α_Z and β_Z from the following two Cox models:

Figure 1.

Causal diagram of the underlying model.

$$\lambda (t;X_0,Z)={\lambda }_0(t)exp({\alpha }_{Z}Z+{\alpha }_0{X}_0)$$ (1)

$$\lambda (t;X_0,X_1,Z)={\lambda }_1(t)exp({\beta }_{Z}Z+{\beta }_0{X}_0+{\beta }_1{X}_1).$$ (2)

Although the two models may be technically incompatible, as discussed in Lin et al. (1997), (1) is a good approximation of the marginal hazard induced from (2) if the failure time outcome is rare, that is, ${\Lambda }_2(t)={\int }_0^t{\lambda }_2(s)ds$ is small, or otherwise if β₁ is small. Hence, if β_Z is much closer to 0 compared to α_Z, we can reasonably conclude that X substantially mediates the relationship between Z and Y.

We assume that biomarker values (X₀, X₁) are measured with mean zero classical measurement error, so that W_j = X_j + U_j, where U_j is independent of X_j given Z_j, j = 0, 1. As a naive approach, we replace X = (X₀, X₁) with W = (W₀, W₁) in the above models:

$$\begin{array}{c}\lambda (t;W_0,Z)={\lambda }_2(t)exp(a_{Z}Z+a_0{W}_0)\\ \lambda (t;W_0,W_1,Z)={\lambda }_3(t)exp(b_{Z}Z+b_0{W}_0+b_1{W}_1)\end{array}$$

Since (X₀, U₀) are pre-randomization variables and typically independent of Z, a_Z is expected to be close to α_Z. However, (X₁, U₁) are post-randomization variables whose distributions may depend on Z. In this case, using b_Z to approximate β_Z may involve a large bias, and lead to incorrect conclusions about mediation. We will focus on reducing bias in β_Z estimation.

The induced hazard from model (2) is

$$\lambda (t;\mathit{W},Z)={\lambda }_1(t)E\{exp({\beta }_{Z}Z+{\mathit{\beta }}_X^T\mathbf{X})|\stackrel{\sim }{T}⩾t;\mathit{W},Z\},$$ (3)

where β _X = (β₀, β₁)^T. We denote the k distinct failure times in a cohort study by {t₁, t₂, …, t_k}, and let i be the index of the individual failing at t_i. The corresponding partial likelihood can be written as

$$PL(\mathbf{\beta })=\mathbf{\prod }_{i=1}^k\frac{E\{exp({\beta }_Z{Z}_i+{\mathit{\beta }}_X^T{\mathit{X}}_i)|\stackrel{\sim }{T}⩾t_i,{\mathit{W}}_i,Z_i\}}{{\sum }_{j\in R(t_i)}E\{exp({\beta }_Z{Z}_j+{\mathit{\beta }}_X^T{\mathit{X}}_j)|\stackrel{\sim }{T}⩾t_i;{\mathit{W}}_j,Z_j\}},$$ (4)

which typically depends on λ₁(t).

2.2 Mean-Variance Regression Calibration

Under the rare disease assumption Pr(T̃ ⩾ t|X, Z) ≈ 1 for all follow-up times t, the induced hazard λ(t; W, Z) in (3) can be approximated by

$$\lambda (t;\mathit{W},Z)\approx {\lambda }_1(t)E\{exp({\beta }_{Z}Z+{\mathit{\beta }}_X^T\mathit{X})|\mathit{W},Z\},$$ (5)

and we replace “≈” in (5) by “=” subsequently. This approximation implies that the joint distribution of (X, U|T̃ ⩾ t, Z) is constant over time. If (X, U|Z) is jointly normal

$${({\mathit{X}}^T,\mathit{U})}^T|Z\sim N({({\mathit{M}}_Z^T,0)}^T,\mathit{\text{diag}}({\mathbf{\sum }}_Z,{\mathbf{\Delta }}_Z)).$$ (6)

the conditional distribution of (X|W, Z) is also normal with mean E(X|W, Z) and variance V(X|W, Z). Then the induced hazard can be written as

$$\lambda (t;\mathit{W},Z)={\lambda }_1(t)exp\{{\beta }_{Z}Z+{\mathit{\beta }}_X^T\mathit{E}(\mathit{X}|\mathit{W},Z)+\frac{1}{2}{\mathit{\beta }}_X^T\mathit{V}(\mathit{X}|\mathit{W},Z){\mathit{\beta }}_X\},$$ (7)

which can by written as a Cox model with covariates W, Z and their interactions:

$$\lambda (t;\mathit{W},Z)={\lambda }_4(t)exp({\gamma }_0{W}_0+{\gamma }_1{W}_1+{\gamma }_{2}Z+{\gamma }_3{W}_{0}Z+{\gamma }_4{W}_{1}Z).$$ (8)

Here γ = {γ₀, γ₁, γ₂, γ₃, γ₄} is a function of β = (β_z, β₀, β₁) and distribution parameters 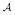= {M_z, Σ_z, Δ_Z; Z = 0, 1}. When 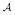is known, maximizing the partial likelihood for (8) as a function of β using, for example, the Newton-Raphson method gives estimates of β. Otherwise, a consistent estimate is needed for plugging into the partial likelihood. We discuss how to obtain in Section 3.

This approach is similar to that proposed in Wang et al. (2001), except that we assume normality to avoid higher order moments of the distribution of X given (W, Z). Compared to conventional regression calibration, expression (7) makes use of both the conditional mean and variance. Hence, we refer to this method as a mean-variance regression calibration (MVC). Under the rare disease assumption, this approach is expected to provide hazard ratio estimates with reduced biases compared to either a naive approach or a conventional regression calibration approach without the conditional variance term.

2.3 Follow-up Time Regression Calibration

While we expect MVC to provide better estimates compared to other approaches just mentioned, its performance may deteriorate under departure from the rare disease assumption. In this section, we modify MVC in an attempt to reduce any such deterioration.

To compute the exact partial likelihood (4), the joint distributions (X, W|T̃ ⩾ t, Z) at all failure times would be needed. When the number of failures is large, it is computationally intensive to calibrate at every failure time. Also, at later failure times, calibration accuracy may be low due to limited risk set sizes. In contrast, with MVC, we assume the conditional distribution of (X, W|T̃ ⩾ t, Z) is constant over time t, then only one calibration is needed. There can be remaining biases in parameter estimates due to differential changes in the covariate distribution over time between treatment arms.

We propose a follow-up time regression calibration (FUC) to avoid the two extremes described above. We divide the time axis into L intervals: [I₁, I₂), [I₂, I₃), …, [I_L, I_{L + 1}), where I₁ = 0 and I_{L + 1} = ∞; then calibrate at each I_i, i = 1, 2,…, L. This way, we assume covariate distribution is constant within each interval, but may differ between intervals. By adjusting L, we can balance between accuracy and computational burden. If L = 1, this is the MVC. If L = k + 1 and I_i+1 = t_i, i = 1, 2,…, k, calibration is done at time 0 and at each failure time. This corresponds to a special case of risk set regression calibration.

Specifically, we approximate the partial likelihood by

$$PL(\beta )\approx \mathbf{\prod }_{l=1}^L\mathbf{\prod }_{i:t_i\in [I_l,I_{l+1})}\frac{E\{exp({\beta }_Z{Z}_i+{\mathit{\beta }}_X^T{\mathit{X}}_i)|{\stackrel{\sim }{T}}_i⩾I_l,{\mathit{W}}_i,Z_i\}}{{\sum }_{j\in R(t_i)}E\{exp({\beta }_Z{Z}_j+{\mathit{\beta }}_X^T{\mathit{X}}_j)|{\stackrel{\sim }{T}}_j⩾I_l,{\mathit{W}}_j,Z_j\}}$$

We further assume that (X,U|T̃ ⩾ I_l, Z_i) is jointly normal with distribution parameters = {M_Z(I_l), Σ_Z(I_l), Δ_Z; Z = 0, 1}, l = 1, 2,…, L, and

$${({\mathit{X}}^T,{\mathit{U}}^T)}^T|\stackrel{\sim }{T}⩾I_l,Z\sim N({({\mathit{M}}_Z{(I_l)}^T,0)}^T,\mathit{\text{diag}}({\mathit{\sum }}_Z(I_l),{\mathbf{\Delta }}_Z)).$$ (9)

Now the paratial likelihood reduces approximately to

$$PL(\beta )=\mathbf{\prod }_{l=1}^L\mathbf{\prod }_{i:t_i\in [I_l,I_{l+1})}\frac{exp\{{\beta }_Z{Z}_i+{\mathit{\beta }}_X^T\mathit{E}({\mathit{X}}_i|{\mathcal{A}}_{I_l},{\mathit{W}}_i,Z_i)+\frac{1}{2}{\mathit{\beta }}_X^T\mathit{V}({\mathit{X}}_i|{\mathcal{A}}_{I_l},{\mathit{W}}_i,Z_i){\mathit{\beta }}_X\}}{{\sum }_{j\in R(t_i)}exp({\beta }_Z{Z}_j+{\mathit{\beta }}_X^T\mathit{E}({\mathit{X}}_j|{\mathcal{A}}_{I_l},{\mathit{W}}_j,Z_j)+\frac{1}{2}{\mathit{\beta }}_X^T\mathit{V}({\mathit{X}}_j|{\mathcal{A}}_{I_l},{\mathit{W}}_j,Z_j){\mathit{\beta }}_X\}},$$ (10)

where E(X_j| 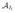, W_j, Z_j) and V(X_j| 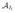, W_j, Z_j) are the corresponding conditional mean and variance. If the joint distribution (X, U|T̃ ⩾ I_l, Z) is not normal, equation (10) can be considered as a second-order Taylor approximation. With this approximated partial likelihood, we first derive the conditional mean and variance of X at each I_l, l = 1, 2,…, L, and then plug them into the partial likelihood to get MLE β̂ . Theoretically, dividing time into shorter intervals may lead to a less biased β̂ . However, we do not recommend choosing a large L due to the increasing computation time and unstable performance at later intervals. From numerical evaluation, it is preferable to choose I_l as the l^th L-quantile of all failure times, to have similar information accumulation within each time interval. The procedures of estimating 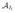, l = 1, 2, …, L are discussed in detail in Section 3.

The idea of FUC was mentioned in Liao et al. (2011) without a detailed development. This approach relaxes the constant covariate distribution assumption, thus is expected to be less sensitive to the rare disease assumption. Allowing control of the number of calibrations (L) opens the possibility of estimates that are both reliable and computationally efficient.

2.4 Asymptotic Properties

We use techniques similar to those discussed in Andersen and Gill (1982) to develop asymptotic properties for the two calibration approaches. MVC can be considered as a special case of FUC with L = 1. Under some mild regularity conditions, we have Theorem 1 for consistency and Theorem 2 for asymptotic normality:

Theorem 1: Under regularity conditions, $\widehat{\mathit{\beta }}\stackrel{P}{\to }{\mathit{\beta }}^{\ast }$, where β^∗ is the true value of β in the approximate induced hazard model (10).

Theorem 2: Under regularity conditions,

$$n^{1/2}(\widehat{\mathit{\beta }}-{\mathit{\beta }}^{\ast })\stackrel{D}{\to }N(0,\mathrm{\Omega }{({\mathit{\beta }}^{\ast })}^{-1}\{B({\mathit{\beta }}^{\ast })+D({\mathit{\beta }}^{\ast })\}\mathrm{\Omega }{({\mathit{\beta }}^{\ast })}^{-1}),\mathit{\text{as}}n\to \infty .$$

Theorem 1 shows that β̂ is consistent for a value β^*, that typically differs somewhat from β. However, the bias |β^* − β| tends to be small in many contexts, as will be shown in Section 4 simulation studies. Theorem 2 states that β̂ has a sandwich-form variance. The middle part of the variance arises from two sources: one from the regular estimating equation, another from the variability in estimating distribution parameters 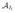, l = 1, 2, …, L. Detailed regularity conditions, proof of both theorems and explicit formula for Ω(.), B(.) and D(.) are given in Web Appendix A.

2.5 Extension to Multiple Mediators and to Other Sampling Designs

When there are K(K > 1) biomarkers measured for each subject, one can ask whether these biomarkers jointly mediate the relationship between Z and Y. It is straightforward to extend MVC and FUC to multiple mediators: X, U, W become 2K × 1 vectors. The approximate induced hazards (7) and (10) are the same, with joint conditional means and variances of the K markers plugged in. All the other steps follow as for a univariate biomarker.

Prentice (1986) proposed the case-cohort design as a way to reduce data collection burden for large cohort studies with infrequent failures. A subcohort of sample size n_sc is randomly selected from the entire cohort of sample size n at the beginning of the study. Covariate histories are only assembled for the subcohort members and the cases. Barlow (1994) viewed this design as a weighted cohort study with pseudo-partial likelihood

$$PL\ast (\beta |\mathit{X},Z)=\mathbf{\prod }_{i=1}^k\frac{w_i(t_i)exp({\mathit{\beta }}_X^T{\mathit{X}}_i+{\beta }_Z{Z}_i)}{{\sum }_{j\in R(t_i)}{w}_j(t_i)exp({\mathit{\beta }}_X^T{\mathit{X}}_j+{\beta }_Z{Z}_j)},$$

where at time t_i, case i has weight 1, at risk members in the subcohort have weight equal to the inverse sampling rate n/n_sc, and other subjects have weight 0. MVC and FUC can be easily adopted. The induced pseudo-partial likelihood is approximated by

$$\mathbf{\prod }_{l=1}^L\mathbf{\prod }_{i:t_i\in [I_l,I_{l+1})}\frac{w_i(t_i)exp[{\beta }_Z{Z}_i+{\mathit{\beta }}_X^{T}E({\mathit{X}}_i|{\mathit{W}}_i,Z_i,{\mathcal{A}}_{I_l})+\frac{1}{2}{\mathit{\beta }}_X^{T}V({\mathit{X}}_i|{\mathit{W}}_i,Z_i,{\mathcal{A}}_{I_l}){\mathit{\beta }}_X]}{\sum _{j\in R(t_i)}{w}_j(t_i)exp[{\beta }_Z{Z}_j+{\mathit{\beta }}_X^{T}E({\mathit{X}}_j|{\mathit{W}}_j,Z_j,{\mathcal{A}}_{I_l})+\frac{1}{2}{\mathit{\beta }}_X^{T}V({\mathit{X}}_j|{\mathit{W}}_j,Z_j,{\mathcal{A}}_{I_l}){\mathit{\beta }}_X]}$$

with FUC of L intervals: [I₁, I₂), [I₂, I₃), …, [I_L, L_L+1), and MVC as a special case with L = 1.

A nested case-control study can be viewed as a cohort study with outcome-dependent weighting, and analyzed through the inverse probability weight estimator framework (Cai and Zheng, 2011). Both MVC and FUC can be applied similarly to the weighted partial likelihood as in the case-cohort design.

3 Measurement Error Model and Biomarker Process Modeling

So far, we restricted U to be normally distributed mean zero classical measurement error. In this section, we consider a class of measurement error models, and discuss the estimation of corresponding distribution parameters under data structures arising in mediation analysis.

3.1 Measurement Error Model

Although modeling W is not our primary interest, we can usefully decompose it to understand its variability. There are at least three sources of random variations that could be associated with the observed W_ij, which is the j^th measure on the i^th subject (Diggle et al., 2002, Chapter 5): subject-specific random effects, temporal variation and technical error:

$$W_{ij}=\mu (Z_i,t_j)+b_i(Z_i,t_j)+S_{ij}(Z_i,t_j)+{\epsilon }_{ij}.$$ (11)

Here, μ(Z_i, t_j) is a fixed population mean, which may differ by treatment Z_i and time t_j. Also b_i(Z_i, t_j) is a subject-specific random effect. It represents the difference between the mean of the i^th subject's measures and the population mean and has mean zero. S_ij(Z_i, t_j) is the temporal variation, which also has mean zero. The within-subject correlation is typically weaker as the time separation increases. Finally, ε_ij is the noise, which is assumed to have mean zero and to be uncorrelated with ε_ik if j ≠ k. We refer to ε_ij as the technical error, even though ε_ij may incorporate local temporal variation beyond that attributable to the measurement technology. These four parts are assumed to be independent of each other given (Z_i, t_j) and independent between subjects. With this decomposition, we specify two formulations of measurement errors: uncorrelated and correlated measurement errors.

By uncorrelated measurement errors, we are considering the following specification:

$$\begin{array}{cc}{X}_{ij}=\mu (Z_i,t_j)+b_i(Z_i,t_j)+S_{ij}(Z_i,t_j),& U_{ij}={\mathrm{\epsilon }}_{ij}\end{array}$$

We consider the technical error as the only source of measurement error, and the targeted X_ij is the true biomarker value of subject i at time t_j. Under this definition, measurement errors are independent between and within subjects: with z = 0, 1,

$${\mathit{M}}_z={({\mu }_0,{\mu }_{z+1})}^T,{\mathbf{\sum }}_z=\left(\begin{array}{cc}{\sigma }_0^2& {\rho }_z{\sigma }_0{\sigma }_{z+1}\\ {\rho }_z{\sigma }_0{\sigma }_{z+1}& {\sigma }_{z+1}^2\end{array}\right),{\mathbf{\Delta }}_z=\mathit{\text{diag}}({\sigma }_{e0}^2,{\sigma }_{e(z+1)}^2),$$ (12)

This distribution may be further simplified. For example, it may be appropriate to assume that the variance of X is constant over time (i.e., ${\sigma }_1^2={\sigma }_2^2$). Also, one could consider assumptions that the measurement error distribution does not depend on X or Z (i.e., ${\sigma }_{e0}^2={\sigma }_{e1}^2={\sigma }_{e2}^2$), or that variance ratios are constant (i.e., k₀ = k₁ = k₂, where $k_i=\frac{{\sigma }_{ei}^2}{{\sigma }_i^2}$).

By correlated measurement errors, we are considering the following model:

$$\begin{array}{cc}{X}_{ij}=\mu (Z_i,t_j)+b_i(Z_i,t_j),& U_{ij}=S_{ij}(Z_i,t_j)+{\mathrm{\epsilon }}_{ij}\end{array}.$$

With this specification, measurement error includes both the technical error and the temporal variation, thus measurement errors within a subject are correlated. The targeted X_ij is a subject-specific mean biomarker level, which may change with time and treatment. In the important special case where both μ(Z_i, t_j) and b_i(Z_i, t_j) do not change with t_j, X_ij is considered as the subject's long-term average biomarker value. Under this specification,

$${\mathit{M}}_z={({\mu }_0,{\mu }_{z+1})}^T,{\mathbf{\sum }}_z=\left(\begin{array}{cc}{\sigma }_0^2& {\rho }_z{\sigma }_0{\sigma }_{z+1}\\ {\rho }_z{\sigma }_0{\sigma }_{z+1}& {\sigma }_{z+1}^2\end{array}\right),{\mathbf{\Delta }}_z=\left(\begin{array}{cc}{\sigma }_{e0}^2& r_z{\sigma }_{e0}{\sigma }_{e(z+1)}\\ r_z{\sigma }_{e0}{\sigma }_{e(z+1)}& {\sigma }_{e(z+1)}^2\end{array}\right),$$ (13)

with z = 0, 1 and ρ₀ = 1. Note the correlation between X₀ and X₁ becomes exactly 1 in the control group, and measurement errors are correlated with each other (i.e., r₀, r₁ ≠ 0). Again, further constraints may be suitable in applications.

The choice between uncorrelated and correlated measurement errors depends substantially on the research question of interest. If the long-term average biomarker level is more relevant to disease risk mediation, then correlated measurement error model is of interest. If one simply wishes to conduct mediation analysis that is adjusted for technical error, then uncorrelated measurement error is more appropriate.

3.2 Biomarker Process Modeling

To estimate E(X|W, Z, 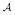) and V(X|W, Z, 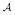) in MVC, one needs to estimate 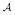. The likelihood of the observed W can be written based on the joint normal distribution in (6) and detailed parameter specifications in (12) and (13). Notice that with uncorrelated measurement error, there are 8 variance-covariance parameters (i.e., ${\sigma }_0^2,{\sigma }_1^2,{\sigma }_2^2,{\sigma }_{e0}^2,{\sigma }_{e1}^2,{\sigma }_{e2}^2,{\rho }_0,{\rho }_1$), but only 5 unique components in the covariance matrix of W (i.e., ${\sigma }_0^2+{\sigma }_{e0}^2,{\sigma }_1^2+{\sigma }_{e1}^2,{\sigma }_2^2+{\sigma }_{e2}^2,{\rho }_0{\sigma }_0{\sigma }_1,{\rho }_1{\sigma }_0{\sigma }_2$). Similarly, with correlated measurement error, there are more parameters than unique components in the covariance matrix. To solve this idenfibility problem, additional information is needed. First, we can consider some constraints as discussed above. Second, we can sometimes obtain estimates of some parameters from external data. For example, one may be able to assume that (ρ₀, ρ₁) in the uncorrelated measurement error scenario, and (ρ₁, r₀, r₁) in the correlated measurement error scenario, or variance ratios k_i are similar across studies. If there is a study with the same biomarker measured longitudinally, we can estimate these parameters to be plugged into the likelihood of W. If unfortunately there is no external information, sensitivity studies on the above mentioned distribution parameters will be needed to cover a range of possible values.

With FUC, additional steps are needed to estimate 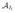, l = 2, …, L. Notice that we let both M _Z(.) and Σ _Z(.) vary with time, but Δ_Z is not time-varying. This is because study subjects with longer survival time may have different characteristics in X, but measurement error U does not affect survival time. In addition, we expect differential changes of X distribution in the two treatment arms. Thus we allow common parameters in the distribution specification (12) and (13), such as μ₀ and ${\mathrm{\sigma }}_0^2$, to be updated separately within treatment groups. At each cutoff timeI_l, l = 2, …, L, we maximize the likelihood within each treatment arm on subjects still at risk, with Δ̂ _z estimated at t = 0 plugged in. This way, we get estimate 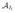, and can subsequently estimate Ê (X|W, Z, 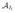), V̂(X|W, Z, ).

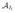When joint mediation effect of multiple biomarkers is of interest, ideally one would model their joint distribution. Thus in addition to the covariance matrix of each marker, one needs to specify the between-biomarker correlation structures. With relatively limited external information, fitting such a model may lead to unstable performance, which can adversely influence the calibration performance. Hence, it may be preferable to calibrate biomarkers individually. This individual calibration approach, however, could result in some efficiency loss. More comprehensive biomarker process models can be applied when the external dataset is large and longitudinal.

With a case-cohort design, similar methods can be applied to estimate distribution parameters, but only subcohort members at risk at the time of calibration are used. This approach is expected to provide approximately unbiased distribution parameter estimates, as the subcohort is a random sample of the population. However the performance can be unstable if the subcohort is small. With a nested case-control design, we may estimate distribution parameters similarly as in a cohort design with inverse probability weights.

4 Simulation Studies

In this section, we conduct several simulation studies to investigate the performances of the two proposed mediation analysis measurement error correction methods.

We specify μ₀ = μ₁ = 0, μ₂ = 0.5, ${\sigma }_0^2={\sigma }_1^2=1,{\sigma }_2^2=1.2$, and β₀ = β₁ = 1, β_Z = log(1.5) ≈ 0.41, λ₁(t) = 1. In the uncorrelated measurement error setting, we assume ${\sigma }_{e0}^2={\sigma }_{e1}^2={\sigma }_{e2}^2=0.5$, and (ρ₀, ρ₁) = (0.95, 0.9). In the correlated measurement error setting, we assume ${\sigma }_{e0}^2={\sigma }_{e1}^2=0.5,{\sigma }_{e2}^2=1$, (ρ₁, r₀, r₁) = (0.9, 0.7, 0.5). Half of the subjects are assigned to active treatment. We compare the performance of the naive approach which replaces X with W (Naive), MVC and FUC with 4 and 8 intervals (FUC4, FUC8). Censoring probabilities are chosen as 80% to 95% under two censoring mechanisms. Under the first mechanism, all subjects are censored at a fixed time point C_end (Censor I). We define intervals as [0, Q_T,1/L), [Q_T,1/L, Q_T,2/L),…,[Q_T,(L-1)/L, ∞), where Q_{T, k/L} is the k^th L-quantile of all failure times. Under the second mechanism, censoring time follows an exponential distribution within each arm, and the censoring rates differ between arms (Censor II). We let the censoring probability in the treatment group to be 5% higher than that in the control group. For example, censoring probabilities in treatment and control group are 97.5% and 92.5% respectively, to achieve 95% overall censoring probability. In this setting, we define intervals as [0, Q_{T, 1/L}), [Q_T,1/L, Q_T,2/L), …, [Q_{T,(L‒1)/L, z=1,} ∞), where Q_{T,k/L, Z=1} is the k^th L-quantile of failure times in the treatment group, to ensures there are enough treated subjects at each calibration. Cohort size varies with censoring probability to achieve 500 expected failures. Simulation results are based on 1000 replications.

First assume that distribution parameters (ρ₀, ρ₁) and (ρ₁, r₀, r₁) in the two settings are known. Simulation results of β_Z are summarized in Table 1. Naive biases in β_Z are generally non-ignorable. MVC does not reduce bias with 80% censoring probability, but its performance improves with higher censoring probability. This is expected from the underlying rare disease assumption of MVC. FUC4 and FUC8 provide considerably smaller biases in all scenarios. Theoretically, more calibrations will result in smaller biases. However, FUC8 does not improve much upon FUC4. This suggests that with 500 events, dividing time into 4 intervals is accurate enough for β_Z estimation. With uncorrelated measurement error and censoring probability 0.95, we actually observe that the bias of β_Z tends to increase from negative to 0 as number of calibrations increases, and more calibrations has the potential to make it further increase over 0, resulting in an over-correction. MVC and FUC are associated with slightly larger biases with the second censoring mechanism. This is because the time span is longer with this mechanism, and censoring time distributions are differential between the two arms. The proposed estimated standard errors agree well with simulation standard errors, especially when bias is small. Coverage probabilities are generally close to 95%.

Table 1.

Summary statistics for β_z. Distribution parameters (ρ₀, ρ_S) in the uncorrelated measurement error setting and (ρ_i, r₀, r₁) in the correlated measurement error setting are assumed to be known.

βz		Censor I					Censor II
P(censor)	method	β̂z	bias	Sim SEa	Est SEb	CPc	β̂z	bias	Sim SE	Est SE	CP
Uncorrelated Measurement Error
0.8	Naive	0.435	0.029	0.100	–	–	0.438	0.033	0.104	–	–
	MVC	0.356	-0.049	0.202	0.190	0.864	0.333	-0.072	0.210	0.254	0.954
	FUC4	0.397	-0.008	0.204	0.192	0.944	0.375	-0.030	0.217	0.260	0.980
	FUC8	0.404	-0.001	0.208	0.196	0.951	0.384	-0.021	0.219	0.265	0.983
0.9	Naive	0.465	0.059	0.097	–	–	0.466	0.061	0.109	–	–
	MVC	0.374	-0.032	0.191	0.176	0.916	0.333	-0.072	0.227	0.223	0.945
	FUC4	0.399	-0.007	0.193	0.188	0.956	0.363	-0.042	0.231	0.247	0.950
	FUC8	0.403	-0.002	0.195	0.191	0.961	0.369	-0.037	0.231	0.250	0.952
0.95	Naive	0.485	0.079	0.099	–	–	0.516	0.111	0.132	–	–
	MVC	0.393	-0.013	0.190	0.178	0.935	0.352	-0.053	0.273	0.251	0.937
	FUC4	0.411	0.005	0.192	0.187	0.953	0.368	-0.038	0.275	0.269	0.950
	FUC8	0.414	0.008	0.193	0.190	0.958	0.371	-0.034	0.276	0.269	0.950
Correlated Measurement Error
0.8	Naive	0.527	0.122	0.105	–	–	0.505	0.099	0.109	–	–
	MVC	0.311	-0.094	0.283	0.364	1.000	0.288	-0.117	0.295	0.366	0.998
	FUC4	0.384	-0.021	0.257	0.275	0.988	0.369	-0.036	0.273	0.316	0.976
	FUC8	0.397	-0.008	0.260	0.272	0.980	0.391	-0.015	0.271	0.309	0.975
0.9	Naive	0.576	0.171	0.102	–	–	0.534	0.128	0.118	–	–
	MVC	0.330	-0.076	0.235	0.277	0.990	0.306	-0.100	0.264	0.283	0.973
	FUC4	0.376	-0.029	0.228	0.241	0.985	0.360	-0.045	0.270	0.294	0.984
	FUC8	0.385	-0.021	0.229	0.239	0.980	0.375	-0.031	0.269	0.292	0.982
0.95	Naive	0.611	0.205	0.104	–	–	0.566	0.161	0.142	–	–
	MVC	0.357	-0.049	0.216	0.227	0.972	0.316	-0.089	0.331	0.309	0.960
	FUC4	0.389	-0.017	0.217	0.214	0.959	0.350	-0.055	0.326	0.329	0.967
	FUC8	0.394	-0.011	0.218	0.213	0.957	0.359	-0.046	0.325	0.328	0.970

^aSimulation Standard Error

^bMean Estimated Standard Error

^cCoverage Probability

To investigate the robustness of results to distribution parameters specification, a simulation study with (ρ₀, ρ₁) and (ρ₁, r₀, r₁) in the two measurement error settings estimated from an external data was conducted. Model specification is similar as before, and we assumed a common censoring time with 95% of subjects censored. External datasets are simulated as described in (11), (12) and (13). Simulation results of β_z are summarized in Table 2. Compared to when (ρ₀, ρ₁) are known, both MVC and FUC still reduce β_Z bias, and the bias decreases as the number of intervals increases. As distribution parameter estimates become less precise, bias tend to increase, especially with correlated measurement error, and more calibrations are likely to cause over-correction. Standard errors tend to increase as well, which agrees with our proposed variance estimates. This increase is generally quite small with uncorrelated measurement error, but can be large with correlated measurement error. The differences between the simulated standard errors and estimated mean standard errors in correlated measurement error scenarios are related to the remaining biases in β₀ and β₁ (see Web Appendix B). These remaining biases are mostly due to the variability in ρ̂₁. Hence, for correlated measurement error, we recommend a careful evaluation of distribution parameters, as results can be quite sensitive to their specification.

Table 2.

Summary statistics for β_z. Distribution parameters (ρ₀, ρ₁) in uncorrelated measurement error setting and (ρ₁, r₀, r₁) in correlated measurement error setting are estimated from external datasets of sample size 1000 and 500.

βz	nE = 1000					nE = 500
method	β̂Z	bias	Sim SE	Est SE	CP	β̂Z	bias	Sim SE	Est SE	CP
Uncorrelated Measurement Error
Naive	0.485	0.079	0.099	–	–	0.485	0.079	0.099	–	–
MVC	0.392	-0.014	0.191	0.189	0.944	0.394	-0.012	0.190	0.199	0.947
FUC4	0.412	0.007	0.193	0.195	0.954	0.415	0.009	0.192	0.201	0.959
FUC8	0.415	0.009	0.194	0.197	0.960	0.418	0.012	0.192	0.203	0.959
Correlated Measurement Error
Naive	0.611	0.205	0.104	–	–	0.611	0.205	0.104	–	–
MVC	0.384	-0.021	0.757	0.741	0.958	0.512	0.106	1.376	1.407	0.958
FUC4	0.409	0.004	0.591	0.535	0.963	0.460	0.054	0.576	0.669	0.974
FUC8	0.408	0.003	0.594	0.509	0.968	0.463	0.057	0.584	0.651	0.968

Next we investigate the robustness of MVC and FUC to non-normality. We assume that X is normally distributed, while U is non-normal. This corresponds to the situation where, under a suitable transformation, X becomes approximately normal while U is generated from a multivariate non-normal distributions with mean 0 and unit variance using methods described in Vale and Maurelli (1983). Two skewness and kurtosis combinations: (0,6/5) and (1,3) are investigated. Here (0,6/5) is chosen to resemble a logistic distribution, which is close to a normal distribution but has heavier tails. The combination of (1, 3) is chosen to allow the distributions to be both skewed and with heavy tails. Other model assumptions are the same with 95% censoring at a common time. Results of β_z are summarized in Table 3. As measurement error distribution becomes further away from normal, the naive bias in β_z tends to increase. Both MVC and FUC show the ability to reduce bias, but over-correction can become serious with severe violation of normality. This is because FUC assumes normality at each calibration, which evidently relies on the normal assumption more heavily than MVC. In this example with relatively high censoring probability, MVC is expected to perform well. The proposed variance estimator is not accurate when violation of normality is severe, as it is derived under normality assumption.

Table 3.

Summary statistics for β_z. Measurement errors are generated from multivariate distribution with violation of normality assumption.

βz	(sk, ku) = (0, 6/5)					(sk, ku) = (1, 3)
method	β̂z	bias	Sim SE	Est SE	CP	β̂z	bias	Sim SE	Est SE	CP
Uncorrelated Measurement Error
Naive	0.491	0.086	0.102	–	–	0.517	0.111	0.106	–	–
MVC	0.403	-0.003	0.197	0.164	0.915	0.444	0.039	0.192	0.125	0.855
FUC4	0.424	0.018	0.201	0.173	0.933	0.464	0.058	0.198	0.134	0.897
FUC8	0.427	0.022	0.202	0.176	0.937	0.467	0.062	0.200	0.136	0.901
Correlated Measurement Error
Naive	0.614	0.209	0.108	–	–	0.629	0.223	0.112	–	–
MVC	0.356	-0.050	0.220	0.215	0.970	0.399	-0.006	0.220	0.186	0.965
FUC4	0.389	-0.017	0.220	0.200	0.958	0.430	0.024	0.219	0.166	0.929
FUC8	0.395	-0.011	0.220	0.199	0.959	0.435	0.029	0.219	0.164	0.928

Simulation results for β₀ and β₁ are provided in Web Appendix B. Naive biases in these two parameters are generally larger than that those of β_Z in our simulation settings, partially due to larger β₀ and β₁ values. MVC and FUC both reduce biases greatly. However, the remaining bias is typically non-negligible, suggesting that more calibrations may be needed if these parameters are of substantial interest.

5 Postmenopausal Hormone Therapy Application

We now re-examine the mediation of postmenopausal hormone therapy effects on breast cancer by serum sex hormones, in the WHI randomized controlled trials. There were two major trials: 16,608 women with uterus were randomized to 0.625 mg/day conjugated equine estrogen plus 2.5 mg/day medroxyprogesterone acetate (E+P) or placebo; and 10,739 post-hysterectomy women were randomized to this same estrogens preparation without the progestin (E-alone) or placebo. Both hormone therapy trials stopped early due to adverse health events. An elevation in invasive breast cancer risk was pivotal in the early stopping of the E+P trial (Rossouw et al., 2002; Chlebowski et al., 2009), while the E-alone trail showed a surprising reduction in breast cancer incidence with treatment (Anderson et al., 2004, 2012).

A nested case-control study was conducted within each hormone therapy trial toward understanding the divergent trial results, with the major changes in plasma hormones induced by these regimens as natural candidates for breast cancer effects mediation. The study included 348 and 235 cases in the E+P trial and E-alone trial, and corresponding 1-1 matched controls. Concentrations of sex hormones were measured at baseline and 1-year following randomization. Major serum estrogens, including estradiol, estrone, and estrone sulfate, were approximately doubled by these hormone therapies, as was the sex hormone binding globulin (SHBG) (Edlefsen et al., 2010; Farhat et al., 2013). However, the sex hormone changes were nearly identical with E-alone and with E+P, presumably reducing the likelihood that these changes can substantially explain the divergent hormone therapy effects on breast cancer. The mediation analyses given here exclude cases occurring during the first year following randomization. Cox model analyses of the randomization indicator variable and log-transformed baseline sex hormone variables were carried out without, and with, the addition of 1-year log-transformed sex hormone concentrations to the model. Matching variables age and race, were included in the regression for confounding control.

As an external dataset, blind duplicate sex hormone assessments were available from 120 women who were screened for WHI participation, but did not enroll. Differences between the log-transformed assessments from the duplicate samples are assumed to be due to technical error. Variance ratios, k₀, are estimated to be 0.13, 0.07, 0.19, and 0.02 for estradiol, estrone, estrone sulfate, and SHBG. We assume that variance ratios in the uncorrelated measurement error model only change with hormone therapy treatment assignment, and provide sensitivity analyses with k₀ = k₁, while k₂ varies. Only MVC is applied to these data, since only about 2% of women developed breast cancer during the intervention phases of these clinical trials. Table 4 presents some results from mediation analyses, on the left with estradiol as potential mediator, and on the right with the four sex hormones considered as possible joint mediators.

Table 4.

Hazard ratios of treatment in E+P and E-alone trials, with and without measurement error correction. Matching variables, age and race, are adjusted in all models.

Potential Mediator	Estradiol		Estradiol,Estrone, Estrone Sulfate, SHBG
Trial	E+P	E-alone	E+P	E-alone
	HRa (95% CIb)	HR (95% CI)	HR (95% CI)	HR (95% CI)
Baseline Biomarkers Only	1.64 (1.28, 2.10)	0.59 (0.45, 0.78)	1.71 (1.32, 2.20)	0.68 (0.51, 0.91)
Baseline+Year 1 Biomarkers
No MEc Correction	1.35 (0.98, 1.84)	0.59 (0.41, 0.83)	1.47 (0.98, 2.20)	0.84 (0.51, 1.38)
Uncorrelated ME Correction
k1 = k2 = k0	1.31 (0.94, 1.82)	0.59 (0.41, 0.86)	1.43 (0.92, 2.22)	0.87 (0.50, 1.50)
k1 = k0, k2 = 1.5k0	1.29 (0.92, 1.81)	0.59 (0.41, 0.86)	1.39 (0.89, 2.16)	0.94 (0.55, 1.62)
k1 = k0, k2 = 2k0	1.27 (0.90, 1.80)	0.59 (0.40, 0.87)	1.36 (0.86, 2.15)	0.95 (0.54, 1.65)
Correlated ME Correction
k0 = k1 = k2 = ks	1.09 (0.70, 1.68)	0.66 (0.35, 1.26)	–	–
k0 = k1 = k2 = 1.5ks	0.99 (0.54, 1.82)	0.65 (0.31, 1.34)	–	–
k0 = k1 = k2 = 2ks	0.89 (0.45, 1.77)	0.68 (0.28, 1.65)	–	–

^aHazard ratio

^bConfidence interval

^cMeasurement error

Serum estradiol appears to partially mediate a substantial effect of E+P on breast cancer risk, even without measurement error correction, with estimated hazard ratio (HR) dropping from 1.64 to 1.35 when 1-year estradiol was added to the analysis. Allowance for uncorrelated measurement error gave HR estimates a little closer to the null. Allowing measurement errors to be correlated, as may be necessary to address mediation by sex hormone levels over the entire trial intervention period, shows the possibility of rather complete mediation by estradiol with HR estimates in the vicinity of one. These are purely sensitivity analyses, however. In order to maintain a non-negative correlation between measurement errors, the smallest possible k₀ for estradiol is 0.95 for the E+P trial and 1.1 for the E-alone trial. We denote these numbers by k_s and vary k_i, i = 0, 1, 2 from k_s to 2k_s. Note that confidence intervals are quite wide, in line with simulation study findings of sensitivity to error distribution parameter specifications. Mediation of the E+P effect on breast cancer was not enhanced by bringing in the other sex hormones. In contrast, the reduced HR with E-alone is evidently minimally explained by the change in serum estradiol, regardless of measurement error correction. However, when the four sex hormones are considered simultaneously as potential mediators, there is evidence of partial mediation without measurement error correction, and rather complete mediations when allowing for technical measurement error. The interpretation of mediation analyses can be complex. Here, specifically, mediation of the risk elevation with E+P seems to be related to removal of a baseline estradiol effect following treatment, whereas the E-alone risk reduction may reflect SHBG increase that offsets the serum estrogen increase (Zhao et al., 2013).

6 Discussion

This article discusses covariate measurement error correction methods in the context of mediation analysis with failure time data. The proposed mean-variance regression calibration is suitable under a rare disease assumption, and the follow-up time regression calibration further extends this applicability. Simulation studies demonstrate that both measurement error correction methods have desirable performances under various biomarker process scenarios.

A requirement of these methods is that some additional information about the biomarker process be available. In application, it might be challenging to obtain such information for novel biomarkers, such as in our WHI hormone therapy trial example. The need for a reliability dataset has always been important in measurement error area. In our more complicated mediation analysis setting, investigators need to plan the reliability study to have sufficient sample size with suitable longitudinal measures.