Non-Bayesian noun generalization in 3- to 5-year-old children: Probing the role of prior knowledge in the suspicious coincidence effect

Abstract

It is unclear how children learn labels for multiple overlapping categories such as “Labrador,” “dog,” and “animal.” Xu and Tenenbaum (2007a) suggested that learners infer correct meanings with the help of Bayesian inference. They instantiated these claims in a Bayesian model, which they tested with preschoolers and adults. Here, we report data testing a developmental prediction of the Bayesian model—that more knowledge should lead to narrower category inferences when presented with multiple subordinate examples. Two experiments did not support this prediction. Children with more category knowledge showed broader generalization when presented with multiple subordinate examples, compared to less knowledgeable children and adults. This implies a U-shaped developmental trend. The Bayesian model was not able to account for these data, even with inputs that reflected the similarity judgments of children. We discuss implications for the Bayesian model including a combined Bayesian/morphological knowledge account that could explain the demonstrated U-shaped trend.

1. Introduction

A central issue in the study of cognitive development is how children learn labels for multiple overlapping categories. “Animal,” “mammal,” “dog,” “Labrador,” and “Rover” are all categories that include the same common object—for example, the Labrador named Rover. Thus, when a child hears a novel label applied to an object like a dog, the correct interpretation is ambiguous: does the unknown label correspond to the species, to the breed, to the individual animal, or something else? Learning hierarchically nested categories like those above presents unique challenges. Unlike the broader ambiguities discussed by Quine (1960) concerning which object in a complicated scene a novel label refers to, ambiguities about hierarchically nested categories for the same object are more difficult for children to solve. Many of the tools children might rely on when learning basic level categories for the first time would fail them when they progress to nested categories. Mutual exclusivity, for example (Markman, 1991), is counterproductive in cases where two categories are not mutually exclusive, but instead include some of the same objects. Golinkoff, Hirsh-Pasek, Bailey, & Wenger’s (1992) N3C constraint— the idea that children tend to assign novel labels to currently unlabeled categories—is similarly unhelpful. For instance, if a child knows that “dog” refers to the four-legged animal in the scene and is asked to point to the “Labrador,” the N3C constraint might direct the child to erroneously attend to the most novel item which could be any other unlabeled object.

Learning subordinate-level categories (e.g., “Labrador”) might be the most difficult of all. Some of children’s hypotheses about the meaning of broad categories, such as those at the basic (“dog”) and superordinate (“animal”) levels, can be ruled out with negative evidence. For example, if a child observes both a pig and a dog labeled “fep,” then “fep” must mean “mammal” or something broader, and all narrower hypotheses can be discarded. Incorrect hypotheses for narrow, subordinate-level categories like “Labrador,” however, can never be ruled out by example. More evidence may make learners more or less confident in their guesses, but no number of examples can entirely rule out the possibility that “fep” refers to dogs in general, even when it only means “Labradors.” In the face of examples alone (not explicit explanation of category extents), there is always a chance that the other dogs in the category just have not been seen and labeled yet. Due to this ambiguity, children are always forced to make assumptions and inferences when learning narrow categories without explicit definitions.

Xu and Tenenbaum (2007a) recently proposed that children use Bayesian inference when learning the extensions of hierarchically nested categories like “Labrador.” Theories of Bayesian inference posit that people begin with prior assumptions regarding the probability of different hypotheses about the world and combine these with the likelihood of each hypothesis given a certain observed outcome. By combining these two estimates, one arrives at a posterior probability distribution: the probability of each hypothesis being correct, given both prior knowledge and current evidence. This distribution can then be used to make inferences about the extent and inclusion of an unfamiliar category and to guide behavior.

Xu and Tenenbaum further suggested that the likelihood portion of Bayesian inference does much of the work in explaining how children and adults learn and extend hierarchically nested categories. Children begin by observing how novel labels are applied to different exemplars. If they hear the same label applied to many exemplars that all look very similar, then they can recognize what Xu and Tenenbaum called a “suspicious coincidence:” a suspiciously low likelihood of having seen that particular set of exemplars in a row, given the broad array of possible objects children might encounter in the world. Such situations favor narrow, subordinate-level interpretations of the novel category. This is because narrow categories have the highest likelihood of producing multiple similar exemplars in a row, since they usually only contain similar exemplars. Thus, recognizing a suspicious coincidence could lead children to interpret that a new label refers to a category at the subordinate level, even though they lack definitive evidence.

Consider a concrete example: a child hears the word “fep” applied to a Labrador. After just one labeling event, the category “fep” is ambiguous—it could refer to a specific individual, a species, or any animal. Imagine that a few minutes later, however, the child hears “fep” applied to a distinctly different Labrador. Now, the child has enough information to calculate the likelihood of having witnessed this series of labeling events given different possible hypotheses about the meaning of the category “fep.” Broad hypotheses in this example are less likely, because if “fep” means something broad like “all dogs,” then it would be a “suspicious coincidence” if the first two labeled examples that the child heard were both members of the same breed. Xu and Tenenbaum suggested that children are aware of these probabilities, leading them to favor the narrower hypothesis that the category “fep” includes only Labradors in this example.

Xu and Tenenbaum (2007a) tested whether 42- to 60-month old children and adults do, in fact, detect suspicious coincidences. They predicted that participants shown one specific breed of dog (like a Labrador), labeled “fep” one time, would not have any strong rational inferences about the meaning of “fep” and would therefore broadly generalize the label to a variety of objects at different hierarchical levels when given a varied comparison (test) set—to other Labradors, different breeds of dogs, and even a few other species of animals, like seals. In contrast, they predicted that participants shown three separate Labradors, all labeled “fep” once, would generalize the novel label more narrowly. As predicted, child and adult participants who saw only one labeled exemplar generalized the label more broadly than those who saw three exactly matching labeled exemplars. Xu and Tenenbaum captured these data quantitatively using a Bayesian model that accurately replicated the pattern of children’s and adults’ performance.

Note that in Xu and Tenenbaum’s methodology, experimenters overtly labeled objects while attending to participants. This is an important theoretical detail, because it highlights that there is a pedagogical nature to the suspicious coincidence effect. Suspicious coincidences can be observed even when objects are not pedagogically labeled, such as when a word learner overhears a conversation. However, the effect should be most potent when a learner is given labels directly by an informed person (e.g. a caregiver or experimenter) in an intentional, pedagogical way, since that is when the information should be most reliable (see Xu & Tenenbaum, 2007b; see also Bonawitz, Shafto, Gweon, Goodman, Spelke, & Schulz, 2011; Shafto & Goodman, 2008; and Gweon, Tenenbaum, & Shulz, 2010 for a discussion of pedagogy as a tool in children’s learning and contexts in which it most matters).

The “suspicious coincidence” effect reported by Xu and Tenenbaum is theoretically important because it is not predicted by other prominent models of word learning (for discussion, see Xu & Tenenbaum, 2007a). It also provides a solution to the difficult problem of identifying the extensions of narrow categories when confronted with hierarchically nested categories. In the present report, we build on this research and examine how children’s ability to identify suspicious coincidences changes as they acquire more category knowledge over development.

Children’s category knowledge changes dramatically in early development as they learn a large variety of categories that include concrete objects at different hierarchical levels (e.g., “Fluffy”, “kitty” and “pet” all for family cat), objects categorized by less typical dimensions such as texture or material substance (Samuelson and Smith, 1999) and even abstract categories such as ‘people I trust’ (Harris, 2012). As children acquire categories, how might their ability to detect suspicious coincidences change? The suspicious coincidence effect reflects a contrast in the probability of generalizing at the basic level when one versus multiple subordinate-level exemplars are presented and labeled. Intuitively, one would expect this effect to get stronger over development as children acquire more adult-like category knowledge. Early in development, children might have little prior knowledge about how basic-level and subordinate-level categories are organized. Thus, when shown a ‘Labrador’, some children might not entertain any subordinate-level hypotheses, while other children might not have much psychological distance (in, for instance, a metric similarity space) between a subordinate-level hypothesis about ‘Labrador’ and a basic-level hypothesis about this item. Both cases should yield only a weak suspicious coincidence effect. As children add more subordinate and basic-level hypotheses into their prior knowledge, however, and distinguish these hypotheses from each other more strongly, the likelihood of showing a suspicious coincidence effect should become greater.

To date, no previous studies have examined how children’s ability to detect suspicious coincidences changes as they acquire more category knowledge. Instead, researchers either used a priori assumptions about children’s knowledge (Griffiths, Sobel, Tenenbaum, & Gopnik, 2011; Xu & Tenenbaum, 2007b; Tenenbaum, Kemp, Griffiths, & Goodman, 2011), or they used measures of adult category knowledge when simulating children’s performance with the Bayesian model (Xu & Tenenbaum, 2007a).

Thus, in the present study, our goal was to examine how developmental changes in children’s category knowledge impact the suspicious coincidence effect. Before proceeding to our empirical probes of this issue, we first turn to a detailed discussion of the Bayesian model and how this model generates the suspicious coincidence effect. We use the model to quantitatively confirm the Bayesian account’s predictions about how the suspicious coincidence effect should change over development. We then test these predictions in the remainder of the paper.

2. Modeling 1: The Bayesian model and developmental predictions

In this section, we examine how the suspicious coincidence effect should change over development according to the Bayesian model. We begin with an overview of the model, and then describe a Monte Carlo approach to simulating developmental predictions. Additional details and discussion of the Bayesian model can be found in Xu and Tenenbaum (2007a).

2.1. Overview of the Bayesian model

The heart of the Bayesian model is the set of equations that calculate Bayesian posterior probabilities for different possible meanings of novel categories, that is, the probability that a novel word like “fep” might mean “Labradors” versus “dogs” or “animals.” Posterior probability in the Bayesian model takes into account initial category knowledge (in the form of the “prior”), modifications to the prior that represent a basic level word learning bias, and the likelihood of observed exemplars, given each hypothesis. The posterior probability equation can be expressed as:

$$p(h|X)=\frac{p(X|h)p(h)}{{\sum }_{h\text{'}\in H}p(X|h\text{'})p(h\text{'})}$$

Here, h = a given hypothesis about a word's meaning that a word learner might consider and that we wish to know the posterior probability for, h’ = each of the total number of hypotheses that might be considered (contributing to the sum in the denominator), X = the set of labeled exemplar toys shown to the child at the start of a trial, and H = the space of all considered hypotheses. We discuss the factors that contribute to this equation, its inputs, and its outputs in the following sections.

2.1.1. Likelihood

Likelihood, p(X | h), is the probability of having seen the exemplars observed, given each hypothesis about word meaning. It is computed in a special way in the Bayesian model. The likelihood of any given hypothesis h is biased according to the size or extension of the hypothesis and the number of consistent examples from that hypothesis that are presented, n (in Xu and Tenenbaum’s task, n is the number of toy exemplars labeled):

$$p(X|h)={[\frac{1}{\mathit{\text{size}}(h)}]}^n$$

According to this equation, then, hypotheses with larger extensions (greater “size”), like “animal,” are weighted more weakly than hypotheses with smaller extensions, like “Labrador,” assuming that both are consistent with the data. Moreover, this difference in weighting is exponentially greater when more consistent examples are presented. Xu and Tenenbaum call this the “size principle.” This principle embodies the reasoning that if a representative sample is being seen, then it is much more statistically likely to see three Labradors in a row labeled “fep” if “fep” means “Labradors” than if “fep” means “dogs.” Every new Labrador shown to the model reinforces the narrowest hypotheses exponentially more than other hypotheses. Consequently, narrow hypotheses dominate the posterior conclusions of the model when multiple subordinate examples are presented relative to when a single example is presented. This explains the suspicious coincidence effect.

2.1.2. Prior probability

The prior, p(h), is the second factor involved in calculating a posterior probability. Xu and Tenenbaum (2007a) used a hierarchical cluster tree as the prior probability input. In a hierarchical cluster tree, every toy used in the behavioral experiment is grouped together with other toys one at a time sequentially, forming hierarchical clusters, until all toys are contained under a single overall cluster. The tree structure used by Xu and Tenenbaum (2007a) was derived from adults’ pairwise similarity judgments for the toys used in their experiments. Xu and Tenenbaum used this tree structure to model both children’s and adults’ behavior.

Each cluster in the tree represents a single, valid hypothesis that the objects in that cluster are members of a labeled category (e.g. “fep”). Some hypotheses are more probable than others, though. The prior probability of each hypothesis in the model is proportional to that hypothesis’ cluster height and the height of the next highest (parent) cluster, according to this equation:

$$p(H)\propto \mathit{\text{height}}(\mathit{\text{parent}}[h])-\mathit{\text{height}}(h)$$

The model only represents a subset of all logically possible hypotheses. That is, while there are logically over 30,000 different ways to combine 15 toys into different sets, Xu and Tenenbaum's model considers only the 12 most likely hypotheses, which are derived from adult ratings by a clustering method. In terms of a typical Bayesian model, this can be interpreted as every other hypothesis having a prior probability of zero.

2.1.3. Basic level bias

Basic level bias is an additional factor involved in calculating the prior. It is an atypical parameter in Bayesian models. Xu and Tenenbaum included this term because prior work suggests early word learners have a bias towards the basic level (Golinkoff, Mervis, & Hirsh-Pasek, 1994; Markman, 1989). The basic level bias is represented as a simple scalar value, which multiplies the prior probability for basic level hypotheses only. For animal stimuli, for example, the prior probability of the hypothesis that includes all five types of dog toys and nothing else would be multiplied by the basic level bias. Basic level bias is a free parameter in the Bayesian model, set to whatever value leads to the best match between the simulated and the behavioral data.

2.1.4. Input to the model

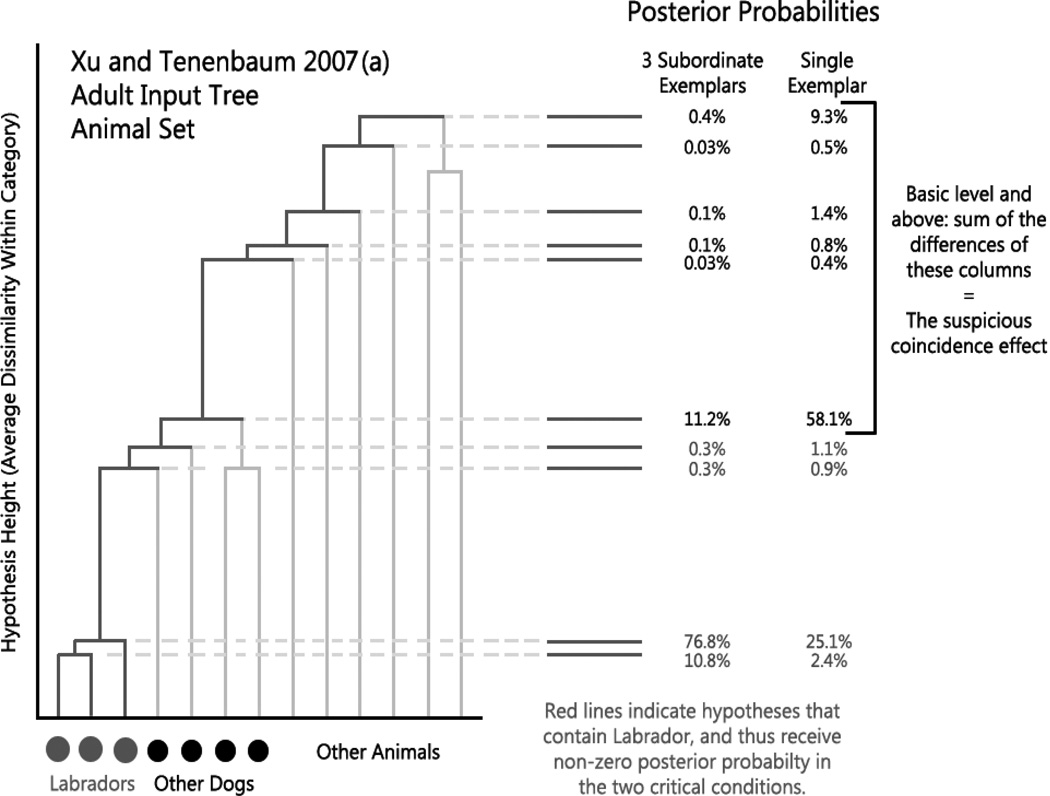
In Fig. 1, we have included a diagram showing a portion of the hierarchical similarity tree that Xu and Tenenbaum (2007a) used to estimate children’s and adults’ prior knowledge—the input to the Bayesian model. The tree is composed of clusters (horizontal lines), each of which is connected to smaller clusters or to the bottom of the diagram. Each cluster is a potential hypothesis about what a novel word might mean, and thus each represents a potentially meaningful category that the person might consider.

Figure 1.

Xu and Tenenbaum’s 2007(a) cluster tree, animal set only, is shown on the left of the figure. The identity of individual tree “leaves” (intersection points along the horizontal axis) are labeled, and hypotheses relevant to the suspicious coincidence effect are highlighted in bold gray. Posterior probabilities in the two conditions relevant to the suspicious coincidence effect are shown to the right of the figure. Please refer to the text for a more in-depth explanation.

Each intersection point on the x-axis at the bottom of the diagram represents a single unique toy in Xu and Tenenbaum’s behavioral study. The gray dots represent exactly matching items (which belong to the same subordinate-level category, like Labradors¹). The black dots represent items that match at a basic categorical level (like other breeds of dogs, terriers for example). The remaining items to the right are items that match at the superordinate categorical level, but not at a basic level (like other non-dog animals).

The height of any given hypothesis (horizontal line) represents the average dissimilarity of pairs of items within that category. Thus, very similar items will tend to be connected to each other by hypotheses low in the tree. Very dissimilar items will require traveling up through the tree to higher levels of hypotheses that connect less similar items to each other in the diagram. Both the equations for the likelihoods and priors in the Bayesian model utilize the heights in this diagram (i.e., the y-axis in Fig. 1). Note that the likelihood equation calls for the “size” of a hypothesis. Xu and Tenenbaum (2007a) approximated hypothesis size by substituting the height of each hypothesis from the tree diagram + 0.05 (to avoid dividing by zero for identical objects with zero dissimilarity).

2.1.5. Output of the model

The model outputs the probability that a participant will generalize a given label (‘fep’) applied to a set of objects (e.g., three Labradors) to other objects (e.g., a terrier) given a particular similarity tree. To explain how this gives rise to the suspicious coincidence effect, it is first important to emphasize that the suspicious coincidence effect reflects a contrast between two conditions: how people generalize the novel label to basic-level items after having seen one exemplar (one condition) versus three subordinate-level exemplars (the alternative condition) labeled. We will consider a concrete case to illustrate: assume that the participant has been shown a Labrador labeled ‘fep’ in one condition versus three Labradors each labeled ‘fep’ in the second condition. The question for the model is: how should this participant generalize ‘fep’ when shown a terrier, pug, husky, or sheepdog in each condition? The suspicious coincidence effect is derived from the model’s generalization output to these other dog breeds in each of the exemplar conditions.

The first step in generating the posterior probability is to identify which hypotheses are relevant given the labeled object(s), in this case, Labradors. In Fig. 1, we have highlighted (in bold gray on the tree itself) all the relevant hypotheses for this case. All other hypotheses are considered to have zero probability because they do not contain Labradors. Next, we can compute the posterior probability for each hypothesis for each condition. These values are shown to the right of the bold gray lines in Fig. 1 for the one example case and the three subordinate-level case. Posterior probability is affected by several variables, but the difference between the two conditions in particular is driven mostly by the “n” variable in the size principle described above. “n” is the number of exemplars shown, and it is in an exponent, so when there are three subordinate-level objects shown, the likelihood for hypotheses that contain these three items are weighted exponentially more strongly than in the one-exemplar condition.

In a concrete example, let’s assume that Labradors were used for exemplars, and we want to know whether the model will generalize the label seen with Labradors to a terrier test item. First, we calculate the posterior probabilities for all hypotheses that contain Labradors: the ones that could potentially match the novel label. Next, we sum up the posterior probabilities for all hypotheses that also contain terriers. This includes all hypotheses at the basic level and above (dogs, mammals, animals, etc.). When we sum these values up for the one exemplar condition, the model predicts a probability per trial of generalizing ‘fep’ to the terrier of 71%. When we sum these values up for the three exemplar condition, the model predicts a probability per trial of generalizing ‘fep’ to the terrier of 12%. This difference across conditions (specifically when the probability is higher in the one-exemplar condition) is the suspicious coincidence effect.²

2.2. Predictions of the Bayesian model with respect to category knowledge

Now that we have introduced the key details of the Bayesian model, we are in a position to quantify what the model predicts when a word learner’s category knowledge changes over development. Recall from our example that only the subset of hypotheses that include the exemplars as part of their extension are relevant for the suspicious coincidence effect—the hypotheses highlighted in bold gray in Fig. 1. All other hypotheses such as “birds” would be assigned zero posterior probability if the exemplar was, for instance, a Labrador. Thus, for any given novel word generalization trial in the suspicious coincidence task, the input to the Bayesian model is simply a one-dimensional list of hypotheses that differ in relative heights.

To investigate how the suspicious coincidence effect should change over development, we performed a Monte Carlo simulation of the suspicious coincidence effect across 1000 simulated children. For each simulated child, we first generated 10 random numbers between zero and one, representing the final hierarchical cluster tree for that child at the end of “development” when the child had acquired all 10 hypotheses shown in Fig 1 (clusters in the simulated tree). We then input the list of numbers into the Bayesian model, and allowed it to calculate posterior probabilities for the one exemplar condition and the three-subordinate exemplars condition. Then, we removed one hypothesis at random from the list, going backward in developmental time (when the simulated participant knew fewer categories), and calculated the posterior probabilities again for each condition, and so on until the list was empty.

Next, we calculated the suspicious coincidence effect at each developmental step as the probability of generalizing to basic-level test items in the one-exemplar minus the three-subordinate-exemplars conditions. To determine the probability of generalizing to basic-level test items, we simply added up the combined posterior probability of all hypotheses 5–10 (the same number of hypotheses at the top of the list that were “basic level” or higher in Xu & Tenenbaum’s similarity data) for any hypotheses that happen to exist at a given step in developmental time. These are the categories for which the exemplars (e.g. Labradors) and their basic-level-only test items (e.g. terriers) would overlap.

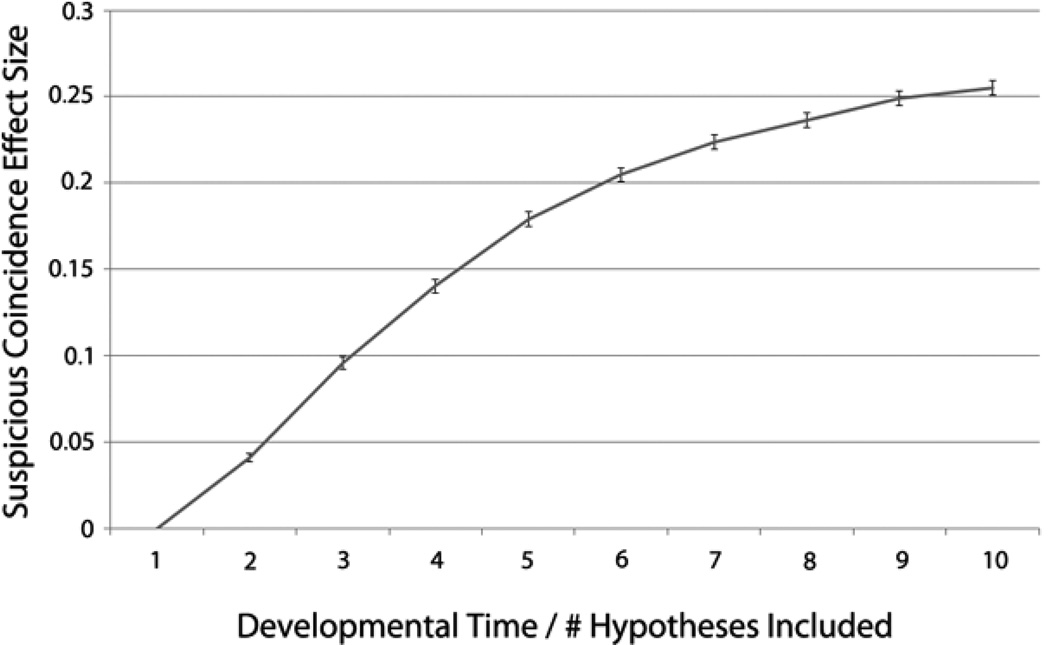
The average suspicious coincidence effects for 1,000 simulated children at each developmental step are shown in Fig. 2. As the number of known categories increases (X-axis), the magnitude of the suspicious coincidence effect also steadily increases. Thus, the model predicts a gradually strengthening suspicious coincidence effect over developmental time as children acquire more category knowledge. Note that the type of category knowledge that matters most for the suspicious coincidence effect is subordinate-level and basic-level category knowledge. Posterior probability tends to “pool” in the narrower hypotheses due to the size principle in the three-exemplar condition, and the basic-level bias draws a larger share of posterior probability in the one-exemplar condition. Thus, it is important to have both narrow hypotheses and basic-level hypotheses to create the strongest contrast between conditions for a robust suspicious coincidence effect. Not possessing these hypotheses will weaken or eliminate the effect.

Figure 2.

The Bayesian model’s output of suspicious coincidence effect size is shown here as a function of how many of ten total hypotheses were inputted to the model on a given simulation run. Number of hypotheses abstractly represents developmental time, since children would acquire more hypotheses as they develop. The suspicious coincidence gets gradually stronger as overall number of hypotheses known increases, almost asymptoting near full, adult-like knowledge (as defined by Xu and Tenenbaum’s 2007a cluster trees).

In the next sections, we empirically test these predictions of the Bayesian model. In particular, we gathered information about children's knowledge of the exact categories used in Xu and Tenenbaum's (2007a) experiment. According to the Bayesian model, children with greater category knowledge—particularly knowledge at the basic and subordinate levels—should show a stronger suspicious coincidence effect than children with less category knowledge.

3. Experiment 1

Our first experiment was an exact replication of Xu and Tenenbaum's (2007a) Experiment 3, which was designed to investigate whether children show the suspicious coincidence effect. Our only modification to the procedure reported by Xu and Tenenbaum was that parents of participants completed an additional questionnaire during the experiment that was designed to measure children’s prior category knowledge. This survey was a critical addition, allowing us to determine whether children with more category knowledge do, in fact, show a stronger suspicious coincidence effect as predicted by the Bayesian model.

3.1. Materials and methods

3.1.1. Participants

Fifty-four monolingual children from a Midwestern town, who were between the ages of 42 and 60 months (M = 51.7), participated. Thirteen participants were excluded from analysis: seven for generalizing to at least one distractor item from the incorrect superordinate category³, one for fussiness, two due to experimenter error, and three for not following instructions. Therefore, 41 participants were included in analyses (M age = 4 years, 3 months; range 3 years, 6 months to 5 years, 0 months). This is a slightly older sample overall than the sample studied by Xu and Tenenbaum (M age = 4 years, 0 months) but covers the same age range of Xu and Tenenbaum’s sample. Each participant was randomly assigned to one of two experimental conditions: a three-subordinate-exemplars condition (N = 20) or a one-exemplar condition (N = 21). Parents of participants were contacted for recruitment via mail and a follow-up phone call and provided informed consent for the study. Each participant received a small toy for participating.

3.1.2. Materials

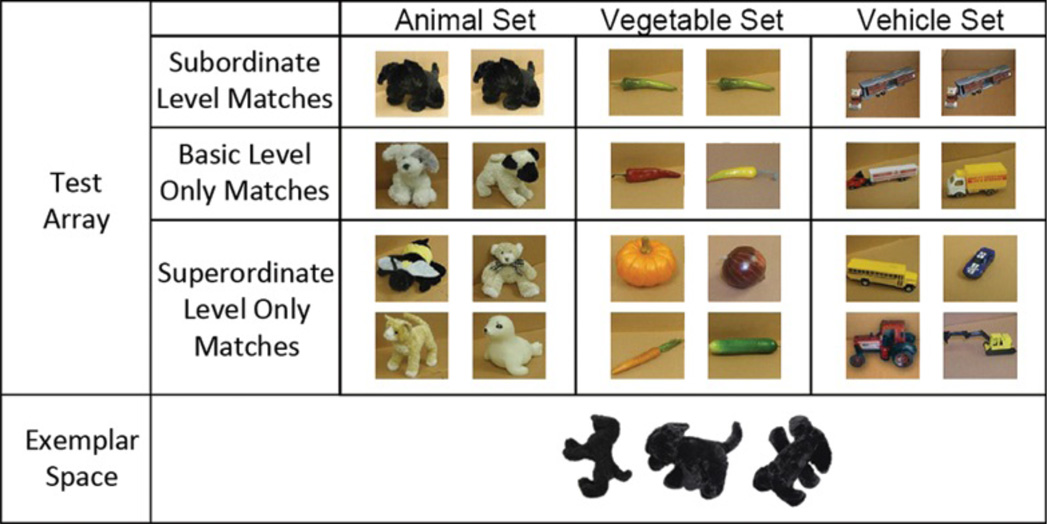
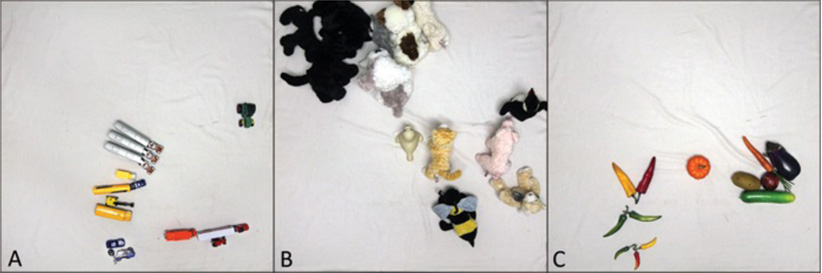
The stimulus set was chosen based on the stimuli used by Xu and Tenenbaum (2007a). The 45 total toys were divided into three superordinate categories (referred to as “sets”): 15 animals, 15 vehicles, and 15 vegetables. Each set was then further divided into six superordinate-level-only matches, which were toys that all belonged to the same superordinate set but came from different basic level categories (e.g., different species of animals, see Fig. 3), four basic-level-only matches, which were toys from the same basic level category, but different subordinate level categories (e.g., various breeds of dog), and five subordinate-level matches, which were toys from the exact same subordinate level category (e.g., all the same breed of dog). For example, the category structure of the 15 animals was as follows: six superordinate-level-only matches (penguin, pig, cat, bear, seal, bee), four basic-level-only matches (husky, sheepdog, pug, terrier), and 5 subordinate-level matches (5 instances of Labradors). Seven toys from each set (three subordinate-level matches, two basic-level-only matches, and two superordinate-level-only matches) were reserved as possible exemplars used for novel labeling events. Three of these seven—the three subordinate-level matches—were central to the conditions discussed in this paper. The rest are relevant to additional conditions which we ran to fully replicate Xu and Tenenbaum’s procedure. We discuss these additional conditions in the Appendix. The remaining eight toys per set not reserved as exemplars were placed in a test array that encompassed all three sets to probe children’s generalization of the familiarized novel words. All the test items are shown in Fig. 3.

Figure 3.

An overhead layout of Experiments 1–3 as seen by children. Children were seated above the top edge of this figure, and experimenters below the bottom edge. Shown is a three-exemplar trial, with three nearly exactly matching subordinate level Black Labrador toys lined up in the exemplar space and labeled once each (Experiments 1 and 2) or multiple times each (Experiment 3). In one-exemplar trials, there would be one Black Labrador in the exemplar space instead, labeled three times (Experiments 1 and 2) or multiple times (Experiment 3). In Experiment 2, the three-exemplar subordinate trial included slightly modified stimuli (a random two of the three exemplars shown had ribbons added). The test array was the same for all children in all conditions, and included all of the toys shown here. During actual trials, the order of test items was scrambled.

A prior category knowledge survey was developed to quantify children’s existing knowledge of the stimuli used in the task. The survey was filled out by parents during the study and included an entry for each unique type of toy used in the experiment across all conditions. There were a total of 45 physical toys used in the experiment divided into three sets (animals, vehicles, vegetables) with 15 toys each (five “target” objects like Labrador, four basic-level matches, and six superordinate-level matches). There were, however, only 30 unique types of toys represented on the survey. For each set we only included one of the five identical matching “target” toys (−12 unique objects). Likewise, Xu and Tenenbaum (2007a) re-used the same red and yellow peppers as both exemplar objects and test objects but we eliminated this duplication on the survey (−2 unique objects). Finally, Xu and Tenenbaum also used two tractors which shared the same category label; thus, we only counted one on the survey (−1 unique object). In total, then, the survey asked each parent to tell us about each participant’s existing knowledge of the 30 unique types of toys used in the task.

Each entry of the survey included a photograph of a toy, a free-response prompt, and yes/no checkboxes next to labels for each hierarchical adult category that would apply to that toy (e.g., a Labrador would have three checkboxes for “animal,” “dog,” and “Labrador”). Parents were verbally instructed to write the word which children would spontaneously use to label each object on the free response line, and to mark the checkboxes if children would recognize that the pictured object was a member of the named category. Although we were interested in asking parents to report each participant’s basic- and subordinate-level knowledge for each item—since knowledge at these category levels is central to the suspicious coincidence—some of the items had no clear subordinate-level label we could include on the survey. For example, the pig toy was merely a generic pig, not clearly any particular breed or variety like a “Yorkshire pig,” nor was the eggplant any obviously nameable variety of eggplant. In total, the survey contained examples / checkboxes for all three category levels (superordinate, basic, subordinate) for 13 unique items (Labrador, sheepdog, pug, terrier, husky, green pepper, yellow pepper, red pepper, livestock semi, delivery truck, fire department semi, fuel semi, garbage truck), and only superordinate and basic-level examples / checkboxes for the remaining 17 unique items (pig, seal, penguin, cat, teddy bear, bee, cucumber, onion, pumpkin, carrot, eggplant, potato, tractor, digger, school bus, car, motorcycle).

The most important data for our purposes was the narrowest level category that each parent checked for each item. Recall that posterior probability in the Bayesian model tends to “pool” in the narrower hypotheses due to the size principle. Thus, it is particularly important to have narrow, subordinate-level hypotheses that contrast with broader, basic-level hypotheses to generate robust suspicious coincidence effects. To quantify the narrowness of children’s category knowledge, therefore, we added up the total number of times that each parent checked the narrowest category level available for each item into a “category score.” The maximum category score was 30 (since there were 30 unique items on the survey). A child receiving a high category score was rated by the parent as knowing many subordinate-level categories (for the 13 items with clear subordinate-level labels) and many basic-level categories (for the remaining 17 items).

3.1.3. Procedure

Every child participated in either a one exemplar condition or a three exemplars condition⁴. In both conditions, the testing session was divided into three trials, each with a familiarization phase followed by a test (generalization) phase. Each trial consisted of presenting exemplars and asking test questions about one of the unique sets of toys used—animals, vegetables, or vehicles. The child and experimenter sat on the floor of the experiment room. The test array and a space for familiarization exemplars were laid out in the middle of the room between them, with the exemplar space nearest the experimenter. The test array was laid out on a 36 by 24 inch faux leather mat, and the exemplars on a 36 by 6 inch mat. All toys were spread out evenly, about 6 inches apart. Any distractions around the room were covered with beige curtains suspended from the ceiling. A camera was positioned behind the left shoulder of the experimenter, providing a view of all the test items and of the participant. The parent sat quietly in a chair behind the child.

During the familiarization phase of the one-exemplar condition, the experimenter pulled out one subordinate-level match toy, placed it on the exemplar mat, and labeled it three times in a row. In the three-subordinate-exemplars condition, the experimenter pulled out three subordinate-level match toys (e.g., three Labradors) and labeled each once. The positions and labeling order of the three toys were randomly chosen for each trial. Novel labels such as “fep,” were used in both conditions (see Xu and Tenenbaum, 2007a). Participants in both conditions heard three object-word pairings per set overall.

The experimenter used a stuffed frog named “Mr. Frog” as an intermediary for interacting with the child. The novel labels used were described as part of “Mr. Frog’s language,” and the children were “helping Mr. Frog” to find toys that were like the toys that he told them the words for. This was replicated from Xu and Tenenbaum’s (2007a) original procedure, and a detailed description of the dialogue used with regard to Mr. Frog can be found there (see p. 256).

During the test phase, the experimenter selected one of the test objects from the test array, held it up and said “Is this a fep?” Following the child’s yes/no response, this was repeated for a total of 10 items in the test array. The items probed always included two subordinate-level matches, two basic-level only matches, four superordinate-level only matches, and any two distractors from the other two sets of toys (randomly chosen to test for a “yes” bias).The order of the 10 items in each trial was randomly chosen before the experiment.

While we replicated the details of Experiment 1 as closely as possible, there were a few minor differences compared to Xu and Tenenbaum’s study (2007a). First, a handful of the specific stimuli used differed slightly from Xu and Tenenbaum’s study (we substituted, for instance, a fuel tanker semi-trailer for a dry goods semi-trailer, due to the availability of toys). Second, we do not know whether Xu and Tenenbaum performed their task on the floor like us, or on a low table, nor whether our toy spacing was the same as theirs. These details were not available in their paper, but are not be theoretically important in current accounts.

3.2. Results

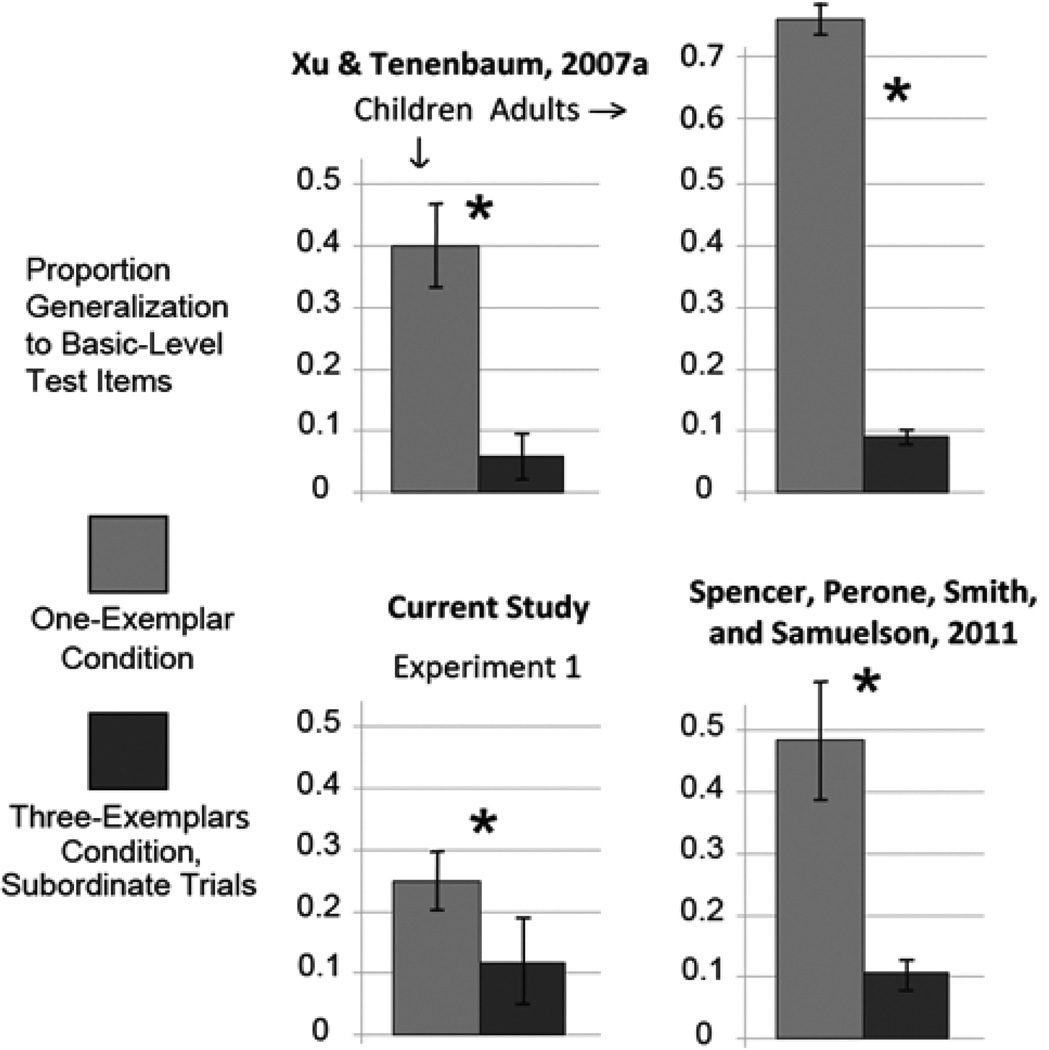
In Xu and Tenenbaum’s task which we replicated here, evidence of the suspicious coincidence effect would be less frequent generalization of a novel label to basic level test items when children are shown three subordinate-level exemplars compared to when they are shown a single exemplar. As can be seen in Fig. 4, we replicated Xu and Tenenbaum’s finding of narrower basic-level novel label generalization overall, following labeling of three identical instances of a category compared to labeling of one, t(39) = 1.72, p < 0.05, although the size of this effect was smaller than in Xu and Tenenbaum’s study (the difference in number of trials with generalization across conditions was 2.83 times smaller in our study than Xu and Tenenbaum’s difference across conditions). The smaller magnitude of this effect is consistent with other reports showing that the suspicious coincidence effect is statistically robust, but varies in magnitude (see, e.g., the replication with adults reported by Spencer, Perone, Smith & Samuelson, 2011).

Figure 4.

Children in Experiment 1 (right panel) replicated the suspicious coincidence effect found by Xu and Tenenbaum 2007, left panel). Children in the one-exemplar condition generalized our novel label to basic level hierarchy matches (e.g., other breeds of dog when shown a Black Labrador) significantly more often than children in three-exemplar condition did (during subordinate trials).

We next examined the relation between children’s prior category knowledge and generalization performance. Recall that the maximum possible category score (“CS”) was 30, but no child received this (M = 16.83, median = 16, range = 12 to 23). An initial analysis showed that the results of our category knowledge survey were not correlated with age (r = −0.04, ns). A median split on CS was thus used to divide children into “low-CS” (n = 21) and “high-CS” (n = 20) groups. Based on our analysis of the Bayesian model, we expected that high-CS children would show a stronger suspicious coincidence effect than low-CS children.

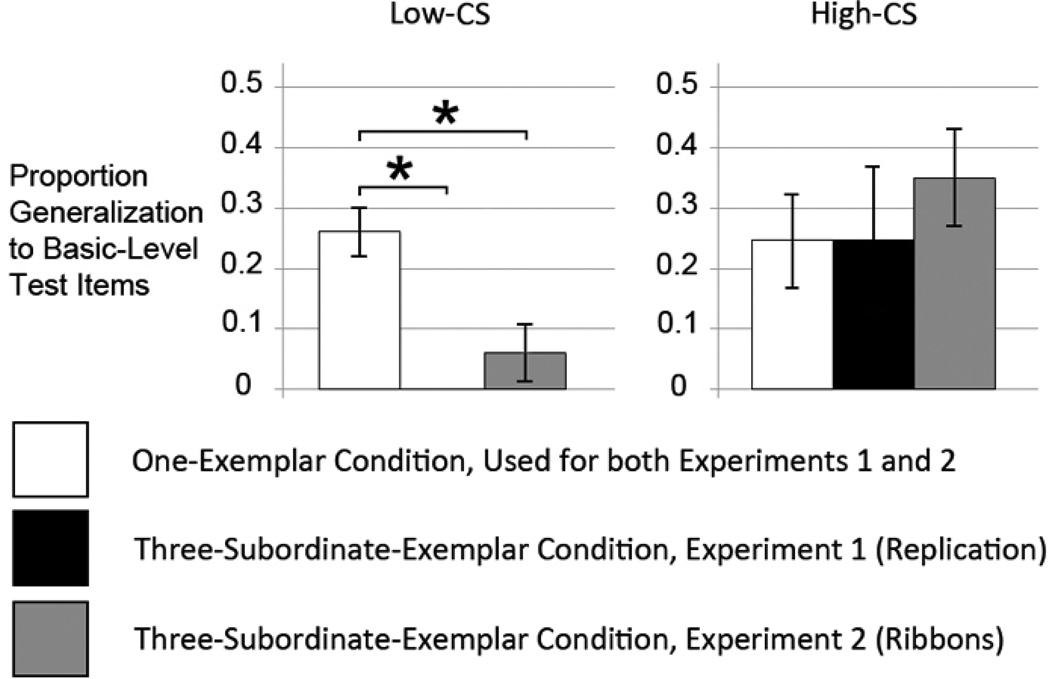
The noun generalization performance for the high and low-CS groups is presented in Fig. 5. As can be seen in the figure, there was a dramatic difference in the generalization patterns of children in the two groups. The low-CS children showed a significant drop in basic-level generalization from the one-exemplar condition (26% generalization) to the three-subordinateexemplars condition (0% generalization), demonstrating a strong suspicious coincidence effect, t(19) = 5.21, p < 0.0001, Cohen’s d = 2.73. By contrast, the high-CS children showed no difference in generalization to basic-level test objects across the one-exemplar and three-subordinate-exemplars conditions.

Figure 5.

After performing a median split on CS from Experiment 1, we can see that the low-CS children are driving the entire suspicious coincidence effect previously seen in the overall data (white versus black bars). With the addition of ribbons to exemplars in Experiment 2, the same pattern is seen – low-CS children show a suspicious coincidence effect, but high-CS children show no effect, if anything trending in the opposite direction (white versus gray bars).

3.3. Discussion

The goal of Experiment 1 was to examine whether children with more subordinate- and basic-level category knowledge would show a stronger suspicious coincidence effect than children with less category knowledge, as predicted by the Bayesian model. Our data replicated Xu and Tenenbaum’s (2007a) findings at the overall group level—we found a statistically robust suspicious coincidence effect across all participants. Nevertheless, when prior category knowledge was factored in, we observed a different developmental pattern than what was predicted by the Bayesian model: The suspicious coincidence effect was inversely related to children's prior category knowledge. That is, low-CS children showed a strong suspicious coincidence effect, while high-CS children showed no effect. These results were unexpectedly the opposite of the pattern predicted by the Bayesian model over development. Our findings suggest an apparent U-shaped developmental trend in the suspicious coincidence effect—the suspicious coincidence effect is evident early in development when children have less category knowledge, it weakens as they acquire more category knowledge, and it returns again later in adulthood (see, e.g., Xu & Tenenbaum, 2007a). Given the unexpected nature of our findings, we asked whether these results would replicate in a second sample. Experiment 2 probes this issue.

4. Experiment 2

To notice suspicious coincidences, children must notice that each named exemplar is a unique instance of an item within the same subordinate-level category. In our experiment, as in Xu and Tenenbaum’s (2007a), the subordinate-level exemplars in a trial were presented to the child in clear view. This should encourage children in the three exemplar condition to treat each object as a unique instance. It is possible, however, that the subordinate exemplars we used were too similar to one another and that some children failed to distinguish them as unique instances. Thus, in Experiment 2, we added distinctive ribbons to two of the three subordinate exemplars in the three-subordinate-exemplars condition, ensuring that each instance of the subordinate-level category was unique. This experiment also served as a replication of the key data from Experiment 1, to probe whether the unexpected finding of a U-shaped developmental trend in the three-subordinate-examples condition was robust in a second sample of children.

4.1. Materials and methods

4.1.1. Participants

Twenty seven participants aged 45–57 months (M = 49.6) were recruited in the same manner as in Experiment 1. Four participants total were excluded from analysis: one was excluded for choosing at least one distractor item, and three were excluded for experimenter error. All of the remaining 23 participants were run in a three-subordinate-exemplars condition. We compared children’s performance to the one-exemplar condition from Experiment 1 (n = 21). The total number of children across experiments being compared was therefore 44, of which the low- and high-CS splits across experiments contribute 22 children each.

4.1.2. Materials

The same category survey, toys, familiarization set, and test set organization from Experiment 1 were used, with the exception that “ribbons” (colored electrician's tape) were attached to two of the exemplars in the three-subordinate-exemplars condition. Positions and labeling order of the two toys with ribbons were randomly chosen.

4.1.3. Procedure

All procedural details were identical to Experiment 1.

4.2. Results and discussion

Category scores were similar to those in Experiment 1 (M = 16.96, median = 17, range = 13 to 22). Overall, there was not a robust suspicious coincidence effect, t(42) = 0.56, ns. Nevertheless, Experiment 2 did replicate the high- and low-CS results of Experiment 1 (see Fig. 5). The suspicious coincidence effect was robust among low-CS children, with a significant drop in basic level generalization from the one-exemplar condition in Experiment 1 (26%) to the three-subordinate-exemplars condition here (6%), t(20) = 4.11, p < 0.01, Cohen’s d = 1.83. High- CS children, by contrast, showed no significant effect, and in fact an opposite trend, increasing from their basic level generalization in the one exemplar condition of Experiment 1 (25%) to the three-subordinate-exemplars condition here (35%), t(20) = 0.93, ns. Thus, as in Experiment 1, only low-CS children showed the suspicious coincidence effect. Note that the broader generalization at the basic level for the high-CS children in the three-subordinate-exemplars condition explains why we did not replicate the suspicious coincidence effect overall.

To further examine the CS result with increased statistical power, we pooled the data from Experiments 1–2 and ran mixed model regressions with CS treated as a continuous variable rather than a binary one (as was the case with the median split). Specifically, we conducted a pair of mixed effects logistic regressions, with category score as an independent variable and generalization responses as a fixed-effect dependent variable. Generalization responses were summed for each child on every basic level test trial—the trials relevant to the suspicious coincidence effect. Both regressions included subject and set type (animal/vehicle/vegetable) as random effects.

In the first regression, category score was scored holistically. That is, for every trial, the data point for the dependent variable was the child’s overall category score across all set types. Holistic category score showed a significant fit to basic level generalization behavior, consistent with our median split findings: higher category scores were associated with weaker suspicious coincidence effects (see Table 1).

Table 1.

Mixed Model Logistic Regression with "Holistic" CS

AIC	BIC	Log Likelihood	Deviance
135	146.8	−63.51	127

Fixed Effects	Estimate	Std. Error	z Value	p(>|z|)
Intercept	−8	2.15	−3.72	0.0002
CS, Holistic	0.34	0.11	3.22	0.0013

In the second regression, we examined the effect of more specific, “matched” category knowledge on the detection of suspicious coincidences. We computed a category score for each superordinate category set separately (animal/vehicle/vegetable) and matched this to the specific noun generalization trials children completed. For example, if Mr. Frog was labeling various breeds of dogs as “feps” on a given trial, we only considered the animal portion of the participant’s category score as a dependent variable for that trial. Matched category score also led to a significant model fit (see Table 2). Indeed, the matched logistic regression model yielded a better fit than the holistic model, although not significantly so (see Burnham and Anderson, 2002 regarding AIC-based model comparisons).

Table 2.

Mixed Model Logistic Regression with "Matched" CS

AIC	BIC	Log Likelihood	Deviance
133.3	145.1	−62.7	125.3

Fixed Effects	Estimate	Std. Error	z Value	p(>|z|)
Intercept	−4.82	1.11	−4.33	0.000015
CS, Holistic	5.05	1.45	3.48	0.00051

Both regression analyses support the results of our median split analyses: children with more relevant category knowledge (i.e., higher-CS children) do not generalize novel labels narrowly when presented with three subordinate-level exemplars. This runs counter to the predictions of the Bayesian model.

5. Modeling 2: Checking the validity of the category score and reparameterizing the Bayesian model

Given that data from Experiments 1 and 2 were not consistent with predictions of the Bayesian model, we conducted additional simulations in an attempt to understand why. The first issue we probed is whether the category score we used truly captured the category knowledge relevant to the suspicious coincidence effect in the model. To probe this, we asked whether models given input matching the knowledge of high-CS children would show a stronger suspicious coincidence effect than models given input matching the knowledge of low-CS children. If so, this would be consistent with the predictions we simulated in Modeling 1. The second question we asked in this section is whether the Bayesian model could capture the Ushaped pattern from Experiments 1 and 2 if the model were reparameterized.

5.1. Category score validity check

First, we scrutinized the predictive validity of our category score in greater detail. To do this, we used the Bayesian model to simulate the performance of actual children with lower and higher category scores. The question: does the model predict that high-CS children should have a stronger suspicious coincidence effect than low-CS children? If so, this would give us more confidence that the category score is a measure directly relevant to the suspicious coincidence effect.

Instead of running Monte Carlo simulations with randomized hypothesis heights over development as in Modeling 1, we gave the Bayesian model a representation of the actual categories parents reported children knew on the CS surveys from Experiment 1. The goal was to construct priors that reflected the knowledge of each child. To construct a cluster tree specific to each child, we started with the adult cluster tree used by Xu and Tenenbaum (2007a). It was necessary to first regularize the subordinate-level clusters across, for instance, dogs because in Xu and Tenenbaum’s pairwise similarity task, adults rated multiple instances of the subordinate-level dog exemplar (e.g., Labradors), but only one instance of the other dogs (e.g., terrier). Thus, the cluster trees had subordinate-level hypotheses for one type of dog, but none for the other dogs (and likewise for the vegetables and vehicles). To regularize this, we created one subordinate-level hypothesis for each type of dog (and pepper and truck) and assigned this a height of 0.05 (the default height of exactly matching stimuli in Xu and Tenenbaum’s tree).

Next, we created a cluster tree for each individual child. Recall that the parent questionnaire asked whether each child knew the subordinate-level category label for 13 items (Labrador, sheepdog, pug, terrier, husky, green pepper, yellow pepper, red pepper, livestock semi, delivery truck, fire department semi, fuel semi, garbage truck), and basic-level category labels for the remaining 17 items. From these data, we calculated a subordinate-level score for each superordinate category: how many subordinate-level dog categories did the child know, how many subordinate-level pepper categories did the child know, and how many subordinate-level truck categories did the child know. We also calculated a basic-level score for each superordinate category (e.g., how many non-dog basic-level animal categories did the child know). To create a cluster tree for each child and each superordinate type (animal, vegetable, vehicle), we then took the subordinate-level score for the child and randomly selected that number of subordinate-level dog categories from the regularized Xu and Tenenbaum trees. Similarly, we took the basic-level score and randomly selected that number of basic-level animal categories. In the final step, we pruned away any unselected hypotheses and fixed any broken lines in the cluster tree due to this pruning. For instance, if “terrier” was not selected as a “known” category, then we had to remove the terrier “leaf” and the lowest hypothesis that contained terriers in the cluster tree. In some cases, the lowest hypothesis might have contained another item (e.g., ‘pug’). In this case, we would connect the remaining exemplar (‘pug’) directly to the next-higher hypothesis in the tree.

The result of this process was 41 unique cluster trees, one for each child in Experiment 1. Note that in the process of creating these trees, we decided to not examine the vegetable set further. There were only 3 unique subordinate-level exemplars in this set (red pepper, yellow pepper, and green pepper). Critically, all three were the same species of pepper (the toys were from the same mold with different colored plastic) and, consequently, parents typically checked all the peppers or none. Thus, the pepper set contributed little useful variance in the simulations.

We then simulated the Bayesian model as in Modeling section 1 (basic level bias = 1; see child simulations in Xu & Tenenbaum, 2007a) to compute the magnitude of the suspicious coincidence effect for these 41 simulated “children” for the animal set (with Labrador as the subordinate-level exemplar) and the vehicle set (with livestock semi as the subordinate-level exemplar). This yielded two category scores per child from the parent questionnaire (animal, vehicle) and two suspicious coincidence scores per child (animal, vehicle). We then repeated this process 4 more times for each set, using each dog as the subordinate-level exemplar once (e.g., replacing Labrador with terrier as the exemplar shown once or three times) and using each truck as the subordinate-level exemplar once (e.g., replacing livestock semi with garbage truck). This essentially ran the Bayesian model through every possible variant of the suspicious coincidence experiment. In total, we ran 10 simulations per “child”, yielding 10 suspicious coincidence scores, 5 for each set (animal, vehicle).

Finally, we iterated this entire process ten times (4100 total simulations) to ensure that the cluster tree generated for each child was representative of that child’s category score and was not biased by the particular categories randomly selected at each level as “known”. Table 3 shows results from these 10 iterations. To analyze the simulation data from each iteration, we correlated the category scores with the suspicious coincidence scores. As can be seen in the table, every iteration yielded a strong correlation between category scores and the magnitude of the suspicious coincidence effect, with a mean correlation coefficient of 0.82 (SD = 0.01). Thus, the model strongly predicts that children with greater relevant category knowledge as measured by the category score should show a greater suspicious coincidence effect. This runs counter to data from Experiments 1 and 2.

Table 3.

Correlation Coefficients Between Child Category Scores and Matched, Simulated Suspicious Coincidence Effect Sizes

Simulation	Correlation
1	0.8
2	0.83
3	0.8
4	0.8
5	0.83
6	0.82
7	0.81
8	0.83
9	0.83
10	0.82
Mean	0.82
Standard Dev.	0.01

5.2. Reparameterization test

We next attempted to reparameterize the Bayesian model to simulate data from Experiments 1 and 2. The question was whether we could change some aspect of the model to reproduce the U-shaped trend observed empirically. There are two readily apparent ways one might modify the Bayesian model: (1) The basic level bias parameter can be adjusted, and (2) different prior probabilities can be used for low- vs. high-CS children. Since altering the model's priors would require new behavioral data to estimate children’s perception of object similarity, we first attempted to match behavioral results from Experiments 1 and 2 by modifying only the basic level bias parameter. In particular, we considered basic level bias to be a free parameter that could be changed independently for each of the two levels of CS. We ran simulations with every possible combination of basic level bias values within a range from 1–10.⁵

5.2.1. Analysis

We compared the output from each simulation to the low- and high-CS results for Experiments 1–2, focusing on the data most central to the suspicious coincidence effect— basic-level responding in the one-exemplar and three-subordinate-exemplars conditions. To quantify the fit of the model, we focused on the relative difference between these conditions. In particular, we calculated the effect size of the suspicious coincidence effect as the difference between basic-level rate of responding in the one-exemplar condition and basic level rate of responding in the three-subordinate-exemplars condition (the same measure of the suspicious coincidence effect in earlier modeling). For example, if generalization was 50% in the single-exemplar condition and 40% in the three-subordinate-exemplars condition, the suspicious coincidence score would be: 0.5 – 0.4 = 0.1 (expressed as a decimal to emphasize that this is an absolute numerical difference, not a ratio). We report the suspicious coincidence score for both the experimental data and for the model. In the latter case, this was based on the posterior probability outputs of each simulation—specifically, the sum of posteriors for basic level and higher hypotheses across the two relevant experimental conditions (the same as in previous modeling sections above).

The suspicious coincidence score from each simulation was compared to all four suspicious coincidence scores from our behavioral experiments (low- and high-CS groups in each of two experiments). The final quantitative measure of model fit—called the model “inaccuracy score”—was defined as the absolute value of the difference between the behavioral suspicious coincidence scores and the simulated suspicious coincidence scores. Essentially, this is a measure of how closely the model captured the strength and direction of the suspicious coincidence effect. For example, if children showed a suspicious coincidence score of −0.1 (e.g., one-exemplar condition basic generalization of 20% and three-subordinate-exemplars condition basic generalization of 30%), and the model showed a suspicious coincidence score of 0.3, the model inaccuracy score would be 0.4 (absolute value of −0.1 – 0.3). Higher inaccuracy scores reflect poorer model performance. For every set of behavioral data, we report the results of the best fitting model. That is, we report the model with parameters that result in the lowest inaccuracy score compared to that set of behavioral data. We also report the mean inaccuracy score for the full range of parameters examined.

To provide a context for the inaccuracy scores, we also calculated inaccuracy scores for a random/baseline model: a model that randomly guesses a suspicious coincidence score off of a number line, without any theoretical basis. suspicious coincidence scores can range from −1 to +1, so with an accuracy of two decimal places, a truly random model would eventually choose amongst the 201 possible suspicious coincidence scores with an equal, flat probability. Thus, we simulated a random model by beginning with a flat distribution. We generated all possible suspicious coincidence scores (to two decimals) exactly once and compared each one to the four behavioral suspicious coincidence scores from Experiments 1–2. The resulting average inaccuracy scores serve as a baseline of comparison for the Bayesian model’s performance.

5.2.2. Results and discussion

The best and average fits of the model to each set of behavioral data are shown in the left columns of Table 4. The fits of the random model are shown in the right column of Table 4. As can be seen in the table, the Bayesian model did not capture our data sufficiently, even when looking only at the best fits and with generous assumptions (i.e., reinterpreting basic level bias to be two separate free parameters, one for each CS group). The Bayesian model is only somewhat more accurate at capturing our behavioral results overall than the random model: the Bayesian model accumulates a 0.39 inaccuracy score on average versus the random model's 0.51 inaccuracy score.

Table 4.

Inaccuracy Scores from Modeling Section 1

Experiment	Behavior to match	Inaccuracy score of model (best fit)	Inaccuracy score of model (average fit)	Inaccuracy score random chance (Average fit)
1a	Replication Low-CS	0.18	0.22	0.53
1b	Replication High-CS	0.44	0.48	0.50
2a	Ribbons Low-CS	0.28	0.32	0.51
2b	Ribbons High-CS	0.50	0.54	0.50
	Total	0.35	0.39	0.51

Note.

^aBehavior trended in direction of suspicious coincidence effect

^bBehavior trended opposite from suspicious coincidence effect.

Interestingly, the Bayesian model’s success correlates well with whether the participants being modeled showed a suspicious coincidence effect (see Table 4). The model’s output fit behavior well in conditions where children behaviorally showed a suspicious coincidence effect (indicated by the “a” superscript in Table 4). In the other conditions (indicated by the “b” superscript in Table 4), the model fared poorly. This indicates that while the Bayesian model is sufficient to explain the basic underlying suspicious coincidence effect, varying basic level bias alone fails to explain why the suspicious coincidence effect disappears in high-CS children.

5.3. Discussion

In summary, our simulations using the Bayesian model thus far demonstrate that the model predicts a stronger suspicious coincidence effect over development in both Monte Carlo simulations and simulations using our category score. This pattern is not consistent with children’s behavior in Experiments 1 and 2. Our simulations also show that basic level bias changes are insufficient to close this gap between the Bayesian model and children’s behavior.

Two other possibilities remain. First, the model might be able to capture our data with different priors. We examine this issue in the following two sections. The second possibility, which we explore in the General Discussion, is that the Bayesian model alone is not sufficient to explain our findings.

6. Experiment 3

It is possible that the inability of the Bayesian model to capture the full range of results from Experiments 1 and 2 primarily reflects the use of adult similarity ratings to choose the hypotheses and priors for modeling child behavior. Perhaps with child-generated priors, the model would capture children's behavior more accurately. Thus, in Experiment 3, we collected similarity data from children to use as prior category input to the model.

To obtain an estimate of children’s priors directly comparable to the data used by Xu and Tenenbaum (2007a), children would need to rate the similarity of every pair of toys used in our experiments. Such data could then be used to form a hierarchical cluster tree. Unfortunately, 3.5- to 5-year-old children will not tolerate making the dozens of standard, pairwise similarity judgments per set needed to form the cluster tree.

Thus, in the present experiment, we used the spatial arrangement method (SpAM) developed by Perry, Cook and Samuelson (2013) that provides similarity judgments for an entire set of stimuli on each trial. This task was derived from original work with adults by Goldstone (1994), where adults were asked to move pictures around on a computer monitor such that similar objects were close together and dissimilar objects were placed far apart. Goldstone found that similarity judgments in this task—the measured pairwise distances between objects— aligned well with more traditional similarity measures (pairwise comparison ratings, sorting objects into distinct groups, and confusability of objects). This is consistent with recent studies that have used the placement task due to its efficiency at measuring the similarity of large sets and its reliability with other measures of similarity (Hout, Goldinger, & Ferguson, 2012; Kriegeskorte, 2012; Perry, Cook, & Samuelson, 2013). Goldstone also noted that the task was particularly well-suited for measuring conceptual similarity, almost to the point of showing a conceptual bias amongst adults. Since we are interested in hierarchically-nested category structures, this strength is a desirable one. Note also that the object placement task is similar to spatial memory tasks which have shown that both adults’ and school-age children’s spatial placements are strongly influenced by conceptual categories (Hund & Plumert, 2003; Recker & Plumert, 2008).

6.1. Materials and methods

6.1.1. Participants

Forty-four participants were recruited in the same manner as in Experiment 1. Participants were between the ages of 41.6 and 57.8 months (M = 49.9) for the “regular stimuli” condition, which utilized the stimuli from Experiment 1. Participants were aged between 42.5 and 57.5 months (M = 49.7) for the “ribbons stimuli” condition, which utilized the stimuli from Experiment 2. Data from five participants were excluded from analysis: one for fussiness, and four for experimenter error. Parents provided informed consent prior to the study. Each participant received a small toy for participation.

6.1.2. Stimuli

Participants in the regular stimuli condition judged the similarity of all the toys from Experiment 1, with the exception that only three of the exact match subordinate-level test objects were used (instead of five) to simplify the number of objects children had to compare. Participants in the ribbons stimuli condition judged the similarity of the stimuli used in Experiment 2. This set was identical to the regular stimulus set, except ribbons were attached to two of the subordinate level toys. A second set of toys, not used in earlier experiments, was used to familiarize the children with the similarity procedure. These were of the same general size and the same level of familiarity to children as those in Xu and Tenenbaum's (2007a) task. Fig. 6 provides images of these stimuli, shown in the order they were presented during the familiarization procedure. The first group of familiarization toys included two identical red apples, one green apple, red grapes, and a green car. The second set of familiarization toys included two highly similar—but not identical—yellow ducks, a pink duck, a toy banana, and a yellow elephant.

Figure 6.

Children in Experiment 4 were led through three training trials before experimental data trials began. First (A), the experimenter introduced toys in an intuitive, increasingly complex order, and then placed the toys in a reasonable order on the table, which includes spatial placement based on multiple different dimensions. Next (B), the experimenter introduces new toys in an equally intuitive and helpful order, but the child is asked to place the toys (in the same order) instead of the experimenter. Finally (C), the number of toys is increased, they are introduced and handed to children in a random order, and the children place the toys on the table.

Familiarization and test trials all took place in an unadorned experiment room. A sturdy, square, wooden table was positioned near the center of the room, upon which toys were arranged. The table measured 48 inches square by 12 inches high. The table was covered by a layer of white felt. Children were easily able to reach all parts of the table. A digital camcorder was mounted to the center of the ceiling above the table to record the experiment and to allow for accurate distance measurements between objects anywhere on the table.

The same parental category survey used in Experiments 1–2 was completed by parents of children participating in Experiment 3.

6.1.3. Procedure

The experiment included six trials—three familiarization trials followed by three test trials. The structure of the familiarization trials is shown in Fig. 6. These trials were designed to introduce young children to the concepts of “same” and “different” and the idea of using distance as a metaphor for similarity. Children began familiarization by sitting on the floor across the table from the experimenter. The experimenter first asked the children whether they knew what it means for two things to be the same. Trials were structured the same way regardless of the child’s answer to this question, except that children who said “no” were allowed slightly longer to appreciate the examples described and to examine toys or propose their own arrangements.

Next, the experimenter introduced the first set of familiarization stimuli, without placing them in any particular position on the table. Each toy was shown to the child, and some representative “same” and “different” relationships were described, to remind or instruct the child about the meaning of the concepts of “same” and “different.” For example, the experimenter would describe a green car and a green apple as “a little the same, because they are both green, and they both roll” but also “they are a lot different, because they are different shapes, and you can’t eat a car.” Perceptual features like size, color, and shape, as well as conceptual features like function, animacy, and edibility, were routinely discussed in example comparisons.

Then the experimenter said, “Now, what I like to do is play a game with my toys, called the same and different game. The way we play the same and different game is that we take toys that are a lot the same like these [holding up the two red apples] and put them close together on the table [with an arm gesture moving the two close together in the air], and we take toys that are a lot different like these [holding up a red apple and the green car] and put them far apart on the table [with an arm gesture moving the two far apart in the air]. I'll play the first time to show you how the game works, and you can help me next time.” The experimenter then lined up all the toys on the edge of the table and proceeded to place them according to the rules of the game.

The apples were placed close together on the table. The red apples nearly touched each other, while the green apple was then placed near, but clearly separate from, the red apples. This arrangement highlights both the perceptual similarity of the apples and they fact they are all the same kind of thing. The grapes were placed on the other side of the red apples about as far as the green apple, again indicating similarity in kind (fruit) but also differences in specific kind and the equality of different feature dimensions—in this case, size and color are treated about equally for overall similarity. Finally, the green car, the only non-fruit item, was placed farther away from any of the other stimuli, but closest to the green apple, to indicate that even though it was the same color of green as the apple, it was a different kind of thing, and that multiple dimensions matter at once. With each new toy, the experimenter pointed out a variety of comparisons and contrasts to other toys introduced already, to encourage children to attend to a diverse set of available information. For example, when placing the red grapes, the experimenter might say “Now, these grapes are a lot the same as these apples: they are red like this apple, they are both round, and they are both fruits you can eat! But they are also a little different, because there are lots of grapes, they are smaller, and grapes are a different kind of fruit than apples.” The experimenter ended the first familiarization trial by introducing the camera in the ceiling, and said, “click!” with the children. The spoken “click” was used by coders to identify screenshots of final placements.

Next, the second set of familiarization toys was introduced (the two yellow ducks, a pink duck, a toy banana, and a yellow elephant). Similarly to the first set, the ducks provide an easy comparison for children to pick out first, and the other toys force them to consider more advanced comparisons. This time, after the rules of the game were repeated, children were asked to arrange the objects. The objects were presented to children in the same order they were introduced, as an aid to the children. The trial ended with the experimenter saying “click” to identify the time to capture a screenshot.

In the final familiarization trial, all of the toys from the first two trials were brought out on the table and lined up along the edge in no particular order. Children were reminded briefly of some comparisons from earlier, and the experimenter pointed out that objects from across the trials could be compared as well (e.g., “this [pink] duck is a little bit the same as this [red] apple, because pink is a little bit like red.”). After repeating the rules of the game, children were asked to choose their favorite toy as a means of randomly selecting a toy to be placed in the middle of the table. After putting the favorite toy in the center of the table, the experimenter handed the other toys in a random order to children to place on the table. This was the most difficult familiarization trial, since children were in charge of placement and the toys were considered in random order.

In familiarization trials 2 and 3, experimenters were instructed to look the children directly in the eyes while the children made placements, and no feedback was given, except after “invalid” placements. Invalid placements were defined only as placements that clearly violated the logic of the task across every emphasized dimension (kind relationships, color, shape, size, function, animacy, etc.) and that were not accompanied by any featural explanation by the child (“because they are both happy” would be an acceptable featural explanation, while “because I felt like putting them there” would not). As an example of an invalid placement, placing anything closer to a red apple than the other red apple would be defined as invalid, since identity is necessarily the highest form of similarity. Also invalid would be placing the green car and a red apple closer than the green apple and a red apple. Kind relations, size, color, shape, function, linguistic category, etc., are all insufficient to explain these placements. In these cases, the experimenter reminded the children of the rules of the game and suggested the smallest possible change to the layout that would fit the task instructions in at least one dimension. These corrections were only permitted during familiarization and were made on the minority of toy placements: out of all toy placements made by the 20 participants sampled for this analysis (400 placements total), 27% were corrected by the experimenter, suggesting that children largely understood the demands of the task as intended by the experimenter. The frequency of corrections also decreased substantially over familiarization, from 43% corrected placements in familiarization trial 2 to 20% corrected placements in familiarization trial 3. This suggests that our series of familiarization examples was successful in training children to better perform the SpAM task.

The three test trials followed a similar procedure to the third familiarization trial, but without experimenter commentary on the relationships between items or correction of any placements. First, a set of test items was placed on the table, and the experimenter commented, “Look! Lots of shapes, lots of sizes, lots of colors.” The child was encouraged to inspect and ideally handle every toy in the set. No specific labels were used by the experimenter during this inspection of the toys, and the experimenter gave only neutral responses (such as “oh yeah?” or no response) to any commentary by the child. The toys were then lined up on the edge of the table, the experimenter reminded the child of the rules of the game, and the child picked his or her favorite toy to be placed in the center. The remaining toys were then handed to the child to place in a random order, a “picture was taken,” and the experimenter asked about placement decisions. Each test trial used the toys from one of the superordinate categories from Xu and Tenenbaum (2007a).

6.1.4. Coding method

The primary data from this experiment were screenshots of children's final toy placements. Coders used a Matlab (version 2009a; MathWorks, Inc.) script to load these images and select the center of each object on the screen via a crosshair, in a predetermined order for each trial type. Centers of objects were determined by coders, according to an algorithm that is graphically depicted in Fig. 7.

Figure 7.

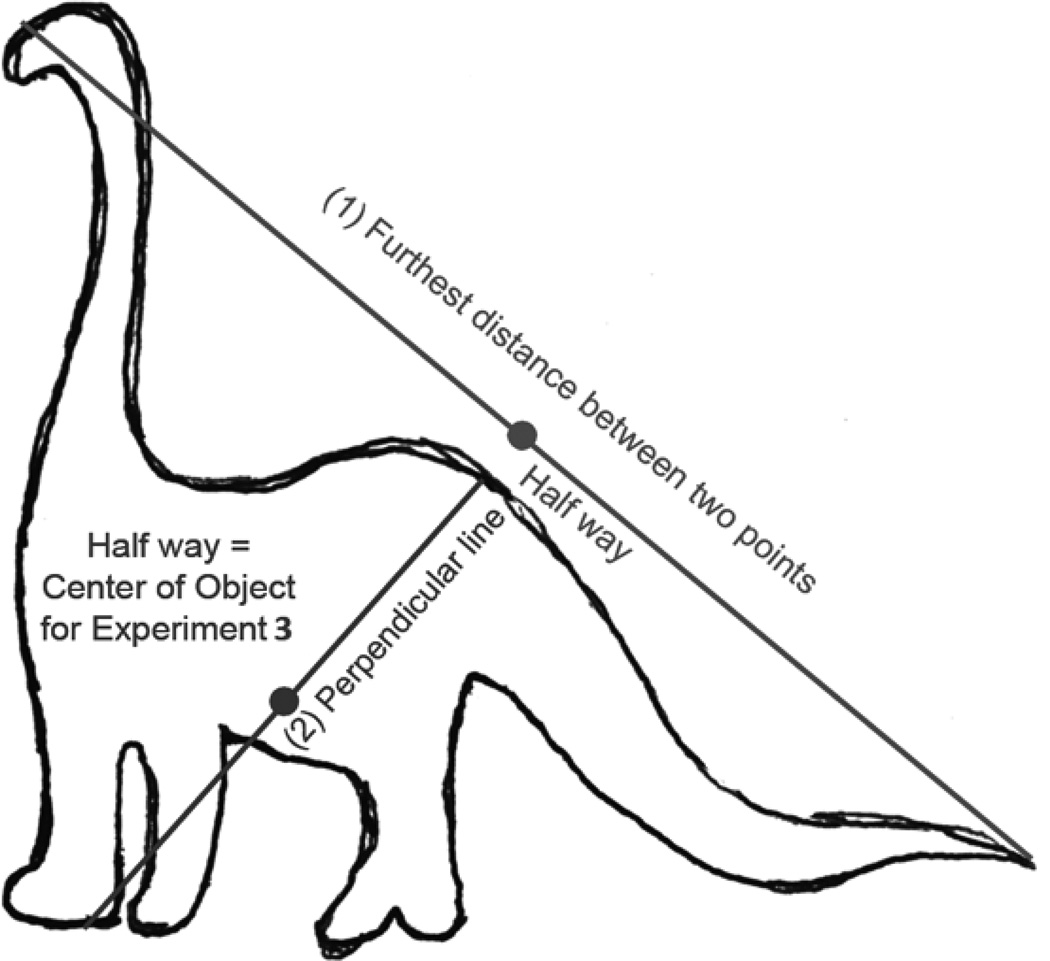
To locate the centers of objects from overhead screenshots, coders first located the two points of the object furthest away from one another. Imagining a line between these two points, coders determined the midpoint of that line, and projected a perpendicular line from that point, spanning between the furthest two points of the object intersecting it. The midpoint of this second line was coded as the center of the object for distance calculations.

The script then automatically calculated the distances of all 78 pairs of toys, excluding any toys that were occluded or indiscernible in the screenshot (less than 1% of toys were excluded by coders for this reason). Since we were interested in relationships between types of toys, not absolute distances, the distances were then normalized across all trials and individuals in the experiment, to control for individual differences in how widely or closely different children tended to place objects overall. The resulting dissimilarity matrix (larger distances in our game correspond to higher dissimilarity) was fed into Matlab's hierarchical cluster analysis function, to produce cluster tree plots of the same kind used by Xu and Tenenbaum (2007a).

6.2. Analysis

6.2.1. Reliability

To assess the robustness and reliability of children’s ratings, we compared dissimilarity scores between the placements for the ‘regular’ and ‘ribbons’ stimulus sets. Recall that these stimulus sets were identical except for small ribbons placed on two of the subordinate-level exemplars. Reliability across these two sets was good overall: the average dissimilarity scores for all 78 pairs of objects were strongly correlated between the regular stimuli and ribbons stimuli, r = 0.60, p < 0.01. We also assessed reliability by computing the standard deviation of dissimilarity scores across conditions. The SD was a moderate 21 units (where 100 is the maximum distance between any two objects for each participant). Moreover, the number of outlying individual distance measurements (> 2 standard deviations from the mean across participants) was low: 3.2% of toy pairs were outliers with regular stimuli and 2.2% were outliers with ribbons stimuli.

6.2.2. Results and discussion

Children organized their placements in a variety of ways. One common pattern is shown in Fig. 8A—a feature-based, perceptual organization. In this example, the child shows a strong bias to organize the objects by color. For example, many children placed the motorcycle and car next to each other (they are both blue), whereas Xu and Tenenbaum's adults rated them as very dissimilar vehicles. Other types of organizational patterns were also evident in the data. For instance, the data in Fig. 8B show an adult-like, hierarchical organization, with subordinate-level items close together, basic-level items adjacent, and other members of the superordinate category placed in a separated region of the table. Finally, as can be seen in Fig. 8C, some children showed a mixed pattern with rough groupings of subordinate and basic-level items (peppers here), but simultaneous organization by size, color, etc., often at different spatial scales (in this case, size was used to organize within the larger, hierarchical grouping of peppers). We classified children’s responses into the three categories shown in Fig. 8. Across all trials for all participants, 43% of arrangements were featurally organized, 15% were hierarchically organized, 16% showed mixed organization, and 27% showed neither clear featural nor hierarchical organization. Overall, these numbers show a substantial difference in children’s performance relative to the overall hierarchical organization of adult judgments from Xu and Tenenbaum (2007a).

Figure 8.

An example of three placements from children showing characteristic category patterns. (A) Featural (color) organization; (B) Taxonomic organization; (C) Feature and taxonomy mixed organization.

We next examined how children’s arrangements in the SpAM task were related to parents’ responses on the category checklist. This gave us a way to assess how parents’ judgments of children’s category knowledge were related to our more direct, child-driven measure of children’s category knowledge. We performed two mixed effect linear regressions with category score as the independent variable and a measure of adult-like similarity from our SpAM task as the DV. In particular, we used the following DV: [average distance between all pair of toys matching at the basic level] / [average distance between all pairs of toys matching at the subordinate level]. The higher this ratio, the more a child’s placements were consistent with adult-like, hierarchical category divisions. Subject and set type were treated as random factors, as with our earlier logistic regressions. In addition, we again performed one regression treating CS as a holistic variable (Table 5) and one regression treating CS as a set type-matched variable (Table 6).

Table 5.

Mixed Model Linear Regression with "Holistic" CS

AIC	BIC	Log Likelihood
610.1	624	−300.1

Fixed Effects	Estimate	Std. Error	t-value	p-value
Intercept	−0.91	1.83	0.5	0.62
CS, Holistic	0.15	0.11	1.42	0.17

As can be seen in the tables, the holistic regression did not reach statistical significance. By contrast, the regression using the matched score found a significant effect of the category data on generalization. The matched regression was also significantly better fitting relative to the holistic regression as indexed by AIC (Burnham & Anderson, 2002). Thus, category score is significantly and linearly related to children’s underlying category knowledge in the SpAM task. This provides direct evidence that the parent category checklist we used in Experiments 1 and 2 provides a robust measure of what children know about the categories used in the noun generalization task.

In summary, the SpAM task yielded reliable, quantitative measures of children's category knowledge for the stimuli used in Experiments 1 and 2. Children’s similarity judgments showed substantial differences compared to the similarity judgments of adults (see Xu & Tenenbaum, 2007a), with children showing a less hierarchically-organized pattern. This suggests that measuring children’s category knowledge directly might be critical when considering the priors they bring to novel noun generalization tasks. We examined this issue in the following section by asking whether cluster trees derived from children’s responses in the SpAM task could improve the fit of the Bayesian model.

7. Modeling 3: Bayesian simulations with child priors

In our previous simulations, we examined whether the Bayesian model could capture data from Experiments 1 and 2 when we used an estimate of children’s category knowledge (the category scores) and considered the basic level bias to be a free parameter. The critical question here is whether the child-generated hypotheses and priors from Experiment 3 could improve the model’s ability to capture our empirical findings.

7.1. Materials and methods

This series of simulations was procedurally the same as our previous model simulations with two modifications. First, we used the child-generated priors from Experiment 3, instead of adult-generated priors. Second, we were forced to make a slight change to how we applied the basic level bias parameter. Children’s similarity ratings did not show the same hierarchical organization as those of adults. In particular, “basic level” toys were scattered across multiple clusters in children’s cluster trees. Thus, to denote the basic level hypotheses to which the basic level bias in the model could be applied, we took the closest approximation of a basic level grouping for each of the three superordinate category types (animals, vegetables, and vehicles). That is, we conservatively defined the “basic level” cluster for the child data as the narrowest cluster that included all basic level toys. After implementing this assumption, we simulated the Bayesian model as before and examined the best and average model fits to the data across experiments.

7.2. Results and discussion

Results are presented in Table 7. Using children's similarity ratings as inputs to the model improved the model's overall inaccuracy score from 0.35 to 0.13 (calculated from best fits), eliminating almost two thirds of all modeling inaccuracy. Looking across conditions, however, it is evident that although overall error was lowered, the same pattern observed previously was still present: the model captured conditions where children showed a suspicious coincidence effect with an impressively small 0.05 inaccuracy (“a” superscripts), but it failed to capture conditions where children showed the opposite effect with an average 0.21 inaccuracy score (“b” superscripts).

Table 7.

Inaccuracy Scores from Modeling Section 2

Experiment	Behavior to match	Inaccuracy score of model (best fit)	Inaccuracy score of model (average fit)	Inaccuracy score random chance (Average fit)
1a	Replication Low-CS	0.01	0.01	0.53
1b	Replication High-CS	0.16	0.16	0.50
2a	Ribbons Low-CS	0.09	0.09	0.51
2b	Ribbons High-CS	0.26	0.26	0.50
	Total	0.13	0.13	0.51

Note.

^aBehavior trended in direction of suspicious coincidence effect

^bBehavior trended opposite from suspicious coincidence effect.

We can draw two major conclusions from the results of this most recent modeling run. First, improving our assessment of children’s knowledge (the priors) greatly improves the fit of the Bayesian model to our data. The model’s inaccuracy score was cut by almost two thirds when child inputs were used. Thus, prior knowledge—and developmental changes in prior knowledge—is clearly a key variable in explaining children's noun generalization behavior. Second, despite impressive improvements in the model fits overall, the Bayesian model was still systematically off in its account of children's behavior in Experiments 1–2, with inaccuracy scores of 0.16 and 0.26 in the two high-CS groups. This is an unacceptably high number considering that the suspicious coincidence effect itself had a magnitude of 0.20–0.25 (see Fig. 5). To account for all of the data, therefore, the Bayesian model must be modified, supplemented, or replaced. We discuss these implications below. We also provide one example of a supplemental hypothesis that might explain why high-CS children fail to show the suspicious coincidence effect and how this additional hypothesis—along with the Bayesian model—might explain both sides of the U-shaped developmental trend.

8. General discussion

Hierarchical structure is one of the key features of language that makes our communication efficient and powerful, and Xu and Tenenbaum's suspicious coincidence effect is a simple, elegant, and intuitive example of how we might expect a hierarchical category system to influence behavior and learning. The effect has been replicated several times under certain conditions (e.g., Xu & Tenenbaum, 2007b; Gweon, Tenenbaum, & Schulz, 2010). Moreover, Xu and Tenenbaum have offered a formal Bayesian model that captures this basic effect. This is currently the only formal model to have done so, making the effect and the model important theoretically.

In the present report, we examined how children’s ability to identify suspicious coincidences changes as they acquire more category knowledge over development. This is important because children’s category knowledge changes dramatically in early development. Moreover, the Bayesian model predicts that children will show a progressively stronger suspicious coincidence effect as they gain more category knowledge. We modeled this prediction quantitatively (see section 1.4.3) and then tested it across two experiments where we measured children’s category knowledge via a parental checklist and had children complete Xu and Tenenbaum’s (2007a) task. Results from the experiments revealed that children with greater relevant category knowledge show a weaker suspicious coincidence effect. This is a surprising finding that is opposite the predicted effect from the Bayesian model. Data from a subsequent experiment showed that the category knowledge score from the parental checklist was related to a direct assessment of children’s category knowledge using the SpAM task. Considered together, these data suggest that there is a U-shaped trend in novel noun generalization for hierarchically-nested categories over development: children with less category knowledge show a suspicious coincidence effect, children with more category knowledge do not, and adults show this effect once again when tested in the canonical task (see Xu & Tenenbaum, 2007a).

Importantly, our modeling efforts suggest that the Bayesian model in its current form cannot capture the U-shaped trend in isolation. In Section 5, we made generous modeling assumptions and chose the best-fitting values for all parameters. The model still failed to account for our data: overall, the Bayesian model fits were only modestly better than fits of a model that randomly chose effect sizes. One potential explanation for this poor fit is that—like Xu and Tenenbaum (2007a)—we used adult priors to fit child data. Thus, in Section 7, we used cluster trees derived from children’s placements in the SpAM task. Critically, use of child-generated priors in the model did improve the fit of the Bayesian model considerably: the inaccuracy measure from the overall fit was cut by almost two-thirds. Nevertheless, the model still failed to capture data from the high-CS conditions where we did not observe the suspicious coincidence effect.

In summary, the present study makes three central contributions to our understanding of the development of novel noun generalization in the context of overlapping category extensions. First, we identified robust and replicable changes in the suspicious coincidence effect as children develop more category knowledge, revealing a U-shaped trend in the suspicious coincidence effect. Second, we showed that measuring children’s prior category knowledge directly can enhance the fit of Bayesian models to empirical data. Third, we revealed key new challenges for the Bayesian account proposed by Xu and Tenenbaum and, more generally, for models of early word learning and category extension.

The primary challenge facing the Bayesian model is its demonstrated lack of generality to cases where children do not show a suspicious coincidence effect. At some level, this is not surprising because the suspicious coincidence effect is inherent in the model’s likelihood equation (the “size principle”):

$$p(X|h)={[\frac{1}{\mathit{\text{size}}(h)}]}^n$$

Since a narrower category must always be of a smaller size than a broader one, narrow hypotheses will always be weighted more strongly than broad hypotheses, and exponentially so as the number of exemplars (n) increases. The only way for the Bayesian model to capture the absence of the suspicious coincidence effect (or its reversal, see Spencer et al., 2011), therefore, is for the underlying structure of the model to be changed.

For example, Xu and Tenenbaum (2007b) reported a reversal of the suspicious coincidence effect in a “learner-driven” generalization condition, in which participants—rather than a knowledgeable teacher—selected a set of exemplars. Xu and Tenenbaum predicted this effect based on the assumption that when learning novel words learners treat items selected by a teacher as more informative and reliable than their own selections. To capture the reverse effect in the Bayesian model, Xu and Tenenbaum switched out the likelihood function used to capture performance between the teacher and learner conditions. That is, in the teacher condition, the authors used one likelihood function (see equation 4; Xu & Tenenbaum, 2007b) while in the learner condition, the authors used a different likelihood function (see equation 5; Xu & Tenenbaum, 2007b). In this way, Xu and Tenenbaum were able to quantitatively capture data from the two conditions with a Bayesian model.

Might the same approach be used with our data—could we modify the likelihood function over development such that the model shows a U-shaped trend? Following from Xu and Tenenbaum (2007b), for instance, is it possible that high-CS children assumed that the experimenter was an uninformative teacher in Experiments 1 and 2? We have no reason to think that these children thought the experimenter was uninformative, particularly given that all children completed the same procedure with random assignment across conditions. More generally, in our view, using different likelihood functions to capture a reversal of the suspicious coincidence effect has only modest explanatory power, because two different models are then used to capture two different patterns of data. In such cases, the models are no longer doing much heavy theoretical lifting. That work is instead left to the modeler who decides which model to run in each case. For instance, in Xu and Tenenbaum’s 2007(b) report, the most important theoretical claim is that there is some psychological process—which is not a part of the Bayesian model—that causes children to treat information differently in the teacher and learner conditions.

Still, although less satisfying than a single, unified, formal model, this type of verbal explanation can help move our understanding forward. Is there a similar, supplementary verbal explanation for our findings? One possibility is that children with greater category knowledge might have learned that, in general, subordinate level categories are labeled with compound labels, like “sheepdog,” “delivery truck” or “Bell pepper.” Basic level categories, on the other hand, tend to have single morpheme labels like “dog,” “truck,” and “pepper.” When faced with a single label in “frog language,” like “fep,” “dax,” or “blick” it is possible that the high-CS children generalized at the basic level based on this statistical regularity.

To examine this possibility, we performed two analyses, using databases of adult and child-directed speech. We first performed a quantitative analysis of adult-directed English using Wordnet (Princeton University, 2010), a searchable database that includes hierarchical category relationships. We used this tool to gather a random sample of 79 basic level terms—ones belonging to “animal,” “vegetable,” and “vehicle” categories. We also randomly sampled 142 subordinate levels terms, by searching members of the “dog,” “pepper,” and “truck” categories. We found that 23% of the basic level categories were labeled with compound nouns, while 56% of the subordinate categories were labeled with compound nouns. Thus, compound labels were two and a half times more common for subordinate categories in our sample than for basic ones.

Second, we performed a similar analysis of child-directed speech using the CHILDES corpus (MacWhinney, 2000), which consists of child-directed conversations. Unlike Wordnet, CHILDES does not contain hierarchy information, however, it does contain some sentence morphology information. Thus, we performed the opposite analysis as we did with Wordnet. We took a random sample of 162 compound nouns used in child-directed speech (all those that we found in the morphology coded database), and coded them ourselves for hierarchical category level. We found that 76% of compound nouns sampled were subordinate, while 24% were basic. Out of a corresponding sample of 162 single-morpheme nouns, only 4% were subordinate and 94% were basic.

These findings suggest that basic level categories are consistently biased toward single-morpheme labels, while subordinate level categories are biased toward compound labels. Critically, all of the novel words used in our study and in Xu and Tenenbaum’s study (2007a) were short (“fep”, “dax”, and “blick”), and none were compounds. It is possible, therefore, that high-CS children might have employed their stronger knowledge of morphological regularities and inferred that our novel labels were more likely to refer to basic level categories than subordinate ones. This would result in high-CS children being biased toward basic level generalization behavior relative to low-CS children. Adults, on the other hand, may be better able to separate the influence of English morphology from their generalizations about Mr. Frog’s language, making them more likely to resist morphological biases and once again show a suspicious coincidence effect.

Future studies that manipulate the usage of single versus compound novel labels will be needed to test this possibility directly. Moreover, such future work will have to assess whether high-CS children do indeed have stronger knowledge of morphological regularities. Note that even if the morphological hypothesis is born out, this explanation of the U-shaped developmental trend does not replace the Bayesian model—it supplements the model to explain what might be driving the different behavior of high-CS children in particular. One must still rely on the Bayesian account to explain the underlying suspicious coincidence effect shown by both low-CS children and adults.

Although a complete explanation of the U-shaped developmental trend reported here will require more data, our findings clearly suggest that children's prior knowledge matters greatly in the case of hierarchically-nested categories and matters in unexpected ways that do not conform to the Bayesian model. Most critically, we did not find an increase in Bayesian inference as children accumulated more category knowledge. Rather, knowledge appears to be reorganized and used in new and different ways that are not always rational over development. This is consistent with other findings showing unexpected and nonlinear results as children reorganize knowledge, such as the appearance of early speech delays (Beckage, Smith, & Hill, 2011), overgeneralizations (Rumelhart & McClelland, 1986; Marcus, et al., 1992; Goldin-Meadow, 2004; Samuelson, Horst, Schutte, & Dobbertin, 2008), and changes in performance in tasks that ostensibly test the same concepts (e.g., Samuelson, Schutte, & Horst, 2009). Any full explanation of the suspicious coincidence effect or of word learning at large will likely need to include an account of how such reorganization of knowledge happens and what consequences it has for the processes involved in category learning and generalization.

This brings us back to the more general issue of early word learning. The goal of word learning theories is to explain both the specifics of what children do in individual laboratory tasks and what children do in the real world as they encounter new instances and build category knowledge over time. On the former front, the Bayesian model certainly fares well: predicting novel laboratory findings—even if they turn out to be robust only in narrow circumstances—is impressive. But the lack of generality of this effect and its mismatch with children’s developmental trajectories raises questions about whether the Bayesian account is sufficient to explain word learning in the wild. Our sense is that either supplemental accounts are needed to work with the Bayesian model (like our morphology explanation), or alternative accounts are needed to explain the entire U-shaped set of developmental data from a fresh perspective. The most likely candidates are accounts that link the step-by-step details of children’s emerging category knowledge to word learning and that allow for the nonlinear and unexpected directions children take during learning (Perry, Samuelson, Malloy & Schiffer, 2010; Samuelson, 2002; Smith and colleagues, 2002; Samuelson, Spencer, & Jenkins, 2013). Future work will be needed to sharpen the contrasts among these different theories of word learning. Our hope is that the Ushaped trend revealed here will usefully contribute to these theoretical debates.

Table 6.

Mixed Model Linear Regression with "Matched" CS

AIC	BIC	Log Likelihood
600.5	614.4	−295.3

Fixed Effects	Estimate	Std. Error	t-value	p-value
Intercept	1.43	0.87	1.64	0.11
CS, Matched	3.81	1.5	2.53	0.013

Appendix

Xu and Tenenbaum (2007) did not only test one-exemplar and three-subordinate-exemplar conditions. Conditions were also run with three basic level exemplars (e.g., Labrador, pug, and Husky), and with three superordinate level exemplars (e.g., Labrador, penguin, and pig). We replicated these conditions in Experiments 1–3, but did not report the results of these two additional conditions previously, since they are not directly relevant to the suspicious coincidence effect of primary interest. Generalization rates to all types of test items and standard errors for all four conditions are shown in the table below.

Novel noun generalization for subordinate and superordinate-level-only test items was also measured. The results were primarily as expected in these other conditions and test cases. Typically, generalization to subordinate level test items was near ceiling for almost all conditions, at around 80–90%, and generalization to superordinate-level-only test items was near floor, usually less than 10% (except, unsurprisingly, when children were shown superordinate exemplars, and generalization climbed to 20–30%). Generalization to basic-level test items was highest when basic-level exemplars were shown, and somewhat lower when superordinate-level exemplars were shown. This latter effect was somewhat surprising. We do not have an explanation for it, although since it is not relevant to the suspicious coincidence effect, this was not of primary concern to us (the generalization is also still at least higher than in the 1-exemplar or 3-subordinate-exemplar conditions).

Novel Noun Generalization for Test Items : Standard Error, for All Conditions

Exp.	Type of test item	1-exemplar generalization generalization	3-subordinate- exemplar generalization	3-basic- exemplar generalization	3-superord.- exemplar generalization
1a	Subordinate	0.94 : 0.03	0.88 : 0.06	0.88 : 0.06	0.79 : 0.08
All	Basic	0.25 : 0.04	0.12 : 0.06	0.65 : 0.10	0.32 : 0.10
CS	Superordinate	0.01 : 0.01	0.01 : 0.01	0.06 : 0.02	0.16 : 0.06
1a	Subordinate	0.94 : 0.04	0.80 : 0.11	0.80 : 0.11	0.70 : 0.11
Low-	Basic	0.26 : 0.04	0.00 : 0.00	0.50 : 0.15	0.05 : 0.05
CS	Superordinate	0.01 : 0.01	0.00 : 0.00	0.03 : 0.03	0.08 : 0.04
1b	Subordinate	0.93 : 0.05	0.95 : 0.05	0.95 : 0.05	0.89 : 0.11
High-	Basic	0.25 : 0.08	0.25 : 0.11	0.80 : 0.13	0.61 : 0.14
CS	Superordinate	0.01 : 0.01	0.03 : 0.03	0.10 : 0.04	0.25 : 0.11
2a	Subordinate	Same as Exp. 1	0.95 : 0.02	0.75 : 0.09	0.88 : 0.07
Low-	Basic		0.06 : 0.03	0.25 : 0.14	0.25 : 0.25
CS	Superordinate		0.00 : 0.00	0.00 : 0.00	0.00 : 0.00
2b	Subordinate	Same as Exp. 1	1.00 : 0.00	1.00 : 0.13	0.75 : 0.13
High-	Basic		0.35 : 0.07	1.00 : 0.00	0.25 : 0.25
CS	Superordinate		0.22 : 0.17	0.50 : 0.18	0.38 : 0.18

Note.

^aBehavior trended in direction of suspicious coincidence effect.

^bBehavior trended opposite from suspicious coincidence effect.