Abstract
In research aimed at improving human health care, animal studies still play a crucial role, despite political and scientific efforts to reduce preclinical experimentation in laboratory animals. In animal studies, the results and their interpretation are not always straightforward, as no single study is executed perfectly in all steps. There are several possible sources of bias, and many animal studies are replicates of studies conducted previously. Use of meta-analysis to combine the results of studies may lead to more reliable conclusions and a reduction of unnecessary duplication of animal studies. In addition, due to the more exploratory nature of animal studies as compared to clinical trials, meta-analyses of animal studies have greater potential in exploring possible sources of heterogeneity.
There is an abundance of literature on how to perform meta-analyses on clinical data. Animal studies, however, differ from clinical studies in some aspects, such as the diversity of animal species studied, experimental design, and study characteristics. In this paper, we will discuss the main principles and practices for meta-analyses of experimental animal studies.
Keywords: meta-analysis, experimental animal studies, systematic review, guidance, principles and practices
Introduction
Animal experimentation plays a vital role in research aimed at improving human health and health care. For example, in 2012, more than 4 million animal studies took place in Great Britain in a research context (Winston 2013), and in a country as small as The Netherlands, almost 600,000 animal experiments were conducted (Netherlands Food and Consumer Product Safety Authority 2013). Many of the animal studies were replicates of studies conducted previously. This is not a surprise, as replication of study results is one of the main principles of science. However, how do we decide when we have enough (reliable) information about a specific topic for decision making? Meta-analysis of animal studies might be of use herein.
In general, meta-analysis is a tool to evaluate the efficacy of an intervention using all available information. In addition, meta-analysis, especially cumulative meta-analysis, can help to minimize unnecessary duplication of animal studies (Lau et al. 1992; Sena, Briscoe et al. 2010). A cumulative meta-analysis is a series of meta-analyses in which each successive meta-analysis incorporates one additional study. When the meta-analyses are sorted chronologically, the display shows how the evidence accumulated, and how the conclusions have shifted over a period of time (Borenstein et al. 2009a). For example, a cumulative meta-analysis conducted by Sena et al. in 2010 on recombinant tissue plasminogen activator (rtPA) in stroke showed that the estimate of efficacy was already stable in 2001, after data from some 1500 animals had been reported. However, this meta-analysis was conducted in 2010, and after 2001 another 1888 animals were used, which was not necessary to establish the effect of rtPA for stroke (Sena, Briscoe et al. 2010). However, note that a number of these studies were not performed to establish the efficacy of rtPA but used rtPA as a positive control or as a comparator for novel interventions. Nevertheless, meta-analyses of animal experiments are an important tool in reducing the number of unnecessary animal studies.
There is an abundance of literature on how to perform meta-analyses on clinical data. Animal studies, however, differ from clinical studies in some aspects. For example, animal studies are much more diverse in their populations (e.g., species), design, and study characteristics. In this paper, we will discuss the main principles and practices for meta-analyses of experimental animal studies.
Meta-analysis in the Context of Systematic Reviews
When a scientist has an important research question to answer, there are often a variety of scientific approaches possible. One option is to design a new animal study. Another somewhat less common option is to conduct a systematic review of all animal studies. In a systematic review, all research evidence relevant to a specific question is identified, appraised, and synthesized in order to draw evidence-based conclusions. In general, a systematic review results in a transparent overview of the available information, for example, about the safety and efficacy of a treatment. It offers new information that was not available by analyzing each study individually. So, a systematic review might result in a better answer to the research question than that provided by a new animal experiment.
Systematic reviews are almost standard practice in clinical studies but are not yet widely conducted in the field of laboratory animal science. Fewer than 250 systematic reviews of preclinical animal studies had been published prior to 2010, as opposed to almost 6000 Cochrane Reviews of clinical studies to date (Ritskes-Hoitinga et al. 2014). Given that many studies using laboratory animals aim at improving human health (and health care), it seems reasonable that research using animals be reviewed in a similar way and adhere to similarly high quality standards. Some scientists even suggested that a more rigorous assessment of the results of animal studies in the form of a systematic review should be a prerequisite before starting studies in patients (Sandercock and Roberts 2002).
Eight different steps need to be taken when a systematic review is conducted (Figure 1). In one of these steps (step 7), the results of all individual studies are reported and compared, and when possible combined by means of a meta-analysis. This results in a quantitative summary of the knowledge that is available. However, a meta-analysis may also aim to assess the dispersion between the individual study effects. Although many systematic reviews contain meta-analyses, systematic reviews are also frequently published without a meta-analysis, especially when the included studies are too heterogeneous or seem to be seriously biased.
Figure 1.
Steps to be taken in a systematic review (SR) and meta-analysis (MA) of animal studies. Figure 1 is partly based on the general methods for Cochrane reviews (Higgins and Green 2008).
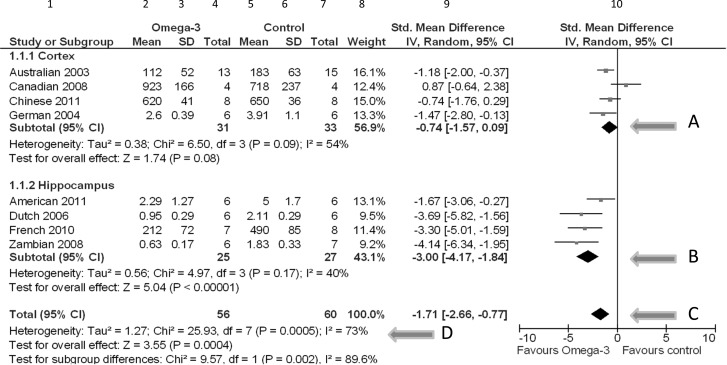
The results of a meta-analysis are displayed in a forest plot; see, for example, Figure 2. This plot allows readers to visualize and interpret the results of a meta-analysis. Figure 2 represents a forest plot summarizing fictive results of eight individual studies on the effects of omega-3 fatty acid supplementation on neuronal cell death in experimental Alzheimer's disease (AD). Four studies assessed the amount of neuronal cell death in the cortex, the other four studies in the hippocampus. These are presented separately, as subgroups.
Figure 2.
Forest plot, summarizing fictive results of eight individual studies, comparing the effects of omega-3 fatty acid supplementation vs. control treatment. Abbreviations: SD: standard deviation; Std. Mean Difference: standardized mean difference; IV, Random: a random-effects meta-analysis is applied, with weights based on inverse variances; 95% CI: 95% confidence interval; df: degrees of freedom; Tau2 and I2: heterogeneity statistics; Chi2: the chi-squared test value; Z: Z-value for test of the overall effect; P: p value.
The first column shows the references of the included studies. Columns 2 through 7 show the raw data (mean, standard deviation [SD], and sample size [total]) of both the experimental omega-3 group and the control group concerning the amount of neuronal cell death due to omega-3 fatty acid supplementation in experimental AD. Neuronal death is measured using different scales; therefore, the means of the various studies vary considerably (0.63 to 923). In this case, some studies present cell death per inch2 and others per mm2.
Based on the raw data, an effect estimate for each study can be calculated. In column 9, the study effects are represented as standardized mean differences (mean difference/SDpooled), so that the differences are expressed on a uniform scale; the fact that the scales of measurement varied across studies is no longer a problem. On the right, these differences, with their 95% confidence intervals (CIs), are presented with a central square and a horizontal line in the forest plot. The size of the central square is roughly equal to the size of the study, or more exactly, to the weight (column 8) that the study contributes to the combined effect (Perera and Heneghan 2009). The weight of a study varies with the statistical model used to pool the results (either fixed- or random-effects model). The vertical line represents the line of no effect.
In this example, it was decided to combine the results of the individual studies. The resulting summary effects are depicted as black diamonds, per subgroup (arrows A and B) and for all studies combined (C). The locations of the diamonds represent the point estimates (direction and size) of the treatment effect, and the width of the diamonds represent the 95% CI. In this fictive example, the diamond corresponding to the total effect (C) is located completely left of the vertical no-effect line. Therefore, we can conclude that there is a statistically significant reduction in the amount of neuronal cell death due to omega-3 fatty acid supplementation in experimental animal models for AD.
Last but not least, in this forest plot the amount of heterogeneity is also shown, expressed as Tau2 (τ2), together with a chi-squared test result (D). The τ2 is an estimate of the between-study variation. The corresponding chi-squared test assesses whether the τ2 is larger than zero, but it is of limited importance because it is not very powerful when the number of studies is small and it gives no information on the extent of heterogeneity (Deeks et al. 2008b). The I2 (also at D) is a measure of inconsistency between the study results and quantifies the proportion of observed dispersion that is real (i.e., due to between-study differences and not due to random error) (Higgins et al. 2003). It reflects the extent of overlap of the CIs of the study effects. If I2 is low (<25%), almost all observed variance is probably spurious. If the heterogeneity is large (e.g., I2 >50%), we should speculate about reasons for the large “real” variance (Deeks et al. 2008b). Animal studies are often quite exploratory and heterogeneous with respect to species, design, intervention protocols, etc., compared to clinical trials. Exploring this heterogeneity is one of the added values of meta-analyses of animal studies and might help to inform the design of a clinical trial.
Reasons to Conduct a Meta-Analysis of Animal Studies
Although meta-analyses of animal studies are not yet routine in laboratory animal experimentation there are many advantages to conducting them.
Results from a systematic review that includes a meta-analysis of animal studies may be more robust than results from single animal studies if the meta-analysis is based on multiple high-quality studies. Therefore, the knowledge about the efficacy or side effects of a treatment or intervention may be more comprehensive. No single research endeavor is perfect, and experts are prone to bias. Combining studies that meet specific predefined criteria regarding content and quality may result in more reliable conclusions (Ioannidis and Lau 1998).
In many situations, human evidence is lacking, for example, in toxicity studies (Peters et al. 2006). A critical evaluation of animal experiments, leading to information about the efficacy and possible side effects, can therefore inform clinical trial design and improve patient safety. For example, single animal studies are often too small to show whether or not a side effect is relevant or to present the full spectrum of side effects. When multiple small animal studies are combined, this will increase the power of the analysis and give more insight in the significance of a side effect. A meta-analysis about the effects of nimodipine (a calcium channel blocker) for acute stroke showed that there was no convincing evidence from the animal studies to substantiate the decision to start trials with nimodipine in large numbers of patients. However, at the time of the meta-analysis of the animal experiments, 29 clinical trials with approximately 7500 patients were already conducted (Horn et al. 2001).
As mentioned above, another added value of meta-analyses of animal studies is the new knowledge that can be obtained by the evaluation of the heterogeneity between the studies. For example, a meta-analysis can make the impact of methodological quality on the effect size transparent. Bebarta et al. showed in 2003 that animal studies that do not utilize randomization or blinding are more likely to report a difference between study groups than studies that employ these methods (Bebarta et al. 2003). Part of the heterogeneity between animal studies can also be caused by differences in biological study characteristics (such as species, sex, age, dose, intervention schedule, etc.) on the main effect. The impact of such characteristics can be investigated by subgroup analyses or meta-regression (meta-analytical techniques to assess the relationship between study level covariates and effect size). A recent review about the effects of ischemic preconditioning (IPC) on ischemic reperfusion injury (IRI) in the animal kidney showed, for example, that the timing of the ischemic preconditioning greatly influenced the efficacy. The late window of protection (IPC more than 24 hours prior to IRI) appeared to be much more effective than the early window of protection. In addition, it was demonstrated that the IPC was more effective in rats than in mice (Wever et al. 2012). These results obtained from the subgroup analyses resulted in the design of a new clinical trial focusing on the late window of protection instead of the early window that had been used so far. This shows how meta-analyses may affect the design of future animal or clinical experiments.
So far, many papers and guidelines have been published regarding meta-analyses for clinical data (Borenstein et al. 2009b; Higgins and Green 2008; Nordmann et al. 2012). Guidance has also been published for animal data, albeit not to the same extent (Vesterinen et al. 2013). Animal studies differ from clinical studies in some aspects, which must be taken into account when performing a meta-analysis.
Differences Between Meta-Analyses of Animal and Human Studies
In human research, the goal of a meta-analysis of clinical trials is generally to estimate the overall effect size of an intervention in order to aid decision making in clinical practice. In contrast, meta-analyses of animal studies are more exploratory and their results can be used to generate new hypotheses and guide the design of clinical trials. The purpose might be to summarize the effect of an intervention, to establish the relation between two variables, to summarize a parameter in a single group, or to evaluate heterogeneity between studies. The size of an effect, for example, of an intervention effect in an animal model, is in itself not particularly useful information. This is partly because animal studies are so diverse in their populations (e.g., species), design, and study characteristics; a pooled effect size is less meaningful compared to clinical trials. However, as the studies in a meta-analysis are addressing a similar question, the direction of the effects is meaningful.
In addition, because animal studies offer a wider range of possibilities to examine toxicity of interventions or study pathology and mechanisms of disease than provided by clinical trials, meta-analyses of animal studies have a greater potential in exploring possible sources of heterogeneity compared to meta-analyses of clinical studies (Mapstone et al. 2003; Vesterinen et al. 2013). We believe that one of the major added values of meta-analyses of animal studies is the insight that can be obtained by the evaluation of the heterogeneity between the studies.
The methods used for meta-analysis of animal studies are largely similar to clinical meta-analyses, but in some aspects they are somewhat different (Vesterinen et al. 2013). For example, an animal study may contain both a placebo group and sham groups. In addition, animal studies are in general much smaller and more heterogeneous than clinical trials. Furthermore, the methodological quality of the included animal studies is often poor, which increases the risk of bias (Kilkenny et al. 2009).
Meta-Analysis of Animal Studies Step by Step
As mentioned before, a meta-analysis is often part of a systematic review. Once the review is started (i.e., once the scientific research question has been formulated), the objectives, study selection criteria, outcomes of interest, and methodological approach should be described prospectively in a meta-analysis protocol. A protocol format for systematic reviews of animal intervention studies is submitted by RBM deVries, CR Hooijmans, MW Langendam, M Leenaars, M Ritskes-Hoitinga, and KW Wever. We also recommend that authors register and/or publish the protocol, thereby allowing feedback on the proposed methodology and insight into changes during the review process. When the studies have been selected and the relevant study results gathered, the statistical synthesis of the results—the meta-analysis—can be performed. This can be done for each outcome of interest, thus a systematic review can contain several meta-analyses per research question, for example, a meta-analysis for the outcome measure mortality, and one for the number of animals with weight increase. Each meta-analysis summarizes with statistical methods the results of those studies that reported on that outcome. A meta-analysis requires that at least two but preferably more studies are available.
We suggest the following key elements and steps, among others inspired by the Cochrane Handbook (Higgins and Green 2008) which all will be taken in a reproducible sequence when performing a meta-analysis of animal studies.
A. Check Whether or not the Included Studies are Homogenous Enough to Conduct a Meta-Analysis
An important feature of a systematic review—and thus also of the meta-analyses in the review—is that the systematic review often addresses a broader research question than was addressed by the primary studies. Consequently, the selected studies may show diversity in animal species, types of outcomes, measurement times, etc. However, in order to be able to provide a meaningful answer to a research question like “what is the effect of this intervention on weight increase,” a group of studies must be sufficiently homogeneous in terms of animals, interventions, designs, and outcomes. Heterogeneity can be diminished by prospectively defining strict inclusion and exclusion criteria and making only sensible comparisons. It is therefore important to conduct a meta-analysis always in collaboration with an expert from the field.
On the other hand, if the aim of the meta-analysis was to determine factors (study characteristics) that influence the overall effect, especially the variation in the effect size is of interest and much more diverse studies may be included. In this case, where the focus of the meta-analysis is the relation between characteristics of the studies and the outcome, a wider diversity between studies is appropriate than when the focus is mainly on the summary effect across a series of studies.
B. Assemble the Relevant Study Data
For each outcome of interest (e.g., weight change), data must be gathered for each study and treatment group, as in columns 2 through 7 in the forest plot (Figure 2). Most of these can be extracted from the original publications. If data were presented only in graphs, they could be measured with digital ruler software. When the required data are missing, the authors of the study should be contacted, which can take some time.
Study results may be expressed on different scales of measurement: counts (e.g., number of animals deceased) and mean values with standard deviations (e.g., for weight increase) are most common. Preferably, data per group (counts or means and SDs and the total number of animals) are gathered for each study. If only medians and ranges or interquartile ranges are provided, these must be collected. If only summary effects are provided (e.g., in the form of odds ratios with a standard error or CI), these must be used. If no more detailed information is available, even only p values and numbers of animals per group, or the direction of the effect size (positive or negative) can be useful (Borenstein et al. 2009b).
Also, the study design is important. It must be recorded what type of animals were used, timing of the measurements, details on the intervention, and other study characteristics that may be useful for the interpretation of the result. For example, if there are two control groups, including a sham group, or if control groups are shared by several experiments, this must be recorded. Animals receiving the same intervention are often group housed, altering the experimental unit into cage instead of individual animal. Furthermore, the animal experiments included in a meta-analysis are often not independent: control groups may be shared by two or more experimental studies.
C. Choose an Effect Size Measure.
Once the relevant study results are gathered, they may be used in the meta-analysis. If count data were gathered, you can choose whether you want to present the result of the meta-analysis in odds ratios, risk ratios, or risk differences.
When the study results are continuous, like weight change, the choice is between “normal” differences of the group means, standardized mean differences, and normalized mean differences. For example, when weight changes are measured in different species, the interpretation of an intervention effect of 6 g in a study with mice is completely different from the same effect in a study with beagles. In such situations, standardized differences are a useful effect size measure, because they express the difference between the groups relative to the standard deviation. For instance, the weight changes of the mice might vary between -5 g and +12 g, and the SD is 4 g. An increase of 6 g corresponds thus to an increase of 1.5 SD. However, beagles weight on average 10 to 11 kg, and the individual changes in weights will be much larger than for mice. If the SD of the weight changes of beagles is 500 g, the increase of 6 g corresponds to a minor change of 0.012 SD. The relevance of the effect is thus much better reflected by standardized differences than by the original differences. An additional advantage is that the scale in the forest plot automatically indicates the relevance of the summary result. This is also clearly shown in the forest plot (Figure 2). A normalized mean difference can be used when the score of a normal, untreated, unlesioned sham animal is known or can be inferred. One of the advantages of this method is that the absolute difference in means can be expressed as a proportion of the mean in the control group, which might be more easy to interpret (Vesterinen et al. 2013). For mean differences, standardized and normalized differences the same data must be extracted from each study: mean values, SDs, and total number of animals per group.
When time to a certain event (e.g., death) is the topic of interest, survival data must be provided. See Vesterinen and colleagues (2013) for details.
D. Calculate the Effect Size for Each Study / Study Subgroup
Once all the relevant data are collected and an effect size is chosen, study results must be prepared so that they can be used in the meta-analysis. In the most simple situation, each study provided separate data for both treatment groups; these data can be directly used to calculate effect sizes per study. However, from time to time, data must be preprocessed, for example, when median values and ranges or interquartile ranges are reported instead of means and SDs. If the data seem sufficiently normally distributed, medians and ranges can be used to construct means and SDs (Hozo et al. 2005).
If results of some of the selected studies are not presented per group but combined as effect sizes, they can also be used in the meta-analysis. Take, for example, a set of five studies. Three studies show weight increase data per group (mean, SD, and total number of animals), and two studies present only the mean difference between the groups with a 95% CI. In this case, the result of each study must be transformed into a mean difference with corresponding standard error before it can be used in the meta-analysis.
In animal studies, often the same control group is used for multiple experimental groups. Sharing a control group makes the comparisons of the experimental groups dependent upon each other. When such comparisons are presented as independent comparisons in a meta-analysis the animals in the control group will be counted twice and the comparisons will receive too much weight in the estimation of the summary effect. Therefore, some adjustment must take place. A simple option is to diminish the number of animals in the shared control group by splitting the “shared” group into two or more groups with smaller sample size (Higgins et al. 2008). For example, a study with two experimental groups sharing a control group with 12 animals results in two comparisons, each with six animals in the control group. For advice on other complicated situations, see the guidance of Vesterinen and colleagues (Vesterinen et al. 2013).
E. Choose a Random-Effects or Fixed-Effects Meta-Analysis Model
Random-effects and fixed-effects models are two statistical approaches that are used to combine the study results. They are based on different assumptions.
A fixed-effects model assumes that all observed variation between the studies is because of chance (Riley et al. 2011) and that there exists only one true underlying effect. In other words, the variation between the study results is only because of variation in sample sizes. This assumption is reflected in the calculations of the study weights. Larger studies receive more weight.
A random-effects model allows that the underlying effect size differs between studies, thus an effect size can truly be larger or smaller depending on the study characteristics. This heterogeneity is reflected by I2 and was discussed above. The assumption that effect sizes truly differ is in general not implausible, because studies may have used different doses, routes of administration, animals, or procedures, or there may be other, unknown differences. The random-effects model results in an “average” effect estimate, whereas the fixed-effects model results in an estimate of the one, true, underlying effect (Higgins et al. 2009; Riley et al. 2011). The confidence interval of a random-effects estimate will reflect that there is some possible variation in the true study effects besides chance alone and, therefore, may be wider than that of a fixed-effects estimate. The two sources of variance are also taken into account in the assigned study weights.
Whether a fixed-effects or a random-effects model will be used must be decided before the meta-analysis is performed, and although one may be tempted to look at the level of I2, the decision must be a priori (Higgins et al. 2003) and based on substantive arguments, independent of the level or significance of I2 (Riley et al. 2011). Due to the nature of and diversity in animal studies, random-effects models may better reflect reality.
Once the meta-analysis is done, the interpretation of the results should be consistent with the model that was chosen. Take, for example, a fixed-effects meta-analysis comparing treatments A and B, that results in a mean difference of 1.75 and a 95% CI from 1.5 to 2. Here, 1.75 is the best estimate of the common treatment effect, and the CI reflects the uncertainty around this estimate. As zero is not in the CI, we can be quite sure that treatment A is superior to B. However, if the same numbers are the result of a random-effects meta-analysis, the interpretation is different. Now we can be rather sure that, on average, treatment A is superior to B, but the true treatment effect may differ between settings. See Higgins and colleagues (2009) and Riley and colleagues (2011) for more information.
F. Specify Subgroups, if Applicable
Sometimes it is expected that the effect size varies across subsets of studies, for instance, if there are variations between species or between dosages or administration routes of an intervention. In other cases, we may observe heterogeneity in the results of the meta-analysis and want to find an explanation. In both situations, subgroup analysis or meta-regression may give insight in the relation between study characteristics and the effect size. For example, our forest plot shows separate subgroups for studies that assessed the amount of neuronal cell death in the cortex and in the hippocampus. This stratified meta-analysis partitions the heterogeneity and shows that the estimated between-study variation is smaller in the subgroups: τ2 in the subgroups is 0.38 and 0.56, whereas τ2 in the pooled analysis is larger than the sum: 1.27. This suggests that there may be subgroup differences, which is confirmed by the test for subgroup differences.
Subgroup analyses play a very important role in meta-analyses of animal studies. This is to some extent due to the exploratory character of animal studies, but also related to the aims of meta-analyses of animal studies. Many meta-analyses are especially conducted to investigate which factors influence the effect size. If subgroups significantly differ in the effects, this may be an indication not to pool the overall results. It is, however, important to realize that the results of subgroup analyses can be misleading, especially if subgroups are not prespecified. When subgroup analyses are not prespecified, the risk of false positive findings (i.e., nonexisting relations between effect size and study characteristics) increases. Further, subgroup analyses are often observational and not based on randomized comparisons (Deeks et al. 2008a). In addition, subgroup analyses are often conducted on small numbers of studies, which impairs the power of the analyses. Therefore, the results should be interpreted with caution (Reade et al. 2008). Results of subgroups are hypothesis generating.
G. Calculate the Summary Effect, Per Subgroup and Overall
In general, the summary effect size is based on the effect sizes and the weights of the individual studies. It can be calculated by hand, but there are also packages that will perform the calculations and provide forest plots, for example RevMan (www.ims.cochrane.org/revman/download), which is free software developed by the Cochrane Collaboration. CMA (Comprehensive meta-analysis [www.meta-analysis.com]) is not free but offers simpler data entry and more options than RevMan. Stata (StataCorp, College Station, TX) and R (www.R-project.org/) also provide meta-analysis packages. In case of more complicated designs, like multiple treatment groups sharing one control group, or studies with two control groups instead of one, it is advisable to consult a statistician.
The way the weights of the individual studies are calculated for the overall analyses is dependent of the model (fixed-effects or random-effects) that was chosen (step E). In random-effects models, small studies get larger weights and are thus relatively more important than in fixed-effects models.
If heterogeneity is the main topic of interest, differences between subgroups are of special importance. Subgroup analyses or meta-regression of the outcome in relation to study characteristics (e.g., species) can give more insight into possible causes of heterogeneity but should be conducted with caution (see step F).
If the results of the selected studies are considered too heterogeneous for pooling, a comparison between the number of studies with findings in one direction, and those with findings in the other direction (irrespective of whether or not the findings were significant) can be done with a sign test (Borenstein et al. 2009b). If pooling of the studies is considered completely inappropriate, no combined estimate can be provided.
H. Conduct a Sensitivity Analysis
A sensitivity analysis is conducted to assess the robustness of the findings from the meta-analysis. Assumptions underlying the initial meta-analysis can be challenged by performing another meta-analysis with different assumptions. If the results of both meta-analyses are similar, then they seem robust. For example, a scientist decided that the duration of an intervention might affect the results. Initially, a short intervention was defined as between 0 and 45 minutes. In the sensitivity analyses, the threshold was set at 30 minutes. What happens to the results if the threshold is changed? When the conclusions of a meta-analysis significantly change, this should be discussed.
Also, the quality of the primary studies is crucial for the reliability of the meta-analysis results and can be assessed with a variety of tools (Hooijmans et al. 2014; Krauth et al. 2013). If some of the studies are suspected to present biased results, the meta-analysis can be performed once without those studies in order to investigate the robustness of the combined result.
I. Minimize Publication Bias
Reliability of results can also be diminished by unpublished studies or unpublished parts of studies. The risk of publication bias can be estimated by means of funnel plots (Reade et al. 2008). Funnel plots are also provided by standard software for meta-analysis.
At the start of the systematic review, a serious attempt to gather all relevant study results must be made, in order to minimize possible reporting bias. Reporting bias, or publication bias, is the consequence of not all relevant data being available. In general, the decision to publish study results may depend on the direction of the study results, and negative studies, which are often relatively small in sample size, are sometimes not published. In case of publication bias, meta-analyses may overestimate the true effect size (Sena, van der Worp et al. 2010). Publication bias is no less of an issue for animal studies than for human studies (ter Riet et al. 2012).
J. Interpretation of Results
A meta-analysis will result in a summary or overall effect with a 95% CI and a p value. In our forest plot, the overall effect was a standardized mean difference of −1.71, with a 95% CI ranging from −2.66 to −0.77 (arrow C). The pooled estimate, −1.71, is an average effect, and effects of the original studies will be spread out around this average effect. The summary effect of a meta-analysis is expressed as a number, for example, an OR of 0.6. However, in animal studies, it is often wiser to focus on the direction of the effect than on the size itself. This is in large parts due to the unavoidable heterogeneity between animal studies (large variation in species, intervention protocols, etc.) and the exploratory nature of animal studies compared to clinical research.
The confidence interval contains all likely effect sizes. If a 95% CI for an OR ranges from 0.4 to 0.9, this means that the true effect is most likely an OR between 0.4 and 0.9. If the 95% CI of an OR contains the value 1 or the 95% CI of mean difference contains the value 0, this means that the treatment groups are not statistically significantly different at a significance level of 5%. This is also reflected in a p value above 0.05. If groups are not statistically significantly different, this does not necessarily mean that the treatment groups are similar; the only conclusion that can be drawn from the meta-analysis is that there is insufficient evidence to prove that the groups are different. Note that, in general, in case of multiple testing, the significance level should decrease.
Interpretation of the results of subgroup analyses (steps F and G) is even more challenging. Subgroups in meta-analyses of animal studies are often very small and remain quite heterogeneous as multiple characteristics in animal studies vary. Results of subgroup analyses should therefore be used to generate rather than test hypotheses.
The forest plot resulted in a p value of 0.0004 for the overall intervention effect. In general, a p value below 0.05 means that the treatment groups are statistically significantly different. However, this does not necessarily mean that the groups are different in a relevant way. It may be that the meta-analysis was based on many studies and thus had high power, whereas the effect size was only minor. In such a situation the meta-analysis will result in a p value below 0.05, but the difference between the interventions may be irrelevant. Therefore, not only the p value but especially knowledge of the direction and size of the effect including the 95% CI are essential for the interpretation.
Another result of the meta-analysis is the extent of heterogeneity, presented with τ2 and I2, and tested with a chi-squared test. In this paper we focus on I2, a reflection of the inconsistency between the effects estimated by the individual studies in a meta-analysis. It describes the percentage of total variation across studies that is due to heterogeneity rather than chance, and lies between 0% and 100%. A value of 0% indicates no observed heterogeneity, larger values show increasing heterogeneity (Higgins et al. 2003). When I2 is 40%, for example, this means that 40% of the observed variation of the study effects is due to heterogeneity (τ2) and 60% due to chance. An I2 value near 100% means that the observed variation of the study effects is almost completely due to heterogeneity. The Cochrane Handbook (Deeks et al. 2008b) states that an I2 between 50% and 90% might be interpreted as substantial heterogeneity. In this case, it may be useful to evaluate whether some study characteristics may be the reason of this high heterogeneity, in order to prevent this in future animal studies. Note, however, that when a subgroup is found that seems to be the cause of the variation between the study results, this should be interpreted with caution.
Finally, the strength of the conclusions from the meta-analysis also depends on the findings of the sensitivity analysis (H) and the evaluation of possible publication bias (I).
Conclusion
In this paper we address why meta-analyses of animal studies are a valuable addition for science aimed at improving health and healthcare. By conducting a meta-analysis of animal experiments, often new and very valuable information can be obtained from the already-published animal experiments. In other words, the decision not to conduct a meta-analysis of animal studies may result in a waste of information, animals, and financial resources.
The steps of a meta-analysis of animal studies are in general comparable to the steps taken in a clinical meta-analysis, and software designed for clinical meta-analyses can be used for most of these steps. It is important that only sensible comparisons are made in order to reduce the risk of false positive findings and diminish heterogeneity. It is therefore important to conduct meta-analysis always in collaboration with an expert from the field.
Furthermore, it is very important that each scientist conducting a meta-analysis of animal studies realizes that the quality of a meta-analysis is also dependent on the quality of the primary studies. Especially if the purpose of the meta-analysis is to inform healthcare policy or practice, the original research needs to be both applicable and of sufficient quality. On the other hand, if the primary studies appear to be biased, meta-analyses may provide the empirical evidence for the impact of the bias. This might stimulate the use of adequate experimental design in future animal studies. As we learned from systematic reviews in the clinical field (Mullen and Ramirez 2006), it is to be expected that the methodological quality of animal studies will increase as a consequence of conducting systematic reviews.
Briefly summarizing: meta-analyses of animal studies expand the knowledge resulting from animal experiments.
Acknowledgments
This article was published Open Access, thanks to the support of the Netherlands Organisation for Scientific Research (NWO).
References
- Bebarta V, Luyten D, Heard K. Emergency medicine animal research: does use of randomization and blinding affect the results? Acad Emerg Med. 2003;10:684–687. doi: 10.1111/j.1553-2712.2003.tb00056.x. [DOI] [PubMed] [Google Scholar]
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Introduction to Meta Analysis. Chichester, UK: John Wiley & Sons; 2009a. Cumulative Meta-Analysis. [Google Scholar]
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Introduction to Meta-Analysis. Chichester, UK: John Wiley & Sons; 2009b. Meta-analysis Methods Based on Direction and P-values. [Google Scholar]
- deVries RB, Hooijmans CR, Tillema A, Leenaars M, Ritskes-Hoitinga M. A search filter for increasing the retrieval of animal studies in Embase. Lab Anim. 2011;45:268–270. doi: 10.1258/la.2011.011056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- deVries RB, Hooijmans CR, Tillema A, Leenaars M, Ritskes-Hoitinga M. Updated version of the Embase search filter for animal studies. Lab Anim. 2014;48:88. doi: 10.1177/0023677213494374. [DOI] [PubMed] [Google Scholar]
- Deeks JJ, Higgins JPT, Altman DG. Analysing data and undertaking meta-analyses. In: Higgins JPT, Green S, editors. Cochrane Handbook for Systematic Reviews of Interventions. Chichester, UK: John Wiley & Sons; 2008a. [Google Scholar]
- Deeks JJ, Higgins JPT, Altman DG. Identifying and assessing heterogeneity. In: Higgins JPT, Green S, editors. Cochrane Handbook for Systematic Reviews of Interventions. Chichester, UK: John Wiley & Sons; 2008b. [Google Scholar]
- Higgins JPT, Deeks JJ, Altman DG. Special topics in statistics. In: Higgins JPT, Green S, editors. Cochrane Handbook for Systematic Reviews of Interventions. Chichester, UK: John Wiley & Sons; 2008. [Google Scholar]
- Higgins JPT, Green S. Cochrane Handbook for Systematic Reviews of Interventions. Chichester, UK: John Wiley & Sons; 2008. [Google Scholar]
- Higgins JPT, Thompson SG, Deeks JJ, Altman DG. Measuring inconsistency in meta-analyses. BMJ. 2003;327:557–560. doi: 10.1136/bmj.327.7414.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higgins JPT, Thompson SG, Spiegelhalter DJ. A re-evaluation of random-effects meta-analysis. JR Stat Soc Ser A Stat Soc. 2009;172:137–159. doi: 10.1111/j.1467-985X.2008.00552.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooijmans CR, Rovers MM, deVries RB, Leenaars M, Ritskes-Hoitinga M, Langendam MW. SYRCLE's risk of bias tool for animal studies. BMC Med Res Methodol. 2014;14:43. doi: 10.1186/1471-2288-14-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooijmans CR, Tillema A, Leenaars M, Ritskes-Hoitinga M. Enhancing search efficiency by means of a search filter for finding all studies on animal experimentation in PubMed. Lab Anim. 2010;44:170–175. doi: 10.1258/la.2010.009117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn J, de Haan RJ, Vermeulen M, Luiten PG, Limburg M. Nimodipine in animal model experiments of focal cerebral ischemia: a systematic review. Stroke. 2001;32:2433–2438. doi: 10.1161/hs1001.096009. [DOI] [PubMed] [Google Scholar]
- Hozo SP, Djulbegovic B, Hozo I. Estimating the mean and variance from the median, range, and the size of a sample. BMC Med Res Methodol. 2005;5:13. doi: 10.1186/1471-2288-5-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannidis JP, Lau J. Can quality of clinical trials and meta-analyses be quantified? Lancet. 1998;352:590–591. doi: 10.1016/S0140-6736(98)22034-4. [DOI] [PubMed] [Google Scholar]
- Kilkenny C, Parsons N, Kadyszewski E, Festing MF, Cuthill IC, Fry D, Hutton J, Altman DG. Survey of the quality of experimental design, statistical analysis and reporting of research using animals. PLoS One. 2009;4:e7824. doi: 10.1371/journal.pone.0007824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krauth D, Woodruff TJ, Bero L. Instruments for assessing risk of bias and other methodological criteria of published animal studies: a systematic review. Environ Health Perspect. 2013;121:985–992. doi: 10.1289/ehp.1206389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau J, Antman EM, Jimenez-Silva J, Kupelnick B, Mosteller F, Chalmers TC. Cumulative meta-analysis of therapeutic trials for myocardial infarction. N Engl J Med. 1992;327:248–254. doi: 10.1056/NEJM199207233270406. [DOI] [PubMed] [Google Scholar]
- Leenaars M, Hooijmans CR, van Veggel N, ter Riet G, Leeflang M, Hooft L, van der Wilt GJ, Tillema A, Ritskes-Hoitinga M. A step-by-step guide to systematically identify all relevant animal studies. Lab Anim. 2012;46:24–31. doi: 10.1258/la.2011.011087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mapstone J, Roberts I, Evans P. Fluid resuscitation strategies: A systematic review of animal trials. J Trauma. 2003;55:571–589. doi: 10.1097/01.TA.0000062968.69867.6F. [DOI] [PubMed] [Google Scholar]
- Mullen PD, Ramirez G. The promise and pitfalls of systematic reviews. Annu Rev Public Health. 2006;27:81–102. doi: 10.1146/annurev.publhealth.27.021405.102239. [DOI] [PubMed] [Google Scholar]
- Netherlands Food and Consumer Product Safety Authority. Zodoende 2012; Annual review of the Dutch Food and Consumer Product Safety Authority on animal experiments and laboratory animals. 2013. Utrecht.
- Nordmann AJ, Kasenda B, Briel M. Meta-analyses: what they can and cannot do. Swiss Med Wkly. 2012;142:w13518. doi: 10.4414/smw.2012.13518. [DOI] [PubMed] [Google Scholar]
- Perera R, Heneghan C. ACP Journal Club. Interpreting meta-analyses in systematic reviews. Ann Intern Med. 2009;150:JC2–2. doi: 10.7326/0003-4819-150-4-200902170-02002. JC2–3. [DOI] [PubMed] [Google Scholar]
- Peters JL, Sutton AJ, Jones DR, Rushton L, Abrams KR. A systematic review of systematic reviews and meta-analyses of animal experiments with guidelines for reporting. J Environ Sci Health B. 2006;41:1245–1258. doi: 10.1080/03601230600857130. [DOI] [PubMed] [Google Scholar]
- Reade MC, Delaney A, Bailey MJ, Angus DC. Bench-to-bedside review: avoiding pitfalls in critical care meta-analysis–funnel plots, risk estimates, types of heterogeneity, baseline risk and the ecologic fallacy. Crit Care. 2008;12:220. doi: 10.1186/cc6941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley RD, Higgins JP, Deeks JJ. Interpretation of random effects meta-analyses. BMJ. 2011;342:d549. doi: 10.1136/bmj.d549. [DOI] [PubMed] [Google Scholar]
- Ritskes-Hoitinga M, Leenaars M, Avey M, Rovers M, Scholten R. Systematic reviews of preclinical animal studies can make significant contributions to health care and more transparent translational medicine. Cochrane Database Syst Rev. 2014;3:ED000078. doi: 10.1002/14651858.ED000078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandercock P, Roberts I. Systematic reviews of animal experiments. Lancet. 2002;360:586. doi: 10.1016/S0140-6736(02)09812-4. [DOI] [PubMed] [Google Scholar]
- Sena ES, Briscoe CL, Howells DW, Donnan GA, Sandercock PA, Macleod MR. Factors affecting the apparent efficacy and safety of tissue plasminogen activator in thrombotic occlusion models of stroke: systematic review and meta-analysis. J Cereb Blood Flow Metab. 2010;30:1905–1913. doi: 10.1038/jcbfm.2010.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sena ES, van der Worp HB, Bath PM, Howells DW, Macleod MR. Publication bias in reports of animal stroke studies leads to major overstatement of efficacy. PLoS Biol. 2010;8:e1000344. doi: 10.1371/journal.pbio.1000344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ter Riet G, Korevaar DA, Leenaars M, Sterk PJ, Van Noorden CJ, Bouter LM, Lutter R, Elferink RP, Hooft L. Publication bias in laboratory animal research: a survey on magnitude, drivers, consequences and potential solutions. PLoS One. 2012;7:e43404. doi: 10.1371/journal.pone.0043404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vesterinen HM, Sena ES, Egan KJ, Hirst TC, Churolov L, Currie GL, Antonic A, Howells DW, Macleod MR. Meta-analysis of data from animal studies: A practical guide. J Neurosci Methods. 2013;221C:92–102. doi: 10.1016/j.jneumeth.2013.09.010. [DOI] [PubMed] [Google Scholar]
- Wever KE, Menting TP, Rovers M, van der Vliet JA, Rongen GA, Masereeuw R, Ritskes-Hoitinga M, Hooijmans CR, Warle M. Ischemic preconditioning in the animal kidney, a systematic review and meta-analysis. PLoS One. 2012;7:e32296. doi: 10.1371/journal.pone.0032296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winston R. Animal experiments deserve a place on drug labels. Nat Med. 2013;19:1204. doi: 10.1038/nm1013-1204. [DOI] [PubMed] [Google Scholar]