Abstract
There is growing interest in the study of individual differences in face recognition, including one of its hallmarks, holistic processing, which can be defined as a failure of selective attention to parts. These efforts demand that researchers be aware of, and try to maximize, the reliability of their measurements. Here we report on the reliability of measurements using the composite task (complete design), a measure of holistic processing that has been shown to have relatively good validity. Several studies have used the composite task to investigate individual differences, yet only one study has discussed its reliability. We investigate the reliability of composite task measurements in eight datasets from five different samples of subjects. In general, we found reliability to be fairly low but there was substantial variability across experiments. Researchers should keep in mind that reliability is a property of measurements, not a task, and the ways in which measurements in this task may be improved, before embarking on individual differences research.
Introduction
Faces, unlike many of the visual stimuli that we encounter each day, are processed holistically. That is, we are unable to attend to a single face part when it is presented in the context of a whole face; rather, numerous behavioral studies have revealed interference from the ostensibly unattended face parts. In a seminal paper, Young, Hellawell, and Hay (1987) found that subjects were slower to identify a face half (e.g., top or bottom) when it was aligned with the complementary half of a different face than when the two halves were misaligned. In contrast, in similar paradigms but in the absence of extensive experience or training, such effects are not seen for other visual object categories: subjects can selectively attend to parts of these objects without difficulty. Holistic processing may offer an insight into what is special about face recognition (McKone, Kanwisher, & Duchaine, 2007; Richler, Cheung, & Gauthier, 2011b), explain what is different about populations with particularly poor face recognition abilities (e.g. Busigny, Joubert, Eelician, Ceccaldi, & Rossion, 2010; Gauthier, Klaiman, & Schultz, 2009; Palermo et al., 2011), or shed light on what is learned when we become experts with a particular category of objects (Gauthier, Williams, Tarr, & Tanaka, 1998; Richler, Wong, & Gauthier, 2011; Wong, Palmeri, & Gauthier, 2009).
One issue that has complicated progress in understanding holistic processing is that there are numerous different meanings and measures of holistic processing in the literature (see Richler, Palmeri, & Gauthier, 2012 for a review). Perhaps the best validated of these measures is the complete design of the composite task1 (Gauthier & Bukach, 2007). Like Young et al.'s (1987) task, described above, this task involves making decisions about one half of a composite face while ignoring the other half. Faces are presented sequentially; a study face composed of two face halves is shown, followed by a blank screen or mask, and then a test face. The task is to indicate by button press whether the cued half of the test face is the same as, or different from the study face. Both the cued and the to-be-ignored face parts can be associated with the same correct response (both parts same or both parts different; congruent trials), or with different correct responses (one part same, the other part different; incongruent trials). Holistic processing is defined by an interaction between congruency and alignment. On congruent trials, a failure to selectively attend to the cued part should facilitate performance, whereas, on incongruent trials, a failure to selectively attend to the cued part should hinder performance. This difference in performance between congruent and incongruent trials is reduced on misaligned trials (e.g., Richler, Tanaka, Brown, & Gauthier, 2008). Finally, it is worth noting that, while we refer to the observed behavior as a failure of selective attention, it does not necessarily imply that the mechanism is attentional. The congruency effect observed in this task may be the result of attentional (Chua, Richler, & Gauthier, in press) or perceptual (Rossion, 2013) mechanisms.
The complete design is a good candidate for a measure of holistic processing as not only does it have good face validity but it also captures an effect that is specific to faces and objects of expertise (e.g. Gauthier, Williams, Tarr, & Tanaka, 1998; Richler, Wong, & Gauthier, 2011; Wong, Palmeri, & Gauthier, 2009). In addition, studies that have investigated the relationship between face recognition ability, measured with the Cambridge Face Memory Test (CFMT; Duchaine & Nakayama, 2006), and holistic processing measured with the complete design have reported a robust relationship between the two (DeGutis, Wilmer, Mercado, Cohan, 2013; McGugin, Richler, Herzmann, Speegle & Gauthier, 2012; Richler et al., 2011b), again suggesting that it measures something that is relevant to understanding face recognition.
However, beyond the issue of validity, conclusions in individual differences studies must be evaluated in the light of another basic concern, that of the reliability of the measurements. There are several reasons to think that the reliability of holistic processing measured using the composite task may be fairly low. First, the measure of holistic processing, congruency x alignment, is calculated by subtracting the difference between congruent and incongruent misaligned trials from the difference between congruent and incongruent aligned trials (e.g. Richler et al., 2011b). Unfortunately, difference scores are often less reliable than the scores from which they are computed (Peter, Gilbert, Churchill, & Brown, 1993), though this depends on the reliability, and the relative variability, of the constituent measures (Malgady & Colon-Malgady, 1991; Rogosa, Brandt, & Zimowski, 1982). Second, while there is only one published report of the reliability of measurements using the complete design of the composite task (DeGutis et al., 2013), it was low enough to raise concerns for anyone interested in doing individual differences work (Guttmans λ2 value of .102). In that case, the authors were looking for a relationship between subjects’ CFMT score and their composite task score. Fortunately, the CFMT was highly reliable (λ2 = .88), which together led to a theoretical upper limit for the correlation between them, computed as the geometric mean of the two reliabilities (Schmidt & Hunter, 1996), of ~0.3. Such low reliability could be prohibitive if researchers wish to relate composite task performance with anything less reliable. It would also reduce the power to find such relationships, as well as the power to find a difference between this and other relationships.
DeGutis et al. (2013) suggested one method that may improve the reliability of these measurements. Rather than using a difference of differences (i.e., aligned congruency effect – misaligned congruency effect) they suggested that it might be better to use the residuals (i.e., regress the congruency effect for misaligned trials out of the congruency effect for aligned trials). Their reasoning, which was mainly driven by considerations of validity, was that the misaligned condition is a control condition which should not contribute as much as the aligned condition to the final estimates of holistic processing – rather it makes more sense to partial out the variability in the misaligned condition, presumed to be irrelevant to holistic processing, which may be present in both conditions. More importantly for the current discussion, DeGutis et al. (2013) found that the reliability of the regression measure of holistic processing was higher than that for the difference measure (λ2 = .24).
Here, we aim to investigate the reliability of the composite task measure of holistic processing in five experiments (eight datasets) from our lab. We also aim to explore whether regression always provides a more reliable measure of holistic processing than difference scores.
Method
Studies
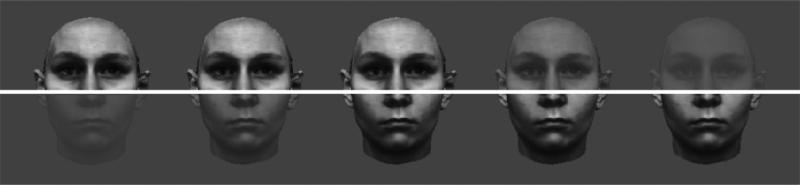
We use data from five different experiments, with four of these experiments including two independent measurements of holistic processing from the same sample of subjects and taken from blocks of trials separated by a few minutes (Table 1). The first 3 experiments come from unpublished datasets and used task parameters that are relatively standard and commensurate with the several dozens of uses of this task in the literature. In contrast, experiments 4 and 5 used modified designs with the explicit motivation to explore whether such changes might produce better reliability. Specifically, in Expt. 4 we manipulated the contrast of the tops and bottoms (details in stimuli section) with the aim of getting more variability in each trial in order to better cover the range of holistic processing ability in the population (see Figure 1). We hypothesized that varying the contrast of the top or bottom would make it more or less difficult to selectively attend to a given part by reducing or increasing its saliency. For example, it might be easier to attend to the top part of a face (i.e. ignore the bottom part) if the bottom part is low contrast, that is, it might be less distracting. Likewise, attending to the top part may be more difficult if it is low contrast and the bottom is high contrast. Thus, we hypothesized that this manipulation could add more variability into the trials, such that on some trials almost everybody might show some evidence of holistic processing, and on other trials only a subset of people would show evidence of holistic processing. Indeed, while such variability in trials is not usually a consideration for group analyses it is central to the idea of measuring individual differences. In Expt. 5 we restricted the number of different face parts (tops and bottoms) to five, rather than 20 as in the other experiments. The rationale was that there may be variability in learning across subjects, over the course of an experiment, and using fewer faces may cause subjects’ performance to asymptote more quickly, reducing the influence of such effects. The various task parameters are listed in Table 1 and discussed below.
Table 1.
Demographics and experiment design in each of the five experiments.
| Stimulus Set | N | Age(SD) | Sex (m/f) | Number of Faces | Fixation (ms) | Study (ms) | Mask (ms) | Test (ms) |
|---|---|---|---|---|---|---|---|---|
| Expt 1. | ||||||||
| MPI female | 85 | 21.0(3.4) | 33/52 | 20 | 200 | 200 | 2000 | 200 |
| G&R | ||||||||
| Expt 2. | ||||||||
| MPI female | 67 | 21.3(3.3) | 25/42 | 20 | 200 | 200 | (blank) 500 | 200 |
| MPI female | ||||||||
| Expt 3. | ||||||||
| MPI female | 91 | 22.5( 4.3) | 27/39 | 20 | 200 | 200 | (blank) 500 | 200 |
| G&R | ||||||||
| Expt 4. | ||||||||
| MPI female | 53 | 24.5(6.8) | 18/35 | 20 | 200 | 200 | 1000 | 150 (or less) |
| MPI male | ||||||||
| Expt 5. | ||||||||
| MPI female | 43 | 19.3(2.1) | 6/33 | 5 | 200 | 200 | (blank) 500 | 200 |
Figure 1.
Sample stimuli used in Expt. 4.
Stimuli
Face images in each experiment were either drawn from the Max Planck Institute Database (MPI, Troje & Bulthoff, 1996) or from a set of 20 face stimuli used by Goffaux & Rossion (G&R, 2006). Both the male and female MPI faces were used, but not within the same experiment (see Table 1). In the Goffaux & Rossion (2006) stimulus set, the male and female faces were intermixed within a single study block. In all cases the stimuli were converted to grayscale and cut in half to produce a set of top and bottom halves, which were randomly recombined on every trial. The faces were also all cropped to remove hair, in the case of the MPI faces they retained some external features (ears, jaw shape, neck) whereas the Goffaux & Rossion (2006) faces had all external features removed. Recombined faces were presented on a grey background with a white line separating the top and bottom halves. Misaligned stimuli were created by horizontally offsetting the top and bottom half such that the edge of one half fell approximately in the center of the other half (see Table 1 for more details of the stimuli/design in the each experiment).
In addition to this standard stimulus construction, the top and bottom face parts used in Expt. 4 were adjusted to create three different levels of contrast (Full, Medium and Low). These parts were then combined to create five possible stimulus types: Top-Full/Bottom-Low, Top-Full/Bottom-Med, Top-Full/Bottom-Full, Top-Med/Bottom-Full and Top-Low/Bottom-Full (see Figure 1). As described earlier, this manipulation was designed so that some trials (when the relevant part is lower in contrast) may provide more information to discriminate subjects with a presumed low degree of holistic processing, whereas other trials (where the relevant part is higher in contrast) may provide more information to discriminate subjects with a presumed high degree of holistic processing. In Expt. 5, all faces were shown with a single level of contrast as in Expts. 1 to 3, but we used only 5 top halves and 5 bottom halves for the entire experiment. Reducing the set of face parts was done in the hope that this would reduce spurious variability attributable to subjects learning to identify the larger set of face parts over the course of the experiment.
Procedure
For all experiments, on each trial, a fixation cross was presented (200ms), followed by a study face (200ms) and then either a mask or a blank screen for 500 – 2000ms, depending on the experiment (see Table 1). Next , a test face was presented for 200ms, with the exception of Expt. 5 in which the test face was presented for 150ms (this was done to try to avoid ceiling, since there may be faster learning of individual parts in this experiment) . In all cases, subjects were instructed to respond by key press if the top part of the test face matched the top part of the study face. In Expt. 1, 2, 3 and 4, there were two blocks using different stimuli (see table 1). The blocks were separated by a screen instructing participants that they could take a break if they wished (the order of blocks was the same for all participants). As the number of trials influences reliability and all of the reported experiments contained at least 160 trials, we decided to only analyze the first 160 trials in each experiment (it is also close to the 144 trials used by DeGutis et al, 2013), with 40 trials in each of the experimental conditions (congruent-aligned, incongruent-aligned, congruent-misaligned, and incongruent-misaligned).
Results
We first checked each dataset, removing any univariate or multivariate outliers and confirming that at the group level all five of our experiments showed the typical congruency x alignment interaction (see Table 2). The present effect sizes are comparable to those in prior studies (a meta-analysis of 48 experiments found an effect size for versions of this task for upright faces of eta2partial =.31, Richler & Gauthier, submitted). Next, individual scores for holistic processing were calculated both by subtracting the congruency effect in misaligned d’ (congruent misaligned – incongruent misaligned) from the congruency effect in aligned d’ (congruent aligned – incongruent aligned), and by regressing the congruency effect for misaligned trials from the congruency effect for aligned trials. Both subtraction (Konar et al., 2010; Richler et al., 2011b) and regression (De Gutis et al., 2013) methods have been reported in individual differences work in the literature.
Table 2.
Group level analysis and split-half reliability in each of the five studies. Note that as we only had one data set from subjects in Expt. 5, we do not report split half reliability. Holistic processing is calculated as the interaction between congruency and alignment.
| Stimulus Set | Subjects Included | Holistic processing (Δd′, σ) | p-Value | Effect size (eta2partial) | Split-Half Subtraction | Split-Half Regression |
|---|---|---|---|---|---|---|
| Expt 1. | ||||||
| MPI female | 76/85 | 0.30 (0.96) | <.05 | 0.09 | 0.05 | 0.13 |
| G&R | 77/85 | 0.53 (0.98) | <.05 | 0.22 | ||
| Expt 2. | ||||||
| MPI female | 60/67 | 0.53 (1.00) | <.05 | 0.21 | 0.04 | 0.11 |
| MPI female | 60/67 | 0.90 (0.84) | <.05 | 0.53 | ||
| Expt 3. | ||||||
| MPI female | 89/91 | 0.58 (0.86) | <.05 | 0.31 | 0 | 0.15 |
| G&R | 86/91 | 0.81 (0.89) | <.05 | 0.46 | ||
| Expt 4. | ||||||
| MPI female | 52/53 | 0.18 (1.20) | > .05 | 0.02 | 0 | 0.12 |
| MPI male | 50/53 | 0.52 (0.81) | < .05 | 0.29 | ||
| Expt 5. | ||||||
| MPI female | 40/53 | 0.86 (0.93) | < .05 | 0.46 |
We calculated the reliability of the composite task in two ways. First, we used a split-half measure of reliability, making use of the four experiments in which we had two independent samples (with the same participants) and calculating the correlation between d’ scores in the two parts (these are expected to present low estimates of reliability because the stimulus sets differ). We did this using both the difference scores and the residuals (Table 2).
Second, following DeGutis et al. (2013) we used Guttmans λ2, which may provide a more appropriate measure of reliability in the composite task than Cronbach's alpha, because it is robust when measures include multiple factors (Callender & Osburn, 1979). Because failures of selective attention indicative of holistic processing are observed on aligned trials, and are significantly reduced or abolished on misaligned trials, in the following calculations the congruency effect on aligned trials is considered to be the primary measure, and the congruency effect on misaligned trials is considered as the control measure.
The formula we used to calculate the of reliability of the difference score, ρ(D), took the difference in variance between the primary measure, ρ(X1), and the control measure, ρ(X2), into account (see Rogosa et al., 1982):
| (1) |
Whereby, σx1 is the standard deviation of the primary measure, σx2 is the standard deviation of the control, and ρx1x2 is the correlation between the primary and control condition.
In contrast, the formula we used to calculate the reliability of the residuals, ρ(U), did not directly include any terms to describe the variance of the primary and control conditions, as they do not effect the reliability of regression (Malgady & Colon-Malgady, 1991)3:
| (2) |
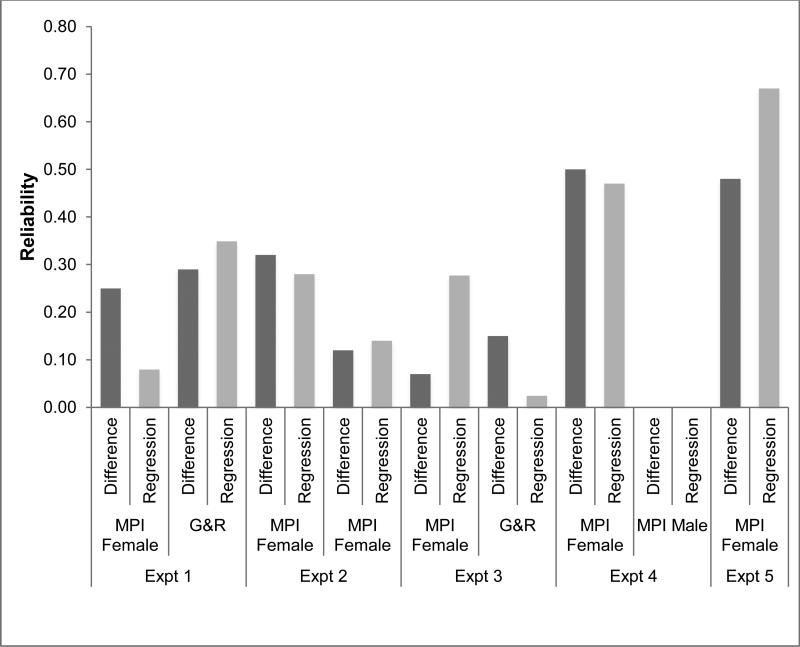
Figure 2 summarizes the results of the difference-score and residual reliability calculations using both formulas, as well as the split-half measure of reliability within each dataset and across the two datasets in experiments 1, 3 and 4. It is worth noting that some of the computed reliability estimates were n computed reliability estimates were negative. However, as i t is generally accepted that negative values are not theoretically meaningful, these values are displayed as zero (see Discussion). as zero (see Discussion) Reliability (λ2) for the difference scores (dark grey bars) ranged between -0.22 and 0.50, μ = 22, 95% CI [7.63, 36.37], and the reliability of the residuals (light grey bars) ranged between -0.54 and 0.57, μ = 19, 95% CI [-3.21, 41.21]. While we have included the mean and 95% CIs, as it may be of interest to some readers, it is important not to interpret these values as reflecting the reliability of the composite task. Fundamentally, reliability is a property of the measurement. While the reliability of the two measures are highly correlated (r = 0.90), as would be expected because both depend at least on the variability of the aligned congruency effect, in four of the nine datasets (Expt. 1 MPI, Expt. 2 MPI female, Expt. 3 G&R., & Expt. 4 MPI female) we found female that difference scores were more reliable. This is perhaps surprising, as a number of authors have suggested that residuals may be more reliable than difference scores (DeGutis et al., 2013; Peter et al., 1993).
Figure 2.
Reliability (Guttmans λ2) across the eight datasets calculated using difference scores and regression. Note that negative reliability estimates have been set to zero as values less than zero are generally assumed not to be theoretically meaningful.
Discussion
Here we have reported the reliability of the composite task in five different experiments (nine datasets). Perhaps most striking is that reliability often appears to be fairly poor, and it is also quite variable from experiment to experiment. This might be surprising to anyone tempted to consider reliability as a property of a task, but this is not a valid interpretation, since reliability is a property of measurements and is sample-dependent. However, the considerable range in reliability we obtain cannot solely be attributed to sample differences (which, we should point out, were all samples from the same undergraduate population). While the differences in reliability between Expts. 2 and 3 with MPI female faces can only be attributed to the samples (since the measure was identical), the differences between the two measurements for each of the three samples (in Expts. 1, 3 and 4) can only be attributed to the different face sets (or to an order effect), since all other task parameters were identical. Finally, beyond differences due to samples and the specific set of faces used in an experiment, our efforts to increase reliability by changing aspects of the task seems to also have had an influence. Indeed, the highest reliabilities we achieved were in Expts. 4 and 5, using the few faces and contrast manipulation designs that were explicitly motivated as efforts to increase reliability. This success is dampened by the fact that in Expt. 4, the contrast manipulation achieved a reasonable level of reliability with the female face set, and negative reliability with the male face set (this is despite holistic processing being obtained at the group level effect for male and not female faces). However, it is interesting to note that of all the tasks reported here, the measure of holistic processing in Expt 4 (using the contrast manipulated female MPI faces) had the most between participant variability, σ = 1.20. This goes someway towards supporting the idea that our manipulation was improved reliability by adding relevant variability in participants measured holistic processing. It is unclear whether to attribute this to an order effect: while Expts. 2 and 3 see some reduction in reliability from one block to the other, Expt. 1 shows the reverse pattern. This is also the only one of our experiments using this specific stimulus set (MPI males), and so we do not have sufficient bases to attribute this effect to the stimulus set either. As a whole, these results suggest that while it is generally inappropriate to quote the reliability of a task from prior work (Thompson, 1994), it is particularly inadequate in the context of this task. Like other tasks that rely on a comparison to a baseline (e.g., Stroop task, Eide, Kemp, Silberstein, Nathan, & Stough, 2002; Strauss, Allen, Jorgensen, Cramer, 2005), measurements of holistic processing using the composite task often result in poor reliability. Besides sample dependence, there appears to be an influence of the faces used, although we cannot explain why some faces yield more reliable measurements than others. Our explorations of contrast manipulations or using a few faces are encouraging and suggest that there may be ways to improve the reliability of such measurements by changing aspects of the paradigm, although the space of parameters that may have an influence is large, including for instance the number and discriminability of the faces involved, and the study, retention and maximum response durations, as well as other aspects of the tasks such as the relative contrast manipulation we used in Expt. 4. As it stands, a combination of using a few faces and/or the contrast manipulation we used, together with a larger number of trials, may help achieve reliabilities closer to .7, typically considered as acceptable in the early stages of construct validation research (Nunnally & Bernstein, 1994). Whenever possible, collecting more data from each subject should also increase reliability.
Unlike DeGutis et al. (2013), who found a large difference in the reliability of residuals compared to difference scores, we did not find much evidence to suggest that regression provides a more reliable measure of holistic processing than difference scores. In fact, there were a number of datasets in which the difference scores were more reliable than residuals. Whether residuals or difference scores are more reliable depends on the precise relationships between the component measures (Chiou, & Spreng, 1996; Llabre, Spitzer, Saab, Ironson & Schneiderman, 1991; Malgady & Colon-Malgady, 1991; Zimmerman, & Williams, 1998). Residuals are known to be , more reliable, albeit not by very much, when the reliability of the primary condition exceeds the reliability of the control condition, (Malgady & Colon-Malgady, 1991).
However, whether residuals or difference scores are preferred should not be entirely driven by concerns of reliability. Difference scores and residuals make different assumptions about what is being measured. Difference scores are fairly easy to interpret. Consider just the aligned trials in the composite task. In this case, taking the difference between the congruent and incongruent trials provides a measure of the congruency effect. Neither condition is obviously a baseline, since it is theoretically possible that congruency facilitates and incongruency hinders performance. That is, both conditions potentially contain useful information about the construct of interest, which is the degree to which the to-be-ignored part has an influence. Regressing out one of the conditions from the other would remove all the variance associated with that condition, and this is only appropriate if one assumes that all of the variance in the condition being regressed out is irrelevant to the construct of interest.
This decision is slightly more difficult in the case of regressing out performance on misaligned trials from aligned trials. On the one hand, misaligned trials are generally considered to be a baseline, with any variance in the congruency effect reflecting some general interference and not genuine holistic processing. On the other hand, if this were true, then it is not clear why the misaligned condition is necessary to measure individual differences in holistic processing (which is theoretically well defined by aligned congruent – aligned incongruent). Previous studies have shown that the misaligned condition is important for distinguishing face-like holistic processing from other kinds of interference effects in the composite task, for instance contextual influences on spatial attention (see Richler et al., 2011, for a review). One particularly problematic finding for the idea of the misaligned condition as a baseline is that, for non-face objects in novices, when the misaligned condition uses images that are misaligned at study and at test (rather than only at test, as in all experiments in the current paper), a congruency effect is obtained on both aligned and misaligned trials that are randomized together (Richler, Bukach & Gauthier, 2009). This congruency effect is not obtained for these objects in novices when the misaligned trials use an aligned study image, and it is not obtained on aligned trials when alignment is blocked, so these results indicate that the context of certain kinds of misaligned trials can influence performance on aligned trials. Until such issues are more fully understood, we would advise researchers interested in measuring holistic processing not to take one specific model for granted. Indeed, it may be that, in a normal population, the congruency effect for the misaligned trials is unrelated to the congruency effect for the aligned trials, in which case regressing it out does not achieve anything (Richler & Gauthier, submitted). Supporting this to some extent, in the current set of studies the Pearson's r correlation between the misaligned and aligned congruency effects were low, ranging between r = -0.19 – r = 0.20. In this case, collecting data for twice as many aligned trials might be much more productive then collecting data from misaligned trials, only to remove the small amount of variance shared between the aligned and misaligned conditions.
While individual differences research has a long history, it is not necessarily familiar territory for cognitive psychologists, especially in the area of high-level vision. Our results demonstrate that reliability can vary a great deal across different implementations of the composite task. We urge researchers interested in measuring individual differences in holistic processing not to rely on prior estimates of reliability but to report the reliability of their own measurements and to consider how said reliability constrains their claims.
Acknowledgements
This work was supported by the NSF (Grant SBE-0542013), VVRC (Grant P30-EY008126) and NEI (Grant R01 EY013441-06A2). We thank Riaun Floyd and Magen Speegle for help with data collection and stimulus construction, and Jeremy Wilmer and Joseph DeGutis for helpful discussions.
Footnotes
A version of the composite task featuring half the trials has been referred to as the “partial design” in the literature (Gauthier & Bukach, 2007), however, the partial design confounds response and congruency (all same trials are incongruent and all different trials are congruent), which has been found to be problematic because congruency produces a response bias which cannot be separated from sensitivity without the other half of the trials (see Cheung, Richler, Palmeri, & Gauthier, 2008; Richler, Cheung, & Gauthier, 2011a; Richler & Gauthier, in press).
Note that this reliability was computed for 144 trials, and we report reliabilities for 160 trials in the present work.
Note that DeGutis et al.'s (2013) reproduction of this formula included a minor error in which the primary and control conditions were switched.
References
- Busigny T, Joubert S, Felician O, Ceccaldi M, Rossion B. Holistic perception of the individual face is specific and necessary: evidence from an extensive case study of acquired prosopagnosia. Neuropsychologia. 2010;48:4057–4092. doi: 10.1016/j.neuropsychologia.2010.09.017. [DOI] [PubMed] [Google Scholar]
- Callender JC, Osburn HG. An empirical comparison of Coefficient Alpha, Guttman's Lambda – 2, and MSPLIT maximized split-half reliability estimates. Journal of Educational Measurement. 1979;16(2):89–99. [Google Scholar]
- Cheung OS, Richler JJ, Palmeri TJ, Gauthier I. Re-visiting the role of spatial frequencies in the holistic processing of faces. Journal of Experimental Psychology: Human Perception and Performance. 2008;34:1327–1336. doi: 10.1037/a0011752. [DOI] [PubMed] [Google Scholar]
- Chiou J, Spreng RA. The reliability of difference scores: A re-examination. Journal of Consumer Satisfaction, Dissatisfaction and Complaining Behavior. 1996;9:158–167. [Google Scholar]
- Chua K-W, Richler JJ, Gauthier I. Becoming a Lunari or Taiyo expert: Learner attention to parts drives holistic processing. JEP:HPP; in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeGutis J, Wilmer J, Mercado RJ, Cohan S. Using regression to measure holistic face processing reveals a strong link with face recognition ability. Cognition. 2013;126:87–100. doi: 10.1016/j.cognition.2012.09.004. [DOI] [PubMed] [Google Scholar]
- Duchaine B, Nakayama K. The Cambridge Face Memory Test: Results for neurologically intact individuals and an investigation of its validity using inverted face stimuli and prosopagnosic faces. Neuropsychologia. 2006;44:576–585. doi: 10.1016/j.neuropsychologia.2005.07.001. [DOI] [PubMed] [Google Scholar]
- Eide P, Kemp A, Silberstein RB, Nathan PJ, Stough C. Test-retest reliability of the emotional Stroop task: Examining the paradox of measurement change. The Journal of Psychology. 2002;136(5):514–520. doi: 10.1080/00223980209605547. [DOI] [PubMed] [Google Scholar]
- Gauthier I, Bukach C. Should we reject the expertise hypothesis? Cognition. 2007;103:322–330. doi: 10.1016/j.cognition.2006.05.003. [DOI] [PubMed] [Google Scholar]
- Gauthier I, Klaiman C, Schultz RT. Face composite effects reveal abnormal face processing in autism spectrum disorders. Vision Research. 2009;49:470–478. doi: 10.1016/j.visres.2008.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauthier I, Williams P, Tarr MJ, Tanaka J. Training ‘greeble’ experts: a framework for studying expert object recognition processes. Vision Research. 1998;38:2401–2428. doi: 10.1016/s0042-6989(97)00442-2. [DOI] [PubMed] [Google Scholar]
- Goffaux V, Rossion B. Faces are “spatial” – Holistic face perception is supported by low spatial frequencies. Journal of Experimental Psychology: Human Perception and Performance. 2006;32:1023–1039. doi: 10.1037/0096-1523.32.4.1023. [DOI] [PubMed] [Google Scholar]
- Konar Y, Bennett PJ, Sekuler AB. Holistic processing is not correlated with face-identification accuracy. Psychological Science. 2010;21(1):38–43. doi: 10.1177/0956797609356508. [DOI] [PubMed] [Google Scholar]
- Llabre MM, Spitzer SB, Saab PG, Ironson GH, Schneiderman N. The reliability and specificity of delta versus residulized change as measures of cardiovascular reactivity to behavioral challenges. Psychophysiology. 1991;28(6):701–711. doi: 10.1111/j.1469-8986.1991.tb01017.x. [DOI] [PubMed] [Google Scholar]
- Malgady RG, Colon-Malgady G. Comparing the reliability of difference scores and residuals in analysis of covariance. Educational and Psychological Measurement. 1991;51:803–807. [Google Scholar]
- McGugin RW, Richler JJ, Herzmann G, Speegle M, Gauthier I. The Vanderbilit Expertise Test reveals domain-general and domain-specific sex effects in object recognition. Vision Research. 2012;69(15):10–22. doi: 10.1016/j.visres.2012.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKone E, Kanwisher N, Duchaine B. Can generic expertise explain special processing for faces? Trends in Cognitive Science. 2007;11:8–15. doi: 10.1016/j.tics.2006.11.002. [DOI] [PubMed] [Google Scholar]
- McKone E, Robbins The evidence rejects the expertise hypothesis: reply to Gauthier and Bukach. Cognition. 2007;103:331–336. doi: 10.1016/j.cognition.2006.05.014. [DOI] [PubMed] [Google Scholar]
- Nunnally JC, Bernstein IH. Psychometric Theory. 3rd ed. McGraw – Hill; New York: 1994. [Google Scholar]
- Palermo R, Willis ML, Rivolta D, McKone E, Wilson EC, Calder AJ. Impaired holistic coding of facial expression and facial identity in congenital prosopagnosia. Neuropsychologia. 2011;49(5):1226–1235. doi: 10.1016/j.neuropsychologia.2011.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter J, Gilbert A, Churchill J, Brown TJ. Caution in the use of difference scores in consumer research. Journal of Consumer Research. 1993;19:662–665. [Google Scholar]
- Richler JJ, Bukach CM, Gauthier I. Context influences holistic processing of nonface objects in the composite task. Attention, Perception & Psychophysics. 2009;71(3):530–540. doi: 10.3758/APP.71.3.530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richler JJ, Cheung OS, Gauthier I. Beliefs alter holistic face processing... if response bias is not taken into account. Journal of Vision. 2011a;11(13):17, 1–13. doi: 10.1167/11.13.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richler JJ, Cheung OS, Gauthier I. Holistic processing predicts face recognition. Psychological Science. 2011b;24(4):17, 464–471. doi: 10.1177/0956797611401753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richler JJ, Gauthier IG. A meta-analysis and review of holistic processing. Psychological Bulletin. doi: 10.1037/a0037004. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richler JJ, Mack ML, Palmeri TJ, Gauthier I. Inverted faces are (eventually) processed holistically. Vision Research. 2011;51(3):333–342. doi: 10.1016/j.visres.2010.11.014. [DOI] [PubMed] [Google Scholar]
- Richler JJ, Palmeri TJ, Gauthier I. Meanings, mechanisms, and measures of holistic processing. Frontiers in Psychology. 2012;3:1–6. doi: 10.3389/fpsyg.2012.00553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richler JJ, Tanaka JW, Brown DD, Gauthier I. Why does selective attention to parts fail in face processing? Journal of Experimental Psychology: Learning, Memory and Cognition. 2008;34:1356–1368. doi: 10.1037/a0013080. [DOI] [PubMed] [Google Scholar]
- Richler JJ, Wong YK, Gauthier I. Perceptual expertise as a shift from strategic interference to automatic holistic processing. Current Directions in Psychological Science. 2011;20:129–134. doi: 10.1177/0963721411402472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogosa D, Brandt D, Zimowski M. A growth curve approach to the measurement of change. Quantitative Methods in Psychology. 1982;92(3):726–748. [Google Scholar]
- Rossion B. The composite face illusion: A whole window into our understanding of holistic face perception. Visual Cognition. 2013;21:139–253. [Google Scholar]
- Schmidt FL, Hunter JE. Measurement error in psychological research: Lessons from 26 research scenarios. Psychological Methods. 1996;1(12):199–223. [Google Scholar]
- Strauss GP, Allen DN, Jorgensen ML, Cramer SL. Test-Retest Reliability of Standard and Emotional Stroop Tasks An Investigation of Color-Word and Picture-Word Versions. Assessment. 2005;12(3):330–337. doi: 10.1177/1073191105276375. [DOI] [PubMed] [Google Scholar]
- Thompson B. Guidelines for authors. Educational and Psychological Measurement. 54:837–847. [Google Scholar]
- Troje N, Bulthoff HH. Face recognition under varying poses: The role of texture and shape. Vision Research. 1996;36:1761–1771. doi: 10.1016/0042-6989(95)00230-8. [DOI] [PubMed] [Google Scholar]
- Wang R, Li J, Fang H, Tian M, Liu J. Individual differences in holistic processing predict face recognition ability. Psychological Science. 2012;23(2):169–177. doi: 10.1177/0956797611420575. [DOI] [PubMed] [Google Scholar]
- Wong ACN, Palmeri TJ, Gauthier I. Conditions for face-like expertise with objects: Becoming a Ziggerin expert – but which type? Psychological Science. 2009;20(9):1108–1117. doi: 10.1111/j.1467-9280.2009.02430.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young AW, Hellawell D, Hay DC. Configurational information in face perception. Perception. 1987;16:747–759. doi: 10.1068/p160747. [DOI] [PubMed] [Google Scholar]
- Zimmerman DW, Williams RH. Reliability scores under realistic assumptions about properties of pre-test and post-test scores. British Journal of Mathematical & Statistical Psychology. 1998;51:343–351. [Google Scholar]