Predicting power-optimal kinematics of avian wings

Abstract

A theoretical model of avian flight is developed which simulates wing motion through a class of methods known as predictive simulation. This approach uses numerical optimization to predict power-optimal kinematics of avian wings in hover, cruise, climb and descent. The wing dynamics capture both aerodynamic and inertial loads. The model is used to simulate the flight of the pigeon, Columba livia, and the results are compared with previous experimental measurements. In cruise, the model unearths a vast range of kinematic modes that are capable of generating the required forces for flight. The most efficient mode uses a near-vertical stroke–plane and a flexed-wing upstroke, similar to kinematics recorded experimentally. In hover, the model predicts that the power-optimal mode uses an extended-wing upstroke, similar to hummingbirds. In flexing their wings, pigeons are predicted to consume 20% more power than if they kept their wings full extended, implying that the typical kinematics used by pigeons in hover are suboptimal. Predictions of climbing flight suggest that the most energy-efficient way to reach a given altitude is to climb as steeply as possible, subjected to the availability of power.

1. Introduction

Predictive simulation is a theoretical method that can be used to explore the evolution of animal locomotion. Rather than analyse the motion of the animals, predictive methods discover a catalogue of different motions, offering clues about why certain locomotive modes are selected over others. This strategy is particularly insightful when there are unresolved hypotheses on the evolution of a specific locomotive mode. For this reason, avian flight stands out as a strong candidate for investigation using predictive simulation.

Predictive models have been used extensively to simulate terrestrial bipedal locomotion, with applications to biomechanics research [1–4], robotics [5–7] and computer animation [8–10]. These methods lend themselves equally well to other terrestrial motions, such as jumping [11] and hopping [12], and have also been applied to synthesize quadrapedal locomotion [4,13,14].

The same approach has been applied to aquatic locomotion. Previous studies include analytical treatments of rigid and flexible swimming plates [15], numerical parametric studies of carangiform and anguilliform swimming [16,17] and numerical optimization of swimming kinematics [18–21]. These studies demonstrate the capability of predictive methods in simulating locomotion driven by fluidic forces, and it is therefore unsurprising that the same approach has been used to investigate flight. Perhaps the most frequent application to flight has been the optimization of kinematics of two-dimensional aerofoils [22–26]. A commonly cited engineering application of these works is the design of flapping-wing air vehicles. Consequently, recent predicted methods have been used to analyse more physically representative cases of three-dimensional wings, both in hover [27] and in forward flight [28,29].

From a zoological perspective, predictive methods have been used to simulate insect wing kinematics in hover [30,31]. More recently, forward flight has been tackled through a model that predicts the amplitude and frequency of planar models of bird and bat wings [32]. A model of jointed avian wings has also been developed that encapsulates a broader subset of kinematics, including wing pronation–supination, flexion–extension and stroke–plane inclination [33]. However, it has only been applied to hover and cruising flight, and has neglected the inertial properties of the wing which influence the choice of optimal kinematics. The specific contribution of this paper is to detail a predictive model of avian rectilinear flight that includes both aerodynamic and inertial loads on the wings, and can be used to model hover, cruise, climbing and descending flight conditions. Simulations will be based on a model of the pigeon, Columba livia, and the results will be compared against previous experimental data.

2. Method

2.1. Modelling philosophy

The philosophy adopted here is to develop a holistic model of avian flight physics, which balances the level of complexity of the aerodynamic model, inertia model, wing kinematics and optimization objective function. As predictive simulation is a relatively new method of investigating animal flight, the author feels that constructing a robust, balanced theoretical model will lay the appropriate foundations for this field [32]; future work may then incorporate more advanced models of avian aerodynamics [34,35] or species-specific wing mass distributions [36], for example.

2.2. Flight apparatus

The flight apparatus is required to generate aerodynamic force for propulsion and weight support. Birds generate this load primarily using their wings. The drag generated by a bird's body, referred to as parasitic drag, is known to have a significant impact on flight power consumption at high speeds [37,38]. The tail generates some aerodynamic force [39,40], but its small surface area and flapping speed suggest that it generates significantly less than the wings; at 6 m s⁻¹ cruise a pigeon's tail, spread at 60° [41], generates only 5% of the weight support assuming a lift coefficient of 1 [39]. It is likely that the main role of the tail in cruise is for stability and control [42]. Therefore, this work will neglect the dynamics of the tail, and model only the wing dynamics and the body drag; this will offer a tractable model that captures the most fundamental aspects of avian flight dynamics necessary for simulating rectilinear flight.

2.3. Bird dynamics

The axis systems employed are similar to those used in a previous model [33] (figure 1). The velocity of the bird with respect to the Earth is given by the freestream velocity vector, V_∞. In this work, forces and velocities described as acting ‘horizontally’, ‘laterally’ and ‘vertically’ are defined as acting in the same direction as the positive x_E-, y_E- and z_E-axes, respectively. ‘Thrust’ and ‘weight support’ are the horizontal and vertical components of aerodynamic force generated by the wings, whereas ‘axial’, ‘lateral’ and ‘normal’ components act in the positive x₀-, y₀- and z₀-directions. The average axial and normal aerodynamic forces on the wings, and the drag on the body, are shown in figure 1b as , 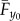and D₀.

Figure 1.

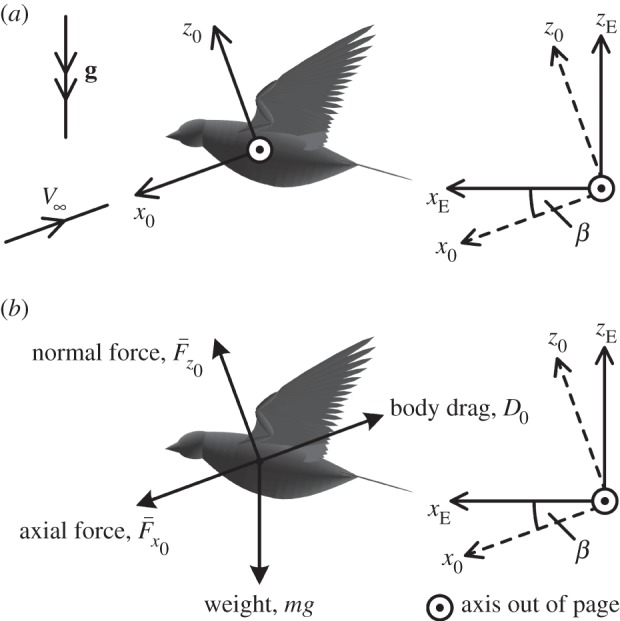
(a) Earth axes (subscript ‘E’) have a fixed position with respect to the Earth, and are oriented with the z_E axis opposing the gravity vector, g, the x_E axis pointing in an arbitrary heading, and the y_E axis perpendicular to x_E and z_E to form a right-handed set. The freestream wind axes (subscript ‘0’) translate with the movement of the bird with respect to the Earth; the x₀ axis is aligned with the freestream velocity vector.

The equations of motion describing rectilinear, cruising flight of the bird are given as

2.1

and

2.2

where β is the descent angle (−β is the ‘climb angle’). The body drag is computed as

2.3

where ρ is the local air density, S_b is the body reference area and 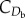is the body drag coefficient.

2.4. Shoulder kinematics

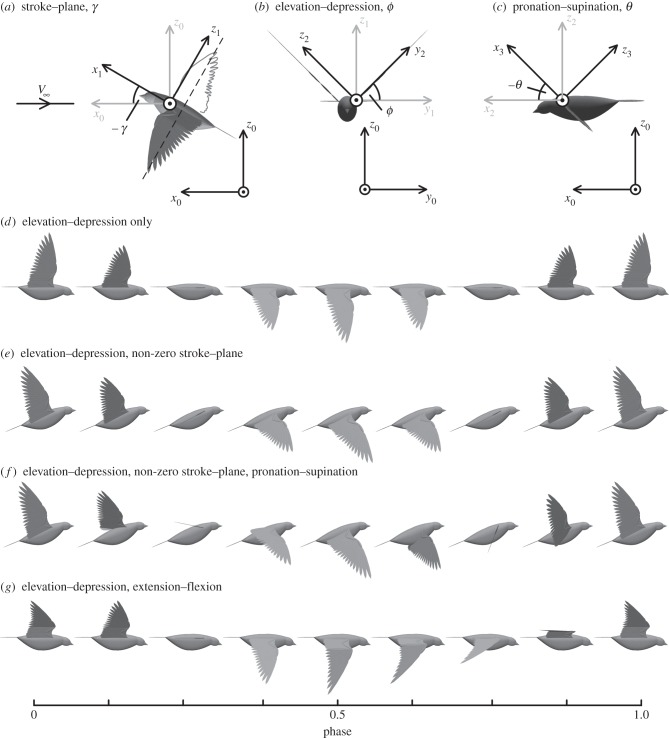
This work models the rotation of the wing about the shoulder joint, and also wing flexion. The shoulder of most modern birds is a hemi-sellar (half saddle) joint with three degrees of freedom and can be modelled as a ball and socket [43]. The degrees of freedom are represented as three Euler rotations of the form y–x–y, which define the commonly used terms of stroke–plane angle (γ; figure 2a), wing elevation–depression (+ϕ and −ϕ, respectively; figure 2b), and wing pronation–supination (+θ and −θ, respectively; figure 2c). Figure 2d–f illustrates the shoulder rotations through depictions of three examples of kinematics modes.

Figure 2.

Illustrations of the three shoulder rotation angles: (a) wings beating with a negative stroke–plane angle, −γ; (b) positive values of ϕ represent wing elevation, whereas negative values represent wing depression; (c) positive values of θ represent pronation, whereas negative values represent supination. Example wing kinematics over a single wingbeat, with the start of the downstroke at phase = 0, mid-downstroke at phase = 0.25, end of downstroke (or start of upstroke) at phase = 0.5 and mid-upstroke at phase = 0.75: (d) wing elevation–depression, with zero stroke–plane, no pronation–supination and a fully extended wing; (e) wing elevation–depression at a constant, negative stroke–plane angle with no pronation–supination and a fully extended wing; (f) wing elevation–depression at a constant, negative stroke–plane angle, with pronation on the downstroke and supination on the upstroke and a fully extended wing; (g) wing elevation depression at zero stroke–plane, with no pronation–supination, and the wing fully extended on the downstroke and partially flexed on the upstroke; the angles between individual feathers and the wing chord are proportional to the wing extension, e, such that when the wing is fully flexed the feathers are aligned with the chord. The body orientation is included for completeness, and is drawn with the major axis normal to the stroke–plane.

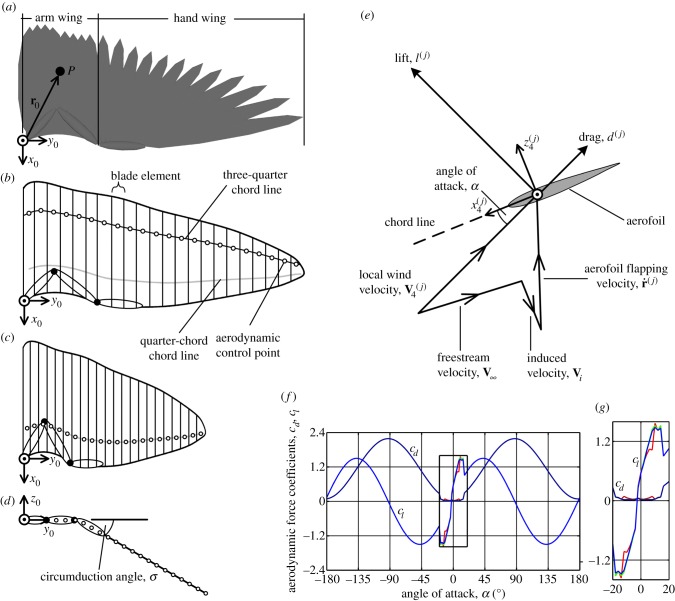
Equation (2.4) defines the position on the wing of a point, P, after being rotated from its initial position, r₀, to its current position r (measured from the shoulder joint; figure 3a), following shoulder rotations γ, ϕ and θ:

2.4

where R_γ, R_ϕ and R_θ are the alibi rotation matrices

2.5

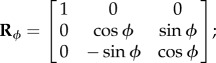2.6

2.7

these equations are used in formulating the wing inertial and aerodynamic models.

Figure 3.

(a) Wing planform geometry illustration and control point, P, given by position vector r₀. (b) Blade-element representation of the wing. (c,d) Blade-element model of wing flexion viewed along the −z₀ and −x₀ axes, respectively. (e) Model of two-dimensional aerodynamic force coefficients. (f) Force coefficients for the full range of angles of attack, from −180° to +180°. Force coefficients in the low angle of attack range (−18° < α < 14°) are taken from previous panel method computations of aerofoil geometries that were constructed from experimental measurements of avian wings [34,44], with data points interpolated using cubic splines. (g) Zoomed-in graph showing the low angle of attack model. In (f,g), light red, green and blue are lift coefficients, and dark red, green and blue are drag coefficients at Reynolds numbers of 1 × 10⁵, 1.5 × 10⁵ and 2 × 10⁵, respectively. Numerical data are included in the electronic supplementary material. (Online version in colour.)

2.5. Wing flexion kinematics

A key distinction between the biomechanics of insect flight and bird flight is that birds can actively flex and extend their wings. Birds' wings are comprised multiple skeletal segments that can be rotated around their respective joints to flex the wing towards the body. The movement of each segment is not completely independent; skeletal and muscular mechanisms couple the rotations about the elbow and wrist joints, providing underactuated flexion and extension. These mechanisms have been described in detail from a biomechanical perspective through surgical examination and observation in flight [45,46].

Wing flexion is significant as it alters the aerodynamic and inertial characteristics of the wing. Flexion reduces the exposed wing surface area, which may be beneficial for reducing drag. It also reduces the wing length, which reduces the wing-tip velocity and angle of attack for typical shoulder kinematics in forward flight; this may allow useful aerodynamic force to be generated during the upstroke for weight support and propulsion. It has also been proposed that wing flexion is beneficial for reducing the moment of inertia of the wing, and thus the energy consumed, during the upstroke [36,47]. However, these proposals neglected the energy consumed in flexing and extending the wing, and so this remains an ongoing area of research [48]. This work will incorporate wing flexion kinematics in both the aerodynamic, and dynamic models of the wing.

2.6. Wing dynamics

This work uses a parsimonious representation of the wing inertial effects by modelling the wing as a point mass, m. Even this simple inertia model overcomes a limitation of a previous predictive model that considered aerodynamic loads only [33]. Here, inertia prevents the predictive method from selecting kinematic modes with unrealistically high frequencies; it is also necessary to make accurate predictions of mechanical power at low cruise speeds when the flapping velocity and acceleration tend to be largest. The point mass wing model implicitly captures the energy required to flex and extend the wing. A previous experimental study of bat wings revealed quantitative data on flexion dynamics, but this information is currently unavailable for birds [48]. Therefore, this work postulates that the spanwise position of the point mass is proportional to the degree of wing extension, which is believed to be the simplest possible representation of wing flexion dynamics. The point mass position is governed by equation (2.4), with r₀ = [0 r_me 0], where r_m is the spanwise distance from the shoulder joint to the centre of mass of the outstretched wing, and e is the normalized wing extension, which has a value of zero for a fully flexed wing and one for a fully extended wing. For flight at a constant freestream velocity, the equation governing the translation of the point mass in the freestream axes is given by Newton's Second Law

2.8

where F_air and F_g are the aerodynamic and gravitational loads, and F_act is the load applied by the wing actuation system. Preliminary tests using the present model found the gravitational force on the wing to be less than 5% of the peak aerodynamic and inertial forces in cruising flight, and therefore it has been neglected from the simulations presented here.

The power consumed by the wing actuation system can be modelled as the product of actuation force and velocity of the point mass

2.9

an equivalent expression for power consumption of a rotating wing can be derived as the product of applied torque and angular velocity [31]. This work assumes that actuation energy is consumed for both positive and negative power requirements, and that no elastic energy is stored; previous experiments have suggested modest energy storage might occur, of up to 8% of the combined work output of the two major flight muscles [49]. The mean power consumption is thus given as the integral of the modulus of the actuation power over a wingbeat

2.10

where T is the wingbeat time period.

2.7. Aerodynamics

The key challenge in evaluating equation (2.9) is defining the aerodynamic load, F_air. As with previous predictive models, a blade-element model is used which is robust and computationally inexpensive [30,31,33]. These properties make the model effective for predictive simulation owing to the large number of function evaluations that may occur during numerical optimization. Blade-element theory models a wing as a series of quasi-two-dimensional aerofoils, or elements [50] (figure 3a,b). The instantaneous aerodynamic lift, l, and drag, d, are calculated at the jth aerodynamic control point as

2.11

and

2.12

where ρ is the local air density, V₄ is the local wind velocity, s is the element reference area and c_l and c_d are the local element lift and drag coefficients. The local wind velocity comprises the freestream velocity, V_∞, the control point velocity in the freestream axes, 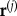and the induced velocity, V_i. The induced velocity is necessary in the model in order to make plausible predictions of elevation amplitude in forward flight. Without it, the optimal wing kinematics tend to minimize the elevation amplitude to unrealistically small values. The induced velocity is calculated iteratively using an actuator disc model that predicts uniform flow velocity normal and tangential to the disc [51]. The actuator disc is aligned with the stroke–plane, and the disc area is given as the area swept by the wings. This kind of wake model is less computationally expensive than those that attempt to resolve the flowfield [52–54]. The control point velocity is evaluated numerically with a first-order central differencing scheme, using the control point position at 400 evenly spaced time points throughout the wingbeat. A total of 32 spanwise control points were used. A detailed description of the numerical aerodynamic calculations is given elsewhere [51]. At the minimum power cruise speed of the pigeon, doubling the number of time steps or spanwise control points leads to less than a 0.7% change in mean actuation power, or 0.04% change in net aerodynamic force.

The lift and drag coefficients are derived from the local angle of attack, α, defined as the angle between the local wind velocity vector and the aerofoil chord line. In this work, the aerodynamic control points are located at the three-quarter chord line in order to implicitly capture the effective camber that arises owing to rotation about the wing major axis [50,55]. This effect is found to yield around an 11% saving in mechanical power consumption in hover, and this saving diminishes with increasing cruise speed.

At high angles of attack, lift and drag coefficients are defined using trigonometric functions (figure 3f) based on methods devised for rotary wing aerodynamics [33,50]. In the light of recent experimental findings, this work also employs a low angle of attack model to capture the high-lift-to-drag ratios that can be achieved by avian wing aerofoils [34,44]. The present model is relatively insensitive to the small fluctuations in the c_l–α and c_d–α curves that are seen at α = −12° and α = 8° in figure 3f,g; for the minimum power cruise kinematics increasing the force coefficients at these angles of attack by 10% only causes a 0.6% change in mechanical power consumption and a 0.5% change in aerodynamic force. Of greater importance is the mean lift–curve slope in the pre-stall region, which is close to 2π—the theoretical value predicted by thin aerofoil theory. Similar values of lift–curve slope were found in another theoretical analysis of avian aerofoils [56].

The aerodynamic model neglects losses in lifting capability that would occur owing to the presence of wing-tip and wing-hinge vortices. To quantify the effect of neglecting tip vortices, the model was used to simulate a revolving pigeon wing, emulating a previous experiment [57]; wing planform geometry, root offset and rotation speed were taken from the experimental data. The simulated revolving wing predicts a maximum vertical aerodynamic force coefficient of 1.61, in comparison with the experimentally recorded maximum of 1.5. In terms of predicting wing kinematics, this means that the model would underpredict the rotational speed required to generate the same vertical force as the real wing by around 3.5%.

Wing flexion is modelled primarily as a reduction in overall wing length, which reduces the blade element areas and moves each element closer to the shoulder joint (figure 4c,d). Automated rotation of the hand wing during wing flexion is captured through the circumduction angle, σ [46].

Figure 4.

Example kinematic modes predicted from numerical optimization of the pigeon wing kinematics at the minimum power cruise speed (13.6 m s⁻¹). Numerical data are included in the electronic supplementary material.

2.8. Species physical parameters

Model physical parameters were taken from previous experimental measurements of pigeons where available, and the remaining variables were estimated using allometric scaling equations (table 1). The wing planform geometry was taken from images of pigeon wings [60].

Table 1.

Model physical parameters. Wing mass and centre of mass position were estimated using allometric scaling equations [36]. An intermediate value of body drag coefficient was selected based on the traditional default value of 0.4 [58] and more recent range suggested of 0.09–0.38 [59]; however, the model was found to be relatively insensitive to changes in this value. All other parameters were taken from experimental measurements of pigeons [37,41].

variable	value
mass, m (kg)	0.4
wing mass (kg)	0.0258
body frontal area, S0 (m2)	0.0036
wing length (m)	0.32
wing centre of mass spanwise position, rm (m)	0.0969
body drag coefficient,	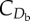0.25
hand : wing length ratio	0.74

2.9. Optimization objective, variables and constraints

Optimization is used to minimize an undesirable property of a system, known as a cost or objective. The mean mechanical power output will be used here as the optimization objective, which will be minimized by adjusting the wing kinematics. To form a tractable problem, the kinematics must be defined by a finite set of variables. Using a greater number of optimization variables leads to a more sophisticated model that can capture a wider variety of movements. The penalty for this is a more complex numerical optimization problem to solve, which requires greater computational cost. A phenomenological approach is taken here, using the minimum number of kinematic variables that allow the model to capture typical flight conditions. This includes cruising at varying speed, hovering, climbing and descending.

The shoulder elevation and pronation angles are defined as

2.13

and

2.14

where Φ and Θ are amplitudes and Φ₀ and Θ₀ are the offsets of elevation and pronation angle, respectively. ξ is the pronation phase lag and f is the wingbeat frequency. A pronation phase lag of π/2 radians is used here to ensure the maximum pronation angle is concurrent with the maximum wing flapping velocity at the mid-downstroke. Angle offsets are assumed to be zero, so the wings elevate and depress by equal amounts, and pronate and supinate by equal amounts, during a wingbeat. This reduces the subspace of possible kinematic modes, but still allows predictions to be made for hovering and forward flight conditions. These conditions can be achieved only by varying the stroke–plane angle, γ, which is modelled here as a constant value throughout the wingbeat. Previous predictive simulations of cruising pigeons found that with a constant stroke–plane the simulated wing-tip paths closely resemble those measured experimentally, and that nonlinearities in wing-tip paths are mainly owing to combinations or wing flexion and pronation–supination rather than changes in stroke–plane [51]. Thus, the optimization variables that describe the shoulder kinematics are the elevation amplitude, Φ, pronation amplitude, Θ, wingbeat frequency, f and stroke–plane angle, γ.

The normalized wing extension is defined as

2.15

where E is the extension amplitude, defined as the ratio of the wing length on the mid-upstroke to the maximum wing length. ζ is the extension ratio phase lag, and is set equal to π/2 radians, so that the wing is fully extended at the mid-downstroke. As examples of wing extension, amplitudes of E = 0, E = 0.5 or E = 1 mean that at the mid-upstroke the wing is fully flexed (e = 0), 50% flexed (e = 0.5) or fully extended (e = 1), respectively.

The key optimization constraint in the model is that the net axial and normal aerodynamic force generated by the wings must balance the body drag and gravitational forces, as given by equations (2.1) and (2.2). Additional constraints are used to limit the wing joint ranges of motion and wingbeat frequency to plausible values (table 2). In hover and low-speed cruise, the simulations tend towards the maximum constrained value of wing elevation amplitude to reduce the power consumption by lowering the induced drag and inertial loads. Interestingly, this even occurs when the elevation amplitude constraint is increased beyond 90°, meaning that the power-optimal mode tends towards a rotary wing solution.

Table 2.

Constraints on optimization variables for cruising flight simulations. Constraints on wingbeat frequency are defined using an allometric scaling prediction for frequency, f_s, [36], with the minimum constraint set equal to 0.5f_s and maximum constraint set as 1.5f_s. Maximum elevation amplitude was defined according to peak values recorded experimentally for pigeons [37].

variable	minimum constraint	maximum constraint
wingbeat frequency, f (Hz)	3	9
elevation amplitude, Φ	0	75°
pronation amplitude, Θ	0	90°
stroke–plane angle, γ	−90°	0°
extension amplitude, E	0	1

A gradient-based numerical optimizer (sequential quadratic programming algorithm) is used to find kinematic modes which satisfy the constraints while minimizing mechanical power. For each flight condition, the optimizer was initiated with multiple starting locations for the optimization variables in order to resolve the local and global solutions. Starting locations were defined at the minimum and maximum constraint values for each variable, and also at the mid-interval value of these constraints; these three starting locations from each of the five variables led to a total of 243 (3⁵) starting locations. A further increase in the number of defined starting locations, or the introduction of random starting locations, did not alter the minimum power solutions that are presented here.

A sensitivity analysis was performed to explore the region in the optimization space that surrounded the global solution. For minimum power cruising flight, the optimized kinematics variables were incremented and decremented, and the change in objective value was examined. The objective function was found to be most sensitive to a combined increase in frequency, elevation amplitude, pronation amplitude and extension amplitude, and a decrease in stroke–plane angle; a 1% change in these variables led to a 5% change in objective function.

3. Results and discussion

3.1. The range of flight modes

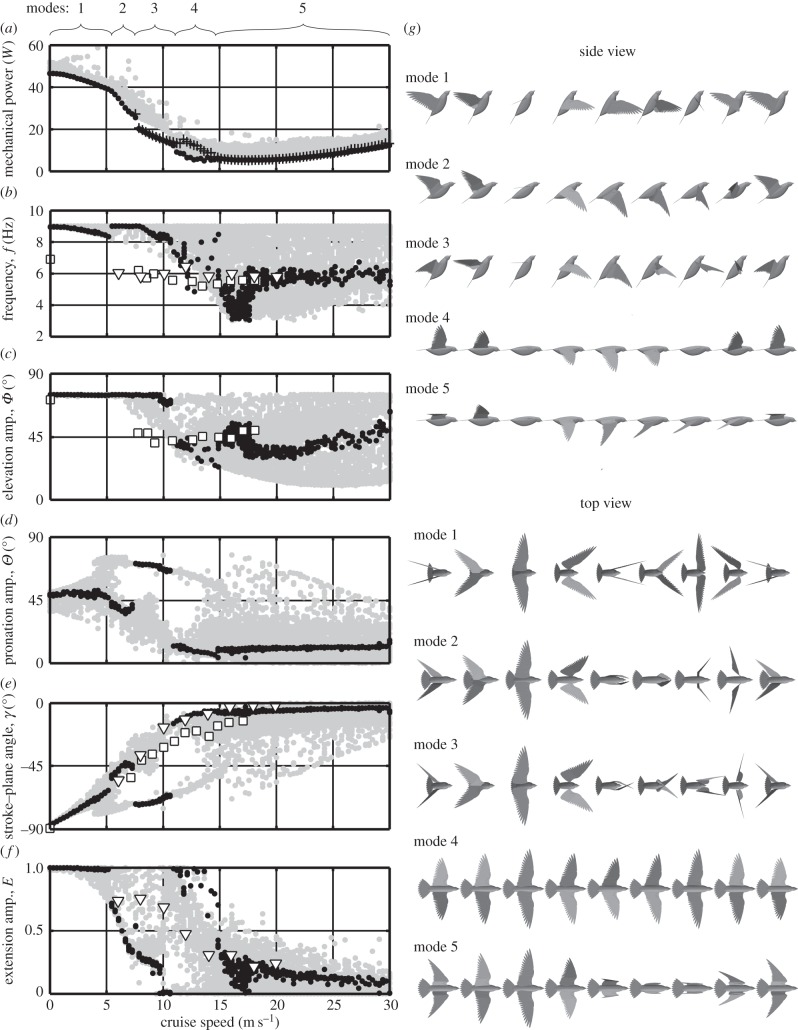
A striking feature of the results is that a diverse range of possible wing kinematics was discovered for a given flight condition, exemplifying many possible modes of flying. This parallels findings from optimization studies of human walking where different gait patterns were found to achieve stable locomotion [61]. At the minimum power cruise speed, a ‘stiff-wing mode’ was discovered (figure 4), in which the wing remains fully extended and flaps with a low frequency of 5.1 Hz and an elevation amplitude of 36°. At the same speed, a ‘flex mode’ was found, where the wing flexes to around half its outstretched length at the mid-upstroke, but uses a much higher frequency of more than 8 Hz. And a ‘flex–twist mode’ was also found, which used significant wing flexion, shoulder pronation–supination, and a steeply inclined stroke–plane. This particular mode highlights that the model does not prevent the wings from intersecting, which can occur when the wings are depressed, and the supination angle or hand circumduction angle is large. Other intermediate modes were discovered that used combinations of the kinematic features discussed here.

3.2. Kinematics with varying cruise speed

With varying cruise speed, the model again discovers various kinematic solutions that satisfy the optimization constraints (figure 5). The following discussion focuses mainly on the minimum power, or ‘global’, solutions, at each cruise speed. ‘Near-global’ solutions are included in figure 5a–f that fall within 5% of the minimum power solution for a given cruise speed. Local minima are also included for completeness, to illustrate the broad range of kinematics that could potentially be used for cruising flight at various speeds.

Figure 5.

Predicted wing kinematics of the pigeon at cruise speeds varying from 0 (hover) to 30 m s⁻¹. (a–f) Filled circles are kinematic variables predicted through simulation; black dots are global and near-global solutions, that fall within 5% of the minimum power solution for a given cruise speed; grey dots are local solutions, which still satisfy the optimization constraints and therefore represent valid cruising kinematics, but use more than 5% of the minimum power solution for a given cruise speed. Crosses are the simulated power consumption for a control case when the model is constrained to an upstroke extension amplitude of E = 0.25. Square symbols are data from previous experiments, for which the current model used the same mass, wing planform geometry and body frontal area [37]. Triangular symbols are data from previous experiments on pigeons with a lower average body mass and wing length [41]. (g) Illustrations of kinematic modes 1–5 are global optimum solutions at cruise speeds of 2.7, 6.4, 9.1, 12.7 and 16.1 m s⁻¹. Numerical data are included in the electronic supplementary material.

In low-speed flight, the predicted power (figure 5a) is greater than in previous theoretical models. For example, at 6 m s⁻¹ cruise, the present model predicts a power consumption of more than 34 W, whereas a previous aerodynamic model predicted less than 7 W [62]. This is largely owing to the inclusion of inertial effects here; in the present model, if the wing mass is neglected, the predicted power at 6 m s⁻¹ decreases to 8.7 W. At low-cruise speeds, the predicted frequency and elevation amplitude, and therefore, the wing flapping velocities, are greater than the experimental values (figure 5b,c). The high frequencies also mean high wing accelerations and inertial loads. So while including inertial effects is important for making accurate predictions of power, the combined overprediction of flapping velocity and acceleration leads to excessive predictions of power (equation (2.9)). For real pigeons, the power consumption in low-speed cruise is expected to lie between the values predicted by conventional aerodynamics models that neglect inertial effects, and the values predicted here that overestimate inertial effects.

At cruise speeds above the minimum power speed, the simulated and experimental flapping velocities are similar, so in these conditions, the inertial effects and power consumption are not believed to be overestimated. The minimum power consumption is predicted here to be 5 W, which is similar to previous theoretical predictions of 4.8 W [62]; the corresponding predictions of minimum power cruise speed are also similar, being predicted as 13.6 m s⁻¹ in the present work and 12 m s⁻¹ in the previous model.

Discontinuities in the power curve correspond to abrupt changes in optimal kinematics with changes in cruise speed. These abrupt changes highlight five kinematic modes of flight (figure 5a,g); for terrestrial locomotion, these could be considered as gaits, but the term is avoided here owing to the historical use of ‘gaits’ for descriptions of wakes of flying animals. As with terrestrial locomotion, the results here illustrate the energetic benefits of switching between different kinematic modes at different speeds. Figure 5a includes the power consumption data for a control case where the extension amplitude was constrained to a value of 0.25, which is the optimal value at 17–18 m s⁻¹ cruise in mode 5. At lower cruise speeds, the optimal solution switches to fully extended wing kinematics in mode 4, which reduces power consumption by up to 55% compared with the control case. A similar test can be performed at low cruise speeds with a constrained fully extended upstroke (E = 1): in moving from mode 1 to mode 2, the optimal kinematics switch to a flexed upstroke, which consumes up to 25% less power than a fully extended upstroke.

In modes 1–3, large frequency and elevation amplitude yield large flapping velocities. This compensates for the low freestream velocity, allowing sufficient aerodynamic force to be generated for weight support in slow cruise. Conversely, at higher cruise speeds, a low flapping velocity is needed, and frequency and elevation amplitude are lower in modes 4 and 5. From examining the local minima solutions, a clear trade-off was found between elevation amplitude and frequency. Solutions with high elevation amplitudes and low frequencies benefit from low induced drag and low inertial force on the wing. But in cruising flight, large wing elevation angles cause a greater component of the aerodynamic force to be vectored laterally, which is essentially wasted as it is cancelled by the force on the other wing. So while solutions were found for cruise with both high and low elevation amplitudes, those with intermediate values consumed less power.

With increasing cruise speed the wings must generate a greater axial component of aerodynamic force to overcome increasing drag on the body. The aerodynamic force is vectored axially by increasing the stroke–plane angle (figure 5e). In modes 1 and 2, the stroke–plane angle increases with increasing cruise speed, up to around −45° at around 7 m s⁻¹ cruise. The main discrepancy between the predicted stroke–plane and the experimental measurements is the sudden reduction in stroke–plane angle in mode 3, which is coupled with an increase in pronation angle. From around 5 to 15 m s⁻¹, the local minima fall into two distinct groups, which use a combination of low stroke–plane and high pronation, or high stroke–plane and low pronation (figure 5d,e); equal changes in these two variables cancel out to yield the same wing orientation at the mid-downstroke. As with the flex–twist mode discussed previously, the combination of wing depression, supination and hand circumduction causes the wings to intersect (figure 5g) making this an implausible solution. If the intersection of the wings were included as a model constraint, the group of solutions with low stroke–plane and high pronation would violate this constraint. Modes with lower pronation amplitudes and higher stroke–plane angles then prevail as the power-optimal solutions, and the simulated stroke–plane angles follow the experimental trend mode closely.

Previous experiments found that at high cruise speeds birds tend to flex their wings on the upstroke [63]. Modes 4 and 5 capture this trend, with all local and global solutions tending towards lower wing extension amplitudes at high cruise speed (figure 5f). The experimental data for pigeons show a smooth reduction in wing extension from around 7.5 to 20 m s⁻¹. The model also shows a reduction in wing extension, but from 0 to 10 m s⁻¹. Unlike the experiments, the model repeats this trend at higher cruise speeds. This yields two modes—mode 1 and mode 4—where the wing is almost fully extended on the upstroke.

Here, the optimal power solution reverts to a fully extended wing mode at low cruise speeds and in hover. This flight mode reflects the kinematics used by hummingbirds, which can be expected to be optimized for efficient hovering flight [63]. However, other species, including pigeons are known to flex their wings on the upstroke during hover. No flexing-wing solutions were found at all in hover, highlighting a limitation of the model. The imposed constraints on frequency and elevation amplitude limit the flapping velocity, and thus the aerodynamic force that can be generated on the downstroke. This means that a significant proportion of the force must be generated on the upstroke, and this is achieved by keeping the wing fully extended.

If the wing were able to move faster on the downstroke less force would be required on the upstroke and the wing could be flexed. To test this hypothesis, the maximum constraint on frequency was removed, and the optimal kinematics were determined in hover. Under these conditions, solutions were obtained that used flexed wings on the upstroke. These solutions generated more than 95% of the weight support on the downstroke alone. To achieve this, the wingbeat frequency was greater than 12 Hz, which is much higher than in experimental measurements of pigeons; a similar flexing-wing upstroke can be achieved with a lower frequency by using a faster downstroke and a slower upstroke. The key finding here is that the flexed-wing upstroke consumes around 20% more power in hover than the global solution, and the power-optimal mode is still the extended-wing upstroke shown in figure 5.

3.3. Wing kinematics in climb and descent

Wing kinematics were predicted for the pigeon for a climb angle range of −60° to 60°, at 4 m s⁻¹, to emulate flight conditions observed in previous experiments on pigeons [64]. With varying climb angle, the predicted wing kinematics only changed in terms of the stroke–plane, frequency and pronation amplitude, whereas the wing remained fully extended with maximum elevation amplitude (figure 6).

Figure 6.

Wing kinematics predicted for the pigeon for a climb angle range of −60° to 60° with a flight speed of 4 m s⁻¹, an intermediate speed between the upper and lower limits seen in experiments on climbing pigeons [64]. The same model physical parameters were used as in the cruising flight simulations. Upper constraint on frequency was increased to 9.4 Hz here to capture the frequency range that has been observed in the climbing experiments. Numerical data are included in the electronic supplementary material.

The predicted wingbeat frequencies at steep descent and climb angles are similar to experimental measurements, but, at shallow angles, the model tends to overpredict frequency (figure 7a). The stroke–plane angle predictions capture the experimental findings more closely over the full range of climb angles, showing an almost linear increase with climb angle (figure 7b). To understand better the reasons behind the change in stroke–plane angle, it is more intuitive to consider stroke–plane measured with respect to an Earth-fixed reference, such as the horizontal plane (figure 7c). Both the simulations and the experiments found that as the angle of climb or descent increases the stroke–plane is oriented at a shallower angle with respect to the horizontal plane. Previous discussions proposed that this variation in stroke–plane was related to the reductions in flight speed seen in climbing and descending flight [64]. However, the present model assumes a fixed flight speed for all climb angles, but still captures the trend in stroke–plane.

Figure 7.

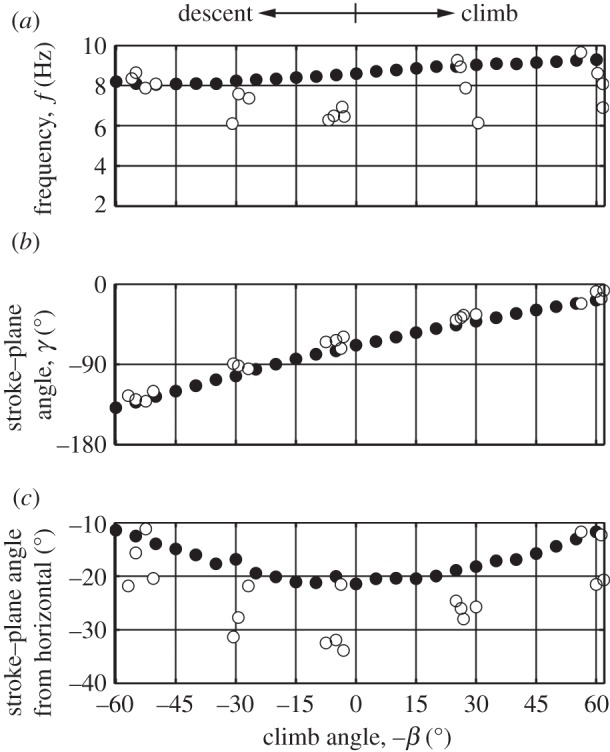
Filled circles are simulated predictions and open circles are experimental data [64] of wing kinematics of pigeons in descent and climb. Numerical data are included in the electronic supplementary material.

The rotation of the stroke–plane can be explained by considering the orientation of the lift force vector on the wing. At low flight speeds, the majority of the lift acts normal to the stroke–plane. So, in horizontal flight, the stroke–plane is inclined to generate a horizontal component of lift to overcome drag on the body and wings. Conversely, in steep climb, the stroke–plane is closer to the horizontal, as only a small horizontal component of lift is needed. In the extreme case of vertical climb or descent, no horizontal component of lift is needed, so a horizontal stroke–plane can be used just as it is in hover.

3.4. The cost of climbing

This section takes a new approach to examining climbing flight by attempting to identify the optimum climb angle and flight speed. It is postulated here that optimum climbing flight is that which reduces the amount of energy consumed to reach a given altitude, i.e. the cost of vertical transport, given by the ratio of power consumed to vertical flight velocity, 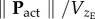. This metric is equivalent to the ‘cost of transport’, which is commonly used in assessing optimum horizontal cruising flight conditions.

Optimal wing kinematics were predicted for the pigeon, varying both the flight speed and the climb angle. At each climb angle, the flight speed was identified at which the cost of vertical transport is minimum. Figure 8a shows how the predicted minimum cost of vertical transport reduces with increasing climb angle. These predictions suggest that it is favourable to climb at steeper angles to reduce the mechanical energy needed to reach a given altitude.

Figure 8.

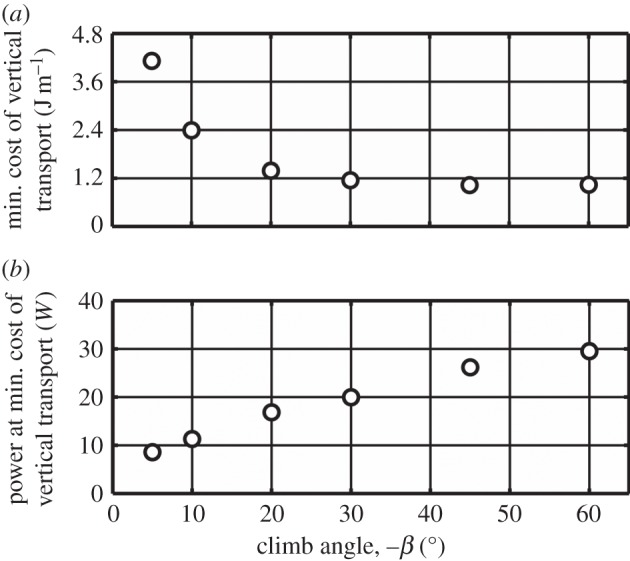
The energetics of climbing. Solutions are taken from simulations of the pigeon model which minimize the ratio of power to vertical speed. Numerical data are included in the electronic supplementary material.

The penalty for climbing more steeply is greater power requirements: while the energy expenditure reduces with climb angle at a diminishing rate, power continues to increase at an approximately linear rate (figure 8b). Climbing at 60° requires the actuation system to generate over five times the amount of power needed for minimum power cruise (figure 5). For real birds, this demand on the flight muscles to operate away from optimal conditions would most likely lead to a drop in performance. Moreover, high power consumption would indicate a requirement of having larger muscles. Carrying this additional muscle mass would be detrimental to flight performance in cruise and other flight conditions and would only benefit birds whose behavioural repertoire was dominated by climbing.

4. Conclusion

The predictive model presented here provides insights into why nature selects certain kinematic modes for flight, and why others get left behind. Avian cruising flight is typified by a near-vertical stroke–plane and flexion of the wing on the upstroke, and the predictive model captured this mode, illustrating that it is power-optimal. But, in addition to this, numerous other modes of flight were discovered. Although less efficient, these modes represent plausible methods of flying that may have once been used. So when considering the evolution of flight, commonality in kinematics should not be assumed between extinct and extant flying birds.

Some instances where the simulations did not capture experimental observations highlight limitations of the existing model. For example, if the model prevented wing intersection, the results would match more closely the experimental measurements at intermediate cruise speeds. In other instances where the predictions did not match the experiments, some useful lessons can be learnt about the role that evolution has played in selecting wing kinematics. For example, the model showed that in hover the power-optimal kinematic mode for a pigeon maintains an extended wing on the upstroke, as used by hummingbirds. The fact that real pigeons use a suboptimal hovering mode by flexing their wings implies that other evolutionary pressures overshadow the desire to minimize power in hover. It is likely that the flight apparatus of pigeons, and other birds, has evolved to be optimal in their more common flight condition of cruise; the wings may be incapable of being fully extended on the upstroke owing to limitations on structural strength or power availability for example, and hence more efficient flight modes cannot be taken advantage of in hover. Similarly, in climbing flight, the wing actuation system may not be able to generate sufficient instantaneous power to climb steeply, which pushes the more energy-efficient steep climb modes outside of the flight envelope for birds.

Funding statement

I acknowledge that this research was supported through the EPSRC doctoral prize fellowship.