Emergence of multicellularity in a model of cell growth, death and aggregation under size-dependent selection

Abstract

How multicellular life forms evolved from unicellular ones constitutes a major problem in our understanding of the evolution of our biosphere. A recent set of experiments involving yeast cell populations have shown that selection for faster sedimenting cells leads to the appearance of stable aggregates of cells that are able to split into smaller clusters. It was suggested that the observed evolutionary patterns could be the result of evolved programmes affecting cell death. Here, we show, using a simple model of cell–cell interactions and evolving adhesion rates, that the observed patterns in cluster size and localized mortality can be easily interpreted in terms of waste accumulation and toxicity-driven apoptosis. This simple mechanism would have played a key role in the early evolution of multicellular life forms based on both aggregative and clonal development. The potential extensions of this work and its implications for natural and synthetic multicellularity are discussed.

1. Introduction

One of the key major transitions of evolution involved the emergence of multicellular life forms from single-cell systems [1,2]. The standard view is that groups of cooperating cells are able to take advantage of division of labour in order to better exploit external resources, avoid predators or improve given adaptive traits [3,4]. Yet, the transition multicellularity (MC) encapsulated in this picture involves an increase in overall complexity [5] and thus increasing costs for coordinated cooperating behaviour. The main problem is then to understand what makes the trade-off between these two sides balance out.

Available phylogenetic techniques have shed light on how and when the roots of MC got established [6–9]. Particularly, comparative analyses of different clades of multicellular organisms have proven to be very useful in delineating of the genetic toolkit required for multicellular existence [10]. These studies show that cell–cell communication and adhesion genes were co-opted from ancestral functions unrelated to multicellular phenotypes into robust developmental processes. In this vein, many unicellular species have the potential to behave (at least in some circumstances) as cooperative ensembles of cells [11,12].

Two major paths towards MC have been identified [7]. The first is clonal development [6,8] which involves the evolution of a life cycle that requires all cells to display adhesion molecules capable of maintaining them together and for all cells to share the same genotype. The second is aggregative development. This alternative path does not require clonality and is present in some well-known but rare systems, such as slime moulds [1]. In this scenario, MC aggregates can form under some conditions and disaggregate into non-clonal individual cells. More recently, it has been found that some unicellular species display an MC pattern of development based on aggregative dynamics [13]. These remarkable findings suggest that non-clonal developmental processes might have played an important role in the early evolution of multicellular life forms [14].

In a recent set of experiments [15–18], artificial selection of cell clusters under gravity constraints was performed. The authors took advantage of the fastest sedimentation speed of cell aggregates of increasing size as a shortcut for selecting for more complex cell assemblies and potential mutations favouring them. Remarkably, after a relatively short number of generations, obtained by repeated culture transfers, the so-called snowflake phenotypes appeared in a predictable way. These are rounded clusters of cells that appear attached to each other. The authors also studied the role played by cellular interactions and cluster structure on the underlying reproductive processes. It was found that clusters do not reproduce through events associated with single cells, but instead involved a cluster-level set of events and—it was argued—a division of labour resulting from an apparently active control of apoptosis. The sequence of events as reported from this microcosm experiments has important consequences for our understanding of the evolution of MC and potential scenarios for recreating the first steps from single cells to cooperating ensembles and organisms. The claim that evolved apoptotic paths might be at work is specially appealing.

Performing actual experiments involving physical aggregates is a necessary step towards reconstructing the events that pervaded the rise of MC. Most theoretical models consider genetic traits, but typically ignore embodiment: both individual cells and aggregates are mapped into non-dimensional, point objects, but including the actual embodiment makes a difference [19]. In this paper, we present a computational model of the experiments of Ratcliff et al., by dealing with a simple set of assumptions that support an alternative interpretation, based on the accumulation of toxic products—such as acetic acid or ammonia—inherent to yeast metabolism [20,21], which could take place inside a large cluster instead of programmed cell death [22]. The model involves a physical, embodied implementation of cellular aggregates falling in a given medium. Our model enables reproduction of the basic experimental results and provides a computational framework to analyse alternative scenarios for the emergence of MC.

2. Methods

The above-summarized experiments include a selection process obtained by sequentially growing yeast in a well-mixed medium and selecting for the cells displaying faster sedimentation. This approach immediately makes larger clusters of cells to be preferentially selected as in reference [15]. Here, we examine these results under the light of a simple, embodied computational model using the NetLogo programming language, which enables simulation of Newtonian physics [23] on groups of interacting particles. Here, cells are represented as objects having a given position and velocity. Cell–cell interactions are modelled by simple, but physically meaningful spring-like interactions. Similarly, the interaction between cells and the fluid environment within which they move (essentially under free fall) is also introduced in a realistic manner. Additional rules related to nutrient and waste diffusion and consumption are also introduced.

2.1. Computational model

Our model considers a spatially extended description of the individuals and their interactions (figure 1a–c). For the sake of simplicity, we assume a two-dimensional spatial domain Γ. In this area, cells are described as point physical objects interacting (figure 1b), when attached to each other, through springs (figure 1c). Moreover, these objects are subjected to gravitation fields when appropriate, or display a random walk otherwise (see §2.3).

Figure 1.

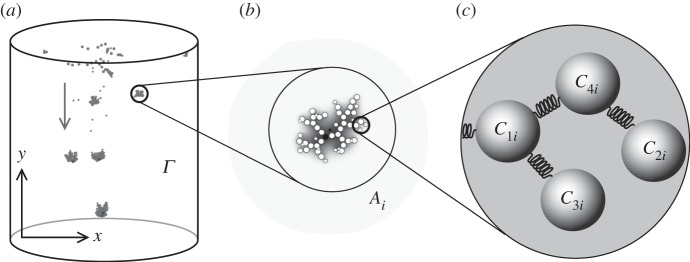
Modelling evolution of multicellular aggregates. Following the experimental set-up described in Ratcliff et al. [15], we consider a physically embodied description of aggregates growing and falling under the action of gravity (a). For the sake of simplicity, the spatial domain is confined to a two-dimensional lattice. In it, yeast cells have a limited number of potential attached cells and, in response to the local concentration of chemical species, cells can divide or die. They can remain attached to daughter cells owing to failure of separation, thus forming aggregates (b). Such aggregates are modelled in terms of simple repelling particles connected by springs (c). The physical displacement or breakage of these aggregates is introduced by cell death (see text).

The experiment starts with a population of single cells located on random positions along Γ. Cells increase in biomass through the consumption of the nutrients available to them and, if a particular threshold is surpassed, a cell can divide and asymmetrically split the resources between the two resulting cells (see figure 2). Stochastically, these two new cells can fail to separate correctly and become an aggregate, which, in turn, determines some of the individual properties of the cells (namely the sedimentation speed). Yeast cells are considered to have a limited number of potential attached cells owing to geometrical constraints. As such, aggregates in the simulation are, in essence, Bethe lattices with k_n neighbours (we consider k_n = 4 as the upper limit owing to physical constraints).

Figure 2.

The basic set of rules used in our model approach to the evolution experiments. The model introduces a cellular death mechanism based on metabolic by-product accumulation. A given aggregate A_i, here composed by just three cells, is shown in (a). It can experience three different types of processes: cell division without (b) and with (c) an increase of aggregate size and (d) cell death. The last scenario takes place if the waste concentration of—say—the third cell C_3i is above a critical threshold δ_c. If the first cell, C_1i, has a mass larger than another threshold M_c and has fewer than four spring-connected relatives, it will split generating an additional cell. This new cell can leave the aggregate (b) or remain attached (c) with probabilities 1 − p_1i and p_1i, respectively. (Online version in colour.)

Following the original set-up [15], the simulated experiments include two distinct phases: growth and sedimentation. In the former, cells are grown in a well-mixed tank until a certain number is reached. In this phase, cells move by random walking through Γ, consume nutrients in order not only to grow and multiply, but also generate generic waste by-products that can cause their death. In the second stage, cells fall under the action of a gravitational field, modelled by a biased random walk using Stoke's law for the vertical component of the bias. This selection step is considered sufficiently short, so that cells neither divide nor die. After a given time—the settling time—those aggregates collected at the lower part of Γ are used to seed back the next round of the process, to be located again randomly all over the spatial domain.

The basic components of the models presented here are cells or clusters of cells resulting from birth and death processes. At any time t in a given simulation, the total population will be composed by a set 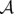of n(t) aggregates, namely

2.1

Each aggregate A_i is formed by a set of linked cells, i.e.

2.2

Let us label as |A_i| the size of the ith aggregate. The mass of each (i) cell within a given (j) aggregate will be indicated as M_ij. Cells in the model have a constant uptake of resources from their immediate surroundings. At the same time, nutrient diffuses and is homogeneously replenished in Γ. To take into account these processes, nutrient concentration change in the finite-element ϕ_ij is given by the following partial differential equation

2.3

The Heaviside function Θ_ij is used to indicate the presence or absence of cells in that particular patch of the lattice (so we have Θ_ij = 1 if a cell is present and zero otherwise). In this same term, the parameter ρ represents the intake rate of nutrients from the culture medium. The last two terms of the equation are introduced as a replenishment process to ensure that, in the absence of cells, the nutrient field recovers its initial value ϕ₀. Here, the diffusion operator ∇²ϕ_ij is numerically computed (using the NetLogo libraries) by means of a standard discretization form

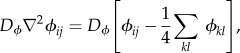2.4

where D_ϕ accounts for the diffusion coefficient. The energy change for ith cell in the jth aggregate is

2.5

Here, β_c represents the maintenance costs and Δ_ij accounts for the number of divisions this particular cell has undergone, causing cells to increasingly spread their divisions. If the energy value of a particular cell reaches its division threshold, a new cell is created and the original energy value is split asymmetrically between the cells. Conversely, cells also generate generic waste as a by-product of their metabolic activity. The change in finite-element W_ij is

2.6

Similar to the nutrient concentration, waste is created in those positions of the lattice occupied by cells (Heaviside function Θ_ij), in a quantity proportional to the maintenance costs of the cell (γM_ij). Waste is also subjected to diffusion and decays proportionally to the current amount. Cells initiate apoptosis if the following threshold condition is met: W_ij ≥ δ_c, where δ_c is the upper bound that cells can withstand.

In figure 3, we show an example of how aggregates grow in size, with increasing levels of waste until some cells meet this threshold and die. As a result, a few smaller aggregates are created, which can export—through passive diffusion—enough waste to avoid death. This pattern of growth until a critical size has been reached appeared quite robust to parameter changes (listed in the caption of figure 3), which were arbitrarily chosen and have arbitrary units.

Figure 3.

Growth and sequential splitting of an aggregate owing to cell death. (a–e) Here, five spatial snapshots are shown at different times within the in silico growth phase. Living and apoptotic cells are shown as blue and red circles, respectively. After a fixed number of algorithm cycles, apoptotic cells disappear with their springs, causing the breakage of the aggregate into smaller clusters (b,c and e). The waste field appears as a continuously shaded gradient, darker areas indicating higher concentration levels. As expected, the core of the aggregate is highly enriched in by-products, eventually causing the death of cells when it surpasses a certain threshold. A different view of the waste field of snapshot e is given in (f). The simulation times in algorithm cycles for the snapshots are: 200, 250, 300, 350 and 400. The parameter's values used in this simulation are: D_Φ = 0.1, D_W = 0.1, ρ = 0.1, β_c = 0.01, M_c = 80, κ = 0.25, γ = 0.2, δ_c = 4.5, δ_Φ = 0.1, δ_W = 0.01, initial concentrations Φ₀ = 20 and W₀ = 0, and a non-evolving adhesion probability p = 1. (Online version in colour.)

2.2. Mutation

Little is known about the genetic changes behind the establishment of the snowflake phenotype reported by Ratcliff et al. Whether it involved extensive rewiring of basic adhesion toolkit genes or slight tuning of interactions in gene networks we do not know, but experiments involving different sedimentation times clearly show that correct separation between cells is not a binary, all or nothing, process.

In order to make less assumptions about the genetic changes taking place in Ratcliff et al., our model enables evolution of only one cell parameter: p_ij, which stands for the probability of remaining attached to the offspring in the event of a division, and condenses the effect of multiple genes related to adhesion mutating independently. As such, p_ij is a continuous variable constrained between 0 and 1. This parameter is inherited by daughter cells with very small variations, namely a flat distribution ±0.05 is applied at each division event.

2.3. Selection process

In Ratcliff et al.'s [15] paper, the researchers made use of gravity as the external force facilitating the differential deposition of cell aggregates. Physically, this corresponds to a simple property of increasingly large objects falling within a fluid medium with a given friction and a fixed gravity field. In our model, we have used a simplified, two-step process to emulate the experimental set-up used by Ratcliff et al.

At the beginning of each simulation, a set of cells were created with random positions in the virtual space, and were grown until 500 cells were obtained under agitation conditions (no sedimentation). Afterwards, we let the cells/aggregates fall until a fixed number simulation cycles had passed, the aforementioned settling time. Then, individuals located at the bottom, below a given critical height h_c, were uplifted to new random positions leaving intact their history and traits. Moreover, the virtual medium was refreshed to homogeneous nutrient (ϕ₀) and waste (W₀) levels.

When growing, cells move in a random-walk fashion, which is an approximation to continuously shaken media. Because they have no preferential direction of movement, they tend to be homogeneously distributed through the simulation space. When settling, we use a biased random walk as an approximation of a sedimentation process. The bias introduced is computed using Stoke's law. During this phase, all cells/clusters tend to go towards the bottom, eventually reaching the selection zone.

3. Results

Several traits of the multicellular aggregates emerging through the simulation can be measured with the above-discussed experimental results. In our study, we have followed both average values of aggregate size over generations as well as those selected traits (such as cell–cell adhesion) favouring the selection process towards larger aggregates. We can estimate the probability of finding aggregates of a given size |A_i|, given by

3.1

In figure 4a, we display the evolution of the mean aggregate size as a function of time, calculated from

3.2

We can appreciate a logistic-like growth pattern, thus exhibiting attrition after a given number of steps. The standard deviation is also displayed as a shaded envelope around the mean. Two snapshots of the aggregate spatial distribution at the end of two selection phases are shown. These correspond to transfers 100 and 150, marked by arrows in figure 4a. In these particular transfers, had reached 0.25 (figure 4b) and 0.75 (figure 4c). A yellow region is included as a visual help to differentiate the selected region. In figure 4d, we display the size distribution of aggregate sizes above (black) and below (red) the h_c for T = 150 and 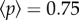. It is possible to appreciate the progressive displacement towards higher aggregate sizes in the selected region (yellow) as a result of the sedimentation process.

Figure 4.

(a) Time evolution of average aggregate sizes using the same parameters described before (figure 3) but with free, evolving p_i. Values shown (black dots) are averages of 30 replicate experiments, and the shaded area represents 1 s.d. of the dataset. In (b,c), we show two snapshots, obtained at the end of transfers 100 and 150, respectively (marked by arrows in a), which correspond to 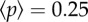and (data not shown). In (d), we also show the size distribution for t = 150, both in the selected and non-selected area (red and black, respectively). (Online version in colour.)

A specially relevant result seems to support our view. In Ratcliff's paper, it was shown that a highly nonlinear correlation exists between the size of the aggregate and the fraction of cells undergoing death within them (figure 5a, inset). In a nutshell, what is observed is that little death is found in a given aggregate size, whereas it rapidly grows once we cross this threshold. However, similar nonlinearity is obtained in our evolution model, as shown in figure 5a (main plot), where we display the statistics of cell death against the size of the aggregates. A nonlinear relationship is also found in our model, which is due to the nonlinearities associated with the thresholds of survival as well as the nonlinear relationships owing to the geometric constraints imposed by our system.

Figure 5.

Nonlinear relation between death rates and aggregate size (a). Our diffusion-driven model predicts a slow increase in death rates (here measured as the observed fraction of dead cells within a cluster) up to a certain aggregate size, from which death rapidly increases. Such a nonlinear relation was also found in the experiments (inset, adapted from Ratcliff et al. [15]) and considered evidence for a selection process for programmed cell death. However (main plot), the diffusion-limited model discussed here predicts a very similar outcome, with low death rates below a given aggregate size and a sharp increase beyond that threshold. Localized cell death (b): 90.55% of the 2 × 10⁴ observed apoptotic cells were among the 25% of cells closest to the centre of the aggregate. Below, we show a sample cluster with its cells classified in four groups after their centrality, the different shades of grey correspond to the quartiles shown in the pie chart. (Online version in colour.)

4. Discussion

Unravelling the mechanisms responsible for the emergence of multicellular life forms from single-cell systems represents a major challenge for our understanding of biological complexity. The traditional approach to this problem was based either on data-driven, experimental and phylogenetic analysis or on mathematical and computer models of simple cell-like units and their emerging interactions [24]. The experimental work described in reference [15] provides a novel way of addressing this problem through a simple and elegant design of a selection-driven experimental set-up. Despite the differences existing between wild and laboratory microorganisms [25], we can safely conjecture that the mechanisms responsible for generating and disaggregating cell clusters should be universal.

Although the experimental results suggested an interpretation of the evolutionary dynamics in terms of an evolved, regulated response, the results reported here suggest a simpler, alternative interpretation in terms of a diffusion-limited process of aggregate growth where the cluster of cells keeps growing provided that enough waste is excreted passively into the medium. Once its size is large enough though, cells occupying the inner layers of the aggregate will start to trigger apoptotic mechanisms shown to occur in natural strains owing to the accumulation of endogenous chemical cues, such as acetic acid or ammonia. This alternative view does not disprove that the observed apoptotic rates are a consequence of adaptation, but offers a clear substrate from which evolution could act, increasing the prevalence of an already existing mechanism.

Accordingly, our interpretation does not diminish the relevance and implications of the experimental evolution experiments. On the contrary, we think that this interpretation suggests a potentially interesting framework concerning the steps followed by primitive aggregates predating the first multicellular life forms. Aggregates breaking up owing to internal cell death through toxicity results in a mechanism of splitting that clearly goes beyond the single-cell level, but is based on physical (or physico-chemical) constraints instead of actively operating regulatory mechanisms and signals. This role played by physics over the cell's molecular machinery is consistent with a view of evolving MC based on an early dominance of physical mechanisms over genetic ones [18,26–28].

Our model provides a simple computational framework that can be expanded in different ways. It also provides a useful system to design new forms of evolving multicellular aggregates. In this context, an interesting avenue can be considered here involving the use of synthetic biology, where specific engineered circuits for population size control or programmed cell death have been designed using microbial models. As a result of such work, it is fair to talk about designing cell–cell interactions in order to provide new, controlled scenarios of multicellular evolution [29]. In this context, we could take advantage of new engineered forms of cellular aggregation that can then be evolved over time. Such a synthetic multicellular approach will offer a whole pathway of inquiry into the problem of how complex life might evolve or how we can evolve it.

Funding statement

This work was supported by the Botín Foundation (S.D.N., R.S.), MINECO BES-2010-038940 fellowship (S.D.N.) and by the Santa Fe institute, where most of the research was done.