Quantifying long-term evolution of intra-urban spatial interactions

Abstract

Understanding the long-term impact that changes in a city's transportation infrastructure have on its spatial interactions remains a challenge. The difficulty arises from the fact that the real impact may not be revealed in static or aggregated mobility measures, as these are remarkably robust to perturbations. More generally, the lack of longitudinal, cross-sectional data demonstrating the evolution of spatial interactions at a meaningful urban scale also hinders us from evaluating the sensitivity of movement indicators, limiting our capacity to understand the evolution of urban mobility in depth. Using very large mobility records distributed over 3 years, we quantify the impact of the completion of a metro line extension: the Circle Line (CCL) in Singapore. We find that the commonly used movement indicators are almost identical before and after the project was completed. However, in comparing the temporal community structure across years, we do observe significant differences in the spatial reorganization of the affected geographical areas. The completion of CCL enables travellers to re-identify their desired destinations collectively with lower transport cost, making the community structure more consistent. These changes in locality are dynamic and characterized over short timescales, offering us a different approach to identify and analyse the long-term impact of new infrastructures on cities and their evolution dynamics.

1. Introduction

Cities, as the core of modern society, are playing increasingly important roles through global urbanization, providing people with housing, transportation, communication and functional institutions for various social activities. Enabled by the transportation infrastructure layer, diverse social interactions among various entities shape a city's interaction layers, creating social economic outputs, which further spur the growth of the cities themselves [1–4]. Created by individuals' trips for work, school, shopping and other social activities, intra-urban movement is a crucial part of these spatial interactions. Intra-urban movements exhibit strong spatial and temporal patterns, which play an important role in urban planning and traffic forecasting [5–7]. Taking travel demand as an example, previous studies have focused on developing models to estimate current and predict future interaction intensity based on social and infrastructural input for planning purposes [8–13]. Although extensive efforts have been made using travel diary data collected from household surveys and interviews [6,7], studies on individual/collective movement still suffers from their small sampling shares, high cost, infrequent periodicity and limited accuracy. As a result, despite the observations telling us that near things are more related than distant things' geographically [14], studies trying to integrate the infrastructure and interaction layers have remained limited due to the lack of detailed longitudinal data measuring change at high spatial and temporal resolutions.

The emerging individual-based large-scale datasets have allowed us to trace our daily behaviour pattern in detail, shifting our understanding on individual mobility from random to predictable [15–17]. The smart card data also show pronounced advantages in depicting the structure of collective encounter networks given the large share of public transit (capturing more than 63% of total mobility in Singapore) [18]. Besides revealing mobility regularity, these datasets also help us further understand human mobility-induced spatial interactions, which are crucial to various urban diffusion processes such as epidemic spreading, knowledge-spillover and social contagions [19–21]. Thus, recent studies demonstrate an increasing use of network theory to model diverse types of interactions (from transportation to digital communication) on multiple scales (state, country and global) [22], documenting the importance of such interactions among spatial units in shaping network typologies [23–27]. This paper analyses intra-urban movements using three one-week transit use data, including both bus and metro systems, from 3 years (11–15 April 2011; 19–23 March 2012; and 8–12 April 2013) in Singapore. We place special emphasis on the study of a key transportation infrastructure—the extended Circle Line (CCL; Mass Rapid Transit service), which provides us an ideal natural observation to investigate how such large infrastructures influence human mobility, and how the resulting spatial interactions shape the structural evolution of a city. The first stage of the CCL (the Eastern half; figure 4d, coloured orange) has been in operation since 2010. After the competition of the second Western half, the CCL has been fully operational (35.7 km in total; figure 4e) since October 2011. This metro line cost about 10 billion Singapore dollars (roughly 8 billion US dollars), carrying about half a million passengers daily today (0.37 million per day in stage 1 and 0.53 million per day after opening stage 2). It seems reasonable that such a large infrastructure project should affect local/global mobility patterns and city structure, by first influencing individual travel patterns, and then by prompting second-order effects such as new businesses and real estate. Indeed, such effects can be measured by looking at the usage patterns of the extension and the geographical space where it occurs [28]. However, these approaches suffer notable limitations when analysing city-wide movements. First, we miss how this local change affects global/city-scale patterns: we cannot tell whether the new service alters mobility patterns by merely looking at local travel patterns. Second, there might be changes of mobility patterns enabled by the new infrastructure we are not aware of yet. Taking advantage of emerging network analysis, this paper tries to present some steps to overcome this knowledge gap.

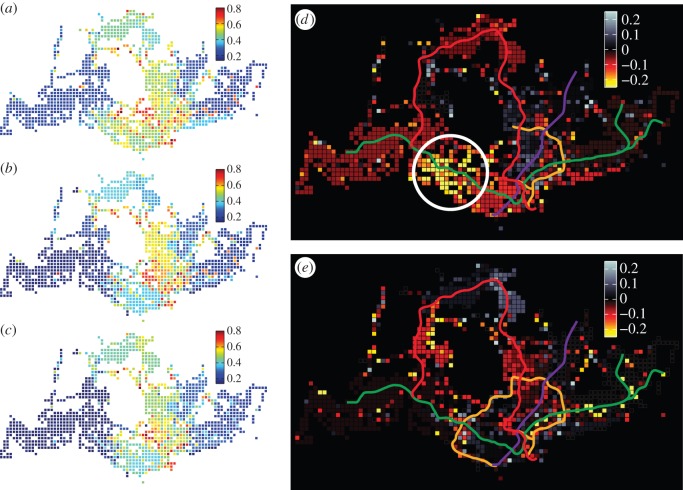
Figure 4.

Spatial distribution of mutability ϕ_i from 06.00 to 21.00: (a–c) ϕ_i,11, ϕ_i,12 and ϕ_i,13 in the year 2011, 2012 and 2013, respectively. (d) The difference of mutability from 2011 to 2012 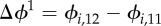. (e) The difference of mutability from 2012 to 2013 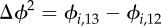. Given that the full completion of CCL was in October 2011, panel (a) shows the mutability of stage 1 while both (b,c) show the mutability of stage 2. Thus, panel (d) actually shows the change of mutability from stage 1 to stage 2, while both ϕ_i,12 and ϕ_i,13 are in stage 2 for panel (e).

2. Results

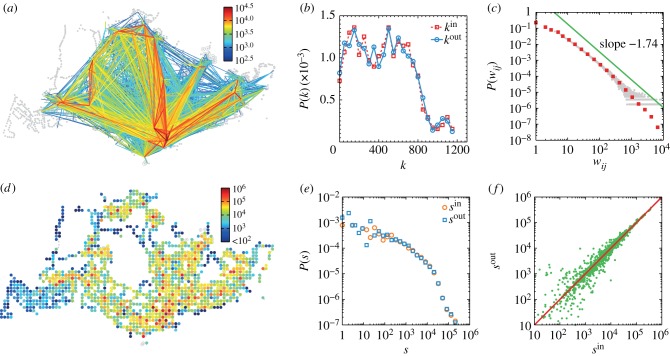
To sketch the geographical structure of intra-urban movement from collective transit use, we divided the island city–state Singapore into zones of 500 × 500 m, indexing all transit journeys with their origin–destination (OD) pairs (see the electronic supplementary material for defining spatial zones and transit journey). By aggregating all transit journeys across weekdays using OD indexes in 2012, we obtained a directed and weighted spatial interaction network, which demonstrates symmetrical in/out-degree distributions (figure 1a,b). This network—with spatial zones as its vertices and the time-resolved commuting flows as its edges—is the basis of our analyses. To explore its statistical properties, we first measure interaction intensity w_ij as total passenger flow travelling from zone i to j, finding that when w_ij ≥ 10, the tail of distribution P(w_ij) is well characterized by a power law 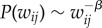with an exponent β = 1.744 ± 0.002 (figure 1c) using statistical tools provided in [29]. This indicates that intra-urban movement displays a strong heterogeneity: most ODs have small flows, but a few ODs involve massive demands. Note that a similar scaling is reported for London Underground [5], suggesting that such scaling of interaction intensity might be a fundamental property of urban spatial interactions. To quantify the importance of individual zones in shaping the aggregate interaction network, we measured in/out-strength of vertex i as its total inflows and outflows ( 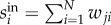and 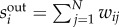) on weekdays, respectively. As figure 1d shows, the spatial distribution of zone strength also exhibits a strong heterogeneity across the city. Although it is difficult to identify a deterministic function to characterize zone strength distributions 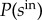and 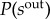, we still find the same heavy tail characterizing both of them and observe an intrinsic balance across all zones (figure 1e,f). Different from a previous study about the dependency of vertex strength s on vertex degree k in the worldwide airport network [23], we found an exponential increase s(k) ∼ exp(λk) instead of a power law s(k) ∼ k^β (with β > 1), suggesting that the network demonstrates a much faster increase of s than k (see the electronic supplementary material, figure S1). In fact, considering the strong heterogeneity of w_ij, degree k, which merely counts the presence of edges and exhibits a saturation process with time, is not appropriate to capture the time-varying architecture and the backbone of this interaction network (electronic supplementary material, figures S2 and S3). To check whether these properties hold over time, we applied these analyses for year 2011 and 2013 as well. Despite the completion of the CCL during the study period, we found indistinguishable aggregate properties for the 3 years.

Figure 1.

Structure of intra-urban public transport movements in Singapore. (a) Aggregated spatial interaction network across weekdays (from 19 to 23 March 2012). For simplicity, we only show the top 1% of edges with highest total interaction intensity w_ij + w_ji in an undirected manner. The grey markers show the spatial locations of transit infrastructures, including both bus stops (dots) and metro stations (circles). (b) In/out-degree distribution P(kⁱⁿ) and P(k^out) measured on the aggregated network. (c) Probability density function P(w_ij) of interaction intensity across all OD pairs. Grey dots show the original histogram and red squares correspond to a log-binned histogram. As a guide, the green line shows a power law with an exponent β = 1.74. (d) The spatial distribution of total strength 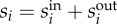of each cell. (e) Probability density function P(sⁱⁿ) of in-strength and P(s^out) of out-strength. Both of them exhibit heavy-tailed properties. (f) Symmetrical plot of sⁱⁿ and s^out. Most dots are scattered around the red line, suggesting the homogeneous inflow and outflow spatially.

A key property in understanding the dynamics of a spatial network is its community structure, defined as vertex partitions which have more connections within themselves than between each other. The importance of community lies in revealing the intermediate scales of network organization and identifying hidden structure in network theory. However, in practice the detection of communities is a difficult task to apply. The state-of-the-art approach to find these partitions is to maximize modularity Q [30]

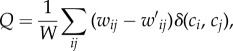2.1

where 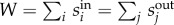is the total network traffic, 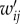is the expected interaction intensity estimated from a null model and δ is an indicator function: δ(c_i, c_j) = 1 if zone i and j belong to the same partition and δ(c_i, c_j) = 0 otherwise. The approach has been successfully applied on various spatial interaction networks at different resolutions, such as identifying effective administrative borders and finding hidden structures of countries and cities [24–27]. In practice, an appropriate null model is crucial to get a meaningful expectation 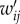to reveal corresponding network structural attributes. Without accounting for spatial attributes, we adopted the default null model for defining modularity, i.e. 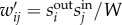(see the electronic supplementary material, figure S2). Note that one may replace the null model for special considerations; for example, 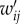is determined using a gravity model to exclude the dependency on distance in [26].

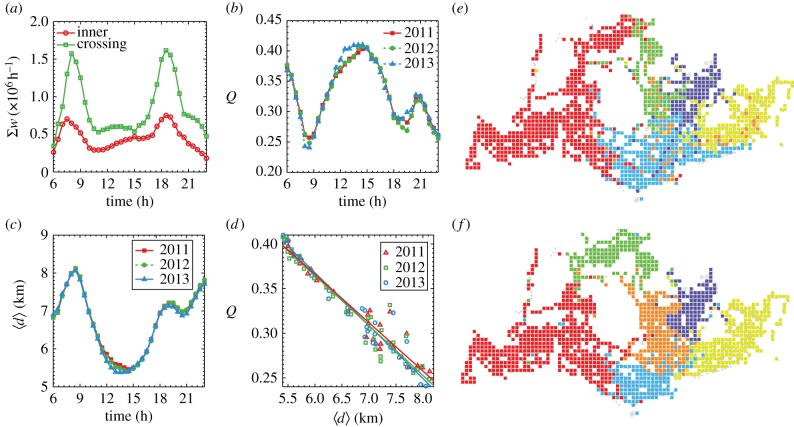
To find partitions that maximize modularity Q, we applied the well-established Louvain method on the aggregated network across weekdays [31]. Although the detection process employs only interaction intensity (without using any geographical information), we still observe a clear spatial consistency from 2011 to 2013 (see the electronic supplementary material, figure S4), suggesting that collective movements are remarkably constant across years. Yet, we may miss the temporal evolution of these community structures by merely analysing the aggregated network. To explore this evolution over the day, we grouped all transit journeys according to their transaction times (see the electronic supplementary material for details). Based on these temporally grouped journeys, we created a series of sub-networks and applied the community detection processes on each of them. In figure 2a, we summed intra- and inter-community flows and measured their temporal variations using 2012 data. Although community structure is well defined spatially and intra interactions are much stronger than inter interactions 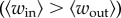, the total number of journeys crossing communities is still higher than that of intra community trips 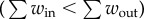, suggesting that people are not confined to a spatial community but show wider destination choices. Likewise, we repeated this analysis for the other years for comparison, finding that temporal variations of modularity Q are essentially indistinguishable across years (figure 2b and electronic supplementary material, figures S6–S8). This indicates that temporal intra-urban movements (or collective mobility) might be comparable as well. Given the clear geographical consistence of these communities, modularity Q is actually a measure of spatial mobility patterns embedded in temporal activities. To explore the variability of collective mobility over time, we measured the average trip distance 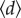for each sub-network. Not surprisingly, we also found high degree of similarity of 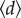across years (figure 2c), indicating that temporal travel behaviours of populations are essentially comparable over 3 years as well. Next, we compared Q and 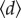jointly to explore how collective movement shapes the time-varying community structure. If communities are well identified as spatial clusters, the longer people travel, the higher the chance that one jumps out of a community. However, the relation is unclear without the assumption. For example, taking only structured metro trips will give rise to high modularity and long travel distance, whereas short and random local trips will lead to low modularity and short distance. We find that they are linked by a universal and substantial negative correlation 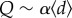(figure 2d; with ρ₂₀₁₁ = −0.9718 [p < 10⁻⁴], ρ₂₀₁₂ = −0.9623 [p < 10⁻⁴] and ρ₂₀₁₃ = −0.9763 [p < 10⁻⁴]); and once again, we observed similar structural patterns across years, independently of the completion of the CCL. Therefore, using time-varying travel displacement as an indicator, we confirmed that temporal variation of collective movement plays a crucial role in expressing the dynamic community structures.

Figure 2.

Structure and temporal variation of intra-urban spatial interactions. (a) Temporal variation of total movements within communities (red-circled line) and across communities (green-squared line) in the year 2012. The summation of these two parts is the total transit flows. (b) Temporal change of modularity Q in 3 years. Modularity Q is characterized by a wave with pronounced troughs (at 08.30 and 19.30) and peaks (at 14.30 and 21.00). (c) Temporal variation of average trip distance 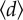in 3 years. (d) The scatter plot of temporal modularity Q and average trip distance 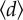. The solid lines represents linear regressions of 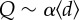, with α₁₁ = −0.69 ± 0.03, α₁₂ = −0.70 ± 0.04 and α₁₃ = −0.72 ± 0.03 (the subscripts represent years), respectively. (e,f) Community structures identified for 08.30 and 14.30 in 2012.

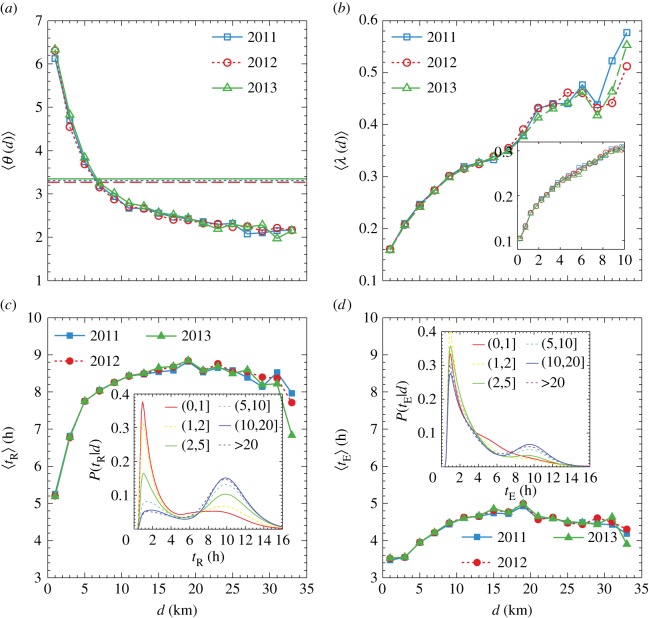
To explore how distance affects systematic/occasional travel behaviour, we quantified the variation of two distance-related diversity measures. Without considering individual identity, we first quantify the degree of heterogeneity of bi-directional flows by measuring a diversity index of OD (i, j) as 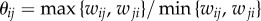(for OD pairs with 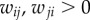). If the collective attribute θ_ij is independent of distance, we expect to find θ_ij being characterized by a determined distribution free from d_ij. However, on the contrary, we do find a significant and consistent reduction of 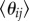with d_ij, indicating that bi-directional transit flows at a collective level become more and more balanced with distance. Still, this is not sufficient to show homogeneity at the individual level. Taking advantage of the anonymized card ID, we further investigated the similarity of users travelling between i and j for each day using the Jaccard index 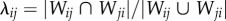, where W_ij represents the set of individuals travelling from i to j; thus, λ_ij is close to one if all individuals travel symmetrically each day, and zero if no one returns to previously visited locations (i.e. 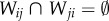). After measuring λ_ij for all OD pairs across weekdays, we show the dependence of 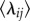on d_ij in figure 3b, finding another consistent (increasing) trend across 3 years. Therefore, despite previous observations characterizing exploration/preferential return behaviour [32], we found that shorter travel distances are associated with higher exploration; and correspondingly, previously visited locations are more preferred for longer distance journeys. Moreover, these properties are also stable across years, independent of the new metro line.

Figure 3.

The impact of distance on spatial interaction patterns. (a) The average diversity index θ_ij with given displacement d_ij. The dashed line demonstrations a null model assuming that θ is independent of d. (b) The average correlation 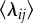with d_ij. The inset illustrates the change of 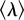when 0 < d ≤ 10 km. (c) Stay duration t_R(d) in between round trips (i, j) and (j, i), averaged over d_ij for both years. The inset shows the distribution P(t_R|d) for groups characterized by different d using kernel smoothing. (d) The same plot as in panel (c), however, for the stay duration t_E(d) in between trip chain. The inset shows the corresponding conditional distribution P(t_E|d).

Large-scale human mobility patterns have been described by three indicators: trip distance distribution P(d), temporal variation of radius of gyration r_g(t) and number of visited locations S(t). However, the duration of stay at one location, as another important attribute in understanding why people move rather than why people stay, is seldom considered in the literature. To investigate recurrence and periodicity of travel behaviour and the patterns of stay in terms of both exploration/preferential return behaviours, we classified transit usage based on the pattern [33]: round journeys (with two trips i → j and j → i) and trip chains with two trips (i → j and j → k, where i ≠ k), and measured the duration of stay at zone j for each. In figure 3c,d, we show the change of average duration of stay for both round journeys 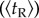and exploratory trip chains 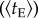as a function of distance d_ij, finding that both 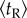and 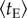display an consistent increase with d in the beginning and reach saturation after d = 10 km. In comparing them, we find that t_R is significantly longer than t_E (p < 10⁻⁴, Wilcoxon rank-sum test), suggesting that people tend to stay longer at the destination of round trips. To further distinguish t_R from t_E, we group journeys with similar travel distance d_ij and determine the distribution P(t_R|d) of stay duration (by measuring the interval between journey i → j and journey j → i) and P(t_E|d) (by measuring the interval between two journeys i → j and j → k) for each group. As the insets of figure 3c,d show, both P(t_R|d) and P(t_E|d) can be approximately characterized by a mixture distribution of a short stopover (secondary activity around 1 h, such as shopping, eating and leisure activities) and a long primary activity (around 10 h, such as work and school). We note that the key difference between t_R and t_E is their composition: the proportion of primary activity in return journeys is significantly higher than that of a trip chain. Thus, figure 3c,d also implies a strong correlation between trip purpose and travel distance, further confirming the role of distance in shaping spatial interaction structure. Taken together, we show that travel distance not only determines the balance of intra-urban movement and a traveller's exploration/preferential return behaviour, but also with the type of journey. Not surprisingly, we once again observe a clear consistency of t_R and t_E across the 3 years.

Previous analyses has shown that intra-urban movement is consistent over the 3 years, exhibiting patterns independent of the key infrastructure project, suggesting that human mobility may display universal patterns invariant to the change of transportation infrastructures. However, as mentioned, with time-varying interactions during a day, the resulting structural communities should be changing simultaneously over time (such as the continuous changing of boarders and emergence of new communities). This effect offers us more insight into how spatial interactions shape the city. To quantify it, we define neighbourhood variability γ_i(t₁, t₂) of zone i between the sub-networks at time t₁ and t₂ as

2.2

where C_i(t) represents the community which zone i belongs to at time j. Hence, γ_i(t₁, t₂) is close to one if the intersection contains only i and zero if C_i does not change from time t₁ to t₂. Using continuous observations during 1 day, we quantified the overall spatial evolution of zone i by calculating mutability index ϕ_i as average neighbourhood variability from t₀ till t_max [34]

2.3

where t₀ is the time step when we start observing the temporal evolution and t_max is the last time step. Thus, ϕ_i quantifies the overall evolution of community structure for each individual zone, characterizing the robustness/fragility of the spatial community to which zone i belongs. Essentially, ϕ_i quantifies community transition rate of zone i when other zones are also changing simultaneously. A high ϕ_i typically indicates that zone i is attached to diverse communities over time and vice versa. In other words, the mutability index ϕ_i used here could also be interpreted as a measure to quantify the diversity of temporal community attachment. By setting t₀ = 6 and t_max = 23 (from 06.00 to 23.00 in 1 h intervals, see the electronic supplementary material for details), we determined the value of ϕ_i,y for each individual zone i in year y. As shown in figure 4a–c, we find that mutability displays clear and comparable spatial patterns: one can easily distinguish the borders between regions with different mutability. Particularly, the central/southern area displays a higher mutability and the western/eastern parts are generally stable across 3 years.

To further compare mutability across years, we calculated Δϕ (as 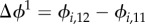and 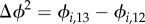) and map the results in figure 4d,e, respectively. Notably, although the temporal change of Q, 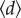and other collective mobility indicators are essentially indistinguishable, we do observe a significant difference when using 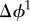as an indicator, while not much difference is observed when measuring 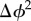. We think that the completion of the CCL appears as a main factor for this difference (figure 4d). As mentioned, only the right half of the CCL was in operation in 2011 (stage 1), while the full metro line has come into service since October 2011 (stage 2). Given the definition of ϕ_i, the implication of Δϕ_i > 0 are twofold. On one hand, for those zones that have not changed their membership during a day, such as most zones in the eastern/western community, the decrease of ϕ_i suggests that the community to which zone i belongs becomes more consistent over time. On the other hand, for those zones that changed their membership during a given time, a decreasing ϕ_i implies that zone i changes less frequently and strengthened its dependency to the attached community. In fact, the completion of stage 2 (the western half of the circle) enables travellers to find their desired destination choices collectively in a structured manner with lower cost, instead of making diverse choices individually. In this sense, the completion of stage 2 of CCL may make zones in southern area (the white circle in figure 4d) more accessible to either the western community or the central community (as shown in the electronic supplementary material, figures S6–S8). We next perform statistical tests on Δϕ_i for zones within the white circle (radius 4 km, 124 zones nearby the extended CCL) and zones outside the circle (1170 zones). We find that 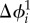in the nearby area are significantly lower than others (p < 10⁻⁴; left side Wilcoxon rank-sum test), while there is no clear evidence to show 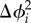in the nearby area are different from the others (p = 0.213; Wilcoxon rank-sum test).

3. Discussion

Understanding spatial interactions is crucial to urban planning, traffic forecasting and various mobility-related urban diffusion processes such as epidemic spreading and social contagions. More importantly, coupled with the transportation infrastructure layers of a city, social economic outputs are shaped by these interactions [35,36]. Although the study of mobility has a long history, previous works were almost all based on modelling these interactions for planning purposes owing to a lack of longitudinal data detailed enough across both spatial and temporal scales. Yet, the evolution of urban structure with these temporal interactions is merely revealed: it remains a challenge to distinguish the natural variability in the city's mobility from large deviations, using either coarse-grained or short-timescale mobility data.

Taking advantage of population-scale smart card datasets spanning 3 years, we study the structure of Singapore's intra-urban interaction network and present how it is influenced by a key transportation infrastructure project (the CCL in this case). Despite that Singapore has been a dynamic, fast-changing city, we show that human mobility displays invariant aggregate patterns across the years, even when seeing a large infrastructure project. As a city evolves over the years, how can we distinguish large deviations in mobility from statistical fluctuations in a city's mobility patterns? Our study suggests that commonly used tools and statistics do not offer sufficient sensitivity to identify key changes in the city's mobility structure.

We present evidence for this by first examining the temporal community structure that emerges from collective travel behaviour, and study its variation across years. Using modularity as an indicator, we find that the community structure varies consistently with the spatial–temporal characteristics of collective mobility, indicating that distance acts as a powerful constraint to keep universal mobility patterns in place over 3 year period, and therefore, does not allow us to discriminate the impact of the completion of the CCL. Moreover, we found that both modularity Q and average journey distance 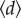demonstrate clear and consistent temporal homogeneity, exhibiting remarkable robustness to the competition of the extended CCL as well. Taking stay-durations as another indicator quantifying human mobility, we showed that travel distance not only determines individual's exploration and preferential return behaviour, but also associates with one's purpose of travelling. However, none of these indicators help us identify the global impact of CCL.

Notably, despite other structural and behavioural dynamic indicators being almost consistent and indistinguishable over the long-term, we do observe a significant difference of mutability. Mutability, which is defined as the average ratio of community members changed across time, emerges as a highly sensitive tool to understand the position of individual zones in the overall evolution and real-time evolving borders of community structure. In fact, it is sensitive to the differences in mobility caused by major transportation infrastructure change, showing the evolving borders in community structure, and with this the way people interact to shape, sustain or reform a city.

Our findings and analysis framework offers analytical tools to better sense the evolution of mobility patterns in cities, providing insights for urban planning, modelling and understanding the evolution of cities through the coupling of infrastructure and interaction networks. Given that ICT is being fast embedded in our daily-life, spatial–temporal digital traces helping us to follow cities will become available in various forms, overcoming the limits of field surveys and interviews. In the near future, much urban data which are generated in real-time will become available for urban planning, improving the quality of life. Despite the privacy concerns, taking full advantage of such data in planning would surely help us further understand urban dynamics and make our cities smarter. Taken together, our study offers a quantitative and general strategy to understand the dynamic evolution in multiple temporal scales and serve as a basis to further track and model such evolution [37].

Funding statement

This study was supported by National Research Foundation of Singapore, which is the funding authority of the Future Cities Laboratory, Singapore-ETH Centre. M.C. is funded by the Australian Government as represented by the Department of Broadband, Communications and Digital Economy and the Australian Research Council through the ICT Centre of Excellence programme.