Multi-haem cytochromes in Shewanella oneidensis MR-1: structures, functions and opportunities

Abstract

Multi-haem cytochromes are employed by a range of microorganisms to transport electrons over distances of up to tens of nanometres. Perhaps the most spectacular utilization of these proteins is in the reduction of extracellular solid substrates, including electrodes and insoluble mineral oxides of Fe(III) and Mn(III/IV), by species of Shewanella and Geobacter. However, multi-haem cytochromes are found in numerous and phylogenetically diverse prokaryotes where they participate in electron transfer and redox catalysis that contributes to biogeochemical cycling of N, S and Fe on the global scale. These properties of multi-haem cytochromes have attracted much interest and contributed to advances in bioenergy applications and bioremediation of contaminated soils. Looking forward, there are opportunities to engage multi-haem cytochromes for biological photovoltaic cells, microbial electrosynthesis and developing bespoke molecular devices. As a consequence, it is timely to review our present understanding of these proteins and we do this here with a focus on the multitude of functionally diverse multi-haem cytochromes in Shewanella oneidensis MR-1. We draw on findings from experimental and computational approaches which ideally complement each other in the study of these systems: computational methods can interpret experimentally determined properties in terms of molecular structure to cast light on the relation between structure and function. We show how this synergy has contributed to our understanding of multi-haem cytochromes and can be expected to continue to do so for greater insight into natural processes and their informed exploitation in biotechnologies.

1. Introduction

Cytochromes form a large family of proteins. They display a wide range of functionalities and yet the vast majority of these proteins contain c-haem, namely, iron coordinated by protoporphyrin IX that is covalently linked to the peptide by thioether bonds (figure 1). These bonds typically arise from a Cys-X1-X2-Cys-His haem-binding motif that provides a His axial ligand to the haem iron and where X can be any amino acid. Mono-haem cytochromes c with His/Met axial ligation of the haem iron make significant contributions to apoptosis and have well-established roles as electron shuttles in both aerobic and anaerobic respiration [1]. Also well studied are proteins containing multiple mono-haem cytochrome c domains [1]. However, this review takes as its subject the more recently recognized and rapidly expanding family of multi-haem cytochromes c whose members are able to transfer electrons over relatively long distances both within and outside cells.

Figure 1.

(a) Two different haem types found in biological systems. The structure of haem c includes covalent thioether linkages to the protein. (b) Binding of haem c via the C-X1-X2-CH-binding motif (providing the proximal axial histidine ligand) and with histidine as the distal axial ligand.

Multi-haem cytochromes are defined by the presence of two, or more, c-haems positioned to bring neighbouring irons within 15.5 Å of one another [2,3]. The haems typically have His/His axial ligation and support rapid electron transfer (ET) through a series of intraprotein ET steps involving the ferric/ferrous redox couple. This concept of electron transport along a protein cofactor chain over several nanometres is indeed widely used in bioenergetic systems. Prominent examples include respiratory enzymes like the complexes in the mitochondrial inner membrane (IM) [4] which couple exergonic electron flow to endergonic proton membrane translocation, or the technologically promising hydrogenases [5,6]. In photosynthesis, cofactor ET chains enable the rapid separation of the photochemically created electron–hole pair [7,8]. A number of different redox-active cofactors are in use in these systems; apart from haems, iron–sulfur clusters of varying stochiometry or small organic compounds like quinones (Q) can be found. These cofactors can be spaced 10 Å or more apart from edge to edge, with the protein matrix often filling the space in between. By contrast, multi-haem cytochromes feature closely packed haems, often in van der Waals contact. Within or alongside, the resulting haem chain sites for redox catalysis can be incorporated and the accessible distances of electron transport can be extended by interactions between two or more multi-haem cytochromes such that these proteins are versatile ET modules. In Nature, multi-haem cytochromes are predominantly associated with bacteria and their cycling of N, S and Fe in processes that contribute to the harnessing of energy from diverse and chemically stratified environments. These processes are also of immediate societal impact through their contributions to infection, food security and regeneration of the Earth's atmosphere (e.g. [1–3,9,10] and references therein) and metabolic pathways supported by multi-haem cytochromes contribute to the deployment of bacterial communities in strategies ranging from the bioremediation of contaminated soils to the harnessing of bioenergy (e.g. [11–15] and references therein). Looking forward, there are also opportunities to use multi-haem cytochromes in bespoke molecular machines and during the microbial electrosynthesis of fuels and chemical feedstocks [11–16].

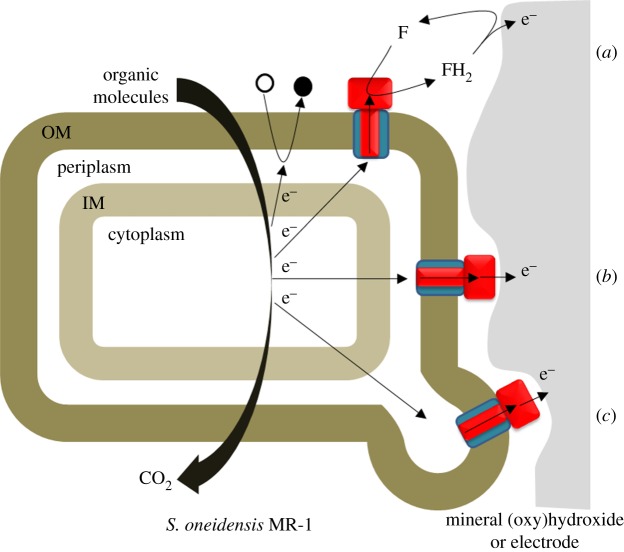
Numerous bacteria contain multi-haem cytochromes. Of these, Shewanella oneidensis MR-1 is noteworthy for its respiratory versatility. This species is a facultative anaerobe able to use more than 10 terminal electron acceptors in the absence of O₂ and in processes that exploit the large number of multi-haem cytochromes encoded within its genome [10,13,17,18]. The respiratory reduction of N and S oxides and oxyanions employs multi-haem cytochromes that have homologues in numerous other bacteria [2,3,13]. However, and in perhaps the most striking respiratory capability of S. oneidensis, two recently discovered families of outer membrane (OM) associated multi-haem cytochromes are responsible for ET to insoluble metal oxides of Fe(III) and Mn(III/IV) that may be located more than 50 µm from the cell surface [10,19–22]. Not only is this kind of biochemistry important for metal cycling in natural environments, it can support electron exchange with electrodes to underpin the harnessing of bioenergy and routes to the microbial synthesis of fuels and chemical feedstocks [16,23,24]; these prospects have motivated ongoing research efforts into the biochemistry of insoluble substrate reduction focusing on S. oneidensis as a model organism. Three mechanisms have been proposed to account for the respiratory reduction of extracellular electron acceptors by S. oneidensis (figure 2): (i) direct ET following contact of the extracellular substrate and redox-active multi-haem cytochromes on the cell surface, (ii) flavin-mediated ET between the extracellular substrates and multi-haem cytochromes on the cell surface, and (iii) ET along extracellular appendages, referred to as nanowires and recently identified as multi-haem cytochrome-containing extensions of the OM that span distances greater than 100 Å to link cells to each other or to establish contact to solid substrates [19,25–27].

Figure 2.

Overview of strategies for respiratory electron transport during the anaerobic growth of S. oneidensis. The oxidation of organic molecules releases electrons to the IM. From the IM electrons may pass to soluble terminal electron acceptors (black circle) that enter the periplasm. Alternatively, the electrons may cross the periplasm and the OM to be delivered to extracellular terminal electron acceptors. ET from the cell surface may be mediated by flavin (F) (a), occur directly from an extracellular cytochrome (b) or involve cellular appendages called nanowires (c). OM spanning complexes homologous to MtrAB are represented by the blue rectangle with a red stripe. Extracellular cytochromes homologous to MtrC are represented by the red rectangle.

We trust that this brief introduction has conveyed some of the importance, and the present excitement, surrounding the contributions of multi-haem cytochromes to electron transport and catalysis in both intra- and extracellular processes. Here, we aim to illustrate the particular opportunities that exist for fruitful synergy of experimental and computational approaches to elucidate the properties of these proteins; experiments can reveal the structure and macroscopic properties of the protein and computational approaches can use the structural information to deconvolute and interpret the properties at a molecular level of detail. Given the multitude of S. oneidensis MR-1 multi-haem cytochromes, their homologues in many other species but also the extracellular examples, we take this ensemble of proteins and their electron transport network as our focus and as reviewed in §2. This sets the stage for an in-depth discussion of individual cytochromes that begins in §3 where we present known structures of multi-haem cytochromes and the available structural information for cytochromes not crystallized thus far. Properties of multi-haem cytochromes are discussed in §4, focusing both on intraprotein ET and interaction with solid and soluble substrates and other cytochromes. This leads to an analysis of structure–function relationships in §5, drawing on the structural findings presented in §3 and the functional insight from §4. Building on this, we turn our intention to possible future developments in §6 and discuss how experimental and simulation approaches can continue to complement each other in furthering our understanding of multi-haem cytochromes. Conclusions and a summary are provided in §7.

2. Overview of multi-haem cytochromes in the metabolism of Shewanella oneidensis

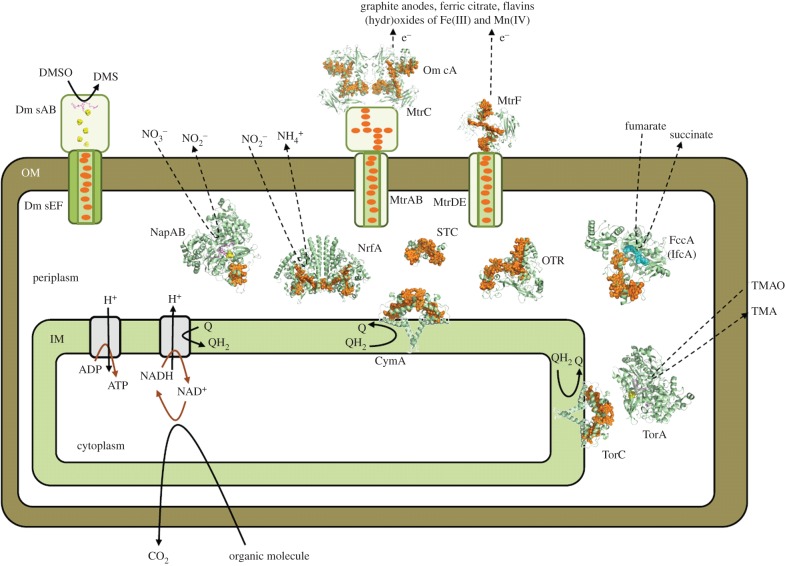
The multitude of multi-haem cytochromes produced by S. oneidensis is perhaps most readily appreciated when their metabolic role is understood. Each of the multi-haem cytochromes contributes to mechanisms that allow the bacterium to harness energy from the available nutrients such that the cellular fuel ATP can be made. ATP synthesis through substrate-level phosphorylation or catalysed by the molecular motor ATP synthase is driven by the oxidation of organic molecules in the cell interior [28]. The oxidation occurs in the bacterial cytoplasm (figure 3). The electrons released by that process must then be transferred through a network of redox proteins to reach a terminal electron acceptor that is present in the bacterium's environment. The multi-haem cytochromes underpin the ET network.

Figure 3.

Multi-haem cytochromes from S. oneidensis illustrated schematically to indicate their cellular location and roles. High-resolution structures are presented for proteins from S. oneidensis STC (pdb entry: 2K3V), NrfA (3UBR), OTR (1SP3), FccA (1QJD), MtrF (3PMQ) and OmcA (4LMH) and their homologues NapAB (1OGY), CymA (2J7A), TorC (2J7A) and TorA (1TMO). Cartoons illustrate the OM spanning porin : cytochrome complex for which no structures are available and the IM associated processes that generate ATP and pass electrons to Q in the IM. The arrangement of cofactors in DmsAB is based on that in the homologue NarGH (1R27). Haems (orange), FeS clusters (yellow/green), FAD (cyan) and molybdopterin (purple).

Shewanella oneidensis can use a diversity of terminal electron acceptors. In the absence of O₂, these acceptors include fumarate, nitrate, trimethylamine oxide (TMAO), dimethyl sulfoxide (DMSO), sulfite, thiosulfate, elemental sulfur and oxidized metals such as Fe(III), Mn(III), Mn(IV) and U(VI) that may be present either as soluble complexes or within solid mineral (hydr)oxides [29–33]. This respiratory versatility makes S. oneidensis competitive in complex aquatic and sedimentary systems. It also underpins the biotechnological contributions made by S. oneidensis. For example, the reduction of soluble U(VI) and Cr(VI) to insoluble precipitates of U(IV) and Cr(III) offers routes to remove dilute metal pollutants in both natural and contained storage sites. The large amounts of sulfide produced from thiosulfate and sulfur allow toxic metals to be immobilized as insoluble metal sulfides. In addition, the oxidation of organic pollutants by anaerobic bioremediation of waste water can be driven by the positive reduction potentials of Fe(III) and Mn(III/IV) as terminal electron acceptors or the anodic potential in a microbial fuel cell.

The ET partners supporting anaerobic respiration include cytochromes, Fe–S proteins and quinols (QH₂). These partners form a network originating in the IM, spanning the periplasm and OM and extending into the extracellular environment (figure 3). This extensive network is demanded by the cellular locations of the key processes. Whereas organic molecules are taken into the cell for oxidation within the cytoplasm, the reduction of terminal electron acceptors occurs outside the bacterium or within the periplasm separating the cytoplasm from the cell exterior. Some of the ET partners supporting anaerobic respiration contribute to the reduction of multiple terminal electron acceptors such that they can be considered as sites for distributing electrons across a branched ET network.

Electrons enter the network at the IM. QH₂ are IM soluble electron carriers produced on reduction of Q by cytoplasmic oxidations. Continued cytoplasmic oxidation requires Q regeneration. Two multi-haem cytochromes with high sequence similarity are able to catalyse this process, TorC and CymA. Both of these enzymes are anchored to the IM by a single α-helix (figure 3). The tetra-haem containing periplasmic domains catalyse QH₂ oxidation and present the resulting electrons to periplasmic redox partners. TorC has a single redox partner, the TMAO reductase TorA. CymA is a menaquinol oxidase [34] able to transfer electrons to partners that result in the reduction of fumarate, nitrate, nitrite, mineral (hydr)oxides of Fe(III) and Mn(III/IV), complexes of Fe(III), DMSO, flavins and electrodes (see [33,35–37] and references therein). This difference in the biochemistry of CymA and TorC is reflected in the genome [13]. TorC and TorA are produced from the same operon. CymA is produced from an orphan gene that allows its synthesis to be regulated independently of that of its redox partners.

Sulfite, nitrate, nitrite and fumarate are terminal electron acceptors able to cross the OM for reduction in the periplasm by multi-haem cytochromes (see table 1 and figure 3). Sulfite and nitrite are reduced by the SirA octa- and NrfA penta-haem cytochromes, respectively [38,39]. Another octa-haem cytochrome, OTR, has been purified from S. oneidensis [40,41]. This enzyme is able to reduce a range of N and S oxides and oxyanions in vitro but its cellular role has yet to be established. Like CymA and TorC, these enzymes use a c-haem as the basis for catalytic substrate reduction. The nitrate and fumarate reductases incorporate additional cofactors for their catalytic activities. In the NapAB nitrate reductase, the catalytic cofactor is Mo. In the fumarate reductases, FccA and IfcA, that cofactor is flavin adenine dinucleotide (FAD).

Table 1.

Multi-haem cytochromes of Shewanella oneidensis MR-1. ‘E’ stands for extracellular, ‘IM’ for inner membrane, ‘OM’ for outer membrane and ‘P’ for periplasmic.

protein	no. c-haems	additional cofactors	main role	cellular location	gene(s)	molecular weight (kDa)
MtrC	10	—	metal and flavin reduction	E	SO_1778	75
MtrF	10	—	metal and flavin reduction	E	SO_1780	74
OmcA	10	—	metal and flavin reduction	E	SO_1779	83
MtrA	10	—	ET	OM	SO_1777	35
MtrD	10	—	ET	OM	SO_1782	38
DmsE	10	—	ET	OM	SO_1427	38
SO4360	10	—	ET	OM	SO_4360	38
OTR	8	—	reduction of nitrite or tetrathionate	P	SO_4144	54
SirA	8	—	sulfite reduction	P	SO_0479	80
NrfA	5	—	nitrite reduction	P	SO_3980	53
FccA (Fcc3)	4	FAD	fumarate reduction	P	SO_0970	64
IfcA (Ifc3)	4	FAD	fumarate reduction	P	SO_1421	64
STC (CctA)	4	—	ET	P	SO_2727	12
NapB	2	—	ET to NapA nitrate reductase	P	SO_0845	16
CymA	4	MQ	quinol oxidation coupled to ET to periplasmic and OM proteins	IM	SO_4591	21
TorC	4	—	quinol oxidation coupled to ET to TMAO reductase (TorA)	IM	SO_1233	20

The reduction of extracellular terminal electron acceptors by S. oneidensis requires ET across the OM. This is a process supported by deca-haem cytochromes of which the best studied is MtrA [10,42,43]. MtrA (35 kDa) forms a complex with the 28 strand β-barrel porin MtrB (85 kDa). An extracellular deca-haem cytochrome MtrC (75 kDa) co-purifies with MtrAB. Support for the role of MtrAB and MtrCAB in trans-OM ET comes from the ability of these complexes to support transmembrane ET when incorporated in a liposome [42,43].

The S. oneidensis genome contains parallogues of MtrA (MtrD, DmsE and SO4360), MtrB (MtrE, DmsF and SO4359) and MtrC (MtrF and OmcA). Porin : cytochrome complexes are predicted for the MtrAB parallogues such that these proteins are implicated in ET to extracellular redox partners. Indeed, the porin : cytochrome complex may form a phylogenetically widespread module for ET across bacterial OMs [42]. In S. oneidensis MR-1, the Mtr/OmcA proteins support the reduction of extracellular metals, flavins and electrodes. MtrF, MtrD and MtrE are proposed to form an OM-spanning complex, MtrFDE, with the same overall structure as MtrCAB. In vivo and in vitro experiments provide evidence that OmcA associates with MtrC in a 2 : 1 stochiometry [44–46]. Extracellular complexes comprised of deca-haem cytochromes may then contribute to extracellular respiratory ET. DmsEF is a porin cytochrome complex that supports trans-OM ET to the catalytic extracellular subunits required for DMSO reduction, DmsAB [32] (figure 3). The role of the predicted porin cytochrome complex SO4359_60 and its associated subunits, SO4361_62, has yet to be resolved [47].

Three mechanisms proposed to support ET to extracellular terminal electron acceptors were introduced in §1. The reduction of DMSO by DmsABEF is an example of the first mechanism, whereby direct ET occurs between the substrate and enzyme following complex formation. The mechanism(s) supporting extracellular ET to solid surfaces have been harder to establish and it seems likely that two, or more, of the mechanisms operate simultaneously. MtrCAB incorporated within a liposome model for trans-OM ET can supply electrons directly to mineral oxides of iron at a rate sufficient to support anaerobic respiration [43]. In addition, the expression of mtrCAB in Escherichia coli confers low, but significant, capacity for reduction of the mineral oxide hematite on the host [48]. However, ET between S. oneidensis and solid extracellular surfaces in the absence of direct contact has been shown in a number of studies. The reduction of Fe(III) oxide located in alginate or nano-porous glass beads was demonstrated [20,21]. In addition, comparable electrical current was sustained by a biofilm grown over an insulating layer with holes designed to allow, or exclude, direct contact with the electrode [22]. In experiments of the latter type, a significant, but recoverable, decrease in the electrical current on rinsing the biofilm without damaging its structural integrity provided evidence that low-molecular weight mediators in the form of flavins secreted by S. oneidensis make a significant contribution to ET to electrode and mineral surfaces [25,49]. Flavin reduction is dependent on the respiratory pathway(s) provided by the Mtr/OmcA proteins [36].

The number of Mtr parallogues makes it likely that these proteins are tailored to reduce specific substrates or be used during different growth conditions. In support of this suggestion, mtrDEF is most highly expressed during biofilm growth [50] and MtrC has been proposed to play the major role in reduction of flavin mononucleotide (FMN), whereas OmcA is selective for riboflavin [51]. Nevertheless, there appears to be some modularity in the respiratory network at the level of the Mtr/Omc proteins with one able to take the role of another under certain conditions [47]. MtrF, but not OmcA, can support low rates of ferric citrate reduction in the absence of MtrC and MtrD can support ferric citrate and FMN reduction in the absence of MtrA. In addition, hybrid complexes can form from MtrCAB and MtrFDE components [47,52].

The third mechanism proposed to support ET from S. oneidensis to solid surfaces involves conductive appendages that have been called nanowires [26,53]. These cellular appendages are several micrometres long and exhibit electric conductances rivalling those of synthetic semiconducting materials (about 1 S cm⁻¹). Nanowires produced by a ΔmtrC/ΔomcA double mutant are not conductive such that the structures may contain MtrC/OmcA for conductivity, or the MtrCAB/OmcA₂ complex may be required for ET across the OM to the nanowires. These extracellular appendages are not essential for extracellular ET [54].

Having surveyed the majority of multi-haem cytochromes present in the respiratory network of S. oneidensis, it is appropriate to finish this section with mention of the protein : protein interactions that may support ET across the respiratory network that they form. It is fair to say that this is a topic that requires further analysis for a clear picture to emerge. In vivo studies found that the flux of ET from MtrCAB to FccA dropped by 80% on deletion of either menaquinone or CymA [16]. Specific protein partners, rather than a periplasmic pool of proteins, may then provide the pathways for facile ET between IM and periplasmic or OM proteins. In vitro studies have presented evidence for both stable and transient complexes involving a number of multi-haem cytochromes in S. oneidensis [55–59]. It is also relevant here that the tetra-haem cytochrome STC (CctA) with no obvious catalytic site is abundant in the periplasm. This protein has been reported to reduce soluble Fe(III) [60] but seems likely to play a role supporting ET throughout the respiratory ET network through interactions with redox enzymes in the IM, periplasm and OM [57,61,62].

3. Structures

The multi-haem cytochromes of S. oneidensis contain predominantly His/His-ligated haems. At the time of writing, high-resolution structures have been resolved for six of these proteins and structures can be predicted for a further four on the basis of their homology to structurally resolved proteins from other organisms. These structures reveal close-packed haem arrangements. It is striking that certain constellations of neighbouring haems are observed in multiple proteins despite very different amino acid compositions and protein folds. These constellations may be optimized to impose control over ET rates and direction. This section discusses the arrangement of haems within protein monomers and where the haems have His/His axial ligation unless stated otherwise.

There are a limited number of ways in which two c-haems can pack tightly within a folded polypeptide. The two haems in NapB have parallel planes [63]. These units are offset relative to one another such that they are in van der Waals contact, yielding a ‘stacked’ arrangement (figure 4a). This brings the closest atoms of each ring within 4 Å of each other and results in an Fe–Fe distance of 9.9 Å (values similar for stacked pairs in other multi-haem cytochromes). Closer alignment of the haems is prevented by the methyl carbon of one haem being within van der Waals distance of an axial His ligand to the second haem. Close packing of two His/His-ligated c-haems can also arise when the haem planes are perpendicular, or ‘T-shaped’, with either face-to-edge or edge-to-edge alignment (figure 4b), resulting in slightly larger ring edge-to-ring edge distances of around 6 Å and Fe–Fe distances of 11–13 Å. Proteins with more than three c-haems where neighbouring haems take the T-shaped arrangement belong to the cytochrome c₃ family. However, the majority of multi-haem cytochromes from S. oneidensis contain alternating stacked and T-shaped planes, while a third packing haem motif (figure 4c) is found between some haem pairs of the extracellular deca-haem cytochromes. The latter motif features parallel porphyrin planes but without the vertical offset that allows ring carbon van der Waals contact in the stacked motif; this yields a ‘coplanar’ arrangement of haems with slightly larger edge-to-edge distances of 6–7 Å and Fe–Fe distances of 13–14 Å.

Figure 4.

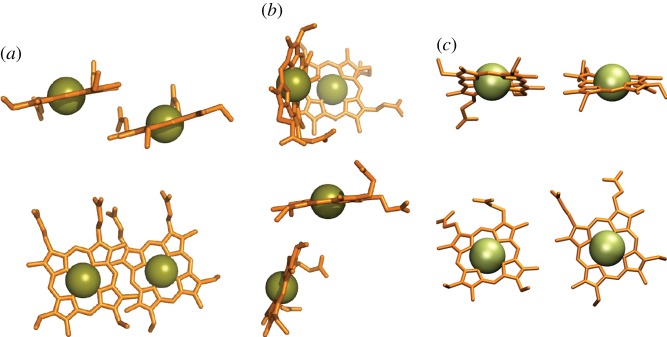
Haem packing motifs found in multi-haem cytochromes. (a) ‘Stacked’; (b) perpendicular or ‘T-shaped’; (c) ‘coplanar’. In each panel the lower images show the haems rotated by 90° relative to the upper images.

STC, FccA, IfcA, CymA and TorC each contain four haems (figure 5). The arrangements of these haems are best considered by referring to the haems in the order that their Cys-X1-X2-Cys-His-binding motifs occur in the relevant primary sequence. The arrangement of haems in CymA and TorC can be predicted from the X-ray structure of a close homologue, NrfH from Desulfovibrio vulgaris [64] (figure 5a). Haem pairs I/II and III/IV take a stacked alignment, while haems II and III lie approximately perpendicular in a T-shaped arrangement. The quinol oxidase activity of these enzymes is imparted by haem I that in CymA has axial ligands of His and water [55]. In STC, the stacking of the haem pairs is reversed [65] (figure 5b). Haem pairs I/II and III/IV take a T-shaped arrangement, while haems in the II/III pair lie stacked. For all haem pairs, the distance of closest approach between ring atoms is 6 Å or lower, the Fe–Fe distance 12 Å or lower. Haems I, II and III in the much larger fumarate reductases FccA and IfcA (64 kDa) can be overlaid on those in STC [66,67]. However, haem IV lies further from haem III (15.6 Å Fe–Fe distance) to accommodate ET to FAD within the site for catalytic fumarate reduction (figure 5c). Gene fusion followed by haem IV repositioning in the fumarate reductases is most likely to have optimized the position of haem IV to allow extension of the intramolecular ET chain that is not required by STC.

Figure 5.

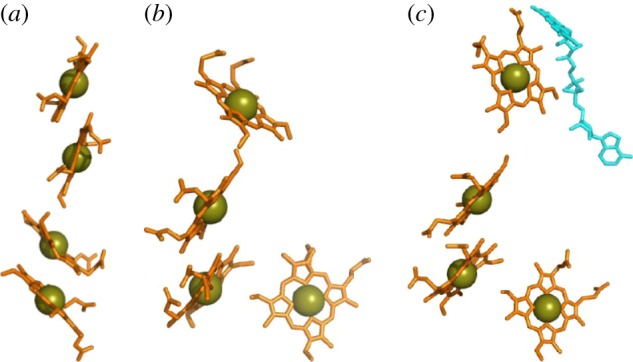
Haem chains in tetra-haem cytochromes from S. oneidensis. (a) The quinol oxidase CymA (haem chain from the homologous NrfH from D. vulgaris shown in lieu of resolved structure for CymA). (b) The periplasmic electron shuttle STC. (c) The fumarate reductase FccA, also including the FAD cofactor (cyan). PDB codes as for figure 3.

A c-haem modified to perform a catalytic function is a feature not just of CymA and TorC but also of the penta-haem NrfA and octa-haem OTR proteins [41,68]. In both of these proteins, the catalytic haem is found within a group of three stacked haems with edge–edge distances below 4 Å to allow direct π-interactions of the rings (figure 6). The catalytic haem receives axial ligation from lysine and water. The latter ligand is exchanged for substrate, then intermediates and product during catalysis. In NrfA, the lysine ligand to the haem comes from the relatively novel Cys-X1-X2-Cys-Lys haem-binding motif. A Cys-X1-X2-Cys-His motif binds the catalytic haem in OTR but the His is oriented away from the haem and a Lys that is remote in the primary sequence becomes an axial ligand to the haem. The active site and haems of NrfA adopt a constellation that is reproduced in OTR. In both proteins, the arrangement of His/His-ligated haems creates a bifurcated pathway allowing electrons to reach the active site from two sites located on opposite sides of the proteins.

Figure 6.

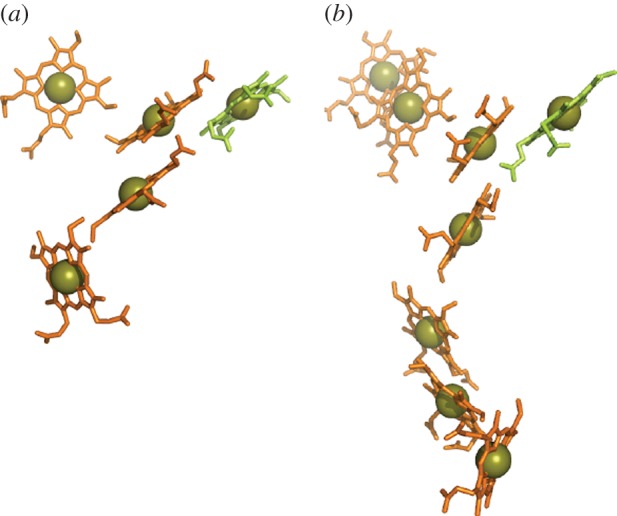
Haems in two periplasmic N/S oxoanion reductases from S. oneidensis: (a) NrfA and (b) OTR. The catalytic haem is highlighted in green for each cytochrome. PDB codes as for figure 3.

MtrC and its parallogues OmcA and MtrF are prototypical members of three of the four major clades of extracellular cytochromes in species of Shewanella [69]. The fourth clade is represented by the undeca-haem UndA from Shewanella HRCR-6. These clades of extracellular cytochromes are distinguished by their size and amino acid composition; these properties will in turn define the specificity of their interactions with protein partners, solid surfaces and flavins (§4.2). Structures have been resolved for MtrF, OmcA and UndA that reveal these proteins are folded as four distinct domains [70–72]. Domains 1 and 3 form Greek-key split β-barrel structures (figure 7a). Domains 2 and 4 are haem-binding domains. In MtrF and OmcA, haems 5,4,3,1,6,8,9 and 10 form an octa-haem chain that extends across the lengths of domains 4 and 2. Haems 2 and 7 are positioned on the flanks of that chain facing domains 1 and 3, respectively. Haems 2,1,6 and 7 form a tetra-haem chain. The additional haem in UndA is positioned adjacent to haem 7 of OmcA and MtrF. A structure has yet to be presented for MtrC but it is predicted to display the defining conserved features of OmcA, MtrF and UndA.

Figure 7.

Haems in OM-associated deca-haem cytochromes from S. oneidensis. (a) The staggered cross from the OM cytochrome MtrF (pdb entry: 3PMQ). (b) Model for the haem arrangement in MtrA (associated with the periplasmic side of the OM) based on two NrfB units (2OZY).

Detailed structural insights into the nature of the OM-spanning porin : cytochrome complexes that permit trans-OM ET are lacking. Of the relevant cytochromes, MtrA is the most extensively studied. It can be purified as a stable soluble protein with rod-like dimensions; 104 Å in length with an elliptical cross section approximately 25 by 50 Å at its largest cross section [73]. This would allow for MtrA insertion within the 28-strand β-barrel porin that is predicted for MtrB [43]. The arrangement of haems within MtrA (and MtrD) is unlikely to map onto those of the extracellular cytochromes that are essentially circular in one plane and with a diameter of 70 Å. Sequence analysis suggests that MtrA may have resulted from duplication of a gene encoding a penta-haem cytochrome. The penta-haem cytochrome NrfB from E. coli provides a structural model for such a protein [74] (figure 7b). In NrfB, the haems are arranged in a semi-linear arrangement as alternating stacked (I, II and III, IV) and T-shaped (II, III and IV, V) haem pairs. The haem chain spans 40 Å such that its duplication could provide a sufficiently long haem wire to traverse the approximately 80 Å width of the OM [62].

This section presented and compared the structures of multi-haem cytochromes from Shewanella, with a focus on analysing haem cofactor arrangements and their conservation between different groups of cytochromes. This sets the stage for an extensive discussion of the functional properties of multi-haem cytochromes in §4, on the levels of both whole proteins and individual subparts and cofactors. As we shall see, the specific structural elements discussed so far have strong functional implications, as is further discussed in §5. But functional properties are not determined by haem arrangement alone; §4 will also elucidate the role of the protein environment surrounding the haems.

4. Properties of multi-haem cytochromes

To understand how multi-haem cytochromes are used to reduce a varied range of soluble and insoluble substrates, it is necessary to understand both their intraprotein electron transport properties as well as their interaction with substrates. Intraprotein electron transport can be broken down into individual ET steps between adjacent haems; it was found that this haem-to-haem ET is well described by Marcus theory in the non-adiabatic limit [75]

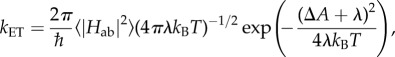4.1

where the ET rate k_ET is determined by the driving force ΔA, the reorganization free energy λ and the thermal average of the square of the electronic coupling matrix element H_ab. In the interaction with external acceptors, the additional question of binding sites and substrate affinities arises.

In the following, we discuss intraprotein ET (§4.1) and review interactions with external acceptors in §4.2.

4.1. Intraprotein electron transfer

In the following, we present the knowledge gained so far about ET within multi-haem cytochromes, with regard to individual Marcus parameters (redox potentials, reorganization free energies) and resulting rates of ET and through-protein transport.

4.1.1. Redox potentials

The close distance of the redox-active sites in multi-haem cytochromes enables the redox state of one haem to affect the redox potentials of close-by haems. Thus, redox potentials determined via successive oxidation/reduction of a multi-haem cytochrome (as is done in many experimental set-ups, e.g. voltammetric or potentiometric measurements) are macroscopic in nature, describing the collective behaviour of the haems when the electrochemistry of the cytochrome as a whole is probed. By contrast, microscopic redox potentials refer to the oxidation/reduction of a particular haem for a fixed redox state of all other haems or redox microstate (e.g. all-oxidized if transport of a single electron through the cytochrome is considered). Thus, the driving force ΔA in equation (4.1) can be described as the difference of microscopic redox potentials of the two cofactors involved in the ET (for the respective redox microstate under which the ET takes place); macroscopic redox potentials, on the other hand, serve to describe the aforementioned whole-protein electrochemical response. In the following, we discuss both kinds of redox potentials: how they are obtained experimentally and computationally and results obtained for multi-haem cytochromes so far.

Macroscopic redox potential windows. Most experimental probes of protein redox activity define the potential window across which the protein is redox active. This can be established both for a protein in solution and for a surface immobilized protein on an electrode as discussed in [76] and references therein. The latter kind of arrangement is used in protein film voltammetry where the current due to electron exchange between an electrode and an adsorbed protein film is recorded as a function of electrode potential. Figure 8 compares cyclic voltammograms illustrating the redox-active windows of several multi-haem cytochromes from S. oneidensis. These windows are similar which appears plausible given that ET is not coupled to energy transduction across the network formed by these proteins. This is in contrast to the mitochondrial electron transport chain where ET to the terminal electron acceptor is intimately coupled to energy transduction. In S. oneidensis, it may be beneficial to minimize the dissipation of free energy across the ET network from CymA to terminal electron acceptors.

Figure 8.

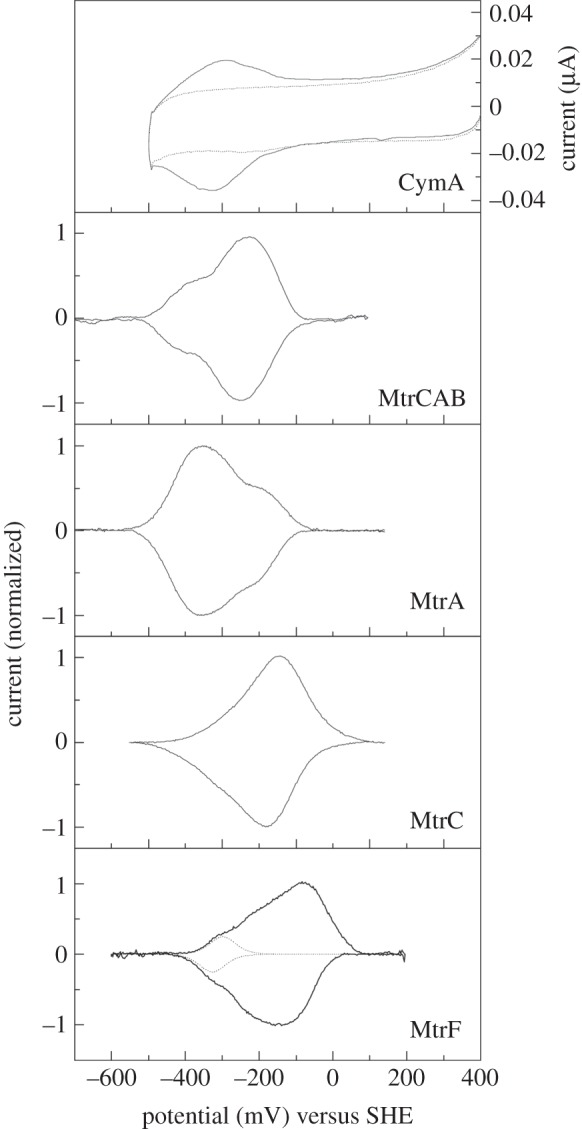
Protein film electrochemistry of multi-haem cytochromes from S. oneidensis. Cyclic voltammetry of CymA (solid line) adsorbed on an 8-mercaptoctanol modified template stripped gold electrode at a 10 mV s⁻¹ scan rate, pH 7.4 is compared to a voltammogram recorded in the absence of CymA (broken line) (redrawn from [34]). Baseline-subtracted cyclic voltammograms are presented for MtrCAB, MtrA, MtrC and MtrF adsorbed on graphite electrodes. Voltammetry was recorded at 30 mV s⁻¹, pH 7 and the peaks are presented as normalized to their respective peak currents (redrawn from [42,72]). For MtrF, a single n = 1 response with average E_m of −312 mV accounts for one-tenth of the peak area and describes the low-potential flanks of the peaks.

The area of each peak in the cyclic voltammogram of an adsorbed protein quantifies the number of moles of electrons exchanged between the electrode and the protein. As a consequence, each redox event contributes to the total area in proportion to the electron stoichiometry of the corresponding half-reaction. The peak shape is a sum of the responses arising from the macroscopic redox properties of the protein. For example, in the case of MtrF, the low-potential flank of the peaks contains a feature that accounts for one-tenth of the total peak area and that can be fit to the theoretical response for an isolated n = 1 centre with a macroscopic redox potential of approximately −310 mV versus SHE (figure 8) [72]. However, it is not possible to assign this, or other redox potentials, deduced from voltammetric peaks to specific haem centres within the protein. Such assignments may be possible when a protein's redox activity is defined by spectropotentiometric titration of the protein, adsorbed on an electrode or in solution, as a function of the sample potential. For CymA, the quinol-oxidizing haem is high-spin in contrast to the low-spin His/His-ligated haems. As a consequence optical spectroscopy of CymA at visible wavelengths allows redox transformation of the high-spin haem to be distinguished from that of the low-spin haems [55]. Plots of signal intensity versus sample potential can be fit to the Nernst equation to yield electron stoichiometry and macroscopic redox potentials.

Optical spectroscopies are typically unable to resolve the redox chemistry of individual His/His-ligated haems. By contrast, electron paramagnetic resonance (EPR) spectroscopy resolves different signatures for such ferric haems with parallel imidazole planes, perpendicular imidazole planes and imidazolate ligation. As a consequence, potentiometric titration of multi-haem cytochromes is routinely monitored by EPR spectroscopy. In this way, it was proposed that haems 2, 4, 5, 6, 7 and 8 of MtrF that display near parallel His ligands in the crystal structure titrate with macroscopic redox potentials between 0 and −260 mV [72]. Haems 1, 3 and 9 have near-perpendicular His ligands and were proposed to have macroscopic redox potentials between −100 and −260 mV. An imidazolate-ligated haem was proposed to contribute the lowest redox potential centre in the protein and that may correlate with haem 10. Thus, spectroscopic methods allow redox potential assignments to be proposed for sub-sets of haems within multi-haem cytochromes but rarely allow for complete assignment of redox potentials to structurally defined haems. One example of the latter case is cytochrome c₅₅₄ from Nitrosomonas europaea where a combination of EPR and Mossbauer spectroscopy enabled the assignment of potentials to all four individual haems [77].

Here, computational approaches could prove helpful in complementing experimental assignments. An early computational study used single-point continuum electrostatics calculations to compute the macroscopic redox potentials for the tetra-haem chain in the reaction centre of Rhodopseudomonas viridis and was able to qualitatively reproduce the experimental values [78]. An improvement in accuracy is offered by computational titration methods familiar from protein pKa (continuum electrostatics) calculations [79,80]. The continuum treatment allows for a very efficient estimation of the free energy of the many possible redox (and protonation) microstates (2^N for N redox sites), so that their Boltzmann occupation probability can be readily computed for a given electrode potential (and pH) using, for example, Monte Carlo sampling. The resultant occupation probability of each redox microstate as a function of electrode potential can be fit to a simple analytical expression (e.g. of the Henderson–Hasselbalch form) to obtain midpoint potentials that could be compared to macroscopic redox potentials. Such a Monte Carlo-based titration was performed, for example, in [81] for hydroxylamine oxidoreductase (HAO) and the aforementioned cytochrome c₅₅₄ from Nm. europaea. For the latter cytochrome, the experimental assignments [77] could be reproduced. For HAO, the experimental macroscopic potentials [82] were reproduced quite well; in regard to potential assignments to individual cofactors, the study confirmed some experimental assignments [83] but interestingly introduced an alternative hypothesis in regard to one assignment. As is also suggested in [81], further improvements in accuracy can be conceived in the framework of explicit protein dynamics sampling via molecular dynamics (MD) simulations; in principle, this would allow one to treat the molecular interactions determining redox potentials more accurately. At the time of writing, we are not aware of any such implementations for redox potential calculations; this might be an area for future developments.

Microscopic redox potentials of individual cofactors. The experimental determination of microscopic redox potentials requires a means of distinguishing the different redox centres. Nuclear magnetic resonance (NMR) spectroscopy can be employed for this purpose as the (highly redox-sensitive) signals for methyl groups of different haems can be distinguished in spite of the overall nearly identical chemical nature of bis-His-ligated c-haems [84,85]. At the same time, electrostatic interactions between haems can be established, quantifying how the redox potential of one haem is shifted by a different redox state of another haem. These interactions can become quite significant for very short iron–iron distances but quickly decay with distance, as can be rationalized by a simple electrostatic shielding model [86]. This is illustrated by the four haems in FccA (see figure 3b for the haem arrangement): the interaction between the stacked haems II and III reaches around 100 meV but is only around 20 meV for the further separated adjacent haems I and II [85]. Where the interaction does become significant, it could contribute to the cytochrome's electron transport functionality [85].

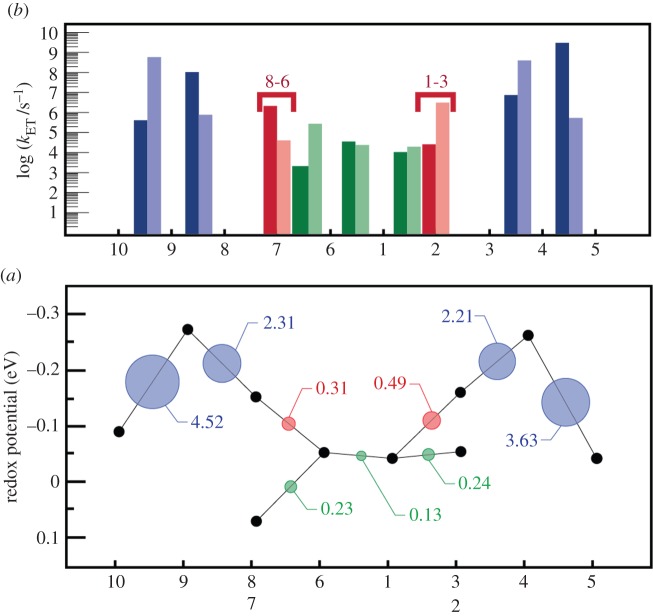
Despite these capabilities of NMR to deconvolute redox properties of individual haems, its applicability has limits. Specifically, measurements become more challenging with increasing protein size, with FccA being the largest cytochrome so far for which microscopic redox potentials could be established via NMR [85]. An appealing alternative in this situation are in silico calculations of microscopic redox potentials; these merely suffer from an increase in computational cost with increasing cytochrome size. If experimental macroscopic redox potentials are known, computational estimation of the aforementioned cofactor electrostatic interactions in the context of continuum electrostatics (akin to the work in [78]) enables the deconvolution of macroscopic into microscopic redox potentials [87,88]. Alternatively, the microscopic potentials can be calculated from scratch for which free energy simulation methods are well suited. Such calculations are well established for mono-haem cytochromes and other proteins with single redox-active cofactors (e.g. [89,90]); recently, the first set of computed microscopic redox potentials has been published for a deca-haem cytochrome, specifically MtrF from S. oneidensis [91]. As the other Marcus quantities have been obtained for this cytochrome as well (see §§4.1.2 and 4.1.3), allowing for the calculation of haem-to-haem ET rates and analysis of structure–function relationships, we discuss the redox potentials for MtrF and the resulting free energy landscape in more detail.

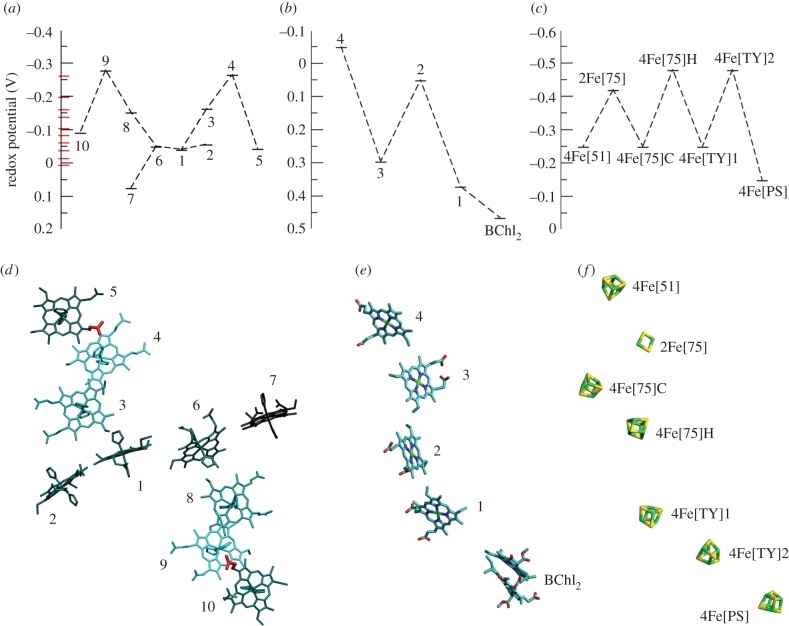
Microscopic redox potentials for all 10 haems in MtrF in the all-oxidized state were calculated using classical MD with a thermodynamic integration protocol; the calculations were long enough to allow for the construction of a statistically significant free energy profile for single-electron conduction along the staggered-cross haem wire. The resulting profile is shown in figure 9a [91] (see figure 9d for the haem arrangement in MtrF). Each small bar along the broken line represents the redox potential of one cofactor along the octa-haem chain, with the potentials of haems 2 and 7 (the two cofactors not part of the octa-haem chain) branching off from haem 1 and 6, respectively. The red bars along the y-axis denote the 10 macroscopic redox potentials obtained from a fit to protein film voltammetry (PFV) data [72]. The microscopic redox potentials obtained from computation range from −0.28 to 0.07 V, spanning 0.35 V, slightly larger than the range of macroscopic potentials obtained from experiment, −0.26 to 0.0 V. This agreement is very encouraging. The small discrepancy can be attributed to several sources of errors. First, the computed range is affected by the high redox potential of haem 7, which might be overestimated (see discussion in [91]). Second, the difference between microscopic and macroscopic redox potentials can reach several 10 meV as mentioned above. Third, in these classical MD calculations, it is assumed that the redox potential difference between the haems is entirely due to the protein and water. Possible electronic polarization effects of the haem groups due to the different environments surrounding the haems are neglected.

Figure 9.

Comparison of cofactor arrangements and free energy landscapes for MtrF (microscopic redox potentials), a bacterial photosynthetic reaction centre and mitochondrial complex I (both macroscopic potentials). (a–c) Present free energy landscapes for each system; see corresponding in (d–f) for the respective cofactor arrangement. (a) Free energy landscape for the 10 haems in MtrF [91]. The red bars along the vertical axis represent (unassigned) macroscopic potentials derived from the protein film voltammetry presented in [72]. (Adapted from [91].) (b) Free energy landscape for the four haems and the bacteriochlorophyll dimer (BChl₂) in the photosynthetic reaction centre of Rps. viridis [92]. (c) Free energy landscape for the FeS cluster ET chain in bovine mitochondrial complex I [93,94], including estimates for the three low-potential clusters (below −0.4 V) [88]. (d) Visualization of the free energy landscape within the molecular structure of MtrF: haems are coloured according to their redox potential, with lighter colours corresponding to lower redox potentials and thus a higher position in the free energy landscape. The two proprionates exerting a strong influence on the potentials of haems 4 and 9, respectively, are highlighted in red. (Adapted from [91].) (e) The haem chain+BChl₂ dimer in the photosynthetic reaction centre of Rps. viridis (pdb entry 1PRC [95]). (f) The FeS cluster chain in bovine mitochondrial complex I of (pdb entry 4UQ8 [96]).

Intriguingly, the free energy landscape in figure 9a exhibits two energetic uphill steps (around 0.2 eV), as opposed to a constant downward slope that one might intuitively expect (as positive reaction free energies lower the rate of ET—see equation (4.1)). However, such ‘roller coaster’ free energy landscapes with uphill steps of 0.2 eV or more are indeed often found in other cofactor ET chains as well [97]. Examples include the haem chain in the aforementioned photosynthetic reaction centre of Rps. viridis [92], the FeS cluster chain in mitochondrial complex I [88,98] and the FeS cluster chain in the NiFe hydrogenase of Desulfovibrio gigas [99]. (These are macroscopic potentials, though; the electrostatic interactions between cofactors can exacerbate the differences in macroscopic midpoint potentials, which would mean smaller differences for microscopic potentials in an all-oxidized protein [88]. See also the discussion of this aspect below for MtrF under reduced conditions.) To put the free energy landscape for MtrF into perspective, we compare it to the potential landscapes of the haem chain in the photosynthetic reaction centre and the FeS cluster chain in mitochondrial complex I in figure 9 which also shows the different cofactor chains.

The classical MD simulations allowed us to analyse the calculated redox potentials in terms of contributions of individual protein residues, with positively charged residues in the vicinity of a given cofactor increasing its redox potential and negative residues decreasing it. Figure 9d depicts the 10 haems in MtrF coloured according to their redox potential (darker for higher redox potential) and also highlights two particularly important side chains thus found: one proprionate from both haem 5 and haem 10; these are very close to the two haems with the lowest potentials (4 and 9) and were found to strongly contribute to their low potentials [91]. Still, the free energy profile observed poses the question of how the low-potential haems are incorporated without slowing down through-protein electron transport.

A last aspect to consider is the redox interactions between individual haems. We would like to emphasize again that the calculated redox potentials are for the all-oxidized state, which are the relevant potentials for electron transport through the all-oxidized haem wire. Haem–haem interactions have not been calculated, but the distance dependence of the interactions (specifically, the screened-interaction model from [86]) allows for some rough considerations. Assuming the absence of non-electrostatic effects like redox-state-dependent conformational changes, the presence of an excess electron on an adjacent haem would decrease the redox potential of a given haem, with the magnitude of the effect dependent on the distances between the haems in question. The fit in fig. 2 in [86] would suggest an effect of around 20 meV for the coplanar pairs with iron–iron distances of 13–14 Å, ca 30 meV for the T-shaped pairs (iron–iron distance ca 12 Å) and perhaps 50 meV for the stacked pairs (iron–iron distance ca 10 Å). With these shifts being larger for the haems whose all-oxidized microscopic potentials are lower to begin with (haems 4 and 9 interacting with two stacked neighbours each and haems 3 and 8 with one stacked and one T-shaped neighbour each), this could lead to a ‘stretching’ of the free energy landscape under all-reduced conditions (in the case of hole transport) in comparison to the all-oxidized landscape in figure 9a, without changing the qualitative aspects of the profile (akin to the stretching of the macroscopic potential landscape compared to the microscopic one in [88]).

4.1.2. Reorganization free energies

In experiment, the two main approaches to determine the reorganization free energy λ are to vary either the driving force or the temperature for a given ET process and use the known dependence of the ET rate on either parameter to derive λ [100]. However, there are potential obstacles for both of these methods: inferring λ from the rate dependence on driving force requires the manipulation of proteins to modify the driving force in a controlled manner (specifically, such that λ can be determined with sufficient precision); and using the temperature dependence of k_ET requires knowledge of the temperature dependence of the driving force [101]. (However, λ can be experimentally determined for heterogeneous ET to an electrode whose potential and therefore driving force to/from the cytochrome can be precisely controlled.) Measurements of λ for single ET steps in a multi-haem cytochrome would furthermore require the ability to measure rates of individual steps. Again, computational approaches are able to complement experimental insight by providing access to this quantity. In the framework of linear response theory, the reorganization free energy for an ET can be expressed as [102]

4.2

where the vertical (instantaneous) ET energy (for a fixed nuclear configuration), ΔE_o, is averaged over the initial (A) and final (B) state (i.e. prior to and after ET), respectively [103]. This formalism allows one to calculate λ via sampling of ΔE_o with MD. This approach has been successfully employed for ruthenium-tagged cytochromes [103,104] as well as for the terminal ET step in cytochrome c oxidase [105] and has recently been used for the first time to obtain reorganization free energies for all the single ET steps in a multi-haem cytochrome [106]. These calculations done on MtrF, combined with the previously obtained redox potentials and hence driving forces [91], yielded activation free energies for all single ET steps in the protein and allowed the construction of Marcus free energy parabolas. Table 2 lists the values for λ thus obtained for each haem pair in MtrF together with the resulting activation free energies in both directions of ET. Reorganization free energies are known to vary widely in aqueous solution, ranging from more than 2 eV for solvated metal ions [107–110] to 0.25–1.5 eV in redox proteins, the latter depending to a large extent on the solvent exposure of cofactors [111]. Within MtrF, their variation was found to be less pronounced with a range of 0.75–1.13 eV; this smaller range can be rationalized by the relative similarity of cofactor environments in MtrF, with most haems being partially solvent exposed.

Table 2.

Reorganization energies λ and activation free energies ΔE^‡ for ET between adjacent haems in MtrF as obtained from molecular simulation. ‘Forward’ and ‘backward’ for pair x → y refers to ΔE^‡ for x → y and y → x, respectively. Table from [106].

pair	λ (eV)	ΔE‡ forward (eV)	ΔE‡ backward (eV)
1 → 2	1.129	0.291	0.274
1 → 3	0.963	0.307	0.183
1 → 6	0.942	0.241	0.231
3 → 4	0.750	0.242	0.140
4 → 5	0.835	0.112	0.335
6 → 7	1.058	0.206	0.330
6 → 8	0.873	0.273	0.170
8 → 9	0.931	0.300	0.174
9 → 10	0.993	0.163	0.351

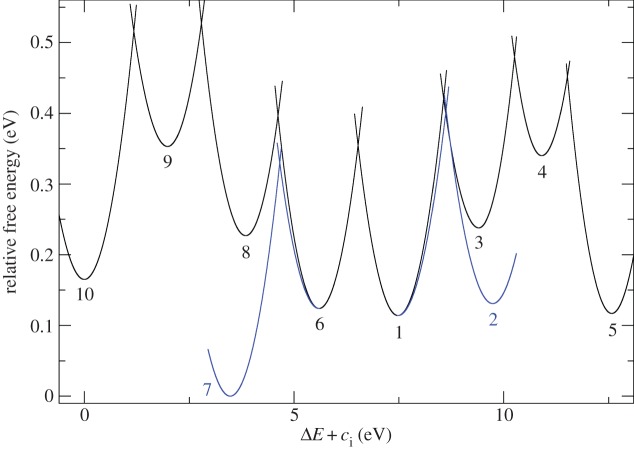
Also, this range of λ values is by and large consistent with partial solvent exposure: reorganization free energies below 0.9 eV are usually expected for solvent-shielded cofactors, with higher values typical for one solvent-exposed cofactor [111]. The activation free energies in the last two columns in table 2 show that the reorganization free energies somewhat ameliorate the impact of the free energy barriers but do not remove it, with ΔE^‡ still being largest for the uphill steps 10 → 9 and 5 → 4. This also becomes apparent in the graphical depiction of Marcus free energy curves in figure 10 (arrangement of haems as in figure 9).

Figure 10.

Marcus free energy parabolas for ET through MtrF [106] as obtained from redox potentials and reorganization free energies [106]. Haem arrangement as in figure 9. (Adapted from [106].)

4.1.3. Electronic couplings

Empirical. Other than by using Stark spectroscopy to determine transition dipole moments for ET (to be used in the framework of generalized Mulliken–Hush theory), H_AB is not a typical experimental observable and cannot be easily measured directly; the conventional way to obtain H_AB from experiment is to measure the rate k_ET and then calculate H_AB provided the Franck–Condon factor (i.e. the exponential term in equation (4.1)) is known. For example, an estimate for the coupling between haem a and haem a₃ in cytochrome c oxidase was derived thereby [105]. For ideal driving forces (i.e. ΔG = −λ and hence Franck–Condon factor = 1) and long donor–acceptor distances, k_ET was found to decay exponentially with distance, justifying a square-barrier tunnelling picture where the barrier height is determined by a protein ‘packing density’ ρ [112]. This model has come to be known as the ‘Moser–Dutton ruler’ after its main authors. An alternative description decomposes the total tunnelling into individual tunnelling pathways, each featuring covalent, hydrogen bond and through-space bridge contacts with fitted coupling constants [113,114]; within this model, couplings can be analysed in terms of specific structural elements.

Neither of these models was designed to predict the quantum mechanical tunnelling between closely spaced cofactors. The packing density model only takes into account the distance between the cofactors but not their respective orientation. While adequate for large distances, this approximation seems to be less suitable for short (van der Waals) distances, where the coupling is determined by the overlap of the redox-active orbitals of donor and acceptor. These orbitals are typically highly anisotropic. Hence, the overlap and coupling are highly sensitive on the orientation of donor and acceptor [115]. (It remains unclear also what the effective packing density should be for close cofactor contacts: for the haem pair in cytochrome c oxidase with an edge-to-edge distance of ca 7 Å, a packing density reduced by a third was suggested [105].) While the orientational aspect is not excluded in the pathway model (as the relative orientation of two cofactors determines, for example, the lengths of different through-space contacts), the latter still does not take into consideration the actual coupling orbital shapes (and treats all through-space contacts as equally important). Hence, the calculation of electronic couplings in multi-haem cytochromes calls for higher level methods that explicitly include electronic structure information.

Non-empirical. In explicit electronic structure approaches, the electronic coupling can be calculated from the explicitly constructed initial and final diabatic states. Many procedures to construct these diabatic states for use in ET calculations have been devised, for example generalized Mulliken–Hush theory (where diabatic states are constructed from adiabatic states by transforming the adiabatic dipole moment matrix) [116,117], fragment orbital approaches (where suitably charge-localized wave functions are taken as diabatic states) [118,119] and constrained density functional theory (CDFT; diabatic states are constructed by constraining the electron density to yield localized charges) [120,121]. When calculating H_ab in multi-haem cytochromes, several factors are relevant:

• (1) It needs to be clarified whether the coupling is mediated by cofactor orbitals only or also by the intervening protein medium (i.e. protein-mediated tunnelling versus through-space tunnelling); the latter possibility might render the explicit inclusion of certain protein residues in the electronic structure calculation necessary.

• (2) Even in the case of through-space tunnelling, the protein environment might still indirectly affect the coupling by polarizing the orbitals on the cofactors. This would require an inclusion on the level of classical electrostatics, as in quantum mechanics/molecular mechanics (QM/MM) coupling schemes.

• (3) The accuracy of explicitly calculated coupling values cannot be expected to be better than 0.1 meV due to the finite basis set, integration grids and numerical noise [122]. Hence, direct calculation using electronic structure methods is only possible if the cofactors are relatively close (in contrast to empirical methods).

• (4) As the cofactors are embedded in a protein matrix at roughly room temperature, thermal motion cannot a priori be ignored and the ensemble average 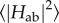becomes important; hence H_AB needs to be calculated for a set of sampled configurations.

Ideally, all of these conditions should be taken care of in calculating 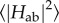for cofactor pairs in a multi-haem cytochrome. For example, couplings were estimated for the three consecutive haem pairs in flavocytochrome c₃ fumarate reductase (Ifc₃) from Shewanella frigidamarina [119] using a fragment orbital approach where the coupling cofactors were simultaneously optimized using DFT with a hybrid functional; however, this was done for a single configuration only, neglecting effects of thermal motion. CDFT prevents spurious delocalization between monomers and can enable the use of (computationally cheaper) generalized-gradient approximation density functionals for intermolecular ET [123–125] as between haem cofactors, but can still be computationally demanding due to the need to converge the constraint as well. An approach that per construction enforces charge localization by piecing together orbitals for individual monomers is fragment orbital density functional theory (FODFT) [125–127]. Here, the diabatic states are constructed by combining (and bi-orthogonalizing) the optimized Kohn–Sham orbitals for the isolated monomers, i.e. orbitals that contain no interaction between monomers at all. This ignores polarization effects but automatically provides localized charges while at the same time reducing the computational complexity from one dimeric system to two monomeric systems which can be treated with standard ground state DFT. Polarization effects can then be approximately incorporated via a correction factor derived from comparing FODFT and CDFT couplings for a small set of reference configurations; these correction factors were found to be relatively small (factor 1.3–1.8) [115,124]. This approach has been successfully applied to calculate the thermal averages 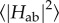for all adjacent cofactors in the deca-haem cytochrome MtrF [115].

Case example: couplings in MtrF. Recently, the first extensive calculations on 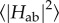for the nine cofactor pairs in the deca-haem cytochrome MtrF were published [115]. Figure 11 shows the couplings H_AB as obtained for all pairs and sampled configurations plotted versus the porphyrin edge-to-edge distance of the respective pair (together with the resulting maximal ET rate on the opposite axis). The full lines represent two exponential fits using bin averages (black circles); the dashed and dotted line represent the Moser–Dutton ruler using the default (dotted) and a reduced (dashed) packing density, respectively. The couplings in MtrF fall in two different exponential regimes, one with a decay constant of 2.25 Å⁻¹ (blue data points, distance smaller than 5.0 Å) and one with a smaller decay constant of 0.8 Å⁻¹ and a somewhat larger scatter (red and green data points, distances larger than 5.0 Å). The colour-coding corresponds to the three pair motifs described in §3: blue for stacked pairs, red for T-shaped pairs and green for coplanar pairs. As can be seen, the specific distance regimes of these motifs translate into corresponding regimes for the respective couplings. The corresponding coloured triangles represent the couplings for the crystal structures only. Not only do these values fall into the respective range of thermally sampled points, but the thermal RMS average 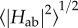for each pair is very similar to the respective crystal structure value, with the increase due to finite temperature never larger than a factor of 2 and in some cases no significant temperature influence at all. This is in agreement with the small differences in edge-to-edge distances between crystal structure and thermal averages, and the by and large small fluctuations in the thermally sampled distances. This observation in turn might be related to the relatively tight incorporation of haems in MtrF via two coordinative ligand bonds and two covalent cysteine linkages.

Figure 11.

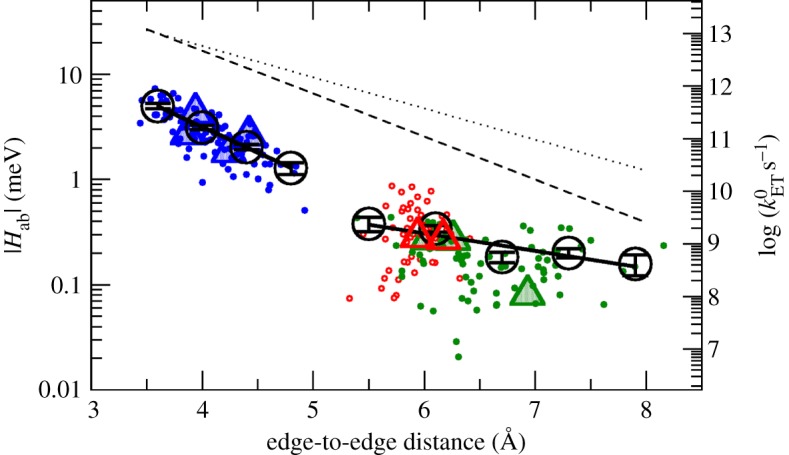
Thermally sampled couplings (|H_ab|, left vertical axis) and resulting maximal ET rates (right vertical axis) for the nine haem pairs in MtrF plotted versus the respective haems' edge-to-edge distance. The colour code corresponds to the three haem pair motifs described in §3: stacked (blue), T-shaped (red) and coplanar (green). Triangles represent couplings obtained for the crystal structure; black circles represent RMS bin averages; black solid lines show exponential fits to the bins; and the dotted and dashed line represent the Moser–Dutton ruler with the default (dotted) and a reduced packing density (dashed), respectively. (Adapted from [115].)

When comparing the calculated couplings to the ones obtained by applying the Moser–Dutton ruler (broken black lines), it becomes obvious that the computational values are consistently lower. For close contacts, the Moser–Dutton ruler is based on a small number of known rates for bacterial reaction centre and photosystem proteins; the geometrical overlap in the special pair in the reaction centre protein is significantly larger than for a stacked pair in MtrF, in spite of comparable edge-to-edge distances. This illustrates that for close contacts, as in the case of multi-haem cytochromes, the coupling is not determined by distance alone: due to the complicated nodal shape of the orbitals involved, the mutual orientation of donor and acceptor becomes crucial (see above).

A further interesting observation in the calculated couplings was the influence of the protein environment: the chosen FODFT protocol enables us to either treat both cofactors in isolation or include the protein's electrostatic influence as point charges (QM/MM). Both approaches yielded essentially the same couplings, indicating that 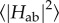is purely determined by molecular geometry for close-contact multi-haem cytochromes. This suggests that the ‘coupling landscape’ could be the same for the MtrF homologues MtrC, OmcA and UndA (see also §2) and that the findings for this specific cytochrome could in fact carry significance for a family of OM cytochromes.

No other estimates for couplings in MtrF are available so far; however, together with microscopic redox potentials and reorganization free energies, the couplings obtained enable us to calculate the haem-to-haem k_ET rates, and these allow for an (albeit indirect) comparison to experimental results (see below).

4.1.4. Electron transfer kinetics

Generally, experimental rate measurements for intramolecular ET between redox cofactors in a protein are based on inducing the ET in a controlled manner, e.g. by photochemical excitation or rapid reduction of one cofactor [128], and following the transfer process spectroscopically. The rate of haem a to haem a₃ ET in cytochrome c oxidase was established as around 1 ns⁻¹ in such measurements [129,130] (inducing ET via photolytic dissociation of a CO ligand). However, measuring rates of individual ET steps in multi-haem cytochromes in such a manner is complicated by additional issues: first, the close arrangement of cofactors in such cytochromes poses a greater challenge for spatial control of ET induction (e.g. controlling where an external electron is injected); and second, determining k_ET for individual steps requires distinguishing these steps spectroscopically (or halting the electron flow along the cofactors at a suitable place). So far, such studies have not been carried out for cytochromes with more than two haems. An alternative is to compute k_ET for the individual haem-to-haem steps using Marcus parameters obtained experimentally or computationally.

Using the values for ΔA, λ and H_AB for the nine cofactor pairs in MtrF as described in previous sections, k_ET could thus be calculated for each of the pairs [115]. Figure 12a shows the rates for each pair in forward and backward direction (dark bars: forward direction, defined as 10 → 5, 7 → 6, 1 → 2; light bars: opposite directions). It becomes apparent that the rates for the energetic uphill steps (ΔA ca 0.2 eV) 10 → 9 and 5 → 4 are in fact a bit larger than along the ‘plateau’ 6-1-2. This somewhat surprising feature can be explained by juxtaposing the thermodynamic landscape with the RMS electronic couplings 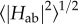for each pair (figure 12b): the steepest uphill steps also feature the highest couplings, whereas couplings are smallest for the central tetra-haem chain (including the free energy plateau 6-1-2). Thus, the electronic couplings compensate for the rate-reducing features of the free energy landscape. This is further discussed in §5.

Figure 12.

Kinetics of ET through MtrF as obtained via equation (4.1), and juxtaposition of constituent quantities. (a) Individual ET rates for each pair in forward (left → right, dark bars) and backward direction (right → left, light bars). (b) The free energy landscape for ET through MtrF (as in figure 9) together with the RMS coupling 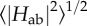for each pair (circles, area proportional to the coupling). The colour code of the circles corresponds to the three haem pair motifs as in figure 11. (Adapted from [115].)

4.1.5. Electron transport through a cytochrome

For multi-haem cytochromes that putatively serve to move electrons along their entire length, the overall electron transport behaviour is also of interest. The overall transport behaviour is in principle somewhat more amenable to experimental measurements given that individual ET steps do not need to be resolved; however, unless the electron flow measured is purely between protein cofactors, the intraprotein electron transport properties can be obscured by the ET steps into and out of the protein. Specifically, unless these initial and final ET steps are faster than the smallest intraprotein step, overall transport rates thus measured will only yield a lower bound on the cytochrome's intrinsic transport rate. To ensure that during measurement the cytochrome does reach its maximal internal transport rate, electrons should continuously be fed into the first haem and removed from the last haem (‘steady state’), rather than just measuring the one-time oxidation of an initially reduced cytochrome (‘transient state’). This set-up is also more relevant to the physiological scenario where metabolic electrons are continuously produced and need to be drained via the OM cytochromes [43]. In a scale-up study involving kinetic measurements at successively larger system scales, transient-state reduction of goethite by isolated MtrC and OmcA was compared to steady-state reduction by membrane fragments (containing OM cytochromes) and whole cells, respectively, and found to be two to three orders of magnitude slower [131]; however, it has been pointed out that this might arise precisely from these different electron supply conditions [43]. An electron transport measurement for a membrane-embedded MtrCAB complex under steady-state conditions was performed in [43]: the cytochrome complex was inserted in a proteoliposome which was filled with methyl viologen as a strong electron donor; electron flow through the membrane complex was initiated by addition of different nanocrystalline ferric oxides and measured spectroscopically. Depending on the ferric oxide used, methyl viologen oxidation rates (and hence overall electron transport rates) of ca 1100–8500 s⁻¹ were observed, indicating that the final ET step from protein to iron oxide was rate-limiting. Thus, the highest transport rate observed in this study can be used as a lower limit on the intrinsic maximal flow rate through the MtrCAB complex and hence through MtrC. Given the postulated strong similarity between MtrC and its crystallized homologue MtrF (§3), this intrinsic rate can also be used as an estimate for MtrF (in lieu of own experimental data for the latter). Comparing then the through-protein transport rates resulting from the individual rate constants k_ET as obtained for each haem-to-haem step (see §4.1.4) to this estimated lower limit provides a first consistency check for the purely computationally derived k_ET rates and hence for their constituent Marcus parameters.

This comparison has been made [115] modelling electron flow through MtrF under steady-state conditions, i.e. assuming excess electron donor and acceptor (of constant concentration), injecting electrons into haem 10 and extracting them from one of the other three terminal haems (2, 5 and 7), respectively. Thus assuming an electron current constant along the entire haem chain allows one to calculate the population of each haem and the current itself [132,133] (under the assumption that haem electron population does not significantly feed back on the ET parameters, specifically ΔA). While the injection rate (from the very low-potential methyl viologen) can be assumed to be faster than any intraprotein rate, the extraction rate was experimentally found to be rate-limiting; its exact value is unknown. Therefore, the total current J was calculated as a function of the final haem-mineral ET rate k_out; in the limit of k_out → ∞, J should converge to the protein's intrinsic maximal transport rate.

Figure 13 shows the modelled current J as a function of k_out for the three exit haems 2, 5 and 7 (black curves), together with the overall transport rates observed for the different ferric oxides in experiment (red horizontal lines). It can be seen that the maximal current for each exit haem (i.e. the limit of J for high k_out) lies above the highest of the three experimental mineral reduction rates. Furthermore, while the intrinsic rate to exit haem 7 is an order of magnitude larger than the highest experimental rate, the rates to haems 2 and 5 are only slightly larger. While this alone does not prove the accuracy of the rates k_ET as obtained from the computed haem-to-haem rates, it does strengthen the credibility of these numbers.

Figure 13.

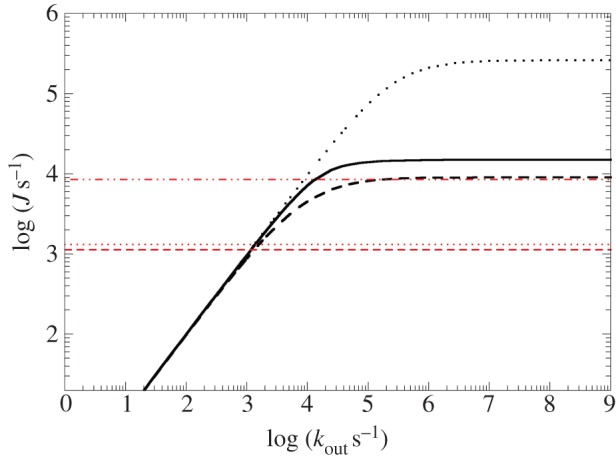
Modelling of steady-state electron flow J through MtrF based on the individual haem-to-haem ET rates in figure 11 (and as a function of the terminal heterogeneous rate, k_out). Black solid line: 10 → 5; black dashed line: 10 → 2; black dotted line: 10 → 7. The red horizontal lines represent experimentally measured electron fluxes through MtrCAB towards different iron oxides (lepidocrocite (dashed dotted), hematite (dotted) and goethite (dashed)). (Adapted from [115].)

4.2. Electron transfer to external acceptors

In principle, three types of external redox partners are possible: solid substrates, soluble (non-protein) substrates and other proteins. All three types of intermolecular interaction have been experimentally demonstrated in vitro; however, while the protein–protein interaction of periplasmic and OM cytochromes as a requirement for extracellular substrate reduction has been established (e.g. [43,47]), the exact circumstances of electron flow from OM cytochromes to a solid substrate have still not been conclusively clarified, as has been discussed in §2. To recap, the suggested mechanisms include direct cytochrome–solid contact, soluble redox shuttles and conductive appendages, and it seems likely that more than one of these mechanisms is relevant in vivo.

In the following, we discuss ET to each of these external acceptors (proteins, soluble substrates and solid substrates), considering both in vitro and in vivo scenarios. A special in vitro set-up is explained in §4.2.4: tunnelling spectroscopy (TS) experiments (using a scanning tunnelling microscope, STM) measuring the tunnelling current through a single cytochrome between a tip and a conductive substrate surface as a function of an external bias voltage (I–V response). Although formally a specific case of interactions with solid substrates, these measurements significantly differ from other in vitro studies not only by the non-zero bias voltage but also by the (thus far) non-aqueous environment.

4.2.1. Protein–protein interactions

With some light already shed on properties of individual proteins supporting electron transport from the IM to the terminal electron acceptors of S. oneidensis, it is now important to resolve the combinations and interactions of redox-active partners within the electron transport network. There is still much to learn in this area as indicated in §2—specifics like contact/binding sites, affinities, association kinetics and interprotein ET rates. Studies of purified multi-haem cytochromes provide some insight into the details of the protein–protein interactions that are likely to underpin the electron transport network. We discuss that evidence here.

The crystal structure of the NrfA dimer [68] provides an example of a complex between two multi-haem cytochromes such that the binding interface features a close interprotein haem contact of 5.5 Å (edge-to-edge). This close approach is possible in spite of the proprionates lying between the two porphyrins as the relative positions of the haems prevents steric clashes. The complex is stable in solution and it has been suggested not only that the close haem contact enables electron flow between the monomers during catalytic substrate reduction, but also that the active sites themselves interact [134].

OmcA was also crystallized as a dimer, providing an example of a protein–protein interaction among the deca-haem cytochromes [70]. The two monomers are stacked on top of each other in the deca-haem plane, with the two haems 5 forming a contact with an edge-to-edge distance of 9.4 Å. If this were indeed the geometry adopted in the MtrC/OmcA₂ complex, it would suggest stacking of this dimer on top of a membrane-associated MtrC. However, pure OmcA in solution is monomeric, giving rise to the question if the crystal structure merely shows a weak interaction not relevant to the cytochrome in solution [70].

In solution it is possible to study protein–protein complex formation via NMR. In general, binding regions can be elucidated, for example, by mapping strength of binding-induced changes in chemical shifts onto specific regions of the proteins involved [135,136] or by deriving distance constraints from paramagnetic relaxation enhancements [137]. In the case of multi-haem cytochromes specifically, only complexes that bring haems close together so as to enable interprotein ET are of interest, and thus it is reasonable to focus on chemical shift perturbations of haem methyl groups. This has made it possible to propose, or exclude, ET-relevant interactions among the periplasm-associated cytochromes CymA, FccA, STC, ScyA and MtrA in [57] and for FccA and STC even the haem involved in interprotein contact could be determined. Interestingly, the latter two cytochromes use the same haem to contact both CymA and MtrA—thus, they could not possibly form a ternary complex to bridge the periplasm between CymA at the IM and MtrA at the OM. Rather, they need to rock back and forth between these two cytochromes so as to bring their contact haem to facing the respective cytochrome. The measurements also quantified dissociation constants K_d; these were always in the μM range, indicating transient interactions so as to optimize the turnover rate (and once more excluding the formation of stable complexes).

No such details are so far available for interactions between the deca-haem cytochromes, though, with the aforementioned OmcA dimer crystal structure being the only piece of data so far. However, a few inferences can be made from the structural and network information presented in §§2 and 3. The homologies and modularities among the multi-haem cytochromes of S. oneidensis strongly suggest that the protein–protein interactions should show analogies as well: i.e. the interaction of MtrA with MtrC via the porin MtrB should have similarities to that of MtrD with MtrF via MtrE. The structure of MtrF [72] provides a basis for considering ET between an extracellular deca-haem cytochrome and the OM-spanning porin : cytochrome complex with which it is complexed. The haem arrangement in MtrF makes the end haems of the octa-haem chain the most likely contact points for MtrA/D (as contact via one of the tetra-haem chain members would require the cytochrome to lie flat on the membrane); furthermore, protein–protein interface prediction modelling together with experimental temperature factors suggested haem 10 to be the entrance haem in MtrF [72]. Thus, the working hypothesis for the interaction between MtrA/D and MtrF is based on electron transduction along the length of MtrA (crossing the membrane in the process) and ET towards the first of the octa-haem chain cofactors in MtrF. Conceivable contact points for further partner cytochromes would then be the opposite end of the octa-haem chain (haem 5 in MtrF) or the central tetra-haem chain. Furthermore, if the trans-OM conduits constitute stable assemblies, association kinetics of their constituent cytochromes should be of secondary importance (once such a complex is set up and operating). It is not clear to what extent these considerations should apply to other OM-associated cytochrome interactions as well; for example, OmcA features a putative hematite-binding motif close to haem 10 and the same motif can be found in the sequence of MtrC close to its tenth haem-binding motif as well (§4.2.3). Thus, it might be that these cytochromes connect to the transmembrane complex via haem 5 rather than haem 10.

Hence, while some insight could be gained already on periplasmic cytochrome interactions, details of the interactions between the OM-associated cytochromes are still in the dark. We present an outlook on this topic in §6.2.1.

4.2.2. Soluble substrates

As for interactions between cytochromes, the interesting aspects for soluble substrates are binding sites, affinities, association kinetics and ET rates. However, the interaction with soluble substrates is much easier to study experimentally in several regards. Firstly, their smaller size in principle renders crystallization of a cytochrome–substrate complex much more feasible. Secondly, reduction rates can easily be determined (although the issue with convoluted association kinetics and actual ET rates remains).

The OM cytochromes of S. oneidensis have been found to reduce a vast range of soluble substrates, including different Fe(III) chelates, U(VI) and flavin redox shuttles [71,72,138]. It is, however, generally not clear whether these substrates are reduced at specific sites or if multiple haems act as non-specific electron donors [71]. Clues for the existence of specific reduction sites were provided by crystal structures of the undeca-haem cytochrome UndA in complex with two different soluble substrates [71]: Fe(III)-nitrilotriacetate (Fe-NTA) and Fe(III)-citrate. Both of these substrates were bound to the same region close to UndA's haem 7 (figure 14), suggesting that this is a non-specific reduction site for iron chelates and perhaps for other soluble substrates as well. Furthermore, the local structure of UndA is not perturbed by substrate binding (with no significant change in position of side chains), suggesting that substrate binding is based on electrostatics only rather than a specific induced-fit docking. Fe(III)-ethylenediaminetetraacetate could not be co-crystallized with UndA and at the same time is reduced by UndA more than 100 times faster than Fe-NTA and Fe-citrate [138], suggesting the interpretation that it binds to UndA much weaker, dissolves more easily and therefore yields a higher total reduction rate.

Figure 14.

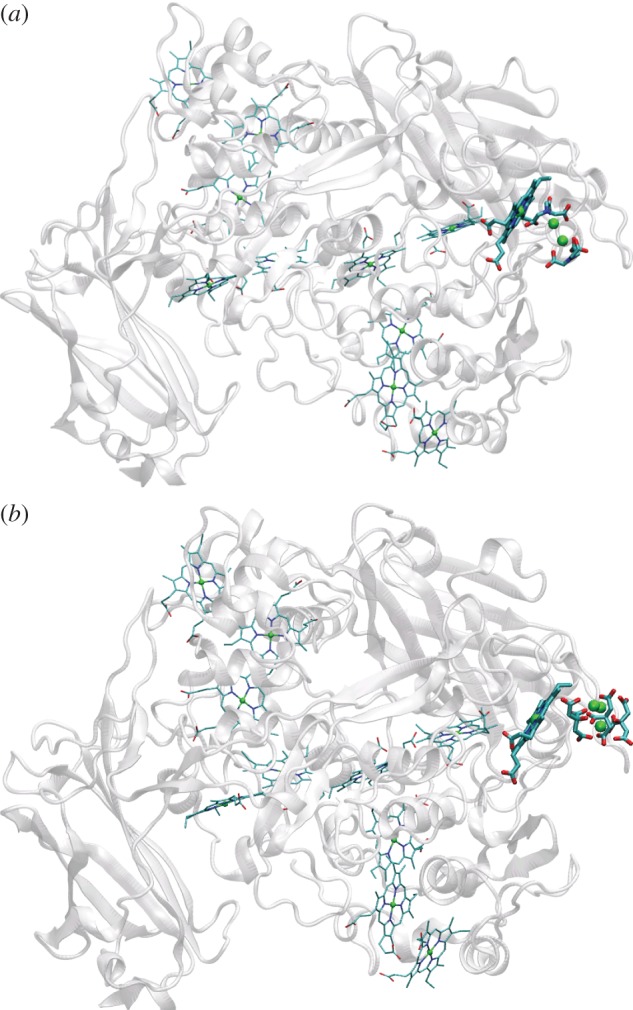
UndA with soluble substrates bound. (a) Fe(III)-NTA and (b) Fe(III)-citrate trimer. The close-by haem (7 in UndA's numbering) is emphasized.

As for the case of cytochrome–cytochrome interactions discussed above [57], NMR studies in solution can reveal information on interactions between soluble substrates and multi-haem cytochromes close to the haem cofactors as well as dissociation constants. In [84], the interaction of several OM cytochromes of S. oneidensis with several redox shuttles was thus investigated, yielding only in some cases interactions close to a haem. However, even in these cases the interaction could not be localized to a specific cofactor or set of cofactors. Again, this is where computational approaches can help and [84] indeed supplemented the experimental studies by ligand-docking simulations, showing how experimental and computational approaches can be deployed within the same study.

The association of soluble substrates to proteins is regularly studied via docking methods which aim to describe the binding of a molecule to the protein by relatively simple empirical models [139]. For the case of docking to multi-haem cytochromes as in [84], the problem is of course that it is not even known which one(s) of the many solvent-exposed haem cofactors might be potential binding site(s) for a given substrate to begin with. Therefore, such docking studies need to be done in a ‘blind’ manner, searching all relevant regions of the cytochrome (e.g. all surface regions not farther away than a certain distance from any haem, or in the extreme case the entire protein surface). Relatively recently, such protocols have been established however and successfully applied for ligands of sizes comparable to flavins docking to relatively large proteins [140,141]. For OmcA, such a blind docking protocol yielded binding sites for riboflavin and FMN close to haems 9 and 2, respectively [84]. Interestingly, haems 2 and 7 have been proposed as potential flavin-binding sites in MtrF based on extended Greek-key split-barrel structures (a common flavin-binding motif) in domains I and III [72].

The affinities reported in [84] fell into the μM range (similar to the cytochrome–cytochrome interactions from §4.2.1), suggesting only transient interactions as would be consistent with the role as an electron shuttle. While a role for flavins as electron shuttle has also been established experimentally [49,142], their exact role or portfolio of roles is still a matter of debate: a recent study [51] suggests the OM cytochromes MtrC and OmcA in fact stably bind flavin molecules as cofactors which then interact with solid substrates. Such a bound flavin cofactor that does not engage in electron shuttling would then need some other function, for example possibly more favourable interactions with certain substrates than the haem cofactors themselves.

4.2.3. Solid substrates

For the interaction of multi-haem cytochromes with solid substrates, affinities, modes of attachment including binding sites and ET parameters are again of interest. However, given that the mineral- or electrode-reducing cytochromes are fixed on the cell surface, contact formation to the solid substrate is determined by the cell as a whole rather than by diffusion of the cytochromes themselves; thus, association kinetics do not play the same role as in the interaction between mobile cytochromes in the periplasm or between cytochromes and soluble substrates.

A protein cannot be co-crystallized with a solid substrate as opposed to soluble substrates or partner proteins; on the other hand, surface-based analysis techniques can be deployed to probe the interaction of a cytochrome with a solid substrate. Specific binding between individual cytochromes and solids could be demonstrated via atomic force microscopy measurements between a hematite-coated tip and a cytochrome-coated surface, demonstrating bonding of both OmcA and MtrC to the iron oxide with OmcA binding stronger and MtrC bonding more frequently [143]. Some insight into how cytochromes interact with a solid surface could be gained via neutron reflectivity which revealed that in binding to a hematite surface, the ellipsoidal OmcA lies flat on the surface, maximizing the contact area with the mineral [144]. However, in vitro modes of contact do not necessarily translate to the situation in vivo as by virtue of their assembly on the cellular surface, cytochromes do not have the same freedom of approach to a surface in vivo as they have in vitro. For example, MtrF is hypothesized to form contact to the MtrDE transmembrane complex via domains I and IV [72] which would imply an erect position on the cell surface, with the opposite end of the octa-haem chain (haem 5) as the likely electron egress site towards solid substrates.

While the molecular-level details of the interactions between cytochrome and solid substrate are still unclear, a putative hematite-binding peptide motif was discovered via in vitro evolution [145]. The core part of this sequence (Ser/Thr-Pro-Ser/Thr) was found in the peptide sequence of OmcA and MtrC close to the C-terminus and the last haem-binding motif, suggesting that it might indeed be employed to facilitate binding between hematite and the protein with the terminal haem 10 brought close to the surface. By contrast, MtrF does not contain such a sequence.

Methods to measure rates of ET from cytochromes to solid substrates include absorbance change measurements [72,146] as well as PFV [147]. Transient-state measurements of metal oxide reduction yielded ET rates of the order of 10⁻² s⁻¹ for MtrC and OmcA with ferrihydrite and manganese oxide [146], while MtrF reacted with ferrihydrite two orders of magnitude slower [72]; MtrC coated on a graphite electrode yielded a higher ET rate of 100 s⁻¹ [146].

However, as in the case of intraprotein electron transport (§4.1.4), steady-state measurements where electrons are continuously fed into the cytochrome have an advantage over transient-state measurements that measure the one-time electron depletion of an initially reduced cytochrome: in the latter case, the observed rate is affected not only by the interfacial ET from terminal haem to substrate but by the time it takes to ‘flush’ all electrons from the cytochrome (whereas in the steady-state case, a steady flow of electrons to the terminal haem is provided). As discussed in §4.1.4, a steady-state measurement featuring the intact MtrCAB complex embedded in a lipid vesicle yielded rates of the order of 10³–10⁴ s⁻¹ depending on the nanocrystalline ferric oxide used as acceptor (specifically, ca 8500 s⁻¹ for lepidocrocite, 1300 s⁻¹ for hematite and 1100 s⁻¹ for goethite) [43]. The dependence on the substrate in turn establishes the heterogeneous ET step as rate-limiting such that the measured rates can be taken as MtrC-ferric oxide ET rates under steady-state conditions. Another important advantage of the vesicle set-up is that it features the OM cytochrome in its in vivo assembly in the MtrCAB complex, rather than approaching the substrate in complete rotational freedom.

Computational methods can be used to investigate several aspects of cytochrome–solid substrate interaction, again with the advantage of atomistic resolution. So far, the mineral interaction of MtrC and its homologues as the terminal mineral reductases has not been studied in this manner, but simulations on the smaller sized and therefore more tractable small tetra-haem cytochrome (STC) in contact with a hematite surface were able to address several aspects of binding and ET [148]. Simulation of STC binding to the surface suggested a major role for haem proprionates and charged amino acids in forming the surface bond; the preferred haem angle to the surface (perpendicular or near-perpendicular) was also found to be favourable in terms of couplings. An upper limit on the haem-hematite ET of 1000 s⁻¹ was estimated, concluding that the interfacial ET step could be a bottleneck in cytochrome-mineral ET. It is not clear how far the results of this study carry over to the OM metal oxide reductases. Interestingly, STC does contain the putative hematite-binding sequence Thr-Pro-Ser right next to a terminal haem, and yet this motif was not reported as a factor in binding to the mineral surface.

4.2.4. Tunnelling spectroscopy

As mentioned in the introduction to §4.2, a special experimental probe of cytochrome ET properties is TS, often performed with a STM because of its ability to spatially resolve a single protein molecule. TS measures the nano- to picoampere current (I) that flows between an atomically sharp metal tip and a conductive substrate, often a flat metallic surface, at a separation of a few angstroms, typically as a function of an applied bias voltage (V). TS can be performed in vacuum, air or controlled atmosphere, or in solution. If a single cytochrome can be physically immobilized in the gap between the tip and substrate, e.g. by self-assembly or chemical linking to the substrate, then the measured I–V tunnelling conductance can be influenced by redox potentials in the cytochrome.

With respect to multi-haem cytochromes, potentials of interest to probe are those associated with haem-to-haem ET, such as the lowest unoccupied molecular orbital on an oxidized haem group. A key aspect is that such states would have to lie at energies between the Fermi levels of the tip and substrate to possibly mediate current flow. The measurement is thus experimentally challenging because it depends on the extent of electronic coupling between the protein and the substrate and the protein and the tip, and on either redox potentials in the protein or on whether or not the protein can be immobilized on the substrate but electronically decoupled such that protein states can be electrochemically swept into the correct potential window to assist electron tunnelling between the tip and substrate. If performed in electrolyte solution using a three electrode cell (substrate/cytochromes as working electrode, plus reference electrode and counter electrode), and the cytochrome is electronically decoupled sufficiently from the substrate, potentials in the cytochrome can be tuned into resonance using a bipotentiostat to independently control the cytochrome redox potential with respect to the reference electrode, and the tip–substrate bias voltage [149]. If performed in air, and the cytochrome can be protected from dehydrating and denaturing, it is desirable to electronically couple the cytochrome to the substrate and probe for redox states in the cytochrome that by chance might lie within the bias voltage sweep between the tip and substrate. The instrumental mechanics of how these kinds of measurements are accomplished is beyond the present scope.

TS was successfully performed on self-assembled monolayers of the OM cytochromes OmcA and MtrC covalently linked to Au(111) thin films, in air and protected from dehydration by an overlayer of detergent [150,151]. Despite similarities in their haem count, charge-carrying amino acid content and molecular mass, the tunnelling conductance of OmcA is significantly different from that of MtrC (figure 15a). The OmcA conductance follows a smooth symmetric exponential behaviour, whereas MtrC conductance shows significant breaks in slope at positive tip bias (electrons tunnelling from the gold substrate to the tip through MtrC). Inflections in conductance appear as peaks in the differential conductance dI/dV. When normalized to I/V, the bias-dependence of the tunnelling transmission probability is removed, and the peaks lie on a flat zero current background. Peaks that appear in the (dI/dV)/(I/V) spectra approximately correspond to redox states in the cytochrome energetically situated between the Fermi levels of the tip and substrate that can participate in the tunnelling process. These normalized differential conductance spectra plotted for OmcA and MtrC reveal significant differences in the conductance mechanism for the two cytochromes (figure 15b). For MtrC, two Gaussian-like peaks are observed at positive tip bias, at approximately −81 and −365 mV versus NHE (figure 15b), within the range expected from PFV measurements [147]. These peaks represent energy regions of enhanced current through MtrC, attributed to mediation of the tunnelling current by redox states in MtrC. The peaks were fit by a model for vibrationally incoherent multi-step ET, which assumes that the involved redox states are transiently occupied by tunnelling electrons; nuclear reorganization of the protein is fast enough to respond to and stabilize electrons at such sites during current flow. The model suggests that the full width at half-height of the peaks in the normalized differential conductance curves is related to the reorganization energy λ. If the involved redox centre(s) in MtrC is a haem or set of haems, λ would derive from the energy to distort bonds in the participating haem orbitals and the energy to repolarize the surrounding polypeptide and solvent to a configuration consistent with the locally reduced state. The orbital mediated tunnelling features for MtrC imply λ values between 0.3 and 0.6 eV [151], in good agreement with STM measurements on azurin [152,153]. As the measurements were carried out in an interfacial setting without bulk water surrounding the cytochromes, lower λ values than those found for haem-to-haem ET in solvated MtrF (0.75–1.13 eV; §4.1.2) are indeed to be expected.

Figure 15.

TS experiments. (a) I–V tunnelling conductance spectra of OmcA (red) and MtrC (blue) single molecules within monolayers (inset) on Au(111) (black) showing deviations from the smoothly varying exponential dependence of the tunnelling probability for MtrC. Redrawn from [150]. (b) The normalized differential conductance from these deviations comprises peaks in the densities of states (DOS) of MtrC at the tip, that can be fit with a vibrationally incoherent electron tunnelling model consistent with participation of haem cofactors assisting the electron conductance. (Adapted from [151].)

In contrast to MtrC, tunnelling conductance of OmcA shows no deviation from a smooth exponential tunnelling profile [150,151]. This suggests that the two cytochromes have different ET properties, and thus different roles on the OM of Shewanella, consistent with the functional differences established in other experiments (§2). The lack of discrete conductance features for OmcA and the agreement between the STM and PFV data for MtrC support a conclusion that OmcA is less electroactive than MtrC.

5. Structure–function relationships

The previously discussed findings for Shewanella's OM cytochromes, specifically MtrF, enable an investigation of structure–function relationships on the molecular level, both for individual ET parameters like redox potentials as well as with respect to the interaction of different aspects and parameters.

The first interesting functional feature was found in the free energy landscape for one-electron transduction through MtrF (§4.1.2), presenting two energetic barriers of 0.2 V, raising the question of how and why these potential kinetic ‘speed bumps’ are incorporated. A possible functional reason for the low potentials of haems 4 and 9 may lie in reduction of soluble substrates, specifically flavin redox shuttles: with a redox potential of −0.219 V [154], FMN (which is known to be rapidly reduced by MtrF in vitro [72]) would only be spontaneously reduced by these two cofactors (assuming that the free energy difference can be taken as the difference in redox potential of isolated donor and acceptor). If these two haems were in fact the binding sites of FMN in MtrF, this might be advantageous: the total rate of soluble substrate reduction at a given haem is not only determined by the corresponding Marcus ET parameters but also by the substrate-binding kinetics; hence, it would make sense to avoid an additional rate penalty for this external ET due to an energetic uphill step (as would arise if the haem in question had a higher redox potential) by instead incorporating this uphill step into the haem chain itself. This line of reasoning would imply the flavin-binding sites to be different from what has been suggested based on the crystal structure (haems 2 and 7 as the tetra-haem termini close to the beta-barrel domains, figure 16) [72]. It is interesting to note though that haems 4 and 9 might still be accessible for a small soluble molecule like FMN if the haems in the tetra-haem chain were already forming contact to a solid substrate.

Figure 16.

Solvent accessibilities of haems in MtrF and possibilities for flavin-binding sites. Haems are coloured according to estimated solvent accessibilities [72], with lighter colour corresponding to higher solvent accessibility. Four FMN molecules are shown: the yellow ones next to haems 4 and 9 as the thermodynamically favourable reduction sites and the orange ones next to haems 2 and 7 as the sites with possible binding motifs [72].

Substrate-binding sites in MtrF have not been identified yet. Interestingly, eight out of 10 haems have a relatively large solvent accessibility (out of these, haems 1 and 6 have the lowest), suggesting that any of these haems could serve as a docking site. Only haems 3 and 8 are buried inside the protein [72] suggesting that these two haems are the least likely binding sites (figure 16). Solvent exposure in general tends to increase reorganization energies [111]. (No clear correlation was found in MtrF; however the lowest reorganization free energies involved the buried cofactors.) This lends support to the idea that all haems apart from 3 and 8 are potentially involved in substrate interaction. (For otherwise, increased burial of cofactors could be beneficial.)

The electronic couplings show a clear correlation with the ET free energies despite the fundamentally different nature of these two quantities: the latter arise from the specific electrostatic environment for each cofactor (as the cofactors themselves are chemically identical in MtrF), while the former describe an electronic interaction and are proportional to the overlap between haem orbitals (hence the exponential decay in figure 11). The correlation is such that the single-step ET rates for the large uphill steps 10 → 9 and 5 → 4 are not smaller than along the energetically flat plateau 6-1-2 (but actually even a bit larger). As a consequence of this, these steps do not become bottlenecks for through-protein ET. Instead, the lowest rates are found along the plateau 6-1-2 and out towards haem 3 or 8, all falling into the region of 10⁴ s⁻¹ (7 → 6 is smaller with 10³ s⁻¹, but haem 7 is not a likely entrance point for electrons). If this correlation was removed, the steep uphill steps would become bottlenecks and the maximal through-protein transport would correspondingly decrease (shifting the uphill steps in free energy to the coplanar pairs or coplanar coupling values to the uphill pairs would result in a decrease by a factor of ca 20 [115]). While the physiological requirements for through-protein transport rates are not known, the decreased rates would fall below the lower limit inferred from experiment (8500 s⁻¹ for the homologue MtrC, §4.1.5).

As a consequence of the symmetry in both redox potentials and couplings along the octa-haem chain (and of the relatively homogeneous reorganization free energies), the profile of ET rates is symmetric as well, resulting in virtually the same through-protein transport rates in both directions: MtrF can conduct electrons in both directions equally well. It is not clear yet if this feature is of physiological relevance. The fact that electron transport along the octa-haem chain is also almost thermoneutral might be beneficial by minimizing free energy dissipation, though.

The fundamentally different nature of couplings and redox potentials was found to have a remarkable consequence [115]: couplings were virtually the same no matter if the protein was taken into account (via electrostatic point charges) or not. Thus, a modification of the electrostatic environment would affect redox potentials but not couplings. Vice versa, if cofactor distance and orientation were to change without significantly perturbing the protein matrix and positions of charges, this should change couplings but not the free energy landscape. Thus, these two quantities can in principle be modulated independently from each other. If one were to redesign an electron transduction protein for maximal through-transport rates starting from MtrF, one could for example try to flatten the free energy hills in the stacked trimers and bring haems 1 and 6 closer together, ideally in a stacked manner, so as to remove present and potential bottlenecks.

The functional role of the preserved staggered-cross motif is still unclear. In regard to the couplings, it is very interesting to note that these should be very similar among MtrF and its homologues featuring the same cofactor arrangement: they differ mainly in their protein matrix, but the protein environment was found to not impact the couplings between cofactors in MtrF. Where haem dimer geometries are preserved, the findings for the couplings should carry over to MtrF's homologues as well (some differences occur, for example, in specific haem edge-to-edge distances as for haems 4 and 5 in MtrF and UndA, respectively). While definitive claims on the significance of the staggered cross are not possible, some considerations can be made. The presence of the central tetra-haem chain including two branched-off cofactors that are not part of the trans-protein octa-haem chain strongly suggests that MtrF and its homologues interact with substrates not only at the ends of the octa-haem chain but also half-way along the chain. This is in line with the suggested flavin-binding motifs at haems 2 and 7 in MtrF [72] and the binding of iron citrate to the additional haem in UndA (next to MtrF's haem 7). However, the interaction with small soluble compounds would not per se necessitate a central tetra-haem chain branching off from the main octa-haem chain (although of course the specific location of substrate-binding sites as hypothesized for MtrF could play a role in this regard). The long-stretched tetra-haem chain (with cofactors arranged coplanarly, thus reaching the greatest possible horizontal extent) might be advantageous if a large contiguous contact area was required, e.g. for a solid substrate; this line of reasoning could not apply to all of MtrF's homologues, though, as the central penta-haem chain in UndA is in fact mostly buried. An alternative possibility might be the necessity to extend the tetra-haem chain as far as possible in order to simultaneously form cytochrome–cytochrome contacts at the tetra-haem termini 2 and 7 (e.g. as in OmcA₂-MtrC or in two-dimensional networks which have been proposed in one modelling study of a bacterial nanowire [155]). Even so, the question remains if ET rates along the tetra-haem chain could be increased by bringing the haems a little closer together (possibly shifting them a little bit such that they approach each other more in a stacked than in a coplanar manner). It might be that higher rates simply would not yield any metabolic benefit (if the rate-limiting steps occur elsewhere, as in the steady-state vesicle studies with MtrCAB [43]).

6. Prospects and future developments

As has been presented in detail in the preceding sections, much insight could already be gained into the properties and functional features of multi-haem cytochromes; however, there are just as many open questions still, concerning many different aspects of these proteins' properties. For intraprotein ET properties, for which detailed insight was obtained computationally at least for one representative specimen (MtrF; with some potential transferability to its homologues), the main challenge is the connection to experiment. The situation is different for the interaction with substrates: here, many aspects have been elucidated neither in experiment nor in simulation. Some interactions, specifically among periplasmic cytochromes and between a sample cytochrome and solid substrate (STC and hematite), have already been studied in some detail (the former experimentally, the latter computationally) and the techniques used might or might not be transferable, for example, to the large OM-associated deca-haem cytochromes. For the interactions with soluble substrates, techniques used for other protein classes might provide a way forward to a more detailed understanding.

A special case is the behaviour of multi-haem cytochromes in STM-based I–V measurements: here, there is experimental data available that so far cannot be clearly explained in terms of a specific electron conduction mechanism.

In the following, we discuss how both experimental and computational approaches could help tackle the many remaining open questions about multi-haem cytochromes and their functions.

6.1. Experimental approaches to intraprotein electron transport

Intraprotein ET properties are difficult to probe experimentally for multi-haem cytochromes with chemically identically haems (see discussion in §4.1); however, novel approaches could make the kinetics of haem-to-haem ET amenable to experiment. The main issue with measuring intraprotein electron transport is the definition of a start point and an endpoint for the electron flow being measured (with the endpoint of measurement not necessarily identical to the final (thermodynamic) endpoint of electron flow; the electron might still move on after its arrival on the endpoint of measurement has been detected). This simultaneous control might be achievable by combining different strategies at once; controlled electron injection into a specific site (and thus a defined start point for intraprotein electron transport) could be achieved by attaching an electron donor next to a specific haem while a controlled endpoint might be created by modifying the coordination environment of some other haem to make it spectroscopically distinguishable. Ruthenium-based cofactors have already been used to induce ET processes involving mono-haem cytochromes in a controlled manner by covalently attaching them to cysteine residues [156]; photochemical excitation then leads to rapid ET to the close-by haem, allowing for spectroscopic observation of the subsequent ET of interest. As discussed before, the close arrangement of haems in a multi-haem cytochrome can render the use of any arbitrary haem as injection site difficult; however, this issue could be circumvented by attaching the Ru-cofactor at any of the terminal haems of the staggered cross such that the distance to the second-last haem is significantly larger. (This might require site-directed mutations to introduce a cysteine for attachment at the appropriate location.) This restriction for the start point for the electron transport measurement would not actually limit the investigation of individual ET steps along the chain as no such restriction exists regarding the choice of the endpoint: a haem cofactor could be made spectroscopically distinguishable by exchanging one of its axial ligands for another ligating residue (e.g. methionine); this would be possible for any cofactor. Thus, electron transport from one terminal haem to any of the three others could be measured, and successively setting the reporter haem one position closer to the terminal haem where the electron ‘originates’ could allow indirect resolution of individual ET steps. These electron transport measurements could then be directly compared to rates from kinetic modelling using computationally derived ET parameters.

As an aside, such haem coordination modifications also strongly affect individual redox potentials. Hence, they might also be deployed to experimentally deconvolute voltammetric responses in terms of individual cofactors (by observing the impact of a given haem modification on the voltammogram). Also, the NMR methods to determine microscopic redox potentials of individual haems could possibly be extended to larger cytochromes as well in combination with ¹³C-labelling of haem methyl groups [84,157].

6.2. Elucidating the interaction with substrates

While not too much detail is known thus far about the interaction of multi-haem cytochromes with their substrates (be they soluble, solid or other cytochromes), methods to study such protein–substrate interactions, both experimental and computational, are established and the interesting question is which methods could be used for multi-haem cytochromes and their complexes.

6.2.1. Protein–protein interactions

Using NMR, some light could already be shed on the interactions between cytochromes in the periplasm (§4.2.1). It is primarily the details of the interactions between the OM-associated deca-haem cytochromes that are still obscured, with the dimeric crystal structure of OmcA being the only piece of data available so far. While co-crystallization of OmcA with MtrC seems at least in principle possible (after all, the two cytochromes already form a complex in solution), this might not actually yield the complex geometry occuring in vivo as MtrC already forms part of the transmembrane MtrCAB complex, excluding certain conceivable ways of interacting with OmcA. Crystallizing such a transmembrane complex would be made difficult not only by the necessity to crystallize a complex of three large proteins at once but also by the porin MtrB/E being a lipophilic membrane protein while the deca-haem cytochromes are hydrophilic. The need for detergents for the membrane proteins would also render small angle X-ray scattering difficult; and while the transmembrane complexes are already comparably large, they are still too small for structure resolution via cryo-electron microscopy. It might therefore be a more viable approach to try to crystallize the proteins individually and study their assembly via some other means. On the experimental side, mutation studies are able to identify residues whose identity has an impact on interprotein ET rates and which thus should be associated with binding/contact sites (with the caveat that impacts on ET rates can also arise from redox potential modulation) [158]. Employment of the NMR methods mentioned in §4.2.1 is also conceivable in principle. However, the NMR measurements in [57] were done at most on tetra-haem cytochromes, and trying such measurements for the larger OM deca-haem cytochromes might encounter additional complications.

Interprotein ET rates can be determined in a similar fashion as for intraprotein ET if a complex is stably bound (e.g. [159]) as might be the case for the transmembrane complexes; in the most general case, however, ET rates and complex association kinetics can be convoluted and may need to be resolved. Affinities and association kinetics may be inferred from measured macroscopic ET rates and analysis in terms of individual reaction steps [160].

On the computational side, Brownian dynamics (BD) simulations have been commonly used to study protein–protein ET complexes (as these interactions might exceed the limits of atomistic MD on both the spatial and temporal scale). Examples of the capabilities of BD in this regard include identifying protein-binding domains from scratch using the individual structures only [161] or using an experimentally known complex structure to analyse complex formation in solution (e.g. regarding importance of electrostatic forces [162]). Binding free energies and kinetics of complex formation can also be obtained and analysed [161,163] and total ET rates can be analysed and, for example, be established as activation- or diffusion-limited [164]. These computational studies have dealt with complexes involving smaller redox proteins like cytochrome c or cytochrome b₅, though, and the large multi-haem cytochromes might present additional challenges.

In general, the most promising way forward appears to be elucidation of individual deca-haem cytochrome structures as a basis for subsequent experimental (NMR, mutation experiments) or computational (BD) studies of interactions and complex formation between the different OM-associated deca-haem cytochromes. For stable complexes, the same computational techniques that have already been successfully employed for intraprotein ET in a single cytochrome (MtrF) should also be applicable to investigate interprotein ET (although the larger system size would drive up the computational costs); even the experimental approaches suggested in the previous subsection for intraprotein electron transport might be applicable. Transient complexes, however, might require techniques capable of deconvoluting ET and association kinetics.

6.2.2. Soluble substrates

As pointed out in §4.2.2, the interaction of multi-haem cytochromes with soluble substrates is in principle more amenable to experimental approaches than the interaction with other cytochromes; for instance, crystal structures of a specific multi-haem cytochrome with bound substrates have been resolved for two substrates. However, this should be the more feasible the higher the affinity of a given substrate for a cytochrome. Some substrates (specifically flavins) are suggested to act as mobile electron shuttles. Hence it would not be surprising if they also exhibited correspondingly lower affinities (as found for flavins [84]) and only transient interactions. This could explain why, for example, MtrF could not be co-crystallized with FMN despite having been shown to reduce FMN in vitro [72]. Transient complexes can still be accessible to studies in solution, though, specifically to NMR studies as presented in §4.2.2.

Docking simulations already provided some insight on possible substrate-binding sites and can be expected to do so in the future when more crystal structures become available, e.g. for MtrC. However, the free energies of binding (and thus affinities) obtained from these docking methods are rather crude; therefore, it would be desirable to obtain more accurate binding free energies via more sophisticated methods. For (putative) binding sites found via docking, binding free energies could be calculated via different atomistic MD protocols (e.g. [165]). This could serve to, for example, energetically discriminate between several potential binding sites for a given ligand, and if experimental affinities are missing and the computational accuracy is high enough computed affinities could also help clarify how a given substrate interacts with a cytochrome (see discussion in §4.2.2 of stable association versus redox shuttling).

As discussed in §4.2.2, effective ET rates from multi-haem cytochromes to soluble substrates can be measured in vitro; however, as for protein–protein interactions, the actual ET rates for a substrate in contact with the cytochrome can be convoluted with the association kinetics of the cytochrome–substrate complex.

6.2.3. Solid substrates

The study of multi-haem cytochrome interaction with solid substrates could also greatly benefit from further computational investigation. A natural next step after the study of the tetra-haem STC (§4.2.3) would be simulations of one of the large OM cytochromes. In addition to the natural oxide substrates, binding to and interaction with artificial substrates like electrodes would be very interesting to study as this bears directly on the utilization of multi-haem cytochromes in nanobioelectronic settings and could help to come to understand the STM experiments discussed in §4.2.4 where cytochromes immobilized on a gold surface yielded tunnelling currents in the nA regime (six orders of magnitude higher than the steady-state measurements in solution) for moderate bias voltages. It is not clear at the moment if such high currents can be faithfully modelled using standard ET rate theories (such as Marcus theory), which assume that the relaxation time of the environment (protein and water) is much faster than the ET. We expect that this condition is almost certainly not fulfilled for nA ET through the haem wire (see, for example, [166] for relaxation times in cytochrome c). It may well be that one has to go beyond the usual rate description and propagate the electron dynamics explicitly by solving the time-dependent Schrödinger equation, e.g. in the framework of non-adiabatic MD (e.g. [167] and references therein).

7. Conclusion

In this Headline Review, we presented a thorough overview of our current knowledge of and insight into multi-haem cytochromes in S. oneidensis, presenting and discussing the multiple levels of functionality involved, from the overall network of interactions of multi-haem cytochromes in S. oneidensis' versatile metabolism via properties of single proteins down to the molecular level of the individual haem cofactors. The knowledge gained so far on functionality particularly on the molecular level allows one one to relate structure to function to yield insight inaccessible before.

In all this, the synergy between experimental and computational methods has hopefully been highlighted convincingly, with experiments providing structures and macroscopic properties while simulations can build on this to elucidate microscopic properties on the molecular level. We therefore discussed the different experimental and computational methods employed to study multi-haem cytochromes, discussing both their respective capabilities and limitations, and providing an outlook on how the many still obscure aspects about S. oneidensis' multi-haem cytochromes could perhaps be approached both in experiment and simulation.

With the field having come quite some way already, both in terms of knowledge established and methods applied so far, it was timely to provide an overview of past achievements and of suggestions that could advance the field further.

Funding statement

M.B. gratefully acknowledges an IMPACT studentship co-sponsored by University College London and Pacific Northwest National Laboratory (PNNL) through the US Department of Energy Office of Biological and Environmental Research (OBER) Subsurface Biogeochemistry Research Science Focus Area (SBR-SFA) programme at PNNL, the latter of which provided support for K.M.R. J.B. thanks the Royal Society for a University Research Fellowship. J.N.B. thanks the UK Biotechnology and Biological Sciences Research Council (most recently through BB/G007519/1 and BB/K009885) and the SBRSFA programme at PNNL for their generous, long-standing support of multi-haem cytochrome research at the University of East Anglia.