Memory-endowed US cities and their demographic interactions

Abstract

A quantitative understanding of cities' demographic dynamics is becoming a potentially useful tool for planning sustainable growth. The concomitant theory should reveal details of the cities' past and also of its interaction with nearby urban conglomerates for providing a reasonably complete picture. Using the exhaustive database of the Census Bureau in a time window of 170 years, we exhibit here empirical evidence for time and space correlations in the demographic dynamics of US counties, with a characteristic memory time of 25 years and typical distances of interaction of 200 km. These correlations are much larger than those observed in a European country (Spain), indicating more coherent evolution in US cities. We also measure the resilience of US cities to historical events, finding a demographical post-traumatic amnesia after wars (such as the American Civil War) or economic crisis (such as the 1929 Stock Market Crash).

1. Introduction

One half of the human population lives in urban areas [1]. Asking whether the present population's growth rates are economically and ecologically sustainable is a recurrent question [2] that justifies efforts directed towards the development of quantitative unified theories of urban living [3]. A countless number of degrees of freedom is involved in a city's evolution, that is, a host of individual contributions, involving millions of people, acting on their own free will. Devising a unified theory constitutes a formidable challenge. However, despite this intrinsic difficulty, many advances have been made in recent years. During the twentieth century, many regularities were reported, such as Zipf's law in the city population rank distribution [4–8], or the celebrated Gibrat's law of proportional growth applicable to cities [9–14]. In addition, empirical data show that the scaling with population of internal degrees of freedom in an urban body such as (i) the structure of road networks or urban sprawl patterns [10,15,16] and (ii) metrics such as wages or crime rates [17,18], do follow predictable tendencies that can be mathematically described. In addition to a city's growth, electoral processes and many other social phenomena have been successfully modelled as well [6,8,19–23]. Also, collective modes emerge when cities are considered as entities that evolve and interact in a coherent fashion. The interaction between cities [14] (as measured by, for instance, the number of crossed phone calls [24] or human mobility [25]) displays predictable characteristics. Indeed, an analogy between the evolution of the population of an ensemble of cities and the random movement of particles in a fluid was made by conjoining Gibrat's law of proportional growth with Brownian motion. In such an approach, the size X at time t of the ith geometrical Brownian walker follows the dynamical equation [9–13,26]

1.1

where the dot denotes a time derivative and v_i(t) is the growth rate, which is described as a Wiener coefficient with covariance 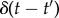—δ standing for the delta function and σ_v for the standard deviation of the growth rates—i.e. uncorrelated and memoryless dynamics. Considering a new variable defined as u_i(t) = ln X_i(t) [26], we recover all the properties of the physical ideal gas in what one may call the scale-free ideal gas [13,27]. Exhaustive empirical observations of the dynamics of Spain's population demonstrate that this analogy can be used to formulate a thermodynamics of population flows [28]. Moreover, we have recently shown that this assumption of uncorrelated evolution fails for cities that are close neighbours [14]. Additionally, the evolution of cities' populations exhibits memory, indicating that we deal with a non-Markovian process. These results are indicative of (i) a rich and complex phenomenology underlying population flows, and (ii) that our models should go beyond the ideal gas to include pairwise interactions and inertia, as in the case of real gases in statistical physics. The presence of some kind of correlations has also been independently proposed in [4], where it is shown, via numerical experiments, that it is necessary to introduce conditioned sampling to reproduce Zipf's law, simulating what the authors call ‘coherence’. These advances, both in the internal structure and in the functionality of cities, as well as in the properties of an ensemble of interacting cities, encourage the search for a unified theory.

We present in this work empirical evidence of such correlations in the population dynamics of US counties and compare our results with previous observations on the population of Spanish cities. In §2.1, we first analyse the statistical properties of cities' growth rates, confirming Gibrat's law with finite size effects for small populations. We pass next to analyse, in §2.2, the memory of the growth rates, using data from a time window of 170 years, which includes relevant historical events, such as the American Civil War, both world wars and the economic crisis after the 1929 Stock Market Crash. We continue, in §2.3, with the analysis of city–city correlations as functions of the distance between them, which leads us to define a characteristic correlation distance. Finally, a discussion and conclusion are given in §3.

2. Results

2.1. Stochastic properties of US growth rates

We look for quantitative space–time patterns underlying US demographics and ascertain which trends are universal and which are local by comparison with [14], related to Spanish cities. An exhaustive analysis of the US population is made using the Census Bureau database of counties' populations [29]. We have used data from 1830 to 2000 (170 years), in a time window that covers relevant historical events such as the American Civil War, both world wars, and the 1929 Stock Market Crash. More than 3000 counties (all of them with available data) are considered in our study, whose spatial distribution is depicted in figure 1.

Figure 1.

(a) Spatial distribution [30] and population of US counties [29] (greater darkness implies larger population). (b) Standard deviation σ of county's growth rate as a function of the total population X (orange dots). The median (red line and dots) clearly follows the proportional Gibrat's law for populations larger than 35 000 inhabitants (slope 1 in a log–log representation), while it follows the expected trend of FSN for smaller populations (slope 1/2). Dashed lines follow the linear fit performed per each contribution (see text).

Administrative and legal boundaries do not reflect, in all cases, an exact definition of what can be considered as a coherent urban nucleus. Indeed, many counties may include several independent population centres, or split big cities into several units. There have been many efforts to find an accurate and natural definition of city through clustering (e.g. [31,32]). Indeed, these definitions become relevant for predicting the shape of the city size rank distribution, for which Zipf's law generally emerges when natural boundaries are used instead of legal ones. However, these definitions do not become so relevant with respect to the dynamics described by equation (1.1), as shown in [28]. As we are here interested in the dynamical patterns exhibited by populations and not in size distributions, we can safely extend our findings beyond the particular definition of city or population nucleus.

We first verified, using the counties database, the validity of Gibrat's law, including the correction for smaller populations, discovered in [13]. To this effect, we added a new term to the proportional law, a ‘finite size noise’ (FSN), of the form

2.1

where w_i(t) is an independent Wiener coefficient. This term is a direct consequence of the Central Limit Theorem, as shown in [13,28], due to the independent nature of the w_i(t). The variation of the population X_i is much smaller than the variation of the growth rates. Thus, for the later, the standard deviation , in our time windows, becomes

2.2

where σ_v and σ_w are the deviations of the proportional and FSN, respectively.

For comparing the raw data with our predictions, we take into account that population data have an strong scale-free behaviour and are characterized by long-tailed distributions. In these circumstances, mean values do not converge or do so very slowly, their estimation becoming numerically unstable. We recommend working with medians instead, as they are numerically more stable and also invariant under several transformations—indeed, med[log(X)] = log(med[X]) but . Following this recipe, we produced the results in figure 1, depicting the empirical versus population, for every county, in a log–log scale, and also the median of the former. Two trends are immediately observed: one for lower populations (X < 35 000 inhabitants) and a second one for larger populations (X > 35 000). Remarkably, a linear fit to the log–log representation—where power laws become straight lines with slope values linked to the exponents—gives for the exponents 0.508 ± 0.025 (with log(σ_w) = 2.6 ± 0.2) for the first trend and 1.04 ± 0.02 (with log(σ_v) = −3.1 ± 0.2) for the second one, with a coefficient of determination R² of 0.96 and 0.994, respectively. As these values almost coincide with the expected ones (1/2 for FSN at lower population and 1 for proportional grow for larger population), we can regard the Gibrat plus FSN law as verified, a rather significant observation. We find, however, that the exponent for proportional growth is slightly larger than 1 according to the confidence interval. In [13], similar cases of exponents larger than 1 are also reported. They emerge as a consequence of the massive migration from small villages to big cities. Even if this deviation from Gibrat's law is mild, it is persistent for our fitting-procedure. Thus, we expect it to also be the signature of fast-growing urban population in US demographics.

2.2. Measuring memory

To check whether US counties exhibit memory effects, we appeal to the Pearson's product–moment correlation coefficient , using as samples the list of counties' growth rates for (i) the year y and (ii) any precedent time t for which data are available. We find that the averaged time correlation over n_y = 12 samples (from 1890 to 2000), defined as and calculated for consecutive census instantiations (Δt = 10 years), exhibits a behaviour similar to that found for Spanish cities [14]: large cities show greater inertia. We can attribute the smaller counties' loss of memory to the FSN term, which becomes important for them (figure 2a). For larger intervals of time Δt, we find a clear decay of the averaged time correlation. Remarkably, the correlations are much larger than those found for Spanish cities (figure 2b). Considering only the first 40 years, a fit to an exponential decay (figure 2b, inset)—in a similar fashion as that effected for Spanish cities—gives us a characteristic time of 25 ± 7 years (R² = 0.990), but surprisingly, the correlation eventually becomes negative after approximately 60 years.

Figure 2.

Averaged time correlations in population growth. (a) Averaged time correlations after 10 years versus town sizes X (dot-line). The shaded area represents the width determined by 1 s.d. Horizontal dashed lines are asymptotic levels to follow the decrease of the correlation at lower populations. (b) Averaged time correlation for the relative growth of towns populated by more than 10 000 inhabitants. Shaded areas represent widths determined by 1 s.d. The time correlation for Spanish cities is also shown for comparison's sake (grey dashed line and dots). Inset: same data in semi-log scale, compared with the exponential fits (straight lines).

In order to gain a deeper understanding of this unexpected trend, and also to check whether it is caused by a non-homogeneous behaviour of the correlations, we have independently studied all the contributions c_y(t) for several years y (and precedent times t (figure 3)). We find that, although for all y a decay of the correlation with time is always present, historical events clearly modulate these correlations. For the growth rates from 1890 to 1950, we find that, irrespective of the year, no memory remains in the demographics of US counties from the years that precede the American Civil War, in a kind of ‘post-traumatic amnesia’ (figure 3a). For the second half of the twentieth century, we find, in general, a slower decay—larger memory—than for other time periods. The most important historical event that one immediately detects (by simple inspection), regarding cities' memory, is the economic crisis after the 1929 Stock Market Crash. Again, irrespective of the year, one still encounters (i) a correlation's fall and (ii) loss of memory regarding precedent decades (figure 3b). Thus, instead of a homogeneous year-independent decay of the correlations with time, we find a decay with a strong dependence on historical events.

Figure 3.

Time correlations in population growth c_y(t) of the year y with all previous years denoted by t. Historical events as the American Civil War (CW), the First World War (WWI), the 1929 Stock Market Crash (C29) and the Second World War (WWII), are marked via shadows. (a) Correlations for years y = 1950 (red circles), 1940 (yellow squares), 1930 (green diamonds), 1920 (turquoise up-triangles), 1910 (blue down-triangles), 1900 (navy small circles) and 1890 (purple empty squares). In all cases, the correlation becomes almost zero after the American Civil War. (b) Correlations for the last half of twentieth century: years y = 2000 (red circles), 1990 (yellow squares), 1980 (green diamonds), 1970 (blue up-triangles) and 1960 (purple down-triangles). A general pattern of decay is apparent for all years, and remarkably, the five curves drop (or suffer larger decay) from 1930 to 1920 after the Stock Market Crash of 1929 (however, note that years 1950 and 1940 in (a) do not drop to zero after the crash, see text).

However, some unanswered questions remain, such as (i) the reason for the strong fluctuations between the years 1990 and 2000 or (ii) why do the years 1940 and 1950 seem to be not strongly afflicted by amnesia? Regarding the latter question, figure 3 indicates that for small time intervals, inertia is more important than historical events. Only after a few decades, the amnesia becomes apparent. Whether this period of inertia is related to the characteristic memory time of approximately 25 years, is something that cannot be tested with the present data, but it is a reasonable hypothesis for future research. If such were the case, two mechanisms would take place defining short- and long-term memories, only the latter being affected by historical events. Deeper insights into how these inertial mechanisms work would indeed shed some light on how information is stored in collective social systems. Accordingly, more research along this line remains to be undertaken.

2.3. Measuring interactions

We consider now spatial correlations. The pairwise Pearson product–moment correlation coefficient of the ith and jth counties is obtained using as samples the evolution of the growth rates of each county in a given time window. We speak here of the twentieth century, from 1900 to 2000 (10 sample sets). We compare the value obtained per each pair with the distance between counties d_ij. The averaged value—obtained as C(d) = ∑_ijC_ijδ(d − d_ij)/∑_ijδ(d − d_ij)—exhibits a clear dependence on distance, demonstrating the entanglement between US population nuclei. The tail of the decay displays a long-range behaviour (figure 4), and the pertinent curve can be nicely fitted to an analytical expression of the form

2.3

with C(0) = 0.62 ± 0.02, d₀ = 215 ± 32 km and α = 0.71 ± 0.04, for a R² coefficient of 0.997. Remarkably, the correlations are much larger than those observed for Spain [14], with a larger characteristic distance (215 km versus 80 km for Spanish cities) and a much slower decay (α = 0.71). Note that for an inverse-square law, α = 2.

Figure 4.

Pairwise correlation C versus distance between counties d. The mean value for a given distance is indicated (red line and dots) together with 1 s.d. (darker shadow) and by two of them (lighter shadow). The black line follows the analytical fit of equation (2.3). The spatial correlation for Spanish cities is also shown for comparison's sake (grey line and dots).

The comparison between USA and Spain is illustrated by figure 4. Results confirm the conjecture that US cities evolve in a more coherent fashion than the cities in Spain, notwithstanding the fact that the US surface is 20 times larger than Spain's, while its population is 6.5 times larger. We may speak of an integration coherence for US cities that seems to be lacking in Europe, as has also been proposed in [4]: Zipf's law emerges when the largest US cities are considered but not when this is done on a state-by-state basis, whereas in Europe, Zipf's law emerges for each country as a whole, and not when all the European continent is considered. The standard deviation observed for the US is approximately 0.4 and does not change with distance. The expected theoretical width for a bivariate normal distribution for the same number of samples is 1/3 [33], 20% smaller than the measured one. Thus, we gather that additional factors are involved in the US pairwise correlation. One can attribute to the distance factor 80% of the city–city entanglement. We expect that some of these extra contributions could be associated with local factors, such as the transportation network, the particular socio-economical status of the city and/or special historical links between some population nuclei. A detailed analysis of the pairwise correlations of a selected county—instead of the coarse-grained viewpoint adopted here—when crossed with other relevant metrics, may help to gain a deeper understanding of the particular demographic and/or economic status, present and future, of a given urban area.

3. Summary and conclusion

Demographic US patterns display a rich and complex phenomenology, including both space and time correlations. US cities exhibit a strong link with their past. In an exercise of quantitative history, we have found that relevant historical events, such as the American Civil War and the 1929 economic crisis, leave a strong imprint in the demographic dynamics, which one may call ‘post-traumatic amnesia’. Remarkably, this amnesia only takes place after a few decades, indicating the potential existence of short- and long-term memories in the social system. The mechanisms underlying this inertia are still unknown. On the other hand, the spatial correlations, much larger than those observed in Europe, indicate a high level of coherence and suggest that the evolution of any single city cannot be understood without taking the whole collective of cities into account. We feel that these empirical findings are relevant to understanding the country at a collective macroscopic level. Also, some microscopic insights are gained that may help city planners to improve their panoply of tools [29,34].

Funding statement

This work was partially supported by Social Thermodynamics Applied Research (SThAR).