Abstract
Compression of a stiff film on a soft substrate may lead to surface wrinkling when the compressive strain reaches a critical value. Further compression may cause a wrinkling–folding transition, and the sinusoidal wrinkling mode can then give way to a period-doubling bifurcation. The onset of the primary bifurcation has been well understood, but a quantitative understanding of the secondary bifurcation remains elusive. Our theoretical analysis of the branching of surface patterns reveals that the wrinkling–folding transition depends on the wrinkling strain and the prestrain in the substrate. A characteristic strain in the substrate is adopted to determine the correlation among the critical strain of the period-doubling mode, the wrinkling strain and the prestrain in an explicit form. A careful examination of the total potential energy of the system reveals that beyond the critical strain of period-doubling, the sinusoidal wrinkling mode has a higher potential energy in comparison with the period-doubling mode. The critical strain of the period-doubling mode strongly depends on the deformation state of the hyperelastic solid, indicating that the nonlinear deformation behaviour of the substrate plays a key role here. The results reported here on the one hand provide a quantitative understanding of the wrinkling–folding transition observed in natural and synthetic material systems and on the other hand pave the way to control the wrinkling mode transition by regulating the strain state in the substrate.
Keywords: period-doubling wrinkling pattern, prestrain, wrinkling pattern transition, post-buckling analysis, nonlinear finite-element analysis
1. Introduction
Surface instability is frequently observed in squeezed soft materials [1–6]. The physics of this nonlinear phenomenon could be harnessed to create tuneable patterns, to fabricate functional surfaces and to understand the correlation between growth and morphogenesis in some natural systems. Therefore, it has received considerable attention of many scientists and engineers [7–14]. Biot [15] made a pioneering effort to understand surface instability of a neo-Hookean solid subject to plane strain compression. His linear perturbation analysis leads to a critical compressive (nominal) strain of 45.6% for the onset of surface instability. Recent analysis [11] based on Koiter's elastic stability theory reveals that surface wrinkling of a neo-Hookean solid is highly unstable because of the nonlinear interaction among the multiple modes associated with the critical compressive state. Concomitantly, wrinkling is sensitive to exceedingly small initial imperfections and spontaneously collapses into a local crease. The nonlinear analysis of Hohlfeld & Mahadevan [7,10] and Hong et al. [8] indicates that a crease/sulcus represents a subcritical instability mode, which is energetically favourable when the nominal compressive strain is beyond 35.4%. The surface instability of a stiff film resting on a soft substrate (bilayer system) is usually believed to be fundamentally different from that of a hyperelastic solid. In the former, surface wrinkles are rather stable, especially when the modular ratio of the film to substrate is large, and could be reliably observed over a wide loading range [14]. This paper is concerned with an interesting experimental phenomenon observed by Brau et al. [5] in Poly(dimethylsiloxane) (PDMS) film/substrate systems and illustrated by our experiments (figure 1). The experiments show that the sinusoidal wrinkling mode will transform to the period-doubling mode when the overall compressive strain reaches around 19%. This phenomenon was recently confirmed by nonlinear finite-element simulations [11]. Moreover, the nonlinear analysis [11] reveals that the critical condition for the onset of the wrinkling pattern transition largely depends on the nonlinear deformation behaviour of the substrate. Precompression favours the occurrence of folding while pre-stretch will retard the wrinkling mode transition; over pre-stretch may lead to a mountain ridge mode [12]. Hutchinson [14] investigated the role of substrate nonlinearity on the wrinkling of thin films bonded to a compliant substrate within the initial post-bifurcation range when wrinkling first emerges. His insightful analysis revealed that when the elastic modulus of the film is about five times greater than that of the substrate, the wrinkling bifurcation will be stable, whereas for a relatively soft film, the wrinkles can be unstable. However, the initial post-bifurcation expansion does not capture the unusual wrinkling modes observed at compressive strains well above the bifurcation strain such as period-doubling, folding [5,11,16] and ridging [12,17,18]. These previous studies help us to understand the physics behind the wrinkling pattern evolution in hyperelastic bilayer systems. However, a quantitative understanding of the wrinkling mode transition from sinusoidal to period-doubling in bilayer systems with the presence of substrate pre-deformation has thus far remained elusive.
Figure 1.

Wrinkling morphology observed in the experiments with substrate with no pre-stretch. (a) Sinusoidal wrinkling observed when the compressive strain was 0.1; (b) period-doubling mode observed at the overall compressive strain of 0.19. The experimental phenomenon is similar to that observed by Brau et al. [5]. PDMS was the substrate in our experiments. The stiff film was generated after the PDMS was subjected to a UV-ozone treatment for 10 min. Experiments details are given in appendix A. (Online version in colour.)
This paper is organized as follows. A theoretical analysis is first performed in §2 on the branching of the wrinkling mode to characterize the correlation between the wrinkling transition strain and the parameters of the system. Computational studies are carried out in §3 to explore the deformation behaviour of the substrate in the vicinity of the second bifurcation point. A characteristic (nominal) strain in the substrate is identified at the incipient occurrence of the period-doubling, which corresponds to a critical point beyond which the period-doubling mode is energetically favourable in comparison with the sinusoidal wrinkling mode. In §4, explicit solutions are given to predict the critical overall strain for the onset of the period-doubling mode in the cases with and without substrate pre-deformation, which are validated by numerical simulations and experiments. Section 5 gives some concluding remarks.
2. Theoretical analysis of wrinkling pattern transition
(a). Model
To determine the critical compressive strain for the onset of a period-doubling mode, we first perform a theoretical analysis on the wrinkling mode branching. For the system illustrated in figure 2, we explore a displacement-controlled loading procedure. The upper surface of the thin film is traction-free. Here, x is coordinate of the initial configuration and ℓ and h are the length and thickness of the film, respectively, and ℓ is assumed to be much larger than the wrinkling wavelength of the system. We assume that the film follows the generalized Hooke's law and the substrate is an incompressible neo-Hookean material. The overall compressive strain in the film in the fundamental state is δ. In the plane strain case, the resultant membrane stresses in the film in the fundamental state can be obtained by
| 2.1 |
where and , with E and ν being Young's modulus and Poisson's ratio, respectively.
Figure 2.
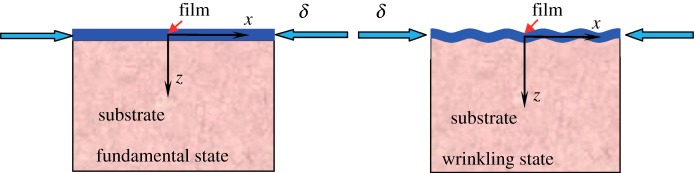
Schematic of compression induced surface wrinkling in the film/substrate bilayer system. (Online version in colour.)
The nonlinear von Kármán plate equations [19–21] are used to model the film in the wrinkling state (figure 2)
| 2.2a |
and
| 2.2b |
where w(x) is the additional deflection of the film from the fundamental state. F is the stress function and
| 2.3 |
refers to a Taylor series of the resistant force of the foundation to the film. R0 is a constant term in the expansion of R. If the expansion is up to the linear term, R0 is zero, ensuring that the total vertical resistant force is zero. However, R0 may be non-zero for a nonlinear foundation, but it can be seen from subsequent analysis that R0 has no contribution to the potential energy of the system. The linear stiffness coefficient of the foundation is given by K=cμs [11,14] with μs being the initial shear modulus of the incompressible neo-Hookean substrate. The wavenumber of the wrinkling state is p and , where λ0 is the pre-stretch ratio of the substrate. The constant K2 is proportional to the initial shear modulus and depends on the deformation state of the substrate as described in the sequel. The stress function F(x,y) gives the additional stresses from the fundamental state by
| 2.4 |
where α,β,γ=1,2 and δαβ= is the Kronecker delta. In this study, we investigate the cases where the ratio of the modulus of the film to the substrate is relatively large, e.g. greater than 50. The strain in the film is assumed to be small. In this case, it is reasonable to assume that the film is linear elastic. Dervaux et al. [21] showed that at low strains, hyperelastic film/substrate systems also satisfy the Föppl–von Kármán equations. Our finite-element simulations in the sequel also demonstrate that the assumption of the film as linear elastic or hyperelastic basically has no effect on the wrinkling mode evolution when the modular ratio is relatively large.
Linearizing equation (2.2a) about the pre-buckling state gives the following buckling equation:
| 2.5 |
where represents the linearized mode. Equation (2.5) admits the following solution:
| 2.6 |
where A refers to the amplitudes of .
Substituting equation (2.6) into (2.5) gives
| 2.7 |
Minimizing equation (2.7) with respect to p gives
| 2.8 |
Equation (2.8) permits us to determine the critical condition for the onset of sinusoidal wrinkling and has been derived in a previous study [11]. These results will be used in the following wrinkling mode branching analysis.
(b). Wrinkling mode branching
Now consider the sinusoidal wrinkling mode with the additional deflection expressed by
| 2.9 |
with b0 being the amplitude of wrinkling mode.
Equation (2.2) admits the stress function in the following form:
| 2.10 |
where a1 and a2 represent the change of average membrane stresses along the x- and y−directions, respectively.
Invoking the following compatibility conditions [9,22]:
| 2.11 |
we have
| 2.12 |
Substituting equations (2.9) and (2.10) into the following potential energy function
| 2.13 |
we obtain
| 2.14 |
Equation (2.13) can be derived from the potential energy function given by Cai et al. [9], and the last term in equation (2.13) refers to the elastic energy of the foundation.
Minimizing the potential energy with respect to b0, ∂PI[w,F]/∂b0=0, the following relationship is obtained
| 2.15 |
Equation (2.15) gives the evolution of the wrinkling amplitude and is consistent with the results in previous studies [23,24]. It is interesting to note that the nonlinear term of the foundation stiffness relevant to K2 has no influence on the potential energy for this wrinkling mode when we take the resistant force of the foundation in the form of equation (2.3) and omit higher order terms.
Next, we consider the following period-doubling mode:
| 2.16 |
The stress function is solved from the nonlinear von Kármán plate equations as
| 2.17 |
From the compatibility condition in equation (2.11), we have
| 2.18 |
Inserting equations (2.16) and (2.17) into (2.13) gives the variation of the potential energy of the system from the fundamental state to the period-doubling wrinkling state as
| 2.19 |
where we have neglected the terms of . The increment of the potential energy from the sinusoidal mode to the period-doubling mode is
| 2.20 |
Substituting equation (2.15) into (2.20) gives
| 2.21 |
where
| 2.22 |
For a linear foundation, i.e. K2=0, ΔP is always positive, indicating that the sinusoidal wrinkling mode has a lower potential energy and the system is unlikely to evolve into the period-doubling mode. Our finite-element simulations have also demonstrated that the system will maintain the sinusoidal mode if the substrate is assumed to be a linear foundation. This demonstrates that the nonlinear behaviour of the substrate deformation plays a fundamental role in the occurrence of the period-doubling mode in film/substrate bilayer systems. For a nonlinear foundation, ΔP=0 determines the critical overall compressive strain δ2 in the film for the transition from sinusoidal wrinkling to a period-doubling pattern, which gives
| 2.23 |
It is worth mentioning that Brau et al. [5] have performed an insightful theoretical analysis on the occurrence of the period-doubling mode. They considered an inextensible film with δc=0 but did not explore the effect of substrate pre-stretch, i.e. λ0=1. In this case, equation (2.23) degenerates to
| 2.24 |
where according to equation (2.22). Therefore, following the assumption of Brau et al. and for the case of λ0=1, equation (2.24) gives
| 2.25 |
which is consistent with the result given by equation (36) in the electronic supplementary material of Brau et al. [5]. Equation (2.23) indicates that δ2 depends on λ0 and δc as well. Provided that K2 is known, the function f(δ2,λ0,δc) can be determined and then δ2 can be solved from equation (2.23). However, it is by no means trivial to determine K2 analytically. Without considering the substrate compression, Brau et al. [5] have obtained an analytical solution for K2, which is zero for an incompressible substrate; with this value, δ2 predicted by equation (2.25) will be infinite and inconsistent with nonlinear finite-element simulations [11]. Very recently, Hutchinson [14] made an effort to calculate K2. He also obtained K2=0 in the absence of substrate compressive deformation. His analysis [14] revealed that K2 strongly depends on the pre-deformation of the substrate and the boundary condition at the upper surface, for which an analytical solution is difficult to obtain if realistic interfacial conditions are taken into account. Bearing this in mind, a nonlinear finite-element analysis is carried out in this paper to explore the deformation behaviour of the substrate at the onset of the period-doubling mode. We will derive an explicit solution to predict δ2 without solving K2 directly.
3. Nonlinear finite-element analysis
(a). Computational model
Nonlinear finite-element analysis is carried out to investigate the plane strain problem (λ3f=λ3s=1) of a neo-Hookean bilayer system at compressive strain levels well beyond the bifurcation strain. We concentrate on the deformation behaviour of the substrate when the wrinkling mode evolves from the sinusoidal pattern to the period-doubled pattern. Plane strain finite-element simulations were performed via the commercial software ABAQUS [25]. The incompressible neo-Hookean material model is adopted for both the film and the substrate, and the anticipated wavelength is much greater than the element size. The hybrid element (CPE8RH in ABAQUS) was used which is applicable for simulations of incompressible materials.
In the post-buckling analysis, two schemes were used to introduce the stress-free geometric imperfections to the system to initiate growth of the post-bifurcation modes [11]. With the absence of substrate pre-stretch, a linear perturbation was first accomplished using the ‘BUCKLE’ function in ABAQUS. The critical eigenmode scaled by a very small factor (e.g. 0.005 h) was introduced as a geometric imperfection into the mesh. With the presence of substrate pre-stretch, finite-element simulations were first run by specifying a sinusoidal surface deflection at the upper surface. The computed displacement field was then introduced as a stress-free geometric imperfection into the mesh. Displacement-controlled loading is employed with u1 (independent of x2) and zero shear traction specified on the vertical sides of the model. The nominal compressive overall strain imposed on the system after the film is attached to the substrate, δ, is defined in terms of the film stretch, λ1f, calculated from the relative difference between u1 on the two sides of the model. The displacement u2 and the shear traction on the bottom surface of the model are taken to be zero. The computational model has a width of the order of 10 wavelengths of the sinusoidal wrinkling mode. The depth of the substrate is taken to be more than 10 times the sinusoidal wavelength and, thus, sufficiently deep such that the substrate can be regarded as infinite. In order to capture the occurrence of the period-doubling mode, a pseudo-dynamic algorithm was adopted in the loading paths. Both loading and unloading procedures were explored to show the effect of damping on the deformation behaviour of the substrate at the bifurcation point. The results indicate that the unloading procedure permits the identification of the critical overall strain for the onset of the period-doubling mode more accurately as shown in detail below.
(b). A characteristic strain at the onset of period-doubling mode
Figure 3 shows the nominal compressive strain of the centre of the peak in the substrate along the loading direction in both loading and unloading paths. Electronic supplementary material, Video S1, shows the evolution of the wrinkling morphology of the film–substrate system for the case without substrate pre-stretch. The strain in figure 3 is the maximum compressive strain in the substrate when the wrinkling mode of the system is sinusoidal. The location of this strain is shown in figure 4. A positive value in figure 3 refers to a compressive strain. In theory, the loading and unloading paths should coincide with each other, since the system is hyperelastic. However, the occurrence of a period-doubling mode may not be captured when the pseudo-dynamic algorithm is not adopted in our simulations. Therefore, the pseudo-dynamic algorithm is used in the loading paths, but not in the unloading paths (β is the damping factor). It can be seen that the two paths are not consistent with each other around the bifurcation point (figure 3) because of the effects of damping. The difference of the two paths is deceased when β becomes smaller. However, figure 3 shows that two unloading paths are consistent for the two different damping factors β and the loading path will basically coincide with the unloading path when β tends to zero. Thus, the unloading procedure permits us to identify the occurrence of period-doubling more accurately. The results of the unloading path show that when the nominal strain reaches a maximum value (0.381, point d in figure 3), the strain in the centre of the peak is released and strain localization occurs in the substrate (figure 3c). Point d in figure 3 is regarded as the bifurcation point for the onset of the period-doubling mode. The nominal compressive strain at point d is defined as the characteristic strain εc, and εc≈0.381. The overall compressive strain at point d is defined as the critical overall strain δ2, which is approximately 0.185. To understand the physics underpinning this characteristic strain, we examine the total potential energy of the system during the wrinkling pattern evolution.
Figure 3.
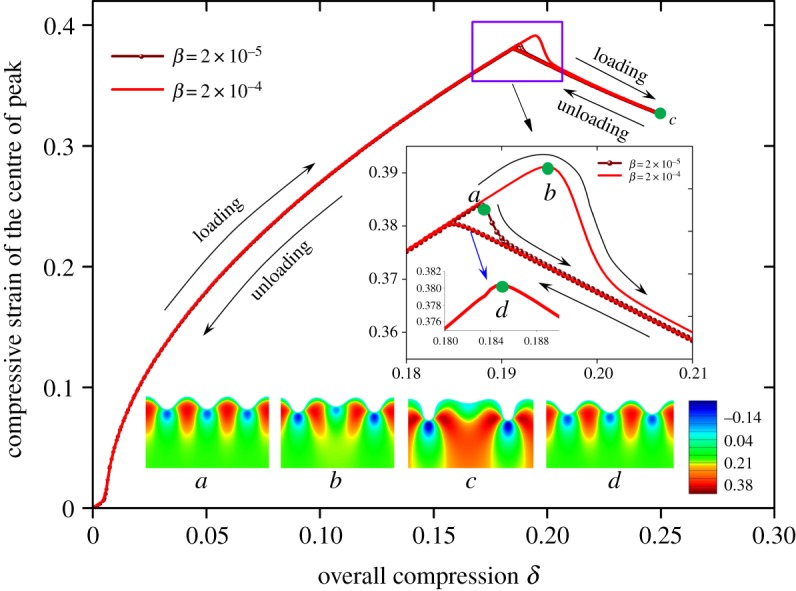
The nominal compressive strain of the centre of the peak in the substrate along the loading direction in both loading and unloading paths. This nominal strain is the maximum compressive strain ( in the substrate when the substrate deformation is sinusoidal. The location of this strain is shown in figure 4. When period-doubling appears, this strain dissipates and strain localization occurs. The strain at point d is defined as the characteristic strain εc(≈0.381). β is the damping factor. The cloud pictures in the figure show the nominal compressive strain distributions of some feature points. (Online version in colour.)
Figure 4.
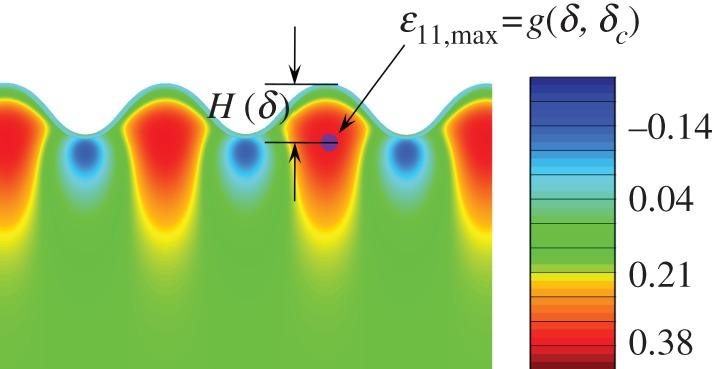
The location of the maximum nominal compressive strain along the loading direction in the substrate when the wrinkling mode is sinusoidal. is a function of δ and δc in the case of no-pre-stretch. H(δ)≈0.18×2π/p in the fundamental state, which is largely insensitive to the compression δ. It should be mentioned that when the system has evolved into the period-doubling mode, the strain of the point shown in this figure is no longer the maximum strain in the substrate. (Online version in colour.)
In finite-element simulations, without perturbation the system may keep the sinusoidal wrinkling mode even when the overall compressive strain is greater than δ2, which permits us to evaluate the total potential energy Ps corresponding to the sinusoidal wrinkling mode. With the presence of perturbation for instance by introducing the damping factor, the system will evolve from the sinusoidal mode to the period-doubling wrinkling mode; in this case, the total potential energy Pa can be obtained from finite-element results. Here, Pa corresponds to the unloading path. Figure 5 shows the potential energy difference ΔP*=Pa−Ps between the wrinkling mode that actually occurs and the sinusoidal wrinkling mode. It can be seen that when the nominal compressive strain at the point shown in figures 4 and 5 reaches the value of 0.381, the sinusoidal wrinkling mode gives way to the period-doubling mode. Beyond this critical point, the period-doubling mode is energetically favourable in comparison with the sinusoidal mode. The corresponding overall compressive strain at the bifurcation point is approximately 0.185.
Figure 5.
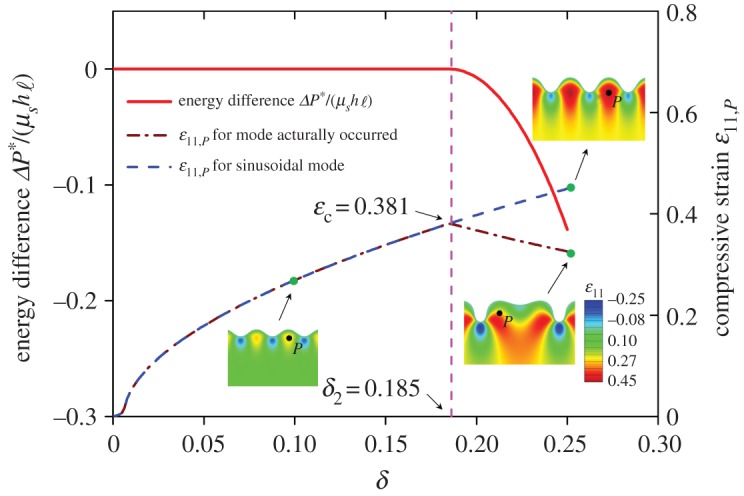
Energy difference between the sinusoidal wrinkling mode and the wrinkling mode that actually occurred. Without perturbation, the system may maintain the sinusoidal wrinkling mode in the post-buckling stage. The strain shown in the figure is the nominal compressive strain of point P, which is shown in figure 4 as well. The modular ratio of the system is 774 and λ0=1. (Online version in colour.)
Our analysis shows that the characteristic strain εc is basically independent of the modular ratio of the film to the substrate and insensitive to the geometric imperfection introduced in the system, as shown in figures 6 and 7. The parameter η in figure 7 represents the ratio of the imperfection amplitude to the film thickness. The strain εc is not far from the crease strain identified by Hohlfeld & Mahadevan [7,10] and Hong et al. [8]. But the connection between these two strains remains unclear. We also explored the case with substrate pre-stretch, i.e. λ0≠1. Our results show that εc basically linearly depends on λ0 (figure 8). A linear function with εc=0.381+0.15(λ0−1) is used to fit the results.
Figure 6.
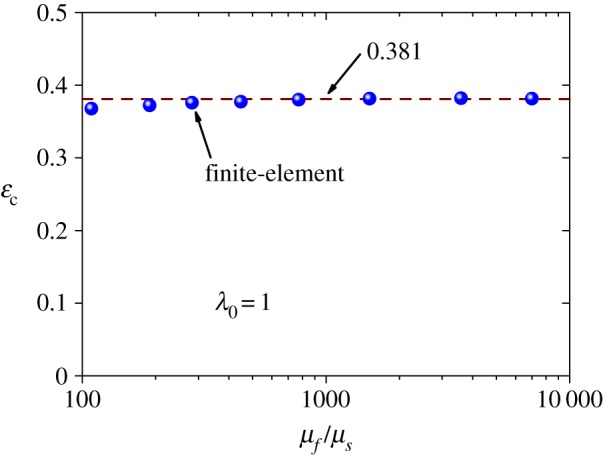
The characteristic strain defined in figure 3 is basically a constant for different modular ratios. The pre-stretch ratio of the substrate is 1. (Online version in colour.)
Figure 7.
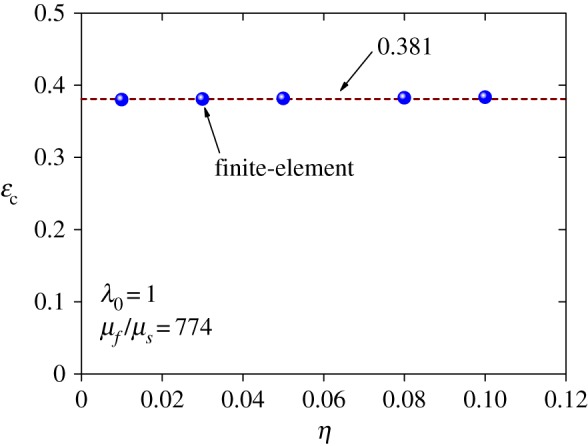
The characteristic strain with different imperfection amplitudes. η refers to the ratio of the imperfection amplitudes to the film thickness. (Online version in colour.)
Figure 8.
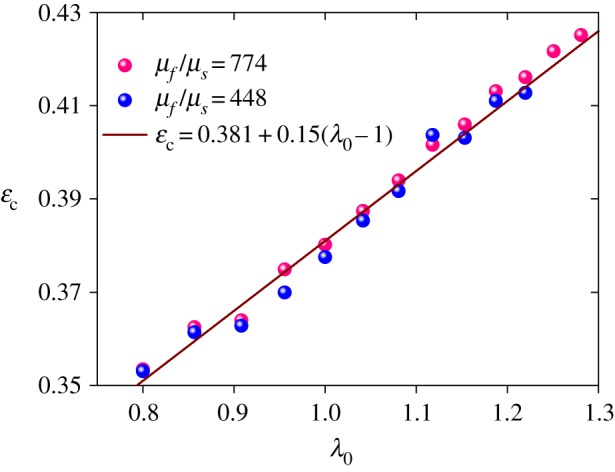
The characteristic strain with different pre-stretch ratios for two finite-element models. A linear function is used to fit the finite-element results (points). (Online version in colour.)
The characteristic strain identified here and the analysis on the total potential energy of the system may not only help us understand the physics behind the occurrence of the period-doubling mode and localized folding in bilayer systems but also provide a means to determine the critical overall compressive strain at the onset of the wrinkling mode transition. This issue will be further addressed below.
4. Explicit solutions to predict the critical overall strain for the onset of period-doubling
In this section, we show that the characteristic strain identified in §3 permits the determination of δ2 in an explicit form. Our analysis reveals that δ2 depends on λ0 and δc, i.e.
| 4.1 |
Without substrate pre-stretch, i.e. λ0=1,
| 4.2 |
Based on the characteristic strain identified in §3, we provide a means to determine the function f1 and δ2 in equation (4.2). For the sinusoidal wrinkling mode, the maximum nominal strain along the loading direction depends on δc and the overall compressive strain δ without substrate pre-stretch (figure 4).
When reaches εc, δ will have the value of δ2, i.e.
| 4.3 |
Therefore, provided that the function g is known, we can determine the function f1 in equation (4.2). Based on the nonlinear finite-element simulations in §2, we have determined the function g. This function gives the correlation between , δ and δc as
| 4.4 |
The last term in equation (4.4) ensures that when δ=δc. 2/hp(δ−1/2 δ2−δc+ 1/2 δc2)1/2 can well describe the evolution of the wrinkling amplitude given by finite-element simulations. For illustration, the function g determined from a finite-element example is shown in figure 9.
Figure 9.
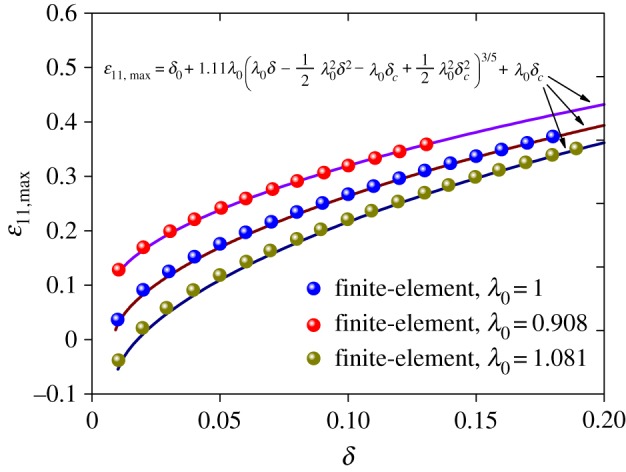
Comparison of function g (equations (4.4) and (4.6.)) with respect to finite-element results, where we take μf/μs=448 in the finite-element simulations. (Online version in colour.)
From equations (4.3) and (4.4), δ2 is derived in the explicit form:
| 4.5 |
indicating that the dependence of δ2 on δc is rather weak when the modular ratio μf/μs is large. For instance, when μf/μs>50, equation (4.5) gives δ2≈0.185, as shown in figure 10. Figure 11 shows that δ2 is insensitive to the geometric imperfections introduced in the post-buckling analysis. The solution given by equation (4.5) is consistent with our experimental results (figure 1) and finite-element simulations performed by Cao & Hutchinson [11].
Figure 10.
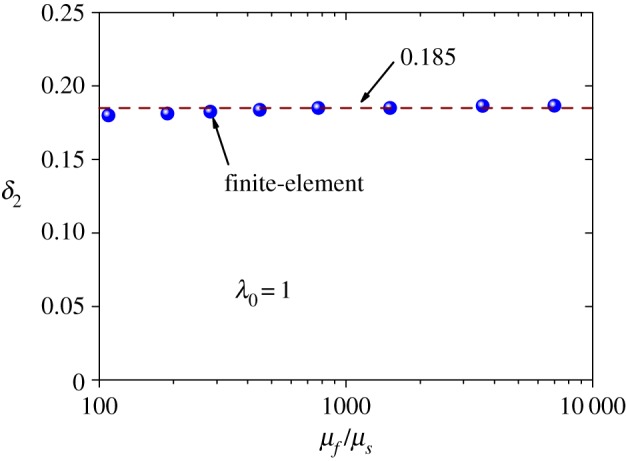
Comparison of δ2 predicted from equation (4.5) for different modular ratios with our finite-element results. (Online version in colour.)
Figure 11.
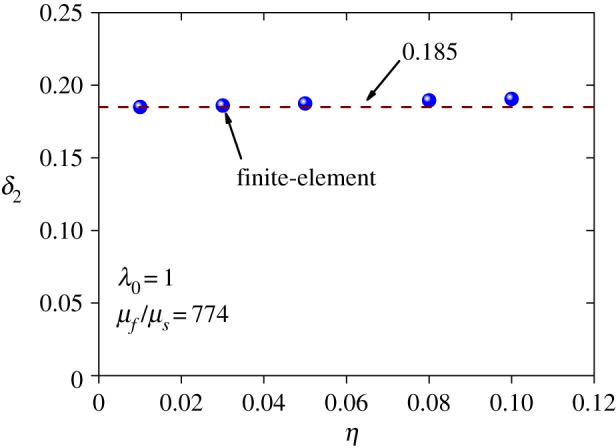
The critical overall strain δ2 for the onset of the period-doubling mode corresponding to different imperfection amplitudes. (Online version in colour.)
In the case of λ0≠1, our theoretical analysis shows that δ2=f1(λ0,δc), and the prestrain in the substrate is δ0=1−λ0. In the presence of pre-stretch, the maximum (nominal) compressive strain in the substrate based on the finite-element results is given by
| 4.6 |
Note that equation (4.6) reduces to equation (4.4) in the case of λ0=1. The comparison of equation (4.6) with the finite-element simulations shown in figure 9 indicates that equation (4.6) is a very good approximation. When , the period-doubling occurs. This condition together with equation (4.6) gives
| 4.7 |
where εc=0.381+0.15(λ0−1). We have compared the predicted δ2 given by equation (4.7) with our finite-element simulations. The results are plotted in figure 12 for two different modular ratios and various pre-stretch ratios. Equation (4.7) matches the finite-element results well. It is also seen that the pre-stretch has pronounced effects on δ2. With the increase of λ0 from 0.8 to 1.3, δ2 increases by a factor of five.
Figure 12.
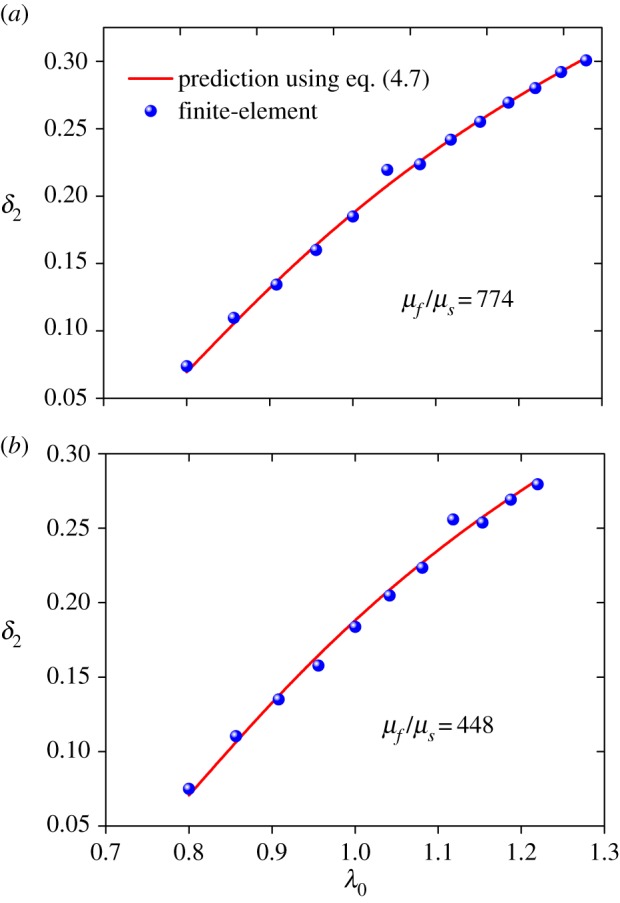
Comparison of δ2 predicted from equation (4.7) for different pre-stretch ratios with finite-element results. (a) Modular ratio μf/μs=774; (b) modular ratio μf/μs=448. (Online version in colour.)
To validate further our analysis and equation (4.7), experiments have been performed. PDMS bulk was chosen as the soft substrate, and the stiff film was generated by subjecting the PDMS to a UV-ozone treatment for 10 min. Experimental details are given in appendix A. The surface wrinkling morphology of the PDMS bulk with occurrence of period-doubling is shown in figure 13 for λ0=0.83, 0.9, 1, 1.1, respectively. It is a challenging issue to accurately determine δ2 in our experiments; therefore, it is difficult to quantitatively validate equation (4.7). However, figure 13 indeed shows that the onset of period-doubling strongly depends on the pre-stretch ratio and the experimental results basically support our theoretical and numerical results. Equations (4.5) and (4.7) are valid for the systems with relatively large modular ratio μf/μs; when the modular ratio is small, say smaller than 10, some localized buckling modes may occur instead of period-doubling [11], which is beyond the scope of this study. Very recently, Auguste et al. [26] studied the post-wrinkling bifurcations in films on pre-stretched substrate through a combination of simulations and experiments. They found the interesting ‘chaotic’ wrinkling when λ0=0.7. In our experiments, the minimum pre-stretch ratio λ0=0.83 at which stable period-doubling was observed.
Figure 13.
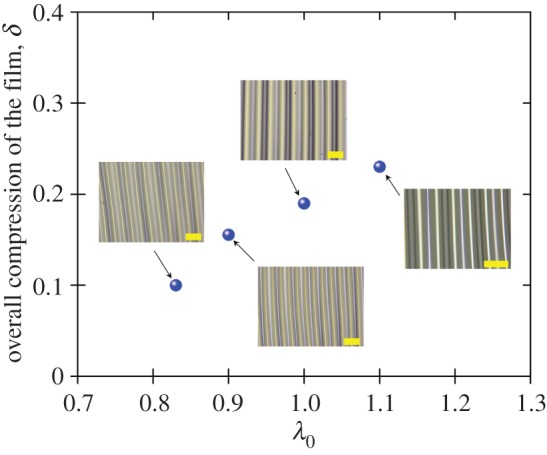
Surface wrinkling morphology of the PDMS with the occurrence of the period-doubling mode for the pre-stretch ratio λ0=0.83, 0.9, 1, 1.1, respectively. Scale bar, 100 μm. (Online version in colour.)
The solution in equation (4.7) allows us to predict the critical condition for the onset of the period-doubling mode, and thus it provides a guideline for controlling surface wrinkling patterns by tuning the stress state in the substrate. Understanding the morphogenesis and origin of shapes has long been a central goal of developmental biology [27–29]. Growth is responsible for the morphogenesis of biological organs and tissues, which consists of a series of orchestrated steps [30]. Besides genetic and chemical effects, mechanical environments play a significant role in regulating pattern formation. Differential growth or atrophy of tissues and organs could induce residual stresses, which are important in the morphogenesis and physiological functions of soft tissues and organs [28,31–33]. Recently, Ben Amar & Jia [34] have studied the surface wrinkling and the zigzag mode of a hyperelastic bilayer soft tissue. In their study, differential growth of the soft tissue elicits residual stresses which lead to surface instability. In this paper, we have studied the development of a period-doubling mode in the plane strain compression of film/substrate bilayer systems with focus on the effects of prestresses. Equation (4.7) clearly demonstrates that prestresses in the substrate affect the evolution of wrinkling patterns and therefore it would be interesting to take this factor into account in understanding the correlation between the growth and morphogenesis of biological organs and tissues.
It should be pointed out that this study is limited to the system with a flat surface. In this sense, although figure 11 shows that δ2 is insensitive to geometric imperfections introduced in the post-buckling analysis, the geometric imperfections should be smaller than the film thickness in order to use equations (4.5) or (4.7) as appropriate. To illustrate this point further, we explore a case where geometric imperfections are introduced based on a buckled deformation corresponding to the sinusoidal mode. In the initial configuration, the buckled amplitude of film is much greater than its thickness. Electronic supplementary material, Video S2, shows the deformed configurations of the system at different overall compressive strains. In this case, equation (4.5) is no longer valid to predict the critical overall compressive strain δ2 for the onset of period-doubling. However, it is interesting to find that period-doubling still occurs when the local nominal strain in the substrate at the centre of the peak (figure 4) reaches the characteristic strain εc. Both this example and the solution in equation (4.5) indicate that the period-doubling mode employs the sinusoidal wrinkling mode as the base state and is almost independent of the overall strain in the fundamental state given in figure 2. Besides the wavelength, the sinusoidal wrinkling mode is primarily characterized by its amplitude. This may help us to understand why the critical condition for period-doubling is given in terms of the characteristic maximum nominal strain in the substrate.
5. Concluding remarks
Understanding the unusual wrinkling modes at compressive strains well above the bifurcation strain such as period-doubling and folding is a challenging issue [5,11,16,34]. In this paper, we have studied the occurrence of a period-doubling mode in the plane strain compression of film/substrate bilayer systems. Our analysis shows that the overall compressive strain δ2 in the film for the onset of the period-doubling mode depends on the substrate pre-stretch ratio and the critical overall strain for the onset of wrinkling. When the modular ratio of the film to the substrate is large, say greater than 50, δ2 only depends on the substrate pre-stretch and is insensitive to the wrinkling strain. Nonlinear finite-element analysis (compressing and unfolding the system) reveals a characteristic strain of 0.381 (with no substrate pre-stretch) for the onset of period-doubling. When maximum compressive strain reaches the value of εc, the period-doubling mode occurs and the potential energy of system in this case is lower than that of the sinusoidal wrinkling mode. This indicates that the period-doubling mode is indeed energetically favourable and likely to occur in practical systems. Finally, explicit solutions based on the characteristic strain have been formulated to predict the overall compressive strain for the onset of the period-doubling in the cases with or without substrate pre-stretch. The solutions proposed here match both experimental and finite-element results well.
Acknowledgements
The authors thank the valuable and insightful comments and remarks of Prof. J. W. Hutchinson (Harvard University) on this study.
Appendix A. Experimental details
(a) Materials
PDMS bulk was prepared by mixing the base and curing agent (Sylgard 184, Dow Corning) in a ratio of 40:1 by weight. The mixture was then cured at 60° for 3 h, after being degassed for 1 or 2 h to remove excess bubbles. The PDMS bulk was cut into cuboids of size 20×15×7 mm in the experiment. The initial shear modulus of the PDMS bulk was measured as being around 0.043 MPa through performing indentation tests by using the Bose ElectroForce3100 test instrument.
(b) Surface treatments of Poly(dimethylsiloxane)
The PDMS (with or without pre-stretch) was subjected to a UV-ozone treatment for 10 min. A thin, stiff film was then formed onto the PDMS surface. Wrinkles formed when the film/substrate system was compressed. The tensile/compressive tests were performed using a locally made uniaxial tensile instrument. UV-ozone conditioning was provided by a UV-ozone cleaner. The modulus of the film induced by the UVO treatment is of the order 10 GPa [35].
(c) Examination of surface morphology
The PDMS surface was observed using a laser scanning microscope (VK-X100 K, Keyence, Japan). We observed the surface morphology while applying compression to the treated PDMS bulk. The compressive strain δ in figure 13 corresponded to the situation where the period-doubling mode was clearly observed.
Funding statement
Supports from the National Natural Science Foundation of China (grant nos 11172155, 11432008), Tsinghua University and 973 Program of MOST (2010CB631005) are acknowledged.
References
- 1.Bowden N., Brittain S., Evans AG, Hutchinson JW, Whitesides GM. 1998. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature 393, 146–149 (doi:10.1038/30193) [Google Scholar]
- 2.Genzer J., Groenewold J. 2006. Soft matter with hard skin: from skin wrinkles to templating and material characterization. Soft Matter 2, 310–323 (doi:10.1039/b516741h) [DOI] [PubMed] [Google Scholar]
- 3.Tokarev I., Minko S. 2009. Stimuli-responsive hydrogel thin films. Soft Matter 5, 511–524 (doi:10.1039/b813827c) [Google Scholar]
- 4.Chen X., Yin J. 2010. Buckling patterns of thin films on curved compliant substrates with applications to morphogenesis and three-dimensional micro-fabrication. Soft Matter 6, 5667–5680 (doi:10.1039/c0sm00401d) [Google Scholar]
- 5.Brau F., Vandeparre H., Sabbah A., Poulard C., Boudaoud A., Damman P. 2011. Multiple-length-scale elastic instability mimics parametric resonance of nonlinear oscillators. Nat. Phys. 7, 56–60 (doi:10.1038/nphys1806) [Google Scholar]
- 6.Li B., Cao YP, Feng XQ, Gao H. 2012. Mechanics of morphological instabilities and surface wrinkling in soft materials: a review. Soft Matter 8, 5728–5745 (doi:10.1039/c2sm00011c) [Google Scholar]
- 7.Hohlfeld E. 2008. Creasing, point-bifurcations, and the spontaneous breakdown of scale-invariance. PhD thesis, Harvard University, Cambridge, MA, USA. [Google Scholar]
- 8.Hong W., Zhao X., Suo Z. 2009. Formation of creases on the surfaces of elastomers and gels. Appl. Phys. Lett. 95, 111901 (doi:10.1063/1.3211917) [Google Scholar]
- 9.Cai S., Breid D., Crosby AJ, Suo Z., Hutchinson JW. 2011. Periodic patterns and energy states of buckled films on compliant substrates. J. Mech. Phys. Solids 59, 1094–1114 (doi:10.1016/j.jmps.2011.02.001) [Google Scholar]
- 10.Hohlfeld E., Mahadevan L. 2011. Unfolding the sulcus. Phys. Rev. Lett. 106, 105702 (doi:10.1103/PhysRevLett.106.105702) [DOI] [PubMed] [Google Scholar]
- 11.Cao YP, Hutchinson JW. 2012. Wrinkling phenomena in neo-Hookean film/substrate systems. J. App. Mech. 79, 031019 (doi:10.1115/1.4005960) [Google Scholar]
- 12.Zang JF, Zhao X., Cao YP, Hutchinson JW. 2012. Localized ridge wrinkling of stiff films on compliant substrates. J. Mech. Phys. Solids 20, 1265–1279 (doi:10.1016/j.jmps.2012.03.009) [Google Scholar]
- 13.Cao YP, Hutchinson JW. 2012. From wrinkles to creases in elastomers: the instability and imperfection-sensitivity of wrinkling. Proc. R. Soc. A 468, 94–115 (doi:10.1098/rspa.2011.0384) [Google Scholar]
- 14.Hutchinson JW. 2013. The role of nonlinear substrate elasticity in the wrinkling of thin films. Phil. Trans. R. Soc. A 371, 20120422 (doi:10.1098/rsta.2012.0422) [DOI] [PubMed] [Google Scholar]
- 15.Biot MA. 1963. Surface instability of rubber in compression. Appl. Sci. Res. 12, 168–182 [Google Scholar]
- 16.Sun JY, Xia S., Moon MY, Oh KH, Kim KS. 2012. Folding wrinkles of a thin stiff layer on a soft substrate. Proc. R. Soc. A 468, 932–953 (doi:10.1098/rspa.2011.0567) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ebata Y., Croll AB, Crosby AJ. 2012. Wrinkling and strain localizations in polymer thin films. Soft Matter 8, 9086–9091 (doi:10.1039/c2sm25859e) [Google Scholar]
- 18.Cao C., Chan HF, Zang J., Leong KW, Zhao X. 2014. Harnessing localized ridges for high-aspect-ratio hierarchical patterns with dynamic tunability and multifunctionality. Adv. Mater. 26, 1763–1770 (doi:10.1002/adma.201304589) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Timoshenko SP, Gere JM. 1961. Theory of elastic stability. New York, NY: McGraw-Hill [Google Scholar]
- 20.Koiter WT. 2009. Applications. In Elastic stability of solids and structures. (ed. van der Heijden AMA.), 166–169 Cambridge, UK:Cambridge University Press. [Google Scholar]
- 21.Dervaux J., Ciarletta P., Ben Amar M. 2009. Morphogenesis of thin hyperelastic plates: a constitutive theory of biological growth in the Föppl–von Kármán limit. J. Mech. Phys. Solids 57, 458–471 (doi:10.1016/j.jmps.2008.11.011) [Google Scholar]
- 22.Chen X., Hutchinson JW. 2004. Herringbone buckling patterns of compressed thin films on compliant substrates. J. App. Mech. 71, 597–603 (doi:10.1115/1.1756141) [Google Scholar]
- 23.Huang R. 2005. Kinetic wrinkling of an elastic film on a viscoelastic substrate. J. Mech. Phys. Solids 53, 63–89 (doi:10.1016/j.jmps.2004.06.007) [Google Scholar]
- 24.Huang ZY, Hong W., Suo Z. 2005. Nonlinear analyses of wrinkles in a film bonded to a compliant substrate. J. Mech. Phys. Solids 53, 2101–2118 (doi:10.1016/j.jmps.2005.03.007) [Google Scholar]
- 25.ABAQUS analysis user's manual 2010, v.6.10. http://www.simula.com. [Google Scholar]
- 26.Auguste A., Jin L., Suo Z., Hayward RC. 2014. The role of substrate pre-stretch in post-wrinkling bifurcations. Soft Matter 10, 6520–6529 (doi:10.1039/C4SM01038H) [DOI] [PubMed] [Google Scholar]
- 27.Sharon E., Marder M., Swinney HL. 2004. Leaves, flowers and garbage bags: making waves. Am. Sci. 92, 254–261 (doi:10.1511/2004.47.932) [Google Scholar]
- 28.Liang H., Mahadevan L. 2009. The shape of a long leaf. Proc. Natl Acad. Sci. USA 106, 22049–22054 (doi:10.1073/pnas.0911954106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Thompson DW. 1942. On growth and form. Cambridge, UK: Cambridge University Press [Google Scholar]
- 30.Taber LA. 1995. Biomechanics of growth, remodeling, and morphogenesis. Appl. Mech. Rev. 48, 487–545 (doi:10.1115/1.3005109) [Google Scholar]
- 31.Goriely A., Ben Amar M. 2005. Differential growth and instability in elastic shells. Phys. Rev. Lett. 94, 198103 (doi:10.1103/PhysRevLett.94.198103) [DOI] [PubMed] [Google Scholar]
- 32.Dervaux J., Ben Amar M. 2008. Morphogenesis of growing soft tissues. Phys. Rev. Lett. 101, 68101 (doi:10.1103/PhysRevLett.101.068101) [DOI] [PubMed] [Google Scholar]
- 33.Li B., Cao YP, Feng XQ, Gao H. 2011. Surface wrinkling of mucosa induced by volumetric growth: theory, simulation and experiment. J. Mech. Phys. Solids 59, 758–774 (doi:10.1016/j.jmps.2011.01.010) [Google Scholar]
- 34.Ben Amar M, Jia F. 2013. Anisotropic growth shapes intestinal tissues during embryogenesis. Proc. Natl Acad. Sci. USA 110, 10525–10530 (doi:10.1073/pnas.1217391110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chan EP, Crosby AJ. 2006. Spontaneous formation of stable aligned wrinkling patterns. Soft Matter 2, 324–328 (doi:10.1039/b515628a) [DOI] [PubMed] [Google Scholar]


