Identifying Optimal Biomarker Combinations for Treatment Selection via a Robust Kernel Method

Summary

Treatment-selection markers predict an individual’s response to different therapies, thus allowing for the selection of a therapy with the best predicted outcome. A good marker-based treatment-selection rule can significantly impact public health through the reduction of the disease burden in a cost-effective manner. Our goal in this paper is to use data from randomized trials to identify optimal linear and nonlinear biomarker combinations for treatment selection that minimize the total burden to the population caused by either the targeted disease or its treatment. We frame this objective into a general problem of minimizing a weighted sum of 0–1 loss and propose a novel penalized minimization method that is based on the difference of convex functions algorithm (DCA). The corresponding estimator of marker combinations has a kernel property that allows flexible modeling of linear and nonlinear marker combinations. We compare the proposed methods with existing methods for optimizing treatment regimens such as the logistic regression model and the weighted support vector machine. Performances of different weight functions are also investigated. The application of the proposed method is illustrated using a real example from an HIV vaccine trial: we search for a combination of Fc receptor genes for recommending vaccination in preventing HIV infection.

1. Introduction

Heterogeneity exists among individual subjects’ responses to treatment in many disease settings. Biomarkers associated with treatment-response heterogeneity can help individuals select therapies in order to optimize clinical outcome. As a single marker typically has limited ability to predict the heterogeneity in treatment response, statistical methods for combining biomarkers are critically needed for optimizing treatment selection.

Among others, one common approach for identifying marker combinations in treatment selection relies on modeling of the disease risk, conditional on biomarkers and treatment assignment; subsequent treatment recommendation is made based on the difference in the disease risk between non-treated and treated. For example, Song and Pepe (2004) adopted the standard logistic regression for disease risk modeling; Foster et al. (2011) proposed a ‘virtual twin’ method with tree-based estimators of disease risk; Qian and Murphy (2011) and McKeague and Qian (2013) adopted a L1-penalized least squares approach for estimating treatment-selection rules; Lu et al. (2013) developed an A-learning method for linear outcomes that requires correct modeling of the treatment-marker interaction but is robust to modeling of the marker’s main effect.

Performance of the treatment-selection rules based on risk modeling relies critically on the correct specification of the model, which is challenging given the complexity of biological mechanisms. A different approach that is more robust to model misspecification is to write down a desired criterion function associated with treatment selection, and search for the marker combination that optimizes the criterion function. For example, Orellana et al. (2010) considered parametric and semiparametric dynamic regime marginal structural models for optimizing expected utility. To optimize the population mean outcome, Zhang et al. (2012a, b) proposed finding marker combinations that optimize the empirical or double-robust estimates of population mean outcome within a pre-specified parametric class. Since these estimates of population mean outcome involve a non-smooth, non-convex 0–1 loss, the optimization procedure can be computationally challenging. Zhao et al. (2012) transformed the optimization problem into an outcome-weighted learning problem and derived the optimal treatment-selection rule using a weighted support vector machine method by approximating the 0–1 loss with a convex hinge loss function.

In this paper, we propose a new method to identify marker combinations that directly optimize the targeted criterion function as did Zhang et al. (2012a) and Zhao et al. (2012). In particular, we consider the objective of minimizing unfavorable outcomes in the population. These outcomes possibly include 1) events of a targeted disease, and 2) adverse side effects or monetary cost incurred by treatment. Furthermore, in a randomized trial setting, the optimization problem can be reformulated as one of minimizing a weighted sum of 0–1 loss. We propose to solve this via the difference of convex functions algorithm (DCA). Like the outcome-weighted support vector machine in Zhao et al. (2012), our estimator allows for flexible linear and nonlinear combinations of biomarkers to account for the possibly complicated relationship between biomarkers and treatment. However, our estimator is more effective at minimizing the targeted criterion function through the adoption of a more precise approximation of 0–1 loss. Fisher consistency and asymptotic consistency of the proposed estimator are derived. Different choices of weight functions are also investigated through numerical studies.

Next, in Section 2, we describe a general framework for optimizing treatment-selection rules. In Section 3, we propose a penalized estimator that minimizes the penalized weighted sum of a ramp loss function and develop its theoretical properties. In Section 4, we evaluate the performance of the estimator and compare it with common approaches through numerical studies. In Section 5, we illustrate the methodology with an example from a recent HIV vaccine efficacy trial in Thailand. Finally, we end the paper with a discussion.

2. Method

Here we consider the problem of optimizing the treatment regimen for an unfavorable clinical outcome denoted by Y, based on a set of markers X with dimension p ≥ 1. In this paper we focus on a binary disease outcome Y, 0 for non-diseased and 1 for diseased. The methods developed work for continuous outcomes as well. Let A(X) indicate the marker-based treatment-selection rule. A = 0 stands for not treating and A = 1 for treating. An important measure for quantifying the treatment-selection benefit of A(X) is E_A(X)(Y), the expected disease rate as a result of treatment selection (Song and Pepe, 2004). Here the expectation is averaged over the decision A(X). This measure has become more widely recognized in the literature in recent years (Zhao et al., 2012; Zhang et al., 2012a).

While E_A(X)(Y) characterizes the burden of disease upon the population, more generally, one may be concerned with additional burden associated with treatment. In practice there are often unpleasant aspects associated with treatment such as its side effects and/or monetary cost. A treatment-selection strategy that takes these aspects into consideration is thus preferred. One way to combine the disease and treatment burdens is to pre-specify a treatment/disease harm ratio such that each burden type can be put on the same scale. As in the decision-theoretic framework proposed in Vickers et al. (2007), let δ be a pre-specified ratio of the burden per treatment relative to the burden per disease event, and let Y(1) and Y(0) indicate the potential disease outcome if a subject were to receive or not receive the treatment. Here we set the burden per targeted disease event as 1. Then the total burden due to disease and treatment for a treatment-selection rule A(X), represented in the unit of the burden per disease event, equals

$$\theta =E_{A(\mathit{X})}(Y)+E\{\delta \times A(\mathit{X})\}=\sum _{a=0}^{1}E[Y(a)\times I\{A(\mathit{X})=a\}]+\delta \times E\{A(\mathit{X})\}.$$ (1)

An optimal treatment-selection rule can thus be found by minimizing θ.

In practice, it is often difficult to agree upon δ. Choosing δ = 0 such that θ = E_A(X)(Y) corresponds to the special case where the criterion function to be minimized is the burden due to the targeted disease alone, as in Zhang et al. (2012a) and Zhao et al. (2012). While detailed discussion about the choice of δ in treatment selection is beyond the scope of this paper, the development of a generalized framework allowing for nonzero δ is, however, important for a method to be applicable to practical scenarios where there are sensible ways to pre-specify δ. For example, δ was chosen to be 5% for treating breast cancer with adjuvant chemotherapy in Vickers et al. (2007) according to a patient survey. In Rapsomaniki et al. (2012), δ was chosen to be 2% for cost of preventive treatment per year for cardiovascular disease relative to the value of an event-free life year.

Suppose we have data from a two-arm randomized trial with T = 0, 1 indicating assignment to the untreated and treated arm, respectively. Let n₀ and n₁ indicate the number of subjects untreated and treated respectively. We have i.i.d. samples {Y_i, X_i, T_i} for i = 1, …, n with n = n₀ + n₁. We make the following assumptions: (i) stable unit treatment value (SUTVA) (Rubin, 1980) and consistency: Y(0), Y(1) of one subject is independent of the treatment assignments of other subjects, and given the treatment a subject actually received, a subject’s potential outcomes equal the observed outcomes; (ii) ignorable treatment assignments assumption: T ⊥ Y(0), Y(1)|X. Assumption (i) is plausible in trials where participants do not interact with one another and assumption (ii) is ensured by randomization. Algebra (as in Web Supplementary Appendix A) shows that

$$\theta =E[Y\times \{1-A(\mathit{X})\}\mid T=0]+E[Y\times A(\mathit{X})\mid T=1]+\delta \times P\{A(\mathit{X})=1\}$$ (2)

$$=E(Y\mid T=0)-E[A(\mathit{X})\times \{{\mathit{Risk}}_0(\mathit{X})-{\mathit{Risk}}_1(\mathit{X})-\delta \}],$$ (3)

where Risk₀(X) = P(Y = 1|X, T = 0) and Risk₁(X) = P(Y = 1|X, T = 1) are the risk of Y conditional on X among untreated and treated, respectively. Therefore an optimal rule A(X) in the sense of minimizing θ is A(X) = 1 if Risk₀(X) − Risk₁(X) > δ and A(X) = 0 otherwise. In other words, the reduction in the disease burden from treatment needs to be more significant than the burden of treatment itself for one to recommend it for a subject. Note that E(Y |T = 0) − θ is the net benefit of A(X) as defined in Vickers et al. (2007), i.e., the difference in the total burden comparing treating none with A(X). It equals E[A(X) × {Risk₀(X) − Risk₁(X) − δ}] by equation (3) and is maximized by the optimal rule A(X) = I{Risk₀(X) − Risk₁(X) > δ}. Related results have been shown by others. For example, in the setting where Y is defined to be a favorable outcome, Zhang et al. (2012b) showed that the optimal A(X) when δ = 0 is to treat if Risk₁(X) − Risk₀(X) > 0; Baker et al. (2012) showed that the average treatment benefit in Y needs to be larger or smaller than δ among subjects with A(X) = 1 or 0 respectively, in order for A(X) to be more beneficial than treating none and treating all: A(X) = I{Risk₁(X) − Risk₀(X) > δ} satisfies these conditions. Standard regression-based methods can be used to estimate Risk₀(X) and Risk₁(X) in order to derive the optimal treatment-selection rule. As pointed out by Zhang et al. (2012a), however, when the risk model is misspecified, performance of the treatment-selection rule derived this way can be sub-optimal.

To make treatment selection more robust to model misspecification, we follow the strategy of Zhang et al. (2012a) and Zhao et al. (2012), and consider a class of rules that make treatment recommendation based on whether a marker combination score is greater than zero. In particular, let A(X) = I{f(X) > 0} with I the indicator function, f(X) = b+γ(X) with γ(X) a function of markers X. Then θ in (2) can equivalently be represented as

$$\theta =\frac{E\{Y\times T\times I\{f(\mathit{X})>0\}]}{P(T=1)}+\frac{E[Y\times (1-T)\times I\{f(\mathit{X})\le 0\}]}{P(T=0)}+\delta \times P\{f(\mathit{X})>0\}.$$

The optimal f(X) can be found by minimizing the empirical estimate of θ, i.e.,

$$\begin{array}{l}\widehat{f}={\text{argmin}}_f\sum _{i=1}^n\left[\frac{Y_i\times T_i\times I\{f({\mathit{X}}_i)>0\}}{n_1}+\frac{Y_i\times (1-T_i)\times I\{f({\mathit{X}}_i)\le 0\}}{n_0}+\delta \times \frac{I\{f({\mathit{X}}_i)>0\}}{n}\right]\\ ={\text{argmin}}_f\sum _{i=1}^n-\{Y_i\times T_i/n_1-Y_i\times (1-T_i)/n_0+\delta /n\}\times I\{f({\mathit{X}}_i)\le 0\}.\end{array}$$

Therefore, we can formulate this problem as the minimization of a weighted sum of 0–1 loss. That is, f̂ can be found as the minimizer of

$$\sum _{i=1}^n{W}_{i}I\{f({\mathit{X}}_i)\le 0\}/n\propto \sum _{i=1}^n\mid W_i\mid I\{sgn(W_i)\times f({\mathit{X}}_i)\le 0\}/n$$ (4)

with the subject-specific weight

$$W_i=W_{1i}=-\left\{\frac{Y_i\times T_i}{n_1/n}-\frac{Y_i\times (1-T_i)}{n_0/n}+\delta \right\}.$$ (5)

Note that in the special case where δ = 0, we have W_1i = 0 when Y_i = 0, which implies that we only need to measure biomarkers among cases to derive the optimal treatment-selection rule. In subsequent numerical studies, we name this set of weights the ‘case-only weights’.

Second, note that θ can also be represented as E(Y|T = 0) + E[(1 − Y) × (1 − T) × I{f(X) > 0}]/P(T = 0) − E[(1 − Y) × T × I{f(X) > 0})]/P(T = 1) + δ × P{f(X) > 0}. So to estimate f(X) we can minimize ${\sum }_{i=1}^n\{(1-Y_i)\times (1-T_i)/n_0-(1-Y_i)\times T_i/n_1+\delta /n\}\times I\{f({\mathit{X}}_i)>0\}$, which is equivalent to minimizing the weighted sum of 0–1 loss (4) with the weight

$$W_i=W_{2i}=-\left\{\frac{(1-Y_i)\times (1-T_i)}{n_0/n}-\frac{(1-Y_i)\times T_i}{n_1/n}+\delta \right\}.$$ (6)

Note that for δ = 0, using this set of weights only requires collection of biomarker information among controls since W_2i = 0 for Y_i = 1. In subsequent numerical studies, we name this set of weights the ‘control-only weights’.

Since the minimizer of two different sets of loss will also be the minimizer of the linear combination of the two sets of loss, we can choose weights in loss (4) as a weighted average of the case-only weights (5) and the control-only weights (6) with weight p and 1 − p respectively for arbitrary p. This is equivalent to minimizing (4) with

$$W_i=W_{3i}=-\left[\{p\times Y_i-(1-p)\times (1-Y_i)\}\times \left(\frac{T_i}{n_1/n}-\frac{1-T_i}{n_0/n}\right)+\delta \right].$$ (7)

In subsequent numerical studies, we choose p = 1/2 and name the set of weights the ‘case-control weights’. All three sets of weights W₁, W₂, W₃ do not require modeling of the disease risk conditional on the marker and the treatment.

Finally, we consider substituting the doubly robust estimator of E_A(X)(Y) (Zhang et al., 2012a) for estimating θ in (2). This estimator augments the inverse probability weighted estimator of E_A(X)(Y) with a term that involves the risk of Y given X and T. It has the double robustness property in that it is consistent for E_A(X)(Y) if either P(T = 1|X) (the propensity score for treatment) or the risk model is correctly specified. In a randomized trial, the propensity score for treatment is known, so consistency of the estimator is always achievable. Using the augmented term is expected to have the added advantage of improving efficiency, as shown in Zhang et al. (2012a) for continuous outcomes. Using a working model to obtain risk estimates ${\widehat{\mathit{Risk}}}_0(\mathit{X})$ and ${\widehat{\mathit{Risk}}}_1(\mathit{X})$ leads to the estimate of θ as

$$\begin{array}{l}\widehat{\theta }=\sum _{i=1}^n\left[\frac{Y_i\times (1-T_i)\times I\{f({\mathit{X}}_i)\le 0\}}{n_0}+\frac{Y_i\times T_i\times I\{f({\mathit{X}}_i)>0\}}{n_1}+\delta \times \frac{I\{f({\mathit{X}}_i)>0\}}{n}\right]\\ -\frac{{\sum }_{i=1}^n((1-T_i)\times I\{f({\mathit{X}}_i)<0\}+T_i\times I\{f({\mathit{X}}_i)>0\}-P[I\{f({\mathit{X}}_i)>0\}=T\mid {\mathit{X}}_i])\times \widehat{m}(Y_i;f)}{P[I\{f({\mathit{X}}_i)>0\}=T\mid {\mathit{X}}_i]},\end{array}$$

where P[I{f(X) > 0} = T| X] = π × I{f(X) > 0} + (1 − π) × I{f(X) ≤ 0} for π = P(T = 1), $\widehat{m}({\mathit{X}}_i;f)={\widehat{\mathit{Risk}}}_0({\mathit{X}}_i)\times I\{f({\mathit{X}}_i)\le 0\}+{\widehat{\mathit{Risk}}}_1({\mathit{X}}_i)\times I\{f({\mathit{X}}_i)>0\}$. As shown in Web Supplementary Appendix B, this corresponds to minimization of (4) with the weight

$$W_i=W_{4i}=-\left[\frac{Y_i{T}_i}{n_1}-\frac{Y_i(1-T_i)}{n_0}+\frac{\pi -T_i}{1-\pi }\times \frac{{\widehat{\mathit{Risk}}}_0+{\widehat{\mathit{Risk}}}_1}{n}+\frac{\delta }{n}\right].$$ (8)

We names this set of weights the ‘double-robustness weights’.

In subsequent numerical studies, we evaluate the performance of our estimators based on the above four special weights. We note, however, the existence of alternative ways to generate the weights. In particular, since the minimization of (3) is equivalent to the minimization of E[I{f(X) ≤ 0} × {Risk₀(X) − Risk₁(X) − δ}], any consistent estimate of Risk₀(X) − Risk₁(X) − δ can serve as W in (4). Similar observation has been made for the problem of minimizing E_A(X)(Y) (Zhang et al., 2012b).

2.1 Penalized Weighted Ramp Loss Estimator

In this section we consider the minimization of the loss function (4) conditional on a pre-specified set of weights W. Minimization of a weighted sum of 0–1 loss is computationally challenging due to the non-convexity of the indicator function. We propose to derive the marker combination through a difference of convex functions algorithm (Liu et al., 2005; Wu and Liu, 2007). Specifically, we approximate the indicator function I(u ≤ 0) with a ramp loss function h_s(u) as shown in Figure 1(a), where h_s(u) = 1 if u/s ≤ −1/2; h_s(u) = −u/s + 1/2 if −1/2 ≤ u/s < 1/2; and h_s(u) = 0 if u/s > 1/2, with s > 0 a scale factor. For any given u ≠ 0, the value of this loss function moves towards 0 or 1 and becomes 0 or 1 at some point as s → 0. Identifiability issues exist in minimizing the weighted sum of ramp loss because h_s(|u|) is greater than or equal to h_s(c|u|) for c > 1 and the ramp loss function satisfies h_s(|u|) = h_s=1(|u|/s). We handle the identifiability problem and at the same time control the model complexity by setting s = 1 and adding a penalty term to the weighted ramp loss. Using h(u) to indicate h_s(u) with s = 1, we propose to estimate f(X) = b + γ(X) by minimizing a penalized weighted sum of ramp loss

Figure 1.

(a) Different approximations of the 0–1 loss function. (b) Representing the ramp loss as the difference of two convex functions.

$$\frac{1}{n}\sum _{i=1}^n\mid W_i\mid h\{sgn(W_i)\times f({\mathit{X}}_i)\}+\frac{1}{2}{\lambda }_n{\Vert f\Vert }^2,$$ (9)

where λ_n is a tuning parameter and ||f|| is some norm for f. To solve this minimization problem, we represent the ramp loss function h as the difference between two convex functions as shown in Figure 1(b): h(u) = h₁(u) − h₂(u), where h₁(u) = (1/2 − u)₊ and h₂(u) = (−1/2 − u)₊. This allows application of a difference of convex functions algorithm (DCA) for minimization as will be presented in the following section. Next we consider derivation of treatment-selection rules based on linear and nonlinear marker combinations consecutively.

2.2 Identification of Linear Marker Combinations

First, we consider optimizing a linear marker combination f(X) = b + X^Tβ. We propose to solve for b and β by minimizing the weighted sum of ramp loss (9) with L2-norm penalty

$$\frac{1}{n}\sum _{i=1}^n\mid w_i\mid h\{z_i(b+{\mathit{x}}_i^T\mathit{\beta })<0\}+\frac{1}{2}{\lambda }_n{\Vert \mathit{\beta }\Vert }_2^2,$$ (10)

with z_i = sgn(w_i).

Let ${\eta }_i=z_{i}f({\mathit{x}}_i)=z_i\left(b+{\mathit{x}}_i^T\mathit{\beta }\right)$, and write h(u) = h₁(u) − h₂(u), minimization of (10) can be carried out in the following steps:

• Step 1. Start with an initial guess for η and call it η⁰.

• Step 2. Solve

  $$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }}{\text{argmin}}\sum _{i=1}^n\mid w_i\mid \left\{h_1({\eta }_i)-{\widehat{h}}_2\left({\eta }_i,{\eta }_i^0\right)\right\}/n+{\lambda }_n{\Vert \mathit{\beta }\Vert }_2^2/2,$$

  where ${\widehat{h}}_2({\eta }_i,{\eta }_i^0)=h_2({\eta }_i^0)+h_2^{\prime }({\eta }_i^0){\eta }_i$, and $h_2^{\prime }(u)=-\mathrm{I}(u<-1/2)$ is the first derivative of h₂(u) with respect to u, except 0 at u = −1/2.

• Step 3. Compute η⁰ and go back to step 2 until the change in the penalized weighted sum of ramp loss is less than a pre-specified threshold.

In Step 2 of the algorithm above, we solve a convex optimization problem. As h₁ and ĥ₂ are not smooth functions, a standard optimization strategy is to convert it to a constrained smooth optimization problem by introducing slack variables ξ_i to replace h₁ and adding two sets of constraints. This leads to

$$\begin{array}{c}\underset{\xi ,\mathit{\beta },b}{min}\frac{1}{n}\sum _{i=1}^n\mid w_i\mid \{{\xi }_i-h_2^{\prime }({\eta }_i^0){\eta }_i\}+\frac{1}{2}{\lambda }_n{\Vert \mathit{\beta }\Vert }_2^2\\ \text{subject}\text{to}{\xi }_i\ge \frac{1}{2}-{\eta }_i,\text{and}{\xi }_i\ge 0,\end{array}$$ (11)

where we have dropped terms void of ξ or β. The constraints in the above optimization problem are challenging to work with; therefore we seek to find its dual problem via the Lagrange method. The primary Lagrangian is

$$L_p=\frac{1}{n}\sum _{i=1}^n\mid w_i\mid \{{\xi }_i-h_2^{\prime }({\eta }_i^0){\eta }_i\}+\frac{1}{2}{\lambda }_n{\Vert \mathit{\beta }\Vert }_2^2-\frac{1}{n}\sum _{i=1}^n{\alpha }_i\left({\xi }_i+{\eta }_i-\frac{1}{2}\right)-\frac{1}{n}\sum _{i=1}^n{\gamma }_i{\xi }_i,$$

where α and γ are vectors of non-negative Lagrange multipliers, corresponding to the two sets of constraints in (11). As detailed in Web Supplementary Appendix C, this leads to the dual problem of

$$\begin{array}{c}\underset{\mathit{\alpha }}{min}{\mathit{\alpha }}^T\mathit{Q}\mathit{\alpha }-{\{\underset{\_}{\mathbf{1}}-2{\mathit{Qh}}_{2,w}^{\prime }({\mathit{\eta }}^0)\}}^T\mathit{\alpha }\\ \text{subject}\text{to}0\le {\alpha }_i\le \mid w_i\mid ,\text{and}\sum _{i=1}^n{a}_i{z}_i+\sum _{i=1}^n{z}_i\mid w_i\mid h_2^{\prime }({\eta }_i^0)=0,\end{array}$$ (12)

where Q is a square matrix whose [i, i′]^th element is 〈z_ix_i, z_i′x_i′〉/(nλ_n), $\underset{\_}{\mathbf{1}}={\{1\}}_{i=1}^n$, and ${\mathit{h}}_{2,w}^{\prime }({\mathit{\eta }}^0)={\{\mid w_i\mid h_2^{\prime }({\eta }_i^0)\}}_{i=1}^n$. The optimization problem (12) has a set of simple box constraints and can be solved via many quadratic programming methods. As shown in Web Supplementary Appendix C, we have $\mathit{\beta }={\sum }_{i=1}^n{z}_i\{\mid w_i\mid h_2^{\prime }({\eta }_i^0)+{\alpha }_i\}{\mathit{x}}_i/(n{\lambda }_n)$. The estimate of b can be found by averaging { $1/2z_i-{\mathit{x}}_i^T\mathit{\beta }=1/2z_i-\mathit{Q}\times \{{\mathit{h}}_{2,w}^{\prime }(\mathit{\eta })+\mathit{\alpha }\}/z_i:\mid w_i\mid >{\alpha }_i>0$}. Having found the best combination, the treatment-selection rule for a new observation x_new will be A(x_new) = I{f(x_new) > 0} where $f({\mathit{x}}_{\mathit{new}})=b+{\mathit{x}}_{\mathit{new}}^T\mathit{\beta }$.

2.3 Identification of Nonlinear Marker Combinations

As the most optimal marker combination for treatment selection may not be among linear combinations of the input markers, we may wish to enlarge the feature space via basis expansion and find the best linear combination in the enlarged space. One such approach is via the so called “kernel methods”. Let ϕ_i = ϕ(x_i) denote the feature vector for subject i in the enlarged feature space. For example, with two markers {x₁, x₂} to derive a treatment-selection rule, we may wish to go beyond their linear combinations and look at the second order trends as well as the interaction between the two markers. Then ϕ_i in the enlarged feature space, will equal {x_1i, x_2i, $x_{1i}^2,x_{2i}^2$, x_1ix_2i}. We can specify a kernel K corresponding to the inner product in the mapping ϕ, i.e., K(x_i, x_j) =< ϕ_i, ϕ_j >. Conversely, for any continuous, symmetric, and positive semidefinite kernel function K : 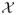× 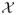→ ℝ, Mercer theorem (Vapnik, 1995) shows that there exists such a mapping ϕ such that K(x_i, x_j) =< ϕ_i, ϕ_j >. Examples of common nonlinear kernels include the polynomial kernel with d^th degree K(x_i, x_j) = (1+ < x_i, x_j >)^d, the radial basis function (RBF) kernel K(x_i, x_j) = exp(−γ||x_i − x_j||²) with γ a tuning parameter, and the identical-by-state (IBS) kernel $K({\mathit{x}}_i,{\mathit{x}}_j)={\sum }_{p=1}^P\{2\times I(x_{ip}=x_{jp})+I(\mid x_{ip}-x_{jp}\mid =1)\}/(2p)$ for x_ip = 0, 1, 2 (Wessel and Schork, 2006).

Let be the associated reproducing kernel Hilbert space (RKHS). We generalize equation (10) to find a combination of markers f ∈ through the minimization of the penalized weighted sum of ramp loss ${\sum }_{i=1}^n\mid w_i\mid h\{z_{i}f({\mathit{x}}_i)\}/n+{\lambda }_n{\Vert f\Vert }^2/2$, with ||·|| the norm in . This is the same as (10), when K is the linear kernel. The algorithm developed in Section 2.2 can be adapted to solve the minimization problem. In step 1 we can let η_i ← 0. In step 2, the dual problem that needs to be solved has the same form as (12), where Q is now a square matrix whose [i, i′]^th element is $\langle z_i{\mathit{\varphi }}_i,z_{i^{\prime }}{\mathit{\varphi }}_{i^{\prime }}\rangle /(n{\lambda }_n)=z_{i}K({\mathit{x}}_i,{\mathit{x}}_i^{\prime })z_i^{\prime }/(n{\lambda }_n)$. Having solved the dual problem, it is not necessary to translate it back to the primal problem because step 3 calls for η. With $\mathit{\beta }={\sum }_{i=1}^n{z}_i\{\mid w_i\mid h_2^{\prime }({\eta }_i^0)+{\alpha }_i\}{\mathit{\varphi }}_i/(n{\lambda }_n)$, we have $\mathit{\eta }=\mathit{z}·\left(b+\mathbf{\Phi }\widehat{\mathit{\beta }}\right)=\mathit{z}·\widehat{b}+\mathit{Q}\times \{{\mathit{h}}_{2,w}^{\prime }({\mathit{\eta }}^0)+\mathit{\alpha }\}$, where · is the element-wise multiplication operator, and Φ = (ϕ₁, …, ϕ_n)^T. This shows that even though ϕ_i may be infinite-dimensional, η_i always has a finite-dimensional representation. As shown in Web Supplementary Appendix C, the marker combination score for a new data x_new is $f({\mathit{x}}_{\mathit{new}})=b+{({\mathit{\varphi }}_{\mathit{new}})}^T\mathit{\beta }=b+{\sum }_{i=1}^n\{{\mathit{h}}_{2,w}^{\prime }(\mathit{\eta })+{\alpha }_i\}{z}_{i}K({\mathit{x}}_{\mathit{new}},{\mathit{x}}_i)/(n{\lambda }_n)$.

In practice, having the flexibility of modeling nonlinear marker effect is important for achieving good treatment-selection performance. This is especially true in the presence of nonzero treatment burden. Using the GLM model as an example: suppose the disease risk conditional on the markers and treatment follows g{P(Y = 1|X, T)} = β₀ + β₁T + β₂μ(X) + β₃ν(X)T with μ(X) and ν(X) being some functions of X. Based on (3), the optimal treatment-selection rule is to treat if the difference between Risk₀(X) = P(Y = 1|X, T = 0) and Risk₁(X) = P(Y = 1|X, T = 1) is greater than the treatment/disease burden ratio δ. Using the GLM model the optimal treatment-selection rule, given δ = 0, is to treat if β₁ + β₃ν(X) > 0 and to not treat otherwise, since sgn{Risk₀(X) − Risk₁(X)} = sgn{β₁ + β₃ν(X)}. In other words, only the main effect of treatment and the marker-treatment interaction need to be modeled correctly to derive the optimal A(X) for δ = 0. This is no longer true, however, for positive δ, since the sign of Risk₀(X) − Risk₁(X) − δ also depends on the intercept term and the main effect of the marker in the risk model for nonlinear link function g (which makes it more challenging to closely model the marker combination). Note that if there exists an underlying monotone transformation q such that q{Risk₀(X) − Risk₁(X)} = c + γ(X) for some constant c, then the optimal rule is to recommend treatment if c + γ(X) > q(δ) or equivalently if c − q(δ) + γ(X) > 0. This optimal rule belongs to the class of treatment-selection rules we study in this paper.

2.4 Theoretical Results

We consider the problem of minimizing E[|W| × I{sgn(W) × f(X) ≤ 0}], the expectation of (4) with respect to a measureable function f, where W is a random variable indicating individual-specific weight. We make the following assumptions: (i) f is a measurable function: 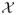→ ℝ; (ii) Y ∈ ℝ is bounded; (iii) |W| for W ∈ ℝ is bounded above. Fisher consistency of the treatment-selection rule based on minimizing the weighted sum of the ramp loss can be derived as shown in Theorem 1.

Theorem 1

For any measureable function f, if f̂ minimizes E[|W| × h{sgn(W) × f(X)}], then f̂ also minimizes E[|W| × I{sgn(W) × f(X) ≤ 0}].

Theorem 1 states that the treatment-selection rule minimizing the weighted sum of ramp loss will also minimize the weighted sum of 0–1 loss. The approximation of the 0–1 loss with the ramp loss does not affect the best treatment-selection performance. Proof of Theorem 1 is shown in Web Supplementary Appendix D.

Furthermore, let f̂_n be the penalized ramp estimator of f proposed in Section 2.1 based on a sample size of n; one can show that the weighted sum of ramp loss estimated based on f̂_n is consistent for that based on f as presented in Theorem 2.

Theorem 2

For a sequence of λ_n > 0 such that λ_n → 0 and λ_nn → ∞, we have that in probability lim_n→∞{θ_h(f̂_n) − inf_{f ∈ H̄k} θ_h(f)} = 0, where 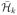denotes the closure of and θ_h(f) = E[|W| × h{sgn(W)f}].

Proof of Theorem 2 is presented in Web Supplementary Appendix E.

2.5 Alternative Estimator of Marker Combinations

In this section, we briefly discuss an alternative way to minimizing the weighted sum of 0–1 loss in (4) based on the weighted support vector machine technology. Since ${\sum }_{i=1}^n{W}_i\times I\{f({\mathit{X}}_i)\le 0\}\propto {\sum }_{i=1}^n\mid W_i\mid \times I[sgn(W_i)\ne sgn\{f({\mathit{X}}_i)\}]$, minimizing the weighted sum of 0–1 loss ${\sum }_{i=1}^n{W}_i\times I\{f({\mathit{X}}_i)\le 0\}$ can be translated into an equivalent problem of minimizing a weighted sum of classification error ${\sum }_{i=1}^n{W}_i^{★}\times I[sgn(W_i)\ne sgn\{f({\mathit{X}}_i)\}]$, where $W_i^{★}$, the weight for the new classification problem, equals |W_i|. In other words, our minimization problem can be formulated into a problem of minimizing the weighted sum of classification error where $Y_i^{★}=sgn(W_i)=\{-1,1\}$ is the true binary classes, sgn{f(X_i)} is the predicted binary class based on X, and $W_i^{★}$ is the subject-specific weight. This type of weighted classification error problem can thus be resolved using the weighted support vector machine (Lin and Wang, 2002) based on X_i, $Y_i^{★}$, and $W_i^{★}$ (sketched in Web Supplementary Appendix F). The outcome-dependent estimator of Zhao et al. (2012) is a special case of this class with weights W^★ corresponding to the case-only weights W₁ (5) in the scenario where δ = 0.

This alternative approach is essentially approximating the 0–1 loss with a hinge loss function g(u) = max(0, 1 − u), and minimizing the weighted sum of hinge loss. As shown in Figure 1(a), the hinge loss does not approximate the 0–1 loss adequately. Use of a suboptimal approximation could compromise the performance of the estimated marker combinations. Next, in simulation studies, we include the weighted support vector machine estimator as a comparison estimator. We also assess the impact of different choices of weights relative to the outcome-dependent weight adopted in Zhao et al. (2012).

3. Simulation

In this section, we investigate the performance of the proposed estimator that minimizes the penalized weighted sum of ramp loss for treatment selection (W-RAMP). For three different simulation settings of 1:1 randomized trial, we study two common kernels for combining two biomarkers X₁ and X₂: the linear kernel for finding linear marker combinations and the RBF kernel for identifying nonlinear combinations. For each simulation setting, we consider the treatment/disease burden ratio δ = 0 and 0.01, and evaluate four different sets of weights: a) the case-only weights (W₁); b) the control-only weights (W₂); c) the average case+control weights (W₃); and d) the double-robustness weights (W₄). Performance of the W-RAMP estimators is compared with the common linear logistic regression model and the weighted support vector machine (W-SVM) estimators described in Section 2.5. In the linear logistic regression, the risk of Y is modeled as a function of the main effect for treatment status and for each biomarker, as well as the interaction between treatment status and each biomarker. This is also the risk model used for constructing the double-robustness weights. For comparison, we also applied the genetic algorithm (W-GENOUD) to find linear marker combinations that minimize the weighted sum of 0–1 loss (4) as did in Zhang et al. (2012a).

In each Monte Carlo simulation, a training sample of size n = 100 is generated; 5-fold cross-validation is used to identify the optimal tuning parameter λ_n and γ (for RBF kernel) within a range of 0 to 5 after ${\sum }_{i=1}^n\mid W_i\mid /n$ is scaled to be 1; a treatment-selection rule Â(X) is then estimated from the training sample using the selected tuning parameter. To evaluate the performance of the estimated rule, a test set of n = 100, 000 is generated in each simulation, based on which we estimate θ with ${\sum }_{i=1}^n(1-T_i)\times Y_i\times \left\{1-\widehat{A}({\mathit{X}}_i)\right\}/n_0+{\sum }_{i=1}^n{T}_i\times Y_i\times \widehat{A}({\mathit{X}}_i)/n_1+\delta \times {\sum }_{i=1}^n\widehat{A}({\mathit{X}}_i)/n$. Distribution of the test set performance over 500 Monte-Carlo simulations is evaluated. For ease of comparison, here we present the percent reduction in θ using a marker-based rule compared to the optimal treatment strategy in the absence of marker information. The latter is defined as treating all if the difference in disease prevalence between the untreated and the treated is larger than δ, or treating none otherwise.

Setting 1 includes two sub-settings. In the first sub-setting (1A), we simulate two biomarkers (X₁, X₂) from a bivariate normal distribution with mean 0, variance 1 each, and correlation 0.2. Risk of Y conditional on X₁, X₂ and T follows a linear logistic model logitP (Y = 1|X₁, X₂, T) = −1.6 − X₁ − X₂ − T × (2.5 + 2.5X₁ + 2.5X₂). In the second sub-setting (1B), 10% outliers are added to the data, where the outliers consist of independent markers X₁, X₂ each with mean 2 and variance 2, with the risk of Y conditional on X₁, X₂ and T following a logistic model $\text{logit}P(Y=1\mid X_1,X_2,T)=2+1.1X_1^3+1.1X_2^3-T\times (1.3X_1^2+1.3X_2^2+1.3X_1{X}_2)$. Disease prevalences among untreated and treated are 0.244 and 0.236 respectively for setting 1A and 0.318 and 0.307 respectively for setting 1B.

Setting 2 also includes two sub-settings. In the first sub-setting (2A), we simulate two biomarkers (X₁, X₂) from a bivariate normal distribution with mean 0, variance 1 each, and correlation 0.2. Risk of Y conditional on X₁, X₂ and T follows a logistic model $\text{logit}P(Y=1\mid X_1,X_2,T)=-1.5+0.2X_1-0.2X_2+T\times (-3-X_1-X_2+X_1^2+X_2^2)$. In the second sub-setting (2B), 10% outliers are added where the outliers consist of independent markers X₁, X₂ each with mean 2 and variance 1.5, with the risk of Y conditional on X₁, X₂ and T following a logistic model $\text{logit}P(Y=1\mid X_1,X_2,T)=-1.5+0.2X_1-0.2X_2+T\times (-3-X_1-X_2-0.1X_1^2-0.1X_2^2+0.4X_1^3+0.4X_2^3)$. Disease prevalences among untreated and treated are 0.185 and 0.175 respectively for setting 2A and 0.192 and 0.190 respectively for setting 2B.

In setting 3, we simulate two independent biomarkers (X₁, X₂) each from a mixture of 90% uniform(−1,1) and 10% uniform (0,2). Risk of Y conditional on X₁, X₂ and T follows logitP(Y = 1|X₁, X₂, T) = −1+T ×[0.5 − 6X₁X₂ × I {(X₁ > 0&X₂ > 0)|(X₁ < 0&X₂ < 0)}]. Disease prevalences among untreated and treated are 0.269 and 0.256 respectively.

Tables 1 shows simulation results for δ = 0. In setting 1A, where the linear logistic model holds, the marker combination based on the linear logistic model achieves the largest treatment-selection benefit with the highest precision. The performance of the linear W-RAMP estimator is inferior to the linear logistic model, but significantly better than the linear W-SVM estimator (p-value≤ 0.001 comparing θ based on the paired t-test for each set of weights). Moreover, the performance of the linear W-SVM estimator is sensitive to the choice of weights, with the double-robustness weights greatly outperforming the other three sets of weights including the case-only weights. In contrast, the performance of the linear W-RAMP estimator is fairly insensitive to the choice of weights. When the RBF kernel is used, the double-robustness and the case-only weights work best for both the W-RAMP and the W-SVM estimators; the W-RAMP estimator significantly outperforms the W-SVM estimator with the double-robustness weights (p-value=0.008 comparing θ based on the paired t-test) while the two have comparable performance with respect to the other three weights.

Table 1.

Percent reduction in θ using marker-based rule compared to the best treatment strategy in the absence of marker information, for δ = 0, training size n = 100. Five-fold CV is used for selecting tuning parameters.

Scenario	ρ0	ρ1	Method	Weights for Ramp and SVM
				Case-only		Control-only		CCa		DRb
				Mean	SE	Mean	SE	Mean	SE	Mean	SE
I-A	0.244	0.236	Linear logistic	21.15	(0.25)
			W-GENOUD, Linear	10.81	(0.34)	3.89	(0.34)	8.31	(0.34)	18.52	(0.34)
			W-Ramp, Linear	14.12	(0.43)	13.90	(0.42)	14.94	(0.42)	14.73	(0.44)
			W-SVM, Linear	7.09	(0.44)	0.98	(0.25)	2.40	(0.29)	12.08	(0.48)
			W-Ramp, RBF	8.80	(0.38)	5.59	(0.33)	6.72	(0.31)	11.01	(0.39)
			W-SVM, RBF	8.78	(0.39)	6.06	(0.34)	6.66	(0.32)	9.82	(0.37)
I-B	0.318	0.307	Linear logistic	1.56	(0.35)
			W-GENOUD, Linear	4.71	(0.37)	2.15	(0.37)	4.38	(0.37)	4.95	(0.37)
			W-Ramp, Linear	5.23	(0.35)	4.59	(0.36)	5.11	(0.38)	5.19	(0.36)
			W-SVM, Linear	−0.58	(0.16)	−0.09	(0.18)	−0.59	(0.16)	−0.43	(0.17)
			W-Ramp, RBF	4.53	(0.27)	3.12	(0.24)	4.35	(0.24)	5.04	(0.26)
			W-SVM, RBF	4.33	(0.26)	3.10	(0.24)	4.36	(0.24)	4.63	(0.25)
II-A	0.185	0.175	Linear logistic	30.81	(0.65)
			W-GENOUD, Linear	31.14	(0.53)	16.03	(0.53)	26.92	(0.53)	33.22	(0.53)
			W-Ramp, Linear	31.19	(0.67)	30.41	(0.65)	32.27	(0.62)	31.44	(0.67)
			W-SVM, Linear	24.17	(0.83)	12.07	(0.74)	17.43	(0.77)	23.45	(0.83)
			W-Ramp, RBF	32.62	(0.68)	23.30	(0.7)	30.86	(0.67)	32.42	(0.69)
			W-SVM, RBF	32.47	(0.68)	22.75	(0.71)	30.45	(0.68)	32.64	(0.66)
II-B	0.192	0.19	Linear logistic	15.57	(0.68)
			W-GENOUD, Linear	21.99	(0.53)	10.85	(0.53)	19.72	(0.53)	23.49	(0.53)
			W-Ramp, Linear	21.06	(0.57)	19.30	(0.62)	21.08	(0.59)	21.77	(0.58)
			W-SVM, Linear	12.76	(0.62)	7.55	(0.53)	9.12	(0.54)	12.51	(0.60)
			W-Ramp, RBF	31.31	(0.64)	23.94	(0.68)	29.47	(0.63)	32.62	(0.61)
			W-SVM, RBF	31.46	(0.64)	23.81	(0.67)	29.55	(0.64)	32.11	(0.60)
III	0.269	0.256	Linear logistic	−0.54	(0.23)
			W-GENOUD, Linear	1.94	(0.25)	−0.06	(0.25)	1.79	(0.25)	2.31	(0.25)
			W-Ramp, Linear	1.19	(0.22)	0.10	(0.21)	0.76	(0.22)	1.16	(0.22)
			W-SVM, Linear	−0.24	(0.19)	−1.01	(0.21)	−1.20	(0.18)	−0.87	(0.18)
			W-Ramp, RBF	5.19	(0.31)	1.53	(0.25)	3.38	(0.26)	4.04	(0.28)
			W-SVM, RBF	5.17	(0.31)	1.48	(0.26)	3.39	(0.26)	4.28	(0.26)

CC^a: Case-control weights; DR^b: double-robustness weights

With outliers added (settings 1B), linear marker combinations identified by the W-RAMP estimator have much improved performance compared to either the linear logistic model or the W-SVM. Again, the performance of the W-RAMP is insensitive to the choice of weights. Nonlinear marker combinations identified using the RBF kernel have improved performance compared to linear marker combinations for W-SVM, with the performance comparable between the W-RAMP and the W-SVM.

In setting 2A, where interactions exist between treatment and polynomial marker effect, the linear W-RAMP estimator has a sightly better treatment-selection performance compared to the linear logistic model, whereas the linear W-SVM estimator has the worst performance. With the RBF kernel, both the W-RAMP and the W-SVM estimators have slightly improved performance compared to linear marker combinations, especially for the case-only weights and the double-robustness weights. The performance is comparable between the W-RAMP and the W-SVM. When 10% outliers are added to the data (setting 2B), among linear marker combinations, the W-RAMP estimator significantly outperforms the linear logistic model or the linear W-SVM. Using the RBF kernel allowing for nonlinear effect leads to a large improvement in treatment-selection benefit compared to the linear kernel with the performance comparable between the W-RAMP and the W-SVM.

In setting 3, where the optimal marker combination for treatment selection is highly nonlinear, the linear logistic model and the linear W-SVM lead to marker combinations that perform worse than the strategy of treating all. The linear W-RAMP estimator, in contrast, still has better performance compared to treating all. The RBF kernel improves the performance over linear kernel for both the W-RAMP and the W-SVM estimators with performance similar between the two.

For finding linear combinations, the relative performance of the W-RAMP and the W-GENOUD varies with the weights and settings, but overall the two seem to have comparable performance. Computation times for W-GENOUD, W-RAMP, and W-SVM are around 4.6, 0.3, and 0.1 sec respectively for a training size of 100.

Tables 2 shows simulation results for δ = 0.01. The pattern for comparing different estimators is fairly similar to that in Table 1. In general, linear marker combinations derived from the proposed W-RAMP estimator have greater performance compared to those from the linear W-SVM. With the presence of nonlinear effect or outlying observations, using a nonlinear kernel such as the RBF kernel improves the performance of the W-RAMP or the W-SVM. The performance of the two algorithms using the RBF kernel are comparable in various simulations when tuning is performed using 5-fold CV.

Table 2.

Percent reduction in θ using marker-based rule compared to the best treatment strategy in the absence of marker information, for δ = 0.01 and training size n = 100. Five-fold CV is used for selecting tuning parameters.

Scenario	ρ0	ρ1	Method	Weights for Ramp and SVM
				Case-only		Control-only		CCa		DRb
				Mean	SE	Mean	SE	Mean	SE	Mean	SE
I-A	0.244	0.246	Linear logistic	17.32	(0.37)
			W-GENOUD, Linear	7.68	(0.37)	4.19	(0.37)	7.64	(0.37)	17.24	(0.37)
			W-Ramp, Linear	11.53	(0.41)	14.94	(0.40)	14.69	(0.40)	13.72	(0.41)
			W-SVM, Linear	6.24	(0.40)	1.41	(0.21)	3.10	(0.28)	10.96	(0.43)
			W-Ramp, RBF	5.78	(0.39)	6.88	(0.32)	6.49	(0.29)	9.10	(0.36)
			W-SVM, RBF	5.62	(0.39)	7.14	(0.29)	6.08	(0.28)	8.48	(0.34)
I-B	0.318	0.317	Linear logistic	2.60	(0.27)
			W-GENOUD, Linear	3.92	(0.34)	2.83	(0.34)	4.86	(0.34)	5.61	(0.34)
			W-Ramp, Linear	4.60	(0.32)	5.99	(0.34)	6.09	(0.34)	5.76	(0.34)
			W-SVM, Linear	0.77	(0.15)	1.28	(0.18)	0.97	(0.15)	0.93	(0.14)
			W-Ramp, RBF	3.84	(0.27)	5.10	(0.23)	5.15	(0.22)	5.53	(0.24)
			W-SVM, RBF	3.88	(0.27)	5.18	(0.21)	5.26	(0.22)	5.24	(0.22)
II-A	0.185	0.185	Linear logistic	26.71	(0.60)
			W-GENOUD, Linear	26.19	(0.53)	15.50	(0.53)	25.70	(0.53)	32.13	(0.53)
			W-Ramp, Linear	28.90	(0.61)	28.92	(0.63)	31.65	(0.58)	30.80	(0.60)
			W-SVM, Linear	23.35	(0.76)	12.94	(0.69)	19.09	(0.72)	23.25	(0.75)
			W-Ramp, RBF	28.54	(0.69)	22.76	(0.62)	28.58	(0.61)	31.34	(0.59)
			W-SVM, RBF	29.08	(0.71)	23.14	(0.60)	28.27	(0.62)	30.57	(0.62)
II-B	0.192	0.2	Linear logistic	12.89	(0.59)
			W-GENOUD, Linear	15.43	(0.52)	7.09	(0.52)	15.50	(0.52)	20.37	(0.52)
			W-Ramp, Linear	15.64	(0.58)	15.63	(0.58)	18.09	(0.56)	18.14	(0.54)
			W-SVM, Linear	9.28	(0.57)	4.35	(0.52)	6.75	(0.51)	10.14	(0.59)
			W-Ramp, RBF	24.74	(0.66)	19.66	(0.59)	25.76	(0.58)	28.04	(0.60)
			W-SVM, RBF	25.04	(0.66)	21.02	(0.57)	25.78	(0.57)	28.21	(0.58)
III	0.269	0.266	Linear logistic	−0.03	(0.11)
			W-GENOUD, Linear	3.97	(0.25)	2.38	(0.25)	3.96	(0.25)	4.20	(0.25)
			W-Ramp, Linear	2.41	(0.24)	1.97	(0.23)	2.32	(0.22)	2.48	(0.22)
			W-SVM, Linear	0.90	(0.17)	0.55	(0.20)	0.78	(0.17)	0.63	(0.16)
			W-Ramp, RBF	6.07	(0.37)	4.19	(0.32)	5.74	(0.27)	6.05	(0.27)
			W-SVM, RBF	5.31	(0.33)	3.26	(0.25)	5.80	(0.26)	5.97	(0.26)

CC^a: Case-control weights; DR^b: double-robustness weights

In Supplementary Tables 1 and 2 we show additional simulation results where an independent tuning set of size 1000 is generated in each Monte Carlo simulation, reflecting an “ideal” setting where there is little uncertainty in choosing tuning parameters. Under this kind of “ideal” tuning, appreciable improvement in performance of both the W-RAMP and the W-SVM are observed compared to 5-fold CV for tuning, with the W-RAMP in general performing significantly better than the W-SVM using both the linear and the RBF kernel. The potential of using better tuning methods to improve the performance of the W-RAMP merits further investigation.

4. Data Example

We illustrate the proposed estimators of marker combinations with a real example from an HIV vaccine study. As a prevention measure, vaccines typically have low cost related to treatment, thus we set δ = 0. The example comes from the RV144 Thailand HIV vaccine trial, the first HIV vaccine trial that demonstrates a positive vaccine efficacy in preventing HIV infection (with an estimated hazard ratio of vaccine vs placebo of 31.2% and p-value 0.04). The trial included 16,402 participants aged 18–30 who were 1:1 randomized into a vaccine and a placebo arm (Rerks-Ngarm et al., 2009).

A followup RV144 host-genetic study was conducted to investigate the effect of genotypes of Fc receptor gene on vaccine efficacy. Overall 148 single nucleotide polymorphisms (SNPs) covering five Fc-γ receptor genes Fc-γR2a, Fc-γR2b, Fc-γR2c, Fc-γR3a, and Fc-γR3b, and 42 SNPs covering the Fc-α receptor gene were genotyped on 125 cases (74 placebo recipients and 51 vaccine recipients), and 225 controls (20 placebo recipients and 205 vaccine recipients). After exclusion of SNPs with minor allele frequency less than 5% and SNPs highly correlated with one another (with Pearson correlation greater than 0.80), four SNPs, each categorized into a binary variable, were identified to have significant interactions with the vaccination status based on the univariate case-only analysis (Li et al., 2014).

Here we explore combinations of the four SNPs to recommend the use of vaccine in order to minimize the rate of HIV infection in the population. We consider the following five treatment strategies: (i) the strategy of not vaccinating anyone; (ii) the strategy of vaccinating everyone; (iii) the strategy of selective vaccinating based on a linear logistic model selected using the Akaike Information Criteria (AIC) defined as 2× number of parameters −2×log(likelihood), where the predictors considered are the main effects for treatment and for each SNP and the interaction between treatment and each SNP; and iv) the W-RAMP estimator for four different set of weights (where the linear logistic risk model as in (iii) is used to construct the double-robustness weights); and (v) the W-SVM estimator. For the W-RAMP and the W-SVM, we consider both the linear and the IBS kernel, and use 5-fold CV for tuning parameter selection. Based on the entire dataset, the tuning parameter identified, and corresponding estimated treatment-selection rules using the linear W-RAMP and the linear W-SVM are presented (Web supplementary Table 3). Also presented is the estimated treatment-selection rule based on the logistic regression model.

In Table 3, we show estimated performance of these different strategies for deriving treatment-selection rules. Naive estimates of θ are obtained by applying the treatment-selection rule estimated using the full dataset to the same data. Moreover, a random cross-validation procedure is performed for the computation of θ correcting for overfitting bias. In particular, the data are randomly split into five folds stratified on the disease and the treatment status, 4 folds for training and the remaining 1 fold for testing. Based on each random training subset, a 5-fold CV is performed to select the tuning parameter specific for the subset, which is then used to derive a treatment-selection rule using the random training subset; the estimated rule is then applied to the random test subset to estimate θ. The procedure is repeated 100 times with the average θ computed. In Table 3, we present both the naive and the cross-validated estimates of θ. Percentile bootstrap confidence intervals are provided for those measures. In the bootstrap procedure, 100 resamplings are performed stratified on the disease and the treatment status; the procedure of computing the naive and the cross-validated θ estimates is then applied to each resampled data.

Table 3.

Estimates of θ/1000 and percentile bootstrap CIs for different methods of deriving SNP combinations in the RV144 host-genetics study.

Method	Weight	Naive		Cross-validated
		Est	95% CI	Est	95% CI
Treat None		9.26	(7.45, 10.87)	8.68★	(6.99, 11.77)
Treat All		6.41	(4.94, 8.03)	6.57	(4.94, 7.82)
Linear Logistic		6.14	(4.50, 7.58)	6.80	(5.38, 7.85)
W-RAMP, Linear	W1	4.96	(3.79, 5.88)	5.74	(4.02, 6.71)
	W2	8.75	(6.40, 10.65)	8.74	(6.88, 9.91)
	W3	8.62	(6.79, 10.84)	9.08	(7.01, 10.42)
	W4	5.49	(4.70, 7.32)	6.92	(5.15, 7.58)
W-SVM, Linear	W1	4.96	(3.98, 6.41)	6.53	(4.25, 7.15)
	W2	9.41	(6.00, 9.80)	9.06	(6.80, 9.98)
	W3	9.41	(5.67, 9.80)	9.04	(6.73, 9.97)
	W4	6.14	(4.96, 6.41)	6.63	(4.99, 7.73)
W-RAMP, IBS	W1	4.96	(3.79, 6.01)	5.68	(4.11, 6.75)
	W2	8.75	(6.79, 10.72)	9.14	(7.07, 10.34)
	W3	9.41	(6.66, 11.17)	9.18	(7.04, 10.41)
	W4	6.14	(4.84, 7.72)	7.01	(5.26, 7.60)
W-SVM, IBS	W1	5.75	(4.11, 6.41)	6.54	(4.25, 7.17)
	W2	9.41	(6.00, 9.80)	9.07	(6.78, 9.82)
	W3	9.41	(6.00, 9.80)	9.04	(6.74, 9.96)
	W4	6.14	(4.96, 6.41)	6.61	(4.97, 7.73)

^★net benefit (Vickers et al., 2007) of a treatment-selection rule equals θ of treating none (8.68/1000) minus θ of the rule. For example, net benefit of treating all = (8.68−6.57)/1000=2.11/1000; net benefit of W-RAMP, IBS = (8.68−5.68)/1000=3/1000. Bootstrap is performed on the efficacy trial data stratified on the treatment status for “treat none” and “treat all” and stratified on the disease and the treatment status for other algorithms.

From Table 3, the strategy of treating none and treating all lead to an estimated HIV infection rate of 9.26 and 6.41 per 1000 persons respectively, consistent with the positive vaccine efficacy we observed in the RV144 trial. Severe over-optimism is observed in naive estimates of marker-based treatment-selection performance. For most methods, the naive estimates show reduced HIV infection rate compared to the treating all strategy. After using cross-validation procedure to correct for the overfitting bias, the proposed W-RAMP estimator with either the linear or the IBS kernel and the case-only weights lead to reduced HIV infection rates: 5.74 per 1000 persons (95% CI: 4.02 to 6.71) for linear and 5.68 per 1000 persons (95% CI: 4.11 to 6.75) for IBS, compared to 6.57 per 1000 persons (95% CI: 4.94 to 7.82) for the treating all strategy. For comparison, the logistic model selected by AIC has θ estimate 6.80 (95% CI: 5.41 to 7.99) per 1000 persons, which is 3.5% above treating-all; the best W-SVM estimators (with the linear or IBS kernel and the case-only weights) have θ values fairly close to treating all. Using the W-RAMP with the case-only weights, 58.2% (95% CI: 45.8% to 73.8%) and 58.6% (95% CI: 44.2% to 73.3%) subjects will be recommended for vaccination based on cross-validation, using the linear and the IBS kernel respectively.

5. Discussion

We proposed a general framework for deriving the optimal treatment-selection strategy using biomarkers, towards the goal of minimizing the total disease and treatment burden to the population. The proposed estimation method has an attribute similar to the work of Zhang et al. (2012a) and Zhao et al. (2012) in that the optimal marker combination is identified through directly minimizing an unbiased estimate of the criterion function, and thus is more robust to model misspecification than standard regression-based methods.

Direct minimization of an estimated criterion function poses high computational challenges due to the involvement of a non-convex 0–1 loss function. To address this issue, we proposed the use of the difference of convex functions algorithm to minimize a penalized weighted sum of ramp loss. The ramp loss serves as an approximation to the 0–1 loss. It is demonstrated to 1) be a more precise approximation than the hinge-loss approximation underlying the standard support vector machine methods; and 2) lead to better or comparable estimators of marker combinations in various scenarios. For binary disease outcomes, we found the performance of the ramp estimator to be relatively insensitive to the choice of weights, with the case-only and the double-robustness weights performing best overall, and we therefore recommend the use of the two kinds of weights in practice. The good performance of the case-only weights is appealing when the criterion function to be optimized is the average disease rate, since the computation of the case-only weights in this scenario requires only measurements of markers among case samples and is thus cost-effective under limited resources.

As mentioned in Section 2.1, unlike the case of δ = 0, in the presence of positive δ, the optimal treatment-selection rule can not be represented as a simple function of the main treatment effect and the marker-treatment interaction in the disease risk model. This makes the modeling of the marker combination more challenging and calls for greater flexibility in estimation methods. Our proposed kernel-estimator is appealing given its ability to allow for flexible modeling of marker combinations. In practice, it is necessary to put the disease burden and the treatment burden on the same scale to determine δ. For example, as in Rapsomaniki et al. (2012), if one can associate a monetary cost with the reduction in the rate of the targeted disease through treatment, and a monetary cost with treatment (including the cost of conducting the procedure and the cost due to secondary events), then δ can be computed as the rate of the latter relative to the former. In practice, a series of δ might also be chosen for sensitivity analysis. More detailed investigation is warranted for evaluating the performance of our estimators in the presence of positive cost ratios.

Finally, note that Janes et al. (2013) considers a more general decision-theoretical approach that allows the burden of disease and treatment to vary with biomarkers. The framework in Vickers et al. (2007) is a special case of this general formulation assuming these burdens do not depend on the marker value. The method developed in the paper, however, can be readily extended to address the general situation through specification of utility parameters that character the association between biomarkers and the disease and treatment burdens.

6. Web Supplementary Appendix

Web Appendices and Tables referenced in Sections 2, 2.1–2.5, 3, and 4, and example R code for implementing the proposed method are available with this paper at the Biometrics website on Wiley Online Library.