A free plate model can predict guided modes propagating in tubular bone-mimicking phantoms

Abstract

The goal of this work was to show that a non-absorbing free plate model can predict with a reasonable accuracy guided modes measured in bone-mimicking phantoms that have circular cross-section. Experiments were carried out on uncoated and coated phantoms using a clinical axial transmission setup. Adjustment of the plate model to the experimental data yielded estimates for the waveguide characteristics (thickness, bulk wave velocities). Fair agreement was achieved over a frequency range of 0.4 to 1.6 MHz. A lower accuracy observed for the thinnest bone-mimicking phantoms was caused by limitations in the wave number measurements rather than by the model itself.

1. Introduction

Assessment of osteoporotic fracture risk is still largely unpredictable. Cortical bone is recognized as playing a key role in the mechanical strength of bone. Recent quantitative ultrasound (QUS) approaches based on guided waves seem promising for the assessment of cortical bone.¹ A specific appealing aspect is the ability of guided waves to account for material properties or structure of the waveguide.² The cortical thinning and the porosity increasing observed with aging and in the case of increased fracture risk, change the propagation characteristics of the guided modes. Thus, applied to long bones such as the radius or tibia, guided waves based approaches would be expected to provide estimates of important bone quality factors like cortical thickness and stiffness which cannot easily be captured by X-ray densitometry techniques.^3–5 Measurements of guided waves in long bones have shown some diagnostic promises ex vivo^6,7 and in vivo.^8–10

We assume that identifying the true structural and material properties of cortical bone, will provide a more reliable estimate of the bone quality and fracture risk than currently available clinical techniques. Toward this goal, several model-based approaches are being developed in which properties of cortical bone are retrieved from spectral analysis of measured guided waves by solving an inverse problem.^3–5

Accuracy of estimates for bone characteristics depends on the chosen model for ultrasound propagation in the cortical bone (which represents the “forward problem”) and on its ability to account for the complexity of the waveguide, including not only the elastic anisotropy, the tubular shape of bone and the presence of soft tissues, but also a variable thickness, irregular geometry, inhomogeneity, and absorption, for example. In previous investigations, more or less complex waveguide models, such as free plate⁵ and tube models,^3,4,11 or bilayer models,^12–14 were applied and found to conform fairly well to experimental dispersion curves of guided modes in bone mimicking phantoms^3,5,12,14 and in ex vivo bone specimens.^3–5,13 On the other hand, more complex models involving more physical parameters would make the solution of the inverse problem more difficult to find. These considerations have implications regarding the choice of the model. The question arises as to whether a simple free plate model is relevant to tube-like bones covered with a layer of soft tissue. The purpose of this letter is to explore the extent to which the physical properties of bone mimicking waveguides with dimension typical of those of human long bones can be retrieved with a reasonable accuracy using a free plate model. The advantage of performing measurements on bone mimicking waveguides rather than bone samples is that the true values of the characteristics of the waveguides are known. This facilitates assessment of models and of the inverse procedure. The disadvantage of performing measurements on phantoms, of course, is that they only approximate the true bone structure. Plate or tube phantoms utilized in the present investigation, have previously been used and their usefulness in developing approaches for bone quantitative ultrasound has been demonstrated.^3,5,12

2. Materials and methods

2.1. Samples

Experiments were carried out on custom-made tubular bone mimicking phantoms made of epoxy mixed with aluminum oxide powder.^14,15 All tubes had a length of 120 mm and a transverse circular cross-section with an external radius of curvature of 8 mm. Five wall thicknesses from 1 to 5 mm [known to an accuracy of ±0.05 mm (Ref. 14)] were used (Fig. 1). These dimensions are typical of those encountered in the human radius. Reference values for mass density ρ is 2.3 g cm⁻³ and for the shear and compression bulk velocities of the material, c_T and c_L, respectively, are 1550 and 3000 m s⁻¹ (Ref. 14). Absorption at 1 MHz was approximately 10 dB cm⁻¹ (unpublished data). These phantoms were measured first without coating and then with a custom-made 2.5 mm-thick soft tissue mimicking coating (Fig. 1) consisting of a mixture of silicone rubber and glycerol with a bulk compression velocity (c_L) of 1250 m s⁻¹ and a mass density of 1.1 g cm⁻³ (Ref. 14).

Fig. 1.

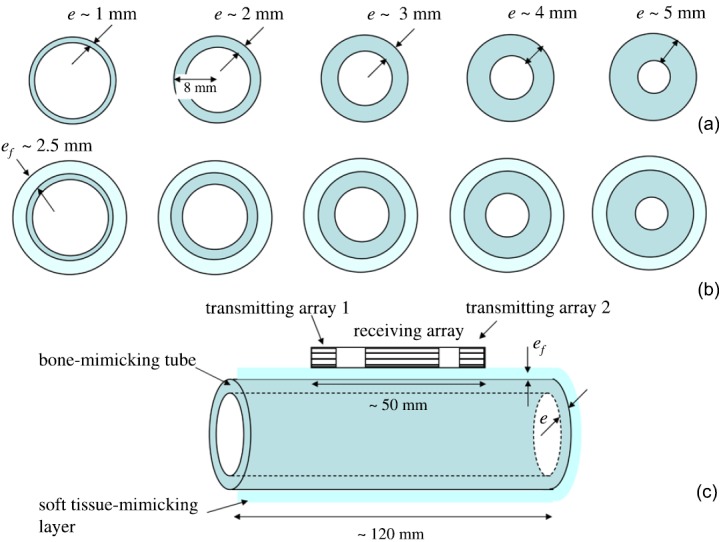
(Color online) (a) Uncoated and (b) coated bone mimicking phantoms, and (c) geometry of the experimental set up.

2.2. Ultrasonic method

Measurements were done using the axial transmission technique¹⁶ with a custom-made probe (Vermon, Tours, France) consisting of a 24 element receiving array placed between two arrays of five transmitters each.^5,17 The probe, aligned with the axis of the tube, was in contact with the phantom (Fig. 1). Ultrasonic gel was used for coupling. A custom-made electronic device (Althaïs, Tours, France) was used to transmit ultrasonic pulses (center frequency, 1 MHz, −6 dB; frequency bandwidth, 800 kHz) and to record the received ultrasound signals. An ensemble of 240 rf signals corresponding to all possible pairs of transmitter/receiver elements were digitized (12 bits, 20 MHz, 1024 samples) and time averaged (16 times).

The experimental dispersion curves, representing the frequency-dependent wave numbers of guided modes propagating in the waveguide, were extracted using a method described in our previous publications.^16,17 Briefly, (1) the rf signals were Fourier transformed; (2) a singular value decomposition was applied to the response matrix at each frequency; (3) enhancement of signal-to-noise ratio was achieved by eliminating the singular vectors associated with the lowest singular values; (4) the projection of a testing vector (an attenuated spatial plane wave with a complex wave number¹⁶) onto the singular vector basis yielded the so-called Norm function, whose maxima correspond to the wave numbers of the guided modes. The bidirectional correction, combining the data acquired from the two transmitting arrays, was applied to the measurements. This correction, initially proposed for the first arriving signal to compensate for the lack of parallelism between the probe and the measured sample surface caused by uneven soft tissues thickness, has been generalized to guided mode measurements.¹⁷

The data obtained with the uncoated and coated 4 mm-thick tube are presented as representative examples of the results. First, one out of ten repeated measured Norm functions is displayed in Figs. 2(a) and 2(b). The detected wave numbers, corresponding to the maxima of the Norm function, are shown with dots. The same wave number values are reported in Figs. 3(d) and 3(i). In order to illustrate measurement repeatability, the wave numbers corresponding to ten measurements are shown in Figs. 2(c) and 2(d). The standard deviation of the wave numbers, observed at a fixed frequency, is on the order of 0.1 rad mm⁻¹ for the uncoated tube and 0.15 rad mm⁻¹ for the coated tube. Similar standard deviation values are observed for the other experiments.

Fig. 2.

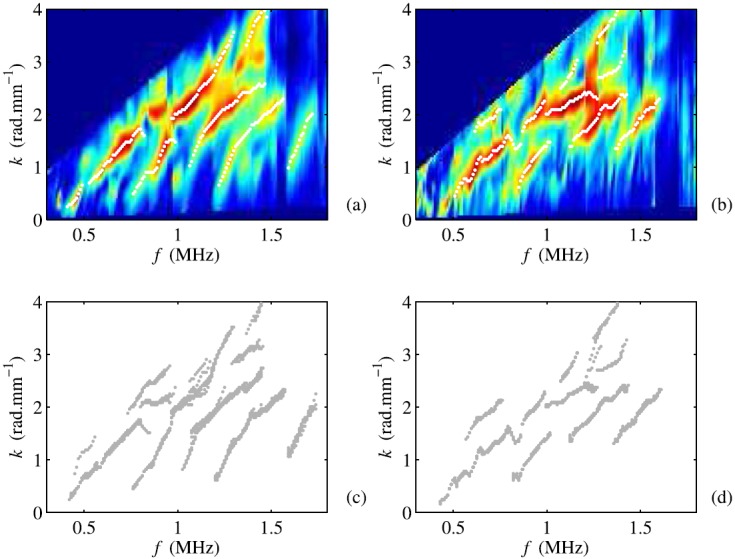
(Color online) Representative example for the Norm function computed for the (a) uncoated and (b) coated 4 mm-thick tube with the associated extracted wave numbers (dots). The data shows one out of ten repeated measurements. The wave numbers of the ten measurements are shown in (c) and (d). Similar standard deviation values are observed for the other experiments. Because of interference with the probe front, wave numbers associated with phase velocities smaller than 2 mm μs⁻¹ are not represented.

Fig. 3.

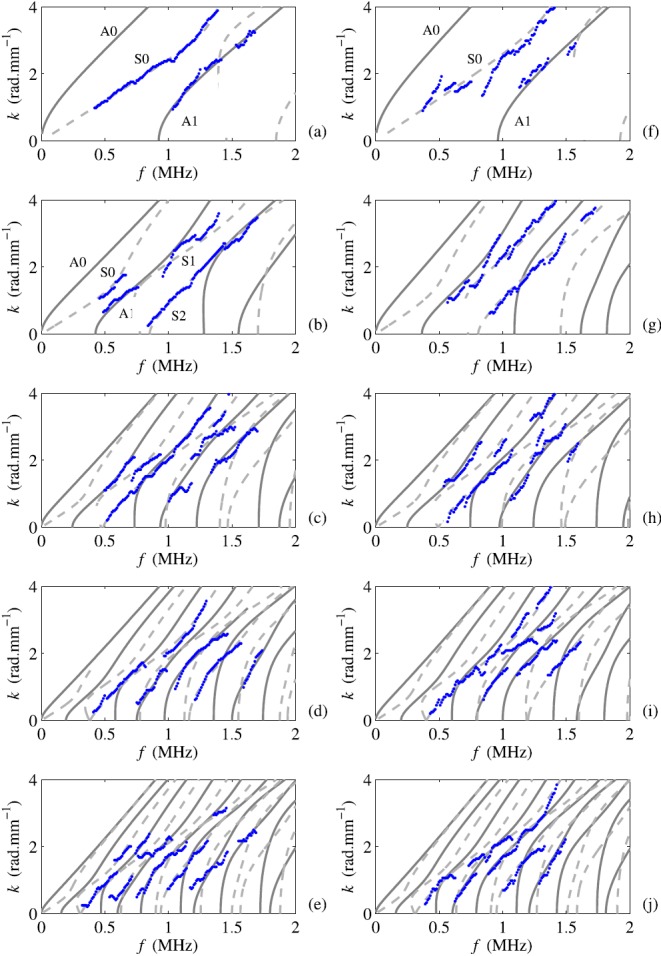
(Color online) Representative examples of experimental wave numbers for one out of ten repeated measurements (dots) are plotted together with the best fitting dispersion curves computed from a non-absorbing free isotropic plate model. Antisymmetric and symmetric modes are represented as continuous and dashed lines, respectively. The results for uncoated phantoms are represented in the left panels numbered (a) to (e) and for coated phantoms in the right panels numbered (f) to (j). Tubes with increasing thickness from 1 to 4 mm in step of 1 mm are represented from top to bottom. The estimated waveguide characteristics are shown in Table 1.

Identification of the waveguide characteristics was achieved by fitting a model to the experimental dispersion branches. For simplicity, a non-absorbing free isotropic plate model, i.e., the Lamb model, was considered here. Indeed, waves guided by a hollow cylinder fall into different classes according to the symmetry of the displacement, exactly as plate modes fall into A and S modes:² longitudinal waves (axially symmetric), flexural waves (non axially symmetric), and torsional wave modes. The third class (torsional) is not considered here with the excitation source used. While the non-axisymmetric sources used in axial transmission are supposed to generate both longitudinal waves and flexural components, mainly longitudinal waves have been observed in previous experimental reports.⁵ We believe that this may be because of the fact that transducer height was large in comparison with the array pitch. Moreover, except for a small frequency × thickness product,³ longitudinal branches are known to coincide with Lamb branches.² Thus, experimental dispersion branches measured on the tubular phantoms, were logically compared with Lamb dispersion curves.

The Lamb dispersion curves are determined by plate thickness, e, and bulk velocities, c_L and c_T. The theoretical dispersion curves, labeled A0 to An and S0 to Sn, depending on their symmetry and order with respect to the increasing frequency are shown in Fig. 2 for plates with a thickness of 1 to 5 mm. The raw data were first grouped into experimental trajectories, and then each trajectory was associated with a specific Lamb curve.⁵ For example, eight theoretical guided modes and four experimental branches (associated with S0, A1, S1, and S2) can be observed in Fig. 3(b) (uncoated phantom of reference thickness e = 2 mm). The A0 and S0 modes, overlapping with modes propagating in the probe front layer,^5,16 cannot be properly evaluated. Bulk velocities and thickness of the phantom were determined by minimization of the error function χ defined by

$$\chi =\sum _{n=1}^N\sum _i{(f_{\hspace{0.17em}\text{exp}\hspace{0.17em}}^n(k_i)-f_{\text{calc}}^n(k_i))}^2,$$ (1)

with k the wave number, f^exp and f^calc the experimental and calculated frequencies, and n the mode label. A similar procedure has been described for an isotropic¹⁸ and a transverse isotropic material.⁵ Optimization was done using the inbuilt non-linear least-squares algorithm from MATLAB (The MathWorks Inc., Natick, MA) using Optimization Toolbox 6.0. This three-step procedure (data acquisition, dispersion curve extraction and identification of the wave guide characteristics) was repeated ten times for each phantom in order to assess measurement precision (given by the standard deviation of the ten consecutive measurements). The measurement error (accuracy) was given by the difference between measured values and the reference value. Average accuracy was computed as the root-mean-square deviation, i.e., standard deviation of the differences between the measured and reference values.

3. Results and discussion

Figure 3 shows experimental wave numbers and theoretical modes, calculated with the best fitting model, for uncoated [Figs. 3(a)–3(e)] and coated phantoms [Figs. 3(f)–3(j)] for one of the ten measurements. Although the material was highly dissipative (∼10 dB cm⁻¹), experimental wave numbers were measured. Overall, a fair agreement in the frequency dependence of the experimental wave numbers and theoretical Lamb dispersion curves is evident over a range at 0.4 to 1.6 MHz: in all tested cases, the experimental branches could be associated with a Lamb dispersion curve computed using the non-absorbing isotropic free plate model, suggesting that, in the considered frequency bandwidth, the best fitting model may be considered as a reasonable approximation for the phantoms under testing. These empirical results, taken collectively, suggest that guided mode wave numbers observed in the cortical bone mimicking phantoms are primarily determined by the thickness and stiffness of the material. The fair agreement observed for the coated tubes suggests that the presence of a soft tissue mimicking coating does not influence significantly the results. With our device, low wave number values, close to the cut-off frequencies, are measured. These wave numbers, associated with high values of the phase velocity, depend mainly on the waves propagating in the tube and are thus little influenced by the soft tissue-mimicking layer.¹²

The waveguide characteristics and accuracy errors obtained with the best fitting models are summarized in Table 1. Thickness was estimated with a fairly good average accuracy of 0.11 mm without coating and 0.21 mm with coating. Relative accuracy was defined as the ratio of the accuracy to the reference value. For the uncoated phantoms, the relative accuracy decreases from about 8% to 1.25% when the wall thickness increases. For the coated phantoms, it decreases from about 20% to 6% for increasing wall thickness. This better relative accuracy for thick tubes compared with thin tubes, can be explained by the fact that for thick waveguides higher order modes with a higher sensitivity to thickness can be measured (for the working frequency bandwidth considered).¹⁸

Table 1.

Estimated waveguide characteristics (mean ± SD) for uncoated and coated phantoms. The standard deviation (SD) was calculated from 10 measurements without repositioning. Values in parentheses correspond to accuracy.

eref (mm)	e (mm)	cL (ms−1)	cT (ms−1)
Uncoated phantoms
1.00	0.92 ± 0.02 (−0.08)	2680 ± 40 (−320)	1700 ± 20 (+150)
2.00	1.90 ± 0.02 (−0.10)	2950 ± 20 (−50)	1620 ± 10 (+70)
3.00	3.15 ± 0.02 (+0.15)	2950 ± 20 (−50)	1540 ± 20 (−10)
4.00	4.05 ± 0.06 (+0.05)	3040 ± 40 (+40)	1570 ± 20 (+20)
5.00	4.85 ± 0.06 (−0.15)	2910 ± 10 (−90)	1520 ± 20 (−30)
Coated phantoms
1.00 ± 0.05	0.80 ± 0.05 (−0.20)	2630 ± 80 (−370)	1540 ± 40 (−10)
2.00 ± 0.05	1.95 ± 0.05 (−0.05)	3150 ± 80 (+150)	1420 ± 40 (−130)
3.00 ± 0.05	3.20 ± 0.05 (+0.20)	3120 ± 80 (+120)	1590 ± 40 (+40)
4.00 ± 0.05	3.80 ± 0.1 (−0.20)	3010 ± 80 (+10)	1520 ± 40 (−30)
5.00 ± 0.05	4.70 ± 0.1 (−0.30)	2840 ± 80 (−160)	1490 ± 40 (−60)

Accuracy of the bulk velocities was on the average 150 m s⁻¹ (c_L, uncoated), 200 m s⁻¹ (c_L, uncoated), and approximately 75 m s⁻¹ for c_T (uncoated and coated). The largest measurement errors were observed for the thinnest tubes. In this case, only two modes, S0 and A1, were measured. While the A1 cutoff frequency, given by c_T/2e,² can be estimated, the value of c_T reached asymptotically by the modes in the high frequency range was, in contrast, not measurable in the frequency bandwidth used.¹⁸ It implies that the value of c_T derived from the ratio c_T/2e will be affected by the biased thickness estimate, which has already been mentioned above. Moreover, c_L was not correctly estimated because the wave numbers of the modes which are the most sensitive to c_L (such as S1 and S2), were not measured for thin tubes in the frequency bandwidth considered.¹⁸

Measurements were done on cortical bone mimicking phantoms to investigate the influence of bone curvature on the accuracy of estimating the characteristics of the wave guide (i.e., cortical thickness, bulk velocities) using a rather simple non-absorbing free plate model. Results reported suggest that a reasonable accuracy can be reached in thickness and in the estimates of elastic properties. The lower accuracy observed for the thinnest bone mimicking phantoms was caused by limited wave numbers measured rather than by the model itself.

While the results suggest that a free plate model can be adequate for bone characterization, extrapolation to clinical measurements still requires additional work. Only effects of a circular curvature and absorption were considered in the current study. In practice, there are additional complexities, in real bones, such as elastic anisotropy, heterogeneity, non-circular curvature and variable thickness. These factors could conceivably be significant sources of model sophistication. More research is needed in this area.

Generality of our results may be limited by the frequency band (0.6–1.4 MHz, −6 dB). In particular, earlier studies by Moilanen et al. suggest that, at low ultrasound frequencies (<0.4 MHz), the effects of bone curvature³ and coating^14,19 must be accounted for by the model, so as to properly evaluate the characteristics (such as wall thickness) of the solid waveguide. Sensitivity to such geometrical details with decreasing frequency could be true and explained by wavelength, which then becomes longer, and absorption, which then becomes weaker. Further research is needed to address the question whether the choice of the simplest suitable model is dependent of frequency.