Validation of a deformable image registration technique for cone beam CT-based dose verification

Abstract

Purpose:

As radiation therapy evolves toward more adaptive techniques, image guidance plays an increasingly important role, not only in patient setup but also in monitoring the delivered dose and adapting the treatment to patient changes. This study aimed to validate a method for evaluation of delivered intensity modulated radiotherapy (IMRT) dose based on multimodal deformable image registration (dir) for prostate treatments.

Methods:

A pelvic phantom was scanned with CT and cone-beam computed tomography (CBCT). Both images were digitally deformed using two realistic patient-based deformation fields. The original CT was then registered to the deformed CBCT resulting in a secondary deformed CT. The registration quality was assessed as the ability of the dir method to recover the artificially induced deformations. The primary and secondary deformed CT images as well as vector fields were compared to evaluate the efficacy of the registration method and it’s suitability to be used for dose calculation. plastimatch, a free and open source software was used for deformable image registration. A B-spline algorithm with optimized parameters was used to achieve the best registration quality. Geometric image evaluation was performed through voxel-based Hounsfield unit (HU) and vector field comparison. For dosimetric evaluation, IMRT treatment plans were created and optimized on the original CT image and recomputed on the two warped images to be compared. The dose volume histograms were compared for the warped structures that were identical in both warped images. This procedure was repeated for the phantom with full, half full, and empty bladder.

Results:

The results indicated mean HU differences of up to 120 between registered and ground-truth deformed CT images. However, when the CBCT intensities were calibrated using a region of interest (ROI)-based calibration curve, these differences were reduced by up to 60%. Similarly, the mean differences in average vector field lengths decreased from 10.1 to 2.5 mm when CBCT was calibrated prior to registration. The results showed no dependence on the level of bladder filling. In comparison with the dose calculated on the primary deformed CT, differences in mean dose averaged over all organs were 0.2% and 3.9% for dose calculated on the secondary deformed CT with and without CBCT calibration, respectively, and 0.5% for dose calculated directly on the calibrated CBCT, for the full-bladder scenario. Gamma analysis for the distance to agreement of 2 mm and 2% of prescribed dose indicated a pass rate of 100% for both cases involving calibrated CBCT and on average 86% without CBCT calibration.

Conclusions:

Using deformable registration on the planning CT images to evaluate the IMRT dose based on daily CBCTs was found feasible. The proposed method will provide an accurate dose distribution using planning CT and pretreatment CBCT data, avoiding the additional uncertainties introduced by CBCT inhomogeneity and artifacts. This is a necessary initial step toward future image-guided adaptive radiotherapy of the prostate.

1. INTRODUCTION

Onboard kilovoltage (kV) cone-beam computed tomography (CBCT) systems installed on modern linear accelerators enable online image guidance and are most commonly used for 3D pretreatment patient setup verification and localization.^1,2 This capability allows the delivery of conformal dose distributions with high accuracy even for hypofractionated regimes, e.g., stereotactic body radiotherapy (SBRT).³ CBCT images can potentially be used for routine dose recalculation during the course of treatment, when plan reoptimization is desirable due to large anatomy changes or motion. However, establishing a standard protocol for CBCT dose calculation is not straightforward due to differences in recorded Hounsfield units (HUs) compared with conventional CT, poorly understood HU-electron density relationship, presence of artifacts, and limited image quality of this modality.⁴

To overcome the limitation related to unconventional HU numbers of CBCT, many efforts have been made to correct these values through electron density calibration. There is a rich literature on CBCT-based dose calculation using this method for phantoms and patient data for various treatment sites.^5–18 In this method, the relation between the average CBCT numbers for several regions of interest in a phantom with several material inserts, and the known electron density of the materials is examined. Using the obtained fit function, the CBCT numbers are replaced by the corresponding CT HU numbers in each voxel. Examples of calibration phantoms are Catphan⁵ and Gammex.⁹ Most of these studies found up to 3% discrepancy between the doses calculated on the planning CT and the calibrated CBCT images. This residual discrepancy is partly due to the inherent CBCT artifacts caused by scatter, beam hardening, or other effects, leading to HU nonuniformities across tissues. Although several techniques to correct the CBCT scatter artifacts have been proposed, e.g., using collimators, antiscatter grids and blockers, a standard approach remains unclear.^19–24

In this study, we investigated the feasibility of using deformable image registration (dir) to create a modified planning CT that closely replicates the CBCT image as a basis of dose calculation for adaptive intensity modulated radiotherapy (IMRT) of the prostate. This method is hypothesized to be feasible due to the emergence of sophisticated dir techniques capable of handling multimodal image registration. The novelty of this work lies in the evaluation of the potential accuracy of the dir algorithm for CT to CBCT deformable registration, for direct use of the deformed planning CT in dose evaluation rather than relying on CBCT image processing and artifact reduction techniques. We also explored the application of CBCT preprocessing to enhance the dir performance as suggested by other groups.^25,26 Several previous studies have aimed to evaluate the performance of multimodal deformable registration and found promising geometric matching using different software and deformation algorithms for different sites.^27–34 Other studies have used dir as a tool to better compare the dose calculated on the CT and calibrated CBCT.³⁵ However, residual discrepancies due to inaccuracies of dir might exist, which have not been addressed. A recent study has taken a similar approach to verify a CT to CBCT dir method for potential IMRT adaptive dose calculation in the head and neck.³⁶ The main limitation of this work could be considered the lack of “gold standard” data, to decouple the effects of anatomy variations and accuracy of the dir method.

To the best of our knowledge, this is the only study to date that aims to assess the performance of modern dir algorithms³⁷ as a tool to enable accurate adaptive radiotherapy dose verification for prostate and pelvis. The CT–CBCT deformable registration was performed using plastimatch software, based on the B-spline algorithm. Using a rigid pelvic anthropomorphic phantom allowed for a robust and reliable comparison by providing a ground truth, in the sense that any residual deformations between the primary CT and CBCT could be avoided and any discrepancies were purely related to the dir performance. Known deformation patterns were applied to both images, and the quality of CT to deformed CBCT registration was assessed by direct quantitative comparison of image HUs and vector fields (vfs) as well as dose distributions. This comparison illustrates the potential feasibility of applying dir for accurate dose calculation on the deformed planning CT rather than the daily CBCT images.

2. METHODS

2.A. Phantom scans

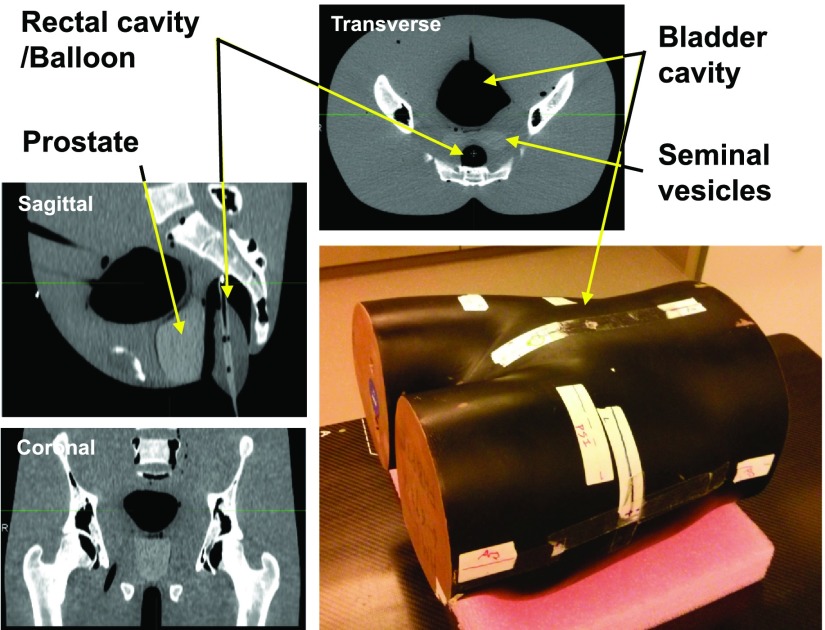
To establish a ground truth for this comparative study, a custom-built full-size rigid anthropomorphic pelvic phantom was used. This phantom features a realistic geometry and size of pelvis [31 cm (RL) × 23 cm (AP) and section height: 37 cm (IS)] including real human bones, two rigid air cavities to customize the bladder and rectal contents, and a built-in prostate in a uniform body with relative electron density of 1.04 and 1.02, respectively. Figure 1 shows the detailed schematics of this phantom. An endorectal balloon was inserted in the rectal cavity, as would be in patient treatments at our site. For various filling levels of the bladder cavity [completely full (∼170 ml of water), half full (∼85 ml), or completely empty], the phantom was separately scanned by CT, followed immediately by CBCT. This variation was applied to assess the performance of the dir algorithm for different tissue heterogeneities close to regions of high deformation and not to simulate intertreatment bladder variability, which was already included in the virtual deformation fields. Note that the presence of no initial deformation between CT and CBCT (owing to the rigidity of the phantom) was the basis for the ground-truth condition. The CT scanner was a GE RT16 simulator (GE Healthcare, Waukesha, WI) and CBCT images were acquired using the XVI onboard kV x-ray volumetric imaging system (Elekta, Crawley, UK). Care was taken for CT and CBCT setup at each bladder level to be identical, regarding the positioning and bladder filling. The phantom surface markers and BBs were aligned with respect to the room lasers in each case. The CT images were 512 × 512 voxels per slice and included 136, 1.25 mm-thick slices. CBCT scans were taken using the M20 FOV filter for an increased field of view and a bowtie filter to reduce artifacts. The images included 410 × 410 voxels per slice with 1 mm slice thickness.

FIG. 1.

Schematics of the rigid anthropomorphic pelvic phantom and transverse, sagittal, and coronal CT slices, illustrating its internal structure.

2.B. dir validation workflow

plastimatch was used as the preferred dir software in this work.^38–40 It is a free, open source, and high-performance image registration tool that provides the option for applying several registration algorithms and control parameters in single- or multistage modes. It permits optimization of specific parameters (e.g., the cost function metric, subsampling rate, and more) for a more precise and customized registration. In this study, the B-spline deformation algorithm was implemented in three stages using multiresolution method. The sum of squared differences (SSD) similarity measure was used as found to yield superior results in parallel with CBCT preprocessing, compared to mutual information (MI). The preprocessing was done in the form of HU calibration that is explained in Sec. 2.C.

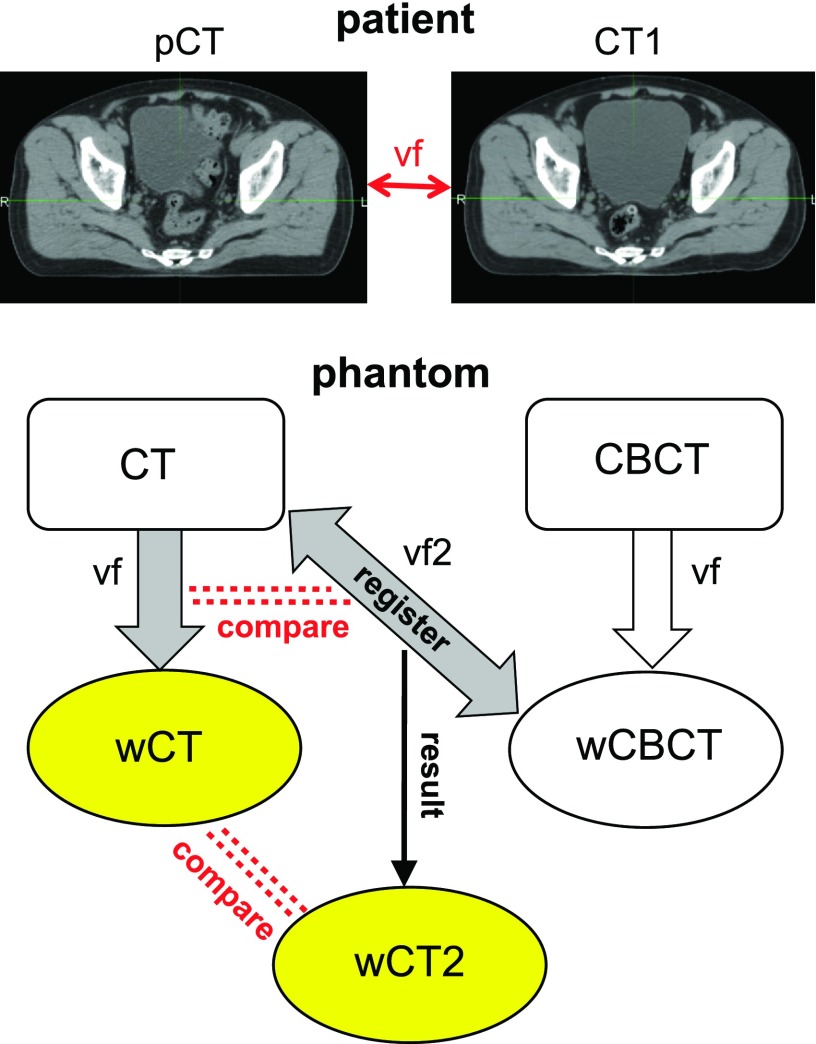
Figure 2 summarizes the workflow for validation of plastimatch CT to CBCT registration accuracy. First, both CT and CBCT images of the pelvic phantom in each bladder filling level were artificially deformed by two representative vfs, created by deformable registration between the pretreatment planning CT (pCT) and a mid-treatment CT (CT1) of two patients. The vector fields are intended to mimic realistic variations in setup of prostate, hip bones, and skin surface. The first vf was extracted using a B-spline algorithm. To emphasize the extent of clinically possible bladder changes, it was manually modified using landmark-based warping based on the Wendland function to extend the bladder volume even further. The second vf was created using the Demons algorithm using the data of a different patient. This vf represented a larger prostate movement and a realistic bladder size reduction. No manual bladder change was applied in the second case. Due to the use of rectal balloon in the patient cohort, rectum deformations were minimal.

FIG. 2.

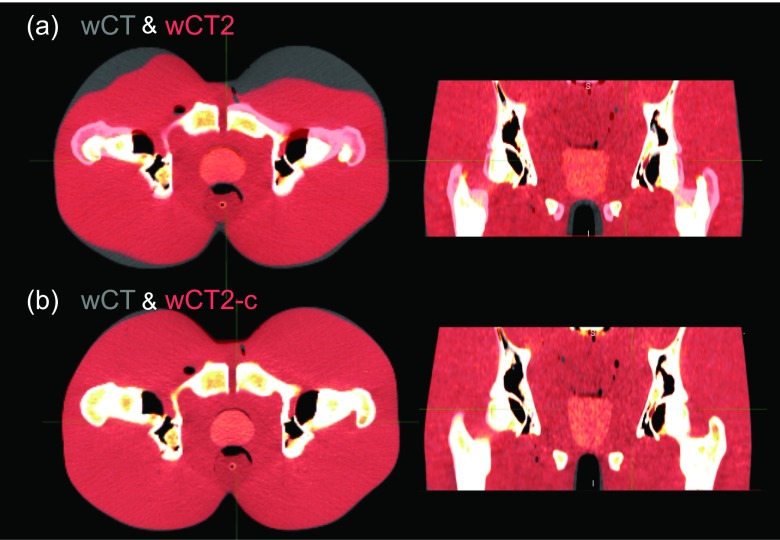
Workflow for validation of plastimatch for CT to CBCT deformable registration. vf extracted from patient variations is applied to the phantom CT and CBCT to yield wCT and wCBCT. CT is then registered to wCBCT through vf2 to yield wCT2 to be compared with wCT to assess the registration quality.

Consequently, warped CT (wCT) and warped CBCT (wCBCT) refer to the results of phantom CT and CBCT deformation using vf. The phantom CT was then registered to wCBCT using dir through purely B-spline algorithm, yielding wCT2 via vector field vf2. The match between wCT and wCT2 as well as vf and vf2 indicated how accurately plastimatch deformable registration could capture the entire magnitude of the deformation, recovering the originally deformed CT.

The workflow was repeated for different bladder filling levels individually without cross registration. Since the ground truth was based on identical primary images, cross registration was not relevant.

2.C. Geometric evaluation

Voxel-based HU number and vector field length (vfl) analyses were performed for a quantitative assessment of the geometric deformation. HU analysis included computing the differences of mean, standard deviation (STD), the quartiles, and the 95% percentile of HU distribution for nonair voxels (HU > − 400) between wCT and wCT2. Choosing this HU limit for both images effectively eliminated the treatment couch from the analysis. The analysis was performed for the whole phantom as well as for prostate and bones only to assess the performance of dir in the vicinity of the tissue boundaries where larger heterogeneities exist. Larger resulting HU differences (ΔHU) indicate less accurate registration performance. Similarly, vector field analysis was performed by finding the mean, STD, median, and 95 percentile of difference in vector field length (Δvfl) between vf and vf2 for the corresponding voxels.

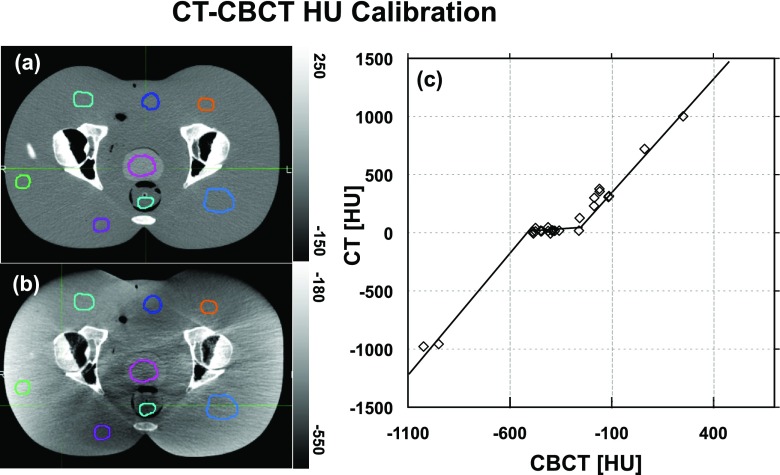
An important step to ensure a more reasonable and accurate CBCT handling by plastimatch was to calibrate the CBCT HU numbers before the registration. This calibration was led by a curve correlating the CT vs CBCT numbers within the same phantom tissues (similar to Refs. 5–18). This curve, shown in Fig. 3, is a linear piecewise fit of data points found by averaging the voxel HU numbers within 26 volumetric regions of interest (ROIs) overlaid on rigidly registered images. The ROIs were placed in various locations, i.e., within the soft issue, pelvic and femoral head and neck bones, and air. Since soft tissue in CBCT is not homogeneous due to scatter artifacts, a small range of CT HU numbers (−20 to 30) corresponded to a much larger range of CBCT numbers (−500 to −250) as seen in Fig. 3. The middle portion of the piecewise linear fit could contribute to decreasing the CBCT nonuniformities. The validation workflow was then repeated using the calibrated CBCT images. It is worthy to note that this calibration curve is case-specific and we recommend that the process be repeated for each patient. The shape of the curve might slightly change due to the inherent sensitivity of CBCT values and artifacts to patient size and shape.

FIG. 3.

Rigidly registered phantom (a) CT and (b) CBCT showing ROIs used for the calibration curve. (c) Calibration curve correlating CT and CBCT HU values. Note that the grayscale window is different on the two images.

2.D. Dosimetric evaluation

To assess the potential clinical impact of possible HU discrepancies between images, IMRT treatment planning and dose calculation was performed. RayStation (RaySearch Laboratories, Sweden) was used to create a seven-field coplanar IMRT plan on the original phantom CT image using multicriteria optimization. The clinical target volume (CTV) was defined as the prostate and received the total dose of 79.2 Gy. Organs at risk (OARs) consisted of bladder and rectum and were delineated in addition to prostate and skin. The plan was created and optimized on the phantom CT with no deformation and full bladder. The optimization objectives aimed to minimize dose to the bladder and rectum. The dose was calculated on 2 × 2 × 2.5 mm grids. The resulting dose distribution was recomputed on the two warped CT images (wCT, wCT2), using the same beam isocenter as the original plan.

Differences in D98, Dmean, and D2 between X (wCT2, wCT2-c, wCBCT-c) and wCT for the warped CTV, bladder, and rectum were calculated as a percentage of wCT dose. The symbol -c refers to cases where CBCT was calibrated,

$${\displaystyle \Delta D=\frac{\left(D\left(X\right)-D\left(\text{wCT}\right)\right)}{D\left(\text{wCT}\right)}\times 100.}$$ (1)

The resulting dose distributions were further compared using gamma analysis for all three bladder fullness levels. The agreement was assessed at the tolerance levels of 2%/2 mm and 1%/1 mm for the γ < 1 test, within the region with dose >10% of the maximum dose.^41,42

3. RESULTS

3.A. CBCT calibration

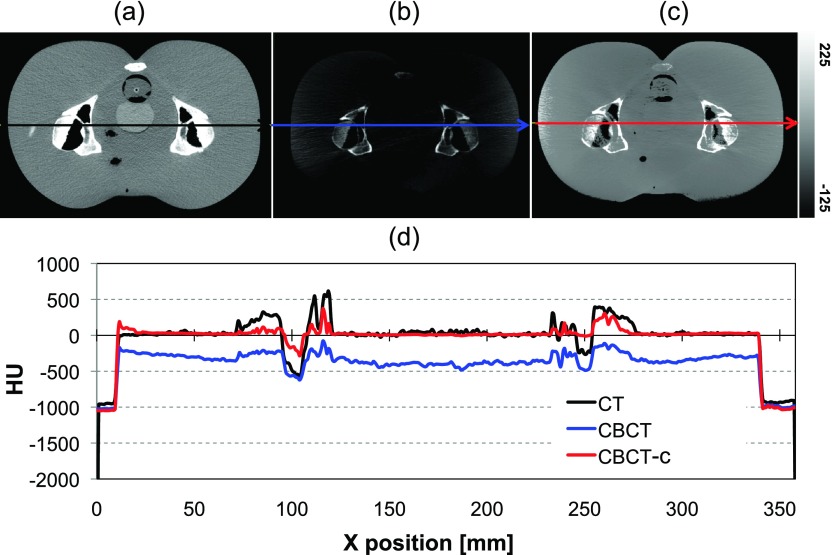
A comparison of CT with uncalibrated and calibrated CBCT images is illustrated in Fig. 4. Note that unlike Fig. 3, the images are displayed on the same contrast window. The calibrated CBCT image has HU numbers much closer to the CT range compared to the uncalibrated image. Choosing a linear piecewise curve increased the homogeneity and reduced image artifacts [compared to Fig. 3(b)], especially in the soft tissue region. Lateral profiles comparing the HU values for the corresponding slice of rigidly registered CT, CBCT and calibrated CBCT images are shown in Fig. 4(d). It is apparent that the calibration rescales the intensity of the CBCT image and brings the range of HU closer to that of the CT. However, the degree of improvement varies from one profile to another, and low-contrast variations are lost. Since the CBCT calibration was performed solely to improve the dir rather than for dose calculation, the quality of the presented calibration was determined to be sufficient.

FIG. 4.

Rigidly registered (a) CT and (b) uncalibrated and (c) calibrated CBCTs shown on the same gray scale. (d) Comparison of HU numbers for CT, CBCT, and calibrated CBCT for a single lateral line profile [lines in (a), (b), and (c)].

3.B. Geometric comparison

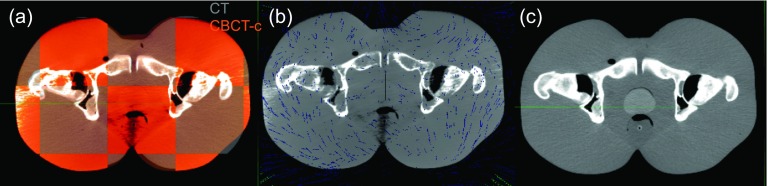
Figure 5 illustrates the process of CT to wCBCT-c deformable registration and geometric matching. A rigid fusion of the two images is shown in Fig. 5(a) for the full-bladder scenario and the first of the two deformation fields. The vector field is visualized in Fig. 5(b) and the final registered wCT2-c is shown in Fig. 5(c). It is apparent from Fig. 6 that when the CBCT values are calibrated, the resulting registration is improved. For instance, not only the skin but also the soft tissue and bones agree much more closely when the calibrated CBCT is used for registration. The large discrepancy seen in the anterior skin surface for the uncalibrated case is due to the combination of inherent heterogeneity of the soft tissue HU, low image intensity compared to CT, and relatively shallow anterior skin gradient in the phantom CBCT image. On the other hand, after CBCT calibration, all organs visually match more accurately.

FIG. 5.

CT-CBCT deformation process, (a) CT and calibrated CBCT are rigidly fused, (b) the registration is performed via a volumetric vector field, (c) the deformed CT matches the CBCT image.

FIG. 6.

Comparison of using (a) uncalibrated and (b) calibrated CBCTs, for CT deformable registration.

Table I summarizes the geometric voxel-based analysis and provides a quantitative confirmation of the visual inspection. The corresponding voxels were compared after rigid fusion of the images. Both patient deformation fields as well as three different tissue regions (whole phantom, bones, and prostate) and the three levels of bladder filling are included in the analysis. The size of the air cavity in the bladder does not seem to affect the registration quality. However, on average, the mean, median, and 95 percentile of ΔHU distribution for the whole phantom derived using the calibrated CBCT were 55%, 31%, and 62% smaller than those calculated from the uncalibrated CBCT, respectively. Similarly, the average differences between mean, median, and 95 percentile vf lengths in the corresponding voxels of the vector fields are comparable for the three bladder fullness scenarios and are decreased by 67%, 74%, and 63% when using calibrated CBCTs compared to uncalibrated ones for the whole phantom. Similar patterns were observed for both deformation fields tested. The clinical relevance of the absolute differences was determined by examining the impact on the organ dose (Sec. 3.C).

TABLE I.

Differences between mean, STD, quartiles, and 95 percentile of HU distribution and vfl for wCT vs wCT2 and wCT2-c, for all bladder fullness levels.

		ΔHU						Δvfl (mm)
Image	Bladder fullness	Mean	STD	Q1	Median	Q3	95%	Mean	STD	Median	95%
First deformation
Whole
wCT2	Full	105.3	211.7	6.0	13.0	41.0	617.0	11.7	8.2	9.6	28.9
	Half full	98.9	211.5	6.0	13.0	36.0	629.0	9.9	7.0	8.2	23.8
	Empty	107.8	216.7	5.0	13.0	49.0	637.0	10.5	7.8	8.7	26.8
wCT2-c	Full	40.9	131.9	4.0	9.0	18.0	177.0	3.8	4.4	2.3	10.4
	Half full	42.5	134.3	4.0	9.0	19.0	199.0	3.5	4.1	2.0	10.2
	Empty	41.4	132.8	4.0	9.0	18.0	189.0	3.4	4.0	2.0	9.8
Bones
wCT2	Full	212.5	199.4	62.0	151.0	302.0	632.0	8.5	5.1	8.0	17.7
	Half full	203.2	194.7	56.0	141.0	290.0	612.0	7.6	4.8	7.1	15.6
	Empty	213.3	199.9	62.0	152.0	302.0	632.0	8.5	5.5	7.7	18.5
wCT2-c	Full	83.8	113.4	17.0	42.0	104.0	316.0	1.2	0.4	1.2	2.0
	Half full	89.1	114.6	19.0	46.0	112.0	329.0	1.2	0.3	1.2	1.7
	Empty	83.0	108.2	17.0	43.0	105.0	308.0	1.2	0.3	1.2	1.7
Prostate
wCT2	Full	56.9	121.2	12.0	21.0	34.0	313.0	10.8	7.5	8.9	26.8
	Half full	53.5	115.8	12.0	20.0	33.0	285.0	9.2	6.1	7.8	21.6
	Empty	58.9	124.7	12.0	21.0	35.0	327.0	10.0	7.1	8.3	25.3
wCT2-c	Full	22.4	38.5	8.0	16.0	25.0	50.0	2.5	2.7	1.6	6.9
	Half full	23.0	38.4	8.0	16.0	25.0	53.0	2.2	1.9	1.5	6.6
	Empty	22.2	37.2	8.0	15.0	24.0	52.0	2.1	1.8	1.4	6.2
Second deformation
Whole
wCT2	Full	106.8	228.9	6.0	13.0	37.0	685.0	11.2	6.9	9.8	25.0
	Half full	112.2	235.9	6.0	13.0	40.0	716.0	11.1	7.1	9.5	24.9
	Empty	119.5	242.4	6.0	13.0	51.0	738.0	11.3	7.3	9.6	25.9
wCT2-c	Full	56.3	177.3	4.0	10.0	20.0	307.0	3.8	4.2	2.7	9.6
	Half full	57.9	178.7	4.0	10.0	21.0	332.0	3.6	3.9	2.7	8.6
	Empty	57.1	177.1	4.0	10.0	20.0	319.0	3.7	3.9	2.7	8.9
Bones
wCT2	Full	225.2	217.5	69.0	160.0	313.0	666.0	9.4	5.5	8.8	19.3
	Half full	226.7	218.5	69.0	161.0	315.0	669.0	9.4	5.7	8.5	19.7
	Empty	227.7	219.0	69.0	163.0	316.0	669.0	9.6	6.0	8.6	20.8
wCT2-c	Full	90.7	137.3	17.0	43.0	108.0	339.0	1.5	1.1	1.3	2.9
	Half full	95.0	133.4	19.0	47.0	118.0	353.0	1.5	0.9	1.4	2.9
	Empty	90.1	126.3	18.0	45.0	113.0	331.0	1.6	1.1	1.4	3.3
Prostate
wCT2	Full	59.2	134.5	12.0	21.0	34.0	306.0	11.2	6.6	9.9	24.6
	Half full	61.0	137.8	12.0	21.0	35.0	323.0	10.9	6.7	9.5	24.6
	Empty	64.0	141.7	12.0	21.0	36.0	346.0	11.1	7.0	9.5	25.8
wCT2-c	Full	26.9	73.5	8.0	16.0	26.0	55.0	2.9	2.3	2.1	7.5
	Half full	25.1	54.0	9.0	16.0	26.0	56.0	2.7	1.9	2.1	6.6
	Empty	24.7	52.6	8.0	16.0	25.0	58.0	2.8	2.0	2.0	7.0

In regions close to tissue–bone interfaces, the mean and median of both ΔHU and Δvfl were up to a factor of 2 and 12 larger compared with the whole phantom, respectively. In turn, in tissue–prostate interface, approximately twofold decrease of mean and twofold increase of median of ΔHU and Δvfl were found compared with the whole phantom. For both regions, the relative improvement of the dir due to the CBCT calibration was comparable to the whole body results.

3.C. Dose comparison

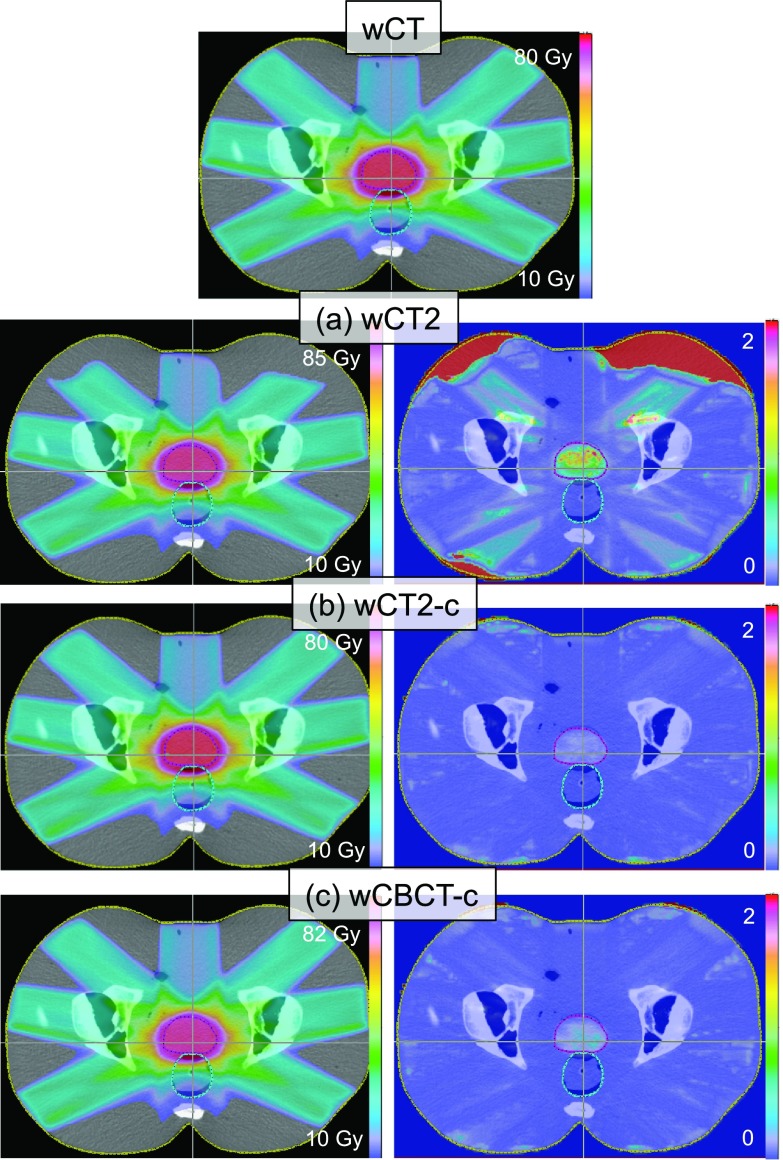
Figure 7 shows the dose distribution calculated on the wCT, wCT2, wCT2-c, and wCBCT-c for the phantom with full bladder using the first deformation. Gamma index distributions are also displayed for each case in the right column.

FIG. 7.

Dose distribution calculated on the original CT and recomputed on the deformed CT, (a) CT registered to deformed CBCT, (b) CT registered to calibrated deformed CBCT, and (c) calibrated CBCT. Gamma distributions comparing each row with wCT (on top) are shown in the right column. The regions with gamma larger than 2 indicate the voxels that failed the gamma test.

Table II lists the absolute dose and the percent differences of D98, Dmean, and D2, comparing wCT to wCT2, wCT2-c, and wCBCT-c, as defined by Eq. (1), for CTV, bladder, and rectum and both patient-based deformations. Overall, the calculated dose for wCT2-c matched wCT very well for all levels of the bladder fullness. The ΔDmean averaged over all organs (prostate, bladder, and rectum) for the bladder full scenario was 0.2% for wCT2-c compared with 0.5% and 3.9% for wCBCT-c and wCT2, respectively. Although wCBCT-c also had good dose agreement, average dose differences were generally up to 1.1% larger than wCT2-c case.

TABLE II.

Dose (Gy) and percent differences (%) (in parenthesis) between D98, Dmean, and D2 of wCT vs wCT2, wCT2-c, and wCBCT-c, for prostate, bladder, and rectum, and for all bladder fullness levels.

		Prostate			Bladder		Rectum		Prostate gamma index pass% (γ < 1)
Bladder filling	X	D98	Dmean	D2	Dmean	D2	Dmean	D2	2%/2 mm	1%/1 mm
First deformation
Full	wCT2	79.2 (1.3)	82.3 (3.9)	84.1 (4.9)	6.0 (2.9)	35.5 (5.8)	29.9 (2.9)	80.5 (3.6)	84.8	46.8
	wCT2-c	78.2 (0.1)	79.3 (0.2)	80.4 (0.3)	5.9 (0.3)	33.7 (0.4)	29.1 (0.0)	78.1 (0.6)	100.0	100.0
	wCBCT-c	78.4 (0.3)	79.6 (0.5)	80.7 (0.7)	5.9 (0.2)	33.8 (0.5)	29.1 (0.2)	78.5 (1.0)	100.0	100.0
Half full	wCT2	79.0 (1.1)	81.7 (3.2)	83.2 (3.6)	6.1 (2.2)	35.3 3.9	29.8 (2.2)	80.0 (2.9)	82.8	46.6
	wCT2-c	78.3 (0.2)	79.4 (0.2)	80.5 (0.3)	6.0 (0.2)	34.1 (0.3)	29.2 (0.0)	78.3 (0.7)	100.0	100.0
	wCBCT-c	78.4 (0.3)	79.6 (0.5)	80.8 (0.6)	5.9 (−0.7)	34.1 (0.4)	29.2 (0.2)	78.4 (0.9)	100.0	100.0
Empty	wCT2	79.1 (1.2)	82.1 (3.6)	84.2 (4.4)	7.8 (9.1)	36.5 (6.8)	30.1 (2.6)	80.4 (3.1)	81.7	44.8
	wCT2-c	78.3 (0.1)	79.4 (0.2)	80.9 (0.3)	7.2 (1.4)	34.0 (−0.6)	29.3 (0.0)	78.4 (0.6)	100.0	100.0
	wCBCT-c	78.5 (0.4)	79.7 (0.6)	81.2 (0.7)	7.2 (0.6)	34.1 (−0.3)	29.4 (0.3)	78.5 (0.7)	100.0	99.9
Second deformation
Full	wCT2	75.7 (1.6)	80.7 (2.9)	82.5 (3.5)	10.3 (2.3)	39.2 (2.8)	28.5 (0.5)	75.4 (2.3)	89.2	58.4
	wCT2-c	74.8 (0.3)	78.6 (0.2)	79.9 (0.3)	10.1 (0.3)	38.0 (−0.3)	28.4 (0.1)	74.0 (0.4)	100.0	100.0
	wCBCT-c	74.7 (0.3)	78.9 (0.5)	80.1 (0.6)	10.1 (0.2)	38.3 (0.5)	28.4 (0.4)	74.8 (1.5)	100.0	99.8
Half full	wCT2	76.0 (1.8)	80.8 (3.0)	82.9 (3.7)	10.5 (3.0)	39.6 (3.0)	28.6 (0.6)	75.7 (2.5)	89.3	58.5
	wCT2-c	74.9 (0.3)	78.6 (0.2)	80.2 (0.4)	10.3 (0.4)	38.4 (−0.2)	28.5 (0.2)	74.1 (0.3)	100.0	100.0
	wCBCT-c	74.8 (0.2)	78.9 (0.5)	80.2 (0.4)	10.2 (0.2)	38.2 (−0.8)	28.5 (0.3)	74.8 (1.3)	100.0	100.0
Empty	wCT2	75.9 (−1.1)	81.1 (3.2)	83.9 (4.3)	13.0 (7.8)	39.7 (4.8)	28.9 (1.1)	76.1 (2.8)	87.7	57.2
	wCT2-c	75.1 (−2.2)	78.7 (0.2)	80.7 (0.4)	12.1 (0.0)	37.7 (−0.3)	28.6 (0.2)	74.2 (0.2)	100.0	100.0
	wCBCT-c	74.9 (−2.4)	79.0 (0.6)	80.8 (0.5)	12.0 (−0.1)	37.4 (−1.1)	28.7 (0.4)	74.8 (1.0)	100.0	99.9

The gamma analysis showed 100% pass rate using 2%/2 mm and 1%/1 mm criteria for both wCT2-c and wCBCT-c and 81.7%–89.3% (2%/2 mm) and 44.8%–58.5% (1%/1 mm) pass rate for wCT2, which increased with the increasing bladder filling.

4. DISCUSSION

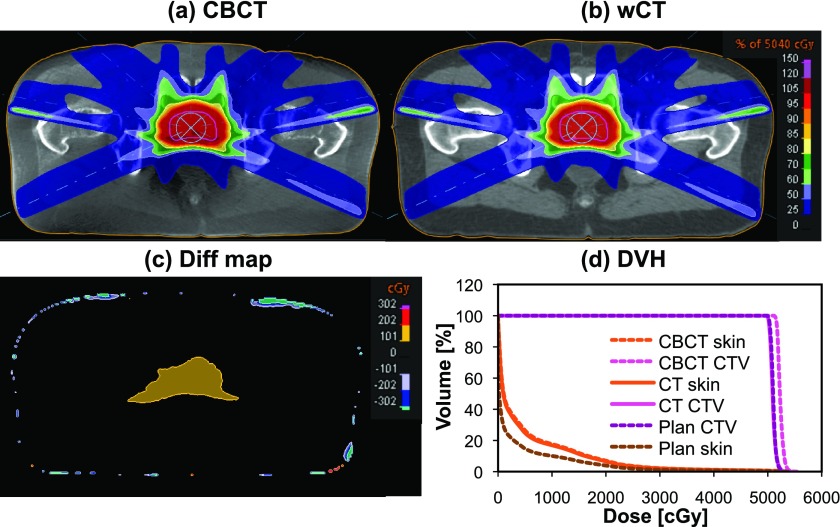
With radiation therapy fast evolving toward adaptive image-guided techniques, it is important to establish validated methods to use CBCT data not only for patient positioning but also dose delivery verification. This work presented the validation of a dir method that enables using CBCT data for routine dose verification. It was found to offer improved accuracy over dose calculation directly on calibrated CBCT. This method is currently applied in a research study at our institution to determine the delivered IMRT dose to patients participating in a clinical trial and compare with the planned dose to measure the plan robustness against interfractional variations. A representative example showing the usability of this technique in a patient case is shown in Fig. 8. According to the dose difference map and dose volume histogram (DVH), the residual dose differences between the warped CT and the calibrated CBCT are comparable for the patient skin. However, the CTV mean, minimum, and maximum dose calculated on the CBCT was 2.5% higher than both deformed and original planning CTs. This can be mainly attributed to calibration inaccuracies and CBCT artifacts since the residual deformations between CBCT and warped CT after matching the bladder volume were not large enough to be responsible for this dose increase. Therefore, upon accurate dir to match pCT to CBCT, the dose calculation could be considered more reliable than using calibrated CBCT directly, especially for heterogeneous patient tissue.

FIG. 8.

Patient IMRT dose distribution calculated on the planning CT and recomputed on (a) the calibrated CBCT and (b) CT registered to the calibrated CBCT. The dose difference between (a) and (b) is shown in (c). DVH for the skin and CTV is shown in (d).

Our results were comparable to the only previous study that used CT-CBCT dir as a basis for adaptive IMRT dose calculation for head and neck patients.³⁶ They found an average mean dose difference of 0.1% between deformed planning CT and a replan CT when they manually delineated the structures on the secondary image. However, this observation may not be directly comparable with our results due to the differences in magnitude of deformations between the two sites and using patient retrospective data instead of phantoms, where no robust ground truth could be established.

Other studies reporting on dose calculation directly on the calibrated CBCT images in the prostate/pelvic region have found somewhat larger dose discrepancies. Guan et al. used a pelvic phantom to explore the CBCT dose calculation accuracy using the intensity calibration approach.⁵ They found dose differences of up to 2.5% for IMRT plans using a 6 MV Linac. Hüttenrauch et al. have found dose recalculation uncertainties of up to 3% using 7 prostate cancer patients.¹⁵ In a similar work by Boggula et al., dose deviation as large as 3% was observed for prostate.¹⁴ Richter et al. and Rong et al. showed 2% dose discrepancies for pelvic patients and CIRS phantoms, respectively.^8,9

A point of strength in our study was the presence of gold standard for validating our method, which is not practical in patient studies. This was mainly possible by using a rigid phantom that allowed for having identical CT and CBCT scans. Although the use of a nonrigid phantom might have been more desirable, it would have been challenging to avoid residual deformations when transporting the phantom from the CT scanner to the Linac facility. Artificial digital phantom deformations were deemed to be appropriate for our purposes, as they represented real-patient deformation data for two different cases.

Due to the poor quality and contrast of CBCT images acquired with a Linac-based scanner, plastimatch may not always capture the full extent of the soft tissue variations. An additional landmark-based deformation could easily be activated within the software platform that is capable of handling larger deformations, e.g., the bladder volume. This could effectively eliminate the need for structure delineation on all CBCT images. The choice of optimal registration parameters in plastimatch was an important factor. The B-spline algorithm was preferred due to smoother, more regularized results. We chose the SSD similarity measure as it yielded superior registration results compared to MI when accompanied by subject-specific image calibration. This might, however, be dependent on the choice of dir software. Furthermore, as plastimatch is actively maintained and improved, functional enhancements, such as the handling of the unconventional CBCT intensities, might be introduced in the future to eliminate the need for CBCT calibration prior to registration.

Using patient CBCT compared with phantom is not expected to pose additional complications in the dir process, as similar levels of artifacts and HU range can be observed. Whether or not the differences in tissue heterogeneity and contrast might work in favor of or against using patient versus phantom data is unclear and is subject to further investigations.

A potential clinical application of the presented method is adaptive prostate radiotherapy, where the treatment plan is mapped on pretreatment CBCT images to verify the target coverage and OAR dose, in case larger than usual anatomy changes are observed. If this assessment proves the plan to be clinically unacceptable, the treatment could be postponed until a new plan is generated and approved. Online CBCT-based replanning is also foreseen in the near future.

5. CONCLUSION

The findings of this work suggest the feasibility of using CT–CBCT deformable registration for IMRT dose calculation and potentially adaptive treatments of prostate. Instead of calculating the dose on the calibrated CBCT, we proposed to deform the planning CT to the calibrated CBCT for a more accurate dosimetry to avoid the inaccuracies related to the inherent CBCT artifacts. While more rigorous testing of this method might be necessary before clinical implementation, this study found deformable image registration to be a potentially reliable and accurate method for routine dose monitoring during the course of radiotherapy. This can be considered an initial step toward fully dynamic and adaptive prostate treatments.