Abstract
Background
To identify best-fitting input sets using model calibration, individual calibration target fits are often combined into a single “goodness-of-fit” (GOF) measure using a set of weights. Decisions in the calibration process, such as which weights to use, influence which sets of model inputs are identified as best-fitting, potentially leading to different health economic conclusions. We present an alternative approach to identifying best-fitting input sets based on the concept of Pareto-optimality. A set of model inputs is on the Pareto frontier if no other input set simultaneously fits all calibration targets as well or better.
Methods
We demonstrate the Pareto frontier approach in the calibration of two models: a simple, illustrative Markov model and a previously-published cost-effectiveness model of transcatheter aortic valve replacement (TAVR). For each model, we compare the input sets on the Pareto frontier to an equal number of best-fitting input sets according to two possible weighted-sum GOF scoring systems, and compare the health economic conclusions arising from these different definitions of best-fitting.
Results
For the simple model, outcomes evaluated over the best-fitting input sets according to the two weighted-sum GOF schemes were virtually non-overlapping on the cost-effectiveness plane and resulted in very different incremental cost-effectiveness ratios ($79,300 [95%CI: 72,500 – 87,600] vs. $139,700 [95%CI: 79,900 - 182,800] per QALY gained). Input sets on the Pareto frontier spanned both regions ($79,000 [95%CI: 64,900 – 156,200] per QALY gained). The TAVR model yielded similar results.
Conclusions
Choices in generating a summary GOF score may result in different health economic conclusions. The Pareto frontier approach eliminates the need to make these choices by using an intuitive and transparent notion of optimality as the basis for identifying best-fitting input sets.
INTRODUCTION
The rapid growth of computing power has enabled health policy models to be constructed with increasing complexity in an effort to more closely approximate reality (1). Natural history models describe disease processes, of which some (such as disease progression rates) may be only partially or indirectly observable. Therefore, model parameters describing these processes are often highly uncertain (1-5). Calibration is the process by which values or ranges of uncertain parameters can be estimated so that model outputs match observed clinical or epidemiological data (the calibration targets) (1-5). Comprehensive models often include calibration targets from multiple data sources making model calibration a non-trivial task.
Model calibration broadly consists of three steps (4-6): (i) identify the input parameters to be estimated through calibration and the calibration targets; (ii) generate potential sets of input values; and (iii) assess how well model outputs resulting from each input set fit the calibration targets and identify a subset of input sets that best fit the targets (the focus of this paper). When there are multiple calibration targets, individual fits are typically combined into a summary goodness-of-fit (GOF) score, providing a single measure on which to assess the overall quality of the fit (5). To compensate for differences in data quality, different measurement scales, and preferences for fitting some calibration targets over others, analysts often choose a set of weights and define the GOF score to be the weighted sum of the individual target fits (4,6).
At every stage of the calibration process, the analyst makes decisions such as what search method to use to generate potential input sets, how to assess individual target fits, and how to weight individual targets into a summary GOF score (Table 1). These decisions can influence which input sets are identified as best-fitting and, by extension, the health economic conclusions of the analysis (7). Some have suggested that the assumptions and decisions necessary to the calibration process should be subject to sensitivity analysis, just as are other sources of uncertainty (7). However, this may not be computationally feasible for many models; reducing the number of choices involved in the calibration process may be a more practical approach.
Table 1.
A summary of some of the different options for calibration search and fit assessment. For an overview of model calibration methods, see (5).
| Search algorithms | Fit assessment
|
|
|---|---|---|
| Individual targets | Overall | |
|
| ||
|
||
In this paper, we present an alternative method for identifying the best-fitting input sets which we call the Pareto frontier approach. This approach eliminates the need to produce a single summary measure of fit (and the choices associated with it) by using an intuitive and transparent notion of optimality from the multi-objective optimization literature as the basis for identifying best-fitting input sets. The principle of Pareto-optimality has been used in multi-objective optimization in a variety of fields. For example, it is the principle underlying the efficient frontier in cost-effectiveness analysis, representing the optimal tradeoff between costs and quality-adjusted life-years, and the receiver operating characteristic (ROC) curve in the evaluation of diagnostic tests, representing the tradeoff between test sensitivity and specificity (8-10). In the context of model calibration, a set of model inputs is Pareto-optimal if it is undominated, meaning that there is no other input set that produces outputs that simultaneously fit all calibration targets at least as well or better. Together, the Pareto-optimal input sets form the Pareto frontier. On the Pareto frontier, any attempt to improve the fit to one calibration target by moving from one Pareto-optimal input set to another would worsen the fit to one or more of the other targets.
In this paper, we describe how to apply the concept of Pareto-optimality to the calibration of disease natural history models. We demonstrate its implementation in the calibration of two example models: a simple, illustrative Markov model and a larger, more complex model used in a previously-published cost-effectiveness analysis. Using these two example models, we compare the Pareto frontier approach to different summary GOF scoring systems for identifying best-fitting input sets. We explore how these different methods influence estimates of input uncertainty, expected health economic outcomes, and decision uncertainty.
METHODS
Overview
We conducted model calibration on two example models. The first was a simple, four-state Markov model of a hypothetical disease and intervention developed for the purposes of this analysis. The second model was used in a previously-published analysis of the cost-effectiveness of transcatheter aortic valve replacement (TAVR) in the management of patients with severe, symptomatic aortic stenosis (11). For each example model, we identified the inputs to be estimated through calibration and defined multiple calibration targets. We randomly generated a large sample of candidate input sets, ran the model for each input set, and calculated the fit of the resulting model outputs to each calibration target (Figure 1). We then identified the input sets whose outputs best fit the calibration targets (the ‘best-fitting’ input sets) using three approaches to model calibration: the Pareto frontier approach and two different summary GOF scoring systems. We compared which input sets were classified as ‘best-fitting’ and the resulting estimates of expected health economic outcomes using these different approaches.
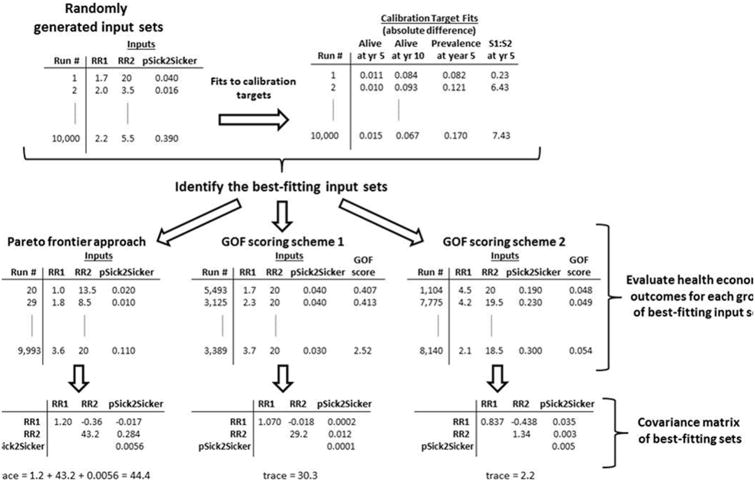
Figure 1.
An overview of the method by which we generated three groups of best-fitting sets using Example 1: Simple Markov Model.
Example Application 1: Simple Markov model
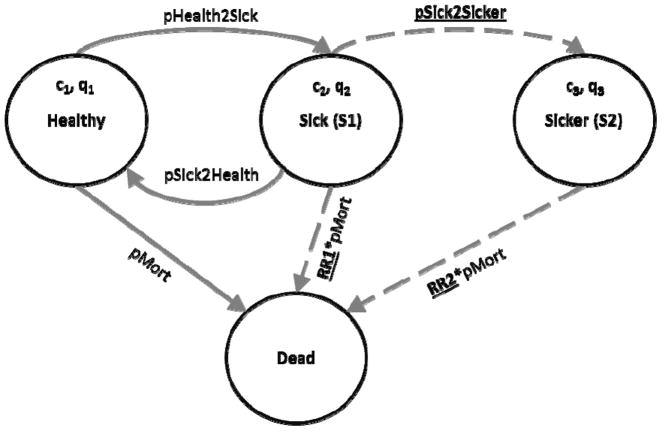
The simple Markov model developed for this analysis consisted of four health states: Healthy, two stages of illness (S1, S2), and Dead (Figure 2). In the model, healthy individuals may develop the illness and progress to the first disease stage (S1). From S1, they might eventually recover (returning to the healthy state) or their disease might further progress to a more severe stage (S2). We assume that as the disease progresses, mortality and healthcare costs increase and quality of life decreases. In this example, we assume that whether an individual is healthy or sick is observable, but it is difficult to distinguish between the two stages of disease. We used model calibration to identify parameter values for the relative risk of death in each stage of disease and the rate of disease progression from S1 to S2 (i.e., unobservable parameters) that were most consistent with calibration targets. Model parameter values and ranges used in calibration for unobservable parameters are given in Table 2.
Figure 2.
State transition diagram of a simple Markov model consisting of four health states: Healthy, two illness states (S1 and S2), and Dead. We assume that the illness is associated with higher mortality (RR1, RR2>1), higher healthcare costs (c1<c2<c3), and reduced quality-of-life (ql>q2>q3). Parameters to be varied in calibration are underlined and corresponding transitions are represented with dashed arrows.
Table 2.
Input values, plausible ranges for unknown parameters, and calibration targets for the simple Markov model.
| Parameter | Value or Range |
|---|---|
|
| |
| Time Horizon | 30 years |
| Annual discount rate | 3% |
| Annual transition probabilities | |
| Disease onset (healthy to S1) | 0.15 |
| Recovery (S1 to healthy) | 0.5 |
| Disease progression (S1 to S2) | (0.01 – 0.48) |
| Annual probability of death | |
| Healthy individuals | 0.005 |
| Relative risk in S1, relative to healthy | (1.0 – 4.5) |
| Relative risk in S2, relative to healthy | (1.0 – 20) |
| Annual costs | |
| Healthy individuals | $2,000 |
| Sick individuals in S1 | $4,000 |
| Sick individuals in S2 | $15,000 |
| Quality-of-life | |
| Healthy individuals | 1.00 |
| Sick individuals in S1 | 0.75 |
| Sick individuals in S2 | 0.50 |
| Intervention effects | |
| Annual treatment cost per sick individual | $12,000 |
| Quality-of-life of treated individuals in S1 | 0.95 |
|
| |
| Calibration Target | Target Value |
|
| |
| Overall 5-year survival | 98% |
| Overall 10-year survival | 84% |
| Prevalence of disease in year 5 | 15% |
| Ratio of S1:S2 | 8:1 |
We calibrated the model to four calibration targets: two observations of the survival of the cohort (at years 5 and 10), the prevalence of disease in the cohort at year 5, and the ratio of patients in S1 to S2 at year 5. The first three calibration targets could have come from an observational study of a typical cohort. The fourth calibration target might have come from a study in which an invasive test was used to determine a patient’s stage of disease. To calibrate the model, we randomly generated 10,000 input sets by sampling uniformly from the plausible ranges on input parameters. For each calibration target, we measured fit as the absolute difference between the calibration target value and the corresponding model output.
In this hypothetical example, the Markov model was used to evaluate the cost-effectiveness of an intervention that improves the quality of life of those afflicted with the disease, but only while in the earlier stage, S1. However, because a patient’s stage of disease cannot be determined easily, the policy decision is whether or not to treat all sick individuals at a cost of $12,000 per patient per year. We evaluated this decision over a 30-year time horizon, discounting costs and benefits at 3% per year. We implemented the model in Matlab 2012a (Mathworks Inc., Natick, MA).
Example Application 2: Natural history model of severe aortic stenosis
Our second example uses a previously published Markov model of the natural history of severe aortic stenosis developed to evaluate the cost-effectiveness of transcatheter aortic valve replacement (TAVR) compared to medical management for patients with New York Heart Association (NYHA) class III/IV level symptoms who are ineligible for surgical aortic valve replacement. Full model details are available elsewhere (11). The model includes health states based on symptom status (NYHA class I/II or class III/IV level symptoms) and major complications (stroke, vascular complication, and bleed) (Figure 3). We implemented the model in TreeAge Pro 2009 Suite (TreeAge Software Inc., Williamstown, MA).
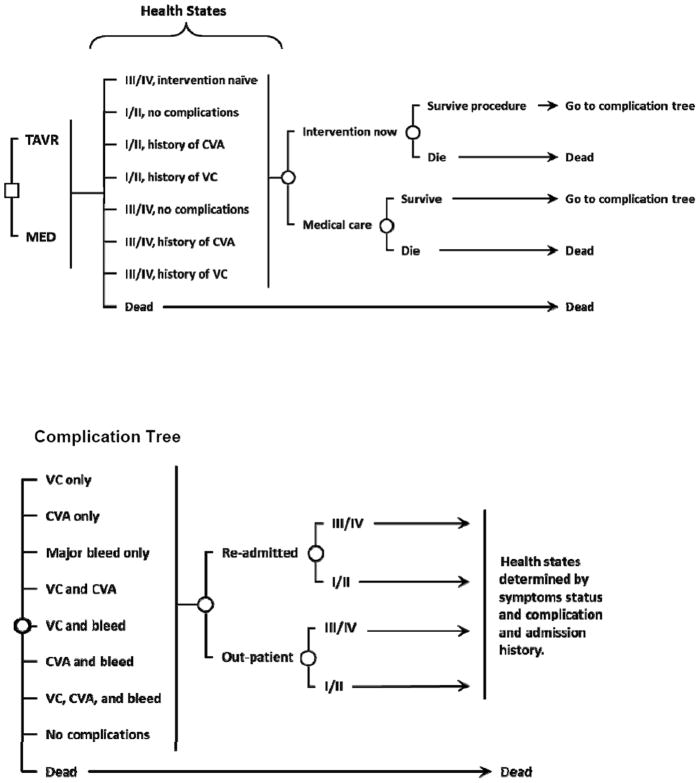
Figure 3.
Aortic stenosis model schematic. The square indicates the policy decision of TAVR or medical management. There are 8 mutually exclusive health states defined by the patient’s symptom status and complication history. Circles represent chance events that can occur within a cycle. Each cycle, patients may develop one or more, potentially fatal, complications and may be re-hospitalized. The health state to which patients transition depends on their current health state and their procedural, hospitalization, and complication history (individuals were classified by the most severe complication in their history).
TAVR = transcatheter aortic valve replacement, MED = medical management, CVA = stroke, VC = vascular complication, III/IV = NYHA class III/IV level symptoms, I/II = NYHA class I/II level symptoms.
Complication Tree
We estimated model parameters from the PARTNER trial (12) and medical literature. We estimated the values and distributions of 15 model variables, including the monthly probability of death and baseline rates of complications and re-hospitalizations, through the calibration of modeled outcomes to those observed in the PARTNER trial. We estimated the range of plausible input values for each of the 15 variables from the literature and clinical judgment (Appendix Table 1). We identified 5 sets of time-series data as calibration targets with from the PARTNER trial outcomes (12): the proportion dead, the proportion dead or hospitalized, total number of strokes, symptom status, and rate of symptom status change over time (Appendix Table 2).
To calibrate the model, we simulated the patient cohort and intervention arms of the PARTNER trial. Specifically, we simulated a cohort of 83 year-olds, which was the average patient age in the trial, with severe symptomatic aortic stenosis through two intervention strategies: in the first, all patients received TAVR immediately; in the second, simulating the medical management arm of the PARTNER trial, 64% of patients received the intervention of balloon aortic valvuloplasty immediately and, of the remaining 36%, 56% receive valvuloplasty during their remaining lifetime. We ran the model for 20,000 randomly-generated sets of input values, recording the outcomes of death, stroke, hospitalization, and symptom status for each set. For each calibration target, we calculated two measures of fit for the model output to the calibration target values at each observed time point: the squared difference and the percent absolute error.
Identifying best-fitting sets
Pareto frontier approach
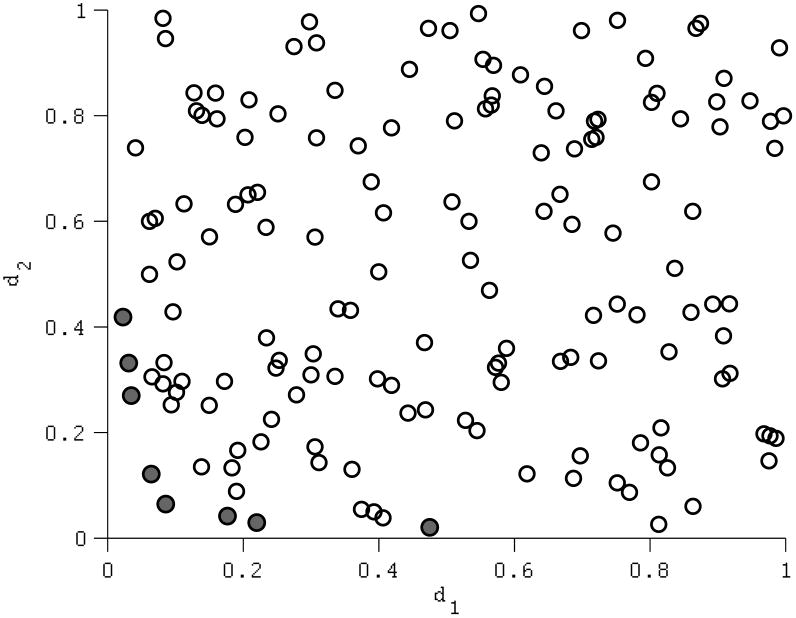
A set of model inputs is on the Pareto-frontier if no other input set produces model outputs that simultaneously fit all calibration targets at least as well, with a strictly better fit on at least one target. As an illustration, consider calibrating a model with two calibration targets. For an input set i, let the absolute difference between the resulting model output and each calibration target be d1(i) and d2(i). The lower d1(i) and d2(i), the better the input set fits the calibration targets. A population of input sets is plotted according to their calibration fits, d1 and d2 (Figure 4). An input set is dominated if there is at least one input set with lower values for both d1 and d2. An input set i is Pareto-optimal if, compared to all input sets with the same or better fit on one calibration target, it achieves a strictly better fit on the other calibration target (i.e., input set i is Pareto-optimal only if d1(j) ≤ d1(i) and d2(j) > d2(i) or if d2(j) ≤ d2(i) and d1(j) > d1(i) for all input sets j≠i). Pareto-optimality is based only on relative relationships (whether a quantity is less than or greater than another) therefore, which input sets are on the Pareto frontier will not change for fit metrics with the same rank-ordering (as is the case with absolute or squared difference, percent absolute error, Chi-squared, or any other scaled measure of difference). In many practical examples, a fit metric based on log-likelihood (for example, a Normal likelihood function) would also result in the same ranking as a metric based on difference, though this is not generally the case (for example, an asymmetric likelihood function such as the Poisson). Two metrics whose ranks are different may identify different input sets as being on the frontier.
Figure 4.
An illustration of Pareto-optimality in context of two calibration targets. Model input sets are plotted in terms of their fit on each target, d1 and d2, measured, in this case, as the absolute difference between the model output and the calibration target value. Thus, lower values of d1 and d2 represent better fits. Filled circles denote the input sets forming the Pareto-frontier.
To identify input sets on the Pareto-frontier, the calibration fits of each input set must be compared to those of every other input set. Generally this comparison is computationally intensive: standard procedures have a computational complexity on the order of O(MN3), where M is the number of calibration targets and N is the number of input sets to be compared, making the comparison of large numbers of input sets difficult (13,14). To conduct these comparisons efficiently, we implemented a previously-published efficient sorting algorithm for comparing multiple calibration targets (see Deb et al. 2002 (14)).
Summary goodness-of-fit (GOF) score
One common method used to assess the overall fit of model outputs to calibration targets is to compute a weighted sum of the individual calibration target fits, given by
Where fi is the fit of the parameter set to calibration target i and Wi is the weight associated with that calibration target. The optimal input set(s) is/are then those sets achieving either minimal (when fit is measured in distance from the calibration target) or maximal (when fit is measured as log-likelihood) GOF scores. Possible weighting schemes include an equal weighting of all calibration target fits, a normalization weighting to put the measures of fit on similar numerical scales, or a weighting that reflects a preference for prioritizing fitting some calibration targets over others (3-6,15,16). This preference may be driven by differences in the quality of the data informing calibration target values or in the relative significance of the calibration targets to the analysis. For the first example model, we used absolute difference to measure individual target fit and considered two weighting schemes: (i) an equal weighting of all calibration targets and (ii) a weighting scheme that puts a higher weight on targets 1-3. For the second example model, both GOF scoring systems assume equal weighting of all targets and instead we consider two different measures of fit: (i) squared difference and (ii) percent absolute error.
Comparisons across best-fitting sets
The number of input sets on the Pareto frontier varies with the number of inputs estimated through calibration, the number of calibration targets, and the extent to which tradeoffs exist between calibration targets. To facilitate comparison, we first identified the number of input sets on the Pareto frontier and then selected the same number of top-fitting input sets as ranked by the two different summary GOF scoring systems to be the ‘best fitting’ sets for each model.
Dispersion of the selected inputs
We first compared input parameter uncertainty across the three groups of best-fitting input sets for each model (the input sets on the Pareto frontier and the best-fitting input sets identified using the two GOF scoring systems). To measure how spread out each group of inputs was in the input parameter space, we calculated the covariance matrix of the inputs for each group. As a summary measure of total variance in the inputs, we calculated the sum of the diagonal elements (the matrix ‘trace’). An example calculation for the simple Markov model is presented in Figure 1.
Health economic outcomes
We also explored how the choice of method for identifying best-fitting sets influenced the health economic outcomes and decision uncertainty. For each of the three groups of best-fitting input sets, we calculated the expected incremental costs, quality-adjusted life-years (QALYs), incremental cost-effectiveness ratio (ICER), and incremental net monetary benefit (NMB) at a willingness to pay threshold of $100,000 per QALY gained for each model (17). We assumed a uniform distribution over the input sets in each best-fitting group with each input set being selected with probability 1/N, where N is the number of best-fitting input sets in each group. To evaluate differences in decision uncertainty attributable to the parameters estimated through calibration, we present the proportion of input sets in each group for which the intervention has the greatest net monetary benefit at various willingness-to-pay thresholds (a cost-effectiveness acceptability curve). This is analogous to performing a probabilistic sensitivity analysis varying only the input parameters estimated through calibration.
RESULTS
Example Application 1: Simple Markov model
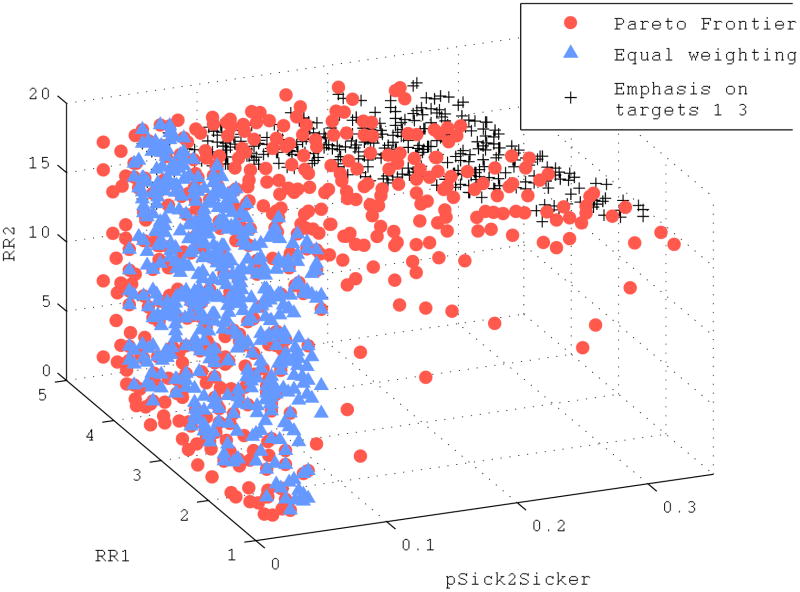
In the calibration of the illustrative Markov model, of the 10,000 randomly sampled input sets, 506 formed the Pareto frontier. For comparison, we selected the top 506 input sets for each of the two GOF weighting schemes: (i) an equal weighting of all calibration targets and (ii) a weighting scheme that puts a higher weight on targets 1-3. The best-fitting input sets identified by the Pareto frontier approach and the two weighting schemes are shown in Figure 5. Note that the two GOF weighting schemes select for virtually non-overlapping regions of the input space: with an equal weighting of calibration targets, the best-fitting input sets are those with a low rate of disease progression from S1 to S2; with a weighting emphasizing targets 1-3, the best-fitting input sets are those with a high relative risk of death in disease stage S2. Input sets on the Pareto frontier span both of these regions and also include other points in the input space. Quantitatively, this is reflected by input sets on the Pareto frontier exhibiting greater variance in each input dimension (diagonal entries of the covariance matrix) and greater overall variance (trace of the covariance matrix) than the best-fitting input sets under either GOF weighting schemes. Input sets on the Pareto frontier had a total variance of 44.4, while the total variance of best-fitting sets under equal weighting or a weighting emphasizing calibration targets 1-3 was 30.3 and 2.2, respectively (Figure 1).
Figure 5.
Input sets on the Pareto frontier (circles) and top 506 best-fitting sets ranked according to an equal weighting of calibration target fits (triangles) and a weighting scheme emphasizing calibration targets 1–3 (crosses) for a simple Markov model. Each input set contains a value for the relative mortality risk in S1 (RR1), the relative mortality risk in S2 (RR2), and the annual probability of transitioning from S1 to S2 (pSick2Sicker).
We then evaluated the incremental costs and QALYs (Figure 5a), incremental cost effectiveness ratio, and a cost-effectiveness acceptability curve (Figure 5b) of the intervention compared to no intervention for each of the input sets on the Pareto frontier and the top 506 best-fitting input sets ranked according to the two weighting schemes (Table 3). When evaluated using the input sets on the Pareto frontier, the hypothetical intervention was cost-effective with a median ICER of $79,000 [95% CI: $64,900 to $156,200] per QALY gained and was the preferred alternative for 70% of input sets on the frontier (using a willingness-to-pay threshold of $100,000 per QALY gained). The two GOF weighting schemes resulted in very different cost-effectiveness estimates and levels of decision uncertainty (the proportion of input sets for which the intervention would be considered cost-effective): at a willingness-to-pay threshold of $100,000 per QALY, the intervention was preferred for all best-fitting inputs identified by an equal-weighting GOF score (median ICER of $79,300 [95% CI: $72,500 – $87,600] per QALY gained); however, using the best fitting inputs identified by a GOF weighting scheme emphasizing targets 1-3, the intervention had a median ICER of $139,700 [95% CI: $79,900 – $182,800] and the intervention was preferred for only 17% of the best-fitting input sets.
Table 3.
Mean and empiric 95% confidence intervals of the health economic outcomes for the simple Markov model example.
| Fit metric for individual calibration targets | Pareto Frontier Rank based on squared difference | GOF scoring scheme 1 Squared difference | GOF scoring scheme 2 Squared difference |
|---|---|---|---|
|
| |||
| Weighting scheme | - | Equal weighting | Emphasis on targets 1-3 |
|
| |||
| Number of “best fitting” sets * | 506 | 506 | 506 |
|
| |||
| Incremental costs - $ | 55,800 (49,600 – 63,800) | 55,100 (51,300 – 60,200) | 61,000 (52,400 – 66,700) |
| Incremental QALYs | 0.64 (0.41 – 0.77) | 0.69 (0.66 – 0.73) | 0.47 (0.36 – 0.65) |
| Incremental cost effectiveness ratio - $ per QALY gained (median) | 79,000 (64,900 – 156,200) | 79,300 (72,500 – 87,600) | 139,700 (79,900 – 182,800) |
| WTP of $100,000/QALY gained | |||
| Incremental net monetary benefit - $ | 8,000 (-22,600 – 27,000) | 14,200 (8,600 – 19,700) | -14,200 (-30,100 – 13,200) |
| Proportion of input sets for which intervention has the highest net monetary benefit | 70% | 100% | 17% |
The number of “best-fitting” sets was determined by the number of input sets on the Pareto frontier. The same numbers of top-fitting sets were classified as “best fitting” using each of the GOF scoring schemes.
Example Application 2: Natural history model of severe aortic stenosis
We generated 20,000 randomly sampled input sets for the calibration of the aortic stenosis natural history model. Of these input sets, 260 were on the Pareto frontier. For comparison, we selected the top 260 input sets ranked according to two different GOF scoring schemes: (i) the (equally-weighted) sum of the squared error between each target and corresponding model output and (ii) the (equally-weighted) sum of the absolute percent error between each target and the corresponding model output. When comparing across the three groups of best-fitting input sets, we again found that input sets on the Pareto frontier exhibited greater total variance in the input space (14.0) than the best-fitting input sets under a summary scoring scheme of either the sum of squared errors (11.7) or sum of absolute errors (12.9).
We then evaluated the incremental costs and QALYs (Figure 6a), incremental cost effectiveness ratio, and a cost-effectiveness acceptability curve (Figure 6b) of TAVR compared to medical management for each of the input sets on the Pareto frontier and the top 260 best-fitting input sets ranked according to the two summary GOF scoring schemes (Table 4). The median ICER of TAVR compared to medical management was $108,600 [95% CI: $74,700 – $216,100] per QALY gained using the Pareto frontier approach, $97,500 [95% CI: $70,400 – $149,100] per QALY gained using GOF scoring scheme (i), and $121,200 [95% CI: $74,600 – $252,200] per QALY gained using GOF scoring scheme (ii). Therefore, at a willingness to pay threshold of $100,000 per QALY gained, adopting TAVR was only preferred if evaluated over the best-fitting input sets identified by GOF scoring scheme (i). Decision uncertainty, represented by the proportion of input sets for which TAVR had an ICER of less than $100,000 per QALY gained, was also very different across the best-fitting input sets. TAVR was the preferred alternative for 38.1% of input sets on the Pareto frontier, in comparison to 55.0% and 26.5% of best-fitting input sets ranked by GOF scoring schemes (i) and (ii), respectively.
Figure 6.
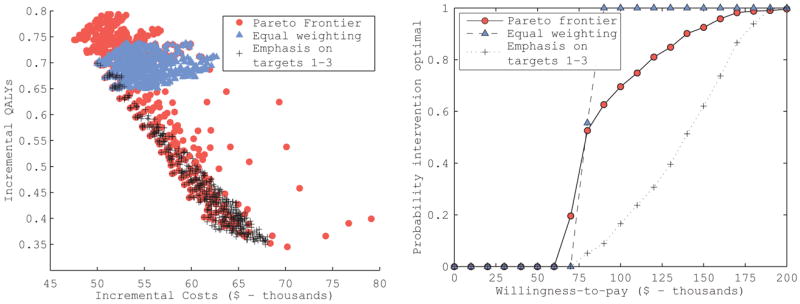
Cost-effectiveness results of the hypothetical intervention in the Markov model example. The incremental costs and QALYs of the intervention compared to no intervention for each input set on the Pareto frontier (circles) and the top 506 best-fitting sets ranked according to an equal weighting of calibration target fits (triangles) and a weighting scheme emphasizing calibration targets 1–3, which would be based on observational studies (crosses) are plotted. These results were used to generate the cost-effectiveness acceptability curves for the intervention that would be estimated under the different input set ranking approaches.
Table 4.
Mean and empiric 95% confidence intervals of the health economic outcomes for the TAVR cost effectiveness analysis.*
| Fit metric for individual calibration targets | Pareto Frontier Rank based on squared difference | GOF scoring scheme 1 Squared difference | GOF scoring scheme 2 Percent absolute error |
|---|---|---|---|
|
| |||
| Weighting scheme | - | Equal weighting | Equal weighting |
|
| |||
| Number of “best fitting” sets ** | 260 | 260 | 260 |
|
| |||
| Incremental costs - $ | 91,800 (61,200 – 130,200) | 92,900 (67,300 – 128,900) | 87,100 (55,000 – 127,300) |
| Incremental QALYs | 0.86 (0.29, 1.59) | 0.97 (0.51, 1.55) | 0.76 (0.24, 1.52) |
| Incremental cost effectiveness ratio - $ per QALY gained (median) | 108,600 (74,700 – 216,100) | 97,500 (70,400 – 149,100) | 121,200 (74,600 – 252,200) |
| WTP of $100,000/QALY gained | |||
| Incremental net monetary benefit - $ | -5,500 (-36,600 – 37,500) | 3,900 (-27,300 – 41,500) | -11,000 (-36,600 – 32,900) |
| Proportion of input sets for which intervention has the highest net monetary benefit | 38.1% | 55.0% | 26.5% |
Note that these values only reflect uncertainty due to calibration parameters and thus do not precisely match results presented in (11), which are based on a full probabilistic sensitivity analysis of all model parameters.
The number of “best-fitting” sets was determined by the number of input sets on the Pareto frontier. The same numbers of top-fitting sets were classified as “best fitting” using each of the GOF scoring schemes.
DISCUSSION
In this paper, we described how the concept of Pareto-optimality can be applied to model calibration, identifying input sets as best-fitting on the basis that no other input set simultaneously fits all calibration targets as well as or better than the given set. The Pareto frontier consists of all such undominated input sets. Without additional information about preferences for fitting some targets over others, no input set on the frontier is superior to any other. The Pareto frontier approach is a clear, transparent, and intuitive definition of ‘best-fitting’ in the context of multi-target model calibration, with a solid grounding in the theory of multi-objective optimization (8). The Pareto frontier approach simplifies the decision of how to measure of fit between the model output and calibration targets (as it effectively uses the rank of fits to make comparisons across input sets) and eliminates the need to produce a single summary GOF measure.
When calibrating a simulation model with multiple targets, an analyst would ideally have information about the full joint probability distributions of the calibration targets so that a single joint-likelihood-based measure can be used to assess overall fit. Since this information is often unavailable, especially when calibration targets come from multiple sources, health decision analysts have traditionally used a weighted sum of individual target fits as a summary GOF measure to rank input sets (e.g., (6,15,16)). However, these weighting schemes generally do not fully account for the tradeoffs that exist in fitting multiple, potentially conflicting, targets. As a result, this approach may inadvertently identify best-fitting input sets that all achieve a good GOF score in a common way (i.e., all fit mortality targets well, but none fit the disease stage distribution). In order to compensate, the analyst might change the weighting scheme, perhaps only to overcompensate and create a new problem. The Pareto frontier approach avoids this problem entirely because it eliminates the need to produce a single summary measure of fit.
Beyond eliminating the decision of how to summarize goodness-of-fit, the Pareto frontier approach may have additional desirable properties. We observed that input sets identified through the Pareto frontier approach maintained greater input uncertainty (higher variance) than top-ranked input sets under a summary GOF scoring system. This is because the Pareto frontier approach selects input sets on the basis of their diversity in fitting calibration targets and avoids identifying sets which all fit calibration targets in a similar way. Greater uncertainty is not necessarily superior, but reductions in input variance attributable to (sometimes arbitrary) analyst decisions in the calibration process are clearly not the goal of calibration. In practice, the true uncertainty about unobservable parameters is unknown and can only be estimated through methods such as those employed here or through other Bayesian approaches to parameter distribution estimation (18-20).
Just as we found considerable differences in which input sets were considered best-fitting under the different approaches, the resulting estimates of health economic outcomes, when evaluated over these different best-fitting input sets, were also substantially different. In the Markov model example, one GOF scoring scheme resulted in the intervention being cost-effective for all best-fitting input sets. However, under the other GOF scoring scheme, the intervention was not cost-effective on average and only preferred for 17% of the best-fitting input sets. Either GOF scoring scheme could be justified based on analyst preferences and data quality; yet these decisions would result in opposite conclusions of the value of the intervention. In contrast, when the Pareto frontier approach was used to identify best-fitting input sets, both regions of the input space (one where the intervention is valuable, the other where it is not) were represented in the Pareto frontier input sets, potentially presenting a more representative estimate of the uncertainty in the intervention’s incremental costs and benefits than either GOF weighting scheme alone.
While the Pareto frontier approach maintains greater diversity among best-fitting input sets than a summary GOF scoring system, it still cannot compensate for incomplete or inefficient searching of the input parameter space. The Pareto frontier approach identifies Pareto-optimal input sets among an initial population of input sets. However, if that initial population is not fully representative of the overall input space, the Pareto frontier approach cannot recover that lost diversity. The Pareto frontier approach is therefore not guaranteed to identify the global set of Pareto optimal input sets and the quality of the identified Pareto frontier will depend upon the diversity and representativeness of the initial population. Thus, it is important that the Pareto frontier approach be integrated with an effective and sufficiently thorough search procedure appropriate to the dimensionality and complexity of the calibration task.
Though we used random search in our demonstrations, it is important to note that the Pareto frontier approach can be integrated into directed search algorithms such as Nelder-Mead (21,22), simulated annealing (23,24), and genetic algorithms (14,23,25,26), in which the process of generating input sets is integrated with the method of assessing fit in an iterative process. It has been shown that directed search methods are more computationally efficient and identify input sets with higher quality fits to individual calibration targets than random search methods (6,13,14). Directed search algorithms using GOF scoring may be more likely to identify a relatively homogenous set of inputs and may be more sensitive to bias introduced by the selection of scoring weights due to the reinforcement of these effects with each iteration. Incorporating the Pareto frontier approach into a directed search algorithm allows the analyst to capitalize on the benefits of directed search, while still maintaining diversity in how those fits are achieved and ensuring that the final set of best-fitting input sets do not over-fit a set of scoring weights. The optimization literature contains several excellent descriptions of how to combine directed search algorithms with the Pareto frontier approach (14,22,24).
For probabilistic analysis, as we have done in our demonstrations, it is common for analysts to assume a uniform distribution over the best-fitting input sets identified through calibration. However, use of the Pareto frontier approach to identify best-fitting input sets does not preclude the assignment of differential weights to input sets identified to be on the Pareto frontier. Weighting may be desirable to reflect differences in likelihood of some input sets over others, data quality, to prioritize calibration targets that are most important to the analysis, or to exclude input sets with unacceptably poor fits on certain targets. Furthermore, analysts may wish to reduce the number of input sets used in probabilistic analysis for computational reasons. In such a situation, a sub-set of top weighted Pareto-optimal input sets (e.g. the top 50 input sets) could be used for analysis.
In this analysis, we have applied the Pareto frontier approach to the calibration of cohort Markov models, which produce deterministic outcomes for a given set of input parameter values. However, microsimulation is another common modeling approach, which incorporates stochastic elements of disease progression. The calibration of these models presents additional challenges due to the uncertainty in model outputs. In future work, we plan to adapt the Pareto frontier approach to the calibration of stochastic models, drawing on approaches such as Stochastic Frontier Analysis and other analogous methods from the multi-objective optimization literature to incorporate noise into the calibration process.
The concept of Pareto-optimality has been applied to problems of multiple competing objectives in a variety of fields, including the calibration of hydrologic models in civil engineering (27,28) and optimal design in systems engineering (29,30). However, the application of this method to the calibration of disease natural history models for health economic evaluation has not been previously described. Model calibration is a critical step in the development of these models, as the input parameters estimated through calibration are often highly uncertain. The process of calibration requires the analyst to make many decisions, which should be transparently reported (3) and systematically evaluated for their influence on results (7). The Pareto frontier approach is a method that is less sensitive to choice of fit metric and does not require that individual calibration targets be summarized into a single GOF score. As models for evaluating new medical technologies and public health programs increase in complexity, applying multi-objective optimization methods will be critical for efficient and effective model calibration.
Figure 7.
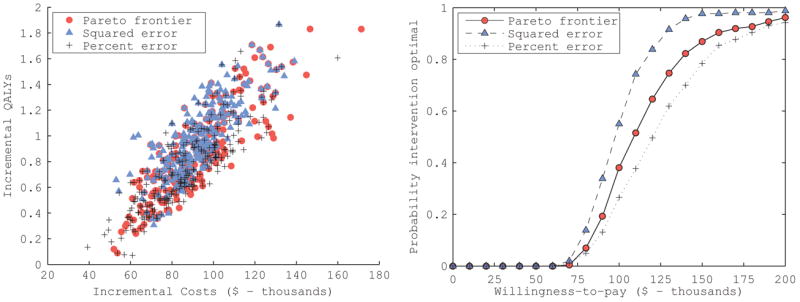
Cost-effectiveness results of transcatheter aortic valve replacement (TVAR) the compared to medical management for patients with severe aortic stenosis. The incremental costs and QALYs of the TAVR for each input set on the Pareto frontier (circles) and the top 260 best-fitting sets ranked according to an equal weighting of fits measured as the squared difference (triangles) or the absolute percent difference (crosses) between each calibration target and the corresponding model output are plotted. These results were used to generate the cost-effectiveness acceptability curves for the intervention that would be estimated under the different input set ranking metrics.
Acknowledgments
Financial support for this study was provided in part by the National Cancer Institute (K25CA133141). The funding agreement ensured the authors’ independence in designing the study, interpreting the data, writing, and publishing the report.
Appendix
Appendix Table 1.
Aortic stenosis natural history model inputs estimated using calibration
| Variable | Description | Range | Notes* |
|---|---|---|---|
| Hazard Ratio (HR) on Age-Specific Mortality Rate | |||
| NYHA class I/II symptoms | |||
| A | 2 to 6 months | 2-5.6 | A > B |
| B | 7+ months | 1.1-2.9 | |
| NYHA class III/IV symptoms | |||
| C | 2 to 6 months | 5.8-13.9 | C > D |
| D | 7 to 12 months | 4.1-12.8 | |
| E | 13+ months | 1.2-7.9 | E > B |
| Annual rate of hospitalization (per 10,000) | |||
| NYHA class I/II symptoms | |||
| F | 2+ months | 0-1,000 | |
| NYHA class III/IV symptoms | |||
| G | ≤ 12 months | 0-15,000 | G > F |
| H | 13+ months | 7,000-60,000 | H > G |
| Annual rate of progressing from NYHA class I/II to class III/IV symptoms (per 10,000) | |||
| TAVR | |||
| I | 2 to 6 months | 0-1,500 | |
| J | 7+ months | 0-6,000 | J > I |
| Balloon valvuloplasty | |||
| K | 2 to 6 months | 0-10,000 | |
| L | 7+ months | 0-5,000 | L < K |
| Annual rate of stroke (per 10,000) | |||
| TAVR | |||
| M | 2 to 6 months | 0-2000 | |
| N | 7+ months | 0-2000 | N < M |
| Balloon valvuloplasty | |||
| O | 2+ months | 0-2000 | 0 < N |
NYHA -- New York Heart Association
If the randomly drawn value for the parameter does not satisfy the constraint, the value is replaced by the closest value satisfying the constraint
Appendix Table 2.
Calibration targets for the aortic stenosis natural history model estimated using (12)
| Description | TAVR Mean (95% CI of target) | PARTNER OMM Mean (95% CI of target) |
|---|---|---|
| Death by any cause | ||
| 1 month | 5% (2-8%) | 2.8% (0-5%) |
| 6 months | 23% (17-31%) | 30% (22-38%) |
| 12 months | 31% (23-39%) | 52% (41-63%) |
| 18 months | 37% (26-49%) | 60% (45-75%) |
| 24 months | 43% (24-62%) | 66% (39-93%) |
| Death or hospitalization | ||
| 1 month | 11% (6-15%) | 12% (7-17%) |
| 6 months | 36% (27-44%) | 50% (40-61%) |
| 12 months | 43% (33-52%) | 72% (60-85%) |
| 18 months | 48% (35-61%) | 81% (65-97%) |
| 24 months | 56% (35-77%) | 90% (60-100%) |
| Stroke | ||
| 1 month | 5.0% (3.3-6.7%) | 1.8% (0.8-2.7%) |
| 12 months | 7.8% (5.8-9.8%) | 3.9% (2.5-5.4%) |
| Proportion of patients with NYHA class I/II symptoms | ||
| 1 month | 63% (56-70%) | 26% (19-32%) |
| 6 months | 60% (52-68%) | 19% (12-26%) |
| 12 months | 49% (41-58%) | 19% (10-27%) |
| Rate of change in symptom status (% change per month) | ||
| 1 to 6 months | -0.6% | -1.4% |
| 6 to 12 months | -1.8% | 0% |
| 1 to 12 months* | -0.6% |
NYHA -- New York Heart Association
The rate of change from 1 to 12 months was used instead of the rate of change from 6 to 12 months for the GOF scoring scheme 2 (percent error) to avoid dividing by zero.
References
- 1.Weinstein MC. Recent developments in decision-analytic modelling for economic evaluation. Pharmacoeconomics. 2006;24(11):1043–53. doi: 10.2165/00019053-200624110-00002. [DOI] [PubMed] [Google Scholar]
- 2.Russell LB. Exploring the unknown and the unknowable with simulation models. Med Decis Making. 2013;31(4):521–3. doi: 10.1177/0272989X11412078. [DOI] [PubMed] [Google Scholar]
- 3.Stout NK, Knudsen AB, Kong CY, McMahon PM, Gazelle GS. Calibration methods used in cancer simulation models and suggested reporting guidelines. Pharmacoeconomics. 2009;27(7):533–45. doi: 10.2165/11314830-000000000-00000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Taylor DCA, Pawar V, Kruzikas D, Gilmore KE, Pandya A, Iskandar R, et al. Methods of Model Calibration. Pharmacoeconomics. 2010;28(11):995–1000. doi: 10.2165/11538660-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 5.Vanni T, Karnon J, Madan J, White RG, Edmunds WJ, Foss AM, et al. Calibrating Models in Economic Evaluation: a seven-step approach. Pharmacoeconomics. 2011;29(1):35–49. doi: 10.2165/11584600-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 6.Kong CY, McMahon PM, Gazelle GS. Calibration of disease simulation model using an engineering approach. Value Health. 2009;12(4):521–9. doi: 10.1111/j.1524-4733.2008.00484.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Taylor DCA, Pawar V, Kruzikas DT, Gilmore KE, Sanon M, Weinstein MC. Incorporating calibrated model parameters into sensitivity analyses: deterministic and probabilistic approaches. Pharmacoeconomics. 2012;30(2):119–26. doi: 10.2165/11593360-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 8.Marler R, Arora J. Survey of multi-objective optimization methods for engineering. Struct Multidiscip Optim. 2004;26(6):369–95. [Google Scholar]
- 9.Gold MR, Siegel JE, Russel LB, Weinstein MC, editors. Cost-effectiveness in health and medicine. Oxford University Press; 1996. [Google Scholar]
- 10.Drummond M, O’Brien B, Stoddart G, Torrance G. Methods for the economic evaluation of health care programmes. Oxford University Press; 1997. [Google Scholar]
- 11.Simons CT, Cipriano LE, Shah RU, Garber AM, Owens DK, Hlatky MA. Transcatheter Aortic Valve Replacement in Nonsurgical Candidates With Severe, Symptomatic Aortic Stenosis: A Cost-Effectiveness Analysis. Circ Cardiovasc Qual Outcomes. 2013 doi: 10.1161/CIRCOUTCOMES.113.000280. in press. [DOI] [PubMed] [Google Scholar]
- 12.Leon MB, Smith CR, Mack M, Miller DC, Moses JW, Svensson LG, et al. Transcatheter aortic-valve implantation for aortic stenosis in patients who cannot undergo surgery. N Engl J Med. 2010;363(17):1597–607. doi: 10.1056/NEJMoa1008232. [DOI] [PubMed] [Google Scholar]
- 13.Srinivas N, Deb K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol Comput. 1995;2(3):221–48. [Google Scholar]
- 14.Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput. 2002;6(2):182–97. [Google Scholar]
- 15.Karnon J, Czoski-Murray C, Smith KJ, Brand C. A hybrid cohort individual sampling natural history model of age-related macular degeneration: assessing the cost-effectiveness of screening using probabilistic calibration. Med Decis Making. 2009;29(3):304–16. doi: 10.1177/0272989X08327491. [DOI] [PubMed] [Google Scholar]
- 16.Kim JJ, Kuntz KM, Stout NK, Mahmud S, Villa LL, Franco EL, et al. Multiparameter calibration of a natural history model of cervical cancer. Am J Epidemiol. 2007;166(2):137–50. doi: 10.1093/aje/kwm086. [DOI] [PubMed] [Google Scholar]
- 17.Weinstein MC, Skinner JA. Comparative effectiveness and health care spending--implications for reform. N Engl J Med. 2010;362(5):460–5. doi: 10.1056/NEJMsb0911104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Henrion M. Propagation of uncertainty in Bayesian networks by probabilistic logic sampling. Proc 2nd Conf Uncertain Artif Intell; 1986. pp. 149–63. [Google Scholar]
- 19.Shachter R, Peot M. Simulation approaches to general probabilistic inference on belief networks. Proc 5th Conf Uncertain Artif Intell; 1989. pp. 311–8. [Google Scholar]
- 20.Dias S, Sutton AJ, Welton NJ, Ades AE. Evidence Synthesis for Decision Making 6: Embedding Evidence Synthesis in Probabilistic Cost-effectiveness Analysis. Med Decis Making. 2013;33(5):671–8. doi: 10.1177/0272989X13487257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nelder J, Mead R. A simplex method for function minimization. Comput J. 1964;7(4):308–13. [Google Scholar]
- 22.Ghiasi H, Pasini D, Lessard L. Pareto frontier for simultaneous structural and manufacturing optimization of a composite part. Struct Multidiscip Optim. 2009;40(1-6):497–511. [Google Scholar]
- 23.Davis L. Genetic algorithms and simulated annealing. Pitman Publishing. 1987 [Google Scholar]
- 24.Bandyopadhyay S, Member S, Saha S, Member S, Maulik U, Deb K. A Simulated Annealing-Based Multiobjective Optimization Algorithm : AMOSA. 2008;12(3):269–83. [Google Scholar]
- 25.Holland JH. Adaptation in natural and artificial systems. Ann Arbor, MI: U Michigan Press; 1975. [Google Scholar]
- 26.Goldberg DE. Genetic algorithms in search, optimization, and machine learning. Addison-Wesley; 1989. [Google Scholar]
- 27.Boyle DP, Gupta HV, Sorooshian S. Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour Res. 2000;36(12):3663–74. [Google Scholar]
- 28.Khu ST, Madsen H. Multiobjective calibration with Pareto preference ordering: An application to rainfall-runoff model calibration. Water Resour Res. 2005;41(3) W03004. [Google Scholar]
- 29.Jourdan DB, de Weck OL. Multi-objective genetic algorithm for the automated planning of a wireless sensor network to monitor a critical facility. In: Carapezza EM, editor. Proc SPIE. 2004. pp. 565–75. [Google Scholar]
- 30.Smaling R, De Weck O. Assessing Risks and Opportunities of Technology Infusion in System Design. Syst Eng. 2007;10(1):1–25. [Google Scholar]