Methods for Specific Electrode Resistance Measurement during Transcranial Direct Current Stimulation

Abstract

Background

Transcranial Direct Current Stimulation (tDCS) is investigated to treat a wide range of neuropsychiatric disorders, for rehabilitation, and for enhancing cognitive performance. The monitoring of electrode resistance before and during tDCS is considered important for tolerability and safety, where an unusually high resistance is indicative of undesired electrode or poor skin contact conditions. Conventional resistance measurement methods do not isolate individual electrode resistance but rather measures overall voltage. Moreover, for HD-tDCS devices, cross talk across electrodes makes concurrent resistance monitoring unreliable.

Objective

We propose a novel method for monitoring of the individual electrode resistance during tDCS, using a super-position of direct current with a test-signal (low-intensity and low-frequency sinusoids with electrode– specific frequencies) and a single sentinel electrode (not used for DC).

Methods

To validate this methodology, we developed lumped-parameter models of two and multi-electrode tDCS. Approaches with and without a sentinel electrode were solved and underlying assumptions identified. Assumptions were tested and parameterized in healthy participants using forearm stimulation combining tDCS (2 mA) and sinusoidal test-signals (38 μA and 76 μA peak to peak at 1 Hz, 10 Hz, and 100 Hz) and an in vitro test (where varied electrode failure modes were created). DC and AC component voltages across the electrodes were compared and participants were asked to rate subjective pain.

Results

A sentinel electrode is required to isolate electrode resistance in a two-electrode tDCS system. For multi-electrode resistance tracking, cross talk was aggravated with electrode proximity and current/resistance mismatches, but could be corrected using proposed approaches. Average voltage and average pain scores were not significantly different across test current intensities and frequencies (two-way repeated measures ANOVA) indicating the test signal does not itself confound electrode stability or sensation. DC-resistance to AC-impedance ratio was ~1:08, averaged across frequencies.

Conclusion

Using the methods developed here, a test signal can predict DC electrode resistance. Since unique test frequencies can be used at each tDCS electrode, specific electrode resistance can be resolved for any number of stimulating channels – a process made still more robust by the use of a sentinel electrode. These findings provide the first method for monitoring individual electrode resistance during tDCS that integrated into devices may minimize irritation at electrodes.

Introduction

Transcranial Direct Current Stimulation (tDCS) is investigated to treat a range of neuropsychiatric disorders, for rehabilitation, and for altering cognitive performance [1, 2]. When standard protocols are followed, tDCS is well tolerated with common adverse events limited to transient skin sensation and erythema. When established protocols are not followed, tDCS can produce significant skin irritation. Given that skin-sensation [3, 4, 5] and skin irritation are the primary risks of tDCS [6, 7], proper electrode preparation and then monitoring of electrode resistance are important to ensure the stimulation is reproducible and well tolerated (as well as sham reliability in clinical trials). The monitoring of electrode resistance before and during tDCS is considered important for tolerability and safety [8, 9, 10], where an unusually high electrode resistance is indicative of undesired electrochemical changes [11] or poor skin contact conditions. Yet, conventional methods to monitor electrode resistance are flawed conceptually and technically.

“Electrode resistance” during tDCS in fact reflects an aggregate metric of conditions in the electrodes (e.g. over-potential; [12]) and skin (see discussion for terminology). Resistance is conventionally measured between two electrodes by applying a test current before tDCS or measuring voltage during tDCS, and dividing the voltage by the current [13]. While convenient, this method does not distinguish the contribution from each electrode. Non-linear tissue impedance and tissue generated potentials, themselves a function of the applied current, also confound measurement. Moreover, when multiple electrodes are used (as in HD-tDCS) the problem is aggravated with cross talk across electrodes making concurrent resistance monitoring unreliable. Here we present the first approach that allows measurement of individual electrode resistance using any number of electrodes or electrode configurations.

The need to combine electrode resistance measurement with current flow for neuromodulation raises special concerns not previously addressed. For example, electrode resistance measurement during EEG is achieved by testing individual pairs of electrodes sequentially [14, 15], such that at any given instant only one pair is activated. While this approach could be applied prior to tDCS, during tDCS all electrodes need to be active for neuromodulation. A potential solution is a super-position of direct current stimulation with a test-signal; but, to be meaningful, such a test signal should provide information related to DC-resistance of the electrodes. Similarly, in Electrode-Impedance-Tomography (EIT refer to measuring tissue resistance using electrodes, not measuring electrode resistance), electrode pairs can be tested sequentially and independently and care is taken to avoid changing or measuring the resistance of electrodes [16, 17, 18]. Continuous direct current is avoided in all these applications because it generates changes in electrode impedance and it precludes time or frequency multiplexing. Thus methods for using a low-intensity test signal in combination with direct current stimulation remains to be proposed and tested. Here we validated methodology for monitoring of individual electrode resistance during two or multi-channel tDCS by using a low-intensity low-frequency test signal (sinusoids) with electrode-specific frequencies and an additional sentinel electrode that is not used for direct current stimulation.

Materials and Methods

Participants

Six healthy volunteers (all male; age range 20–30 years; mean age 22.8 ± 2.4) participated in this study. The experiment was conducted after receiving approval from the CCNY local Ethics Committee and all participants gave written informed consent before participating in the experiment. They were seated in a relaxed position with their stimulated arm on a bench top.

Stimulation

The main input signal superimposed a direct current source (2 mA) with an alternating current source (38 μA and 76 μA pk-pk at 1 Hz, 10 Hz, and 100 Hz) applied on the subjects arm for 4 min. We aimed to establish a relationship between the DC and the test signal (AC) to predict electrode resistance (as defined in discussion). A sentinel (none DC current carrying) electrode was used to isolate electrode impedance and eliminate tissue resistance contamination from one or more sources. A trapezoidal current input composed of a 30 s test signal (AC, 38 μA or 76 μA) followed by a DC ramp up to 2 mA (30 s duration), a 2 min stimulation phase composed of superimposed AC and DC signal (main input signal), a DC ramp down (30 s), and a post stimulation test signal (AC, 30 s) was applied through tin electrodes (EASYCAP, Herrsching, Germany) on the subjects’ forearm. The LabVIEW (National Instruments, TX, USA) generated voltage signal output from a NI 9263 cDAQ Module (National Instruments (NI), TX, USA) was converted to a constant current through an analog current controller (A-M Systems Analog Stimulus Isolator, WA, USA).

Subject experimental procedures

A combined DC and test-signal was used to stimulate forearms of the six healthy participants under different current amplitudes (38 μA and 76 μA) and frequencies (1 Hz, 10 Hz, and 100 Hz). Prior to simulation, the skin was cleaned with dilute saline. Rubber straps and electrode holders from Soterix Medical Inc. (NY, USA) were secured on the forearm (10.2 cm apart) and uniformly filled with a conductive gel (Signa, NJ, USA). The anode and cathode electrodes were positioned proximal and distal to the hand, respectively, and connected to the analog current isolator/stimulator. Voltage was recorded across the stimulator. A manual switch was placed in series with the circuit to avoid transient current spikes and ensure that the skin impedance doesn’t change until the stimulation session begins.

In vitro electrode testing

While conducting in vitro electrodes testing on parafilm sheets, the electrodes were positioned on top of conductive gel (Signa). In case of Type A error and method of correction using a sentinel electrode, 2 mA DC (Source 1 (S1)) was passed through anode and cathode and a test signal (38 μA pk-pk at 10 Hz as Source 2 (S2)) was passed through the anode (shared) and sentinel. Voltage was recorded across sentinel and shared anode. In Type B error and method for correction using sinusoidal test signal, first source (S1) with test signal (38 μA at 10 Hz) superimposed on top of DC (0.5 mA) energized anode1 and cathode1 and a DC current (second source (S2)) of 2 mA was passed through anode 2 and cathode 2. Voltage across anode 1 and cathode 1 was acquired for this approach.

Data recording and Impedance analysis

Unless otherwise stated, voltage data from stimulation were acquired using NI 9229; an analog input module and Lab VIEW. In experiment where independent current sources were used, data were collected using multi-meters. Acquired voltage signal (Fig. 3A) was first isolated into test signal (sinusoid) voltage using high pass filter (Fig. 3B) and DC signal using low pass filter (Fig. 3E). Specific cut-off frequencies were selected for all stimulation frequencies. Test signal was converted into RMS (root mean squared) voltage (Fig. 3C) and divided by the RMS current to calculate the AC-impedance (Fig. 3D). DC-resistance was determined by dividing DC voltage component by the DC current (Fig. 3F).

Figure 3. Representative analysis for combined DC resistance and AC impedance measurement.

(A) Voltage signal measured across the electrodes. 2 mA DC current is applied for 2 min with an additional ramp-up and ramp-down across a subject’s forearm. A 10 Hz, 38 μA test sinusoidal current (pk-pk) is also applied prior, during (superimposed on the DC), and post stimulation. (B) High pass filtered signal revealing the test signal: AC component. (C) RMS voltage of the AC component. (D) Calculated AC impedance. (E) Low pass (DC component) voltage filtered signal. (F) Calculated DC resistance.

Pain analysis

Subjective pain was acceded by asking every participant to rate their pain level during every 30 s of stimulation phase excluding pre and post-stimulation. Participants rated their skin sensation in the scale of 1–10; visual analogue scale (VAS) [7].

Statistical analysis

The data were evaluated using MATLAB (MA, USA). Two-way repeated measures ANOVAs (analysis of variance) were used for each output measures (pain sensation, average voltage and DC-resistance to AC- impedance ratio) with current intensities and frequencies as factors to analyze interactions between the two factors and to account testing within each participants. Critical value < 0.05 was accepted as a statistical difference between groups.

Results

In the first part of results, we define the problem - which is unrecognized in current tDCS and HD-tDCS - and our proposed solution. This also allows us to identify assumptions of our solution. The second part tests those assumptions experimentally. The third part illustrates the solution through experiment.

Part 1: Problem Definition, Solution, and Assumptions to be tested

The non-triviality of resistance measurement during two electrode tDCS

Fig. 1B is a simplified lumped parameter model of electrode resistance during tDCS. The complete “cell” across which net resistance can be measured (at the output terminals of the stimulator) includes two electrodes and tissue. The stimulator (current source, S1) generates current (I1) across the cell and the resulting voltage is measured (voltmeter) as indicative of electrode resistance. The presence of multiple elements in itself makes it impossible to determine the contributing element to a resistance increase (e.g. is electrode 1, electrode 2, and/or tissue) as shown in the following equation.

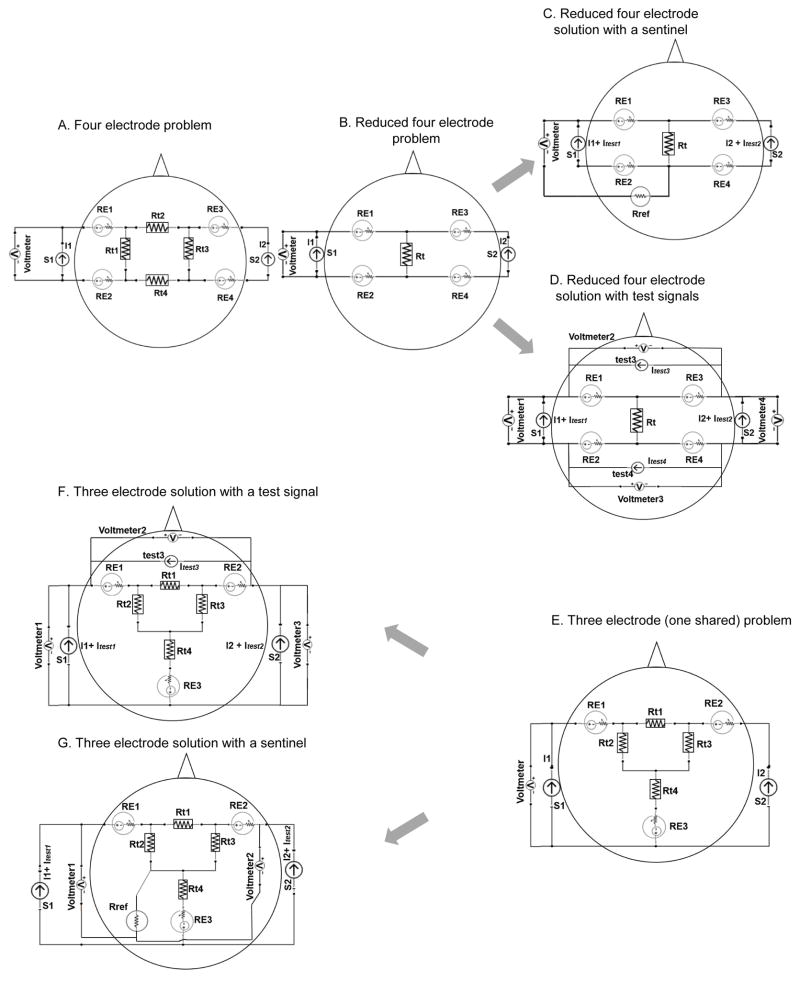
Figure 1. Lumped circuit analysis of transcranial Direct Current Stimulation (tDCS) using two electrodes with an additional sentinel electrode that does not carry direct current.

(A) Illustrates our assumption of using a test signal (test) and a sentinel (Rref) to predict DC-voltage. This example includes two sources, S1 (DC) and a test AC signal, two active electrodes used for DC simulation: RE1 and RE2, and a sentinel electrode (Rref). We assume that the AC voltage detected across RE1 and Rref can predict the DC voltage (hence DC resistance) of RE1. (B) Illustrates the need for methodology to detect single electrode resistance changes. The schematic has two electrodes (RE1 & RE2) and a DC source (S1). The resulting voltage drop across these electrodes is function of tissue impedance (Rt) and the resistance of both electrodes. (C) Presents a solution for the problem indicated in B based on the assumptions outlined in A, where a sentinel electrode (Rref) is used to selectively monitor an stimulating electrode (in this case RE1) of interest. In this case a single source produced a combined direct current with superimposed test AC signal. And sentinel electrode (not used for DC stimulation) is required, but not additional current sources.

$$Vt=I1(RE1+Rt+RE2)$$ (i)

where the total voltage (Vt) measured across two active electrodes (RE1 & RE2) is found assuming a linear relationship between current I1 and sum of electrodes resistance and tissue impedance (Rt). The matter is further complicated by the complex non-linear impedance of each electrode reflecting the electrochemistry as the electrode surface before and during direct current stimulation [11]. For illustration, we simplify this electrode resistance (as defined in discussion) as a voltage source, reflecting electrode over-potential, and a non-linear resistance, reflecting how current application produces a further voltage across the electrode. Tissues (skin, bone, fat, brain, etc.) also offer complex impedances (current and time dependent) and generate potentials, but for convenience are also considered a resistance. Equation (i) is thus not strictly valid. Simplistically, the “resistance” reported during tDCS (see discussion) is the measured voltage (Vt) divided by the applied current (I1). But the voltage measured across the cell, before or during direct current stimulation is not a trivial function of “electrode resistance”. For example, the electrode over-potential contributes to Vt and the impedance is itself a function of the amount of current applied [13]. Our purpose here is to simply develop a measure to resolve the voltage across a single resistance (e.g. the voltage across RE1) during two and multi-electrode tDCS.

Use of test signal and sentinel electrode

Fig. 1C illustrates a schematic for our basic solution. The use of a third “sentinel” electrode (Rref) that is not involved in stimulation is common in electrochemical analysis [19]. The potential measured between any given active electrode and the sentinel electrode, reflects only voltage drop across that active electrode and tissue voltage contribution as shown in the equation below:

$$Vt=(I1+\mathit{Itest})\left(\frac{Rt1.Rt2}{(Rt1+Rt2+Rt3)}+RE1\right)$$ (ii)

where Rt1, Rt2, and Rt3 are tissue resistances and Vt reflects the voltage drop across RE1. This step in itself enhances the fidelity of electrode resistance measurement by isolating a single electrode. If RE1 is significantly larger than the tissue impedances, then Vt is assumed to largely reflect the impedance of RE1 (Vt = I1 + Itest)RE1). More generally, assuming linear relation, equation (ii) cannot be applied.

Up to this point we have considered application of only direct current and measurement of the resulting voltage. We proposed the addition of a further current (“Itest” in Fig. 1C), a low-intensity and frequency test signal that generates a characteristic voltage across the active electrode, which in turn will be a sinusoid component in Vt superimposed on the voltage generated by the direct current stimulation. The central assumption of this report is that this sinusoidal voltage is representative in magnitude of the voltage generated across RE1 by the passage of direct current. This assumption is trivial where one assume Ohmic current flow. But given the complexity of the electrode interface, including electrode over-potential, this assumption requires validation.

Fig. 1A rephrases the lump-parameter model to clarity this assumption. Passage of DC current (I1) by S1 produces complex over-potential and impedance changes in electrode RE1 and a direct voltage across RE1. This is the “DC impedance” of the electrode, which is the so-called “resistance” of interest in tDCS. Will a sinusoidal current simultaneously passed across RE1, produce a sinusoidal voltage that is related to this direct voltage? At face value, the addition of a test signal does not provide more information in a two electrode system, however if this test signal predict DC resistance of an electrode, it can be leveraged during multi-electrode tDCS, as explained next.

In exploring sinusoid test-signal tracking of DC resistance, we will test a range of frequencies and intensities. And we further will evaluate if the passage of sinusoidal current itself does not change the electrical performance of the electrode or skin impedance, as well as that the subject sensation is not a function of test signal intensity or frequency.

Further cross talk during resistance measurements in multi-electrode tDCS

Here, we represented two independent current sources (S1 and S2) though this analysis can be extended to any number of electrodes and sources (Fig. 2). In a four electrode example, each current source is connected to distinct two stimulating electrode (RE1, RE2 to S1 & RE3, RE4 to S2; Fig. 2A, 2B, 2C, & 2D) while in the three electrode example (RE1, RE2, RE3), one electrode (RE3) is shared by the stimulation sources (Fig. 2E, 2F, & 2G). Tissue impedance is again represented as multiple lumped parameters for the purpose of illustration (such as Rt, Rt1, Rt2, Rt3, Rt4, etc.). Voltage measurement can be obtained across the current sources (the voltage being produced by the current source accessible at the output leads) or using additional voltmeters and a sentinel electrode (Rref). For each electrode, the electrode potential and non-linear impedance are represented by a single lumped parameter but we emphasize again these quantities are a complex function of time and current passage.

Figure 2. Lumped circuit analysis of transcranial Direct Current Stimulation (tDCS) using four or three DC stimulating electrodes with solutions for electrode resistance tracking solutions using either an additional sentinel electrode or additional current sources.

(A) Representation of a four-electrode arrangement problem which is reduced to a simpler form as shown in (B). (C) First solution for problem in (B) using a sentinel electrode and a test signal superimposed on an existing current source. (D) Second proposed solution with using additional test current sources but no additional electrodes. (E) Representation of a stimulation montage using three electrodes when there are two independent electrodes (RE1 & RE2) and a common shared electrode (RE3). (F) Illustration of the first solution of problem situation in (E) where a test signal produced by additional current sources are passed across two active electrodes to resolve specific DC-electrode resistance. (G) Another solution of the same problem where a sentinel is used without requiring additional current sources. For all of the cases, confound of tissue resistance is also shown (see text).

For two independent sources that do not share electrodes (Fig. 2A), the voltage measured across source S1, is also influenced by the current source S2 and a function of specific tissues impedances. Assuming linearity the voltage across S1 is:

$$Vt=I1\left(RE1+\frac{Rt1(Rt2+Rt3+Rt4)}{(Rt1+Rt2+Rt3+Rt4)}+RE2\right)+I2\left(\frac{Rt3.Rt1}{(Rt1+Rt2+Rt3+Rt4)}\right)$$ (iii)

The degree of cross-talk from S2 to the voltage recording across S1 is a function of tissue resistivities. Depending on polarity, the voltage across S2 may be higher or lower. However, even for tissue resistivities leading to relatively low coupling (e.g. Rt3 ≪ Rt2), a large S2 source (e.g. 2 mA) may contribute significantly to the voltage across a smaller S1 source (e.g. 0.1 mA). By further extension, for a multiple channel system (e.g. 10 sources with 0.2 mA) the voltage measured at any given source may be significantly contaminated by tissue coupling across other sources making “electrode impedance” calculation unreliable.

To illustrate our solution, a further simplified four stimulating electrode lumped circuit is shown in Fig. 2B which is governed by the following equation assuming linearity:

$$Vt=I1(RE1+RE2+Rt)+I2(Rt)$$ (iv)

where DC current (I2) from S2, and by extension additional sources, would confound the voltage (Vt) reading across S1.

For the four-electrode example, two solutions that both remove this electrode-cross talk and furthermore allow isolation of single-electrode impedance are shown. The first solution using a test signal and sentinel electrode is shown in Fig. 2C, where the voltmeter (tuned to the frequency of test1) will detect the sinusoid test1, which under the assumptions explained above (illustrated in Fig. 1A), would predict the DC electrode impedance of RE1. The total voltage across S1 assuming linearity is given by:

$$Vt=(I1+\mathit{Itest}1)(RE1+Rt)+(I2+\mathit{Itest}2)Rt$$ (v)

But considering only the test frequency, the contributing voltage will be:

$$Vt(\mathit{test})=\mathit{Itest}1(RE1+Rt)+\mathit{Itest}2(Rt)$$ (vi)

Here, assuming RE1≫Rt, and our overall assumption, provide a measure of single electrode impedance. A similar approach (not shown) can be used to determine the DC electrode resistance of RE3. A test sinusoid signal, test2, can be applied across RE2 and RE3 but with a distinct frequency as test1, such that there is no cross talk across these test signals. The DC electrode impedance of RE3 and RE4 can be measured using a voltmeter across RE3 and RE4 or Rref, where that voltmeter is tuned to the frequency of test2. Some powerful analysis can be obtained from this solution: 1) only one additional electrode is needed (Rref); 2) no additional current sources are needed if a single current source can produce both DC and test signals; 3) as long as Rref does not fail, the system is robust to the failure of any given electrode.

For the four-electrode case, the second solution (Fig. 2D) does not involve the use of a sentinel electrode (no Rref electrode). Here, two additional current sources (test3, and test 4) generate test signals of unique frequencies, with associated voltmeters. Two test signals are also provided with the DC sources (test1 and test 2). A total of four voltmeters (four equations) and four electrodes (four unknowns) provide a substrate for solving for the impedance of each electrode where assuming linearity, the voltage across the S1 voltmeter is given by:

$$Vt=(I1+\mathit{Itest}1)(RE1+RE2+Rt)+(I2+\mathit{Itest}2)Rt+\mathit{test}3(RE1)$$ (vii)

A similar equation can be provided for each voltmeter and, after removing all tissue impendences under the assumption they are smaller than electrode impendences, all solves simultaneously to calculate the impedance of each electrode as:

$$Vt=(I1+\mathit{Itest}1)(RE1+RE2)+\mathit{test}3(RE1)$$ (viii)

Note that in this solution: 1) no additional electrodes are needed but additional current sources are; 2) if any electrode fails completely (source open) it may not be possible to obtain a solution for any of the electrode impedances. The underlying assumption for test signal predicting DC-resistance is still required.

Finally, we considered the case of two current sources (S1 and S2) and three stimulating electrodes (RE1, RE2, RE3) such that one stimulating electrode (RE3) is shared by the two current sources (Fig. 2E). When a stimulating electrode is shared by two sources, two measurements (two voltages) and three key unknowns (three electrode impedances) arise and thus do not allow identification of faulty electrode responsible for any increase in resistance. Assuming linearity, the voltage across S1 is given by:

$$Vt=I1\left[Rt2\frac{Rt1+Rt3}{(Rt1+Rt2+Rt3)}+RE1+RE3+Rt4\right]+I2\left(\frac{Rt2.Rt3}{(Rt1+Rt2+Rt3)}+RE3+Rt4\right)$$ (ix)

Again if our assumption of electrode resistance being greater than that of tissue impedances is supported, this equation can be further reduced (assuming linearity) to:

$$Vt=I1(RE1+RE3)+I2(RE3)$$ (x)

For this case, two solutions are illustrated with a sentinel electrode (Fig. 2G) and without a sentinel but with an extra current sources (Fig. 2F). As with the four-electrode case, both solutions allows calculation of individual electrode resistance, but for the solution without a sentinel electrode, an additional test current sources are needed and must be connected across novel combinations of electrodes. For the first solution with the sentinel, the voltmeter across S1 will detect (assuming linearity):

$$Vt=(I1+\mathit{Itest}1)\left[\frac{Rt2(Rt1+Rt3)}{Rt1+Rt2+Rt3}+RE1\right]+(I2+\mathit{Itest}2)\left(\frac{Rt2.Rt3}{Rt1+Rt2+Rt3}\right)$$ (xi)

If one assumes RE1 is greater than any tissue resistance, and consider only the test1 frequency, this reduces to

$$Vt(\mathit{test})=\mathit{Itest}1(RE1)$$ (xii)

For the second solution to the three-electrode case without a sentinel, the S1 voltmeter will detect:

$$Vt=(I1+\mathit{Itest}1)\left[\frac{Rt2(Rt1+Rt3)}{(Rt1+Rt2+Rt3)}+RE1+RE3+Rt4\right]+(I2+\mathit{Itest}2)\left(\frac{Rt2.Rt3}{Rt1+Rt2+Rt3}+RE3+Rt4\right)+\mathit{test}(RE1)$$ (xiii)

A similar equation can be provided for each voltmeter and, after removing all tissue resistance under the assumption they are smaller than electrode resistance, all can be solved simultaneously.

Part 2: Testing of assumptions, and identification of effective test signals

This section aims at testing the underlying assumptions of the proposed solution (not illustrating its application per se which is left for Part 3). The core assumption to be tested is the tracking of DC-resistance by the AC test signals; several intensities and frequencies are compared. Secondary assumptions include that the selected signals do not confound the application or tolerability of tDCS as indicated by average voltage and subjective pain (Fig. 4). Experiments were conducted on in a parafilm sheet (gel base) and on the forearms of subjects. All participants tolerated the stimulation hence none of the experimental sessions were interrupted.

Figure 4. Interaction of AC test signal with electrical performance and subjective sensation.

(A) Subjective average pain score, (B) average voltage, (C) average DC-resistance to AC-impedance ratio during forearm testing and (D) average DC-resistance to AC- impedance ratio during in vitro test. Values represent the average during the phase of constant current (excluding ramp up and ramp down). Average pain scores were based on subjective VAS ratings. Results demonstrate that using AC test signal at different amplitudes and frequencies did not change pain score or the overall impedance trajectory. The averaged DC-resistance to AC-impedance ratio was also consistent (~1.08) across frequencies and intensities. The resistance ratio was found to be lower at 76 μA (pk-pk) compared to 38 μA (pk-pk) in vitro.

Pain analysis during Stimulation

A two-way repeated measures ANOVA of current intensities (38 μA & 76 μA) and frequencies (1 Hz, 10 Hz, and 100 Hz) during stimulation was conducted. The main effect of current intensities and frequencies on pain sensation was not significant; F (1, 5) =2.8, p=0.16 & F (2, 10) =3.3, p=0.08 as shown in Fig. 4A. The interaction between these two factors was not significant, F (2, 10) =0.16, p=0.86.

Average voltage during Stimulation

Average voltage was independent of current intensities and stimulation frequencies, F (1, 5) =0.05, p=0.83 & F (2, 10) =0.7, p=0.57. The interaction was not significant, F (2, 10) =0.59, p=0.57 (Fig. 4B).

Comparing DC-resistance from AC-impedance on forearm

DC-resistance to AC-impedance ratio across stimulation frequencies was significantly different, F (2, 10) =31.03, p=0.0001 (Fig. 4C). The resistance ratio was slightly higher at 1 Hz (DC:AC_{1 Hz} =1.14) compared to that at 10 Hz (DC:AC_{10 Hz} =1.02) and 100 Hz (DC:AC_{100 Hz}=1.12). No significant difference was found at the different current levels, F (1, 5) =1.46, p=0.28. Further analysis of the interaction between current intensities and frequencies was not significant, F (2, 10) =0.21, p=0.82.

Error percentage in Predicting Electrode Resistance

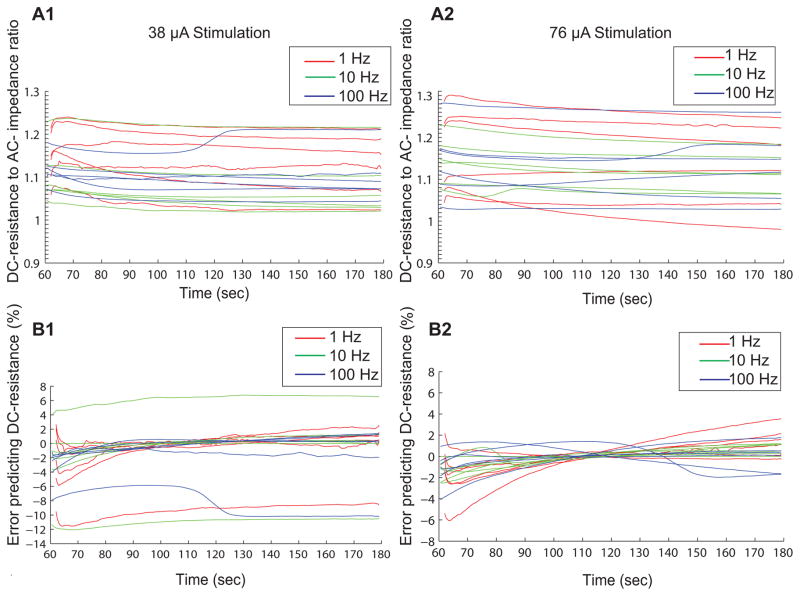
The error percentage ([predicted DC-resistance − actual DC-resistance]/actual DC-resistance, where the predicted DC-resistance = DC:AC ratio × actual AC-impedance) in predicting DC-resistance by AC-impedance was −2.56 ± 3.98 (mean ± SD) at 38 μA and −1.27 ± 1.72 at 76 μA (at the onset of the stimulation phase, 60 s), −1.09 ± 4.16 at 38 μA and 0.26 ± 0.34 at 76 μA (120 s after the onset of stimulation), and −0.74 ± 4.48 at 38 μA and 0.71 ± 1.22 at 76 μA (at the end of stimulation, 180 s). The inter-individual variability contributes to an over- or under-estimation of the prediction error as seen in Fig. 5B1 and Fig. 5B2.

Figure 5. Reliability of predicting DC-resistance by AC-impedance.

Average DC-resistance to AC-impedance ratio and error percentage in predicting DC- resistance at 38 μA (A1, B1) and at 76 μA (A2, B2) during forearm stimulation at different stimulation frequencies.

DC-electrode resistance to AC-impedance ratio in gel, comparison with skin

The DC-resistance to AC-impedance ratio in forearm stimulation was found to be higher than that of the in vitro test (Wilcoxon rank sum test: p<0.05, Fig. 4D). Though interesting, our focus here is on application, so we do not diagnose here the source of this difference between forearm (in vivo) and gel (in vitro) testing; contribution may include frequency dependence of tissue impedance of tissue, which would decrease AC impedance [20], as well as tissue, namely skin, generated potentials [21] that would increase the DC potential. The precision of prediction (above) is thus specific to the DC- resistance to AC-impedance ratio determined from in vivo testing, while the in vivo to in vitro difference reinforces the complex nature of tissue impedance and the none-triviality of developing an approach to track electrode impedance during tDCS.

Part 3: Application of solutions in experiment

Using in vitro electrode testing, we consider two types of resistance measurement errors and test the correction provided by our invention: Type A errors related to cross talk across systems and Type B errors identifying failing electrode.

Correction of Type A error

Type A error result when a single electrode fails resulting in a voltage increase across the entire two-electrode system. We demonstrated this error and method of correction using three-electrode system (Fig. 6A1 & 6B1), where two electrode are connected to a DC current source and a test sinusoid is passed between one of the active electrodes (shared) and a third sentinel electrode. This test was carried out with electrodes in conductive gel. We mimicked electrode failure (of the shared electrode) by using a corroded tin electrode and by reducing the contact area of this electrode and the conductive gel after 100 s of stimulation for about 20 s. Likewise, we also demonstrated another electrode failure condition (electrode connected to DC source only) after 145 s for 20 s too. While the measured voltages across the shared electrode and sentinel increased (shown in Fig. 6A1 in terms of DC-resistance), only by inspecting the test signal, it was possible to determine the electrode of interest was failing.

Figure 6. In vitro demonstration of failures to detect single electrode impedance changes (electrode faults) with specificity and methods to correct.

(A1, B1) Type A error and method of correction using a sentinel electrode and test signal. A DC source (S1) energizes an anode and cathode with 2 mA. A second source (S2) passes a test sinusoidal current (38 μA pk-pk at 10 Hz) between the anode (shared) and a sentinel electrode (not used for direct current). At any instance (here around 100–120 s of stimulation; A1) when the anode electrode becomes faulty - in this case intentionally through reduced electrode gel contact area - the voltage/resistance increases across the DC current source and at the time the AC voltage/impedance increases across the second test source. In contrast, when a fault is created at the cathode, DC-resistance across the first source again increases but AC-impedance at the second course is unaffected. (A2, B2) Type B error and method for correction using sinusoidal test signal. Two independent sources pass direct current (DC) across independent pairs of electrodes. Source 1 (S1) generates superimposed test signal (38 μA) on top of a DC (0.5 mA) while Source 2 (S2) generates 2 mA DC. S2 is activated transiently (around 100 to 150 s). Whereas the DC voltage/resistance across S1 is contaminated by the voltage produced when S2 is energized, the AC voltage/impedance is not affected.

Correction of Type B error

Type B error are generated when two current sources are active and one current source produces a voltage that is detected by the other current source resulting in an error in resistance prediction – this error does not require that current source share an electrode when the error voltage is generated across tissue. We demonstrated this error and method for correction using a simple four electrode system (in conductive gel) with two independent current sources connected to four electrodes (Fig. 6A2 & 6B2). One current source (S1) has a superimposed test sinusoid on top of DC while the other source was a tDCS. The test signal impedance did not change upon the introduction of a second source (Fig. 6B2). In contrast, the DC-impedance sharply increased (Fig. 6A2) as the second source (S2) was turned on (100–149 s) and decreased when S2 was turned off (150 s). Hence, an introduction of a second current source or a faulty electrode in a multi-channel stimulation can result in contaminated electrode impedance. Therefore, a test signal across electrodes can precisely predict DC-resistance correcting for Type B error.

Discussion

Clarification of “electrode resistance” during tDCS

The electrochemical performance of electrodes under DC, as well as tissue, has been addressed elsewhere [12] - our focus here is on practical remedy rather than theory. None-the-less, context is necessary to inform rational design. tDCS is current controlled with the voltage output (also called here the total source-voltage) of the stimulator adjusted to maintain a controlled current application. In tDCS, when “resistance” is described, it is generally referring to the voltage at the output of the current source divided by the current applied – through the application of ohms law. However, the electrode and tissue are not simply resistive (e.g. explained by ohms law). “Impedance” refers to broader relation between current applied and the voltage associated with maintaining that current flow. Linear impedance includes frequency specific responses (e.g. the response to sinusoids of varied frequencies). The electrode and tissue are complex non-linear impedance. For example, the impedance may change over time and both electrodes and tissue may generate internal potentials. For electrodes, this is the over-potential from the electrode interface [11] and for tissue this includes skin potentials [24]. How then does this complex system of impedance inform monitoring of “electrode resistance” for tDCS safety? It is accepted that during tDCS, significantly increased voltage (at the current source output), which is associated with increased cell impedance, suggests a non-optimal conditions at the electrode or electrode skin interface. This is biophysically justified since maintaining a low electrode over-potential voltage (see [11] for detailed discussion) at the electrodes and high conductivity (e.g. good gel/saline contact with the electrode and skin) are associated with minimized chemical reactions and good contact. These in turn promote, but do no guarantee, tolerated stimulation. During tDCS, the voltage drop across a given electrode divided by the DC current across that electrode is what we refer to as the electrode resistance, while acknowledging it is not a simple resistance. Thus, we aimed to develop a system that allows measurement of a test-signal that is correlated with the electrode resistance during tDCS (passage of mA over minutes). We refer to electrode resistance equivalently as DC-electrode resistance to contrast with measurement derived from test signals. Our goal is further to resolve the electrode resistance of any given electrode during two or multi-channel tDCS.

Importance of electrode resistance measurement in tDCS and limitations of existing measurement approaches

The common adverse events associated with tDCS is skin irritation; conditions at the electrode are considered critical for tolerated stimulation [5]. The passage of electrical current across electrodes, and especially direct current, will strain electrode conditions that, if significant, can herald skin irritation. The most robust way to minimize skin irritation is through limiting current applied (e.g. total charge per session), use of well-designed electrodes (e.g. designed for tDCS), and following protocols for electrode assembly and skin preparation. None-the-less, none ideal conditions can arise. Subject reporting of sensation, general observation of electrode/skin conditions, and the monitoring of “electrode resistance” during stimulation are the only methods to monitor electrode conditions – and of these, electrode resistance is the only device controlled and objective measures. Electrode resistance is thus universally relied on in tDCS.

However, as discussed above, the “electrode resistance” monitored is, in fact, the voltage at the current stimulator output (as the voltage is adjusted to maintain constant current) divided by the applied current. This voltage reflects many non-linear processes at both electrodes and the tissue (equations i to xiii). While valuable in tDCS monitoring, since large excursions in voltage are indicative of non-ideal electrode conditions, this is not a measure of single electrode resistance or even strictly resistance, since electrode over-potentials contribute as well. Rational development of tDCS can benefits from recognizing the none-triviality of this “electrode impedance” measurement.

Then multiple electrodes are used but the challenges in measuring single electrode resistance still exist where electrode impedances are confounded through cross talk. Measurements of “electrode resistance” (as extrapolated from the voltage as one of the current sources) may be misleading such that poor electrode conditions are not detected (false negative) or good electrode conditions as reported as poor (false positive). While our method for single electrode impedance is valuable for two electrode tDCS, for multi-electrode tDCS it becomes essential.

Commonalties and contrast with Electrode Impedance Tomography

Four electrode systems (tetra polar) are commonly used in tissue impedance measurements [22, 23], and still more sophisticated multi-electrode methods do exist or have been developed for Electrode Impedance Tomography (EIT). But the application here is different in key regards. First, our measurand of interest is the electrode impedance with the goal to minimize contribution from tissue, while in EIT the measurand of interest is tissue impedance with efforts taken to minimize contribution of electrodes. Second, significant current must be passed across electrodes for stimulation that results in changing electrode impedance, while in EIT minimal current is used. During tDCS, the changes in electrode impedance and electrode-over potential are particularly significant. None-the-less, to extend our solutions here, key techniques can be adapted from EIT including time or frequency multiplexing. What we demonstrated here is how to combine approaches used in EIT to resolve electrode impedance (more generally over-potential) during multi-channel direct current stimulation.

Assumptions to solution

The fundamental assumption to our solutions (both with and without a sentinel) is that the passage of a low-intensity and low-frequency sinusoidal current across an electrode (used for tDCS) produces a sinusoidal voltage across the electrode that predicts the DC-voltage across that same electrodes. Thus, the sinusoidal test impedance should predict the DC impedance of the electrode during tDCS.

A further assumption is that electrode resistance (at DC and also to the test signal) is greater than tissue resistance. We consider this assumption valid in the sense that poor electrode conditions will result in high electrode resistance and therefore will be detected. If a high resistance measurement is made, this is indicative of a poor electrode condition (not tissue conditions). If electrode resistance is low, and so comparable to tissue resistance, the resulting low measurement is regardless not of concern.

We also assumed and tested that the passage of the test current does not, in itself, confound either the tolerability of tDCS or electrode performance - meaning the test signal is presumed innocuous. These assumptions appear valid for the conditions tested here as physiological actions on peripheral nerves or skin properties could be reflected by a chance in sensation or resistance, respectively. Since the current densities at the brain are much lower than the skin [9] where changes could not be detected, and experimentally based on prior neurophysiologic observations [24, 25], the test signals used here are predicted not to influence brain function.

Two distinct technological solutions are shown, both of which rely on our tested fundamental assumption, that AC-impedance can track DC-resistance. One approach requires the use of a single additional sentinel electrode, that is used a reference for AC voltage measurement across each stimulation electrode of interest. In this first approach, no additional current sources are needed, but existing current sources provide a small test AC current superimposed on DC, which is technically incremental. In the second approach, no additional electrodes are required but additional current sources providing only test signal are required at a number that is a function of the montage and stimulating source configuration, which is technically feasible. However, the first solution using a sentinel electrode may be advantageous as it is easily scalable and the second approach may fail if a single electrode fails completely.

Article Highlights.

• First approach that allows measurement of individual electrode resistance using any number of electrodes or electrode configuration has been coined and tested.

• Methodologies for monitoring individual electrode resistance during multi-channel electrode impedance using a low-intensity and low-frequency sinusoids with electrode-specific frequencies and an additional sentinel electrode (not used for direct current stimulation) were tested and parameterized.

• Both validated methodologies rely on our tested fundamental assumption, that AC-impedance can track DC resistance.

• Possible errors in resistance measurement were considered and tested through our invention; Type A error related to cross talk across system and Type B errors that identifies electrode failure.