Accurate field mapping in the presence of B₀ inhomogeneities, applied to MR thermometry

Abstract

Purpose

To describe how B₀ inhomogeneities can cause errors in proton resonance frequency (PRF) shift thermometry, and to correct for these errors.

Methods

With PRF thermometry, measured phase shifts are converted into temperature measurements through the use of a scaling factor proportional to the echo time, TE. However, B₀ inhomogeneities can deform, spread, and translate MR echoes, potentially making the ‘true’ echo time vary spatially within the imaged object and take on values that differ from the prescribed TE value. Acquisition and reconstruction methods able to avoid or correct for such errors are presented.

Results

Tests were performed in a gel phantom during sonication, and temperature measurements were made with proper shimming as well as with intentionally-introduced B₀ inhomogeneities. Errors caused by B₀ inhomogeneities were observed, described, and corrected by the proposed methods. No statistical difference was found between the corrected results and the reference results obtained with proper shimming, while errors by more than 10% in temperature elevation were corrected for. The approach was also applied to an abdominal in vivo dataset.

Conclusion

Field variations induce errors in measured field values, which can be detected and corrected. The approach was validated for a PRF thermometry application.

INTRODUCTION

Thermal therapies such as high intensity focused ultrasound (HIFU) (1–4), radio-frequency (5–8), microwave (9,10) and laser (11,12) ablations offer minimally-invasive alternatives to conventional surgeries. Temperature monitoring and image guidance can be a critical component of such treatments, and MRI is routinely employed in this role. During HIFU ablations for example, MRI may help monitor temperature at the targeted location while also detecting any additional unintended heating spot(s) along the focused ultrasound (FUS) beam. The proton resonance frequency (PRF) method (13–16) is the most commonly-used MR temperature monitoring technique, although many other MR-based alternatives have been proposed (17).

B₀ inhomogeneities can cause errors in the temperature values measured with the PRF method (18,19). The present work aims to further describe and avoid such errors. In the PRF method, a precise knowledge of the echo time (TE) is required to convert phase shifts in the MR signal into accurate temperature measurements. By definition, TE is the time between signal excitation and the peak of a field echo, and k-space center is typically where such echoes are expected to occur. However, in the presence of B₀ inhomogeneities echoes may be displaced in k-space. B₀ inhomogeneities can deform, spread, and translate k-space signals, making the ‘true’ echo time both spatially-variable within the imaged object and different from the nominal user-prescribed value. As discussed for example by Yang et al. (20), B₀ inhomogeneities introduce an additional intravoxel dephasing term into the imaging equation, whose effect may be to shift the location of maximum MR signal away from k-space center. In extreme cases, signal from parts of the imaged object may even be shifted all the way outside of the sampled k-space region causing signal voids. B₀ inhomogeneities are typically caused by spatial variations in magnetic susceptibility, such as air-tissue transitions. For example, in transcranial MR-guided HIFU, magnetic susceptibility effects near the sphenoid sinus (20), orbitofrontal cortex and inferior temporal lobes (21) can prove especially challenging. Materials within the heating device (22) and the treated tissues themselves (19) may also cause significant field variations.

When k-space signals are displaced away from k-space center, the nominal (user-prescribed) TE value may not be appropriate anymore for converting phase shifts into temperature measurements. The nominal TE value marks the moment when data at k-space center is sampled, but in the presence of B₀ inhomogeneities a more relevant moment might be the echo formation, which may occur away from k-space center at some time TE+ΔTE. To complicate matters further, because B₀ inhomogeneities vary spatially, signals from different locations in the object may form echoes at different locations in k-space (23) thus making ΔTE vary spatially as well. The TE error, ΔTE, is inversely proportional to the imaging bandwidth; accordingly, echo-planar imaging (EPI) sequences are especially vulnerable to this problem because of their low effective bandwidth in the y (phase-encoded) direction. For example, even with an echo-spacing as short as 500 μs, a single-shot EPI sequence would have an imaging bandwidth of only 2 kHz along the y direction, making signal shifts along k_y both likely and commonplace. Even in non-EPI PRF-based thermometry, because a low readout bandwidth is usually selected, there may also be non-negligible shifts in the frequency-encoding k_x direction.

Three distinct strategies are presented here to avoid these types of temperature-measurement errors. In the first method presented, pulse sequence and reconstruction settings are sought that can make PRF thermometry immune to susceptibility-induced temperature errors, without having to calculate ΔTE explicitly. Although convenient, such immune methods may not be optimal in terms of temperature-to-noise (TNR) properties and overly constraining in terms of acquisition parameters. The second method presented is more general and less constraining, allowing more favorable acquisition and reconstruction parameters to be selected and higher TNR to be achieved. The last method presented is the most flexible of the three in terms of pulse sequence design but is more intricate in terms of reconstruction. It is worth noting that the purpose of these methods is to avoid and/or correct for susceptibility-induced temperature measurement errors but not necessarily to correct for other susceptibility-induced problems that may affect MR images, such as geometrical distortions and signal voids. Other strategies such as accelerated imaging to avoid distortions and/or z-shimming (20,24), tailored RF pulse (25) and local shimming coils (26) to avoid signal losses are expected to prove readily compatible with the methods proposed here.

The tests performed here involved imaging a gel phantom during FUS sonication with proper shimming as well as with intentionally de-adjusted high-order shim (HOS) parameters, to introduce B₀ inhomogeneities in a controlled manner. The effects of B₀ inhomogeneities on temperature measurements are characterized, and the ability of the proposed methods to avoid and/or correct for these effects are assessed. Corrected temperature measurements, obtained with de-adjusted shim parameters, are compared with reference results obtained with proper shimming. In vivo abdominal results in a human volunteer were also obtained, in the absence of any external heating source.

The immediate goal of this work was to create methods capable of providing accurate temperature measurements even in tissues located close to air-tissue or water-fat transitions. It may be noted, however, that PRF thermometry is part of a larger class of MR methods that are based on field mapping, which also includes for example susceptibility and susceptibility-weighted imaging (27,28) as well as Dixon-based fat-water separation methods (29,30). The type of inhomogeneity-induced errors and the correction methods described here may hopefully prove relevant to other MR field-mapping methods beyond the current PRF thermometry application.

METHODS

Susceptibility-induced temperature errors

With the PRF method, temperature changes can be calculated from the corresponding phase change, Δϕ(r⃗,t), as measured at time t and location r⃗:

$$\mathrm{\Delta }T(\overrightarrow{r},t)=\frac{\mathrm{\Delta }\varphi (\overrightarrow{r},t)}{\lambda },$$ [1]

where λ represents the temperature sensitivity. Phase changes Δϕ are measured with respect to a non-heated reference, for example a pre-heating time frame and/or non-heated spatial locations within the image (17,31). The temperature sensitivity can be expressed as:

$$\lambda =2\pi \times \gamma \times \alpha \times B_0\times \tau ,$$ [2]

where γ is the gyromagnetic ratio for hydrogen (42.58 MHz/T), α is the PRF change coefficient (−0.01 ppm/°C), B₀ is the main field strength, and τ is the time duration available for phase evolution. For most pulse sequences used in PRF thermometry, such as ‘fast imaging with steady state precession’ (FISP), τ would simply be equal to the echo time, TE. It is worth noting that in more elaborate multi-pathway sequences, τ may take on different and possibly even negative values (32). For example, for signal obtained from a reverse-FISP (PSIF) pathway τ would be equal to (TE − TR), a negative value.

B₀ inhomogeneities can lead to distortions and displacements of k-space signals over the k-space matrix, thus affecting the timing of echoes and the ‘true’ value of TE. A more exact version of τ that would take these effects into account is sought:

$$\widehat{\tau }=\tau +\mathrm{\Delta }\tau ,$$ [3]

where the caret symbol indicates the corrected version of τ. Inserting τ̂ in place of τ in Eqs 1 and 2 allows a corrected temperature measurement, ΔT̂, to be obtained. Three distinct strategies to obtain ΔT̂ are introduced below, in order of increasing complexity and general applicability.

A dual-echo method immune to susceptibility-induced temperature errors

Consider a pulse sequence as depicted in Fig. 1, where at least two echoes are sampled within the TR period. One could obtain temperature values based on the first one of these echoes, ΔT̂₁, or based on the second echo, ΔT̂₂. The combined temperature measurement, ΔT̂, would be obtained from a weighted sum:

$$\mathrm{\Delta }\widehat{T}=\frac{w_1\mathrm{\Delta }{\widehat{T}}_1+w_2\mathrm{\Delta }{\widehat{T}}_2}{w_1+w_2}.$$ [4]

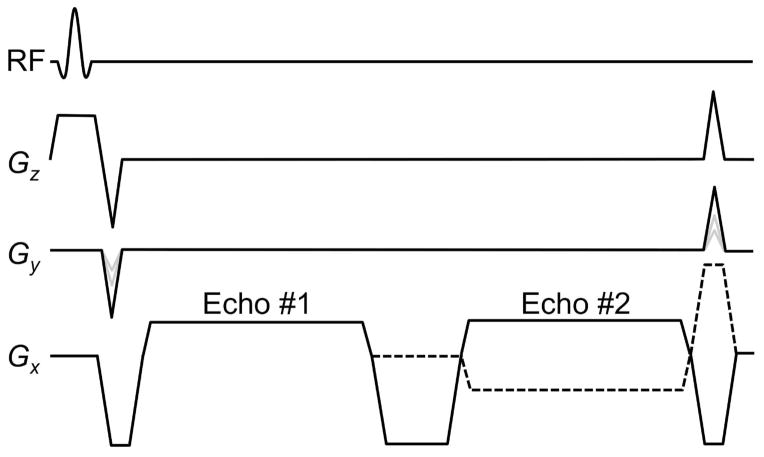
Fig. 1.

Diagram of the dual-echo steady-state sequence used here. The two echoes were sampled either with the same imaging bandwidth (solid G_z line) or opposed ones (dashed line). See text for more details.

The most common way to generate temperature measurements from a two-echo sequence may be to compare the phase difference between the two echoes before heating to that after heating; such processing can readily be shown equivalent to setting w₁ = −|λ₁| and w₂ = |λ₂| in Eq. 4. Another common choice might be to consider the total phase evolution rather than the difference between echoes, as obtained by setting w₁ = |λ₁| and w₂ = |λ₂| in Eq. 4. When echoes are generated from different signal pathways and may very much differ in terms of signal strength, a measure of expected signal amplitude may further be included into the chosen weights, to help improve TNR (32).

A solution is sought here that would be naturally immune to susceptibility-induced temperature errors, such that:

$$w_1\mathrm{\Delta }{\widehat{T}}_1+w_2\mathrm{\Delta }{\widehat{T}}_2=w_1\mathrm{\Delta }{T}_1+w_2\mathrm{\Delta }{T}_2.$$ [5]

In other words, errors from the first temperature measurement, ΔT₁, should be made to exactly cancel out errors from the second measurement, ΔT₂. Using the fact that in the absence of noise and other sources of error the corrected temperatures ΔT̂₁ and ΔT̂₂ should be the same, Eq. 5 becomes:

$$w_1\times \left(1-\frac{\mathrm{\Delta }{T}_1}{\mathrm{\Delta }{\widehat{T}}_1}\right)+w_2\times \left(1-\frac{\mathrm{\Delta }{T}_2}{\mathrm{\Delta }{\widehat{T}}_2}\right)=0.$$ [6]

Replacing the definitions from Eqs 1–3 into Eq. 6 one obtains:

$$\frac{\mathrm{\Delta }{\tau }_1}{\mathrm{\Delta }{\tau }_2}=-\frac{w_2\times {\tau }_1}{w_1\times {\tau }_2}.$$ [7]

The error on the evolution time, Δτ, is expected to be proportional to the evolution time and inversely proportional to the imaging bandwidth, BW, such that:

$$\frac{\mathrm{\Delta }{\tau }_1}{\mathrm{\Delta }{\tau }_2}=\frac{{BW}_2}{{BW}_1}\times \frac{{\tau }_1}{{\tau }_2}.$$ [8]

For a 2D Cartesian acquisition, BW would refer to the sampling bandwidth along k_x, while for EPI imaging the effective sampling bandwidth along k_y would be considered instead. Combining Eqs 7 and 8 one obtains:

$$w_2=-\frac{{BW}_2}{{BW}_1}\times w_1,{BW}_1\ne {BW}_2.$$ [9]

Eq. 9 is the condition for obtaining a PRF method naturally immune to susceptibility-induced temperature errors. One simple solution to Eq. 9 involves w₂ = w₁ and BW₂ = −BW₁, as depicted in Fig. 1 with a dashed line, where readout gradients have equal magnitude but opposite polarities. For improved TNR, a choice w₁ = ±|λ₁| and w₂ = |λ₂| would be preferable, and through Eq. 9 it leads to BW₂ = ∓BW₁×|λ₂|/|λ₁|. Note that using the same bandwidth for both echoes, BW₁ = BW₂, is not an option here as it would lead to w₂ = −w₁ and to an indeterminate zero-divided-by-zero value for ΔT̂ in Eq. 4. The two echoes may be of the same signal type (e.g., two FISP echoes), or of mixed types (e.g., a PSIF and a FISP, with τ_FISP = TE_FISP and τ_PSIF = TE_PSIF − TR). Of special note here is that ΔT̂ can be calculated here without any explicit knowledge of Δτ and ΔTE values, as errors from both temperature measurements simply cancel out.

Equation 9 links reconstruction parameters, w₁ and w₂, to acquisition parameters, BW₁ and BW₂. It might be desirable to set these parameters independently instead. Explicit calculations of Δτ₁ and Δτ₂ would then be required, as detailed below.

Calculating ΔT̂ based on temperature discrepancies

Using a sequence with two (or more) echoes and calculating relative temperature measurements from each would lead to values ΔT₁ and ΔT₂. These temperature measurements can be expected to disagree when B₀ inhomogeneities are present. The approach presented here involves finding the offsets Δτ₁ and Δτ₂ that would be required to erase such discrepancy, and to obtain a corrected measurement ΔT̂ based on these offsets.

By posing ΔT̂₁ = ΔT̂₂ and using definitions from Eqs 1–3, an expression was obtained that involves the acquired MR phase information (Δϕ₁ and Δϕ₂), known imaging parameters (τ₁, τ₂, BW₁ and BW₂) and the unknown timing errors (Δτ₁ and Δτ₂). Replacing Δτ₂ with its expression from Eq. 8, an expression for Δτ₁ is obtained:

$$\mathrm{\Delta }{\tau }_1=-\frac{{\tau }_1\times (\mathrm{\Delta }{\varphi }_1\times {\tau }_2-\mathrm{\Delta }{\varphi }_2\times {\tau }_1)}{\mathrm{\Delta }{\varphi }_1\times {\tau }_2\times ({BW}_1/{BW}_2)-\mathrm{\Delta }{\varphi }_2\times {\tau }_1},{BW}_1\ne {BW}_2.$$ [10]

The Δτ₁ value obtained from Eq. 10 can be used to evaluate Δτ₂ through Eq. 8, and the corrected temperature measurement, ΔT̂, can then be calculated from Eq. 4. The value of ΔT̂ becomes indeterminate for BW₁ = BW₂ and/or for Δϕ₁, Δϕ₂ = 0, in other words, Eq. 10 can only be used where/when significant heating is present and for a pulse sequence having at least two echoes of different bandwidth, BW₁ ≠ BW₂. These bandwidths may differ in polarity and/or in magnitude. A more general approach less constraining in terms of pulse sequence design and applicable to non-heated as well as heated voxels is presented below.

Calculating ΔT̂ based on field maps and their derivatives

The main problem with the methods presented above is that they require two or more echoes sampled with bandwidths of different polarity and/or size. In the presence of susceptibility-induced field variations, different bandwidths lead to different geometrical distortions and/or chemical shifts, which may complicate any pixel-by-pixel processing. Gradient timing errors and/or eddy currents could also, in principle at least, introduce undesirable TE-dependent effects when using different bandwidths for different TEs. To circumvent all of these potential problems, a more general approach is presented here which could be used with a single-echo sequence and/or a multi-echo sequence with no constraints on bandwidth.

For the time being it is assumed that a field map, B₀(r⃗), is available. Gradients in B₀(r⃗) are responsible for shifting signal in k-space:

$$\mathrm{\Delta }{\overrightarrow{k}}_{j,i}(\overrightarrow{r})=2\pi \times \gamma \times {\widehat{\tau }}_{j,i}\times \nabla B_{0,i}(\overrightarrow{r}),$$ [11]

where j is an echo number and i an iteration number. A pulse-sequence specific function, f_s(k⃗), is defined that returns the time at which any given k⃗ point is sampled within TR, with k⃗ = 0 representing k-space center. Using Δk⃗_j,i(r⃗) from Eq. 11 as an input to the f_s(k⃗) function gives the ‘true’ value for TE for an object element located at r⃗, which by definition is also given by TE_j + ΔTE_j,i(r⃗):

$${TE}_j+\mathrm{\Delta }{TE}_{j,i}(\overrightarrow{r})=f_s\left(\mathrm{\Delta }{\overrightarrow{k}}_{j,i}(\overrightarrow{r})\right).$$ [12]

With a pulse sequence including two echoes per TR, a field map B₀(r⃗) could be obtained on a frame-by-frame basis:

$$B_{0,i}\left(\overrightarrow{r}\right)=\frac{1}{2\pi \times \gamma }\times \frac{{\varphi }_2(\overrightarrow{r})-{\varphi }_1(\overrightarrow{r})}{{\tau }_{2,i}-{\tau }_{1,i}}.$$ [13]

An iterative approach is employed, with initial values τ_j,0 = τ_j for the 0^th iteration. The τ_j,i values are used in Eq. 13 to evaluate B_0,j(r⃗), which gives $\mathrm{\Delta }\overrightarrow{k_{j,i}}(\overrightarrow{r})$ though Eq. 11, then ΔTE_j,i(r⃗) and τ_j,i+1 through Eq. 12 (e.g., for a FISP echo τ_j,i+1 = TE + ΔTE_j,i). Upon convergence, the resulting τ_j values are used to calculate ΔT̂_j and the ΔT̂ result, through Eq. 4. Convergence is not guaranteed, but in the present work a couple iterations proved sufficient to very much suppress susceptibility-induced temperature errors. As part of evaluating the spatial gradients in B_0,i(r⃗), a Savitzky-Golay filter was employed (5-point window, 2^nd order least-square fit using magnitude data as weight).

Experimental setup

The pulse sequence from Fig. 1 was implemented on a 3.0 T MR system (GE Healthcare, Milwaukee, WI, Signa HDxt Twin Speed, 40 mT/m, 150 T/m/s) with a receive-only eight-channel head coil. A 1.5 MHz single-element ultrasound transducer (100-mm radius of curvature, 100-mm of diameter) was used to generate heating. The setup also included a function generator (Fluke, Everett, WA, Model 396), an RF amplifier (E and I, Rochester, NY, model 240L), a power meter (Hewlett Packard, Palo Alto, CA, model 438A), a dual directional coupler (Werlatone, Brewster, NY, model C1373) and fiber-optic temperature probes (Neoptix, Québec City, Canada). Table 1 provides a list of MRI and ultrasound parameters that were used for the various experiments performed here. Pre-heating images were used as a phase reference to calculate temperature changes. The image reconstruction and data analysis were performed in the MATLAB programming language (MathWorks, Natick, MA).

Table 1.

Scan parameters

	Sequence	BW1 / BW2 (kHz)	TE (ms)	TR (ms)	Resolution (mm)	Matrix size	FOV cm2	Flip angle	FUS sonication
1.	FSPGR	Varied	10	17	1.5×1.5×5.0	128×128	19.2×19.2	30°	78 W, 20 s
2.	FISP-FISP	±10 / ∓10	7.2 and 17.8	25	1.5×1.5×5.0	128×128	19.2×19.2	30°	53 W, 30 s
3.	FISP-FISP	±10 / ±10	6.0 and 16.6	25	1.5×1.5×5.0	128×128	19.2×19.2	30°	53 W, 30 s
4.	GRE	±5.81	7.0 or 9.0	20	3.0×3.0×5.0	128×128	38.0×38.0	20°	None

Phantom experiments

All three methods proposed here and expressed through Eqs 9, 10 and 11–13, respectively, were tested through phantom experiments. The transducer was mounted at the bottom of an acrylic tank, a tissue-mimicking gel phantom (InSightec, Tirat Carmel, Israel) was placed above the transducer (ATS Laboratories, Bridgeport, CT) (33) and the tank was filled with water that was both degassed and deionized (see Fig. 2). The phantom was stored in the magnet room overnight to ensure temperature equilibrium was reached before scan time. An axial imaging plane was prescribed so it would include the transducer’s focal point, as located through a series of low-power short-duration sonication tests performed using a conventional gradient echo (GRE) sequence. Heating experiments were separated by periods of cooling of at least 30-min to allow temperature to return near baseline. The full-width-half-maximum size of the focal region heated by the transducer was about 10 mm and 5 mm in the axial and lateral directions, respectively.

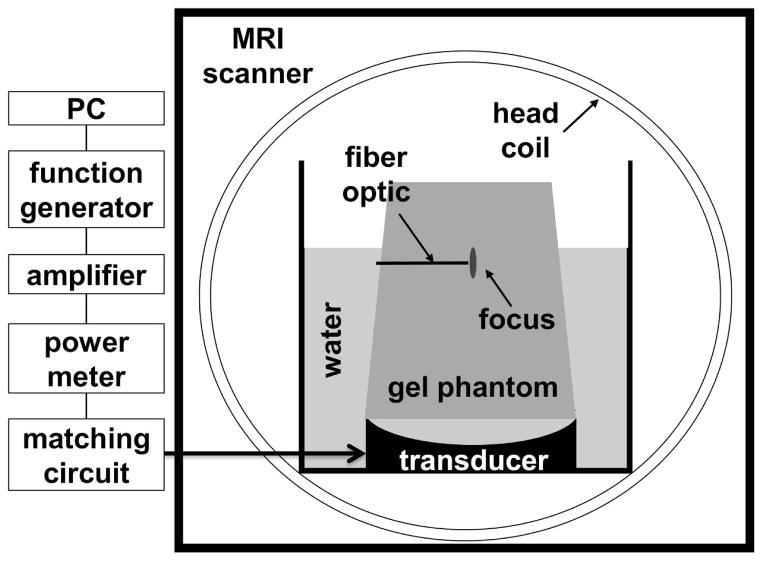
Fig. 2.

Axial view of the FUS experimental set-up used here. The transducer was attached at the bottom of a custom-built tank and immersed in a bath of degassed, de-ionized water. The size of the tank was designed to fit into an eight-channel head coil. A gel phantom was placed over the transducer. The focused ultrasound beam was delivered through water into the gel phantom, with focus within the phantom. Temperature mapping images were acquired in the axial plane that included the focal location.

A dozen heating experiments were performed either with properly-adjusted HOS parameters or with intentionally de-adjusted shim parameters. Temperature measurements obtained from properly-shimmed scans were used here as a reference, and success was defined as obtaining results from improperly-shimmed scans that would be nearly identical to reference ones. The readily-available product HOS procedure on our scanner was employed, which consisted of a pair of spiral GRE multi-slice scans acquired with different TE values, for B₀ field mapping. Nine shim currents were automatically computed and set, and one or more of these currents could be manually altered to intentionally introduce B₀ inhomogeneities in a controlled manner. Experiments involved introducing a non-linear field term (a 3.8 Amp offset was manually added to the x²+y² shim coil) and/or a linear field term (a 0.308 or 0.169 mT/m offset was added to the vertically-oriented, physical-y orientation). These settings were chosen to be roughly representative of field gradients that might be encountered in vivo, with values of 0.1 and 0.5 mT/m previously reported for breast and brain applications, respectively (34,35).

Non-linear B₀ inhomogeneities cause a smear of the k-space content as signals from different spatial locations in the object suffer k-space shifts that differ in size and/or direction, and the effect in the object domain is to warp the image. A field map was obtained to allow the acquired images to be unwarped if needed. Linear field terms, on the other hand, simply shift the k-space content and introduce a phase ramp across the object. For unwarping purposes, the field maps were obtained using a pair of steady-state GRE scans acquired with different TE settings (TR = 50 ms, matrix size = 128×128, flip angle = 30°, FOV = 19.2×19.2 cm², BW = ±15.63 or ±10.00 kHz, TEs = 5/7 ms).

In vivo experiments

In vivo breath-held abdominal scans were performed in a single healthy volunteer, in the absence of any external heating, with GE auto-shim parameters, to assess how distorted temperature measurements would have been due to B₀ inhomogeneities. The scans were a pair of steady-state GRE sequences for field mapping (TR = 20 ms, matrix size = 128×128, flip angle = 20°, FOV = 38.0×38.0 cm², BW = ±5.81 kHz, TEs = 7/9 ms, 8-channel cardiac array, 7 s breath-hold duration). Experiments were performed shortly after IRB-approved informed consent was obtained. These tests were performed to provide relevant information as to how significant the corrections proposed would be in a typical in vivo environment.

Unwarping

Unwarping had to be used every time images acquired with different bandwidths were compared. However, the last method (Eqs 11–13) is applicable even when BW₁ = BW₂, in which case all images are similarly deformed and un-warping becomes optional. But for the methods from Eqs 9 and 10, with BW₁ ≠ BW₂, un-warping was needed before any further processing could be applied. The unwarping algorithm was essentially identical to the well-known warping algorithm available on all commercial scanners to correct for the non-linearity of the imaging gradients, except that the input to the algorithm was a field map instead of a model description of gradient errors. All field maps are subject to the type of TE errors described here, the field maps used for unwarping are no exception, and the correction from Eqs 11–13 was applied to these maps before using them for unwarping purposes.

RESULTS

Demonstration of inhomogeneity-induced temperature errors

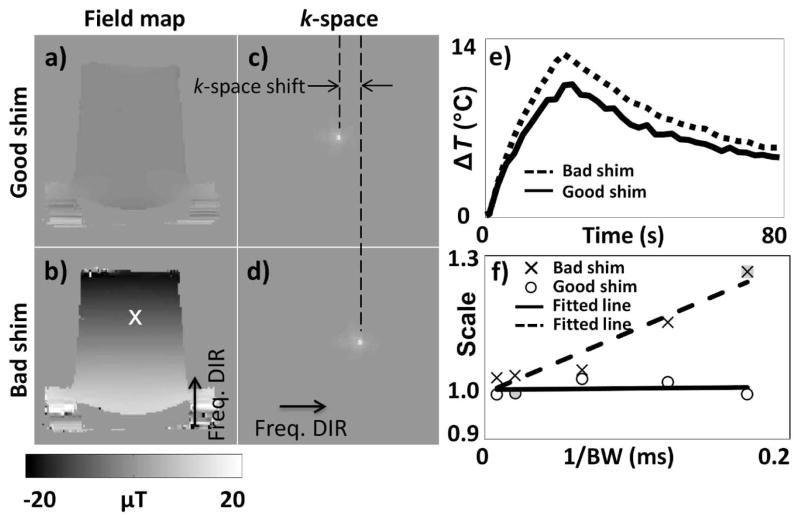
Field maps obtained with properly-adjusted and manually de-adjusted shim parameters are shown in Fig. 3a and 3b, respectively, along with associated k-space data in Fig. 3c and 3d. The white ‘×’ symbol in Fig. 3b marks the transducer’s focal point. Ten phantom heating experiments were performed both with proper and with de-adjusted shim parameters while varying the sampling bandwidth, BW (regular single-echo GRE sequence, parameters listed on line #1 of Table 1). A temperature curve was obtained for a 1×3 pixel region located at focus for each one of these experiments, and two examples are shown in Fig. 3e: One for proper shimming and high-bandwidth setting, and one for de-adjusted shimming and low-bandwidth setting. Using the former as a reference, a linear fit between the two curves showed the latter to be off by a multiplicative factor of 1.26. Such multiplicative factor was calculated for each one of the heating experiments performed, and the resulting multiplicative factors are plotted in Fig. 3f as a function of 1/BW, both for proper and for de-adjusted shim parameters. Because it corresponds to the reference curve from Fig 3e, one of the points in Fig. 3f has a value of exactly 1 (shaded ‘○’ symbol). Another point, shown as a shaded ‘×’ symbol in Fig. 3f, corresponds to the dashed line from Fig. 3e and to a scaling factor of 1.26 as mentioned above.

Fig. 3.

Field maps and associated k-space data were obtained using: Properly adjusted shim parameters (a,c), and manually de-adjusted shim parameters (a 0.308 mT/m offset was added to the vertically oriented, physical-y orientation) (b,d). The manually introduced shim term was spatially linear in this case, which caused a simple global shift in k-space in (d). Several heating experiments were performed while varying the imaging bandwidth, with proper and with de-adjusted shimming. e) The heating curve obtained at focus is shown for the case BW = ±5.8 kHz and de-adjusted shimming (dashed curve) and for the case BW = ±50 kHz and proper shimming (solid curve). The two curves were found to differ by a multiplicative factor of 1.26 in this case. Such multiplicative factor, obtained for each heating experiment using the solid line from (e) as a reference, is plotted in (f) as a function of the inverse of the imaging bandwidth, 1/BW. Regardless of bandwidth, properly-shimmed experiments yielded accurate results, as determined by the fact that a scaling factor of about 1.0 was obtained (see ‘○’ symbols in (f)). As expected, temperature results obtained with de-adjusted shim parameters were affected through a multiplicative factor that increased linearly with 1/BW (‘×’ symbols). Gray-filled symbols in (f) represent the two cases exemplified in (e): An ‘○’ and an ‘×’ symbol with scaling value of 1.00 and 1.26, respectively.

Figure 3f shows that as expected, the presence of B₀ inhomogeneities caused errors in the measured temperature values. These errors took the form of a multiplicative factor that increased linearly with 1/BW, with a slope that depends on local field gradients at the transducer’s focus (‘×’ symbols in Fig. 3f). Through careful shimming, local field gradients could be mostly removed, leading to more accurate measurements and scaling factors in the vicinity of 1.00 at all sampled 1/BW settings (‘○’ symbols in Fig. 3f). The proposed work aims at enabling accurate measurements even in the presence of B₀ inhomogeneities.

Interestingly, the field changes induced by the hotspot itself through the PRF effect also cause errors in TE. In our experiments at 3 T where heating reached 10 °C, the field change reached about −0.3 μT over a transition region of about 5 mm, producing field gradients of about 0.06 mT/m. A field gradient about five times larger, 0.308 mT/m, was created in Fig. 3f which led to errors by up to 26%, depending on bandwidth. Accordingly, errors up to only 5% or so might be expected from gradients caused by the hotspot itself, depending on bandwidth. This error would be expected to increase with greater and/or more rapid temperature elevations at the hotspot.

Method immune to susceptibility-induced temperature errors – Testing Eq. 9

A heating experiment was performed using the dual-echo sequence from Fig. 1 and parameters from line #2 in Table 1, with properly-adjusted as well as with de-adjusted shim parameters (extra linear term). Figure 4a shows an example where, in the presence of B₀ inhomogeneities, temperature measurements from the first and second echoes of the dual-echo sequence overestimate and underestimate temperature changes, respectively, as compared to reference data acquired with a product GRE sequence and proper shimming (‘○’ symbols in Fig. 4a). With BW₁ = −BW₂ (see Fig. 1, dashed line), Eq. 9 requires w₁ = w₂ for the resulting method to be immune to inhomogeneity-induced temperature errors, which means from Eqs 4 and 5 that the corrected ΔT̂ measurement is simply the arithmetic average of the two erroneous measurements from Fig. 4a. The resulting corrected results are shown in Fig. 4a using a solid line. Note that results obtained from the immune method in the presence of B₀ inhomogeneities (solid line in Fig. 4a) closely match the reference properly-shimmed results ‘○’ symbols). Corrected and reference results were further compared using a scatter plot and a Bland-Altman plot in Fig 4b and 4c, 6respectively. Linear regression (solid line in Fig. 4b) yielded slope and intercept values of 1.01 and 0.01, respectively (R² = 0.996). The solid line in Fig. 4c shows a mean difference of 0.06 °C, and dashed lines correspond to a 95% confidence interval of ±0.36 °C.

Fig. 4.

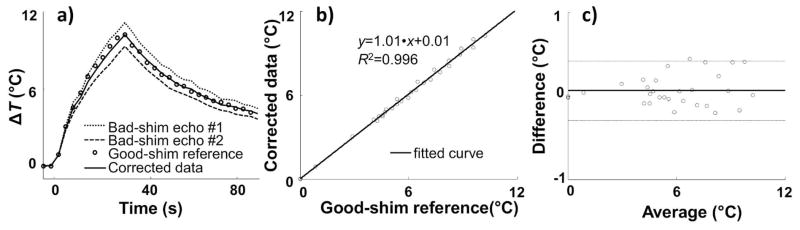
a) Heating as measured in a 1×3 pixel ROI located at the focus is plotted as a function of time (dual-echo pulse sequence from Fig. 1, BW₂ = −BW₁, under manually de-adjusted linear shim, 0.169 mT/m offset was added to the vertically-oriented, physical-y orientation). Dotted and dashed curves represent measurements from echo #1 and echo #2, respectively, while the solid line shows corrected results obtained through Eq. 9. The corrected results agreed very well with reference results, shown with ‘○’ symbols and obtained using a properly-shimmed product GRE sequence. A scatterplot (b) and a Bland-Altman plot (c) were used to compare the corrected temperature measurements to the reference ones. From (c): Slope/intercept = 1.01/0.01 and R² = 0.996. From (d): Mean difference = 0.06 °C (solid line), 95% confidence intervals = ±0.36 °C (±1.96 standard deviation, dashed lines).

As mentioned in the Methods section, images had to be un-warped before they could be analyzed and results from Fig. 4 could be generated. The un-warping algorithm required a field map, and as previously mentioned all field maps may suffer from the type of problems being treated here, not just temperature measurements. The field maps before and after correction are compared in Fig. 5.

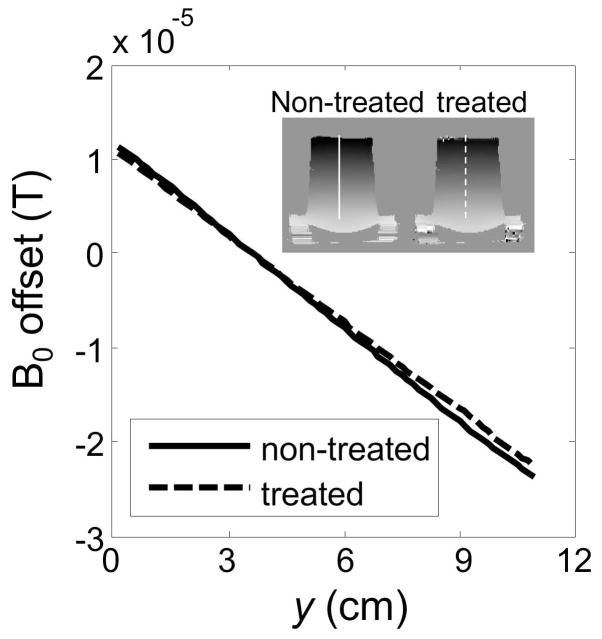
Fig. 5.

The field maps used here for unwarping, like any other field map, can be corrected as proposed through Eqs 11–13. A 1D profile as marked in inset is plotted here, for the corrected as well as the non-corrected field map. In this particular case, the manually-introduced shim was linear (Fig. 3b); for this reason and as seen here, the field error was simply proportional to the field itself, so that treated and untreated results appear here as straight lines intersecting at a zero field offset.

Method based on temperature discrepancies – Testing Eq. 10

When using the pulse sequence from Fig. 1, data from the second echo is more heavily temperature-encoded by virtue of its longer TE, and for TNR purposes greater weight should be given to these data compared to those from the first echo. By setting w₁ = w₂ through Eq. 9 a TNR penalty was paid, as equal weight was given to data from both echoes. Using the same data as above and using Eq. 10 instead, corrected results were obtained in Fig. 6a that proved very similar to those from Fig. 4a except for an improvement in TNR. In theory, weights w₁ = TE₁×exp(−TE₁/T₂*) and w₂ = TE₂×exp(−TE₂/T₂*) would be optimal, but in general T₂* may not be precisely known and weights w₁ = TE₁ and w₂ = TE₂ were used here instead. Temperature noise was calculated over the 5×5 ROI shown in Fig. 6b, leading to a TNR of 129 for the data in Fig. 6 as compared to 102 for that from Fig. 4. Good agreement was found between reference and corrected data in Fig. 6a (95% confidence intervals = ±0.35 °C).

Fig. 6.

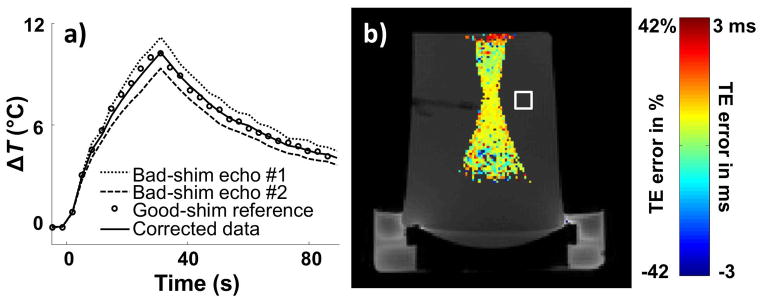
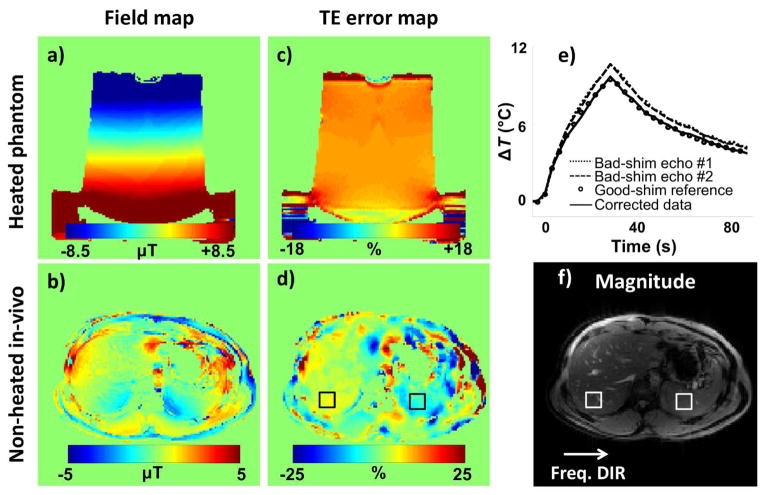
The same data as in Fig. 4 were reconstructed a second time using Eq. 10 rather than Eq. 9. a) Temperature measurements at focus are very similar to those from Fig. 4a: Corrected temperature measurements agreed very well with reference values. b) Equation 10 allows errors in τ, simply equal to TE for a regular gradient-echo signal, to be explicitly calculated wherever significant heating was present. A map of ΔTE for echo #1 (TE = 7.2 ms) is overlaid on a magnitude image, and as expected from an extra linear shim term the value of ΔTE is mostly constant spatially (value of about 0.7 ms or 10%, as measured at focus). The main advantage of using Eq. 10 (as done here) rather than Eq. 9 (as in Fig. 4) is an improved TNR. In the square ROI shown in (b), the TNR was 129 here for results calculated from Eq. 10 compared to 102 for results from Fig. 4 and Eq. 9.

Using the processing from Eq. 10 allowed ΔTE to be evaluated everywhere significant heating is present and a map of ΔTE (for echo #1, TE = 7.2 ms) is shown as a color overlay in Fig. 6b. In the presence of B₀ inhomogeneities created by a linear shim term the ΔTE map should be nearly constant spatially; the processing encountered problems near the edge of the phantom where higher values can be seen. At focus, a ΔTE value of 0.7 ms for the first echo, or 10%, was measured.

Method based on field maps and their derivatives – Testing Eqs 11–13

A heating experiment was imaged using a dual-echo sequence whereby both echoes had the same bandwidth, BW₁ = BW₂, and parameters from line #3 in Table 1. Data were acquired both with proper and de-adjusted shim parameters (extra linear and quadratic term). The data acquired under proper shimming (‘○’ symbols in Fig. 7e) was used as reference. In a manner similar to Figs 4 and 6, Fig. 7 shows that inhomogeneity-induced errors could be corrected. While Eqs 11–13 were also used to help generate accurate field maps for un-warping purposes for the data from Figs 4 and 6, no un-warping was required for data in Fig. 7 because of the BW₁ = BW₂ setting. Good agreement was found between reference and corrected data in Fig. 7e (95% confidence intervals = ±0.26 °C).

Fig. 7.

a,c) A manually-introduced linear and second-order shim term was used to create B₀ inhomogeneities (3.8 Amp offset was manually added to the x²+y² shim coil and a 0.169 mT/m offset was added to the vertically-oriented, physical-y orientation), and a field map as well as a ΔTE map (for echo #2, TE = 16.6 ms) were obtained through Eqs 11–13 after two iterations. The same bandwidth was used for both FISP readout windows. Field maps and ΔTE maps were independently created for each acquired time frame, and the ones shown here correspond to that with maximum heating. e) As in Fig. 4 and 6, measurements from individual echoes differed from the reference measurements while corrected result showed good agreement (95% confidence intervals = ±0.26 °C). b,d,f) Abdominal images of a healthy volunteer (35 yo, male) were obtained during breath-holding, in the absence of any external heating source. The same bandwidth was used for both FISP echoes. A field map, a ΔTE map (for the echo with TE = 9 ms) and a corresponding magnitude image are shown. ΔTE values of 4.84±0.64% and 7.96±1.02% were measured in ROIs placed over the liver and spleen, respectively. These relative errors on TE would lead to similar errors on relative temperature measurements.

In vivo abdominal results

Figure 7 also includes field values calculated from in vivo abdominal data (breath-held, two single-echo GRE scans with different TE of 7/9 ms, BW₁ = BW₂, acquired using the parameters listed on line #4 of Table 1). Corrected field and evolution time values were computed from Eqs 11–13. The field map and the percentage error 100×(τ₁ − τ̂₁)/τ₁, the scaling factor that would normally affect temperature measurements, are shown in Fig. 7b and 7d, respectively. A 5×5 median filter was applied to the TE error map before displaying it in Fig. 7d. ROIs (5×5 pixels in size) were placed over the liver and the spleen, as shown in Fig. 7d, and mean errors of 0.44±0.06 ms (4.84±0.64%) and 0.72±0.11 ms (7.96±1.20%) were measured, respectively. Of course, because no heating was present, there were no actual temperature-measurement errors in the present datasets, but Fig. 7d provides a map of how large such errors would have been if heating had been applied. Although anecdotal in nature, the in vivo results from Fig. 7d seem to support the phantom results in suggesting that temperature errors corrected here may readily reach 10% in size, contingent on the imaged subject, anatomy, and selected bandwidth.

DISCUSSION

Temperature-measurement errors caused by B₀ inhomogeneities have been described and characterized, and methods have been proposed to avoid them. Of special interest is the more general version proposed here, as described through Eqs 11–13, because it does not impose any particular constraint on imaging and reconstruction parameters and it generates a corrected field map as part of the solution. The method could be applied to a single-echo sequence as well as multi-echo sequences, but in such case the required field map(s) would have to be independently acquired. The temperature errors detected and corrected for here were quite significant, especially when a narrow imaging bandwidth was chosen to help boost SNR, and readily reached a 10% level in phantom and human data. The method is expected to prove especially useful when the heated region is located near transitions such as air-water interfaces.

When using phantoms and simple object geometries, proper shimming can often nearly erase B₀ inhomogeneities. For in vivo scans however, B₀ inhomogeneities can prove much more difficult to address through shimming, especially in the abdomen where several air-water transitions are present. Furthermore, no amount of shimming could or should erase legitimate field variations that convey useful information, which are the target of MR phase imaging methods. For example, heating itself causes phase variations to appear within the object, and it is no coincidence that the focus location can be faintly seen in the ΔTE map shown in Fig. 7c. Phase changes caused by heating, which could not and should not be shimmed away, displace signals in k-space and cause errors on temperature measurements that can be addressed here. For example, as a heating spot gets created and evolves, B₀ inhomogeneities also evolve, and the present method can adapt to the evolving situation by creating time-resolved corrected field maps.

The present study was limited in many ways, as validations were to a large extent limited to thermometry and all heating experiments were performed in phantom. Attempts were made to validate MR-derived temperature results in phantoms with measurements from a fiber-optic system (see Fig. 2), but sudden changes in fiber-optic measurements when the ultrasound beam was turned on/off suggested the ultrasound field might deposit energy directly into the heat-sensitive material of the fiber-optic probe, and that the resulting measurements might not be representative of the temperature of surrounding tissues. For in vivo results, percentage values have been obtained to describe errors that would have been obtained if heating had been applied but no actual heating and errors were measured to corroborate these predictions. Furthermore, complicating factors such as signal losses and/or voxels made of multiple chemical species were not considered here. B₀ inhomogeneities can create TE errors of such magnitude that signal falls outside of the readout window, causing a loss of signal and of temperature information. Methods geared toward avoiding signal losses such as z-shimming (20,24), tailored RF pulse (25) and/or local shimming coils (26) should prove compatible with the present work. The possibility that voxels might consist of a mixture of chemical species was also overlooked here. Because of the chemical shift effect, different chemical species found in a same voxel originate from different spatial locations within the object and may be associated with different field values when B₀ inhomogeneities are present (36). Versions of the TE-correction methods developed here capable of handling a mixture of chemical species would be desirable but are considered beyond the scope of the present work.

PRF thermometry measures temperature-induced field changes, and is in nature a field-mapping method. The type of errors described and corrected for here would presumably be present in any field-mapping MR application, not just thermometry. Interestingly, field maps used for un-warping purposes (not for temperature mapping) also showed improvements here when treated through the algorithm from Eqs 11–13. MR phase-imaging methods such as susceptibility imaging, fat-water separation, shimming or thermometry are by nature akin to phase mapping, and it is hoped that the methodology presented here might not be limited to thermometry.

CONCLUSION

B₀ inhomogeneities create errors in temperature measurements, which can be detected and corrected using the proposed strategies. The use of the proposed methodology to help generate corrected field maps for un-warping purposes provides an enticing hint to a possibly larger range of applicability for the proposed approach beyond thermometry.