Abstract
Microtubules, the primary components of the chromosome segregation machinery, are stabilized by longitudinal and lateral noncovalent bonds between the tubulin subunits. However, the thermodynamics of these bonds and the microtubule physicochemical properties are poorly understood. Here, we explore the biomechanics of microtubule polymers using multiscale computational modeling and nanoindentations in silico of a contiguous microtubule fragment. A close match between the simulated and experimental force–deformation spectra enabled us to correlate the microtubule biomechanics with dynamic structural transitions at the nanoscale. Our mechanical testing revealed that the compressed MT behaves as a system of rigid elements interconnected through a network of lateral and longitudinal elastic bonds. The initial regime of continuous elastic deformation of the microtubule is followed by the transition regime, during which the microtubule lattice undergoes discrete structural changes, which include first the reversible dissociation of lateral bonds followed by irreversible dissociation of the longitudinal bonds. We have determined the free energies of dissociation of the lateral (6.9 ± 0.4 kcal/mol) and longitudinal (14.9 ± 1.5 kcal/mol) tubulin–tubulin bonds. These values in conjunction with the large flexural rigidity of tubulin protofilaments obtained (18,000–26,000 pN·nm2) support the idea that the disassembling microtubule is capable of generating a large mechanical force to move chromosomes during cell division. Our computational modeling offers a comprehensive quantitative platform to link molecular tubulin characteristics with the physiological behavior of microtubules. The developed in silico nanoindentation method provides a powerful tool for the exploration of biomechanical properties of other cytoskeletal and multiprotein assemblies.
Introduction
Microtubules (MTs) are essential for health and viability of eukaryotic cells. Stable MTs are fairly rigid,1 which enables them to serve as important structural and organizing elements. MTs form long and durable linear tracks for neuronal transport, and the mechanical properties of MTs help to define cell architecture and polarity.2 The dynamics of MTs, i.e., their ability to undergo stochastic cycles of polymerization and depolymerization, also play a prominent role in many cellular processes.3,4 MTs play a vital role during cell division, when they form a mitotic spindle;5 as a result, different MT disrupting or stabilizing drugs are widely used as chemotherapeutic agents.6 Importantly, the disassembling MTs have been proposed to serve as a primary biological motor for poleward chromosome motion during mitosis.7,8 However, understanding the underlying mechanisms for different MT functions is impeded by a lack of quantitative knowledge about the thermodynamics and biomechanics of these complex cytoskeletal structures.
MTs are hollow protein cylinders that contain lateral assemblies of protofilaments: the linear strands of longitudinally arranged αβ-tubulin dimers (Figure 1A).9 A biologically relevant form of MT contains 13 protofilaments that are arranged in a left-hand 3 start helix. Such a multi-protofilament structure makes it difficult to establish a direct correspondence between molecular tubulin characteristics and observed MT properties in vitro. Theoretical approaches have played an important role in providing such a link, for example, by exploring different mechanisms of MT dynamics and force generation.10−13 Theoretical studies have identified several microscopic properties that are critically important for understanding the MT behavior. These features include the thermodynamic characteristics of interfaces between adjacent tubulins, i.e., the energy of lateral and longitudinal bonds, and the mechanical flexural rigidity of individual tubulin protofilaments. To date, it has not been possible to probe these properties via direct experimental measurements, which explains why virtually every aspect of MT thermodynamics and mechanics is still controversial.
Figure 1.
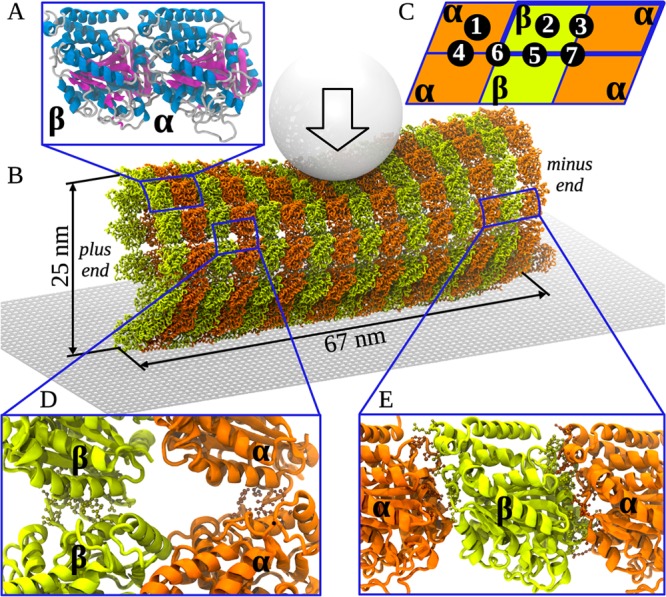
Schematic of SOP model for nanoindentations and subunit interactions. (A) Atomic model of αβ-tubulin heterodimer showing the secondary structure: helices (blue), sheets (red), and loops/turns (gray). (B) The Cα-based representation of an MT lattice fragment (MT8/13) with tubulin heterodimers shown in brown (α-tubulin) and green (β-tubulin). In simulations, the cantilever tip (gray ball) produces indentations of MT lattice (arrow shows direction of force). (C) Schematic of MT fragment with locations of 7 specific points for indentation: for points 1, 2, and 3 the force is applied onto the surface of the α-tubulin, β-tubulin, and dimer–dimer interface, respectively; for points 4 and 5 force is applied at the interfaces between two α- and two β-tubulins, respectively; for points 6 and 7 force is applied between protofilaments at the junction connecting four tubulin dimers, and within two dimers, respectively. (D) Atomic structure of the lateral (α–α and β–β) interfaces between adjacent protofilaments. (E) Atomic structure of the longitudinal interfaces: interdimer (α–β; left) and intradimer (β–α, right).
It is generally agreed that in the MT lattice the longitudinal tubulin–tubulin bonds are stronger than the lateral bonds, because during MT disassembly the lateral tubulin bonds dissociate prior to the longitudinal ones. This is evident from the presence of curled “ram horns” at the ends of shortening polymers14 and is in agreement with computer calculations based on tubulin structure.15 However, the absolute values of the tubulin–tubulin bond energies are not known. Traditional thermodynamic analyses of these bonds have led to ambiguous results mainly because of the complexity of pathways for tubulin assembly and disassembly.16 Indeed, the binding rate constants for tubulin attachment to various sites at the ragged MT tip can vary due to the differences in the number and location of neighboring subunits.17 Additional difficulty concerns the dissociation rate, which can be affected by the number of lateral contacts for a given dimer, as well as by the rigidity of MT protofilaments, which bend concomitantly with tubulin disassembly. The energy of lateral and longitudinal bonds’ dissociations have previously been estimated using different kinetic and mechanical MT models; the energy values vary significantly from 3 to 15 kBT for the lateral bonds, and from 6 to 20 kBT for the longitudinal bonds.18−23 Quantum calculations have also been employed, but the obtained estimates are unrealistically large (up to 186 kBT for the lateral bonds and 158 kBT for the longitudinal bonds24,25). The shapes of the free energy profiles and even the geometry and number of the sites for tubulin–tubulin interactions in the MT models are debated.18,20,22,23,26
The flexural rigidity of MT protofilaments is also a subject of debate. Previous theoretical estimates of this quantity vary by an order of magnitude, from 1,500 to 28,000 pN nm2,27,28 which correspond to energies of 3.7 to 64 kBT per dimer for full protofilament straightening. Accurate determination of protofilament rigidity is experimentally difficult because protofilaments are fragile transient structures. Knowing flexural rigidity, however, is important, because it has direct implications for mechanisms of force generation during MT depolymerization. Indeed, MT depolymerization can generate a large force in vitro and in vivo,29,30 but the underlying mechanism is controversial.27 In the power stroke based mechanism of force generation, the bending protofilaments are thought to transmit a large force available from tubulin–tubulin energetics, but this energy can be used to move the associated cargo only if protofilaments are fairly rigid.10
The various functional roles played by MTs in eukaryotic cells necessitate rigorous quantitative analysis of their thermodynamic and mechanical properties. Recently, considerable progress has been achieved in the mechanical testing of biological protein assemblies,31 including the MT response to compressive force.32,33 Such dynamic force measurements present a unique methodology to deform or rupture the noncovalent bonds of the MT lattice, opening an experimental avenue to determine the underlying microscopic characteristics. The published experimental force–indentation spectra for the MT reveal a complex multistep deformation mechanism.32,33 However, a detailed structure-based interpretation of these results has been lacking. Here, we have carried out the controlled in silico nanoindentations of the MT by combining molecular dynamics (MD) simulations accelerated on graphics processing units (GPUs)34,35 of the atomic tubulin structure and the Cα-based self-organized polymer (SOP) model36−40 of the MT fragment, which contains 13 protofilaments, each 8 tubulin dimers in length (Figure 1). The computational acceleration on GPUs has enabled us to apply the experimentally relevant force-loading rate (cantilever velocity vf= 1.0 μm/s) and to span the experimental time scale (∼50 ms). Close agreement between experimental and simulated force spectra has allowed us to resolve structural transitions in the MT lattice that underpin the MT lattice biomechanics in the experimentally inaccessible sub-nanometer scale of length. Importantly, using our novel methodology of nanoindentation in silico we were able to directly calculate the energies of lateral and longitudinal tubulin–tubulin contacts and to obtain an independent estimate of the flexural rigidity of single tubulin protofilaments.
Results
SOP Model Provides Accurate Description of the Experimental Force–Indentation Spectra
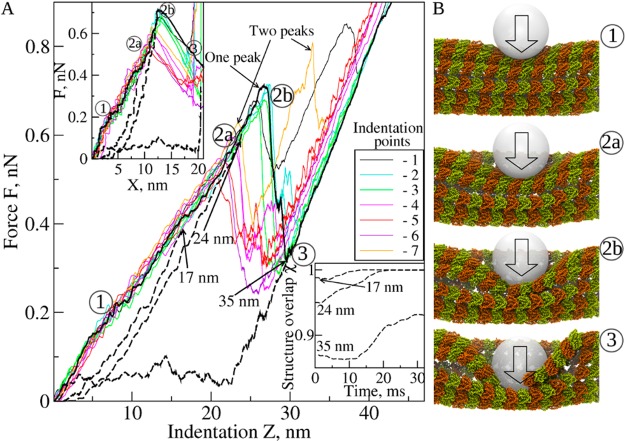
The simulated force–indentation spectra, i.e., the profiles of the indentation force F vs the cantilever tip displacement (indentation depth) X (the FX curves) and the profiles of F vs the virtual cantilever base (or piezo) displacement Z (the FZ curves), are presented in Figure 2A. Importantly, these curves are very similar to the corresponding experimental spectra (see Figure 1C in ref (32)). The FZ and FX curves exhibit the single-step transitions, characterized by a single force peak, and multistep transitions with several force peaks. Although the force spectra show some variability depending on the location of indentation points, each spectrum reveals three distinct regimes (see Supporting Movie S1 in the Supporting Information): (1) the linear-like regime of continuous elastic deformation (Z < 15–20 nm; X < 6–8 nm); (2) the transition regime where the MT lattice undergoes discrete structural transitions (15–20 nm < Z < 25–30 nm; 6–8 nm < X < 11–13 nm); and (3) the postcollapse regime (Z > 25–30 nm; X > 11–13 nm) (Figure 2). We estimated the spring constant KMT from the initial slope of the FZ curves (linear-like regime), and extracted the values of critical force F* (peak force in FZ curves) and the critical distance Z*, at which the transition to the collapsed state occurs. These values are in good quantitative agreement with their experimental counterparts (compared in Table 1). The slightly higher theoretical values of F* and Z* are due to our using a faster cantilever velocity (vf = 1.0 μm/s vs vf ≈ 0.2 μm/s used in refs (32, 33)). Thus, the SOP model provides a very good description of the physicochemical properties of the MT lattice. In the simulations described above, we imposed hard constraints at the ends of the MT fragment (see Materials and Methods) to mimic the long persistence length of the MT polymers (microns to millimeters). However, the force spectra were very similar when the soft (harmonic) constraints were applied, and the relative differences between the values of F*, Z*, and X* from simulations with soft constraints and hard constraints were within the standard deviations (data not shown).
Figure 2.
Force indentations in silico. (A) The force–deformation (FZ) curves for 7 indentation points (Figure 1C), each depicted with different color. Results were obtained with vf =1.0 μm/s and Rtip = 10 nm (see Figure S1 in the Supporting Information for Rtip = 15 nm). Z is the displacement of the virtual cantilever base (piezo in AFM). Dashed black curves represent the FZ profiles for the tip retraction simulations, which followed the forward indentations (solid black curve) with Z = 17, 24, and 35 nm as initial conditions. The top inset shows the corresponding FX curves for the forward indentation (solid curves; colors as in A) and backward tip retraction (dashed black curves). X is the displacement of the cantilever tip. The bottom inset shows the time profiles of the structure overlap χ for MT lattice restructuring during tip retraction (starting from Z = 17, 24, and 35 nm indentations). (B) The MT structure snapshots 1, 2a, 2b, and 3 illustrating the mechanism of MT deformation and collapse. Structure 1: continuous deformation (Z < 15–20 nm; elastic regime). Structures 2a and 2b: disruption of lateral and longitudinal interfaces, respectively (20–25 nm < Z < 25–30 nm; transition regime). Structure 3: postcollapse evolution (Z > 25–30 nm). These structures correspond to the accordingly numbered regions in FZ and FX curves in panel A.
Table 1. Comparison of the Mechanical Properties of the MT Lattice Determined from Indentations in Vitro and in Silicoa.
| indentation | KMT, pN/nm | F*, nN | Z*, nm |
|---|---|---|---|
| in silico (Rtip = 10 nm) | 51.8 ± 2.8 | 0.62 ± 0.07 | 23.8 ± 2.2 |
| in silico (Rtip = 15 nm) | 61.4 ± 6.6 | 0.76 ± 0.04 | 26.9 ± 1.3 |
| in vitro (Rtip = 20 nm) | 74.0 ± 13.0 | 0.4 ± 0.1 | 17.2 ± 3.5 |
Values are means with standard deviations: MT spring constant, KMT; critical force, F*; and critical distance, Z* (cantilever velocity vf = 1.0 μm/s). Experimental data in vitro are from the results of de Pablo et al.32 and Shaap et al.,33 who used vf ≈ 0.2 μm/s and Rtip ≈ 15–20 nm. The experimental values of KMT were extracted from the experimental histogram (Figure 2 in ref (33)); the values of F* and Z* were taken from the experimental force–indentation curves (Figure 1 in ref (32)). Theoretical values of KMT, F*, and Z* were obtained by averaging over 3 simulation runs for each indentation point 1–7.
MT Is a Network of Rigid Elements Interconnected via Elastic Lateral and Longitudinal Bonds
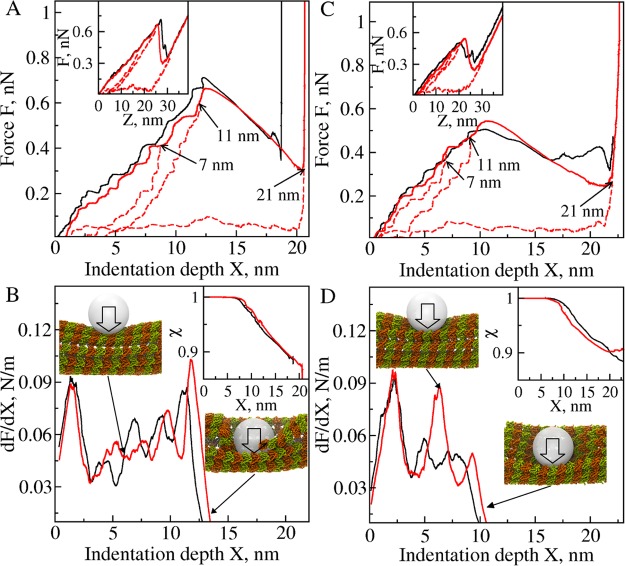
Simulations for 7 indentation points were carried out using tips of different size. The summarized description of all observed transitions is provided in Table S1 in the Supporting Information. Comparison of the FZ and FX curves for a 10 nm tip (Figure 2) vs a 15 nm tip (Figure S1 in the Supporting Information) shows that the force spectra are similar, although the values of F*, X* (critical indentation depth), and KMT increase slightly with tip size (Table 1). Consider examples of the forward indentation for the 10 nm tip followed by tip retraction at the surface of a protofilament (indentation points 2 and 3; Figures 3A and 3B) and between protofilaments (indentation points 6 and 7; Figures 3C and 3D). The critical force F* and critical indentation depth X* depend on where the compressive force is applied: F* = 0.65–0.7 nN and X* ≈ 12 nm for compressing a protofilament (Figure 3A) are larger than F* = 0.5–0.55 nN and X* ≈ 10 nm for compressing the interface between protofilaments (Figure 3C). We also profiled the slope of the FX curve (dF/dX), a measure of mechanical compliance of the MT. We found that dF/dX varies largely with X (Figures 3B and 3D): steep increases interrupted by sudden drops of dF/dX indicate that the MT lattice behaves as a soft material. The heights of the peaks of dF/dX mark the limits of deformability of the MT cylinder. The MT resists the mechanical collapse longer (strong last peak of dF/dX) when indented on the protofilament rather than between the protofilaments (weak last peak of dF/dX). This indicates that the lateral interfaces between tubulins are softer (more compliant mechanically) than between longitudinal tubulins within a protofilament. We arrive at similar conclusions when considering the results obtained with a 15 nm tip for indentation points 1, 3, and 5, 7 (Figure S2 in the Supporting Information). The profiles of structure overlap χ (defined in the Supporting Information) show that the collapsed MT lattice remains ∼80–90% similar to the uncompressed state (the insets to Figures 3B and 3D, and Figures S2B and S2D in the Supporting Information). This implies that stress-dependent changes are mainly localized to the lateral and longitudinal interfaces. Hence, the network of lateral and longitudinal bonds is the origin of elasticity for the MT lattice.
Figure 3.
Force spectra for indentation and retraction and deformation-induced MT structure alterations. Shown are results for indentation points 2 (black) and 3 (red) in panels A and B, and for indentation points 7 (black) and 6 (red) in panels C and D obtained with vf = 1.0 μm/s and Rtip = 10 nm (see Figure S2 in the Supporting Information for results obtained with Rtip = 15 nm). (A, C) The FX curves for forward indentation (solid black and red lines). The insets show the FZ curves. Curves for backward tip retraction (dashed red lines) were generated using the structures obtained from forward indentation for X = 7, 11, and 21 nm (indicated on the graphs). (B, D) The slope dF/dX for force spectra from panels A and C. Snapshots show the side views of the MT structure before dissociation of the lateral bonds and after dissociation of the longitudinal bonds. The insets show the profiles of structure overlap χ vs X.
MT Deformation and Collapse Occur via Specific Multistep Mechanism
Our study demonstrates a qualitative similarity between the FX curves and profiles of dF/dX and χ for different indentation points (Figures 2 and 3 for 10 nm tip, and Figures S1 and S2 in the Supporting Information for 15 nm tip). Analysis of structures generated under different indentation conditions has revealed that the MT transition to the collapsed state occurs by a surprisingly conserved pathway (Supporting Movie S1 in the Supporting Information), which we illustrate for two examples of MT indentation (Figure 4). Initially, the MT lattice resists deformation, as seen from the increase of dF/dX (the inset in Figure 4), which results in small variations in the local curvature of the MT cylinder under the tip (Figure S3A in the Supporting Information). This is the linear-like regime of (continuous) elastic deformation as evidenced from the quasi-linear dependence of F on X (white region in Figure 4); this regime persists until X ≈ 6–8 nm (structure 1 in Figure 2, Figure S1 in the Supporting Information, and Figure 4; see Figure S3A in the Supporting Information). The compressive force loads an increasingly larger portion of the MT surface leading to the MT cylinder flattening (“buckling”). Indentation beyond X ≈ 6–8 nm can no longer be accommodated by the MT bending alone. At this point, the MT system enters the transition regime (gray region in Figure 4) in which discrete structural changes occur. In this regime, mechanical tension exceeds the strength of lateral and longitudinal bonds, which results in their sequential rupture: the lateral bonds dissociate first at X ≈ 6–8 nm (structure 2a, Figure 4), and the longitudinal bonds dissociate second at X ≈ 11–13 nm (structure 2b, Figure 4). The latter event triggers the MT lattice rapid transitioning to the collapsed state, which results in a sharp force drop (force peak in Figure 4). This crossover from the continuous deformation to the multistep discrete dissociation transitions was observed in all indentation simulations (21 runs), regardless of where the compressive force was applied. Importantly, we detected the dissociation of the longitudinal interdimer bonds but not the intradimer bonds, consistent with tubulin heterodimer being a major structural unit for MT disassembly. Disruption of the lateral interfaces between the α-tubulins occurred simultaneously with loss of lateral contacts between the β-tubulins. Beyond X ≈ 20 nm indentation, which corresponds to the postcollapse regime, the tip indented the lower portion of the MT cylinder (not shown), and the resulting events were not analyzed.
Figure 4.
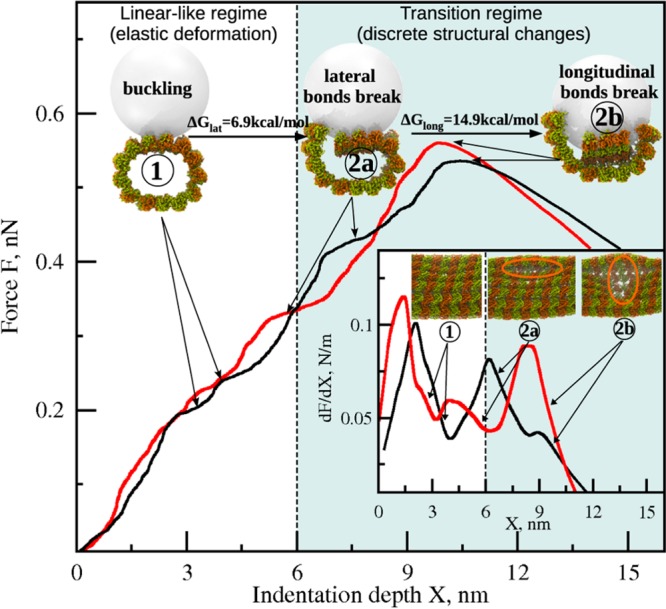
Summary of the MT deformation mechanics. The FX curves for force application between protofilaments at the junction connecting four tubulin dimers (indentation point 6, red curve) and within the adjacent dimers (point 7, black curve) illustrate that the sequence of transitions is overall similar. Images of the MT lattice and tip on the main graph are shown in an MT cross-section view. White area indicates the linear-like regime for elastic deformations, represented by the buckled MT cylinder (structure 1, X ≈ 3–4 nm). Gray area corresponds to the transition regime, characterized by the rupture of lateral (structure 2a, X ≈ 6–8 nm), then longitudinal contacts (structure 2b, X ≈ 9–11 nm). The inset shows the slope dF/dX vs X, so the peaks correspond to the activated system states for the buckling and dissociation transitions. Images in the inset are the same structures 1, 2a, and 2b (with no tip) viewed from the top; areas circled in orange contain the disrupted lateral and longitudinal interfaces (see also Figure S3 in the Supporting Information).
Dissociation of the Lateral but Not Longitudinal Contacts Is Reversible
We carried out simulations of the force-quenched tip retraction with 10 nm tip (Figures 2 and 3) and 15 nm tip (Figures S1 and S2 in the Supporting Information), in which we reversed the direction of cantilever motion thereby gradually decreasing to zero the amplitude of compressive force (see Supporting Movie S2 in the Supporting Information). We used the MT structures from the simulations of forward deformation for X = 7, 11, and 21 nm indentation. These structures correspond to the buckled MT (X ≈ 7 nm), the MT with disrupted lateral bonds (X ≈ 11 nm), and the MT with disrupted lateral and longitudinal bonds (X ≈ 21 nm). To monitor the progress of MT lattice remodeling, we analyzed the structure overlap χ (the inset to Figures 2 and S1 in the Supporting Information). In full agreement with experiment (Figures 1 and 5 in ref (33)), we found that the deformation is fully reversible for small indentations (X < 7 nm), partially reversible with small hysteresis for larger indentations (7 nm < X < 11 nm), and irreversible with large hysteresis for indentations larger than critical (X* ≈ 11–13 nm). These findings are also supported by the results from the dynamics of MT lattice remodeling, which show that MT restructuring is 100% complete (χ ≈ 1) over 10–20 ms for X = 7 and 11 nm indentation, but is incomplete (χ ≈ 0.90–0.93) for X = 21 nm indentation (the bottom inset in Figures 2 and S1 in the Supporting Information). This demonstrates that ruptured lateral contacts between the adjacent protofilaments can be efficiently restored over the time scale of a few tens of microseconds. The disruption of longitudinal bonds, however, inflicts irreparable damage on the MT lattice.
SOP Model Predicts Strong Interactions at the Longitudinal and Lateral Tubulin Interfaces
Our finding that the MT lattice structure in the collapsed state is ∼85–90% similar to the native state (Figures 3 and S2 in the Supporting Information) strongly suggests that the compression-induced alterations in the MT lattice are mostly localized to the lateral and longitudinal interfaces, consistent with recent results from other groups.41 This property allowed us to probe the thermodynamics of MT deformation. We analyzed the FX curves for forced indentation and force-quenched retraction (Supporting Movie S2 in the Supporting Information) to determine the enthalpy change ΔH, reversible work wrev, and free energy change ΔG for the MT transitioning from the native state (X = 0) to the collapsed state (X = 20 nm) (see the Supporting Information for more detail). Next, we calculated the enthalpy change and free energy change for disruption of the contacts at the lateral interface (ΔHlat and ΔGlat) and longitudinal interface (ΔHlong and ΔGlong). The number of lateral/longitudinal contacts was determined using a conservative estimate of the distance characteristic of contact disruption (see the Supporting Information). A comparison of ΔHlat, ΔHlong, and ΔGlat, ΔGlong demonstrates that these state functions show little variation with tip size and tip position on the MT (Table S2 in the Supporting Information). The changes in enthalpy, free energy, and entropy for the disruption of one lateral bond and one longitudinal bond are summarized in Table 2. Importantly, the obtained values of ΔGlat = 6.9 ± 0.4 kcal/mol and ΔGlong = 14.9 ± 1.5 kcal/mol indicate that the intra-protofilament longitudinal tubulin–tubulin bonds are roughly twice as strong as the lateral inter-protofilament tubulin–tubulin bonds. This is consistent with our finding that the lateral bonds dissociate prior to the longitudinal bonds. Interestingly, the difference in entropy for the rupture of longitudinal bonds vs lateral bonds is roughly 4-fold (Table 2). This large TΔS difference can be understood from the increased flexibility of the newly created protofilament ends. We also estimated the range for tubulin–tubulin interactions (see Supporting Information), and found that the longitudinal bonds are characterized by the longer interaction range (Δylong ≈ 1.25–1.5 nm) compared to the lateral bonds (Δylat ≈ 0.85–1.1 nm). Both of these values lie within the 1.5–2 nm interaction range characteristic of protein complexes.42,43
Table 2. Thermodynamic Characteristics Deduced from in Silico Indentations: Change in Enthalpy ΔH, Entropy TΔS, and Free Energy ΔG (with Standard Deviations) Associated with the Disruption of a Single Lateral Bond (Interface) and Longitudinal Bonda.
| interface | ΔG, kcal/mol | ΔH, kcal/mol | TΔS, kcal/mol |
|---|---|---|---|
| lateral | 6.9 ± 0.4 | 9.3 ± 0.8 | 2.5 ± 0.7 |
| longitudinal | 14.9 ± 1.5 | 25.7 ± 2.2 | 10.8 ± 2.5 |
Averaging is performed over all indentation points (1–7, Figure 1C) and for 10 and 15 nm tip.
Nanoindentation Spectra of a Single Protofilament Suggest That It Has Large Flexural Rigidity
We analyzed mechanical deformations of the MT cylinder using a thin-shell approximation (see Supporting Information).32 For the average slope of the FX curves of KMT = 51.8 ± 2.8 pN/nm (for simulations with 10 nm tip; Table 1), the MT flexural rigidity EI comes to (25,400 ± 1,500) × 103 pN nm2, which corresponds to the MT persistence length Lp = EI/kBT of 6.18 ± 0.36 mm. To estimate the flexural rigidity of tubulin strands, we performed simulations of bending deformation of single protofilaments formed by 8 (PF8/1), 16 (PF16/1), 24 (PF24/1), and 32 (PF32/1) dimers (see Supporting Movie S3 in the Supporting Information for PF16/1). In these simulations, the protofilament ends were clamped and the bending in response to forced indentations was examined. The simulated force–deformation spectra, i.e., the profiles of the deformation force F vs the cantilever tip displacement (deformation) X (the FX curves), and the corresponding profiles of the deformation energy (obtained by calculating the area under the FX curve) vs X are presented in Figure S5 in the Supporting Information. Using the harmonic approximation valid for small 2–3 nm deformations we find that the values of EI for these protofilament fragments are in the range of 18,000–26,000 pN nm2 (Figure S5 in the Supporting Information, Table 3), which corresponds to the 4.5–6.6 μm range for the persistence length (Table 3).
Table 3. Mechanical Bending Parameters Deduced from in Silico Deformationsa.
| system | PF8/1 | PF16/1 | PF24/1 | PF32/1 |
|---|---|---|---|---|
| EI × 10–26, N m2 | 1.8 ± 0.1 | 2.3 ± 0.2 | 2.6 ± 0.1 | 2.6 ± 0.1 |
| Lp, μm | 4.5 ± 0.3 | 5.7 ± 0.4 | 6.3 ± 0.2 | 6.3 ± 0.3 |
Values are averages with standard deviations of the flexural rigidity (EI) and persistence length (Lp) obtained from 5 bending simulation runs for single protofilaments of 8 (PF8/1), 16 (PF16/1), 24 (PF24/1), and 32 (PF32/1) tubulin dimers.
Discussion
A Novel Approach to Multiscale Modeling of MT Polymer
Dynamic, mechanical, and force-generating properties of MTs play important roles in many cellular processes, but little is known about the thermodynamics of tubulin–tubulin interactions and mechanics of individual protofilaments that form the MT lattice. Previously, the energies of lateral and longitudinal bonds’ dissociations were estimated with the help of molecular-mechanical models, in which the tubulin monomer/dimer was the smallest unit.19−21 The major drawback of this approach is that tubulin energies are derived from the dynamic parameters of MT assembly and disassembly, which report on the thermodynamics of tubulin–tubulin interactions only indirectly. In contrast, the AFM-based dynamic force measurements provide a more straightforward experimental avenue, because in these experiments the protofilaments’ deformation and tubulin–tubulin bond rupture events are recorded with high spatial and temporal resolution.32,33 However, due to the complexity of the multi-protofilament MT structure, the molecular interpretation of experimental force–indentation spectra at the level of protein–protein bonds is not trivial, as it requires the structure-based understanding of fine features of the experimental spectra.
We have overcome this limitation by carrying out the dynamic force measurements in silico using the amino acid as the smallest structural unit. Our computer-based experiments mimic the AFM based dynamic force experiments in vitro. The full control over the system we have during the entire course of forced deformation (contact point and direction of force application, constrained residues, indenter size) and the structural resolution (intact versus disrupted lateral/longitudinal interfaces) allows us to directly correlate the energy changes with the structure alterations at the residue level. Our approach to forced indentation in silico involves following stochastic dynamics of mechanical deformation of a biological particle, which is microscopically reversible when a force loading is sufficiently slow. In this regime of compressive force application, the rate of force increase is slower than the rate of system re-equilibration at each point along the deformation reaction path (quasi-equilibrium). This can be gleaned, e.g., from the comparison of FX curves for the 24 dimer long protofilament fragment PF24/1 obtained using varying cantilever velocities (see Figure S6 in the Supporting Information). We see that as vf decreases, the FX curves become less and less different. For example, the FX curves obtained for PF24/1 with vf = 1.0 and 0.5 μm/s look almost identical, implying similar mechanical responses (Figure S6 in the Supporting Information). These results show that in silico indentation experiments reported here are carried out under near-equilibrium force-loading conditions.
The dynamic force spectroscopy in silico was previously applied by us to examine the forced unfolding of fibrin polymers44 and to map the free energy landscape for deformation of the Cowpea Chlorotic Mottle Virus capsid.45 This approach is made possible by combining the atomic-level and Cα-based coarse-grained modeling with nanomanipulation of the MT lattice in silico.34,35 By taking advantage of the computational acceleration on a GPU we were able to carry out detailed exploration of MT biomechanics on a long time scale (∼50 ms) using the experimentally relevant conditions of force application.32,33 With this approach, the atomic-level details underlying the lateral and longitudinal interactions are implicit in the SOP model of the MT cylinder. The next-neighbor interactions that stabilize MT structure and the lattice confinement for individual dimers are explicitly described. Within the context of these advances, although this model can be applied to describe processes that occur on a millisecond time scale, given current computational limitations it cannot be applied to much slower processes, such as the rupture of tubulin bonds and protofilament bending during MT depolymerization.
Here, we have determined the thermodynamic and mechanical characteristics of the MT that are difficult to access experimentally by analyzing the force–deformation curves from in silico nanoindentation simulations. The area under the FX curve is the total work performed on the system, and the reversible part of work can be linked to the Gibbs free energy change. Hence, the obtained free energies for the tubulin bonds’ dissociation are based on theoretical analyses of in silico experiments, in which these bonds are directly manipulated. The only free parameter of the SOP model is εh, but the values of this quantity for each group of contacts between amino acids were calculated using the all-atom MD simulations (Table S3 in the Supporting Information). The SOP model based nanoindentation assays provided the force–indentation curves which agree well with the experimental AFM spectra.32,33 Thus, the agreement between the experiment and simulations was achieved without model fitting and without adjustment of free parameters. The detailed understanding of the mechanisms of MT deformation and structural collapse that we have achieved offers unique insights into the mechanochemistry of the MT lattice.
Insights into the Thermodynamics of Tubulin–Tubulin Interactions in the MT Lattice
First, we found that the compressed MT behaves as a system of rigid elements interconnected through a network of lateral and longitudinal elastic bonds. Large rigidity of tubulin monomers agrees well with the results of prior computational modeling study, in which tubulin monomers were found to have a stable central core.46 Accordingly, under small deformations the MT cylinder responds elastically, while undergoing continuous deformation characteristic of long wavelength modes. The importance of slow global modes in mechanical deformation of the MT lattice has also been revealed in a recent elastic network modeling study.47 Beyond 3–4 nm compression, the αβ-tubulin dimers buckle, leading to flattening of the MT cylinder. With further compression the lateral contacts between the adjacent protofilaments dissociate (both α–α and β–β lateral bonds behave similarly), which is then followed by the rupture of longitudinal interdimer but not intradimer bonds (Figure S4 in the Supporting Information); these discrete structure changes are characteristic of short wavelength modes. Importantly, the sequence of microscopic events during mechanical MT compression defined here is likely to provide a blueprint for a pathway of normal MT disassembly. Indeed, in the course of mechanical compression tubulin bonds dissociate in the same order as during normal MT disassembly (lateral bonds prior to the longitudinal ones). Since the Gibbs free energy change for any bond dissociation is a state function and, therefore, does not depend on the exact cause of transition, our findings from nanoindentation experiments are directly applicable to describe and model the molecular events during MT disassembly.
Second, our work provides direct estimates of the free energies of dissociation of the lateral and longitudinal tubulin–tubulin bonds. We show that interfaces between tubulin subunits in the MT wall are characterized by strong noncovalent interactions. Structural analyses revealed that (i) the α–α and β–β lateral interfaces are formed by a total of 19 and 21 stable residue–residue contacts, respectively, and that (ii) the longitudinal intradimer bonds and interdimer bonds are stabilized by 78 and 38 total contacts, respectively. In both the lateral and longitudinal interfaces, the most stable residue–residue contacts are hydrophobic bonds and salt bridges (Figure S4A–D in the Supporting Information), consistent with a recent molecular modeling study48 (major structural determinants in tubulin monomers involved in the intermonomer contacts’ formation are accumulated in Table S4 in the Supporting Information). The difference between the obtained energies of the lateral and longitudinal bonds, ΔΔG = ΔGlong – ΔGlat = 8.0 kcal/mol (∼13.3 kBT), is close to the 11 kBT estimate reported earlier.15,19 Importantly, the large strength of the tubulin–tubulin bonds reported here should prompt a re-evaluation of current molecular models of MT dynamics and stability, where these characteristics play a significant role.
Third, our results reveal that the rupture of the lateral tubulin–tubulin bond is highly reversible. This finding provides an important clue for understanding the molecular mechanisms of MT rescue, an abrupt switch from MT depolymerization to polymerization. We suggest that high reversibility of lateral bond dissociation can promote “sealing” of the cracks between shortening protofilaments in the MT wall, thereby inhibiting the depolymerization. Another insight from our study concerns the geometry of contacts in the lateral tubulin interfaces. Previously, it has been suggested that the steplike “gaps” in the force–indentation curves obtained with AFM reflect the existence of two additional interaction sites between the dimers in adjacent protofilaments.22 Our results demonstrate that a single pair of lateral interaction sites can account for all features of the experimental force spectrum, and the steplike gaps appear to result from the dissociation of lateral bonds under 6–8 nm deformations (Figure 4). Interestingly, subjecting the MT lattice to mechanical stress can lead to the formation of small defects at the junction points connecting α- and β-tubulins; these defects grow in size with increasing force load (Figure S3 in the Supporting Information). Such defects could also emerge due to the mechanical “fatigue” of an MT lattice that repeatedly experiences large deformations, similar to the behavior of carbon nanotubes.49,50 However, since the local force to cause such a crack is large (>300 pN), thermal vibrations of the MTs are highly unlikely to lead to the MT lattice fatigue,33 so they cannot explain the MT “aging” in vitro.51 Yet, crack formation might be pertinent to the activity of MT-severing enzymes, which are thought to exert large local forces while pulling the tubulins out of the MT wall.52
We found that the rupture of the longitudinal tubulin–tubulin bond is irreversible on the time scale of a few tens of microseconds. The corresponding irreversibility of the MT lattice restructuring is directly related to the long time scale required for the re-formation of all the longitudinal bonds and recovery of the MT lattice structure upon large indentation, a feature that was also detected in the original AFM experiments.32,33 The authors found that it would take ∼4 min for the MT lattice to fully self-heal (in the absence of free tubulin in solution) following an indentation beyond 10 nm. Hence, this finding shows that even after disruption of lateral and longitudinal bonds the lattice is able to recover, but only on a long time scale of a few minutes. To further explore this (ir)reversibility aspect, we carried out simulations of force-induced forward indentation followed by force-quenched backward tip retraction, but for the short protofilament fragment PF8/1. The results are presented in Figure S7 in the Supporting Information. Interestingly, we found that, following the initial dissociation of the longitudinal bond between the 4th and 5th dimers, when the direction of tip motion was reversed, the bond re-formed and the protofilament unbent completely over a 10–20 ms time scale (Figure S7 in the Supporting Information). Hence, the longitudinal bond dissociation in short protofilament fragments (such as PF8/1) is fully reversible on the millisecond time scale. This can be explained by lower entropic barriers for reassociation of tubulin dimers in single protofilaments compared to the MT lattice.
Implications for the Models of Force Generation by the Depolymerizing MT
The large flexural rigidity of individual protofilaments reported here implies that tubulin protofilaments are fairly rigid. Our estimates (18,000–26,000 pN nm2, Table 3) come close to the experimental values from several studies (Table 1 in ref (18)) and agree with those from a recent all-atom MD simulation study (EI = 27,740 pN nm2).28 This large protofilament’s rigidity supports the idea that almost the entire energy from GTP hydrolysis is stored as mechanical tension in a straightened protofilament.53,54 The obtained value of the persistence length for the MT cylinder Lp = 6.18 mm agrees well with the experimentally measured value 3.45 mm (ref (1)) and with the estimates from other computation studies,28,47,55 demonstrating the validity of SOP modeling. Importantly, our results imply that tubulin protofilaments are about 3 orders of magnitude more flexible than the intact MT cylinder (of comparable length), which is in tune with some but not all previous estimates.27,48,56 We also obtained a similar 3 orders of magnitude difference for the persistence length, i.e., 6.18 mm for the MT cylinder vs 4.5–6.6 μm for the tubulin protofilaments (Table 3), implying a stabilizing role played by the lateral tubulin–tubulin bonds.
Our work has important implications for the mechanism of force generation by the disassembling MTs. The ability of shortening MTs to transport a large cargo in vitro (up to 30 pN)30 has been proposed to result from different mechanisms, including the biased-diffusion and power stroke based models.10,27 Only the latter mechanism takes a direct advantage of the tubulin dissociation pathway during which the lateral tubulin bonds dissociate prior to the longitudinal ones, causing a splaying of the protofilaments into the “ram’s horns” structures.14,58 This structural transition has been proposed to exert a power stroke, capable of moving the appropriately attached cargo.21,57,59 Although SOP modeling does not allow one to calculate directly the MT disassembly due to the prohibitively large computational time, it is interesting to discuss the estimates obtained here in the framework of the current models for MT force generation. The work to straighten the 8–32 dimer long protofilament with the intradimer bending angle of 0.4 rad can be estimated from the protofilament’s rigidity, assuming that the protofilament behaves as a Hookean spring: ∼39–58 kBT. This large bending energy suggests that a significant portion of this chemical energy can be converted into useful work.53,54 Therefore, both the large flexural rigidity of tubulin protofilaments and high tubulin–tubulin dissociation energies obtained here support the proposal that the disassembling MT can serve as a strong depolymerization motor.10,21 We hope that future advances in computational molecular modeling and availability of high-resolution, nucleotide specific tubulin structures will enable a direct testing of these conclusions. The modeling tools we have developed here can also be applied to study other complex biological assemblies when their detailed physicochemical characteristics cannot be resolved using modern experimental approaches.
Materials and Methods
Computer Model of MT Lattice
The structure of a finite-length fragment of the MT lattice was obtained from the 13 subunit ring structure of αβ-tubulin dimers, as in ref (60). This ring structure utilizes atomic coordinates of the αβ-tubulin dimer (PDB code: 1JFF),61 in which the E-site in β-tubulin contains GDP. The finite-length fragment of GDP-tubulin MT lattice (MT8/13, Figure 1A) was constructed by replicating the ring structure 8 times using the shift distance of 85 Å to obtain an MT construct of 8 dimers in length (MT8/13; see Figure 1B). We used the all-atom molecular dynamics simulations in implicit water (SASA and GB models of implicit solvation) to obtain an accurate parametrization of the SOP model, as described below (see Table S3 in the Supporting Information). The structures of 8, 16, 24, and 32 dimer long single protofilaments (PF8/1, PF16/1, PF24/1, and PF32/1) were extracted starting from the structure of MT8/13.
Self-Organized Polymer (SOP) Model
We used the SOP model of the polypeptide chain36 to describe each monomer (α-tubulin and β-tubulin). In the topology-based SOP model, each amino acid is represented by a single interaction center (Cα-atom), and the Cα–Cα covalent bond with the bond distance a = 3.8 Å (peptide bond length). The potential energy function of the protein conformation USOP specified in terms of the coordinates {ri} = r1, r2, ..., rN (N is the total number of amino acid residues) is given by USOP = UFENE + UNBATT + UNB. The finite extensible nonlinear elastic potential UFENE = −∑i=1N–1(k/2)(R02){log[1 – (ri,i+1 – ri,i+1)2/R02]} with the spring constant k = 14 N/m and the tolerance in the change of a covalent bond distance R0 = 2 Å describes the backbone chain connectivity. The distance between residues i and i + 1 is ri,i+1, and ri,i+10 is its value in the native (PDB) structure. We used the Lennard-Jones potential UNB = ∑i=1N–3∑j=i+3εh[(rij0/rij)12 – 2(rij/rij)6]Δij to account for the noncovalent (nonbonded attractive) interactions that stabilize the native folded state. We assumed that if the noncovalently linked residues i and j (|i – j| > 2) are within the cutoff distance RC = 8 Å in the native state, then Δij = 1, and it is zero otherwise. The value of εh quantifies the strength of the nonbonded interactions. The non-native (nonbonded repulsive) interactions UNBREP = ∑i=1εl(σl/ri,i+1)6 + ∑i=1N–3∑j=i+3εl(rij0/rij)6(1−Δij) are treated as repulsive. An additional constraint was imposed on the bond angle formed by residues i, i+1, and i+2 by including the repulsive potential with parameters εl = 1 kcal/mol and σl = 3.8 Å. These determine the strength and the range of the repulsion.
Parameterization of Cα-Based SOP Model
A more detailed description of the SOP model parametrization is presented in the Supporting Information. In short, in the SOP model, the parameter εh defines the average strength of noncovalent residue–residue contacts that stabilize the native state. Importantly, the values of εh were calculated directly using MD simulations of an atomic structure model MT8/13 of the MT lattice at T = 300 K. The atomic-level details that determine the type and number of binary contacts between amino acids and their energies were ported to the SOP model of the MT lattice. Three 10 ns simulation runs were performed to calculate for each group of contacts the average nonbonded energy (Enb), given by the sum of the van der Waals energy (Lennard-Jones potential) and the electrostatic energy (Coulomb potential), and the average number of binary contacts between amino acids (Nnb) that stabilize the native MT structure (native contacts). We assumed that a pair of residues formed a contact if the distance between their Cα-atoms in the native state does not exceed the cutoff distance RC. We used a standard choice of the cutoff distance RC = 8 Å. All the native contacts were divided into five groups (contact types): (1) the intramonomer contacts in the α-tubulin monomers; (2) the intramonomer contacts in the β-tubulin monomers; (3) the intradimer contacts that stabilize the dimer’s structure; (4) the longitudinal interdimer contacts between any two dimers along the MT cylinder axis; and (5) the lateral interdimer contacts between the α-tubulin monomers and between the β-tubulin monomers in adjacent protofilaments. To calculate the energy for nonbonded interactions, we employed the Solvent Accessible Surface Area (SASA)62 and Generalized Born (GB)63 models of implicit solvation, which are based on the CHARMM19 force-field.64 We used the output from SASA model based simulations (coordinate and energy files) to calculate the values of Enb and Nnb for the contact groups 1–3. Since electrostatic interactions are important for the formation of longitudinal and lateral tubulin–tubulin bonds, we used a more accurate GB model to calculate Enb and Nnb for the contact groups 4 and 5. Finally, dividing Enb by the corresponding value of Nnb for each contact group, we obtained the value of εh (see Table S3 in the Supporting Information), which were used in all simulations reported here.
Dynamic Force Measurements in Silico
Nanoindentation measurements were performed at different points on the MT surface using the spherical tip of radius Rtip = 10 and 15 nm (Figure 1C), similar to the 15 nm tip used in atomic force microscopy (AFM) experiments.32,33 In the simulations of mechanical indentation of the MT cylinder and deformation of single protofilament fragments, the tip–MT lattice interactions and the tip–protofilament interactions were modeled by the repulsive potential, Utip = εtip[σtip/(ri– Rtip)]6, where ri is the position of the ith particle, εtip = 4.18 kJ/mol, and σtip =1.0 Å. In the forward indentation measurement, the tip exerted the time-dependent compressive force f(t) = f(t)n in the direction n perpendicular to the MT or protofilament surface (Figure 1B). The force magnitude f(t) = rft was increased with the force-loading rate rf = κvf, where vf = 1.0 μm/s (for MT indentations) and vf = 0.2 μm/s (for protofilament deformations) is the velocity of the cantilever base (piezo) represented by a virtual particle, and κ = 0.05 N/m is the cantilever spring constant. The force f(t) is transmitted to the tip through the cantilever spring, and the resisting indentation force (for MT lattice) or deformation force (for the protofilament) F is calculated using the energy output from simulations. In the simulations of backward (tip) retraction, the direction of tip (or piezo) motion was reversed, which resulted in a gradual decrease of the compressive force to zero.
Simulations of Mechanical Indentation of MT
These simulations were performed using the SOP model of MT8/13 and Langevin simulations accelerated on a GPU.34,35 To account for the long persistence length of MTs (microns to millimeters),65 positions of the Cα-atoms for a total of 9 residues 248, 253, 257, 262, 325, 326, 329, 348, 349 in each tubulin monomer at the plus MT end, and positions of the Cα-atoms for 9 residues 98, 176, 177, 180, 221, 224, 225, 403, 407 in each tubulin monomer at the plus MT end, were constrained (Figure 1). We implemented hard constraint conditions, in which the positions of all 9 constrained residues were fixed, and soft harmonic constraints, in which we connected these same 9 residues to a virtual wall through a harmonic spring with the spring constant of κ = 0.1 nN/nm. A total of 42 indentation runs were generated (using hard constraints): 3 runs per indentation point 1–7; 21 runs for each Rtip value. We profiled the dependence of the indentation force F in dynamic force experiments on the cantilever tip displacement X (indentation depth) and Z (the piezo displacement) for all indentation points (Figure 1C). The FX curves show higher sensitivity to the MT deformation dynamics than FZ curves, and so X is a better reaction coordinate. However, for the purpose of comparing the results of experiments with simulations, we analyzed the FZ and FX curves (Figure 2A).
Simulations of Bending Deformation of MT Protofilaments
These simulations were performed using the SOP models of protofilament fragments PF8/1, PF16/1, PF24/1, and PF32/1 and Langevin simulations on a GPU. To constrain a protofilament, we fixed the same positions of the Cα-atoms at the N-terminus of the first monomer and at the C-terminus of the last monomer. The cantilever tip was set to move in the direction perpendicular to the protofilament axis, as shown in Figure S5 in the Supporting Information. A total of 12 indentation runs for indentation point 3 were generated for all four protofilament fragments: 3 runs per fragment (Rtip = 10 nm). We profiled the dependence of the deformation force F on the cantilever tip displacement X for the protofilament fragments (Figure S5 in the Supporting Information). Flexural rigidity of the protofilament fragments was calculated in the harmonic approximation as described in the Supporting Information. Because the harmonic approximation is valid only in the regime of small deformations, we analyzed the initial quadratic 2–3 nm portion of the FX curves (Figure S5 in the Supporting Information). This deformation translates to the average dimer–dimer bending angle of 1–2°.
Free Energy Estimation
To obtain accurate estimates of the Gibbs free energy change associated with the disruption of single lateral interface and longitudinal interface (ΔGlat and ΔGlong), we determined the mechanical work performed on the MT (area under the FX curve). Since it is not possible to apply infinitely slow force loading, which would correspond to the equilibrium conditions of mechanical force application (and reversible work), the total work (w) in our indentation cycle contains the reversible part wrev, which is spent to deform the MT lattice, and to dissociate the lateral and longitudinal bonds, as well as the irreversible part wirrev (see hysteresis in the FX curves in Figures 2 and 3; see also Figures S1 and S2 in the Supporting Information). We calculated the reversible part of work wrev using the Crooks theorem (see the Supporting Information).
Analyses of the Simulation Output
These analyses for mechanical compression of MT8/13, and bending deformation of PF8/1, PF16/1, PF24/1, and PF32/1, including the structure visualization and determination of the thermodynamic quantities (ΔG, ΔH, and TΔS), flexural rigidity (EI), persistence length (Lp), and the range of lateral and longitudinal bonds (Δy), are described in detail in the Supporting Information.
Acknowledgments
We thank J. R. McIntosh for critical reading of the manuscript and A. Zaytsev for help with videos. This work was supported in part by National Institutes of Health Grant R01-GM098389 to E.L.G.; by the National Science Foundation CAREER Award MCB-0845002 to R.I.D.; and by Russian Fund for Basic Research (13-04-40188-H, 13-04-40190-H) and Presidium of Russian Academy of Sciences (Mechanisms of the Molecular Systems Integration and Molecular and Cell Biology programs) to F.I.A.
Supporting Information Available
Additional description of multiscale MT modeling approach, construction of MT model, main features of SOP model, its parametrization and dynamic force measurements in silico, and methods for data analysis. Tables: Summary of microscopic transitions in the MT lattice, comparison of the mechanical and thermodynamic parameters from indentations at different points, and parametrization of the SOP model for the MT lattice. Movies: Forced indentation of MT lattice, forward indentation and backward tip retraction of the MT lattice, and force deformation of 16 dimer long MT protofilament. Figures: Mechanism of MT lattice nanoindentation with Rtip = 15 nm, detailed information about structure changes during force indentation, atomic representation of lateral and longitudinal tubulin–tubulin interfaces, force–deformation spectra for single protofilament fragments, dependence of force–deformation spectra on cantilever velocity, and reversibility of longitudinal bonds’ dissociation observed for single protofilament fragment. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Valdman D.; Atzberger P. J.; Yu D.; Kuei S.; Valentine M. T. Biophys. J. 2012, 102, 1144–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dogterom M.; Surrey T. Curr. Opin. Cell Biol. 2013, 25, 23–29. [DOI] [PubMed] [Google Scholar]
- de Forges H.; Bouissoua A.; Pereza F. Int. J. Biochem. Cell Biol. 2012, 44, 266–274. [DOI] [PubMed] [Google Scholar]
- Desai A.; Mitchison T. J. Annu. Rev. Cell Dev. Biol. 1997, 13, 83–117. [DOI] [PubMed] [Google Scholar]
- Walczak C. E.; Cai S.; Khodjakov A. Nat. Rev. Mol. Cell Biol. 2010, 11, 91–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakhoum S. F.; Compton D. A. Curr. Opin. Cell Biol. 2012, 24, 64–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh J. R.; Volkov V. A.; Ataullakhanov F. I.; Grishchuk E. L. J. Cell Sci. 2010, 123, 3425–3434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joglekar A. P.; Bloom K. S.; Salmon E. D. Curr. Opin. Cell Biol. 2010, 22, 57–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nogales E.; Whittaker M.; Milligan R. A.; Downing K. H. Cell 1999, 96, 79–88. [DOI] [PubMed] [Google Scholar]
- Grishchuk E. L., McIntosh J. R., Molodtsov M. I., Ataullakhanov F. I.. Force generation by dynamic microtubule polymers. In Comprehensive Biophysics, Molecular Motors and Motility; Academic Press: Oxford, 2011; Vol. 4, pp 93–117. [Google Scholar]
- Bowne-Anderson H.; Zanic M.; Kauer M.; Howard J. Bioessays 2013, 35, 452–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dogterom M.; Kerssemakers J. W. J.; Romet-Lemonne G.; Janson M. E. Curr. Opin. Cell Biol. 2005, 17, 67–74. [DOI] [PubMed] [Google Scholar]
- Gardner M. K.; Hunt A. J.; Goodson H. V.; Odde D. J. Curr. Opin. Cell Biol. 2008, 20, 64–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandelkow E. M.; Mandelkow E.; Milligan R. A. J. Cell Biol. 1991, 114, 977–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sept D.; Baker N. A.; McCammon J. A. Protein Sci. 2003, 12, 2257–2261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vulevic B.; Correia J. J. Biophys. J. 1997, 72, 1357–1375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner M. K.; Charlebois B. D.; Jánosi I. M.; Howard J.; Hunt A. J.; Odde D. J. Cell 2011, 146, 582–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanBuren V.; Cassimeris L.; Odde D. J. Biophys. J. 2005, 89, 2911–2926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanBuren V.; Odde D. J.; Cassimeris L. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 6035–6040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efremov A.; Grishchuk E. L.; McIntosh J. R.; Ataullakhanov F. I. Proc. Natl. Acad. Sci. USA 2007, 104, 19017–19022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molodtsov M. I.; Grishchuk E. L.; Efremov A. K.; McIntosh J. R.; Ataullakhanov F. I. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 4353–4358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z.; Nogales E.; Xing J. Biophys. J. 2012, 102, 2687–2696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z.; Wang H.-W.; Mu W.; Ouyang Z.; Nogales E.; Xing J. PLoS One 2009, 4, e7291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drabik P.; Gusarov S.; Kovalenko A. Biophys. J. 2007, 92, 394–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayoub A. T.; Craddock T. J. A.; Klobukowski M.; Tuszynski J. Biophys. J. 2014, 107, 740–750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molodtsov M. I.; Ermakova E. A.; Shnol E. E.; Grishchuk E. L.; McIntosh J. R.; Ataullakhanov F. I. Biophys. J. 2005, 88, 3167–3179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asbury C. L.; Tien J. F.; Davis T. N. Trends Cell Biol. 2011, 21, 38–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafmüller A.; Voth G. A. Structure 2011, 19, 409–417. [DOI] [PubMed] [Google Scholar]
- Nicklas R. B. J. Cell Biol. 1983, 97, 542–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volkov V. A.; Zaytsev A. V.; Gudimchuk N.; Grissom P. M.; Gintsburg A. L.; Ataullakhanov F. I.; McIntosh J. R.; Grishchuk E. L. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 7708–7713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roos W. H.; Bruinsma R.; Wuite G. J. L. Nat. Phys. 2010, 6, 733–743. [Google Scholar]
- de Pablo P. J.; Schaap I. A. T.; MacKintosh F. C.; Schmidt C. F. Phys. Rev. Lett. 2003, 91, 098101–098104. [DOI] [PubMed] [Google Scholar]
- Schaap I. A. T.; Carrasco C.; de Pablo P. J.; MacKintosh F. C.; Schmidt C. F. Biophys. J. 2006, 91, 1521–1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhmurov A.; Dima R. I.; Kholodov Y.; Barsegov V. Proteins: Struct., Funct., Bioinf. 2010, 78, 2984–2999. [DOI] [PubMed] [Google Scholar]
- Zhmurov A.; Rybnikov K.; Kholodov Y.; Barsegov V. J. Phys. Chem. B 2011, 115, 5278–5288. [DOI] [PubMed] [Google Scholar]
- Hyeon C.; Dima R. I.; Thirumalai D. Structure 2006, 14, 1633–1645. [DOI] [PubMed] [Google Scholar]
- Theisen K. E.; Zhmurov A.; Newberry M. E.; Barsegov V.; Dima R. I. J. Phys. Chem. B 2012, 116, 8545–8555. [DOI] [PubMed] [Google Scholar]
- Dima R. I.; Joshi H. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 15743–15748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z.; Thirumalai D. Structure 2012, 20, 628–640. [DOI] [PubMed] [Google Scholar]
- Hyeon C.; Onuchic J. N. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 17382–17387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alushin G. M.; Lander G. C.; Kellogg E. H.; Zhang R.; Baker D.; Nogales E. Cell 2014, 157, 1117–1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoefling M.; Gottschalk K. E. J. Struct. Biol. 2010, 171, 52–63. [DOI] [PubMed] [Google Scholar]
- Selzer T.; Schreiber G. Proteins: Struct., Funct., Bioinf. 2001, 45, 190–198. [DOI] [PubMed] [Google Scholar]
- Zhmurov A.; Brown A. E.; Litvinov R. I.; Dima R. I.; Weisel J. W.; Barsegov V. Structure 2011, 19, 1615–1624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kononova O.; Snijder J.; Brasch M.; Cornelissen J.; Dima R. I.; Marx K. A.; Wuite G. J.; Roos W. H.; Barsegov V. Biophys. J. 2013, 105, 1893–903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng L. X.; Hsu M. T.; Bonomi M.; Agard D. A.; Jacobson M. P. PLoS Comput. Biol. 2014, 10, e1003464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deriu M. A.; Soncini M.; Orsi M.; Patel M.; Essex J. W.; Montevecchi F. M.; Redaelli A. Biophys. J. 2010, 99, 2190–2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafmüller A.; Noya E. G.; Voth G. A. J. Mol. Biol. 2013, 425, 2232–2246. [DOI] [PubMed] [Google Scholar]
- Suhr J.; Victor P.; Ci L.; Sreekala S.; Zhang X.; Nalamasu O.; Ajayan P. M. Nat. Nanotechnol. 2007, 2, 417–421. [DOI] [PubMed] [Google Scholar]
- Pampaloni F.; Florin E. L. Trends Biotechnol. 2008, 302–310. [DOI] [PubMed] [Google Scholar]
- Su X.; Ohi R.; Pellman D. Trends Cell Biol. 2012, 22, 567–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp D. J.; Ross J. L. J. Cell Sci. 2012, 125, 2561–2569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mickey B.; Howard J. J. Cell Biol. 1995, 130, 909–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caplow M.; Ruhlen R. L.; Shanks J. J. Cell Biol. 1994, 127, 779–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sept D.; MacKintosh F. C. Phys. Rev. Lett. 2010, 104, 018101. [DOI] [PubMed] [Google Scholar]
- Gittes F.; Mickey B.; Nettleton J.; Howard J. J. Cell Biol. 1993, 120, 923–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grishchuk E. L.; Molodtsov M. I.; Ataullakhanov F. I.; McIntosh J. R. Nature 2005, 438, 384–388. [DOI] [PubMed] [Google Scholar]
- Chrétien D.; Fuller S. D.; Karsenti E. J. Cell Biol. 1995, 129, 1311–1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koshland D. E.; Mitchison T. J.; Kirschner M. W. Nature 1988, 331, 499–504. [DOI] [PubMed] [Google Scholar]
- Wells D. B.; Aksimentiev A. Biophys. J. 2010, 99, 629–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe J.; Li H.; Downing K. H.; Nogales E. J. Mol. Biol. 2001, 313, 1045–1057. [DOI] [PubMed] [Google Scholar]
- Ferrara P.; Apostolakis J.; Caflisch A. Proteins: Struct., Funct., Bioinf. 2002, 46, 24–33. [DOI] [PubMed] [Google Scholar]
- Hawkins G. D.; Cramer C. J.; Truhlar D. G. J. Phys. Chem. 1996, 100, 19824–19839. [Google Scholar]
- MacKerell A. D.; Bashford B.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Nguyen D. T.; Prodhom B.; Reiher W. E. III; Roux B.; Schlenkrich M.; Smith J. C.; Stote R.; Straub J.; Watanabe M.; Wiorkiewicz-Kuczera J.; Yin D.; Karplus M. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- Pampaloni F.; Lattanzi G.; Jonas A.; Surrey T.; Frey E.; Florin E. L. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 10248–10253. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.