Best Fitting Prediction Equations for Basal Metabolic Rate: Informing Obesity Interventions in Diverse Populations

Abstract

Basal Metabolic Rate (BMR) represents the largest component of total energy expenditure and is a major contributor to energy balance. Therefore, accurately estimating BMR is critical for developing rigorous obesity prevention and control strategies. Over the past several decades, numerous BMR formulas have been developed targeted to different population groups. A comprehensive literature search revealed 248 BMR estimation equations developed using diverse ranges of age, gender, race, fat free mass, fat mass, height, waist-to-hip ratio, body mass index, and weight. A subset of 47 studies included enough detail to allow for development of meta-regression equations. Utilizing these studies, meta-equations were developed targeted to twenty specific population groups. This review provides a comprehensive summary of available BMR equations and an estimate of their accuracy. An accompanying online BMR prediction tool (available at http://www.sdl.ise.vt.edu/tutorials.html) was developed to automatically estimate BMR based on the most appropriate equation after user-entry of individual age, race, gender, and weight.

1. Introduction

Obesity is the result of a positive imbalance between energy intake and energy expenditure ¹. The basal metabolic rate (BMR), defined as the energy required for performing vital body functions at rest, is the largest contributor to energy expenditure. Therefore estimating the total contribution of individual BMR to total daily energy expenditure is an important calculation for understanding, developing, and executing weight related interventions.^{1, 2} For example, BMR estimation is applied to determine target energy intake in weight loss programs, develop dynamic prediction models of weight gain and loss, identify patients with potential metabolic abnormalities, inform the design of public health programs promoting obesity prevention in diverse populations, and assess potential energy deficits in metabolically stressed patients, such as burn victims. Direct measurement of BMR through indirect calorimetry ³ is not feasible for frequent and timely individual use. As a result, the majority of BMR estimates obtained for weight loss interventions rely on BMR prediction equations. Over the past few decades, a large body of obesity related literature has been devoted to development of BMR equations targeted to specific population demographics.

BMR and the terms resting metabolic rate and resting energy expenditure are often used interchangeably⁴, however, some investigators differentiate between these terms based on the conditions under which they are measured ⁵. We limited our review of BMR studies to experiments that have measured the dependent variable, consistent with the definition of BMR ^6,7 measured in the post-absorptive state, after at least 10 hours of fasting, determined through direct or indirect calorimetry^6,7.. The extensive literature on BMR equations is based on the pioneering work of Harris and Benedict ⁸ and includes covariates such as age ^{2, 8–14}, body composition (i.e. fat mass and fat free mass) ¹³, gender and race ¹⁵ on BMR. Most of the developed equations have focused on cross sectional data from targeted subpopulations (for example the young adults) and have used a specific equation structure. A review by Frankenfield et al. ¹⁶ compares commonly applied BMR prediction equations including Mifflin et al. , ¹⁷ Owen et al., ^{18, 19} Harris and Benedict ⁸ and WHO report²⁰ to determine the most reliable prediction equation. However current reviews often fail to include different equation structures and populations with different age ranges and race. In fact, a single equation cannot adequately capture the variations across age, race, gender, and body composition.

The purpose of the current paper is to combine, analyze and categorize a comprehensive review of studies that estimate the relationship between BMR and known covariates. The results of the analysis were combined to determine the best fitting BMR prediction equations targeted to different population characteristics. A simple online tool¹ that determines the best BMR estimate after user input of age, race, gender, weight, and height was developed to enhance clinical application of study results.

2. Methods

Overview

Models that predict BMR, include different determinants and metabolically active components at four different levels of molecular (Fat mass and fat free mass), cellular (extracellular fluid, and extracellular solids), tissue/organ and whole body (Body Mass). ²¹ In this Systematic Review, our purpose is to find all regression equations reported in the literature for predicting BMR based on molecular or whole body level factors. More detailed levels of cellular or tissue/organ components, while very important for advancement of our understanding of drivers of BMR, are not considered due to the complexity involved in quantifying those factors which reduces their value for widespread clinical application. In our review, the selected papers contain prediction models for healthy obese or non-obese individuals, differentiated based on their race, gender and age. Due to limited number of primary studies that account for dynamic changes in metabolic rate of a single individual over time (See ^{22, 23} for notable exceptions), our analysis focuses on equations using cross-sectional data. Then we apply a meta-regression analysis to generate a combined equation that is more robust in predicting BMR for each sub-population group. In our study we refer to meta-regression analysis as a method to develop a single regression equation that summarizes the findings of multiple regressions found in a number of studies.

Literature Search and Filtering

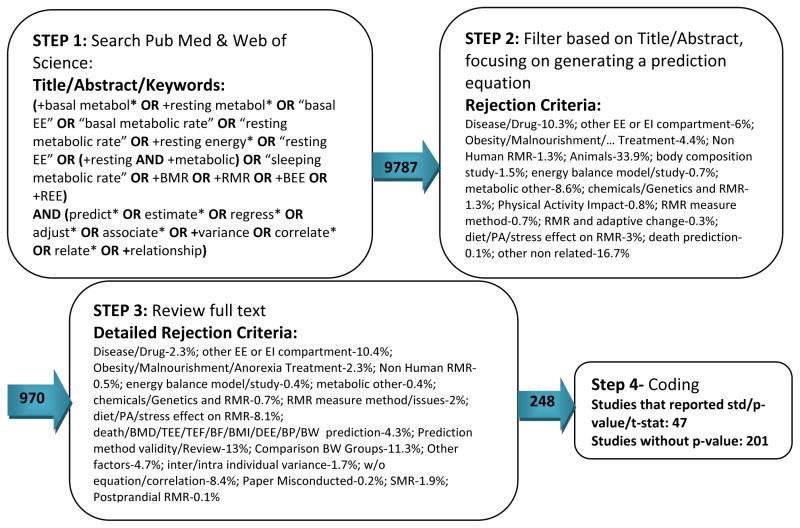
The comprehensive search of the literature was performed in four stages to identify all studies that predict a BMR equation based on an empirical dataset. The specific keywords, used to search PubMed and the Web of Science databases for studies published in any language between the earliest available date October 31, 1923 and March 3, 2011, are shown in Figure 1. Search terms are selected so that any publication, which finds a prediction model for BMR or its alternative terms (Resting Metabolic Rate (RMR), Resting Energy Expenditure (REE) or Basal Energy Expenditure (BEE)), is included. Retrieved articles were reviewed in two steps. First abstracts were reviewed and items obviously not fitting were excluded. Then the full text for the remaining articles were obtained and reviewed to select the articles that included a regression equation based on the criteria above. In a parallel process reference tracking helped identify additional studies not retrieved through automated search.

Figure 1.

Flowchart of literature search and selection process

Literature Coding

The regression equations reported in the remaining sample were extracted into a database. These studies fall into two categories, first, those studies that lack estimates of variance for reported regression coefficients. These are coded by including the data sample size and determinants used to estimate BMR for future research, but are not further analyzed in this paper because they lacked enough specificity to allow parametric meta-regression. The second group consisted of studies that include some measure of variance such as standard deviation, p-value, or t statistic. The details of the data set used in the study and the equations developed were extracted from this group (See online supporting information S1). Variance or standard deviation of reported regression parameters is needed for conducting meta-regression analysis. Therefore we follow a set of procedures to consistently extract/estimate this factor, which is described in online supporting information S2. The full set of references without estimates of variance is reported in online supporting information S4.

Meta-Regression Analysis

Resulting equations are grouped based on sub-populations they were developed for (based on gender, age group, and race) and the structure of the regression equation (i.e. independent variables included and the transformations used). Within each group with homogenous population and equation structure, we combined all the extracted equations to form a single new equation that aggregates different previous findings. If a study estimates a single equation for two different groups (e.g. 18–50 and >50 years old groups), we used that equation separately in estimating the aggregate equations for each of the groups.

There are different approaches in the literature for synthesizing coefficients (slopes) of a set of similar regressions found in different studies into a single slope, ²⁴ which in this paper we refer to as meta-regression². The more statistically precise methods, such as the multivariate Generalized Linear Square approach, ²⁴ require the covariance between different slopes. However the covariance matrices are rarely reported in studies. In fact none of the studies found in the literature search for this paper included the covariance matrix of slopes. Instead we used an alternative method that has been applied to different problems in the literature, ^26–28 and only requires the regression coefficients and the standard error for each coefficient. In this method the meta-coefficient for each factor is calculated using a weighted average of the same coefficient across the different studies. The weights are reciprocal of the variance of those coefficients and also allow us to calculate the variance of the meta-coefficient (See online supporting information S2). The meta-regression analysis is conducted in Microsoft Excel (2010).

3. Results

The initial search identified 9787 studies, including 39 studies identified from cross-referencing, that cover a broad range of items. All of the titles and abstracts of these studies were reviewed in the first step to filter out the clearly un-related papers. The full set of exclusion criteria are shown in step 2 of Figure 1. Next, by reviewing the full text of 970 remaining studies, 712 studies were excluded due to different criteria reported in Figure 1, including (but not limited to) those that focus on inter/intra individual variance of BMR, studies just describing correlation values between BMR and different factors (but no regression equation), those focusing on sleeping metabolic rate or postprandial BMR (i.e. not after 10–12 hours fasting), those finding the relation between BMR and factors at a cellular level, such as blood adipocytokines, pulse pressure and protein turnover. After this screening process, 248 studies that generate a regression equation for predicting BMR based on a data set of healthy obese or non-obese individuals were reviewed and coded.

The final set of 248 papers is categorized into two groups. The first category, those lacking enough details to allow analytical meta-regression included 201 studies (See online supporting information S4 for the full list). The final category with enough details to enable meta-regression includes 47 studies. These papers report regression results for BMR as the independent variable and different sets of determinants. Both coefficients and their corresponding standard deviation (or a related concept such as p-value or t-statistic) are coded in a database.

The final set of studies is categorized into different groups based on the structure of the regression equation and the population subgroups distinguished by age, gender, and race. As a result seventeen categories of Regression Models and twenty subpopulation groups are identified. Note that age ranges for children, adult, and older adult vary slightly across different subpopulation groups due to variations in the definitions used for different studies (See online supporting information S3 for a summary table).

For each population group (based on age, gender, and race) and each regression structure meta regression formulas (See online supplement S2) are applied to estimate a single meta regression equation. These results are shown in Table 1. For each subpopulation, a list of resulting meta-regression equation results, the original references that were combined, and the range, mean, and standard deviation of R² (a commonly reported measure of goodness of fit) for the original studies are reported.

Table 1.

Master table including meta-regression equations estimated for different equation structures and population groups. Meta-regression coefficients (standard error) are reported in each cell. Also reported are the number of studies, Range of R², and average (Standard Error) of R².

Female													Male
	Structure	References	Range R2	Average R2 (SD)	β0 = Intercept	β1 W	β2 H	β3 A	β4 FFM	β5 FM	β6 WHR	β7 BMI	Range R2	Average R2 (SD)	β0 = Intercept	β1 W	β2 H	β3A	β4 FFM	β5FM	β6 WHR	β7 BMI
White 5–18	1	35, 36, 37	0.48–0.859	0.65 (0.158)	84.7(50.3)	11.1(0.398)	5.46 (0.753)	−24.8(3.03)					0.6–0.859	0.695 (0.113)	220(50.5)	11.3(0.409)	5.82 (0.77)	−25.5(3.15)
	2	38							28.3(0.824)	6.61(1.43)									29.7 (0.682)	4.37(2.99)
	3	37		0.59	901(73.8)	9.8 (0.72)								0.59	933(73.8)	12.2(0.72)
	5	39, 40, 41, 37	0.57–0.7	0.625 (0.058)	218(25.9)				23.9(1.4)				0.47–0.7	0.583 (0.0943)	219(26.2)				25.4(1.44)
	8	37		0.31	1600(139)			15.8(9.6)						0.31	848(139)			94.9(9.6)
	9	37		0.59	870(44.5)			−6.69(3.29)	23.7(0.837)					0.59	870(44.5)			−6.69(3.29)	23.7 (0.837)
	10	37		0.59	909(46)	12(0.418)		−13.6(3.41)						0.59	1150(46)	12(0.418)		−13.6(3.41)
	11	14, 36, 37, 42	0.47–0.79	0.642 (0.12)	513(33.2)			−7.77(1.48)	15.4(1.3)	12.1 (0.819)			0.59–0.79	0.678 (0.074)	680(33.3)			−7.61(1.49)	16.9(1.36)	12.8 (0.868)
	15	37		0.41	−708(327)		15.8 (2.04)							0.41	−1320(327)		21 (2.04)
	16	37		0.47	890(109)							25.6 (2.93)		0.47	639(109)							41.8 (2.93)
	17	37		0.58	956(72.2)					17.4 (1.41)				0.58	954(72.2)					23.9(1.41)
Black 5–17	5	39, 40, 41	0.5–0.7	0.57 (0.113)	53.5(27.5)				29.5(2.81)				0.51–0.7	0.587 (0.1)	55(27.5)				30 (2.77)
	11	14		0.79	−235(53.8)			−15 (7.31)	19.8(6.4)	7.6(5.03)				0.79	−111(53.8)			−15(7.31)	19.8 (6.4)	7.6(5.03)
Hispanic 4–6	5	43	0.384–0.792	0.588 (0.288)	28.6(26.6)				13(1.63)				0.384 – 0.792	0.588 (0.288)	28.6(26.6)				13 (1.63)
White 18–57	1	44, 45, 46, 37	0.449–0.75	0.619 (0.129)	301(65.1)	10.2 (0.152)	3.09 (0.385)	−3.09 (0.168)					0.6–0.75	0.671 (0.0619)	522(65.8)	10.4 (0.156)	3.19 (0.388)	−3.1(0.169)
	2	38							28.3(0.824)	6.61(1.43)									29.7 (0.682)	4.37(2.99)
	3	47, 48$, 37, 49$	0.449–0.9	0.645 (0.188)	632(33.3)	10.9 (0.324)							0.59 – 0.9	0.745 (0.219)	778(39.1)	11.7 (0.339)
	4	50$, 51, 52, 53, 47	0.526–0.91	0.804 (0.15)	360(29.5)				21(0.494)	4.68 (0.455)			0.612 – 0.91	0.809 (0.135)	361(30.8)				21.1 (0.498)	4.77(0.483)
	5	48$, 54, 55 , 56, 53, 57, 58, 37, 59	0.53–0.922	0.675 (0.115)	473(15.5)				20.1 (0.43)				0.53 – 0.922	0.674 (0.121)	503(15.6)				18.3 (0.436)
	6*	12		0.806	4.65 (0.229)			−0.00125 (0.000405)	0.624** (0.202)	0.0907*** (0.0294)				0.806	4.71(0.229)			−0.00125 (0.000405)	0.624** (0.202)	0.0907*** (0.0294)
	8	37		0.33	2020(33)			−5.02 (0.668)						0.33	2640(33)			−8.37 (0.668)
	9	37, 45	0.588–0.59	0.589 (0.00141)	838(22.8)			−2.41 (0.176)	19.7 (0.287)				0.588 – 0.59	0.589 (0.00141)	830(22.8)			−2.41 (0.176)	19.7 (0.287)
	10	37, 60	0.42–0.6	0.51 (0.127)	781(22)	11 (0.178)		−3.45 (0.232)					0.6 – 0.69	0.645 (0.0636)	1050(22.2)	11(0.178)		−3.53 (0.236)
	11	61, 44, 53 , 42, 62$, 63, 64, 65, 66, 37 , 67, 68, 46	0.425–0.88	0.66 (0.136)	682(25)			−3.08 (0.194)	12.9 (0.47)	5.9(0.313)			0.45 – 0.88	0.711 (0.208)	898(27.1)			−3.32 (0.207)	14.3 (0.507)	6.46(0.374)
	12	45		0.657	1380(59.6)			−6.18 (0.744)		11.5 (0.462)				0.657	1930(59.6)			−6.18 (0.744)		11.5(0.462)
	13	45		0.647	886(72.2)			−6.08 (0.742)				26.8 (1.07)		0.647	1440(72.2)			−6.08 (0.742)				26.8 (1.07)
	14	69		0.736	560(131)	5.39 (2.15)			14.1 (3.73)					0.736	560(131)	5.39(2.15)			14.1 (3.73)
	15	37		0.38	−417(203)	13.9 (1.18)								0.38	−1390(203)		21.3 (1.18)
	16	37		0.47	794(53.2)							23.4 (1.28)		0.47	985(53.2)							30.4 (1.28)
	17	37		0.57	631(43.4)					21.7 (0.882)				0.57	856(43.4)					30.4(0.882)
White >50	1	44, 45, 46, 37	0.449–0.75	0.619 (0.129)	301(65.1)	10.2 (0.152)	3.09(0.385)	−3.09(0.168)					0.6 – 0.75	0.671 (0.0619)	522(65.8)	10.4(0.156)	3.19 (0.388)	−3.1 (0.169)
	3	47, 37	0.59–0.9	0.745 (0.219)	568(39.1)	11.1 (0.339)							0.59 – 0.9	0.745 (0.219)	743(39.1)	11.7(0.339)
	4	70$, 51, 52, 53, 47	0.526–0.89	0.751 (0.149)	290(32.4)				19.9 (0.541)	4.71 (0.466)			0.612 – 0.89	0.789 (0.121)	291(34.3)				20 (0.547)	4.64(0.497)
	5	37, 59, 57, 53	0.59–0.74	0.669 (0.0642)	429(17.9)				20.9 (0.53)				0.59 – 0.74	0.669 (0.0642)	464(17.9)				18.6 (0.53)
	6*	12		0.806	4.65 (0.229)			−0.00125 (0.000405)	0.624** (0.202)	0.0907*** (0.0294)				0.806	4.71(0.229)			−0.00125 (0.000405)	0.624** (0.202)	0.0907*** (0.0294)
	7	71, 72			479(80.6)			−1.99 (0.928)	16.1 (0.606)	6.09 (0.434)	118 (34)				893(80.6)			−7.06 (0.928)	16.1 (0.606)	6.09(0.434)	118 (34)
	8	37, 71, 72		0.33	1950(30.5)			−4.72 (0.572)					0.33–0.33	0.33	2570(30.5)			−8.29 (0.572)
	9	37, 45, 59	0.588–0.77	0.649 (0.105)	838(22.8)			−2.43 (0.175)	19.8 (0.283)				0.588 – 0.77	0.649 (0.105)	829(22.8)			−2.43 (0.175)	19.8 (0.283)
	10	37, 60, 59	0.42–0.74	0.587 (0.16)	784(21.9)	10.9 (0.173)		−3.47 (0.231)					0.6 – 0.74	0.677 (0.0709)	1050(22.1)	10.9(0.173)		−3.55 (0.235)
	11	61, 44, 53, 42, 62$, 63, 64, 65, 66, 37, 67, 68, 46	0.425–0.88	0.66 (0.136)	682(25)			−3.08 (0.194)	12.9 (0.47)	5.9 (0.313)			0.45 – 0.88	0.711 (0.208)	898(27.1)			−3.32 (0.207)	14.3 (0.507)	6.46(0.374)
	12	45		0.657	1380(59.6)			−6.18 (0.744)		11.5 (0.462)				0.657	1930(59.6)			−6.18 (0.744)		11.5(0.462)
	13	45		0.647	886(72.2)			−6.08 (0.742)				26.8 (1.07)		0.647	1440(72.2)			−6.08 (0.742)				26.8 (1.07)
	15	37		0.38	−417(203)		13.9 (1.18)							0.38	−1390(203)		21.3 (1.18)
	16	37		0.47	794(53.2)							23.4 (1.28)		0.47	985(53.2)							30.4 (1.28)
	17	37		0.57	631(43.4)					21.7 (0.882)				0.57	856(43.4)					30.4(0.882)
Asian 18–30	1	63		0.834	−101(337)	11.5 (1.1)	5.59 (2.01)	−3.3 (0.598)					****	0.834	883(471)	11.5(1.1)	5.59 (2.01)	−3.3 (0.598)
	3	73			593(133)	10.9 (2.72)
	10	74&											****	0.41	860(152)	11.6(1.3)		−3.37 (1.03)
Black 18–50	1	46		0.675	883(471)	8.7 (1.4)	−0.342 (2.94)	−3.9 (0.8)						0.675	1100(471)	8.7 (1.4)	−0.342 (2.94)	−3.9 (0.8)
	3	49, 75&		0.548	302(148)	13.2 (3.55)								0.548	500(96.5)	15.6 (1.6)
	4	76	0.75–0.84	0.783 (0.0441)	397(79.5)				20.6 (2.72)	1.9 (0.575)			0.75 – 0.84	0.783 (0.0441)	421(82.8)				20.6 (2.72)	1.9(0.575)
	5	59, 76 ,75&	0.66–0.83	0.748(0.0695)	400(42)				16.6 (0.949)				0.66 – 0.83	0.73 (0.0718)	392(39.1)				17.4 (0.861)
	11	64, 46	0.68–0.71	0.695 (0.015)	678(92.8)			−3.28 (0.485)	13.6 (1.16)	5.95 (1.03)			0.68 – 0.71	0.695 (0.015)	787(92.8)			−3.28 (0.485)	13.6 (1.16)	5.95(1.03)
Black >50	1	46		0.675	883(471)	8.7 (1.4)	−0.342 (2.94)	−3.9 (0.8)						0.675	1100(471)	8.7 (1.4)	−0.342 (2.94)	−3.9 (0.8)
	3	49&		0.63	302(148)	13.2 (3.55)
	4	76	0.75–0.84	0.783 (0.0441)	397(79.5)				20.6 (2.72)	1.9 (0.575)			0.75 – 0.84	0.783 (0.0441)	421(82.8)				20.6 (2.72)	1.9(0.575)
	5	59, 76	0.66–0.83	0.748 (0.0695)	400(42)				16.6 (0.949)				0.66 – 0.83	0.748 (0.0695)	400(42)				16.6 (0.949)
	9	59		0.69	1260(262)			−11.2 (3.4)	15.9 (5.52)					0.69	1260(262)			−11.2 (3.4)	15.9 (5.52)
	10	59		0.67	1420(281)	7.6 (0.7)		−11.4 (3.5)						0.67	1590(281)	7.6 (0.7)		−11.4 (3.5)
	11	64, 46	0.68–0.71	0.695 (0.015)	678(92.8)			−3.28 (0.485)	13.6 (1.16)	5.95 (1.03)			0.68 – 0.71	0.695 (0.015)	787(92.8)			−3.28 (0.485)	13.6 (1.16)	5.95(1.03)
>50 Hispanic	3	77		0.75	394(105)	13.6 (1.62)								0.75	502(105)	13.6 (1.62)
18–50 Native American	11	65		0.88	705(60.3)			−2.2 (0.8)	15 (1.1)	4.4 (0.7)				0.88	829(60.3)			−2.2 (0.8)	15 (1.1)	4.4(0.7)

^*Structure 6 estimates log_eBMR.

^**Coefficient for log_eFFM

^***Coefficient for log_eFM

^****The age group is 18–50.

^$This reference only applies to the female equation.

^&This reference only applies to the male equation.

Abbreviations- W: Weight (kg); H: Height (cm); A: Age (years); FFM: Fat-Free Mass (kg); FM: Fat Mass (kg); WHR: Waist-to-Hip-Ratio; BMI: Body Mass Index (kg/m²). F: Female; M: Male; T: White; B: African American; P: Hispanic; S: Asian; I: Pima Native American; Equation Structures- 1: β₀ + β₁W + β₂H + β₃A; 2: β₄FFM + β₅FM; 3: β₀ + β₁W; 4: β₀ + β₄FFM + β₅FM; 5: β₀ + β₄FFM; 6: β₀ + β₃A + β₄logeFFM + β₅logeFM; 7: β₀ + β₃A + β₄FFM +β₅FM + β₆WHR; 8: β₀ + β₃A; 9: β₀ + β₃A + β₄FFM; 10: β₀ + β₁W + β₃A; 11: β₀ + β₃A + β₄FFM + β₅FM; 12: β₀ + β₃A + β₅FM; 13: β₀ + β₃A + β₇BMI; 14: β₀ + β₁W + β₄FFM; 15: β₀ + β₂H; 16: β₀ + β₇BMI; 17: β₀ + β₅FM;

Using the Resulting Equations

For a concrete example, consider calculating the expected BMR for a 35-year-old white female who weighs 75 kg (165 lb) and is 165 cm (5’ 5”) tall. With this information we can look up the designated rows in Table 1 (identified as “White 18–57”; the left hand columns for female) and identify equation structures 1, 3, 10, and 15 for which meta regression equations are available. Based on R² values, structures 1 and 3 are deemed more accurate. Equation structure 1 can be read as: BMR=301+10.2W+3.09H-3.09A, calculating this with W=75kg, H=165cm, and A=35, we obtain a BMR of 1467.7 kcal/Day. This value is close to the predictions obtained from Harris and Benedict ⁸ (H&B) equation³ (1513.8), World Health Organization (WHO) report ²⁰ equation⁴ (1558.7) and Institute of Medicine (IOM) report ²⁹ equation⁵ (1475.9). While offering results consistent with more commonly used equations for typical cases, Table 1 can provide empirically estimated equations for older ages (Note that the Harris Benedict sample was under 45, and WHO equations do not include age) and when additional data items are available (e.g. fat free mass (FFM) and waist to hip ratio (WHR); neither included in WHO, IOM, or H&B equations). Table 1 can also provide estimated variations across different ethnicities (not included in WHO, IOM, or H&B equations). Such flexibility can be beneficial in making the best use of available data for research and clinical applications. We also have developed an online tool, which predicts BMR for subjects in different demographic groups depending on what information (e.g. age, weight, and height) is available about them. In addition to the meta-regression results developed in this paper, the tool includes the relevant predictions from IOM and WHO reports for each subject, allowing the user to make comparisons and reach an informed consensus. Details are reported in online supplement S5.

Impact of Body Composition

Overall, consistent with previous findings, Fat-Free Mass is the best independent predictor of BMR ¹³ as evidenced by good predictive power of equation structure 5 (β₀ + β₄FFM) in many population groups. Weight is almost as good a predictor as Fat-Free Mass, based on comparing the effect sizes for different independent variables. FM has a moderately positive coefficient and provides a slight improvement in predictive power. Comparing structures 4 (β₀ + β₄FFM+ β₅FM) and 5 (β₀ + β₄FFM), it appears that impact of FM and FFM are independent, i.e. inclusion of FM does not change the FFM coefficient. Moreover, logarithmic functions may describe the FFM and FM effect as well as, if not better than, linear effects (comparing structures 6 and 11). In fact with logarithmic functional forms for FFM/FM the intercept shrinks considerably, suggesting that with the logarithmic nonlinearity FM and FFM can explain the majority of variation in BMR.

Impact of Age

The direct impact of age is most pronounced for the children but is also significant in adults, and is consistently negative. The age impact is slightly stronger in male than female. Age also has a more subtle interaction with other factors. Comparing equation structures 4 (β₀ + β₄FFM+ β₅FM) and 11 (β₀+ β₃A + β₄FFM + β₅FM), we note that by including Age, the coefficient for FFM shrinks (from ~20 to ~13 kcal/kg/day for adults) while the constant term becomes larger, i.e. age and a constant term can replace a significant portion of FFM contribution to BMR. This may suggest a reduction in tissue-specific organ metabolic rates as people age. ³⁰ The underlying mechanisms to explain the compensating effects of FFM and Age may require cellular level measures in BMR estimation³¹ yet inclusion of Waist to Hip Ratio (WHR) among the independent variables restores some of the direct effect of FFM (structure 7: β₀ + β₃A + β₄FFM +β₅FM + β₆WHR), suggesting that WHR is informative in understanding the interaction of Age and FFM. Other predictors including height and BMI are statistically significant when included, but their significance may be attributed to lack of controls for fat-free mass or weight in those equations.

Best Fitting Equations for Subpopulations

We elaborate on the best fitting equation structures for each major subpopulation separately. For Female-White-5–18 group, equation structures 1 (β₀ + β₁W + β₂H + β₃A), 2 (β₄FFM + β₅FM), 5 (β₀ + β₄FFM) and 11 (β₀+ β₃A + β₄FFM + β₅FM), are the results of combining 3 or more studies. Structures 1 and 11 have the highest average R², but structure 5 is also very close (average R²=0.625). Nevertheless including Age, Height, and FM can all lead to more precise BMR predictions. The same conclusions hold for ‘Male-White-5–18 and, should the required information be available, we suggest applying either structure 1 or 11 for predicting BMR in this sub-population as well. Only two equation structures have been estimated for African-American youth (4.7–17 years old). While more studies have used structure 5, structure 11 offers a better fit and thus can be recommended. A single equation structure is available for Hispanic children (4–6 years).

For adult white groups (male and female, 18–50 and 50+ groups) structures 1, 2, 3 (β₀ + β₁W), 4 (β₀ + β₄FFM + β₅FM), 5, 9 (β₀ + β₃A + β₄FFM), 10 (β₀ + β₁W + β₃A) and 11 are estimated based on multiple studies.

Structures 4, 5 and 11 have higher average R² with 4 and 11 providing a good balance in terms of precision and empirical support (more than 5 studies and R² between 0.7 and 0.8). For the adult African American groups, equations 4, 5, and 11 are well supported and offer good fits with R² values typically between 0.6 and 0.8. For other population groups (Asians, Native Americans and adult Hispanics) a single regression exists for each equation structure and therefore available choices are limited.

4. Conclusions

This study provides a comprehensive review of the BMR prediction equation literature to develop meta-predictive equations using seventeen different structures and for twenty different subpopulations. Providing robust equations for predicting expected BMR, the results can inform obesity interventions in diverse populations. For example the equations can inform setting energy intake goals in weight loss programs, help build dynamic models of weight gain and loss, speed up the calibration of personalized obesity interventions, enable the identification of patients with potential metabolic abnormalities, estimate energy deficits for metabolically stressed individuals, and inform the design of public health programs promoting obesity prevention in diverse populations. The equations provide enough flexibility for accommodating a host of different independent variables, depending on the availability of data for the application at hand. The accompanying BMR prediction tool simplifies the application of results by practitioners.

From the 248 studies with predictive equations that we retrieved, only 19% included enough detail regarding their estimated equations to allow for reliable comparison and meta-regression. Mathematical models ³² increasingly rely on regression equations such as those summarized here. Weight change experiments and commercial weight loss centers often depend upon BMR regression equations to design their interventions. Explicit quantification of variance is a critical factor for pooling data and models, improving these models, and appropriately informing health care providers on the accuracy and limitations of developed models.

In practice, application of a best fitting equation is also limited by data availability. While FFM, FM, and waist and hip circumference are significant predictors of BMR, these variables may not be available to researchers or individuals. We take a step towards addressing this challenge by providing meta-regression equations with different independent factors, including those that only rely on a subset of easily measured covariates (weight, age, height, gender, and race).

Several areas for future research can improve these results. Individual life histories can provide additional predictive variables not included in our meta-regression equations due to the limited number of longitudinal primary studies. For example rapid weight loss can lead to sustained BMR reduction even if FFM is sustained, effectively changing the coefficient for FFM ²². Such information may be especially relevant for designing individualized interventions. Methodologically, the meta-regression formulations we used, while commonly applied in the literature ^26–28, assume independence among estimated coefficients, which could not be verified in the absence of the correlation matrix for coefficients. This may have led to under-estimation of variance in meta-coefficients. Moreover, researchers will be interested in the net value of adding each independent variable in balancing equation complexity against the predictive power of a model. If different models (with different combinations of independent variables) are estimated on the same data, measures such as Bayesian ³³ and Akaike ³⁴ Information Criteria can be used to tradeoff model parsimony against predictive power. Such comparisons are not feasible in the current study because each equation is estimated on a different dataset, nevertheless estimated parameter variances provide related information on marginal value of different BMR predictors. Improved meta-regression techniques could be developed to correct for these potential shortcomings. Individual-level data can also be used to empirically compare the precision of different equation structures we have identified.