Towards Biomimetic Virtual Constraint Control of a Powered Prosthetic Leg

Abstract

This brief presents a novel control strategy for a powered prosthetic ankle based on a biomimetic virtual constraint. We first derive a kinematic constraint for the “effective shape” of the human ankle-foot complex during locomotion. This shape characterizes ankle motion as a function of the Center of Pressure (COP)–the point on the foot sole where the resultant ground reaction force is imparted. Since the COP moves monotonically from heel to toe during steady walking, we adopt the COP as a mechanical representation of the gait cycle phase in an autonomous feedback controller. We show that our kinematic constraint can be enforced as a virtual constraint by an output linearizing controller that uses only feedback available to sensors onboard a prosthetic leg. Using simulations of a passive walking model with feet, we show that this novel controller exactly enforces the desired effective shape whereas a standard impedance (i.e., proportional-derivative) controller cannot. This work provides a single, biomimetic control law for the entire single-support period during robot-assisted locomotion.

I. Introduction

Estimates indicate that by 2050 the United States will incur a two-fold increase in the incidence of limb loss, due in large part to vascular disease [1]. High-performance prostheses could significantly improve the quality of life for lower-limb amputees, whose ambulation is slower, less stable, and requires more energy than that of able-bodied persons [2], [3].

Modern prosthetic legs have mechanically passive joints that attempt to mimic human joint impedance (i.e., stiffness and viscosity) [4], [5]. This approach fails to replicate the ability of human muscles to generate large amounts of mechanical power, which is why transfemoral amputees expend excessive amounts of energy climbing inclines and stairs. The recent advent of mechanically powered legs (e.g., [6]–[10]) presents new opportunities, as well as challenges, for prosthetic control systems. The Vanderbilt legs [7], [8] extend the traditional impedance control paradigm by changing proportional-derivative (PD) gains according to discretized phases of the gait cycle. The iWalk ankle [9] also uses a finite state machine but trades the simplicity of impedance models for the biomimetic behavior of muscle reflex models. These increasingly complex prostheses are limited by the need to manually tune multiple control models for each user and task, and their time-varying strategies are not necessarily robust to external perturbations that push joint kinematics (i.e., angles and velocities) forward or backward in the gait cycle.

These limitations could potentially be addressed by a unifying control model based on a mechanical representation of the gait cycle phase (i.e., the location in an oscillation), which could be continuously sensed by a prosthesis to match the body’s progression through the cycle. The prosthetic ankle SPARKy [10] is the first prosthetic control system to employ phase-based control by tracking able-bodied human data (e.g., ankle angles from level ground walking) as a function of the shank angle and velocity. However, without defining a general constraint function this control strategy does not readily generalize to arbitrary users or tasks.

Feedback controllers for autonomous walking robots have been developed that produce joint torques to “virtually” enforce kinematic constraints [11]–[16], which define desired joint patterns as functions of a mechanical phase variable (e.g., the stance leg angle or hip position). This approach has proven successful in experimental bipedal robots such as RABBIT [14] and MABEL [15]. In particular, using feedback control to linearize the output dynamics associated with the constraints enables more accurate tracking and faster walking than is possible with PD control [15]. A biomimetic virtual constraint and phase variable could make prosthetic legs more robust and easily tuned than with current prosthetic control approaches.

Recent evidence suggests that the progression of human joint patterns during locomotion is coupled with the heel-to-toe movement of the center of pressure (COP)–the point on the foot sole where the resultant ground reaction force is imparted. Hansen et al. have shown that during human walking, geometric relationships exist between stance leg joints and the COP [17]–[20]. Viewed from a shank-based reference frame, the ankle and foot together produce a COP trajectory resembling a circular rocker shape (coined “effective shape”), which is invariant over walking speeds, heel heights, and body weights. The fact that the COP moves monotonically from heel to toe during steady gait [21] suggests that the COP can serve as the phase variable of a virtual constraint. However, without the availability of state feedback from the human body, it is unclear how a prosthetic control system can linearize its output dynamics to enforce a virtual constraint.

The practical contributions of this paper are two-fold: (i) we propose the COP as a phase variable and show that the effective shape between the COP and ankle joint corresponds to a simple kinematic constraint, which (ii) can be enforced as a virtual constraint by an output linearizing controller using feedback available to sensors onboard a prosthetic leg. The theoretical contribution is then the derivation of an output linearizing control law for a dynamical system subject to external forces and holonomic constraints. This controller drives ankle patterns as a function of the COP, a novel choice of phase variable that unifies the single-support cycle in a prosthetic control system. We simulate a biped model to show that stable gaits can be achieved for a range of effective shapes enforced by output linearization, whereas an impedance controller cannot exactly enforce these shapes.

II. Leg Model

In this paper we use a simple model without knees to design an ankle controller and to simulate walking. The human ankle merely lifts the foot to facilitate ground clearance during the swing period, so in this paper we focus on the control of a prosthetic ankle bearing weight during stance. The planar biped of Fig. 1 (left) has a hip joint and ankle joints with constant-curvature rocker feet to approximate the deformation of human feet during walking [22]. We consider the stance leg (shown in solid gray) to be a prosthesis, which connects to the body (dashed black) at the hip. We will separately model the stance leg for the control derivation in Section III and return to the full biped model for simulations in Section IV.

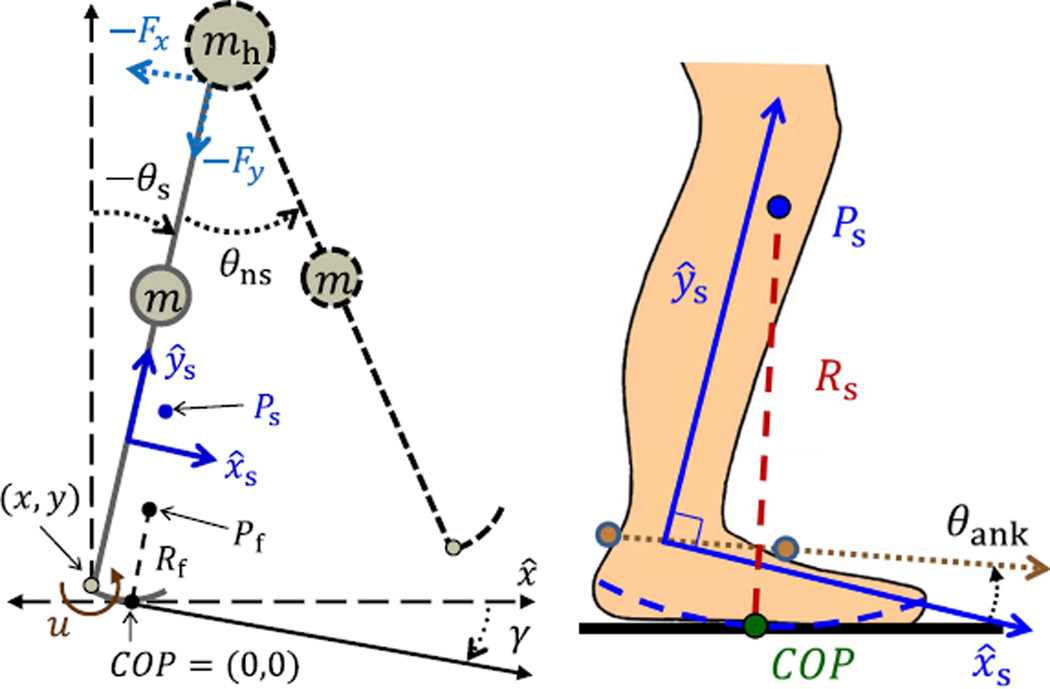
Fig. 1.

Left: biped model with the prosthesis shown in solid gray and the body shown in dashed black. The COP is defined at the origin, where the orientation of the global reference frame is defined with respect to horizontal (dashed) axis x̂. The origin of the shank-based coordinate frame (solid axes x̂_s, ŷ_s) is drawn above the ankle for visual clarity but is actually modeled to coincide with the ankle joint (which is located at the heel for simplicity). Right: diagram of human ankle-foot effective shape with a radius of curvature R_s, which is constant for walking tasks. The COP moves along the shape (dashed curve) about the center of rotation P_s in the shank-based coordinate frame. Note that in this diagram the relative angle θ_ank between the shank x_s-axis and foot (dotted axis) is shown instead of the global leg angle θ_s.

We model the prosthesis by first describing the continuous dynamics of its kinematic chain with respect to the COP. We then derive a kinematic constraint that forces the COP to move along the rocker foot in the continuous dynamics. Note that this constraint is different than the effective shape, which depends on both the foot curvature and ankle motion. We will model and control the effective shape in Section III.

A. Dynamics

The configuration of the stance leg is given by q = (x, y, θ_s)^T, where x, y are the Cartesian coordinates of the ankle/heel center (for simplicity the ankle is defined at the heel) with respect to the COP (defined at the origin), and θ_s is the leg angle defined with respect to vertical. The state of the dynamical system is given by vector z = (q^T, q̇^T)^T, where q̇ contains the joint velocities. During the continuous single-support period, the state trajectory evolves according to a differential equation of the form

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+N(q)+A^T(q)\lambda =\tau$$ (1)

where M is the inertia/mass matrix, C is the matrix of Coriolis/centrifugal terms, N is the vector of gravitational torques, A is the constraint vector for the rocker foot (modeling inherent foot compliance), and λ is the Lagrange multiplier providing the forces to enforce the foot constraint. The vector of external forces τ = Bu + J^T (q)F is composed of actuator torques and interaction forces with the body, respectively. Ankle actuation is provided by scalar torque input u and mapped into the leg’s coordinate system by B = [0, 0, 1]^T. We now describe force F and Jacobian J.

B. Interaction Forces

The interaction force F ∈ ℝ³ at the socket (i.e., the connection between the prosthesis and the body) is composed of linear forces in the plane and the moment about the normal axis. This force vector at the end-point of the kinematic chain is mapped to torques and forces at the leg joints by the Jacobian matrix (cf. [23])

$$J(q)=\left(\begin{array}{ccc}\hfill \text{cos}({\theta }_{\mathrm{s}})\hfill & \hfill \text{sin}({\theta }_{\mathrm{s}})\hfill & \hfill -\ell \hfill \\ \hfill -\text{sin}({\theta }_{\mathrm{s}})\hfill & \hfill \text{cos}({\theta }_{\mathrm{s}})\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),$$ (2)

where ℓ is the leg length. Note that force F can be measured by a 3-axis load cell attached to the socket (located at the hip in our model). We now show how to model the rocker foot constraint in the context of equation (1).

C. Modeling the Foot

We model the rocker foot by constraining the heel point (x, y) to an arc that has radius R_f and intersects the COP, which we have defined at the origin. The center of rotation P_f is defined in a moving reference frame such that the vector between P_f and the COP is always normal to the ground with radius ‖P_f − COP‖ = R_f. This constraint is given in model coordinates by k(q) = 0, where

$$k(q)={(x-R_{\mathrm{f}}\text{sin}(\rho ))}^2+{(y+R_{\mathrm{f}}\text{cos}(\rho ))}^2-R_{\mathrm{f}}^2$$

for $\rho =\gamma +2\text{arcsin}\left(\frac{d}{2R_{\mathrm{f}}}\right)$, slope angle γ, and distance $d=\sqrt{x^2+y^2}$ between the COP and the heel. Following the method in [23], we derive the constraint vector A = ∇_qk and Lagrange multiplier λ = λ̂ + λ̃u + λ̄F, where

$$\widehat{\lambda }={(A{M}^{-1}{A}^T)}^{-1}(\dot{A}\dot{q}-A{M}^{-1}(C\dot{q}+N))\tilde{\lambda }={(A{M}^{-1}{A}^T)}^{-1}A{M}^{-1}B\overline{\lambda }={(A{M}^{-1}{A}^T)}^{-1}A{M}^{-1}{J}^T.$$ (3)

Recall that this rocking constraint only pertains to the foot, whereas the effective shape characterizes the pendular trajectory of the stance leg about the ankle-foot complex. We now use this leg model to derive a kinematic constraint and controller that mimics the human effective shape.

III. Effective Shape Control

We wish to design a prosthetic control system that mimics the effective shape of the biological ankle-foot complex during various locomotor tasks [20]. This shape characterizes how the ankle moves as the COP travels from heel to toe. We now derive the kinematic constraint of the effective shape and two possible controllers for enforcing a desired shape.

A. Kinematic Constraint

The effective shape is the COP trajectory mapped into a shank-based reference frame (axes x̂_s, ŷ_s in Fig. 1). Able-bodied humans have effective shapes specific to activities such as walking or stationary swaying [20], and each shape can be characterized by the curvature of the COP trajectory with respect to a point P_s = (X_s, Y_s)^T attached to the shank reference frame (Fig. 1). This can be expressed as the coordinate-free distance relationship

$$\Vert P_{\mathrm{s}}-COP\Vert =R_{\mathrm{s}}(COP),$$ (4)

where the radius of curvature R_s is a function of the COP. At heel strike the COP is co-linear with our model’s stance leg and condition (4) is necessarily satisfied, so the y_s-component of P_s is given by $Y_{\mathrm{s}}=\sqrt{R_{\mathrm{s}}^2(0,0)-X_{\mathrm{s}}^2}$.

The x-component of the COP moves monotonically from heel to toe during steady walking; this can be measured in a variety of ways, as discussed in Section V. The COP can therefore serve as the phase variable of a virtual constraint corresponding to (4). We can express this constraint in the COP reference frame (i.e., global axes x̂, ŷ in Fig. 1), for which the effective center of rotation is given by $P_{\mathrm{s}}^{COP}(q)={(x,y)}^T+S({\theta }_{\mathrm{s}})P_{\mathrm{s}}$, where S(θ_s) is the standard rotation matrix parameterized by angle θ_s. Equation (4) is then given in our model coordinates by the kinematic constraint h(q) = 0 for

$$h(q)={(x+X_{\mathrm{s}}\text{cos}({\theta }_{\mathrm{s}})-Y_{\mathrm{s}}\text{sin}({\theta }_{\mathrm{s}}))}^2+{(y+X_{\mathrm{s}}\text{sin}({\theta }_{\mathrm{s}})+Y_{\mathrm{s}}\text{cos}({\theta }_{\mathrm{s}}))}^2-R_{\mathrm{s}}^2(x,y).$$ (5)

This kinematic constraint represents the desired behavior of the prosthetic ankle, which we can attempt to enforce in two ways: impedance control or output linearizing control.

B. Impedance Control

Assume that h(q) = 0 can be solved for the leg angle θ_s = ϕ(x, y), where map ϕ depends on function R_s and constant P_s. (This assumption is valid for walking tasks, where R_s is a constant.) The COP could then drive the progression of ankle kinematics with the PD controller

$$u=-K_{\mathrm{p}}e-K_{\mathrm{d}}\dot{e},$$ (6)

where e ≔ θ_s − ϕ(x, y) is the tracking error.

This linear control law will not exactly enforce the desired constraint (5) due to nonlinearities in the system dynamics. For this purpose we now derive a model-based control law, which will not require us to explicitly solve (5) for θ_s.

C. Output Linearizing Control

We wish to design a model-based control law for a prosthetic ankle that enforces (5) as a virtual constraint. We cannot expect to have a good model of the human user or state measurements from intact joints in a clinically viable system. We therefore use only our model of the prosthetic leg and feedback provided by onboard sensors, specifically state z = (q^T, q̇^T)^T and interaction force F.

The coupled dynamics (1) of the weight-bearing prosthesis can be given in a modified control-affine form (cf. [24]):

$$\dot{z}=f(z)+g(z)u+j(z)F,$$ (7)

where the vector fields are defined as

$$f(z)=\left(\begin{array}{c}\hfill \dot{q}\hfill \\ \hfill -M{(q)}^{-1}(C(q,\dot{q})\dot{q}+N(q)+A^T(q)\lambda )\hfill \end{array}\right),g(z)=\left(\begin{array}{c}\hfill 0_{3\times 3}\hfill \\ \hfill M^{-1}(q)B\hfill \end{array}\right),j(z)=\left(\begin{array}{c}\hfill 0_{3\times 3}\hfill \\ \hfill M^{-1}(q)J^T(q)\hfill \end{array}\right).$$ (8)

Letting output ξ ≔ h(z), our goal is to define a feedback control law for u that drives ξ to zero in system (7). We first examine the output dynamics of the above system:

$$\dot{\xi }=({\nabla }_{z}h)\dot{z}=L_{f}h+(L_{g}h)u+(L_{j}h)F,$$ (9)

where the Lie derivative L_fh ≔ (∇_zh) f characterizes the change of h along flows of vector field f [24], and it is easily shown that L_gh = 0 and L_jh = 0 for all z. Noting that no acceleration or control terms appear in L_fh, output ξ has relative degree greater than one (cf. [24]) and we must take another time-derivative to expose the control input u:

$$\ddot{\xi }=L_f^{2}h+(L_g{L}_{f}h)u+(L_j{L}_{f}h)F.$$ (10)

Because the Lagrange multiplier defined in (3) explicitly depends on the external joint torques, so does the second Lie derivative $L_f^{2}h=\widehat{L_f^{2}h}+(\widetilde{L_f^{2}h})u+(\overline{L_f^{2}h})F$, where

$$\widehat{L_f^{2}h}=({\nabla }_q{L}_{f}h)\dot{q}-({\nabla }_{\dot{q}}{L}_{f}h)M^{-1}(C\dot{q}+N+A^T\widehat{\lambda })\widetilde{L_f^{2}h}=-({\nabla }_{\dot{q}}{L}_{f}h)M^{-1}{A}^T\tilde{\lambda }\overline{L_f^{2}h}=-({\nabla }_{\dot{q}}{L}_{f}h)M^{-1}{A}^T\overline{\lambda }.$$ (11)

Note that vector A depends on foot radius R_f, which reflects the compliance of the foot and can be measured a priori [19].

Grouping the control input terms from (10), we can solve for the control law that inverts the output dynamics:

$$u=\frac{1}{D}(-\widehat{L_f^{2}h}-(\overline{L_f^{2}h}+L_j{L}_{f}h)F+v),$$ (12)

where the denominator $D=L_g{L}_{f}h+\widetilde{L_f^{2}h}$ only depends on q and is strictly greater than zero for feasible walking configurations. We then choose auxiliary input v to render the output dynamics linear and exponentially stable:

$$\ddot{\xi }=v≔-K_{\mathrm{p}}\xi -K_{\mathrm{d}}\dot{\xi },$$ (13)

for K_p, K_d > 0. Given sensor measurements of z and F and actuation of u, we can obtain the closed-loop output dynamics (13), which imply ξ(t) → 0 exponentially fast as t → ∞ for ξ(0) ≠ 0. During steady-state walking controller (12) will maintain zero output error, so these PD gains will only serve to correct errors resulting from perturbations. We now present the full biped model for simulations with these controllers.

IV. Biped Model and Simulations

Now that we have designed two possible controllers for the prosthetic leg, we wish to study both during simulated walking with the full biped model of Fig. 1 (left). This requires us to consider the coupled dynamics of the body and the controlled prosthesis. In order to generate stable walking patterns for the entire biped, we will exploit the existence of passive gaits.

Passive walking harnesses momentum and gravity to propel forward motion without any control or actuation whatsoever [25], [26]. Passive gaits arise on declined surfaces when the potential energy converted into kinetic energy during each step cycle replenishes the energy dissipated at impact events. This behavior reflects certain characteristics of human walking, such as ballistic motion during early stance [27] and energetic efficiency down slopes [28].We will start with an uncontrolled, passive gait in the full biped model and augment the stance leg with each of our prosthetic controllers.

A. Biped Model

For simplicity we do not distinguish between legs from step to step (as in the case of a bilateral amputee). Each leg in this symmetrical model employs the same control law during single support with mass m, moment of inertia I_rot, and length ℓ. We do not model the swing ankle because the foot is assumed to be massless.

The configuration vector of the full biped is denoted by q̆ = (q^T, θ_ns)^T, where θ_ns is the hip (i.e., non-stance) angle. The biped’s dynamics during single support are governed by a differential equation of the form (1) until the swing foot contacts the ground, which initiates the transition into the next step cycle. We define a function H_γ(q̆) to give the height of the heel of the swing foot above ground with slope angle γ, so heel strike occurs when the state trajectory intersects the switching surface G = {q̆ | H_γ(q̆) = 0}. The subsequent double-support transition is modeled as an instantaneous impact event with a perfectly plastic (inelastic) collision as in [12]. The state trajectory is therefore subjected to the discontinuous impact map Δ (which also changes the values of θ_s, θ_ns to re-label the stance/swing legs) in the hybrid dynamical system:

$$\begin{array}{cc}\hfill \stackrel{⌣}{M}(\stackrel{⌣}{q})\ddot{\stackrel{⌣}{q}}+\stackrel{⌣}{C}(\stackrel{⌣}{q},\dot{\stackrel{⌣}{q}})\dot{\stackrel{⌣}{q}}+\stackrel{⌣}{N}(\stackrel{⌣}{q})+{\stackrel{⌣}{A}}^T(\stackrel{⌣}{q})\stackrel{⌣}{\lambda }=\stackrel{⌣}{\tau }& \text{for}\stackrel{⌣}{q}\notin G\hfill \\ \hfill ({\stackrel{⌣}{q}}^{+},{\dot{\stackrel{⌣}{q}}}^{+})=\mathrm{\Delta }({\stackrel{⌣}{q}}^{-},{\dot{\stackrel{⌣}{q}}}^{-})& \text{for}\stackrel{⌣}{q}\in G\hfill \end{array}$$

where superscripts +/− respectively denote the post- and pre-impact states, τ̆ = [B^T, 0]^T u (i.e., the swing leg moves passively), and other accented terms associated with the full model are defined as in Section II.

Note that during heel contact (x = y = 0) we use an alternate constraint matrix A that fixes the heel position to the ground (i.e., acts as a point foot since the rocker does not go beyond the heel). We switch back to the rocker constraint (3) when the unconstrained accelerations point in the positive x-direction. Control torques are zeroed during heel contact because virtual constraint (5) is automatically satisfied.

Walking gaits correspond to cyclic solutions of this hybrid system, which we will analyze to determine gait stability.

B. Hybrid Solutions

Let $\stackrel{⌣}{z}={({\stackrel{⌣}{q}}^T,{\dot{\stackrel{⌣}{q}}}^T)}^T$ be the state vector for the full biped. Walking gaits correspond to solution curves z̆(t) of the hybrid system such that z̆(t) = z̆(t + T) for all t ≥ 0 and some minimal T > 0. These solutions define isolated orbits in state space known as hybrid limit cycles, which correspond to equilibria of the Poincaré map P : G → G. This return map represents a hybrid dynamical system as a discrete system between impact events, sending state z̆_j ∈ G ahead one step to z̆_j+1 = P(z̆_j). A periodic solution z̆(t) then has a fixed point z̆* = P(z̆*).

We verify stability about a fixed point z̆* by approximating the linearized map ∇_z̆P(z̆*) through a perturbation analysis in simulation [25], [26]. The linearized discrete system is exponentially stable if the eigenvalues of ∇_z̆P(z̆*) are within the unit circle, by which we can infer local stability of the hybrid limit cycle. We now simulate the biped model with our controllers to generate walking gaits and verify their stability.

C. Simulation Parameters

During a normal walking task the radius of curvature R_s is constant (i.e., the effective shape is a circular arc as in Fig. 1, right). Since passive gaits typically involve short steps, we will produce natural step lengths by adopting a large effective radius of R_s = 0.45 m. The effective center of rotation $P_{\mathrm{s}}={(X_{\mathrm{s}},\sqrt{R_{\mathrm{s}}^2-X_{\mathrm{s}}^2})}^T$ is located behind the shank with X_s = 5 mm (for walking in the negative x-direction) based on the human studies of [17]. In order to compare the gait characteristics resulting from passive walking, impedance controller (6), and output linearizing controller (12), we now describe the initial passive gait and define our control gains.

1. Passive Gait: We adopt the model parameters of Table I based on adult (male) mean values reported by [29] with trunk masses grouped at the hip. The rocker foot radius is set to three-tenths of the leg length ℓ, which is typical of human foot compliance [22]. Given these parameters we can find a passive walking gait (u = 0) on slope γ = 0.0075 rad using the methods described in [26]. We will use this underlying gait to study the effect of our prosthetic ankle controllers.

2. Impedance Control: For control law (6) we adopt K_p = 6(m_h + 2m) Nm/rad based on normalized measurements of human ankle stiffness from [30], and we choose a viscosity value of $K_{\mathrm{d}}=2\zeta \sqrt{K_{\mathrm{p}}}$ with damping ratio ζ = 0.7.

3. Output Linearization: The dynamics, interaction forces, and control law (12) are simultaneously computed from both the full biped model and the prosthesis model in MATLAB. Although the control gains have different units than the impedance controller, we again choose K_p = 6(m_h + 2m) Nm/m² and $K_{\mathrm{d}}=2\zeta \sqrt{K_{\mathrm{p}}}$ to achieve damping ratio ζ = 0.7 in the linearized output dynamics (13).

TABLE I.

Model Parameters

Parameter	Variable	Value
Hip mass	mh	31.73 [kg]
Leg mass	m	13.5 [kg]
Leg inertia	Irot	0.2 [kg·m2]
Leg length	ℓ	0.856 [m]
Slope angle	γ	0.0075 [rad]
Foot radius	Rf	0.26 [m]
Effective radius	Rs	0.45 [m]
Effective center	Xs	0.005 [m]
Proportional gain	Kp	352.38 [Nm/rad]
Derivative gain	Kd	26.281 [Nm·s/rad]

We now present and compare results from these simulations.

D. Results

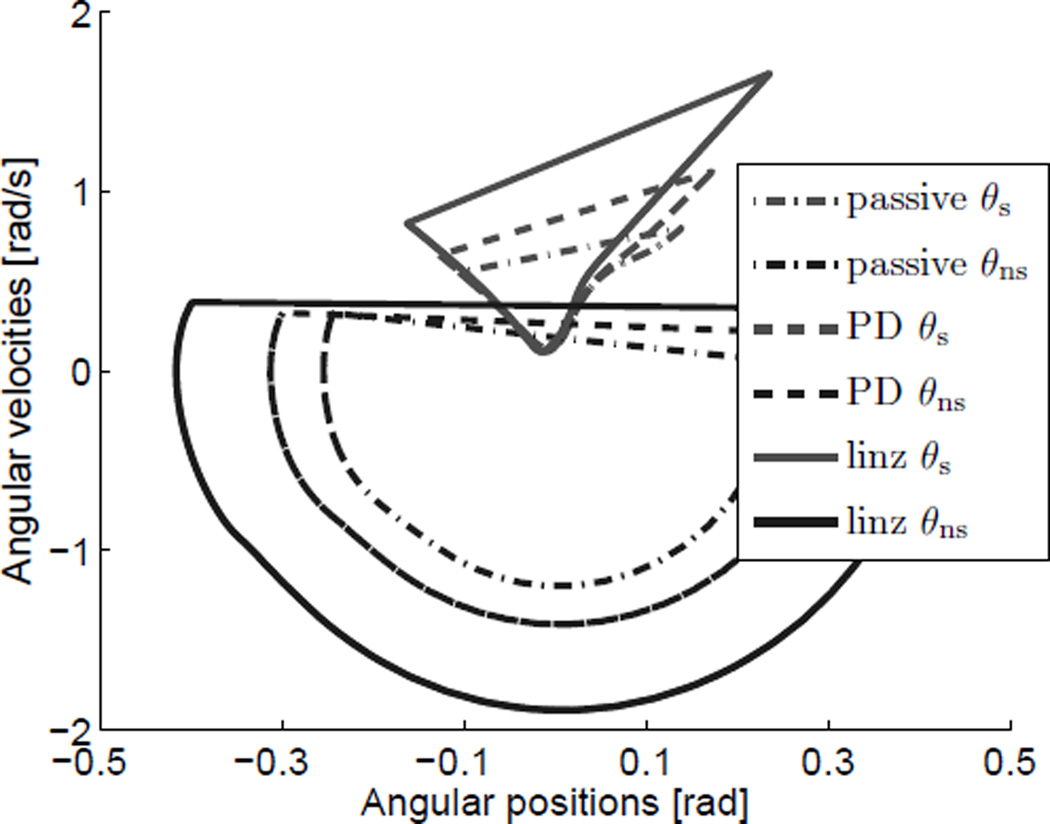
Starting with the previously described passive gait, we implement each control law and allow the simulation to converge to a steady-state walking gait (i.e., a fixed point). We verify that for each control strategy the associated fixed point is locally exponentially stable, using the procedure described in [26]. The hybrid limit cycles for all three gaits are superimposed in the phase portrait of Fig. 2.

Fig. 2.

Phase portrait of angular states from the hybrid limit cycles simulated with R_s = 0.45 for three control modes: passive walking, impedance control (PD), and output linearization (linz). The smaller orbits (shown in gray) correspond to the prosthetic ankle joint and the larger orbits (shown in black) correspond to the body’s hip joint.

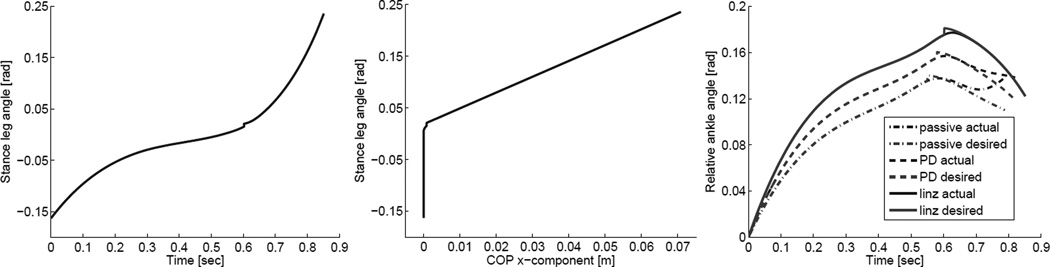
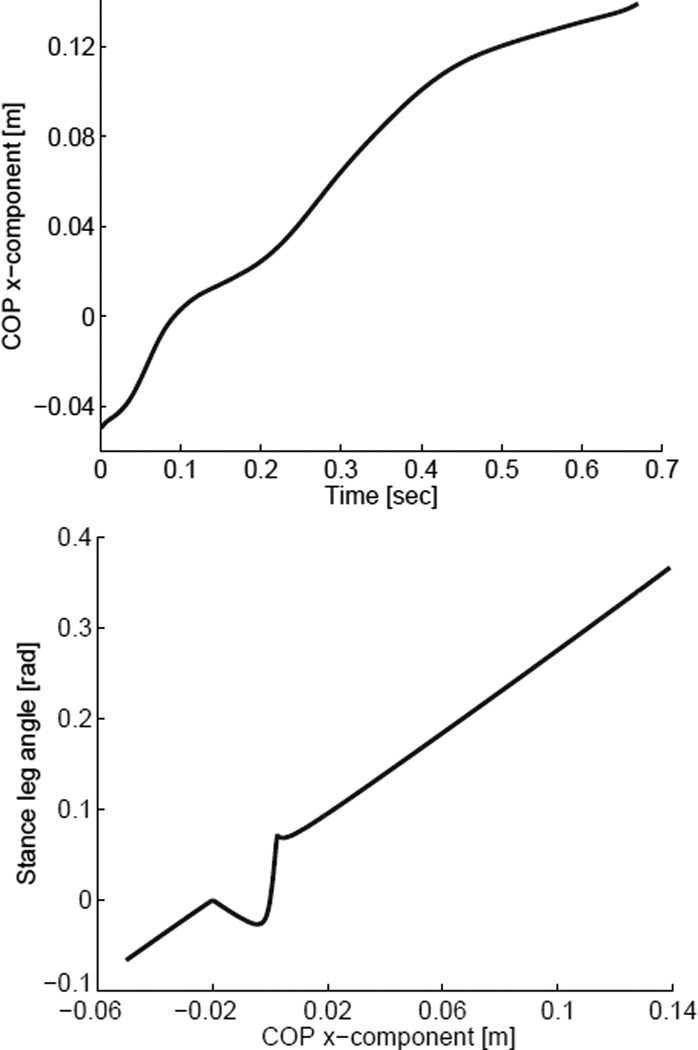
Using the COP trajectory of the linearized gait, we compute the desired stance leg angle ϕ(x, y) satisfying constraint (5). Fig. 3 shows the desired trajectory over both time and COP x-component (i.e., the phase variable). The desired leg angle is equal to the actual leg angle for the first 550 ms of the stance period, when the heel point is in contact with the ground. This period causes the desired leg angle as a function of COP to be non-unique (Fig. 3, center). We will discuss how this differs from human walking in Section V.

Fig. 3.

Desired stance leg angle ϕ(x, y) over time (left) and over COP (center) from simulation using linearizing controller (12). Right: Actual and desired trajectories of relative ankle angle θ_ank (zeroed at heel strike for the sake of comparison) from passive walking, impedance control (PD), and output linearization (linz) simulations. Note that the small jumps in the desired trajectories are caused by numerical imprecision when switching contact constraints.

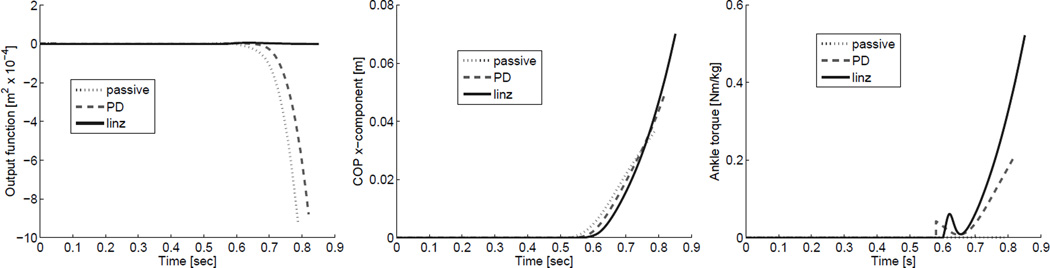
We see in Fig. 4 that output linearization outperforms the impedance controller in several ways. The linearized gait has no output error during steady-state walking, whereas error grows immediately after the foot starts rolling in the impedance and passive cases (Fig. 4, left). Output linearization causes more foot-rocking motion (which we would expect with R_s > R_f), as seen in the COP time-trajectory (Fig. 4, center) and the effective shape (Fig. 5, top). Similarly, this controller causes more ankle range of motion with wider steps in Fig. 3 (right). An interesting consequence of exactly enforcing the desired effective shape is greater control torque prior to contralateral heel strike (Fig. 4, right), which resembles the power generation of the human ankle at toe-off [21].

Fig. 4.

Comparison between steady-state gaits for passive walking, impedance control (PD), and output linearization (linz): output ξ (left), COP x-component (center), and ankle torque (right) over time. Recall that ξ ≡ 0 corresponds to perfect enforcement of the effective shape, which we see with output linearization.

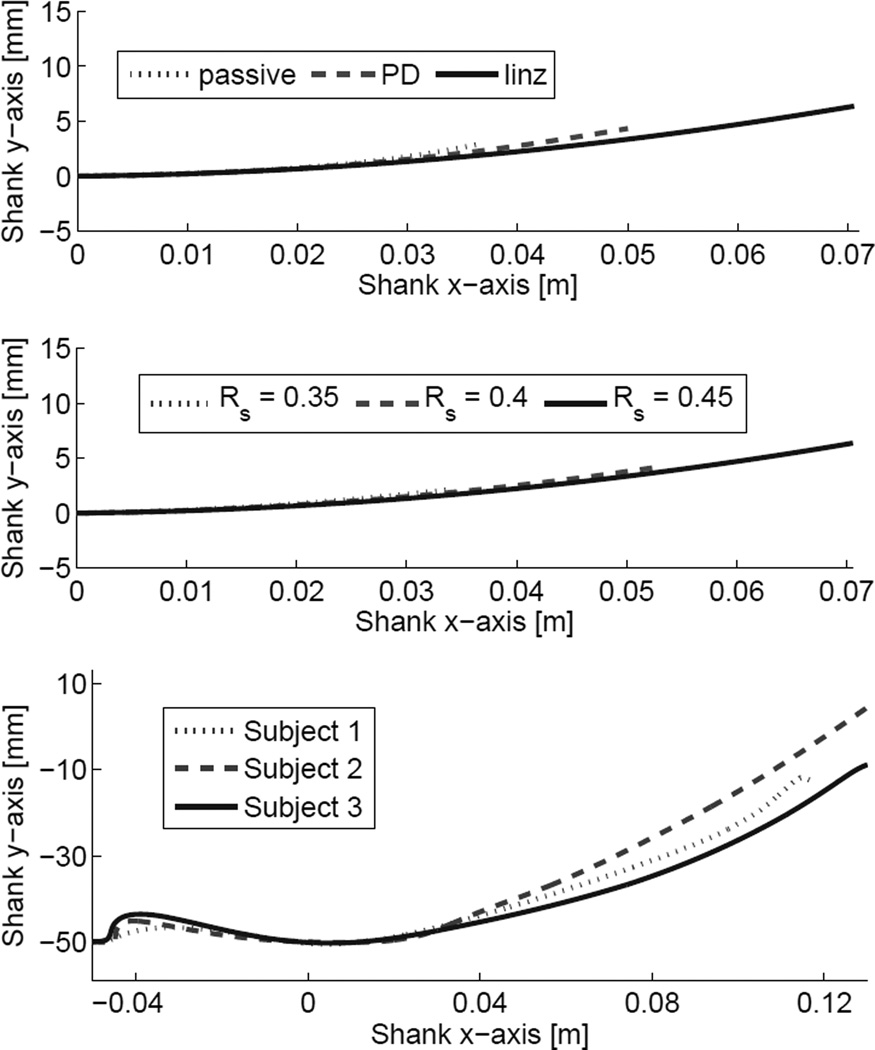
Fig. 5.

Effective shapes (i.e., COP trajectories in shank coordinates) for three control modes simulated with R_s = 0.45 (top), three effective radii simulated under output linearization (middle), and three able-bodied human subjects (bottom). Note that the human ankle joint is 50 mm above the heel, causing an offset along the shank y_s-axis.

Different effective radii are exactly enforced by output linearization in Fig. 5 (middle). We see that the COP range of motion increases with the effective radius. In general we find that a larger radius implies faster walking with a wider step length and a longer stance period (see Table II). Supplemental videos of the animated walking gaits for R_s = 0.45 and R_s = 0.35 are available at http://vimeo.com/38050625 and http://vimeo.com/38052820respectively.

TABLE II.

Influence of Effective Radius

Gait Descriptor	Rs = 0.45	Rs = 0.40	Rs = 0.35
x-COP Range [m]	0.070	0.053	0.034
Step Length [m]	0.269	0.224	0.169
Step Duration [s]	0.851	0.841	0.831
Step Velocity [m/s]	0.316	0.266	0.203

V. DISCUSSION

Although our simple biped model has limitations, the proposed control strategy has important advantages including biomimetic performance and clinical viability.

A. Positive Force Feedback

Although we did not explicitly design a push-off phase into the control strategy, enforcing the effective shape provided a biomimetic period of power generation as the COP approached the toe. A positive feedback loop arises when COP movement causes a positive ankle torque, which in turns causes the COP to move further forward. This biomimetic behavior, resembling the muscle reflex model in [9], might prevent compensatory work production at the hip (cf. [4]) and allow lower-limb amputees to expend normal levels of energy when walking.

B. Clinical Viability

This strategy requires tuning of only four control parameters (R_s, X_s, K_p, K_d) for the entire single-support period, whereas other control approaches have many more parameters during stance (e.g., 18 for event-based impedance control [8], 14 for a muscle model [9], or a human data set [10]). The effective radius R_s is a trivial function of the user’s leg length and the rotation center X_s determines the amount of ankle flexion, offering a simple tuning procedure. Moreover, the output linearization approach can accurately enforce constraints with much smaller gains than standard PD control [15], which is desirable for stability in the presence of feedback time delay and for safety when interacting with humans.

We showed that output linearization can be achieved on a powered prosthetic leg using measurements of interaction forces in place of state feedback from the human body. The COP can be sensed with a 3-axis load cell between the foot and ankle joint or with a pressure sensor grid in the foot or shoe insole [31]. Load cells are common in modern prosthetic legs (e.g., [6]–[8]), and advanced filtering techniques for rhythmic patterns can help estimate the COP [32]. A motorized ankle would likely use an encoder to measure the relative angle θ_ank between the shank and foot (Fig. 1, right) rather than the global angle used in our model. We can convert between angles by ${\theta }_{\mathrm{s}}=2\text{arcsin}\left(\frac{d}{2R_{\mathrm{f}}}\right)+\gamma -{\theta }_{\mathrm{a}\mathrm{n}\mathrm{k}}$, but this requires knowledge of the slope angle and the foot compliance. Fortunately the radii of curvature for many prosthetic feet have already been characterized in [19], and various methods have been proposed for measuring the slope angle during locomotion (e.g., inertial measurement units or passive mechanical devices [33]).

C. Zero Dynamics

Output linearization provides ξ ≡ 0 in steady state, implying that the surface Z = {z̆ | ξ = 0, ξ̇ = 0} is invariant¹ under the closed-loop dynamics. This surface is also hybrid invariant since ξ = ξ̇ = 0 immediately after impact. The hybrid system can therefore be restricted to its hybrid zero dynamics on surface Z, which exactly characterize the biped as a lower-dimensional hybrid system. Since output ξ represents the error of the prosthetic control system, the hybrid zero dynamics represent the coupled body. In our simulations we rendered this system minimum phase (i.e., stabilized the zero dynamics [24]) by exploiting the existence of an intrinsically stable passive gait. This allowed the entire biped to converge to a stable limit cycle even though the prosthetic ankle joint did not coordinate with the body’s hip joint. We hypothesize that the highly adaptable human neuromuscular system would provide this minimum phase property in a real prosthetics application.

D. Model Limitations

The biped model we used to simulate our controller has several limitations, including limited COP motion, the lack of a knee joint, and an instantaneous double-support phase. Although humans have strictly monotonic COP trajectories during steady walking (Fig. 6, top), our model has no COP movement until 550 ms into the stance period (Fig. 4, center). Numerical imprecision at this transition from heel contact to rolling contact results in a small discontinuous jump in ankle torque observed in Fig. 4 (right). It should also be noted that the COP is not truly a position variable as modeled in this paper, but rather a function of forces (i.e., a second-order variable) [21]. However, COP movement during human walking is associated with continuous foot deformation that resembles rolling [18], [20], so feet are commonly modeled as rockers to approximate the behavior of the ankle-foot complex, including the COP [22]. A rocker foot model can then be employed to derive the model-based prosthesis control law (12) for a human application, where we can expect COP motion to be more natural than in our passive walking model.

Fig. 6.

Top: COP x-component trajectory from one able-bodied human subject. Bottom: desired stance leg angle ϕ(x, y) over COP x-component from human data. To model the human foot we used a generalized form of constraint (5) that includes a non-zero height (0.05 m) between the heel and ankle joint with R_s = 0.26 m, X_s = 0.01 m from Fig. 5 (bottom).

To demonstrate that our kinematic constraint applies to realistic COP motion, we examine de-identified human data from [30], in which able-bodied subjects walked 400 times across a force plate at self-selected speeds. Subjects gave written informed consent in accordance with the Northwestern University Institutional Review Board. The mean effective shapes (Fig. 5, bottom) have approximately constant curvature as in our simulations (recall that we intentionally chose an abnormally large radius to accelerate the slow passive gait). We use the mean COP trajectory and R_s, X_s values from one subject to compute the desired leg angle ϕ(x, y) in Fig. 6 (bottom). This COP-ankle relationship could similarly be enforced via output linearization.

The lack of a knee joint also limits the anthropomorphism of our model, but our control strategy can be extended to a two-degree-of-freedom transfemoral prosthesis. Hansen et al. showed that the knee-ankle-foot (KAF) effective shape–the COP trajectory transformed into a coordinate frame attached to the thigh–also has constant curvature during walking [18]. This provides a second kinematic constraint from which the desired knee angle can be determined from the COP and ankle angle. Control of the knee could then be integrated into our proposed controller using a vector output ξ. This control approach could be tuned in a sequential manner, starting with the ankle-foot constraint, which does not depend on the knee angle, and ending with the KAF constraint.

A non-trivial double-support period could be modeled using a compliant ground contact model, which has been done in the context of output linearization [34]. However, the constant-curvature property of the COP trajectory in shank coordinates does not hold after contralateral heel strike. The main challenge is then to extend the kinematic model of the effective shape into the double-support period, possibly using the theoretical COP of the support polygon (which can be located between the two feet).

By relying on passive dynamics to generate joint patterns, we were limited to testing our controller with a downhill walking task. We can mimic human behavior on different slopes by rotating the effective center of rotation P_s by the slope change [17]. Stationary fore-aft swaying also has a constant effective radius–about six times that of a walking task [20]. Kinematic constraint (5) allows the radius of curvature R_s to be a function of the COP, which may be the case for a stair climbing task. It is possible that (5) cannot be solved for θ_s when R_s is non-constant, but unlike impedance control, our linearizing controller does not require this form.

Despite these limitations, this simple model allowed a proof-of-concept demonstration of our new control strategy. The simplicity of this model is also beneficial for elucidating biomechanical principles that are important in lower-limb prostheses, such as quasi-stiffness [35].

VI. Conclusion

We showed that the effective shape between the COP and ankle joint corresponds to a simple kinematic constraint, which can be enforced as a virtual constraint by an output linearizing control law using only feedback available to sensors onboard a prosthetic leg. This controller exactly enforced the desired effective shape during simulated walking, whereas an impedance controller did not. Due to the invariance of the effective shape over walking speeds, body weights, and heel heights [17], this choice of constraint will allow the prosthesis to naturally adapt to the user. The constraint can also be systematically tuned to produce the effective shapes corresponding to different activities, such as stationary swaying or stair climbing, by changing the center of rotation or the curvature radius/function.

Future work could integrate our control strategy with a neural interface (e.g., via electromyography from residual muscles [36]) to allow the user to subconsciously adapt the constraint when anticipating a task change. Our formulation of output linearization for prosthetics can also be used with constraints unrelated to the effective shape. This general framework motivates a new control theory for wearable robots, including powered orthoses [37], [38], that will exploit hybrid zero dynamics in assisted human locomotion.

We plan to implement our effective shape controller on the Vanderbilt leg [8] at the Rehabilitation Institute of Chicago. Ongoing work also includes perturbation experiments with able-bodied human subjects to test our hypothesis that joint patterns depend on the COP as a phase variable. Our hope is that this work will elucidate the control mechanisms behind human locomotion and enable translational designs for clinically viable wearable robots.