GENERAL THEORY FOR INTERACTIONS IN SUFFICIENT CAUSE MODELS WITH DICHOTOMOUS EXPOSURES

Abstract

The sufficient-component cause framework assumes the existence of sets of sufficient causes that bring about an event. For a binary outcome and an arbitrary number of binary causes any set of potential outcomes can be replicated by positing a set of sufficient causes; typically this representation is not unique. A sufficient cause interaction is said to be present if within all representations there exists a sufficient cause in which two or more particular causes are all present. A singular interaction is said to be present if for some subset of individuals there is a unique minimal sufficient cause. Empirical and counterfactual conditions are given for sufficient cause interactions and singular interactions between an arbitrary number of causes. Conditions are given for cases in which none, some or all of a given set of causes affect the outcome monotonically. The relations between these results, interactions in linear statistical models and Pearl’s probability of causation are discussed.

1. Introduction

Rothman’s sufficient-component cause model [21] postulates a set of different causal mechanisms each sufficient to bring about the outcome under consideration. Rothman refers to these hypothesized causal mechanisms as “sufficient causes”, conceiving of them as minimal sets of actions, events or states of nature which together initiate a process resulting in the outcome.

Thus each sufficient cause is hypothesized to consist of a set of “component causes”. Whenever all components of a particular sufficient cause are present, the outcome occurs; within every sufficient cause, each component would be necessary for that sufficient cause to lead to the outcome. Models of this kind have a long history: a simple version is considered by Cayley [3]; it also corresponds to the INUS model introduced by Mackie [11] in the philosophical literature. Much recent work has sought to relate the model to other causal modelling frameworks [7, 8, 29, 31, 32].

In traditional sufficient-component cause [SCC] models the outcome and all the component causes are events, or equivalently, binary random variables. An SCC model with k component causes, implies a set of 2^k potential outcomes. Conversely, in section 2 we show that for any given list of potential outcomes there is at least one SCC model which represents this set. However, in general there may be many such SCC models.

One question concerns whether, given a set of potential outcomes implied by some (unknown) SCC model, one may infer that two component causes are present within some sufficient cause in the unknown SCC model. In general, it is possible that two SCC models both imply the same set of potential outcomes yet although A and B occur together in some sufficient component cause in the first model, A and B are not present together in any sufficient component cause in the second. In [32] two sufficient component causes are said to form a ‘sufficient cause interaction’ (or to be ‘irreducible’) if they are both present within at least one sufficient cause in every SCC model for a given set of potential outcomes. Of course, in general, the distribution of potential outcomes for a given population is also unknown, though it is constrained (marginally) by the observed data from a randomized experiment. In [32] empirical conditions are given which are sufficient to ensure that for any set of potential outcomes compatible with experimental data, all compatible SCC models will contain a sufficient cause involving A and B. These results are an improvement upon earlier empirical tests for the existence of a two-way interaction in an SCC model [22], which required the assumption of monotonicity; see also [1, 9, 10, 15, 30]. The new results are able to establish the existence of an interaction in situations where monotonicity does not hold. In this paper we develop empirical conditions that are sufficient for the existence of a sufficient cause containing a given subset of an arbitrary number of variables both with and without monotonicity assumptions.

As illustrative motivation for the theoretical development we will consider data presented in a study by [26], summarized in Table 1, from a case-control study of bladder cancer examining possible three-way interaction between smoking (1 =present), and genetic variants on NAT2 (0 = R, 1 = S genotype) and NAT1 (1 for the *10 allele) for Caucasian individuals. We return to this example at the end of this paper to examine the evidence for a sufficient cause containing all three of smoking, the S genotype on NAT2 and the *10 allele on NAT1.

Table 1.

Smoking	NAT2	NAT1*10	Cases (n = 215)	Controls (n = 191)	Odds Ratio (95% CI)
0	0	0	6	13	1
0	0	1	8	16	1.1	(0.3, 3.9)
0	1	0	16	31	1.1	(0.4, 3.5)
0	1	1	6	10	1.3	(0.3, 5.3)
1	0	0	42	32	2.8	(1.1, 8.3)
1	0	1	41	26	3.4	(1.2, 10.1)
1	1	0	61	51	2.6	(0.9, 7.3)
1	1	1	35	12	6.3	(2.0, 20.3)

The remainder of this paper is organized as follows: Section 2 presents the sufficient-component cause framework as formalized by VanderWeele and Robins [32]. Section 3 describes general n-way irreducible interactions (aka ‘sufficient cause interactions’) and characterizes these in terms of potential outcomes. Section 4 derives empirical conditions for the existence of irreducible interactions both with and without monotonicity assumptions. Section 5 describes ‘singular’ interactions which arise in genetic contexts, provides a characterization, derives empirical conditions that are sufficient for their existence, and relates this notion to Pearl’s probability of causation. Section 6 discusses the relation between singular and sufficient cause interactions and linear statistical models. Section 7 provides some comments regarding stronger interpretations of sufficient cause models, and returns to the data presented in Table 1. Finally section 8 offers some possible extensions to the present work.

2. Notation and Basic Concepts

We will use the following notation: An event is a binary random variable taking values in {0, 1}. We use uppercase roman to indicate events (X), boldface to indicate sets of events (C), and lowercase to indicate specific values both for single random variables (X = x), and, with slight abuse of notation, for sets {C = c} ≡ {∀i, (C)_i = (c)_i}, and {a ≤ b} ≡ {∀i, (a)_i ≤ (b)_i}; 1 and 0 are vectors of 1’s and 0’s; the cardinality of a set is denoted |C|. We use fraktur ($\mathfrak{B}$) to denote collections of sets of events.

The complement of some event X is denoted by $\overline{X}\equiv 1-X$. A literal event associated with X, is either X or $\overline{X}$. For a given set of events C, $𝕃\left(\mathbf{C}\right)$ is the associated set of literal events:

$$𝕃\left(\mathbf{C}\right)\equiv \mathbf{C}\cup \{\overline{X}\mid X\in \mathbf{C}\}.$$

For a literal $L\in 𝕃\left(\mathbf{C}\right)$, and an assignment c to C, (L)_c denotes the value assigned to L by c. The conjunction of a set of literal events $\mathbf{B}=\{F_1,\dots ,F_m\}\subseteq 𝕃\left(\mathbf{C}\right)$ is defined as:

$$\bigwedge \left(\mathbf{B}\right)\equiv \prod _{i=1}^m{F}_i=\min \{F_1,\dots ,F_m\};$$

note that Λ(B) = 1 iff for all i, F_i = 1. We also define B₁ ∧B₂ ≡ Λ {B₁, B₂}. We will use $𝕀\left(A\right)$ to denote the indicator function for event A. There is a simple correspondence between conjunctions of literals and indicator functions: let B = {X₁, …, X_s} and C = {Y₁, …, Y_t}, then

$$\bigwedge \left(\right\{X_1,\dots ,X_s,{\overline{Y}}_1,\dots ,{\overline{Y}}_t\left\}\right)=1\iff 𝕀\left(\right\{\mathbf{B}=1,\mathbf{C}=0\left\}\right)=1.$$ (2.1)

Similarly, the set of literals corresponding to an assignment c to C is defined:

$${\mathbf{B}}^{\left[\mathbf{c}\right]}\equiv \{L\mid L\in 𝕃(\mathbf{C}),{\left(L\right)}_{\mathbf{c}}=1\}$$

so that $\bigwedge \left({\mathbf{B}}^{\left[\mathbf{c}\right]}\right)=𝕀(\mathbf{C}=\mathbf{c})$; note that |B^[c]| = |C|. The disjunction of a set of binary random variables is defined as:

$$\bigvee \left(\right\{Z_1,\dots ,Z_p\left\}\right)\equiv \max \{Z_1,\dots ,Z_p\};$$

note that ∨({Z₁, …, Z_p}) = 1 iff for some j, Z_j = 1. Similarly we let B₁ ∨ B₂ ≡ ∨{B₁, B₂}. Given a collection of sets of literals $\mathfrak{B}=\{{\mathbf{C}}_1,\dots ,{\mathbf{C}}_q\}$ we define:

$$\bigvee \bigwedge \left(\mathfrak{B}\right)\equiv {\bigvee }_i(\bigwedge ({\mathbf{C}}_i\left)\right).$$

We use $\stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$ to denote the set of subsets of $𝕃\left(\mathbf{C}\right)$ that do not contain both X and $\overline{X}$ for any X ∈ C, more formally:

$$\stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)\equiv \left\{\mathbf{B}\mid \mathbf{B}\subset 𝕃\left(\mathbf{C}\right),\text{for all}X\in \mathbf{C},\{X,\overline{X}\}⊈\mathbf{B}\right\}.$$

Note that if $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, and |B| = |C|, so that for all C ∈ C, exactly one of C or $\overline{C}$ is in B, then an assignment of values b to B induces a unique assignment c to C and vice versa.

2.1. Potential Outcomes Models

Consider a potential outcome model [14, 23, 24] with s binary factors, X₁, …, X_s, which represent hypothetical interventions or causes and let D denote some binary outcome of interest. We use Ω to denote the sample space of individuals in the population and use ω for a particular sample point. Let D_x1…xs(ω) denote the counterfactual value of D for individual ω if the cause X_j were set to the value x_j for j = 1, …, s. The potential outcomes framework we employ makes two assumptions: first, that for a given individual these counterfactual variables are deterministic; second, in asserting that the counterfactual D_x1…xs(ω) is well-defined, it is implicitly assumed that the value that D would take on for individual ω is determined solely by the values that X₁, …, X_s are assigned for this individual, and not the assignments made to these variables for other individuals ω′. This latter assumption is often called ‘no interference’ [6], or the Stable Unit Treatment Value Assumption (SUTVA) [25]. An example of a situation where this assumption might fail is a vaccine trial where there is ‘herd’ immunity.

We will use D_x1…xs(ω), D_{X1=x1,…,Xs=xs}(ω), D_c and D_C=c(ω), with C = {X₁, …, X_s} interchangeably. In this setting there will be 2^s potential outcomes for each individual ω in the population, one potential outcome for each possible value of (X₁, …, X_s); we use $\mathcal{D}(\mathbf{C};\omega )$ to denote the set of all such potential outcomes for an individual, and $\mathcal{D}(\mathbf{C};\Omega )$ for the population. Note that if G = g(C) is some deterministic function of C then G_C=c(ω) = g(c), and hence is constant; thus our usage is consistent with the definition of (L)_c in the previous section.

The actual observed value of D for individual ω will be denoted by D(ω) and similarly the actual value of X₁, …, X_s by X₁(ω), …, X_s(ω). Actual and counterfactual outcomes are linked by the Consistency Axiom which requires that

$$D_{X_1=X_1\left(\omega \right),\dots ,X_s=X_s\left(\omega \right)}\left(\omega \right)=D\left(\omega \right),$$ (2.2)

i.e. that the value of D which would have been observed if X₁, …, X_s had been set to the values they actually took is equal to the value of D which was in fact observed [?]. It follows from this axiom that D_{X1(ω),…,Xs(ω)}(ω) = D is observed, but it is the only potential outcome for individual ω that is observed.

Example 1. Consider a binary outcome D with three binary causes of interest, X₁, X₂ and X₃. Suppose that the population consists of two individuals. The potential outcomes (LHS) and actual outcomes (RHS) are shown in Table 2.

Table 2.

All potential outcomes and actual outcomes for three binary causes X₁, X₂ and X₃, in a population with two individuals.

Individual	D 000	D 001	D 010	D 011	D 100	D 101	D 110	D 111	(X1,X2,X3)	D
1	0	1	1	0	0	1	1	0	(1, 0, 1)	1
2	0	1	1	0	0	1	1	1	(0, 0, 0)	0

We use the notation A ⫫ B | C to indicate that A is independent of B conditional on C in the population distribution.

2.2. Definitions for sufficient cause models

The following definitions generalize those in [32] to sub-populations, $\varnothing \ne {\Omega }^{\ast }\subseteq \Omega$:

Definition 2.1 (Sufficient Cause). A subset B of the putative (binary) causes $𝕃\left(\mathbf{C}\right)$ for D forms a sufficient cause for D (relative to C) in sub-population Ω* if for all c ∈ {0, 1}^|C| such that (Λ(B))_c = 1, D_c(ω) = 1 for all ω ∈ Ω* ⊆ Ω. (We assume that there exists a c* such that (Λ(B))_c* = 1.)

Observe that if B is a sufficient cause for D then any intervention setting the variables C to c with (Λ(B))_c = 1 will ensure that D_c(ω) = 1 for all ω ∈ Ω*. We restrict the definition to non-empty sets Ω*, to preclude every set B being a sufficient cause in an empty sub-population. Likewise we require that there exists some c* such that (Λ(B))_c* = 1 in order to avoid logically inconsistent conjunctions, e.g. $X_1\wedge {\overline{X}}_1$, being classified (vacuously) as a sufficient cause. As a direct consequence, for any binary random variable X, at most one of X and $\overline{X}$ appear in any sufficient cause B.

Proposition 2.2. In Ω* if B is a sufficient cause for D relative to C then B is sufficient for D in any set C* with B ⊆ C* ⊆ C.

B may be sufficient for D relative to C in Ω*, but not relative to C′ ⊃ C.

Proposition 2.3. If B is a sufficient cause for D relative to C in Ω* then B is sufficient for D relative to C in any subset $\varnothing \ne {\Omega }^{\ast \ast }\subseteq {\Omega }^{\ast }$.

B may be sufficient for D relative to C in Ω*, but not in Ω′ ⊃ Ω*.

Definition 2.4 (Minimal Sufficient Cause). A set $\mathbf{B}\subset 𝕃\left(\mathbf{C}\right)$ forms a minimal sufficient cause for D (relative to C) in sub-population Ω* if B constitutes a sufficient cause for D in Ω* but no proper subset B* ⊂ B also forms a sufficient cause for D in Ω*.

Note that (in some Ω*) B may be a minimal sufficient cause for D relative to C, but not relative to C* ⊂ C, so the analog of Proposition 2.2 does not hold. For individual 2 in Table 2 {X₁, X₃} is a minimal sufficient cause relative to {X₁, X₂, X₃}. However, if we suppose that for ω = 2, X₂ is not caused by X₁ and X₃, so for all x₁, x₃, X_2X1=x1,X3=x3(ω = 2) = X₂(ω = 2), then {X₁, X₃} is not a minimal sufficient cause relative to {X₁, X₃}:

$$\begin{array}{cc}\hfill D_{X_1=0,X_3=1}(\omega =2)& =D_{X_1=0,X_2=0,X_3=1}(\omega =2)=1,\hfill \\ \hfill D_{X_1=1,X_3=1}(\omega =2)& =D_{X_1=1,X_2=0,X_3=1}(\omega =2)=1,\hfill \end{array}$$

(since X₂(ω =2) = 0) hence X₃ is a sufficient cause of D relative to {X₁, X₃}, hence {X₁, X₃} is not minimal relative to {X₁, X₃} for ω = 2.

Similarly, if B is a minimal sufficient cause for D relative to C in Ω*, it does not follow that B is a minimal sufficient cause for D relative to C in subsets Ω** ⊆ Ω*, so the analog to Proposition 2.3 does not hold. In particular, it may be the case that for all ω ∈ Ω*, B is not a minimal sufficient cause for D in {ω}.

In the language of digital circuit theory [12], sufficient causes are termed ‘implicants’, and minimal sufficient causes are ‘prime implicants’.

Definition 2.5 (Determinative Set of Sufficient Causes). A set of sufficient causes for D, $\mathfrak{B}=\{{\mathbf{B}}_1,\dots ,{\mathbf{B}}_n\}\subseteq \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, is said to be determinative for D (relative to C) in sub-population Ω* if for all ω ∈ Ω* and for all c, D_c(ω) = 1 if and only if ${(\bigvee \bigwedge (\mathfrak{B}\left)\right)}_{\mathbf{c}}=1$.

We will refer to a determinative set of sufficient causes for D as a sufficient cause model. Observe that in any sub-population Ω* for which there exists a determinative set of sufficient causes, the vectors of potential outcomes for D are identical, so $\mathcal{D}(\mathbf{C},\omega )=\mathcal{D}(\mathbf{C},{\omega }^{\prime })$ for all ω,ω′ ∈ Ω*.

Definition 2.6 (Non-redundant Set of Sufficient Causes). A determinative set of sufficient causes $\mathfrak{B}$, for D, is said to be non-redundant (in Ω*, relative to C) if there is no proper subset ${\mathfrak{B}}^{\ast }\subset \mathfrak{B}$ that is also determinative for D.

Note that sufficient causes are conjunctions, while sets of sufficient causes form disjunctions of conjunctions; minimality refers to the components in a particular conjunction, that each component is required for the conjunction to be sufficient for D; non-redundancy implies that each conjunction is required for the disjunction of the set of conjunctions to be determinative. If for some set of sufficient causes $\mathfrak{B}\subseteq \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, for all X ∈ C, and all $\mathbf{B}\in \mathfrak{B}$, either X ∈ B or $\overline{X}\in \mathbf{B}$ then $\mathfrak{B}$ is a non-redundant set of sufficient causes.

Example 1 (Revisited). The set ${\mathfrak{B}}_1=\left\{\right\{X_1,X_2\},\{X_2,{\overline{X}}_3\},\{{\overline{X}}_2,X_3\left\}\right\}$ forms a determinative set of sufficient causes for the individual ω = 2, since:

$$D_{\mathbf{c}}(\omega =2)={\left((X_1\wedge X_2)\vee (X_2\wedge {\overline{X}}_3)\vee ({\overline{X}}_2\wedge X_3)\right)}_{\mathbf{c}}$$ (2.3)

as does ${\mathfrak{B}}_2=\left\{\right\{X_1,X_3\},\{X_2,{\overline{X}}_3\},\{{\overline{X}}_2,X_3\left\}\right\}$:

$$D_{\mathbf{c}}(\omega =2)={\left((X_1\wedge X_3)\vee (X_2\wedge {\overline{X}}_3)\vee ({\overline{X}}_2\wedge X_3)\right)}_{\mathbf{c}}.$$ (2.4)

As this example shows, determinative sets of sufficient causes are not, in general, unique.

2.3. Sufficient cause representations for a population

As noted, if B is a sufficient cause for D in Ω*, then all the units in Ω* will have D = 1 for any assignment c to C, such that (Λ(B))_c = 1. In most realistic settings it is unlikely that any set B will be sufficient to ensure D = 1 in an entire population. Consequently different sets of sufficient causes will be required within different sub-populations. A sufficient cause representation is a set of sub-populations each with its own determinative sufficient cause representation:

Definition 2.7. A sufficient cause representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C};\Omega )$ is an ordered set A = 〈A₁, … A_p〉 of binary random variables, with (A_i)_c = A_i for all i, c, and a set $\mathfrak{B}=\langle {\mathbf{B}}_1,\dots ,{\mathbf{B}}_p\rangle$, with ${\mathbf{B}}_i\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, such that for all ω, c, D_c(ω) = 1 ⇔ for some j, A_j(ω) = 1 and (∧(B_j))_c = 1.

Note that the binary random variables A_i and the sets B_i are naturally paired via the orderings of A and $\mathfrak{B}$; we will refer to a pair (A_i, B_i) as occurring in the representation. The requirement that (A_i)_c = A_i for all i, c implies that A ∩ C = ∅, and further that the A_i are unaffected by interventions on the X_i; this is in keeping with the interpretation of the A_i as defining pre-existing sub-populations with particular sets of potential outcomes for D.

Proposition 2.8. If (A, $\mathfrak{B}$) is a sufficient cause representation for $\mathcal{D}(\mathbf{C};\Omega )$ then B_i is a sufficient cause of D in the sub-population in which A_i(ω) = 1.

Proposition 2.9. If (A, $\mathfrak{B}$) is a sufficient cause representation for $\mathcal{D}(\mathbf{C};\Omega )$, then for all A* ⊆ A, if

$$\varnothing \ne {\Omega }_{\mathbf{A}\backslash {\mathbf{A}}^{\ast }}^{{\mathbf{A}}^{\ast }}\equiv \{\omega \mid forall{A}_i\in \mathbf{A},A_i(\omega )=1iff{A}_i\in {\mathbf{A}}^{\ast }\},$$

then

$${\mathfrak{B}}^{{\mathbf{A}}^{\ast }}\equiv \{{\mathbf{B}}_i\mid {\mathbf{B}}_i\in \mathfrak{B};A_i\in {\mathbf{A}}^{\ast }\}$$

forms a determinative set of sufficient causes (relative to C) for ${\Omega }_{\mathbf{A}\backslash {\mathbf{A}}^{\ast }}^{{\mathbf{A}}^{\ast }}$.

Note that ${\Omega }_{\mathbf{A}\backslash {\mathbf{A}}^{\ast }}^{{\mathbf{A}}^{\ast }}$ consists of the sub-population in which A_i(ω) = 1 for all A_i ∈ A* and A_j(ω) = 0 for all A_j ∈ A\A*.

Proof: Suppose for some $\omega \in {\Omega }_{\mathbf{A}\backslash {\mathbf{A}}^{\ast }}^{{\mathbf{A}}^{\ast }}$, ${\mathbf{B}}_j\in {\mathfrak{B}}^{{\mathbf{A}}^{\ast }}$, and c we have (Λ(B_j))_c = 1. Since $\omega \in {\Omega }_{\mathbf{A}\backslash {\mathbf{A}}^{\ast }}^{{\mathbf{A}}^{\ast }}$, A_j(ω) = 1. It then follows from the definition of a sufficient cause representation that D_c(ω) = 1. Conversely, suppose D_c(ω) = 1. As (A, $\mathfrak{B}$) is a sufficient cause representation, for some j, A_j(ω) = 1 and (Λ(B_j))_c = 1. Since, by hypothesis, $\omega \in {\Omega }_{\mathbf{A}\backslash {\mathbf{A}}^{\ast }}^{{\mathbf{A}}^{\ast }}$, it follows that A_j ∈ A*, hence ${\mathbf{B}}_j\in {\mathfrak{B}}^{{\mathbf{A}}^{\ast }}$.

Theorem 2.10. For any $\mathcal{D}(\mathbf{C};\Omega )$ there exists a sufficient cause representation (A, $\mathfrak{B}$).

Proof: Let p = 2^|C|, and define $\mathfrak{B}\equiv \{\mathbf{B}\mid \mathbf{B}\subseteq \stackrel{.}{\mathbb{P}}(𝕃\left(\mathbf{C}\right)),\mid \mathbf{B}\mid =\mid \mathbf{C}\mid \}\equiv \langle {\mathbf{B}}_1,\dots ,{\mathbf{B}}_p\rangle$, ordered arbitrarily. Further define A_i(ω) ≡ D_Bi=1(ω). Given an arbitrary c, for some j, B^[c] = B_j, by construction of $\mathfrak{B}$. We then have

$$D_{\mathbf{c}}\left(\omega \right)=1\iff D_{{\mathbf{B}}_{j=1}}\left(\omega \right)=1\iff A_j\left(\omega \right)=1\text{and}{(\bigwedge ({\mathbf{B}}_j\left)\right)}_{\mathbf{c}}=1,$$

as required. The last step follows since by definition B^[c] = 1 iff C = c.

[32] proves this for the case of |C| = 2; see also [7] and [29] for discussion of the case |C| = 1.

Example 1 (Revisited). The construction given in the proof of Theorem 2.10 would yield the following sets of sufficient causes to represent $\mathcal{D}(\mathbf{C};\Omega )$ shown in Table 2:

$$\begin{array}{cc}\hfill \mathfrak{B}& =\langle {\mathbf{B}}_1,\dots ,{\mathbf{B}}_8\rangle \hfill \\ \hfill & =\langle \{X_1,X_2,X_3\},\{X_1,X_2,{\overline{X}}_3\},\{X_1,{\overline{X}}_2,X_3\},\{X_1,{\overline{X}}_2,{\overline{X}}_3\},\hfill \\ \hfill & \{{\overline{X}}_1,X_2,X_3\},\{{\overline{X}}_1,X_2,{\overline{X}}_3\},\{{\overline{X}}_1,{\overline{X}}_2,X_3\},\{{\overline{X}}_1,{\overline{X}}_2,{\overline{X}}_3\}\rangle \hfill \end{array}$$ (2.5)

with A₁ = A₄ = A₅ = 0, A₂ = A₃ = A₆ = A₇ = 1, $A_8=𝕀\left(\right\{\omega =2\left\}\right)$.

3. Irreducible conjunctions

We saw in Example 1 above with ω = 2 that an individual’s potential outcomes may be such that there are two determinative sets of common causes $\mathfrak{B}$ and ${\mathfrak{B}}^{\prime }$ and {X₁, X₂} is in $\mathfrak{B}$, but not in ${\mathfrak{B}}^{\prime }$. However, certain conjunctions are such that in every representation either the conjunction is present or it is contained in some larger conjunction; such conjunctions are said to be ‘irreducible’:

Definition 3.1. $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$ is said to be irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ if in every representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$ there exists ${\mathbf{B}}_i\in \mathfrak{B}$, with B ⊆ B_i.

[32] also refer to irreducibility of B for $\mathcal{D}(\mathbf{C},\Omega )$ as a ‘sufficient cause interaction’ between the components of B. (Note, however, that if B is irreducible, this does not in general imply that B is either a minimal sufficient cause, or even a sufficient cause, only that there is a sufficient cause that contains B.) It can be shown (via Theorem 3.2 below) that {X₂, ${\overline{X}}_3$} and {${\overline{X}}_2$, X₃} are irreducible for $\mathcal{D}(\mathbf{C};\Omega )$ in Table 2. In §7 we provide an interpretation of irreducibility in terms of the existence of a mechanism involving the variables in B. We now characterize irreducibility:

Theorem 3.2. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, |B| = |C₁|, then B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ iff there exists ω* ∈ Ω and values ${\mathbf{c}}_2^{\ast }$ for C₂ such that: (i) $D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=1$; (ii) for all L ∈ B, $D_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=0$.

Here ${\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$ indicates the disjoint union of C₁ and C₂. Thus B is irreducible if and only if there exists an individual in Ω, who would have response D = 1 if every literal in B is set to 1, but D = 0 whenever one literal is set to 0 and the rest to 1 (in some context ${\mathbf{C}}_2={\mathbf{c}}_2^{\ast }$). Note that conditions (i) and (ii) are equivalent to:

$$D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)-\sum _{L\in \mathbf{B}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)>0.$$ (3.1)

Proof: (⇒) We adapt the proof of Theorem 2.10, to show that if for all ω ∈ Ω and assignments ${\mathbf{c}}_2^{\ast }$ to C₂, at least one of (i) or (ii) does not hold, then there exists a representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$ such that for all ${\mathbf{B}}_i\in \mathfrak{B}$, B ⊆ B_i.

Define:

$$\begin{array}{cc}\hfill {\mathfrak{B}}^{†}& \equiv \langle {\mathbf{B}}_i^{†}\rangle \equiv \left\{{\mathbf{B}}^{\ast }\mid {\mathbf{B}}^{\ast }\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right),\mid {\mathbf{B}}^{\ast }\mid =\mid \mathbf{C}\mid ,\mathbf{B}⊈{\mathbf{B}}^{\ast }\right\},\hfill \\ \hfill {\mathfrak{B}}^{‡}& \equiv \langle {\mathbf{B}}_i^{‡}\rangle \equiv \left\{{\mathbf{B}}^{\ast }\mid {\mathbf{B}}^{\ast }\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right),\mid {\mathbf{B}}^{\ast }\mid =\mid \mathbf{C}\mid -1,\mathbf{B}\backslash {\mathbf{B}}^{\ast }=\left\{L\right\},L\in \mathbf{B}\right\},\hfill \end{array}$$

under arbitrary orderings. Thus ${\mathfrak{B}}^{†}$ is the set of subsets of exactly |C| literals that do not include B as a subset, while ${\mathfrak{B}}^{‡}$ contains those subsets of size |C| − 1 that contain all but one literals in B.

• For ${\mathbf{B}}_i^{†}\in {\mathfrak{B}}^{†}$ define the corresponding ${\mathbf{A}}_i^{†}\left(\omega \right)\equiv D_{{\mathbf{B}}_i^{†}=1}\left(\omega \right)$;

• For ${\mathbf{B}}_i^{‡}\in {\mathfrak{B}}^{‡}$ define ${\mathbf{A}}_i^{‡}\left(\omega \right)\equiv D_{{\mathbf{B}}_i^{‡}=1,L_i=0}\left(\omega \right)D_{{\mathbf{B}}_i^{‡}=1,L_i=1}\left(\omega \right)$, where $\left\{L_i\right\}\equiv \mathbf{B}\backslash {\mathbf{B}}_i^{‡}$.

The representation is given by $(\mathbf{A},\mathfrak{B})\equiv ({\mathbf{A}}^{†}\cup {\mathbf{A}}^{‡},{\mathfrak{B}}^{†}\cup {\mathfrak{B}}^{‡})$, where ${\mathbf{A}}^{†}\equiv \langle A_i^{†}\rangle ,{\mathbf{A}}^{‡}\equiv \langle A_i^{‡}\rangle$. To see this, first note that if for some ω and c, there is a pair (A_j, B_j) in (A, $\mathfrak{B}$) such that A_j(ω) = 1 and (Λ(B_j))_c = 1 then by construction of A^† and A^‡ it follows that D_c(ω) = 1. For the converse, suppose that for some c and ω, D_c(ω) = 1. There are two cases to consider:

(Λ(B))_c=0. In this case B ⊈ B^[c], so for some j, ${\mathbf{B}}_j^{†}={\mathbf{B}}^{\left[\mathbf{c}\right]}$, hence $A_j^{†}\left(\omega \right)\equiv D_{{\mathbf{B}}_j^{†}=1}\left(\omega \right)=D_{\mathbf{c}}\left(\omega \right)=1$, as required.

(Λ(B))_c =1. Let c be partitioned as (c₁, c₂). Since (i) holds with ${\mathbf{c}}_2^{\ast }={\mathbf{c}}_2$, (ii) does not. Thus for some L ∈ B, D_{B\{L}=1,L=0,C2=c2}(ω) = 1. By construction of ${\mathfrak{B}}^{‡}$, for some j, ${\mathbf{B}}_j^{‡}={\mathbf{B}}^{\left[\mathbf{c}\right]}\backslash \left\{L\right\}$, so ${(\bigwedge ({\mathbf{B}}_j^{‡}\left)\right)}_{\mathbf{c}}=1$. Since 1 = D_c(ω) = D_{B\{L}=1,L=0,C2=c2}(ω), we have $A_j^{‡}\left(\omega \right)=1$, as required.

(⇐) Suppose for a contradiction, that for some ω* and ${\mathbf{c}}_2^{\ast }$, (i) and (ii) hold, but B is not irreducible. Then there exists a representation (A, $\mathfrak{B}$) such that for all ${\mathbf{B}}_i\in \mathfrak{B}$, B ⊈ B_i. By (i), $D_{\mathbf{B}=1,{\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=1$. Thus for some pair (A_j, B_j), A (ω*) = 1, and ${\mathbf{B}}_j\subseteq \mathbf{B}\cup {\mathbf{B}}^{\left[{\mathbf{c}}_2^{\ast }\right]}$. Since B ⊈ B_j there exists some L ∈ B \ B_j, but then since A_j(ω*) = 1 and ${(\bigwedge ({\mathbf{B}}_j\left)\right)}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}=1$, we have $D_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=1$, which is a contradiction.

Corollary 3.3. If B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ then for any Ω* ⊃ Ω, B is irreducible for $\mathcal{D}(\mathbf{C},{\Omega }^{\ast })$.

Proof: By Theorem 3.2, since if Ω satisfies (i) and (ii) then so does Ω*.

3.1. B irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ with |B| = |C|

In the special case where |B| = |C|, the concepts of minimal sufficient cause for some ω* and irreducibility coincide.

Proposition 3.4. If $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$ and |B| = |C| then B is a minimal sufficient cause for some ω* ∈ Ω relative to C i B is irreducible for $\mathcal{D}(\mathbf{C},\omega )$.

Proof: If |B| = |C| then condition (i) in Theorem 3.2 (taking C₂ = ∅) holds iff B is a sufficient cause for D for ω*, and similarly condition (ii) holds iff B is a minimal sufficient cause for D (for ω*).

Thus we have the following:

Corollary 3.5. If $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, |B| = |C| and B is a minimal sufficient cause for D for some ω* ∈ Ω then $\mathbf{B}\in \mathfrak{B}$ for every representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$.

Proof: Immediate from Proposition 3.4.

3.2. B irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ with |B| > |C|

When |B| < |C| the conditions for irreducibility and for being a minimal sufficient cause are logically distinct. Condition (i) in Theorem 3.2 requires $D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=1$ for one assignment ${\mathbf{c}}_2^{\ast }$ (and some ω*), while if B is a sufficient cause (for ω*) then this condition is required to hold for all assignments ${\mathbf{c}}_2^{\ast }$; in contrast condition (ii) in Theorem 3.2 requires that there exists a single ${\mathbf{c}}_2^{\ast }$ (and some ω*) such that for all $L\in \mathbf{B},D_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=0$, while for B to be a minimal sufficient cause for ω* merely requires that for all L ∈ B, there exists an assignment ${\mathbf{c}}_2^L$ such that $D_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2^L}\left({\omega }^{\ast }\right)=0$.

Example 1 (Revisited). Let C = {X₁, X₂, X₃}, = {2}. Relative to C, {X₁, X₂} is a minimal sufficient cause for ω = 2 since D₁₁₁(2) = D₁₁₀(2) = 1, and D₀₁₁(2) = D₁₀₀(2) = 0. However {X₁, X₂} is not irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ because we have D₁₀₁(2) = D₀₁₀(2) = 1, hence condition (ii) in Theorem 3.2 is not satisfied for either X₃ = 0, or X₃ = 1. Conversely {X₁} is irreducible for = {2} since D₁₁₁(2) = 1, while D₀₁₁(2) = 0, but {X₁} is not a sufficient cause because D₁₀₀(2) = 0.

Though irreducibility of B for $\mathcal{D}(\mathbf{C},\Omega )$ neither implies, nor is implied by B being a minimal sufficient cause for some ω ∈ Ω, it does imply that every sufficient cause representation for $\mathcal{D}(\mathbf{C},\Omega )$ contains at least one conjunction B_j of which B is a (possibly proper) subset. However, prima facie this still leaves open the possibility that, for example, every representation either includes B ∪ {L} or $\mathbf{B}\cup \left\{\overline{L}\right\}$, for some L, but no representation includes both. However, this cannot occur:

Corollary 3.6. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$ if B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ then there exists a set ${\mathbf{B}}^{\ast }\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, with |B*| = |C| such that in every representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$ there exists ${\mathbf{B}}_j\in \mathfrak{B}$, with B ⊆ B_j ⊆ B*.

Thus irreducibility of B further implies that there is a set B* of size |C| such that in every representation there is at least one conjunct containing B that is itself contained in B*. However, it should be noted that, in general, there may be more than one conjunct B_j with B ⊆ B_j ⊆ B*.

Proof: Immediate from Theorem 3.2, taking ${\mathbf{B}}^{\ast }=\mathbf{B}\cup {\mathbf{B}}^{\left[{\mathbf{c}}_2^{\ast }\right]}$.

Finally, we note that a conjunction that is both irreducible and a minimal sufficient cause corresponds to an ‘essential prime implicant’ in digital circuit theory [12]. The Quine-McCluskey algorithm [13, 18, 19] finds the set of essential prime implicants for a given Boolean function, which here corresponds to the potential outcomes $\mathcal{D}(\mathbf{C},\omega )$ for an individual.

3.3. Enlarging the set of potential causes

As noted in §2.2 a set B may be a minimal sufficient cause for C but not a superset C′. Irreducibility is also not preserved without further conditions. To state these conditions we require the following:

Definition 3.7. X′ is said to be not causally influenced by a set C if for all ω ∈ Ω, the potential outcomes $X_{\mathbf{C}=\mathbf{c}}^{\prime }\left(\omega \right)$ are constant as c varies.

We will also assume that if every X′ ∈ C′ is not causally influenced by C then the Relativized Consistency Axiom holds:

$$D_{\mathbf{C}=\mathbf{c},{\mathbf{C}}^{\prime }={\mathbf{C}}^{\prime }\left(\omega \right)}\left(\omega \right)=D_{\mathbf{C}=\mathbf{c}}\left(\omega \right),$$ (3.2)

i.e. that if variables in C′ are not causally influenced by the variables in C then the counterfactual value of D intervening to set C to c is the same as the counterfactual value of D intervening to set C to c and the variables in C′ to the values they actually took on.

We now have the following Corollary to Theorem 3.2:

Corollary 3.8. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, |B| = |C₁|. If B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$, C′ ∩ C = ∅ and for all X′ ∈ C′, X′ is not causally influenced by C, then B is irreducible for $\mathcal{D}(\mathbf{C}\cup {\mathbf{C}}^{\prime },\Omega )$.

Proof: By Theorem 3.2 there exists ω* ∈ Ω and an assignment ${\mathbf{c}}_2^{\ast }$ to C₂ such that (i) and (ii) hold. Let c′ = C′(ω*). Since variables in C′ are not causally influenced by C, for all assignments b:

$$D_{\mathbf{B}=\mathbf{b},{\mathbf{C}}_2={\mathbf{c}}_2^{\ast },{\mathbf{C}}^{\prime }={\mathbf{c}}^{\prime }}\left({\omega }^{\ast }\right)=D_{\mathbf{B}=\mathbf{b},{\mathbf{C}}_2={\mathbf{c}}_2^{\ast },{\mathbf{C}}^{\prime }={\mathbf{C}}^{\prime }\left({\omega }^{\ast }\right)}\left({\omega }^{\ast }\right)=D_{\mathbf{B}=\mathbf{b},{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right),$$

the second equality here follows from (3.2). It follows that ω* and (${\mathbf{c}}_2^{\ast }$, c′) obey (i) and (ii) in Theorem 3.2 with respect to C ∪ C′.

The assumption that every variable in C′ is not causally influenced by C, is required because otherwise we may have C′(ω*) ≠ (C′)_B=b* (ω*) for some assignment b* to B. For example, let C = {X₁, X₂, X₃}, and suppose that

$$\begin{array}{cc}\hfill D_{X_1=x_1,X_2=x_2,X_3=x_3}\left(\omega \right)& =x_3\hfill \\ \hfill {\left(X_3\right)}_{X_1=x_1,X_2=x_2}\left(\omega \right)& =x_1\wedge x_2\hfill \end{array}$$

for all ω ∈ Ω. In this case {X₁, X₂} is irreducible for $\mathcal{D}\left(\right\{X_1,X_2\},\Omega )$, but not for $\mathcal{D}\left(\right\{X_1,X_2,X_3\},\Omega )$. We saw earlier that if B is a minimal sufficient cause for C then this does not imply that B is a minimal sufficient cause with respect to subsets of C. Here we see that if B is irreducible with respect for $\mathcal{D}(\mathbf{C},\Omega )$ then this does not imply irreducibility for supersets C* ⊃ C, unless every variable in C* \ C is not causally influenced by a variable in C.

4. Tests for irreducibility

In this section we derive empirical conditions which imply that a given conjunction B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$. Our first approach is via condition (3.1).

4.1. Adjusting for Measured Confounders

To detect that (3.1) holds requires us to identify the mean of potential outcomes in certain subpopulations. This is only possible if we have no unmeasured confounders [??]:

Definition 4.1. A set of covariates W suffice to adjust for confounding of (the effect of) C on D if:

$$D_{\mathbf{C}=\mathbf{c}}⫫\mathbf{C}\mid \mathbf{W}=\mathbf{w}$$ (4.1)

for all c, w.

Proposition 4.2. If a set W suffices to adjust for confounding of C on D and P (C = c, W = w) > 0 then

$$E[D_{\mathbf{C}=\mathbf{c}}\mid \mathbf{W}=\mathbf{w}]=E[D\mid \mathbf{C}=\mathbf{c},\mathbf{W}=w].$$

The proof of this is standard and hence omitted.

Note that if W is sufficient to adjust for confounding of C on D, then W is also sufficient to adjust for confounding of B on D, where $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, |B|=|C|.

4.2. Tests for irreducibility without monotonicity

Theorem 4.3. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, |B| = |C₁|. If W is sufficient to adjust for confounding of C on D, and for some c₂,w,

$$\begin{array}{cc}\hfill 0<E[D\mid & \mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2,\mathbf{W}=\mathbf{w}]\hfill \\ \hfill -& \sum _{L\in \mathbf{B}}E[D\mid \mathbf{B}\backslash \{L\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2,\mathbf{W}=\mathbf{w}]\hfill \end{array}$$ (4.2)

then B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$.

Proof: We prove the contrapositive. Suppose that B is not irreducible for $\mathcal{D}(\mathbf{C},\Omega )$. Then by Theorem 3.2, for all ω ∈ Ω, and all c₂,

$$D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2}\left(\omega \right)-\sum _{L\in \mathbf{B}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left(\omega \right)\le 0.$$

Hence for any w,

$$E=\left[D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2}-\sum _{L\in \mathbf{B}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2}\phantom{\mid }\mid \mathbf{W}=\mathbf{w}\right]\le 0.$$

Applying Proposition 4.2 to each term implies the negation of (4.2).

The condition provided in Theorem 4.3 can be empirically tested with t-test type statistics if W consists of a small number of categorical or binary variables or using regression or inverse probability of treatment weighting methods [20, 34] otherwise.

It follows from Corollary 3.8 that condition (4.2) further establishes that B is irreducible for $\mathcal{D}(\mathbf{C}\cup {\mathbf{C}}^{\prime },\Omega )$ so long as every variable in C′ is not causally influenced by variables in C.

It may be shown that condition (4.2) is the sole restriction on the law of (D, C, W) implied by the negation of irreducibility.

4.3. Graphs

In the next section we develop more powerful tests under monotonicity assumptions. However, to state these conditions we first introduce some concepts from graph theory:

Definition 4.4. A graph $\mathfrak{G}$ defined on a set B is a collection of pairs of elements in B, $\mathfrak{G}$ ≡ {E | E = {B₁, B₂} ⊆ B, B₁ ≠ B₂}.

This is the usual definition of a graph, except that the vertex set here is a set of literals. We will refer to sets in $\mathfrak{G}$ as edges, which we will represent pictorially as B₁ — B₂.

Definition 4.5. Two elements L, L* ∈ B are said to be connected in $\mathfrak{G}$ if there exists a sequence L = L₁, …, L_p = L* of distinct elements in B such that {L_i, L_i+1} ∈ $\mathfrak{G}$ for i = 1, …, p – 1.

The sequence of edges joining L and L* is said to form a path in $\mathfrak{G}$.

Definition 4.6. A graph $\mathfrak{G}$ on B is said to form a tree if $\mid \mathfrak{G}\mid =\mid \mathbf{B}\mid -1$, and any pair of distinct elements in B are connected in $\mathfrak{G}$.

In a tree there is a unique path between any two elements.

Proposition 4.7. Let $\mathfrak{T}$ be a tree on B. For each element R ∈ B there is a natural bijection:

$${\varphi }_R^{\mathfrak{T}}:\mathbf{B}\backslash \left\{R\right\}\leftrightarrow \mathfrak{T}$$

given by ${\varphi }_R^{\mathfrak{T}}\left(L\right)=\mathbf{E}=\{L^{\prime },L\}$ where $\mathbf{E}\in \mathfrak{T}$ is the last edge on a path from R to L.

It is not hard to show that for a graph $\mathfrak{G}$, if the bijections described in Proposition 4.7 exist then $\mathfrak{G}$ is a tree.

Theorem 4.8 (Cayley [4]). On a set B there are |B|^|B|−2 different trees.

4.4. Monotonicity

Sometimes it may be known that a certain cause has an effect on an outcome that is either always positive or always negative.

Definition 4.9. B_i has a positive monotonic effect on D relative to a set B (with B_i ∈B) in a population Ω if for all ω ∈ Ω and all values b_−i for the variables in B \ {B_i}, D_{B{Bi}=b−i,Bi=1}(ω) ≥ D_{B{Bi}=b−i,Bi=0}(ω).

Similarly we say that L has a negative monotonic effect relative to B ∪ {L} if $\overline{L}$ has a positive monotonic effect relative to $\mathbf{B}\cup \left\{\overline{L}\right\}$. Note that the case in which D_{B{Bi}=b−i,Bi=1}(ω) = D_{B{Bi}=b−i,Bi=0}(ω) for all ω, and hence B_i has no effect on D relative to B, is included as a degenerate case.

The definition of a positive monotonic effect requires that an intervention does not decrease D for every individual, not simply on average, regardless of the other interventions taken. This is thus a strong assumption; see [33] for further discussion.

Proposition 4.10. The set of potential outcomes that are compatible with monotonicity is given by the Sperner number S(n).

*** Cite Dedekind again?

4.5. Tests for irreducibility with monotonicity

Knowledge of the monotonicity of certain potential causes allows for the construction of more powerful statistical tests for irreducibility than those given by Theorem 4.3.

Theorem 4.11. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, $\mathbf{B}=(\mathbf{B}+\stackrel{.}{\cup }{\mathbf{B}}^{\prime })\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, |B|=|C₁| and suppose that every L ∈ B₊ has a positive monotonic effect on D relative to C. If for some tree $\mathfrak{T}$ on B₊, ω* ∈ Ω and some c₂ we have:

$$\begin{array}{cc}\hfill 0<& D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)\hfill \\ \hfill & -\sum _{L\in \mathbf{B}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)+\sum _{\mathbf{E}\in \mathfrak{T}}{D}_{\mathbf{B}\backslash \mathbf{E}=1,\mathbf{E}=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right).\hfill \end{array}$$ (4.3)

then B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$.

If we know that X has a negative monotonic effect on D, then we may use this Theorem to construct more powerful tests of the irreducibility of sets containing $\overline{X}$ with respect to $\mathcal{D}(\mathbf{C},\Omega )$. Under the assumption that every L ∈ C has a monotonic effect on D we have shown via direct calculation using cddlib [?] that for |C| ≤ 4, the conditions (4.3) are the sole restrictions on the law of (D, C, W) implied by the negation of irreducibility. We conjecture that this holds in general.

Proof: By Theorem 3.2 it is sufficient to prove that under the monotonicity assumption on B₊, (4.3) implies (3.1). Suppose that (3.1) does not hold, so that for all values c₂, and all ω* ∈ Ω,

$$D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)-\sum _{L\in \mathbf{B}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)\le 0.$$

Then for each ω* ∈ Ω there exists R ∈ B₊ such that

$$D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)-\sum _{L\in {\mathbf{B}}^{\prime }\cup \left\{R\right\}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)\le 0.$$

For a given tree $\mathfrak{T}$, the remaining terms on the RHS of (4.3) are:

$$\begin{array}{cc}\hfill -& \sum _{L\in {\mathbf{B}}_{+}\backslash \left\{R\right\}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)+\sum _{\mathbf{E}\in \mathfrak{T}}{D}_{\mathbf{B}\backslash \mathbf{E}=1,\mathbf{E}=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)\hfill \\ \hfill & =\sum _{L\in {\mathbf{B}}_{+}\backslash \left\{R\right\}}\left(D_{\mathbf{B}\backslash {\varphi }_R^{\mathfrak{T}}\left(L\right)=1,{\varphi }_R^{\mathfrak{T}}\left(L\right)=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)-D_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2}\left({\omega }^{\ast }\right)\right),\hfill \end{array}$$

by Proposition 4.7. Finally since ${\varphi }_R^{\mathfrak{T}}\left(L\right)=\{L,L^{\prime })\subseteq {\mathbf{B}}_{+}$, L′ has a positive monotonic effect on D relative to C, thus no term in the sum is positive. Consequently for all ω* ∈ Ω, (4.3) does not hold for any tree $\mathfrak{T}$.

Example 2. In the case B = {X₁, X₂} = B₊ = C, where there is only one tree on B₊, consisting of a single edge X₁ — X₂. Thus if X₁ and X₂ have a positive monotonic effect on D (relative to C) then Theorem 4.11 implies that if the following inequality holds for some ω ∈ Ω then

$$D_{11}\left(\omega \right)-\left(D_{10}\right(\omega )+D_{01}(\omega \left)\right)+D_{00}\left(\omega \right)>0$$

then {X₁, X₂} is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$.

Example 3. If B = {X₁, X₂, X₃} = B₊ = C, then there are three trees on B₊, see Figure 1. These correspond to the following conditions:

1. D₁₁₁(ω) − (D₁₁₀(ω) + D₁₀₁(ω) + D₀₁₁(ω)) + (D₀₁₀(ω) + D₀₀₁(ω)) > 0;

2. D₁₁₁(ω) − (D₁₁₀(ω) + D₁₀₁(ω) + D₀₁₁(ω)) + (D₁₀₀(ω) + D₀₀₁(ω)) > 0;

3. D₁₁₁(ω) − (D₁₁₀(ω) + D₁₀₁(ω) + D₀₁₁(ω)) + (D₁₀₀(ω) + D₀₁₀(ω)) > 0.

Thus B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ if at least one holds for some ω ∈ Ω.

Fig 1.

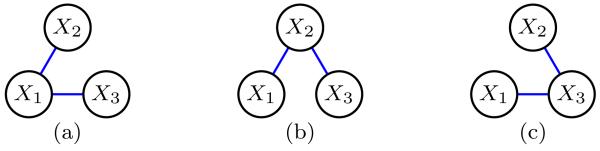
The three trees on {X₁, X₂, X₃}.

Corollary 4.12. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, $\mathbf{B}=(\mathbf{B}+\stackrel{.}{\cup }{\mathbf{B}}^{\prime })\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$ |B| = |C₁|. Suppose that every L ∈ B₊ has a positive monotonic effect on D relative to C, and W is sufficient to adjust for confounding of C on D. If for some tree $\mathfrak{T}$ on B₊, and some c₂, w we have:

$$\begin{array}{cc}\hfill 0<E[D\mid \mathbf{B}& =1,{\mathbf{C}}_2={\mathbf{c}}_2,\mathbf{W}=\mathbf{w}]\hfill \\ \hfill -\sum _{L\in \mathbf{B}}& E[D\mid \mathbf{B}\backslash \{L\}=1,L=0,{\mathbf{C}}_2={\mathbf{c}}_2,\mathbf{W}=\mathbf{w}]\hfill \\ \hfill & +\sum _{\mathbf{E}\in \mathfrak{T}}E[D\mid \mathbf{B}\backslash \mathbf{E}=1,\mathbf{E}=0,{\mathbf{C}}_2={\mathbf{c}}_2,\mathbf{W}=\mathbf{w}],\hfill \end{array}$$ (4.4)

then B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$.

Proof: Directly analogous to the proof of Theorem 4.3.

The special case of the previous Corollary where |B₊| = |C| = 2, and W = ∅, appears in Rothman and Greenland [22]; see also Koopman [10].

Theorem 4.8 implies that if every literal in B has a positive monotonic effect on D then we will have |B|^|B|−2 conditions to test, each of which is sufficient to establish the irreducibility of B for $\mathcal{D}(\mathbf{C},\Omega )$. As before, the conditions (4.4) may be tested via t-test type statistics or using various statistical models.

As with the results in §4.2, we may apply Corollary 3.8 to establish that B is irreducible for D(C ∪ C′,) if every variable in C′ is not causally influenced by variables in C.

4.6. Tests for a minimal sufficient cause under monotonicity

As noted in section §3.1 if |B| = |C| then irreducible conjunctions are also minimal sufficient causes. Thus in this special case the tests of irreducibility given in Theorem 4.3 and Corollary 4.12 also establish that B is a minimal sufficient cause relative to C. When |B| < |C| these tests do not in general establish this. However, under positive monotonicity assumptions on C₂, such tests may be obtained by taking c₂ = 0:

Proposition 4.13. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, |B|=|C₁|. Suppose every L ∈ C₂ has a positive monotonic effect on D relative to C. If (i) D_B=1,C2=0(ω*) = 1 and (ii) for all L ∈ B, $D_{\mathbf{B}\backslash \left\{L\right\}=1,L=0,{\mathbf{C}}_2=0}\left({\omega }^{\ast }\right)=0$, then B is a minimal sufficient cause for D relative to C for ω*.

Proof: For any c₂, D_B=1,C2=c2(ω) ≥ D_B=1,C2=0(ω) by the monotonicity assumption. Hence B is a sufficient cause for D relative to C for ω*. Minimality follows directly from condition (ii).

We have the following corollaries which provide conditions under which B is a minimal sufficient cause for D relative to C for some ω ∈, in addition to being irreducible for $\mathcal{D}(\mathbf{C},\Omega )$:

Corollary 4.14. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$,$\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$ |B| = |C₁|. Suppose every L ∈ C₂ has a positive monotonic effect on D relative to C and W is sufficient to adjust for confounding of C on D. If (4.2) holds with c₂ = 0 for some w then B is a minimal sufficient cause of D relative to C for some ω ∈ Ω.

Proof: Immediate from Proposition 4.13 and Theorem 4.3.

Corollary 4.15. Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, $\mathbf{B}=(\mathbf{B}+\stackrel{.}{\cup }{\mathbf{B}}^{\prime })\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, |B| = |C₁|. Suppose that every L ∈ B₊ ∪ C₂ has a positive monotonic effect on D relative to C, and W is sufficient to adjust for confounding of C on D.

If (4.4) holds with c₂ = 0 for some w and some tree $\mathfrak{T}$ on B₊ then B is a minimal sufficient cause of D relative to C for some ω ∈ Ω.

Proof: Immediate from Proposition 4.13 and Corollary 4.12.

5. Singular interactions

In the genetics literature, in the context of two binary genetic factors, X₁ and X₂, ‘biologic’ or ‘compositional’ epistasis [2, 5, 17] is said to be present if for some ω*, D₁₁(ω*) = 1 but D₁₀(ω*) = D₀₁(ω*) = D₀₀(ω*) = 0; in this case the effect of one genetic factor is effectively masked when the other genetic factor is absent. If {X₁, X₂} is a minimal sufficient cause of D relative to {X₁, X₂} for ω* then although this implies D₁₁(ω*) = 1 and D₁₀(ω*) = D₀₁(ω*) = 0, it does not imply D₀₀(ω*) = 0. This motivates the following:

Definition 5.1. A minimal sufficient cause B for D relative to C for ω* is said to be singular if there is no ${\mathbf{B}}^{\prime }\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, B′ ≠ B, forming a minimal sufficient cause for D relative to C for ω*. B is singular for $\mathcal{D}(\mathbf{C},\Omega )$ if B is singular relative to C for some ω* ∈ Ω.

If B is singular for $\mathcal{D}(\mathbf{C},\Omega )$ then we will also refer to a singular interaction between the components of B. We now characterize singularity in terms of potential outcomes:

Theorem 5.2. Let C = C₁∪C₂, $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, |B| = |C₁| then B is singular for $\mathcal{D}(\mathbf{C},\Omega )$ iff there exists ω* ∈ Ω such that

$$forallvalues{\mathbf{c}}_2^{\ast },\mathbf{b}:D_{\mathbf{B}=\mathbf{b},{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=1\iff \mathbf{b}=1.$$ (5.1)

Note that (5.1) is equivalent to:

$$D_{\mathbf{C}=\mathbf{c}}\left({\omega }^{\ast }\right)={(\bigwedge (\mathbf{B}\left)\right)}_{\mathbf{c}}\text{for all}\mathbf{c}.$$ (5.2)

Thus if B is singular for $\mathcal{D}(\mathbf{C},\Omega )$ then there is some individual ω* whose potential outcomes are given by the single conjunction B.

Proof: By definition, B is a sufficient cause for D for ω* iff $(\mathbf{b}=1\Rightarrow D_{\mathbf{B}=\mathbf{b},{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}({\omega }^{\ast })=1)$. Thus it is sufficient to show that, assuming B is a minimal sufficient cause for D for ω*, there are no other minimal sufficient causes of D for ω* iff $\left(D_{\mathbf{B}=\mathbf{b},{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\right({\omega }^{\ast })=1\Rightarrow \mathbf{b}=1)$.

Suppose B is the only minimal sufficient cause for D for ω*, but that for some b* ≠ 1, $D_{\mathbf{B}={\mathbf{b}}^{\ast },{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=1$. Let ${\mathbf{B}}^{†}\equiv {\mathbf{B}}^{[\mathbf{B}={\mathbf{b}}^{\ast },{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }]}$, B^† forms a sufficient cause for D for ω*, and B ⊈ B^†. Hence there is some B′ ⊆ B^† that is a minimal sufficient cause for D for ω*, and B ≠ B^†, a contradiction.

Conversely suppose $\left(D_{\mathbf{B}=\mathbf{b},{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\right({\omega }^{\ast })=1\Rightarrow \mathbf{b}=1)$ but there exists another minimal sufficient cause B′ for D for ω*, and B ≠ B^†. Since B′ is minimal, B ⊈ B′. Thus there exists a $\tilde{\mathbf{c}}$ such that ${\left(\mathbf{B}\right)}_{\tilde{\mathbf{c}}}\ne 1$, but ${\left({\mathbf{B}}^{\prime }\right)}_{\tilde{\mathbf{c}}}=1$ and hence $D_{\mathbf{C}=\tilde{\mathbf{c}}}\left({\omega }^{\ast }\right)=1$, a contradiction.

Corollary 5.3. For $\mathcal{D}(\mathbf{C},\Omega )$, if B is singular then B is irreducible.

Proof: Immediate from (5.1) and the definition of irreducibility.

Theorem 5.4 relates singular interactions to properties of the set of sufficient cause representations for $\mathcal{D}(\mathbf{C},\Omega )$.

Theorem 5.4. Let $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$. B is singular for $\mathcal{D}(\mathbf{C},\Omega )$ iff there exists ω* ∈ Ω such that in every representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$, (i) for all ${\mathbf{B}}^{\ast }\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, with |B*| = |C| and B ⊆ B* there exists ${\mathbf{B}}_i\in \mathfrak{B}$ with B_i ⊆ B* and A_i(ω*) = 1; (ii) for all ${\mathbf{B}}_i\in \mathfrak{B}$ such that B ⊈ B_i, A_i(ω*) = 0.

Proof: Let $\mathbf{C}={\mathbf{C}}_1\stackrel{.}{\cup }{\mathbf{C}}_2$, where $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, and |B| = |C₁|.

(⇒) Suppose B is singular for $\mathcal{D}(\mathbf{C},\Omega )$, so that some ω* ∈ Ω satisfies (5.2). Then for any representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$ and any B* such that |B*| = |C| and B ⊆ B* we can select values ${\mathbf{c}}_2^{\ast }$ so that ${\mathbf{B}}^{\ast }{=}^{[\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }]}$. Since $D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=1$ there exists A_i ∈ A, ${\mathbf{B}}_i\in \mathfrak{B}$ with A_i (ω*) = 1 and ${(\bigwedge ({\mathbf{B}}_i\left)\right)}_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}=1$. Thus B_i ⊆ B*, so (i) holds. For all ${\mathbf{B}}_i\in \mathfrak{B}$ such that B ⊈ B_i, we can choose $\tilde{\mathbf{B}}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right({\mathbf{C}}_1\left)\right)$, $\mid \tilde{\mathbf{B}}\mid =\mid {\mathbf{C}}_1\mid$ with $\tilde{\mathbf{B}}\ne \mathbf{B}$ and values ${\tilde{\mathbf{c}}}_2$ so that ${\mathbf{B}}_i\subseteq {\mathbf{B}}^{[\tilde{\mathbf{B}}=1,{\mathbf{C}}_2={\tilde{\mathbf{c}}}_2]}$. Since $D_{\tilde{\mathbf{B}}=1,{\mathbf{C}}_2={\tilde{\mathbf{c}}}_2}\left({\omega }^{\ast }\right)=0$ we have A_i(ω*) = 0 since ${(\bigwedge ({\mathbf{B}}_i\left)\right)}_{\tilde{\mathbf{B}}=1,{\mathbf{C}}_2={\tilde{\mathbf{c}}}_2}=1$, so (ii) holds as required.

(⇐) Suppose there exists ω* ∈ such that every representation (A, $\mathfrak{B}$) satisfies (i) and (ii). We will show that (5.1) holds. For any values ${\mathbf{c}}_2^{\ast }$ let ${\mathbf{B}}^{\ast }\equiv {\mathbf{B}}^{[\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }]}$, so |B*| = |C| and B ⊆ B*. Thus by (i) there exists ${\mathbf{B}}_i\in \mathfrak{B}$ with B_i ⊆ B* and A_i(ω*) = 1. Hence $D_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=1$ since A((ω*) = 1 and ${(\bigwedge ({\mathbf{B}}_i\left)\right)}_{\mathbf{B}=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}=1$. Conversely for any b′ ≠ 1, let B′ ≡ B^[B=b′]. so |B′| = |C₁| with B′ ≠ B. Thus for all ${\mathbf{B}}_i\in \mathfrak{B}$ such that ${(\bigwedge ({\mathbf{B}}_i\left)\right)}_{{\mathbf{B}}^{\prime }=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}=1$, B ⊈ B_i and thus by (ii) A_i (ω*) = 0. Hence $D_{{\mathbf{B}}^{\prime }=1,{\mathbf{C}}_2={\mathbf{c}}_2^{\ast }}\left({\omega }^{\ast }\right)=0$.

We now consider results relevant for testing for singular interactions with or without monotonicity assumptions.

Theorem 5.5. Let $\mathbf{B}={\mathbf{B}}_{+}\stackrel{.}{\cup }{\mathbf{B}}^{\prime }\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, |B| = |C| and suppose that every L ∈ B₊ has a positive monotonic effect on D relative to C. If for some tree $\mathfrak{T}$ on B₊ and some ω* ∈ Ω we have

$$\begin{array}{cc}\hfill D_{\mathbf{B}=1}\left({\omega }^{\ast }\right)& -\sum _{L\in {\mathbf{B}}_{+}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0}\left({\omega }^{\ast }\right)\hfill \\ \hfill & -\sum _{\tilde{\mathbf{B}}:\varnothing \ne \tilde{\mathbf{B}}\subseteq {\mathbf{B}}^{\prime }}{D}_{\mathbf{B}\backslash \tilde{\mathbf{B}}=1,\tilde{\mathbf{B}}=0}\left({\omega }^{\ast }\right)+\sum _{\mathbf{E}\in \mathfrak{T}}{D}_{\mathbf{B}\backslash \mathbf{E}=1,\mathbf{E}=0}\left({\omega }^{\ast }\right)>0\hfill \end{array}$$ (5.3)

then B is singular for $\mathcal{D}(\mathbf{C},\Omega )$.

Proof: By Theorem 5.4 B is singular for $\mathcal{D}(\mathbf{C},\Omega )$ iff

$$\text{for some}{\omega }^{\ast }\in \Omega ,D_{\mathbf{B}=1}\left({\omega }^{\ast }\right)-\sum _{\tilde{\mathbf{B}}\subseteq \mathbf{B}}{D}_{\mathbf{B}\backslash \tilde{\mathbf{B}}=1,\tilde{\mathbf{B}}=0}\left({\omega }^{\ast }\right)>0.$$ (5.4)

Suppose for a contradiction that (5.4) does not hold but (5.3) holds for some ω* ∈ Ω. Since B₊ has a positive monotonic effect on D relative to C, if $\tilde{\mathbf{B}}\subseteq \mathbf{B}$ is such that $\tilde{\mathbf{B}}\cap {\mathbf{B}}_{+}\ne \varnothing$ then $D_{\mathbf{B}\backslash \tilde{\mathbf{B}}=1,\tilde{\mathbf{B}}=0}\left({\omega }^{\ast }\right)=1$ implies $D_{\mathbf{B}\backslash \left\{L\right\}=1,L=0}\left({\omega }^{\ast }\right)=1$ for some $L\in \tilde{\mathbf{B}}$. Hence for all ω ∈ Ω

$$D_{\mathbf{B}=1}\left(\omega \right)-\sum _{L\in \mathbf{B}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0}\left(\omega \right)-\sum _{\tilde{\mathbf{B}}\subseteq {\mathbf{B}}^{\prime },\mid \tilde{\mathbf{B}}\mid \ge 2}{D}_{\mathbf{B}\backslash \tilde{\mathbf{B}}=1,\tilde{\mathbf{B}}=0}\left(\omega \right)\le 0.$$ (5.5)

By applying the same argument to the first two terms on the LHS of (5.5) as was applied in the proof of Theorem 4.11 we have that (5.3) does not hold for all ω ∈, which is a contradiction.

The following corollary to Theorem 5.5 generalizes the discussion in [27,28] to an arbitrary number of dichotomous factors:

Corollary 5.6. Let $\mathbf{B}={\mathbf{B}}_{+}\stackrel{.}{\cup }{\mathbf{B}}^{\prime }\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, |B| = |C|. Suppose that every L ∈ B₊ has a positive monotonic effect on D relative to B, and W is sufficient to adjust for confounding of C on D. If for some tree $\mathfrak{T}$ on B₊, and some w we have:

$$\begin{array}{cc}\hfill 0<E& [D\mid \mathbf{B}=1,\mathbf{W}=\mathbf{w}]-\sum _{L\in {\mathbf{B}}_{+}}E[D\mid \mathbf{B}\backslash \{L\}=1,L=0,\mathbf{W}=\mathbf{w}]\hfill \\ \hfill & -\sum _{\tilde{\mathbf{B}}:\varnothing \ne \tilde{\mathbf{B}}\subseteq {\mathbf{B}}^{\prime }}E[D\mid \mathbf{B}\backslash \tilde{\mathbf{B}}=1,\tilde{\mathbf{B}}=0,\mathbf{W}=\mathbf{w}]\hfill \\ \hfill & +\sum _{\mathbf{E}\in \mathfrak{T}}E[D\mid \mathbf{B}\backslash \mathbf{E}=1,\mathbf{E}=0,\mathbf{W}=\mathbf{w}]\hfill \end{array}$$ (5.6)

then B is singular for $\mathcal{D}(\mathbf{C},\Omega )$.

Proof: By applying Proposition 4.2 to each term in (5.3).

Condition (5.6) leads directly to a statistical test of compositional epistasis. This is notable since some claims in the genetics literature appear to suggest that such tests did not exist [5].

As stated in the next corollary, from Theorem 5.5 if all or all but one of the elements of B have positive monotonic effects on D then singularity and irreducibility coincide:

Corollary 5.7. Suppose |B| = |C| and that for all or all but one of B_i ∈ B, B_i has a positive monotonic effect on D relative to B then B is singular for $\mathcal{D}(\mathbf{C},\Omega )$ i B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$.

An important consequence of this corollary is that when there is at most one variable that does not have a positive monotonic effect condition (4.4) establishes that B is singular in addition to being irreducible for $\mathcal{D}(\mathbf{C},\Omega )$.

Proof: Let B′ denote the one or zero elements of B that do not have a monotonic effect on D relative to C. If B is irreducible for $\mathcal{D}(\mathbf{C},\Omega )$ then by Theorem 4.11,

$$D_{\mathbf{B}=1}\left({\omega }^{\ast }\right)-\sum _{L\in \mathbf{B}}{D}_{\mathbf{B}\backslash \left\{L\right\}=1,L=0}\left({\omega }^{\ast }\right)+\sum _{\mathbf{E}\in \mathfrak{T}}{D}_{\mathbf{B}\backslash \mathbf{E}=1,\mathbf{E}=0}\left({\omega }^{\ast }\right)>0.$$

Since the third term on the LHS of (5.3) vanishes when |B′| ≤ 1, it follows that B is singular for $\mathcal{D}(\mathbf{C},\Omega )$. The converse is given in Corollary 5.3.

Corollary 5.8. Suppose |B| = |C| and that for all or all but one of $B_i\in \mathbf{B}\stackrel{.}{\cup }{\mathbf{C}}^{\prime }$, B_i has a positive monotonic effect on D relative to B ∪ C, for all X′ ∈ C′, X′ is not causally influenced by C and B is singular for $\mathcal{D}(\mathbf{C},\Omega )$ then B is singular for $\mathcal{D}(\mathbf{C}\cup {\mathbf{C}}^{\prime },\Omega )$.

Proof: By Corollary 5.7, B is irreducible relative to $\mathcal{D}(\mathbf{C},\Omega )$. Hence by Corollary 3.8 B is singular relative to $\mathcal{D}(\mathbf{C}\cup {\mathbf{C}}^{\prime },\Omega )$. The conclusion then follows from a further application of Corollary 5.7.

5.1. Relation to Pearl’s Probability of Causation

Pearl [16, chapter 9] defined the probability of necessity and sufficiency (PNS) of cause X for outcome D to be P (D_X=1(ω) = 1, D_X=0(ω) = 0). In other words PNS(D, X) is the probability that D would occur if X occurred and would not have done so had X not occurred. We generalize this to the setting in which there are multiple causes B:

Definition 5.9. For $\mathbf{B}\subseteq \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, the probability of necessity and sufficiency of B causing D, is:

$$\mathrm{PNS}(D,\mathbf{B})\equiv P(D_{\mathbf{B}=1}=1andforall\mathbf{b}\ne 1,D_{\mathbf{B}=\mathbf{b}}=0).$$

Thus PNS(D, B) is the probability that D would occur if every literal L ∈ B occurred and would not have done so had at least one literal in B not occurred.

Proposition 5.10. If |B| = |C| then PNS(D, B) > 0 i B is singular for $\mathcal{D}(\mathbf{C},\Omega )$.

Proof: Follows directly from Theorem 5.4 and Definition 5.9.

This connection also provides an interpretation for condition (5.6).

Proposition 5.11. Under the conditions of Corollary 5.6, with W = ∅ = B₊ PNS(B, D) is bounded below by the RHS of (5.6).

Proof:

$$\begin{array}{cc}\hfill \mathrm{PNS}(D,\mathbf{B})& =P(D_{\mathbf{B}=1}=1andforall\mathbf{b}\ne 1,D_{\mathbf{B}=\mathbf{b}}=0)\hfill \\ \hfill & \ge P(D_{\mathbf{B}=1}=1)+P(forall\mathbf{b}\ne 1,D_{\mathbf{B}=\mathbf{b}}=0)-1\hfill \\ \hfill & =P(D_{\mathbf{B}=1}=1)-P(forsome\mathbf{b}\ne 1,D_{\mathbf{B}=\mathbf{b}}=1)\hfill \\ \hfill & \ge P(D_{\mathbf{B}=1}=1)-\sum _{\mathbf{b}\ne 1}P(D_{\mathbf{B}=\mathbf{b}}=1)\hfill \\ \hfill & =E[D=1\mid \mathbf{B}=1]-\sum _{\mathbf{b}\ne 1}E[D\mid \mathbf{B}=\mathbf{b}]\hfill \end{array}$$

which is the RHS of (5.6) with W = ∅ = B₊.

This generalizes some of the lower bounds on PNS(D, X) given by Pearl [16, §9.2]. The assumption in Proposition 5.11 that B and D are unconfounded, so W = ∅, and the absence of monotonicity assumptions so B₊ = ∅, are for expositional convenience.

6. Relation to Statistical Models with Linear Links

In related work [32] it is noted that the presence of interaction terms in statistical models do not in general correspond to sufficient conditions for irreducibility. Consider for example a saturated Bernoulli regression model for D with identity link and binary regressors C = {X₁, …, X_p}:

$$E[D\mid \mathbf{C}=\mathbf{c}]=\sum _{\tilde{\mathbf{B}}\subseteq \mathbf{C}}{\beta }_{\tilde{\mathbf{B}}}{(\bigwedge (\tilde{\mathbf{B}}\left)\right)}_{\mathbf{c}}.$$ (6.1)

Note that with c = (x₁, …, x_p) then ${(\bigwedge (\tilde{\mathbf{B}}\left)\right)}_{\mathbf{c}}={\Pi }_{X_i\in \tilde{\mathbf{B}}}{x}_i$, the usual multiplicative interaction term. The conditions, given earlier, for detecting the presence of irreducibility and singularity lead to linear restrictions on the regression coefficients ${\beta }_{\tilde{\mathbf{B}}}$:

$$\sum _{\tilde{\mathbf{B}}\subseteq \mathbf{C}}{m}_{\tilde{\mathbf{B}}}{\beta }_{\tilde{\mathbf{B}}}>0.$$ (6.2)

Note that (6.2) includes an intercept β_∅. First we define

$${\mathrm{deg}}_{\mathfrak{T}}\left(L\right)\equiv \{\mathbf{E}\mid \mathbf{E}\in \mathfrak{T},L\in \mathbf{E}\},$$

the degree of L in a tree $\mathfrak{T}$, to be the number of edges in $\mathfrak{T}$ that contain L.

Proposition 6.1. Under the conditions of Theorem 4.11, with B = C, condition (4.3) is equivalent to restriction (6.2) with $m_{\tilde{\mathbf{B}}}=m_{\tilde{\mathbf{B}}}^{\mathrm{irred}}$ where:

$$m_{\tilde{\mathbf{B}}}^{\mathrm{irred}}\equiv 1-\mid \mathbf{B}\backslash \tilde{\mathbf{B}}\mid +\mid \mathfrak{T}\mid -\sum _{L\in \tilde{\mathbf{B}}\cap {\mathbf{B}}_{+}}{\mathrm{deg}}_{\mathfrak{T}}\left(L\right)+\mid \{\mathbf{E}\mid \mathbf{E}\in \mathfrak{T},\mathbf{E}\subseteq \tilde{\mathbf{B}}\cap {\mathbf{B}}_{+}\}\mid .$$ (6.3)

Note that since $\mathfrak{T}$ is a tree on B₊, the last term in (6.3) has a natural graphical interpretation as the number of edges in the ‘induced subgraph’ of $\mathfrak{T}$ on the subset $\tilde{\mathbf{B}}$. Definition (6.3) also subsumes condition (4.2) given in Theorem 4.3 (without monotonicity), in which case the last three terms in (6.3) vanish. Though Proposition 6.1 assumes that C₂ = ∅, the condition given by (6.2) and (6.3) continues to apply in the case where c₂ = 0 as in Corollaries 4.14 and 4.15; obvious extensions apply to the case where c₂ ≠ 0.

Proof: This follows by counting the number (and sign) of expectations in (4.3) for which $\tilde{\mathbf{B}}$ is a subset of the variables assigned the value 1 in the conditioning event. The first two terms in (4.3) correspond, respectively, to the first two terms in (6.3). The remaining three terms in (6.3) correspond to the last sum in (4.3): |$\mathfrak{T}$|, the number of edges in $\mathfrak{T}$, is the total number of terms in the sum. The sum over degrees subtracts the number of terms in which some $L\in \tilde{\mathbf{B}}$ is assigned zero. Since this double counts terms corresponding to edges contained in $\tilde{\mathbf{B}}$, the last term corrects for this.

Proposition 6.2. Under the conditions of Theorem 5.5, with B = C, condition (5.3) is equivalent to restriction (6.2) with $m_{\tilde{\mathbf{B}}}=m_{\tilde{\mathbf{B}}}^{\mathrm{sing}}$ where:

$$m_{\tilde{\mathbf{B}}}^{\mathrm{sing}}\equiv m_{\tilde{\mathbf{B}}}^{\mathrm{irred}}+(\mid {\mathbf{B}}^{\prime }\backslash \tilde{\mathbf{B}}\mid )-(2^{\mid {\mathbf{B}}^{\prime }\backslash \tilde{\mathbf{B}}\mid }-1).$$ (6.4)

Proof: Expression (6.4) follows from another counting argument similar to the proof of Proposition 6.1, together with the observation that conditions (4.3) and (5.3) only differ in that the terms in the sum over L in (4.3) for L ∈ B′ are replaced by a sum over all subsets of B′.

Example 4 (Two-way interactions). Consider the saturated Bernoulli regression with with identity link with C = {X₁, X₂}:

$$E[D\mid X_1=x_1,X_2=x_2]={\beta }_{\varnothing }+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_{12}{x}_1{x}_2.$$

Suppose that X₁ and X₂ are unconfounded with respect to D, so (4.1) holds with W = ∅. Proposition 6.1 implies that {X₁, X₂} is irreducible relative to C if β₁₂ > β_∅; Proposition 6.2 implies that {X₁, X₂} is singular relative to C if ₁₂ > 2 _∅. If one of X₁ or X₂ have positive monotonic effects on D relative to C then Proposition 6.1 and Corollary 5.7 imply that {X₁, X₂} is both irreducible and singular relative to C if β₁₂ > β_∅ If X₁ and X₂ have positive monotonic effects on D relative to C then Proposition 6.1 and Corollary 5.7 imply that {X₁, X₂} is both irreducible and singular relative to C if β₁₂ > 0.

Thus only under the assumption of positive monotonic effects for both X₁ and X₂ does the sufficient condition for the irreducibility and singularity of {X₁, X₂} coincide with the classical two-way interaction term β₁₂ being positive.

It also follows from Proposition 3.4 that if {X₁, X₂} is irreducible relative to C then there exists some ω ∈ for whom {X₁, X₂} is a minimal sufficient cause relative to C (since |B| = |C|).

Example 5 (Three-way interactions). The saturated Bernoulli regression with three binary variables and a identity link can be written as:

$$E[D=1\mid X_1=x_1,X_2=x_2,X_3=x_3]={\beta }_{\varnothing }+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_3+{\beta }_{12}{x}_1{x}_2+{\beta }_{13}{x}_1{x}_3+{\beta }_{23}{x}_2{x}_3+x_{123}{x}_1{x}_2{x}_2.$$

Suppose that C = {X₁, X₂, X₃} is unconfounded for D. Proposition 6.1 implies that {X₁, X₂, X₃} is irreducible relative to C if

$${\beta }_{123}>2{\beta }_{\varnothing }+{\beta }_1+{\beta }_2+{\beta }_3.$$ (6.5)

It follows from Proposition 3.4 that if {X₁, X₂, X₃} is irreducible relative to C then there exists some ω ∈ Ω for whom {X₁, X₂, X₃} is a minimal sufficient cause relative to C (since |B| = |C|).

Proposition 6.2 implies {X₁, X₂, X₃} is singular relative to C if

$${\beta }_{123}>6{\beta }_{\varnothing }+2{\beta }_1+2{\beta }_2+2{\beta }_3.$$

However, if X₁, X₂ and X₃ have positive monotonic effects on D (relative to C) then Proposition 6.1 implies {X₁, X₂, X₃} is irreducible relative to C if any of the following hold:

$${\beta }_{123}>{\beta }_1,{\beta }_{123}>{\beta }_2,{\beta }_{123}>{\beta }_3;$$ (6.6)

equivalently, β₁₂₃ > min{β₁, β₂, β₃}. By Corollary 5.7 this also establishes that {X₁, X₂, X₃} is singular relative to C.

If only X₁ and X₂ have positive monotonic effects on D relative to C then Proposition 6.1 implies that {X₁, X₂, X₃} is irreducible relative to C if

$${\beta }_{123}>{\beta }_{\varnothing }+{\beta }_1+{\beta }_2.$$ (6.7)

By Corollary 5.7 condition (6.7) also implies that {X₁, X₂, X₃} is singular relative to C (since only X₃ does not have a positive monotonic effect on D). As we would expect condition (6.7) is weaker than (6.5) but stronger than any of the conditions (6.6). If only one potential cause has a monotonic effect on D relative to C then we can only use (6.5) to establish irreducibility.

Thus for three-way interactions β₁₂₃ > 0 does not correspond to any of the sufficient conditions for irreducibility or singularity of {X₁, X₂, X₃} relative to C, regardless of whether or not monotonicity assumptions hold.

7. Interpretation of sufficient cause models

As mentioned in §2.1 the observed data for an individual (C(ω), D(ω)) represents a strict subset of the potential outcomes $\mathcal{D}(\mathbf{C},\omega )$; this is the ‘fundamental problem of causal inference’. Further, as we have seen, for a given set of potential outcomes there can exist different determinative sets of minimal sufficient causes B for the same set of potential outcomes; see (2.3) and (2.4). Thus we have the following for an individual:

$$\begin{array}{ccccc}\hfill ⋮\hfill & \hfill \searrow \hfill & \hfill ⋮\hfill & \hfill \searrow \hfill & \hfill \hfill \\ \hfill \mathfrak{B}\hfill & \hfill \to \hfill & \hfill \mathcal{D}(\mathbf{C},\omega )\hfill & \hfill \to \hfill & \hfill \left(\mathbf{C}\right(\omega ),D(\omega \left)\right).\hfill \\ \hfill ⋮\hfill & \hfill \nearrow \hfill & \hfill ⋮\hfill & \hfill \nearrow \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \text{many-one}\hfill & \hfill \hfill & \hfill \text{many-one}\hfill & \hfill \hfill \end{array}$$ (7.1)

It is typically impossible to know the set of potential outcomes for an individual $\mathcal{D}(\mathbf{C},\omega )$, even when C = {X}, even from randomized experiments. However possession of this knowledge would permit one to predict how a given individual would respond under any given pattern of exposures C = c.

The results in this paper demonstrate that, given data from a randomized experiment (or when sufficient variables are measured to adjust for confounding) it is possible to infer the existence of an individual for whom all sets of minimal sufficient causes $\mathfrak{B}$ have certain features in common. However, given the double many-one relationship (7.1), and the fact that the set of potential outcomes $\mathcal{D}(\mathbf{C},\omega )$, if they were known, apparently address all potential counterfactual queries, it is natural to ask what is to be gained by considering such representations. We now motivate our results by presenting several different interpretations of sufficient cause representations.

7.1. The descriptive interpretation

Under this view sets of minimal sufficient causes are merely a way to describe the set of potential outcomes $\mathcal{D}(\mathbf{C},\Omega )$. The representation (A, $\mathfrak{B}$) may be more compact; compare Table 2 and (2.5). Extending this to a population Ω, the variables A in a representation (A, $\mathfrak{B}$) merely describe subpopulations with particular patterns of potential outcomes. Knowing that there exists an individual for whom all representations $\mathfrak{B}$ have certain features in common provides qualitative information about the set of potential outcomes.

For two binary causes {X₁, X₂}, Theorem 3.2 implies that {X₁, X₂} is irreducible relative to C for ω* if D₁₁(ω*) = 1 and D₁₀(ω*) = D₀₁(ω*) = 0. Such a pattern is of interest insofar as it indicates that the causal process resulting in this individual’s potential outcomes D(C, ω*) is such that (for some setting of the variables in C \ {X₁, X₂}), D = 1 if both X₁ = 1 and X₂ = 1, but not when X₁ = 1 and X₂ = 0 or vice versa.

Similarly it follows from Theorem 5.2 that if {X₁, X₂} is singular relative to C for ω* if D₁₁(ω*) = 1 and D₁₀(ω*) = D₀₁(ω*) = D₀₀(ω*) = 0. Hence the causal process producing $\mathcal{D}(\mathbf{C},{\omega }^{\ast })$ is such that, for some setting of the variables in C \ {X₁, X₂}, D = 1 if both X₁ = 1 and X₂ = 1, but not when either X₁ = 0 or X₂ = 0.

In contrast to the classical notions of interaction arising in linear models (see §6), irreducibility and singularity are causal in that they relate to the potential outcomes. §4 and §5 contain empirical tests for the presence of irreducible or singular interactions.

7.2. Generative mechanism interpretations

A minimal sufficient cause representation may be interpreted in terms of a ‘generative mechanism’:

Definition 7.1. A mechanism M(ω) relative to C takes as input an assignment c to C, and outputs a ‘state’ M_c(ω) which is either ‘active’ (1) or ‘inactive’ (0). A mechanism is said to be generative for D if whenever it is active, the event D = 1 is caused, so that M_c(ω) = 1 implies D_c(ω) = 1. Conversely, a mechanism is said to be preventive for D if whenever M_c(ω) = 1, D_c(ω) = 0 is caused.

Though this definition refers to a mechanism ‘causing’ D = 1 or D = 0, we abstain from defining this more formally in terms of potential outcomes until the next section. Our reason for proceeding in this way is that there may be circumstances in which an investigator is able to posit the existence of a causal mechanism causing D = 1 or D = 0, e.g. based on experiments manipulating the inputs C and output D, but lacks sufficiently detailed information to posit well-defined counterfactual outcomes involving interventions on these (hypothesized) mechanisms.

Definition 7.2. A set of generative mechanisms M = 〈M¹, …, M^p〉 will be said to be exhaustive for a given set of potential outcomes $\mathcal{D}(\mathbf{C},\Omega )$ if for all ω ∈ Ω, and all c, if D_c(ω) = 1 then for some Mⁱ ∈ M, $M_{\mathbf{c}}^i\left(\omega \right)=1$.

Note that if M forms an exhaustive set of mechanisms for $\mathcal{D}(\mathbf{C},\Omega )$, then it follows that in a context in which no mechanism Mⁱ is active, D = 0.

Proposition 7.3. If M = 〈M¹, …, M^p_W〉 forms an exhaustive set of generative mechanisms for $\mathcal{D}(\mathbf{C},\Omega )$ then $\mathcal{D}=\bigvee \left(\mathbf{M}\right)$ and $D_{\mathbf{c}}\left(\omega \right)=\bigvee \left({\mathbf{M}}_{\mathbf{c}}\right(\omega \left)\right)$.

Proof: Follows Definitions 7.1 and 7.2. 2

Proposition 7.4. Suppose M forms an exhaustive set of generative mechanisms for $\mathcal{D}(\mathbf{C},\Omega )$. If $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, |B| = |C| and B is irreducible for $\mathcal{D}(\mathbf{C};\Omega )$ then there exists an individual ω* and a mechanism Mⁱ such that $M_{\mathbf{B}=1}^i\left({\omega }^{\ast }\right)=1$ but for all L ∈ B, $M_{\mathbf{B}\backslash \left\{L\right\}=1,L=0}^i\left({\omega }^{\ast }\right)=0$.

Thus if there exists an exhaustive set of generative mechanisms for $\mathcal{D}(\mathbf{C},\Omega )$ and B is irreducible then there is an individual ω* and a mechanism Mⁱ such that Mⁱ is active when all the literals in B take the value 1, and is inactive when any one literal is 0 and the rest continue to take the value 1.

Proof: By Theorem 3.2, since B is irreducible for $\mathcal{D}(\mathbf{C};\Omega )$, there exists ω* ∈ Ω such that D_B=1(ω*) = 1 and for all L ∈ B, D_B\{L}=1,L=0(ω). Since M is an exhaustive set of generative mechanisms for $\mathcal{D}(\mathbf{C},\Omega )$, we have that for all c, $D_{\mathbf{c}}\left({\omega }^{\ast }\right)=\bigvee \left({\mathbf{M}}_{\mathbf{c}}\right(\omega \left)\right)$. Since D_B=1(ω*) = 1, for some M_i ∈ M, $M_{\mathbf{B}=1}^i\left({\omega }^{\ast }\right)=1$. Since for all L ∈ B, D_B\{L}=1,L=0(ω*) = 0 we have that $M_{\mathbf{B}\backslash \left\{L\right\}=1,L=0}^i\left({\omega }^{\ast }\right)=0$.

Proposition 7.5. Suppose M forms an exhaustive set of generative mechanisms for $\mathcal{D}(\mathbf{C},\Omega )$. If $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, |B| = |C| and B is singular for $\mathcal{D}(\mathbf{C};\Omega )$ then there exists an individual ω* and a mechanism Mⁱ such that $M_{\mathbf{B}=\mathbf{b}}^i\left({\omega }^{\ast }\right)=1$ iff b = 1.

Hence under the conditions of Proposition 7.5, if B is singular then there is an individual ω* and a mechanism Mⁱ such that Mⁱ is active if and only if all the literals in B take the value 1.

Proof: Similar to the proof of Proposition 7.4, replacing Theorem 3.2 by Theorem 5.2.

As the next example shows, the assumption that there exists an exhaustive set of generative mechanisms is substantive, and does not hold in all cases.

Example 6. Suppose C = {X₁, X₂} where X₁ and X₂ denote the presence of a variant allele at two particular loci. Let M¹ and M² denote two different proteins such that Mⁱ is produced iff X_i = 0, i.e. the associated allele is not present. Finally let D denote some characteristic whose occurrence is blocked by the presence of either M¹ or M² (or both). In this example

$$\begin{array}{cc}\hfill M_{x_1{x}_2}^i\left(\omega \right)& =(1-x_i)\hfill \\ \hfill D_{x_1{x}_2}\left(\omega \right)& =(1-M_{x_1{x}_2}^1)\vee (1-M_{x_1{x}_2}^2)=x_1{x}_2.\hfill \end{array}$$

By De Morgan’s Law, the second equation here may also be expressed as:

$$1-D_{x_1{x}_2}\left(\omega \right)=M_{x_1{x}_2}^1\left(\omega \right)M_{x_1{x}_2}^2\left(\omega \right)=1-x_1{x}_2.$$

The mechanisms M¹ and M² are preventive for D, so that D = 1 only occurs when both mechanisms are inactive. An exhaustive set of generative mechanisms does not exist because in this example there are no generative mechanisms.

It is natural to suppose that mechanisms are ‘modular’ and thus may be isolated or rendered inactive without affecting other such mechanisms. This may be formalized via potential outcomes:

Definition 7.6. An exhaustive set of generative mechanisms M for $\mathcal{D}(\mathbf{C},\Omega )$ are said to support counterfactuals if there exist well-defined potential outcomes D_C=c,M=m(ω) and D_M=m(ω) such that

$$D_{\mathbf{C}=\mathbf{c},\mathbf{M}=\mathbf{m}}\left(\omega \right)=D_{\mathbf{M}=\mathbf{m}}\left(\omega \right)={(\bigvee (\mathbf{M}\left)\right)}_{\mathbf{m}}.$$

The important assumption here is the existence of the potential outcomes D_m(ω) and D_c,m(ω). Note that if M supports counterfactuals then interventions on C do not affect D if interventions are also made on M.

Proposition 7.7. If the exhaustive set of generative mechanisms M support counterfactuals then

$$D_{\mathbf{M}=\mathbf{M}\left(\omega \right)}\left(\omega \right)=D_{\mathbf{C}=\mathbf{C}\left(\omega \right),\mathbf{M}=\mathbf{M}\left(\omega \right)}\left(\omega \right)=D\left(\omega \right)$$

so that consistency holds for the potential outcomes D_m(ω) and D_c,m(ω).

Proof: This follows because

$$D_{\mathbf{C}=\mathbf{C}\left(\omega \right),\mathbf{M}=\mathbf{M}\left(\omega \right)}\left(\omega \right)=D_{\mathbf{M}=\mathbf{M}\left(\omega \right)}\left(\omega \right)=\bigvee \left(\mathbf{M}\right(\omega \left)\right)=D\left(\omega \right).$$

7.3. Counterfactual interpretation of a minimal sufficient cause representation

If we have an exhaustive set of generative mechanisms which supports counterfactuals, and further each mechanism is a conjunction of literals, then there will be a minimal sufficient cause representation that itself supports counterfactuals.

Definition 7.8. A representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$ will be said to be structural if for each pair (A_i, B_i), A_i ∈ A, ${\mathbf{B}}_i\in \mathfrak{B}$ there exists a generative mechanism (or mechanisms) Mⁱ such that Mⁱ = A_i ∧ (Λ(B_i)) and

$${M^i}_{\mathbf{C}=\mathbf{c}}\left(\omega \right)=A_i\left(\omega \right)\wedge {(\bigwedge ({\mathbf{B}}_i\left)\right)}_{\mathbf{c}}.$$

Thus if (A, $\mathfrak{B}$) is structural then each pair (A_i, B_i), A_i ∈ A, ${\mathbf{B}}_i\in \mathfrak{B}$ corresponds to a mechanism Mⁱ. Thus in this case the variables A_i(ω) may be interpreted as indicating whether the corresponding mechanism(s) Mⁱ is ‘present’ in individual ω. We may thus associate potential outcomes with the A_i, corresponding to removing (or inserting) the corresponding mechanism(s). This interpretation of the A_i’s is consistent with the notion of ‘co-cause’ which arises in the literature on minimal sufficient causes.

We note that ‘structural’ is often used as a synonym for ‘causal’. However, even under the weak interpretation, a sufficient cause representation is causal in that it represents a set of potential outcomes. The word is used in Definition 7.8 to connote that the structure of the representation itself represents (additional) potential outcomes arising from intervention on a set of mechanisms M that correspond with the pairs (A_i, B_i), A_i ∈ A, ${\mathbf{B}}_i\in \mathfrak{B}$. Note that there need not be a unique structural representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$. There might be several functionally equivalent generative mechanisms corresponding to a given pair (A_i, B_i).

Proposition 7.9. If a representation (A, $\mathfrak{B}$) for $\mathcal{D}(\mathbf{C},\Omega )$, where A = 〈A₁, …, A_p〉, is structural then the associated set of generative mechanisms 〈M¹, …, M^p〉 is exhaustive.

Proof: This follows from Definitions 2.7 and 7.2. 2.

Proposition 7.10. Suppose that M forms an exhaustive set of generative mechanisms for $\mathcal{D}(\mathbf{C},\Omega )$ and M supports counterfactuals. If for all Mⁱ ∈ M there exists ${\mathbf{B}}_i\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$, and an A_i such that for all c, and ω ∈ Ω, if A_i(ω) = 1 then (Mⁱ)_c(ω) = Λ(B_i)_c, then (A = 〈A₁, …, A_p〉, $\mathfrak{B}=\langle {\mathbf{B}}_1,\dots ,{\mathbf{B}}_p\rangle$) forms a representation for $\mathcal{D}(\mathbf{C},\Omega )$ that is structural.

Proof: This follows from Definitions 2.7 and 7.8.

Proposition 7.11. If there is some representation (A, $\mathfrak{B}$) that is structural and $\mathbf{B}\in \stackrel{.}{\mathbb{P}}\left(𝕃\right(\mathbf{C}\left)\right)$ is irreducible for $\mathcal{D}(\mathbf{C};\Omega )$ then there exists a mechanism M_i that is active only if B = 1.

Proof: If B is irreducible for $\mathcal{D}(\mathbf{C};\Omega )$ then there exists ${\mathbf{B}}_i\in \mathfrak{B}$ with $\mathbf{B}\subseteq {\mathbf{B}}_i$; the mechanism Mⁱ = A_i ∧ (Λ(B_i)) is such that Mⁱ = 1 only if B = 1.

Note that the conclusion of Proposition 7.11, unlike those of Propositions 7.4 and 7.5, does not make reference to an individual ω*. This is because Proposition 7.11 assumes that there is a representation (A, $\mathfrak{B}$) that is structural: in this representation the A_i variables may be seen as a constituent part of the corresponding mechanism M_i.

Note that there may exist a set of exhaustive generative mechanisms, but these mechanisms may not themselves be conjunction of literals so that there is no sufficient cause representation for $\mathcal{D}(\mathbf{C};\Omega )$ that is structural:

Example 7. Suppose C = {X₁, X₂} where X₁ and X₂ again denote the presence of variant alleles, acquired by maternal and paternal inheritance respectively, at a particular locus. Let M denote a protein that is produced iff either X₁ = X₂ = 1 or X₁ = X₂ = 0 and let D denote some characteristic that occurs iff M = 1. Suppose we can intervene to remove or add the protein. We then have that

$$\begin{array}{cc}\hfill M_{x_1{x}_2}\left(\omega \right)& =x_1{x}_2\vee (1-x_1)(1-x_2)\hfill \\ \hfill D_{x_1{x}_2}\left(\omega \right)& =M_{x_1{x}_2}\left(\omega \right)\hfill \\ \hfill D_{x_1{x}_{2}m}\left(\omega \right)=D_m\left(\omega \right)& =m.\hfill \end{array}$$

Thus {M} constitutes an exhaustive set of generative mechanisms for $\mathcal{D}(\mathbf{C},\Omega )$. We have a representation for $\mathcal{D}(\mathbf{C},\Omega )$:

$$D_{x_1{x}_2}\left(\omega \right)={\left(A_1\right(\omega )X_1{X}_2\vee A_2(\omega \left)\right(1-X_1\left)\right(1-X_2\left)\right)}_{x_1{x}_2}$$

with A₁(ω) = A₂(ω) = 1 for all ω ∈. However, this representation is not structural because A₁(ω)X₁X₂ and A₂(ω)(1−X₁)(1−X₂) do not constitute separate mechanisms for which interventions are conceivable; there is only one mechanism M, the protein. Since for anyω ∈, D₁₁(ω) = 1 and D₁₀(ω) = D₀₁(ω) = 0, {X₁, X₂} is irreducible relative to C; however it is not the case that there is a mechanism M_i that is active only if X₁X₂ = 1 since for the only mechanism M it is the case that M = 1 if X₁ = X₂ = 0. Note, however, in this example there is still a mechanism, namely M, that will be ‘active’ if X₁ = X₂ = 1 but will be ‘inactive’ if only one of X₁ or X₂ is 1.

Example 8. To illustrate the results in the paper we consider again the data presented in Table 1. We let D denote bladder cancer, X₁ smoking, X₂ the S NAT2 genotype, and X₃ the *10 allele on NAT1. As discussed in Example 5, if the effect of C = {X₁, X₂, X₃} is unconfounded for D and and we fit the model

$$E[D=1\mid X_1=x_1,X_2=x_2,X_3=x_3]={\beta }_{\varnothing }+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_3+{\beta }_{12}{x}_1{x}_2+{\beta }_{13}{x}_1{x}_3+{\beta }_{23}{x}_2{x}_3+{\beta }_{123}{x}_1{x}_2{x}_2$$ (7.2)

then if X₁, X₂ and X₃ have positive monotonic effects on D (relative to C) then {X₁, X₂, X₃} is irreducible relative to C if any of the following hold:

$${\beta }_{123}>{\beta }_1,{\beta }_{123}>{\beta }_2,{\beta }_{123}>{\beta }_3.$$

We cannot fit the model (7.2) directly with case control data. However, under the assumption that the outcome is rare (reasonable with bladder cancer) so that odds ratios approximate risk ratios, we can fit the model:

$$E[D=1\mid X_1=x_1,X_2=x_2,X_3=x_3]∕E[D=1\mid X_1=0,X_2=0,X_3=0]={\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+{\theta }_{12}{x}_1{x}_2+{\theta }_{13}{x}_1{x}_3+{\theta }_{23}{x}_2{x}_3+{\theta }_{123}{x}_1{x}_2{x}_2$$ (7.3)

and the conditions for the irreducibility of {X₁, X₂, X₃} relative to C under monotonicity of {X₁, X₂, X₃} become:

$${\theta }_{123}>{\theta }_1,{\theta }_{123}>{\theta }_2,{\theta }_{123}>{\theta }_3.$$

If we fit model (7.3) using maximum likelihood, we find that

$$\begin{array}{cc}\hfill {\theta }_{123}-{\theta }_1& =1.21(9.5\%\mathrm{CI}:-3.83,6.26),\hfill \\ \hfill {\theta }_{123}-{\theta }_2& =2.93(9.5\%\mathrm{CI}:-2.85,8.72),\hfill \\ \hfill {\theta }_{123}-{\theta }_3& =2.97(9.5\%\mathrm{CI}:-2.80,8.74).\hfill \end{array}$$

In each case the point estimate suggests evidence of irreducibility, under monotonicity of {X₁, X₂, X₃}, but the sample size is not sufficiently large to draw this conclusion confidently. With monotonicity of {X₁, X₂, X₃}, irreducibility also implies a singular interaction for {X₁, X₂, X₃}. If we assume that only {X₁, X₂} or {X₁, X₃} or {X₂, X₃} are monotonic relative to C then the conditions for irreducibility in Example 5 can be expressed respectively as:

$${\theta }_{123}>1+{\theta }_1+{\theta }_2,{\theta }_{123}>1+{\theta }_1+{\theta }_3,{\theta }_{123}>1+{\theta }_2+{\theta }_3.$$

From model (7.3) we have that

$$\begin{array}{cc}\hfill {\theta }_{123}-(1+{\theta }_1+{\theta }_2)& =0.09(9.5\%\mathrm{CI}:-4.77,4.96),\hfill \\ \hfill {\theta }_{123}-(1+{\theta }_1+{\theta }_3)& =0.13(9.5\%\mathrm{CI}:-4.69,4.95),\hfill \\ \hfill {\theta }_{123}-(1+{\theta }_2+{\theta }_3)& =1.86(9.5\%\mathrm{CI}:-3.41,7.12).\hfill \end{array}$$

Again, in each case the point estimate suggests evidence of irreducibility, under monotonicity of just two of the three exposures, but the sample size is not sufficiently large to draw this conclusion confidently. With monotonicity of two of the three exposures, irreducibility also implies a singular interaction for {X₁, X₂, X₃}. The test for irreducibility in Example 5 without assumptions about monotonicity can be expressed as:

$${\theta }_{123}>2+{\theta }_1+{\theta }_2+{\theta }_3.$$

From model (7.3) we have that

$${\theta }_{123}-(2+{\theta }_1+{\theta }_2+{\theta }_3)=-0.99(95\%\mathrm{CI}:-5.86,3.88).$$

In this case, not even the point estimate is positive.

If {X₁, X₂, X₃} is in fact irreducible and if there exists a representation that is structural then it follows by Proportion 7.11 that there exists a mechanism that is active only if X₁ = 1, X₂ = 1, X₃ = 1.

8. Concluding Remarks

In this paper we have developed general results for notions of interaction that we referred to as ‘irreducibility’ (aka ‘a sufficient cause interaction’) and ‘singularity’ for sufficient cause models with an arbitrary number of dichotomous causes. The theory could be extended by developing notions of sufficient cause, irreducibility and singularity for causes and outcomes that are categorical and/or ordinal in nature.