An Augmented Two-Layer Model Captures Nonlinear Analog Spatial Integration Effects in Pyramidal Neuron Dendrites

Abstract

In pursuit of the goal to understand and eventually reproduce the diverse functions of the brain, a key challenge lies in reverse engineering the peculiar biology-based “technology” that underlies the brain’s remarkable ability to process and store information. The basic building block of the nervous system is the nerve cell, or “neuron,” yet after more than 100 years of neurophysiological study and 60 years of modeling, the information processing functions of individual neurons, and the parameters that allow them to engage in so many different types of computation (sensory, motor, mnemonic, executive, etc.) remain poorly understood. In this paper, we review both historical and recent findings that have led to our current understanding of the analog spatial processing capabilities of dendrites, the major input structures of neurons, with a focus on the principal cell type of the neocortex and hippocampus, the pyramidal neuron (PN). We encapsulate our current understanding of PN dendritic integration in an abstract layered model whose spatially sensitive branch-subunits compute multidimensional sigmoidal functions. Unlike the 1-D sigmoids found in conventional neural network models, multidimensional sigmoids allow the cell to implement a rich spectrum of nonlinear modulation effects directly within their dendritic trees.

I. INTRODUCTION

Whether the goal is a scientific one—to understand the computing functions of neural tissue, or an engineering one—to imitate some aspect of brain function using neuromorphic technology, it is crucial to develop simplified models of individual neurons that concisely describe their computing functions, while abstracting away nonessential biological details. The cost of not having good single-neuron models is potentially high: if in studying a neural circuit, the neuroscientist operates under flawed assumptions regarding the capabilities of the various neuron types that make up the circuit, he/she may fail to design appropriate experiments, encounter difficulties interpreting experimental data, and be steered away from correct conclusions as to how the circuit works. Pitfalls also await the neuroengineer who attempts to build neuromorphic hardware without a solid understanding of the computing capabilities of individual neurons: the large investment of time and money required to move through the hardware development cycle may be wasted if critical capabilities of individual neurons are omitted from the design.

In this paper, we review both the history and recent progress in our understanding of the computing functions of individual neurons, with the following limitations in scope. First, we focus on dendritic integration in the pyramidal neuron (PN), one of a multitude of neuron types in the central nervous system (CNS), but a particularly important one as it is the principal cell of the neocortex and hippocampus. Some of our conclusions will likely apply to other neuron types, while others may not. Second, we focus on spatial integration of synaptic inputs, where multiple synapses are activated in fixed spatial arrangements on one or more dendrites, and time-averaged responses are measured at the soma. Third, we focus on the principles of synaptic integration within a dendritic tree or subtree consisting of a relatively homogeneous set of dendrites emanating from a central node. In a stellate-form cell, this might correspond to the entire dendritic tree. In a PN, subtrees fitting this general description include the basal tree emanating from the soma, and tuft dendrites emanating from the main apical branch point [1]. More global interactions between subtrees are beyond the scope of this paper, but have been discussed elsewhere [2]–[11].

For previous reviews and a broad range of perspectives on the topic of dendritic inte.gration and single neuron computation, see [12]–[23].

II. THE TRADITIONAL VIEW OF THE NEURON

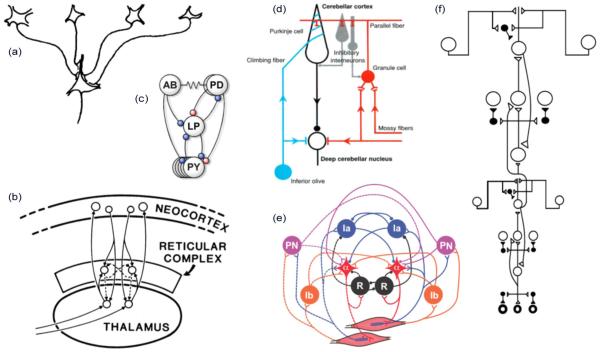
The classical view of dendritic integration in neurons of the CNS is that excitatory and inhibitory synaptic currents collected from across the dendritic arbor are funneled to the soma, where the net current determines the cell’s output firing rate. This view that dendrites exist mainly to increase a neuron’s receptive surface area, but confer no additional processing capabilities [24], [25], is in keeping with the long-running tendency to leave dendrites out of the picture in multineuron models covering virtually every part of the brain and aspect of brain function [26]–[48] (Fig. 1). The notion that dendrites are computationally superfluous has also been reinforced by the introduction of numerous dendrite-less “point neuron” models in the neural computation literature [49]–[54] (see [55] for a commentary on [49]); though it should be emphasized that the use of point neuron models may be entirely appropriate for certain questions and/or levels of analysis.

Fig. 1.

Examples of neural circuit models constructed from “point neurons” containing a single integrative node. (a) Model of a “simple” cell in visual cortex [34]. (b) “Seachlight” model of attention [56]. (c) Subset of the stomatogastric ganglion circuit [36]. (d) Cerebellar circuit [43]. (e) Spinal cord circuit [42]. (f) Circuit in visual cortex [57].

III. CHALLENGES TO THE POINT NEURON HYPOTHESIS

The key assumption in a point neuron model is that the cell has a single integrative node at the soma where all excitatory and inhibitory effects are combined. Though it continues to enjoy broad acceptance, this radically simplified view of the neuron began to face serious challenges already decades ago, both 1) from neurophysiological data indicating that dendrites are capable of generating “active” spike-like responses with varying degrees of locality and based on a variety of ionic mechanisms [1], [6], [11] (see [14] for more references from the pre-1990 literature), [58]–[82]; and 2) from biophysical studies showing that a neuron’s cable properties promote spatially restricted synaptic interactions [61], [65], [83]–[104]. Taken together, these two effects mean that a neuron is capable, in principle, of carrying out multiple local computations simultaneously within its dendritic tree. But what local computations? How many can occur simultaneously, and what are their allowable spatial arrangements in the dendritic arbor? And how are the results of the local computations combined from across the dendritic tree to determine the cell’s overall output?

IV. THERE HAVE BEEN A VARIETY OF IDEAS ABOUT DENDRITIC COMPUTATION

Early theorists proposed that dendrites might engage in a variety of local computations, and they contemplated different ways that the results of those computations might be combined at the soma. Koch et al. introduced the notion of a dendritic “subunit” [88], a subregion within the dendritic tree in which local synaptic computations can take place with relatively little interaction with other subunits. They also showed that the divisive interaction between an excitatory synapse and a shunting or “silent” inhibitory synapse (i.e., whose reversal potential is at or near the cell’s resting potential) could provide a logical and–not operation, where the inhibition acts like a local “veto” signal. They suggested that this operation, repeated in many different subunits across the dendritic tree, could provide a biophysical mechanism for direction selectivity [89], along the lines proposed by Barlow and Levick [105]. Shepherd and Brayton [100] demonstrated that voltage-dependent Na⁺ channels could implement logical and and or operations between nearby synapses, and proposed that a dendritic tree might act like a hierarchical boolean logic network [12]. Rall and Segev [98] showed that mixtures of active and passive spines could produce complicated and varied nonlinear interactions between inputs to multiple branches of a dendritic tree. Zador et al. [106] showed that a voltage-dependent K⁺ channels could produce a xor interaction between inputs delivered to two different dendritic sites. Other early models of dendritic integration included the “contextron,” a simplified neuron model in which a set of dedicated modulatory inputs enabled different dendritic subunits at different times [107]; the “sigma-pi” unit, in which the dendrites provided a set of low-order product terms between groups of synapses that were summed at the soma [108]–[110]; and the “clusteron,” a model neuron that captured the fact that dendrites containing N-methyl-D-aspartate (NMDA) and voltage-dependent Na⁺ channels exhibit the property of “cluster sensitivity,” that is, they respond more strongly to excitatory synapses activated in multiple spatial clusters in comparison to the same total amount of input delivered diffusely [67], [92]–[94], [111].

The idea that a neuron computes a sum of nonlinear terms, where each term represents the interaction between a group of nearby synaptic inputs, is more or less explicit in several of the aforementioned models. This abstraction of dendritic integration has the advantage that it is specific regarding the mathematical operations that are supposed to be taking place in the dendritic tree, but is vague regarding the constraints that exist on the spatial distribution of dendritic sites that can be simultaneously involved in these local nonlinear operations, in relation to the physical branching structure of the neuron. For example, when a distal site is synaptically activated and a local computation takes place, should the result of that computation, as it flows to the cell body, influence or not influence an ongoing computation at a more proximal site? Do the neuron’s computational subunits have soft or hard boundaries, and to what extent are the boundaries warped by branch points, the soma, etc.? Are dendritic subunits organized hierarchically, and if so, is the hierarchy shallow or deep?

V. THE TWO-LAYER MODEL

In search of a model of dendritic integration that retained the same basic sum-of-nonlinear-terms form as several earlier models, but which was more explicit about the relationship between the structure of a PN dendritic tree and the structure of the overall computation, we introduced the “two-layer model” (2LM) (Fig. 2). The 2LM incorporates several morphology-related simplifications. First, it aims to describe the behavior of only a portion of the overall dendritic arbor, specifically, a subtree consisting of a uniform set of thin dendrites emanating from a central node. Second, given that most of the excitatory synapses impinging on PN thin dendrites lie on long, unbranched terminal sections [112]–[114], we assumed that the tree consisted only of unbranched terminal dendrites. Third, given that cable theory tells us that voltage communication within a dendrite is relatively efficient whereas communication between dendrites is relatively poor [88], [97], [104], we assumed communication within a dendrite was perfect and communication between dendrites was negligible.

Fig. 2.

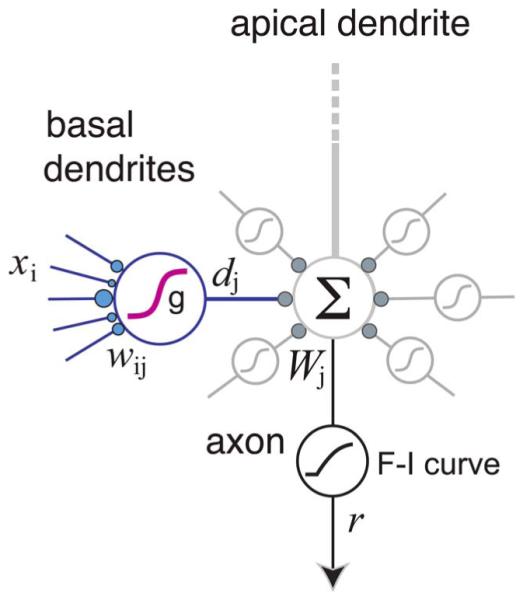
Two-layer model of a pyramidal neuron dendritic subtree. Each dendritic “subunit” computes a weighted sum of its inputs (weights are shown as blue circles), and then applies a nonlinear subunit function g(·) to produce the dendritic output d. These outputs are then summed with weights and fed into the global F–I curve to produce the neuron’s response r. A model of this form was used to predict average spike rates produced by a biophysically detailed compartmental model [96]. Depiction here is intended to suggest the basal subtree; apical oblique and apical tuft dendrites are thought to behave similarly [1], [91], though the model for the cell as a whole also involves nonlinear interactions between subtrees [6], [7], [11], [18] (see Fig. 8).

In addition to assuming that each dendrite is a separate subunit, the basic 2LM also assumed that: 1) the effect of the ith synapse onto the jth subunit is fully described by its activation rate x_i times its weight w_ij; 2) a subunit’s input–output (I–O) function is a linear–nonlinear (LN) cascade, first combining its synaptic inputs linearly followed by a stereotyped nonlinear subunit function g(·); 3) the dendritic output “currents” d_j are summed at the soma with branch weights W_j; and 4) the total somatic current is fed into the axo-somatic F–I curve to determine the cell’s output firing rate r (Fig. 2).

All of these features of the basic 2LM are captured by

$$d_j=g\left(\sum _i{w}_{ij}{x}_i\right)$$ (1)

$$r=\mathrm{F}-\mathrm{I}\left(\sum _j{W}_j{d}_j\right).$$ (2)

Besides providing a simple model of dendritic integration, this scheme brought three additional advantages. First, the 2LM is isomorphic to a feedforward artificial neural network (ANN), with the dendrites providing a layer of nonlinear computing subunits (also knows as codons, conjunctions, basis functions, hidden units, higher order features, etc.) interposed between the inputs and the output. This isomorphism allows the theory of ANNs, including their learning rules and their various uses as classifiers, function approximators, density estimators, etc., to be brought to bear in the effort to understand how individual neurons contribute to neural circuit function [115]. Second, the idea that a neuron pools the outputs of a set of discrete LN subunits suggests a connection between dendritic form/function and neurophysiological data: the receptive fields (RFs) of sensory neurons have frequently been described as having a two-layer sum-of-subunits structure. Most notably, the receptive fields of V1 “complex cells” are typically modeled as a sum of multiple “simple cell” subunits [34], [116]–[118]. A similar scheme involving the pooling of subunits is thought to account for the increasing spatial invariance of receptive fields along the visual cortical form processing pathway [119]–[123], raising the possibility that dendritic subunits are the physical substrate for a neuron’s functional subunits [83], [85], [88], [91], [124]–[135]. Third, the partitioning of the dendritic tree into discrete integrative units of a specific size facilitates the analysis of memory or processing capacity [130], [136]–[138].

VI. SUPPORT FOR THE TWO-LAYER MODEL

A. Modeling Studies

Given the technical difficulties associated with stimulating real neurons at multiple precisely defined locations and maintaining the health of neurons while recording their responses to large stimulus sets, the first direct support for the 2LM came from computer simulations. In these studies, a biophysically detailed compartmental model was used as a surrogate for a real neuron, and its responses were compared to the predictions of an abstract 2LM over a systematically constructed stimulus set. The logic of this model-to-model comparison strategy is as follows: if the responses of a very complicated, realistic compartmental model, whose evaluation involves numerical integration of thousands of coupled nonlinear differential equations, can be predicted by a model that is so simple that it can be evaluated by hand, then to the extent that the detailed model is a faithful representation of a real neuron, and the stimulus set is a faithful representation of the relevant stimulus space, then the simple model is a useful abstraction of the real neuron’s integrative capabilities. Furthermore, the ways in which the simple model fails to capture the complex model’s behavior can provide valuable clues as to the deficiencies in one or both of the models, or the stimulus set, or the response measure, or all of the above. For example, the detailed model might lack ionic currents crucial for a behavior of interest, or the ion channels that are included might be inappropriately distributed or incorrectly parameterized. The stimulus set used to test the models might be too simple, like testing the performance of a scientific calculator only on problems involving single-digit arithmetic, or functionally inappropriate, like testing the ability to play tennis with a bow and arrow. Even if the task is appropriate, the response measure might be off base, like assessing the quality of a musician’s recorded performance using the video track rather than the sound track. The simple model may also be deficient, either by including invalid simplifications, or by leaving out valid ones. Thus, the model-to-model comparison process is not only a means of testing ideas about single-neuron function and the biophysical basis thereof, but has the added advantage that it produces information useful for improving both the realistic and abstract models.

Several studies have proceeded using this approach. Archie and Mel [83] showed using a compartmental model that a dendritic tree containing four basal dendrites emanating from the soma—a “ball and sticks” morphology—produced firing rates that were more consistent with the predictions of a 2LM with an accelerating subunit function than of a point neuron. Moreover, the model cell captured the response nonlinearities of V1 complex cells whose receptive fields had been previously described by a two-layer “energy” model [117], [139]. However, given the simplified dendritic morphology and stimulus set used in the study, and the lack of a quantitative assessment of prediction performance under different 2LM assumptions, the strength of the conclusions that could be drawn from that study was limited. A more demanding test of the 2LM was carried out using a more biophysically realistic compartmental model of a CA1 pyramidal cell, using a larger, more complex stimulus set [96]. We found the 2LM with a sigmoidal subunit function outperformed the other variants tested, and explained 67% of the firing rate variance that could be attributed to variations in the spatial distribution of synaptic inputs—compared to 11% for a point neuron model.

This test of the 2LM was also lacking, however, in that the simulation experiments did not control for within-branch spatial variations, made no allowance for dendrite-specific subunit nonlinearities, and could not distinguish direct voltage-dependent interactions between dendrites in the first layer from nonlinear interactions occurring in the second layer arising from the cell’s axo-somatic F–I curve. Lacking these controls, it was not possible to decide whether the substantial fraction (33%) of unexplained firing rate variance seen in this study was due to either a fundamental breakdown of the 2LM’s core assumption of subunit independence, versus an inadequate representation of the subunit and somatic nonlinearities. In a recent follow-up study, we found that when the nonlinear dendritic I–O functions are properly characterized in terms of the steady state currents they produce, and the somatic F–I curve is properly taken into account, the two core assumptions of the 2LM—that 1) synaptic integration occurs independently in different subunits, and 2) subunit outputs combine linearly at the soma—are upheld with remarkable accuracy [84].

B. Experimental Studies

A basic prediction of the 2LM is that the responses to two inputs delivered to the same dendritic branch should combine as if the inputs are summed by an LN subunit with a sigmoidal nonlinearity, whereas the responses to two inputs delivered to two different branches should combine linearly at the soma—as long as the cell remains subthreshold for somatic spiking [95], [96], or the somatic F–I curve happens to be linear [84]. These predictions were confirmed in experiments in brain slices [74], with a caveat discussed in Section VII.

The idea that thin terminal dendrites are the main integrative compartments in PNs has also received support from anatomical data: dendritic spine volumes and postsynaptic density sizes measured in EM images were found to decrease steadily along the length of CA1 oblique dendrites [140]. This gradual falloff in synaptic “weight” moving from the branch origin, where the input resistance is low, to the branch tip, where the input resistance is high, suggests that as a group these synapses are “designed” to be uniform contributors to voltage signaling in that specific dendritic compartment, rather than at the soma. (For a related point on the role of spines in equalizing local voltage responses, see [141]). Additional circumstantial support for dendritic subunitization lies in the evidence that dendrites are, or contain, or would benefit from being or containing, synaptic plasticity compartments [92], [106], [127], [128], [130], [136], [138], [142]–[154]; for review, see [22].

VII. PROBLEMS WITH THE 2LM ASSUMPTION THAT DENDRITES ARE LOCATIONLESS

A core assumption of the basic 2LM is that a dendrite sums its inputs independent of their location within the subunit. Notwithstanding its value in linking dendritic trees to ANNs and other equivalent layered computational frameworks, the assumption that a dendrite is a locationless LN unit is a crude approximation from the perspective of cable theory, and has become increasingly untenable as evidence accumulates regarding the location dependence of synaptic integration effects in PN dendrites.

Several lines of evidence suggest that modeling a PN dendrite as a locationless integrative unit is too simple. It has been known for decades that dendritic structures, unlike uniform cables, exhibit highly asymmetric voltage attenuation and summation effects [61], [65], [89], [97], [102], [104], [155], [156]. These asymmetries arise both from the difference in input impedance at the two ends of the dendrite (high at the distal tip, low at the perisomatic end; see [157, Ch. 3]), and from the fact that the “readout” of a dendrite is at the proximal end, since it is only the current reaching the soma that participates in the cell’s second layer of processing. (This statement ignores the effect of direct dendro–dendritic communication, which do occur [158] but are beyond the scope of this paper.)

A striking illustration of the importance of location within a PN dendrite lies in the systematic change in a dendrite’s sigmoidal I–O curve when a single focal excitatory stimulus is applied at different distances from the soma [61], [62], [71] (Fig. 3). When the intensity of dendritic excitation is gradually increased and the response is measured at the soma, the I–O curve typically exhibits these three general features: an initial slow rise at low stimulus intensities, followed by a steep jump in amplitude when the local dendritic spike threshold is crossed, followed by a saturation of the response magnitude at high stimulus intensities [1], [70], [76], [159]. The parameters of the sigmoid vary systematically with dendritic location, however. As the stimulation site moves farther out along the branch, the spike threshold decreases steadily, given that it is inversely related to the input resistance [65], [99], [156]. The amplitude of the sigmoid also declines steadily, given the distance-dependent attenuation of a dendritic spike as it passively propagates from the site of initiation to the soma [61], [65], [71], [159] [Fig. 3(b) and (c)]. Other parameters can influence the I–O curve as well, including the spatial spread of the excitation about its center [61], [67], [92]–[94], [160], and the spine neck resistance [84], [141], [161], both of which alter the sigmoidal nonlinearity. Thus, depending on its center, spread, and other parameters that may depend on location, each excitatory input to a dendrite can choose from a spectrum of different sigmoidal I–O curves—a fact that is irreconcilable with the locationless LN subunit assumption.

Fig. 3.

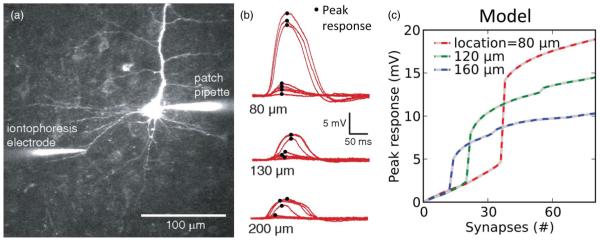
Example of location dependence of dendritic I–O curves. (a)–(b) Data from [71] showing location dependence of NMDA spikes. (a) Illustration of experimental setup: glutamate iontophoresis activates synapses at specific dendritic locations. (b) Voltage traces recorded at the soma for various stimulus sites along the dendritic length. As stimulation intensity is increased, a threshold is crossed and a local “NMDA spike” is generated. (c) Compartmental model from [61] shows a similar location dependence of the threshold and peak somatic voltage response. Curves show peak voltage responses recorded at the soma [similar to the peak of the traces shown in (b)] for stimulus sites at increasing distances from the soma (modified from [61]).

An interesting side effect of the spatial dependence of a dendrite’s sigmoidal I–O curve is that conventional notions of synaptic integration can be turned on their head. For example, an excitatory stimulus of a given intensity can have a larger effect on the soma when it is delivered to a distal site compared to more proximal sites, if the intensity is sufficient to cross the local spike threshold distally but not proximally [compare blue to red and green curves in Fig. 3(c) for 12 synapses]. Or, the somatic response can be largest for a stimulus delivered at mid-dendrite compared to the same stimulus delivered more proximally or distally [compare green to red and blue curves in Fig. 3(c), for 30 synapses].

In summary, even when only a single excitatory input pathway is activated, let alone an arbitrary spatial pattern of excitation, the asymmetric passive cable properties interacting with location-dependent dendritic spike thresholds means that a PN thin dendrite cannot be described as an LN function with a stereotyped sigmoidal nonlinearity. But what is the alternative? In Section VIII, we discuss our recent efforts to capture with greater generality the spatial integration capabilities of a single active dendrite, including both pure excitatory, as well as excitatory–inhibitory spatial interactions.

VIII. WHEN MULTIPLE INPUTS ARE ACTIVATED, THE SUBUNIT ACTS LIKE A MULTIDIMENSIONAL SIGMOID

In the first experimental test of the 2LM model, we compared summation of two colocalized inputs within the same dendrite to summation of two inputs delivered to different dendrites [74]. In a final experiment in that study in which two inputs to the same branch were increasingly separated, we showed that the within-branch summation rule changed qualitatively as a function of separation distance. Both the data and theory available at the time were insufficient to describe the effect in any generality, however.

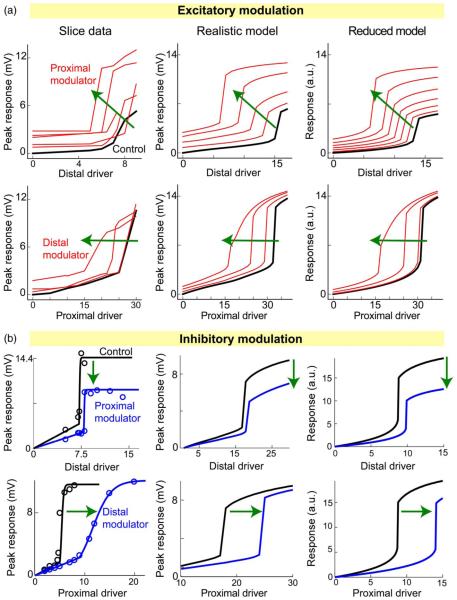
To address this, we carried out a more extensive set of two-input summation experiments both in brain slices and computer models, and in both excitatory–excitatory [61] and excitatory–inhibitory [65] configurations. To facilitate interpretation of the results, in each case, one of the inputs was designated the “driver” input, whose sigmoidal I–O curve was plotted along the abscissa, while the other input, whether more proximal or more distal, and whether excitatory or inhibitory, was designated the “modulator.” The effect of the modulator on the driver’s I–O curve was then analyzed. Fig. 4 shows examples of the data gathered in the slice experiments, and comparable results from two different types of models: 1) a “realistic” model, consisting of a reconstructed PN morphology discretized into 443 compartments, containing multiple types of ion channels and time-varying synaptic conductances, and whose somatic response was calculated through numerical integration of thousands of coupled nonlinear differential equations using the NEURON simulation package [162]; and 2) a “reduced” model, consisting of two compartments with time-invariant synaptic conductances and whose response was the solution of one nonlinear algebraic equation. The effects of the modulator on the driver’s sigmoidal I–O curve were similar in all three “models” (slice, realistic, and reduced), for both excitatory and inhibitory modulation at both proximal and distal sites (Fig. 4). This similarity is important as it tells us that the reduced model, though radically simplified compared to the realistic model, not to mention a real neuron, is nonetheless adequate to describe the time-averaged analog location-dependent interactions of two spatially separated inputs to an active dendrite.

Fig. 4.

Location-dependent two-input synaptic integration effects. (a) Excitatory–excitatory interactions, adapted from [61]. Left column shows peak somatic responses recorded in brain slices as a function of excitatory stimulus intensity (“Driver”), similar to Fig. 3(c). Each red curve was generated for a fixed value of the excitatory modulation. Distal/proximal labels indicate location of the driver or modulator relative to the soma. Middle column shows comparable results in a realistic 443-compartmental model with full membrane and synaptic dynamics. Right column is from a time-invariant two-compartment model. (b) Plots are organized as in (a) but for an inhibitory modulatory input (from [65]).

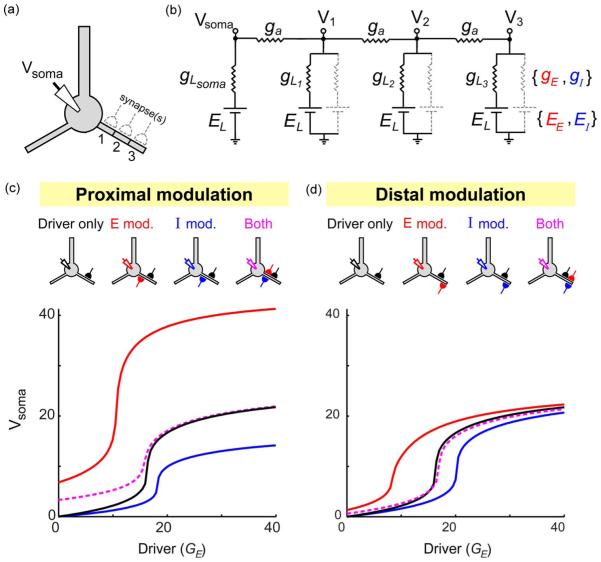
The general rules of two-input summation are summarized in Fig. 5. First, a proximal modulator affects both the threshold and the amplitude of the driver’s I–O curve, lowering the threshold and increasing the amplitude in the case of an excitatory modulator, and raising the threshold while decreasing the amplitude in the case of an inhibitory modulator [Fig. 5(c)]. In contrast, a distal modulator affects only the threshold of the driver’s input-output curve, lowering the threshold (i.e. left-shifting the I–O curve) when the modulator is excitatory, and raising the threshold when the modulator is inhibitory (Fig. 5(d); see also [99], [156]). Finally, as suggested by the first two generalizations, excitatory and inhibitory modulators have similar effects, but in opposite directions. Consistent with this, when excitatory and inhibitory modulators are applied simultaneously at the same location, their effects on the threshold and amplitude roughly cancel [Fig. 5(c) and (d), dashed magenta curves].

Fig. 5.

Excitatory and inhibitory spatial modulation effects are roughly equal but opposite. (a) Schematic shows neuron with three potential sites of synaptic input. (b) Circuit model with three dendritic and one somatic compartments. Parameters were: g_L1 = 10, g_L2 = 2, g_L3 = 1, g_a = 6, E_L = −70 mV, E_E = 0 mV, E_I = −70 mV. Excitatory synapses were modeled as voltage-dependent NMDA-type channels, with g_E = G_E/(1 + exp(−(V_x + 23:7)/12:5)) where V_x is the voltage at the synapse location. Conductances were in arbitrary units. (c) Schematics of neurons/synapses show an excitatory “Driver” input delivered to mid-dendrite (black synapse), coupled with a proximal excitatory (red) or inhibitory (blue) modulator input, or both. I–O curves are shown for each case (see legend for color code). Excitatory and inhibitory modulator conductances were G_E = 40 and g_I = 18. The somatic voltage was calculated using the method described in [65]. (d) Similar to (c), but for distal modulation (G_E = 60 and g_I = 24).

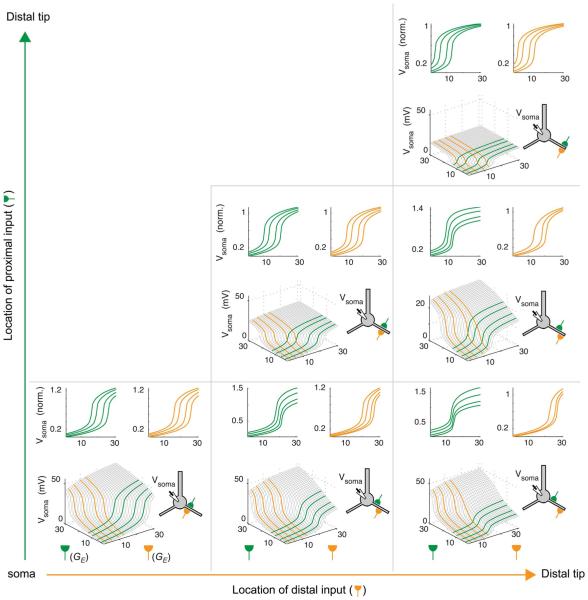
To gain a more comprehensive overview of the space of two-input spatial integration effects, including the effects of both relative and absolute location, we systematically varied the locations of two inputs to a dendrite, and for each input configuration, plotted the somatic response as a 2-D surface plot (Fig. 6). The three subplots on the main diagonal show cases with two colocalized inputs at increasing distances from the soma. The plots are all symmetric 2-D sigmoids (and thus effectively degenerate to 1-D sigmoids as in the basic 2LM), but with lower threshold and amplitude as the distance from the soma increases. This is consistent with the distance-dependent changes in sigmoid parameters seen for a single input to a PN (Fig. 3). In each subplot in Fig. 6, several 1-D slices are collected into vertically normalized “marginal” plots, so that the effects of proximal modulation (green) and distal modulation (orange) can be explicitly viewed. Given the rough interchangeability of excitatory and inhibitory modulation effects (see Fig. 5), the 1-D slice plots can be interpreted as showing either type of modulation, where inhibition pushes the curves to the right, and excitation pushes the curves to the left.

Fig. 6.

Spectrum of two-input location effects. Surface plots show effect of conjoint stimulation by two inputs (schematic of neuron shows locations). Inputs are given in normalized conductance units (similar to Fig. 5). Three panels on the main diagonal show cases with colocalized inputs at different distances from the soma. Green and orange line plots in top row of each panel show color-coded slices from surface plots to highlight the effect one input has on the I–O curve of the other.

In the lower right subplot, which corresponds to the case with maximally separated inputs, the 2-D sigmoid is most asymmetric, clearly showing the distinction between threshold plus amplitude modulation by the proximal input (green) versus pure threshold modulation by the distal input (orange).

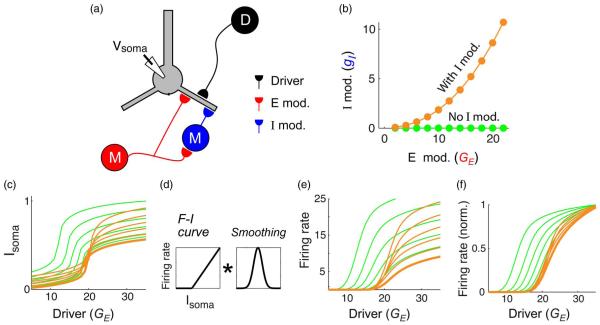
IX. MULTIPLE MODULATION EFFECTS CAN BE COMBINED

The rough cancellation of the excitatory and inhibitory modulators illustrated in Fig. 5 raises the intriguing possibility that multiple modulators may be combined to achieve a rich spectrum of modulation effects. To illustrate this idea, we constructed an example in which a driver input (D) projects to mid-dendrite, while a modulatory input (M) acts both through a monosynaptic excitatory input to a proximal site, and a disynaptic inhibitory input to a distal site via a dendrite-targeting interneuron (I) [Fig. 7(a)]. According to the “rules” of proximal–distal modulation laid out in Figs. 5 and 6, as the modulatory input increases, its effects should be to: 1) lower the threshold and boost the amplitude of the driver’s I–O curve due to the proximal excitatory modulator, while 2) raising the threshold of the driver’s I–O curve without affecting the amplitude due to the distal inhibitory modulator. If the two modulatory effects combine “rationally,” in the sense that the two opposing threshold effects cancel, the net result of the modulation should be a relatively pure multiplicative scaling of the driver’s I–O curve. The orange scatter data in Fig. 7(b) show the slightly superlinear relation between the levels of modulatory excitation and inhibition needed to achieve the multiplicative scaling effect. (This type of gentle superlinear relation could arise from various sources. For example, the interneuron could have an accelerating F–I curve, or the excitatory synapses onto the interneuron could have facilitating short-term synaptic dynamics.) The effect of this compound modulator is shown by the orange curves in Fig. 7(c)–(e), where the lowest orange curve is the driver’s I–O curve with no modulation. For comparison, the green curves show the result where the inhibition is “blocked,” leaving only the excitatory proximal modulation effect [as seen in Fig. 5(c)]. When the set of orange curves is passed through a typical F–I nonlinearity and a temporal/spatial averaging operation to represent the transformation from subthreshold voltage signals to firing rates under in vivo-like conditions, the result is a roughly multiplicative modulation [Fig. 7(e)]. To make the approximate scaling relationship clearer, the I–O curves are also shown vertically normalized [Fig. 7(f)].

Fig. 7.

Compound modulation circuit for multiplicative scaling. (a) Schematic of input configuration. (b) Orange scatter data show relation between excitatory modulation strength [red input in (a)] and inhibitory modulation strength [blue input in (a)]. Green data points indicate the case with only excitatory modulation, i.e., with inhibitory modulation “blocked.” (c) Orange curves show subthreshold voltage calculated using the four-compartmental model shown in Fig. 5. The effect of the compound modulator is primarily an increase in amplitude with a slight lowering of the threshold. For comparison, green curves show modulation with inhibition blocked [comparable to the red curve in Fig. 5(c)]. (d) Transformation to firing rate is modeled by applying a threshold-linear F–I curve followed by convolution with a smoothing kernel. (e) Firing rate curves obtained by applying the transformation in (d) to the data in (c). Orange curves resulting from compound modulation show approximate multiplicative scaling. The case without inhibition is shown for comparison (green curves). (f) Height-normalized firing rate curves from panel (e) illustrating the near invariance in orange I–O curves up to a variable scaling factor.

To summarize, a PN’s nonlinear analog spatial processing capabilities provide the local circuit with access to a broad spectrum of modulation effects that could be useful in many different types of computations. In particular, a modulatory pathway (whether contextual, attentional, cross-modal, etc.) would distribute its excitatory contacts nonuniformly along the proximal–distal axis of the PN’s thin dendrites to achieve a desired mixture of threshold lowering versus amplitude boosting, while biasing its projections onto different classes of interneurons to achieve the desired mixture of threshold elevation versus gain suppression [163]. The diversity of computations that can be implemented through this type of compound modulation effect has barely begun to be explored.

X. DISCUSSION

A. Current State of the 2LM

A major theme of this review is that a key assumption of the original 2LM is too simple: thin dendrites emanating from a soma or main trunk are not well described as locationless LN subunits. Rather, based on close agreement between experimental and modeling studies, we have arrived at the following conclusions: 1) given that a single input pathway can produce a spectrum of 1-D sigmoids depending on its location and other parameters, and that two input pathways can produce an even richer spectrum of 2-D branch functions depending on their locations and parameters, and there is evidence that this process continues to higher dimensions [164], it is appropriate to describe a PN thin dendrite as a multidimensional sigmoidal unit; 2) the multidimensional sigmoidal interactions between synapses within a PN dendrite can be reproduced by simple time-invariant circuits, which may open the door to compact analog hardware implementations of dendrites in the future [165]; 3) the distinct effects of distal versus proximal modulation are straightforward to state: distal modulation has a pure threshold-altering effect, whereas proximal modulation has combined threshold and amplitude effects [65]; for related ideas, see [89], [99], [102], [156], and [166]; 4) excitatory and inhibitory modulators have similar effects but in opposite directions; and 5) to the limited extent that the issue has been explored, the effects of multiple modulators combine rationally, in the sense that their effects on threshold and amplitude roughly “add” when they act in the same direction, and roughly “cancel” when they act in opposite directions (Fig. 7).

In contrast to the LN subunit assumption, which is clearly in need of revision, the other key assumption of the 2LM—that thin dendrites act as independent subunits [74], [83], [95], [96]—has received further support in recent years [1], [84], [140], [155]. Thus, our current working model of a PN subtree retains its two-layer structure, but includes an upgraded definition of the subunit function

$$d_j=g(E\left(x\right),I\left(x\right))$$ (3)

where E(x) and I(x) are the spatial patterns of excitation and inhibition, respectively, impinging on a dendrite. No analytical expression is currently available for function g(E(x); I(x)) for arbitrary spatial patterns of excitation and inhibition. However, to the extent that the E(x) and I(x) patterns can be captured by a coarse spatial quantization, such as in the single-input, two-input, and three-input cases discussed above, the time-averaged response of the dendrite can be evaluated by solving a circuit like the one shown in Fig. 5 (or using a table lookup). While these multidimensional branch functions arising from spatial interactions are more complicated than the locationless 1-D subunit functions of the original two-layer model, they are far less complicated than a biophysically detailed compartmental model of a dendrite, and are therefore valuable as abstractions of dendritic spatial processing capabilities.

B. Scope and Extensions of the Model

To reiterate the limitations in our scope in this paper, the augmented 2LM that includes within-dendrite spatial effects as shown in Fig. 8 is most appropriate for describing the integrative behavior of a dendritic tree or subtree whose synapses lie predominantly on a uniform set of long, unbranched terminal dendrites emanating from a common central node. This “ball and sticks” structure applies to many types of CNS neurons, however, so that our conclusions may have broad applicability. It is also important to note that the augmented 2LM is a generalization of the basic 2LM model, and so encompasses single-neuron models that do not make use of their within-dendrite spatial processing capabilities [83], [130], [132], [133], [136]–[138]. The simplest way this “degeneracy” could occur is if excitatory inputs project to dendrites in a spatially unbiased fashion. A further limitation has been our focus on time-averaged spatial integration behavior. While spatial integration is clearly important, many interesting forms of dendritic processing will likely involve timing in some critical way [89], [155], [167]–[170]. How best to include timing effects into a model that has no representation of time is not clear, especially if the goal is to retain a model that is simple enough so that it can be evaluated practically by hand.

Fig. 8.

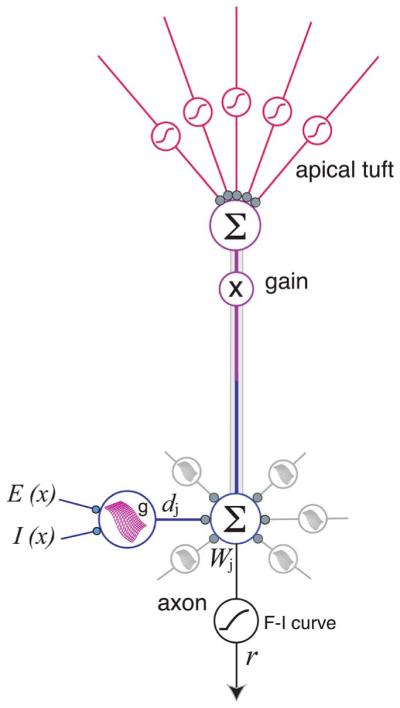
Augmented model of the PN is an elaboration of the 2LM shown in Fig. 2. Dendritic subunits are shown having multidimensional sigmoidal I–O functions that depend on the spatial distributions of excitatory and inhibitory inputs to that dendrite [61], [65]. Output of apical tuft is shown setting the response gain for the whole cell [1], [6], [7], [175]. Apical tuft and oblique dendrites may also show within-branch location effects, but this has not yet been tested.

Even within the realm of spatial processing, a number of additional parameters will likely interact with the location effects we have discussed here, including 1) the NMDA–AMPA ratio, which will influence the maximum achievable slope of the sigmoidal nonlinearity; 2) short-term synaptic dynamics, which can significantly change the integrative “arithmetic” of the cell [21], [171], [172], and 3) ion channel gradients, which may introduce additional location-dependent summation effects even within individual branches [62], [173].

A further elaboration of the two-layer model, in which the core assumption of subunit independence is relaxed, is also likely to be needed to capture the breadth of synaptic integration effects in the CNS. It is obvious that few real dendritic trees conform faithfully to the assumption that all of their dendrites are terminal, unbranched, and emanate directly from a central node, i.e., the morphology that would tend to maximize dendritic independence. Instead, thin dendrites within a typical subtree are electrically coupled to varying degrees, such that branches that are close, particularly sister branches joined at a branch point, show nontrivial levels of subthreshold voltage interaction that leads to a partial breakdown of their functional independence [1], [84], [159]. One interesting possibility is that the sharing of subthreshold voltage signals between nearby subunits is a feature rather than a bug. For example, fully independent subunits might be the appropriate targets for statistically independent channels of information, e.g., see [174], whereas immediately neighboring subunits whose responses are correlated by subthreshold voltage communication may be appropriate targets for partially correlated information channels. More work will be needed to sort out this issue.

XI. CONCLUSION

The past 30 years have brought major progress in our understanding of the principles of synaptic integration in active dendritic trees. The modern view of the neuron, supported by the triad of experimental data, mathematical analysis, and computer modeling, has evolved based on an accumulation of insights from many corners, and has brought us to a point where, though we are still far from having a complete picture of the roles that individual neurons play in the circuits of the brain, it can now be said with confidence that a neuron’s information processing capabilities go well beyond the capacity to integrate and fire. Recent advances in the ability to measure dendritic processing in the intact brain will make it much easier to pin down the computing functions of individual pyramidal neurons and other cells types moving forward, so that our 100+ year wait to learn what a single neuron does may be approaching its end [11], [68], [73], [79], [176], [177].

Biographies

Monika P. Jadi received the B.E. degree in electronics and power engineering from the National Institute of Technology, Nagpur, India, in 1995, the M.S. degree in electrical engineering from the University of Missouri, Rolla, MO, USA, in 1997, and the Ph.D. degree in biomedical engineering from the University of Southern California, Los Angeles, CA, USA, in 2010.

From 1995 to 1997, she worked as a Research and Teaching Assistant at the University of Missouri. From 1997 to 2004, she worked as a Senior Staff Engineer at Motorola, contributing to the architecture and development of real-time software for paging and cellular base stations. From 2004 to 2010, she worked as a Research and Teaching Assistant with the Department of Biomedical Engineering, University of Southern California. She is currently a Postdoctoral Fellow in the laboratory of Terrence Sejnowski at the Salk Institute for Biological Sciences, La Jolla, CA, USA. Her broad research interest includes neural computation at various levels in the brain from the synapse, to single neuron to networks of neurons. She has studied the contribution of inhibitory neurons in the brain to single-neuron computation as well as oscillatory dynamics in neural networks.

Dr. Jadi has been a recipient of the Dean’s Fellowship at the University of Missouri, Women in Science and Engineering Fellowship at the University of Southern California, and the National Eye Institute Training Fellowship at the Salk Institute. She has been a member of the Society for Neuroscience since 2004.

Bardia F. Behabadi received the B.S. degree in biomedical engineering from The Johns Hopkins University, Baltimore, MD, USA, in 2002 and the Ph.D. degree in biomedical engineering from the University of Southern California, Los Angeles, CA, USA, in 2011.

From 2004 to 2011, he worked as a Research and Teaching Assistant with the Department of Biomedical Engineering, University of Southern California. Since 2012, he has been a Senior Engineer at Qualcomm Research, San Diego, CA, USA. His research interests include neural computation, machine learning, and artificial intelligence.

Alon Poleg-Polsky was born in Magnitogorsk, Russia, in 1980, and immigrated to Haifa, Israel, in 1990. He received the MD and Ph.D. degrees in neuroscience from the Technion—Israel Institute of Technology, Haifa, Israel, in 2007 and 2009, respectively. The main focus of his Ph.D. training, under the supervision of Prof. J. Schiller, was to examine dendritic signal processing in fine dendrites and NMDA spike generation using experimental and modeling approaches.

Between 2008 and 2010, he combined his medical and scientific training as a medical director of a startup company, Nephera, in Haifa, Israel. In 2010, he joined Jeffrey S. Diamond’s lab at the National Institutes of Health (NIH), Bethesda, MD, as a visiting fellow. In his current postdoctoral studies. he is applying his skills in understanding retinal physiology, specifically focusing on direction selectivity circuit.

Dr. Poleg-Polsky is a member of the Society for Neuroscience. He serves as a reviewer for the Journal of Neuroscience and the Journal of Physiology. During his studies, he received numerous awards, including the Wolf prize for graduate students (2005) and the Rothschild Fellowship (2010).

Jackie Schiller was born in 1960. She received the Ph.D. degree in neurobiology from the Hebrew University, Jerusalem, Israel, in 1993.

She was a Postdoctoral Fellow in the Laboratory of Bert Sakmann at the Max-Planck Institute of Medical Sciences between 1993 and 1995. Between 1995 and 1997, she was a Postdoctoral Fellow in the Laboratory of David Clapham at the Mayo. She joined the Technion—Israel Institute of Technology, Haifa, Israel, as a faculty member in 2000 and became a full Professor with the Faculty of Medicine in 2011. She currently heads the Rappaport Neuroscience center at the Technion. Her work focuses on understanding the processing capabilities of principle cortical neurons with special emphasis on the nonlinear computational capabilities of dendrites in cortical pyramidal neurons. She uses advanced electrophysiological, imaging, histology, and modeling tools to decipher the properties of dendrites. She has recently been exploring the role of active dendritic processing in the cortex of awake behaving animals.

Prof. Schiller has been a Principle Investigator on grants from Israel Science Foundation, United States-Israel Binational Science Foundation, German-Israel Foundation for Scientific Research and Development and Minerva Foundation.

Bartlett W. Mel was born in Berkeley, CA, USA, in 1960. He received the B.S. degree in electrical engineering and computer science from the University of California at Berkeley, Berkeley, CA, USA, in 1982 and the Ph.D. degree in computer science from the University of Illinois at Urbana-Champaign, Urbana, IL, USA, in 1989.

He was a Postdoctoral Fellow in the Laboratory of Christof Koch at the California Institute of Technology (Caltech), Pasadena, CA, USA, from 1989 to 1994. He has been on the faculty of the Biomedical Engineering Department, University of Southern California (USC), Los Angeles, CA, USA, since 1994, with joint appointments in Psychology and the Neuroscience Ph.D. Program. His work focuses on understanding the information processing mechanisms of the brain, with intertwined scientific and engineering goals. A major focus has been to study the “arithmetic” underlying synaptic integration in the dendritic trees of CNS neurons using computer models at multiple levels of abstraction, and to explore how the computing capabilities of individual neurons may contribute to the sensory, motor, and memory-related functions of the brain. On the engineering side, he has focused on the development of neurally inspired algorithms in the attempt to reproduce the remarkable functions of the visual cortex, including algorithms for edge detection, contour extraction, feature learning, and viewpoint-invariant object recognition.

Dr. Mel has been a Principal Investigator on grants from the Office of Naval Research (ONR), the Army Research Office (ARO), the Defense Advanced Research Projects Agency (DARPA), the National Science Foundation (NSF), the National Institutes of Health (NIH), and the Israel–U.S. Binational Foundation, and has served on grant review panels for NSF and NIH. He has been the recipient of a Hewlett-Packard/AEA Fellowship, a McDonald-Pew Foundation Fellowship, and an NSF Career Award. In 2010–2011, he served as Program Chair and General Chair of the Computational and Systems Neuroscience (COSYNE) conference.