Covariate Imbalance and Adjustment for Logistic Regression Analysis of Clinical Trial Data

Abstract

In logistic regression analysis for binary clinical trial data, adjusted treatment effect estimates are often not equivalent to unadjusted estimates in the presence of influential covariates. This paper uses simulation to quantify the benefit of covariate adjustment in logistic regression. However, International Conference on Harmonization guidelines suggest that covariate adjustment be pre-specified. Unplanned adjusted analyses should be considered secondary. Results suggest that that if adjustment is not possible or unplanned in a logistic setting, balance in continuous covariates can alleviate some (but never all) of the shortcomings of unadjusted analyses. The case of log binomial regression is also explored.

1 Introduction

In the analysis of binary data from a clinical trial comparing two treatment groups, common unadjusted estimates of treatment effect include the risk difference (RD), relative risk (RR), and odds ratio (OR). While the RD and RR have relatively simple interpretations, the interpretation of the odds ratio is less intuitive as the concept of “odds” is not easy to grasp. Thus, in a clinical trial setting it makes sense to use RD or RR to determine treatment effect. However, these raw, unadjusted estimates are no longer appropriate if analysis requires adjustment for a covariate known to influence primary outcome.

Generalized linear models (GLMs) with an identity or log link function allow for adjusted estimation of RD or RR, respectively, but these two methods have the potential to result in estimated probabilities outside of [0,1]. Modeling RD (or RR) with identity (or log) link function assumes a linear (exponential) relationship between probability of outcome and treatment/covariate effect(s). While easy to interpret, these assumptions may not always be valid. In addition, the log binomial model (for RR) oftentimes results in convergence issues in model fitting that result in unstable estimates, especially when outcomes are not uncommon (e.g., they occur with probability near 0.50) (Deddens and Peterson, 2008; Blizzard and Hosmer, 2006). In simulations from Blizzard and Hosmer (2006), the log binomial model resulted in non-convergence or out-of-bounds predicted probabilities as much as 59% of the time in some scenarios. As a result, the GLM with logit link (for OR) remains more popular for analysis of binary data in clinical trials (Agresti and Hartzel, 2000). A problem arises, however, when assuming an underlying logistic relationship among outcome, treatment effect, and covariate effect in that adjusted model treatment effect estimates are not equivalent to unadjusted model treatment effect estimates (Gail et al., 1984). This inequality has the potential to result in incorrect conclusions about the magnitude and direction of treatment efficacy on outcome in clinical trial settings. When trying to determine whether efficacy of a given investigational product is “statistically significant” the conclusion based on clinical trial data may depend on whether the unadjusted or adjusted effect is of interest. This is illustrated below.

Let η denote the linear predictor in modeling the parameter of interest, p (the probability of successful outcome). Without loss of generality, let η = β₀ + β_txT + β_xX, where β₀ is an intercept term, β_tx is the treatment effect, T is an indicator variable for active treatment group, and β_x is the covariate effect for a one unit increase in continuous covariate X. Let h(η) be the function relating the linear predictor (η) to the parameter of interest, such that p = h(η). Then h(η) = exp(η) for the log binomial model (for RR), h(η) = η for the linear binomial model (for RD), and $h(\eta )=\frac{\mathit{\text{exp}}(\eta )}{1+\text{exp}(\eta )}$ for the logit model (for OR). Let ${\beta }_{tx}^{*}$ correspond to the treatment effect when the covariate (X) is not included in the linear predictor for the model at hand. Under this notation, Gail et al. (1984) have shown that the “bias” of ${\beta }_{tx}^{*}$ can be approximated using Taylor series expansion:

$${\beta }_{tx}^{*}-{\beta }_{tx}\approx \frac{1}{2}{\beta }_x^2{\sigma }_x^2[\frac{h″({\beta }_{tx})}{h\prime ({\beta }_{tx})}-\frac{h″({\beta }_0)}{h\prime ({\beta }_0)}],$$ (1)

where ${\sigma }_x^2$ is the variance of X. It can be shown that in the linear and exponential settings, unadjusted treatment effect estimates $({\beta }_{tx}^{*})$ are equivalent to adjusted treatment effect estimates (β_tx) and equation (1) is zero. This is the case when assuming a linear relationship to model RD or an exponential relationship to model RR. However, if one assumes that the underlying relationship among outcome, covariate effect, and treatment effect is logistic such that $p=\frac{\mathit{\text{exp}}(\eta )}{1+\mathit{\text{exp}}(\eta )}$, then unadjusted treatment effect estimates will be “biased”. That is, the estimate of treatment effect based on an unadjusted model will not be equivalent to the adjusted treatment effect estimate, and thus conclusions based on unadjusted effects may be misleading. The direction and magnitude of this inequality is determined by the expression in brackets in equation (1). In the logistic framework, it tends to be true that if treatment effect is positive (i.e., β_tx > 0), then “bias” $({\beta }_{tx}^{*}-{\beta }_{tx})$ will be less than zero, and the unadjusted coefficient estimate ${\beta }_{tx}^{*}$ will underestimate the true treatment effect.

This is the mathematical illustration of the noncollapsibility property of the OR (i.e., The overall OR does not necessarily equal the weighted average of the stratum-specific ORs) (Kent et al., 2009; Greenland et al., 1999; Robinson and Jewell, 1991). In modeling RR or RD, this problem of noncollapsibility does not exist (Gail et al., 1984), but modeling the OR in logistic regression is often preferred in practice because this setup ensures estimated probabilities in [0,1] and has better convergence properties (Agresti and Hartzel, 2000; Deddens and Peterson, 2008; Blizzard and Hosmer, 2006).

Hernández et al. (2004) use simulations to illustrate this point, and the authors further show that this biased treatment effect estimation results in detrimental effects on power for unadjusted analysis of binary data. However, the International Conference on Harmonization (ICH) states that covariate adjustment must be pre-specified in the Statistical Analysis Plan (SAP) for a clinical trial. If an unplanned adjusted analysis is conducted, it should be considered secondary (ICH, 1999). Historically there has been more emphasis on unadjusted, easily interpretable analyses that are not based on statistical models (Austin et al., 2010; Hauck et al., 1998; Hernández et al., 2004; Peduzzi et al., 2002; Pocock et al., 2002). Thus, there are two conflicting arguments. One comes from the statistical literature, and it states that adjustment is essential for appropriate inferences about treatment efficacy based on statistical analyses; and the other side of the argument comes from the more practical point of view, suggesting analysis should be carried out precisely as planned, and interpretation should be as simple and generalizable as possible.

In the case of binary outcomes, covariate adjusted and unadjusted treatment effect estimates should essentially be the same for RD or RR. However, previous work (Ciolino et al., 2011a) has shown that in the linear setting (RD), seemingly trivial covariate imbalance can result in nontrivial discrepancies between unadjusted and adjusted treatment effect estimates that become evident in comparing power or type I error rate across the two analysis methods.

It has been argued that unadjusted estimates will always be “biased” estimates of adjusted estimates in the logistic regression framework, regardless of covariate imbalance (Gail et al., 1984; Hernández et al., 2004). One of the main goals of this paper is to examine the relationship between continuous covariate imbalance and under/overestimation of treatment effect (from this point on the under/overestimation of unadjusted treatment effect estimates will be referred to as bias), power, and type I error rate for an unadjusted analysis of binary data when underlying relationships are truly logistic.

We first compare several measures of baseline covariate imbalance to determine an appropriate measure to be used in assessing these statistical parameters in unadjusted analyses. Next, we attempt to determine whether continuous baseline covariate balance results in decreased bias and better statistical properties for unadjusted analyses. Thus, when adjusted analysis is not possible or not planned for a binary outcome, we determine whether balance in continuous covariate distributions can remedy some of the issues that unadjusted analysis presents. The exponential (RR) setup is also briefly examined. This paper further explores the relationship between covariate imbalance and statistical parameters (power, type I error rate, bias) in a properly adjusted analysis in order to determine whether both imbalance control (through covariate adaptive treatment allocation algorithms) and covariate adjustment are required for sound statistical analysis of binary data.

2 Motivating Example

The National Institutes of Neurological Disorders and Stroke (NINDS) tissue plasminogen activator (tPA) dataset (NINDS, 1995) serves as a motivating example for this research. In 1996, as a result of the NINDS clinical trial, the Food and Drug Administration (FDA) approved the use of tPA for the treatment of ischemic stroke. Despite the trial’s success and the FDA’s approval of tPA, tPA is administered to a surprisingly low percentage (between 0% and 10% depending on the population and hospital) of ischemic stroke patients (Ingall et al., 2004). This may be because relatively few acute stroke patients are eligible to receive tPA, but imbalance in baseline disease severity across treatment groups in the NINDS tPA study is one major source of controversy surrounding this trial that raises concerns about the true efficacy of tPA (Frey, 2005; Ingall et al., 2004; Hertzberg et al., 2008). The active treatment group was favored at baseline with repsect to baseline disease severity or the National Institutes of Health Stroke Scale (NIHSS) score. NIHSS is a score ranging from 0 to 42 that measures stroke severity–the higher the score, the more severe the stroke. This measurement can also be used as an outcome measure, usually at three months post randomization (NINDS, 1995). Although this imbalance was insignificant at the 5% level (t=1.48, p-value=0.14), a closer look at the data suggests that this imbalance may have resulted in an inflated type I error rate (Ciolino et al., 2011b).

The primary outcome measure in the NINDS tPA study was a global measure that encompassed four commonly used scales to measure three month functional outcome following ischemic stroke, but these simulations will focus on the Modified Rankin Scale (mRS) (NINDS, 1995). The mRS ranges from a score of 0 (no symptoms) to 6 (dead), with varying levels of disability in between, and common practice is to define “favorable outcome” as a score of 0 or 1 (Graham, 2003).

In the NINDS tPA trial, the proportion of subjects experiencing a favorable outcome at three months was significantly larger in the active treatment group when compared to the placebo group, but it is questionable whether the effects of influential covariates such as NIHSS were truly controlled (Ciolino et al., 2011b). In the original article reporting the overall trial results, analyses did not adjust for baseline NIHSS (NINDS, 1995). For this particular study, adjusted reanalysis continues to suggest that there is in fact a significant treatment effect favoring tPA, despite the severe imbalances in baseline stroke severity (Ingall et al., 2004; Hertzberg et al., 2008). These simulations use the NINDS dataset as a model for some scenarios, and they determine the effect of such statistically “insignificant” baseline imbalances on type I error rate.

3 Methods

3.1 Simulation outline

The methods of these simulations closely resemble those of previous work of Ciolino et al. in which imbalance was assessed for its relationship with continuous outcome analysis (Ciolino et al., 2011a). Simulation studies were conducted in R that simulated a clinical trial involving two treatment arms with equal allocation (using a permuted block allocation scheme to ensure equal sample sizes), one predictive baseline continuous covariate, and a binary primary outcome. In the simulated clinical trial, we assume either (a) no treatment effect on outcome, or (b) treatment effect corresponding to 80% power for a simple unadjusted chi-squared test for binomial proportions. Thus, we simulate the situation of designing a clinical trial with a simple planned analysis (two-sample chi-squared test for binomial proportions) for a binary outcome, and investigate several scenarios in which these analysis results may or may not lead to incorrect conclusions about treatment efficacy (e.g., an unforeseen covariate influences primary outcome, relationship between outcome and covariate/treatment is truly logistic, etc.). The simulation logic is outlined below:

1. Simulate covariate (X) from a specified distribution (choices are normal, lognormal, bimodal).

2. Assign X values sequentially to one of two treatment arms ensuring equal sample sizes.

3. Determine the probability p of successful outcome based on the underlying assumed relationship between p, X, and treatment assignment (T). This relationship was assumed to be logistic such that

   $$p=\frac{\mathit{\text{exp}}({\beta }_0+{\beta }_{tx}T+{\beta }_{x}X)}{1+\mathit{\text{exp}}({\beta }_0+{\beta }_{tx}T+{\beta }_{x}X)},$$ (2)

   and T = 0 for assignment to placebo arm and T = 1 for assignment to active treatment arm.

   The treatment effect β_tx was simulated (a) to be equivalent to zero, or (b) that which would be observed if 80% power in an unadjusted analysis was desired. The covariate effect (β_x) was simulated to be equivalent to 0, 0.6β̃_tx, β̃_tx, or 1.5β̃_tx, where β̃_tx is β_tx correspdonding to 80% power (since β_tx = 0 when simulating no treatment effect, we define β̃_tx so that covariate effects are comparable when simulating no treatment effect versus simulating a treatment effect). Note that in a few scenarios, the relationship between p and η = β₀ + β_txT + β_xX was assumed to be exponential (for modeling RR), but there were restrictions placed on the levels of covariate inlfluence (β_x) that were examined since in order to have a valid probability of successful outcome, η must be less than or equal to zero. Levels simulated for these scenarios were β_tx = 0, 0.6β̃_tx, 0.68β̃_tx.

4. Simulate responses (success/failure) based on the probability p found in step 3.

5. Conduct an unadjusted two-sample chi-squared test for binomial proportions at the end of each simulated trial, capturing one-sided p-value and unadjusted estimated treatment effect (RD).

6. Fit a logistic (or log binomial) regression model to simulated data that properly adjusts for the influential covariate (X), capturing one-sided model Wald p-value associated with treatment effect and use back-transformation to estimate adjusted treatment effect in terms of proportions (RD).

7. Calculate measurements of imbalance for covariate X. Several measures are compared. They include:

   1. The independent two-sample t-statistic comparing mean covariate values across treatment groups
   2. The Wilcoxon rank-sum (WRS) statistic comparing covariate ranks across treatment groups
   3. A variation of the Kolmogorov-Smirnov statistic (KS) that captures directional imbalance in empirical covariate distribution functions across treatment groups
   4. The area under the curve of cumulative imbalance (AUC) across two treatment groups (Ciolino et al., 2011b,a). To calculate cumulative imbalance, first count the number of subjects at each level (in order) of the covariate (i.e., at each one unit increment) in both the treatment and placebo groups, then calculate the difference across groups at each level, and sum each of these differences in order. Since AUC is always positive, direction of imbalance is realized by multiplying AUC by the sign associated with the t-statistic. This measure of imbalance is denoted sAUC.

8. Return to step 1.

All possible combinations of covariate distribution (normal, lognormal, bimodal), level of covariate influence (β_x = 0, 0.6β̃_tx, β̃_tx, 1.5 β̃_tx), and treatment effect (corresponding to 2.5% power and 80% power) were simulated (for a total of 24 simulation scenarios) 5000 times each. The nominal one-sided significance level for test of treatment effect was set at 2.5%, and thus the treatment effect associated with 2.5% power is equivalent to zero. Each of the 24 scenarios were examined for sample sizes of 100, 300, 500, and 1000, and the treatment effects in terms of RD corresponding to 80% power for unadjusted analysis for these sample sizes were approximately 28%, 16%, 13%, and 9%, respectively.

Treatment was simulated to positively affect outcome, and positive levels (t>0, WRS>0, KS<0, sAUC>0) of imbalance corresponded to larger values of the covariate in the active treatment group. For that reason, β_x was made positive when there was no simulated treatment effect in order to determine inflation of type I error rate, while β_x was made negative when there was a simulated treatment effect in order to determine detrimental effects on power (as opposed to inflation, since underpowered studies are of more interest). This change in direction of association was done for ease of interpretation and reporting of results.

3.2 Simulating an Exponential Relationship Using NINDS data as a Template

Due to the problems associated with assuming an exponential relationship among the probability of successful outcome, treatment, and covariates, the NINDS dataset was used as a starting point for these simulation scenarios. When analyzing the NINDS dataset using the log binomial GLM, there is a convergence issue as discussed earlier. Despite this issue, the estimated adjusted treatment effect in the log binomial model corresponds to a RR of about 1.27. That is, in this dataset, tPA treatment increases probability of successful outcome by an estimated 27% compared to placebo. This estimate was based on adjustment for standardized covariate(s) (e.g. NIHSS value minus mean of NIHSS, divided by standard deviation of NIHSS) so that the new standardized variable was centered at zero with variance one. In examining the simulation scenarios outlined above, the scenario corresponding to a clinical trial with N=500 subjects and 80% power (RD=13%, RR=1.26) closely resembled this situation. A normally distributed covariate centered at zero with variance one was simulated, and any values falling outside of three standard deviations were resampled until they fell within appropriate ranges (in order to simulate practical scenarios as well as to have some control over simulating excessively large probabilities).

Recall that the simulated logistic scenarios examined covariate effects of 0, 0.6β̃_tx, β̃_tx, and 1.5β̃_tx, but in the exponential relationship, η must be less than or equal to zero. It was determined that under the conditions outlined above (N=500, 80% power, X ~ N(0, 1)), β_x could not exceed approximately 0.68β̃_tx. As a result, under these conditions, only slight levels of covariate influence could be simulated for the exponential scenarios. It should be noted, however, that in the analysis of the real NINDS dataset, NIHSS influence was actually larger than 1.5β̃_tx. Therefore, any conclusions made based on the level(s) of influence examined in these simulations were conservative. This is further discussed in Section 4.4.

3.3 Analysis of Simulated Data

After each simulated clinical trial, an indicator variable, detect, was created to capture whether a treatment effect was detected at the one-sided 2.5% level of significance (i.e., p-value<0.025) for both unadjusted and adjusted analyses. Overall power was estimated by

$$\mathit{\text{power}}=\frac{{\sum }_{i=1}^{5000}\mathit{\text{detect}}}{5000}$$ (3)

for each analysis type. To determine the predictive ability of imbalance, the simulated data was used to model detect with each of the imbalance measures (t-statistic, WRS, KS, sAUC) in turn as predictors. As a result, four separate GLMs with logit link functions were fit for each of the simulation scenarios described above. Model Wald p-values associated with the effect of the imbalance measure was used as an initial indicator of predictive ability, and goodness of fit for these models was based Akaike Information Criteria (AIC) (Agresti, 2002), the Hosmer-Lemeshow goodness of fit test (Hosmer and Lemeshow, 1980), and a measure analogous to R-squared (for linear models) denoted D (originally introduced by McFadden (1974) but also mentioned by Agresti (2002)). The D criterion ranges from zero to one (as does R-squared in the linear model setup), but it is used as a relative measure since the value alone is difficult to interpret because it is based on log-likelihoods. These criteria were examined simultaneously for each GLM, and the measure with the most favorable characteristics (i.e., the lowest Wald p-value, lowest AIC, highest Hosmer-Lemeshow p-value, and highest D) overall was chosen the “best” measure for modeling type I error rate (for the scenarios simulating no treatment effect) or power (for the scenarios simulating treatment effect corresponding to 80% power) for unadjusted test for treatment effect on binary outcome. The situation of “ties” between the measures of imbalance was not anticipated; however, if ties did occur, the measure requiring the simplest calculation was chosen as the “best.” This was deemed acceptable since previous work (Ciolino et al., 2011a) has shown strong association between each of these measures of imbalance.

In addition to the GLMs for type I error rate and power, simple linear regression models (LMs) were used to model bias in RD for treatment effect estimation in each scenario. In each of the scenarios, the simulated RD was either (a) zero or (b) that which would result in 80% power for the given sample size. Thus, the estimated RD based on the unadjusted and adjusted (using back-transformation) analyses in each simulated clinical trial was used to calculate the “bias” in RD. Again, the model p-value was used as an initial indicator of predictive ability in modeling bias, and the criteria used to select a “best” measure of imbalance in these models included R-squared and AIC. Though RD is a proportion and using LMs to model it may be inappropriate, model assumptions were checked and no alarming violations were noted, and the distribution of RD bias appeared symmetric and relatively normal. Thus, LMs were deemed an appropriate means of modeling RD bias observed in these simulations. Again, the imbalance measure showing the largest number of favorable characteristics (i.e., lowest AIC and highest R-squared) overall was considered to be the “best” measure for modeling RD bias in an unadjusted test for treatment effect on binary outcome.

Once an ideal measure of imbalance was chosen, the GLMs and LMs were used to predict statistical parameter values (power, type I error rate, bias) for a given level of imbalance. Section 4 reports overall results for the measures’ predictive ability for these statistical parameters, compares power of unadjusted and adjusted analysis, and illustrates the relationship between imbalance and power, type I error rate, and bias. First, we will discuss the hypothesized findings in these simulations.

3.4 Hypotheses for Simulation Results

Based on the results from Gail et al. (1984), we expected that unadjusted analyses in the logistic scenarios would result in biased treatment effect estimation, even in cases of perfect balance in the simulated covariate across treatment groups. However, from previous research (Ciolino et al., 2011a), we expected to see a relationship between unadjusted analysis bias, type I error rate, and power and covariate imbalance, suggesting that balance has the ability to remedy some of the statistical problems associated with unadjusted analyses. On the other hand, since the bias for unadjusted analyses treatment effect estimation in the exponential case (RR) is equivalent to zero (Gail et al., 1984), we expected to see that perfect covariate balance would result in unbiased treatment effect estimation as well as nominal type I error rates and power in unadjusted analyses. We also hypothesized that as the level of covariate imbalance increased, treatment effect estimates for unadjusted analyses (whether in the exponential or logistic scenarios) would become more biased and thus result in detrimental effects on type I error rates and power.

Based on results from preliminary research (Ciolino et al., 2011a), we hypothesized that all measurements of covariate imbalance would be associated. The intent was to determine a measure of imbalance that is robust in its predictive ability for the statistical parameters of interest, but we hypothesized that the t-statistic would be sufficient in capturing continuous covariate imbalance in all scenarios. We also made note of the possibility that the predictive ability of each imbalance measure may change with the nature of outcome and covariate distibution, which explains the comparison of multiple measures.

Finally, we expected that the predictive ability of covariate imbalance would decrease for covariate adjusted analyses in all scenarios. Ciolino et al. (2011b) showed that covariate imbalance has detrimental effects on imbalance even when analysis is properly adjusted in the logistic case, but the authors’ results were inconclusive because it was difficult to determine whether the significance of this relationship was a result of a large number of simulations (millions) or possibly very large (and thus very unlikely) levels of covariate imbalance. These simulations were designed to help alleviate the confusion surrounding this issue.

4 Results

4.1 The Predictive Ability of Imbalance Measurements

Each of the measures of covariate imbalance significantly predicted power, type I error rate, and bias for unadjusted analyses when covariate influence was not equal to zero (p < 2×10⁻¹⁶ in most cases). According to the criteria listed in Section 3.3, the overall “best” measures of imbalance were the t-statistic and WRS when analysis was unadjusted for the logistic scenarios, and the t-statistic was the “best” measurement for the exponential scenarios.

The results for the logistic scenarios varied across different covariate distributions. Both the t-statistic and WRS were very predictive for the scenarios in which X was normal, WRS was the most predictive for most lognormal scenarios, and the t-statistic was most predictive for bimodal scenarios. The discrepancy between the two measures' predictive ability, however, was generally negligible. Table 1 shows each measure’s predictive ability for power for a sample size of 300 and a covariate distributed bimodally in the logistic scenarios. In each scenario listed in Table 1, the t-statistic has the smallest AIC and largest D, suggesting it may be the best predictor of power in the bimodal case. The Hosmer-Lemeshow goodness of fit tests were not as consistent, but in most cases the test does not suggest poor fit for models involving either the t-statistic or WRS. These two measures are also highly significantly and strongly positively correlated in all cases (p < 2 × 10⁻¹⁶, and Pearson’s sample correlation coefficient, r ≈ 0.98, 0.71, and 0.93 for normal, lognormal, and bimodal covariate distribution, respectively). Similar reults can be seen in predicting bias in RD (table ommitted here).

Table 1.

Predictive Ability of Imbalance Measurements for Power, N=300, X ~ Bimodal, (β̃_tx is treatment effect in equation (2) corresponding to 80% power)

Scenario	Measure	Model p-value	AIC	Hosmer-Lemeshow p-value	D
	t	<2E-16	1167.9	0.675	0.063
βx= 0.63β̃tx	WRS	8.34E-16	1178.8	0.499	0.054
βtx = 0	KS	3.55E-12	1187.1	0.016	0.047
	sAUC	2.36E-16	1168.7	0.056	0.062
	t	<2E-16	5401.4	0.011	0.051
βx = −0.6β̃tx	WRS	<2E-16	5429.1	0.744	0.047
βtx = β̃tx	KS	<2E-16	5465.2	0.028	0.040
	sAUC	<2E-16	5410.1	0.006	0.050
	t	<2E-16	1066.5	0.400	0.102
βx = β̃tx	WRS	<2E-16	1090.8	0.861	0.082
βtx = 0	KS	1.16E-15	1097.7	0.394	0.076
	sAUC	<2E-16	1077.0	0.054	0.094
	t	<2E-16	5928.3	0.060	0.109
βx = −β̃tx	WRS	<2E-16	6021.9	0.509	0.095
βtx = β̃tx	KS	<2E-16	6158.0	<0.001	0.074
	sAUC	<2E-16	5948.1	0.063	0.106
	t	<2E-16	977.5	0.679	0.229
βx = 1.5β̃tx	WRS	<2E-16	1019.6	0.924	0.196
βtx = 0	KS	<2E-16	1052.4	0.003	0.170
	sAUC	<2E-16	984.5	0.862	0.224
	t	<2E-16	5503.1	0.619	0.194
βx = −1.5β̃tx	WRS	<2E-16	5722.5	0.843	0.161
βtx = β̃tx	KS	<2E-16	59850	<0.001	0.123
	sAUC	<2E-16	5576.4	<0.001	0.183

Since in all cases, either the t-statistic or WRS was deemed the “best” measure of imbalance in terms of predictive ability for power, type I error rate, and bias, and the discrepancies between the two measures were negligible, the t-statistic was chosen as a means of representing continuous covariate distributional imbalance. The results for the exponential scenarios (omitted here) were comparable to those seen in Table 1. However, the amount of variation in these statistical parameters that was explained by the t-statistic was much less for the exponential models. For example, the largest D observed in models for type I error rate and power was only 0.026 in these scenarios, and the largest R-squared observed in models for bias was only 0.029 (while R-squared frequently reached 0.30 and above in the logistic scenarios). This can be attributed to the fact that only slight levels of covariate influence were simulated in the exponential scenarios. It was thus inferred and hypothesized that larger levels of influence (though not simulated here), would have resulted in even stronger associations between imbalance and these statistical parameters in unadjusted analyses when relationship between p and η was exponential.

4.2 Adjusted versus Unadjusted Analysis

When properly adjusting for the influential covariate, the level of imbalance did not significantly predict power, type I error rate, or bias in any of the simulated data. In the logistic scenarios, the estimated type I error rate (i.e., when simulated treatment effect was zero) was often slightly inflated in the unadjusted case. The mean estimated type I error rate for unadjusted analyses for sample size of 300 was approximately 2.70% while the mean type I error for adjusted analyses was approximately 2.44% (Recall that the simulated type I error rate was 2.5%). Though the impact is slight, adjusted analysis appears to have better ability to conserve type I error rate than unadjusted analysis when the true relationship between outcome, treatment, and covariate is logistic.

Table 2 shows estimated unadjusted and adjusted analysis power for sample size of 100 in the logistic scnenario for a nonzero covariate effect. The power estimates in Table 2 are calculated from equation (3) for each of the scenarios simulated. Adjusted analysis consistently resulted in larger estimated power than unadjusted analysis in all cases. Table 2 also illustrates the RD bias (unadjusted RD minus adjusted RD [after back-transformation]) estimated from the simulated data. As the level of covariate influence increased, the benefit in power of adjusted analysis increased in all scenarios. Also, as the level of influence increased, estimated power dropped drastically below the desired 80% even when analysis was adjusted (This did not happen in the exponential cases). Furthermore, when the covariate had a nonzero effect on outcome, the treatment effect (RD) was underestimated in unadjusted analysis (RD bias was negative). In additon, the magnitude of RD bias increased as the distribution of the influential covariate strayed from normal and as the level of covariate influence increased. The estimated bias for all adjusted analyses was essentially zero. Simulation results were similar for all sample sizes, but the magnitude of bias for an unadjusted analysis decreased as sample size increased. Table 3 shows the same information for sample size of 1000.

Table 2.

Benefit in Power for Adjusted Analysis, N=100, RD Treatment Effect = 28%

X Distribution	βx	Unadjusted Power	Adjusted Power	Benefit	Unadjusted Bias
	−0.6β̃tx	76.78%	79.98%	3.20%	−2.5%
Normal	−1.0β̃tx	66.12%	75.52%	9.40%	−5.3%
	−1.5β̃tx	48.92%	66.46%	17.54%	−9.2%
	−0.6β̃tx	72.46%	78.84%	6.38%	−3.4%
Lognormal	−1.0β̃tx	62.64%	74.20%	11.56%	−6.0%
	−1.5β̃tx	47.90%	65.02%	17.12%	−9.6%
	−0.6β̃tx	58.80%	71.14%	12.34%	−6.9%
Bimodal	−1.0β̃tx	30.56%	50.62%	20.06%	−14.0%
	−1.5β̃tx	14.48%	25.62%	11.14%	−19.2%

Table 3.

Benefit in Power for Adjusted Analysis, N=1000, RD Treatment Effect = 9%

X Distribution	βx	Unadjusted Power	Adjusted Power	Benefit	Unadjusted Bias
	−0.6β̃tx	79.54%	79.22%	−0.32%	−0.1%
Normal	−1.0β̃tx	78.76%	78.90%	0.14%	−0.3%
	−1.5β̃tx	76.08%	78.46%	2.38%	−0.5%
	−0.6β̃tx	78.28%	78.92%	0.64%	−0.3%
Lognormal	−1.0β̃tx	76.66%	78.44%	1.78%	−0.5%
	−1.5β̃tx	71.96%	75.46%	3.50%	−0.9%
	−0.6β̃tx	79.52%	79.86%	0.34%	−0.2%
Bimodal	−1.0β̃tx	74.38%	77.38%	3.00%	−0.7%
	−1.5β̃tx	67.70%	73.80%	6.10%	−1.4%

Table 3 again shows that the estimated adjusted power tended to be larger than the estimated unadjusted power for the logistic scenarios. This benefit in power grew as the covariate distribution strayed from normality and as the level of covariate influence increased. Treatment effect estimates were again biased when analysis was unadjusted, and the situation is less severe in Table 3 than in Table 2. The power estimates in Table 3 are much closer to the 80% power that was simulated, but note that the treatment effect (β_tx) associated with 80% power for sample size of 100 was larger than that for a sample size of 1000. Therefore, the magnitudes of covariate influence (β_x = −0.6β̃_tx,− β̃_tx,−1.5β̃_tx) were also larger for a sample size of 100 than for a sample size of 1000.

As expected, the estimated bias for unadjusted analyses in the exponential scenarios (omitted here) was, on average, zero. The appropriately adjusted (using log binomial models) analyses resulted in consistently larger power than the unadjusted analyses in these scenarios as well. The power for unadjusted analyses in the scenario in which β_x was equal to −0.68β̃_tx was 82.30%, while the appropriately adjusted analyses resulted in estimated power of 84.98%. Type I error rate was conserved for unadjusted as well as adjusted analyses in the exponential scenarios. The next Section further explores the relationship between imbalance in continuous covariate distributions (measured by the t-statistic) and statistical parameters for an unadjusted analysis in both the logistic and exponential cases.

4.3 Predicting Power and Type I Error Rate for Unadjusted Analyses

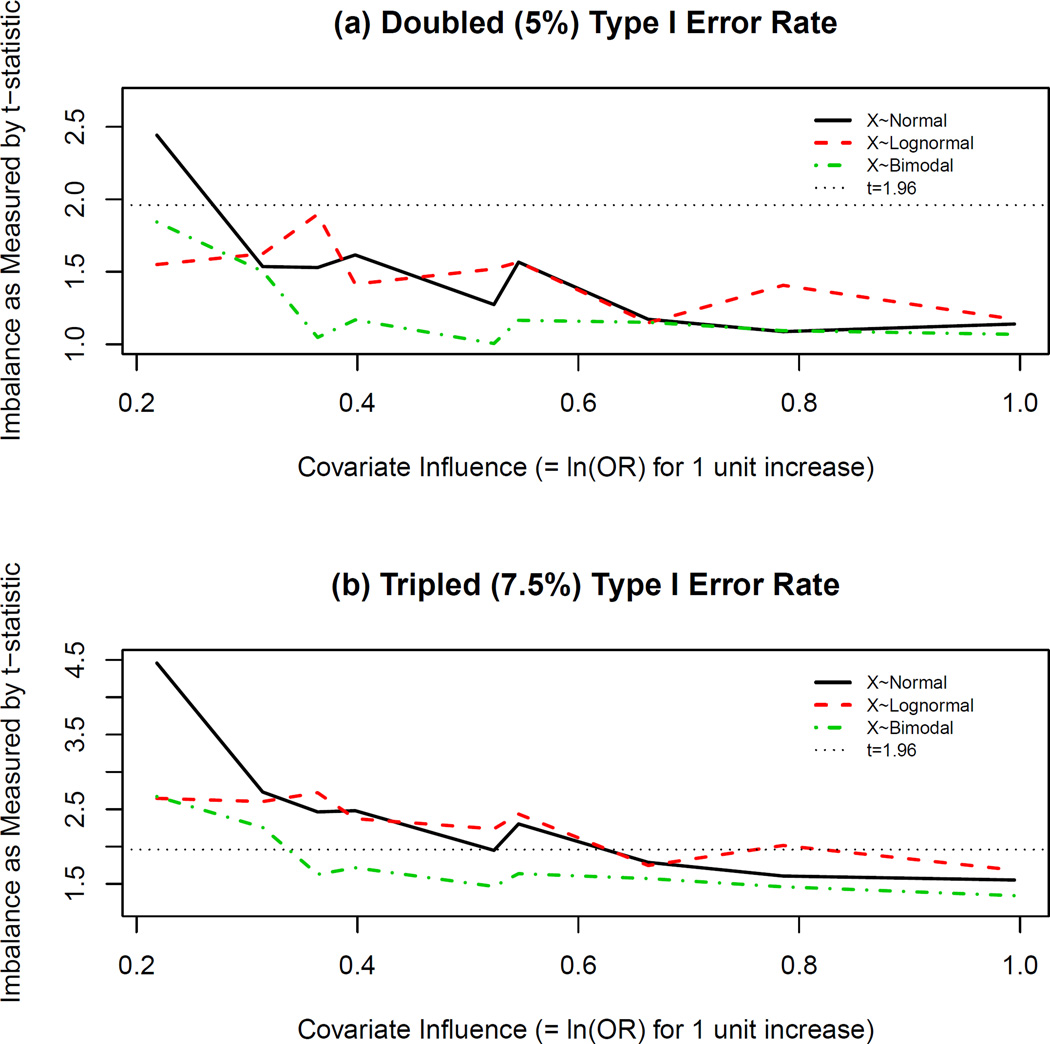
Recall that the overall type I error rate was relatively conserved for unadjusted versus adjusted analysis. However, imbalance predicts type I error rate (Table 1, Section 4.1). In order to determine the magnitude of imbalance that may result in inflated type I error rate when underlying relationships are truly logistic, the models for type I error rate were used to estimate levels of imbalance (t-statistic) in the covariate distribution across treatment groups that correspond to double (5%) and triple (7.5%) the nominal (2.5%) type I error rate for these scenarios. The results are shown in Figures 1(a) and 1(b), respectively. Note that the level of covariate influence in this Figure corresponds to β_x from equation (2).

Figure 1.

Imbalance Levels Corresponding to Type I Error Rate Inflation in Logistic Scenarios. Table 1 shows that imbalance as measured by the t-statistic significantly predicts type I error rate. Using the Generalized Linear Models (GLMs) whose summary information is depicted in Table 1, t-statistic estimates corresponding to estimated type I error rates of (a) 5% and (b) 7.5%, were calculated and plotted for various levels of covariate influence (β_x) in the logistic scenarios. Positive levels of imbalance correspond to a favored active treatment group in these plots. The horizontal line at t=1.96 corresponds to the two-sided critical value for a baseline test comparing covariate distributions at the 5% level of significance. Influential levels of imbalance are thus not discovered by this test as most values fall below this threshold in (a) and (b).

In logistic scenarios, an analysis unadjusted for an influential covariate resulted in type I error rate double that of the desired (simulated) rate when covariate imbalance as measured by the t-statistic was “insignificant” at the 5% level (Figure 1). When β_x ≈ 0.31 (i.e., β_x = 0.6β̃_tx for N=500), an insignificant level of imbalance resulted in an estimated type I error rate that was double that of the nominal (2.5%) level. Furthermore, as the level of covariate influence increased (the horizontal axis in Figure 1), the estimated level of imbalance (vertical axis in Figure 1) corresponding to double or triple the simulated type I error rate in an unadjusted analysis decreased. Thus, influential levels of continuous covariate imbalance for an unadjusted analysis would remain undiscovered by a baseline test for significance, and though the t-statistic is a robust measure of covariate imbalance, the t-test is not an appropriate method of assessing treatment group comparability.

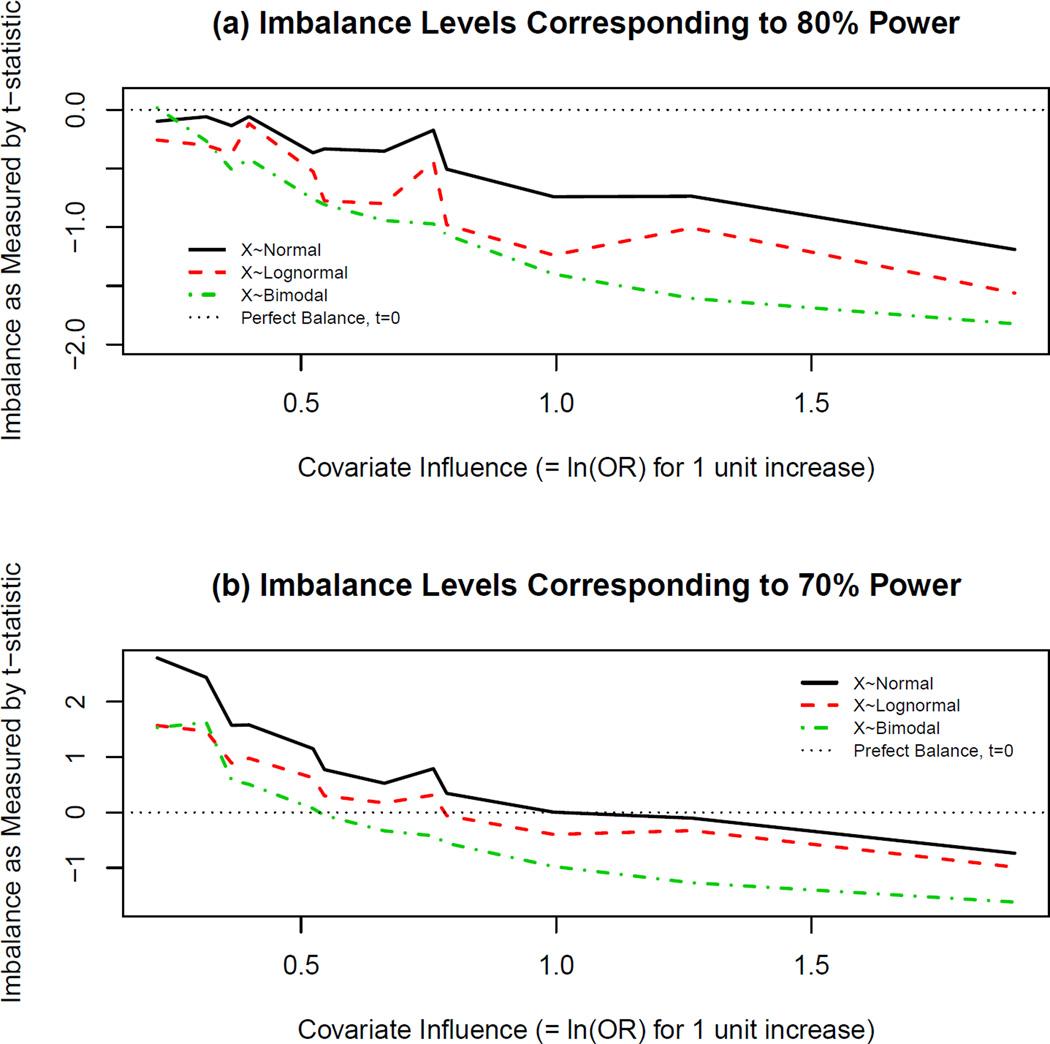
Tables 2 and 3 show that adjusted analyses tended to be better powered than unadjusted analyses when the true relationship between outcome, covariate, and treatment effects was logistic. Perfect balance in influential covariates still resulted in biased treatment effect estimation for unadjusted analyses. Recall that when examining power the covariate was simulated to negatively impact outcome, and positive levels of imbalance (t>0) corresponded to poorer baseline prognosis in the active treatment arm. Figures 2(a) and 2(b) present levels of covariate imbalance (|β_x|) that resulted in estimated power of 80% and 70%, respectively (according to GLMs from the simulated data). From Figure 2(a) it is evident that perfect or nearly perfect balance resulted in the desired 80% power only for slightly influential covariates. However, as the level of covariate influence increased, the estimated imbalance that would result in 80% power for an unadjusted analysis was such that t<0 (i.e., the active treatment group at baseline had a better prognosis than the placebo group). Thus, if a systematic bias in treatment allocation were introduced such that the treatment group was favored at baseline, the desired 80% power would be approximately achieved for an unadjusted analysis. The magnitude of the estimated required amount of imbalance in the proper direction increased as the covariate influence increased.

Figure 2.

Imbalance Levels Corresponding to Specific Levels of Estimated Power in Logistic Scenarios. Using the Generalized Linear Models (GLMs) whose summary information is depicted in Table 1, t-statistic estimates corresponding to estimated power of (a)80% and (b)70%, were calculated and plotted for various levels of covariate influence (β_x in equation (2)). Note that the absolute value of β_x is plotted here, and the covariate negatively influences outcome in this case. Thus, positive levels of imbalance (t>0) correspond to a poorer baseline prognosis in the active treatment arm. The horizontal line at t=0 corresponds to perfect continuous baseline covariate balance, and in most cases, even perfect balance does not result in the desired (a)80% power (or sometimes even (b)70% power). As the imbalance shifts in a negative direction such that the treatment arm is favored, the estimated desired power is achieved.

Figure 2(b) shows that an estimated 10% decrease in power was observed if imbalance was less than significant at the 5% level according to the two-sample t-test comparing mean covariate values across treatment groups at baseline. Once the level of covariate influence reached a certain point (β_x ≈ 0.99 for X ~ Normal, β_x ≈ 0.66 for X ~ Lognormal, and β_x ≈ 0.52 for X ~ Bimodal), a similar phenomemon to that seen in Figure 2(a) occurred, whereby the predicted power reached 70% (10% less than the simulated power) for unadjusted analysis only when the placebo group had a poorer disposition at baseline. Thus, the importance of adjustment for influential covariates in nonlinear settings is evident, and these results assert that even perfect baseline covariate balance does not seem to remedy the problems associated with unadjusted analyses. Furthermore, the baseline significance test is a poor assessment of covariate imbalance.

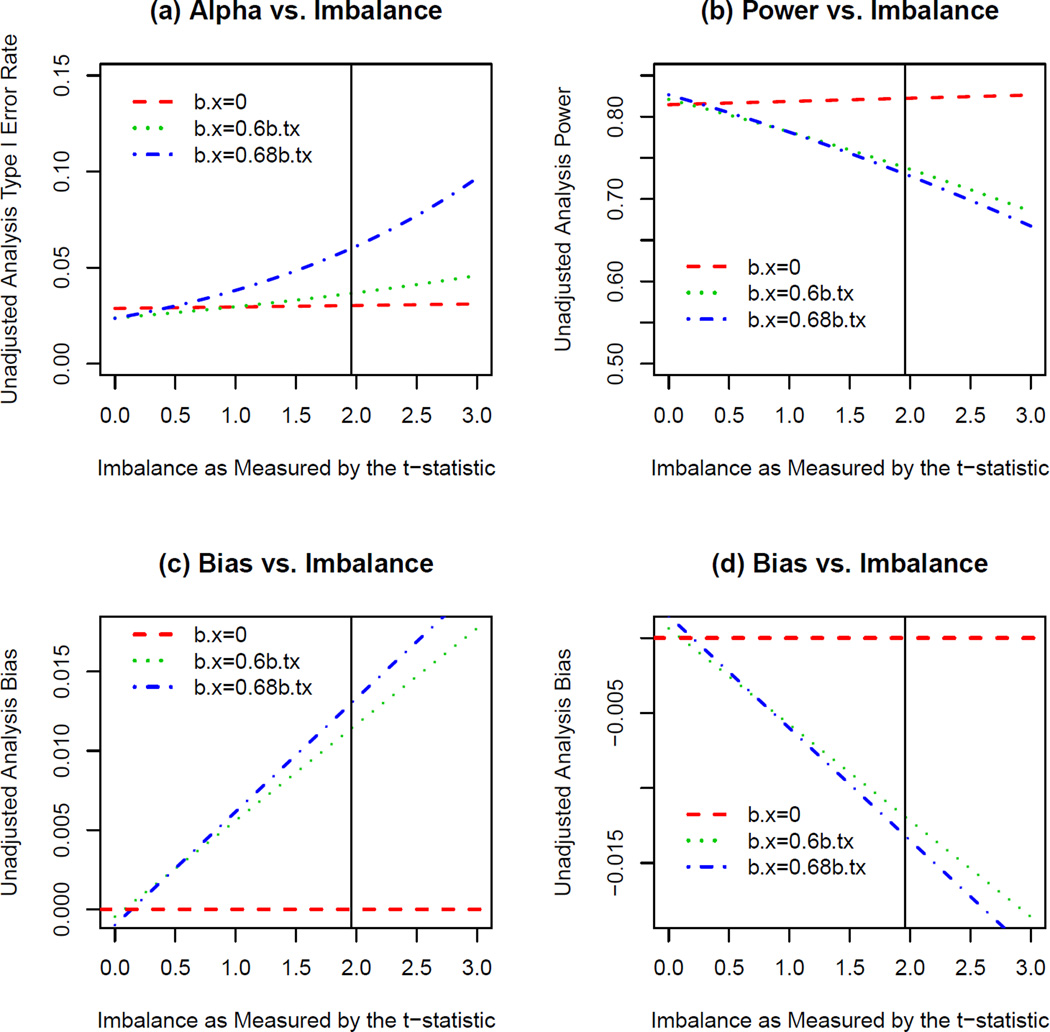
The results from the exponential scenarios also suggested that less than significant levels of covariate imbalance had the potential to result in type I error rate inflation (when no treatment effect was simulated), decreases in power (when treatment effect corresponding to 80% power was simulated), and/or biased treatment effect estimation for unadjusted analyses. The estimates for these statistical parameters given covariate imbalance based on models for the simulated data in the exponential scenarios are illustrated in Figure 3. Though perfect covariate balance did not affect bias, power, or type I error rate, the plots in Figure 3 suggest that for an influential covariate, when underlying relationships between outcome and covariate/treatment were exponential, less than “significant” levels of covariate imbalance resulted in nontrivial effects on these parameters in unadjusted analyses. Note that the level of covariate influence simulated in these simulations was very slight, and that more realistic levels of influence (β_x > 1.5β̃_tx in the NINDS tPA dataset) would most likely have shown even stronger relationships.

Figure 3.

Effects of Imbalance on Unadjusted Analysis when Outcome is Exponentially Related to Treatment and Covariate. These plots show the estimated (a) type I error rate, (b) power, and (c,d) bias for given levels of imbalance defined by the t-statistic comparing mean covariate values across two treatment groups in an unadjusted analysis in the exponential scenarios. The t-statistic values greater than zero correspond to larger values of the covariate in the active treatment group. Plots (a) and (c) correspond to effects on these parameters for a covariate that is positively associated with outcome (treatment group favored at baseline) and plots (b) and (d) correspond to effects on these parameters for a covariate that is negatively associated with outcome (placebo group favored at baseline).

4.4 Estimating Type I Error Rate Inflation in the NINDS tPA Dataset

Recall that part of the controversy surrounding the NINDS tPA trial stems from the observed imbalance in baseline NIHSS (disease severity) that resulted in a better baseline prognosis in the active treatment group. Original analysis of the tPA data did not adjust for NIHSS or several other predictive covariates (NINDS, 1995). Though there were several covariates that were influential on three month functional outcome (mRS), these simulations focused on only one such covariate. The relevant question in regard to the controversy of this trial is: Is the observed treatment effect in these data a result of imbalance in NIHSS at baseline, or is it truly a result of the effect of tPA? In other words, did the imbalance in NIHSS result in a type I error?

The GLMs modeling type I error rate versus imbalance in both exponential and logistic scenarios were used to estimate type I error rate inflation for a trial similar to the NINDS trial. Recall that the baseline imbalance in NIHSS observed in the NINDS dataset corresponded to a t-statistic of 1.48. The GLM for type I error rate in the exponential scenarios (note that these scenarios were simulated based on the tPA dataset, Section 3.2) estimated that this level of covariate imbalance corresponded to approximately double the nominal type I error rate (2.5%), corresponding to an overestimation of the treatment effect (RD) by about 1% (RD). Note that this is a conservative estimate because the actual level of covariate influence in the NINDS dataset was much larger (β_x > 1.5β̃_tx) than was possible to simulate in these scenarios (β_x = 0.68β̃_tx).

In the logistic scenarios that most closely resembled the observed relationships in the NINDS dataset, the estimated type I error rate inflation was almost triple (about 7%) that of the nominal (2.5%) type I error rate for an imbalance of t=1.48. This level of imbalance corresponded to an overestimated treatment effect of about 2% to 3% (RD). Again, these are conservative estimates, and the observed imbalance in the real dataset most likely resulted in more than double the nominal type I error rate and a greater than 3% (absolute RD) overestimation of treatment effect. It should also be noted that there were other covariates that were not examined here (e.g., age) that were also imbalanced at baseline in this dataset (NINDS, 1995; Ciolino et al., 2011b). These imbalances were not necessarily in the same direction as the one observed for NIHSS, and thus may have offset the effects of NIHSS imbalance on type I error rate. The purpose of this exercise was nonetheless meant to illustrate the possible effects of “insignificant” continuous baseline covariate imbalances on unadjusted analyses.

5 Discussion

It has been argued that in clinical trial data analysis, adjustment must be made for influential covariates regardless of their level of observed baseline imbalance (Ford and Norrie, 2002; Gail et al., 1984; Hauck et al., 1998; Hernández et al., 2004; Pocock et al., 2002; Raab and Day, 2000; Senn, 1989, 1994). In the case of continuous outcomes in linear models, the purpose of adjustment is to increase precision, thereby increasing power (Ford and Norrie, 2002; Raab and Day, 2000; Senn, 1989). On the other hand, when primary outcome is binary and the relationship between outcome, treatment, and covariate is logistic, adjusted analysis surprisingly results in decreased precision. The “bias” (underestimation of treatment effect) associated with unadjusted treatment effect estimation, however, outweighs any benefit it may show in precision, and thus, covariate adjustment is still suggested in these cases (Ford and Norrie, 2002; Gail et al., 1984; Hernández et al., 2004; Robinson and Jewell, 1991). These simulations consistently illustrate the benefit in power of adjusted analysis over unadjusted analysis. In logistic scenarios involving no covariate influence, estimated power was slightly larger (<1%) in almost all cases for unadjusted analyses. However, even with slightly influential covariate levels, the estimated power associated with adjusted analysis was substantially larger in almost all cases (Table 2). The benefit in in power of adjusted analyses for the logistic scenarios ranged from about 0% to 20%, and the benefit in power for the few exponential scenarios ranged from about 2% to 3%.

Note that when relationships between binary outcome and treatment/covariate(s) are linear (RD) or exponential (RR), the discrepancies between unadjusted and adjusted treatment effect estimates disappear (Gail et al., 1984). However, this research suggests that baseline covariate imbalance has nontrivial impact on bias, type I error, and power for unadjusted analyses when underlying relationships are linear (Ciolino et al., 2011a) or exponential (Figure 3). As a result, adjusted analyses are still favored in these cases to account for these potential imbalances, but models for RD or RR (using GLM identity or log link, respectively) should be interpreted with caution since they have the potential to result in estimated probabilities outside of [0,1] as well as convergence issues (Agresti and Hartzel, 2000; Deddens and Peterson, 2008; Blizzard and Hosmer, 2006). Thus, despite the ease of interpretation for RD and RR, these quantities are difficult to model when attempting to adjust for influential covariates, and logistic regression remains the most popular method of covariate adjustment when outcome is binary (Agresti and Hartzel, 2000). According to ICH guidelines, however, adjusted analyses should be planned and presented a priori, and any unplanned adjusted analyses should be considered secondary (ICH, 1999).

Furthermore, there has historically been less emphasis on analyses based on adjusted models than those based on unadjusted treatment effect estimates (Hauck et al., 1998; Hernández et al., 2004; Peduzzi et al., 2002; Pocock et al., 2002). The reason for this may be that unadjusted estimates that do not rely on model building are more easily interpretable and generalizable. It also may be the case that influential covariates are not known prior to commencement of the trial, and thus, adjustment cannot be pre-specified in the statistical analysis plan. In order to circumvent this issue, common practice is to show “comparable” treatment groups with respect to influential covariates of interest. That is, most articles reporting clinical trial results present a “Table 1,” reporting baseline covariate descriptive statistics stratified by treatment group. These tables often include p-values associated with baseline tests comparing means or proportions across treatment groups (Austin et al., 2010; Pocock et al., 2002). These tests, however, are invalid ways of evaluating covariate imbalance (Austin et al., 2010; Pocock et al., 2002; Roberts and Torgerson, 1999; Senn, 1989, 1994; Ciolino et al., 2011a). This paper provides further evidence of the inappropriateness of the t-test to compare continuous baseline covariates across treatment arms in a clinical trial. Further, this paper has shown that the t-statistic itself is a robust measure of baseline covariate imbalance, and the t-statistic can serve as a tool to evaluate the extent to which baseline covariate imbalance affects type I error rate, power, and bias in an unadjusted analysis.

Senn (1989, 1994); Ciolino et al. (2011a) have shown that when outcomes are continuous, insignificant levels of imbalance as measured by the t-statistic have potential to result in nontrivial bias, type I error rate inflation, or decrease in power. Ciolino et al. (2011a) suggest that continuous covariate balance can serve as a compromise between the unadjusted analyses (that may not allow for appropriate inference on treatment efficacy) and the less accepted, adjusted analysis of continuous outcome data; however, the standard baseline test using a 5% level of significance is an inappropriate method of evaluating covariate imbalance. Instead, a much more stringent level of significance is required in order to ensure power and type I error of unadjusted analysis are unaffected in the continuous outcome case; the level of imbalance that results in statistical issues with unadjusted analysis depends on the level of outcome-covariate association.

In this paper, imbalance (as measured by the t-statistic) is shown to be predictive of these statistical parameters for the logistic and exponential scenarios, but in some cases, no amount of balance can overcome the bias associated with unadjusted treatment effect estimation for logistic relationships. Thus, attempts should be made to balance known influential covariates at the design phase of a clinical trial, but it is imperative to adjust for any covariates found to be influential throughout the duration of the trial when analyses are based on logistic regression assumptions. Note that selection of covariates a priori is not always an easy task, and it requires a collaborative effort between statisticians and clinicians as well as knowledge from previous research and literature. It is impossible to adjust for all prognostic covariates because they may not all be known or even measureable (Steyerberg et al., 2000). Thus, if adjustment is not possible, one can use results from these simulations in an attempt to determine the magnitude of detrimental effect any baseline imbalances may have on unadjusted analysis. For example, in examining the scenarios closely resembling the NINDS tPA study, we determined that imbalance in baseline disease severity observed in the trial had the potential to result in an approximate tripling of type I error rate that corresponded to overestimation of true treatment effect by about 3% (see Section 4.4).

Finally, in these simulations, imbalance does not appear to have much effect on properly adjusted analysis. Ciolino et al. (2011b) have suggested the possibility that imbalance may have an effect on analysis even when properly adjusted, but the results presented in those cases pertain to large and relatively unlikely levels of imbalance. These simulations were meant to simulate natural levels of covariate imbalance. A blocking scheme was used to ensure equal sample sizes, and large imbalances (|t| > 3) were observed in very few trials out of the simulated 5000. Thus, when imbalance (no matter which way it is measured) is within practical ranges, the association between imbalance and power, type I error rate, and bias for adjusted analyses is negligible. This does not suggest that balance is unimportant if covariate adjustment is planned in the analysis anyway, but adjustment at the end of a trial does have strength to overcome imbalance at baseline. If one plans to adjust for influential covariates in analyses, then ensuring balance through complex treatment allocation algorithms becomes less imperative, but this is only if one can ensure that inferences will be based on adjusted analyses. Balance in important baseline covariates still remains crucial for face validity, secondary outcome analyses, interim analyses, and any other situations in which adjustment may not be possible (McEntegart, 2005), but it is not meant to serve as a replacement for the covariate adjusted analysis, especially in the case of nonlinear logistic relationships among outcome and predictors.