Abstract
Segmentation and parcellation of the thalamus is an important step in providing volumetric assessment of the impact of disease on brain structures. Conventionally, segmentation is carried out on T1-weighted magnetic resonance (MR) images and nuclear parcellation using diffusion weighted MR images. We present the first fully automatic method that incorporates both tissue contrasts and several derived features to first segment and then parcellate the thalamus. We incorporate fractional anisotrophy, fiber orientation from the 5D Knutsson representation of the principal eigenvectors, and connectivity between the thalamus and the cortical lobes, as features. Combining these multiple information sources allows us to identify discriminating dimensions and thus parcellate the thalamic nuclei. A hierarchical random forest framework with a multidimensional feature per voxel, first distinguishes thalamus from background, and then separates each group of thalamic nuclei. Using a leave one out cross-validation on 12 subjects we have a mean Dice score of 0.805 and 0.799 for the left and right thalami, respectively. We also report overlap for the thalamic nuclear groups.
Keywords: Brain imaging, diffusion MRI, magnetic resonance imaging, machine learning, segmentation, thalamus parcellation
1 Introduction
The thalamus is a sub-cortical gray matter (GM) structure in the brain of vertebrates that is symmetric in the midline and located between the cerebral cortex and midbrain [18]. Its principal function is the relaying of sensory and motor signals to the cerebral cortex [18] and the regulation of consciousness, sleep, and alertness. The thalamus consists of lamellae—myelinated fibers—which separate the thalamus into its components and are grouped based on the orientation and location of distinct clusters of neurons. The most well known of these thalamic nuclear groups are the anterior nucleus (AN), medial dorsal (MD), ventral (VNG), pulvinar (PUL), lateral geniculate (LGN) and medial geniculate (MGN)—though each of these groups is made up of several smaller bundles of fibers. These nuclear groups are differentially affected in neurodegenerative diseases such as multiple sclerosis [8], Alzheimer’s disease [4], schizophrenia [6, 10], and Parkinson’s disease [12]. Unfortunately, much of our understanding of the thalamus has come from neuropathological ex-vivo studies [6, 10, 12] which is not surprising considering that thalamic nuclei present minimal contrast in conventional MRI. Diffusion tensor imaging (DTI) presents a greater opportunity to unlock the secrets of the thalamus, as distinct tract connectivities and cytoarchitectures [16] provide a platform to distinguish the nuclear groups in-vivo. However, the exclusive use of DTI would make it impossible to distinguish the thalamus from other adjacent structures.
Previous work [11, 14, 17, 20, 23, 24] has been limited to methods dependent on some level of manual interaction. This work presents two innovations: 1) it is the first fully automatic multi-modal thalamus segmentation algorithm, and 2) it is also the first fully automated thalamic nuclei parcellation—into AN, MD, VNG, PUL, LGN, and MGN—using tensor-based features within the thalamus and cortical connectivity features derived from tractography. Our method starts by generating an estimate of the region of interest (ROI) of the thalamus. Within this ROI, features are computed, including diffusion tensors and their principal directions and probabilistic connectivities between each voxel and lobar labels on the cerebral cortex. These features are used in a hierarchical random forest (RF) classifier framework, where the first RF segments the thalamus within the ROI, and a second RF identifies the collection of nuclear groups. The method is tested against manual delineation and its two phases (thalamic segmentation and nuclear group identification) are compared to other methods.
2 Method
2.1 ROI Identification
To reduce the computational burden of training an RF we estimate bounding boxes for the left and right thalami, denoted
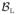 and
and
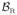 respectively. These ROIs are identified using a tissue segmentation and labeling approach based on topology preservation and fuzzy classification [1]. For voxel j with spatial position xj in the image domain Ω and with MR intensity
respectively. These ROIs are identified using a tissue segmentation and labeling approach based on topology preservation and fuzzy classification [1]. For voxel j with spatial position xj in the image domain Ω and with MR intensity
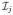 , there are functions ujk which represent the membership of the voxel with respect to structure k. The structures k have an intensity centroid of ck. We introduce rjk as a penalty term that discourages unrealistic configurations such as the thalamus touching the cerebellum. We have prior probabilities pjk coming from a statistical atlas and weights wkm on the intensity difference between the centroids of two classes ck and cm. These terms are combined to form the following energy minimization problem,
, there are functions ujk which represent the membership of the voxel with respect to structure k. The structures k have an intensity centroid of ck. We introduce rjk as a penalty term that discourages unrealistic configurations such as the thalamus touching the cerebellum. We have prior probabilities pjk coming from a statistical atlas and weights wkm on the intensity difference between the centroids of two classes ck and cm. These terms are combined to form the following energy minimization problem,
| (1) |
where q is a fuzziness parameter. The first term, on the right hand side of Equation (1) ensures voxels in the same structure have similar intensity values, while the second term controls the smoothness of the memberships, and the final term regulates the influence of the prior probability. β and γ are weights that balance the relative influence of the terms. The energy is minimized while simultaneously maintaining the topological arrangements of the objects achieved through max membership assignment.
Given a fuzzy segmentation estimate of the left thalamus
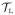 ,
,
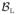 is defined as
is defined as
| (2) |
where lL =
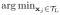 xj, hL =
xj, hL =
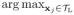 xj, and rL = 0.1 × (hL − lL), which pads
xj, and rL = 0.1 × (hL − lL), which pads
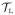 by 10% along each axes. This process is repeated for
by 10% along each axes. This process is repeated for
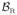 from its corresponding fuzzy segmentation
from its corresponding fuzzy segmentation
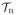 . Henceforth, when we refer to
. Henceforth, when we refer to
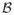 it is implied that the process is repeated for both
it is implied that the process is repeated for both
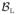 and
and
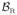 , independently.
, independently.
2.2 Knutsson Space and Edge Maps
DTI is acquired from diffusion weighted MRI, using a gradient spin echo pulse sequence with a known b-value b and gradient direction g. The diffusion signal, S(b, g), at each voxel is an attenuated version of the signal S0 that would be recorded in the absence of diffusion weighting. The relationship can be specified using the Stejskal-Tanner equation,
| (3) |
where D is the 3 × 3 symmetric diffusion tensor,
| (4) |
The eigenvalues (λ1, λ2, λ3) from Equation (4) have eigenvectors (u1, u2, u3).
Two common quantities computed from the eigenvalues are the mean diffusivity (MD) and fractional anisotrophy (FA), denoted
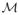 and
and
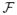 , respectively. The principal eigenvector (PEV) u1 represents the direction of maximum diffusion. As the diffusion occurs either in the direction of u1 or in the opposite direction −u1 with equal probability, it is convenient to represent the direction u as an orientation using the Knutsson map [15], which transforms the eigenvector u from
, respectively. The principal eigenvector (PEV) u1 represents the direction of maximum diffusion. As the diffusion occurs either in the direction of u1 or in the opposite direction −u1 with equal probability, it is convenient to represent the direction u as an orientation using the Knutsson map [15], which transforms the eigenvector u from
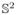 to
to
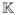 ⊂ ℝ5 by
⊂ ℝ5 by
| (5) |
This mapping takes opposing Cartesian vectors and sends them to the same location in Knutsson space
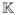 —that is both length and direction are crushed in the transformation to
—that is both length and direction are crushed in the transformation to
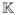 . We can now generate an edge map using orientations in
. We can now generate an edge map using orientations in
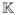 . For v = (v1, …, v5) ∈
. For v = (v1, …, v5) ∈
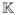 we have the gradient matrix G and its Frobenius norm ||G||F given by
we have the gradient matrix G and its Frobenius norm ||G||F given by
| (6) |
This is an edge map representing a change in the direction of the PEV, which will allow us to distinguish thalamic nuclei.
2.3 Connectivity to the Cortical Mantle
Connectivity to the cortical mantle is calculated using probabilistic tractography [3] implemented in the FSL toolkit. Six cortical masks corresponding to thalamic connection sites are used as the targets for the tractography algorithm. Ml is the set of voxels in a cortical mask and l is the cortical mask label. The six labels for the cortical masks are {frontal, occipital, parietal, temporal, precentral, postcentral}.
Connectivity Cl(x) is defined as the number of times a sample starting at the voxel x forms a pathway connecting to any voxel y belonging to the cortical mask with label l,
| (7) |
5000 samples are initiated per voxel in
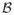 and the path direction is determined by local fiber directions.
and the path direction is determined by local fiber directions.
2.4 Features and Random Forest Framework
The first features input into our RF framework are the relative position of xj ∈
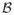 and the MR intensity value at xj,
and the MR intensity value at xj,
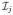 . These intensities provide clues about the boundary of the thalamus with non-thalamus structures. The core distinguishing features of the nuclear groups are fiber orientation and strength. Thus the next set of features are the FA, MD, Knutsson mapping, and Frobenius norm, denoted as
. These intensities provide clues about the boundary of the thalamus with non-thalamus structures. The core distinguishing features of the nuclear groups are fiber orientation and strength. Thus the next set of features are the FA, MD, Knutsson mapping, and Frobenius norm, denoted as
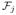 ,
,
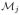 , {K(xj)}, and ||G(K(xj))||F, respectively. The final features are the connectivity between the position xj and the six cortical labels (i.e., the Cl(xj)’s), denoted {C(xj)}. The complete feature vector fj is
, {K(xj)}, and ||G(K(xj))||F, respectively. The final features are the connectivity between the position xj and the six cortical labels (i.e., the Cl(xj)’s), denoted {C(xj)}. The complete feature vector fj is
| (8) |
which gives us an 18-dimensional feature space.
Our hierarchical RF [5] approach uses fj for each voxel in the available training data to build a collection of trees that first distinguishes the thalamus within
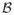 from other tissues. This is a binary classification task identifying thalamus from background. A second RF is then built using the same feature vector, trained to provide a membership for each of the six thalamic nuclear groups given that we know the thalamus from the first stage. The first stage thalamus identification can be quite noisy due to peripheral objects have a thalamus-like appearance. To reduce this artifact, we select the largest connected component foreground object which we then close with a 3 × 3 × 3 structuring element. The learnt RFs can be applied to a new subject, with the classification scores determining the segmentation of the thalamus and subsequent parcellation of the nuclear groups.
from other tissues. This is a binary classification task identifying thalamus from background. A second RF is then built using the same feature vector, trained to provide a membership for each of the six thalamic nuclear groups given that we know the thalamus from the first stage. The first stage thalamus identification can be quite noisy due to peripheral objects have a thalamus-like appearance. To reduce this artifact, we select the largest connected component foreground object which we then close with a 3 × 3 × 3 structuring element. The learnt RFs can be applied to a new subject, with the classification scores determining the segmentation of the thalamus and subsequent parcellation of the nuclear groups.
3 Results
3.1 Data
Our data consists of 12 subjects from a study of cerebellar ataxia. The subject images were acquired on a 3T MR scanner (Intera, Philips Medical Systems, Netherlands) and have undergone standard neuroimaging processing: inhomogeneity correction [19], skull stripping [7], isotropic resampling [22] to 0.828 mm, distortion correction [21], and probabilistic tractography [13]. A subject is shown in Fig. 1 showing some of the input contrasts. We refer to our method as OM 18F, as in our method using 18 features.
Fig. 1.

Shown are (a) the MPRAGE
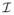 , (b) the FA
, (b) the FA
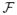 , and (c) the edgemap ||G||F. Thalami estimates from (d) FreeSurfer [9], (e) our method (OM 18F), and (f) a manual delineation.
, and (c) the edgemap ||G||F. Thalami estimates from (d) FreeSurfer [9], (e) our method (OM 18F), and (f) a manual delineation.
A manual rater first used the FA to find the thalamus boundary, then used the Knutsson edge map to delineate nuclear structures that we identify as the AN, MD, PUL, LGN, and MGN nuclei. VG is the complement of these structures, within the thalamus boundary. We use these reproducible manual delineations as a ground truth for our training and testing.
3.2 Thalamus Boundary
Our first results compare our estimate of the thalamus with those from two whole brain segmentation software tools [1, 9]. We used leave-one-out cross-validation to train both our RFs, the results are averaged over the different cross-validation runs and Dice scores are shown in Fig. 2. A paired Wilcoxon rank sum test comparing our method with Bazin and Pham [1] (TOADS) had a p-value < 0.001 for both the left and right thalami (computed independently), indicating significant improvement. A similar test between our method and Dale et al. [9] (FreeSurfer) gives a p-value < 0.001 for the right thalamus; however for the left thalamus the p-value is 0.00684, which is just shy of statistical improvement. We note that in this stage, as in the next, there are two RFs one for the left thalamus and the other for the right stemming from
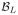 and
and
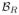 , respectively. Example results and comparison to our ground truth is shown in Fig. 1.
, respectively. Example results and comparison to our ground truth is shown in Fig. 1.
Fig. 2.
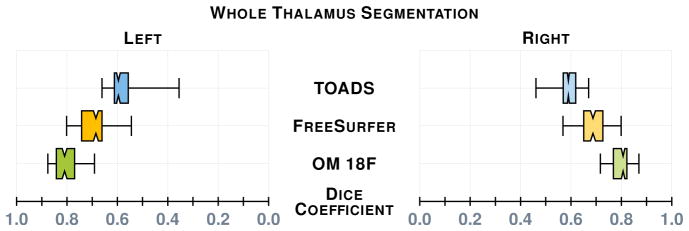
A comparison between our thalamus segmentation (OM 18F) and those of Bazin and Pham [1] (TOADS) and Dale et al. [9] (FreeSurfer 5.3.0). The notches give a 95% confidence interval for the difference in two medians.
3.3 Thalamic Nuclei Segmentation
The second step in our hierarchical RF framework distinguishes thalamic nuclei assuming that the thalamus boundary is known from the first stage. The left and right thalami were those identified in Section 3.2, which were passed through their respective trained RFs to predict the nuclear groups. We also implemented an automated algorithm based on Behrens et al. [2], which used only the cortical labels to parcellate the thalamus. The fiber groupings in Behrens et al. [2] are different to ours, thus for comparison we merged AN & MD (AN+MD). Behrens et al. [2] also excluded LGN and MGN from their parcellation. The comparable nuclear groups—AN+MD; VNG; PUL—are shown in Fig. 3, as well as the additional nuclear groups we can parcellate. A paired Wilcoxon rank sum test comparing the results has a p-value < 0.001 for the VNG and PUL on both thalami. We fail to reach significance when comparing for AN+MD, because we train for AN and MD separately; training on the merging of these groups would perform better. Examples of our parcellation for two subjects are shown in Fig. 4.
Fig. 3.
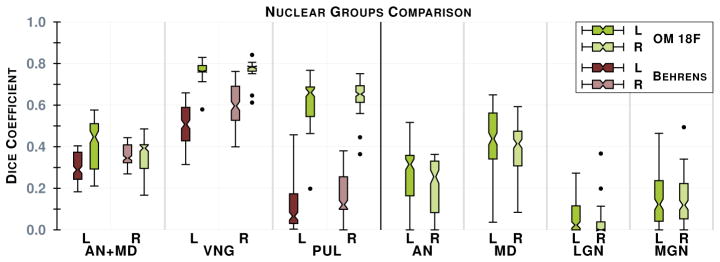
The plot on the left is a comparison of the Dice score between our implementation of Behrens et al. [2] (B) (shades of brown) and our method (OM 18F) (shades of green), see the text for details. On the right is the remaining nuclear groups we can generate. Both plots are for our 12 subjects. Results for left and right thalami are denoted L and R, respectively. The notches give a 95% confidence interval for the difference in two medians.
Fig. 4.
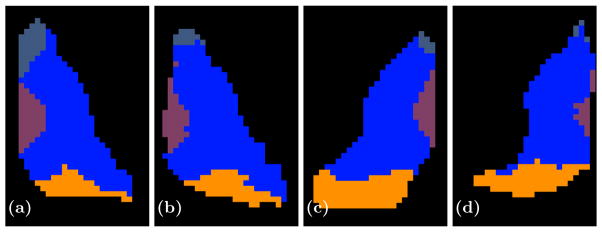
Shown are axial slices of (a) a manual delineation and (b) our parcellation for a right thalamus on one of our better results and (c) a manual delineation and (d) our parcellation of a left thalamus for a bad result. The AN is shown in a slate blue anterior to the thalamus, the VNG is the large blue body in the center of the thalamus, while MD and PUL are shown in purple and orange, respectively.
4 Conclusion
In this paper we have presented the first fully automatic thalamic parcellation method using multi-modal imaging data, and we make two important contributions. Firstly we use a multi-channel framework to segment the thalamus—the first such method. Secondly, we provide a parcellation of the six core nuclear groups of the thalamus in a fully automated fashion.
Acknowledgments
This work was supported by the NIH/NINDS grants R21-NS082891 and R01-NS056307. Jeffrey Glaister is supported by the Natural Sciences and Engineering Research Council of Canada. We would like to thank the MICCAI reviewers for their suggestions in helping improve our approach.
References
- 1.Bazin PL, Pham DL. Homeomorphic brain image segmentation with topological and statistical atlases. Medical Image Analysis. 2008;12(5):616–625. doi: 10.1016/j.media.2008.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Behrens TEJ, et al. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nature Neuroscience. 2003;6(7):750–757. doi: 10.1038/nn1075. [DOI] [PubMed] [Google Scholar]
- 3.Behrens TEJ, et al. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? Neuro Image. 2007;34(1):144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Braak H, Braak E. Alzheimer’s disease affects limbic nuclei of the thalamus. Acta Neuropathologica. 1991;81(3):261–268. doi: 10.1007/BF00305867. [DOI] [PubMed] [Google Scholar]
- 5.Breiman L. Random Forests. Machine Learning. 2001;45(1):5–32. [Google Scholar]
- 6.Byne W, et al. Postmortem Assessment of Thalamic Nuclear Volumes in Subjects With Schizophrenia. Am J Psychiatry. 2002;159(1):59–65. doi: 10.1176/appi.ajp.159.1.59. [DOI] [PubMed] [Google Scholar]
- 7.Carass A, et al. Simple paradigm for extra-cerebral tissue removal: Algorithm and analysis. Neuro Image. 2011;56(4):1982–1992. doi: 10.1016/j.neuroimage.2011.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cifelli A, et al. Thalamic neurodegeneration in multiple sclerosis. Annals of Neurology. 2002;52(5):650–653. doi: 10.1002/ana.10326. [DOI] [PubMed] [Google Scholar]
- 9.Dale AM, et al. Cortical Surface-Based Analysis I: Segmentation and Surface Reconstruction. Neuro Image. 1999;9(2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- 10.Danos P, et al. Volumes of association thalamic nuclei in schizophrenia: a postmortem study. Schizophrenia Research. 2003;60(2–3):141–155. doi: 10.1016/s0920-9964(02)00307-9. [DOI] [PubMed] [Google Scholar]
- 11.Duan Y, et al. Thalamus Segmentation from Diffusion Tensor Magnetic Resonance Imaging. International Journal of Biomedical Imaging. 2007;5(2):1–5. doi: 10.1155/2007/90216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jellinger KA. Post mortem studies in Parkinson’s disease–is it possible to detect brain areas for specific symptoms? J Neural Transm Suppl. 1999;56:1–29. doi: 10.1007/978-3-7091-6360-3_1. [DOI] [PubMed] [Google Scholar]
- 13.Jenkinson M, et al. FSL. Neuro Image. 2012;62(2):782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- 14.Jonasson L, et al. A level set method for segmentation of the thalamus and its nuclei in DT-MRI. Signal Processing. 2007;87(2):309–321. [Google Scholar]
- 15.Knutsson H. Producing a Continuous and Distance Preserving 5-D Vector Representation of 3-D Orientation. IEEE Computer Society Workshop on Computer Architecture for Pattern Analysis and Image Database Management; 1985. pp. 175–182. [Google Scholar]
- 16.Morel A, et al. Multiarchitectonic and Stereotactic Atlas of the Human Thalamus. J Comparative Neurology. 1997;387(4):588–630. doi: 10.1002/(sici)1096-9861(19971103)387:4<588::aid-cne8>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 17.Rittner L, et al. Segmentation of thalamic nuclei based on tensorial morphological gradient of diffusion tensor fields. 7th International Symposium on Biomedical Imaging (ISBI 2010); 2010. pp. 1173–1176. [Google Scholar]
- 18.Sherman SM, Guillery R. Exploring the Thalamus. Elsevier; 2000. [Google Scholar]
- 19.Sled JG, et al. A non-parametric method for automatic correction of intensity non-uniformity in MRI data. IEEE Trans Med Imag. 1998;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- 20.Stough J, et al. Thalamic Parcellation from Multi-Modal Data using Random Forest Learning. 10th International Symposium on Biomedical Imaging (ISBI 2013); 2013. pp. 852–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Studholme C, et al. Accurate alignment of functional EPI data to anatomical MRI using a physics-based distortion model. IEEE Trans Med Imag. 2000;19(11):1115–1127. doi: 10.1109/42.896788. [DOI] [PubMed] [Google Scholar]
- 22.Thévenaz P, et al. Interpolation revisited [medical images application] IEEE Trans Med Imag. 2000;19(7):739–758. doi: 10.1109/42.875199. [DOI] [PubMed] [Google Scholar]
- 23.Wiegell MR, et al. Automatic segmentation of thalamic nuclei from diffusion tensor magnetic resonance imaging. Neuro Image. 2003;19(2):391–401. doi: 10.1016/s1053-8119(03)00044-2. [DOI] [PubMed] [Google Scholar]
- 24.Ye C, et al. Parcellation of the Thalamus Using Diffusion Tensor Images and a Multi-object Geometric Deformable Model. Proceedings of SPIE Medical Imaging (SPIE-MI 2013); Orlando, FL. February 9–14, 2013; 2013. pp. 866909–866909–7. [DOI] [PMC free article] [PubMed] [Google Scholar]


