Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Nov 26;118(51):14827–14832. doi: 10.1021/jp511702w

Poisson–Boltzmann versus Size-Modified Poisson–Boltzmann Electrostatics Applied to Lipid Bilayers

Nuo Wang †, Shenggao Zhou ‡, Peter M Kekenes-Huskey §, Bo Li ‡, J Andrew McCammon †,§,⊥,*
PMCID: PMC4280115  PMID: 25426875

Abstract

graphic file with name jp-2014-11702w_0005.jpg

Mean-field methods, such as the Poisson–Boltzmann equation (PBE), are often used to calculate the electrostatic properties of molecular systems. In the past two decades, an enhancement of the PBE, the size-modified Poisson–Boltzmann equation (SMPBE), has been reported. Here, the PBE and the SMPBE are reevaluated for realistic molecular systems, namely, lipid bilayers, under eight different sets of input parameters. The SMPBE appears to reproduce the molecular dynamics simulation results better than the PBE only under specific parameter sets, but in general, it performs no better than the Stern layer correction of the PBE. These results emphasize the need for careful discussions of the accuracy of mean-field calculations on realistic systems with respect to the choice of parameters and call for reconsideration of the cost-efficiency and the significance of the current SMPBE formulation.

1. Introduction

Mean-field methods provide a way to coarse grain the electrostatic interactions between the solvent and the biomolecules of interest.1 They are commonly used to generate the electrostatic potentials needed for biomolecular diffusion simulations2−5 and are used in calculations of the solvation free energies of biomolecules.6,7

The hundred-year-old Poisson–Boltzmann equation (PBE) is currently the flagship of the mean-field methods.8−10 Despite the success of the PBE,11,12 it is built upon several approximations; for example, the ions in the PBE are considered infinitesimally small. This approximation runs into trouble near highly charged biomolecular surfaces, such as those of typical enzyme active sites.13 The reason is that, under the strong electrostatic attractions near highly charged surfaces, the concentration of the counterion can exceed its maximally allowed value without the restriction from steric hindrance; this will then lead to an overestimation of electrostatic screening and an underestimation of the electrostatic potential exerted by the biomolecule.14,15 To remedy the lack of ion steric hindrance, or ion-size effects, in the PBE, a Stern layer, or ion-exclusion layer, outside of the molecular surface has been used, within which no ion is allowed.16

To improve the PBE, the size-modified Poisson–Boltzmann equation (SMPBE), which incorporates the finite ion sizes through a more physical lattice gas formulation, was developed and has been applied to biomolecular systems.14,17−20 The computational cost of the SMPBE is comparable to that of the PBE when there are only two ion sizes.18 However, in its generalized form that can handle an arbitrary number of different ion sizes, the SMPBE takes much longer to solve.19,21

It is known that mean-field methods are parameter-dependent and that there is no standard way of choosing input parameters that guarantee the optimum accuracy of prediction.22−25 The SMPBE is reported to reproduce experimental18 and molecular dynamics simulation20 results better than the PBE, but there still lacks a comprehensive comparison between these two mean-field methods using a variety of input parameters to determine whether the SMPBE generally outperforms the PBE.

This paper discusses the accuracy of prediction and the cost-efficiency of the SMPBE with respect to the PBE using several different parameter sets. Given that the mean-field methods are parameter-dependent, this work also discusses the existence of a single parameter set with which the mean-field methods give consistent high accuracy of prediction across different ionic strengths and surface charge densities. Specifically, the equilibrium ion distributions outside of neutral and charged lipid bilayers are calculated by the PBE and the SMPBE using eight different parameter sets and are compared to the molecular dynamics (MD) simulation results. The long-term goal of this work is to identify appropriate tools for modeling diffusion dynamics of molecules that are of biological or medical interest.26,27 In these diffusion processes, the system evolves from a nonequilibrium state to the equilibrium state, and this work is an initial step to test the ability of the SMPBE in predicting ion distributions in the equilibrium state. Lipid bilayers are considered here because of their profound importance in the activity of membrane proteins and cross-membrane signaling pathways.28,29

2. Methods

2.1. The SMPBE Implementation

The SMPBE formulation used here is capable of calculating the electrostatic potential and the ion distributions for molecular systems containing an arbitrary number of ion species with different ion sizes.19,21 A brief description of the formulation is included in the Supporting Information (SI) section I. This formulation is an extension of the earlier foundational SMPBE theory by Borukhov et al.,14 which, in its original form, can only handle one same-size cation–anion pair.

This SMPBE formulation is implemented in the Adaptive Poisson–Boltzmann Solver (APBS)30 and is freely available upon request. A brief explanation of the SMPBE routine in APBS is included in section II of the SI.

2.2. Numerical Calculations

Molecular dynamics (MD) simulations can generate the equilibrium ion distributions in a molecular system at higher accuracy and resolution than the mean-field methods but also at significantly greater computational expense.1 In this work, the MD simulation results are used as a standard to assess the accuracy of the PBE and the SMPBE predictions.

2.2.1. Molecular Dynamics Simulations

The dimensions of the lipid bilayer systems used in the MD simulations and the mean-field calculations are illustrated in Figure S1 of the SI. In this work, eight lipid bilayer MD systems are simulated (Table 1).

Table 1. Composition of the Molecular Dynamics Systemsa.
system lipid cation anion bulk salt concentration
1 48 POPC 10 Na+ 10 Cl– 0.060 M
2 48 POPC 20 Na+ 20 Cl– 0.126 M
3 48 POPC 40 Na+ 40 Cl– 0.268 M
4 48 POPC 10 K+ 10 Cl– 0.060 M
5 48 POPC 20 K+ 20 Cl– 0.134 M
6 48 POPC 40 K+ 40 Cl– 0.275 M
7 48 POPS 68 Na+ 20 Cl– 0.170 M
8 48 POPS 68 K+ 20 Cl– 0.169 M
Open in a new tab
a

POPC, 1-palmitoyl-2-oleoylphosphatidylcholine; POPS, 1-palmitoyl-2-oleoylphosphatidylserine. The bulk salt concentration is the averaged salt (NaCl, KCl) concentration at |z| = 60 Å (z, the perpendicular distance to the bilayer center, is defined in Figure S1 of the SI) over the converged portion of the MD trajectories.

1-Palmitoyl-2-oleoylphosphatidylcholine (POPC) is a partially charged, but overall neutral, lipid molecule, and each 1-palmitoyl-2-oleoylphosphatidylserine (POPS) lipid molecule carries one negative charge. All of the systems in Table 1 are built by the online application CHARMM-GUI Membrane Builder.31 The MD simulations are performed by NAMD2.9 software package32 with CHARMM3633 lipid force field34 using mostly the default system settings offered by the CHARMM-GUI Membrane Builder (see section III of the SI). Each system in Table 1 is simulated for 100–150 ns. All of the POPC simulations are 150 ns long and reach convergence after 20 ns. All of the POPS simulations are 100 ns long and converge after 30 ns. The converged MD trajectories are utilized for all of the data analysis (see section III of the SI for the convergence criteria).

2.2.2. Mean-Field Calculations

To test the accuracy of a mean-field method in predicting the ion distributions in an MD system listed in Table 1, three MD frames are evenly sampled from the converged MD trajectory, and a mean-field calculation is performed for each frame; the final mean-field results are averaged over all three calculations. Note that APBS has no periodic boundary conditions in its finite difference routine. To avoid boundary effects, the lipid bilayer structures obtained from the MD simulations are manually extended 0.25 times along the positive and negative x,y-axis, while the mean-field results are only collected above and below the original size of the lipid bilayer as in the MD simulations, see Figure S1 of the SI. A 161(x) by 161(y) by 193(z) finite difference grid is used for all of the mean-field calculations following the APBS electrostatic focusing scheme,30 and the grid spacing is 0.43 Å(x) by 0.43 Å(y) by 0.47 Å(z), a reasonable resolution for calculating ion distributions. The lipid atomic charges and radii are taken from CHARMM36 charges and CHARMM36 van der Waals radii. Both the PBE and the SMPBE are solved in their nonlinear form. The majority of the input parameters for the mean-field methods follow the default settings of the APBS input preparation program PDB2PQR35 except for the ones mentioned in the next section. See section IV of the SI for an example of the APBS input file. Data analysis in this work utilizes GROMACS4.5.5,36 VMD1.9.1,37 and customized scripts.

3. Explanations on the Eight Mean-Field Parameter Sets

The use of different mean-field method input parameters is key to the discussion of the accuracy of predictions of the SMPBE with respect to those of the PBE. Among all of the mean-field calculation input parameters or settings, two are selected for the discussion. First, the ion size is chosen mainly because it is a particularly important input parameter for the SMPBE, and it is also used to define the size of the Stern layer. Second, the definition of molecular surface is chosen for its direct relationship to ion accessibility, thus the ion distributions. Specifically, four definitions of molecular surface, Figure 1, and two sets of ion sizes, Table 2, are tested, yielding a permutation of eight different sets of input parameters.

Figure 1.

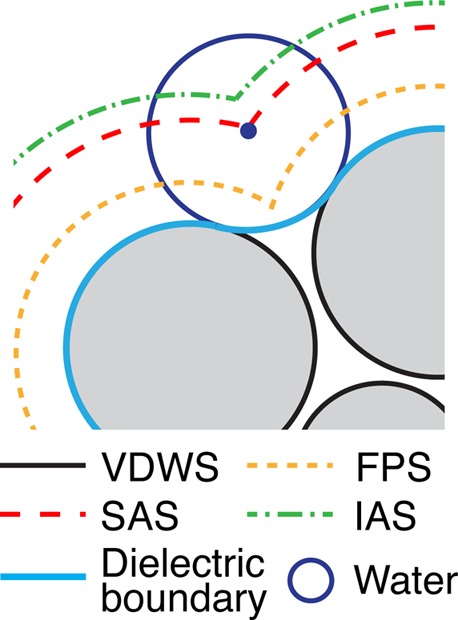
Figure 1

Open in a new tab

Definitions of molecular surface. VDWS: the van der Waals surface, drawn around the lipid atom centers with the CHARMM36 VDW radii, i.e., the Lennard-Jones rmin/2 values. FPS: the first-peak surface, drawn according to the MD cation–lipid carbonyl oxygen radial distribution function (RDF) first-peak positions. SAS: the solvent-accessible surface, drawn by the center of the water probe of radius 1.4 Å38 rolling across VDWS. IAS: the ion-accessible surface, drawn in the same way as the SAS, only that the probe radius is that of the counterion. The dielectric boundaries in all of the mean-field calculations are the same and are defined by the solid light-blue line (or equivalently the solvent-exclusion surface).

Table 2. Two Sets of Ion Radiia.

  VDW radius RDF radius
Na+ 1.4 Å 2.3 Å
K+ 1.8 Å 2.6 Å
Cl– 2.3 Å 4.0 Å
Open in a new tab
a

The van der Waals (VDW) radii are taken from the CHARMM36 ion VDW radii. The radial distribution function (RDF) radii are the first-peak positions of the ion–lipid carbonyl oxygen RDFs from the MD simulations.

Three key points need to be clarified. First, despite the multiple definitions of the molecular surface in Figure 1, only the van der Waals surface (VDWS) is commonly recognized as the molecular surface. Second, the reason for the flexible use of the term molecular surface in this work is as follows. Supposedly, the SMPBE, without the help of the Stern layer, is able to predict solvation properties comparably accurately or more accurately than the PBE with a Stern layer. However, as it is shown later in the Results section, unexpectedly, using the SMPBE outside of the VDWS without a Stern layer leads to large ion concentration overestimation. To carry out further investigations, several alternative molecular surfaces that are further away from the lipid molecules than the VDWS are tested. Finally, the seemingly peculiar use of the first-peak surface (FPS) is inspired by the fact that the MD radial distribution function (RDF) first-peak positions are often smaller than the sum of the VDW radii of the cation and its association partner, the lipid carbonyl oxygen.39 FPS is generated by uniformly expanding the VDWS until the minimum FPS–lipid carbonyl oxygen center distance is equal to the counterion–lipid carbonyl oxygen MD RDF first-peak position. The VDWS is expanded by 0.6 Å for the Na+ FPS and 0.9 Å for the K+ FPS. Using the FPS in the mean-field methods could theoretically reproduce the MD results better. However, this turns out not to be the case as shown in the Results section. The RDF radius is chosen because it was used in a previous work,20 and an alternative set of ion radii is needed to show how the PBE and the SMPBE results change with respect to the change of ion sizes.

4. Results and Discussion

4.1. The PBE vs the SMPBE

Figure 2 shows an array of calculations on the number of Na+ ions bound per POPC molecule. The corresponding results for the K+ ion are shown in the SI (Figure S2). The number of ions bound is calculated by integrating the concentration of ions within 25 Å to the lipid bilayer center. An example of the detailed position-dependent ion concentration is shown in the SI (Figure S3).

Figure 2.

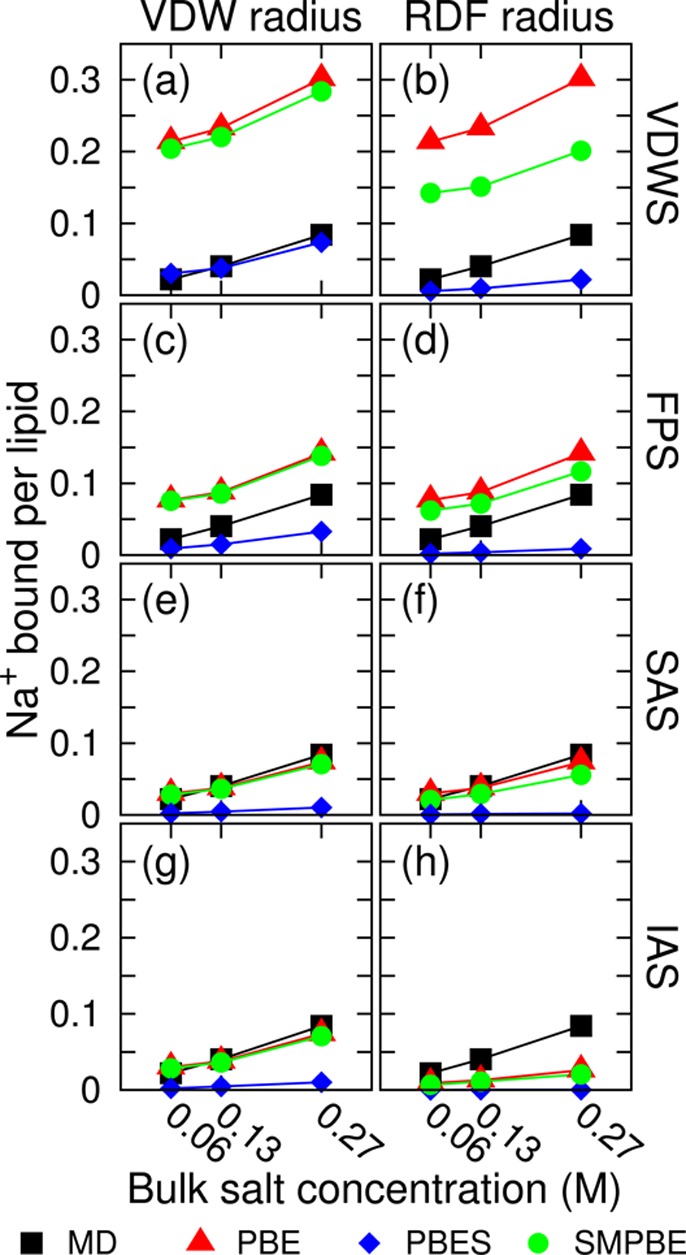
Figure 2

Open in a new tab

Number of Na+ bound per POPC molecule at three NaCl bulk concentrations (systems 1–3 in Table 1). MD: molecular dynamics; PBE: nonlinear Poisson–Boltzmann equation (without Stern layer); PBES: PBE with Stern layer; SMPBE: size-modified Poisson–Boltzmann equation (without Stern layer). Subfigures (a)–(h) use eight different parameter sets; each is a combination of a molecular surface (VDWS, FPS, SAS, IAS, see Figure 1) and an ion radius set (VDW radius, RDF radius, see Table 2). (g) turns out to be identical to (e) because the Na+ VDW radius happens to be the same as the radius of water, 1.4 Å, and so the SAS in (e) is exactly the same as the IAS in (g).

By a crude observation, the PBE and the SMPBE reproduce MD results the best in Figure 2g, while the PBES (the PBE with Stern layer; the size of the Stern layer is always set to be the radius of the cation) performs the best in Figure 2a. However, the PBES calculation in Figure 2a is actually the same as the PBE calculation in Figure 2g. This is because the ion-accessible surface (IAS) used in Figure 2g exactly overlaps with the outer surface of the Stern layer in Figure 2a. Also, it should be reemphasized that the VDWS is the physical molecular surface, and it is only fair to compare the SMPBE results without the use of a Stern layer to the PBE results with the use of a Stern layer. With this said, it can be concluded from Figure 2a and b that when the SMPBE is used outside of the physical molecular surface without a Stern layer, it significantly overestimates the MD ion concentrations compared to the PBE calculation with the aid of a Stern layer; the size-modified correction of the PBE does not seem to be as effective as the Stern-layer-modified correction. This is a surprising result considering the fact that the POPC bilayer has zero net surface charge and yet the capability of the SMPBE is not enough to limit the ion concentrations to the correct range. Furthermore, caution should be taken to distinguish the real source of the corrections or errors. Given the poor performance of the SMPBE in Figure 2a, it is clear that the reproduction of the MD results by the SMPBE in Figure 2g is mainly due to the introduction of an effective Stern layer through the use of the IAS instead of the SMPBE formulation itself. The reason for the underestimation of the MD results by the PBES in Figure 2g is the redundant use of a second Stern layer on top of the IAS.

Fortunately, as expected, at least the use of the SMPBE consistently alleviates the overestimation of ion concentrations by the PBE. The strength of SMPBE correction increases as the molecular surface shrinks (IAS to VDWS), which causes ions to experience a stronger electrostatic potential, and as the ion radii increase (VDW radius to RDF radius), which results in more steric exclusion between ions in the SMPBE formulation. However, in general, the SMPBE gives similar results to the PBE (Figure 2a, c, e, f, g, and h). A previous study has shown that the electrostatic free energies predicted by the PBE and the SMPBE can be quite different,40 but in this work, the PBE and the SMPBE electrostatic potentials are shown to also be very similar under most parameter sets, see Figure S4 of the SI. As mentioned in the Introduction, the SMPBE has a comparable computational cost to the PBE when two ion sizes are used,18 but the cost significantly increases when the SMPBE is generalized to handle an arbitrary number of different ion sizes because the SMPBE can no longer be expressed analytically.19,21 If the simple Newton’s method is used to solve the generalized SMPBE, then the SMPBE is up to hundreds of times slower than the PBE. Without developing a more efficient SMPBE solver, only in the two-ion-size case is SMPBE a cost-efficient choice for its degree of correction on the PBE. However, even with a faster SMPBE solver, the Stern layer remains a more effective correction than the current SMPBE formulation at no extra computational cost.

4.2. Existence of the Best Parameter Set

From Figure 2, it can be said that the VDWS combined with a Stern layer of the size of the VDW radius of the cation is the parameter set that gives the best PBE prediction of ion distributions. However, Figure 3 shows that this does not hold true for a different lipid bilayer surface charge density (the corresponding figure for the K+ ion is Figure S5 of the SI).

Figure 3.

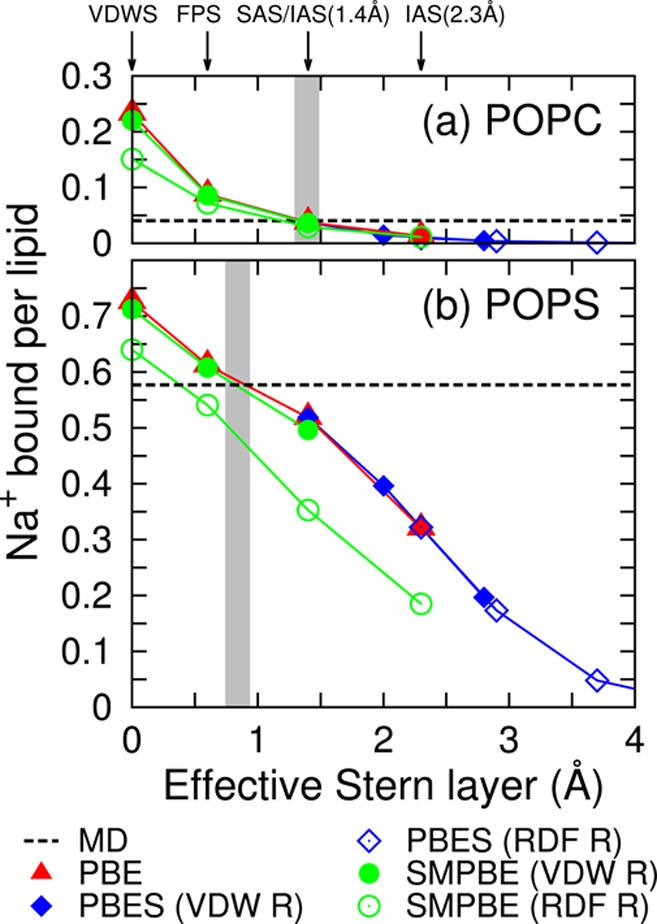
Figure 3

Open in a new tab

Number of Na+ bound per lipid as a function of the effective Stern layer thickness, the minimum distance between the VDWS and the molecular surface used for each calculation. (a) NaCl of bulk concentration 0.13 M outside of the POPC bilayer, system 2 in Table 1. (b) NaCl of bulk concentration 0.17 M outside of the POPS bilayer, system 7 in Table 1; VDW R and RDF R are shorthand for VDW radius and RDF radius. Gray shades mark where the mean-field calculations using the VDW radius agree with MD.

The surface charge density of the simulated POPS bilayer is about 0.28 C/m2 or 1.73 e/nm2 (for reference, the surface charge density of DNA is about 1 e/nm2), a fairly high value. The gray shade positions in Figure 3a and b show that the thickness of the Stern layer for the POPS bilayer needs to be smaller than what is used for the POPC bilayer (the VDW radius of Na+) for the PBE to reproduce the MD ion concentrations. Figure 3 reveals that the same parameter set does not give consistent accuracy of prediction when the surface charge density changes. This is also true, although not as significantly, when the bulk ionic strength, or the bulk ion concentration, varies. When looked at closely, the slopes of the PBE, the PBES, and the SMPBE plots in Figure 2 are always equal to or smaller than that of the MD, leading to inconsistent performances of a parameter set across different ionic strengths. Additionally, the same parameter set does not give the same performance for different ions. For example, for K+, the IAS with VDW radius does not perform as well as it does for Na+, that is, the gray shade in Figure S5 of the SI is not exactly overlapping with the IAS + VDW radius data point like it does in Figure 3. The inconsistency of the performance of a parameter set is partly because mean-field methods are much more simplified than the MD simulations and do not describe several ionic effects such as ion–ion correlations and fluctuations;7 they also ignore the ion–lipid specific interactions modeled in the MD force fields.41,42

The parameter inconsistency can be circumvented if empirical guidelines are available on how to choose parameters on the basis of the characteristics of a system. For example, one can summarize a relationship between the surface charge density and the effective Stern layer thickness. Two data points in this relationship are generated here: at zero surface charge density, the VDW radius can be used as the size of the Stern layer, and at surface charge density 1.73 e/nm2, roughly 0.8 Å for Na+ and 0.6 Å for K+ should be used as the size of the Stern layer. More data points need to be generated for a more complete knowledge of this relationship, and the lipid-type specific ion absorption effects should be considered.

Last but not least, even though theoretically the PBE and the SMPBE become more distinguishable under a stronger electrostatic potential, the strong electrostatic potential exerted by the higher surface charge density of the POPS bilayer is not yet enough to significantly separate the PBE and the SMPBE results when the common VDW ion radii are used, Figure 3b, putting the capability of the SMPBE under further doubt.

5. Conclusion

First, when it comes to studying ion equilibrium distributions, the SMPBE only offers a slight advantage over the PBE for the systems considered here. It is neither faster nor more accurate than the simple Stern layer ion-size correction of the PBE. There may, however, be other physical regimes where the SMPBE has a strong advantage. Further improvements are needed for the SMPBE to be an impactful correction to the PBE. Second, no single parameter set gives consistent mean-field method accuracy of prediction across systems of varying surface charge densities and ionic strengths. Empirical rules may be able to be summarized to guide the choice of parameters of the mean-field calculations.

Acknowledgments

This work is supported by the National Institutes of Health (grants GM31749, GM096188), the National Science Foundation (grants MCB-1020765, DMS-0811259), and the NSF Center for Theoretical Biological Physics (grant PHY-0822283).

Supporting Information Available

A brief description of the SMPBE formulation; the SMPBE routine in APBS; the MD simulation settings; an example of the APBS input file. The supporting figures, Figure S1 to Figure S5. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

# Peter M. Kekenes-Huskey is now at the Department of Chemistry, University of Kentucky, Lexington, KY, 40506.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

jp511702w_si_001.pdf (584.6KB, pdf)

References

  1. van Gunsteren W. F.; Bakowies D.; Baron R.; Chandrasekhar I.; Christen M.; Daura X.; Gee P.; Geerke D. P.; Glättli A.; Hünenberger P. H.; et al. Biomolecular Modeling: Goals, Problems, Perspectives. Angew. Chem., Int. Ed. 2006, 45, 4064–4092. [DOI] [PubMed] [Google Scholar]
  2. McCammon J. A.; Northrup S. H.; Allison S. A. Diffusional Dynamics of Ligand-Receptor Association. J. Chem. Phys. 1986, 90, 3901–3905. [Google Scholar]
  3. Sharp K. A.; Fine R.; Honig B. Computer Simulations of the Diffusion of a Substrate to an Active Site of an Enzyme. Science 1987, 236, 1460–1463. [DOI] [PubMed] [Google Scholar]
  4. McCammon J. A. Theory of Biomolecular Recognition. Curr. Opin. Struct. Biol. 1998, 8, 245–249. [DOI] [PubMed] [Google Scholar]
  5. Eun C.; Kekenes-Huskey P. M.; Metzger V. T.; McCammon J. A. A Model Study of Sequential Enzyme Reactions and Electrostatic Channeling. J. Chem. Phys. 2014, 140, 105101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bardhan J. P. Biomolecular Electrostatics - I Want Your Solvation (Model). Comput. Sci. Discovery 2012, 5, 013001. [Google Scholar]
  7. Ren P.; Chun J.; Thomas D. G.; Schnieders M. J.; Marucho M.; Zhang J.; Baker N. A. Biomolecular Electrostatics and Solvation: a Computational Perspective. Q. Rev. Biophys. 2012, 45, 427–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Davis M. E.; McCammon J. A. Solving the Finite Difference Linearized Poisson-Boltzmann Equation: A Comparison of Relaxation and Conjugate Gradient Methods. J. Comput. Chem. 1989, 10, 386–391. [Google Scholar]
  9. Holst M.; Saied F. Multigrid Solution of the Poisson-Boltzmann Equation. J. Comput. Chem. 2004, 14, 105–113. [Google Scholar]
  10. Boschitsch A. H.; Fenley M. O. A Fast and Robust Poisson–Boltzmann Solver Based on Adaptive Cartesian Grids. J. Chem. Theory Comput. 2011, 7, 1524–1540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dong F.; Olsen B.; Baker N. A. Computational Methods for Biomolecular Electrostatics. Methods Cell Biol. 2008, 84, 843–870. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Sharp K. A.; Honig B. Electrostatic Interactions in Macromolecules: Theory and Applications. Annu. Rev. Biophys. Biophys. Chem. 1990, 19, 301–332. [DOI] [PubMed] [Google Scholar]
  13. Bartlett G. J.; Porter C. T.; Borkakoti N.; Thornton J. M. Analysis of Catalytic Residues in Enzyme Active Sites. J. Mol. Biol. 2002, 324, 105–121. [DOI] [PubMed] [Google Scholar]
  14. Borukhov I.; Andelman D.; Orland H. Steric Effects in Electrolytes: A Modified Poisson-Boltzmann Equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar]
  15. Shapovalov V. L.; Brezesinski G. Breakdown of the Gouy-Chapman Model for Highly Charged Langmuir Monolayers: Counterion Size Effect. J. Phys. Chem. B 2006, 110, 10032–10040. [DOI] [PubMed] [Google Scholar]
  16. Stern O. The Theory of the Electrolytic Double-layer. Z. Elektrochem. Angew. Phys. Chem. 1924, 30, 508–516. [Google Scholar]
  17. Kralj-Iglič V.; Iglič A. A Simple Statistical Mechanical Approach to the Free Energy of the Electric Double Layer Including the Excluded Volume Effect. J. Phys. II France 1996, 6, 477–491. [Google Scholar]
  18. Chu V.; Bai Y.; Lipfert J.; Herschlag D.; Doniach S. Evaluation of Ion Binding to DNA Duplexes Using a Size-Modified Poisson-Boltzmann Theory. Biophys. J. 2007, 93, 3202–3209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Zhou S.; Wang Z.; Li B. Mean-field Description of Ionic Size Effects with Nonuniform Ionic Sizes: A Numerical Approach. Phys. Rev. E 2011, 84, 021901. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kirmizialtin S.; Silalahi A.; Elber R.; Fenley M. The Ionic Atmosphere Around A-RNA: Poisson-Boltzmann and Molecular Dynamics Simulations. Biophys. J. 2012, 102, 829–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Li B.; Liu P.; Xu Z.; Zhou S. Ionic Size Effects: Generalized Boltzmann Distributions, Counterion Stratification, and Modified Debye Length. Nonlinearity 2013, 26, 2899–2922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Dong F.; Vijayakumar M.; Zhou H. X. Comparison of Calculation and Experiment Implicates Significant Electrostatic Contributions to the Binding Stability of Barnase and Barstar. Biophys. J. 2003, 85, 49–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Pang X.; Zhou H. X. Poisson-Boltzmann Calculations: van der Waals or Molecular Surface?. Commun. Comput. Phys. 2013, 13, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Harris R. C.; Boschitsch A. H.; Fenley M. O. Influence of Grid Spacing in Poisson-Boltzmann Equation Binding Energy Estimation. J. Chem. Theory Comput. 2013, 9, 3677–3685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Harris R. C.; Boschitsch A. H.; Fenley M. O. Sensitivities to Parameterization in the Size-modified Poisson-Boltzmann Equation. J. Chem. Phys. 2014, 140, 075102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Spaar A.; Dammer C.; Gabdoulline R. R.; Wade R. C.; Helms V. Diffusional Encounter of Barnase and Barstar. Biophys. J. 2006, 90, 1913–1924. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Cheng Y.; Kekenes-Huskey P.; Hake J. E.; Holst M. J.; McCammon J. A.; Michailova A. P. Multi-scale Continuum Modeling of Biological Processes: from Molecular Electro-Diffusion to Sub-cellular Signaling Transduction. Comput. Sci. Discovery 2012, 5, 015002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Simons K.; Toomre D. Lipid Rafts and Signal Transduction. Nat. Rev. Mol. Cell Biol. 2000, 1, 31–39. [DOI] [PubMed] [Google Scholar]
  29. Phillips R.; Ursell T.; Wiggins P.; Sens P. Emerging Roles for Lipids in Shaping Membrane-Protein Function. Nature 2009, 459, 379–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Baker N.; Sept D.; Joseph S.; Holst M.; McCammon J. A. Electrostatics of Nanosystems: Application to Microtubules and the Ribosome. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 10037–10041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Jo S.; Lim J. B.; Klauda J. B.; Im W. CHARMM-GUI Membrane Builder for Mixed Bilayers and Its Application to Yeast Membranes. Biophys. J. 2009, 97, 50–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Phillips J.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R.; Kale L.; Schulten K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; et al. CHARMM General Force Field: A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Klauda J.; Venable R.; Freites J.; O’Connor J.; Tobias D.; Mondragon-Ramirez C.; Vorobyov I.; MacKerell A. Jr.; Pastor R. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Dolinsky T. J.; Czodrowski P.; Li H.; Nielsen J. E.; Jensen J. H.; Klebe G.; Baker N. A. PDB2PQR: Expanding and Upgrading Automated Preparation of Biomolecular Structures for Molecular Simulations. Nucleic Acids Res. 2007, 35, W522–W525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [DOI] [PubMed] [Google Scholar]
  37. Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
  38. Richards F. M. Areas, Volumes, Packing, and Protein Structure. Annu. Rev. Biophys. Bioeng. 1977, 6, 151–176. [DOI] [PubMed] [Google Scholar]
  39. Böckmann R. A.; Hac A.; Heimburg T.; Grubmüller H. Effect of Sodium Chloride on a Lipid Bilayer. Biophys. J. 2003, 85, 1647–1655. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Silalahi A. R. J.; Boschitsch A. H.; Harris R. C.; Fenley M. O. Comparing the Predictions of the Nonlinear Poisson-Boltzmann Equation and the Ion Size-modified Poisson-Boltzmann Equation for a Low-Dielectric Charged Spherical Cavity in an Aqueous Salt Solution. J. Chem. Theory Comput. 2010, 6, 3631–3639. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pandit S. A.; Bostick D.; Berkowitz M. L. Molecular Dynamics Simulation of a Dipalmitoylphosphatidylcholine Bilayer with NaCl. Biophys. J. 2003, 84, 3743–3750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Lee S. J.; Song Y.; Baker N. A. Molecular Dynamics Simulations of Asymmetric NaCl and KCl Solutions Separated by Phosphatidylcholine Bilayers: Potential Drops and Structural Changes Induced by Strong Na+-Lipid Interactions and Finite Size Effects. Biophys. J. 2008, 94, 3565–3576. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp511702w_si_001.pdf (584.6KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES