Making Microvascular Networks Work: Angiogenesis, Remodeling, and Pruning

Abstract

The adequate and efficient functioning of the microcirculation requires not only numerous vessels providing a large surface area for transport but also a structure that provides short diffusion distances from capillaries to tissue and efficient distribution of convective blood flow. Theoretical models show how a combination of angiogenesis, remodeling, and pruning in response to hemodynamic and metabolic stimuli, termed “angioadaptation,” generates well organized, functional networks.

The main function of the circulatory system is the transport of substances throughout the body and the supply of parenchymal tissues. This is achieved by convection in flowing blood and diffusive exchange between blood and surrounding tissues. The basic physics of these transport processes impose stringent constraints on the structure of the vasculature, which must be satisfied if the system is to perform its function effectively and efficiently. Specifically, the delivery of oxygen and other substrates by diffusion to all tissue cells depends critically on the spatial arrangement of vessels, whereas the distribution of convective blood flow is sensitively dependent on network topology and vessel diameters and lengths. In terminal vascular beds, requirements for both diffusion and convection must be met by the same vascular network.

In recent decades, efforts to understand the biological basis for the structure of the vasculature have largely focused on angiogenesis, i.e., the formation of new blood vessels. The molecular and cellular reactions involved have been extensively reported (4, 16, 17, 20, 26, 34, 66) and will not be reviewed here. The emphasis on angiogenesis is understandable, because the availability of enough microvessels with a sufficient area for exchange is a necessary condition for tissue oxygenation. However, it is not a sufficient condition. As shown by analysis of tumor microvascular beds (5, 55, 56) and vascular structures generated under the influence of increased VEGF levels (78, 79), high vascularity does not guarantee adequate and efficient vascular beds. The processes of vascular adaptation and maturation by which a mesh of blood vessels resulting from angiogenesis is transformed into an organized network, capable of meeting the above-mentioned physical requirements, are equally important (20, 66). Drawing on results from our theoretical models for vascular adaptation and angiogenesis, this review addresses the question of how microvascular networks with adequate transport characteristics are generated, thereby making networks that “work.”

Vascular Networks and Physical Principles of Mass Transport

Vascular networks must be patterned to comply with the basic characteristics of diffusive and convective solute transport (FIGURE 1). Diffusion is driven by the stochastic thermal movement of molecules, and the net solute flux is proportional to the gradient in concentration¹ (FIGURE 1A). Diffusion is therefore effective only over short distances. In the case of oxygen, a further limitation on diffusive transport is the relatively low solubility of oxygen (α) in tissue of about 3 × 10⁻⁵ cm³O₂·cm⁻³·Torr⁻¹. At a typical tissue partial pressure of oxygen (P) of 30 Torr, the concentration (c) is relatively low, at ∼0.001 cm³O₂/cm³ or 45 μM (c = αP). A simple one-dimensional analysis provides an estimate of the maximum diffusion distance (d_t) of oxygen from blood into tissue (70):

$$d_{\text{t}}={\left(2D\alpha P/M_0\right)}^{1/2}$$

where D is the diffusivity (∼1.5 × 10⁻⁵ cm²/s), P is the oxygen partial pressure in the blood, and M₀ is the oxygen consumption rate. For typical consumption rates between 0.01 and 0.3 cm³O₂·cm⁻³·min⁻¹ and partial pressures in blood between 30 and 100 Torr, the resulting diffusion distance is in the range of ∼20–200 μm. Thus tissue oxygenation can only be achieved if oxygenated blood is brought within such a distance of each cell in the tissue, calling for a fine mesh of tiny blood vessels (capillaries), which furthermore provides an interface with a very large area for exchange. Other small solutes (e.g., glucose) exhibit higher maximal diffusion distances and impose less stringent constraints on vascular geometry. Therefore, oxygen delivery is the primary consideration with regard to diffusive transport properties of microvascular networks.

FIGURE 1.

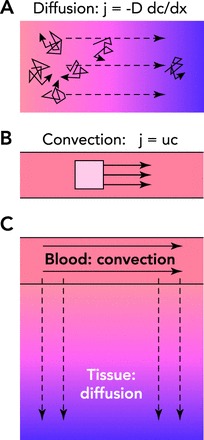
Basic principles of solute transport to tissue

A: diffusive transport depends on the random thermal motion of individual solute molecules (solid arrows). In the presence of a concentration gradient (see footnote 1), this random motion results in a net mass flux (j) down the concentration gradient (dc/dx), proportional to the molecular diffusivity (D). Diffusive transport generally requires a steep gradient in concentration to be effective and is therefore limited to short distances. B: in convective transport, the solute is carried by a flowing fluid. The local mass flux of solute (j) is given by the product of the flow velocity (u, solid arrows) and the concentration (c). The transport distance is limited only by the energy dissipation due to friction of fluid flow. C: modes of solute transport in the microcirculation. Both convective transport and diffusive transport occur in blood and tissue regions. Convective transport is dominant in the blood, whereas diffusive transport is dominant in tissue for oxygen and other low molecular weight solutes.

Organisms with sizes exceeding the maximal diffusion distances for oxygen (including humans) had to evolve convective systems, such as the blood circulation, to achieve transport over large distances (FIGURE 1B) and, acting in concert with diffusion, to provide transport throughout tissues (FIGURE 1C). Whereas diffusion requires only thermal energy, convection requires an energy-consuming fluid pumping mechanism (the heart). For an array of N cylindrical tubes with diameter d and length L connected in parallel, the mechanical power (E) required to pump a fluid at a total flow rate Q can be estimated using Poiseuille's law as

$$E=Q\Delta P=\frac{128\mu }{N\pi d^4}\cdot L{Q}^2$$

where μ is the viscosity of the fluid. If, for a given total intravascular fluid volume, the diameter of individual tubes is decreased to increase their number and exchange surface, the power requirement increases in proportion to 1/d². Pumping fluid through many very narrow tubes is therefore an inefficient means of convective transport, whereas convective transport over large distances is efficiently achieved by a low number of large-diameter vessels (major arteries and veins). A hierarchical structure of branching vessels with widely varying diameters is then needed to connect these large vessels with the capillaries needed for diffusive exchange.

For such hierarchical trees, Murray (52) derived conditions for minimum “work,” defined as the sum of viscous energy dissipation in the vessels and a term proportional to total blood volume. This condition is met if vessel diameters vary through successive branching generations such that flow is proportional to the cube of diameter, which is equivalent to maintaining the same level of wall shear stress throughout the vascular tree. However, it should be noted that real vascular networks exhibit substantial deviations from the stipulations of “Murray's law.” These deviations are both systematic, e.g., arterial shear stress is higher than venous shear stress, and stochastic, e.g., capillary shear stress exhibits a coefficient of variation of >1 (61, 62).

Vascular Network Structures

These features of the circulatory system are well known. Diagrams in textbooks or reviews to symbolize vascular networks frequently show either mesh-like structures (FIGURE 2A) or symmetric tree-like structures (FIGURE 2B). However, neither of these provides an adequate representation of actual mature microvascular networks. Capillary meshes represent a simple structure, reminiscent of structures seen in the primary vascular plexus of the yolk sac (66) or in the chorioallantoic membrane. These structures have relatively low and homogeneous distances between tissue cells and the nearest capillary. However, as already discussed, an extended network of capillary-sized vessels is inefficient for convective transport. Moreover, it would generate an oxygen gradient and thus a gradient of metabolic conditions along the flow direction. On the other hand, a symmetric tree-like structure would provide efficient convective transport, but the large surface for exchange would be restricted to a relatively small zone around the capillaries. In reality, the whole tissue, including the regions close to feeding and draining vessels, has to be supplied with a mesh of capillaries.

FIGURE 2.

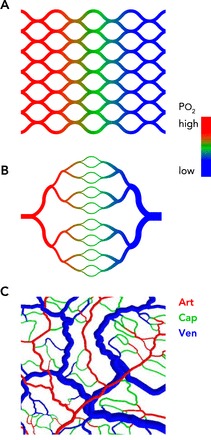
Comparison of idealized and actual structures of microvascular networks

A: a capillary mesh provides a short and homogeneous diffusion distance, but high resistance to blood flow and an oxygen gradient across the tissue is generated. Color coding indicates the intravascular oxygen level. B: a symmetric tree structure provides low resistance to blood flow but short diffusion distances only in the central band containing capillaries. Color coding is as in A. C: a real network structure, based on observations of the rat mesentery, provides short and homogeneous diffusion distances in combination with low flow resistance. Color coding indicates vessel type: Art, arterioles (part of a diverging tree); Cap, capillaries (connecting a divergent with a convergent tree); Ven, venules (part of a converging tree).

To combine the requirements of convection and diffusion, the two types of structures shown in FIGURE 2, A AND B, must somehow coexist throughout the tissue region. The need to serve tissue cells both close to and remote from larger feeding and draining vessels necessarily leads to heterogeneous and more complex network structures (3, 48, 61), as illustrated in FIGURE 2C. Thus the generation of microvascular network structures presents an apparently difficult problem in biological pattern formation to minimize both diffusion distances and energy consumption (55, 68). How is this problem solved by living tissues? One might suppose that vascular geometries are genetically programmed. Indeed, the paths of the major arteries and veins are individually preprogrammed during development (31). However, this does not apply to the microcirculation, which includes a vast number of segments (>10⁹) and is capable of continuous structural changes in response to varying conditions as occur in growth and development, exercise and atrophy, the estrus cycle, wound healing, etc. The question therefore remains: How are microvascular network structures that meet the physical requirements for mass transport generated, maintained, and repaired according to the needs of each tissue?

Angioadaptation: Angiogenesis, Remodeling and Pruning

A sequence of processes involved in formation of the vascular system was outlined by Risau (66). According to this scheme, a primary capillary plexus is formed during early development by the process of vasculogenesis. Subsequent addition of vessels occurs by angiogenesis, involving sprouting or splitting (intussusception). These networks undergo pruning and remodeling in a process of maturation, leading to functional and efficient structures. Here, we adopt the term “angioadaptation” (81) to describe the combined action of angiogenesis, remodeling, and pruning, leading under normal conditions to the formation of functional and efficient networks, as represented schematically in FIGURE 3.

FIGURE 3.

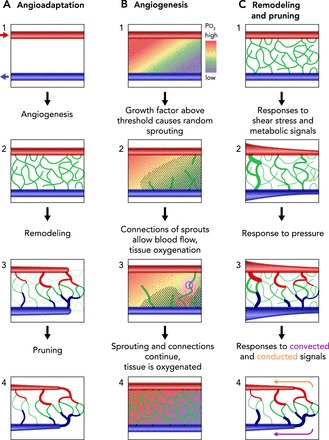
Processes of network formation and maturation

A: overview. Red arrows, arteriolar inflow; blue arrows, venular drainage. 1: initial configuration with underperfused region between arteriole and venule. 2: sprouting angiogenesis leads to formation of an initial disordered mesh of new vessels. 3: structural remodeling results in an orderly progression of segment diameters along flow pathways. Redundant segments shrink in diameter. 4: pruning of redundant segments gives mature network structure. B: sprouting angiogenesis. 1: initial configuration with underperfused region between arteriole and venule. Color scale shows tissue oxygen levels. Growth factor is generated in hypoxic regions. Diagonal hatched lines indicate region with growth factor levels above a threshold level. 2: new sprouts (shown in white) are generated at random locations within region where growth factor level exceeds threshold. 3 and 4: connections between sprouts (pink circle) form continuous flow pathways, allowing flow and providing local tissue oxygenation. C: structural adaptation of vessel diameters. 1: initial disordered mesh of new vessels. 2: response to wall shear stress leads to larger diameters in vessels with higher flow. Response to metabolic signals stabilizes network by maintaining segments that are needed to supply metabolic needs. 3: response to intravascular pressure leads to arterio-venous asymmetry, with larger diameters in venules than in corresponding arterioles. 4: transmission of metabolic signals upstream by conducted responses and downstream by metabolite convection preferentially enlarges diameters on long flow pathways, which would otherwise be underperfused.

Given the huge number of vessels and the ability of the system to adapt to changing demands and conditions, it is obvious that these structural behaviors cannot be predetermined for every individual vessel. A plausible hypothesis, supported by much experimental evidence starting with observations by John Hunter in the reindeer antler in 1787 and the coining of the term “angiogenesis”, is that all vessels are capable of structural responses (36, 40, 42, 49, 51, 67, 76) to several types of stimulus and that the actual behavior of each segment is dictated by the mechanical and biological stimuli that it receives. Thus organized network structures emerge as the result of the more or less autonomous behavior of many individual vessels. Under this hypothesis, the question now becomes: Can the observed structural and functional properties of the microvasculature be achieved by a network of vessel segments exhibiting structural responses to locally available stimuli according to a generic set of “rules”?

Theoretical Model for Angioadaptation

Theoretical simulations are of special importance to address this question (11, 19, 46, 47, 54, 73). Biological or genetic approaches can provide evidence that a specific response characteristic in a network exists and that blocking this response leads to altered network structures. But only a computational model can test whether a given set of hypothesized vascular behaviors and responses is capable of generating the expected network structures (69). It also can be used to simulate the development of the network with time and to test whether it can meet the requirements for adequate and efficient mass transport.

Most previous models in this area have addressed either sprouting angiogenesis or structural adaptation, but not both. Models for sprouting angiogenesis have used a range of approaches, representing sprouts either by a continuous distribution (7, 32, 44, 45) or by discrete, stochastically generated elements (2, 50, 77). Models for structural adaptation (37, 57, 59, 63, 67) have focused mainly on changes of luminal diameter or vessel wall thickness driven by hemodynamic or metabolic stimuli. Few models have included pruning explicitly.

As a consequence of the fourth-power dependence on diameter in Poiseuille's law, flow distributions in vascular networks are highly sensitive to vessel diameters. Simulations of structural adaptation of vessel diameters in networks have established a minimal set of structural responses needed to achieve efficient and realistic flow distribution (57, 59, 63). The effects of these responses are indicated schematically in FIGURE 3C. As already mentioned, the energy required to pump blood through a given network and at a given total blood volume can be minimized if flow is proportional to diameter cubed in each segment or the wall shear stress is held to a fixed level (neglecting variations in blood viscosity) (52). Therefore, a structural response to wall shear stress, such that vessels with high shear stress enlarge, acts to enforce this condition, with diameters decreasing from proximal to distal vessels in the arterial and venous trees. However, such a response, acting alone, causes instability of parallel flow pathways (67). To stabilize the network, a local metabolic response is needed, such that segments subjected to hypoxia experience a growth stimulus (65). The reaction to transmural pressure ensures arterio-venous asymmetry, with smaller diameters, and higher flow resistance and shear stress on the arterial side, and low average capillary pressure (59). The transfer of information derived from the local metabolic signal both upstream by conduction along the vessel wall (right, orange arrow) and downstream by convection with the blood (purple arrow) is critical to avoid functional shunting through relatively large-diameter proximal arterio-venous flow pathways at the expense of longer flow pathways (55, 56). The role of conducted responses is discussed further below. The responses outlined above lead to continued vessel shrinking and eventually to pruning of vessels that are nonfunctional with respect to both convective and diffusive transport. Typically, such vessels have low shear stress and moderate or high oxygen levels and therefore receive a negative net growth stimulus, causing decrease in diameter (FIGURE 3).

The fact that vascular networks must serve tissue regions close to the main supplying vessels as well as more remote regions poses a fundamental problem of dynamic vascular adaptation: avoiding functional shunting (56). The need for distribution of capillaries throughout the tissue implies the presence of both short and long flow pathways connecting the feeding arteriole to the draining venule. As illustrated in FIGURE 4, a short pathway has a very high pressure drop per length and thus very high wall shear stress compared with the feeding arteriole from which it branches. On the other hand, the local oxygen partial pressure and metabolic environment of the two segments are similar. Responses to local signals alone would therefore favor growth in the short pathway, generating a functional arterio-venous (A-V) shunt. To avoid such behavior, an additional mechanism is required that signals differences between arterioles supplying a large number of capillaries and those forming short A-V connections. This mechanism must provide transfer of information upstream along arterioles within vascular networks. A similar consideration applies to vessels in the venular network, where information transfer in the downstream direction, from distal to proximal vessels, is necessary. In this case, convective transport of metabolites may provide the needed signals (55, 63). However, upstream information transfer is not so simply explained.

FIGURE 4.

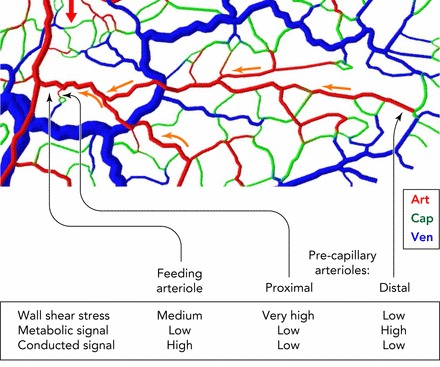
Schematic illustration of signals involved in remodeling of vessel diameters, showing importance of conducted responses

Shown is a section of a mesenteric microvascular network, color-coded for vessel type (Art, arteriole; Cap, capillary; Ven, venule). Red arrow shows blood flow direction in main arteriole supplying region. Two precapillary arterioles are identified: one (proximal) forming part of a short arterio-venous flow pathway; the other (distal) forming part of a long flow pathway. The feeding arteriole of both pathways is shown for comparison. The feeding arteriole and the proximal precapillary arteriole experience equivalent oxygen levels and thus have similar local metabolic signals, but the proximal precapillary arteriole is subjected to a much steeper pressure gradient, leading to high wall shear stress, a growth stimulus. To establish a situation without functional shunting, i.e., high flow in the feeding arteriole relative to a proximal precapillary arteriole, the diameter of the feeding arteriole must be maintained large relative to that of the possible shunt. This condition can be achieved if the feeding arteriole, but not the proximal precapillary arteriole, receives a strong conducted signal transmitted from the high number of supplied capillaries (yellow arrows), ensuring a large vessel diameter and low flow resistance. The distal precapillary arteriole is typically in a low-oxygen region and receives a relatively strong local metabolic signal.

We hypothesized (56, 63) that the necessary upstream information transfer in arteriolar trees is provided by conduction of electrical signals along the vessel wall. This conduction relies on the adequate function of connexins forming gap junctions between cells in the vessel wall (14, 23, 29). Simulations with reduced conducted responses show more heterogeneous tissue perfusion, more generation of functional shunts, and increased tissue hypoxia (55, 63, 68). Model simulations indicated that the length constant of the conducted signal should be above 2 mm (58). A low attenuation of conducted responses with increasing distance along arteriolar vessels has been found in some experimental investigations (23).

Conclusive experimental evidence for this hypothesis has not so far been obtained. Experiments in Cx40 knockout mice showed impaired conducted vasodilation, but structural microvascular defects were not seen (39). A critical experimental test of the concept is difficult to achieve, because the knockout of a single connexin type may have only limited functional impact, whereas elimination of two or more of the four subtypes that are expressed in the cardiovascular system, namely Cx37, Cx40, Cx43, and Cx45 (14), usually results in severe defects and sometimes in lethal phenotypes (28). The evident redundancy in connexin function limits the interpretation of negative results since a given function may be affected only by a combined blockade of more than one connexin type. Furthermore, experimental studies have focused on the role of connexins in the short-term regulation of vascular tone in arteriolar vessels, whereas in the present context the regulation of vessel wall structure in arterioles, capillaries, and venules is addressed. A close relationship between the regulation of tone and structure has been shown in cultured arterioles (6). Therefore, the finding that conducted responses are important in the regulation of tone strongly suggests that they also play a role in structural responses. However, a direct test of the importance of conduction in this context will require experiments assessing long-term vascular adaptation with and without complete blockade of conduction along the vessel wall.

We recently presented a theoretical approach that combines simulations of angiogenesis, remodeling, and pruning in an integrated model (68). In this approach, the simulation of sprouting angiogenesis follows previous work (77), as indicated schematically in FIGURE 5. For any given state of the vascular network, the resulting distributions of blood flow in microvessels and of oxygen in the surrounding tissue are computed, using previously established methods (64, 71). A growth factor, such as VEGF (1, 20, 27), is assumed to be generated in hypoxic regions and to diffuse in the tissue. In regions with growth factor levels above a threshold level, existing vessels form sprouts at randomly chosen locations, which elongate with randomized directions at each time increment of the simulation. The cellular and molecular processes underlying sprout formation and progression, including the role of tip cells and guidance molecules, have been investigated in detail (21, 25, 33, 41, 72, 75, 80) and will not be discussed here. Since a growing sprout is not subject to blood flow and wall shear stress, it is assumed not to be subjected to remodeling, as just described, but to be sustained by cellular reactions to the local growth factor level. Upon elongation, a sprout may make contact with other sprouts or existing vessels, establishing flow. This starts the processes of remodeling and pruning as already described, in which the inherently heterogeneous network structure arising from stochastic angiogenesis is adapted and refined to meet the physical requirements for mass transport (60).

FIGURE 5.

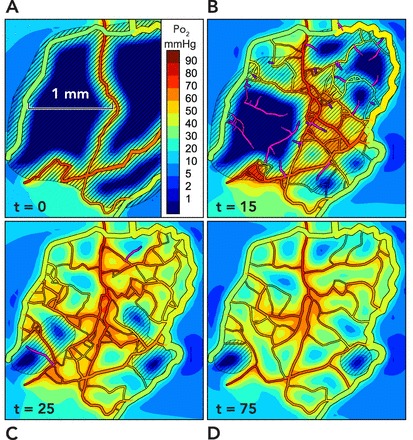
Simulation of angioadaptation

Results are presented from two-dimensional simulations incorporating the mechanisms described in FIGURE 3 and described in detail elsewhere (68). A: the initial configuration is derived from observations of rat mesentery, with all but a few main vessels removed. Colors indicate oxygen levels (see scale bar). The extensive hypoxic regions generate levels of growth factor above the threshold level (diagonal lines) throughout most of the region. B: at 15 days, some regions contain unconnected new sprouts (shown in purple), whereas connected sprouts in other regions carry flow, and tissue is oxygenated. C: at 25 days, most of the tissue is well oxygenated, but some areas of hypoxia are still stimulating sprouting angiogenesis. D: at 75 days, the structure has stabilized with a vasculature capable of supplying nearly all points with oxygen but with pruning of redundant vessels.

To test whether this set of assumed mechanisms is sufficient to “solve” the problem of vascular network pattern formation, we carried out a series of simulations based on observations of microcirculation in the rat mesentery (68). Starting with an observed network structure, we reduced it to a skeleton and simulated the resulting angioadaptation process. A sample of the results obtained is shown in FIGURE 5. Initially, vessel sprouting at existing vessels is triggered by hypoxia-driven production of a vascular growth factor. New sprouts grow in a stochastic process, forming a relatively disordered initial network (FIGURE 5, B AND C). With remodeling and pruning, redundant segments drop out, and a more streamlined and stable structure emerges that is still capable of maintaining tissue oxygenation (FIGURE 5D). Compared with the actual observed capillary network in this particular mesenteric region, the simulated network shows almost identical characteristics with respect to the distributions of tissue oxygen levels and of distances of tissue points to the nearest vessels (68). These simulations demonstrated that the assumed set of biological responses and mechanisms is sufficient to generate networks meeting the physical requirements for mass transport, as already discussed.

Several aspects of this model are noteworthy.

First, the model includes a feedback mechanism by which regions with inadequate oxygen supply can generate a signal leading to formation of additional vessels by angiogenesis. Thus the capillary network structure is automatically “tuned” to provide adequate oxygen supply.

Second, the model provides a mechanism for selecting vessels that are needed for effective mass transport and for removing redundant segments. If the shrinking of a given vessel leads neither to local hypoxia nor to increased wall shear stress, then it receives no increasing growth stimulus and continues to shrink, eventually being pruned. This happens if the local oxygen needs in the vicinity of a given vessel can be met by other nearby vessels and if the vessel in question is not the unique flow source to other necessary segments. In this case, a positive feedback loop is set up, in which a decrease in diameter leads to a decrease in wall shear stress and further shrinkage (67). Conversely, shrinkage of a vessel that is needed for diffusive transport leads to hypoxia and an increased metabolic stimulus for growth (65), whereas shrinkage of a vessel that is needed for convective transport leads to increased wall shear stress, also a stimulus for vessel growth. In each case, the resulting negative feedback loop stabilizes vessel diameter.

Third, angiogenesis, remodeling, and pruning occur in parallel and not as separate processes. FIGURE 6A shows the variation over time of an index of each of these processes. According to the model, the periods of high activity in each process largely overlap, although the peaks in activity are slightly shifted relative to each other in the expected sequence. The stochastic process of angiogenesis inevitably gives rise to some vessels that are redundant and ultimately subject to pruning as just described. Therefore, overabundant generation of new vessels is necessary so that the eventual network has adequate density. Such an overshoot is typical, for example, in wound healing (15). Thus the processes of angiogenesis, structural adaptation, and pruning are intertwined. Their functional regulation and consequences cannot be adequately understood if they are considered separately (FIGURE 6, B AND C).

FIGURE 6.

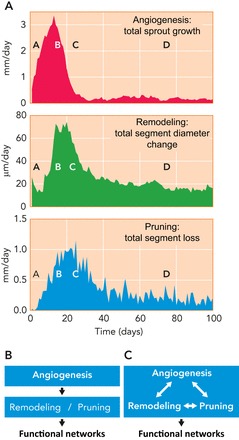
Time course of angiogenesis, remodeling, and pruning during simulated angioadaptation

A: results based on the simulations described in FIGURE 5 show the strong overlap of these processes with some phase shift from angiogenesis to remodeling and to pruning. The letters A to D indicate corresponding time points in FIGURE 5. B: in the past, angiogenesis and structural remodeling/pruning were generally considered as sequential processes and were mostly separate areas of investigation, with angiogenesis receiving much greater emphasis. C: the results presented here, including those in A, indicate that remodeling and pruning occur largely in parallel with angiogenesis and that all three processes interact with each other. Therefore, understanding the formation of vascular networks requires consideration of the integrated processes of angiogenesis, structural adaptation, and pruning.

Fourth, vessel type is not predetermined according to this model but rather emerges from the localization in the network and the resulting hemodynamic and topological conditions. Vessels that were initially capillaries can turn into larger conductance vessels (and vice versa) at any location within the developing network. Redistribution of flow directions can cause transitions from venous to arterial vessel type in response to the resulting hemodynamic and metabolic conditions (22, 53), and flow conditions can thus determine vascular identity (17, 43).

Angioadaptation in Health and Disease

Many normal physiological processes and responses to changing environmental conditions, including tissue growth and regression, exercise, wound healing, and the estrus cycle, lead to changes in functional demands that must be met by the microcirculation. The model proposed here provides a basis for understanding how the combined processes of angiogenesis, remodeling, and pruning are capable of adjusting vascular structures to meet these varying demands. For example, a sustained increase in tissue oxygen demand may lead to hypoxia if the existing structure is inadequate. Such hypoxia is predicted to stimulate outward remodeling of existing vessels and increased convective oxygen delivery (65). If vascular density is not sufficient for adequate diffusive transport, then persistent hypoxia causes production of VEGF and/or other growth factors stimulating angiogenesis. In that case, an overshoot in vascular density followed by a phase of pruning and remodeling is predicted, leading to a structure with higher vascular density (68). Conversely, a decrease in oxygen demand is predicted to cause inward remodeling and pruning. An interesting prediction of the theory is that this system exhibits hysteresis: the increase in vascular density generated during a period of higher demand is only partially reversed if demand returns to its former level (68).

Even in the absence of changes in oxygen demand or other functional requirements, microvascular network structures are dynamic and likely undergo continuous low-level fluctuations. Model simulations show the occasional development of small hypoxic areas in otherwise well oxygenated tissue, which may trigger angiogenesis and network reorganization. Under steady-state conditions, endothelial cells are relatively quiescent, exhibiting a turnover time in the range of ∼30–300 days (18, 35). Such endothelial cell turnover may also trigger local flow changes leading to angioadaptive events. These low-level fluctuations may be significant in allowing the network to adjust to slow changes in functional demands.

Changes in the structure of the microcirculation occur in several disease states and with aging. In tumors, the microvasculature is typically seen to be more tortuous and disorganized than in normal tissues. Tumors often show a relatively high proportion of hypoxic tissue, even if the vascular volume and perfusion are relatively high. This hypoxia has important effects on tumor responses to radiation and chemotherapies, generally reducing their effectiveness. Analysis of hemodynamics and remodeling in tumor microvessel networks suggests that poor oxygenation may result from functional shunting, i.e., failure to distribute flow appropriately between short and long flow pathways, as a consequence of impaired conducted responses (55, 56). Such impairment is plausible given that endogenous VEGF levels are typically elevated in tumor tissues and that VEGF has disruptive effects on vascular wall integrity and gap junction function (74).

These findings relate to anti-angiogenic therapy and the concept of “vascular normalization” with the aim of improving the susceptibility of the tumor to chemotherapy or radiation (30, 38). The dense but highly disordered and functionally deficient vascular networks often observed in tumors can be interpreted as the result of excessive angiogenesis combined with weak or defective remodeling and pruning. Similar patterns with increases of vessel density but not perfusion have been reported to result from VEGF overexpression (78). According to the present concepts, anti-angiogenic therapy, e.g., with anti-VEGF compounds, can restore the balance between angiogenesis and remodeling/pruning, allowing vessels to adapt to local and conducted stimuli and leading to formation of “normal” functionally adequate vascular networks.

Impaired conducted responses may also play a role in the microvascular dysfunction observed in diabetes. Expression of connexin 43 has been found to be reduced in diabetic mice and was related to the development of retinal microvascular lesions (12). However, this finding has to be interpreted with caution since endothelial cells express mainly Cx37 and Cx40 (23), and Cx43 is only present in small amounts in the microcirculation. With aging, a significant reduction in the strength of conducted responses along arterioles was found in skeletal muscle of mice (8). The cause of this reduction has not been established (9, 10); reduced connexin expression in aging may play a role (13, 24).

Conclusions

To fulfill its function of supplying oxygen and other materials throughout the tissue space, the microcirculation must provide low diffusion distances from capillaries to all tissue cells as well as efficient convective distribution of blood flow through larger vessels. Moreover, the structure is inherently heterogeneous, as a result of the stochastic nature of angiogenesis and also of the need to supply tissue points that are near or far from major feeding vessels. The structure cannot be fully predetermined, considering the vast number of vessels and the need to adapt to changing conditions.

Here, we advance the hypothesis that this patterning problem can be “solved” by a combination of sprouting angiogenesis, vascular remodeling, and pruning, in which each segment follows a set of generic responses to available stimuli, such that an adequate structure emerges. This contrasts to an “engineering” solution to a transport problem, such as a heat exchanger, in which a predetermined and often highly symmetrical structure is designed to meet specified criteria. In this hypothesized “biological” solution, an inherently heterogeneous and asymmetrical structure is continually refined in response to several locally acting feedback mechanisms, such that it self-organizes into an adequate and efficient structure.

This hypothesis is supported by a theoretical model (68), which shows that a set of biologically reasonable responses can lead to network structures that are adequate for mass transport and consistent with experimental observations. Note the model is not necessarily complete: other mechanisms not included in the model may be relevant or even essential in the control of microvascular network structure. Nonetheless, the results of the model lead to a number of predictions that merit further experimental investigation, including the overabundant generation of new vessels in sprouting angiogenesis and largely simultaneous action of angiogenesis, remodeling, and pruning. Furthermore, dysfunctional microvascular network structures may arise from disturbances in the processes of angiogenesis, remodeling, and/or pruning. In many situations, including tumors, diabetes, and aging, reduced information transfer via conducted responses along vessel walls is probably an important factor. More generally, it is hoped that this review will challenge the vascular research community to take a more integrated view of the processes underlying vascular structure, where currently angiogenesis and structural remodeling are more or less disjointed areas of investigation.