Combining Ordered Subsets and Momentum for Accelerated X-ray CT Image Reconstruction

Abstract

Statistical X-ray computed tomography (CT) reconstruction can improve image quality from reduced dose scans, but requires very long computation time. Ordered subsets (OS) methods have been widely used for research in X-ray CT statistical image reconstruction (and are used in clinical PET and SPECT reconstruction). In particular, OS methods based on separable quadratic surrogates (OS-SQS) are massively parallelizable and are well suited to modern computing architectures, but the number of iterations required for convergence should be reduced for better practical use. This paper introduces OS-SQS-momentum algorithms that combine Nesterov's momentum techniques with OS-SQS methods, greatly improving convergence speed in early iterations. If the number of subsets is too large, the OS-SQS-momentum methods can be unstable, so we propose diminishing step sizes that stabilize the method while preserving the very fast convergence behavior. Experiments with simulated and real 3D CT scan data illustrate the performance of the proposed algorithms.

I. Introduction

Statistical X-ray CT image reconstruction methods can provide images with improved resolution, reduced noise and reduced artifacts from lower dose scans, by minimizing regularized cost-functions [1]–[4]. However, current iterative methods require too much computation time to be used for every clinical scan. Many general iterative algorithms have been applied to statistical CT reconstruction including coordinate descent [5], [6], preconditioned conjugate gradient [7], and ordered subsets [8], [9], but these algorithms all converge slower to the minimizer than is desired for clinical CT. This paper describes new image reconstruction algorithms that require less computation time.

Recent advances on iterative algorithms in X-ray CT minimize the cost function by using splitting techniques [10]–[12] accompanied with the method-of-multipliers framework [13]. The Chambolle-Pock primal-dual algorithm [14] has been applied to tomography [15], [16]. Momentum techniques [17]-[19] that use previous update directions have been applied to X-ray CT [20]-[22], accelerating a gradient descent update using the Lipschitz constant of the gradient of the cost function.

This paper focuses on momentum techniques that have received wide attention in the optimization community. Nesterov [17], [18] developed two momentum techniques that use previous descent directions to decrease the cost function at the fast convergence rate O (1/n²), where n counts the number of iterations. The rate O (1/n²) is known to be optimal¹ for first-order² optimization methods [23], while ordinary gradient descent has the rate O (1/n). Nesterov's momentum algorithms have been extended to handle nonsmooth convex functions [19], [24], and have been applied to image restoration problems [19], [25].

Momentum techniques in X-ray CT [20]–[22] have been used to accelerate gradient descent methods. However, these “traditional” momentum algorithms do not show significant improvement in convergence speed compared with other existing algorithms, due to the large Lipschitz constant of the gradient of the cost function [11]. Here, we propose to combine momentum techniques with ordered subsets (OS) methods [8], [9] that provide fast initial acceleration. (Preliminary results based on this idea were discussed in [26], [27].) OS methods, an instance of incremental gradient methods [28], approximate a gradient of a cost function using only a subset of the data to reduce computational cost per image-update. Even though the approximation in the method may prevent the algorithm from converging to the optimum, OS methods are widely used in tomography problems for their M-times initial acceleration in run time, where M is the number of subsets, leading to rate O (1/(nM)) in early iterations. Remarkably, our proposed OS-momentum algorithms should have the rate O (1/(nM)²) in early iterations providing a promising M² acceleration compared to the standard Nesterov method.

Conventional momentum methods use either the (smallest) Lipschitz constant or a backtracking scheme to ensure monotonic descent in the gradient step [19]. Here, to reduce computation, we instead use diagonal preconditioning (or majorizing) based on the separable quadratic surrogate (SQS) [9] that is used widely for designing monotonic descent algorithms for X-ray CT. Another advantage of using SQS is that we can further accelerate the algorithm using the nonuniform approach in SQS methods that provides larger updates for the voxels that are far from their respective optima [29].

Combining OS methods with Nesterov's momentum techniques directly is a practical approach for acceleration but lacks convergence theory.³ Indeed, we observed unstable behavior in some cases. To stabilize the algorithm, we adapt the diminishing step size rule developed for stochastic gradient method with Nesterov's momentum in [33]. We view the OS-SQS methods in a stochastic sense and study the relaxation scheme of momentum approach [33]. We investigate various relaxation schemes to achieve both fast initial acceleration and stability (or convergence) in a stochastic sense. (Note that this relaxation (or diminishing step size) is not necessary if OS is not used in the proposed algorithms.)

This paper is organized as follows. Section II explains the problem of X-ray CT image reconstruction and Section III summarizes the OS-SQS algorithms. Section IV reviews momentum techniques and combines them with OS-SQS. Section V suggests a step size relaxation scheme that stabilizes the proposed algorithms. Section VI shows experimental results on simulated and real CT scans. Section VII offers conclusion and discussion.

II. Problem

We consider a (simplified) linear model for X-ray CT transmission tomography:

$$\mathit{y}=\mathit{\text{Ax}}+\mathit{\epsilon },$$ (1)

where y ∈ ℝ^N_d is (post-log) measurement data, $\mathit{A}\triangleq \{a_{\mathit{\text{ij}}}\}\in {ℝ}_{+}^{N_d\times N_p}$ is a forward projection operator [34], [35] (a_ij ≥ 0 for all i, j), $\mathit{x}\triangleq \{x_j\}\in \chi ={ℝ}_{+}^{N_p}$ is an unknown (nonnegative) image (of attenuation coefficients) to be reconstructed and ε ∈ ℝ^N_d is noise.

A penalized weighted least squares (PWLS) [3], [4] criterion is widely used for reconstructing an image x with a roughness penalty and a nonnegativity constraint:⁴

$$\widehat{\mathit{x}}=\underset{\mathit{x}⪰0}{argmin}\{\mathrm{\Psi }(\mathit{x})\triangleq \frac{1}{2}{\Vert \mathit{y}-\mathit{\text{Ax}}\Vert }_{\mathit{W}}^2+R(\mathit{x})\},$$ (2)

where the diagonal matrix W ⪰ 0 provides statistical weighting that accounts for the ray-dependent variance of the noise ε. Here, we focus on smooth⁵ convex regularization functions:

$$R(\mathit{x})\triangleq \sum _{r=1}^{N_r}{\psi }_r({\left[\mathit{\text{Cx}}\right]}_r),$$ (3)

where ψ_r(t) ≜ β_rψ(t), the function ψ(·) is an edge-preserving potential function such as a Fair potential function in [36], the parameter β_r provides spatial weighting [37], and C ≜ {c_rj} ∈ ℝ^{N_r × N_p} is a finite-differencing matrix considering 26 neighboring voxels in 3D image space. The regularizer (3) makes the PWLS cost function Ψ(x) in (2) to be smooth and strictly convex with a unique global minimizer x̂ [38]. Throughout this manuscript, we assume that the objective Ψ(x) is smooth and (strictly) convex.

This nonquadratic PWLS cost function cannot be optimized analytically and requires an iterative algorithm. We propose algorithms combining OS and (relaxed) momentum approaches that minimize a smooth convex objective function Ψ(x) for CT rapidly and efficiently. Although we focus on PWLS for simplicity, the methods may also apply to penalized-likelihood formulations and to cost functions with nonsmooth regularizers, which we leave as future extensions.

III. OS-SQS Algorithms

A. Optimization transfer method

When a cost function Ψ(x) is difficult to minimize, we can replace it by a (simple) surrogate ϕ(x; x⁽ⁿ⁾) at the nth iteration, and generate a sequence {x⁽ⁿ⁾} by minimizing the surrogate as

$${\mathit{x}}^{(n+1)}=\underset{\mathit{x}⪰0}{argmin}\varphi (\mathit{x};{\mathit{x}}^{(n)}).$$ (4)

This optimization transfer method [39] is also known as a majorization-minimization approach [40, Section 8.3].

To monotonically decrease Ψ(x) using an optimization transfer method, a surrogate function ϕ(x; x⁽ⁿ⁾) at nth iteration should satisfy the following majorization conditions:

$$\{\begin{array}{c}\mathrm{\Psi }({\mathit{x}}^{(n)})=\varphi ({\mathit{x}}^{(n)};{\mathit{x}}^{(n)}),\hfill \\ \mathrm{\Psi }(\mathit{x})\le \varphi (\mathit{x};{\mathit{x}}^{(n)}),\forall \mathit{x}\in \chi ={ℝ}_{+}^{N_p}\hfill \end{array}$$ (5)

Surrogates satisfying the conditions in (5) can be constructed using a Lipschitz constant [19], quadratic surrogates [41], and SQS methods [9], [29].

B. SQS algorithms

An optimization transfer method used widely in tomography problems is a SQS method [9] yielding the following surrogate function ϕ(x; x⁽ⁿ⁾) with a diagonal Hessian (second-order derivatives) matrix D ≜ diag{d_j}, at nth iteration:

$$\varphi (\mathit{x};{\mathit{x}}^{(n)})\triangleq \mathrm{\Psi }({\mathit{x}}^{(n)})+\nabla \mathrm{\Psi }{({\mathit{x}}^{(n)})}^{\top }(\mathit{x}-{\mathit{x}}^{(n)})+\frac{1}{2}{\Vert \mathit{x}-{\mathit{x}}^{(n)}\Vert }_{\mathit{D}}^2$$ (6)

for all x, x⁽ⁿ⁾ ∈ χ, which satisfies (5). The standard SQS algorithm [9] uses the following diagonal majorizing matrix

$$\mathit{D}\triangleq \text{diag}\left\{\right[{\mathit{A}}^{\top }\mathit{\text{W A}}+{|\mathit{C}|}^{\top }\text{diag}\{{\ddot{\psi }}_r(0)\}|\mathit{C}|\left]1\right\}$$ (7)

using the maximum curvature ψ¨_r(0) = max_t ψ¨_r(t) [41], where $|\mathit{C}|\triangleq \{|c_{\mathit{\text{rj}}}|\}\in {ℝ}_{+}^{N_r\times N_p}$, and the vector 1 ∈ ℝ^N_p consists of N_p ones. (This D is positive definite because its diagonal entries are all positive.)

Table I gives the outline of the computationally efficient (and massively parallelizable) SQS algorithm, where the operation χ [x] projects x onto a constraint set ${ℝ}_{+}^{N_p}$ by a (simple) element-wise clipping that replaces negative element values to zero. The sequence {x⁽ⁿ⁾} generated from the SQS algorithm in Table I has the following convergence rate [29]:

Table I. SQS Methods.

1: Initialize x(0) and compute D such that (5) and (6) hold.

2: for n = 0, 1, …

3: x(n+1) = χ [x(n) − D−1∇Ψ(x(n))]

$$\mathrm{\Psi }({\mathit{x}}^{(n+1)})-\mathrm{\Psi }(\widehat{\mathit{x}})\le \frac{{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathit{D}}^2}{2(n+1)}$$ (8)

for any diagonal majorizing matrix D satisfying the conditions (5) and (6), including the choice (7), by a simple generalization of [19, Theorem 3.1]. Based on (8), the nonuniform approach [29] (see Section V-E) accelerates SQS methods by providing larger updates for the voxels that are far from their respective optima, which we use in our experiments (in Section VI).

SQS algorithms require many iterations to converge, both due to the O (1/n) rate in (8) and large values in D needed for satisfying the conditions (5) and (6) in 3D X-ray CT problem. Thus we usually combine SQS algorithms with OS algorithms for faster convergence in early iterations [9], [29].

C. OS algorithms

Iterative reconstruction requires both forward and back projection operations Ax and A^⊤y on the fly [34], [35] due to their large-scale in 3D, and thus computation of the gradient ∇Ψ(x) = A ^⊤ W(Ax − y) + ∇R(x) is very expensive. OS methods [8] accelerate gradient-based algorithms such as in Table I by grouping the projection views into M subsets evenly and using only the subset of measured data to approximate the exact gradient of the cost function.

OS methods define the subset-based cost function:

$${\mathrm{\Psi }}_m(\mathit{x})\triangleq \frac{1}{2}{\Vert {\mathit{y}}_m-{\mathit{A}}_m\mathit{x}\Vert }_{{\mathit{W}}_m}^2+\frac{1}{M}R(\mathit{x})$$ (9)

for m = 0,1, …, M − 1, where $\mathrm{\Psi }(\mathit{x})={\sum }_{m=0}^{M-1}{\mathrm{\Psi }}_m(\mathit{x})$ and the matrices y_m, A_m, W_m are sub-matrices of y, A, W for the mth subset, and rely on the following “subset balance” approximation [8], [9]:

$$\nabla \mathrm{\Psi }(\mathit{x})\approx M\nabla {\mathrm{\Psi }}_0(\mathit{x})\approx \cdots \approx M\nabla {\mathrm{\Psi }}_{M-1}(\mathit{x}).$$ (10)

Using (10), OS methods provide initial acceleration of about the factor of the number of subsets M in run time, by replacing ∇Ψ(x) in Table I with the approximation M∇Ψ_m(x) that requires about $\frac{1}{M}$-times less computation, as described in Table II.

Table II. OS-SQS Methods.

1: Initialize x(0) and compute D.

2: for n = 0, 1, …

3: for m = 0, 1, …, M − 1

4: k = nM + m

5: ${\mathit{x}}^{\left(\frac{k+1}{M}\right)}=\mathcal{P}\chi [{\mathit{x}}^{\left(\frac{k}{M}\right)}-{\mathit{D}}^{-1}M\nabla {\mathrm{\Psi }}_m({\mathit{x}}^{(\frac{k}{M})})]$

We count one iteration after all M sub-iterations are performed, considering the use of projection operators A and A^⊤ per iteration, and in practice the initial convergence rate is O (1/(nM)). (Using large M can slow down the algorithm in run time due to the regularizer computation [42].) OS algorithms approach a limit-cycle because the assumption (10) breaks near the optimum [43]. OS algorithms can be modified to converge to the optimum with some loss of acceleration in early iterations [28], [44].

IV. OS-SQS Methods with Nesterov's Momentum

To further accelerate OS-SQS methods, we propose to adapt two of Nesterov's momentum techniques [17], [18] that reuse previous descent directions as momentum towards the minimizer for acceleration. (One could also consider another Nesterov momentum approach [45] achieving same rate as other two [17], [18].) This section reviews both momentum approaches and combines them with OS methods.

The first momentum method [17] uses two previous iterates, while the second [18] accumulates all gradients. Without using OS methods, both Nesterov methods provide O (1/n²) convergence rate. We heuristically expect that combining momentum with OS methods will provide roughly O (1/(nM)²) rates in early iterations, by replacing n by nM. The main benefit of combining OS and Nesterov's momentum is that we have approximately M² times acceleration in early iterations with M subsets, yet the extra computation and memory needed (in using Nesterov's momentum approaches) are almost negligible. We discuss both proposed algorithms in more detail.

A. Proposed OS-SQS methods with momentum 1 (OS-mom1)

Table III illustrates the proposed combination of an OS-SQS algorithm with the momentum technique that is described in [17], where the algorithm generates two sequences $\{{\mathit{x}}^{(\frac{k}{M})}\}$ and $\{{\mathit{z}}^{(\frac{k}{M})}\}$, and line 7 of the algorithm corresponds to a momentum step with Nesterov's optimal parameter sequence t_k. Table III reduces to the ordinary OS-SQS algorithm in Table II when t_k = 1 for all k ≥ 0.

Table III. Proposed OS-SQS methods with momentum in [17] (OS-mom1).

1: Initialize x(0) = z(0), t0 = 1 and compute D.

2: for n = 0, 1, …

3: for m = 0, 1, …, M − 1

4: k = nM + m

5: $t_{k+1}=\frac{1}{2}\left(1+\sqrt{1+4t_k^2}\right)$

6: ${\mathit{x}}^{(\frac{k+1}{M})}=\mathcal{P}\chi [{\mathit{z}}^{(\frac{k}{M})}-{\mathit{D}}^{-1}M\nabla {\mathrm{\Psi }}_m({\mathit{z}}^{(\frac{k}{M})})]$

7: ${\mathit{z}}^{(\frac{k+1}{M})}={\mathit{x}}^{(\frac{k+1}{M})}+\frac{t_{k-1}}{t_{k+1}}({\mathit{x}}^{(\frac{k+1}{M})}-{\mathit{x}}^{(\frac{k}{M})})$

The non-OS version of Table III satisfies the following convergence rate:

Lemma 1: For n ≥ 0, the sequence {x⁽ⁿ⁾} generated by the non-OS version (M = 1) of Table III satisfies

$$\mathrm{\Psi }({\mathit{x}}^{(n+1)})-\mathrm{\Psi }(\widehat{\mathit{x}})\le \frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathit{D}}^2}{(n+1)(n+2)},$$ (11)

where D is a diagonal majorizing matrix satisfying the conditions (5) and (6), such as (7).

The inequality (11) is a simple generalization of [19, Theorem 4.4]. In practice, we expect the initial rate of OS-mom1 for M > 1 to be O (1/(nM)²) with the approximation (10), which is the main benefit of this approach, while the computation cost remains almost the same as that of OS-SQS algorithm in Table II. The only slight drawback of Table III over Table II is the extra memory needed to store the image $\{{\mathit{z}}^{(\frac{k}{M})}\}$.

B. Proposed OS-SQS methods with momentum 2 (OS-mom2)

Table IV summarizes the second proposed OS-SQS algorithm with momentum. This second method, OS-mom2, is based on [18] and uses accumulation of the past (subset) gradients in line 7. Rather than using the original choice of coefficient $t_k=\frac{k+1}{2}$ from [18], Table IV uses the t_k from [46], [47] that gives faster convergence. Both ${\mathit{x}}^{(\frac{k}{M})}$ and ${\mathit{\upsilon }}^{(\frac{k}{M})}$ in Table IV lie in the set χ (e.g., are nonnegative) because of the projection operation 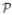χ[·]. Furthermore, ${\mathit{z}}^{(\frac{k}{M})}$ is a convex combination of ${\mathit{x}}^{(\frac{k}{M})}$ and ${\mathit{\upsilon }}^{(\frac{k}{M})}$ and thus also lies in χ. This may improve the stability of OS-mom2 over OS-mom1 that lacks this property.

Table IV.

Proposed OS-SQS Methods with Momentum in [18] (OS-mom2), The Notation (l)_M Denotes l mod M.

1: Initialize x(0) = υ(0) = z(0), t0 = 1 and compute D.

2: for n = 0, 1, …

3: for m = 0, 1, …, M − 1

4: k = nM + m

5: $t_{k+1}=\frac{1}{2}(1+\sqrt{1+4t_k^2})$

6: ${\mathit{x}}^{(\frac{k+1}{M})}=\mathcal{P}\chi [{\mathit{z}}^{(\frac{k}{M})}-{\mathit{D}}^{-1}M\nabla {\mathrm{\Psi }}_m({\mathit{z}}^{(\frac{k}{M})})]$

7: ${\mathit{\upsilon }}^{(\frac{k+1}{M})}=\mathcal{P}\chi [{\mathit{z}}^{(0)}-{\mathit{D}}^{-1}{\sum }_{l=0}^{\mathit{\text{nM}}+m}{t}_{l}M\nabla {\mathrm{\Psi }}_{{(l)}_M}({\mathit{z}}^{(\frac{l}{M})})]$

8: ${\mathit{z}}^{(\frac{k+1}{M})}={\mathit{x}}^{(\frac{k+1}{M})}+\frac{t_{k+1}}{{\sum }_{l=0}^{k+1}{t}_l}({\mathit{\upsilon }}^{(\frac{k+1}{M})}-{\mathit{x}}^{(\frac{k+1}{M})})$

The sequence {x⁽ⁿ⁾} generated by Table IV with M = 1 can be proven to satisfy the inequality (11), by generalizing [18, Theorem 2]. While the one-subset (M = 1) version of Table IV provides O(1/n²), we heuristically expect from (10) for the OS version to have the rate O (1/(nM)²) in early iterations. (The convergence analysis of this algorithm in Table IV is discussed stochastically in the next section.) Compared with Table III, one additional 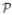χ [·] operation per iteration and extra arithmetic operations are required in Table IV, but those are negligible.

Overall, the two proposed algorithms in Tables III and IV are expected to provide fast convergence rate O (1/(nM)²) in early iterations, which we confirm empirically in Section VI. However, the type of momentum affects the overall convergence when combined with OS. Also, the convergence behavior of two algorithms is affected by the number and ordering of subsets, as discussed in Section VI.

The proposed OS-momentum algorithms in Tables III and IV become unstable in some cases when M is too large, as predicted by the convergence analysis in [33]. To stabilize the algorithms, the next section proposes to adapt a recent relaxation scheme [33] developed for stochastic gradient methods with momentum.

V. Relaxation of Momentum

This section relates the OS-SQS algorithm to diagonally preconditioned stochastic gradient methods and adapts a relaxation scheme designed for stochastic gradient algorithms with momentum. Then we investigate various choices of relaxation⁶ to achieve overall fast convergence.

A. Stochastic gradient method

If one uses random subset orders, then one can view OS methods as stochastic gradient methods by defining M∇Ψ_Sk(x) as a stochastic estimate of ∇Ψ(x), where a random variable S_k at kth iteration is uniformly chosen from {0, 1, …, M − 1}. In this stochastic setting, OS-SQS methods satisfy:

$$\{\begin{array}{l}\mathbb{E}[M{\mathrm{\Psi }}_{S_k}(\mathit{x})]=\mathrm{\Psi }(\mathit{x})\hfill \\ \mathbb{E}[M\nabla {\mathrm{\Psi }}_{S_k}(\mathit{x})]=\nabla \mathrm{\Psi }(\mathit{x})\hfill \\ \mathbb{E}[{(M{\nabla }_j{\mathrm{\Psi }}_{S_k}(\mathit{x})-{\nabla }_j\mathrm{\Psi }(\mathit{x}))}^2]\le {\sigma }_j^2,\forall j\hfill \end{array}$$ (12)

for all x ∈ 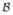, for some finite constants {σ_j}, where 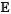is the expectation operator over the random selection of S_k, ∇_j ≜ ∂/∂x_j, and 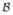is a bounded feasible set that includes x̂. The feasible set 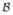can be derived based on the measurement data y [44, Section A.2], and we assume that the sequences generated by the algorithms are within the set 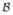. The last inequality in (12) is a generalized version of [33, eqn. (2.5)] for (diagonally preconditioned) OS-SQS-type algorithms. The vector σ ≜ {σ_j} has smaller values if we use smaller M or the subsets are balanced as (10). However, estimating the value of σ:

$${\sigma }_j\triangleq \underset{\mathit{x}\in \mathit{\beta }}{max}{\stackrel{\sim }{\sigma }}_j(\mathit{x}),$$ (13)

where

$$\begin{array}{l}{\stackrel{\sim }{\sigma }}_j^2(\mathit{x})\triangleq \mathbb{E}\left[{(M{\nabla }_j{\mathrm{\Psi }}_{S_k}(\mathit{x})-{\nabla }_j\mathrm{\Psi }(\mathit{x}))}^2\right]\\ =M\sum _{m=0}^{M-1}{\left[{\mathit{A}}_m^{\top }{\mathit{W}}_m({\mathit{A}}_m\mathit{x}-{\mathit{y}}_m)\right]}_j^2-{[{\mathit{A}}^{\top }\mathit{W}(\mathit{\text{Ax}}-\mathit{y})]}_j^2,\end{array}$$ (14)

appears to be impractical, so Section V-F provides a practical approach for approximating σ.

B. Proposed OS-SQS methods with relaxed momentum (OS-mom3)

Inspired by [33], Table V describes a generalized version of OS-SQS-momentum methods that reduces to OS-mom2 if one uses a deterministic subset ordering S_k = (k mod M) and a fixed majorizing diagonal matrix

Table V.

Proposed Stochastic OS-SQS Algorithms with Momentum (OS-mom3). ξ_k is a Realization of a Random Variable S_k.

1: Initialize x(0) = v(0) = z(0), t0 ∈ (0, 1] and compute D.

2: for n = 0, 1, …

3: for m = 0, 1, …, M − 1

4: k = nM + m

5: Choose ${\mathbf{\Gamma }}^{(k)}\triangleq \text{diag}\left\{{\gamma }_j^{(k)}\right\}\mathrm{s}.\mathrm{t}.\{\begin{array}{ll}{\mathbf{\Gamma }}^{(0)}\succ \mathit{D}\hfill & k=0\hfill \\ {\mathbf{\Gamma }}^{(k)}⪰{\mathbf{\Gamma }}^{(k-1)},\hfill & k>0\hfill \end{array}$

6: Choose $t_{k+1}\mathrm{s}.\mathrm{t}.t_{k+1}^2{\mathbf{\Gamma }}^{(k+1)}⪯\left({\sum }_{l=0}^{k+1}{t}_l\right){\mathbf{\Gamma }}^{(k)}$

7: ${\mathit{x}}^{(\frac{k+1}{M})}=\mathcal{P}\chi [{\mathit{z}}^{(\frac{k}{M})}-{[{\mathbf{\Gamma }}^{(k)}]}^{-1}M\nabla {\mathrm{\Psi }}_{{\xi }_k}({\mathit{z}}^{(\frac{k}{M})})]$

8: ${\mathit{\upsilon }}^{(\frac{k+1}{M})}=\mathcal{P}\chi [{\mathit{z}}^{(0)}-{[{\mathbf{\Gamma }}^{(k)}]}^{-1}{\sum }_{l=0}^k{t}_{l}M\nabla {\mathrm{\Psi }}_{{\xi }_l}(\mathit{z}(\frac{l}{M}))]$

9: ${\mathit{z}}^{(\frac{k+1}{M})}={\mathit{x}}^{(\frac{k+1}{M})}+\frac{t_{k+1}}{{\sum }_{l=0}^{k+1}{t}_l}({\mathit{\upsilon }}^{(\frac{k+1}{M})}-{\mathit{x}}^{(\frac{k+1}{M})})$

$${\mathbf{\Gamma }}^{(k)}=\mathit{D}.$$ (15)

For M = 1, the algorithm with these choices satisfies (11) with n = k. However, for M > 1, the analysis in [33] illustrates that using the choice (15) leads to the following inequality

$$\mathbb{E}[\mathrm{\Psi }({\mathit{x}}^{(\frac{k+1}{M})})-\mathrm{\Psi }(\widehat{\mathit{x}})]\le \frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathit{D}}^2}{(k+1)(k+2)}+\frac{(k+3){\mathit{p}}^{\top }\mathit{\sigma }}{3}$$ (16)

for k ≥ 0, where p ≜ {p_j ≜ max_x,x̅∈ 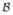|x_j − x̅_j|} measures the diameter of the feasible set . This expression reveals that OS methods (M > 1) with momentum may suffer from error accumulation due to the last term in (16) that depends on the error bounds (σ) in (12). To improve stability for the case M > 1, we would like to find a way to decrease this last term. Using a larger constant denominator, i.e., Γ^(k) = qD for q > 1, would slow the accumulation of error but would not prevent eventual accumulation of error [33].

To stabilize the algorithm for M > 1, we adapt the relaxed momentum approach in [33] as described in Table V with appropriately selected Γ^(k) and t_k satisfying the conditions in lines 5 and 6 in Table V. Then, the algorithm in Table V satisfies the following convergence rate:

Lemma 2: For k = nM + m ≥ 0, the sequence $\{{\mathit{x}}^{(\frac{k+1}{M})}\}$ generated by Table V satisfies

$$\begin{array}{l}\mathbb{E}\left[\mathrm{\Psi }({\mathit{x}}^{(\frac{k+1}{M})})-\mathrm{\Psi }(\widehat{\mathit{x}})\right]\\ \le \frac{1}{{\sum }_{l=0}^k{t}_l}[\frac{{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{{\mathbf{\Gamma }}^{(k)}}^2}{2}+\sum _{l=0}^k\sum _{i=0}^l{t}_i{\Vert \mathit{\sigma }\Vert }_{{({\mathbf{\Gamma }}^{(l)}-\mathit{D})}^{-1}}^2].\end{array}$$ (17)

Proof: See Appendix A.

Lemma 2 shows that increasing Γ^(k) can help prevent accumulation of error σ. Next we discuss the selection of parameters Γ^(k) and t_k.

C. The choice of Γ^(k) and t_k

For any given ${\mathbf{\Gamma }}^{(k)}\triangleq \text{diag}\left\{{\gamma }_j^{(k)}\right\}$, we use t₀ = 1 and the following rule:

$$t_{k+1}=\frac{1}{2{\alpha }_{k+1}}(1+\sqrt{1+4t_k^2{\alpha }_k{\alpha }_{k+1}})$$ (18)

for all k ≥ 0, where ${\alpha }_{k+1}\triangleq {max}_j({\gamma }_j^{(k+1)}/{\gamma }_j^{(k)})$ and α₀ = 1. The choice (18) increases the fastest among all possible choices satisfying the condition in line 6 of Table V (see the proof in Appendix B).⁷

In this paper, we focus on the choice

$${\mathbf{\Gamma }}^{(k)}=\mathit{D}+{(k+2)}^{c_k}\mathbf{\Gamma }$$ (19)

for a nondecreasing c_k ≥ 0 and a fixed diagonal matrix Γ ≜ diag{γ_j} ≻ 0. The choice (19) generalizes [33], enabling more flexibility in the choice of c_k. We leave other formulations of Γ^(k) that may provide better convergence as future work.

For Γ^(k) in (19), computing α_k in (18) becomes

$${\alpha }_{k+1}=1+\frac{{(k+3)}^{c_{k+1}}-{(k+2)}^{c_k}}{{min}_j(d_j/{\gamma }_j)+{(k+2)}^{c_k}}\ge 1.$$ (20)

Overall, the computational cost of Table V with the choices (18) and (19) remains similar to that of Table IV. Using (18) and (19), the proposed algorithm in Table V achieves the following inequality:

Corollary 1: For k = nM+m ≥ 0, the sequence $\{{\mathit{x}}^{(\frac{k+1}{M})}\}$ generated by Table V with the coefficients (18) and (19) satisfies

$$\mathbb{E}[\mathrm{\Psi }({\mathit{x}}^{(\frac{k+1}{M})})-\mathrm{\Psi }(\widehat{\mathit{x}})]\le \left(\underset{0\le l\le k}{max}\sqrt{{\alpha }_l}\right)[\frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathit{D}}^2}{(k+1)(k+2)}+\frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathbf{\Gamma }}^2}{(k+1){(k+2)}^{1-c_k}}+\frac{2{\sum }_{l=0}^k{(l+2)}^{2-c_l}{\Vert \mathit{\sigma }\Vert }_{{\mathbf{\Gamma }}^{-1}}^2}{(k+1)(k+2)}].$$ (21)

Proof: Use Lemma 2 and the inequality conditions of the sequence {t_k} in (18):

$$\begin{array}{c}\frac{k+1}{2\sqrt{{\alpha }_k}}\le t_k\le \frac{k+1}{\sqrt{{\alpha }_k}},\\ \underset{0\le l\le k}{min}\frac{(k+1)(k+2)}{4\sqrt{{\alpha }_l}}\le \sum _{l=0}^k{t}_l\le \underset{0\le l\le k}{max}\frac{(k+1)(k+2)}{2\sqrt{{\alpha }_l}}\end{array}$$

for k ≥ 0, which can be easily proven by induction.

There are two parameters c_k and Γ to be tuned in (19). Based on Corollary 1, the next two subsections explore how these parameters affect convergence rate. (We made a preliminary investigation of these two parameters in [48].)

D. The choice of c_k

In Corollary 1, the choice of c_k controls the overall convergence rate. We first consider a constant c_k = c.

Corollary 2: For k = nM + m ≥ 0 and a fixed constant c_k = c ∈ [0, 2], the sequence $\{{\mathit{x}}^{(\frac{k+1}{M})}\}$ generated by Table V with the coefficients (18) and (19) satisfies

$$\mathbb{E}[\mathrm{\Psi }({\mathit{x}}^{(\frac{k+1}{M})})-\mathrm{\Psi }(\widehat{\mathit{x}})]\le \left(\underset{0\le l\le k}{max}\sqrt{{\alpha }_l}\right)\left[\frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathit{D}}^2}{(k+1)(k+2)}+\frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathbf{\Gamma }}^2}{(k+1){(k+2)}^{1-c}}+\frac{2{(k+3)}^{3-c}{\Vert \mathit{\sigma }\Vert }_{{\mathbf{\Gamma }}^{-1}}^2}{(3-c)(k+1)(k+2)}\right].$$ (22)

Proof: Use the derivation in [33, Section 6.3] using

$$\sum _{l=0}^k{(l+2)}^{2-c}\le {\int }_1^{k+1}{(s+2)}^{2-c}\mathrm{d}s\le \frac{{(k+3)}^{3-c}}{3-c}.$$

In Corollary 2, the choice c_k = 1.5 provides the rate

$$\mathbb{E}[\mathrm{\Psi }({\mathit{x}}^{(\frac{k+1}{M})})-\mathrm{\Psi }(\widehat{\mathit{x}})]\le \left(\underset{\underset{\forall j}{0\le l\le k}}{max}\sqrt{\frac{d_j+{(l+2)}^{1.5}{\gamma }_j}{d_j+{(l+1)}^{1.5}{\gamma }_j}}\right)\times O(\frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathit{D}}^2}{k^2}+\frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathbf{\Gamma }}^2}{\sqrt{k}}+\frac{2{\Vert \mathit{\sigma }\Vert }_{{\mathbf{\Gamma }}^{-1}}^2}{1.5\sqrt{k}}),$$ (23)

achieving, on average, the optimal rate $O(1/\sqrt{k})$ in the presence of stochastic noise⁸. Corollary 2 shows that using c ≤ 1 will suffer from error accumulation, using 1 < c < 1.5 might provide faster initial convergence than c = 1.5 but does not achieve the optimal rate, and c > 1.5 will cause slower overall convergence rate than c = 1.5. So, we prefer 1 < c ≤ 1.5, for which we expect to eventually reach smaller cost function values than the choice Γ^(k) = D (or Γ = 0) in (15), since we prevent the accumulation of error from OS methods by increasing the denominator Γ^(k) as (19). In other words, the algorithm with M > 1 and (19) is slower than the choice of (15) initially, but eventually becomes faster and reaches the optimum on average.

In light of these trade-offs, we further consider using an increasing sequence c_k that is upper-bounded by 1.5, hoping to provide fast overall convergence rate. We investigated the following choice:

$$c_k=1+0.5(1-\frac{\eta }{k+\eta })$$ (24)

for k ≥ 0 with a parameter η > 0. This choice of c_k balances between fast initial acceleration and prevention of error accumulation. In other words, this increasing c_k can provide faster initial convergence than a constant c_k = 1.5 (or η = 0), yet guarantees the optimal (asymptotic) rate $O(1/\sqrt{k})$ as the case c_k = 1.5, based on Corollary 1. We leave further optimization of c_k as future work.

E. The choice of D and Γ

To optimize the choice of Γ^(k) in (19), we would like to minimize the upper bound on the right hand side of (22) with respect to both D and Γ, where we consider a fixed c_k = c for simplicity. In nonuniform SQS [29], to accelerate algorithms in Tables I and II, we suggested to use D that minimizes the right hand side of (8) among all possible choices of D generated by a (general) SQS technique [9], [29] (details are omitted) and thus satisfies (5) and (6). Similarly in our proposed methods, we use the following diagonal majorizing matrix D̂ that minimizes the right hand side of (22):

$$\begin{array}{l}\widehat{\mathit{D}}\triangleq \underset{\underset{\mathit{D}\text{is diagonal and it is generated by SQS}[9],[29].}{\mathit{D}\succ 0}}{argmin}\left\{\frac{2{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathit{D}}^2}{(k+1)(k+2)}\right\}\hfill \\ =\text{diag}\left\{\text{diag}{\{\widehat{\mathit{u}}\}}^{-1}[{\mathit{A}}^{\top }\mathit{\text{W A}}+{|\mathit{C}|}^{\top }\text{diag}\{{\ddot{\psi }}_r(0)\}|\mathit{C}|]\widehat{\mathit{u}}\right\},\hfill \end{array}$$ (25)

instead of (7), where the vector û is defined as

$$\mathit{û}=\{{\mathit{û}}_j\triangleq |x_j^{(0)}-{\widehat{x}}_j|\}\in {ℝ}_{+}^{N_p}.$$ (26)

To choose Γ, we also minimize the upper bound on the right hand side of (22) with respect to Γ. For simplicity in designing Γ, we ignore the ${max}_{0\le l\le k}\sqrt{{\alpha }_l}$ term, and we ignore the “+1” and “+2” factors added to k. The optimal Γ for k (sub)iterations is

$${\widehat{\mathbf{\Gamma }}}_c(k)\triangleq \underset{\underset{\mathbf{\Gamma }\text{is diagonal}.}{\mathbf{\Gamma }\succ 0,}}{argmin}\{\frac{{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{\mathbf{\Gamma }}^2}{k^{2-c}}+\frac{{\Vert \mathit{\sigma }\Vert }_{{\mathbf{\Gamma }}^{-1}}^2}{(3-c)k^{c-1}}\}=\text{diag}\left\{\frac{{\sigma }_j}{\sqrt{3-c}{\mathit{û}}_j}{k}^{1.5-c}\right\}.$$ (27)

It is usually undesirable to have to select the (sub)iteration k before iterating. The choice c = 1.5 cancels out the parameter k in (27) leading to the k-independent choice:

$${\widehat{\mathbf{\Gamma }}}_{1.5}=\text{diag}\left\{\frac{{\sigma }_j}{\sqrt{1.5}{\mathit{û}}_j}\right\}.$$ (28)

Since we prefer the choice of c_k that eventually becomes 1.5 for the optimal rate, we focus on the choice Γ̂_1.5 in (28).

F. The choice of σ and û

The optimized D̂ (25) and Γ̂_1.5 (28) rely on unavailable parameters {σ_j} (13) and {û_j} (26), so we provide a practical approach to estimate them, which we used in Section VI. In practice, the sequences in Table V visit only a part of the feasible set , so it would be preferable to compute σ̃_j(x) in (14) within such part of for estimating σ_j, but even that is impractical. Instead, we use σ̃_j(x⁽⁰⁾) as a practical approximation of σ_j, which is computationally efficient. This quantity measures the variance of the stochastic estimate of the gradient at the initial image x⁽⁰⁾, and depends on the grouping and number of subsets. This estimate of σ_j may be sensitive to the choice of x⁽⁰⁾, and we leave further investigation as future work.

To save computation, we evaluate σ̃_j(x⁽⁰⁾) simultaneously with the computation of D in (7) or (25) using modified projectors A and A^⊤ (see [29, Section III.F]) that handle two inputs.

We further approximate û_j (26) by

$${\mathit{û}}_j\approx \zeta {\overline{u}}_j$$ (29)

for Γ̂_1.5 in (28), where ζ > 0 is an (unknown) constant, and a vector $\overline{\mathit{u}}\in {ℝ}_{+}^{N_p}$ is a (normalized) approximation of û_j, which is computed by applying an edge-detector to the filtered back-projection (FBP) image that is used for the initial x⁽⁰⁾ as described in [29, Section III.E].⁹ In low-dose clinical CT, the root mean squared difference (RMSD¹⁰) within the region -of-interest (ROI) between the initial FBP image x⁽⁰⁾ and the optimal image x̂ is about 30 [HU], i.e., $\Vert {\mathit{û}}_{\text{ROI}}\Vert /\sqrt{N_{p,\text{ROI}}}\approx 30[\text{HU}]$, so we let ζ = 30 [HU] in (29) as a reasonable choice in practice¹¹ where $\Vert {\overline{\mathit{u}}}_{\text{ROI}}\Vert /\sqrt{N_{p,\text{ROI}}}=1$. Then, our final practical choice of Γ becomes

$${\widehat{\mathbf{\Gamma }}}_{1.5}\approx \text{diag}\left\{\frac{{\stackrel{\sim }{\sigma }}_j({\mathit{x}}^{(0)})}{\sqrt{1.5}\zeta {\overline{\mathit{u}}}_j}\right\}.$$ (30)

VI. Results

We investigate the convergence rate of the three proposed OS-momentum algorithms in Tables III, IV and V, namely OS-mom1, OS-mom2 and OS-mom3 in this section, for PWLS reconstruction of simulated and real 3D CT scans. We implemented¹² the proposed algorithm in C and ran on a machine with two 2.27GHz 10-core Intel Xeon E7-8860 processors using 40 threads.¹³

We use an edge-preserving potential function ψ_r(·) in [29, eqn. (45)] with a = 0.0558, b = 1.6395, and δ = 10:

$$\psi (t)=\frac{{\delta }^2}{b^3}(\frac{{\mathit{\text{ab}}}^2}{2}{\left|\frac{t}{\delta }\right|}^2+b(b-a)\left|\frac{t}{\delta }\right|+(a-b)log(1+b\left|\frac{t}{\delta }\right|)).$$

For simulation data, the spatial weighting β_r was chosen empirically to be

$${\beta }_r\triangleq 50\prod _{\forall j,c_{\mathit{\text{rj}}}\ne 0}max\{{\kappa }_j,0.01{\kappa }_{max}\}$$ (31)

for uniform resolution properties [37], where ${\kappa }_j\triangleq \sqrt{\frac{{\sum }_{i=1}^{N_d}{a}_{\mathit{\text{ij}}}{w}_i}{{\sum }_{i=1}^{N_d}{a}_{\mathit{\text{ij}}}}}$ and κ_max ≜ max_j κ_j. We emulated β_r of the GE product “Veo” for the patient 3D CT scans. We use a diagonal majorizing matrix D̂ in (25) using the nonuniform approach [29] with (29) for SQS methods. We investigated 12, 24 and 48 subsets for OS algorithms.

We first use simulated data to analyze the factors that affect the stability of the proposed OS-momentum algorithms, and further study the relaxation scheme for the algorithms. Then we verify the convergence speed of the proposed algorithm using real 3D CT scans. We computed the RMSD between the current and converged¹⁴ image within the ROI versus computation time for 30 iterations (n) to measure the convergence rate.¹⁵

A. Simulation data

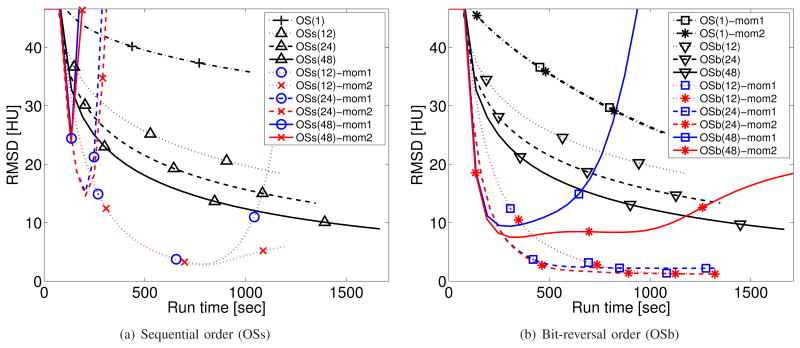
We simulated a 888 × 64 × 2934 sinogram (number of detector columns × detector rows × projection views) from a 1024 × 1024 × 154 XCAT phantom [51] scanned in a helical geometry with pitch 1.0 (see Fig. 1). We reconstructed 512 × 512 × 154 images with an initial FBP image x⁽⁰⁾ in Fig. 1(a) using a (simple) single-slice rebinning method [52]. Fig. 2 shows that SQS-Nesterov's momentum methods without OS algorithms do not accelerate SQS much. OS algorithm itself can accelerate the SQS algorithm better than Nesterov's momentum. Our proposed OS-momentum algorithms rapidly decrease RMSD in early iterations (disregarding the diverging curves that we address shortly). However, the convergence behavior of OS-momentum algorithm depends on several factors such as the number of subsets, the order of subsets, and the type of momentum techniques. Thus, we discuss these in more detail based on the results in Fig. 2, and suggest ways to improve the stability of the algorithm while preserving the fast convergence rate.

Fig. 1.

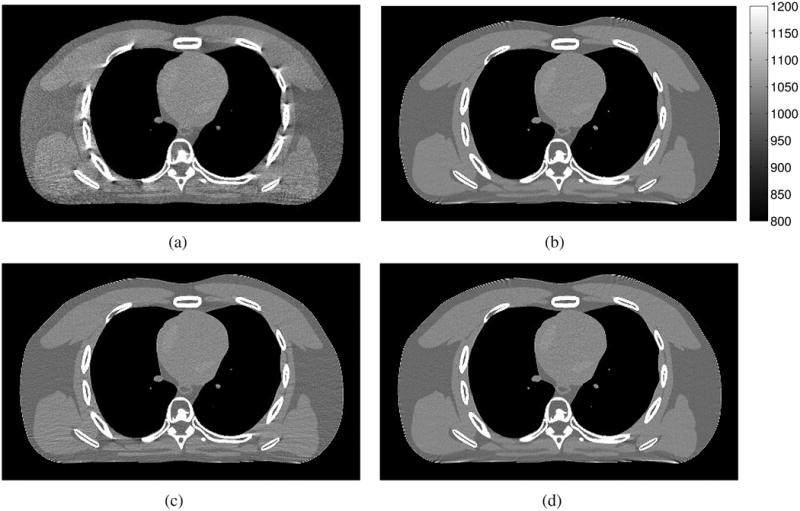
Simulation data: a transaxial plane of (a) an initial FBP image x⁽⁰⁾, (b) a converged image x̂, and two reconstructed images x⁽¹⁵⁾ after 15 iterations (about 680 seconds) of (c) OSb(24) and (d) OSb(24)-mom2. (Images are cropped for better visualization.)

Fig. 2.

Simulation data: convergence rate of OS algorithms (1, 12, 24, and 48 subsets) for 30 iterations with and without momentum for (a) sequential order and (b) bit-reversal order in Table VI. (The first iteration counts the precomputation of the denominator D in (7), and thus there are no changes during the first iteration.)

1. The number of subsets: Intuitively, using more subsets will provide faster initial convergence but will increase instability due to errors between the full gradient and subset gradient. Also, performing many sub-iterations (m) can increase error accumulation per outer iteration (n). Fig. 2 confirms this behavior.

2. The ordering of subsets: Interestingly, the results of the proposed algorithms depend greatly on the subset ordering. Fig. 2 focuses on two deterministic orders: a sequential (OSs) order, and a bit-reversal (OSb) order [53] that selects each order-adjacent subsets to have their projection views to be far apart as described in Table VI. The ordering greatly affects the build-up of momentum in OS-momentum algorithms, whereas ordering is less important for ordinary OS methods as seen in Fig. 2. The bit-reversal order provided much better stability in Fig. 2(b) compared to the results in Fig. 2(a). Apparently, the bit-reversal order can cancel out some gradient errors, because successive updates are likely to have opposite directions due to its subset ordering rule. In contrast, the sequential ordering has high correlation between the updates from two adjacent subsets, increasing error accumulation through momentum. Therefore, we recommend using the bit-reversal order. (Fig. 3(d) shows that random ordering (OSr) performed worse than the bit-reversal order.)

3. Type of momentum: Fig. 2 shows that combining OS with two of Nesterov's momentum techniques in Tables III and IV (OS-mom1 and OS-mom2) resulted in different behaviors, whereas the one-subset versions of them behaved almost the same. Fig. 2 shows that the OS-mom2 algorithm is more stable than the OS-mom1 algorithm perhaps due to the different formulation of momentum or the fact that the momentum term $\{{\mathit{z}}^{(\frac{k}{M})}\}$ in Table III is not guaranteed to stay within the set χ unlike that in Table IV. Therefore, we recommend using the OS-mom2 algorithm in Table IV for better stability.

   Fig. 1 shows the initial image and the converged image and reconstructed images after 15 iterations (about 680 seconds) of conventional OS and our proposed OS-momentum algorithm with 24 subsets and the bit-reversal ordering. The OSb(24)-mom2 reconstructed image is very similar to the converged image after 15 iterations while that of conventional OS is still noticeably different. However, even the more stable OS-mom2 algorithm becomes unstable eventually for many subsets (M > 24) as seen in Fig. 2; the next subsection shows how relaxation improves stability.

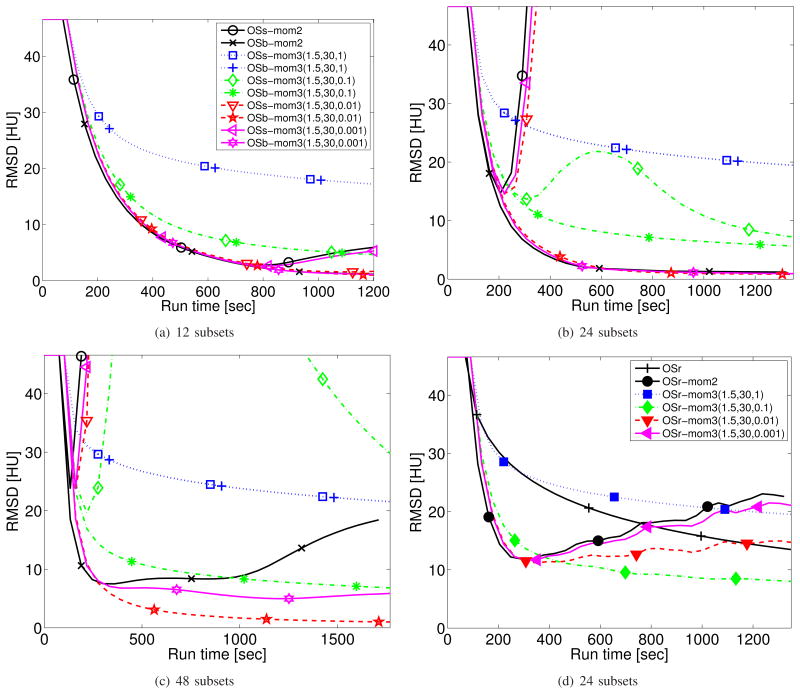
4. The choice of Γ: Section V-E gives an optimized Γ in (19) that minimizes the right term of (22), i.e., the gradient error term, on average. However, since the right term in (22) is a worst-case loose upper-bound, we can afford to use smaller Γ than Γ̂_1.5 in (28) (or (30)). In addition, we may use even smaller Γ depending on the order of subsets. Specifically, the bit-reversal ordering (OSb) appears to accumulate less gradient error than other orderings, including random subset orders (OSr), so the choice (28) (or (30)) may be too conservative. Therefore, we investigated decreasing the matrix Γ̂_1.5 (28) (or (30)) by a factor λ ∈ (0, 1] as

   $$\stackrel{\sim }{\mathbf{\Gamma }}=\lambda {\widehat{\mathbf{\Gamma }}}_{1.5.}$$ (32)

   Fig. 3 shows the effect of the parameter λ for various choices of the number and ordering of subsets. In all cases, λ = 1 is too conservative and yields very slow convergence. Smaller λ ≤ 0.1 values lead to faster convergence, but it failed to stabilize the case of sequential ordering for M > 24. However, λ = 0.01 worked well for the bit-reversal orderings in the simulation data, while the choice λ = 0.001 was too small to suppress the accumulation of error within 30 iterations for 48 subsets. Any value of λ > 0 here will eventually lead to stability as Γ^(k) increases with c_k = 1.5, based on the convergence analysis (22). Particularly, OSs-mom3 algorithm with λ = 0.1 in Figs. 3(b) and 3(c) illustrates this stability property, where the RMSD curve recovers from the initial diverging behavior as the algorithm proceeds.

Table VI.

Examples of Subset Orderings: Two Deterministic Subset Ordering (OSs, OSb) and One Instance of Random Ordering (OSr) for OS Methods with M = 8 Subsets in a Simple Geometry with 24 Projection Views Denoted as (p₀, p₁, …, p₂₃), where those are Reasonably Grouped into the Following 8 Subsets: S₀ = (p₀, p₈, p₁₆), S₁ = (p₁, p₉, p₁₇), …, S₇ = (p₇, p₁₅, p₂₃).

Sequential (OSs): (S0, S1, S2, S3, S4, S5, S6, S7), (S0, S1, …

Bit-reversal (OSb): (S0, S4, S2, S6, S1, S5, S3, S7), (S0, S4, …

Random (OSr): S6, S7, S1, S7, S5, S0, S2, S4, S7, S3, …

Fig. 3.

Simulation data: convergence rate for various choices of the parameter λ in relaxation scheme of OS-momentum algorithms (c, ζ, λ) for (a) 12, (b) 24, (c) 48 subsets with both sequential (OSs) and bit-reversal (OSb) subset orderings in Table VI for 30 iterations. (The plot (b) and (c) share the legend of (a).) The averaged plot of five realizations of random subset ordering (OSr) is illustrated in (d) for 24 subsets.

For Fig. 3(d), we executed five realizations of the random ordering and show the average of them for each curve. Here, we found that λ = 0.01 was too small to suppress the error within 30 iterations, and λ = 0.1 worked the best. Based on Fig. 3, we recommend using the bit-reversal order with λ = 0.01 rather than random ordering.

Figs. 2 and 3 are plotted with respect to the run time of each algorithm. Using larger subsets slightly increased the run time due to extra regularizer computation, but those increases were minor compared to the acceleration given by OS methods. The additional computation required for momentum methods was almost negligible, confirming that introducing momentum approach accelerates OS algorithm significantly in run time.

Overall, the simulation study demonstrated dramatic acceleration from combining OS algorithm and momentum approach. Next, we study the proposed OS-momentum algorithms on patient data, and verify that the parameters tuned with the simulation data work well for real CT scans.¹⁶

B. Patient CT scan data

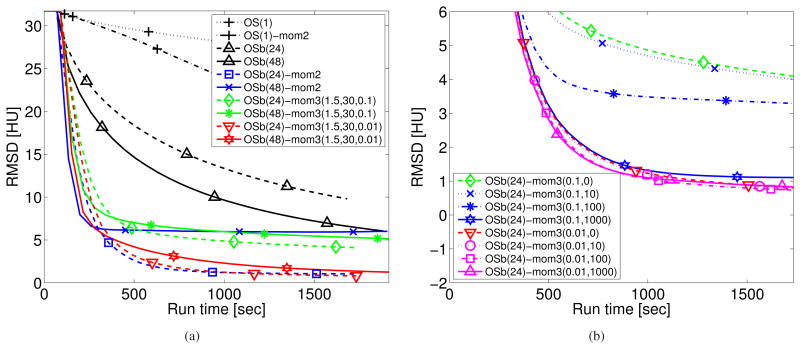
From a 888 × 32 × 7146 sinogram measured in a helical geometry with pitch 0.5, we reconstructed a 512 × 512 × 109 shoulder region image in Fig. 4. Fig. 5 shows the RMSD convergence curves for the bit-reversal subset ordering, where the results are similar to those for the simulation in Fig. 3 in terms of parameter selection. In Fig. 5(a), the parameter λ = 0.01 for both 24 and 48 subsets worked well providing overall fast convergence. Particularly for M = 48, the choice λ = 0.01 greatly reduced the gradient approximation error and converged faster than the un-relaxed OS-momentum algorithm.

Fig. 4.

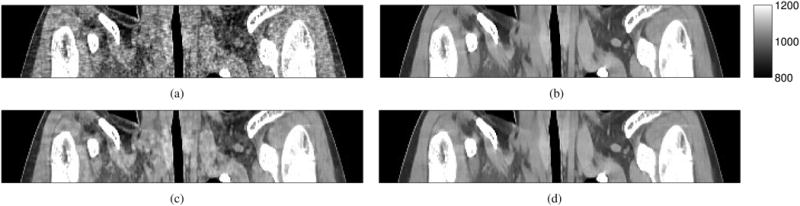
Patient CT scan data: a sagittal plane of (a) an initial FBP image x⁽⁰⁾, (b) a converged image x̂, and two reconstructed images x⁽¹⁵⁾ after 15 iterations (about 865 seconds) from (c) OSb(24) and (d) OSb(24)-mom3 where (c, ζ, λ) = (1.5, 30, 0.01).

Fig. 5.

Patient CT scan data: convergence rate of OSb methods (24, 48 subsets) for 30 iterations with and without momentum for (a) several choices of (c, ζ, λ) with a fixed c_k = c = 1.5 and (b) the choices of (λ, η) for an increasing c_k in (24) with 24 subsets and ζ = 30 [HU].

In Fig. 5(b), we further investigate the increasing c_k (24) in (19) that starts from 1 and eventually becomes 1.5 with a tuning parameter η in (24). Larger η in (24) leads to a slowly increasing c_k, i.e. smaller c_k values in early sub-iterations (k), and thus, the results in Fig. 5(b) show better initial acceleration from using large η. Particularly, using large η for the choice λ = 0.1 showed a big acceleration, while that was less effective in the case λ = 0.01 due to small values of Γ (32) in (19).

Fig. 4 shows the initial FBP image, converged, and reconstructed images from conventional OS and the proposed OS-momentum with relaxation. Visually, the reconstructed image from the proposed algorithm is almost identical to the converged image after 15 iterations.

VII. Conclusion and Discussion

We introduced the combination of OS-SQS and Nesterov's momentum techniques in tomography problems. We quantified the accelerated convergence of the proposed algorithms using simulated and patient 3D CT scans. The initial combination could lack stability for large numbers of subsets, depending on the subset ordering and type of momentum. So, we adapted a diminishing step size approach to stabilize the proposed algorithm while preserving fast convergence.

We have focused on PWLS cost function in this paper, but the proposed algorithms can be applied to any convex cost function for tomography problems, including penalized-likelihood methods based on Poisson models for pre-log sinogram data. The ideas also generalize to parallel MRI problems [54], [55]. We are further interested in studying the proof of convergence of the OS-momentum algorithm for a (bit-reversal) “deterministic” order.

The accumulating error of the proposed algorithms in Section V is hard to measure due to the computational complexity, and thus optimizing the relaxation parameters for an increasing Γ^(k) in (19) remains an open issue. In our experiments, we observed that simply averaging all of the sub-iterations at the final iteration [29] greatly reduces RMSD, particularly when the proposed algorithm becomes unstable (depending on the relaxation parameters). One could consider this averaging technique to improve stability, or alternatively one could discard the current momentum and restart the build-up of the momentum as in [30], [56]. Such refinements could make OS-momentum a practical approach for low-dose CT.

Appendix A: Proof of Lemma 2

We extend the proof of [33, Theorem 7] for diagonally preconditioned stochastic OS-SQS-type algorithms for the proof of Lemma 2. We first use the following lemma:

Lemma 3: For k = nM + m ≥ 0, the sequence $\{{\mathit{x}}^{(\frac{k}{M})}\}$ generated by Table V satisfies

$$\begin{array}{l}\sum _{l=0}^k{t}_l\mathrm{\Psi }({\mathit{x}}^{(\frac{k+1}{M})})-e^{(k)}\le \underset{\mathit{\upsilon }⪰0}{min}{\mathrm{\Phi }}^{(k)}(\mathit{\upsilon })\hfill \\ {\mathrm{\Phi }}^{(k)}(\mathit{\upsilon })\le \sum _{l=0}^k{t}_l\mathrm{\Psi }(\mathit{\upsilon })+\frac{{\Vert \mathit{\upsilon }-{\mathit{z}}^{(0)}\Vert }_{{\mathbf{\Gamma }}^{(k)}}^2}{2}+{\overline{e}}^{(k)}(\mathit{\upsilon }),\hfill \end{array}$$

where

$${\mathrm{\Phi }}^{(k)}(\mathit{\upsilon })\triangleq \sum _{l=o}^k{t}_l[M{\mathrm{\Psi }}_{S_l}({\mathit{z}}^{(\frac{l}{M})})+M\nabla {\mathrm{\Psi }}_{S_l}{({\mathit{z}}^{(\frac{l}{M})})}^{\top }(\mathit{\upsilon }-{\mathit{z}}^{(\frac{l}{M})})]+\frac{{\Vert \mathit{\upsilon }-{\mathit{z}}^{(0)}\Vert }_{{\mathbf{\Gamma }}^{(k)}}^2}{2}$$

that satisfies ${\mathit{\upsilon }}^{(\frac{k+1}{M})}=arg{min}_{\mathit{\upsilon }⪰0}{\mathrm{\Phi }}^{(k)}(\mathit{\upsilon })$,

$$\begin{array}{l}{e}^{(k)}\triangleq \sum _{l=0}^k\sum _{i=0}^l{t}_i{\Vert M\nabla {\mathrm{\Psi }}_{S_l}({\mathit{z}}^{(\frac{l}{M})})-\nabla \mathrm{\Psi }({\mathit{z}}^{(\frac{l}{M})})\Vert }_{{[{\mathbf{\Gamma }}^{(l)}-\mathit{D}]}^{-1}}^2\hfill \\ +\sum _{l=0}^k{t}_l(\mathrm{\Psi }({\mathit{z}}^{(\frac{l}{M})})-M{\mathrm{\Psi }}_{S_l}({\mathit{z}}^{(\frac{l}{M})}))\hfill \\ +\sum _{l=1}^k\sum _{i=0}^{l-1}{t}_i{(\nabla \mathrm{\Psi }({\mathit{z}}^{(\frac{l}{M})})-M\nabla {\mathrm{\Psi }}_{S_l}({\mathit{z}}^{(\frac{l}{M})}))}^{\top }({\mathit{z}}^{(\frac{l}{M})}-{\mathit{x}}^{(\frac{l}{M})})\hfill \end{array}$$

and

$${\overline{e}}^{(k)}(\mathit{\upsilon })\triangleq \sum _{l=0}^k{t}_l[M{\mathrm{\Psi }}_{S_l}({\mathit{z}}^{(\frac{l}{M})})-\mathrm{\Psi }({\mathit{z}}^{(\frac{l}{M})})+{(M\nabla {\mathrm{\Psi }}_{S_l}({\mathit{z}}^{(\frac{l}{M})})-\nabla \mathrm{\Psi }({\mathit{z}}^{(\frac{l}{M})}))}^{\top }(\mathit{\upsilon }-{\mathit{z}}^{(\frac{l}{M})}\left)\right].$$

Proof: Simply generalize the proof of [33, Lemma 2] using the proof of [18, Lemma 1].

Using Lemma 3 with the fact min_υ⪰0 Φ^(k)(υ) ≤ Φ^(k)(x̂) leads to the following:

$$\sum _{l=0}^k{t}_l(\mathrm{\Psi }({\mathit{x}}^{(\frac{k+1}{M})})-\mathrm{\Psi }(\widehat{\mathit{x}}))\le \frac{{\Vert {\mathit{x}}^{(0)}-\widehat{\mathit{x}}\Vert }_{{\mathbf{\Gamma }}^{(k)}}^2}{2}+e^{(k)}+{\overline{e}}^{(k)}(\widehat{\mathit{x}}).$$

Finally, the expectation on the above equation provides Lemma 2, as in [33, Theorem 7].

Appendix B: Choice of coefficients t_k

Lemma 4: For any given $\{{\gamma }_j^{(k)}\}$ satisfying its constraint in line 5 of Table V, the {t_k} generated by t₀ = 1

$$t_{k+1}=\frac{1}{2{\alpha }_{k+1}}\left(1+\sqrt{1+4t_k^2{\alpha }_k{\alpha }_{k+1}}\right),$$

where ${\alpha }_{k+1}\triangleq {max}_j({\gamma }_j^{(k+1)}/{\gamma }_j^{(k)})$ and α₁ = 1, tightly satisfies the following conditions:

$$t_0\in (0,1]\text{and}{\alpha }_{k+1}{t}_{k+1}^2\le \sum _{l=0}^{k+1}{t}_l,\forall k\ge 0,$$

which are equivalent to the conditions in line 6 of Table V.

Proof: Let t₀ have the largest possible value 1.

For k = 0,

$$\begin{array}{l}{\alpha }_1{t}_1^2=t_0+t_1=t_0^2+t_1\\ t_1=\frac{1}{2{\alpha }_1}(1+\sqrt{1+4t_0^2{\alpha }_0{\alpha }_1}).\end{array}$$ (33)

For k > 0, we get

$$\begin{array}{c}{\alpha }_{k+1}{t}_{k+1}^2=\sum _{l=0}^{k+1}{t}_l={\alpha }_k{t}_k^2+t_{k+1}\\ t_{k+1}=\frac{1}{2{\alpha }_{k+1}}(1+\sqrt{1+4t_k^2{\alpha }_k{\alpha }_{k+1}}).\end{array}$$ (34)

This rule for t_k (34) reduces to those used in Tables III and IV when ${\gamma }_j^{(k+1)}={\gamma }_j^{(k)}$ for all k ≥ 0 and j.