Measuring continuous baseline covariate imbalances in clinical trial data

Abstract

This paper presents and compares several methods of measuring continuous baseline covariate imbalance in clinical trial data. Simulations illustrate that though the t-test is an inappropriate method of assessing continuous baseline covariate imbalance, the test statistic itself is a robust measure in capturing imbalance in continuous covariate distributions. Guidelines to assess effects of imbalance on bias, type I error rate, and power for hypothesis test for treatment effect on continuous outcomes are presented, and the benefit of covariate-adjusted analysis (ANCOVA) is also illustrated.

1. Introduction

When properly designed, comparative randomized trials provide the foundation for concrete decisions on efficacy and safety of new therapies.^{1, 2} Green³ explains that the goals of these clinical trials are to determine which of two or more interventions is more effective in treatment or prevention, and to convince the community of the results. The latter is best accomplished when treatment groups are comparable. Comparable treatment groups with respect to covariate distributions are important not only for face validity, but also for achieving maximal power, especially in the case of interim analysis, early stopping, and secondary outcome analyses.⁴ Under random subject allocation, the expected level of imbalance in covariate distributions is zero. However, a single trial is only one experiment that is subject to stochastic phenomena.⁵ Therefore, individual randomized clinical trials will exhibit some level of covariate imbalance, and the questions arise:

1. Did randomization “work” in balancing covariate distributions for a single trial?

2. What level of covariate imbalance will impact overall results and analysis (i.e. bias, type I error rate, power)?

Current practice in reporting clinical trial data generally involves presenting a “Table 1,” displaying baseline variable summary statistics stratified by treatment group. A significance test often accompanies. Pocock et al.⁶ and Austin et al.⁷ reviewed clinical trials reported in four high profile journals from July to September of 1997 and January to June of 2007, respectively. Pocock et al. found that 92% of trials reported this Table 1, and 48% of these tables included baseline significance tests. In the review by Austin et al., 96.5% of articles reported this table with baseline tests for significance occurring 38% of the time. In both reviews, the authors point out inconsistency, lack of clarity in interpretation of these tests, and failure to explain decisions to adjust for influential covariates in subsequent analysis.

Table 1.

Predicting Power and Type I Error Rate, X ~ Lognormal, N=1000

Scenario	Measure	GLM p-value	GLM AIC	Hosmer-Lemeshow p-value	D
ρ = 0.3, Δ = 0	t	<2E-16	1054.6	0.896	0.066
	WRS	1.75E-08	1096.8	0.768	0.028
	KS	2.68E-06	1105	0.157	0.021
	sAUC	8.32E-16	1061.2	0.513	0.060
ρ = –0.3, Δ = 1.8	t	<2E-16	4929.9	0.962	0.040
	WRS	<2E-16	5051.9	0.312	0.016
	KS	2.29E-16	5064.1	0.613	0.013
	sAUC	<2E-16	4970.5	0.107	0.032
ρ = 0.6, Δ = 0	t	<2E-16	1057.1	0.184	0.206
	WRS	<2E-16	1207.8	0.779	0.092
	KS	3.02E-15	1250.9	0.365	0.060
	sAUC	<2E-16	1081	0.353	0.188
ρ = –0.6, Δ = 1.8	t	<2E-16	4046.5	0.360	0.190
	WRS	<2E-16	4616	0.920	0.076
	KS	<2E-16	4690.6	0.063	0.061
	sAUC	<2E-16	4212.5	<0.001	0.157
ρ = 0.8, Δ = 0	t	<2E-16	645.8	0.684	0.384
	WRS	<2E-16	863.9	0.510	0.175
	KS	<2E-16	915.8	0.126	0.125
	sAUC	<2E-16	664.1	0.938	0.367
ρ = –0.8, Δ = 1.8	t	<2E-16	3075.4	0.436	0.386
	WRS	<2E-16	4149.1	0.763	0.171
	KS	<2E-16	4376.5	<0.001	0.126
	sAUC	<2E-16	3432.5	<0.001	0.314

Baseline significance tests seem a natural way of evaluating randomization schemes, but they can be both controversial and uninformative.^6-9 If subject allocation to treatment groups is random, then “statistically significant” imbalances occur 5% of the time. Furthermore, tests for continuous covariate balance usually compare means or medians across treatment groups, and a statistically insignificant difference across treatment groups does not imply distributional balance. Senn⁹ shows that statistically insignificant levels of imbalance, as measured by the two-sample independent Z- or t-statistic, can result in large inflation of type I error rates in analysis of a continuous, normal outcome. Thus, the t-test is an inappropriate way of assessing continuous baseline covariate imbalance across treatment groups, but the t-statistic itself may be a useful measure of baseline covariate imbalance. The level of imbalance (as measured by the t-statistic) resulting in biased treatment effect estimation remains to be discovered and it will be explored in this paper, but the t-statistic as a measure of imbalance relies heavily on the assumption of normality of covariate(s).

This paper compares several candidate measures of imbalance for continuous covariates (including the t-statistic) and uses simulation results to select one of these measures for predicting detrimental effect on power, type I error rate, and bias in an unadjusted analysis for continuous primary outcome. Based on the selected measurement of imbalance, specific levels of imbalance corresponding to nontrivial levels of bias in treatment effect estimation are presented. Section 2 explains several candidate measures of imbalance, and Section 3 outlines simulation methods and criteria for evaluating predictability of each measurement. Section 4 presents simulation results, and the final section discusses overall significance of these results.

2. Candidate measures of imbalance

The statistical literature illustrates a variety of candidate measurements of imbalance for comparing continuous covariate distributions in clinical trials. Evaluation of treatment allocation schemes often involves computer simulation to compare balancing capabilities of different algorithms. Stigsby and Taves¹⁰ assess their rank-minimization algorithm in comparison to other algorithms by comparing t-statistic values from baseline significance tests for different allocation schemes. The allocation algorithm showing the smallest t-statistic is deemed the “best” method of balancing continuous covariates. Greevy et al.¹¹ use absolute difference in means across treatment groups and Wilcoxon rank-sum p-values in comparing balancing capabilities of treatment allocation algorithms. Rosenbaum and Rubin¹² have used a measure similar to the t-statistic known as the “standardized covariate bias.” While the p-values associated with these statistics are not informative measures, the absolute mean difference, t-statistic, the standardized covariate bias, or the Wilcoxon rank-sum statistics themselves are potential candidate measures of imbalance for continuous covariate distributions.

Begg, Iglewicz¹³ and Atkinson^{14, 15} use a precision or efficiency measurement in their simulation studies comparing optimum designs based on linear models. These measures capture precision associated with the treatment effect estimate in a final linear model for primary outcome, and they would therefore be expected to be associated with power and type I error rate. This measure seems logical for statisticians, but remains unintuitive for the less statistically inclined. Furthermore, calculations of this measurement are not universal across all types of outcomes (i.e. Calculation will be different for generalized linear models, proportional hazards models, etc.).^16-19 For these reasons, the simulations to follow do not examine efficiency or precision. The measures compared in these simulation studies are discussed in more detail below.

2.1. The t-statistic

The Z or t-statistic (or variation thereof) is one candidate measure of imbalance that will be evaluated in the simulations that follow. Senn⁹ illustrates that for a normally distributed outcome (Y) and a normally distributed covariate (X) in a clinical trial involving two treatment groups, a one-sided hypothesis test for treatment effect failing to condition on a correlated X can result in inflated type I error rate that is directly related to level of imbalance in that covariate (as measured by the Z or t-statistic). In fact, the actual size α(d_x) of a one-sided unadjusted test for mean treatment effect is equivalent to

$$\begin{array}{cc}\hfill \alpha \left(d_x\right)=& prob\left[Z\ge \frac{Z_{\alpha }}{\sqrt{1-{\rho }^2}}-\frac{\rho d_x}{\sqrt{(1-{\rho }^2){\sigma }_x^2}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\right]\hfill \\ \hfill =& prob\left[Z\ge \frac{Z_{\alpha }}{\sqrt{1-{\rho }^2}}-\frac{\rho d_x^{\ast }}{\sqrt{1-{\rho }^2}}\right]\hfill \end{array}$$ (1)

In this case corr(X,Y) = ρ, ρ_α is the one-sided critical value for a two-sample independent Z-test comparing mean outcome across treatment groups, n₁ (or n₂) is the number of subjects allocated to the active (or placebo) treatment arm, ${\sigma }_x^2$ is the variance of X, d_x is the mean difference in X across treatment groups, and $d_x^{\ast }$ is the standardized mean difference in X across treatment groups (also known as the Z-statistic comparing means in covariate X across treatment groups). It can be easily seen that as d_x or $d_x^{\ast }$ increases for a positively correlated covariate (such that the active treatment group is favored), α(d_x) will also increase. On the other hand, if the placebo group is favored, it can be shown that α(d_x) decreases as the magnitude of imbalance increases, resulting in a conservative test for treatment effect.^{6, 9}

It can further be shown that $d_x^{\ast }$ is also associated with power of an unadjusted test for treatment effect in the situation outlined above. The actual power γ(d_x) of such a test can be represented as follows:

$$\begin{array}{cc}\hfill \gamma \left(d_x\right)=& prob\left[Z\ge \frac{Z_{\alpha }}{\sqrt{1-{\rho }^2}}-\frac{d_x^{\ast }\rho }{\sqrt{1-{\rho }^2}}-\frac{\Delta }{\sqrt{(1-{\rho }^2){\sigma }_y^2}\left(\frac{1}{n_1+\frac{1}{n_2}}\right)}\right]\hfill \\ \hfill =& prob\left[Z\ge \frac{Z_{\alpha }-d_x^{\ast }\rho -d_y^{\ast }}{\sqrt{1-{\rho }^2}}\right]\hfill \end{array}$$ (2)

In this case ${\sigma }_y^2$ is the variance of Y, Δ is the treatment effect as measured by the mean difference in Y across treatment groups, and $d_x^{\ast }$ is the effect size (the standardized mean treatment effect). As $d_x^{\ast }$ increases for a positively associated covariate such that the active treatment group is favored, the actual power γ(d_x) of test for treatment effect will increase (because type I error rate is inflated), but if the placebo group is favored, γ(d_x) will decrease (because type I error rate will be much less than the nominal level). Pocock et al.⁶ also point out that $d_x^{\ast }$ is associated with biased treatment effect estimation.

Since in reality population variances are rarely known, $d_x^{\ast }$ (or Z) can be estimated by the t-statistic (because the t-distribution converges in distribution to the standard normal). Thus, one possible candidate measurement of imbalance is the familiar t-statistic comparing standardized mean covariate values across treatment groups. This measure is tied to normality of the covariate, and it only uses information from the first two moments of the overall covariate distribution. However, balance according to this measurement (i.e. a t-statistic equal to zero) does not necessarily imply overall distributional balance across two treatment groups.

2.2. The large sample Wilcoxon rank-sum statistic

A natural nonparametric extension of the t-statistic is the Wilcoxon rank-sum statistic.²⁰ This statistic measures location differences across two distributions in a similar manner to the t-statistic, but it does not carry the dependence of normality. Thus, it may be a measurement of imbalance that can be applied to a wider range of covariate distributions. The statistic can be explained as follows:

Let R_ij represent the rank of covariate observation x_ij for observation i(i = 1,...,n_i) in treatment group j(j - 1,2), such that R_ij ∈ (1,2..., N – 1, N), where N = n₁ + n₂. Then $W_1={\sum }_{i=1}^{n_1}{R}_{i1}$ represents the Wilcoxon rank-sum statistic whose exact distribution has been determined for specific sample sizes.²⁰ The expectation and variance of this statistic are $E\left(W_1\right)=\frac{n_1(N+1)}{2}$ and $Var\left(W_1\right)=\frac{n_1{n}_2(N+1)}{12}$, respectively. Therefore, the standardized or large sample Wilcoxon Rank-Sum statistic (WRS) is $WRS=\frac{W_1-E\left(W_1\right)}{\sqrt{Var\left(W_1\right)}}$, and this statistic has an asymptotic standard normal distribution under the null assumption of equal distributions.²⁰ The WRS measure is one candidate measure of imbalance that may have better capabilities in capturing distributional information than the parametric t-statistic.

2.4. The Kolmogorov-Smirnov statistic

It is important to note that measures such as the t-statistic and WRS statistic compare standardized means or median differences across treatment groups. They do not capture overall distributional imbalance because they rely on only the first one or two moments of the continuous covariate distribution. A covariate's distribution is not defined by the lower dimension moments alone, but much of the information associated with that distribution may be captured in these moments. If the distributions of a covariate in two treatment groups are the same, the lower dimension moments will be equivalent, but the converse is not true.

Huber ²² has introduced a balance test for observational data using the nonparametric Kolmogorov-Smirnov tests to assess overall covariate distributional differences. In addition, the R function GenMatch (a genetic search matching algorithm that attempts to maximize balance between treatment and control groups in an observational study) maximizes the Kolmogorov-Smirnov test p-value in matching continuous covariate distributions. Sekhon²³ illustrates that this method of matching performs better than using other imbalance metrics relying on empirical quantile-quantile differences. Finally, Rosenberger and Sverdlov²⁴ have also used the Kolmogorov-Smirnov distance in comparing balancing capabilities of various covariate-adaptive response-adaptive allocation schemes.

The Kolmogorov-Smirnov test is a nonparametric test that looks for any distributional differences by using empirical distribution functions. The test itself is very stringent, but this work focuses on a variation of the test statistic (as opposed to the p-value associated with it).

For observation x_ij (i = 1,..., n_i) in treatment group j(j = 1,2) and indicator function I, let $F_{n_1}\left(t\right)=\frac{{\sum }_{i=1}^{n_1}I(x_{i1}\le t)}{n_1}$ and $G_{n_2}\left(t\right)=\frac{{\sum }_{i=1}^{n_2}I(x_{i2}\le t)}{n_2}$ represent the empirical cumulative distribution functions (Ecdfs) for covariate X in the active treatment and placebo arms, respectively. Then the Kolmogorov-Smirnov statistic is $J=\frac{n_1{n}_2}{d}ma{x}_{-\infty <t<\infty }\left(\mid F_{n_1}\left(t\right)-G_{n_2}\left(t\right)\mid \right)$, where d is the greatest common divisor of n₁ and n₂. The exact distribution for selected small sample sizes has been derived,²⁰ but the simulations to follow focus on the large sample statistic, $J^{\ast }=\frac{d}{\sqrt{n_1{n}_{2}N}}J$. It will be imperative to know the direction of imbalance, and for that reason, the actual maximum difference in Ecdfs is used to calculate a variation of this statistic as opposed to the absolute value of this difference. Because it compares Ecdfs, this nonparametric measure may be more useful in capturing distributional imbalances as opposed to mean or median differences for continuous covariates. Thus, this variation of the Kolgmorogov-Smirnov statistic (KS) is used as yet another candidate for measuring continuous baseline covariate imbalance in these simulations.

2.5. The area under the curve of cumulative imbalance

Ciolino et al.²¹ present a novel way of illustrating distributional imbalance for continuous covariates. Let F(x, j) represent the number of subjects randomized to treatment arm j(j = 1,2) with covariate value less than or equal to x. Then D(x) = F(x ,1) − F(x, 2) represents the distribution of cumulative covariate imbalances between the two treatment arms. Ideally, an imbalance at one value of the covariate can be compensated by another imbalance at a nearby value in the opposite direction. Thus, D(x) would be expected to linger around zero in its entire range, indicating a nearly balanced covariate distribution between the two arms. The more the curve strays from zero, the larger the level of distributional imbalance observed. As a result, the area under the curve of cumulative imbalance (AUC) serves as an additional candidate measure of imbalance, and Simpson's Rule is used to numerically estimate the area under D(x) in the simulations to follow. It is essential to determine the direction of overall imbalance, and the area under the curve of imbalance alone cannot accomplish this as it will always be positive. For this reason, the sign associated with the t-statistic multiplied by the estimated AUC, sAUC, is used in determining predictive ability for statistical parameters of interest.

The following section outlines the simulation study conducted to evaluate each of the measurements of imbalance discussed here. It also explains criteria used in choosing a measurement of imbalance with the “best” predictive ability for statistical parameters of interest.

3. Methods

3.1. Simulation outline

Simulation studies were conducted in R that simulated a clinical trial involving two treatment arms with equal allocation (using a blocking scheme), one predictive baseline continuous covariate, and a normally distributed primary outcome. The simulation logic is outlined below:

1. Simulate covariate (X) from a specified distribution (choices are normal, lognormal, bimodal).

2. Assign X values sequentially to one of two treatment arms according to a blocking scheme to ensure equal sample sizes.

3. Simulate normally distributed outcome (Y) conditional on X values, the assumed level of correlation between X and Y (ρ = 0,0.3, 0.6, 0.8), and the treatment effect (Δ may be zero or the treatment effect corresponding to 80% power).

4. Conduct an unadjusted hypothesis test for mean treatment effect on primary outcome at the end of each simulation, capturing one-sided p-value and estimated treatment effect.

5. Calculate measurements of imbalance for covariate X: t-statistic, WRS, KS, and AUC.

6. Return to 1.

All possible combinations of covariate distribution (normal, lognormal, bimodal), level of covariate influence (ρ = 0,0.3, 0.6, 0.8), and treatment effect (corresponding to 2.5% power and 80% power) were simulated (for a total of 24 simulation scenarios). For each of the 24 scenarios, 5000 replications were performed. The nominal one-sided significance level for test of treatment effect was set at 2.5% and thus the treatment effect associated with 2.5% power is equivalent to zero. Each of the 24 scenarios were examined for sample sizes of 100, 300, 500, and 1000 and the mean treatment effects corresponding to 80% power for each of these sample sizes were approximately 5.6, 3.2, 2.5, and 1.8, respectively. Thus, the treatment was simulated to positively affect outcome, and positive levels (t>0, WRS>0, KS<0, AUC>0) of imbalance corresponded to larger values of the covariate in the active treatment group. For that reason, correlation was made positive when there was no simulated treatment effect in order to determine inflation of type I error rate, while correlation was made negative when there was a simulated treatment effect in order to determine detrimental effects on power (as opposed to inflation, since underpowered studies are of more interest). This change in direction of association was done for ease of interpretation and reporting of results.

3.2. Choosing an imbalance measure

Measuring imbalance in covariate distributions is not the same as measuring its impact on primary outcome analysis. However, since statisticians are concerned with the latter, these measures of imbalance were evaluated based on predictive ability for statistical parameters for primary outcome analysis in these simulations. The statistical parameters of importance are power, type I error rate, and bias in treatment effect estimation. Using all of the simulated data, separate models were created for each of these parameters using each of the imbalance measurements in turn as predictors. Specifically, after each simulated clinical trial, an indicator variable was created to capture whether a treatment effect was detected at the one-sided 2.5% level of significance (i.e. p-value < 0.025). Then four separate generalized linear models (GLMs) with logit link functions were fit for this variable using each of the measurements of baseline covariate imbalance as explanatory variables. Goodness of fit for these models was based on magnitude of model Wald p-value associated with the effect of the imbalance measure, Akaike Information Criteria (AIC),²⁵ the Hosmer-Lemeshow goodness of fit test,²⁶ and a measure analogous to R-squared (for linear models) denoted D, originally introduced by McFadden²⁷ but also mentioned by Agresti.²⁵ The D criterion ranges from zero to one (as does R-squared in the linear model setup), but it is used as a relative measure since the value alone is difficult to interpret because it is based on log-likelihoods. These four criteria were examined simultaneously for each GLM, and the measurement with the most favorable characteristics (i.e. the lowest Wald p-value, lowest AIC, highest Hosmer-Lemeshow p-value, and highest D) overall was chosen the “best” measurement for modeling type I error rate (for the scenarios simulating no treatment effect) or power (for the scenarios simulating treatment effect corresponding to 80% power) for unadjusted test for treatment effect on normal outcome.

In addition to the generalized linear models for type I error rate and power, four separate simple linear models (LMs) were used to model bias for treatment effect estimation in each scenario. The criteria used to determine predictive ability in these models included the model p-value associated with the imbalance effect, R-squared, and AIC. Again, the imbalance measure showing the largest number of favorable characteristics (i.e. lowest p-value, lowest AIC, and highest R-squared) overall was deemed the “best” measurement for modeling bias in an unadjusted test for treatment effect on normal outcome.

Once an ideal measure of imbalance was chosen, the GLMs and LMs were used to predict statistical parameter values for a given level of imbalance. Further, the probability of observing levels of imbalance corresponding to large effects on these parameters was calculated under simple random allocation. The next section reports overall results for the measurements' predictive ability, relationships between the measurements, and influential levels of imbalance to be used as guidelines in assessing clinical trial data.

4. Results

4.1. Robustness of the t-statistic in measuring covariate imbalance

For all covariate distributions and sample sizes examined, results were very consistent. For this reason, tables 1 and 2 only present results for scenarios using a sample size of 1000 for the skewed, lognormally distributed covariate. The results are, however, generalizable to essentially all scenarios examined for each sample size (N=100, N=300, N=500, and N=1000) as well as each covariate distribution (normal, lognormal, bimodal). Table 1 illustrates the predictive ability of each measure of covariate imbalance for type I error rate and power when analyses fail to account for the influential covariate. The models for type I error rate are those corresponding to zero treatment effect in table 1, and the models for power are those corresponding to nonzero treatment effect in table 1. Table 2 illustrates the predictive ability of each measure of covariate imbalance for bias.

Table 2.

Predicting Bias, X ~ Lognormal, N=1000

Scenario	Measure	LM R-squared*	LM AIC
ρ = 0.3, Δ = 0	t	0.102	9106.8
	WRS	0.048	9398.2
	KS	0.035	9463.6
	sAUC	0.086	9196.6
ρ = –0.3, Δ = 1.8	t	0.087	9253.3
	WRS	0.038	9513.8
	KS	0.031	9554.7
	sAUC	0.071	9340.4
ρ = 0.6, Δ = 0	t	0.371	7488.7
	WRS	0.178	8831
	KS	0.0122	9159.4
	sAUC	0.324	7851.8
ρ = –0.6, Δ = 1.8	t	0.353	7412.4
	WRS	0.163	8701
	KS	0.124	8923.8
	sAUC	0.301	7794.6
ρ = 0.8, Δ = 0	t	0.622	4511.9
	WRS	0.308	7539.9
	KS	0.233	8057
	sAUC	0.524	5666.8
ρ = –0.8, Δ = 1.8	t	0.633	4712.4
	WRS	0.312	7862.4
	KS	0.236	8386.1
	sAUC	0.534	5916.8

^*In all cases outlined in Table 2, the model p-value was <2E-16, suggesting that imbalance (no matter which way it was measured) significantly predicted bias on all scenarios involving an influential covariate.

None of the imbalance measurements examined were predictive for type I error rate, power, or bias when the covariate X had zero influence on outcome Y (i.e. ρ = 0). However, even with slight correlation (ρ = 0.3) between covariate and outcome, each measure significantly predicts power, type I error rate, and bias for an unadjusted analysis as illustrated by the extremely small model p-values associated with each variable (p < 2×10⁻¹⁶ in most cases, see tables 1 and 2). Not surprisingly, as the simulated level of correlation between X and Y increased, the predictive ability for each measurement of imbalance also increased. Tables 1 and 2 show that the t-statistic unanimously had the lowest AIC for models of power (treatment effect=1.8 in this case, table 1), type I error rate (treatment effect=0, table 1), and bias (table 2). The t-statistic was the most predictive for bias as determined by the R-squared criterion, and it was also the most predictive for power and type I error rate as indicated by the analogous measure D. The Hosmer-Lemeshow goodness of fit test p-value was not as consistent as the other criteria in illustrating one measure's predictive ability over any others, but in all cases, this goodness of fit criterion does not suggest evidence against goodness of fit for models of power or type I error rate involving the t-statistic. The same cannot be said for the KS and sAUC measures. The results observed in tables 1 and 2 are representative of the observed results for each simulated covariate distribution (normal, lognormal, bimodal) for all sample sizes examined (N=100, N=300, N=500, N=1000). For all of these reasons, the t-statistic was chosen as the most predictive measurement of imbalance in these simulated scenarios for a normally distributed outcome when analysis is unadjusted.

4.2. Relationship between measurements of imbalance

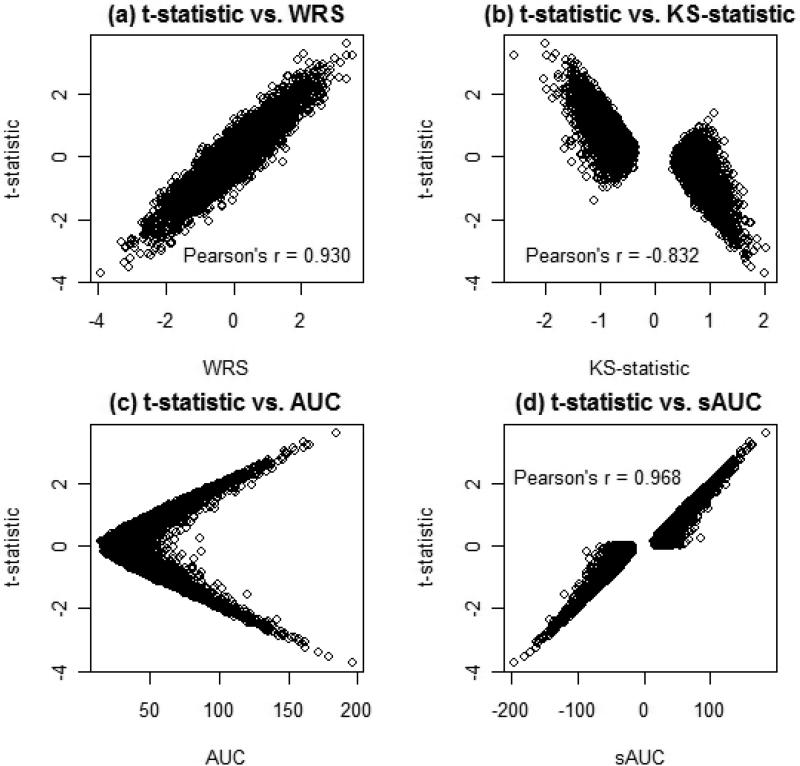
From tables 1 and 2 it is clear that each of the measurements of imbalance examined have some predictive ability for the statistical parameters of interest, and it may be the case that these measures are related to one another. Figure 1 and table 3 illustrate the relationships between these quantities. Table 3 shows the Pearson correlation estimates along with 95% confidence intervals for all possible pairwise comparisons between the four measurements examined. Figure 1 illustrates selected scatter plots that demonstrate these relationships for the bimodal covariate distribution. The t-statistic is strongly positively correlated with the WRS. It is also strongly negatively associated with the KS statistic, and the raw AUC value appears nonlinearly related to the t-statistic. However, if we take the slightly transformed AUC variable, sAUC (to illustrate the direction of imbalance), the t-statistic is highly correlated with this variable (table 3, figure 1). The strength of the relationships between each of the measurements of imbalance changes as the distribution of the covariate changes, but the overall shapes of these relationships remain the same (table 3). The relationship that remained consistent regardless of covariate distributions was that between the nonparametric WRS and KS measures (Pearson's r ≈ −0.89 in all cases). Note that Figure 1 suggests nonlinear associations between the imbalance measures examined, suggesting that linear correlation coefficients may not have the capability of capturing the true nature of the relationship. It is obvious that strong relationships exist among these measures, and although not necessarily entirely appropriate, the Pearson sample correlation coefficients were included in Table 3 in an attempt to numerically quantify the strength of these associations.

Figure 1.

Relationships of imbalance Measure

Table 3.

Correlation Between Imbalance Measures

Distribution	Measure	t	WRS	KS
Normal	t	1
	WRS	0.98 (0.98,0.98)	1
	KS	−0.86 (−0.87,−0.85)	−0.89 (−0.90,−0.89)	1
	sAUC	0.92 (0.92,0.93)	0.91 (0.91,0.92)	−0.86 (−0.87,−0.86)
Lognormal	t	1
	WRS	0.71 (0.70,0.72)	1
	KS	−0.62 (−0.64,−0.60)	−0.89 (−0.90,−0.89)	1
	sAUC	0.91 (0.91,0.91)	0.63 (0.62,0.65)	−0.55 (−0.57,−0.53)
Bimodal	t	1
	WRS	0.93 (0.93,0.93)	1
	KS	−0.83 (−0.84,−0.82)	−0.89 (−0.90,−0.89)	1
	sAUC	0.97 (0.97,0.97)	0.88 (0.87,0.89)	−0.81 (−0.82,−0.80)

Even though the t-statistic appears to be the most predictive of the statistical parameters of interest, each of the measurements of imbalance has some predictive ability since they are each significantly related to each other. These measurements of imbalance are thus capturing similar information about bias, power, and type I error rate. The level of predictive ability for each measure, however, depends on the strength of its association with the t-statistic.

4.3. Resampling from clinical data: The NINDS tPA study

Using data from the National Institutes of Neurological Disorders and Stroke (NINDS) tissue plasminogen activator (tPA) study for acute ischemic stroke,²⁸ additional simulations were conducted in which subjects (covariate, treatment, and outcome included) were resampled with replacement. The outcome variable used in these simulations was 90-day modified Rankin (mRS) scale score. The baseline covariate of interest for these simulations was National Institutes of Health Stroke Scale score (NIHSS), and there were two treatment arms (the active arm, receiving tPA, and the control arm receiving placebo). Subjects (N=200) were drawn from the NINDS tPA study dataset with replacement and statistical analyses were conducted for each of 5000 simulated clinical trials. The four imbalance measurement values were calculated for each simulation, and models for power (GLM) and treatment effect (LM) were developed using each of these measurements in turn as done previously. Relationships between each of these measurements were consistent with those seen in the simulated data. Correlations between the t-statistic and WRS, KS, and sAUC were estimated at 0.983, −0.781, and 0.909, respectively. The t-statistic again proved to be most predictive for power as determined by AIC, Hosmer-Lemeshow goodness of fit criterion, and the D measure. The t-statistic was also most predictive of treatment effect (and thus, bias. Note that we cannot calculate bias in this case as we do not know the “true” treatment effect.) as determined by AIC and R-squared. The predictive ability of the WRS measure was very comparable to that of the t-statistic in these simulations, but the t-statistic showed slightly better predictive ability for power (D=0.144 for the t-statistic versus D=0.142 for WRS) and treatment effect (i.e. bias, R-squared=0.296 for the t-statistic versus R-squared=0.295 for the WRS).

4.4. Threshold levels of imbalance determined by the t-statistic

Based on the GLMs discussed in Section 4.1, estimates for the t-statistic values corresponding to detrimental effects on unadjusted analysis (in terms of type I error and power) were obtained for all sample sizes and each covariate distribution examined. The estimates were similar across sample sizes and covariate distributions. The average estimated t-statistics across these scenarios corresponding to specific decreases in power and increases in type I error rate are reported in table 4. In addition, the probabilities of observing imbalances as large or larger according to the standard normal distribution are reported. It was deemed appropriate to report probabilities according to the standard normal distribution as it is the limiting distribution of the t distribution and sample size is adequately large (N=100, N=300, N=500, or N=1000) in all scenarios to use the normal approximation to the t distribution.

Table 4.

Estimated Power and Type I Error Given Imbalance

ρ	Simulated Power	t- or Z-statistic	Estimated Power|Imbalance	Prob(Z ≥ observed)
−0.3	80.0%	1.2	70.0%	0.115
		2.04	60.0%	0.021
		2.8	50.0%	0.003
0.3	2.5%	1.35	5.0%	0.089
		1.91	7.5%	0.028
		2.35	10.0%	0.009
−0.6	80.0%	0.73	70.0%	0.233
		1.07	60.0%	0.142
		1.38	50.0%	0.084
0.6	2.5%	1.2	5.0%	0.115
		1.43	7.5%	0.076
		1.63	10.0%	0.052
−0.8	80.0%	0.71	70.0%	0.239
		0.9	60.0%	0.184
		1.07	50.0%	0.142
0.8	2.5%	1.27	5.0%	0.102
		1.44	7.5%	0.075
		1.56	10.0%	0.059

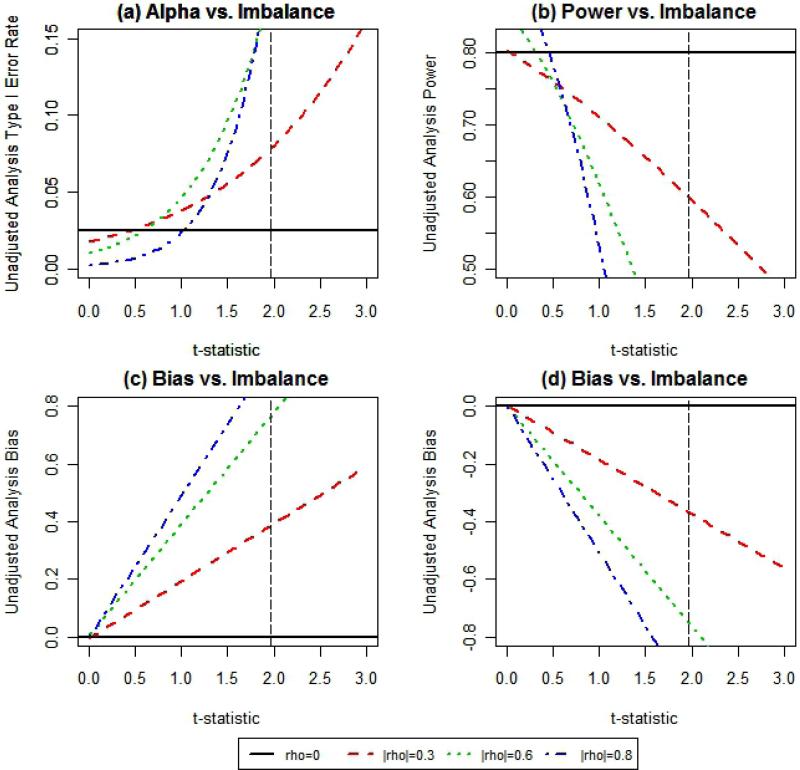
When failing to control imbalance in continuous baseline covariate distributions, an estimated 10% decrease in power (i.e. 70% power in table 4) of unadjusted test for treatment effect on a normally distributed outcome will occur approximately 11.5%, 23.3%, or 23.9% of the time when the correlation between covariate and outcome is 0.3, 0.6, or 0.8, respectively (table 4). In addition, actual estimated type I error rate is twice (i.e. 5% power in table 4) the nominal (2.5%) level approximately 8.9%, 11.5%, or 10.2% of the time for the same respective levels of correlation. Plots of type I error rate, power, and bias estimates for the lognormal scenario can be seen in figure 2. It is evident that as the level of influence of the covariate increases, the impact on these statistical parameters becomes more substantial. In any case, the traditional two-sided 5% level baseline test for significance does not capture these issues (as indicated by the vertical dotted line at 1.96, Figure 2). Thus, the threshold values shown in Table 4 are of more relevance than a baseline test for significance at the 5% level.

Figure 2.

These plots show the estimated (a) type I error rate, (b) power, and (c,d) bias for given levels of imbalance defined by the t-statistic comparing mean covariate values across two treatment groups. The t-statistic values greater than$>$ zero correspond to larger values of the covariate in the active treatment group. Plots (a) and (c) correspond to effects on these parameters for a covariate that is positively associated with outcome and plots (b) and (d) correspond to effects on these parameters for a covariate that is negatively associated with outcome.

4.5.The power of ANCOVA

The same methods outlined in Sections 3.1 and 3.2 were used to examine whether imbalance in influential baseline covariate distributions still has an impact on power, type I error rate, and bias when analysis involves covariate-adjustment in a linear model (analysis of covariance or ANCOVA). The only differences in methodology occurred at the end of each simulation run, where adjusted p-values and adjusted treatment effects were captured in addition to the unadjusted information.

In fitting GLMs and LMs for power, type I error rate, and bias, none of the five measures alone proved to be significant predictors of these outcomes across all sample sizes and all scenarios examined. R-squared values were almost unanimously <0.001 in models for bias, and the analogous D values were also almost all <0.001 with few exceptions (maximum=0.016) in models for power and type I error rate. Thus, it appears that imbalance alone in a linearly related covariate does not seem to have a noticeable effect on covariate-adjusted statistical analysis of a continuous outcome.

Recall that when a treatment effect was simulated, it corresponded to 80% power for the unadjusted hypothesis test for mean treatment effect. This power was approximately observed for the unadjusted statistical analyses, but as the covariate effect increased, the estimated power for adjusted statistical analysis was much larger than 80%. For example, the estimated power (i.e. the proportion of successful treatment effect detections as determined by p-value < 0.025) for the covariate-adjusted analysis of treatment effect was about 99.6% when the correlation between a normally distributed covariate and the outcome was 0.80 for sample size of 100. that imbalance is highly predictive of statistical parameters in the unadjusted test for treatment effect, while we have no evidence of its predictive ability for the adjusted test in these data. The final section to follow discusses the significance of these overall results and concludes with guidelines for statistical analysis in clinical trials involving continuous outcomes with predictive covariates.

5. Discussion

In the clinical research literature, it has been common practice to report baseline variables in “Table 1” in journal articles reporting clinical trial results.^{6, 7} Although baseline significance tests are not an uncommon feature presented in this table, several authors^{6-9, 29-31} have discussed the problems associated with using significance tests to compare baseline covariate distributions across treatment groups. Aside from the fact that p-values associated with these tests are uninformative, Senn²⁹ also illustrates how easy it can be for systematic bias in allocation to go undiscovered using the t-test for baseline imbalance at the 5% level. This paper has shown that statistically insignificant imbalances in covariate distributions can have a substantial effect on power, type I error rate, and bias in a test for treatment effect when analysis fails to adjust for that covariate. Altman⁸ suggests a subjective assessment of baseline imbalance using common sense, but there is an evident disconnect between recommendation from the statistical literature and current practice in assessing baseline imbalance as is evidenced by the reviews of Pocock et al.⁶ and Austin et al.⁷ A possible reason for this discrepancy may be the lack of proper tools for objective assessment of baseline covariate imbalance.

Though a baseline significance test may be an inappropriate way of assessing influential covariate imbalance, the test statistics themselves may have the capacity to capture distributional imbalances that are predictive of biased treatment effect estimation. These simulations have compared four relatively straightforward measurements in order to better characterize the relationship between imbalance and statistical parameters for primary outcome analysis. The results suggest that imbalance in prognostic baseline covariates (no matter how it is measured) is highly predictive of bias, type I error rate, and power for an unadjusted hypothesis test for mean treatment effect in a normally distributed outcome. Of the four measurements of imbalance (t-statistic, WRS, KS, AUC) examined, the t-statistic had the best overall predictive ability for these statistical parameters. This was true whether the covariate distribution was symmetric (normal), skewed (lognormal), or bimodal. Thus, the t-statistic is a robust measurement of baseline covariate imbalance, and the authors recommend its use in evaluating imbalance in continuous covariate distributions across treatment arms in clinical trials.

However, the baseline “significance” test associated with the t-statistic is not a proper way of evaluating imbalance because statistically insignificant imbalances (at the 5% level) still have the potential to result in substantial effects on type I error rate and power for an unadjusted statistical test. The appropriate level of significance (or equivalently, the appropriate amount of imbalance as measured by the t-statistic) for determining influential levels of baseline imbalance depends on the scenario (i.e. the amount of correlation between covariate and outcome and treatment effect). According to these results, a more appropriate one-sided baseline test for significance may have a significance level as high as 23.9%≈24% (or 48% for a two-sided test, see table 4). At the very least, the authors suggest using table 4 as a guideline, but to estimate actual type I error rate of an unadjusted hypothesis test for continuous outcome, use equation (1), replacing ρ with the estimated Pearson correlation coefficient, Z_α with the critical value for the hypothesis test for primary outcome, and $d_x^{\ast }$ with the t-statistic comparing mean covariate values across treatment groups. Similarly, when estimating power for an unadjusted hypothesis test for treatment effect, use equation (2), replacing $d_y^{\ast }$ with the effect size. These equations can also be used in determining a “tolerable” level of imbalance to preserve a given type I error rate or power.

The thresholds presented in table 4 are comparable to those predicted based on Senn's and the authors’ formulas (equations (1) and (2)). As long as sample size is sufficiently large (N>30), the discrepancy between the quantile values from the t-distribution and those from the standard normal distributional are minimal.³² As a result, when using these equations, the quantile values from the t-distribution can be used in place of those from the standard normal as the standard normal is the limiting distribution for the t.

Consistent results were also obtained when resampling from real data. The results of the NINDS tPA study for acute ischemic stroke²⁸ examined in Section 4.3 have been the source of controversy partially due to large, but statistically insignificant imbalances in baseline NIHSS across treatment groups.^{21, 33-35} Baseline NIHSS is a known predictor of three month outcome, and in this dataset the sample correlation coefficient between NIHSS at baseline and 90-day mRS was 0.54. The observed t-statistic comparing NIHSS across treatment groups was −1.48 (smaller values, or less severe strokes were assigned to the treatment group overall, two-sided p-value=0.14) for this trial. If the 90-day mRS score had been the primary outcome (though a global statistic that captured several stroke severity measures at 90 days was actually used in analysis), the estimated type I error for an unadjusted one-sided test for treatment effect (using a critical value corresponding to 2.5% level of significance) was actually about 8.38% according to equation (1). Resampling from real clinical data thus shows support for our results involving simulation of data based on specific underlying relationships.

It should be noted, however, that only one baseline covariate was examined in the monte carlo simulations as well as the bootstrapped sampling. In the NINDS tPA dataset, it is possible that imbalance in additional covariates may have further biased results or offset the biases that were caused by baseline NIHSS imbalances in unadjusted analyses. This is true for any trial making unadjusted inferences on treatment effect in the presence of multiple covariates, and the situation quickly becomes complex with the addition of covariates, interactions, and multiple treatment arms. These situations are beyond the scope of this paper and will be explored in the future.

These simulations have also illustrated that adjustment in a linear model setting can be a very powerful tool in controlling variability associated with influential covariates. Results do not show strong evidence that the level of imbalance in influential covariates is directly associated with power, type I error rate, or bias when using ANCOVA as a means of primary outcome analysis. In these simulations, power of the test for treatment effect in the adjusted analyses was generally much larger than in the unadjusted hypothesis test (99.6% adjusted versus 80% unadjusted). Thus, a conservative approach is to always adjust for known influential covariates when conducting a test for overall treatment effect in a continuous outcome.

Pocock et al.⁶ have suggested that adjustment be made if the correlation between covariate and outcome is estimated to be greater than or equal to 0.50. However, the International Conference on Harmonization (ICH) states that this adjustment should be specified a priori in the clinical trial's protocol, and any unplanned adjusted analysis will be considered secondary analysis.³⁶ Furthermore, there has historically been more emphasis on unadjusted statistical analyses of clinical trial data due to the ease of interpretation and generalizability.^{18, 19} Austin et al.⁷ claim that about 94% of clinical trial articles reviewed presented an unadjusted analysis for primary outcome, while only 34% included an adjusted analysis. Of those including the adjusted results, only 15% clearly pre-specified the adjustment, 18% made the post hoc decision to adjust, and the remaining 67% of trials were unclear as to whether the decisions to adjust in analyses were planned.

Green³ has pointed out that the hope that one can simply adjust away any imbalance is just “wishful thinking.” Imbalance in covariate distributions may not affect adjusted analysis as severely as one may think (as illustrated by these results), but balance is important for face validity, interim analysis, the case of small sample sizes, and secondary outcome analyses (these are all cases in which an unadjusted analysis may be preferred over the adjusted analysis).⁴ Furthermore, Trowman et al.³⁷ show that imbalance in covariate distributions can result in misleading overall conclusions in meta-analyses. The authors use an example to illustrate that imbalance in covariate distributions must be taken into account when conducting meta-analysis in order to obtain a more precise overall estimate of treatment effect using data pooled from multiple studies.

Since both proper adjustment and balance for influential covariates have been shown to be important in analysis and interpretation of clinical trial results, the authors recommend use of the following guidelines:

1. Attempt to control any known influential covariates at the design phase by including them in the treatment allocation scheme as well as planning to adjust for these covariates in the analysis.

2. If this is not possible (i.e. if the covariates were not known to be influential before the commencement of the trial), then an adjusted secondary analysis should be conducted. It should be noted however, that this analysis will not carry as much merit as the unadjusted primary analysis outlined in the clinical trial protocol. Any unplanned analyses will fall under the heading of exploratory analyses, and for that reason, interpretations must be made with caution. Furthermore, trial results based on inferences from unadjusted primary analysis may be questionable if there is imbalance in influential covariate(s). Therefore, proceed to guideline 3.

3. To assess the impact that imbalance may have on an unadjusted primary analysis, we suggest calculating a t-statistic comparing mean covariate value in the active treatment group to the mean covariate value in the placebo group (numerator = x̄_tx − x̄_pbo) as well as the estimated level of covariate influence (measured by the Pearson correlation coefficient between X and Y). If the active treatment group is favored (i.e. if the t-statistic for a positively associated covariate is greater than zero or the t-statistic for a negatively associated covariate is negative), then a nontrivial type I error inflation may occur. For the impact on type I error, refer to table 4 or equation (1). If the placebo group is favored (i.e. the t-statistic for a negatively associated covariate is greater than zero or the t-statistic for a positively associated covariate is less than zero), then a nontrivial decrease in power is possible. For the impact on power, refer to table 4 or equation (2).

Balance in influential covariates is by no means meant to replace adjustment because adjustment should be made for influential covariates regardless of level of imbalance.^{9, 29, 38, 39} Perhaps Senn²⁹ explained it best when he said, “...balance has nothing to do with validity of statistical inference; it is neither necessary nor sufficient for it. Balance concerns the efficiency of statistical inference and valid inference depends on correct conditioning.” Although ensuring covariate balance does not make unadjusted analysis valid, it may be a compromise between the invalid unadjusted analysis and the less accepted and more difficult to plan adjusted analysis. These simulations have shown this to be true for the continuous outcome case for a clinical trial involving two treatment arms, but future work includes examining the impact of imbalance on unadjusted and adjusted analyses when the association between covariate and outcome is nonlinear, the outcome is not normally distributed, the case of more than two treatment groups, and the case of more than one covariate. In addition, evaluation of current treatment allocation schemes is planned in order to examine the distribution of continuous covariate imbalance under commonly implemented algorithms.

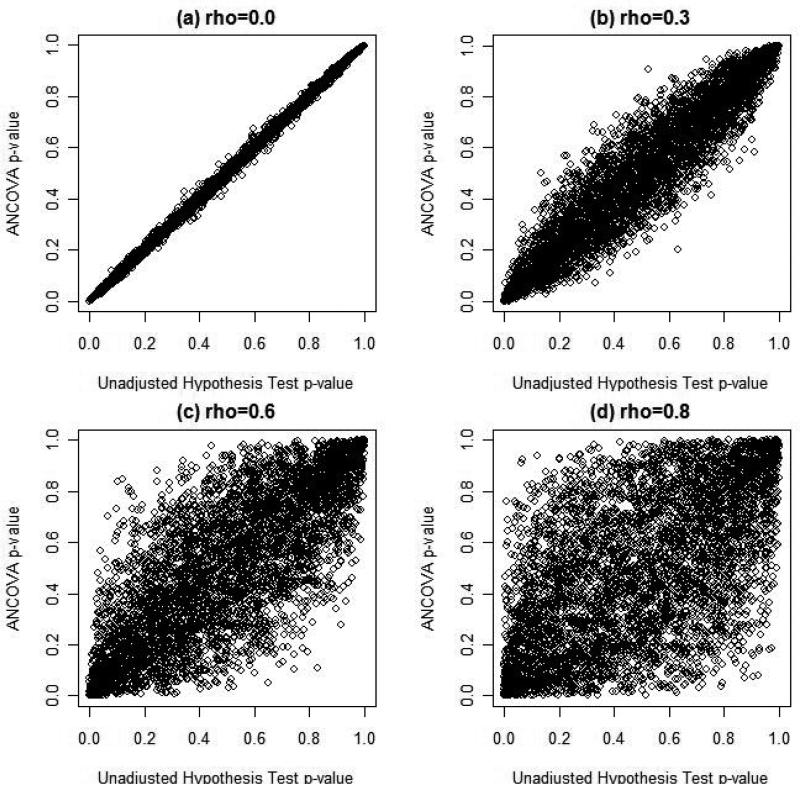
Figure 3. Relationship between AMCOVA and Unadjustment Hyposthesis Tests, N = 1000.

Figure 3 illustrates the relationship between ANCOVA and the standard unadjusted test for treatment effect using the p-values for each test. In each of the plots illustrated, there was no simulated treatment effect and thus the p-values for each type of analysis should be uniformly distributed on (0,1). When there is no association between the covariate and outcome, there is almost perfect correlation between the two tests' p-values (Pearson's r = 0.999). As figure 3 illustrates, as the level of correlation between the covariate and the outcome increases, the strength of the association between the two types of statistical analyses diminishes. Figure 3(d) suggests relatively weak and noisy association between the two statistical tests when the covariate X is strongly associated with outcome Y. Thus, it is not surprising