Abstract
The thioredoxin system, which consists of a family of proteins, including thioredoxin (Trx), peroxiredoxin (Prx) and thioredoxin reductase (TrxR), plays a critical role in the defense against oxidative stress by removing harmful hydrogen peroxide (H2O2). Specifically, Trx donates electrons to Prx to remove H2O2 and then TrxR maintains the reduced Trx concentration with NADPH as the cofactor. Despite a great deal of kinetic information gathered on the removal of H2O2 by the Trx system from various sources/species, a mechanistic understanding of the associated enzymes is still not available. We address this issue by developing a thermodynamically-consistent mathematical model of the Trx system which entails mechanistic details and provides quantitative insights into the kinetics of the TrxR and Prx enzymes. Consistent with experimental studies, the model analyses of the available data show that both enzymes operate by a ping-pong mechanism. The proposed mechanism for TrxR, which incorporates substrate inhibition by NADPH and intermediate protonation states, well describes the available data and accurately predicts the bell-shaped behavior of the effect of pH on the TrxR activity. Most importantly, the model also predicts the inhibitory effects of the reaction products (NADP+ and Trx(SH)2) on the TrxR activity for which suitable experimental data are not available. The model analyses of the available data on the kinetics of Prx from mammalian sources reveal that Prx operates at very low H2O2 concentrations compared to their human parasite counterparts. Furthermore, the model is able to predict the dynamic overoxidation of Prx at high H2O2 concentrations, consistent with the available data. The integrated Prx-TrxR model simulations well describe the NADPH and H2O2 degradation dynamics and also show that the coupling of TrxR- and Prx-dependent reduction of H2O2 allowed ultrasensitive changes in the Trx concentration in response to changes in the TrxR concentration at high Prx concentrations. Thus, the model of this sort is very useful for integration into computational H2O2 degradation models to identify its role in physiological and pathophysiological functions.
Keywords: Mathematical model, Enzyme kinetics, Redox biology, Hydrogen peroxide, Thioredoxin system, ROS scavenging
Introduction
Hydrogen peroxide (H2O2) is a crucial form of reactive oxygen species (ROS), which is involved in cell signaling, and also alters the intracellular redox environment when produced in excess amounts, leading to many pathophysiological conditions [1-3]. Various components of the cell are capable of producing H2O2, with major contribution emerging from mitochondria [4-8]. Two major thiol-dependent antioxidant systems, the thioredoxin (Trx) and glutathione (GSH) systems, that control the degradation of H2O2, are critical for accurate maintenance of the intracellular redox environment in many organisms. In addition to H2O2 metabolism, the Trx system plays an important role in different biological processes, such as ribonucleotides reduction, sulfate assimilation, transcription control, and signal transduction [9-11]. Thus, quantification of the Trx system in the H2O2 degradation is critical for analyzing the role of different H2O2 degradation pathways in the maintenance of redox environment in the cell.
The Trx system, which is composed of a NADPH-dependent thioredoxin reductase (TrxR) and Trx, provides electrons to thiol-dependent peroxidases (peroxiredoxin, Prx) to remove H2O2 (Fig. 1A). Mammalian cells possess two Trx systems, the cytosolic Trx1 and mitochondrial Trx2 systems. Trx2 has only two cysteines in its active site, whereas Trx1 has three additional cysteines, which play an important role in the regulation of enzyme activity and NO signaling [12]. TrxR is a homodimeric flavoprotein member of the pyridine nucleotide-disulfide oxidoreductases family [13, 14]. Three isoforms of TrxR have been identified in mammalian cells: cytosolic TrxR1, mitochondrial TrxR2, and testis-specific thioredoxin glutathione reductase (TGR) [15], which regenerate the reduced Trx (Trx(SH)2) from the oxidized Trx (TrxS2). On the other hand, Prx constitutes a family of peroxidases, which are ubiquitously distributed [16], and participates in the removal of H2O2 with the help of electrons from Trx. Mammalian Prx include six members (Prx1-6), which can be classified as typical 2-Cys Prx isoforms (Prx1-4), atypical 2-Cys Prx isoform (Prx5) and one 1-Cys Prx isoform (Prx6) [17].
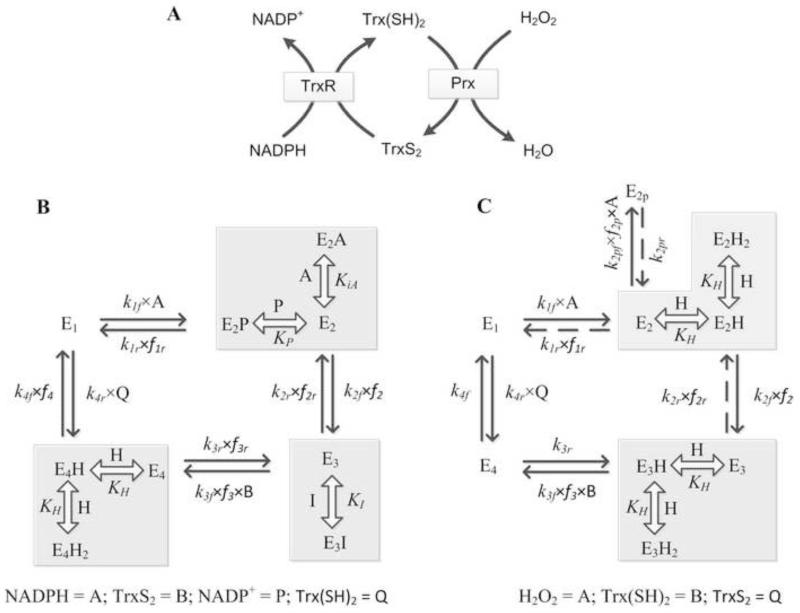
Figure 1. Proposed schematics for the catalytic mechanisms of the Trx system.
A) Coupled system of the TrxR and Prx enzymes; Prx reduces H2O2 to H2O using electrons from Trx(SH)2, and TrxR regenerates Trx(SH)2 from TrxS2 using electrons from NADPH. (B, C) Catalytic mechanisms for the TrxR and Prx enzymes, respectively (see texts for detailed description of the mechanisms). Here, kif and kir represent the forward and reverse rate constants for the respective interactions. E1, E2, E2p, E3 and E4 represent enzyme states and fi indicates the associated binding polynomial for each enzyme state transition. Broken arrows represents for pseudo-reversible steps. KI, KiA and KH represent dissociation constants for the drug auranofin, substrates and protons, respectively.
Several independent kinetic studies performed on TrxR and Prx from various sources/species suggest a ping-pong mechanism for their operations [18-24]. The initial-velocity experiments performed on TrxR from human placenta showed that the enzyme activity is inhibited at high NADPH concentrations [21]. Furthermore, in another study, the initial-velocity experiments performed on mammalian TrxR revealed that the selenium is required for the catalytic action, and the enzyme activity follows a bell-shaped curve with respect to pH with optimal activity near pH 7 [24]. Similarly, several kinetic experiments were performed on typical 2-Cys Prx isoforms derived from parasites to mammalian cells using TrxR as the redox-coupled reaction [18-20, 22, 23]. The initial-velocity experiments performed on Prx from human parasites such as Plasmodium falciparum [18], Vibrio vulnificus [19], Schistosoma mansoni [25], Crithidia fasciculate [26], and bacterium Helicobacter pylori [27] are consistent with a ping-pong mechanism with varied peroxide removal rates. The study by Bang et al. [19] also showed that both Prx1 and Prx2 were differentially optimized to eliminate H2O2, with Prx1 operating at high H2O2 concentrations while Prx2 activated by traces of H2O2 leading to its overoxidation at high H2O2 concentrations. A similar observation is made for S. mansoni Prx1 [25] which also operates at high H2O2 concentrations and prone to overoxidation. Although kinetic experiments were performed on Prx from mammalian sources [20, 22, 23], the same levels of details were not available to determine their mode of action with respect to H2O2 accurately. In all of the mammalian Prx studies, the initial-velocity experiments were performed with Trx as the only varying substrate at a fixed H2O2 concentration (~100 μM), thus leading to uncertainty in the determination of the catalytic mechanisms and kinetic parameters related to H2O2.
Although structural and kinetic information are available on the catalytic mechanisms of these enzymes (TrxR and Prx) [17-24, 28-32], the mathematical models developed so far to represent their kinetics are not well elucidated and are restricted to simple mass action kinetics [33, 34]. Furthermore, none of the developed models are able to describe the experimentally observed NADPH-mediated substrate inhibition of TrxR and pH-mediated bell-shaped behavior of the enzyme activity. In addition, the flux expressions used for TrxR and Prx in the integrated ROS handling models so far are not based on mechanistic details and are restricted to the absence of products, and hence are not suitable for predictions under in vivo conditions. In the current study, we addressed this problem and developed thermodynamically-consistent mathematical models for both enzymes using aforementioned structural and kinetic information. We estimated the rate constants associated with each step in the catalytic cycle, which accurately describe the available data and provide novel insights into the catalytic mechanisms, e.g. the effects of reaction products (NADP+ and Trx(SH)2) on the enzyme activity. By incorporating intermediate enzyme protonation states, we are also able to describe the pH-mediated bell-shaped enzyme (Prx and TrxR) activities. Using the developed models, we predict the behavior of the coupled TrxR and Prx enzyme system under different experimental conditions showing H2O2 degradation, Prx overoxidation, and Trx regeneration. Thus, the models of this sort, which are based on known mechanistic details and are able to describe several independent data sets, can be incorporated into the integrated ROS handling models to understand H2O2 detoxification under physiological and pathophysiological conditions.
Methods
Initial-velocity data on TrxR derived from human placenta [21] and also data on pH-mediated effects on the TrxR activity [24] were used to identify the catalytic mechanism and relevant kinetic parameters for TrxR. Similarly, initial-velocity data on Prx from various sources/species [18-20, 22, 23, 25-27] were used to identify the catalytic mechanism and associated kinetic parameters for Prx.
Proposed catalytic scheme for TrxR
The structure and substrate specificity of mammalian TrxR is different from the well-studied Escherichia coli TrxR [35] and is more similar to the glutathione reductase (GR) [36, 37]. However, in contrast to GR, TrxR contains a selenocysteine (SeCys) residue which is essential for its catalytic activity. TrxR catalyzes reduction of the redox-active disulfide in Trx to reduced Trx using NADPH as the cofactor, as shown by the biochemical reaction: NADPH + TrxS2 ⇔ NADP+ + Trx(SH)2. The first step of the catalytic cycle involves reduction of fully oxidized enzyme by NADPH and formation of a charge transfer intermediate which is also common to GR. The NADPH reduced enzyme is believed to be present in equilibrium with three other principle forms of the enzyme [38, 39]. In the second part of the reaction, the conserved Cys and SeCys residues acts as a second redox center and electrons are transferred from the redox-active disulfide via the redox center at the C-terminal to the substrate TrxS2 yielding a Trx-mixed selenenylsulfide. In the final step, the Trx-mixed selenenylsulfide dissociates to regenerate the selenenylsulfide (fully oxidized enzyme) and Trx(SH)2) [28, 29].
The catalytic cycle described above for TrxR involves at least 6 reversible reactions with 12 unknown rate constants for estimation [28, 29]. We reduce the model complexity by considering rapid equilibrium assumptions for some steps in the catalytic cycle as shown in Figure 1B. Specifically, the fully oxidized enzyme (E1) interacts with NADPH (A) to produce an intermediate enzyme product complex (E2P) which then undergoes charge transfer reactions to form intermediate enzyme forms that are assumed in rapid equilibrium and considered as a single state shown by the square box (E2t). The intermediate form of the enzyme (E2) is assumed then to undergo further charge transfer reactions yielding the enzyme state E3. The enzyme state E3 then interacts with the substrate TrxS2 to generate Trx-mixed selenenylsulfide (E4). In the final step, the enzyme state E4 dissociates to form the fully oxidized enzyme (E1) and Trx(SH)2. In addition, studies with organic gold compounds, such as auranofin (I), indicate a specific inhibition of selenoenzyme by this drug [40]. Thus, inhibitory action of these drugs on the enzyme was incorporated by assuming formation of dead-end products (E3I) at the enzyme state E3 as suggested in the experimental study [21]. Furthermore, we incorporated rapid protonation of Trx-bound enzyme to be in activated form in the catalytic scheme and di-protonated and un-protonated forms were considered to be inactive in the enzyme state E4 to explain the experimentally observed bell-shaped pH-dependent behavior of the TrxR activity [24]. These assumptions reduce the complexity of the TrxR catalytic scheme to only four reversible steps with eight unknown rate constants.
Kinetic flux expression for TrxR
The net reaction velocity for TrxR is derived based on steady-state assumption for the catalytic scheme shown in Figure 1B using our freely available KAPattern Matlab tool for generating rate equations [41]. Assuming A, B, P and Q are the concentrations of NADPH, TrxS2, NADP+, and Trx(SH)2, respectively, the net reaction velocity is given by:
| (1) |
where kif and kir (i = 1-4) represent the forward and reverse rate constants for the interactions shown in Figure 1B; E0 is the total initial concentration of the enzyme; f1r, f2r, f3r, f2, f3 and f4 indicate the corresponding fractional occupancies associated with each state:
| (2) |
where KP and KH represents NADP+ and H+ binding dissociation constants for the enzyme, respectively. KiA and KI represent the inhibition constant for the substrate NADPH and drug auranofin (I), respectively.
At equilibrium, the net reaction rate in Equation (1) is zero, and correspondingly, the ratio of the product of forward rate constants and the product of reverse rate constants is equal to the apparent equilibrium constant (K’eq), which is calculated based on the Gibb’s free energy formation of each species in the biochemical reaction (see Supplementary Material for details), resulting in the following thermodynamic constraint for the kinetic parameters:
| (3) |
Proposed catalytic scheme for Prx
The Prx enzymes are family of peroxidases that reduce H2O2 (or alkyl hydroperoxides) to water (or alcohol), using reducing equivalents provided by thiol-containing proteins [42], as shown by the biochemical reaction: H2O2 + Trx(SH)2 ⇔ 2H2O + TrxS2. All Prx contain a conserved cysteine residue which is the primary site of oxidation by H2O2. The subgroups of Prx differ in number of cysteine residues present with Prx1-5 containing two residues in its active site while Prx6 contains only one. The catalytic reaction schemes for all Prx are similar with slight differences for each member [43]. For all Prx, the first and chemically most interesting step of catalysis is peroxidation. In this, the peroxidatic cysteine (Cys-SPH) attacks the peroxide substrate (e.g. H2O2) and is oxidized to a cysteine sulfenic acid (Cys-SOH). Here, excess H2O2 can lead to further reactions with Cys-SOH yielding more acidic forms of sulfenic acid derivatives (Cys-SO2H and Cys-SO3H). However, at low H2O2, the second step of the peroxidase reaction involving resolution of cysteine sulfenic acid distinguishes these three Prx classes. In the typical 2-Cys Prx, the peroxidatic Cys-SPOH from one subunit is attacked by the resolving cysteine (Cys-SRH), located in the C-terminus of the other subunit which results in a condensation reaction leading to formation of a stable intersubunit disulfide bond. In the atypical 2-Cys Prx, both the peroxidatic and its corresponding resolving cysteine are contained with the same polypeptide resulting in the formation of an intramolecular disulfide bond. In the third and final step, the disulfide bond is cleaved by one of several cell-specific disulfide oxidoreductases such as Trx, Grx, AhpF and tryperedoxin, completing the catalytic cycle.
Figure 1C shows the corresponding mechanistic catalytic scheme proposed for Prx based on the details described above. Here, the reduced Prx enzyme (E1) is oxidized by H2O2 (A) to yield sulfenic acid form of the enzyme (E2). Prolonged exposure to high H2O2 at this stage can further oxidize sulfenic acid residues (−SOH) to sulfinic (−SO2H) and sulfonic acids (−SO3H) and lead to dead-end products with irreversible protein deactivation. However, for initial-velocity studies with low H2O2 (< 100 μM), the H2O2-mediated overoxidation of Prx can be ignored. Sulfenic acid (E2) can then undergo the condensation reaction to form intra/inter molecular disulfide bond leading to formation of enzyme state E3. In the next step, Trx(SH)2 (B) reacts with enzyme state E3 to cleave the disulfide bond and in the process forms an enzyme product complex E4 which then dissociates in the final step to form the reduced Prx enzyme and TrxS2 (Q). Furthermore, we incorporated rapid protonation of enzyme states E2 and E3 to be in activated form in the catalytic scheme, and di-protonated and un-protonated forms were considered to be inactive to explain the experimentally observed pH-dependent behavior of Prx activity [20]. To understand the dynamic overoxidation of Prx by high H2O2, we expanded the catalytic scheme to include the formation of a pseudo-irreversible dead-end complex E2p (−SO2H and −SO3H) from E2 (Fig. 1C) and developed a dynamic model of Prx, coupled with TrxR, as detailed in the Supplementary Materials.
Kinetic flux expression for Prx
A steady-state assumption is not valid with the formation of a pseudo-irreversible dead-end product (E2p) in the catalytic cycle (Fig. 1C). However, the initial-velocity equation for Prx can be derived for low H2O2 where Prx overoxidation by H2O2 can be negligibly small and ignored. Assuming A, B and Q are the concentrations of H2O2, Trx(SH)2, and TrxS2, respectively, for the scheme shown in Figure 1C, the net reaction velocity is given by:
| (4) |
where kif and kir (i = 1-4) represent the forward and reverse rate constants for the interactions shown in Figure 1C; E0 is the total initial concentration of the enzyme; f1r, f2r, f2, and f3 indicate the corresponding fractional occupancies associated with each state:
| (5) |
where KH represents the H+ binding dissociation constants for the intermediate enzyme states. The thermodynamic constraint relating the apparent equilibrium constant to the rate constants is given by:
| (6) |
Parameter estimation and sensitivity analysis
One parameter from the set of unknown parameters for both TrxR and Prx models was constrained using the thermodynamic constraint, and the remaining unknown parameters were estimated using the available experimental data from the literature. A combined least-square estimation technique was used to fit the model simulated outputs to the experimental data:
| (7) |
where Nexp is the number of experiments and Ndata is the number of data points in a particular experiment; are the experimental data and are the corresponding model simulations. The accuracy and robustness of the model fitting to the data are assessed based on the value of the mean square residual error E(φ) and sensitivities of J (φ) to perturbations in the optimal parameter estimates, respectively.
Since experimental data relating the effects of products on the reaction velocities are not available for both TrxR and Prx, the unknown parameters related to reverse reactions were fixed based on known literature information and the sensitivity analysis. The normalized local sensitivity coefficients with respect to the model parameters are computed as:
| (8) |
where φi is the ith parameter; Jj is the model simulation for jth data point; Mi is the number of non-zero sensitivity coefficients (Si,j) for the parameter φi; and Si is the normalized sensitivity coefficient with respect to the parameter φi. Here, a high sensitivity value for a given parameter indicates that a small change in the parameter value will result in a significant change in the model output, and hence deemed as a free parameter to be estimated. On the other hand, a small sensitivity value for a given parameter indicates that the model output is insensitive to the parameter, and hence that should be fixed and removed from the parameter estimation procedure. The values of the insensitive parameters are fixed suitably based on known knowledge on the kinetics and/or thermodynamics of the enzymatic reaction. For example, for water releasing condensation reactions steps in the Prx reaction scheme (E1 to E2 and E2 to E3 in Fig. 1C), the reverse rate constants are fixed at very small numbers. Similarly, for product TrxS2 formation reactions step E4 to E1 in the Prx reaction scheme, the forward rate constant (k4f) is fixed at a very high value, as established in the literature.
Results
In this section, we present detailed parameterization of both the TrxR and Prx models with validation of the proposed catalytic mechanisms using available experimental data from the literature [18-27]. We first independently estimated the unknown parameters of the TrxR model using initial-velocity data in the absence of products [21], and then presented the model description of the experimental data with varying substrates in Figure 2A. Since these experimental studies did not include product-inhibition data, we fixed parameters related to the product inhibition based on sensitivity analysis as described in Methods. The resulting estimated parameter values along with their local sensitivity coefficients are tabulated in Table 1. The parameterized model is then used to simulate the effects of products on the TrxR rates as well as the effects of externally added drug auranofin and pH on the enzyme activity in Figures 2(B-G). We further corroborated the parameterized TrxR model by using an independent experimental study on TrxR from H. pylori [27], for which the model fittings are shown in Figure 2I and the estimated parameter values are reported in Table 1. In addition, we used the developed model to simulate the in vitro and in vivo like behavior of TrxR in the absence and presence of reaction products for different pH in Figure 3.
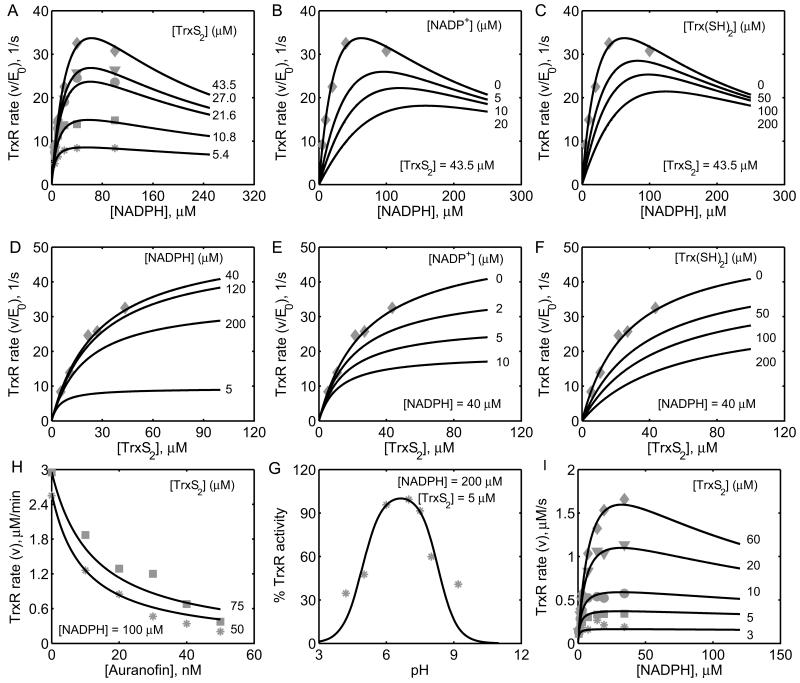
Figure 2. Characterization of the initial-velocity data on TrxR as a function of NADPH, TrxS2, auranofin and pH.
A) Model simulations are compared with the data from Gromer et al. [21] for variable [NADPH] at different fixed [TrxS2] of 5.4, 10.8, 21.6, 27 and 43.5 μM in the absence of the reaction products. B) Model predictions for the effect of the product NADP+ on the enzyme activity for variable [NADPH] at fixed TrxS2 of 43.5 μM and at different fixed [NADP+] of 0, 5, 10 and 20 μM. C) Model predictions for the effect of the product Trx(SH)2 on the enzyme activity for variable [NADPH] at fixed TrxS2 of 43.5 μM and at different fixed [Trx(SH)2] of 0, 50, 100 and 200 μM. D) Model predictions for the variable [TrxS2] at different fixed [NADPH] of 5, 40, 100 and 20 μM in the absence of products. E) Model predictions for the effect of the product NADP+ on the enzyme activity for variable [TrxS2] at fixed [NADPH] of 40 μM and at different fixed [NADP+] of 0, 2, 5 and 10 μM. F) Model predictions for the effect of the product Trx(SH)2 on the enzyme activity for variable [TrxS2] at fixed [NADPH] of 40 μM and at different fixed [Trx(SH)2] of 0, 50, 100 and 200 μM. In plots (B, F), experimental data in the absence of products from plot A are shown for clarity. H) Model simulations are compared with the data from Gromer et al. [21] on the effect of the externally added drug auranofin on the TrxR activity for two different [TrxS2] of 50 and 75 μM for 100 μM [NADPH]. G) Model simulations are compared with the data from Zhong et al. [24] on the effect of pH on the TrxR activity. I) Model simulations are compared to the experimental data on H. pylori TrxR enzyme [27] with varying [NADPH] at fixed [TrxS2] of 3, 5, 10, 20, and 60 μM, as independent validation of the TrxR kinetic model.
Table 1.
Estimated model parameter values for the TrxR kinetic model.
| Gromer et al. [21] | Baker et al. [27] |
||
|---|---|---|---|
|
| |||
| Parameter | Value | Sensitivity | Value |
| k1f (M−1 s−1) | 1.9×106 | 0.42 | 2.5×106 |
| k1r (s−1)a | 1.2×105 | 4.7×10−3 | 1.2×105 |
| k2f (s−1) | 7.9×104 | 0.085 | 2.6×104 |
| k2r (s−1)b | 0.22 | N/A | 0.22 |
| k3f (M−1 s−1) | 2.3×106 | 0.46 | 5.6×106 |
| k3r (s−1) | 1.0×103 | 0.09 | 1.0×103 |
| k4f (s−1) | 3.4×103 | 0.11 | 1.6×102 |
| k4r (M−1 s−1)a | 5.0×106 | 4.7×10−3 | 5.0×106 |
| KH (M) | 2.7×10−8 | N/A | 2.7×10−8 |
| KiA (M) | 1×10−7 | 0.09 | 1×10−7 |
| KP (M)a | 6.0×10−6 | 4.7×10−3 | 6.0×10−6 |
| KI (M) | 3.3×10−9 | N/A | 3.3×10−9 |
| 3.9c | N/A | 3.9c | |
Unidentifiable parameters due to the absence of product inhibition data.
Parameter was calculated based on thermodynamic constraint.
Calculated for the experimental conditions of pH 7.4, temperature 25 °C and ionic strength 0.22 M. N/A: Not applicable as they are fixed parameters.
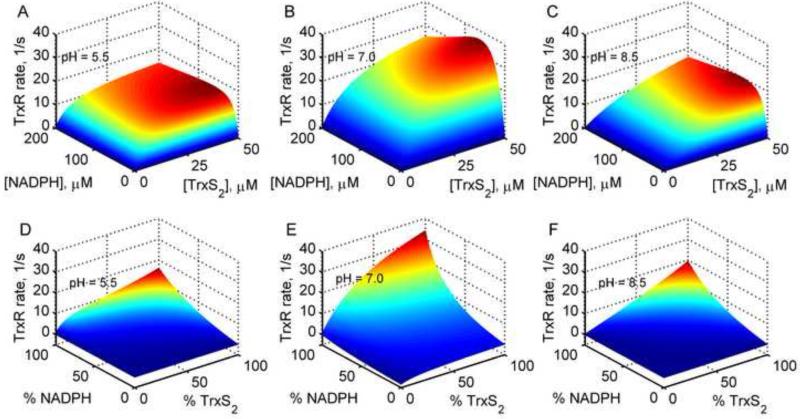
Figure 3. 3-dimentional model simulations for the effects of pH and products on the TrxR activity.
(A-C) Surface plots of the TrxR rate with varying substrates [NADPH] and [TrxS2] in the absence of products for three different pH values of 5.5, 7 and 8.5, respectively. (D-F) Surface plots of the TrxR rate for in vivo like conditions with varying substrate and products with a fixed total pool concentrations of NADP+ (100 μM) and Trx (50 μM) for three different pH values of 5.5, 7 and 8.5, respectively.
Similarly, we independently estimated the unknown parameters of the Prx model using initial-velocity data from various sources/species [18-20, 22, 23, 25-27]. Although the individual catalytic steps in the Prx reaction were known from structural studies and basic biochemistry of the reaction, there were very few detailed kinetic studies available in the literature for mammalian Prx to estimate the associated rate constants. We therefore first used experimental data on Prx from human pathogens such as P. falciparum [18], V. vulnificus [19], S. mansoni [25], C. fasciculata [26] and bacterium H. pylori [27], and estimated the relevant parameters of the model and presented the model description of the data in Figure 4. Subsequently, we used this information and estimated the unknown parameters for the mammalian Prx model and presented the results in Figure 5. The resultant estimated parameter values of the Prx model for the parasites and mammalian Prx are tabulated in Tables 2 and 3, respectively. Finally, we developed a dynamic model of Prx, incorporating high H2O2-mediated dynamic Prx overoxidation, and integrated both the TrxR and Prx models and presented the model simulation results in Figures 6, 7 and 8.
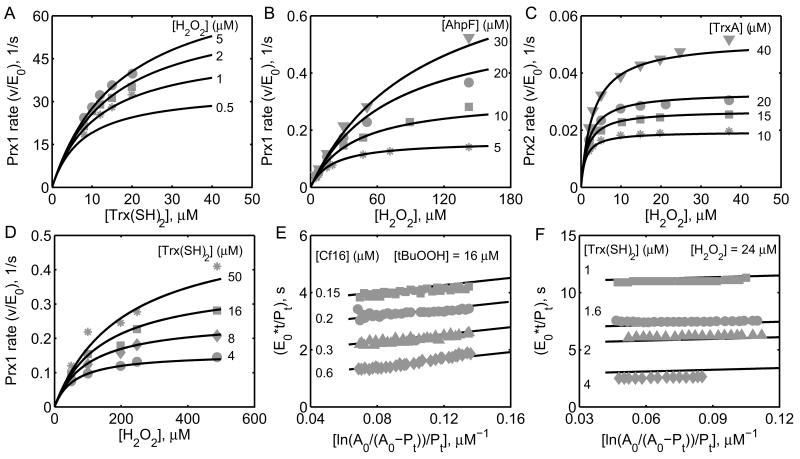
Figure 4. Characterization of the initial-velocity data on human pathogen and bacterial Prx enzymes.
A) Model simulations are compared with the data from Akerman et al. [18] on the Prx1 from human parasite P. falciparum with varying [Trx(SH)2] at four different [H2O2] of 0.5, 1, 2 and 5 μM. (B, C) Model simulations are compared with the data from Bang et al. [19] on the Prx1 from human pathogen V. vulnificus with varying [H2O2] at four different fixed [AhpF] of 5, 10, 20 and 30 μM and on the Prx2 at four different [TrxA] of 5, 10, 20 and 30 μM. D) Model simulations are compared with the data from Sayad et al. [25] on S. mansoni Prx with varying [H2O2] at four different [Trx(SH)2] of 4, 8, 16 and 50 μM. (E, F) Model simulations of the time-integrated data from Nogoceke et al. [26] and H. pylori [27] on C. fasciculata Prx (Cf21) oxidizing tBuOOH (Fig. 4E) and H2O2 (Fig. 4F) at different fixed [Cf16] of 0.15, 0.2, 0.3 and 0.6 μM and [Trx(SH)2] of 1, 1.6, 2 and 4 μM, respectively. Here, A0 is the initial concentration of the substrate (tBuOOH/H2O2). Pt represents product concentrations at time t, and E0 is the total enzyme concentration used in the study.
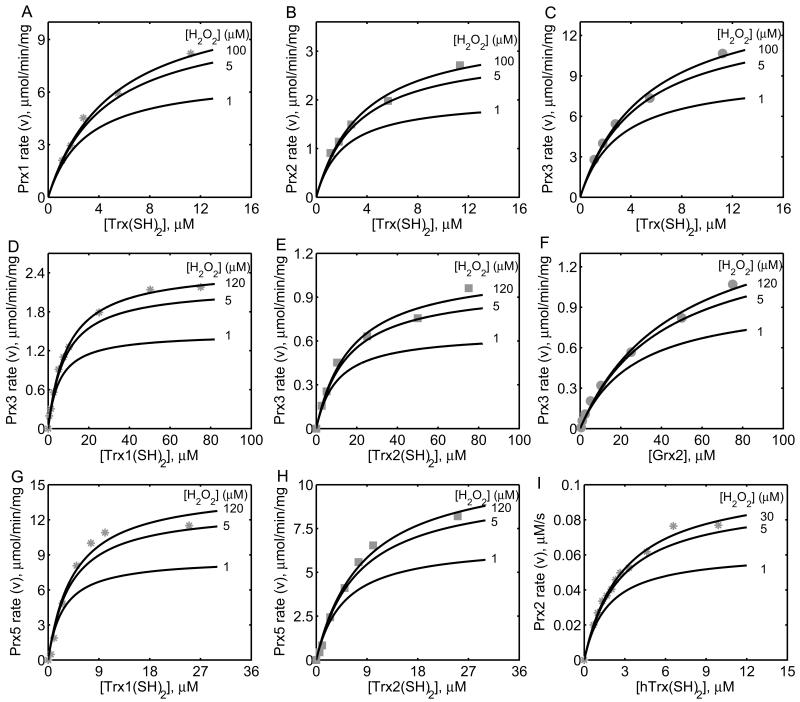
Figure 5. Characterization of the initial-velocity data on mammalian Prx enzyme.
(A, B, C) Model simulations are compared with the data from Chae et al. [20] with varying [Trx(SH)2] for 100 μM of [H2O2] on the mammalian Prx1, 2 and 3. (D, E, F) Model simulations are compared with the data from Hanschmann et al. [22] with varying [Trx(SH)2] for 120 μM of [H2O2] on Prx3 for three different substrates [Trx1(SH)2], [Trx2(SH)2], and [Grx2]. (G, H) Model simulations are compared with the data from Hanschmann et al. [22] with varying [Trx(SH)2] for 120 μM of [H2O2] on Prx5 for two different substrates [Trx1(SH)2] and [Trx2(SH)2]. I) Model simulations are compared with the data on Prx2 from Manta et al. [23] with varying human [Trx(SH)2] for 30 μM of [H2O2]. The figures also show the model predictions for 1 and 5 μM of [H2O2] for all the cases.
Table 2.
Estimated model parameter values for the human parasite and bacterial Prx kinetic model.
| Parameter | Akerman et al. [18] |
Bang et al. [19] | Sayad et al. [25] |
Nogoceke et al. [26] |
Baker et al. [27] |
|
|---|---|---|---|---|---|---|
| Prx1 | Prx1 | Prx2 | Prx1 | Cf21 | AhpC | |
|
k1f (M−1 s−1) |
1.1×108 | 8.3×103 | 1.7×104 | 2.5×103 | 1.6×105 | 2.0×105 |
| k1r (s−1)a | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 |
| k2f (s−1) | 2.6×102 | 17 | 0.34 | 2.0 | 60 | 30 |
| k2r (S−1)a | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 |
|
k3f (M−1 s−1) |
1.3×107 | 1.0×105 | 7×103 | 1.5×103 | 5.7×106 | 2.8×105 |
| k3r (s−1)b | 4.3×102 | 1.0×10−5 | 1.0×10−8 | 5.0×10−7 | 6.0×10−2 | 1.0×10−3 |
| k4f (s−1) | 1.0×106 | 1×106 | 1×106 | 1.0×106 | 1.0×106 | 1.0×106 |
|
k4r (M−1 s−1)a |
1×102 | 1×102 | 1×102 | 1×102 | 1×102 | 1×102 |
| KH (M) | 2.5×10−8 | 1×10−7 | 1×10−7 | 1×10−7 | 1×10−7 | 1×10−7 |
| (M−2)c | 8×1054 | 1×1055 | 1×1055 | 1×1055 | 8×1054 | 1×1055 |
Unidentifiable parameters for the respective data sets due to the absence of product-inhibition data and are suitably fixed based on sensitivity analysis, known knowledge on the reaction kinetics and thermodynamics.
Parameter was calculated based on thermodynamic constraint. The large variation in this parameter for different data sets is due to its correlation with other parameters.
Calculated based on the experimental conditions of the respective data set.
Table 3.
Estimated model parameters for the mammalian Prx kinetic model.
| Parameter | Chae et al. [20] | Hanschmann et al. [22] | Manta et al. [23] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Prx1 | Prx2 | Prx3 | Prx3 | Prx5 | Prx2 | ||||
| Trx1 | Trx2 | Grx2 | Trx1 | Trx2 | |||||
|
k1f (M−1 s−1) |
7.3×106 | 2×106 | 9.8×106 | 1.5×106 | 6.8×105 | 1×106 | 9.1×106 | 7×106 | 3×105 |
| k1r (s−1)a | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 |
| k2f (s−1) | 15.3 | 4.4 | 20 | 3.2 | 1.45 | 2.2 | 19.2 | 14.7 | 0.63 |
| k2r (s−1)a | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 | 1×10−18 |
|
k3f (M−1 s−1) |
3×106 | 1.2×106 | 3.8×106 | 3.4×105 | 8.3×104 | 4.6×104 | 4.2×106 | 1.7×106 | 2.1×105 |
| k3r (s−1)b | 2.5×10−1 | 7×10−3 | 5×10−1 | 1×10−3 | 6×10−5 | 7×10−5 | 5.6×10−1 | 1×10−1 | 3×10−5 |
| k4f (s−1) | 1×106 | 1×106 | 1×106 | 1×106 | 1×106 | 1×106 | 1×106 | 1×106 | 1×106 |
|
k4r (M−1 s−1)a |
1×102 | 1×102 | 1×102 | 1×102 | 1×102 | 1×102 | 1×102 | 1×102 | 1×102 |
| KH (M) | 1×10−7 | 1×10−7 | 1×10−7 | 1×10−7 | 1×10−7 | 1×10−7 | 1×10−7 | 1×10−7 | 1×10−7 |
| (M−1)c | 1×1055 | 1×1055 | 1×1055 | 1×1055 | 1×1055 | 1×1055 | 1×1055 | 1×1055 | 1×1055 |
Unidentifiable parameters for the respective data sets due to the absence of product-inhibition data and are suitably fixed based on sensitivity analysis known knowledge on the reaction kinetics and thermodynamics.
Parameter was calculated based on thermodynamic constraint. The large variation in this parameter for different data sets is due to its correlation with other parameters.
Calculated based on the experimental conditions of the respective data set.
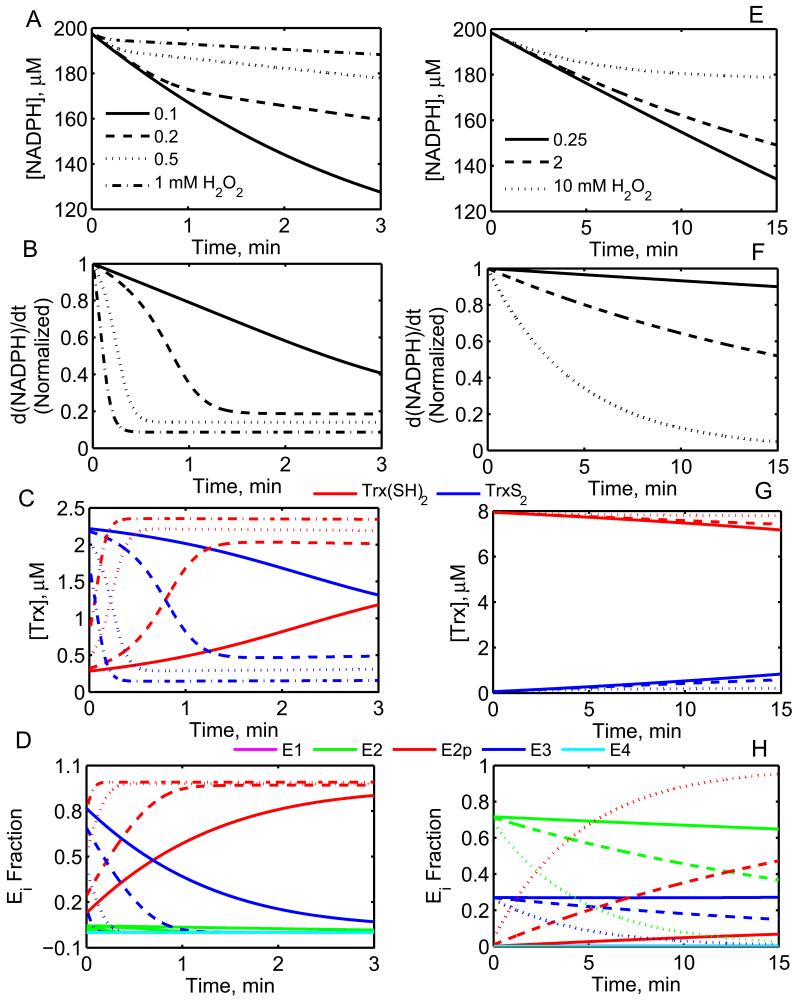
Figure 6. Dynamic model simulations of Prx overoxidation by H2O2 using a coupled system of TrxR and Prx enzymes.
Simulations for the experimental conditions of Yang et al. [46] (200 μM NADPH, 2.4 μM Prx1, 2.5 μM Trx(SH)2, and 150 nM TrxR at pH 7 and 30 °C) on Prx1 (A, B, C, D) and Manta et al. [23] (200 μM NADPH, 0.5 μM Prx1, 8 μM Trx(SH)2, and 1 μM TrxR at pH 7.4 and 25 °C) on Prx2 (E, F, G, H). (A, E) NADPH consumption with time for Prx1 and Prx2. (B, F) Normalized rate of NADPH oxidation, where the rate of NADPH oxidation was normalized with respect to the initial rate at t = 0. (C, G) Trx consumption and regeneration with time for Prx1 and Prx2. (D, H) Fractional enzyme states of Prx1 and Prx2. For the plots in the left side panel (A, B, C and D), solid, dashed, dotted and dash-dotted lines represent [H2O2] of 0.1, 0.2, 0.5 and 1 mM respectively. For the plots in right side panel (E, F, G and H), solid, dashed and dotted lines represent [H2O2] of 0.25, 2 and 10 mM, respectively. Above simulations were performed using the estimated parameter values of Prx1 and Prx2 from Table 3 for Chae et al. [20] and Manta et al. [23], respectively. However, the parameter for overoxidation (k2pf) used was 7.5×103 M−1.s−1 for Prx1 and 1.5 M−1.s−1 for Prx2.
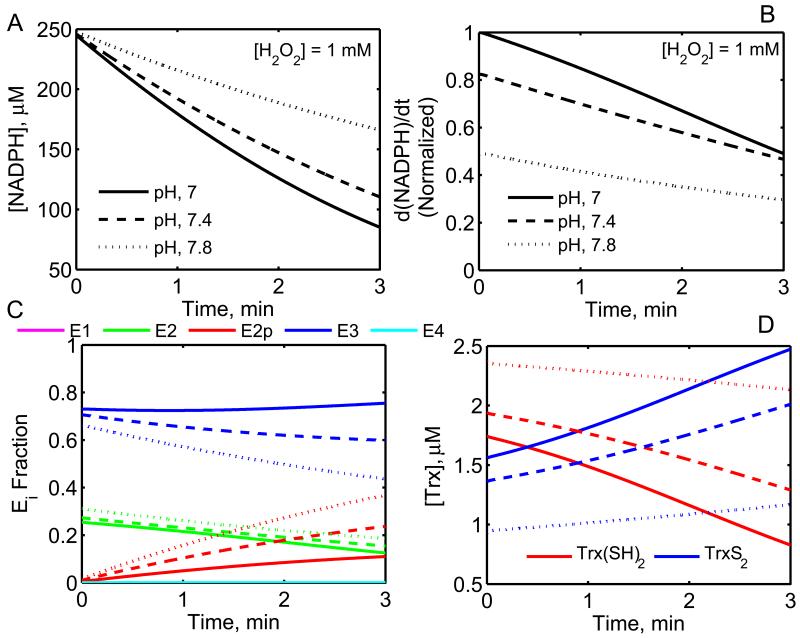
Figure 7. Dynamic model simulations of the effects of pH on the mammalian Prx1 rates using a coupled system of Prx and TrxR enzymes.
A) Model predictions for the [NADPH] consumption time. B) Normalized rate of NADPH oxidation with time, where the rates were normalized with respect to the initial-rate at pH 7 at t = 0. C) Fractional enzyme states of Prx1 with time. D) Dynamics of [Trx] in a coupled system of TrxR and Prx1. Simulations were performed using the experimental conditions of Chae et al. [20] (250 μM NADPH, 0.92 μM Prx1, 3.3 μM Trx(SH)2, 460 nM TrxR and 1 mM H2O2 at 37 °C), for three different pH values of 7 (solid lines), 7.4 (dashed lines) and 7.8 (dotted lines) using the estimated parameters of Prx1 from Table 3 for Chae et al. [20].
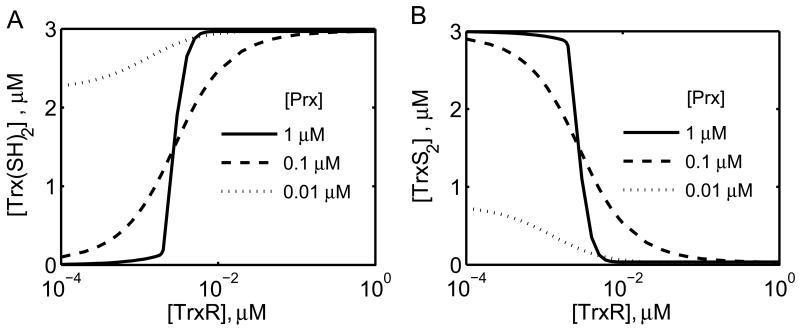
Figure 8. Model simulations of the effects of variations in [TrxR] and [Prx] on the steady-state profiles of [Trx] in a coupled system of TrxR and Prx enzymes.
Steady-state concentrations of [Trx(SH)2] (A) and [TrxS2] (B) with varying [TrxR] for three different [Prx] of 0.01 (dotted), 0.1 (dashed) and 1 (solid line) μM. Here, the model estimated parameters shown Table 3 from Manta et al. [23] were used for simulations at 200 μM NADPH, 3.0 μM Trx(SH)2, and 10 μM H2O2 at pH 7 and 25 °C.
Characterization of catalytic mechanism of TrxR
Gromer et al. [21] who optimized the purification of TrxR protein from human placenta and investigated its catalytic mechanism by performing kinetic studies showed that the enzyme operates by a ping-pong mechanism. The Lineweaver-Burk plots of the initial-velocities in their experiments showed parallel lines until 100 μM [NADPH], which started deviating upside along the y-axis for high [TrxS2], indicating substrate inhibition by NADPH at higher concentrations of both the substrates. Kinetic studies performed on bacterium H. pylori [27] also showed a similar ping-pong mechanism for TrxR. We used these experimental data to test the proposed catalytic mechanism and validate the developed kinetic model for TrxR, by identifying the unknown parameters of the TrxR model. Based on the estimated parameter values, we further used the model to simulate the experimental data on the effect of pH on the TrxR activity [24].
Figure 2A shows the model simulations of the experimental data with varying [NADPH] for five different [TrxS2] in the absence of products. The model was not only able to accurately describe the data, but also able to depict the NADPH-mediated substrate inhibition of the reaction for above 100 μM [NADPH] at high [TrxS2]. The estimated parameter values were then used to simulate the initial-velocity data with varying [TrxS2] for different fixed [NADPH] in the absence of products and the effects of products on the TrxR rates in Figures 2B-F for which experimental data are not available. The model simulations in the presence of the product NADP+ alone show that the TrxR reaction is very sensitive to [NADP+] with 50% inhibition taking place at 20 μM [NADP+] for a fixed [TrxS2] of 43.5 μM (Figs. 2B, E). The product Trx(SH)2 also inhibits the TrxR reaction; however, it is required in higher concentrations to reach the maximum effects (Figs. 2C, F). Furthermore, the model also accurately simulates the experimental data on the auranofin-mediated inhibition of the TrxR activity for two different [TrxS2] of 50 and 75 μM for 100 μM [NADPH] (Fig. 2H) as well as the bell-curve behavior of the TrxR activity with respect to varying pH (Fig. 2G). Here, for Figures 2H and 2G, experimental data was not used in the fitting process (except for KI and KH) and model simulations were exclusively based on the parameter values estimated from Figure 2A. Thus, the minor disagreement of model simulations and experimental data on the effect of pH could be due to this or due to the requirement of additional inactive protonation states of the enzyme in the catalytic cycle. The estimated parameter values of the mammalian TrxR are then used to simulate the initial-velocity data of H. Pylori TrxR with varying [NADPH] for five different [TrxS2] (Fig. 2I). The model is able to simulate the data with few adjustments in some parameter values as reported in Table 1 indicating minor differences in the operation of TrxR in two systems.
We used the estimated parameter values in Table 1 for Gromer et al. [21] to further evaluate the effects of pH and products on the TrxR activity under conditions of no products present and in the presence of products, as shown in Figure 3. The TrxR activity is optimum near pH 7 with both varying substrates, and decreases above and below the optimal pH, indicating a bell-curve behavior of the TrxR activity in the absence of products (Figs. 3A-C). The plots also clearly show the NADPH-mediated substrate inhibition at higher concentrations of both the substrates. However, under in vivo like conditions, where total pool concentration of NADP+ (100 μM) and Trx (50 μM) are maintained, though the bell-curve behavior was unchanged with respect to varying pH, the TrxR rate pattern significantly altered (Figs. 3D-F). The simulations show that the initial-velocity of the TrxR reaction was lowest under conditions of maximal product concentrations.
Characterization of catalytic mechanism of Prx isoforms from various species/sources
The kinetic experiments performed on the mammalian Prx isoforms are not detailed enough to estimate all the unknown parameters of the Prx model accurately [20, 22, 23]. Thus, we initially used Prx isoforms from human pathogens to identify the unknown parameters, and then used them as initial estimates for mammalian Prx isoforms. Figure 4A shows model simulations of the initial-velocity data from 2-Cys Prx from P. falciparum [18] with varying [Trx(SH)2] for three different [H2O2] and model predictions for 0.5 μM [H2O2] in the absence of products. The calculated values of the intrinsic Km (Cleland coefficients, see Supplementary Materials) from estimated rate constants for H2O2 and Trx were 0.78 and 19 μM, respectively. Similarly, we used the experimental data from V. vulnificus [19] for two different Prx isoforms, namely Prx1 (Fig. 4B) and Prx2 (Fig. 4C). Here, the calculated intrinsic Km values of H2O2 for V. vulnificus Prx1 (0.6 mM) and Prx2 (6 μM) indicate that the Prx1 can detoxify higher H2O2 concentrations compared to Prx2. A similar behavior was also observed with S. mansoni Prx1 [25] where the initial-velocity with H2O2 was not saturated (Fig. 4D) and the calculated intrinsic Km value of H2O2 is 0.26 mM.
The developed kinetic model for Prx was also used to simulate the time-integrated experimental data on C. fasciculata Prx (Cf21) and H. pylori Prx (AhpC) as shown in Figures 4E and 4F, respectively. Here, the flux expression for Prx was used to calculate the time profiles of H2O2 degradation and product accumulation, and the corresponding time-integrated plots were compared with the experimental data as described in Forstrom et al. [44]. The model simulations accurately show the observed non-saturation kinetics with respect to varying [H2O2] for both studies with calculated intrinsic Km values of 0.15 and 0.3 mM, respectively. As evident in Figure 4, the single mechanistic scheme proposed for Prx is able to describe the kinetics of several Prx enzymes, however with a different set of parameter values (Table 2). As described in the experimental studies, the model simulations also show that these Prx isoforms operate with different efficiency despite using similar catalytic schemes. This could be due to slight structural differences in the Prx isoforms, which make them to act differently in detoxifying H2O2. In contrast, the developed kinetic model of Prx was not able to describe the S. mansoni Prx3 kinetics [25] (results not shown) as it is evident from the observed non-parallel initial-velocity data in their study indicating the deviation from a ping-pong mechanism.
In contrast to studies on Prx from human parasites [18, 19, 25-27], the mammalian Prx kinetic studies were limited to only single initial-velocity data set with varying [Trx(SH)2] at a fixed [H2O2] of ~100 μM [20, 22, 23]. The experimental data were insufficient to reliably estimate the unknown H2O2-related parameters. Therefore, we initially used parameter estimates from human parasites Prx studies and literature information regarding the Km values of H2O2 and Trx(SH)2 to identify their second order binding rate constants (k1f and k3f) using the correlations between Cleland coefficients and rate constants (see Supplementary Materials) which are tabulated in Table 3. Chae et al. [20] performed initial-velocity studies on the mammalian Prx from various species and classified them into three distinct types, Prx1, 2 and 3, based on their deduced amino acid sequences and immunological reactivity. They showed that all three enzymes display similar kinetic properties. We identified the unknown Prx model parameters from these data as described above. Figures 5A-C show the model descriptions of the initial-velocity data in the absence of products with varying [Trx(SH)2] for 100μM [H2O2] for Prx1, 2 and 3, respectively. Initial-velocity of Prx was increased with [Trx(SH)2] and saturated above 50 μM and the activities were Prx3 > Prx1 > Prx2. The figure also shows the model predictions for two different [H2O2] (1 and 5 μM) indicating that the mammalian Prx saturates for very small concentrations of H2O2 with maximum being around 10 μM based on the apparent Km of H2O2 around 1 μM, consistent with the human pathogen study [18] and Chae et al. [20] study.
Similar kinetic studies performed on mammalian mitochondrial Prx3 by Hanschmann et al. [22] showed that typical 2-Cys Prx3 was reduced not only by both cytosolic and mitochondrial Trx(SH)2, but also can be a substrate for mitochondrial glutaredoxin (Grx2). Figures 5D-F shows the model descriptions of their initial-velocity data for Prx3 with varying cytosolic [Trx1(SH)2], mitochondrial [Trx2(SH)2], and mitochondrial [Grx2], respectively, for a fixed 120 μM [H2O2] in the absence of products. Consistent with other Prx, Prx3 displays similar kinetics with respect to H2O2 and shows saturation behavior at lower concentrations, irrespective of the reducing substrate. Mammalian Prx5 also displays similar characteristics with respect to Trx1(SH)2 and Trx2(SH)2 at a fixed 120 μM [H2O2], as shown in Figures 5(G, H). Prx5 was not reduced by mitochondrial Grx2 as opposed to Prx3. In another study, Manta et al. [23] performed initial-velocity experiments with human erythrocyte Prx2 which revealed that the enzyme displays a fast kinetics with an apparent Km of ~2.4 and ~0.7 μM for human Trx(SH)2 and H2O2, respectively. Figure 5I shows the model descriptions of the experimental data with varying human [Trx(SH)2] at a fixed 30 μM [H2O2]. In all cases, the model predictions for 1 and 5 μM [H2O2] show that Prx saturates at [H2O2] below 10 μM.
Integrated TrxR and Prx enzymes in the removal of H2O2, Prx overoxidation, and the effect of pH on the Prx activity
The kinetic experiments performed on Prx to determine the catalytic mechanism were based on a coupled TrxR and Prx enzyme system [18-20, 22, 23]. In these studies, oxidation of NADPH was used to determine the initial-velocity of Prx assuming a high [TrxR] to maintain [Trx(SH)2] constant so that the Prx reaction is rate limiting. In several such studies, Prx was shown over-oxidizing at high [H2O2] leading to reduction in the rate of NADPH oxidation [19, 20, 23, 25, 45]. In order to simulate such phenomenon, we developed a dynamic model for Prx coupled with TrxR with formation of a pseudo-irreversible dead-end complex E2p from the enzyme state E2 of Prx. We used the estimated parameter values for TrxR and Prx from Table 1 and 3 and allowed the second order rate constant (k2pf) for H2O2 binding to E2 that produce E2p to vary for different studies to understand the overoxidation of Prx at high [H2O2].
Figure 6 shows the dynamic profiles of NADPH oxidation, Trx interconversion, and Prx fractional enzyme states for various high [H2O2] for the experimental conditions of Yang et al. [46] on Prx1 and Manta et al. [23] on Prx2. The model simulations clearly show the reduction in NADPH consumption (Fig. 6A) and decrease in the rate of NADPH oxidation (Fig. 6B) with increased [H2O2] from 0.1 to 1 mM due to the Prx overoxidation. The corresponding Trx dynamics (Fig. 6C) and Prx fractional enzyme state levels (Fig. 6D) suggest that as [H2O2] is increased from 0.1 mM (solid lines) to 1 mM (dash-dotted lines), the entire Prx enzyme resides in the dead-end complex form E2p leading to very small active enzyme turnover to produce the product TrxS2 (blue lines in Fig. 6C) which is the substrate for TrxR. The model simulations are in good agreement with the reported experimental data for Prx1 in Yang et al. [46] for a second order rate constant of 7.5×103 (M.s)−1 for H2O2 binding to E2 (k2pf in Fig. 1C). A similar Prx overoxidation phenomenon was also observed for Prx2 from Manta et al. [23] (Figs. 6E, F, G and H) for high [H2O2] from 0.25 to 10 mM. However, the magnitude of overoxidation was smaller even for high [H2O2] and required very small overoxidation parameter k2pf (1.5 M−1.s−1). The corresponding Prx fractional enzyme states (Fig. 6H) suggest that the dead-end complex formation due to high H2O2 is minimal and requires longer time scales to reach the maximum inactivation owing to the estimated parameter values used for simulation for Prx2 from Manta et al. [23] from Table 3.
The developed integrated Prx and TrxR enzyme model also further used to identify the effect of pH on the Prx activity. Chae et al. [20] performed experiments on the coupled TrxR and Prx enzymes where they measured the absorbance of NADPH at 340 nm for two different pH values (7 and 7.8), indicating reduction in the Prx activity at pH 7.8 for a fixed [H2O2] of 1 mM. We used the developed models and the estimated parameter values from Tables 1 and 3 for TrxR and Prx1 and coupled the two enzymes to predict the pH-effect on the Prx activity. Figure 7 shows model predicted dynamics of NADPH and Trx consumption for the given substrates [Trx(SH)2] and [H2O2] of 3.3 μM and 1 mM, respectively. The proposed pH mechanism for Prx clearly shows that with increased pH, NADPH consumption (Fig. 7A) and the rate of NADPH oxidation (Fig. 7B) decreased independent of Prx overoxidation. The corresponding Prx fractional enzyme states (Fig. 7C) and Trx dynamics (Fig. 7D) suggest that though Prx overoxidation contributes to the decreased rate of NADPH oxidation, but it was majorly due to pH inhibition in the catalytic cycle. In addition, the Prx overoxidation rate (k2pf) was similar in magnitude to that estimated for the experimental data of Manta et al [23].
Using the developed integrated Prx and TrxR enzyme model and the estimated parameter values for the TrxR and Prx enzymes (Tables 1 and 3), we characterized the emergent properties of the coupled enzyme system, specifically the ultrasensitive behavior of [Trx(SH)2] and [TrxS2] to varying [TrxR] for different [Prx] (Figs. 8A and 8B). As shown in the figure, for [H2O2] of 10 μM and a high Prx concentration (1 μM), Trx shows ultrasensitive behavior with respect to varying TrxR concentration (solid lines), with Trx completely reduced above 0.01 μM [TrxR] and completely oxidized below 0.001 μM [TrxR]. However, the ultrasensitive behavior disappeared as the concentration of Prx decreased 10 and 100-fold, as shown by the dashed and dotted lines in Figure 8.
Discussion
ROS such as H2O2 play an important role in physiological cell signaling processes and in the development of pathophysiological states, including neurodegenerative disorders [47] and cardiovascular diseases [48, 49]. Cells possess a network of enzymatic and non-enzymatic antioxidant systems for detoxification of H2O2 to prevent harmful accumulation of hydroxyl radical (OH·) and maintain physiologically-relevant levels of H2O2. The major pathways responsible for H2O2 detoxification in various cell types include the GSH and Trx systems. Mechanistic mathematical models have been recently developed for the GSH system that provides novel quantitative insights into the catalytic mechanisms of GR and GPx enzymes [50, 51] in the removal of H2O2. However, the same level of mechanistic characterization of the Trx system is not available despite several experimental studies performed on the system (Prx and TrxR enzymes). Furthermore, several integrated models of ROS scavenging [45, 52, 53] so far have used phenomenological bi-substrate mechanisms in the absence of products for the Trx system that cannot describe the available kinetic data. Thus, in the current study, we used the available kinetic data on the TrxR [21, 24] and Prx [18-20, 22, 23, 25-27] enzymes, and developed thermodynamically-feasible mechanistic mathematical models of the TrxR and Prx enzymes. The developed models not only well describes the available kinetic data, but also provides crucial quantitative insights into their catalytic actions, including the overoxidation of Prx by high H2O2, effects of reaction products and pH on the enzyme activity, and ultrasensitive response of Trx to the variations in TrxR and Prx concentrations arising from the coupled TrxR-Prx enzyme system.
The developed model for TrxR is able to simulate the NADPH-mediated substrate-inhibition data and the experimentally-observed inhibition pattern with respect to auranofin, indicating the efficiency of the model in depicting the inhibitory effects of substrates and externally added drugs on the enzyme activity [21]. Although experimental data are not available on the effects of products on the TrxR activity with Trx as the substrate, interestingly the developed model, which considers the thermodynamics of the reaction, is able to predict product inhibition of the reaction. Although the rate constants related to the products in our model were not accurately identifiable, the structural and thermodynamics of the TrxR reaction indicate that there is a significant effect of products on the reaction kinetics, similar to the kinetics of GR enzyme [50]. Also experiments performed with the rat TrxR1 enzyme with other model substrates, such as DTNB (5,5′-dithiobis-2-nitrobenzoic acid), suggested that the product NADP+ showed mixed type inhibition with respect to NADPH and DTNB [54], validating our model predictions. However, further kinetic experiments on TrxR or its variants in the presence of varying concentrations of the products NADP+ and Trx(SH)2 are necessary to accurately identify the kinetic parameters related to product inhibition (reverse rate constants). Furthermore, the model predictions performed with different pH values in the absence and presence of products revealed that the kinetic pattern in the absence of products is significantly different from that in the presence of products with in vivo like conditions in which the total NADP+ and Trx pools are fixed (Fig. 3). Thus, the developed model shows the importance of product inhibition studies to determine the catalytic mechanism of TrxR enzyme and need for more experimental data with respect to Trx to accurately estimate the product-related kinetic parameters in the model.
The Prx model analyses of the available kinetic data from human pathogen Prx from P. falciparum [18] and V. vulnificus [19] indicate that both Prx act differently, with fPrx1 and vPrx2 saturating at lower [H2O2] while vPrx1 capable of eliminating higher [H2O2] (Figs. 4A-C). A similar non-saturation behavior with respect to H2O2 was also observed with Prx enzymes in other parasite and bacterial model systems [25-27]. On the other hand, the Prx model analysis of the kinetic information on mammalian Prx suggests that they operate at very low H2O2 concentrations with saturation kinetics below 10 μM. In addition, kinetic mechanisms of mammalian Prx isoforms show a similar kinetic pattern irrespective of the reducing substrate used, however with different maximum velocities (Fig. 5).
The estimated model parameters shown in Table 2 for parasite Prx isoforms indicate that the second order rate constant for H2O2 reduction (k1f) is of the order of 3×103 – 1×108 M−1.s−1 and the second order rate constant (k3f) for reduction of the oxidized enzyme by Trx(SH)2 is of the order of 1×104 – 1×106 M−1.s−1, which is consistent with the experimentally-determined values [18, 19, 25-27, 55, 56]. On the other hand, the second order rate constants for the mammalian Prx isoforms are in the range of 3×105 – 7×106 M−1.s−1 for H2O2 (k1f) and 4×104 – 4×106 M−1.s−1 for Trx(SH)2 (k3f in Table 3). However, the experimentally determined value for Prx2 oxidation by H2O2 (k1f) based on the competition kinetics with horseradish peroxidase were in the range of 10 to 100-fold higher to the estimated values in our model [23, 57]. Although the model can describe the initial-velocity data on Prx2 in Manta et al. [23] using the reported value in the study (1×108 M−1.s−1), however the calculated intrinsic Km value of H2O2 using correlations between rate constants and intrinsic Km values (see Supplementary Materials) is very small (< 1 nM) and is in conflict with the Km value reported in their study (~0.78 μM). In addition, pre-steady state kinetic studies performed on Prx5 using both competitive kinetics and fluorescence techniques to measure the rate constants for Prx5 oxidation by H2O2 determined the value to be 3×105 M−1.s−1 [58] and it is generally assumed in that range for Prx in other studies [42, 55, 56].
The estimated first order rate constant (k2f) for the transformation of sulfenic acid form of the enzyme (E2) to disulfide form of the enzyme (E3) is consistently smaller for all the Prx isoforms studied from different species. Specifically, the k2f value is consistently smaller for mammalian Prx2 from different studies compared to Prx3 and Prx5 (Table 3). The estimated values are in agreement with the experimentally determined values reported in the literature [58-60]. For example, the pre-steady state kinetic experiments performed on Prx5 in Trujillo et al. [58] yielded the rate constant for formation of intramolecular disulfide bond (k2f) as 14.7 s−1, which is close to the estimated value for Prx5 in our study (Table 3). Thus, these observations clearly show that formation of disulfide bond in the catalytic cycle could be one of the rate limiting steps in the catalytic cycle.
A common phenomenon observed in several experimental studies related to the Prx enzyme is its dynamic overoxidation at high H2O2 concentrations leading to the enzyme inactivation. Although, experimental studies were able to see the enzyme inactivation at high [H2O2] [19, 23, 25, 46], however they were not consistent in depicting the magnitude of inactivation correctly for the mammalian Prx enzymes [23, 46]. Using a dynamic model for the integrated Prx and TrxR enzymes, we are able to simulate the Prx overoxidation phenomenon and the model results suggests that the Prx overoxidation is a time dependent process with continuous increase in the dead-end complex (E2p in Fig. 1C) formation depending on [H2O2] (Fig. 6) and the magnitude of the second order rate constant k2pf. The two experimental scenarios simulated in our study for Prx1 [46] and Prx2 [23] suggested that the mammalian Prx1 requires much higher rate of overoxidation rate constant compared to Prx2 (Table 3). However, competitive kinetic studies performed with respect to catalase to determine the Prx2 and Prx3 overoxidation rate constants [59] suggested that their rates (1.2×104 M−1.s−1) are comparable to the Prx1 rate used in our study (7.5×103 M− 1.s−1). In addition to the second order rate constant k2pf, the rate of Prx overoxidation also depends on the rate constant for the disulfide formation, k2f. For example, in an independent experiment performed on Prx2 revealed that the nitration of Prx2 increases its catalytic activity and its resistance to overoxidation owing to the increased value of the rate constant for disulfide formation in the catalytic cycle [60]. Thus, this result and our model simulations suggest that for a fixed k2pf, the rate of overoxidation also depends on the rate of disulfide formation in the catalytic cycle and estimated parameter value of k2f for Prx2 is lower than the other Prx enzymes indicating a greater chance of overoxidation for Prx2 compared to other Prx enzymes.
The proposed catalytic schemes of the TrxR and Prx enzymes with the incorporated pH effect are able to predict the observed bell-shaped behavior of the enzyme activity with respect to variable pH (Fig. 3 and Fig. 7). The effect of pH on the TrxR activity was established by incorporating proton binding steps in the TrxR catalytic scheme by a trial and error method. Iteratively each enzyme state in the catalytic cycle was assumed to be in the single protonated activated form, while the di-protonated and un-protonated form of the enzyme was considered inactive. None of the assumptions except the single protonated activated form of the enzyme state E4 for TrxR enzyme was able to predict the experimentally observed kinetic behavior with respect to pH [24]. Similarly, for Prx we assumed the single protonated activated forms of the enzyme at each step where water is released as the reaction product, namely at intermediate enzyme state E2 and E3. A similar approach was considered in our previous study [51] to identify the pH-mediated kinetic behavior of the mechanistically identical GPx enzyme. The model analyses of the peroxidase enzymes show that the activities of these enzymes are considerably reduced to detoxify H2O2 in the event of acidic pH, leading to higher [H2O2] which is the hallmark of oxidative stress.
The developed mechanistic models of the TrxR and Prx enzymes provide us the unique opportunity to investigate the emergent behavior of the coupled enzyme system in H2O2 detoxification. Using the coupled TrxR-Prx enzyme system, we are able to show the in vitro experimental scenarios in the maintenance of a constant Trx(SH)2 with the availability of NADPH for TrxR (Figs. 6G and 8). Furthermore, in the coupled enzyme system of mammalian TrxR and Prx, the model simulations with the estimated parameter values of the TrxR and Prx enzymes show that the steady-state [Trx] has ultrasensitivity with respect to varying [TrxR] at high [Prx]. These results indicate that under conditions of lower TrxR concentrations in vivo due to its inactivation with inhibitors, the TrxR enzyme may not be sufficient enough to maintain the fully reduced Trx concentrations resulting in lower H2O2 detoxifications by the Trx system.
In conclusion, we have developed thermodynamically-consistent mathematical models for the catalytic mechanisms of TrxR and different Prx isoforms based on known structural information of the enzymes. The models analyses of the available kinetic data provides the precise values of the reaction rate constants in the catalytic cycle and the relations between the rate constants and the Cleland coefficients. The models are able to simulate accurately the inhibitory effects of reaction substrates, Prx overoxidation, and externally added drug effects on the enzyme activity. Furthermore, the models provide a unique opportunity to understand the effects of reaction products and pH on the enzyme activity. Thus, the developed models are suitable for integrating into computational H2O2 detoxification models to understand redox balance under normal and oxidative stress conditions.
Supplementary Material
Acknowledgements
We thank the reviewers for their valuable comments and suggestions, which helped in improving the manuscript. This work was supported by the National Institute of Health grants R01-HL095122.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Kamata H, Hirata H. Redox regulation of cellular signalling. Cellular Signalling. 1999;11:1–14. doi: 10.1016/s0898-6568(98)00037-0. [DOI] [PubMed] [Google Scholar]
- [2].Rhee SG, Yang KS, Kang SW, Woo HA, Chang TS. Controlled elimination of intracellular H2O2: Regulation of peroxiredoxin, catalase, and glutathione peroxidase via post-translational modification. Antioxidants and Redox Signaling. 2005;7:619–626. doi: 10.1089/ars.2005.7.619. [DOI] [PubMed] [Google Scholar]
- [3].Veal EA, Day AM, Morgan BA. Hydrogen peroxide sensing and signaling. Molecular Cell. 2007;26:1–14. doi: 10.1016/j.molcel.2007.03.016. [DOI] [PubMed] [Google Scholar]
- [4].Andreyev AY, Kushnareva YE, Starkov AA. Mitochondrial metabolism of reactive oxygen species. Biochemistry (Moscow) 2005;70:200–214. doi: 10.1007/s10541-005-0102-7. [DOI] [PubMed] [Google Scholar]
- [5].Brand MD, Affourtit C, Esteves TC, Green K, Lambert AJ, Miwa S, Pakay JL, Parker N. Mitochondrial superoxide: Production, biological effects, and activation of uncoupling proteins. Free Radical Biology and Medicine. 2004;37:755–767. doi: 10.1016/j.freeradbiomed.2004.05.034. [DOI] [PubMed] [Google Scholar]
- [6].Loschen G, Flohé L, Chance B. Respiratory chain linked H2O2 production in pigeon heart mitochondria. FEBS Letters. 1971;18:261–264. doi: 10.1016/0014-5793(71)80459-3. [DOI] [PubMed] [Google Scholar]
- [7].Murphy MP. How mitochondria produce reactive oxygen species. Biochem J. 2009;417:1–13. doi: 10.1042/BJ20081386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Turrens JF. Mitochondrial formation of reactive oxygen species. J Physiol. 2003;552:335–344. doi: 10.1113/jphysiol.2003.049478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Arnér ESJ, Holmgren A. Physiological functions of thioredoxin and thioredoxin reductase. European Journal of Biochemistry. 2000;267:6102–6109. doi: 10.1046/j.1432-1327.2000.01701.x. [DOI] [PubMed] [Google Scholar]
- [10].Lu J, Holmgren A. The thioredoxin antioxidant system. Free Radical Biology and Medicine. 2014;66:75–87. doi: 10.1016/j.freeradbiomed.2013.07.036. [DOI] [PubMed] [Google Scholar]
- [11].Nordberg J, Arnér ESJ. Reactive oxygen species, antioxidants, and the mammalian thioredoxin system. Free Radical Biology and Medicine. 2001;31:1287–1312. doi: 10.1016/s0891-5849(01)00724-9. [DOI] [PubMed] [Google Scholar]
- [12].Holmgren A. Antioxidant function of thioredoxin and glutaredoxin systems. Antioxidants and Redox Signaling. 2000;2:811–820. doi: 10.1089/ars.2000.2.4-811. [DOI] [PubMed] [Google Scholar]
- [13].Williams CH, Jr, David Arscott L, Müller S, Lennon BW, Ludwig ML, Wang PF, Veine DM, Becker K, Heiner Schirmer R. Thioredoxin reductase: Two modes of catalysis have evolved. European Journal of Biochemistry. 2000;267:6110–6117. doi: 10.1046/j.1432-1327.2000.01702.x. [DOI] [PubMed] [Google Scholar]
- [14].Koháryová M, Kollárová M. Oxidative stress and thioredoxin system. General Physiology and Biophysics. 2008;27:71–84. [PubMed] [Google Scholar]
- [15].Lu J, Holmgren A. Selenoproteins. Journal of Biological Chemistry. 2009;284:723–727. doi: 10.1074/jbc.R800045200. [DOI] [PubMed] [Google Scholar]
- [16].Sue GR, Ho ZC, Kim K. Peroxiredoxins: A historical overview and speculative preview of novel mechanisms and emerging concepts in cell signaling. Free Radical Biology and Medicine. 2005;38:1543–1552. doi: 10.1016/j.freeradbiomed.2005.02.026. [DOI] [PubMed] [Google Scholar]
- [17].Rhee SG, Woo HA, Kil IS, Bae SH. Peroxiredoxin functions as a peroxidase and a regulator and sensor of local peroxides. Journal of Biological Chemistry. 2012;287:4403–4410. doi: 10.1074/jbc.R111.283432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Akerman SE, Müller S. 2-Cys peroxiredoxin PfTrx-Px1 is involved in the antioxidant defence of Plasmodium falciparum. Molecular and Biochemical Parasitology. 2003;130:75–81. doi: 10.1016/s0166-6851(03)00161-0. [DOI] [PubMed] [Google Scholar]
- [19].Bang YJ, Oh MH, Choi SH. Distinct characteristics of two 2-cys peroxiredoxins of Vibrio vulnificus suggesting differential roles in detoxifying oxidative stress. Journal of Biological Chemistry. 2012;287:42516–42524. doi: 10.1074/jbc.M112.421214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Chae HZ, Kim HJ, Kang SW, Rhee SG. Characterization of three isoforms of mammalian peroxiredoxin that reduce peroxides in the presence of thioredoxin. Diabetes Research and Clinical Practice. 1999;45:101–112. doi: 10.1016/s0168-8227(99)00037-6. [DOI] [PubMed] [Google Scholar]
- [21].Gromer S, Arscott LD, Williams CH, Jr, Schirmeri RH, Becker K. Human placenta thioredoxin reductase. Isolation of the selenoenzyme, steady state kinetics, and inhibition by therapeutic gold compounds. Journal of Biological Chemistry. 1998;273:20096–20101. doi: 10.1074/jbc.273.32.20096. [DOI] [PubMed] [Google Scholar]
- [22].Hanschmann EM, Lönn ME, Schütte LD, Funke M, Godoy JR, Eitner S, Hudemann C, Lillig CH. Both thioredoxin 2 and glutaredoxin 2 contribute to the reduction of the mitochondrial 2-Cys peroxiredoxin Prx3. Journal of Biological Chemistry. 2010;285:40699–40705. doi: 10.1074/jbc.M110.185827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Manta B, Hugo M, Ortiz C, Ferrer-Sueta G, Trujillo M, Denicola A. The peroxidase and peroxynitrite reductase activity of human erythrocyte peroxiredoxin 2. Archives of Biochemistry and Biophysics. 2009;484:146–154. doi: 10.1016/j.abb.2008.11.017. [DOI] [PubMed] [Google Scholar]
- [24].Zhong L, Holmgren A. Essential role of selenium in the catalytic activities of mammalian thioredoxin reductase revealed by characterization of recombinant enzymes with selenocysteine mutations. Journal of Biological Chemistry. 2000;275:18121–18128. doi: 10.1074/jbc.M000690200. [DOI] [PubMed] [Google Scholar]
- [25].Sayed AA, Williams DL. Biochemical characterization of 2-cys peroxiredoxins from Schistosoma mansoni. Journal of Biological Chemistry. 2004;279:26159–26166. doi: 10.1074/jbc.M401748200. [DOI] [PubMed] [Google Scholar]
- [26].Nogoceke E, Gommel DU, Kieß M, Kalisz HM, Flohé L. A unique cascade of oxidoreductases catalyses trypanothione-mediated peroxide metabolism in Crithidia fasciculata. Biological Chemistry. 1997;378:827–836. doi: 10.1515/bchm.1997.378.8.827. [DOI] [PubMed] [Google Scholar]
- [27].Baker LMS, Raudonikiene A, Hoffman PS, Poole LB. Essential thioredoxin-dependent peroxiredoxin system from Helicobacter pylori: Genetic and kinetic characterization. Journal of Bacteriology. 2001;183:1961–1973. doi: 10.1128/JB.183.6.1961-1973.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Cheng Q, Sandalova T, Lindqvist Y, Arnér ESJ. Crystal structure and catalysis of the selenoprotein thioredoxin reductase 1. Journal of Biological Chemistry. 2009;284:3998–4008. doi: 10.1074/jbc.M807068200. [DOI] [PubMed] [Google Scholar]
- [29].Sandalova T, Zhong L, Lindqvist Y, Holmgren A, Schneider G. Three-dimensional structure of a mammalian thioredoxin reductase: Implications for mechanism and evolution of a selenocysteine-dependent enzyme. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:9533–9538. doi: 10.1073/pnas.171178698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Zhong L, Arnér ESJ, Holmgren A. Structure and mechanism of mammalian thioredoxin reductase: The active site is a redox-active selenolthiol/selenenylsulfide formed from the conserved cysteine-selenocysteine sequence. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:5854–5859. doi: 10.1073/pnas.100114897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Rhee SG, Woo HA. Multiple functions of peroxiredoxins: Peroxidases, sensors and regulators of the intracellular messenger H 2O 2, and protein chaperones. Antioxidants and Redox Signaling. 2011;15:781–794. doi: 10.1089/ars.2010.3393. [DOI] [PubMed] [Google Scholar]
- [32].Hanschmann EM, Godoy JR, Berndt C, Hudemann C, Lillig CH. Thioredoxins, glutaredoxins, and peroxiredoxins-molecular mechanisms and health significance: From cofactors to antioxidants to redox signaling. Antioxidants and Redox Signaling. 2013;19:1539–1605. doi: 10.1089/ars.2012.4599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Pillay CS, Hofmeyr JHS, Rohwer JM. The logic of kinetic regulation in the thioredoxin system. BMC Systems Biology. 2011:5. doi: 10.1186/1752-0509-5-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Adimora NJ, Jones DP, Kemp ML. A model of redox kinetics implicates the thiol proteome in cellular hydrogen peroxide responses. Antioxidants and Redox Signaling. 2010;13:731–743. doi: 10.1089/ars.2009.2968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Williams CH., Jr Mechanism and structure of thioredoxin reductase from Escherichia coli. FASEB Journal. 1995;9:1267–1276. doi: 10.1096/fasebj.9.13.7557016. [DOI] [PubMed] [Google Scholar]
- [36].Williams CH., Jr . In: Chemistry and Biochemistry of Flavoenzymes. Muller F, editor. III. CRC Press; Boca Raton, FL.: 1992. pp. 121–211. [Google Scholar]
- [37].Arscott LD, Gromer S, Schirmer RH, Becker KB, Williams CH., Jr. The mechanism of thioredoxin reductase from human placenta is similar to the mechanisms of lipoamide dehydrogenase and glutathione reductase and is distinct from the mechanism of thioredoxin reductase from Escherichia coli. Proceedings of the National Academy of Sciences of the United States of America. 1997;94:3621–3626. doi: 10.1073/pnas.94.8.3621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Gladyshev VN, Jeang KT, Stadtman TC. Selenocysteine, identified as the penultimate C-terminal residue in human T-cell thioredoxin reductase, corresponds to TGA in the human placental gene. Proceedings of the National Academy of Sciences of the United States of America. 1996;93:6146–6151. doi: 10.1073/pnas.93.12.6146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Zhong L, Arnér ESJ, Ljung J, Åslund F, Holmgren A. Rat and calf thioredoxin reductase are homologous to glutathione reductase with a carboxyl-terminal elongation containing a conserved catalytically active penultimate selenocysteine residue. Journal of Biological Chemistry. 1998;273:8581–8591. doi: 10.1074/jbc.273.15.8581. [DOI] [PubMed] [Google Scholar]
- [40].Hill KE, McCollum GW, Boeglin ME, Burk RF. Thioredoxin reductase activity is decreased by selenium deficiency. Biochemical and Biophysical Research Communications. 1997;234:293–295. doi: 10.1006/bbrc.1997.6618. [DOI] [PubMed] [Google Scholar]
- [41].Qi F, Dash RK, Han Y, Beard DA. Generating rate equations for complex enzyme systems by a computer-assisted systematic method. BMC Bioinformatics. 2009:10. doi: 10.1186/1471-2105-10-238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Hofmann B, Hecht HJ, Flohé L. Peroxiredoxins. Biological Chemistry. 2002;383:347–364. doi: 10.1515/BC.2002.040. [DOI] [PubMed] [Google Scholar]
- [43].Seo MS, Kang SW, Kim K, Baines IC, Lee TH, Rhee SG. Identification of a new type of mammalian peroxiredoxin that forms an intramolecular disulfide as a reaction intermediate. Journal of Biological Chemistry. 2000;275:20346–20354. doi: 10.1074/jbc.M001943200. [DOI] [PubMed] [Google Scholar]
- [44].Forstrom JW, Stults FH, Tappel AL. Rat liver cytosolic glutathione peroxidase: Reactivity with linoleic acid hydroperoxide and cumene hydroperoxide. Archives of Biochemistry and Biophysics. 1979;193:51–55. doi: 10.1016/0003-9861(79)90007-9. [DOI] [PubMed] [Google Scholar]
- [45].Yang L, Korge P, Weiss JN, Qu Z. Mitochondrial oscillations and waves in cardiac myocytes: Insights from computational models. Biophysical Journal. 2010;98:1428–1438. doi: 10.1016/j.bpj.2009.12.4300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Yang KS, Kang SW, Woo HA, Hwang SC, Chae HZ, Kim K, Rhee SG. Inactivation of human peroxiredoxin I during catalysis as the result of the oxidation of the catalytic site cysteine to cysteine-sulfinic acid. Journal of Biological Chemistry. 2002;277:38029–38036. doi: 10.1074/jbc.M206626200. [DOI] [PubMed] [Google Scholar]
- [47].Andersen JK. Oxidative stress in neurodegeneration: Cause or consequence? Nature Medicine. 2004;10:S18–S25. doi: 10.1038/nrn1434. [DOI] [PubMed] [Google Scholar]
- [48].Sugamura K, Keaney JJF. Reactive oxygen species in cardiovascular disease. Free Radical Biology and Medicine. 2011;51:978–992. doi: 10.1016/j.freeradbiomed.2011.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Lesnefsky EJ, Moghaddas S, Tandler B, Kerner J, Hoppel CL. Mitochondrial dysfunction in cardiac disease: ischemia-reperfusion, aging, and heart failure. J Mol Cell Cardiol. 2001;33:1065–1089. doi: 10.1006/jmcc.2001.1378. [DOI] [PubMed] [Google Scholar]
- [50].Pannala VR, Bazil JN, Camara AKS, Dash RK. A biophysically based mathematical model for the catalytic mechanism of glutathione reductase. Free Radical Biology and Medicine. 2013;65:1385–1397. doi: 10.1016/j.freeradbiomed.2013.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Pannala VR, Bazil JN, Camara AKS, Dash RK. A mechanistic mathematical model for the catalytic action of glutathione peroxidase. Free Radical Research. 2014;48:487–502. doi: 10.3109/10715762.2014.886775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Cortassa S, Aon MA, Winslow RL, O’Rourke B. A mitochondrial oscillator dependent on reactive oxygen species. Biophysical Journal. 2004;87:2060–2073. doi: 10.1529/biophysj.104.041749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Zhou L, Aon MA, Almas T, Cortassa S, Winslow RL, O’Rourke B. A reaction-diffusion model of ROS induced ROS release in a mitochondrial network. PLoS Computational Biology. 2010:6. doi: 10.1371/journal.pcbi.1000657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Cenas N, Nivinskas H, Anusevicius Z, Sarlauskas J, Lederer F, Arnér ESJ. Interactions of quinones with thioredoxin reductase: A challenge to the antioxidant role of the mammalian selenoprotein. Journal of Biological Chemistry. 2004;279:2583–2592. doi: 10.1074/jbc.M310292200. [DOI] [PubMed] [Google Scholar]
- [55].Cox AG, Peskin AV, Paton LN, Winterbourn CC, Hampton MB. Redox potential and peroxide reactivity of human peroxiredoxin 3. Biochemistry. 2009;48:6495–6501. doi: 10.1021/bi900558g. [DOI] [PubMed] [Google Scholar]
- [56].Kalinina EV, Chernov NN, Saprin AN. Involvement of thio-, peroxi-, and glutaredoxins in cellular redox-dependent processes. Biochemistry (Moscow) 2008;73:1493–1510. doi: 10.1134/s0006297908130099. [DOI] [PubMed] [Google Scholar]
- [57].Peskin AV, Low FM, Paton LN, Maghzal GJ, Hampton MB, Winterbourn CC. The high reactivity of peroxiredoxin 2 with H2O2 is not reflected in its reaction with other oxidants and thiol reagents. Journal of Biological Chemistry. 2007;282:11885–11892. doi: 10.1074/jbc.M700339200. [DOI] [PubMed] [Google Scholar]
- [58].Trujillo M, Clippe A, Manta B, Ferrer-Sueta G, Smeets A, Declercq JP, Knoops B, Radi R. Pre-steady state kinetic characterization of human peroxiredoxin 5: Taking advantage of Trp84 fluorescence increase upon oxidation. Archives of Biochemistry and Biophysics. 2007;467:95–106. doi: 10.1016/j.abb.2007.08.008. [DOI] [PubMed] [Google Scholar]
- [59].Peskin AV, Dickerhof N, Poynton RA, Paton LN, Pace PE, Hampton MB, Winterbourn CC. Hyperoxidation of peroxiredoxins 2 and 3: Rate constants for the reactions of the sulfenic acid of the peroxidatic cysteine. Journal of Biological Chemistry. 2013;288:14170–14177. doi: 10.1074/jbc.M113.460881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Randall LM, Manta B, Hugo M, Gil M, Batthyàny C, Trujillo M, Poole LB, Denicola A. Nitration transforms a sensitive peroxiredoxin 2 into a more active and robust peroxidase. Journal of Biological Chemistry. 2014;289:15536–15543. doi: 10.1074/jbc.M113.539213. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.