Significance
Microbes can discriminate among metabolites that differ only in the stable isotopes of the same element. This stable isotope fractionation responds systematically to environmental variables like extracellular metabolite concentrations and to physiological ones like cell-specific metabolic rates. These observable characteristics define a stable isotope phenotype, as exemplified by the rich database of experimental sulfur isotope fractionations from sulfate-respiring bacteria and archaea. We developed a quantitative model for sulfur isotope fractionation during sulfate respiration that incorporates only experimentally accessible biochemical information. With this approach, stable isotope phenotypes can be decomposed into their physiological, enzymatic, and environmental parts, potentially illuminating the relative influences of these components in natural microbial populations today, as well as how they may have varied in the deep past.
Keywords: dissimilatory sulfate reduction, sulfur isotope fractionation, flux–force relationship
Abstract
We present a quantitative model for sulfur isotope fractionation accompanying bacterial and archaeal dissimilatory sulfate respiration. By incorporating independently available biochemical data, the model can reproduce a large number of recent experimental fractionation measurements with only three free parameters: (i) the sulfur isotope selectivity of sulfate uptake into the cytoplasm, (ii) the ratio of reduced to oxidized electron carriers supporting the respiration pathway, and (iii) the ratio of in vitro to in vivo levels of respiratory enzyme activity. Fractionation is influenced by all steps in the dissimilatory pathway, which means that environmental sulfate and sulfide levels control sulfur isotope fractionation through the proximate influence of intracellular metabolites. Although sulfur isotope fractionation is a phenotypic trait that appears to be strain specific, we show that it converges on near-thermodynamic behavior, even at micromolar sulfate levels, as long as intracellular sulfate reduction rates are low enough (<<1 fmol H2S⋅cell−1⋅d−1).
Dissimilatory sulfate reduction is a respiratory process used by some bacteria and archaea to generate energy under anaerobic conditions. Aqueous sulfate serves as the terminal electron acceptor in this process, leading to the oxidation of organic carbon compounds and sometimes hydrogen and to the production of aqueous sulfide (1). Dissimilatory sulfate respiration was one of the first microbial metabolisms to be isotopically characterized through culture experiments (2), with 32S-bearing sulfate shown to be consumed preferentially to 34S-bearing sulfate. Early experiments identified two critical features of this dissimilatory sulfur isotope fractionation: Its magnitude correlates inversely with the sulfate reduction rate of an individual cell but correlates directly with extracellular sulfate concentrations (3–5).
Through careful regulation of the environmental controls on respiration, more recent experiments have precisely calibrated these relationships and suggest that their particular form may be strain specific (6–11). All experiments, however, show a nonlinear response, where sulfur isotope fractionation increases rapidly with decreasing rate. At the low-rate limit, sulfur isotope fractionation appears to approach levels defined by thermodynamic equilibrium between aqueous sulfate and sulfide (8, 12), the initial reactant and final waste product in the respiratory processing chain.
In parallel with experimental studies, theoretical work has built a broad foundation for understanding the net sulfur isotope fractionation expressed during sulfate respiration (13–17). These efforts initially dealt with sulfur flow through simplified metabolic networks (13) (Fig. 1A) and have expanded to incorporate, for example, electron supply to the reaction cycles of individual respiratory enzymes (17). The reversibility of an individual enzymatic reaction is a central theoretical concept behind these approaches, as it carries the isotopic memory of downstream steps in the pathway (Fig. 1A). Net “back flux” of sulfur from product sulfide to reactant sulfate was an early experimental observation with pure cultures of sulfate-reducing bacteria (18), supported recently by a similar demonstration in a sulfate-reducing coculture (19).
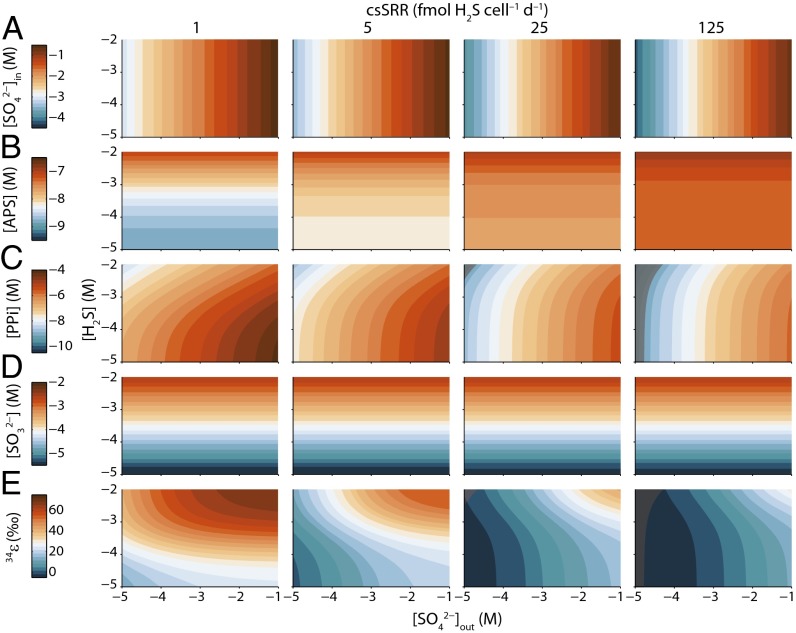
Fig. 1.
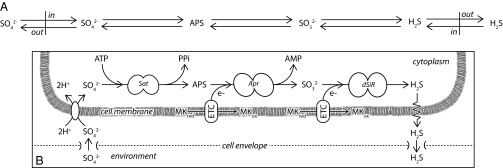
Two illustrations of the dissimilatory sulfate respiration network. (A) Sulfur-focused representation of S-isotope fractionation. Bidirectional arrows represent reversible S transformations. In this framework the “back flux” on any one step is a phenomenological constraint. (B) Metabolite-focused representation used here to quantify back flux. Arrows indicate net flux through the individual steps of the pathway, with the ratio of backward to forward flux controlled by the relative abundances of the reactants and products for each step as well as the kinetics of their associated enzymes. Sat is sulfate adenylyl transferase. Apr is APS reductase. dSiR is dissimilatory sulfite reductase. MKred refers to the reduced form of menaquinone (menaquinol) and MKox refers to the oxidized form of menaquinone. ETC stands for “electron transfer complex.” The likely identities of these complexes in sulfate-reducing microbes are discussed in the text.
Here we describe a quantitative model for sulfur isotope fractionation during microbial sulfate dissimilation that explicitly links fractionation, reaction reversibility, and intracellular metabolite concentrations. Thermodynamic control over isotope fractionation at the low-rate limit is a natural consequence of this approach. It also leads to predictive relationships of fractionation with extracellular sulfate and sulfide concentrations, as well as with intracellular sulfate reduction rates. These relationships are observable characteristics of sulfate-respiring bacteria and archaea, both in the laboratory and in nature. They are the basis for interpreting fossil S-isotope fractionation patterns in the rock record in terms of ancient organisms and their environmental interactions (6, 11, 20). Both in concept and in application, then, sulfur isotope fractionation is a phenotypic trait. Its relationships with environmental metabolites and reduction rate can be thought of as a sulfur isotope phenotype. The approach we advocate here enables past and present variations of the sulfur isotope phenotype to be linked to their physiological, enzymatic, and environmental controls.
A Model for Dissimilatory Sulfur Isotope Fractionation
During the steady-state transformation of a sulfur-bearing reactant (r) to a sulfur-bearing product (p), the net fractionation of 34S from 32S in the reactant relative to the product can be expressed by
| [1] |
where is a fractionation factor characterizing the 34S–32S ratio in the reactant relative to that in the product at equilibrium, is a kinetic fractionation factor that reflects the rate of transformation of 34S-bearing reactant relative to 32S-bearing reactant in the absence of any product, and is the ratio of the rate of formation of reactant from product relative to the rate of product formation from reactant (SI Materials and Methods). This ratio tracks the reversibility of the transformation and varies from 0 for an irreversible transformation to 1 for equilibrium between reactant and product (i.e., complete reversibility). The flux–force relationship connects to the thermodynamic driving force for a chemical transformation,
| [2] |
where R is the gas constant, T is the temperature at which the chemical transformation is taking place, and is the actual free energy change associated with the transformation of interest (SI Materials and Methods) (19, 21, 22). This relationship means that the back flux ratio and, in turn, the sulfur isotope fractionation expressed during a chemical transformation are a function of product and reactant concentrations through
| [3] |
where is the free energy of the reaction at standard-state conditions, is the stoichiometric coefficient for the ith product, and is the stoichiometric coefficient for the jth reactant. The line of reasoning encapsulated in Eqs. 1–3 applies equally well to enzymatically catalyzed biochemical transformations (19, 21–23), illustrating how the concentrations of all metabolic reactants and products ultimately control the net isotopic fractionations that accompany networks of enzymatic reactions.
The kinetics of many reversible enzymatic reactions can be represented with a Michaelis–Menten formalism. Here the net rate of reaction (J) can be decomposed into
| [4] |
where is a constant term that reflects the maximal rate capacity of the reaction and κ is a term that incorporates fractional substrate and product saturation and, like , varies from 0 to 1 (SI Materials and Methods) (23). From this decomposition, Eq. 1 can be expressed as a function of the net rate of reaction (cf. ref. 24):
| [5] |
At the low-rate limit , will approach . When reaction rates are at maximal capacity , enzymes are saturated and will be equal to (25). Importantly, if is greater than , as appears to be the case for individual steps in the dissimilatory sulfate pathway, then the magnitude of the net isotopic fractionation expressed during an enzymatic transformation will vary inversely with the rate of that transformation. We note the variation of net fractionation between equilibrium and kinetic end members (Eq. 5) is not exclusive to sulfur isotopes.
For linear series of reversible enzymatic transformations at steady state, the net isotopic fractionation at any upstream step is given by a recursive relationship that incorporates the net isotopic fractionations associated with all downstream enzymatic transformations (SI Materials and Methods). As a result, the expression for the overall isotopic fractionation associated with a catabolic pathway like dissimilatory sulfate reduction will involve a product of the values for every step in the pathway. The value for each step can be related to the net rate of reaction for that step through expressions like Eq. 4. At steady state, however, the net rates of all steps will be equal to the rate of the overall catabolic transformation . Accordingly, the expression for the overall isotope effect will be a nonlinear, polynomial function of , with the polynomial degree equal to the number of steps in the metabolic pathway.
The approach outlined here can, in principle, explain fundamental characteristics of dissimilatory sulfur isotope fractionation—the inverse nonlinear relationship with cell-specific sulfate reduction rate and the direct correlation with extracellular sulfate concentrations —that have broad empirical support (2–11). To do so, we next discuss the biochemistry of the sulfate respiration pathway, with a focus on general characteristics that are shared among most sulfate-reducing microbes. The discussion is not exhaustive but attempts to provide enough common details to enable us to take our approach from theory to practice.
Overview of Dissimilatory Sulfate Respiration
Dissimilatory sulfate reduction is a respiratory process based on oxidative phosphorylation; substrate-level phosphorylation does not appear to generate enough ATP for growth with hydrogen or lactate as an electron donor (26). Careful accounting of sulfate accumulation within, and sulfate reduction by, dissimilatory sulfate-reducing bacteria demonstrates that the enzymatic reactions leading from sulfate to sulfide occur within the cytoplasm (27). Accordingly, the first step in dissimilatory sulfate reduction is the transport of the sulfate anion from the extracellular environment into the cytoplasm. Microelectrode experiments reveal that the sulfate permeases that facilitate this process are secondary transporters that symport protons or sodium ions with sulfate rather than primary transporters that directly consume ATP (28–30). The stoichiometry of symport is roughly two protons for every sulfate dianion (Fig. 1B and Table S1). Importantly, the overall transport step appears to be reversible (Fig. S1), although the degree of reversibility has not been quantified (30).
Once in the cytoplasm, the ultimate reduction of the sulfate anion to sulfide depends on the presence of ATP (31), indicating that the sulfate needs to be activated into a higher energy form to overcome the unfavorable energetics of a direct transformation to sulfite (32). In the dissimilatory reduction network, adenosine-5′-phosphosulfate (APS) is the free activated intermediate (33), produced along with pyrophosphate (PPi) from ATP and sulfate through the enzymatic activity of sulfate adenylyl transferase (Fig. 1B and Table S1) (34). This reaction is endergonic at standard-state conditions (Table S1) but a cytoplasmic pyrophosphatase “pulls” the reaction toward the products by efficiently hydrolyzing pyrophosphate to phosphate (35).
The enzyme APS reductase catalyzes the efficient reduction of APS to AMP and sulfite, consuming two electrons in the process (35). Sulfate reducers can grow on an energy source of H2 and sulfate (36). However, APS reductase is located in the cytoplasm of sulfate-reducing bacteria (Fig. 1B) (37), whereas hydrogenases that catalyze H2 oxidation are located primarily within the cell envelope (37, 38). This topography requires chemiosmotic energy conservation, in which electrons are partitioned through the cell membrane (Fig. 1B) (37). A suite of quinone-interacting membrane-bound oxidoreductase (Qmo) proteins makes up the electron transfer complex that provides electrons to cytoplasmic APS reductase in Desulfovibrio vulgaris (39, 40). The precise mechanism of APS reduction via Qmo is complicated and may ultimately involve electron bifurcation (41). However, menaquinones (MKox) are the most abundant electron carriers in sulfate-reducing microbes (37), in line with suggestions that membrane-bound menaquinols (MKred) are likely to be the proximal source of electrons to the electron transport complex that, in turn, supplies APS reductase (Fig. 1B and Table S1) (41).
Sulfite produced from APS reduction is the electron acceptor for the final reductive step in the sulfate respiration pathway (Fig. 1B). Dissimilatory sulfite reductase catalyzes the reduction of sulfite to sulfide (42). Sulfate-reducing bacteria have been shown to gain energy solely from sulfite and H2 (43). In light of the disparate topography of their dissimilatory sulfite reductase and hydrogenase enzymes (37), this means that a membrane-bound electron transfer complex (identified as DsrMKJOP) (44) facilitates the exchange of reducing power. The reduction of sulfite to sulfide likely proceeds through a pair of siroheme iron-bound intermediates (, ), consuming two electrons during each of the three proposed conversions catalyzed by dissimilatory sulfite reductase (45). During this reductive transformation, the DsrC protein appears to play a critical role in cycling electrons between the membrane-bound DsrMKJOP complex and cytoplasmic dissimilatory sulfite reductase (46, 47). Within the cell membrane, the oxidation of menaquinol to menaquinone is thought to be the ultimate source of electrons to the transport complex that mediates this process (Fig. 1B and Table S1) (41, 48).
At intracellular pH values, the sulfide produced during sulfite reduction will exist as H2S and HS−. To compensate for the energetic cost of symporting protons across the cell membrane, however, sulfide efflux from the cytoplasm is likely to be as H2S (Fig. 1B) (30). In line with these energetic arguments, limited biophysical measurements indicate that microbial cell membranes are freely permeable to H2S (49), whereas membrane-crossing HS− ion channels have only a small probability of being open (50).
Model Implementation
As outlined above, the backbone of the dissimilatory sulfate respiration pathway involves 13 substrates (Fig. 1). We assumed that each of these substrates exists as a free metabolite rather than a bound metabolic complex. In addition, we assumed that sulfate and sulfide levels within the cell envelope were equal to their external concentrations and that cytoplasmic sulfide concentrations were equal to external ones through efficient H2S permeation (i.e., [H2S]in = [H2S]out = [H2S]) (49) (Fig. 1). Accordingly, we end up with 10 substrates linked by four separate biochemical transformations (Table S1), each of which is separately described by equations like [1]–[3]. With standard-state ΔG values for each substrate (Table S1), kinetic parameters for the transformations in which they are involved (Table S2 and Dataset S1), and equilibrium and kinetic fractionation factors for the isotopologues of each S-bearing substrate (Table S3), we solved these linked equations under the assumption of steady-state kinetics (Materials and Methods and SI Materials and Methods). The relevant equilibrium fractionation factors are well constrained theoretically and experimentally but the relevant kinetic fractionation factors are either inferred from experiments with crude cell extracts or treated as a free parameter (Materials and Methods). As such, the values we use for kinetic fractionation factors should be viewed as “best guesses” to be verified by fractionation experiments with purified enzymes.
We note that the standard-state free energy changes of reaction are positive for the final three steps in the sulfate reduction pathway (Table S1). The activation of sulfate to APS, for example, is widely recognized as endergonic under standard-state conditions, but sulfite reduction is typically considered to be exergonic at standard state (35), in contrast to the results presented here. This is a direct consequence of referencing the standard state to the redox pair, which has a much higher redox potential than the H2/H+ couple that is conventionally used (35). Like the majority of metabolically feasible biochemical reactions (51), sulfite reduction is apparently reversible in vivo and depends strongly on the physiological concentrations of metabolites (e.g., ) to proceed in a net forward direction.
Our solution revealed a handful of important influences on the net S-isotope fractionation (expressed as ) between the external sulfate consumed and the external sulfide produced, during dissimilatory sulfate respiration (SI Materials and Methods). Two are environmental, and [H2S], and are fixed by the living conditions of a particular sulfate-reducing population. The three others are intrinsic to the respiratory pathway: (i) the ratio of reduced to oxidized menaquinone, ; (ii) the kinetic fractionation factor associated with sulfate uptake, ; and (iii) a scaling factor, , that reflects the concentration of active enzymes in whole cells in vivo relative to those in crude cell extracts from in vitro enzyme assay experiments (SI Materials and Methods). We calibrated these important parameters with a combination of physiological reasoning and well-characterized experiments on S-isotope fractionation by sulfate-reducing microbes (Materials and Methods and SI Materials and Methods).
An important result from the calibration exercise is that appears to increase linearly with cell-specific sulfate reduction rate (csSRR) (Fig. S2). As scales with relative enzyme levels (SI Materials and Methods), this prediction can be understood as a specific example of a long-observed physiological response: Overall intracellular protein levels correlate positively with growth rate (52). Other early experiments showed that, under balanced growth, individual protein numbers (53) increase with increasing growth rate as well. Although these observations have theoretical backing (54, 55), supporting proteomic comparisons between sulfate-reducing populations maintained at different specific growth rates have not been performed. We note, however, that there is a clear, coordinated down-regulation of the genes within the sulfate reduction pathway (Fig. 1B) in stationary-phase cultures of D. vulgaris compared with exponentially growing cultures (56). Our results predict approximately fourfold differences in respiratory protein levels (Fig. S2), variations that are well within the range estimated for other metabolic pathways (57) and that could be monitored with targeted transcriptomic or proteomic experiments.
Results and Discussion
Environmental Sulfate and Sulfide Levels Control S-Isotope Fractionation Through the Proximate Influence of Intracellular Metabolites.
Microbial sulfate reduction can occur over a wide span of sulfate and sulfide concentrations. It is sustained at sulfate concentrations from hundreds of millimolar, as found in some hypersaline soda lakes (58), down to tens of micromolar, as shown by precise measurements of the sulfate affinity of actively growing sulfate reducers (59). Sulfide concentrations much higher than tens of millimolar, however, appear to inhibit microbial sulfate reduction (60). This upper limit may be set by sulfide toxicity or by pathway energetics. The lower limit set by physiological sulfide levels is poorly known, with different estimates spanning millimolar (50) to micromolar (61) concentrations. For a given csSRR and constant levels of intracellular redox metabolites, these two environmental boundary conditions are the ultimate controls on sulfur isotope fractionation during dissimilatory sulfate reduction. They determine intracellular metabolite concentrations (SI Materials and Methods and Eqs. S22–S25), which in turn dictate reversibility (Eq. 2) (19) and isotopic fractionations (Eq. 5) (62).
Predictions of intracellular metabolite concentrations show a handful of different responses to these environmental conditions (Fig. 2). First, internal sulfate concentrations are primarily controlled by external sulfate concentrations, relative to which they are enriched by factors of ∼3–100 (Fig. 2A). Accumulation experiments show similar enrichments (30). Enrichments are more pronounced at lower external sulfate concentrations because relatively high internal sulfate levels are required to make favorable the energetics of sulfate activation to APS. Less pronounced intracellular sulfate enrichments at higher csSRR reflect the slower kinetics of sulfate uptake relative to APS formation (Table S2).
Fig. 2.
Predicted metabolite concentrations and isotopic fractionation in a model sulfate reducer. Shown are intracellular concentrations of sulfate (, row A), APS ([APS], row B), PPi ([PPi], row C), and sulfite (, row D) and the net isotopic fractionation between the substrate sulfate and product sulfide (, row E) as functions of extracellular sulfate (, horizontal axis) and sulfide concentrations ([H2S], vertical axis). All concentrations are shown on logarithmic scales. Intracellular metabolite levels are calculated from Eqs. S22–S25, whereas isotopic fractionation is calculated by application of Eqs. 2 and 5. Regions where calculated PPi concentrations (and associated fractionations) are physiologically unlikely are shown as gray shaded fields (SI Materials and Methods) (rows C and E).
On the other hand, intracellular sulfite levels illustrate another control regime. They depend exclusively on sulfide concentrations, do not vary with respiration rate, and range from 0.1 mM to 1 mM for typical environmental sulfide concentrations (Fig. 2D). Maintenance of intracellular sulfite at essentially thermodynamic levels results from the endergonic nature of sulfite reduction at standard state when menaquinone is the electron carrier. Comparison of the redox potentials of sulfite reduction and menaquinol oxidation suggests that menaquinone must be almost completely reduced to reach thermodynamic equilibrium (63). This condition is also inferred here (; SI Materials and Methods) to maintain physiological levels of respiratory metabolites. Intracellular sulfite concentrations have not been reported for sulfate reducers, but cytoplasmic sulfite levels of ∼0.15 mM have been measured in the phototrophic sulfur oxidizer Chlorobaculum tepidum (64). Although the analogy is imperfect, this is a natural example where sulfite is an obligate metabolic intermediate in a bacterium that inhabits anoxic environments. More direct support for our predictions is provided by the reaction rate between isolated siroheme (the inferred catalytic center for dissimilatory sulfite reductase) and sulfite, which is maximized at sulfite concentrations around 0.1 mM (65, 66). Targeted metabolomic studies are clearly needed to test these predictions.
Modeled APS and PPi concentrations show more complex behaviors. At low respiration rates, APS levels are relatively low and PPi levels are relatively high, whereas at high rates the converse is true (Fig. 2 B and C). The negative covariance of APS with PPi reflects the endergonic nature of sulfate activation, which requires that the concentration product of both metabolic products be kept low to sustain net forward reaction. Although this concentration product has not been measured in sulfate-reducing microbes, in vitro rates of APS reduction by APS reductase are ∼80% of measured maximums at APS concentrations of 1 μM (67) and estimates of cytosolic APS levels in growing D. vulgaris are 0.25–5 μM (67). These estimates agree well with the APS concentrations predicted here for high csSRR (0.4–0.6 μM; Fig. 2B), which are required to support high rates of sulfite production. The corresponding PPi concentrations fall to the physiological limit of 1 nM at low external sulfate levels (<10−5 M), indicated by the curved gray fields in Fig. 2D. We note that PPi is an important intermediary in the energy metabolism of sulfate-respiring microbes. Given the multitude of reactions that are likely responsible for maintaining cellular PPi concentrations, the low PPi levels calculated here are best interpreted as a consistency argument that is required for net sulfate reduction to occur. Inorganic pyrophosphatase is an extremely efficient enzyme (68) and may sustain this condition within the cell.
Taken together, these different metabolic responses combine to produce relatively straightforward patterns of S-isotope fractionation. When net respiration is near zero, the magnitude of net S-isotope fractionation is large and responds primarily to sulfide concentrations (Fig. 2E). At a csSRR of 1 fmol H2S⋅cell−1⋅d−1, for example, accessible values increase with increasing sulfide concentrations, approaching the thermodynamic S-isotope fractionation between sulfate and sulfide (∼71‰ at 25 °C) at millimolar levels of sulfide. With increasing sulfide concentrations, the energy yield of the reduction of sulfate to sulfide decreases to zero; thermodynamic equilibrium demands complete reversibility and equilibrium S-isotope fractionation among all of the metabolic intermediates.
As respiration rate increases, external sulfate concentrations become influential as well, with contours of equal following systematic paths of decreasing external sulfate and increasing sulfide concentrations at moderate csSRR (Fig. 2E). At a csSRR of 125 fmol H2S⋅cell−1⋅d−1, accessible values are small, only weakly sensitive to external sulfate, and insensitive to sulfide (Fig. 2E). Together the fractionation characteristics at moderate to high csSRR may explain why most batch experiments with sulfate reducers return isotopic data consistent with a single value of , despite changing sulfate and sulfide levels throughout the course of the experiment. The insensitivity of to csSRR at high rates arises from our prediction that enhanced production of respiratory enzymes will accompany enhanced csSRR (Fig. S2). Because of this, the ratio of csSRR to becomes constant at high csSRR, meaning that the concentrations of respiratory metabolites (SI Materials and Methods and Eqs. S22–S25) and stabilize as well.
S-Isotope Phenotypes Appear to Be Strain Specific.
Recent culture experiments have isolated the effects of single control parameters (csSRR, external sulfate concentration) on fractionation of 33S–32S and 34S–32S (6–11, 14). The broad fractionation patterns in these experiments confirm inferences made from earlier work; decreases with increasing rate and increases with increasing external sulfate (Fig. 3). However, measured strain-specific fractionations are difficult to compare directly because of limited overlap in the experimental conditions under which they were determined. An initial attempt to address this issue suggested that common fractionation behaviors might not accompany sulfate respiration by different strains (69), although, as shown here, the environmental diversity in this important experiment complicates strain-by-strain comparisons. Starting from the metabolic state defined by the model sulfate reducer illustrated in Fig. 2, we constrained a –csSRR relationship for the two recent experiments that looked at the influence of rate on fractionation by different bacterial strains of D. vulgaris (DvH, DMSS-1) and another one that examined how sulfate affected fractionation by the sulfate-reducing archaeon Archaeoglobus fulgidus (Fig. S2). Coupled with unique and for each experiment, this exercise allowed us to extend the strain-specific fractionations to other environmental conditions in a self-consistent fashion.
Fig. 3.
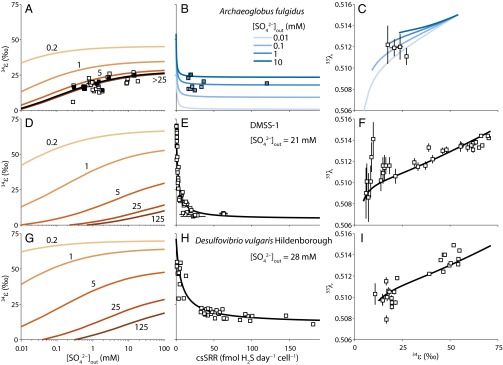
Model calibration to experimental data. (A) Net isotopic fractionation by A. fulgidus grown at 80 °C at constant csSRR (6, 7) as a function of extracellular sulfate concentrations . Orange contours show the value of for different values of csSRR in fmol H2S⋅cell−1⋅d−1. The black curve shows for the harmonic mean of the csSRR values that were reported for some of the experiments (black squares). The csSRR values were not reported for other experiments (white squares), resulting in the scatter around the black curve. (B) Predicted as a function of csSRR for between 10 μM and 100 mM. Experiments for which , csSRR, and were all reported are also shown, color coded by . (C) Predicted fractionation exponent as a function of for the same as in B. Experiments for which minor isotope data exist are also shown (14). (D) Predicted relationship for Desulfovibrio strain DMSS-1 grown at ∼20 °C, 21–14 mM , and 2–7 mM sulfide (8–10). (E) Measured (white squares) and model (black curve) vs. csSRR for the experiments in D. These experiments were run in batch culture, so we assumed the average and external sulfide concentrations for the interval over which vs. csSRRs were determined (SI Materials and Methods). (F) vs. for the experiments in D. Error bars are 1σ reported in the experiments. (G–I) Same as D–F, but for D. vulgaris Hildenborough, grown at 25 °C and with precisely controlled of 28 mM (11). Sulfide concentrations for the model curves were assumed to be 0.1 mM.
Once environmental biases are accounted for, it is clear that the two bacterial strains have different fractionations when respiration rate is the control parameter and that their isotopic responses to changing external sulfate concentrations differ also (Fig. 3 D and G). The fundamental distinction is that DvH is predicted to maintain a higher respiration rate at a given sulfate concentration, giving rise to expanded access to the –csSRR field (Fig. 3G). The fivefold difference in the initial value required by DvH and DMSS-1 to sustain minimal respiration, as well as the more profligate production of respiratory enzymes by DvH with increasing csSRR, underlies this physiological response (Fig. S2 and Table S4). The scaling factor between in vitro and in vivo reaction velocities incorporates catalytic rate constants as well as enzyme levels (SI Materials and Methods). Specific activities for individual sulfate respiration enzymes vary nearly 100-fold (SI Materials and Methods), suggesting that the initial difference identified here may have its roots in structural differences between DvH and DMSS-1 respiratory enzymes. The clear tension between energy yield and protein cost may be behind the distinct responses of to increases in csSRR (Fig. S2) (57); DMSS-1 is a recently isolated strain that may be more economical in producing proteins than the long-transferred, laboratory workhorse DvH.
Comparative predictions for DvH and the archaeal sulfate reducer, A. fulgidus (Fig. 3), reveal S-isotope phenotypes that differ in a number of ways as well. The most obvious difference is at the low-rate limit, where the higher optimal growth temperatures of the archaeon lead to an equilibrium that is ∼20‰ lower than that for DvH. In addition, the archaeal contours are more tightly spaced than those of DvH, representing the lower sensitivity of fractionation to increasing csSRR in A. fulgidus. The domain-level physiological distinctions between these two strains are reflected in the kinetic performance of their respective respiratory enzymes (Table S2), as well as in the values required to reproduce the –csSRR data for DvH and the data for A. fulgidus (Fig. S2 and Table S4). It appears that A. fulgidus needs to produce >10-fold more respiratory enzymes than DvH to cause the same increase in csSRR. Protein degradation rates are temperature sensitive, potentially accounting for the higher predicted production rates in A. fulgidus. For a given external sulfate concentration, this feature leads to an unchanging archaeal and, by inference, a static respiratory metabollome, once csSRR surpasses ∼1 fmol H2S⋅cell−1⋅d−1 (Fig. 3B). Our analysis supports the proposal that the A. fulgidus experiments were run in a regime of control rather than rate control (7).
Unlike the –csSRR and the relationships, phenotypic variability in vs. is less pronounced among sulfate-reducing strains (Fig. 3 C, F, and I). This finding is in marked contrast to the wide range of 33S–32S and 34S–32S fractionations that are predicted by phenomenological models of multiple S-isotope fractionation during microbial sulfate reduction (8, 14, 17). As explored below, this behavior has its roots in the similar and values assigned to the sulfate reducers examined here.
Low Sulfate Concentrations Lead to Less Fractionation, but Not When Coupled to Low Respiration Rates.
Early experiments showed that microbial sulfate respiration in barite-saturated solutions produced limited S-isotope fractionation (3). These observations strongly influenced later interpretations of the geologic record of microbial S-isotope fractionation, where limited variability in whole-rock S values from ancient marine sediments was linked to low levels of seawater sulfate at their time of deposition (70). Later experiments examined respiratory S-isotope fractionation over a wider range of sulfate levels and with a variety of populations of microbial sulfate reducers (6). The general fractionation pattern appeared bimodal, with values near zero below ∼200 μM but widely dispersed at higher concentrations. Recent experiments on microbial sulfate reduction in low-sulfate euxinic lakes have expanded this relationship and slightly blurred its apparent boundaries, with fractionation reported near the thermodynamic limit at (12) and shown to still be sizable (∼20‰) at sulfate levels between ∼100 μM and 350 μM (71). In detail, however, the low sulfate–high sulfate duality is not always obvious. A. fulgidus, for example, shows a positive log-linear relationship between and extracellular (7) (Fig. 3A).
The model described here naturally explains these disparate observations. Whereas fractionation always decreases continuously with decreasing extracellular sulfate levels in a broadly log-linear fashion, the net respiration rate controls the range of values that are accessible at a given . For example, simple estimates of barite saturation at room temperature predict equal concentrations of Ba2+ and near 50 μM (72). At these extracellular sulfate levels, limited S-isotope fractionation is predicted for all strains when respiration rates are greater than those typically seen in pure culture experiments (≥25 fmol H2S⋅cell−1⋅d−1; Figs. 2E and 3 A, D, and G). For a microbe respiring at 25 fmol H2S⋅cell−1⋅d−1 in media with modern seawater (28 mM), however, strain-specific behavior results in a wider range of possible fractionations ( up to ; Fig. 3 A, D, and G). Consistent with fractionation experiments conducted at near-seawater sulfate concentrations (8), can approach the thermodynamic limit between sulfate and sulfide when net respiration rates decrease to <<1 fmol H2S⋅cell−1⋅d−1 (Fig. 3 B, E, and H). In this region, any strain-specific behavior is trumped by the almost perfect two-way metabolic communication between the initial reactant and ultimate product of the sulfate respiration pathway.
However, the most unexpected result of the new model is that this near-thermodynamic reciprocity can be maintained down to extremely low concentrations of external sulfate (Fig. 3 A, D, and G). As anticipated by environmental incubations from sulfate-poor meromictic lakes (12), values of 60–70‰ can occur at sulfate concentrations down to tens of micromolar as long as the right strains (e.g., DvH; Fig. 3G) maintain sluggish net respiration. The major features of published measurements can then be rationalized as follows. First, the wide variation in down to ∼200 μM extracellular most likely represents unique strain-by-strain responses to external sulfate forcing [either in terms of well-known differences in strain-specific sulfate affinities (59) or in terms of more speculative differences in the kinetic fractionation factor associated with sulfate uptake; Table S3]. Second, the limited variability in below ∼200 μM extracellular is only superficial and probably results from the experimental difficulty of sustaining viable cultures at respiration rates as low as those encountered in natural environments. Rate-controlled chemostat experiments of different strains of sulfate reducers at different sulfate concentrations will go a long way toward validating these predictions.
No Single Metabolic Step Controls Fractionation.
Metabolic interpretations of isotope fractionation during sulfate respiration are typically framed in terms of a “rate-limiting” step in the metabolic reaction network (3, 13, 15, 17, 73), with notable exceptions (cf. ref. 62). The catalytic reduction of to H2S is often considered to be the rate bottleneck for respiration (73), leading to the suggestion that larger S fractionations could result if this constraint were released (15). Upstream steps have also been proposed to fulfill the rate-limiting role. In early experiments, for example, fractionation at low rates of respiratory reduction ( ∼ 25‰) was interpreted as the isotopic signature of the conversion of APS to (3). In contrast, a similar claim for this step was drawn from the convergence of on a value of ∼15‰ for six different strains of sulfate reducers in batch culture (74). Likewise the small respiratory fractionations observed at low sulfate levels have been proposed to result from rate limitation by sulfate uptake and the assumption of minor intrinsic fractionation during the uptake process (7, 13). Our calculations support the hypothesis (62) that a fractionation framework based on rate-limiting steps, although potentially correct in theory, is often mistaken in practice. The holistic approach described here acknowledges the relative isotopic influence of each step in the respiratory pathway and reveals their combined controls on fractionation limits.
There are three fractionation limits that bracket the patterns associated with sulfate respiration. The first limit occurs where csSRR approaches zero (Fig. 4A). Here each internal metabolite is in thermodynamic equilibrium with all others in the reaction network, as ultimately dictated by environmental sulfate and sulfide concentrations. As a result, the values for each step are unity, resulting in an overall S-isotope fractionation determined by the product of the equilibrium fractionation factors for each step. The other two limits occur at high respiration rates and at low sulfate levels. Importantly values for sulfate activation and sulfite reduction are always near unity, even at these limits, implying the values for these steps exert minor influence on the isotope phenotype (Fig. S3). As csSRR increases, the reduction of APS emerges early as the primary bottleneck for the respiratory processing chain over a wide range of metabolic states (Fig. 4A). As a result, for this step approaches zero whereas csSRR is still much less than the maximum achievable. The fractionation-free character of sulfate activation to APS (Table S3) means that fractionation control is switched to the sulfate uptake step at this point and, consequently, the drawn-out decay of toward a low constant value with increasing csSRR reflects the slow departure of sulfate uptake from equilibrium (Fig. 4A).
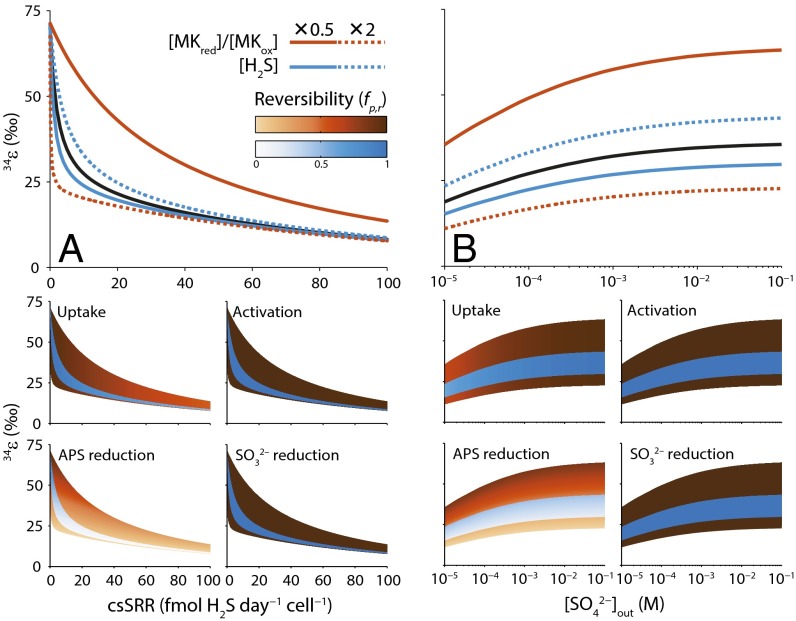
Fig. 4.
Sensitivity of –csSRR (A) and (B) relationships to a halving (solid curves) and a doubling (broken curves) of the default [MKred]/[MKox] (= 100) and [H2S] (= 0.1 mM) values. Fractionation resulting from the default state is shown by the black curves. Shaded envelopes in A and B show the reversibility of the steps in the sulfate reduction pathway resulting from variation of [MKred]/[MKox] and [H2S] for a range of and csSRRs. Values of range from 0.45 to 0.99 for uptake, 0.98 to ∼1 for activation, ∼0 to 0.98 for APS reduction, and 0.99 to ∼1 for reduction.
At variable extracellular sulfate levels, the distribution of fractionation control depends on the initial metabolic state, with the ratio of reduced to oxidized electron carriers and internal sulfide concentrations playing key roles. In all cases, as external sulfate levels decrease, the reversibility of sulfate uptake decreases (sulfate uptake departs from equilibrium; Fig. 4B). Consequently, slowly approaches a low constant value (Fig. 4B). The metabolic state modulates this behavior. For example, at lower values or higher [H2S], reversibility in the APS reduction step is relatively high (Fig. 4B) and sulfate uptake exerts the primary control on fractionation changes at low sulfate levels. The magnitude of is still much larger than that of , meaning that downstream steps continue to exert an isotopic influence at extremely low sulfate levels (<10 μM; Fig. 4B). At higher values or lower [H2S], the path to low is different, with the reduction of APS approaching irreversibility over a wide range of sulfate concentrations (Fig. 4B). The overall fractionation is smaller in this case, reflecting both the low reversibility in the APS reduction step and the decreasing reversibility of sulfate uptake with decreasing sulfate levels (Fig. 4B). In both these cases, however, extremely low sulfate concentrations ( M) appear to be required before for sulfate uptake would approach zero. This appears to rule out the hypothesis of a simple mass transfer control on fractionation, where a low sulfate level confers a small isotope effect (i.e., ) due to conservation of mass. As the control of fractionation is distributed among different enzymatic steps even at these limiting conditions, it seems likely that S-isotope fractionation is never a sole function of a single respiratory enzyme.
Minor Isotope Fractionations Are Uniquely Sensitive to Upstream Steps in the Sulfate Respiration Pathway.
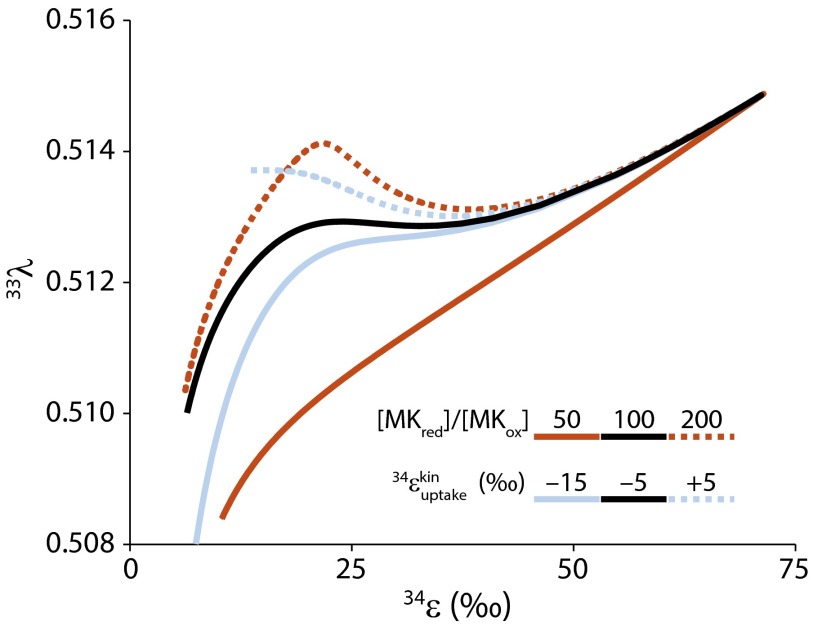
Although the positive correlation of with has been experimentally validated, the causation behind it is still opaque. One defining limit of the relationship is clear. As the rate of sulfate respiration approaches zero, and will be pegged to their thermodynamic counterparts regardless of the responsible sulfate respirer (Fig. 3 C, F, and I). This characteristic suggests that comparative 33S–32S and 34S–32S fractionations will be most biologically informative in the low fractionation limit. The experimental variation of seems to increase as decreases, lending some support to this inference (Fig. 3 C, F, and I). Some of this variability may result from the intracellular ratio of reduced to oxidized electron carriers for the sulfate respiration pathway. Lower values produce relatively steady declines in with , whereas higher ratios introduce cusps that separate fractionation regimes upstream and downstream of APS reduction (Fig. 5). This redox control is also seen in the –csSRR behavior, where lower values give rise to a more gradual decrease in fractionation with rate whereas higher ratios show a more abrupt change in slope (Fig. 4A).
Fig. 5.
Sensitivity of the relationship to the ratio of reduced to oxidized menaquinone ([MKred]/[MKox], orange) and the kinetic isotope fractionation during sulfate uptake (, blue).
To reproduce the measured – patterns, we found that an inverse isotope effect had to be associated with sulfate uptake. For DvH, for example, is , whereas it is for DMSS-1 (Table S3). The isotope effects of transport across cell membranes have been only rarely studied, but the one isotope effect that has been directly observed for active transport [∼14‰ for uptake in Escherichia coli (75)] has a similar absolute magnitude but opposite sign. Although inverse kinetic isotope effects are unusual, we note that early experiments assigned a fractionation of to (3).
An inverse isotope effect is required for sulfate uptake because decreases as approaches zero. For the equilibrium fractionations and temperatures considered here, is always close to 0.515 (Table S3). Under the Swain–Schaad assumption, is very similar to 0.515 as well (Table S3). As a result, when is positive, indicating a normal kinetic isotope effect, will always be positive and will swing between 0.515 at both the high and low fractionation limits, dipping slightly below 0.515 at intermediate fractionations (Fig. 5) because of the nonlinear interaction of fractionation and isotope mixing (14). On the other hand, when is negative, will “cross over” from a positive value to a negative value; this happens slightly before the sign change for . Consequently, will go through a singularity, approaching negative infinity from the right and positive infinity from the left (Fig. 5).
The – relationship for microbial sulfate respiration, then, appears to be a natural example of the abnormal fractionation behavior first identified in a theoretical investigation of the H-D-T system (76). (We stress that this behavior is not the “mass-independent” S-isotope fractionation documented in ancient S-bearing minerals and in photolysis experiments with SO2. The values corresponding to these situations would require vanishingly small values of , and the anomalous fractionation would remain analytically undetectable as a result.) This inference, however, depends on the validity of the Swain–Schaad relationship, particularly for the S-isotope effect associated with sulfate uptake. Although it has been examined only in calculations for H isotopes, this relationship appears computationally robust in the face of the complexity associated with enzyme kinetics (77), but may break down for secondary isotope effects, especially when they become very small (78). It will take a well-designed molecular and isotopic experiment (cf. ref. 75) to determine whether these theoretical results apply to S-isotope effects associated with sulfate uptake or activation.
Summary and Natural Extensions
In this contribution we predict the sulfur isotope phenotypes of sulfate-respiring bacteria and archaea over a wide range of environmental sulfate and sulfide levels and at respiration rates that range from those typical of laboratory cultivation down to the much lower rates associated with natural populations (79). One of our primary conclusions is that S-isotope fractionation reflects the intracellular concentrations of all metabolites involved in the respiratory pathway. Targeted metabolomic analyses should be able to assess this result. Because of this dependence on metabolite levels, it appears that the activity of a single enzyme is unlikely to be the sole control over fractionation. Our approach combines biochemical kinetics and thermodynamics and involves only parameters that can, in principle, be experimentally determined. As it stands, we have been able to reproduce recent S-isotope datasets (with more than 100 total measurements) from three separate strains of sulfate reducers (two bacteria and one archaeon) by considering variations in three model parameters: (i) the ratio of reduced to oxidized membrane-bound menaquinone; (ii) S-isotope fractionation during sulfate uptake; and (iii) a scaling factor, , that reflects the concentration of active enzymes in whole cells relative to those in crude cell extracts.
The calculated S-isotope phenotypes associated with these strains confirm some of the broad fractionation patterns inferred from experimental work, while revealing that others might be artifactual. The positive covariation of 33S–32S and 34S–32S fractionations is a robust isotopic feature, largely because of the thermodynamic anchor point provided at low respiration rates. Sulfate-uptake–induced fractionation and intracellular redox state create isotopic variability in this pattern when 34S–32S fractionations are small. Our results also clarify the long-observed decrease in fractionation with increasing respiration rate. The general grade is essentially preordained, given that equilibrium fractionations in the sulfate respiration pathway have larger magnitudes than their corresponding kinetic counterparts. Individual trajectories, however, are strain specific and reflect primarily differences in the intracellular redox states and enzyme levels of sulfate-reducing microbes. Although our results show a monotonic increase in 34S–32S fractionations with increasing sulfate levels for a given respiration rate, we never calculated a threshold sulfate concentration above which fractionation was expressed and below which it was repressed. Near thermodynamic fractionations appear to be accessible at extremely low sulfate levels (<10 μM), as long as the average respiration rate of a sulfate-reducing population is low enough (79). This feature may neatly unite two conflicting views of S cycling on the Archean earth: large intrasample variability in S values (80, 81) in the face of low marine sulfate concentrations (6, 82).
Although sulfate respiration is particularly well investigated from an isotopic point of view, other microbial metabolic pathways also exhibit the isotopic behaviors explicated here. For example, biosynthetic carbon isotope fractionation is often contrasted as either an equilibrium or kinetic process (83). This dilemma is captured in a pair of long-standing observations; measured intermolecular C isotope fractionations in biosynthetic products have been shown to correlate with fractionations estimated from the calculated intramolecular distribution of C isotopes at thermodynamic equilibrium (25, 84) while measured intramolecular distributions of C isotopes in bacterial fatty acids have been fully explained in terms of kinetic isotope effects (85). These observations may not be incompatible, as physiological state can bridge the divide between equilibrium and kinetic fractionations (Eq. 5). Also consistent with the general principles encompassed in Eq. 5, catabolic pathways with single processing steps exhibit more linear relationships between and rate [e.g., 34S–32S fractionation during dissimilatory S0 reduction (86)] whereas longer processing chains show distinctly nonlinear behavior [e.g., 13C–12C fractionation during methanogenesis (87)]. Nitrogen isotope fractionation during microbial denitrification, however, exhibits a range of behaviors that are not so easily classified. Recent work on respiratory nitrate reduction, for example, reveals a general pattern of increasing with increasing cell-specific nitrate reduction rate until a fractionation plateau is reached (88). Careful experiments on an intermediate step in the denitrification pathway—nitrite reduction—show that rate control by the electron acceptor follows a similar fractionation pattern, whereas rate control by the electron donor produces fractionations that decrease with increasing rate (24, 89). Although the conceptual underpinning for these contrasting isotopic behaviors was sketched out almost 30 y ago (90), the present contribution has the potential to link them under a single quantitative framework. We hope that our approach will enable stable isotope phenotypes like these, as well as similar ones seen in assimilatory N and C metabolisms (91, 92), to be decomposed into their physiological, enzymatic, and environmental parts. This is a necessary first step toward understanding the relative influences of these components in natural microbial populations today and is critical for recognizing how those influences may have varied in the deep past.
Materials and Methods
Reaction Thermodynamics and Kinetics.
We constrained the free energies of reaction at standard-state intracellular conditions (pH 7.0; ionic strength = 0.25; Table S1), using an online biochemical calculator (http://equilibrator.weizmann.ac.il) (93) that is based on an internally consistent database (51) and accounts for speciation at intracellular pH values. The redox potential for [MKred]/[MKox] was from ref. 35. Standard-state free energy values for sulfate uptake have not been previously determined and we constrained these from membrane energetics and sulfate accumulation experiments with sulfate-reducing bacteria (SI Materials and Methods and Fig. S1). Velocities for the individual reactions were taken from experiments with purified enzymes, whole-cell extracts, and, in a few cases, cell suspensions (Table S2). Saturation constants were taken from an online database (www.brenda-enzymes.info) (94) (Table S2).
Isotopic Fractionation Factors.
Published thermodynamic calculations provided equilibrium S-isotope fractionation factors for most individual steps (95), whereas kinetic fractionation factors for 34S–32S were taken from experiments with cell-free extracts where available (Table S3). Kinetic fractionation factors for 33S–32S were calculated from a fractionation exponent based on the Swain–Schaad formalism (96), assuming that S–O bonds were broken (Table S3). We assumed equilibrium fractionation among external, internal, and APS-bound sulfate is negligible. During APS production, S–O bonds are not broken, and no bonds with S are made. Kinetic S-isotope fractionation during this process would be characterized by a secondary isotope effect, which we assumed was insignificant.
Additional Parameters.
Intracellular concentrations of ATP, AMP, and total MK have been measured in sulfate reducers (Table S4) and we maintained these at constant levels in our calculations. Over the range of csSRR investigated here, we chose [MKred]/[MKox] such that intracellular metabolite levels did not exceed 10 mM and were greater than the free physiological limit of 1 nM. Because of the endergonic nature of reactions in the sulfate reduction pathway at standard state (Table S1), the value of [MKred]/[MKox] that fulfills these requirements is ∼100 (SI Materials and Methods).
Note Added in Proof.
Experiments with pure cultures of Desulfobacterium autotrophicum show a positive correlation between per-cell contents of dSiR mRNA and csSRR (97). The slope of this correlation (≈fourfold change in dSiR mRNA for every unit increase in csSRR) compares well with the predictions made here (Fig. S2 and Table S4). We thank Alex Loy (University of Vienna) for bringing this to our attention.
Supplementary Material
Acknowledgments
The farsighted experiments of G. Shearer and D. Kohl (Washington University) on catabolic N-isotope fractionation inspired this work. Discussions with R. Milo (Weizmann Institute of Science) provided focus at critical points in our development of the approach advocated here. We thank W. Fischer (California Institute of Technology), D. Fike and W. Leavitt (Washington University), and A. Pellerin (McGill University) for valuable discussions; D. Stahl and the Stahl research group (University of Washington) for turning on to stable isotopes; J. Singh (McGill University) for finding two important typos; and two anonymous reviewers for their criticism that improved this manuscript in substance and in style. J. Ferry (Johns Hopkins University) made early suggestions that equilibrium thermodynamics might partly account for microbial behavior. I.H. acknowledges funding from a European Research Council Starting grant and from Israel Science Foundation Grant 1133/12. B.A.W. acknowledges support from a National Science and Engineering Research Council of Canada Discovery grant and the Feinberg Foundation Visiting Faculty Program at the Weizmann Institute of Science.
Footnotes
The authors declare no conflict of interest.
See Commentary on page 18102.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1407502111/-/DCSupplemental.
References
- 1.Rabus R, Hansen T, Widdel F. In: Dissimilatory Sulfate- and Sulfur-Reducing Prokaryotes. Rosenberg E, DeLong E, Lory S, Stackebrandt E, Thompson F, editors. Springer; Berlin: 2013. pp. 309–404. [Google Scholar]
- 2.Thode H, Kleerekoper H, McElcheran D. Isotope fractionation in the bacterial reduction of sulphate. Research. 1951;4:581–582. [Google Scholar]
- 3.Harrison A, Thode H. Mechanism of the bacterial reduction of sulphate from isotope fractionation studies. Trans Faraday Soc. 1958;54:84–92. [Google Scholar]
- 4.Kaplan IR, Rittenberg SC. Microbiological fractionation of sulphur isotopes. J Gen Microbiol. 1964;34(2):195–212. doi: 10.1099/00221287-34-2-195. [DOI] [PubMed] [Google Scholar]
- 5.Chambers LA, Trudinger PA, Smith JW, Burns MS. Fractionation of sulfur isotopes by continuous cultures of Desulfovibrio desulfuricans. Can J Microbiol. 1975;21(10):1602–1607. doi: 10.1139/m75-234. [DOI] [PubMed] [Google Scholar]
- 6.Habicht KS, Gade M, Thamdrup B, Berg P, Canfield DE. Calibration of sulfate levels in the Archean ocean. Science. 2002;298(5602):2372–2374. doi: 10.1126/science.1078265. [DOI] [PubMed] [Google Scholar]
- 7.Habicht KS, Salling L, Thamdrup B, Canfield DE. Effect of low sulfate concentrations on lactate oxidation and isotope fractionation during sulfate reduction by Archaeoglobus fulgidus strain Z. Appl Environ Microbiol. 2005;71(7):3770–3777. doi: 10.1128/AEM.71.7.3770-3777.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sim MS, Bosak T, Ono S. Large sulfur isotope fractionation does not require disproportionation. Science. 2011;333(6038):74–77. doi: 10.1126/science.1205103. [DOI] [PubMed] [Google Scholar]
- 9.Sim M, Ono S, Donovan K, Templer S, Bosak T. Effect of electron donors on the fractionation of sulfur isotopes by a marine Desulfovibrio sp. Geochim Cosmochim Acta. 2011;75:4244–4259. [Google Scholar]
- 10.Sim MS, Ono S, Bosak T. Effects of iron and nitrogen limitation on sulfur isotope fractionation during microbial sulfate reduction. Appl Environ Microbiol. 2012;78(23):8368–8376. doi: 10.1128/AEM.01842-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Leavitt WD, Halevy I, Bradley AS, Johnston DT. Influence of sulfate reduction rates on the Phanerozoic sulfur isotope record. Proc Natl Acad Sci USA. 2013;110(28):11244–11249. doi: 10.1073/pnas.1218874110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Canfield DE, Farquhar J, Zerkle AL. High isotope fractionations during sulfate reduction in a low-sulfate euxinic ocean analog. Geology. 2010;38:415–418. [Google Scholar]
- 13.Rees C. Steady-state model for sulfur isotope fractionation in bacterial reduction processes. Geochim Cosmochim Acta. 1973;37:1141–1162. [Google Scholar]
- 14.Farquhar J, et al. Multiple sulphur isotopic interpretations of biosynthetic pathways: Implications for biological signatures in the sulphur isotope record. Geobiol. 2003;1(1):27–36. [Google Scholar]
- 15.Brunner B, Bernasconi SM. A revised isotope fractionation model for dissimilatory sulfate reduction in sulfate reducing bacteria. Geochim Cosmochim Acta. 2005;69:4759–4771. [Google Scholar]
- 16.Johnston D, et al. Multiple sulfur isotope fractionations in biological systems: A case study with sulfate reducers and sulfur disproportionators. Am J Sci. 2005;305:645–660. [Google Scholar]
- 17.Bradley AS, Leavitt WD, Johnston DT. Revisiting the dissimilatory sulfate reduction pathway. Geobiology. 2011;9(5):446–457. doi: 10.1111/j.1472-4669.2011.00292.x. [DOI] [PubMed] [Google Scholar]
- 18.Trudinger P, Chambers L. Reversibility of bacterial sulfate reduction and its relevance to isotope fractionation. Geochim Cosmochim Acta. 1973;37:1775–1778. [Google Scholar]
- 19.Holler T, et al. Carbon and sulfur back flux during anaerobic microbial oxidation of methane and coupled sulfate reduction. Proc Natl Acad Sci USA. 2011;108(52):E1484–E1490. doi: 10.1073/pnas.1106032108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shen Y, Buick R, Canfield DE. Isotopic evidence for microbial sulphate reduction in the early Archaean era. Nature. 2001;410(6824):77–81. doi: 10.1038/35065071. [DOI] [PubMed] [Google Scholar]
- 21.Britton HG. The Ussing relationship and chemical reactions: Possible application to enzymatic investigations. Nature. 1965;205:1323–1324. doi: 10.1038/2051323b0. [DOI] [PubMed] [Google Scholar]
- 22.Beard DA, Qian H. Relationship between thermodynamic driving force and one-way fluxes in reversible processes. PLoS ONE. 2007;2(1):e144. doi: 10.1371/journal.pone.0000144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Noor E, Flamholz A, Liebermeister W, Bar-Even A, Milo R. A note on the kinetics of enzyme action: A decomposition that highlights thermodynamic effects. FEBS Lett. 2013;587(17):2772–2777. doi: 10.1016/j.febslet.2013.07.028. [DOI] [PubMed] [Google Scholar]
- 24.Shearer G, Kohl D. Nitrogen isotopic fractionation and 18O exchange in relation to the mechanism of denitrification of nitrite by Pseudomonas stutzeri. J Biol Chem. 2013;41:D764–D772. [PubMed] [Google Scholar]
- 25.Galimov EM. The Biological Fractionation of Isotopes. Academic; Orlando, FL: 1985. [Google Scholar]
- 26.Peck HD., Jr Evidence for oxidative phosphorylation during the reduction of sulfate with hydrogen by Desulfovibrio desulfuricans. J Biol Chem. 1960;235:2734–2738. [PubMed] [Google Scholar]
- 27.Furusaka C. Sulphate transport and metabolism by Desulphovibrio desulphuricans. Nature. 1961;192:427–429. doi: 10.1038/192427a0. [DOI] [PubMed] [Google Scholar]
- 28.Stahlmann J, Warthmann R, Cypionka H. Na+-dependent accumulation of sulfate and thiosulfate in marine sulfate-reducing bacteria. Arch Microbiol. 1991;155:554–558. [Google Scholar]
- 29.Warthmann R, Cypionka H. Sulfate transport in Desulfobulbus propionicus and Desulfococcus multivorans. Arch Microbiol. 1990;154(2):144–149. [Google Scholar]
- 30.Cypionka H. In: Solute Transport and Cell Energetics. Barton L, editor. Springer; New York: 1995. pp. 151–184. [Google Scholar]
- 31.Peck HD. The ATP-dependent reduction of sulfate with hydrogen in extracts of Desulfovibrio desulfuricans. Proc Natl Acad Sci USA. 1959;45(5):701–708. doi: 10.1073/pnas.45.5.701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Thauer R, Stackebrandt E, Hamilton W. In: Energy Metabolism and Phylogenetic Diversity of Sulphate-Reducing Bacteria. Barton L, Hamilton W, editors. Cambridge Univ Press; Cambridge, UK: 2007. pp. 1–37. [Google Scholar]
- 33.Ishimoto M, Fujimoto D. Biochemical studies on sulfate-reducing bacteria: 10. Adenosine-5′-phosphosulfate reductase. J Biochem. 1961;50:299–304. [Google Scholar]
- 34.Akagi JM, Campbell LL. Studies on thermophilic sulfate-reducing bacteria: 3. Adenosine triphosphate-sulfurylase of Clostridium nigrificans and Desulfovibrio desulfuricans. J Bacteriol. 1962;84(6):1194–1201. doi: 10.1128/jb.84.6.1194-1201.1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Thauer RK, Jungermann K, Decker K. Energy conservation in chemotrophic anaerobic bacteria. Bacteriol Rev. 1977;41(1):100–180. doi: 10.1128/br.41.1.100-180.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Badziong W, Thauer RK, Zeikus JG. Isolation and characterization of Desulfovibrio growing on hydrogen plus sulfate as the sole energy source. Arch Microbiol. 1978;116(1):41–49. doi: 10.1007/BF00408732. [DOI] [PubMed] [Google Scholar]
- 37.Badziong W, Thauer R. Vectorial electron transport in Desulfovibrio vulgaris (Marburg) growing on hydrogen plus sulfate as sole energy source. Arch Microbiol. 1980;125(1-2):167–174. [Google Scholar]
- 38.Bell GR, LeGall L, Peck HD. Evidence for the periplasmic location of hydrogenase in Desulfovibrio gigas. J Bacteriol. 1974;120(2):994–997. doi: 10.1128/jb.120.2.994-997.1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ramos AR, Keller KL, Wall JD, Pereira IA. The membrane QmoABC complex interacts directly with the dissimilatory adenosine 5-phosphosulfate reductase in sulfate reducing bacteria. Front Microbiol. 2012;3:137. doi: 10.3389/fmicb.2012.00137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Krumholz LR, et al. Membrane protein complex of APS reductase and Qmo is present in Desulfovibrio vulgaris and Desulfovibrio alaskensis. Microbiology. 2013;159(Pt 10):2162–2168. doi: 10.1099/mic.0.063818-0. [DOI] [PubMed] [Google Scholar]
- 41.Pereira I, et al. A comparative genomic analysis of energy metabolism in sulfate reducing bacteria and archaea. Front Microbiol. 2011 doi: 10.3389/fmicb.2011.00069. 2:69/1-69/22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kobayashi K, Seki Y, Ishimoto M. Biochemical studies on sulfate-reducing bacteria. 8. Sulfite reductase from Desulfovibrio vulgaris—mechanism of trithionate, thiosulfate, and sulfide formation and enzymatic properties. J Biochem. 1974;75(3):519–529. doi: 10.1093/oxfordjournals.jbchem.a130420. [DOI] [PubMed] [Google Scholar]
- 43.Nethe-Jaenchen R, Thauer R. Growth yields and saturation constant of Desulfovibrio vulgaris in chemostat culture. Arch Microbiol. 1984;137:236–240. [Google Scholar]
- 44.Pereira PM, et al. Energy metabolism in Desulfovibrio vulgaris Hildenborough: Insights from transcriptome analysis. Antonie van Leeuwenhoek. 2008;93(4):347–362. doi: 10.1007/s10482-007-9212-0. [DOI] [PubMed] [Google Scholar]
- 45.Parey K, Warkentin E, Kroneck PM, Ermler U. Reaction cycle of the dissimilatory sulfite reductase from Archaeoglobus fulgidus. Biochemistry. 2010;49(41):8912–8921. doi: 10.1021/bi100781f. [DOI] [PubMed] [Google Scholar]
- 46.Oliveira TF, et al. The crystal structure of Desulfovibrio vulgaris dissimilatory sulfite reductase bound to DsrC provides novel insights into the mechanism of sulfate respiration. J Biol Chem. 2008;283(49):34141–34149. doi: 10.1074/jbc.M805643200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Venceslau SS, et al. Redox states of Desulfovibrio vulgaris DsrC, a key protein in dissimilatory sulfite reduction. Biochem Biophys Res Commun. 2013;441(4):732–736. doi: 10.1016/j.bbrc.2013.10.116. [DOI] [PubMed] [Google Scholar]
- 48.Thauer R, Kunow J. In: Sulfate-Reducing Archaea. Barton L, editor. Springer; New York: 1995. pp. 33–48. [Google Scholar]
- 49.Mathai JC, et al. No facilitator required for membrane transport of hydrogen sulfide. Proc Natl Acad Sci USA. 2009;106(39):16633–16638. doi: 10.1073/pnas.0902952106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Czyzewski BK, Wang DN. Identification and characterization of a bacterial hydrosulphide ion channel. Nature. 2012;483(7390):494–497. doi: 10.1038/nature10881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Noor E, et al. An integrated open framework for thermodynamics of reactions that combines accuracy and coverage. Bioinformatics. 2012;28(15):2037–2044. doi: 10.1093/bioinformatics/bts317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Schaechter M, Maaloe O, Kjeldgaard NO. Dependency on medium and temperature of cell size and chemical composition during balanced grown of Salmonella typhimurium. J Gen Microbiol. 1958;19(3):592–606. doi: 10.1099/00221287-19-3-592. [DOI] [PubMed] [Google Scholar]
- 53.Pedersen S, Bloch PL, Reeh S, Neidhardt FC. Patterns of protein synthesis in E. coli: A catalog of the amount of 140 individual proteins at different growth rates. Cell. 1978;14(1):179–190. doi: 10.1016/0092-8674(78)90312-4. [DOI] [PubMed] [Google Scholar]
- 54.Koch AL. Why can’t a cell grow infinitely fast? Can J Microbiol. 1988;34(4):421–426. doi: 10.1139/m88-074. [DOI] [PubMed] [Google Scholar]
- 55.Molenaar D, van Berlo R, de Ridder D, Teusink B. Shifts in growth strategies reflect tradeoffs in cellular economics. Mol Syst Biol. 2009;5:323. doi: 10.1038/msb.2009.82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zhang W, et al. Global transcriptomic analysis of Desulfovibrio vulgaris on different electron donors. Antonie van Leeuwenhoek. 2006;89(2):221–237. doi: 10.1007/s10482-005-9024-z. [DOI] [PubMed] [Google Scholar]
- 57.Flamholz A, Noor E, Bar-Even A, Liebermeister W, Milo R. Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc Natl Acad Sci USA. 2013;110(24):10039–10044. doi: 10.1073/pnas.1215283110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Oren A. Halophilic Microorganisms and their Environments. Kluwer, Dordecht; The Netherlands: 2002. [Google Scholar]
- 59.Tarpgaard I, Roy H, Jorgensen B. Concurrent low- and high-affinity sulfate reduction kinetics in marine sediment. Geochim Cosmochim Acta. 2011;75:2997–3010. [Google Scholar]
- 60.Cooney MJ, Roschi E, Marison IW, Comninellis C, von Stockar U. Physiologic studies with the sulfate-reducing bacterium Desulfovibrio desulfuricans: Evaluation for use in a biofuel cell. Enzyme Microb Technol. 1996;18(5):358–365. doi: 10.1016/0141-0229(95)00132-8. [DOI] [PubMed] [Google Scholar]
- 61.Kessler D. Enzymatic activation of sulfur for incorporation into biomolecules in prokaryotes. FEMS Microbiol Rev. 2006;30(6):825–840. doi: 10.1111/j.1574-6976.2006.00036.x. [DOI] [PubMed] [Google Scholar]
- 62.Eckert T, Brunner B, Edwards E, Wortmann U. Microbially mediated re-oxidation of sulfide during dissimilatory sulfate reduction by Desulfobacter latus. Geochim Cosmochim Acta. 2011;75:3469–3485. [Google Scholar]
- 63.Wagner GC, Kassner RJ, Kamen MD. Redox potentials of certain vitamins K: Implications for a role in sulfite reduction by obligately anaerobic bacteria. Proc Natl Acad Sci USA. 1974;71(2):253–256. doi: 10.1073/pnas.71.2.253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Rodriguez J, Hiras J, Hanson TE. Sulfite oxidation in Chlorobaculum tepidum. Front Microbiol. 2011;2:112/1–112/7. doi: 10.3389/fmicb.2011.00112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kang L, LeGall J, Kowal AT, Johnson MK. Spectroscopic properties of siroheme extracted from sulfite reductases. J Inorg Biochem. 1987;30(4):273–290. doi: 10.1016/0162-0134(87)80071-5. [DOI] [PubMed] [Google Scholar]
- 66.Soriano A, Cowan J. Sulfite reductase: Active-site residues are “noncatalytic”. Comparison of reaction energetics for enzyme-catalyzed and siroheme-catalyzed reduction of inorganic substrates. J Am Chem Soc. 1995;117:4724–4725. [Google Scholar]
- 67.Yagi T, Ogata M. Catalytic properties of adenylylsulfate reductase from Desulfovibrio vulgaris Miyazaki. Biochimie. 1996;78(10):838–846. doi: 10.1016/s0300-9084(97)84336-2. [DOI] [PubMed] [Google Scholar]
- 68.Bar-Even A, et al. The moderately efficient enzyme: Evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry. 2011;50(21):4402–4410. doi: 10.1021/bi2002289. [DOI] [PubMed] [Google Scholar]
- 69.Detmers J, Brüchert V, Habicht KS, Kuever J. Diversity of sulfur isotope fractionations by sulfate-reducing prokaryotes. Appl Environ Microbiol. 2001;67(2):888–894. doi: 10.1128/AEM.67.2.888-894.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Cameron EM. Sulfate and sulfate reduction in early Precambrian oceans. Nature. 1982;296(5853):145–148. [Google Scholar]
- 71.Gomes M, Hurtgen M. Sulfur isotope systematics of a euxinic, low-sulfate lake: Evaluating the importance of the reservoir effect in modern and ancient oceans. Geology. 2013;41:663–666. [Google Scholar]
- 72.Church T, Wolgemuth K. Marine barite saturation. Earth Planet Sci Lett. 1972;15(1):35–44. [Google Scholar]
- 73.Canfield D. In: Stable Isotope Geochemistry. Valley JW, Cole DR, editors. Vol 43. Chantilly, VA: Mineral Soc Am; 2001. pp. 607–636. [Google Scholar]
- 74.Chambers L, Trudinger P, Smith J, Burns M. Possible boundary condition in bacterial sulfur isotope fractionation. Geochim Cosmochim Acta. 1976;40:1191–1194. [Google Scholar]
- 75.Vo J, Inwood W, Hayes JM, Kustu S. Mechanism for nitrogen isotope fractionation during ammonium assimilation by Escherichia coli K12. Proc Natl Acad Sci USA. 2013;110(21):8696–8701. doi: 10.1073/pnas.1216683110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Stern M, Vogel P. Relative tritium-deuterium isotope effects in absence of large tunneling factors. J Am Chem Soc. 1971;93:4664–4675. [Google Scholar]
- 77.Kohen A, Jensen JH. Boundary conditions for the Swain-Schaad relationship as a criterion for hydrogen tunneling. J Am Chem Soc. 2002;124(15):3858–3864. doi: 10.1021/ja016909e. [DOI] [PubMed] [Google Scholar]
- 78.Hirschi J, Singleton DA. The normal range for secondary Swain-Schaad exponents without tunneling or kinetic complexity. J Am Chem Soc. 2005;127(10):3294–3295. doi: 10.1021/ja0430752. [DOI] [PubMed] [Google Scholar]
- 79.Hoehler TM, Jørgensen BB. Microbial life under extreme energy limitation. Nat Rev Microbiol. 2013;11(2):83–94. doi: 10.1038/nrmicro2939. [DOI] [PubMed] [Google Scholar]
- 80.Bontognali TRR, et al. Sulfur isotopes of organic matter preserved in 3.45-billion-year-old stromatolites reveal microbial metabolism. Proc Natl Acad Sci USA. 2012;109(38):15146–15151. doi: 10.1073/pnas.1207491109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Fischer WW, et al. SQUID-SIMS is a useful approach to uncover primary signals in the Archean sulfur cycle. Proc Natl Acad Sci USA. 2014;111(15):5468–5473. doi: 10.1073/pnas.1322577111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Jamieson J, Wing B, Farquhar J, Hannington M. Neoarchaean seawater sulphate concentrations from sulphur isotopes in massive sulphide ore. Nat Geosci. 2013;6:61–64. [Google Scholar]
- 83.Eiler J. The isotopic anatomies of molecules and mineral. Annu Rev Earth Planet Sci. 2013;41:411–441. [Google Scholar]
- 84.Galimov EM. 1975. Carbon Isotopes in Oil-Gas Geology (National Aeronautics and Space Administration, Washington DC), Vol TTF–682.
- 85.Monson KD, Hayes JM. Carbon isotopic fractionation in the biosynthesis of bacterial fatty acids. Ozonolysis of unsaturated fatty acids as a means of determining the intramolecular distribution of carbon isotopes. Geochim Cosmochim Acta. 1982;46:139–149. [Google Scholar]
- 86.Surkov AV, Böttcher ME, Kuever J. Sulphur isotope fractionation during the reduction of elemental sulphur and thiosulphate by Dethiosulfovibrio spp. Isotopes Environ Health Stud. 2012;48(1):65–75. doi: 10.1080/10256016.2011.626525. [DOI] [PubMed] [Google Scholar]
- 87.Zyakun A. 1996. Potential of 13C/12C variations in bacterial methane in assessing origin of environmental methane. M 66: Hydrocarbon Migration And Its Near-Surface Expression, eds Schumacher D, Abrams M (American Association of Petroleum Geologists, Tulsa, OK), Vol 66, pp 341–352.
- 88.Kritee K, et al. Reduced isotope fractionation by denitrification under conditions relevant to the ocean. Geochim Cosmochim Acta. 2012;92:243–259. [Google Scholar]
- 89.Bryan BA, Shearer G, Skeeters JL, Kohl DH. Variable expression of the nitrogen isotope effect associated with denitrification of nitrite. J Biol Chem. 1983;258(14):8613–8617. [PubMed] [Google Scholar]
- 90.Kohl DH, Shearer G. In: Isotope Effects in Metabolic Studies. Frigerio A, editor. Plenum Press; New York: 1978. pp. 623–640. [Google Scholar]
- 91.Shearer G, Schneider JD, Kohl DH. Separating the efflux and influx components of net nitrate uptake by Synechococcus R2 under steady-state conditions. J Gen Microbiol. 1991;137:1179–1184. [Google Scholar]
- 92.Laws E, Popp B, Bidigare R, Kennicutt M, Macko S. Dependence of phytoplankton carbon isotopic composition on growth rate and [CO2](aq) - theoretical considerations and experimental results. Geochim Cosmochim Acta. 1995;59:1131–1138. [Google Scholar]
- 93.Flamholz A, Noor E, Bar-Even A, Milo R. eQuilibrator—the biochemical thermodynamics calculator. Nucleic Acids Res. 2012;40(Database issue):D770–D775. doi: 10.1093/nar/gkr874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Schomburg I, et al. BRENDA in 2013: Integrated reactions, kinetic data, enzyme function data, improved disease classification: New options and contents in BRENDA. Nucleic Acids Res. 2013;41(Database issue):D764–D772. doi: 10.1093/nar/gks1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Otake T, Lasaga AC, Ohmoto H. Ab initio calculations for equilibrium fractionations in multiple sulfur isotope systems. Chem Geol. 2008;249:357–376. [Google Scholar]
- 96.Swain CG, Stivers EC, Reuwer JF, Jr, Schaad LJ. Use of hydrogen isotope effects to identify the attacking nucleophile in the enolization of ketones catalyzed by acetic acid1-3. J Am Chem Soc. 1958;80:5885–5893. [Google Scholar]
- 97.Neretin LN, et al. Quantification of dissimilatory (bi)sulphite reductase gene expression in Desulfobacterium autotrophicum using real-time RT-PCR. Environ Microbiol. 2003;5(8):660–671. doi: 10.1046/j.1462-2920.2003.00452.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.