Using the Bollen-Stine Bootstrapping Method for Evaluating Approximate Fit Indices

Abstract

Accepting that a model will not exactly fit any empirical data, global approximate fit indices quantify the degree of misfit. Recent research (Chen et al., 2008) has shown that using fixed conventional cut-points for approximate fit indices can lead to decision errors. Instead of using fixed cut-points for evaluating approximate fit indices, this study focuses on the meaning of approximate fit and introduces a new method to evaluate approximate fit indices. Millsap (2012) introduced a simulation-based method to evaluate approximate fit indices. A limitation of Millsap’s work was that a rather strong assumption of multivariate normality was implied in generating simulation data. In this study, the Bollen-Stine bootstrapping procedure (Bollen & Stine, 1993) is proposed to supplement the former study. When data are non-normal, the conclusions derived from Millsap’s (2012) simulation method and the Bollen-Stine method can differ. Examples are given to illustrate the use of the Bollen-Stine bootstrapping procedure for evaluating RMSEA. Comparisons are made with the simulation method. The results are discussed, and suggestions are given for the use of proposed method.

Among dozens of fit indices introduced in structural equation modeling, the chi-square test is important because it can be used to test exact fit. The chi-square test in SEM computes the “exact” discrepancy between the reproduced model-implied covariance matrix and the sample covariance matrix. However the chi-square test statistic may lead to rejection of the model in large samples even when the actual fit is regarded as good (Bentler & Bonett, 1980). In practice, researchers usually report the chi-square statistic and its significance, but seldom rely on it alone.

In contrast to the exact fit test, global indices of approximate fit accept that a model does not fit perfectly and then quantify the degree of misfit. Strictly speaking, approximate fit indices do not support binary decisions of whether the model fits the data. Rather, approximate fit indices show the “relative” degree of model misfit. In practice however, many researchers rely on cut-points to make binary decisions that models fit well or not. The cut-points used are usually recommended values that were obtained by previous simulation studies or experience (e.g., Browne & Cudeck, 1993; Hu & Bentler, 1999; Savalei, 2012; Steiger, 1989). For example, the well-known cut-points for RMSEA are < .05 for a close fit, .05 to .08 for fair fit, .08 to .10 for poor fit, and >.10 for unacceptable fit (Browne & Cudeck, 1993). Using fit indices with fixed cut-points may lead to poor decisions about model fit. Chen, Curran, Bollen, Kirby, and Paxton (2008) challenged the RMSEA cut-point of .05 with empirical evidence from simulation studies. Regardless of using point estimates or using 95% confidence intervals together with the point estimates, the .05 cut-point produced unstable (high or low) rejection rates depending on model misspecification and sample size. Chen et al. (2008) argued that cut-points depend on model specifications, degrees of freedom, and sample size. Other researchers have noted similar problems in using a fixed cut-point for approximate fit indices (e.g., Barrett, 2007; Beauducel & Wittmann, 2005; Fan & Sivo, 2005; Marsh, Hau, & Wen, 2004; Mulaik, 2007; Nevitt & Hancock, 2000; Yuan, 2005). The main argument of these papers was that using particular cut-points is not plausible in all cases. The choice of cut-points depends on model complexity, number of measured variables, the specified model, distributional conditions, and sample size.

Given the conclusions of the recent work on approximate fit indices and cut-points, one can question the usefulness of approximate fit indices in SEM. Barrett (2007) argued that researchers should not generally make model decisions based on approximate fit indices and instead should use only the chi-square test as a basis for judging fit. However, other researchers (Mulaik, 2007; Millsap, 2007) argued that Barrett’s recommendation was too strict. Mulaik (2007) argued that approximate fit can be useful to facilitate further research by using a “heuristic rationale”. A heuristic rationale lets us retain a model that is not perfect but is close to perfect. Millsap (2007) discussed the meaning of retaining a model with approximate overall fit in SEM. As the word “approximate” suggests, it means that we may retain a model, knowing the model has some flaws. In retaining the model, we are effectively arguing that these flaws are small enough to be ignored. For example, suppose that we have a model that has a RMSEA value of .03. This is a value that would indicate good fit to the data using conventional cut-points (i.e., < .05). However, even though we know that a model has a RMSEA of .03, the real nature of the misspecification in the model is unclear. What types of misspecifications are consistent with an RMSEA of .03? Typical practice is to overlook this question, and simply argue, based on the size of the RMSEA, that we should proceed with the misspecified model. We now turn to a procedure that is designed to investigate the possible misspecifications more directly and to evaluate the RMSEA value in light of what is found.

A simulation paradigm in evaluating approximate fit

Suppose that one has a model of interest M0 and has rejected that model using the chi-square test of exact fit in real data. Let F0 be the approximate fit index value found in the real data. The question at hand is then whether F0 is consistent with the idea that M0 offers a good approximation to the unknown model that generated the real data. To address this question, the simulation method poses an alternative model M1 that is only trivially different from M0. In other words, if M1 were the model that generated the real data, we would be happy to say that M0 is a good approximation to M1. For example, suppose that M0 is a conventional one-factor model with six indicators. A possible alternative M1 might be a one-factor model with loadings similar to M0, but with small nonzero covariances among some of the unique factors. If M1 was in fact the model that generated the real data, we might still be satisfied with M0 as an approximation.

With M1 in hand and with all parameters being assigned values in M1, Millsap (2007, 2012) proposed that simulated data be generated repeatedly from M1 in samples whose size is the same as the real sample data. In each of the simulated datasets, M0 is fit to the data and the fit index value F1 is recorded. A distribution of fit index values is then created. In the final step, the fit index value F0 from the real data is evaluated with respect to the distribution of F1 from the simulated data. For example, suppose that the fit index is the RMSEA. If F0 fall in the extreme (e.g., within the top 5%) right tail of the distribution of F1 in the simulated data, it suggests that the fit of M0 in the real data is much worse than expected if M1 had generated the real data. Hence we would reject M0 in this case. In rejecting M0, we conclude that the real data results are inconsistent with the idea that M1 could have generated the real data. In other words, the “story” that M0 is a good approximation in the real data, taking M1 as the model generating the real data, is not plausible. On the other hand, if F0 does not fall in the extreme (e.g., within the top 5%) right tail of the distribution of F1 in the simulated data, we may conclude that the fit of M0 in the real data is adequate and accept the M0. Most importantly, the decision to accept or to reject M0 does not use any conventional cut-points for F0. The decision is based on the location of F0 in relation to a distribution of F1 values generated via simulation.

To be more specific, the steps to be followed can be described as a five-step process.

1. First, fully specify the M1 model as a good approximation to the M0 model. In specifying the M1 model, we should specify the structure of the model and all parameter values. For instance, in the one factor model with six measures illustrated above, we should assign the unique factor covariance values while specifying the M1 model, along with values of all factor loadings and other model parameters. In choosing parameter values in M1, one can use the estimates that were obtained from fitting M0 to the real data for the parameters that were common (e.g., the factor loadings, factor variance, and unique factor variances) in the M0 and M1 models. Then, trivial values can be assigned for the new parameters in the M1 model (e.g., the unique factor covariances). The determination of what values constitute “trivial” values will depend on the context, model, and parameters, but most researchers will have some sense of what should be considered trivial for this purpose (because that is what is being argued in using the approximate fit notion). It may be useful to apply traditional metrics for “small effect sizes” (Cohen, 1988) and then further reduce the value as deemed appropriate.

2. Generate data (e.g., 1,000 datasets) from the M1 model. Multivariate normality is used as the distributional assumption, assuming continuous measured and latent variables. Other multivariate distributions could be considered if there is an empirical basis for doing so.

3. Fit the M0 model in each of the generated data sets in step 2, getting the value of the approximate fit index F1 in each set of data.

4. Gather the approximate fit index values F1 of interest (e.g., RMSEA) in a frequency distribution across the generated datasets. We will call this distribution the “F1 fit index distribution” since it is a distribution of a fit index generated by fitting the M0 model to the data sets that were based on the model M1.

5. The last step is to evaluate the sample fit index value F0 from the real data. Assume for now that the fit index being used is the RMSEA (i.e., large values indicate poor fit). Using the distribution of F1 values from step 4, calculate P1 = P (F1 > F0). P1 is the proportion of the F1 values that are larger than the F0 value. Given a particular P1 value (e.g., P1 < .10), we could make decisions about the M0 model. By locating the relative position of the sample F0 estimate in the F1 fit index distribution, we can get an idea of whether the fit of M0 in data generated from M1 is consistent with the fit of M0 in real data. For example, even if the sample RMSEA estimate F0 is small (e.g., < .05), the value of P1 may be very small as well, indicating that F0 is too large to be considered indicative of a good approximation in the sense of M1. In this case, the argument that M0 provides a good approximate fit in the real data is weakened. The simulation showed that if M1 was the model underlying the real data, fit to the empirical data should have been better. On the other hand, even if the sample RMSEA estimate is large (e.g., > .08), the value of P1 may also be relatively large (e.g., P1= .35), indicating that the fit in the real data is in fact consistent with a good approximation in the sense of M1. In this case, we can argue that if M1 was the model underlying the real data, the F0 value found in the real data is quite plausible, and so the idea that M0 is a good approximation in the real data is supported.

In any real application of this procedure, multiple choices for alternative models M1, M2, M3, … may be created, specified, and used to evaluate the original M0 and F0. The alternative models represent different ways of conceptualizing the possible misspecification in M0. In all cases, the alternative model is specified so that M0 is a “good approximation” to that alternative model. Multiple possible alternative models can be considered because there are multiple ways in which M0 might be mis-specified, while still being an acceptable approximation. We will illustrate how these alternatives might be developed and evaluated in some real examples below and in the discussion at the end of this article.

The above five-step procedure was described in Millsap (2012) and will be denoted the “simulation method” in what follows. The simulation method has some limitations. The data generated under M1 are ordinarily generated under multivariate normality assumptions. Of course, the empirical data may have been derived from a population in which data are not multivariate normal. If we know the population distribution, we could use it to generate simulated data. More commonly however, the appropriate population distribution is unknown. A logical alternative is to use the real sample data and employ resampling. We turn now to this alternative: the Bollen-Stine bootstrapping procedure.

Bollen-Stine bootstrapping

In SEM, we formulate a covariance structure model. The Bollen-Stine (B-S) method (Bollen & Stine, 1993) provides a way of imposing the model on the sample data so that bootstrapping is done under that model. This fact is important when bootstrapping a fit statistic from the sample observations (e.g., chi-square test statistic, T). By imposing the covariance structure model on the sample data, we can study the bootstrapping performance of the fit statistic under the “null hypothesis” that the model fits. Therefore, we should first obtain modified data imposing the null hypothesis covariance structure and then perform bootstrapping. The B-S bootstrapping method can be applied to the simulation method, replacing the simulations with bootstrapping from the real sample data after transformation as suggested in Bollen and Stine (1993). We need to impose the covariance and mean structure of M1 before actually bootstrapping the approximate fit indices.

The modified data can be obtained as follows. Let us denote N as the sample size, p as the number of variables and X^* (Nxp matrix) as the modified data. Then,

$$X^{\ast }=1\mu ’+(X-1\stackrel{‒}{X}’)A^{-1}{T}_1$$ (1)

where, 1 is a unit vector (Nx1), μ₁ is the mean vector implied by M1, X (Nxp matrix) is the sample data, X̄ is the sample mean vector (px1), A (pxp) is a matrix in the triangular factoring of the sample covariance matrix (S = A′A, where S is the sample covariance matrix), and T₁ (pxp) is a matrix in the triangular factoring of the covariance matrix implied by the M1 (Σ₁ = T′₁T₁, where Σ₁ is the covariance matrix implied by M1). Note that Equation 1 expands Equation 17 in Bollen and Stine (1993) to include both mean and covariance structures (Yung & Bentler, 1996).

Applying the B-S method to the simulation method, the researchers impose the covariance and mean structures implied by M1. We factor the covariance matrix implied by M1 and achieve T₁. The researchers also assign parameter values that lead to the mean structure μ₁, if means are modeled. Other values (e.g., X, X̄, and A) are from real data. We can then compute the modified data by Equation (1). After modifying the data implied by the hypothesized model M1, we can perform bootstrapping by resampling (with replacement) the rows of the modified data. In each bootstrap sample, M0 is fit to the data and the F1 value is recorded. We do not need to make any assumptions about the distribution using the bootstrapping method apart from representativeness. Finally, once the bootstrap samples are obtained with corresponding F1 values, we follow the procedures that Millsap (2012) has suggested to evaluate an approximate fit. The simulation method and B-S method will result in nearly identical results when the real data satisfy the multivariate normality assumption. However, when the real data are non-normal, the simulation method can be biased since the generated data are based on the multivariate normality assumption.

Effect of estimator choice and sample size for non-normal data

In SEM, it is known that the chi-square fit statistic is often positively biased using the maximum likelihood (ML) estimator when the data are non-normal (Curran, West & Finch, 1996; Wang, Fan & Wilson, 1996). Therefore, robust estimators that produce corrected chi-square test statistics are recommended with non-normal data. One example of a robust estimator is the maximum likelihood with robust standard errors (MLR) estimator used in Mplus (Muthén & Muthén, 1998-2012). The MLR estimator produces a scaled chi-square test statistic (T₂^*) introduced in Yuan and Bentler (2000). If non-normality is suspected in the real data, researchers may use the MLR estimator in the initial fit of M0 to the real data. The choice of an estimator should not greatly affect the results given by the B-S method (e.g., the P1 value) as long as the same estimator is used to produce the sample fit index value F0 from fitting the M0 model into the real data and the fit index values F1 from fitting the M0 model into the generated samples. Therefore, if non-normal data are suspected, we would use the MLR estimator for both the real data analysis and the analyses of the bootstrap samples to obtain corrected chi-square values.

In SEM, sample size is another consideration when fitting a model to non-normal data. The effect of multivariate non-normality tends to stand out especially when the sample size is small (Lei & Lomax, 2005; Ory & Mokhtarian, 2010). If data are non-normal, the difference between the simulation and B-S method can be substantial when the sample size is small.

In this study, we will present non-normal data examples (examples 3 & 4) using the MLR estimator in a relatively large and relatively small sample size data to investigate if the results vary when comparing the simulation method with the B-S method.

In the next section, four examples of the above procedures are shown using real data. The first example uses the Holzinger and Swineford (1939) dataset. The detailed steps of the B-S method are presented in this first example. The second example utilizes WAIS-R data and will be a replication of what was done in Millsap (2012) but using the B-S method. The third and fourth examples use the COERCE data, illustrating the case when the data are skewed and/or the sample is small. For Examples 2 to 4, the results using the simulation method in Millsap (2012) and the B-S method will be compared.

Example 1: The Holzinger & Swineford (1939) Data

Data

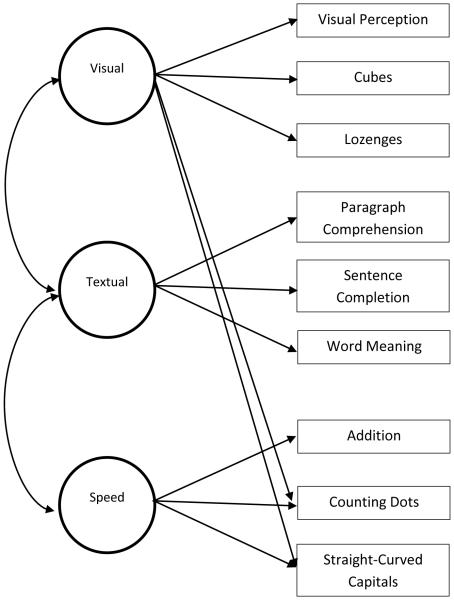
The Holzinger and Swineford (1939) dataset that is included in the R package “lavaan” is used in this example. Nine of the original 26 tests of mental ability were used, and the dataset had 301 observations with no missing data. The nine tests were visual perception, cubes, lozenges, paragraph comprehension, sentence completion, word meaning, addition, counting dots, and straight-curve capitals. These nine tests were originally proposed as a three-factor structure (visualization, verbal, & speed) by Jöreskog (1969). Note that Jöreskog (1969)e used data from only the Grant-White school sample (n = 145). In this example, we used data from both schools (the Grant-White and Pasteur). The M0 model of interest is the model specified in Table 1 (e) in Jöreskog (1969). Figure 1 illustrates the M0 model from Jöreskog (1969). Fitting the M0 model to the complete dataset yielded the following fit indices, χ² (23) = 47.23, p = .002, and RMSEA = .06. The RMSEA fit statistic is of interest in this study. Based on the conventional cut-points for the RMSEA, the M0 model adequately fit the data (Browne & Cudeck, 1993). Our research question is to check whether the conclusion made with the conventional cut-point is support if M1 were the underlying model that generated the real data. If the F0 value (the RMSEA value when M0 is fitted to the real data) is indeed in the range of possible values of F1 (the RMSEA value when M0 is fitted to the generated datasets based on M1 model), we would retain the M0 model. However, if the F0 value is higher than the typical range of F1 values, we would reject the M0 model. We will use a criterion value of P1 = .10 to decide to retain or reject the M0 model. In other words, if P1 < .10, then reject the M0 model. Otherwise, we retain the M0 model.

Table 1.

M1 model parameter values assigned for Example 1 (Holzinger & Swineford data)

	F1	F2	F3	Unique factor variances	Intercepts/Means
X1	1.000			0.589	4.936
X2	0.605			1.100	6.088
X3	0.764			0.826	2.250
X4		1.000		0.490	3.061
X5		1.117		0.543	4.341
X6		0.927		0.375	2.186
X7			1.000	0.441	4.186
X8	0.287		0.873	0.357	5.527
X9	0.567		0.589	0.584	5.374
F1	0.770			0.770	0.000
F2	0.372	0.973		0.973	0.000
F3	0.050	0.089	0.599	0.599	0.000

Note. X1 = visual perception, X2 = cubes, X3 = Lozenges, X4 = paragraph comprehension, X5 = sentence completion, X6 = word meaning, X7 = addition, X8 = counting dots, x9 = straight-curved capitals, F1 = visualization factor, F2 = verbal factor & F3 = speed factor. All other parameter values unspecified in the table were fixed to zero. The part in bold indicates the additional parameter in the M1 model over the M0 model.

Figure 1.

The M0 model for Example 1 (Holzinger & Swineford data).

One alternative model, M1, can be specified as adding the correlation between the visual and speed factor. Note that this correlation was fixed to zero in the M0 model in Figure 1. In M1, we fixed the population covariance between the visual and speed factor at .05, which is a .07 value in correlation metric. This value would be considered trivial or small based on Cohen (1988). The other assigned parameter values for the M1 model are given in Table 1. Another alternative model, M2, can be specified by adding a correlation between the residuals of the cubes test and the straight-curved capitals test from the M0 model. The assigned population values for the M2 model were similar to the M1 model except, (1) the correlation between the visual and speed factor was fixed at 0, and (2) the covariance between the unique factors for the cubes and straight-curved capitals tests was fixed at .08, which is a .10 value in correlation metric. Models M1 and M2 were each used in separate bootstrapping runs to evaluate M0.

General procedure using the Bollen-Stine method

Given M1 and M2 as described above, the next step was to transform the data to conform to each model. We began with M1, creating the modified data using Equation 1. We then resampled rows of the transformed data matrix with replacement, creating bootstrap samples of size n=301 to match the sample size of the real data. We generated 1000 such bootstrap samples. In each sample, M0 was fit to the data and an F1 value (the RMSEA value) was obtained. This process generated an F1 fit index distribution of 1000 values. Let F0 be the sample RMSEA value computed from fitting model M0 to the real data. The F0 for the empirical data was .059. Using the distribution of F1 values, we calculated P1 = P (F1 > F0). This entire process was then repeated using M2 as the alternative model of interest and transforming the original real data using M2 in Equation 1.

To the authors’ knowledge, a limited number of computer programs can perform all the steps described above. One program that implements the B-S method is the “simsem” package in R (Pornprasertmanit et al., 2013). In the present study, all programs were written in R (R Core Team, 2012) to conduct the procedures described here. Software R version 2.13.2 was used to perform the B-S bootstrapping procedures and package Lavaan version 0.5-11 (Rosseel, 2012) in R was used to fit the models and compute RMSEA estimates. The program used for this example (the M1 model case) is given in the Appendix.

Results

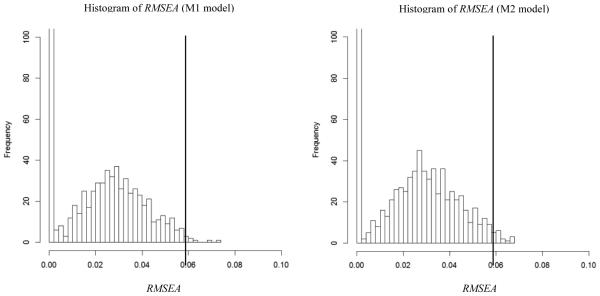
A frequency histogram of the F1 values is shown in Figure 2. The left side of the figure shows the case in which M1 was the alternative model and the right side of the figure shows the case in which M2 was the alternative model. The P1 value for the M1 case was 0.008 which was below the criterion value, P1 = .10. The P1 value for the M2 case was 0.014 which was also below the criterion value. The RMSEA value that corresponds to the P1 = .10 level was .042 for the M1 case and .045 for the M2 case. Both cases indicate that the lack of fit for M0 in the real data is larger than we would expect if either M1 or M2 had generated the real data. This is true even though the F0 value of .06 might ordinarily be taken to indicate acceptable fit to the data. Our analyses suggest that M0 does not offer good approximate fit to the data.

Figure 2.

Results for Example 1 (Holzinger & Swineford data). Left side figure depicts the case where the M1 model was used and right side figure depicts the case where the M2 model was used. Mean_M1 = .016, Max_M1 = .074, Count (RMSEA = 0)_M1 = 464, Mean_M2 = .019, Max_M2 = .068 and Count (RMSEA = 0)_M2 = 389. The vertical reference line shows the value of the RMSEA (.059) in the analysis of empirical data.

Example 2: WAIS-R Data

Data

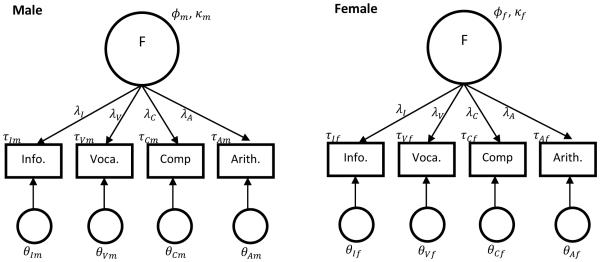
This example uses data reported in Millsap (2012). The WAIS-R standardization sample was analyzed with a multiple-group confirmatory factor analysis model. The groups compared were males (n=940) and females (n=940), with no missing data. The example uses 4 of the original 11 subtests in the WAIS-R: Information, Vocabulary, Comprehension, and Arithmetic. See Table 2 for descriptive statistics of the data. The model M0 of interest is shown in Figure 3. Model M0 implies invariant factor loadings between males and females. The M0 model produced a significant chi-square value (χ² and an RMSEA estimate of .043.

Table 2.

Descriptive statistics for Example 2 (WAIS-R data)

item	n	mean	sd	median	min	max	skew	kurtosis
F_info	940	8.98	2.80	9	1	18	0.20	0.30
F_voca	940	9.25	2.97	9	1	19	0.09	−0.09
F_comp	940	8.89	2.83	9	1	17	0.18	0.11
F_arit	940	9.33	3.06	9	1	19	0.11	−0.16
M_info	940	9.82	3.10	10	1	18	0.06	−0.27
M_voca	940	9.41	3.06	9	1	19	0.23	−0.23
M_comp	940	9.87	3.03	10	2	17	0.18	−0.35
M_arit	940	9.61	3.09	10	2	19	0.15	−0.21

Figure 3.

M0 model for Example 2 (WAIS-R data)

To evaluate whether the RMSEA estimate implies a good approximation, the fit-evaluation paradigm illustrated above was conducted. An alternative model M1 specifies the single-factor model structure as in M0, but three of the four factor loadings were different between groups. The female loadings were specified to be .10 smaller than each of the corresponding male loadings. The parameter values are shown in Table 3. Both the simulation method and the B-S method¹ were compared for illustration. A criterion value of P1 = .10 was used to decide to retain or reject the M0 model. Mplus was used for the simulation method, and R was used for the B-S method. The Mplus syntax can be found in Millsap (2012), and the R syntax is given in the Appendix.

Table 3.

M1 model parameters for Example 2 (WAIS-R data)

Parameter	Male Value	Female Value
τ I	9.82	8.98
τ V	9.41	9.25
τ C	9.61	9.33
τ A	9.50	9.20
λ I	.90	.80
λ V	1.00	1.00
λ C	.88	.78
λ A	.70	.60
κ	0	0
ϕ	8.4	7.8
θ I	2.0	1.8
θ V	1.0	1.2
θ C	4.0	4.0
θ A	3.0	3.0

Results

A frequency histogram of the F1 values is shown in Figure 4. The left side depicts the frequency histogram using the B-S method and the right side depicts the frequency histogram using the simulation method. In both cases, the RMSEA value of .043 from the real data lies near the center of the distribution in Figure 2 (P1 = .70 for the B-S method and P1 = .67 for the simulation method). This indicates that the lack of fit for M0 in the real data is found to be consistent with the misspecification of M0 under the assumption that M1 is the model that generated the real data. Therefore, we retain the M0 model. Note that no substantial differences were found between the results of using the B-S method or the simulation method. These results should have been expected because the WAIS-R example had a sufficiently large sample size (n=940 for each group) and the variables did not deviate strongly from multivariate normality.

Figure 4.

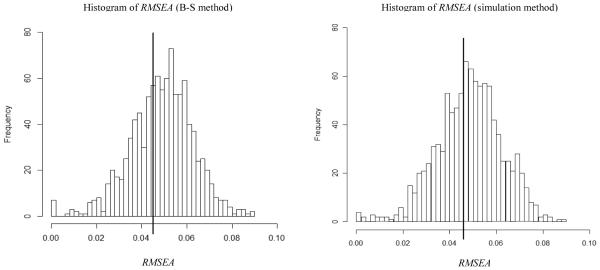
Results for Example 2 (WAIS-R data). Left side graph is the histogram of RMSEAs using the Bollen-Stine method and the right side graph is the histogram of RMSEAs using the simulation method. Mean_B-S = .049, Max_B-S = .089, Count (RMSEA = 0)_B-S = 7, Mean_simulation = .048, Max_simulation = .090 and Count (RMSEA = 0)_simulaiton = 4. The vertical reference line shows the value of the RMSEA (.043) in the analysis of empirical data.

Example 3: COERCE Full Sample Data

Data

Partial data from the Early Steps Multisite Study (Dishion et al., 2008; Shaw et al., 2009) were used for this example. In the Early Steps study, 731 families were recruited and about half (n = 367) of the families were randomly assigned to participate in the Family-Check-Up (FCU) program. Details of the data are well described in Dishion et al. (2008). In the present study, the coder impression data were used (Child and Family Center, 2003). Families were given small tasks (e.g., meal preparation with child), and the parent-child interactions were rated by coders. After, the coders were asked to give their impressions about the family on 51-item questionnaire, using a 1-9 rating scale. Among the 51 items, 8 items were related to “coercive” parenting. See Table 4 for the items.

Table 4.

Items for Example 3 (COERCE full sample) and Example 4 (COERCE random sub-sample)

Factor	Item (variable name)	Question
COERCE	i1	Does the parent seem ‘tired-out’, depressed, or inattentive to the child during the task?
	i2	Does the parent display anger, frustration, and/or annoyance during activities?
	i3	Does the parent threaten the child with any sort of punishment to gain compliance?
	i4	Does the parent criticize or blame the child for family problems or other family difficulties or stressors?
	i5	Does the parent use physical discipline during the observation session?
	i6	Does the parent seem distracted from parenting by a lifestyle of drug and alcohol use?
	i7	Does the parent actively ignore/reject the child?
	i8	Does the parent make statements or gestures that indicate that he or she feels the child is worthless?

Overall 7 observations had missing values for all 8 coerce items, and 2 observations had missing values for two different items. Because the observations with missing values (n = 9) were relatively small compared to the whole sample (n = 731), we deleted the 9 cases. Therefore, a total of 723 observations were analyzed in this study. Note that, in applications having larger proportions of missing cases, Enders (2002, 2005) and Savalei and Yuan (2009) showed how missing data can be handled within the Bollen-Stine approach.

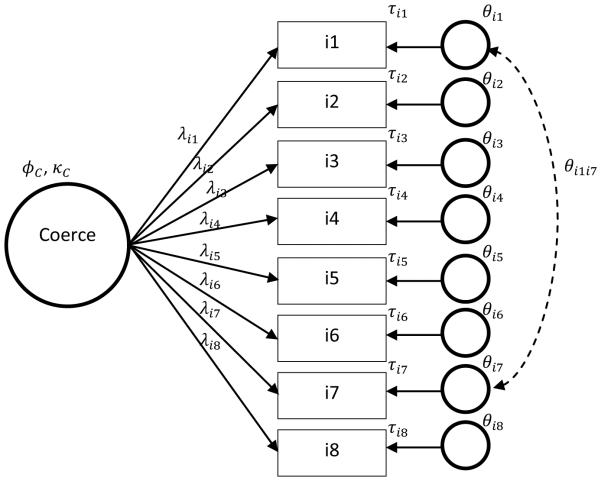
Table 5 summarizes the descriptive statistics of the data. Note that the scale was a 1-9 rating scale, but responses at the higher rating levels were relatively few in number. Thus, the items were all positively skewed, and distributions were peaked for all of the items. Because the COERCE data did not satisfy the multivariate normality assumption, it would be logical to use the MLR estimator. The M0 model was a one factor model with 8 indicators with uncorrelated unique factors (see Figure 5). The RMSEA value fitting the M0 model into the sample data was .101. The contents of item 1 and item 7 (see Table 4) are similar: both ask about “indifference” to the child. After accounting for coercive parenting, there could be some shared variability left in item 1 and item 7 that captures indifference to the child. One method to capture the shared variability is to allow a covariance between the unique factors of item 1 and item 7. Therefore, an alternative model, M1 can be a model similar to M0, but having a small covariance between the unique factors related to items 1 and 7. In this study, the unique factor correlation value between item 1 and 7 was assigned at 0.2 (covariance = 0.17). Table 6 shows the parameter values for M1. Note that the covariance value between item 1 and 7 is shown in Table 6.

Table 5.

Descriptive statistics for Example 3 (COERCE full sample) and Example 4 (COERCE random sub-sample)

	item	n	mean	sd	median	min	max	skew	kurtosis
Full sample (n = 723)	i1	723	2.30	1.37	2	1	9	1.35	2.39
	i2	723	2.33	1.34	2	1	8	1.16	1.35
	i3	723	2.30	1.39	2	1	9	1.20	1.39
	i4	723	1.35	0.66	1	1	6	2.34	7.56
	i5	723	1.64	1.15	1	1	7	1.69	1.88
	i6	723	1.38	0.75	1	1	6	2.40	7.05
	i7	723	1.70	0.94	1	1	8	1.58	4.04
	i8	723	1.44	0.74	1	1	6	1.94	4.55
Random sub- sample (n = 150)	i1	150	2.47	1.47	2	1	8	1.00	0.70
	i2	150	2.26	1.29	2	1	7	1.12	1.08
	i3	150	2.01	1.16	2	1	6	1.01	0.26
	i4	150	1.33	0.69	1	1	5	2.48	6.96
	i5	150	1.56	1.11	1	1	6	1.96	2.87
	i6	150	1.32	0.72	1	1	5	2.81	9.10
	i7	150	1.68	1.03	1	1	8	2.26	8.59
	i8	150	1.42	0.77	1	1	5	2.19	5.46

Figure 5.

M0 and M1 model for Example 3 (COERCE full sample) and Example 4 (COERCE random sub-sample). The dashed line indicates the additional association specified in the M1 model over the M0 model.

Table 6.

M1 model parameters for Example 3 (COERCE full sample) and Example 4 (COERCE random sub-sample).

	COERCE factor	Unique factor variances	i7	Intercepts/Means
i1	1.000	1.425	0.170	2.297
i2	1.358	0.992		2.332
i3	1.063	1.437		2.303
i4	0.739	0.192		1.350
i5	1.279	0.602		1.645
i6	0.693	0.348		1.376
i7	0.896	0.522		1.700
i8	0.822	0.252		1.444
COERCE factor	0.439

Note. The part in bold indicates the additional parameter in the M1 model over the M0 model. Other blank spaces are all fixed at zero.

Two methods were tested, the B-S method and the simulation method. For each method, 1,000 samples were generated from the M1 model, and 1,000 RMSEA values were computed fitting the M0 model into the generated samples. The MLR estimator was used to fit the M0 model to the real data and to data from the generated samples. Mplus was used for the simulation method, and R was used for the B-S method. Both Mplus and R syntax are given in the Appendix.

Results

Figure 6 left shows the histogram of RMSEA values produced by using the B-S method and Figure 6 right shows the histogram of RMSEA values produced by using the simulation method. The RMSEA value from real data (RMSEA = .101) was far out to the right of the histograms (P1 = 0 for both methods). Regardless of the method used (B-S or simulation), we would reject the M0 model, arguing that the sample RMSEA value was higher than any RMSEA value fitting the M0 model to the generated samples from M1. Although the conclusion was the same using both methods, some differences were found between the two methods in the mean RMSEA value (Mean_B-S = .027 and Mean_simulation = .039) and a significant difference in the frequency of RMSEA=0 (Count (RMSEA = 0)_B-S = 132, Count (RMSEA = 0)_simulaiton = 7). The similar conclusions for the simulation and B-S method was anticipated because of the relatively large sample size (n = 723), which suggested that the non-normality would not lead to large differences between the simulation and B-S methods.

Figure 6.

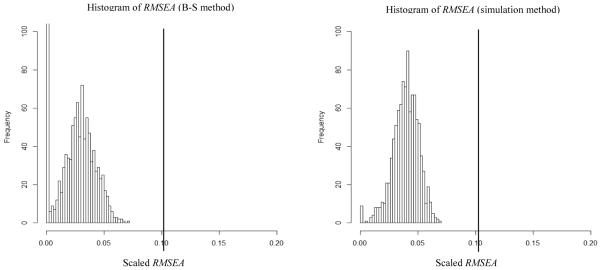
Results for Example 3 (COERCE full sample). Left side graph is the histogram of RMSEAs using the Bollen-Stine method and the right side graph is the histogram of RMSEAs using the simulation method. Mean_B-S = .027, Max_B-S = .070, Count (RMSEA = 0)_B-S = 132, Mean_simulation = .039, Max_simulation = .070 and Count (RMSEA = 0)_simulaiton = 7. The vertical reference line shows the value of the RMSEA (.101) in the analysis of empirical data.

Example 4: COERCE Random Sub-Sample

Data

In Example 3, some differences were observed between the B-S method and simulation method using non-normal data. To illustrate a situation where the difference between the B-S method and the simulation method may be more visible, a random sample with lower sample size (n = 150) was drawn from the COERCE data and analyzed. Table 5 summarizes the descriptive statistics of the random sample. Again, note that the scale was a 1-9 rating scale but none of the observations showed a value of 9 for all items. The items were all positively skewed, and distributions were peaked for most of the items (except item 1 & 3). The same M0 model as in Example 3 was fitted to the data. The sample RMSEA was .117 using the MLR estimator. The M1 model had the same configuration (correlation between the unique factors related with item 1 and 7) and parameter values as Example 3.

The other procedures were the same as above: the B-S and the simulation procedure were performed. Mplus was used for the analysis using the simulation method, and R was used for the analysis using the B-S method. Mplus and R syntax are omitted in this paper because the syntax for Example 4 resembles the syntax for Example 3.

Results

In Figure 7, the left side shows results using the B-S method and the right side shows results using the simulation method. Here, we focused on any differences found between the B-S and simulation method. Results showed that the B-S method and simulation method might lead to different conclusions about the sample RMSEA, depending on the criterion used to accept or reject the M0 model. The P1 value was larger using the B-S method than the simulation method, P1_B-S = .039 versus P1_simulation = .001, respectively. If we were to use a criterion level of .01 for the P1 value, the B-S method would lead us to retain the M0 model, but the simulation method would lead us to reject the M0 model.

Figure 7.

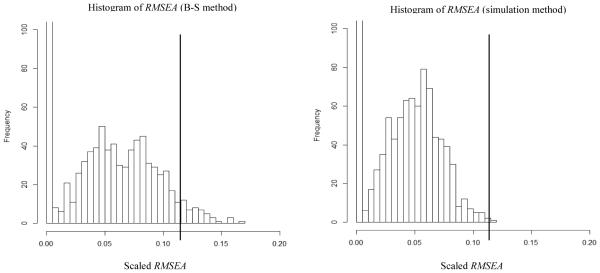
Results for Example 4 (COERCE random sub-sample). Left side graph is the histogram of RMSEAs using the Bollen-Stine method and the right side graph is the histogram of RMSEAs using the simulation method. Mean_B-S = .046, Max_B-S = .166, Count (RMSEA = 0)_B-S = 316, Mean_simulation = .040, Max_simulation = .119 and Count (RMSEA = 0)_simulaiton = 224. The vertical reference line shows the value of the RMSEA (.117) in the analysis of empirical data.

Noticeable differences can be seen between the two distributions in Figure 7. The mean RMSEA, maximum RMSEA, and the zero RMSEA count were all higher for the B-S method than the simulation method, Mean_B-S = .046 versus Mean_simulation = .040, Max_B-S = .166 versus Max_simulation = .119 and Count (RMSEA = 0)_B-S = 316 versus Count (RMSEA = 0)_simulaiton = 224. The main point here is that we should not neglect possible discrepancies in interpreting the sample RMSEA value between the B-S method and the simulation method. Below, we offer a logical way to choose which method (B-S or simulation) to use with non-normal data, and the results from this study are discussed following this perspective.

Alternate Indicators of Approximate Fit

One reviewer of this manuscript asked whether the B-S method would produce similar conclusions on model fit if other fit indices were used as the basis of comparison. To answer this intriguing question, three other widely used fit indices were considered: the Comparative Fit Index (CFI, Bentler, 1990), Tucker Lewis Index (TLI, Tucker & Lewis, 1973), and Standardized Root Mean Square Residual (SRMR, Jöreskog & Sörbom, 1981). The same B-S procedures, but using different fit indices, were applied to the four examples in this study. Higher values of RMSEA and SRMR indicate poor fit to the data. On the other hand, lower values of CFI and TLI show poor fit. To facilitate interpretation, we matched the direction of badness of fit by computing (1 – CFI) and (1 – TLI). If the real data fit value was located higher than the 90% rank of the simulated data fit values, we concluded that the M0 model had a poor fit. Otherwise, we concluded that the M0 model had adequate fit. Table 7 displays the percentile ranks of the real data fit values among the simulated data fit values. As Table 7 suggests, similar conclusions would be made using any of the four fit indices in the four examples included in our study. The only exception was the conclusion from the SRMR for the Holzinger and Swineford (1939) example given the M1 model. The percentile rank for the SRMR F0 value was 89.7% which was at the margin of poor and adequate fit, but might support the acceptance of the M0 model, whereas the M0 model was rejected using all other indicators of fit. Although the conclusion from SRMR might not agree with the results from other fit indices for one of our four examples, we would argue that even though the four fit indices look at divergent aspects of misfit of the model (e.g., SRMR does not penalize for model complexity whereas RMSEA does), using the B-S procedure illustrated in this study often produces convergent conclusions from different fit indices.

Table 7.

Percentile rank of real data fit among the simulated data fit

Example	RMSEA	1–CFI	1–TLI	SRMR
H&S_M1	99.3 (0.059) ^	99.1 (0.027) ^	99.1 (0.043) ^	89.7 (0.045) +^
H&S_M2	98.6 (0.059) ^	98.0 (0.027) ^	98.0 (0.043) ^	94.0 (0.045) ^
WAIS-R	29.6 (0.043) +	28.0 (0.002) +	28.0 (0.004) +	7.4 (0.02) +
COERCE_full	100 (0.101) ^	100 (0.186) ^	100 (0.261) ^	100 (0.063) ^
COERCE_sub	96.1 (0.117) ^	98.1 (0.207) ^	98.1 (0.289) ^	99.4 (0.075) ^

Values in parentheses indicate the real data fit values. Applying a rule of the percentile rank being over 90% meaning poor fit and otherwise meaning adequate fit, + indicates the fit was adequate, ^ indicates the fit was poor and having both + and ^ indicates the fit was marginal.

Discussion

Using conventional cut-points with approximate fit indices leaves the investigator with uncertainty about what misspecifications might be consistent with the level of approximate fit. Carefully looking into the meaning of “approximate fit” leads us to a new approach in evaluating approximate fit, rather than using conventional cut-points for evaluating fit. Accepting that any model of interest M0 will exhibit misfit in the population, we can think of a possible alternative model M1 that does not vary much from the model of interest and that would justify the idea that the model of interest provides a good approximation to real data. After generating samples from M1, we can fit M0 in each of the generated samples and draw a distribution of the fit index estimates. Then we can evaluate M0 by locating the sample fit index estimate within the distribution of fit index estimates in data generated from M1. Millsap’s (2012) simulation method was restricted to assuming multivariate normality in generating the samples. In this study, the multivariate normality assumption was relaxed and the Bollen-Stine (B-S) bootstrapping approach was applied to expand the application of the method. Four data examples were given to illustrate the B-S method and to compare the results with the simulation method.

First of all, the example with the Holzinger & Swineford (1939) data illustrated a situation in which a conclusion based on conventional cut-points of RMSEA can be disputed. Based on conventional cut-points, the sample RMSEA value of .06 indicated that the M0 model adequately fit the data. However, we do not have any idea of misspecifications that might be consistent with this RMSEA value, or how large such misspecifications might be while still leading to the RMSEA value of .06. Assuming that the M1 or M2 model were the underlying model that generated the real data, the P1 value was small enough to conclude that, in fact, the sample RMSEA value .06 was a rather high value in the F1 fit index distribution. Therefore, we have a basis for rejecting the M0 model as a good approximation.

The example with WAIS-R data illustrated the use of the B-S approach integrated with the simulation method when evaluating approximate fit (i.e., RMSEA). Results showed that the P1 value for fit in the empirical data was higher than the pre-assigned critical value (P1 = .10). Therefore, this evidence argues against rejection of M0 as a reasonable approximation for M1 as an alternative model. This result was consistent with Millsap (2012). The consistency of the results was anticipated because the WAIS-R data showed little evidence of non-normality and the sample size was large (n = 940 for each group).

The COERCE data were analyzed to investigate effects of non-normality of the data using the B-S or the simulation method. Example 3 analyzed the original data with 723 observations, and Example 4 analyzed a random sample (n = 150) drawn from the original data. The simulation method assumed multivariate normality in generating data, an assumption that may not be plausible. The B-S method preserves the characteristic of the data and thus may serve as a better method, especially when data are non-normal.

Decision errors may occur when using the simulation method instead of the B-S method with non-normal data with small sample size. In this example, the B-S method had higher P1 values than the simulation method. It was difficult to tell whether there was a difference in the two methods in the third example because the sample RMSEA value was relatively large in all cases (P1 = 0 in all cases). However in Example 4, the difference was more discernable. The P1 value using the B-S method (P1 = .039) was clearly higher than the P1 value using the simulation method (P1 = .001). It is unclear whether this ordering of P1 values would generally be found in non-normal examples. However, if a criterion value of P1 = .01 were used, we would draw a different conclusion based on the method used in the example, which illustrates the different conclusions than can be reached under the two methods.

Apart from the non-normality issue, several general objections to the simulation method can be raised. First, results from many possible alternative true models (e.g., M1, M2, M3…) might be possible, and results might differ substantially across these alternative models. For example, if M1 were a model far from M0, the sample fit estimate might be much smaller than the distribution of simulated fit index values, and we would always retain M0. On the other hand, M2 may be very close to M0; here, the sample fit estimate would be much larger than the distribution of simulated fit index values, and we would reject M0. As a result, alternate M1 models specified by the researcher can yield different results, and any researcher using this method must therefore report the models in detail (with the parameter values given) as well as the fit results in the real and simulated data. The presence of numerous possible alternative models is a reality for all approximate fit decisions, however, and is not unique to the method developed here (Millsap, 2012). Approximate fit indices measure lack of fit, and lack of fit can be evaluated to be small or large depending on different alternative models. The conventional way to evaluate fit hides this problem by avoiding the specification of the “true model” to which the M0 model is an approximation. In contrast, the proposed method clearly specifies the alternative model.

A key point here is that any model fit evaluation must, in a transparent way, explain what “approximate fit” means by building an alternative model that is approximated by the model of interest. The alternative model represents what is meant by an approximation because it is close to the model of interest. Now, multiple ways of defining approximation in this way can be conceived, and hence we have multiple possible outcomes of the fit process. If these outcomes are very different, we must either accept or abandon the original model. The best policy for researchers is to use a set of alternative models deemed viable or plausible and report results based on those. Other investigators are free to evaluate M0 against different choices as needed.

Under either the simulation approach or the B-S method, the proposed fit evaluation procedure resembles methods of power analysis that also involve specification of alternative models, such as those proposed by Satorra and Saris (1985). In those procedures, the power to detect a parameter value of a pre-specified size (or group of parameters) is evaluated conditional on choices for all other model parameters in an alternative model. The goals of a power analysis and of the proposed fit evaluation procedure are different however. In power analysis, the goal is to estimate the probability of rejecting a model that is mis-specified in relation to the target parameter or parameters, under various scenarios involving small, medium, or large values for the target parameter. The alternative model in this case is ordinarily not specified to be only trivially different from the original, mis-specified model. In the proposed fit evaluation procedures investigated in the current study, however, the goal is to evaluate the plausibility of the claim that the original model M0, while mis-specified, is a good approximation to the “true” but unknown model. To evaluate this claim, one or more alternative models that represent possible “true” models are specified, each of which is close to M0 in some explicit sense. These alternative models are not really of intrinsic interest, as their purpose is simply to help evaluate the claim of a “good approximation” for M0. Hence while power analysis and the proposed fit procedure are alike in focusing on alternative models, the purpose and roles for these alternative models are different.

The original simulation procedure proposed by Millsap (2007, 2012) represents an approach to using approximate fit indices that does not rely on a priori cut-points for these indices and instead puts the burden of proof on the investigator by requiring that alternative models be specified to support claims of “approximate fit.” Any investigator who wishes to claim that an imperfect model M0 (i.e., one that is rejected via the chi-square test) is nevertheless adequate as an approximation should be able to state precisely one or more models for which M0 could serve as an approximation. The specified alternative models are then used to generate data that allow one to evaluate the fit of M0 and the claim of approximate fit. An investigator who uses this method will be required to report not only the fit of M0 in the real data, but also all of the alternative models and the simulations results associated with each. Readers, journal editors, and reviewers can then judge the probity of the claims of approximate fit for M0 in a more thorough manner.

The unique contribution of the present paper is to extend the simulation procedure proposed by Millsap (2007, 2012) to use of the Bollen-Stine bootstrapping procedure in generating data under the alternative models. Instead of relying on pre-specified distributional forms for simulated data that may be unrealistic, the extension described here can be applied to a much wider variety of distributional forms. For example, if the real data analyses have already been performed using robust estimation as in the MLR procedure in Mplus (Muthén & Muthén, 1998-2012), the investigator can still implement the fit evaluation procedure described here and thus achieve the goals sought under the simulation procedure described in Millsap (2012). We hope that this extension will prove to be useful in real applications of SEM.

Appendix

R syntax using package Lavaan 0.5-11

[Holzinger & Swineford (1939) example]

### Importing data as a matrix. ###

myvars <- c("x1", "x2", "x3", "x4", "x5", "x6", "x7", "x8", "x9")

HS.data <- HolzingerSwineford1939[myvars]

HS.matrix <- as.matrix(HS.data)

class(HS.matrix) <- "numeric"

### Assigning basic scalars, vectors and matrices needed. ###

n<-nrow(HS.matrix)

one<-array(1,dim=c(n,1))

E<-one%*%t(one)

### Assigning values for the "true model". ###

L<-matrix(c(1.000, 0.000, 0.000,

    0.605, 0.000, 0.000,

    0.764, 0.000, 0.000,

    0.000, 1.000, 0.000,

    0.000, 1.117, 0.000,

    0.000, 0.927, 0.000,

    0.000, 0.000, 1.000,

    0.287, 0.000, 0.873,

    0.567, 0.000, 0.589),nrow=9,byrow=T)

P<-matrix(c(0.770, 0.372, 0.050,

    0.372, 0.973, 0.089,

    0.050, 0.089, 0.599),nrow=3, byrow=T)

TD<-matrix(c(0.589,0.000,0.000,0.000,0.000,0.000,0.000,0.000,0.000,

    0.000,1.100,0.000,0.000,0.000,0.000,0.000,0.000,0.000,

    0.000,0.000,0.826,0.000,0.000,0.000,0.000,0.000,0.000,

    0.000,0.000,0.000,0.490,0.000,0.000,0.000,0.000,0.000,

    0.000,0.000,0.000,0.000,0.543,0.000,0.000,0.000,0.000,

    0.000,0.000,0.000,0.000,0.000,0.375,0.000,0.000,0.000,

    0.000,0.000,0.000,0.000,0.000,0.000,0.441,0.000,0.000,

    0.000,0.000,0.000,0.000,0.000,0.000,0.000,0.357,0.000,

    0.000,0.000,0.000,0.000,0.000,0.000,0.000,0.000,0.584),nrow=9,byrow=T)

tau<-matrix(array(c(4.936, 6.088, 2.250, 3.061, 4.341, 2.186, 4.186, 5.527,

5.374),dim=c(n,9)),nrow=n,byrow=T)

m<-matrix(c(0, 0, 0), nrow=1, byrow=T)

myu<-matrix(rep(m, n),nrow=n, byrow=T)

### Matrix Algebra for Bollen-Stine Bootstrapping. ###

true.mean<-tau+myu%*%t(L)

true.cov<-L%*%P%*%t(L)+TD

sample.mean<-(1/n)*(t(HS.matrix)%*%one)

sample.cov<-((t(HS.matrix)%*%(HS.matrix))-((1/n)*t(HS.matrix)%*%(E)%*%(HS.matrix))*(1/(n-1))

### Cholesky Decomposition. ###

T<-chol(true.cov)

A<-chol(sample.cov)

HS.mod<-(HS.matrix-one%*%t(sample.mean))%*%solve(A)%*%T+true.mean

options(nwarnings=1000)

### Bootstrapping RMSEA values. ###

set.seed(1531)

NBOOT <- 1000

RMSEA <- numeric(NBOOT)

for(b in 1:1000) {

   boot.idx <- sample(1:n, replace=TRUE)

   HS_resamp <- HS.mod[boot.idx,]

   colnames(HS_resamp) <- c("x1","x2","x3","x4","x5","x6","x7","x8","x9") ### Assigning variable names. ###

 HS_resamp <- as.data.frame(HS_resamp) ### Converting matrix into data frame. ###

### HS 3-factor model ###

 M0 <- ' visual =~ x1 + x2 + x3 + x8 + x9

    textual =~ x4 + x5 + x6

    speed =~ x7 + x8 + x9

    visual ~~ 0*speed

 '

fit <- cfa(M0, data=HS_resamp) ### Fitting model to the resampled data. ###

RMSEA[b] <- fitMeasures(fit,"rmsea")   ### Computing RMSEAs ###

}

### Plotting histogram of RMSEA. ###

plt.rmsea<-hist(RMSEA, breaks=40, xlim=c(0, .1), ylim=c(0, 100))

[WAIS-R example]

### Importing data in R ###

WAISRM<-"I:/JWAISRM.dat"

RM<-matrix(scan(WAISRM,n=940*12),940,12,byrow=T)

WAISRF<-"I:/ JWAISRF.dat"

RF<-matrix(scan(WAISRF,n=940*12),940,12,byrow=T)

### Selecting variables of interest ###

M<-matrix(c(RM[,2],RM[,4],RM[,6],RM[,5]),nrow=940,byrow=F)

F<-matrix(c(RF[,2],RF[,4],RF[,6],RF[,5]),nrow=940,byrow=F)

### Defining some basic numbers and matrices for further algebra ###

n1<-nrow(M)     # Number of rows (observations) for males

n2<-nrow(F)     # Number of rows (observations) for females

oneM<-array(1,dim=c(n1,1))   # A vector with elements of “1”s for males

oneF<-array(1,dim=c(n2,1))   # A vector with elements of “1”s for females

E1<-oneM%*%t(oneM)    # A square matrix with elements of “1”s for males

E2<-oneF%*%t(oneF)    # A square matrix with elements of “1”s for females

### Specifying the M1 model ###

L1<-matrix(c(.90, 1.00, .88, .70),nrow=4,byrow=T)  # Factor loadings for male

P1<-8.4         # Factor variance for male

### Residual variances for male ###

TD1<-matrix(c(2.0, 0, 0, 0, 0, 1.0, 0, 0, 0, 0, 4.0, 0, 0, 0, 0, 3.0),nrow=4,byrow=T)

L2<-matrix(c(.80, 1.00, .78, .60),nrow=4,byrow=T)  # Factor loadings for female

P2<-7.8         # Factor variance for female

### Residual variance for female ###

TD2<-matrix(c(1.8, 0, 0, 0, 0, 1.2, 0, 0, 0, 0, 4.0, 0, 0, 0, 0, 3.0), nrow=4, byrow=T)

### Intercepts for male ###

tau1<-matrix(array(c(9.82,9.41,9.61,9.50),dim=c(940,4)),nrow=940,byrow=T)

### Intercepts for female ###

tau2<-matrix(array(c(8.98,9.25,9.33,9.20),dim=c(940,4)),nrow=940,byrow=T)

myu1=array(0,dim=c(n1,1))   # Factor mean for male

myu2=array(0,dim=c(n2,1))   # Factor mean for female

### Computing the implied (by M1) covariance & mean ###

X1<-L1%*%P1%*%t(L1)+TD1    # Implied variance/covariance matrix for male

X2<-L2%*%P2%*%t(L2)+TD2    # Implied variance/covariance matrix for female

U1<-tau1+myu1%*%t(L1)    # Implied mean vector for male

U2<-tau2+myu2%*%t(L2)    # Implied mean vector for female

Mbar<-(1/n1)*(t(M)%*%oneM)    # Sample mean vector for male

Fbar<-(1/n2)*(t(F)%*%oneF)    # Sample mean vector for female

SM<-(t(M)%*%M-(1/n1)*t(M)%*%E1%*%M)*(1/(n1-1))   # Sample variance/covariance for male

SF<-(t(F)%*%F-(1/n2)*t(F)%*%E2%*%F)*(1/(n2-1)) # Sample variance/covariance for female

### Defining the Cholesky factorization matrices ###

T1<-chol(X1)      # Cholesky factorization for males implied var/cov matrix

T2<-chol(X2)      # Cholesky factorization for females implied var/cov matrix

A1<-chol(SM)      # Cholesky factorization for males sample var/cov matrix

A2<-chol(SF)      # Cholesky factorization for females sample var/cov matrix

### Applying the Bollen-Stine correction ###

Mmod<-(M-oneM%*%t(Mbar))%*%solve(A1)%*%T1+U1

Fmod<-(F-oneF%*%t(Fbar))%*%solve(A2)%*%T2+U2

### Calling the “lavaan” package ###

library(lavaan)

### Bootstrapping and fitting the M0 model for the re-samples ###

set.seed(1234)      # Setting seed number for replication

NBOOT <- 1000

RMSEA <- numeric(NBOOT)   # Creating an object named “RMSEA”

for(b in 1:1000) {

boot.idx <- sample(1:940, replace=TRUE)    # Sampling with replacement

Mresamp <- Mmod[boot.idx,]      # Bootstrapping male data

Fresamp <- Fmod[boot.idx,]      # Bootstrapping female data

finM <- cbind(oneM,Mresamp)     # Assigning group indicator for male (=1)

finF <- cbind(2*oneF,Fresamp)     # Assigning group indicator for female (=2)

finT <- rbind(finM,finF)     # Concatenating the male and female data

colnames(finT) <- c("sex","info","voca","comp","arit")   # Assigning column names

finT <- as.data.frame(finT)      # Converting the matrices to data frame

### Model specification (refer to package “lavaan” manual) ###

M0 <- '

    f1 =~ NA*info + 1.0*voca + comp + arit

    f1 ~ 0*1

    info + voca + comp + arit ~ 1

    '

fit <- cfa(M0, data=finT, group="sex", group.equal=c("loadings"))  # Fitting the M0 model

RMSEA[b] <- fitMeasures(fit,"rmsea")   # Computing RMSEA values

}

### Frequency distribution graph of RMSEAs ###

plt<-hist(RMSEA, breaks=40, xlim=c(0, .10), ylim=c(0, 80))

[COERCE example – full sample]

### Reading data into R ###

coerce <- read.csv("I:/coerce_coimps_age2.csv",header=FALSE)

coerce.matrix <- as.matrix(coerce)

class(coerce.matrix) <- "numeric"

### Assigning some basic numbers and matrices for further algebra ###

n<-nrow(coerce)

one<-array(1,dim=c(n,1))

E<-one%*%t(one)

### Assigning values for the "true model". ###

L<-matrix(c(1, 1.358, 1.063, 0.739, 1.279, 0.693, 0.896, 0.822))

P<-matrix(c(0.439), nrow=1, byrow=T)

TD<-matrix(c(1.425,0,0,0,0,0,0.17,0,

     0,0.992,0,0,0,0,0,0,

     0,0,1.437,0,0,0,0,0,

     0,0,0,0.192,0,0,0,0,

     0,0,0,0,0.602,0,0,0,

     0,0,0,0,0,0.348,0,0,

     0.17,0,0,0,0,0,0.522,0,

     0,0,0,0,0,0,0,0.252),nrow=8,byrow=T)

tau<-matrix(array(c(2.297, 2.332, 2.303, 1.350, 1.645, 1.376, 1.700, 1.444),dim=c(n,8)),nrow=n,byrow=T)

myu<-matrix(rep(0, n),nrow=n, byrow=T)

### Matrix Algebra for Bollen-Stine Bootstrapping. ###

true.mean<-tau+myu%*%t(L)

true.cov<-L%*%P%*%t(L)+TD

sample.mean<-(1/n)*(t(coerce.matrix)%*%one)

sample.cov<-((t(coerce.matrix)%*%(coerce.matrix))-((1/n)*t(coerce.matrix)%*%E%*%(coerce.matrix)))*(1/(n-1))

### Cholesky Decomposition. ###

T<-chol(true.cov)

A<-chol(sample.cov)

coerce.mod<-(coerce.matrix-one%*%t(sample.mean))%*%solve(A)%*%T+true.mean

library(lavaan)     ### Activating package "Lavaan". ###

### Bootstrapping RMSEA values. ###

set.seed(1234)

NBOOT <- 1000

RMSEA.MLR <- numeric(NBOOT)

for(b in 1:1000) {

   boot.idx <- sample(1:n, replace=TRUE)

   coerce_resamp <- coerce.mod[boot.idx,]

   colnames(coerce_resamp) <- c("i22","i23","i24","i25","i26","i31","i32","i33") ### Assigning variable names. ###

 coerce_resamp <- as.data.frame(coerce_resamp)      ### Converting matrix into data frame. ###

### M0 model ###

 M0 <- '

  Coerce =~ 1*i22 + i23 + i24 + i25 + i26 + i31 + i32 + i33

    Coerce ~~ Coerce

    i22 + i23 + i24 + i25 + i26 + i31 + i32 + i33 ~ 1

    Coerce ~ 0*1

    '

fit <- sem(M0, estimator = “MLR”, data=coerce_resamp)  ### Fitting model to the resampled data. ###

RMSEA.MLR[b] <- fitMeasures(fit,"rmsea.scaled")  ### Computing RMSEAs using MLR ###}

### Plotting histogram of RMSEA. ###

plt.rmsea.mlr<-hist(RMSEA.MLR, breaks=40, xlim=c(0, .20), ylim=c(0, 100))

Mplus syntax

[COERCE example – full sample]

TITLE: COERCE example (full sample)

MONTECARLO:

NAMES ARE i22 i23 i24 i25 i26 i31 i32 i33;

NOBSERVATIONS = 723;

NREPS = 1000;

SEED = 120489;

RESULTS = coercemonte.dat;

MODEL POPULATION:

coerce BY i22@1 i23@1.358 i24@1.063 i25@0.739

i26@1.279 i31@0.693 i32@0.896 i33@0.822;

[i22@2.297 i23@2.332 i24@2.303 i25@1.350 i26@1.645

i31@1.376 i32@1.700 i33@1.444];

coerce@0.439;

i22@1.425 i23@0.992 i24@1.437 i25@0.192 i26@0.602

i31@0.348 i32@0.522 i33@0.252;

i22 WITH i32@0.17;

MODEL:

coerce BY i22@1 i23* i24* i25* i26* i31* i32* i33*;

[i22* i23* i24* i25* i26* i31* i32* i33*];

coerce*;

OUTPUT: TECH9;