Use of Smoothing Splines for Analysis of Backscattered Ultrasonic Waveforms: Application to Monitoring of Steroid Treatment of Dystrophic Mice

Abstract

Duchenne Muscular Dystrophy is an X-linked genetic disease characterized by progressive weakness and wasting of skeletal and cardiac muscle; boys present with weakness by the age of 5 years and, if left untreated, are unable to walk without assistance by age 10 years. Therapy for DMD has been primarily palliative, with oral steroids are emerging as a first-line approach even though this treatment has serious side-effects. Consequently, low-cost imaging technology suitable for improved diagnosis and treatment monitoring of DMD would be of great value, especially in remote and underserved areas. Previously, we reported use of the logarithm of the signal energy, log[E_f], and a new method for ultrasound signal characterization using entropy, H_f, to monitor prednisolone treatment of skeletal muscle in a dystrophin-deficient mouse model. Three groups were studied: mdx mice treated with prednisolone, a control group of mdx mice treated with saline, and a control group of wild-type mice treated with saline. It was found that both log[E_f] and H_f were required to statistically differentiate the three groups. In the current study we show that preprocessing of the raw ultrasound using optimal smoothing splines prior to computation of either log[E_f] or a rapidly computable variant of H_f, denoted I_f,∞, permits delineation of all three groups by either metric alone. This opens the way for the ultimate aim of this study, which is identification and implementation of new diagnostically sensitive algorithms on the new generation of low-cost hand-held clinical ultrasonic imaging systems.

INTRODUCTION AND LITERATURE

In earlier studies we reported on the application of several entropies: Shannon entropy, H_S, [1] a continuous analog of H_S, denoted H_f, [2–7] a generalization of H_f, the Renyi entropy, I_f(r), which is defined for all r < 2 (r is roughly a reciprocal “temperature”), [8] and a limiting form of I_f(r → 2), I_f,∞, [9] for the detection of changes in backscattered RF (Radio Frequency) ultrasound waveform, f(t). In all of these studies, the sensitivities of entropic measures, or signal receivers, to changes in backscattered RF were compared to the sensitivity of a conventional signal receiver: either the signal energy E_f or more typically its logarithm, log[E_f], with entropic measures having greater sensitivity in all studies but one.[10] Many of these investigations were based on molecular targeting of perfluorocarbon nanoparticle ultrasound contrast agents to neovasculature in tumors. A description of the physical properties of these nanoparticles has been published elsewhere.[11] It was found that detection of targeted nanoparticles in the angiogenic bed, which is highly nonplanar and has sparsely distributed target sites, presented challenges that might require the application of novel types of signal processing.[4–9] We were able to show that signal processing based on a “moving window” entropy analysis using Eq. (4) could detect accumulation of tissue-targeted nanoparticles within 15 minutes of nanoparticle injection. The most notable feature of later studies is that I_f,∞ is computable using an algorithm having a lower operation count than that required to produce B-Mode grayscale images and may thus be computed in real-time.[9, 12]

Analysis based on the entropy I_f(1) = −H_f has also been successfully applied to characterization of diseased and normal smooth muscle.[10] In that study it was shown that H_f images could be used to distinguish normal and prednisolone-treated from untreated dystrophic tissue, and thus, that entropic images could be used to monitor the impact of prednisolone therapy in a dystrophic animal model. However, the time required to execute a H_f analysis was quite lengthy, on the order of tens of hours, and it was unable to distinguish prednisolone-treated mdx mice and normals. However, log[E_f] was able to distinguish these groups but not the mdx treated and untreated groups.

The purpose of the current study is two-fold. The immediate goal is to show that these results ([10]) may be improved in both speed and sensitivity by preprocessing of the RF data with two steps (followed by either entropy, I_f,∞, or energy, log[E_f], analysis). First is application of bandpass filtering, in the frequency domain, to exclude all frequencies outside of the effective bandwidth of the transducer, which was 0–36 MHz for our data. The second step is fitting of an optimal smoothing spline to reduce the impact of noise on the computation of derivatives needed for computation of I_f,∞. The resulting algorithms run in minutes, as opposed to the hours required for H_f analysis, and both have low enough operation counts that with further development real-time operation is feasible. Both steps are required to achieve the results presented below, which demonstrate that the two algorithms are clinically efficacious and have sufficiently low operation count that they are reasonable candidates for clinical implementation.

The results thus support the ultimate aim of this study, which is identification and implementation of new diagnostically sensitive algorithms on the new generation of low-cost hand-held clinical ultrasonic imaging systems. Accordingly, we have focused our efforts on either discovery of new algorithms, e.g., I_f,∞, or simple and fast preprocessing techniques. The aim of this study is not development of sophisticated denoising techniques or signal models for which there is a vast literature.[13–19]

MATERIALS AND METHODS

Entropy-based Image Formation

All results in this study were obtained using the density function, w_f(y) of the continuous function y = f(t), assumed to underlie the sampled RF data. Subsequently, w_f(y) was used to compute the entropy I_f(r) which determined a single pixel value in an “entropy” image. When applied in this manner, each pixel corresponds to a different w_f(y). As described in previous studies w_f(y) corresponds mathematically to the density functions used in statistical signal processing.[8] However, its physical meaning is very different from its meaning in that context where it is typically one of a family of well-known distributions, e.g. that in [13–19]. On the other hand, we assume that the noise levels in our apparatus are low enough so that with sufficient signal averaging, noise may be eliminated, or at least reduced to a low enough level, that derivatives of f(t) may be accurately computed. From these derivatives the density function w_f(y) may be directly computed from the random variable f(t), [8] which then facilitates calculation of the quantities typically discussed in statistical signal processing, e.g., mean values, variances, covariances.[20–22] However, in typical statistical signal processing computations, the density function is usually assumed to be continuous, infinitely differentiable, and to approach zero at infinity. In our case w_f(y) is not well-behaved and has integrable singularities. While this renders calculation of the density function more difficult, applications of entropy imaging based on w_f(y) have shown the cost to be justified in terms of increased sensitivity to subtle changes in scattering architecture that are often undetected by more conventional imaging.

We use the same conventions as in previous studies so that

$$w_f(y)={\sum }_{k=1}^N\mid g_k^{\prime }(y)\mid ,$$ (1)

where N is the number of laps, i.e. regions of monotonicity of f(t), g_k(y) is the inverse of f(t) in the k^th-lap and if y is not in the range of f(t) in the k^th-lap, is taken to be 0. We also assume that all experimental waveforms f(t) have a Taylor series expansion valid in the domain: 0,1.

The mathematical characteristics of the singularities of w_f(y) are important in order to guarantee the existence of the following expression on which we base our analysis of signals in this study:

$$I_{f,\infty }=log\left[{\sum }_{\{t_k\mid f^{\prime }(t_k)=0\}}\frac{1}{f^{″}(t_k)}\right],$$ (2)

which is obtained by an asymptotic analysis of

$$I_f(r)=\frac{1}{1-r}log\left[{\int }_{f_{\mathit{min}}}^{f_{\mathit{max}}}{w}_f{(y)}^{r}dy\right],$$ (3)

as r → 2⁻. I_f(r) known as the Renyi entropy, [23, 24] is similar to the partition function in statistical mechanics with the parameter r playing the role of an “artificial” reciprocal temperature, [8, 25] which is unrelated to the actual physical temperature in the scattering region. Moreover, I_f(r) → −H_f as r → 1, using L’Hôpital’s rule, so that is a generalization of:

$$H_f={\int }_{f_{\mathit{min}}}^{f_{\mathit{max}}}{w}_f(y)log{w}_f(y)dy.$$ (4)

Previous studies have shown that all three quantities: I_f,∞, I_f(r), and H_f, can be more sensitive to subtle changes in scattering architecture than are more commonly used energy-based measures.[7–9] We base our current study exclusively on since this quantity is calculable in real-time.[9]

As stated above, the literature on statistical processing of ultrasonic signals is vast and it is not possible in the space of a research article to provide a complete comparison between our approach and more established techniques. However, a limited comparison of our approach with more established methods in statistical signal processing of ultrasonic signals [13–19] is shown in Figure [1]. In the top panel backscattered RF from the biceps of one of the mice used in our study is shown. A yellow rectangle is also drawn to indicate a selection of RF subsegments that will be subjected to statistical analysis. In a many approaches to statistical ultrasonic signal processing it is assumed that the distribution of values in the ensemble has a Gaussian distribution, e.g. see section III, Figure 5A of [13]. The top panel of the figure shows several sampled RF segments, each 128 points long corresponding to 0.128 μs. The histogram determined by the values of all RF segments in the yellow box is shown at the right hand side of the top panel and it appears that it is indeed approximately Gaussian. This condition permits further, and sophisticated, frequency domain analysis of the spectra of the RF segments, the goal of which is to establish performance bounds and confidence estimates of “spectral parameters and tissue features”.[13] On the other hand, the bottom panel illustrates our approach in graphical form. The same representative RF segments are shown, but to these are fit optimal splines, which are continuous functions. Thus, the RF segments are thought of as truly continuous functions and thus they may be used to compute a density, w_f(y). We note that the individual density functions, w_f(y), are dominated by singularities, which correspond to local extrema in the continuous RF waveforms. These are then used as described above to compute entropy, as in Eq. (3). Thus, in the conventional approach a PDF is assumed for an ensemble or class of waveforms, e.g., backscatter from liver or prostate tissue, which then serves as the basis for subsequent analysis. Often this takes place in the frequency domain. In our approach there is a unique PDF for every RF segment and all analysis takes place in the time domain. The relation between our approach and the more established statistical analyses is similar to that between complexity theory of classes of functions based on ε-entropy, e.g. the set of analytic functions of one variable or the class of continuous functions on one hand and algorithmic information on the other.[26, 27]

Figure 1.

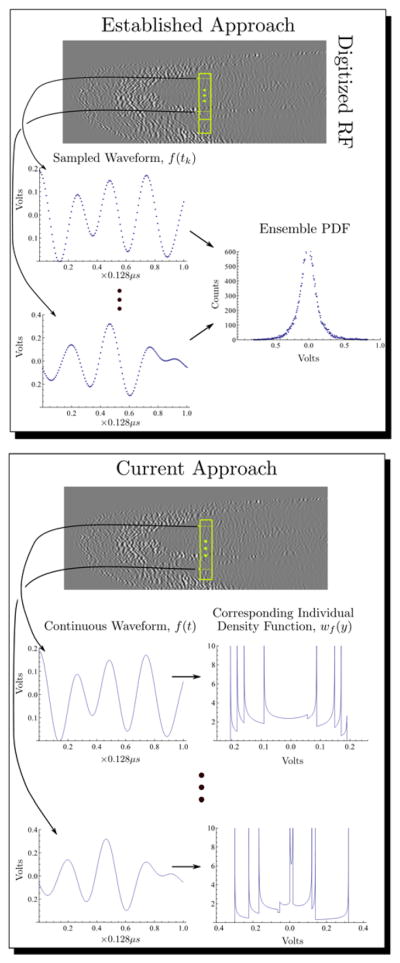
A comparison of (top) established statistical signal processing techniques with (bottom) the approach employed in this study. Comparison of the two techniques shows that the probability density functions have completely different physical origins.

Log Energy-Based Image Formation

By analogy with the expression for the kinetic energy for a mass-spring system, the signal energy of a waveform, f(t), measured over the unit interval is usually defined as

$$E_f={\int }_0^{1}f{(t)}^{2}dt.$$ (5)

This function may also be computed as the second moment of the density, w_f(y), as described elsewhere.[10]

Moving Window Analysis

In the current investigation, both energy-based, log[E_f], and entropy-based, I_f,∞, receiver operators were applied as sliding boxcar, or moving window, filters to 0.128-μs segments of the individual radio-frequency backscatter A-lines. The moving window was moved in 0.016-μs steps to produce either log[E_f] or I_f,∞ images. These were then used in a region of interest analysis (ROI) to compare and assess the complementary nature of the two metrics to differentiate among normal, untreated dystrophic, and steroid-treated dystrophic muscles.

Animal Model and Therapy

The study was performed according to an approved animal protocol and in compliance with guidelines of the Washington University institutional animal care and use committee.

The mdx mouse possesses a genetic mutation that results in the absence of dystrophin in the muscles, and is considered to be a valid model of human Duchenne Muscular Dystrophy (DMD).[28, 29] Dystrophic mdx mice (C57BL/10ScSn-DM Dmdx) and appropriately matched normal controls (C57BL/10ScSn-J) were acquired from the Jackson Laboratory (Bar Harbor, ME) at 8 weeks of age. A total of 8 mdx positive- and 5 negative-control mice were employed for this study. All mice were housed in the same animal facility and cared for within the guidelines set forth by the University’s animal care committee. Food and water were provided ad libitum.

At an age of months, the mdx dystrophic mice were blocked randomly into two groups: receiving steroid treatment, and positive controls. The treated block of animals received daily subcutaneous injections of prednisolone prednisolone sodium succinate, trade name “Solu-Delta-Cortef,” Pfizer Animal Health, Groton, CT, prepared at a dilution of 1 mg/mL saline and dosed at 1 mL solution per 1 kg body mass, e.g., 30 μL for a 30-g mouse. The positive-control block of mdx mice received subcutaneous injections of an equivalent volume of saline, specifically 1 mL per 1 kg body mass. All injections were performed on a daily basis for 14 consecutive days, followed by ultrasonic imaging and data acquisition on day 15 following the start of treatment.

Ultrasonic Data Acquisition

To minimize unwanted motion artifact, each mouse was anesthetized using a single subcutaneous injection of ketamine-xylazine (1:1 mixture, 2 μL per g body weight) immediately prior to acquisition of ultrasonic backscatter data. Sedated animals were partly submerged in a 37°C regulated water bath, with the head above waterline, right forelimb extended and biceps oriented up toward the imaging transducer. Each forelimb was imaged in transverse cross sections using a Vevo-660 (Visualsonics, Toronto, ON, Canada) with a single-element 40-MHz wobbler-transducer (model RMV-704, Visualsonics) sweeping back and forth 15 times per second to achieve a 30-Hz frame rate. The transduction element was 3 mm in diameter and spherically focused to a depth of 6 mm, which is equivalent to an f-number of f/2. The focal zone spot size was 80×1100 μm determined using the −6 dB criterion. The frequency content of the water path-only transmit pulse was centered at approximately 35 MHz with a 40-dB bandwidth ranging from 10 to 60 MHz. Actual bandwidth was significantly reduced by tissue attenuation with usable bandwidth extending up to only 36 MHz at the −20 dB point.

To analyze data from the full volume of each biceps muscle, a sequence of these transverse sector images was acquired from “shoulder” to “elbow”, advancing the transducer longitudinally in 100-μm steps using a 4-axis motion controller (Unidex 12, Aerotech Inc., Pittsburgh, PA). A schematic illustrating the relative placement of the transducer, mouse forelimb, and direction of scan has been published previously.[10] For completeness, we note that the separation between the transducer and the forelimb was adjusted to position the 6-mm focal depth in the middle of the biceps cross-sectional area. At each position of the scan, radio-frequency data from across the entire sector image, 384 radio-frequency scan lines, evenly spaced in a 7.8-degree sector, were digitized using a PC-based acquisition card (Compuscope CS82G, Gage Applied Technologies, Inc., Montreal, Quebec, Canada). Backscatter data were acquired and stored with 8-bit resolution at one GSample/s for 8192-point record lengths.

Data were processed to generate three separate co-registered image representations. First, “Conventional” or log of the analytic signal magnitude. Second, “integrated backscatter”, or 128-point boxcar average of the log energy. Third, “entropy”, or 128-point boxcar information theoretic receiver, H_f.[30] Representative segments of digitized RF are shown in Figure [1].

Ultrasonic Data Analysis: band-pass filtering

Since the real-time entropy depends on the second derivative of the raw data, a potentially noise-enhancing process, all RF data were bandpass filtered in the frequency domain as a first step in data analysis. This was accomplished by multiplying the Fourier transform by the filter function, F(f),

$$F(f)=\frac{1}{4}(1.0+tanh[{\alpha }_l(f-f_{\text{lower}\text{cutoff}})])\times (1.0+tanh[{\alpha }_u(f_{\text{upper}\text{cutoff}}-f)])$$ (6)

where α_l = 0.75, α_u = 0.25, f_{lower cutoff} = 0 MHz and f_{upper cutoff} = 36 MHz. These were chosen to correspond to the 20-dB point of our apparatus at 36 MHz. This function, F(f), has the shape of a smoothed rectangular window turning on near f_{lower cutoff} and turning off near f_{upper cutoff}. The coefficients α_l and α_u govern the sharpness of these transitions. This function was chosen as a gate function since it is infinitely differentiable.

Ultrasonic Data Analysis: simple cubic spline vs. smoothing spline

After filtering, each of the 384 RF lines in the data was fit to one of three types of splines: simple cubic, smoothing cubic spline with smoothing “turned off” and smoothing cubic spline with optimal smoothing.

Simple Cubic Spline

To facilitate comparison with previous results, [10] a simple cubic spline was fit to the data represented by a set of N = 8192 values y_i at times t_i between t₁ and t_n.[31] This “order N” algorithm also produces the second derivative values of the fit function.[31] Next, a moving window analysis was performed on the second derivative data set, using Eq. (2) to compute I_f,∞, by moving a rectangular window 128 points long, which is equivalent to 0.128 μs in 16-point steps, which is equivalent to 0.016-μs steps. This results in 505 window positions within the output image for each time point in the experiment.

Smoothing Cubic Spline

In this case calculation of I_f,∞ via Eq. (2) is accomplished by fitting a smoothing spline to each set of the 128 points obtained as the moving window is swept over the experimentally acquired data array. The algorithm for this was first described by Reinsch in 1967.[32] Assuming, as above, that the backscattered RF is represented by a set of (in this case) N =128 values y_i at times t_i, where i =1, …, N, the corresponding smoothing spline approximation to those values is the function g(t) that minimizes:

$${\int }_{t_0}^{t_N}{g}^{″}{(t)}^{2}dt,$$ (7)

subject to the constraint that

$${\sum }_{i=0}^N\left(\frac{g(t_i)-y_i}{\delta y_i}\right)\le \widehat{S},$$ (8)

where, operationally, δy_i > 0 is the standard deviation of the measured data point y_i. For this study we have taken to be δy_i = 0.01, which was obtained using statistics from the water only regions of our backscattered data. For aesthetic reasons the smoothing parameter Ŝ is multiplied by the number of points N, to define a new smoothing parameter S = Ŝ × N. With this normalization, S =0.0, corresponds to no smoothing: the output of the algorithm is identical to a cubic spline fit. As S → ∞, the output approaches the best fit line to the data. The optimum fit, corresponding to the minimum defined by Eqs. (7) and (8) occurs somewhere near S = 1.0.

As discussed by Reinsch these equations may be combined into the problem of minimizing the functional

$${\int }_{t_0}^{t_N}{g}^{″}{(t)}^{2}dt+p\left\{{\sum }_{i=0}^N\left(\frac{g(t_i)-y_i}{\delta y_i}\right)+z^2-S\right\},$$ (9)

where z is an auxiliary variable, which is needed in addition to the expected Lagrange multiplier p, since Eq. (8) is an inequality instead of an equality. Minimization with respect to p and z may be performed as described by Reinsch after writing g(t) as a cubic spline and substituting this expression into Eq. (9) to obtain a N × N matrix minimization problem that may be solved iteratively. We have found, for the data presented in this study, that at most ten, and on average 9, iterations are required to compute the optimal smoothing spline. As is often the case in matrix minimization problems solution requires use of an algorithm with an operation count of N³ at each iteration. For the Reinsch algorithm this is Cholesky decomposition. Consequently, we expect the smoothing spline approach to be slower by a factor of N² than the simple cubic spline algorithm. In previous studies, [8] upsampling of N was required to improve the accuracy of computed zeros of the derivatives of f(t). In the current approach this is not necessary, so that N = 128, thus mitigating the impact of Cholesky decomposition. The resulting g(t) will replace the raw time domain function, f(t) appearing in Eqs. (2) and (5).

The Reinsch algorithm computes the value of g(t), g′(t) and g″(t) at the t_i. Thus, it is easy to identify the location of critical points by finding zero crossings of the g′(t) array and subsequently solving a quadratic equation. This is done as described in Press et.al. ([31], 2^nd ed., Chapter 5, section 6) to avoid loss of precision in our implementation for calculation of the locations of the critical points. Consequently, we obtain more accurate values of the smoothing spline, and its first and second derivatives at these points at the critical points than was obtained in the algorthim that employed unsmoothed splines.

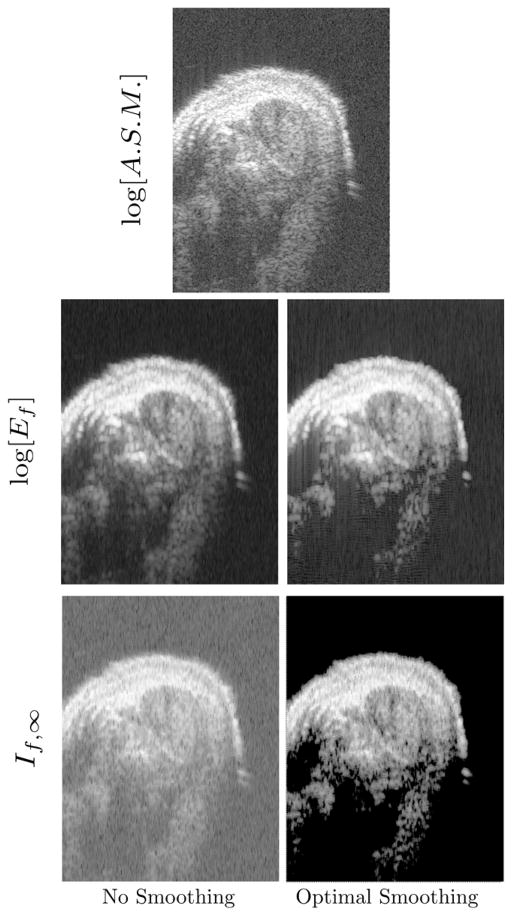
A representative set of these images, which are reconstructions of a transverse B-scan slice of the biceps is shown Figure [2]. All of the images shown were reconstructed from the same raw RF data. In the top row, is the conventional gray scale image, which is a limiting form of the log[E_f] image in the limit of smaller and smaller moving window length. Several features of the two bottom rows, labeled log[E_f] and I_f,∞, deserve mention. First, the I_f,∞ image, while showing roughly the same features as the energy images above it, has negative contrast when compared to energy images. To achieve a consistent image presentation we have therefore shown these images with inverted gray-scale lookup tables. This relationship between energy and entropy images has been observed in previous studies.[8, 9, 12] Second, in the I_f,∞ image obtained using optimal smoothing splines, we note the perfectly white region between the transducer, which is above the mouse, as well as the white region at deeper and thus more highly attenuated regions of the image. These correspond to regions where the smoothing spline algorithm has returned a masked value indicating that a valid value of I_f,∞ can not be obtained. Inspection of the I_f,∞ image shows that these correspond to regions where, on experimental grounds, we expect the signal to be dominated by noise. In fact, the smoothing I_f,∞ algorithm is written, in the C programming language, so that regions, i.e., moving window locations, where the second derivative is less than DBL_EPSILON are masked. In this case, our algorithm returns a masked value chosen to lie outside the range of I_f,∞ values returned at non-noise dominated regions. We point out that this masking is automatic in the sense that it is obtained without setting of any cutoff level. It is imposed by: the optimality criterion, the measured noise level in the water-only region and the limitations of the digital architecture. Thus, the advantage of this approach over the setting of cutoff levels “by hand” is the economy of assumptions it affords and the objectivity with which they are implemented.

Figure 2.

An illustration of representative mdx-saline (positive-control) mouse biceps cross sections. The image depicted in the top row is conventional grayscale [i.e., logarithm of the analytic signal magnitude (ASM)]. The second row are log[E_f] images obtained using the same RF data using (left) unsmoothed or (right) optimal smoothing splines. The bottom row shows the corresponding I_f,∞· images. The direction of insonification is from the top.

Image Analysis

Subsequent analyses were performed with these quantitative images using the public domain ImageJ software.[33] To assist in identifying the boundary of each biceps muscle, frames of the conventional image stacks were first processed with a 5 × 5 median filter to reduce image speckle. We note that this smoothing operation was performed for visualization only, and was not applied to the analyzed data. A region of interest (ROI) was then drawn to circumscribe the muscle interior on each frame that included a biceps cross section, for each image stack. The ROIs were drawn in a blinded and randomized fashion without knowledge of the animal blocking, and all regions were drawn by one operator and reviewed by two others. These ROIs were applied subsequently to the appropriate frame of the corresponding log[E_f] and entropy images to extract average parameters for each biceps. We note that each ROI intersected an average of 80 RF lines on each of 53±8 frames per mouse biceps.

Results

I_f,∞: Simple Cubic Spline

Figure [3] summarizes the results obtained for all three groups if simple cubic splines are used to compute Eq. (2). These results are statistically equivalent to those that were obtained using H_f (Eq. (4)) in a previous study of the same data: statistical separation of the saline vs. prednisolone, and saline vs. normal, with no distinction observed between prednisolone vs. normal groups.[10]

Figure 3.

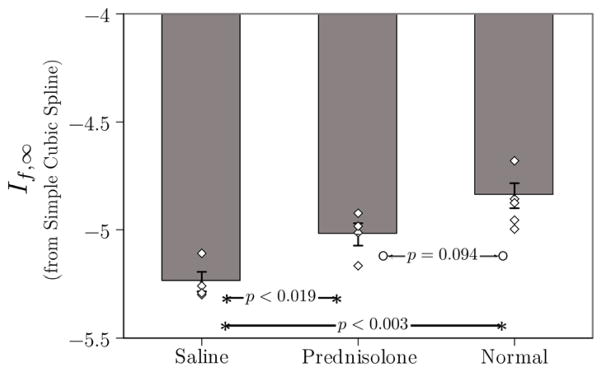
Plot of mean I_f,∞· for the three groups in this study. Individual data points for each member of each group are also shown to give an indication of the scatter in the data. These data were obtained using (2) in conjunction with simple (i.e., non-smoothing cubic) splines. As in a previous study using the same raw RF data, I_f,∞· operating on unsmoothed data are unable to differentiate the prednisolone and normal groups.[10]

It is also possible to execute a smoothing spline analysis with smoothing “turned off” by setting the smoothing parameter S = 0. This analysis has also been performed. The results are indistinguishable from those of Figure [3]. This fact rules out the use of less accurate, but faster, linear interpolation of the second derivative appearing in Eq. (2) as a major factor preventing differentiation of the prednisolone and normal groups which may be obtained if smoothing is used (see below).

I_f,∞: Smoothing Cubic Spline

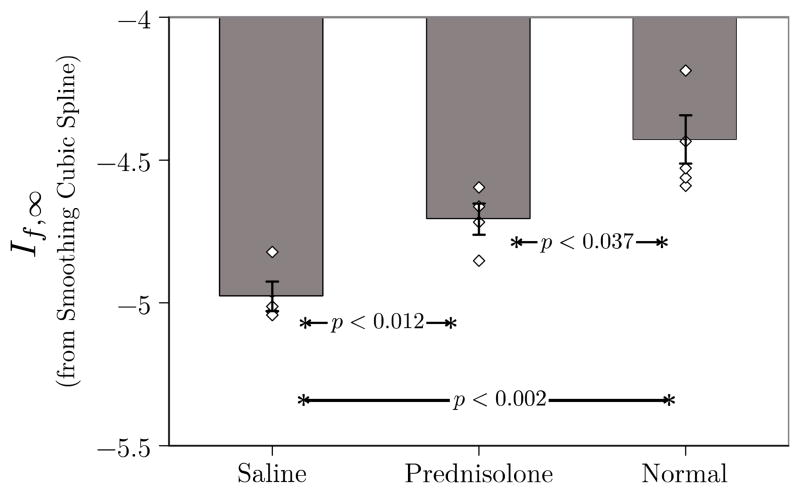
The corresponding results obtained with optimal smoothing (i.e., S = 1) are shown in Figure [4]. The effect of smoothing is demonstrated by the statistical separation of all groups from each other. This result depends critically on the elimination of masked pixels from the analysis (this is possible in ImageJ). Exclusion of the masked pixels is necessary to ensure that significance is not lost. Since there are measurable clinical differences in size and strength between all groups this result implies greater clinical sensitivity and hence utility of the approach based on smoothing splines.

Figure 4.

Plot of mean I_f,∞· for the three groups in this study. Individual data points for each member of each group are also shown to give an indication of the scatter in the data. These data were obtained using (2) in conjunction with optimal smoothing cubic splines. Unlike Fig. 3, I_f,∞· operating on optimally smoothed data are able to differentiate all three groups.

LOG[E_f]: Corresponding Results

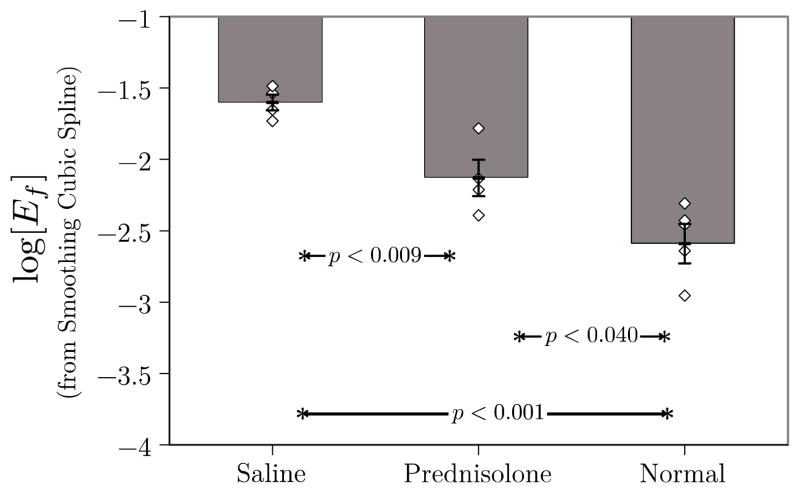
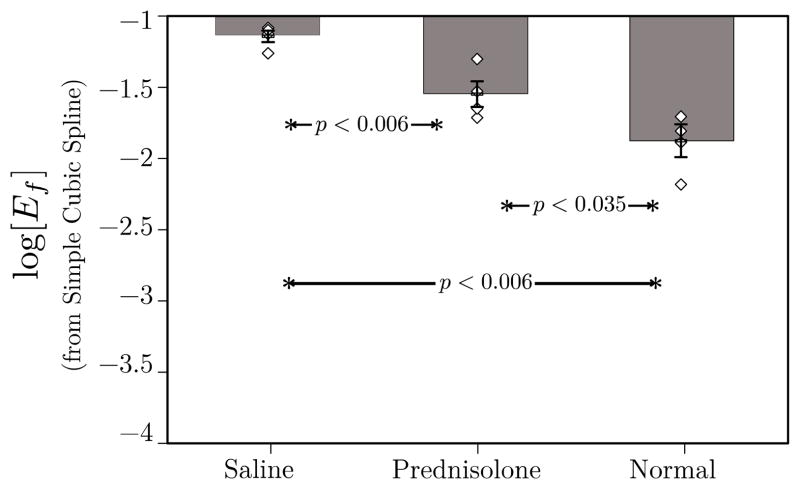
Smoothing splines may also be used in the computation of the logarithm of Eq. (5). The results for all three groups are shown in Figure [5]. They demonstrate essentially equivalent statistical performance with the I_f,∞ analysis shown in Figure [4]. The corresponding results obtained using unsmoothed splines are shown in Figure [6].

Figure 5.

Plot of mean log[E_f] for the three groups in this study. Individual data points for each member of each group are also shown to give an indication of the scatter in the data. These data were obtained using (2) in conjunction with optimal smoothing cubic splines. As in Fig. 4, log[E_f] operating on optimally smoothed data are able to differentiate all three groups. This result may be compared with that shown in Fig. 5 of a previous study that was based on unsmoothed RF. In that case, log[E_f] was unable to differentiate prednisolone-treated from untreated groups.[10]

Figure 6.

Plot of mean log[E_f] for the three groups in this study. Individual data points for each member of each group are also shown to give an indication of the scatter in the data. These data were obtained using (2) in conjunction with optimal smoothing cubic splines. As in Fig. 4, log[E_f] operating on optimally smoothed data are able to differentiate all three groups. This result may be compared with that shown in Fig. 5 of a previous study that was based on unsmoothed RF. In that case, log[E_f] was unable to differentiate prednisolone-treated from untreated groups.[10]

For completeness a statistical summary of these results is shown in Tables I and II. Table I summarizes results obtained using I_f,∞. Results obtained using optimal smoothing are shown immediately above the corresponding results obtained without smoothing, which are enclosed in parentheses. The column labeled σ summarizes standard deviations, and the column labeled α summarizes the standard errors of the mean. Table II summarizes the corresponding results for log[E_f], using the same format. The table shows that the effect of smoothing is to increase slightly the differences between the means of the three groups, especially the difference between the normal and prednisolone treated groups.

Table I.

Effect of smoothing on I_f,∞·

Group	Mean	σ	α, N=4
Saline, S=1.0	−4.97	0.10	0.05
(Saline, S=0.0)	(−5.25)	(0.09)	(0.04)
Prednisolone, S=1.0	−4.71	0.11	0.05
(Prednisolone, S=0.0)	(−5.04)	(0.10)	(0.05)
Normal, S=1.0	−4.43	0.17	0.08
(Normal, S=0.0)	(−4.86)	(0.12)	(0.06)

Table II.

Effect of smoothing on log[E_f]

Group	Mean	σ	α, N=4
Saline, S=1.0	−1.6	0.11	0.06
(Saline, S=0.0)	(−1.15)	(0.08)	(0.04)
Prednisolone, S=1.0	−2.13	0.26	0.13
(Prednisolone, S=0.0)	(−1.57)	(0.19)	(0.09)
Normal, S=1.0	−2.59	0.28	0.14
(Normal, S=0.0)	(−1.91)	(0.24)	(0.12)

Conclusion

The most significant outcome of this study is the essentially equivalent performance of the energy and entropic receivers. In other experimental settings we have found entropic signal receivers to be more sensitive to changes in scattering architecture caused by accumulation of targeted nanoparticles, e.g. I_f,∞ in references [7–9, 34, 35], and to changes in scattering from hard cylindrical scatters, e.g. Shannon entropy and H_f.[30] Consequently, the results of this study on a very different acoustic problem, weak scatterering from long fibers, is interesting since it supports our belief that there does not exist a signal receiver that is better than all others in all scattering regimes. In fact, based on this principal our approach has been the continual development and investigation of multiple signal receivers, based not only on signal energy, but also on a family of entropic quantities. These permit simultaneous evaluation of potential changes in scattering architecture by multiple metrics with the goal of providing more reliable characterization than is possible using a single signal receiver.

Preprocessing of ultrasonic backscatter by band pass filtering followed by computation of the optimal smoothing splines has been shown to increase the sensitivity of both energy-based analysis, log[E_f], and entropic analysis, I_f,∞, for the delineation of treated and untreated dystrophic skeletal muscle. Further improvements in speed of ultrasonic data analysis, or data acquisition, e.g., by reducing sampling rate requirements, might be realized using this technique and will be studied in future investigations.