Abstract
Purpose:
Photon counting detectors (PCDs) are an emerging technology with applications in spectral and low-dose radiographic and tomographic imaging. This paper develops an analytical model of PCD imaging performance, including the system gain, modulation transfer function (MTF), noise-power spectrum (NPS), and detective quantum efficiency (DQE).
Methods:
A cascaded systems analysis model describing the propagation of quanta through the imaging chain was developed. The model was validated in comparison to the physical performance of a silicon-strip PCD implemented on an experimental imaging bench. The signal response, MTF, and NPS were measured and compared to theory as a function of exposure conditions (70 kVp, 1–7 mA), detector threshold, and readout mode (i.e., the option for coincidence detection). The model sheds new light on the dependence of spatial resolution, charge sharing, and additive noise effects on threshold selection and was used to investigate the factors governing PCD performance, including the fundamental advantages and limitations of PCDs in comparison to energy-integrating detectors (EIDs) in the linear regime for which pulse pileup can be ignored.
Results:
The detector exhibited highly linear mean signal response across the system operating range and agreed well with theoretical prediction, as did the system MTF and NPS. The DQE analyzed as a function of kilovolt (peak), exposure, detector threshold, and readout mode revealed important considerations for system optimization. The model also demonstrated the important implications of false counts from both additive electronic noise and charge sharing and highlighted the system design and operational parameters that most affect detector performance in the presence of such factors: for example, increasing the detector threshold from 0 to 100 (arbitrary units of pulse height threshold roughly equivalent to 0.5 and 6 keV energy threshold, respectively), increased the f50 (spatial-frequency at which the MTF falls to a value of 0.50) by ∼30% with corresponding improvement in DQE. The range in exposure and additive noise for which PCDs yield intrinsically higher DQE was quantified, showing performance advantages under conditions of very low-dose, high additive noise, and high fidelity rejection of coincident photons.
Conclusions:
The model for PCD signal and noise performance agreed with measurements of detector signal, MTF, and NPS and provided a useful basis for understanding complex dependencies in PCD imaging performance and the potential advantages (and disadvantages) in comparison to EIDs as well as an important guide to task-based optimization in developing new PCD imaging systems.
Keywords: photon counting detector, cascaded systems analysis, modulation transfer function, noise-power spectrum, detective quantum efficiency, image quality, charge sharing model
1. INTRODUCTION
Photon counting detector (PCD) systems are an emerging medical imaging technology with potential applications in low-dose radiography,1,2 mammography,3–5 tomography,6–8 and energy-resolved imaging.9–11 The detection medium in PCDs includes CdZnTe (Refs. 12–15) and Si-strip detectors,16,17 microchannel plates,18 image intensifier based systems,19 and dual-material detectors.20 These technologies exploit potential advantages of reduced electronics noise and the ability to discriminate the energy of detected x-ray photons, each providing the potential for improved contrast to noise ratio.21 While the underlying physics of PCD systems has been studied extensively over the last decade, with investigation of spectral models,22 detector scatter models,23 and computer simulation,24 there has been less work on the fundamental image quality characteristics, modeling, and analysis of Fourier metrics of modulation transfer function (MTF), noise-power spectrum (NPS), and detective quantum efficiency (DQE).25,26 A cascaded systems model of signal and noise transfer characteristics, as previously developed for flat panel detectors (FPDs)27–29 and other types of energy-integrating detectors (EIDs)30–32 would provide a powerful tool for system development and understanding the factors that govern imaging performance, especially in the early stages of system design, development, and optimization.
Recent work established by Tanguay et al.33 provides a basis for cascaded systems analysis of PCDs. Such work highlights the distinction between previously established models of EIDs—for example, FPDs—and PCD systems involving a signal threshold stage. Specifically, a PCD model should consider the propagation of the probabilistic distribution of image quanta arising from a single x-ray interaction through each stage, rather than simply following the mean signal, MTF, and NPS. The distribution is modeled as a binomial selection process including both the magnitude (probability density) and spatial distribution at each stage, thereby enabling the application of a threshold at the appropriate point in the imaging chain. The threshold amounts to an acceptance of signal above a given energy (recorded as “counts”) and rejection of signal below that energy—potentially eliminating electronic noise, but as shown below, imparting effects on mean signal and spatial resolution as well. The work reported below extends the cascaded systems framework reported by Tanguay et al.25 to consider the spatially dependent transfer implications of thresholding as well as charge sharing, additive noise, and count rate-independent spectral distortion. The model is also validated in comparison to physical measurements with a Si-strip PCD and exercised as a guide to optimizing system performance in selection of optimal threshold values and examining the effect of detector design on DQE. Finally, the model is used to highlight the fundamental advantages (and disadvantages) of photon counting in comparison to energy integration.
2. THEORETICAL METHODS
2.A. A cascaded systems model for PCDs
The PCD imaging chain is modeled as a cascade of stages, where each stage represents a physical process in which the distribution of image quanta changes in number (amplification or loss), spatial distribution (blur or integration), or is sampled at discrete locations. For PCDs, there is an additional stage (Stage 7 below) corresponding to the application of a threshold, which imparts important effects on the mean signal, charge sharing, electronic noise, false counts, and sampling effects—all with direct influence on DQE. Preliminary analysis was presented previously,34 expanded here to include details of the analytical model and an expanded investigation of PCD performance.
The sections below describe the model for signal and noise propagation in the PCD imaging chain, with the gain stages reflecting a binomial selection process as described by Tanguay et al.25 and extension to the spatially varying implications of threshold-dependent gain. For the specific PCD used in this work (MicroDose Si-strip detector, Philips Healthcare, Solna, Sweden), model parameters are derived below and summarized in Table I. Because the system was operated well below the exposure rate at which pulse pileup effects become significant—specifically, ∼6 × 103 x-rays/pixel/s (∼100 x-rays/pixel for a 15 ms x-ray pulse) compared to the count rate limit of ∼3 × 106 x-rays/pixel/s (∼4.5 × 104 x-rays/pixel for a 15 ms x-ray pulse) as shown below and in previous work35—such nonlinearities were not considered in the current model.
TABLE I.
Model parameters for each stage in the imaging chain, with values calculated at nominal operating conditions for the Si-strip PCD system in Fig. 2. For the silicon-strip detector, the sampling distance in the y direction, by, is large, and sampling in the y direction is assumed to be independent (infinitely spaced).
| Model parameter | Description | 35 kVp | 70 kVp |
|---|---|---|---|
| Incident fluence per exposure (X) | 2.88 × 105 x-rays/mm2/mR | 6.64 × 105 x-rays/mm2/mR | |
| Photon interaction probability | 0.68 | 0.26 | |
| Gain in secondary quanta | 8000 electrons | 11 500 electrons | |
| T3 | Charge cloud diffusion | σ3 = 0.015 mm | |
| Charge collection efficiency | 0.99 | ||
| T5 | Aperture | ax = 0.05 mm, ay = 0.55 mm | |
| σ6 | Additive noise | ||
| t7 | Threshold | 1500 electrons | |
| III8 | Sampling function | bx = 0.05 or 0.1 mm | |
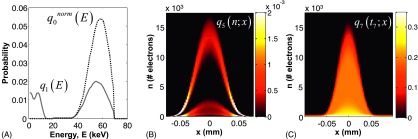
Stage 0: Incident x-ray spectrum. The incident x-ray spectrum was simulated using the spektr implementation36 of TASMIP,37 nominally 35 kVp with added filtration of 2 mm Al and 4 cm water or 70 kVp with added filtration of 2 mm Al and 1.2 mm Cu approximating objects in breast or extremities applications, respectively. As illustrated in Fig. 1(A) for a 70 kVp beam, the normalized spectrum, gives the probability distribution of one incident photon having energy E0.
FIG. 1.
Distribution of quanta at various stages in the imaging chain. Table I provides a summary of system parameters. (A) Normalized incident photon spectrum at 70 kVp (Stage 0) and spectrum of interacting photons (Stage 1). (B) Stage 5 distribution of quanta collected at a distance x from the site of interaction (taken here as y = 0, and aperture size ax = 0.05 mm and ay = 0.55 mm). (C) Distribution of quanta at Stage 7 counted at any location (x) for a given threshold (t7) (also shown for the case y = 0).
Stage 1: Interaction of x-ray quanta. Propagation of the distribution through Stage 1 considers energy-dependent interactions in the detector. Typical models assume a mean interaction probability () derived from the total cross section of the detector material and a binomial selection process with variance in the gain given by . However, the distribution of energies absorbed by the detector is important in analysis of PCD systems, and photoelectric and Compton interactions impart distinct energy distributions that must be considered in the propagation of signal and noise. The supplementary material57 available via EPAPS provides detailed description of the distinct distributions arising from photoelectric and Compton interactions similar to the analysis by Hajdok et al.38 The resulting distribution of interactions at Stage 1 is
| (1) |
where q1PE represents the normalized distribution of photons undergoing a photoelectric interaction in the detector, and q1C represents that undergoing a Compton interaction. The latter accounts for both the scenario of scatter followed by escape [giving the low-energy peak in Fig. 1(A)] and scatter followed by reabsorption (with the total energy deposited equal to the energy of the incident photon). The relative contribution of photoelectric and Compton interactions is combined according to the relative cross section at each energy [ and , respectively], such that . The probability that a photon passes through the detector without interacting gives the “zero-energy” term in the distribution, .
Stage 2: Generation of secondary quanta. Stage 2 describes the conversion of energy to secondary quanta (electron–hole pairs). The distribution of the number (n) of secondary quanta is modeled as
| (2a) |
where is a probability distribution function describing the generation of n electron–hole (e–h) pairs from a single photon interaction at energy E. The mean number of e–h pairs generated at each energy is determined by W, the work function of the detector material. The distribution g2 may be modeled as a Poisson process or by a broader distribution characterized by a Poisson excess, but in materials such as Si the variance is reduced according to the Fano factor (F = 0.115). The distribution of secondary quanta is therefore modeled as a Gaussian distribution that includes the Fano factor
| (2b) |
| (2c) |
with the variance , and N is the number of quanta (continuous variable). The distribution was discretized by evaluating at positive integer values of N and normalizing so that .
Stage 3: Spatial spreading of secondary quanta. At Stage 3, secondary quanta undergo spatial redistribution (stochastic scatter) according to a point spread function, , modeled as a Gaussian
| (3) |
where σ3 is the characteristic width of charge carrier diffusion, and (ξ,η) are spatial dimensions in x and y domains, respectively, corresponding to the relocation of a secondary quantum. For a blur stage, the probability of one quantum continuing to the next stage is , indicating that a spatial blurring stage propagates all quanta from the previous stage, and the number of quanta is preserved. For simplicity, we assume a normally incident x-ray photon and symmetric diffusion, though previous work39,40 has suggested asymmetric spread of secondary quanta for obliquely incident x-rays.
Stage 4: Collection efficiency of secondary quanta. At Stage 4, the loss of secondary quanta due to effects such as e-h absorption or trapping41 is modeled as a binomial selection with loss characterized by the factor, g4. This quantity is assumed independent of position, which is a fair assumption for high-quality semiconductors free of defects.
Stage 5: Integration of secondary quanta. Integration of quanta by the detector aperture at Stage 5 is given by the convolution in Eq. (4b), where x and y denote the displacement between the center of the aperture and the point of interaction in the x and y domain, and ax and ay are the dimensions of the aperture. This considers the effect of the relative displacement between the aperture and the center of , with the distribution at Stage 5 given by
| (4a) |
| (4b) |
Equation (4a) is a binomial distribution representing the collection of n5 secondary quanta generated within a virtual aperture located at any point relative to the interaction. The probability of successfully collecting a single secondary quantum at (x, y) is given by p5(x, y). Equation (4b) assumes uniform collection sensitivity across the (rect function) aperture, though the model allows for more complex aperture models, e.g., a trapezoidal function.42 The distribution of secondary quanta computed at all possible locations in the x domain (taking y = 0 for simplicity) is shown in Fig. 1(C), where the probability distribution (vertical axis) is shown as an intensity map at each x location (horizontal axis) about the point of interaction. Each column in Fig. 1(B) is the now familiar distribution of quanta (including, for example, the Compton peak at low n), and the distribution is modulated at increased x according to the binomial selection in Eq. (4a). The model thereby describes both the statistical (n) and spatial (x) distribution of quanta, with reduced probability of counts recorded at greater distance from the site of interaction <5 × 103 electrons collected for |x| > 0.04 mm in Fig. 1(B).
Stage 6: Additive noise. Stage 6 models the addition of electronics noise prior to readout, modeled as a Gaussian-distributed random variable with characteristic width σadd
| (5a) |
| (5b) |
The probability distribution resulting from the addition of electronics noise is equal to the probability distribution of a sum of two random variables (namely, n5 representing the number of quanta collected in Stage 5 and n6 representing the additive noise) and is given by the convolution of their respective individual distributions in Eq. (5a). Note that is discretized in the same manner as the distribution of secondary quanta discussed in Stage 2.
Stage 7: Threshold. At Stage 7, a threshold (t7) is applied to the distribution, giving q7(t7; x, y), the probability of collecting more than t7 secondary quanta at location (x, y)
| (6) |
The probability of collecting a number of secondary quanta exceeding the threshold is calculated for all possible (x, y) locations of the aperture in Stage 5, implying that a single x-ray photon interaction may result in a count above threshold in multiple apertures. As detailed in Appendix A, depending on the characteristics of the detector system [e.g., the radius of charge carrier diffusion (σ3), the additive noise level (σadd), and the threshold (t7)], such multiple counts (“double counts”) can degrade signal fidelity by introducing false counts. Similarly, additive noise registering above threshold is a potential source of false counts. The relationship of detector threshold to false counts arising from charge sharing and/or additive noise is described in Appendices A and B.
Stage 8: Sampling. Finally, the signal is sampled at Stage 8, represented by multiplication of with a spatial domain comb function, , with the parameters equal to the sampling distance (pixel pitch) in the x and y directions and (x0, y0) the relative displacement between the point of photon interaction and the center of the apertures
| (7) |
Sampling corresponds to convolution in the Fourier domain between the (Fourier transform of the) presampling signal and a comb function at intervals of the sampling frequency (1/bx). While q7 gives the likelihood of recording a count at a given threshold, the recorded signal itself is binary—0 if the signal is below threshold and 1 if the signal (including true and false counts) is above threshold.
2.B. Fourier metrics of imaging performance
The geometry of the Si-strip detector (Fig. 2 and Table I) allows analysis of MTF, NPS, and DQE in terms of a single spatial-frequency (fx) dimension (1D), since the aperture in the y direction (ay = 550 μm) is much greater than the aperture width in the x direction (ax = 50 μm) and the MTF in the y direction is determined by the aperture of a precollimator (not integral to the detector and not used in this work). Additionally, the individual Si wafers are isolated by metal septa in the y direction, preventing electron scatter between adjacent wafers; therefore, correlation in the y direction is considered negligible. The model detailed above provides a general basis for the 2D MTF, NPS, and DQE, and in Secs. 2.B.1–2.B.3, each metric is shown for 2D. In Secs. 3 and 4, analysis is shown in the 1D (fx) domain, since the central slice is a nearly complete representation of the Fourier characteristics of the system due to the large ay aperture.
FIG. 2.
Experimental setup. (A) An imaging bench with an edge-on Si-strip PCD. The detector is capable of readout at multiple detector threshold bins. The edge-on detection geometry is illustrated in (B), where photons are incident along the z direction, and readout is performed in the x direction, with bronze septa separating each Si wafer in the y direction. (C) Diagram of individual Si wafers (not to scale) illustrating the large detector thickness (3.6 mm) in the z direction for increased interaction probability and fine (50 μm) pixel pitch in the x direction. Individual wafers are aligned with the divergent beam, so the tilt angles η and ν are nonzero and different for each wafer depending on its position. (D) An example CT reconstruction of a wrist phantom obtained with the PCD detector (70 kVp, 162 mAs).
2.B.1. MTF
The presampling MTF is computed from the point spread function [PSF(x, y)] at a given threshold t, and taking , where u and v are the Fourier coordinates associated with the x and y directions, respectively. The notation t is interchangeable with t7 (Stage 7, above). Theoretical calculation of the PSF and MTF is based on the distribution q7 shown above, and measurement of the presampling MTF is described below (Sec. 3.B).
2.B.2. NPS
The NPS at a threshold, t, is computed as
| (8a) |
where is the incident x-ray fluence (photons/mm2), γ is the system gain
| (8b) |
and * denotes Fourier domain convolution.
2.B.3. DQE
The system gain, MTF, and NPS are combined to yield the DQE
| (9) |
As described in Stage 7 and Appendix A, “false” counts are defined as the recording of a photon interaction when an interaction did not occur (e.g., due to electronic noise) or also resulted in a count in another detector element (e.g., due to charge sharing) and represents a source of variability in estimation of the total number of photon interactions. The analysis of DQE therefore distinguishes true counts [i.e., true system gain, , defined as the probability of one incident photon yielding exactly one count in the corresponding detector element] and total counts arising from a single incident photon [i.e., the total system gain in Eq. (8b)]. The effects of false counts on the DQE—in particular, the dependence of charge sharing and additive noise effects on detector threshold, and the potential to reduce false counts via coincidence detection—are investigated in Sec. 4.B.
3. EXPERIMENTAL METHODS
3.A. Imaging bench for photon counting CT
As illustrated in Fig. 2, an imaging bench was built to test PCD imaging performance as predicted by the model and serve as a basis for the development of new PCD CT systems. The bench includes an x-ray source (XRS-125-7K-P, Source-Ray, Ronkonkoma, NY), computer-controlled translation and rotation stages (PK266-03A-P1, Velmex, Bloomfield, NY, with minimum step size 0.00635 mm and 0.0125°, respectively), and an edge-on Si-strip PCD (MicroDose, Philips Healthcare, Solna, Sweden) originally developed for mammography, with (0.05 × 0.550) mm2 pixel size (x and y directions) and 3.6 mm thickness (z direction), as illustrated in Fig. 2(C). An example CT reconstruction of a hand phantom (natural human skeleton in tissue-equivalent plastic) is shown in Fig. 2(D), acquired on the PCD bench at 70 kVp, 0.075 mAs per projection, 360 projections over 360° and reconstructed using 3D filtered backprojection.
The detector features coincidence detection logic that identifies when counts are recorded by adjacent pixels within a small time window (τco). With coincidence rejection enabled, the two counts are considered to represent the same photon, and a count is assigned only to the pixel with the higher pulse height. The time window τco determines the so-called dead time extension, as two or more distinct photon interactions occurring over adjacent pixels during this time window will also be considered coincident, resulting in loss of true signal. The model incorporates the effects of coincidence rejection as detailed in Appendix A. Assuming a detector dead time of ∼180 ns as specified by the manufacturer, a coincidence rejection dead time extension of τco = 20 ns,35 and fluence as reported in Table I for a 70 kVp beam, only ∼0.1% of all incident photons are within the dead time window even with coincidence circuitry active. These coincident counts are postprocessed such that the pixel recording the larger pulse height is taken to record the “true” count, and the other count is rejected. In the nominal readout mode, coincidence detection is on by default. For measurements without coincidence detection, the system deactivates every other pixel (giving pixel pitch bx = 0.1 mm) such that a coincident event in adjacent pixels will never be recorded. This scenario of bx = 2ax is not intended for typical image acquisition, but is included as a testing mode for investigating the effects of charge sharing. The measurement of presampling MTF is not affected by sampling distance, so the measurements presented in Sec. 4 are not affected by sampling effects resulting from turning off coincidence rejection.
Measurements were performed at a tube voltage of 70 kVp, added filtration of 2 mm Al plus 1.2 mm of Cu (approximating attenuation by 10 cm water), tube current varied from 1 to 7 mA, x-ray pulse duration of 15 ms, and detector readout at 1 frame/s. A basic calculation of tube output in spektr36 suggests that a typical exposure (70 kVp, 4 mA, 15 ms pulse, 10 cm water equivalent filtration) with a source–detector distance of 653 mm and pixel size of (0.05 × 0.55) mm2 amounts to fewer than 100 photons per pixel per frame, which is well below the count rate limit of this PCD.35
3.B. Measurement of detector signal, MTF, and NPS
The performance of the Si-strip PCD system (Fig. 2) was evaluated in terms of the mean signal, MTF, NPS, and DQE. To relate the measured and predicted detector response, the threshold in secondary quanta (t, with units of secondary quanta) must be converted to the detector pulse height threshold (D, with units of arbitrary detector threshold corresponding to pulse height in millivolts). Section II of the supplementary material provides further discussion of the empirical relationship of t and D, a process governed by the pulse shaper and digitizer in converting charge carriers to a voltage pulse height.57 A comparator determines if a count is above the voltage threshold D, and the pulse height monotonically increases with increased number of charge carriers. Saturation occurs when the pulse height exceeds the capacity of the pulse shaper and digitizer, resulting in a nonlinear mapping of charge carrier threshold and pulse height threshold. The mapping was described by an empirical fit of the form D = c1 − c2e−c3t (for t > c4) and D = c2c3e−c2c3t (for t ≤ c4), where c1 describes the maximum detector threshold, c2 the zero-threshold offset, c3 the saturation rolloff, and c4 the range of linear operation. The parameters c1–c4 were determined by fitting the predicted mean signal and the measured detector signal (at 70 kVp, 4 mA, 15 ms pulse time) and were found to be consistent with previous work35 in mammography (e.g., ∼25 keV saturation energy and ∼3 keV noise floor). These parameters were sufficient for testing the model and could be adjusted according to other potential applications, e.g., higher saturation energy for CT applications involving a higher energy incident spectrum.
The mean detector signal was measured from flood-field images acquired at various settings of detector threshold. Gain correction was performed to account for residual pixel-to-pixel differences after trimming the individual thresholds to adjust for varying pulse height amplification. An empirical fit of the mean signal response (Fig. 3) with and without coincidence rejection suggested a coincidence rejection efficiency of rm = 0.35. This relatively low rejection efficiency is likely due to “leakage” resulting from an inability of the circuitry to distinguish between two simultaneous pulses of similar (saturated) pulse heights at 70 kVp.35
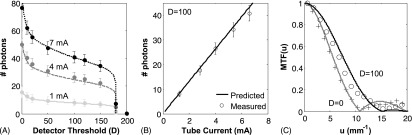
FIG. 3.
Predicted and measured mean signal response as a function of (A) detector threshold and (B) tube current. The detector response is linear over the operating range of the x-ray tube. (C) Presampling MTF at two levels of detector threshold (D = 0 and D = 100).
The MTF was measured using a 0.5 mm thick tungsten edge abutting and parallel to the face of the detector. The beam was collimated to ∼1 × 1 cm2 at the face of the x-ray tube to minimize off-focal radiation. An oversampled edge-spread function (ESF) was formed from 30 images of the tungsten edge in which the edge was translated in increments of 6.35 μm via the computer-controlled translation stage between each image. Data from a continuous row of pixels were analyzed for each image, and the oversampled ESF was generated by interleaving the ESF images according to the displacement of the tungsten edge. A numerical derivative of the ESF was computed, and the tails of the resulting line spread function (LSF) at less than 1% of the peak magnitude were smoothed by a sliding (1 × 7) mean filter to reduce high-frequency noise.43,44 The discrete Fourier transform of the area-normalized LSF was computed to arrive at the presampling MTF.
The NPS was measured from an ensemble of flood-field images at detector threshold values ranging from D = 0 to D = 150 (t range from 0 to 2.4 × 103 electrons). For each threshold, 30 flood-field images were acquired (70 kVp, 2 mm Al and 1.2 mm Cu added filtration, 1–7 mA, 15 ms pulse length). Each flood-field image consisted of ∼100 individual edge-on Si-strip detector wafers, with ∼1500 pixels per wafer. These data were processed in 58 regions of interest (300 pixels each) with continuous adjacent pixels within each wafer, yielding a total of 1740 noise realizations for each setting of milliampere and threshold. These data were linearly detrended to account for anode heel effect, and each image was gain-corrected at each threshold. The mean signal was subtracted from each noise realization, and the squared modulus of the Fourier transform was computed and normalized by the pixel pitch and number of pixels in each realization.45 The resulting 1740 NPS estimates were averaged to yield the ensemble NPS.
4. RESULTS
4.A. Comparison of theory and measurement
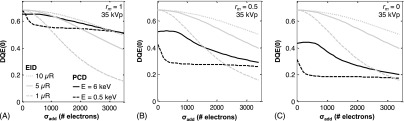
The predictions of mean signal, MTF, and NPS derived from cascaded system analysis were compared to measurements at nominal parameters (70 kVp and without coincidence rejection) as described in Sec. 3. As shown in Fig. 3(A), detector signal response was measured at various milliamperes and detector threshold, with the mean signal predicted as in Sec. 2. The mean signal decreases monotonically as detector threshold is increased, reflecting a larger number of counts rejected at higher threshold. As shown in Fig. 3(B) for a fixed threshold (D = 100), the mean signal, , is linear with exposure (tube current). The system gain for one incident photon, γ, does not exhibit a dependence on exposure over the range of tube currents investigated in the current system. A slight deviation from linearity is observed at tube current greater than ∼7 mA, confirming that the PCD is operating at count rates well below the pileup regime. As shown in Fig. 3(C), the MTF was evaluated at low (D = 0) and nominal (D = 100) detector thresholds, showing an improvement in transfer characteristic at higher threshold. As the distance between the point of photon interaction and the center of the pixel is increased, the likelihood of collecting secondary quanta in the pixel is reduced (per Stages 5 and 7 of the model). Therefore, raising the threshold rejects signal collected far from the point of interaction and improves the effective PSF by reducing the relative contribution of adjacent apertures from multiple counts or detector crosstalk. (See supplementary material Sec. III for analysis of PSF at various levels of detector threshold.57) A potential disadvantage of using a higher threshold is reduced signal, as shown in Fig. 3(A). Overall, theory and measurement were in reasonably good agreement, quantified in terms of a Pearson’s correlation coefficient (R value in a linear regression of measured versus theoretical values). The correlation coefficient was greater than 0.93 for all results shown in Figs. 3–5 except where specifically noted.
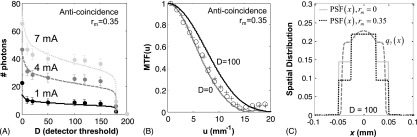
FIG. 5.
Predicted and measured signal response with the coincidence rejection circuit enabled (rm = 0.35). (A) The mean signal as a function of detector threshold. (B) The presampling MTF shows an improvement especially at low thresholds due to rejection of counts resulting from charge sharing. (C) PSF with and without coincidence rejection, showing an improvement (narrowing of the PSF) with reduction of double counts.
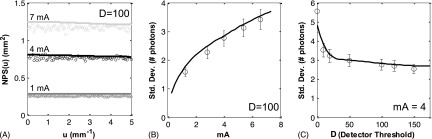
The spatial-frequency-dependent NPS is shown in Fig. 4(A) and is found to be largely uncorrelated at all exposure levels for the nominal operating threshold despite the detector cross talk caused by charge sharing evident in the PSF. The whitening of the NPS arises from undersampling associated with doubling of the sampling distance (bx = 0.1 mm) in this readout mode (see Sec. 3.A) without a corresponding doubling of aperture size. If the detector could be fully sampled in this readout mode (and the aliasing effect correspondingly reduced), then the broadening of the PSF would be more clearly evident in bandlimiting of the NPS.26,46 Such results are demonstrated in the supplementary material, Sec. III.A.57 As shown in Fig. 4(B), individual pixel noise computed from the standard deviation of a single pixel in successive frames was seen to increase with the square root of the exposure, as expected for a Poisson distributed random variable, in good agreement with model predictions. In Fig. 4(C), the individual pixel noise is plotted as a function of threshold (with pixel noise given by the integral of the 2D NPS over the Nyquist region). The frequency dependence of the NPS (not shown) was verified in this readout mode to be white (uncorrelated) for all threshold values, D > 20. At the lowest threshold settings, the magnitude of the noise increases dramatically due to additive noise. This effect is predicted by the model (Appendix B); however, individual pixels with varying behavior in the pulse shapers and small differences in gain (detector trim differences) were found to count additive noise in varying degrees, and the error in gain calibration resulted in a slight overestimation of the noise at D < 10 (giving a reduced correlation coefficient of 0.81).
FIG. 4.
Predicted and measured NPS and pixel noise. (A) The NPS at various exposure levels for a fixed detector threshold (D = 100), showing a “white” NPS with reasonable agreement between theory and measurement. (B) The standard deviation in pixel value (noise) measured and predicted as a function of tube current. (C) Pixel noise measured and predicted as a function of threshold at a fixed exposure level (tube current 4 mA).
4.B. Effect of charge sharing on PCD performance
The effects of charge sharing on PCD performance primarily involve a contribution of false counts [calculated from q7(x, y; t)] from multiple adjacent pixels recording a count for the same photon interaction. As discussed in Appendix A, the effective PSF is a weighted combination of rect functions representing the PSF of a single count, a double count, etc. This suggests that as the threshold is reduced, the contribution from instances of multiple counting is increased, leading to a larger proportion of rect functions from multiple counting and broadening the overall PSF. Supplementary material Sec. III.A provides further analysis and discussion.57 The effects of charge sharing on signal response are shown in Fig. 5(A), where the predicted and measured mean signals are shown for the detector operated with anticoincidence circuitry enabled. A discrepancy at high threshold might be expected due to channel leakage associated with high-energy charge sharing events as previously reported35 for this detector (a reduced correlation coefficient of 0.91 and 0.93 for the case of 4 and 7 mA, respectively). These effects are evident in the measurement of mean signal and spatial resolution, as seen in the 7 mA measurements in Fig. 5. Channel leakage can cause the majority of counts recorded at high threshold to be saturated, which can confound the coincidence rejection logic, resulting in a higher than expected signal. For the nominal detector threshold, however, the linearity of the signal response was preserved when the coincidence rejection circuitry was enabled, indicating that the dead time loss remained largely unchanged. In comparing the mean signal with coincidence rejection as shown in Fig. 5(A) to that without coincidence rejection [Fig. 3(A)], we observe little or no effect on the number of counts reported at high thresholds, since most counts at high thresholds are single counts, whereas at low threshold (D < ∼ 50) the signal is reduced by ∼10%–20% due to the large proportion of double counts.
Analysis of the count coefficients, wm (detailed in Appendix A), showed that coincidence rejection reduced the ratio of double counts (w2) to single counts (w1), which is reflected in Fig. 5 as an improvement in the presampling MTF at all thresholds [e.g., comparing Figs. 5(B) and 3(C)]. The improvement is most pronounced for low thresholds where charge sharing events are strongest, although it is still apparent to a smaller degree at the nominal threshold of D = 100 [Fig. 5(B)]. The dependence of the MTF on threshold in coincidence rejection mode is less pronounced than predicted by the model (with a reduced Pearson’s coefficient of 0.91 and 0.92 for D = 0 and D = 100, respectively), which is attributed in part to the channel leakage effect. The improved MTF [i.e., narrower PSF as shown in Fig. 5(C)] indicates improved spatial resolution associated with coincidence rejection.
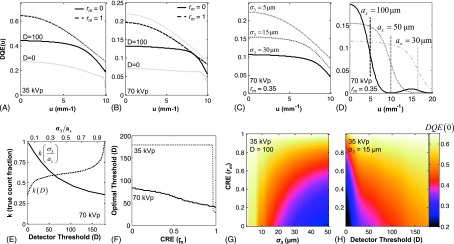
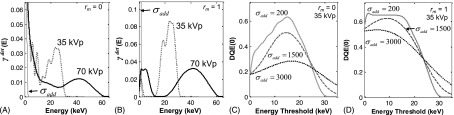
The effects of charge sharing on spatial-frequency-dependent detector performance are further illustrated in Figs. 6(A)–6(D) as a function of exposure conditions (beam energy) and PCD parameters (threshold, charge carrier diffusion, and pixel size). As shown in Fig. 6(A), the DQE at low threshold (D = 0) and low energy (35 kVp) suffers without coincidence rejection due to an increase in false counts. At the same energy, raising the threshold improves both high-frequency DQE and the zero-frequency DQE. A detector with perfect coincidence rejection efficiency (CRE, rm = 1) was simulated, and the resulting DQE at low and high thresholds is shown as dotted lines. With perfect coincidence rejection, the threshold effect is eliminated. At higher tube voltage [70 kVp, Fig. 6(B)], the detector performance at low and high thresholds without coincidence rejection mirrors that at low energy, but with an overall decrease in the DQE due to a reduction in quantum detection efficiency. For a detector with perfect coincidence detection, the DQE at high threshold is worse than that at low threshold due to rejection of true low-energy counts arising from Compton interactions. See Figs. 7(A) and 7(B) and the supplementary material for further discussion of the contribution of low-energy Compton events to true counts.57 The effect is also somewhat apparent at 35 kVp, but at 70 kVp a larger portion of interactions are Compton, making the effect more pronounced.
FIG. 6.
The effects of charge sharing as a function of various system parameters. The frequency dependent DQE(u) is shown at (A) 35 kVp and (B) 70 kVp with 4 and 10 cm of water filtration. The DQE(u) is also shown for various levels of (C) charge carrier diffusion and (D) pixel size with Nyquist frequency demarked by vertical dashed lines. The reduction in DQE(0) at low coincidence rejection efficiency is due to a reduction in the true count fraction, shown in (E). In (F), the optimal detector threshold is shown at 35 and 70 kVp, demonstrating a strong dependence of optimal threshold on kVp. The reduction of charge sharing effects by coincidence rejection is shown to benefit DQE(0) computed as a function of (G) charge carrier diffusion radius and (H) detector threshold.
FIG. 7.
Effect of additive noise on the detected spectrum and DQE. (A) The detected spectrum without coincidence rejection. (B) The detected spectrum with perfect coincidence rejection, showing that charge sharing effects at the nominal additive noise level tend to dominate over additive noise unless coincidence rejection is employed. (C) and (D) Zero-frequency DQE computed as a function of energy threshold (C) without coincidence rejection and (D) with perfect coincidence rejection.
In Fig. 6(C), the effect of charge carrier diffusion is shown for three different diffusion lengths (σ3). Improving the charge carrier spread function (reducing σ3) increases both the high-frequency performance (as expected from reduced blur) and improves DQE(0) due to a reduction in false counts from charge sharing. Similarly, changing the aperture or pixel size [Fig. 6(D)] reflects a tradeoff between a loss in high-frequency performance due to a reduction in the Nyquist frequency and an improvement in the low-frequency DQE from a reduction of charge sharing. It should be noted that increasing the aperture size imparts distinct implications for PCDs compared, for example, to FPDs. Increasing the aperture size does not give an appreciable improvement in the ratio of signal to additive noise, unlike in EIDs.47 Instead, the benefit of larger apertures stems from a reduction in the chance that a single photon will contribute secondary quanta to multiple pixels, i.e., reduced probability of charge sharing.
The true count fraction, k, is defined as k = γtrue/γ and shown in Fig. 6(E). The true count fraction computed as a function of threshold (dotted line) indicates that more than half of all recorded counts at low threshold (D < 20) are false counts (from both charge sharing and additive noise), but at high thresholds (D > 150), almost all counts are true. A “perfect” threshold set equal to the maximum possible number of secondary quanta generated by a photon interaction would yield unity k, but the system gain (γ) would be nearly zero. The solid line shows the true count fraction as a function of the ratio of diffusion radius (σ3) to aperture size (ax). For diffusion radius much smaller than aperture size, nearly all secondary quanta generated by a photon interaction are collected by a single pixel, rendering charge sharing negligible. On the other hand, if the charge carrier diffusion radius is much greater than the aperture size, almost all photon interactions result in multiple pixels receiving some secondary quanta, increasing false counts.
Figure 6(F) shows the optimal detector threshold for various levels of coincidence rejection efficiency at 35 and 70 kVp. The optimal threshold is that which maximizes DQE by best separating the additive noise from the signal and balancing the reduction in charge sharing versus the corresponding reduction in true signal. For a 35 kVp beam, a high threshold is optimal: increasing the threshold rejects relatively few true counts (the low-energy Compton peak is small, Fig. 7) compared to a large number of false counts resulting from charge sharing. For a 70 kVp beam, there is a much larger Compton peak compared to the additive noise, and the optimal threshold balances the rejection of both additive noise and Compton signal with charge sharing rejection.
Figures 6(G) and 6(H) illustrates PCD performance in terms of DQE(0) for a number of pertinent parameters. The zero-frequency DQE is shown for brevity, and since the DQE(u) of Figs. 6(A)–6(D) are nearly flat over a fairly broad range of parameters, the analysis conveys many of the pertinent ramifications of the system design parameters under consideration. Figure 6(G) shows that as charge carrier diffusion increases, coincidence rejection becomes increasingly important. Figure 6(H) shows that for low energies, the choice of detector threshold is less important. At low coincidence rejection efficiency, the detector threshold needs to be selected to balance tradeoffs among additive noise, charge sharing, and collection of true signal as discussed in relation to Fig. 6(F).
4.C. Effects of additive noise on PCD performance and spectral resolution
As detailed in Appendix B, the effects of additive noise on PCD performance primarily involve a contribution of false counts at low thresholds (largely determined by the behavior of the pulse shaper and the ASIC pulse height gain) and a “blurring” effect on the detected energy spectrum. As seen in Fig. 7(A), for the PCD operating without coincidence detection, the nominal additive noise contribution to the signal is relatively small for energies greater than 1 keV. However, comparing with a PCD capable of perfect coincidence rejection [Fig. 7(B)], nearly all of the signal at E < 10 keV (at 35 kVp) [and E < 30 keV at 70 kVp in Fig. 7(A)] is due to charge sharing events registered as counts. Even with perfect coincidence rejection, however, a threshold that is high enough to reject additive noise unavoidably rejects a portion of the low-energy counts resulting from Compton interactions. This is tantamount to a reduction of the quantum detection efficiency of the detector and contributes to the different ranges of optimal detector threshold seen in Fig. 6.
The effects of additive noise and coincidence rejection efficiency on DQE(0) are shown in Figs. 7(C) and 7(D). In addition to the strong dependence of optimal threshold on beam energy shown in Fig. 6(F), the optimum depends on additive noise and coincidence rejection efficiency. Without coincidence rejection [Fig. 7(C)], the optimal threshold exhibits a weak dependence on additive noise until the magnitude of the additive noise overcomes the charge sharing effects contributing to false counts (σadd > 1500). In Fig. 7(D), on the other hand, a detector with perfect coincidence rejection has an optimal threshold with a much stronger dependence on additive noise, since there is no contribution of false counts from charge sharing at low thresholds. The result is intuitive in that reduction of charge sharing effects allows a lower threshold (and higher signal) with reduced effect of additive noise.
4.D. Potential advantages (and disadvantages) of photon counting
While EIDs (for example, FPDs) have been a widespread base technology for x-ray detection for more than 15 years, and PCDs have become increasingly prevalent over the last decade, the fundamental advantages and disadvantages of each has been only somewhat rigorously assessed. For PCDs, the benefit of reduced (effectively zero) electronics noise is often noted by virtue of thresholding, as is the improved energy weighting and the potential for energy discrimination and spectral imaging.48 The latter effects are outside the scope of the current work and were not included in the analysis below. However, at least a portion of the low-energy Compton interactions are lost in selecting a threshold that rejects the entirety of the additive noise distribution [for example, as in Figs. 7(A) and 7(B)]. To compare the fundamental advantages and disadvantages of the thresholding step, consider a hypothetical EID with the same nominal parameters as the PCD system described above (Table I). For purposes of this analysis, the only difference between the PCD and the hypothetical EID is the ability of the former to threshold the detected signal at a voltage pulse height corresponding to the number of collected secondary quanta and the resulting binary nature of the recorded signal. The effects of dead time loss (pulse pileup and chance coincidence) are ignored, as discussed above. The EID therefore has equivalent quantum detection efficiency (g1), gain and spread in secondary quanta (g2 and T3), aperture size (T5), electronics noise (σadd), etc. and was modeled according to well-established cascaded system analysis in previous work.49
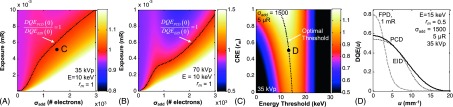
As shown in Fig. 8(A), a PCD system operating with perfect coincidence rejection (rm = 1) at a typical threshold level (E = 6 keV, approximately equal to D = 100 for the system in Sec. 3.A) selected to reject additive noise suffers from a slight reduction in DQE(0) compared to an identically parameterized EID due to the loss of low-energy Compton interactions. Reduction of the threshold (e.g., to E = 0.5 keV, approximately equal to D = 5 for the system in Sec. 3.A) results in an improvement at lower additive noise values, but causes the PCD to suffer as additive noise is increased. Furthermore, Figs. 8(B) and 8(C) show that as the coincidence rejection decreases, the advantage of PCDs at all levels of additive noise and dose decreases appreciably, but still maintains regions of operation at high noise and low dose that are advantageous to that of the hypothetical EID. This analysis allows selection of an optimal threshold that balances the tradeoffs between the loss in Compton counts and the influence of additive noise. With reduced coincidence rejection efficiency, false counts from charge sharing occur at low-energy thresholds [see Fig. 6(A)] and remove the advantage of a low threshold which does not reject the low-energy Compton signal.
FIG. 8.
Performance of a PCD in comparison to a hypothetical EID of equivalent design (but without the ability for signal thresholding). The plot shows DQE(0) for the two systems as a function of additive noise at (A) perfect coincidence rejection efficiency (rm = 1), (B) imperfect coincidence rejection efficiency (rm = 0.5), and (C) no coincidence rejection (rm = 0). The DQE(0) for the PCD is nearly independent of dose and was evaluated at two threshold settings [nominal 6 keV (solid black line) and a low-energy threshold of 0.5 keV (dotted black line)]. The DQE(0) for the EID is shown at three dose levels: 10 μR (dotted gray line), 5 μR (solid gray line), and 1 μR (dashed gray line).
Further comparison between the PCD and the hypothetical, identical EID is shown as a function of dose, additive noise, incident energy, threshold, and coincidence rejection efficiency in Fig. 9. These calculations show the range of operating conditions at low dose and/or high additive noise for which the application of a threshold in the PCD systems is beneficial in comparison to the energy-integrating system. Note, however, that the hypothetical EID enjoys a quantum gain ( electrons) that is much larger than for typical scintillators and less efficient semiconductors, so the performance of the hypothetical system at low dose (and higher additive noise) is greater than should be expected for a realistic EID. The point here is to illustrate the fundamental advantage (and disadvantage) of thresholding, all other factors being equal, and analysis for a realistic EID (viz., a FPD) is shown below.
FIG. 9.
Comparison of a PCD and a hypothetical EID system with the same physical parameters. The ratio of DQE(0) for a PCD to that of an EID is plotted as a function of dose and additive noise at (A) 35 kVp and (B) 70 kVp behind 4 and 10 cm of water, respectively. (C) At fixed additive noise (σadd = 1500 e) and exposure (5 μR), the DQE(0) ratio is evaluated as a function of threshold and coincidence rejection efficiencies. (D) At fixed additive noise (σadd = 1500 e), coincidence rejection (rm = 0.5), exposure (5 μR), and threshold (E = 15 keV), the spatial-frequency-dependent DQE is shown for the PCD and the hypothetical EID in comparison to a FPD.
Perfect coincidence rejection is assumed in Fig. 9(A) for a 35 kVp beam, leaving additive noise as the only contributor of false counts for the PCD. The threshold was fixed at E = 10 keV to give good separation of the additive noise (σadd = 0–3000 electrons) from the true signal spectrum. In the regime of low additive noise and high dose, the EID is shown to slightly outperform the PCD, because the EID is operating in close to ideal circumstances (strongly quantum limited) while the PCD suffers a small loss due to the rejection of the Compton interactions. The effect of frequency was evaluated and found to have minimal effect on the relative performance of the PCD versus the EID. Further evaluation of DQE(u, v) is within the capability of the model and certainly of interest in future work. In Fig. 9(B), the identical scenario is shown for a 70 kVp beam. At higher incident energies, the Compton interaction cross section comprises a larger portion of the total cross section, and a threshold of E = 10 keV therefore rejects a larger portion of the interacting photons. This results in a stronger reduction in DQE(0) and a reduction in the dose range for which the PCD is advantageous in comparison to the EID.
The relative performance of EIDs and PCDs with suboptimal coincidence rejection and different thresholds is discussed further in supplementary materials Sec. III.B, showing the region where PCD performance is equivalent or superior to that of the hypothetical EID is strongly dependent on coincidence rejection efficiency.57 Figure 9(C) summarizes these results—at a fixed dose and additive noise level—as a function of coincidence rejection efficiency and detector threshold. The EID performance is independent of these parameters. For a given additive noise level, dose, and coincidence rejection efficiency, there is an optimal threshold at which PCD performance is maximized (indicated with the dashed black line). At low-energy threshold and low coincidence rejection efficiency, the PCD performance suffers due to the introduction of false counts from charge sharing effects. As the threshold is increased above ∼25 keV, the PCD again suffers in comparison to the EID due to the rejection of true signal (high-energy Compton interactions and photoelectric interactions).
In Fig. 9(D), the spatial-frequency-dependent DQE of the PCD and hypothetical EID is shown at fixed dose, additive noise, threshold, and coincidence rejection efficiency. The PCD shows a modest improvement at low spatial-frequency, and a more pronounced improvement in comparison to the EID at higher frequencies. To provide a realistic base of comparison, and because the gain at Stage 2 is so high (higher than would be expected for a typical EID employing a scintillator), the performance is plotted in comparison to that of a “typical” FPD as modeled in previous work.49–51 The FPD was modeled according to a CsI:Tl scintillator (150 mg/cm2 thickness), , T3 determined by the scintillator thickness, , T5 given by a sinc function for ax = 0.05 mm, and σadd = 1000 e. This more realistic representation of an energy-integrating FPD exhibits lower gain in Stage 2 and a blurrier Stage 3, achieving comparable performance to the PCD only down to ∼1 mR. As shown in Fig. 9(D), the DQE for the FPD (gray dashed curve) is higher at low spatial-frequency due to the higher atomic number of the CsI:Tl scintillator (higher g1); however, the high-frequency performance is limited by blur in the scintillator, which greatly exceeds that of charge carrier diffusion in the silicon-strip detector.
5. CONCLUSIONS
A cascaded systems model has been developed for the analysis of the imaging performance characteristics of PCD systems, building upon more than a decade of well-established modeling of signal and noise propagation in energy-integrating detectors (e.g., FPDs) and extends analysis to include effects that are unique to PCDs. The model was validated in comparison to measurements and illustrates the threshold dependence of the MTF, extending previous work by Acciavatti and Maidment.26 The model also complements recent work in detector physics specifically modeling a single stage—e.g., spectral distortion effects52,53—to include a more complete framework for spatial-frequency-dependent signal and noise characteristics. Among the findings of the current work are (i) illustration of numerous important factors of system performance, such as the effects of detector threshold on DQE as reported by Tanguay et al.,33 (ii) revealing the effects of charge sharing and false counts, (iii) validation of theoretical predictions in comparison to experimental measurements on a PCD benchtop across a wide range of exposure and detector operating conditions, (iv) formulation of a framework for system optimization, and (v) a basis for more rigorous understanding of the potential advantages (and disadvantages) of PCDs in comparison to conventional energy integrators. The model also introduces the concept of a threshold-dependent effective PSF given by a weighted combination of aperture functions and incorporates coincidence rejection in the analytical framework for PCD imaging performance.
The current model is not without limitations, as acknowledged in part in Sec. 2. Among these is the assumption that pulse pileup—in which multiple photons are incident onto the same pixel during the dead time of the detector—and chance coincidence—in which multiple photons are incident on adjacent pixels at a nearly coincident time and blocked by the anti-coincidence logic—are negligible. As demonstrated in the experimental measurements, however, these assumptions appear to be valid for the PCD used in this work over nearly the entire range of operating techniques [kilovolt (peak) and milliamperes], where only a small departure from linearity was observed at the highest exposure rates. For PCD systems with larger pixel size, more compact geometry, and increased dead time compared to the Si detector considered in this work, pileup effects may degrade detector response. Extension of the analytical model to encompass both charge sharing (as shown in this work) and pileup effects (to be considered in future work) would benefit system design and optimization for such configurations.
The model was shown to demonstrate reasonable agreement with the measured signal and noise characteristics of the PCD, including spatial resolution (MTF), spectral characteristics (signal versus threshold), and stochastic noise characteristics (NPS). These aspects of detector performance are important to consider as such PCD systems begin to enter application in various areas of radiographic/mammographic and tomographic imaging. Such characteristics not only govern the fundamental low-dose performance of such systems but also the ability for energy discrimination, which is the subject of future work in extension of the model. The model adapts equally well to a variety of PCD configurations distinct from the Si-strip detector considered in this work. For example, the model allows analysis of the potential benefit of improved quantum detection efficiency of detector materials such as CdTe (higher atomic number) weighed against the tradeoffs of poor charge transport of holes (increased σ3 and reduced g4) and K-fluorescence. In particular, K-fluorescent photons can degrade the resolution and increase charge sharing events. This can be incorporated in the model as a parallel cascade54 representing spatial relocation at Stage 2. As in previous work,55 the distribution for photoelectric and Compton interactions would be split in Stage 1, treated independently in Stages 2–4 (including K-fluorescent effects) and recombined in Stage 5.
Finally, the model provides a rigorous basis for understanding the fundamental performance advantages and limits of PCDs in comparison to conventional energy integrators. Future work includes extension of the model to distributions of quanta in the temporal domain (pulse pileup and chance coincidence), a more complete detector scatter model (Rayleigh and multiple Compton scatter), extension of the model to other detector material types, 3D image reconstruction, and material decomposition in spectral CT.
ACKNOWLEDGMENTS
The research was supported by NIH Grant Nos. 2R01-CA-112163 and T32EB010021. The authors extend thanks to Håkan Langemark, Mathias Beer, and Vignesh Natarajan (Philips Healthcare) for assistance with instrumentation of the PCD used in this work.
APPENDIX A: THE EFFECT OF CHARGE SHARING ON PCD PERFORMANCE
As described in Sec. 2.A, a single photon can contribute counts to multiple detector elements. For example, if the spatial extent of the charge carrier cloud arising at Stage 3 spans more than a single pixel, all pixels that collect charge carriers from a photon interaction have a chance to record a count, resulting in a system gain that can be greater than unity. This phenomenon, called charge sharing or pixel crosstalk, causes a loss of fidelity in the recorded data. Both the true system gain, , and the total system gain, , can be computed from the distribution, derived in Stage 7, as an expectation value of the sampled signal, with consideration for the sampling step in Stage 8 yielding an “unmodulated” signal of 1 when a count is recorded and a signal of 0 if a count is not recorded. A count coefficient, , can be computed to describe the likelihood that a single incident photon at threshold t will contribute counts to exactly m pixels
| (A1) |
For example, m = 1 corresponds to a coefficient describing the probability of one pixel recording one count, m = 2 corresponds to the probability of two pixels recording one count each (for a total of two counts), etc. By definition, , since it is assumed that if a photon generates a detectable signal, then the likelihood of zero counts is zero. Note that the likelihood of interaction of the photon is included in the calculation of q7 from Stage 1.
The effects of charge sharing can be at least partially mitigated in PCD systems, such as the one in this work, by detection of temporally coincident counts in adjacent pixels. This effect can be included in the count coefficient as a modification of for m > 1 by a CRE coefficient, denoted rm, as
| (A2) |
A rejection efficiency of rm = 1 corresponds to perfect coincidence detection (a photon interaction contributes counts only to the pixel directly beneath it) and a rejection efficiency of 0 means nothing is rejected (e.g., a PCD without coincidence detection).
The expected mean signal resulting from a single photon interaction, γ(t), can then be computed as
| (A3) |
where can be equivalently interpreted as the total system gain (detector counts per incident x-ray) and x0 represents the phase difference between the sampling matrix and the photon interaction.56 The expected true system gain is then , where can be equivalently interpreted as the likelihood that one incident photon will contribute one count to the detector element directly under the point of interaction.
The count coefficients, , are ideally limited simply by the quantum detection efficiency (the likelihood of the photon interacting at Stage 1) and the integration of secondary quanta at Stage 5 resulting in a count above threshold. However, with a sufficiently broad spread (σ3) of secondary quanta at Stage 3, a small aperture size (ax) at Stage 5, or a low threshold (t) at Stage 7, the terms wm for m > 1 can be nonzero, meaning that more than one pixel records a count from a single interaction. As a result, γ(t) can in principle exceed unity due to false (alternatively, “double”) counts. The model describes how both charge sharing and additive noise can result in such false counts, presenting a source of error that must be accounted in the propagation of signal and noise.
Furthermore, the PSF associated with a single photon counted by the detector is a rect function, since the detector records photons in a binary fashion (0 or 1) and is therefore unmodulated. However, again due to the charge sharing effect, the width of this rect function is in multiples of ax—i.e., one photon can contribute counts to one pixel resulting in an rect of width ax, two pixels resulting in a rect of width 2ax, etc. The “effective” point spread function is computed as a weighted sum of such rect functions,56 with the weights proportional to the count coefficients computed in Eq. (A2)
| (A4) |
| (A5) |
APPENDIX B: THE EFFECT OF ADDITIVE NOISE ON PCD PERFORMANCE AND SPECTRAL RESOLUTION
There are two potential benefits to application of a threshold in PCDs. The first aims to achieve the highest data fidelity by optimally separating the true count distribution from the false-count distribution. A second benefit is provided by the ability to distinguish incident energies. To this end, the threshold, t (in units of secondary quanta) can be approximately remapped to an energy threshold by , where W is the average energy required to liberate a single charge carrier in the detector material, and Et is the energy threshold equivalent. For notational convenience, the subscripts are dropped in further analysis. It is useful to cite the threshold alternatively in terms of detector threshold (D, units proportional to pulse height), charge carrier threshold (t, units of charge carriers), and energy threshold (E, units of energy). From Appendix A, an expected system gain can be computed for any threshold. The threshold can be converted to energy as above, and the numerical derivative can be performed to arrive at the detected energy spectrum, . The detected spectrum for a PCD operating with and without coincidence rejection is shown in Figs. 7(A) and 7(B). It is important to note that the low-energy “noise” associated with the detected spectrum in detectors without coincidence rejection or some other form of charge sharing rejection can be almost entirely attributed to false counts resulting from charge sharing. This effect is compounded by the presence of additive noise (discussed below), but can be mitigated with proper false-count correction.
Additive noise contributes to the low-energy portion of the distribution in quanta and can contribute false counts if the threshold is selected at a value that is too low. Common practice is to select a threshold well above the additive noise level (i.e., t several times larger than σadd), but as can be seen in the energy spectrum of Fig. 7(B), doing so will also set the threshold above the energy of Compton interactions, resulting in a loss of true signal as well. Reducing the threshold increases the detector signal associated with low-energy interactions, but it increases the probability that a recorded count is due to additive noise instead of a true interaction. For a given threshold, the additive noise distribution for a noninteracting photon is
| (B1) |
where is a convolution of the probability of no photon interaction [q5(n = 0; x)] with the additive noise term defined in Eq. (5b). The resulting additive noise distribution after thresholding (denoted ) is given by
| (B2) |
and is the probability of recording a false count at a given threshold t7 and any location x due solely to additive noise. The expected false signal from additive noise is derived in a similar manner as the expected gain in Eq. (A3)
| (B3) |
with the factor, madd, empirically determined from measurement of noise recorded when no photon is incident. For the PCD system under consideration, madd = 3 provided a reasonable match to measured dark-field distributions, accounting for pulse shaper behavior and pulse height sampling rate. This semiempirical approach accounts for the ratio of false-count events resulting from instances where a photon was not incident on the detector as discussed in Tanguay et al.,25 but characterization of the innate detector processes which leads to this false-count ratio is outside the scope of this work.
REFERENCES
- 1.Francke T. et al. , “Dose reduction in medical x-ray imaging using noise free photon counting,” Nucl. Instrum. Methods Phys. Res., Sect. A 471(1–2), 85–87 (2001). 10.1016/S0168-9002(01)00920-2 [DOI] [Google Scholar]
- 2.Weigel S., Berkemeyer S., Girnus R., Sommer A., Lenzen H., and Heindel W., “Digital mammography screening with photon-counting technique: Can a high diagnostic performance be realized at low mean glandular dose?,” Radiology 271(2), 345–355 (2014). 10.1148/radiol.13131181 [DOI] [PubMed] [Google Scholar]
- 3.Cole E. B., Toledano A. Y., Lundqvist M., and Pisano E. D., “Comparison of radiologist performance with photon-counting full-field digital mammography to conventional full-field digital mammography,” Acad. Radiol. 19(8), 916–922 (2012). 10.1016/j.acra.2012.03.005 [DOI] [PubMed] [Google Scholar]
- 4.Thunberg S. J. et al. , “Dose reduction in mammography with photon counting imaging,” Proc. SPIE 5368, 457–465 (2004). 10.1117/12.530649 [DOI] [Google Scholar]
- 5.Fredenberg E., Hemmendorff M., Cederstroöm B., Åslund M., and Danielsson M., “Contrast-enhanced spectral mammography with a photon-counting detector,” Med. Phys. 37(5), 2017–2029 (2010). 10.1118/1.3371689 [DOI] [PubMed] [Google Scholar]
- 6.Maidment A. D. A. et al. , “Evaluation of a photon-counting breast tomosynthesis imaging system,” Proc. SPIE 6142, 61420B (2006). 10.1117/12.654651 [DOI] [Google Scholar]
- 7.Alivov Y., Baturin P., Le H. Q., Ducote J., and Molloi S., “Optimization of K-edge imaging for vulnerable plaques using gold nanoparticles and energy resolved photon counting detectors: A simulation study,” Phys. Med. Biol. 59(1), 135–152 (2014). 10.1088/0031-9155/59/1/135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schmitzberger F. F. et al. , “Development of low-dose photon-counting contrast-enhanced tomosynthesis with spectral imaging,” Radiology 259(2), 558–564 (2011). 10.1148/radiol.11101682 [DOI] [PubMed] [Google Scholar]
- 9.Silkwood J. D., Matthews K. L., and Shikhaliev P. M., “Photon counting spectral breast CT: Effect of adaptive filtration on CT numbers, noise, and contrast to noise ratio,” Med. Phys. 40(5), 051905 (15pp.) (2013). 10.1118/1.4800504 [DOI] [PubMed] [Google Scholar]
- 10.Wang X., Meier D., Taguchi K., Wagenaar D. J., Patt B. E., and Frey E. C., “Material separation in x-ray CT with energy resolved photon-counting detectors,” Med. Phys. 38(3), 1534–1546 (2011). 10.1118/1.3553401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Alessio A. M. and MacDonald L. R., “Quantitative material characterization from multi-energy photon counting CT,” Med. Phys. 40(3), 031108 (8pp.) (2013). 10.1118/1.4790692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Takahashi T. and Watanabe S., “Recent progress in CdTe and CdZnTe detectors,” IEEE Trans. Nucl. Sci. 48(4), 950–959 (2001). 10.1109/23.958705 [DOI] [Google Scholar]
- 13.Redus R. H., Pantazis J. A., Pantazis T. J., Huber A. C., and Cross B. J., “Characterization of CdTe detectors for quantitative x-ray spectroscopy,” IEEE Trans. Nucl. Sci. 56(4), 2524–2532 (2009). 10.1109/TNS.2009.2024149 [DOI] [Google Scholar]
- 14.Iwanczyk J. S. et al. , “Photon counting energy dispersive detector arrays for x-ray imaging,” IEEE Trans. Nucl. Sci. 56(3), 535–542 (2009). 10.1109/TNS.2009.2013709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ruat M. and Ponchut C., “Characterization of a pixelated CdTe x-ray detector using the timepix photon-counting readout chip,” IEEE Trans. Nucl. Sci. 59(5), 2392–2401 (2012). 10.1109/TNS.2012.2210909 [DOI] [Google Scholar]
- 16.Ohsugi T., Onno Y., Sadrozinski H. F.-W., Yoshida S., and Ohsugi T., “Application of silicon strip detectors to x-ray computed tomography,” Nucl. Instrum. Methods Phys. Res., Sect. A 541(1), 412–420 (2005). 10.1016/j.nima.2005.01.083 [DOI] [Google Scholar]
- 17.Beuville E. et al. , “High resolution x-ray imaging using a silicon strip detector,” IEEE Trans. Nucl. Sci. 45(6), 3059–3063 (1998). 10.1109/23.737664 [DOI] [Google Scholar]
- 18.Shikhaliev P. M., Xu T., Le H., and Molloi S., “Scanning-slit photon counting x-ray imaging system using a microchannel plate detector,” Med. Phys. 31(5), 1061–1071 (2004). 10.1118/1.1695651 [DOI] [PubMed] [Google Scholar]
- 19.Kuhls-Gilcrist A., Jain A., Bednarek D. R., and Rudin S., “The solid state x-ray image intensifier (SSXII) in single photon counting (SPC) mode,” Proc. SPIE 7622, 76221P (2010). 10.1117/12.843785 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Koenig T. et al. , “Imaging properties of small-pixel spectroscopic x-ray detectors based on cadmium telluride sensors,” Phys. Med. Biol. 57(21), 6743–6759 (2012). 10.1088/0031-9155/57/21/6743 [DOI] [PubMed] [Google Scholar]
- 21.Tapiovaara M. J. and Wagner R., “SNR and DQE analysis of broad spectrum x-ray imaging,” Phys. Med. Biol. 30(6), 519–529 (1985). 10.1088/0031-9155/30/6/002 [DOI] [Google Scholar]
- 22.Taguchi K., Frey E. C., Wang X., Iwanczyk J. S., and Barber W. C., “An analytical model of the effects of pulse pileup on the energy spectrum recorded by energy resolved photon counting x-ray detectors,” Proc. SPIE 7622, 76221C (2010). 10.1117/12.843753 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yun S., Tanguay J., Kim H. K., and Cunningham I. A., “Cascaded-systems analyses and the detective quantum efficiency of single-Z x-ray detectors including photoelectric, coherent and incoherent interactions,” Med. Phys. 40 , 041916 (17pp.) (2013). 10.1118/1.4794495 [DOI] [PubMed] [Google Scholar]
- 24.Lundqvist M., Cederstrom B., Chmill V., Danielsson M., and Nygren D., “Computer simulations and performance measurements on a silicon strip detector for edge-on imaging,” in Nuclear Science Symposium, 1999. Conference Record. 1999 IEEE (IEEE, Piscataway, NJ, 1999), pp. 433–438. 10.1109/NSSMIC.1999.842522 [DOI] [Google Scholar]
- 25.Tanguay J., Yun S., Kim H. K., and Cunningham I. A., “The detective quantum efficiency of photon-counting x-ray detectors using cascaded-systems analyses,” Med. Phys. 40 , 41913 (15pp.) (2013). 10.1118/1.4794499 [DOI] [PubMed] [Google Scholar]
- 26.Acciavatti R. J. and Maidment A. D. A., “An analytical model of NPS and DQE comparing photon counting and energy integrating detectors,” Proc. SPIE 7622, 76220I (2010). 10.1117/12.845310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Antonuk L. E. et al. , “Strategies to improve the signal and noise performance of active matrix, flat-panel imagers for diagnostic x-ray applications,” Med. Phys. 27 , (2), 289–306 (2000). 10.1118/1.598831 [DOI] [PubMed] [Google Scholar]
- 28.Siewerdsen J. H. et al. , “Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology,” Med. Phys. 24 , 71–89 (1997). 10.1118/1.597919 [DOI] [PubMed] [Google Scholar]
- 29.Tward D. J. and Siewerdsen J. H., “Cascaded systems analysis of the 3D noise transfer characteristics of flat-panel cone-beam CT,” Med. Phys. 35(12), 5510–5529 (2008). 10.1118/1.3002414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhao W., Ji W. G., Debrie A., and Rowlands J. A., “Imaging performance of amorphous selenium based flat-panel detectors for digital mammography: Characterization of a small area prototype detector,” Med. Phys. 30(2), 254–263 (2003). 10.1118/1.1538233 [DOI] [PubMed] [Google Scholar]
- 31.Hajdok G., Yao J., Battista J. J., and Cunningham I. A., “Signal and noise transfer properties of photoelectric interactions in diagnostic x-ray imaging detectors,” Med. Phys. 33(10), 3601–3620 (2006). 10.1118/1.2336507 [DOI] [PubMed] [Google Scholar]
- 32.Richard S. and Siewerdsen J. H., “Cascaded systems analysis of noise reduction algorithms in dual-energy imaging,” Med. Phys. 35(2), 586–601 (2008). 10.1118/1.2826556 [DOI] [PubMed] [Google Scholar]
- 33.Tanguay J., Yun S., Kim H. K., and Cunningham I. A., “Extension of cascaded systems analysis to single-photon-counting x-ray detectors,” Proc. SPIE 8313, 831310 (2012). 10.1117/12.912941 [DOI] [Google Scholar]
- 34.Xu J. et al. , “Cascaded systems modeling of signal, noise, and DQE for x-ray photon counting detectors,” Proc. SPIE 9033 , 903320 (2014). 10.1117/12.2043515 [DOI] [Google Scholar]
- 35.Fredenberg E., Lundqvist M., Cederström B., Åslund M., and Danielsson M., “Energy resolution of a photon-counting silicon strip detector,” Nucl. Instrum. Methods Phys. Res., Sect. A 613(1), 156–162 (2010). 10.1016/j.nima.2009.10.152 [DOI] [Google Scholar]
- 36.Siewerdsen J. H., Waese A. M., Moseley D. J., Richard S., and Jaffray D. A., “Spektr: A computational tool for x-ray spectral analysis and imaging system optimization,” Med. Phys. 31(11), 3057–3067 (2004). 10.1118/1.1758350 [DOI] [PubMed] [Google Scholar]
- 37.Boone J. M. and Seibert J. A., “An accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kV,” Med. Phys. 24(11), 1661–1670 (1997). 10.1118/1.597953 [DOI] [PubMed] [Google Scholar]
- 38.Hajdok G., Battista J. J., and Cunningham I. A., “Fundamental x-ray interaction limits in diagnostic imaging detectors: Spatial resolution,” Med. Phys. 35(7), 3180–3193 (2008). 10.1118/1.2924219 [DOI] [PubMed] [Google Scholar]
- 39.Acciavatti R. J. and Maidment A. D. A., “Optimization of phosphor-based detector design for oblique x-ray incidence in digital breast tomosynthesis,” Med. Phys. 38(11), 6188–6202 (2011). 10.1118/1.3639999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Badano A., Freed M., and Fang Y., “Oblique incidence effects in direct x-ray detectors: A first-order approximation using a physics-based analytical model,” Med. Phys. 38(4), 2095–2098 (2011). 10.1118/1.3567497 [DOI] [PubMed] [Google Scholar]
- 41.Yin S. et al. , “Direct conversion Si and CdZnTe detectors for digital mammography,” Nucl. Instrum. Methods Phys. Res., Sect. A 448(3), 591–597 (2000). 10.1016/S0168-9002(00)00295-3 [DOI] [Google Scholar]
- 42.Schumann L. W. and Lomheim T. S., “Modulation transfer function and quantum efficiency correlation at long wavelengths (greater than 800 nm) in linear charge coupled imagers,” Appl. Opt. 28(9), 1701–1709 (1989). 10.1364/AO.28.001701 [DOI] [PubMed] [Google Scholar]
- 43.Cunningham I. A. and Reid B. K., “Signal and noise in modulation transfer function determinations using the slit, wire, and edge techniques,” Med. Phys. 19(4), 1037–1044 (1992). 10.1118/1.596821 [DOI] [PubMed] [Google Scholar]
- 44.Samei E., Flynn M. J., and Reimann D. A., “A method for measuring the presampled MTF of digital radiographic systems using an edge test device,” Med. Phys. 25(1), 102–113 (1998). 10.1118/1.598165 [DOI] [PubMed] [Google Scholar]
- 45.Siewerdsen J. H., Cunningham I. A., and Jaffray D. A., “A framework for noise-power spectrum analysis of multidimensional images,” Med. Phys. 29(11), 2655–2671 (2002). 10.1118/1.1513158 [DOI] [PubMed] [Google Scholar]
- 46.Fredenberg E., Lundqvist M., Åslund M., Hemmendorff M., Cederström B., and Danielsson M., “A photon-counting detector for dual-energy breast tomosynthesis,” Proc. SPIE 7258, 72581J (2009). 10.1117/12.813037 [DOI] [Google Scholar]
- 47.Antonuk L. E. et al. , “Initial performance evaluation of an indirect-detection, active matrix flat-panel imager (AMFPI) prototype for megavoltage imaging,” Int. J. Radiat. Oncol. 42(2), 437–454 (1998). 10.1016/S0360-3016(98)00210-7 [DOI] [PubMed] [Google Scholar]
- 48.Cahn R. N., Cederström B., Danielsson M., Hall A., Lundqvist M., and Nygren D., “Detective quantum efficiency dependence on x-ray energy weighting in mammography,” Med. Phys. 26(12), 2680–2683 (1999). 10.1118/1.598807 [DOI] [PubMed] [Google Scholar]
- 49.Siewerdsen J. H., Antonuk L. E., El-Mohri Y., Yorkston J., Huang W., and Cunningham I. A., “Signal, noise power spectrum, and detective quantum efficiency of indirect-detection flat-panel imagers for diagnostic radiology,” Med. Phys. 25 , 614–628 (1998). 10.1118/1.598243 [DOI] [PubMed] [Google Scholar]
- 50.Vedantham S. et al. , “Full breast digital mammography with an amorphous silicon-based flat panel detector: Physical characteristics of a clinical prototype,” Med. Phys. 27(3), 558–567 (2000). 10.1118/1.598895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ganguly A., Rudin S., Bednarek D. R., and Hoffmann K. R., “Micro-angiography for neuro-vascular imaging. II. Cascade model analysis,” Med. Phys. 30(11), 3029–3039 (2003). 10.1118/1.1617550 [DOI] [PubMed] [Google Scholar]
- 52.Taguchi K. and Iwanczyk J. S., “Vision 20/20: Single photon counting x-ray detectors in medical imaging,” Med. Phys. 40(10), 100901 (19pp.) (2013). 10.1118/1.4820371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Yveborg M., Danielsson M., and Bornefalk H., “Performance evaluation of a sub-millimetre spectrally resolved CT system on high- and low-frequency imaging tasks: A simulation,” Phys. Med. Biol. 57(8), 2373–2391 (2012). 10.1088/0031-9155/57/8/2373 [DOI] [PubMed] [Google Scholar]
- 54.Yao J. and Cunningham I. A., “Parallel cascades: New ways to describe noise transfer in medical imaging systems,” Med. Phys. 28 , 2020–2038 (2001). 10.1118/1.1405842 [DOI] [PubMed] [Google Scholar]
- 55.Richard S., Siewerdsen J. H., Jaffray D. A., Moseley D. J., and Bakhtiar B., “Generalized DQE analysis of radiographic and dual-energy imaging using flat-panel detectors,” Med. Phys. 32(5), 1397–1413 (2005). 10.1118/1.1901203 [DOI] [PubMed] [Google Scholar]
- 56.Dobbins J. T. III, “Effects of undersampling on the proper interpretation of modulation transfer function, noise power spectra, and noise equivalent quanta of digital imaging systems,” Med. Phys. 22 , 171–181 (1995). 10.1118/1.597600 [DOI] [PubMed] [Google Scholar]
- 57.See supplementary material at http://dx.doi.org/10.1118/1.4894733 E-MPHYA6-41-015410 for additional figures and explanations of concepts discussed throughout the paper.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1118/1.4894733 E-MPHYA6-41-015410 for additional figures and explanations of concepts discussed throughout the paper.