Measurement of bow tie profiles in CT scanners using a real-time dosimeter

Abstract

Purpose:

Several areas of computed tomography (CT) research require knowledge about the intensity profile of the x-ray fan beam that is introduced by a bow tie filter. This information is considered proprietary by CT manufacturers, so noninvasive measurement methods are required. One method using real-time dosimeters has been proposed in the literature. A commercially available dosimeter was used to apply that method, and analysis techniques were developed to extract fan beam profiles from measurements.

Methods:

A real-time ion chamber was placed near the periphery of an empty CT gantry and the dose rate versus time waveform was recorded as the x-ray source rotated about the isocenter. In contrast to previously proposed analysis methods that assumed a pointlike detector, the finite-size ion chamber received varying amounts of coverage by the collimated x-ray beam during rotation, precluding a simple relationship between the source intensity as a function of fan beam angle and measured intensity. A two-parameter model for measurement intensity was developed that included both effective collimation width and source-to-detector distance, which then was iteratively solved to minimize the error between duplicate measurements at corresponding fan beam angles, allowing determination of the fan beam profile from measured dose-rate waveforms. Measurements were performed on five different scanner systems while varying parameters such as collimation, kVp, and bow tie filters. On one system, direct measurements of the bow tie profile were collected for comparison with the real-time dosimeter technique.

Results:

The data analysis method for a finite-size detector was found to produce a fan beam profile estimate with a relative error between duplicate measurement intensities of <5%. It was robust over a wide range of collimation widths (e.g., 1–40 mm), producing fan beam profiles that agreed with a relative error of 1%–5%. Comparison with a direct measurement technique on one system produced agreement with a relative error of 2%–6%. Fan beam profiles were found to differ for different filter types on a given system and between different vendors.

Conclusions:

A commercially available real-time dosimeter probe was found to be a convenient and accurate instrument for measuring fan beam profiles. An analysis method was developed that could handle a wide range of collimation widths by explicitly considering the finite width of the ion chamber. Relative errors in the profiles were found to be less than 5%. Measurements of five different clinical scanners demonstrate the variation in bow tie designs, indicating that generic bow tie models will not be adequate for CT system research.

1. INTRODUCTION

Bow tie filters are commonly used in computed tomography (CT) scanners to create a nonuniform flux across the x-ray fan beam in order to reduce patient dose, minimize scattered radiation, and reduce the dynamic range requirements of detectors.¹ Knowledge of this fan beam intensity profile is necessary in several areas of research:² (1) dose reduction simulators,³ (2) calculation of radiation dose to an individual patient using Monte Carlo techniques,⁴ and (3) iterative statistical reconstruction algorithms.⁵ Unfortunately, bow tie designs are considered proprietary by manufacturers, and their specifications are not generally available to researchers. To remedy this, Boone and coworkers proposed a noninvasive technique to directly measure fan beam profiles, which they termed the “characterization of bow tie relative attenuation (COBRA).”^6,7 Their method uses a real-time radiation monitor positioned near the edge of the scanner’s field of view (FOV) to measure the temporal signal (kerma rate versus time) during the rotation of the x-ray source about the isocenter during an air scan. From the peaks of the temporal signal, the distance of the probe from the isocenter can be calculated, and with this knowledge both the fan beam angle and relative source intensity at each point on the waveform are determined. Initial results based on simulations and experiments promised a solution for noninvasively determining bow tie profiles in a convenient, efficient manner. The Boone group also noted several limitations to their method: a real-time dosimeter with sufficient sensitivity and fast temporal response is necessary; the probe size must be such that it is completely covered by the projected collimated beam (or alternatively, the collimated beam must be completely contained by the probe) over a whole rotation; and noise in peak value measurements of the waveform can propagate as uncertainties in the bow tie profile.

With the recent introduction of a commercially available real-time dosimeter, we were encouraged to utilize the COBRA method for measuring bow tie profiles in our research. In this paper, we describe extensions to the analysis method that overcome its original limitations with detectors with an intermediate size and report on measurements made on multiple CT scanners.

2. MATERIALS AND METHODS

2.A. CT scanners

Measurements reported here were performed at three institutions (University of Pittsburgh, Washington University in St. Louis, and Virginia Commonwealth University), using five CT scanners made by three vendors (General Electric Healthcare—GE Lightspeed Qx/I, VCT; Siemens Medical Solutions—Sensation 64, Definition AS; and Philips Healthcare—Brilliance CT Big Bore). The studied clinical systems included various multirow-detector scanners, which typically have multiple bow tie filters (e.g., body and head), depending on the selected protocol. In many situations, the ion chamber was attached to the patient’s table, requiring axial (step-and-shoot) protocols to keep the probe stationary with scans restricted to repeated single rotations. This complicated data acquisition with the real-time probe due to the arbitrary timing of start of the x-ray source. Protocols were set such that the CTDI_vol was approximately 20 mGy, with rotation times varying from 0.5 to 2 s, collimations varying from 1 mm (2 × 0.5 mm) to 40 mm (64 × 0.625 mm), and kVp from 90 to 140. In the case of one of the scanners, manufacturer-supplied software allowed sinogram data, which corresponded to intensity measurements, to be extracted from the signal processing path, resulting in an independent assessment of the fan-beam profile.

2.B. Measurement by real-time dosimeter

2.B.1. Data acquisition

Real-time dosimeter measurements were acquired with an Accu-Gold digitizer connected to a 10X6-0.6CT ion chamber (Radcal Corporation, Monrovia, CA). The digitizer has a 10 kHz bandwidth and can record temporal waveforms up to 300 s duration, initiated by self-triggering using the internal “standard” threshold. This provided greater than 5000 sample points per revolution for all measurements. Provided software on a laptop computer controlled acquisition and stored data for later analysis. The cylindrical ion chamber had active dimensions of 20.7 mm length by 6.4 mm diameter.

The ion chamber was placed in the empty (air only) scanner bore with its axis parallel to the scanner axis of rotation near the periphery of the FOV (e.g., 240–300 mm from the isocenter). Patient-positioning lasers were used to approximately center the long axis of the ion chamber in the middle of the collimated fan beam.

Both step-and-shoot (axial/sequential) and helical/spiral protocols were used. For the former, the x-ray tube would power on at random gantry angles, causing the waveform to have truncated end points for an individual rotation, which resulted in less than one complete cycle recorded (usually cycles would have either a centered primary [Fig. 1(b)] or secondary [Fig. 1(c)] peak). This necessitated repeated acquisitions (sometimes up to 4–5 repeats) to get two partial waveforms that contained both peaks and overlapping intermediate regions that could be combined to constitute a dataset representing one complete cycle. In helical mode, multiple rotation cycles were acquired in a single measurement and a complete one-cycle waveform could be extracted [Fig. 1(d)].

FIG. 1.

Data acquisition waveforms from real-time dosimeter are as follows: (a) helical/spiral scans (probe not on table) give multiple rotations, from which a single cycle can be extracted. Note that waveform peaks alternate between high (probe along central ray closest to source) and low (along central ray furthest from source); (b) step-and-shoot single rotation (probe on table) with trigger giving central peak closest to source; (c) step-and-shoot single rotation with trigger giving central peak furthest from source; (d) for bow tie profile analysis, an extracted composite waveform for one-half revolution was formed [here from (b) and (c)], starting with the central ray farthest from the source and ending with the central ray closest to the source. Over this half revolution, there are two samples at each fan beam angle (one with probe far and one with probe near).

2.B.2. Data analysis

The “Characterization Of Bow tie Relative Attenuation” method⁷ (COBRA) to determine the bow tie profile, as described by Boone⁶ is basically a three-step process: First, the displacement of the dosimeter from the isocenter is estimated, from which the trajectory (position as a function of time) of the dosimeter can be calculated. Next, knowing the trajectory, the fan beam angle and the source-to-dosimeter distance can be calculated. Finally, by scaling the measured intensities for their distance from the source, a source intensity profile as a function of fan beam angle is obtained.

In the measurements reported by the Boone group to date, they have assumed that the intensity (I) measured by the dosimeter has a 1/L² dependence on the distance L from the x-ray source X. Such an inverse square law (ISL) is appropriate for a point detector, i.e., one for which the subtended solid angle of the detector is small enough to be completely within the collimated beam; the subtended solid angle of the detector then decreases as 1/L², since the small size of the detector makes the planar flux variation term cos(θ) approximately unity. They also noted that if a larger detector (wider than the collimated beam) was used, then an inverse law (IL) would be appropriate, since then the solid angle subtended by the detector decreases in only one (longitudinal) dimension. See Fig. 2(b).

FIG. 2.

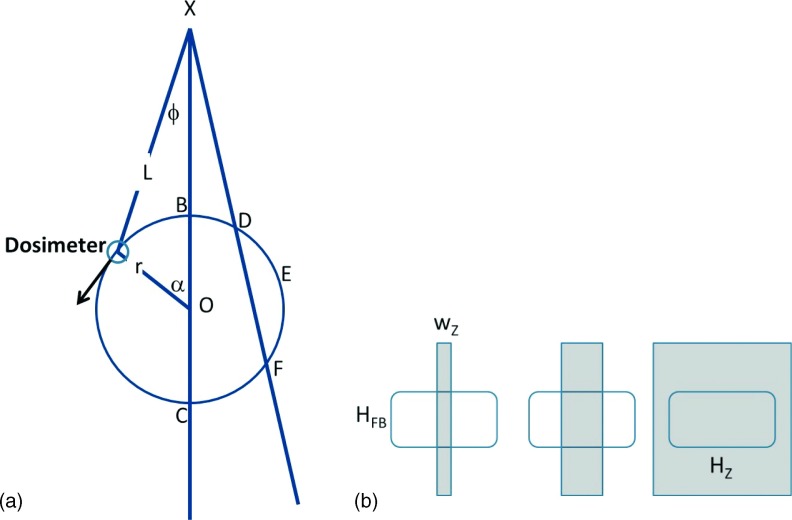
Measurement geometry. (a) In the scanner gantry coordinate system (xy) centered with origin O (isocenter), the dosimeter rotates on circle BDEFCB of radius r with constant dα/dt, being a distance L from the source X at fan beam ϕ w.r.t. the central ray XO. Note that each fan beam angle has two associated dosimeter measurements, corresponding to a near and far position, e.g., B and C, or D and F, except for extremum position E. (b) A detector of size (H_FB × H_z) is illuminated by a collimated beam (gray) that overfills in the fan beam direction and has width w_z in the z-direction. At left, close to the source (e.g., B), the collimated beam width is contained on detector, covering area w_z × H_FB. In center (E), as distance increases the beam width grows linearly but is still contained. At right (C), when detector is overfilled by collimated beam, total area is H_z × H_FB.

Using the point source model and referring to the geometry in Fig. 2(a), the waveform measurements at dosimeter positions B and C (I_B and I_C) along the central ray are related by the ratio of their squared distances from the source, allowing one to solve for the radius of the dosimeter’s position, r, in I_B/I_C = (XO+r)²/(XO − r),² where the source-to-isocenter distance XO is known

$${\displaystyle r=XO*\left(\frac{1-\sqrt{\frac{I_B}{I_C}}}{1+\sqrt{\frac{I_B}{I_C}}}\right).}$$ (1)

Following the first step of determining r and knowing that the gantry rotates at constant speed taking time T per revolution, one can then calculate for any dosimeter point (at time t from start of revolution at B), the distance L from the source

$${\displaystyle L\left(t\right)=\sqrt{{XO}^2+r^2-2*XO*r*cos\left(\frac{2\pi t}{T}\right)}}$$ (2)

and the fan beam angle formed

$${\displaystyle \varphi \left(t\right)=\mathrm{arcsine}\left(\frac{r*sin\left(\frac{2\pi t}{T}\right)}{L\left(t\right)}\right).}$$ (3)

The fan beam profile is then defined as the ratio of the intensity measurement at angle ϕ, weighted by the distance squared, to the intensity measured at the isocenter ray, weighted by the distance squared

$${\displaystyle R\left(\varphi \left(t\right)\right)=\frac{I\left(t\right)*L^2\left(t\right)}{I\left(B\right)*{\left(XO-r\right)}^2}.}$$ (4)

This inverse square law assumption was certainly valid for the simulations of a point dosimeter in Ref. 6 and for the measurements on a clinical scanner in Ref. 7, where a dosimeter having a width of 7 mm was scanned with a collimator width of 38.4 mm. However, the dosimeter that we used was significantly wider (20.7 mm), while on many of the scanners that we wished to measure, the collimator widths varied from 1 to 40 mm. Furthermore, note that these stated collimator widths are referenced to the isocenter, so that as the gantry rotates the effective collimation at the detector location changes due to magnification/demagnification. For example, the effective collimation for the clinical scanner in Ref. 7 varies from 21.5 to 55.2 mm.

In our experiments involving the Radcal dosimeter, applying either of these functional dependencies (1/L, 1/L²) alone to the data resulted in inconsistent data fits. For example, in Fig. 1(d), measurements were made with the dosimeter placed at approximately 250 mm from the isocenter. The ratio of the intensities along the central ray [point B and C in Fig. 2(a)] is 2.92, which would imply a radius of 149 mm from Eq. (1) (or a radius of 279 mm for 1/L dependence), using the logic of Ref. 6. The fact that the measured ratio is between the 1/L and 1/L² values indicates that the ion chamber used was of an intermediate size compared to the collimation width [Fig. 2(b)], i.e., the collimated beam projection on the dosimeter during a rotation of the gantry varied from complete to partial coverage. The Radcal detector has length of 20.7 mm while the effective collimation width due to magnification ranges from 10 to 29 mm for a 20 mm nominal (isocenter) collimation. Off-center positioning and penumbra effects may also contribute to variable distance dependencies.

To accommodate this varying dosimeter coverages, a more complete model was used to relate the intensity of the source at a particular fan beam angle to dosimeter measurements made at some distance L from the source. First, it is assumed that the x-ray density incident on the detector depends on the square of the distance between center of the source and the center of the detector, i.e., effects such as finite focal spot size, beam obliquity, or the heel effect are negligible. These are reasonable assumptions, given that the total subtended angle of the collimation is less than 2° in multirow scanners [corrections tend to vary as cos(θ), 0.1%] and the heel effect has been found to be small⁸ with a dominant linear component⁹ that will average to a constant as the beam magnifies. Therefore, the measured signal depends on the area illuminated on the detector.

In the fan beam angle direction the detector is always overfilled by the projection of the collimator opening, so the dosimeter height H_FB fixes one dimension of the illuminated area [Fig. 2(b)]. In the z-direction, the z width of the beam increases linearly with its distance L from the source based on simple magnification, so w_z = C∗L/SID, with C defined as the collimation at isocenter and SID being the source-to-isocenter distance. Thus, the illuminated area of the detector, A_ill, increases linearly with distance from the source, until the beam overfills the detector, at which point it remains a constant H_z, $A_{\mathrm{ill}}=H_{\mathrm{FB}}\cdot \min \left(H_z,C\cdot L/\mathrm{SID}\right)=A_{\mathrm{dos}}\cdot \min \left(1,L/\Delta \right)$, where Δ ≡ H_Z⋅SID/C is the distance at which the dosimeter becomes completely covered by the collimated beam and A_dos is the dosimeter area. The dosimeter measurement is then related to the source intensity by $I_{\mathrm{dos}}=I_{\mathrm{source}}\cdot A_{\mathrm{dos}}\cdot min\left(1,L/\Delta \right)/L^2$, and the relative fan beam intensities are obtained by applying a weighting factor containing one adjustable parameter Δ, instead of a fixed 1/L or 1/L² factor

$${\displaystyle W\left(L,\Delta \right)=\frac{L^2}{\min \left(\frac{L}{\Delta },1\right)}.}$$ (5)

To determine the parameter Δ, the symmetry of the dosimeter measurements is used, namely that for every half-cycle of the gantry, each fan beam angle is sampled twice, once with the dosimeter close to the source, P₊, [e.g., Fig. 2(a), point D] and once more distant, P₋, [e.g., Fig. 2(a), point F]. (The exception is at the extremum corresponding to the fan beam angle with the ray that is tangential to the circular orbit of the dosimeter, where only one measurement occurs.) By minimizing the difference between the source fan beam intensities (P₊, P₋) derived from two measurements at the same fan beam angle but different source-to-detector distances [e.g., in Fig. 2(a), pairs B and C, or D and F], an iterative procedure can be used to determine parameters r and Δ.

Data analysis begins by extracting a measured waveform corresponding to a one-half gantry revolution. By convention we define the detector measurement corresponding to the central ray furthest from the source as the start position [peak in Fig. 1(c) corresponding to point C in Fig. 2(a)] and the central ray measurement closest to the source as the end position [peak in Fig. 1(b) corresponding to point B in Fig. 2(a)]. For step-and-shoot scans, which have truncated end points due to random beam start angles, two waveforms were combined by locating the central peaks (either secondary or primary) in each of the two scans, registering the overlapping wings of the two scans to each other and then combining them into one complete waveform. For the helical/spiral scans, the centers of the primary/secondary peaks were located, and the data between the two peaks were extracted as one complete half cycle.

To determine the parameters {r, Δ} of our fitting model, we minimize the total mean squared error (MSE) between estimated profile pairs (P₊, P₋) along each fan beam ray (ϕ) using a Nelder–Mead downhill simplex method (fminsearch, matlab, MathWorks, Inc., Natick, MA).

$${\displaystyle \mathrm{MSE}=\frac{1}{{\varphi }_{\max }}\sum _{\varphi =0}^{\varphi ={\varphi }_{\max }}{\left(1-\frac{P_{+}\left(\varphi \right)}{P_{-}\left(\varphi \right)}\right)}^2.}$$ (6)

The results of the analysis are presented by plotting the relative profile versus fan beam angle during a half rotation, which includes two measurements near and far from the source, and the root mean square (rms) error of Eq. (6) is a measure of the precision of the method.

To test the capabilities of this method, an experiment was conducted with the dosimeter positioned at a fixed radius while the collimation (at isocenter) was set to either 12 or 24 mm. Also, a prototype cylindrical slit that was provided by Radcal, Inc., consisting of a lead tube with a 1 mm wide plastic-covered opening, was used to create a point-like detector. For each of the three coverage conditions, three methods (COBRA ISL, COBRA IL, and iterative fitting with variable coverage model) were used to calculate an effective radius (and an effective transition distance Δ for the model fitting). Also at distance Δ, the effective projection beam width B was calculated, including the magnification of the collimator width C and the effect of penumbra due to a finite-sized focal spot (FS) positioned at a distance P_C from the collimator edges

$${\displaystyle B=C*\frac{\Delta }{\mathrm{SID}}+2*\mathrm{FS}*\frac{\left(\Delta -P_C\right)}{P_C}.}$$ (7)

Measurements were performed on five different scanners, varying collimations from 5 to 38 mm, kVp from 80 to 140, and using multiple head and body bow tie filters as available.

3. RESULTS

3.A. Variable coverage method

Including a variable coverage model to account for the beam projection onto the dosimeter accurately fits the experimental results, as seen in Fig. 3. The root mean squared error between the two quarter cycles is 4% in Fig. 3(c) compared to a 7% error with COBRA method in Fig. 3(a). In Fig. 4, three measurements on the same CT scanner are shown that correspond to different beam projections onto the dosimeter: the dosimeter (20.7 mm wide) scanned with 12 and 24 mm collimation, plus a scan with the slit adapter covering the dosimeter to provide an effective 1 mm width (with 24 mm collimation). The measured waveforms show substantial differences in shape [Fig. 4(a)] while the computed bow tie profiles resulting from the analysis are essentially the same [Fig. 4(b)]. Table I presents several aspects for the various fitting models. The radius is calculated in three ways, with the COBRA ISL or IL method resulting in large errors, except for the point detector that is correctly estimated by the ISL. The radii calculated by the variable coverage model agree to better than 1%. The distance Δ, characterizing the transition between 1/L and 1/L², is reported, along with the effective beam width [Eq. (7)] at the transition point Δ. Note that for both collimations the beam width B closely matches the detector width at the distance Δ, as expected. For the point detector, the transition Δ occurs at a distance much closer to the source than the dosimeter actually reaches, indicating a solely ISL behavior.

FIG. 3.

(a) Fan beam profile calculated from Fig. 1(d), using COBRA method with 1/L intensity dependence, showing mismatch between the two measurements at same fan beam angles during gantry rotation—dotted line is gantry rotation from points C to E in Fig. 2(a) and solid line is rotation from E to B; (b) Relative dosimeter measurement as a function of L [inverse of Eq. (5)], showing a transition between 1/L and 1/L² functions (here at a distance of Δ  ∼  700 mm, for a detector length of 20.7 mm and a collimation width of 10 mm at isocenter); and (c) Variable weighting allows a close match of bow tie profiles at each fan beam angle during gantry rotation.

FIG. 4.

Fan beam fittings. (a) Measured profiles with different collimations, top is 16 × 0.75 mm, middle is 16 × 1.5 mm, and bottom is 16 × 0.75 with 1 mm collimated slit. (Order progresses from dependence similar to 1/L to dependence with 1/L².) (b) Fitted fan beam profile plots derived from (a), showing excellent agreement under different acquisition conditions.

TABLE I.

Analysis of three different dosimeter coverage conditions shown in Fig. 4, varying relative beam projection versus detector width, with analysis by COBRA (with ISL or IL) and the model fitting method. Rows show estimated dosimeter-to-isocenter displacement (R) and the rms relative error between measurement pairs at same fan beam angle. For the model fitting, parameters Δ and B(Δ) are shown. It is clear that only the model fitting method provides consistent estimates of dosimeter-to-isocenter displacement (R) and hence consistently low rms error in all three measurement scenarios. [Note that the maximum/minimum source-to-detector physical distances are 390 and 895 mm, so that in the point detector case (detector width = 1 mm) Δ is never reached.].

Detector width (mm)	20.7	20.7	1
Collimation (mm)	12	24	12
ISL: R (mm) [rms error (%)]	155 [27.9]	225 [7.0]	261 [2.5]
IL: R (mm) [rms error (%)]	294 [7.4]	401 [21.8]	449 [26.3]
Model Fit: R (mm) [rms error (%)]	254 [2.8]	257 [2.0]	258 [2.2]
Fitted parameter Δ (mm)	785	486	313
Fitted parameter B(Δ) (mm)	20.5	20.9	6.9

Figure 5 compares the profile calculated by the dosimeter method with profiles measured directly by the gantry detectors using vendor software, at several effective energies. The agreement is generally good (rms error 2%–6%) with some deviation in the wings of the bow tie, where beam hardening occurs. Differences in energy response between ion chamber and solid state CT detectors may be occurring. Figure 6 illustrates selected measured features from different scanners. In (a), the probe was placed outside the scanner FOV, with the profile showing the penumbra at the edge of the fan beam. In (b), profiles for two of the bow ties in a system demonstrate substantial differences in fan beam profiles for different protocols. Finally, plots of body bow tie profiles for three different vendors show substantial differences, indicating that single generic profile would result in significant inaccuracies.

FIG. 5.

Bow tie profiles as function of kVp: left 90 kVp, center 120 kVp, and right 140 kVp. Dosimeter measurements (dots) versus direct measurement from gantry detectors (solid, line extending to 25 degrees). The rms error is 8%–10%, with noticeable differences in the high attenuation portion of the bow tie profile.

FIG. 6.

(a) Bow tie profile with dosimeter placed outside FOV, showing penumbra of the collimator; (b) Profiles of “head” (lower curve) and “body” (upper curve) bow ties, demonstrating change in coverage; (c) Body filter profiles from three vendors, showing significant variation of design, which would preclude the use of one “generic” profile for different systems.

4. DISCUSSION

The need to extend the COBRA method to include intermediate size detectors, such as those now currently commercially available, was demonstrated by analyzing the measured datasets. Regarding the findings that measured fan beam profiles have a complex dependence on detector coverage by the collimated beam, we note that similar phenomena may have been observed in recent work from the Boone group. In the experiments reported by McKenney et al.,¹⁰ where a real-time dosimeter (the same product as used in this paper) was used to make measurements for evaluating the half-value layer of the central ray in a CT scanner, sinusoidal baseline intensity variations were observed (their Fig. 7 on page 369) that could not be completely removed by ISL fittings, indicating that a more complex function might be required.

The model used for beam projection on the probe (an instantaneous transition from IL to ISL) is not exact, as penumbra profile effects and partial coverage are not explicitly included, but the general concept of a transition between a pointlike 2D ISL response and a linelike 1D regime enables the analysis algorithm to accurately handle a range of experimental conditions.

The real-time dosimeter method for acquiring data is convenient and fast. Care must be taken to properly align the probe active area with the center of the collimated beam; otherwise there can be asymmetries in response due to gantry position. Observed inconsistencies between bow tie profiles obtained via different measuring systems may be due to the energy response of detectors, which could be taken into account during analysis.

5. CONCLUSIONS

An improved method was presented for the noninvasive measurement of bow tie profiles using a real-time dosimeter probe. By using an analysis technique that explicitly includes the x-ray beam coverage of intermediate size detectors, a more general class of measurements can be handled, allowing commercially available dosimeters to be used. Results indicate the ability to extract intensity profiles under a wide range of scan protocols, with excellent agreement with profiles obtained from internal scanner measurements.