Abstract
As we explore a scene, our eye movements add global patterns of motion to the retinal image, complicating visual motion produced by self-motion or moving objects. Conventionally, it has been assumed that extra-retinal signals, such as efference copy of smooth pursuit commands, are required to compensate for the visual consequences of eye rotations. We consider an alternative possibility: namely, that the visual system can infer eye rotations from global patterns of image motion. We visually simulated combinations of eye translation and rotation, including perspective distortions that change dynamically over time. We demonstrate that incorporating these “dynamic perspective” cues allows the visual system to generate selectivity for depth sign from motion parallax in macaque area MT, a computation that was previously thought to require extra-retinal signals regarding eye velocity. Our findings suggest novel neural mechanisms that analyze global patterns of visual motion to perform computations that require knowledge of eye rotations.
Introduction
Vision is an active process—we frequently move our eyes, head, and body to acquire visual information to guide our actions. In some cases, self-movement generates visual information that would not be available otherwise, such as the motion parallax cues to depth that accompany translation of the observer1, 2. However, self-movement also complicates interpretation of retinal images. When we rotate our eyes to track a point of interest, we add a pattern of full-field motion to the retinal image, altering the patterns of visual motion that are caused by self-motion or moving objects. The classical viewpoint on this issue is that visual image motion resulting from eye rotations must be discounted by making use of internal signals, such as efference copy of motor commands3. Indeed, there is ample evidence that the brain uses extraretinal signals to attempt to parse out the influence of self-movements on vision4–8.
However, theoretical studies suggest an alternative possibility: under many conditions, the image motion of a rigid scene contains sufficient information to estimate the translational and rotational components of observer movement9, 10. Thus, visual information may also play a role in compensating for self-movement, and there is evidence in the psychophysics literature that the brain makes use of global patterns of visual motion resulting from observer translation11–15.
Consider the case of an observer who translates side to side while counter-rotating their eye to maintain fixation on a world-fixed target (Fig. 1a). This produces dynamic perspective distortions of the image in both stimulus coordinates (here, Cartesian coordinates associated with planar image projection) and in spherical retinal coordinates (Supplementary Movie 1). Under the assumption that the world is stationary (a likely prior), it is sensible for the brain to infer that the resulting images arise from translation and rotation of the eye relative to the scene, rather than from the entire world rotating around a vertical axis through the point of fixation.
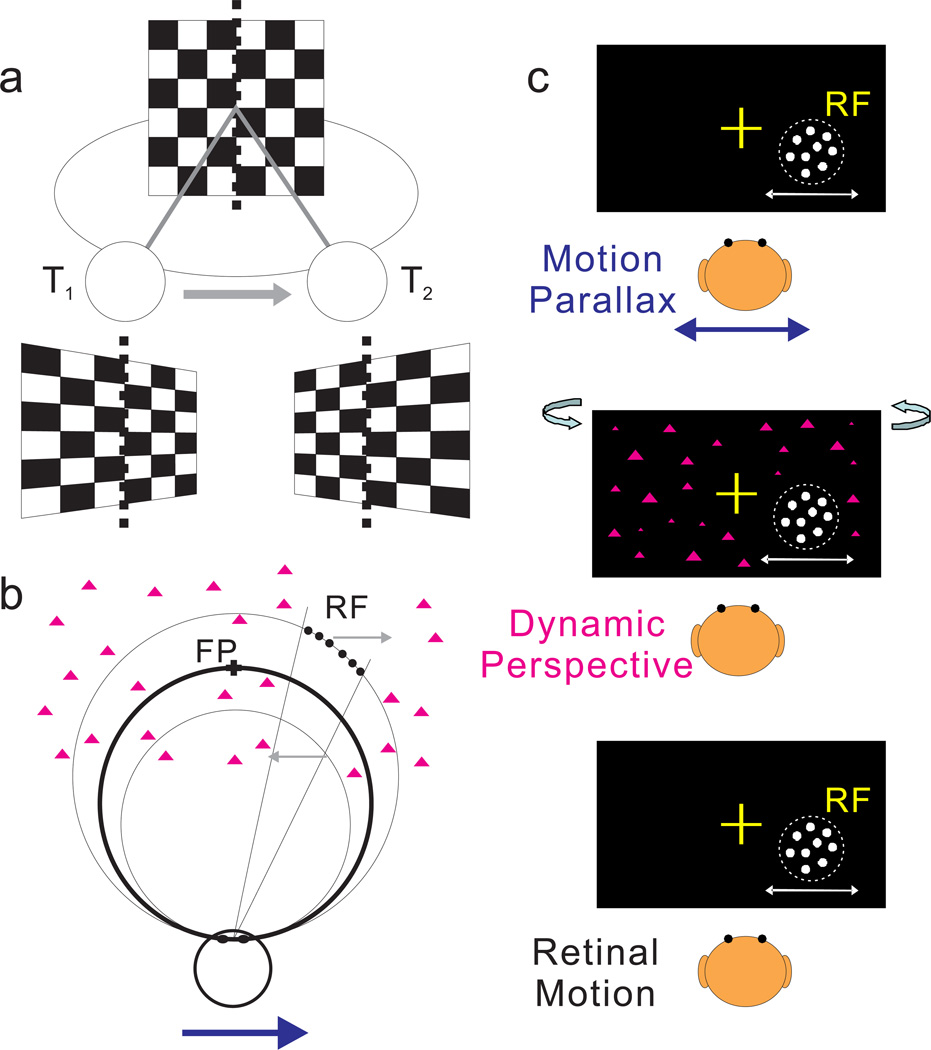
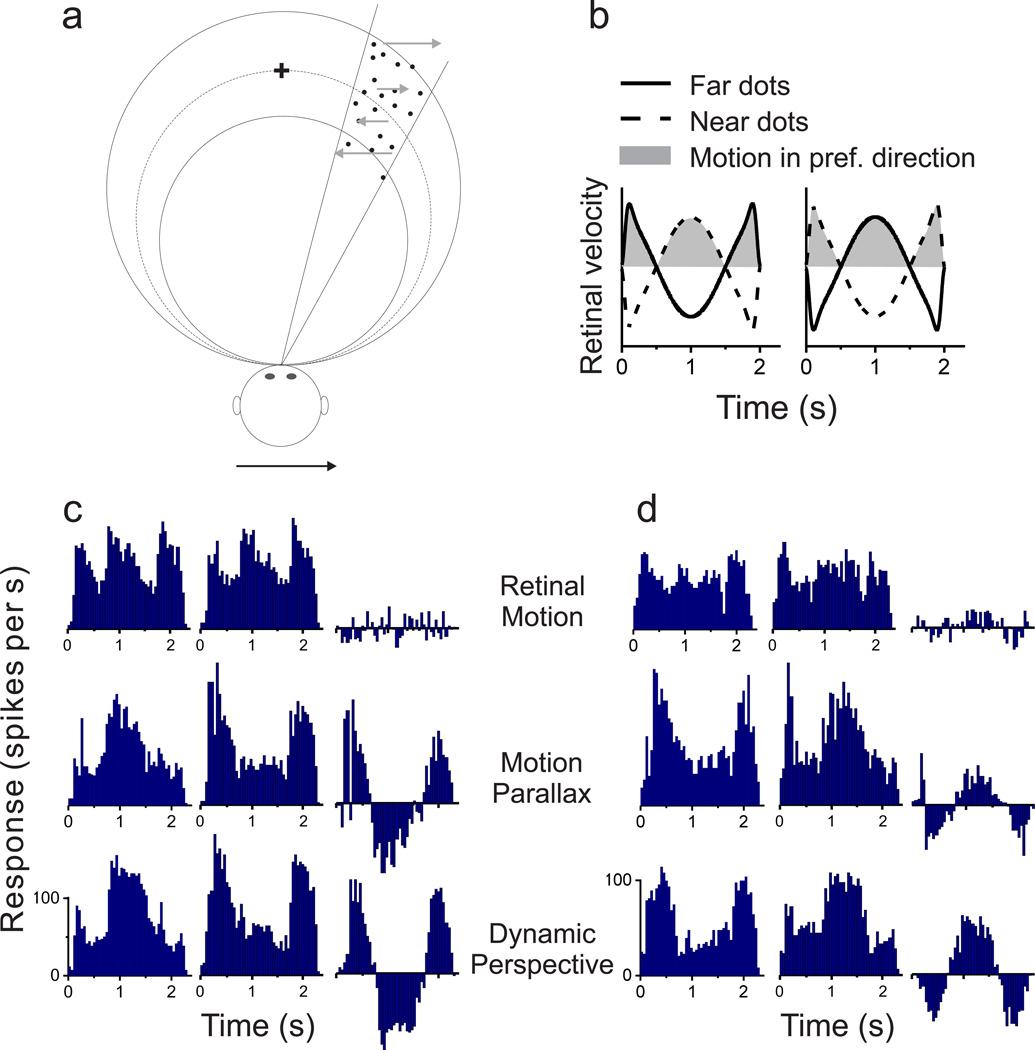
Figure 1. Schematic illustration of dynamic perspective cues and stimuli for measuring depth tuning from motion parallax.
(a) An observer translates from left (at time T1) to right (at time T2) while the observer’s eye (circle) rotates to maintain fixation at the center of a world-fixed checkerboard. As the observer translates, the perspective distortion changes dynamically and is manifest as a rotation of the image (in stimulus coordinates) about a vertical axis through the fixation target (dotted line). Supplementary Movie 1 shows an image sequence resulting from this viewing geometry. (b) Top view illustrating the stimulus geometry. The thick circle represents the locus of points in space for which motion simulates a depth equivalent to zero binocular disparity. The other two circles represent sets of points that have image motion consistent with particular near or far depths (equivalent to −1° and +1° of binocular disparity). Dots within the receptive field (which have no size cues to depth) are shown as filled black circles; background dots (having size cues) are shown as magenta triangles. When the observer moves rightward (blue arrow), near and far dots move in opposite directions (gray arrows). (c) Frontal views for each experimental condition. In the Motion Parallax condition, animals experience full-body translation and make counteractive eye movements to maintain fixation on a world-fixed target (yellow cross). In the Retinal Motion condition, the animal’s head and eyes are stationary, but visual stimuli replicate the image motion experienced in the Motion Parallax condition. The Dynamic Perspective condition is the same as the Retinal Motion condition except that a 3D cloud of background dots was added to the display. Background dots near the receptive field were masked.
Image transformations that accompany translation and rotation of the eye can be described equivalently in either stimulus coordinates or retinal coordinates9, but have different signatures in the two domains. A lateral translation of the eye (Supplementary Fig. 1a) produces no perspective distortion in stimulus coordinates (assuming planar projection), but does induce perspective distortion in (spherical) retinal coordinates (Supplementary Movie 2). By contrast, a pure eye rotation (Supplementary Fig. 1b) is associated with dynamic perspective distortions in stimulus coordinates, but not in retinal coordinates (Supplementary Movie 3). Thus, time-varying perspective distortions in stimulus coordinates can provide information about eye rotation, whereas global motion that lacks perspective distortion in retinal coordinates may be used to infer eye rotation. Here, we refer to the perspective distortions that accompany eye rotation—in stimulus coordinates— as “dynamic perspective” cues16, 17.
Perception of depth from motion parallax provides an ideal system in which to explore whether and how dynamic perspective cues are used in neural computations. In the absence of pictorial depth cues such as occlusion or relative size, the perceived sign of depth (near vs. far) from motion parallax can be ambiguous, unless additional information regarding observer movement is available18, 19. Nawrot and Stroyan20 have demonstrated mathematically that the critical disambiguating variable is the rate of change of eye orientation relative to the scene. This variable could, of course, arise from efference copy of smooth eye movement command signals, and there is overwhelming evidence that eye movement signals are sufficient to perceive depth sign from motion parallax19, 21–23. In addition, we have shown previously that neurons in macaque area MT combine retinal image motion with pursuit eye movement signals, not vestibular signals related to head movements, to signal depth sign from motion parallax24.
Alternatively, dynamic perspective cues (in stimulus coordinates) might also be used to infer the change of eye orientation relative to the scene and to disambiguate perceived depth17. Thus, we tested the hypothesis that dynamic perspective cues could generate depth-sign selectivity in MT neurons, in the absence of physical eye movements. Our results reveal that many MT neurons become selective for depth-sign when dynamic perspective cues are provided via large-field background motion. Moreover, the depth-sign selectivity generated by dynamic perspective cues is generally consistent with that produced by smooth eye movements. Our findings suggest that novel visual mechanisms may play important roles in a variety of important neural computations that involve estimating self-rotations.
Results
We tested whether MT neurons can signal depth sign from motion parallax based on dynamic perspective cues that simulate eye rotation relative to the visual scene (Fig. 1a, b). To compare depth-sign selectivity generated by dynamic perspective and eye movement signals, three stimulus conditions were randomly interleaved (Fig. 1c). In all cases, a small patch of dots overlying the neuron’s receptive field contained motion consistent with one of several depths, but the perceived depth sign (near vs. far) of this stimulus was ambiguous on its own. The motion of the small patch relative to the fixation point was identical in all conditions, and there were no size or density cues to depth within the receptive field. All stimuli for the main experimental conditions (Fig. 1c) were viewed monocularly except for the fixation target, which was presented to both eyes to aid stable vergence.
In the Motion Parallax condition, animals were passively translated along an axis in the frontoparallel plane (determined by the direction preference of the neuron under study) and actively counter-rotated their eyes to maintain fixation on a world-fixed target. In the Dynamic Perspective condition, the animal remained stationary with eyes fixated on a central target while the visual stimulus, including a large-field random-dot background, simulated the same translation and rotation that the eye experienced in the Motion Parallax condition (see Suppl. Movie 4). Finally, in the Retinal Motion control condition, neither eye movement nor dynamic perspective cues were available, such that the depth-sign of the random-dot patch over the receptive field was largely ambiguous (see Suppl. Movie 5). Assuming that the animal maintains gaze accurately on the fixation target, the retinal image motion of the small patch of dots is the same in all conditions.
Example neurons
Responses of a typical MT neuron largely follow retinal image velocity in the Retinal Motion condition (Fig. 2a), with similar response modulations for simulated near and far depths having the same magnitude. As expected from previous studies24–26, the depth tuning curve of this neuron for the Retinal Motion condition is approximately symmetrical around zero depth (Fig. 2d, black curve). We computed a depth-sign discrimination index (DSDI, see Methods)24, 25 to quantify the symmetry of tuning curves. DSDI ranges from −1 to 1, with negative values denoting a near preference and positive values indicating a far preference. For the example neuron, DSDI was not significantly different from zero for the Retinal Motion condition (DSDI = −0.09, P = 0.313, permutation test), reflecting the depth-sign ambiguity of the visual stimulus. Note that depth tuning curves in the Retinal Motion condition typically have a trough centered at zero depth; this reflects speed tuning since the stimulus at zero depth has essentially no retinal image motion.
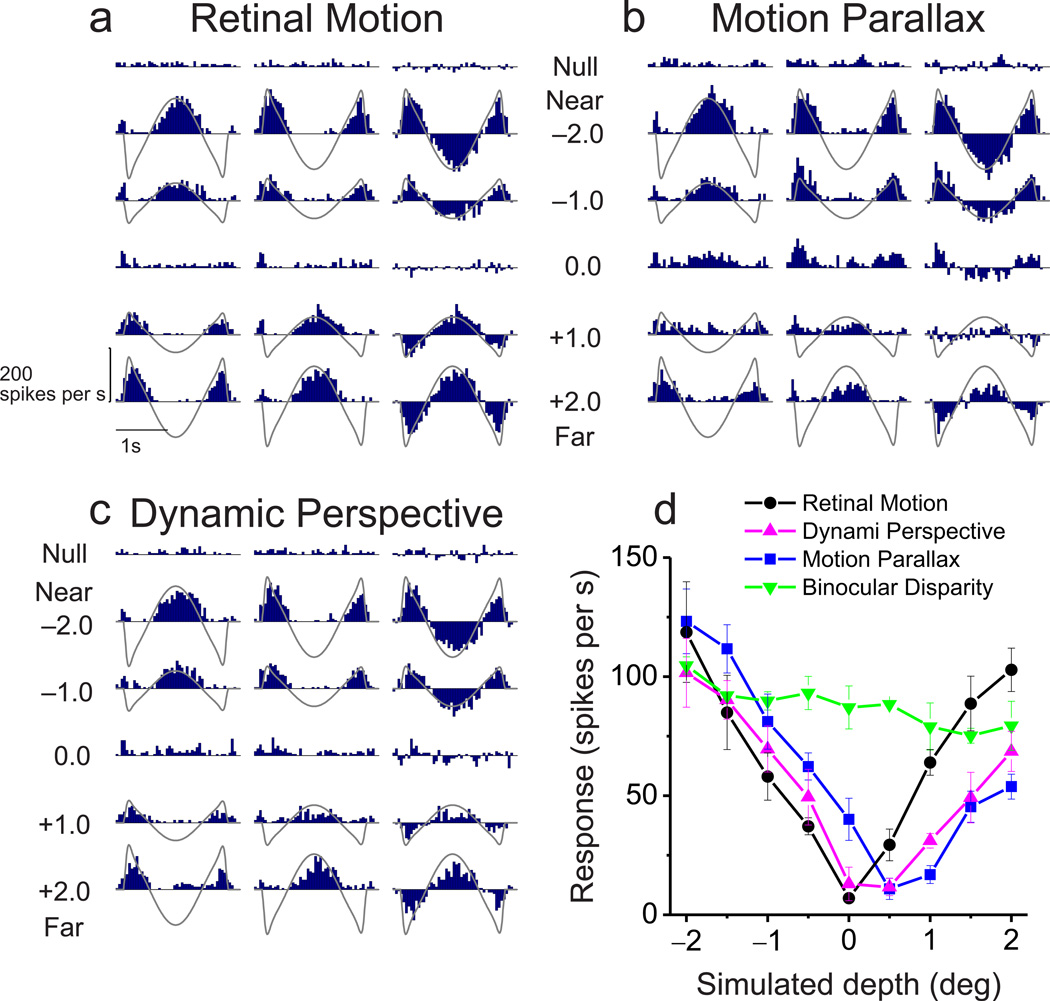
Figure 2. Raw responses and depth tuning curves for an example neuron.
(a–c) Peri-stimulus time histograms (PSTHs) for each experimental condition: Retinal Motion, Motion Parallax, and Dynamic Perspective, respectively. Due to the quasi-sinusoidal trajectory of observer translation, retinal image motion has a phasic temporal profile (gray curves). Rows correspond to different stimulus depths. Left and middle columns indicate data for the two starting phases of motion. The right column shows the difference in response between these two phases. Note that responses to near and far depths are balanced in the Retinal Motion condition, but the neuron responds more to near depths in the Motion Parallax and Dynamic Perspective conditions. (d) For each stimulus condition, depth-tuning curves are shown. Response amplitude is computed as the magnitude of the Fourier transform of the difference response at 0.5Hz. Tuning in the Retinal Motion condition is symmetrical around zero depth (black, DSDI = −0.09), whereas tuning curves show a clear preference for near depths in the Motion Parallax (blue, DSDI = −0.80), Dynamic Perspective (magenta, DSDI = −0.67) and Binocular Disparity conditions (green, DSDI = −0.56). Error bars represent s.e.m.
For the Motion Parallax condition, in which the animal was physically translated and pursued a world-fixed target, responses of the example neuron to far stimuli were suppressed (Fig. 2b). This resulted in a tuning curve with a clear preference for near depths (Fig. 2d, blue, DSDI = −0.80, P < 0.001 permutation test). Thus, as shown previously24–26, smooth eye movement command signals can generate depth-sign selectivity in MT neurons.
The critical question addressed here is whether dynamic perspective cues can also disambiguate depth, in the absence of eye movements. In the Dynamic Perspective condition, responses of the example neuron are similar to the Motion Parallax condition, showing suppressed responses to far stimuli (Fig. 2c, magenta curve in Fig. 2d). This resulted in a highly significant preference for near stimuli (DSDI = −0.67, P < 0.001 permutation test), similar to that for the Motion Parallax condition. Note that a portion of the background motion stimulus roughly three-fold larger than the neuron’s receptive field was masked (Suppl. Movie 4, Supplementary Fig. 2), such that background motion by itself did not evoke responses (Fig. 2c, top row of PSTHs). Rather, a signal (of currently unknown origin) derived from the large-field background motion appears to modulate the response and generate depth-sign selectivity in the absence of extra-retinal signals.
Since most MT neurons are also selective for depth from binocular cues27, 28, we also measured the binocular disparity tuning of each neuron (see Methods). The example neuron shows modest disparity tuning with a preference for near stimuli (Fig. 2d, green, DSDI = −0.56; P = 0.001, permutation test), consistent with depth-sign tuning in the Motion Parallax and Dynamic Perspective conditions. We refer to such neurons, having consistent depth preferences for disparity and motion parallax, as ‘congruent’ cells26. Note that depth tuning curves in the Binocular Disparity condition generally do not have a trough at zero depth since stimuli always moved with the neuron’s preferred direction and speed while binocular disparity was varied (see Methods).
Data from three additional MT neurons are shown in Fig. 3. The first neuron (Fig. 3a) exhibits a robust and highly significant preference for near stimuli in the Dynamic Perspective (DSDI = −0.62, P < 0.001, permutation test) and Motion Parallax (DSDI = −0.56, P < 0.001) conditions, with no significant depth-sign tuning in the Retinal Motion condition (DSDI = 0.01, P = 0.458). This neuron also prefers near depths in the Binocular Disparity condition (DSDI = −0.71, P < 0.001). The second neuron is a congruent cell that prefers far depths (Fig. 3b) in the Dynamic Perspective (DSDI = 0.49, P = 0.005, permutation test), Motion Parallax (DSDI = 0.52, P = 0.001), and Binocular Disparity (DSDI = 0.87, P < 0.001) conditions, with no significant depth-sign selectivity in the Retinal Motion condition (DSDI = 0.03, P = 0.44). Note that all of the congruent cells illustrated here (Figs. 2, 3a,b) have similar depth-sign selectivity in the Dynamic Perspective and Motion Parallax conditions, suggesting that dynamic perspective cues modulate MT responses in a similar manner to actual eye movement signals.
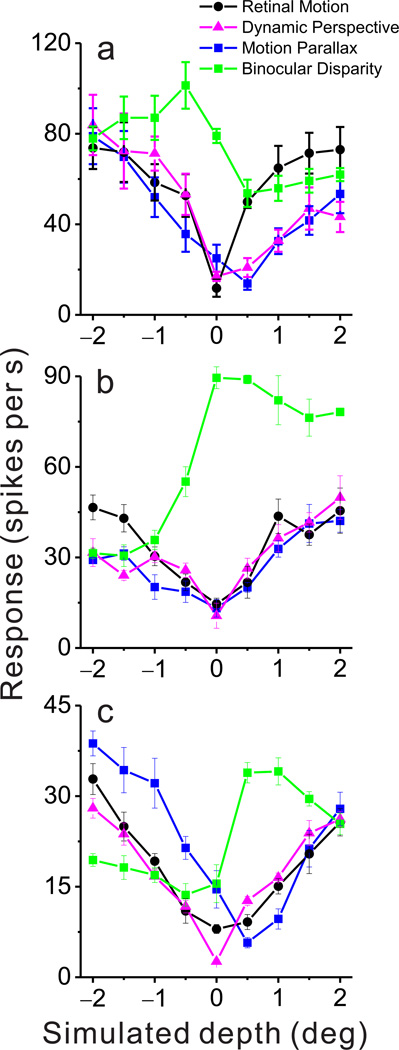
Figure 3. Depth tuning curves from three additional example neurons.
(a) An example congruent cell preferring near depths in the Dynamic Perspective, Motion Parallax and Binocular Disparity conditions. Format as in Figure 2d; error bars represent s.e.m. (b) An example congruent cell preferring far depths in the Dynamic Perspective, Motion Parallax, and Binocular Disparity conditions. (c) An example opposite cell that prefers near depths in the Motion Parallax condition but far depths in the Binocular Disparity condition. This neuron does not show significant depth-sign selectivity in the Dynamic Perspective condition.
We recently reported that the depth-sign preferences of MT neurons for motion parallax and binocular disparity can be either consistent or mismatched, with almost half of MT neurons preferring opposite depth signs for the two cues ('opposite' cells)26. Figure 3c illustrates data for an opposite cell that prefers near depths in the Motion Parallax condition (DSDI = −0.74, P < 0.001, permutation test) and prefers far depths in the Binocular Disparity condition (DSDI = 0.80, P < 0.001). Interestingly, this neuron shows no significant depth-sign selectivity in the Dynamic Perspective condition (DSDI = −0.02, P = 0.474). Indeed, congruency between tuning for motion parallax and disparity was systematically related to depth-sign selectivity in the Dynamic Perspective condition, as demonstrated in the population analyses that follow.
Population summary
We collected sufficient data for 103 MT neurons from two macaque monkeys (48 from monkey 1, 55 from monkey 2). We attempted to record from any MT neuron that could be isolated, except for a small proportion of neurons (5–10%) that preferred fast speeds and did not respond over the range of speeds in our motion-parallax stimuli (~0 to 7 deg/sec). Overall, significant depth-sign selectivity was infrequent in the Retinal Motion condition (29/103 neurons), substantially more common in the Dynamic Perspective condition (67/103 neurons), and most common in the Motion Parallax condition (92/103 neurons) (Fig. 4a, filled bars). As quantified by computing absolute DSDI values, depth-sign selectivity in the Dynamic Perspective condition (median |DSDI| = 0.51) is significantly greater than that for the Retinal Motion condition (median |DSDI| = 0.17; P = 3.6 × 10−10, Wilcoxon signed rank test), but significantly weaker than selectivity in the Motion Parallax condition (median |DSDI| = 0.70; P = 3.0 × 10−7). Thus, dynamic perspective cues produce robust depth-sign selectivity in MT neurons, but slightly weaker than the selectivity generated by eye movement signals.
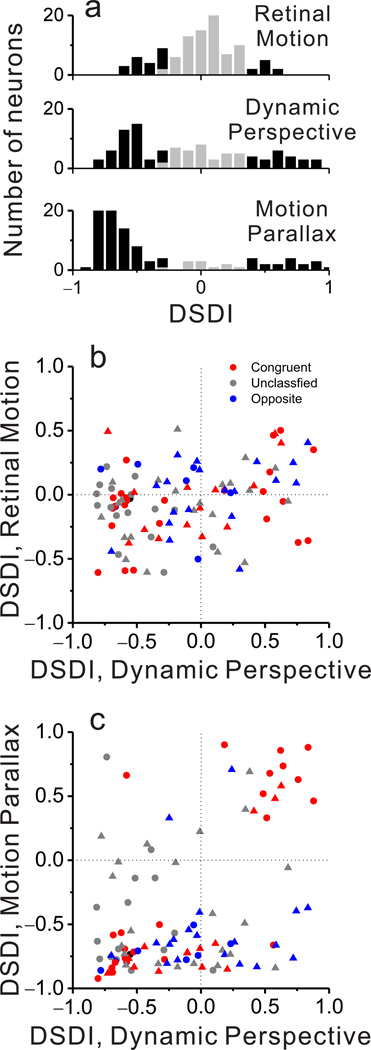
Figure 4. Population summary of depth-sign selectivity.
(a) Histograms of DSDI values for each stimulus condition: Retinal Motion (top), Dynamic Perspective (middle), and Motion Parallax (bottom). Black bars represent DSDI values that are significantly different from zero, whereas gray bars are not significant. (b) DSDI values in the Retinal Motion and Dynamic Perspective conditions are weakly correlated (ρ = 0.25, P = 0.01, Spearman rank correlation). Colors represent congruent (red), opposite (blue), and unclassified (gray) neurons. Circles and triangles denote data from monkeys M1 and M2, respectively. (c) DSDI values for the Motion Parallax and Dynamic Perspective conditions are highly correlated for congruent cells (red, n = 38, ρ = 0.70, P = 2.6 × 10−6), but not for opposite or unclassified cells. Format as in b.
While DSDI provides a useful index of depth-sign selectivity, it does not tell how much information MT neurons carry about depth sign. We also used receiver operating characteristic (ROC) analysis29 to compute how well an ideal observer could discriminate depth sign based on activity from each neuron. Most MT neurons can reliably discriminate depth sign (ROC values significantly different from 0.5, permutation test) in the Motion Parallax and Dynamic Perspective conditions, but not in the Retinal Motion condition (Supplementary Fig. 3). Thus, in terms of information regarding depth sign, the effects of pursuit signals and dynamic perspective cues on MT responses are quite robust.
To evaluate whether dynamic perspective and pursuit signals produce similar depth-sign preferences, we compared signed DSDI values across stimulus conditions. We found no correlation between DSDI values for the Retinal Motion and Motion Parallax conditions (ρ = 0.13, P = 0.196, Spearman rank correlation), as shown previously25. Comparing the Retinal Motion and Dynamic Perspective conditions, we observe a weak but significant positive correlation of DSDI values (Fig. 4b; ρ = 0.25, P = 0.013, Spearman rank correlation), which is notable given that significant depth-sign selectivity in the Retinal Motion condition occurred more frequently (28%) than expected by chance (n = 103, P < 0.001, permutation test). These observations may be explained by the fact that the visual stimulus in the Retinal Motion condition (Suppl. Movie 5) also contains dynamic perspective cues, but they are weak because the stimulus is small.
To test whether the modest depth-sign selectivity in the Retinal Motion condition depends on dynamic perspective cues within the receptive field, we computed a simple metric of dynamic perspective information (DPI) that is derived from a mathematical description of image motion—in stimulus coordinates—that accompanies translations and rotations (see Methods). We found that DPI, computed for the stimulus overlying the receptive field, is significantly correlated with the magnitude of DSDI values in the Retinal Motion condition (n = 103, ρ = 0.24, P = 0.006, Spearman rank correlation; see Supplementary Fig. 4), such that neurons with larger receptive fields that are located away from the horizontal and vertical meridians generally have more depth-sign selectivity. Correspondingly, the distribution of DPI values differs significantly between neurons with and without significant depth-sign tuning in the Retinal Motion condition (two-sample Kolmogorov–Smirnov test, n = 29 and 74 respectively, P = 0.0005, Supplementary Fig. 4). This likely explains the fact that 29/103 neurons exhibit significant depth-sign selectivity in the Retinal Motion condition, as well as the weak but significant correlation between DSDI values in the Retinal Motion and Dynamic Perspective conditions.
Critically, if dynamic perspective signals are used to perceive depth from motion parallax, we would expect MT neurons to exhibit matched depth-sign preferences in the Motion Parallax and Dynamic Perspective conditions. Across our population of 103 neurons, DSDI values are modestly, but significantly, correlated across conditions (Fig. 4c; ρ = 0.36, P = 0.0002, Spearman rank correlation), and the correlation is comparable after accounting for depth-sign tuning in the Retinal Motion condition (n = 103, ρ = 0.35, P = 0.0004, Spearman partial correlation).
While many neurons showed the same depth-sign preferences for the Dynamic Perspective and Motion Parallax conditions, others had mismatched preferences (Fig. 4c, bottom-right and top-left quadrants). We refer to the former neurons as ‘matched’ cells, and the latter as ‘mismatched’ cells. We found that this distinction is strongly related to the congruency of depth-sign preferences between the Motion Parallax and Binocular Disparity conditions. For ‘opposite’ cells, we find no significant correlation between depth-sign preferences in the Motion Parallax and Dynamic Perspective conditions (Fig. 4c, blue, n = 26, ρ = 0.28, P = 0.17, Spearman rank correlation). In striking contrast, for ‘congruent’ cells, depth-sign preferences in the Motion Parallax and Dynamic Perspective conditions are strongly correlated (Fig. 4c, red, n = 38, ρ = 0.70, P = 2.6 × 10−6). A third group of ‘unclassified’ neurons, which do not have significant depth-sign selectivity in both the Motion Parallax and Binocular Disparity conditions, shows results similar to opposite cells (Fig. 4c, gray, n = 38, ρ = −0.02, P = 0.91). These findings, which are consistent across animals (Table 1), demonstrate clearly that dynamic perspective cues and eye movement signals can generate matched depth-sign preferences, but only for neurons having binocular disparity tuning that is also matched to the motion parallax selectivity.
Table 1. Analysis of the relationship between DSDI values in the Motion Parallax and Dynamic Perspective conditions, broken down by animals (M1 and M2).
Each cell gives the correlation coefficient (Spearman rank correlation) between DSDI values for the Motion Parallax and Dynamic Perspective conditions, along with the P value indicating the significance of the correlation and the number of neurons in each group. Rows indicate breakdown by animals; columns indicate breakdown by congruency of motion parallax and binocular disparity tuning. One neuron for which binocular disparity tuning not measured was excluded from this analysis.
| Congruent (n=38) | Opposite (n=26) | Unclassified (n=38) | Total (n=102) | |
|---|---|---|---|---|
| M1 | 0.77 (P=2.0×10−5, n=24) | 0.75 (P=0.07, n=7) | 0.00 (P=1.00, n=16) | 0.54 (P=9.7×10−5., n=48) |
| M2 | 0.65 (P=0.01, n=14) | 0.08 (P=0.74, n=19) | −0.04 (P=0.88, n=22) | 0.20 (P=0.14, n=55) |
| Total | 0.70 (P=2.6×10−6) | 0.28 (P=0.17) | −0.02 (P=0.91) | 0.36 (P=0.0002) |
This strong intervening effect of binocular disparity selectivity was unexpected because all of the visual stimuli in the Retinal Motion, Motion Parallax and Dynamic Perspective conditions are monocular. Thus, the effect of congruency (Fig. 4c) is not a direct influence of binocular disparity on MT responses. Rather, we speculate that disparity selectivity plays some role in establishing the correspondence between dynamic perspective and eye movement signals (see Discussion).
Eye movements
A potential concern is that background motion in the Dynamic Perspective condition might evoke small eye movements that could modulate MT responses and generate depth-sign tuning. To address this issue, we analyzed eye movements and computed pursuit gain, defined as the ratio of actual eye movement velocity to the ideal eye velocity that would be needed to keep the eye on target during observer translation. Consistent with previous studies25, we found that pursuit gain in the Motion Parallax condition was not significantly different from unity (median = 1.00, P = 0.23, signed rank test), indicating that animals pursued the target accurately. For the Retinal Motion and Dynamic Perspective conditions, pursuit gains were very small (median values = 0.028, 0.03, respectively), but the pursuit gain was significantly greater in the Dynamic Perspective condition (Supplementary Fig. 5a; P < 0.05, Wilcoxon signed rank test). Importantly, we found no significant correlation between pursuit gains and absolute DSDI values in the Dynamic Perspective condition (Supplementary Figs. 5b, c; ρ = −0.18, P = 0.22 for monkey 1; ρ = −0.25, P = 0.07 for monkey 2). Results were similar if we correlated pursuit gain with signed DSDI values, instead of absolute values (ρ = 0.1, P = 0.48; ρ = 0.15, P = 0.29). Thus, we find no evidence that depth-sign selectivity in the Dynamic Perspective condition can be accounted for by residual eye movements.
Contributions of dot size and motion asymmetry to depth-sign tuning
We designed the background motion stimulus in the Dynamic Perspective condition such that it contains rich information about rotation of the eye relative to the scene. Background elements had size cues (near dots are bigger than far dots), which might help to interpret background motion. In addition, background elements were distributed uniformly in depth (±20cm) around the fixation target, which means that the nearest dots had faster retinal image motion than the farthest dots in the scene. Both size cues and the asymmetry of motion energy in the background might contribute to generating neural selectivity for depth sign from motion parallax17.
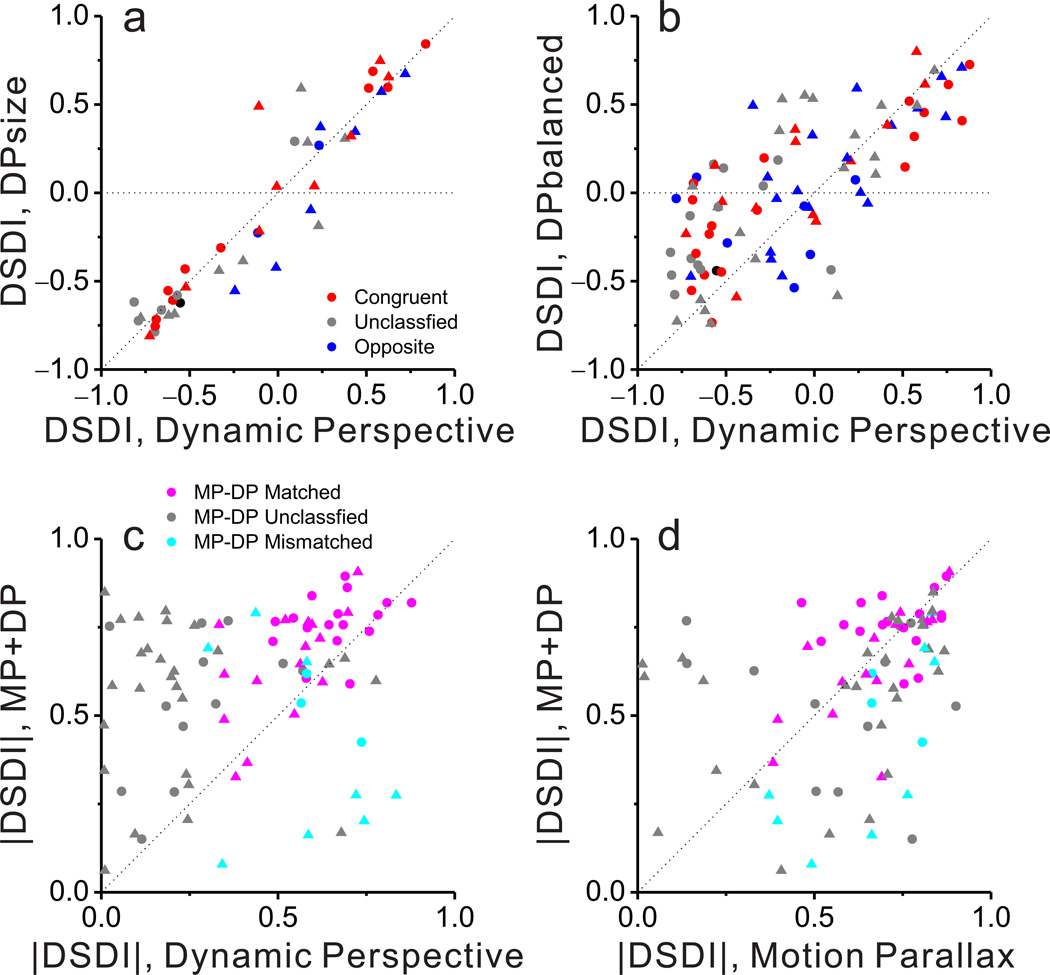
To examine the contribution of these auxiliary cues, we interleaved two additional experimental conditions for a subset of neurons. In the DPsize condition, background elements had the same spatial distribution as in the standard Dynamic Perspective condition, but had a constant retinal size (0.39 deg) independent of their location in depth. Results from 44 neurons show that size cues did not substantially influence the depth-sign tuning of MT neurons (Fig. 5a). DSDI values in the DPsize condition are strongly correlated with those from the Dynamic Perspective condition (n = 44, ρ = 0.94, P = 7.6 × 10−22, Spearman rank correlation), and the median absolute values are slightly but significantly greater for the DPsize condition (0.56) than for the Dynamic Perspective condition (0.52, P = 0.015, Wilcoxon signed rank test). Thus, if anything, removing the dot size cues slightly enhanced depth-sign selectivity.
Figure 5. Effects of auxiliary cues on depth-sign selectivity and effects of cue combination.
(a) Comparison of DSDI values between the DPsize control condition and the standard Dynamic Perspective condition; format as in Figure 4b. Eliminating size cues has little effect on depth-sign selectivity (b) Comparison of DSDI values between the DPbalanced control condition and the standard Dynamic Perspective condition. Eliminating asymmetries in the speed distribution between near and far dots modestly reduces depth-sign selectivity; see text for details. (c) Comparison of absolute DSDI values between the MP+DP condition, in which both eye movement and dynamic perspective cues were present, and the standard Dynamic Perspective condition. Data are shown separately for neurons with depth-sign preferences in the Motion Parallax and Dynamic Perspective conditions that are matched (n = 33, magenta), mismatched (n = 11, cyan), or unclassified (n = 39, gray). (d) Comparison of absolute DSDI values between the MP+DP condition and the Motion Parallax condition; format as in c.
To examine the effect of motion asymmetry between near and far background elements, background dots were distributed uniformly within a 3D volume bounded by two cylinders having equivalent disparities of ±2 deg relative to the fixation target (DPbalanced condition, see Methods). This manipulation ensures that the distribution of retinal image speeds is identical for near and far dots. Size cues were also eliminated in the DPbalanced condition, such that this stimulus represents a ‘pure’ dynamic perspective cue.
With this stimulus, many MT neurons again show significant depth-sign selectivity (50/91), and DSDI values in the DPbalanced condition are strongly correlated with those for the Dynamic Perspective condition (Fig. 5b, n = 91, ρ = 0.703, P = 1.0 × 10−14, Spearman rank correlation). The median absolute value of DSDI in the DPbalanced condition (0.34) is significantly less than that for the Dynamic Perspective condition (0.51; P = 0.0009, Wilcoxon signed rank test), indicating that removal of the motion speed asymmetry between near and far dots reduces depth-sign selectivity. Nevertheless, the median |DSDI| for the DPbalanced condition is significantly greater than that for the Retinal Motion condition (median |DSDI| = 0.17; P = 3.4 × 10−5, Wilcoxon signed rank test), demonstrating that even the purer form of dynamic perspective cue is still effective at generating depth-sign selectivity in area MT. We conclude that size cues make no contribution to depth-sign tuning in the Dynamic Perspective condition, but the neural circuits that process background motion do take advantage of asymmetries in the distribution of velocities in the scene. Critically, however, even an unnatural scene in which near and far elements have identical ranges of retinal speeds is able to disambiguate depth and sculpt depth-sign selectivity in MT neurons. Additional analyses reveal that depth-sign selectivity induced by dynamic perspective cues in the stimulus cannot be attributed to surround suppression (Supplementary Fig. 6).
Combined effect of motion parallax and dynamic perspective cues on depth-sign tuning
Given that both eye movement signals and dynamic perspective cues can generate depth-sign selectivity in MT neurons, we examined whether these two sources of disambiguating information could combine synergistically. In the MP+DP condition, animals were translated by the motion platform and counter-rotated their eyes to maintain fixation on a world-fixed target (as in the Motion Parallax condition); however, a large-field background of dots was present as in the Dynamic Perspective condition. Thus, the MP+DP condition provides both eye movement and dynamic perspective information.
Across our population of MT neurons, the median absolute value of DSDI is significantly greater for the MP+DP condition than the Dynamic Perspective condition (Fig. 5c; n = 83, P = 3.3 × 10−7, Wilcoxon signed rank test). However, this relationship depends on whether depth-sign preferences in the Motion Parallax and Dynamic Perspective conditions are matched, mismatched, or unclassified. Matched cells and unclassified cells showed robust enhancement of depth-sign selectivity in the MP+DP condition (Fig. 5c, magenta and gray symbols, n=33 and P = 0.0001 for matched cells, n = 39 and P = 1.8 × 10−6 for unclassified cells, Wilcoxon signed rank test), indicating that adding eye movement signals enhances the effect of dynamic perspective cues. In contrast, mismatched cells did not show such an enhancement (cyan symbols; n = 11, P = 0.206).
Comparison between the Motion Parallax and MP+DP conditions revealed a somewhat different pattern of results (Fig. 5d). In this case, matched cells show no significant difference in depth-sign selectivity between conditions (n = 33, P = 0.71, Wilcoxon signed rank test), whereas mismatched cells exhibited significantly weaker depth-sign selectivity in the MP+DP condition (n = 11, P = 0.001). Given that depth-sign selectivity is significantly greater for matched cells in the Motion Parallax condition than the Dynamic Perspective condition (n = 33, P = 0.001, Wilcoxon signed rank test), this pattern of results might reflect a ceiling effect whereby addition of dynamic perspective cues to the motion parallax stimulus does not enhance selectivity over that seen in the Motion Parallax condition alone. In contrast, addition of dynamic perspective cues may reduce the depth-sign selectivity of mismatched cells in the MP+DP condition because dynamic perspective and eye movement signals have opposite effects on the depth tuning of these neurons. Together, results from the MP+DP condition are broadly consistent with the notion that eye movement signals and dynamic perspective cues interact to sculpt the depth-sign selectivity of MT neurons.
Dynamics of depth-sign selectivity revealed by noise stimuli
A limitation of the visual stimuli described thus far is that all dots within the receptive field move alternately in the preferred and null directions of the neuron under study. Thus, we can only measure the modulatory effect of dynamic perspective cues during the half of the stimulus period for which dots move in the preferred direction (e.g., Fig. 2), To obtain a clearer picture of the dynamics of response modulation, we tested MT neurons with stimuli in which the dots within the receptive field were uniformly distributed in depth (Fig. 6a).
Figure 6. Response dynamics revealed by random-depth stimuli.
(a) In the random-depth stimulus, dots were distributed uniformly in a range of simulated depths corresponding to equivalent disparities from −2deg to +2deg. (b) Retinal velocity profiles for near (dashed curve) and far (solid curve) dots, for each of the two phases of movement (left and right panels). At all times, half of the dots move in the preferred direction (shaded region). (c) PSTHs from a near-preferring neuron, for the Retinal Motion (top row), Motion Parallax (middle row), and Dynamic Perspective (bottom row) conditions. Left and middle columns indicate responses for the two starting phases of motion, whereas the right column shows the difference in response between the two phases. Responses in the Retinal Motion condition show three equal peaks, such that the difference response is near zero. Responses in the Motion Parallax and Dynamic Perspective conditions are modulated by real or simulated eye rotation, such that difference responses are clearly modulated. (d) Data from a far-preferring neuron; format as in c.
With this random-depth stimulus, either near or far dots are always moving in the neuron’s preferred direction at every point in time (Fig. 6b). As a result, responses of an example neuron in the Retinal Motion condition exhibit three distinct peaks of activity (Fig. 6c, top row). In contrast, responses of the same neuron (to the same visual stimulus) in the Motion Parallax condition reveal clear phasic modulations that depend on the direction of eye movement (Fig. 6c, middle row). For this near-preferring neuron, responses are suppressed when the eye moves toward the null direction of the neuron, whereas responses are little affected when the eye moves toward the preferred direction. The resulting difference in response between the two stimulus phases shows a clear sinusoidal modulation (Fig. 6c, right column). Strikingly, in the Dynamic Perspective condition, background motion resulting from simulated eye rotation modulates responses in a very similar manner (Fig. 6c, bottom row).
Analogous results for a far-preferring neuron (Fig. 6d) demonstrate similar response modulations. In this case, however, responses are suppressed when the eye moves toward the neuron’s preferred direction, or when dynamic perspective cues simulate this direction of rotation. Again, response modulations are very similar in the Motion Parallax and Dynamic Perspective conditions, indicating that eye movements and dynamic perspective cues may modulate MT responses through a similar mechanism to generate selectivity for depth sign.
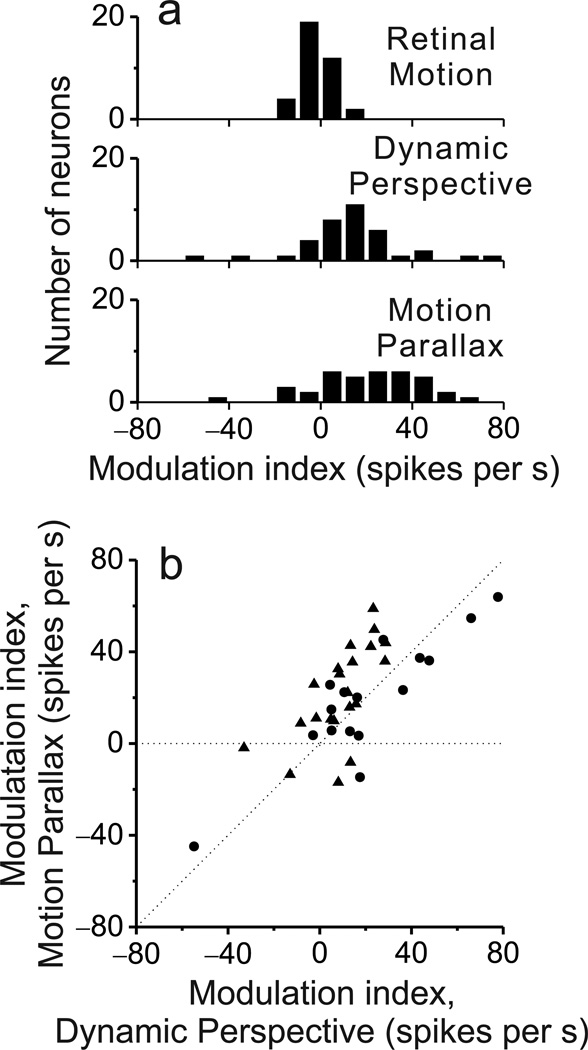
To quantify these patterns of response modulation, we computed the phase and magnitude of the differential response (Fig. 6c, d, right column) by Fourier transform (at the fundamental frequency of 0.5Hz). A Modulation index was then computed as: cos(phase) × magnitude. This Modulation Index will be positive for response modulations having a phase like that in Fig. 6c, and negative for the case of Fig. 6d. Distributions of the Modulation Index reveal values clustered around zero for the Retinal Motion condition, and much broader distributions for the Motion Parallax and Dynamic Perspective conditions (Fig. 7a). The median absolute values of Modulation Index are significantly greater for the Motion Parallax and Dynamic Perspective conditions than for the Retinal Motion condition (n = 37, P = 1.2 × 10−7 and 2.1 × 10−6 respectively, Wilcoxon signed rank test). In addition, Modulation Indices are well correlated between the Motion Parallax and Dynamic Perspective conditions (Fig. 7b, n = 37, ρ = 0.67, P = 3.0 × 10−4, Spearman rank correlation), as expected from the example neurons in Fig. 6. These results reinforce the conclusion that two independent sources of information about eye rotation relative to the scene—efference copy of pursuit eye movements and dynamic perspective cues—appear to modulate MT responses in a nearly identical fashion to represent depth from motion parallax.
Figure 7. Summary of results from random-depth stimuli.
(a) Distributions of the Modulation Index are shown for each of the stimulus conditions. See text for details. (b) Modulation Indices for the Dynamic Perspective and Motion Parallax conditions are significantly and positively correlated (ρ = 0.67, P = 3.0 × 10−4, Spearman rank correlation), indicating that eye movements and dynamic perspective cues have similar effects on MT responses.
Discussion
Our findings demonstrate that dynamic perspective cues are sufficient to disambiguate motion parallax and generate robust depth-sign selectivity in macaque MT neurons. This shows that the brain is able to infer likely changes in eye orientation relative to the scene from global patterns of retinal image motion, and can use these visual cues to perform useful neural computations in lieu of extra-retinal signals. The fact that dynamic perspective cues (in stimulus coordinates) and smooth eye movement command signals are both capable of disambiguating depth-sign is consistent with theoretical considerations20, as both pieces of information are capable of specifying changes in eye orientation relative to the scene. More broadly, our findings suggest that a variety of neural computations that need to account for rotations of the eye or head—such as compensating for eye/head rotations during heading perception6, 30, 31—may be able to take advantage of dynamic perspective cues in addition to relevant extraretinal signals.
Based on our findings, we expect that dynamic perspective cues will also disambiguate humans’ perception of depth sign based on motion parallax. Indeed, preliminary results indicate that this is the case32. How extra-retinal signals and dynamic perspective cues interact to determine perceived depth based on motion parallax will be an important topic for future studies.
Relative benefits of dynamic perspective cues vs. extraretinal signals
Theoretical work has shown that the rate of change of eye orientation relative to the scene is the critical variable needed to compute depth from motion parallax20. Given that smooth eye movement command signals are available to perform this computation, why should the brain process dynamic perspective cues as an alternative? When the head and body do not rotate, changes in eye orientation relative to the scene are equivalent to changes in eye orientation relative to the head, which is the signal conveyed by efference copy of pursuit eye movements. Importantly, however, changes in eye orientation relative to the scene can also be produced by head rotations on the body or body rotations relative to the scene. In general, the brain would need to combine multiple extra-retinal signals to compute change in eye orientation relative to the scene.
In this regard, it may be advantageous to infer eye rotation from visual cues because they directly reflect changes in eye orientation relative to the scene. Regardless of whether eye orientation changes due to eye, head, or body movements, or some complex combination thereof, the net change in eye orientation relative to the scene could be computed by processing perspective cues. On the other hand, dynamic perspective cues may not be very reliable if the visual scene is very sparse or noisy. Thus, it makes sense for the brain to utilize both eye movement signals and dynamic perspective cues to compute depth from motion parallax.
As noted earlier, interpretation of dynamic perspective cues may rely on the assumption (or prior) that the majority of the visual scene is rigid and is not moving relative to the observer. In this regard, the concordance of extra-retinal signals and dynamic perspective cues may enable the system to perform validity checks on this assumption. If extra-retinal signals suggest observer movement that is grossly incompatible with dynamic perspective cues, then this may provide a strong indication that the scene is non-rigid.
Implications for previous and future studies
Our findings likely have important implications for many situations in which the brain must compensate for self-generated rotations. For example, previous physiological studies have examined how neurons tuned for heading compensate for smooth pursuit eye movements33–36. Pursuit eye movements add a rotational component to the optic flow field and alter the radial patterns of visual motion associated with fore-aft translation of the observer30. Some previous physiology studies compared the effects of real and simulated pursuit eye movements on heading tuning and concluded that extraretinal signals related to smooth pursuit are necessary for heading tuning curves to fully compensate for rotation34, 35.
These findings appear to be at odds with our conclusion that global patterns of visual motion can be used to infer eye rotations. Importantly, however, the simulated rotation stimuli used in previous studies34, 35 consisted simply of laminar optic flow that was added to a radial pattern of motion. Laminar motion (presented on a flat display) is not an accurate simulation of the visual motion produced by pursuit eye movements; specifically, it lacks the dynamic perspective cues needed to simulate eye rotation. To our knowledge, no previous study of heading tuning has implemented a proper visual control for pursuit, and some previous studies have not included a visual control at all33, 36. Thus, we predict that the heading tuning of neurons in MSTd or VIP may compensate for eye rotations when dynamic perspective cues are provided. This example highlights the need for future studies to employ accurate visual simulations of eye or head rotations.
It is unclear to what extent dynamic perspective cues will be involved in other neural computations that require information about eye and head rotations, but it is conceivable that phenomena that have previously been attributed to the action of extra-retinal signals may have been mediated, at least in part, by visual computations.
Binocular disparity and matching of depth sign preferences
If both dynamic perspective cues and eye movement command signals disambiguate depth, we might expect them to produce consistent depth-sign preferences in MT neurons. Curiously, we found this matching to be contingent on the binocular disparity tuning of MT neurons (Fig. 4c). This contingency cannot be a direct effect of binocular disparity cues because the visual displays in the Motion Parallax and Dynamic Perspective conditions are monocular. Rather, we suggest that disparity cues may play some sort of instructive role in establishing the convergence of dynamic perspective and pursuit eye movement signals onto MT neurons. When the depth-sign preference from disparity does not match that in the Motion Parallax condition (opposite cells), dynamic perspective cues generally do not produce the same depth-sign selectivity as eye movement signals.
Further research will be needed to understand how disparity signals influence the development of depth-sign selectivity in congruent and opposite cells, as well as to understand the functional roles of opposite cells. We have speculated previously that opposite cells may play important roles in detecting discrepancies between binocular disparity and local retinal image motion that result when objects move in the world26.
The source of dynamic perspective signals
Where in the brain do neurons process dynamic perspective cues to signal eye rotation? It is unlikely that these perspective cues are processed within area MT (or upstream areas) for the following reasons. First, processing of dynamic perspective cues probably requires mechanisms that integrate motion signals over large regions of the visual field, for the same reasons that vertical binocular disparities are thought to be processed using large-field mechanisms37, 38. If dynamic perspective cues were sufficiently reliable on the spatial scale of MT receptive fields, we might have expected to observe stronger depth-sign selectivity in the Retinal Motion condition. Second, the background motion was masked with an annulus 2–3 fold larger than the MT receptive field (Supplementary Fig. 2). This limits the possibility that neighboring neurons with nearby receptive fields are the source of modulation.
It is important to emphasize that we have described dynamic perspective cues in stimulus coordinates, not retinal coordinates. In spherical retinal coordinates, a pure eye rotation causes no perspective distortion. Thus, neural mechanisms that attempt to infer eye rotations from visual motion may be selective for global components of retinal image motion that lack perspective distortion in retinal coordinates. This would require mechanisms that operate over large portions of the visual field.
We speculate that dynamic perspective cues are analyzed in brain areas that process large-field motion (such as CIP, VIP and MSTd) and signals are fed back to MT. CIP neurons show selectivity for the static tilt of a planar stimulus based on perspective cues39. Thus, CIP responses might also modulate with dynamic perspective cues, although this possibility has not been tested directly. VIP neurons40 are selective for patterns of optic flow in large-field stimuli41, and some neurons also show pursuit-related responses40; thus, VIP could be a place where both dynamic perspective cues and smooth eye movement signals are represented.
Another candidate source of dynamic perspective signals is area MSTd, where neurons are selective to complex patterns of large-field motion42–44, and project back to area MT45. Notably, Saito et al42 measured responses of MSTd neurons in anesthetized monkeys to rotation-in-depth (i.e., rotation around an axis in the fronto-parallel plane) of a hand-held textured board that was presented monocularly. They reported that a small number of MSTd neurons are selective for the direction of rotation in depth (“Rd” cells). Although rotation in depth was confounded with angular subtense in these stimuli, it seems likely that responses of Rd neurons may by modulated by dynamic perspective cues.
MSTd neurons are also selective for the direction of smooth pursuit eye movements46. Moreover, MSTd neurons respond only to volitional pursuit, not to the rotational vestibular-ocular reflex (rVOR)47, and this property may be beneficial for disambiguating depth from motion parallax. Because rVOR compensates for head rotation and does not change eye orientation relative to the scene, an rVOR-related signal produced by head rotation is not necessary for the computation of depth from motion parallax. Together, these previous findings suggest that MSTd may represent eye orientation relative to the scene from both extra-retinal signals and dynamic perspective cues, and this is a topic of current investigation in the laboratory.
Another possible source of dynamic perspective signals may be eye movement planning areas such as the frontal eye field (FEF), which sends feedback connections to area MT48. Since FEF neurons receive input from visual areas49 and a portion of FEF represents smooth pursuit eye movements50, this area could provide a generalized signal about eye rotation relative to the scene, which is necessary to compute depth from motion parallax20. Further investigation of where and how dynamic perspective cues may be processed and integrated with eye movement commands is likely to provide new insights into how visual and non-visual signals cooperate to perform a variety of neural computations that must account for active rotations of an observer’s eye, head, or body.
Methods
Subjects and surgery
Two male monkeys (macaque mulatta, 8–12 kg) participated in the experiment. Standard aseptic surgical procedures under gas anesthesia were performed to implant a head holder. A Delrin (Dupont) ring was attached to the skill with dental acrylic cement, which was anchored by bone screws and titanium inverted T-bolts. To monitor eye movements, a scleral search coil was implanted under the conjunctiva of one eye.
To target microelectrodes to area MT, a recording grid made of Delrin was affixed inside the head-restraint ring using dental acrylic. The grid (2 × 4 × 0.5 cm) contains a dense array of holes (spaced 0.8 mm apart). Small burr holes were drilled vertically through the recording grid to allow penetration of microelectrodes into the brain via transdural guide tubes. All surgical procedures and experimental protocols were approved by the University Committee on Animal Resources at the University of Rochester.
Experimental apparatus
Animals were seated in a custom-made primate chair that was mounted on a six degree-of-freedom motion platform (MOOG 6DOF2000E). In some experimental conditions (detailed below) the motion platform was used to passively translate the animal back and forth along an axis in the fronto-parallel plane. The trajectory of the platform was controlled in real time at 60 Hz51. A field coil frame (C-N-C Engineering) was mounted to the top of the motion platform and was used to monitor eye movements using the scleral search coil technique.
Visual stimuli were rear-projected onto a 60×60 cm tangent screen using a stereoscopic projector (Christie Digital Mirage S+3K) which was mounted on the motion platform51. The tangent screen was mounted on the front side of the field coil frame. To restrict the animal’s field of view to the visual stimuli presented on the tangent screen, the sides and top of the field coil frame were covered with black matte material.
To generate visual stimuli that accurately simulate the observer’s movement through a virtual environment, visual stimuli were generated using OpenGL libraries and the OpenGL camera was moved along the exact trajectory of movement of the animal’s eye. The dynamics of the motion platform, including any delays, were compensated by measuring a transfer function that accurately characterized the relationship between motion trajectory command signals and actual platform movement. Synchronization was confirmed by presenting a world-fixed target in the virtual environment and superimposing a small spot by a room-mounted laser pointer while the platform was in motion51.
Electrophysiological recording
We recorded extracellular single unit activity using tungsten microelectrodes having typical impedances in the range from 1–3 MOhm (FHC Inc.). The sterilized microelectrode was loaded into a transdural guide tube and was advanced into the brain using a hydraulic micro-manipulator (Narishige). The voltage signal was amplified and filtered (1 kHz – 6 kHz, BAK Electronics). Single unit spikes were detected using a window discriminator (BAK Electronics), whose output was time-stamped with 1ms resolution.
Eye position signals were sampled at 200 Hz and stored to disk (TEMPO, Reflextive Computing). The raw voltage signal from the electrode was also digitized and recorded to disk at 25 kHz (Power1401 data acquisition system, Cambridge Electronic Design). If necessary, single units were re-sorted off-line using a template-based method (Spike2, Cambridge Electronic Design).
The location of area MT was initially identified by registering the structural MRI for each individual monkey with a standard macaque atlas (CARET)52. The approximate coordinates for vertical electrode penetrations were estimated from the MRI-based areal parcellation scheme, as mapped onto the MRI volume for each animal. The approximate location of area MT in the posterior bank of the superior temporal sulcus (STS) was projected on the horizontal plane of the recording grid, and the corresponding grid holes were explored. Patterns of gray matter and white matter along electrode penetrations aided our identification of area MT. Upon reaching the STS, we typically first encountered neurons with very large receptive fields and selectivity for visual motion, as expected for area MSTd. Following a very quiet region (the lumen of the STS), area MT was then the first area encountered. Compared to MSTd neurons, MT receptive fields are much smaller53, and MT neurons typically give robust responses to small visual stimuli (a few degrees in diameter) whereas MSTd neurons typically respond poorly to such small stimuli. MT neurons also often exhibit clear surround suppression54. Within area MT, we observed a gradual change of the preferred direction of multiunit responses, as expected from the known topographic organization of direction in MT28, 55.
Visual stimuli
Visual stimuli were generated using software custom-written in Visual C++, along with the OpenGL 3D graphics rendering library. Stimuli were rendered using a hardware-accelerated graphics card (NVIDIA Quadro FX 1700). To generate accurate motion parallax stimuli, the OpenGL camera was located at the same position as the animal's eye, and the camera imaged the scene using perspective projection. We calibrated the display such that the virtual environment has same spatial scale as the physical space through which the animal moves. Stereoscopic images were rendered as red/green anaglyphs, and were viewed by animals through custom-made goggles containing red and green filters (Kodak Wratten 2 Nos. 29 and 61). The crosstalk between eyes was very small (0.3% for the green filter and 0.1% for the red filter).
A random dot patch was created in the image plane using a fixed dot size of 0.39 deg and a density of 1.4 dots/deg2, and this patch was presented over the receptive field of a neuron under study. To present the random-dot stimulus at a particular simulated depth (based on motion parallax), we used a ray tracing procedure to project points from the image plane onto a virtual cylinder of the appropriate radius25. Different depths correspond to cylinders having different radii. A horizontal cross-section through the cylinder is a circle, and the circle corresponding to zero equivalent disparity passes through the fixation point as well as the nodal point of the eye (Fig. 1b, thick curve), whereas circles corresponding to near and far stimuli have smaller or larger radii, respectively (Fig. 1b). Through this procedure, the retinal image of the random-dot patch remains circular, but the patch appears as a concave surface in the virtual workspace, as though it were painted onto the surface of a transparent cylinder of the appropriate diameter. This procedure ensures that patch size, location, and dot density are identical in the retinal image while the simulated depth varies. Hence, all pictorial depth cues that might otherwise disambiguate depth sign are eliminated. Because the random-dot patch was rendered at a fixed location in the virtual environment on each trial, the whole dot aperture moves over the receptive field in retinal coordinates (see Supplementary Movies 4 and 5). However, this motion is the same across the different stimulus conditions. The dot patch was sized to be a bit larger than the receptive field of the neuron under study, such that it always overlapped most of the receptive field as it moved.
As simulated depth deviates from the point of fixation (either near or far), the speed of motion of the dot patch will increase on the display. In practice, even the 0° equivalent disparity stimulus (passing through the fixation point) contains very slight retinal image motion due to the fact that the animal is translated along a fronto-parallel axis rather than along a segment of the Vieth-Muller circle. To eliminate occlusion cues when the random dot patch overlaps the fixation target, the stimulus was always transparent. Size cues were eliminated from stimuli that were presented over a neuron’s receptive field by rendering dots with a constant retinal size (0.39 deg). In contrast, size cues were available in some of the background motion conditions described below. In most stimulus conditions, visual stimuli were presented only to the eye contralateral to the recording hemisphere (as detailed below).
For horizontal (left/right) translations of the head and eyes, the set of cylinders specifying our stimuli are oriented vertically. However, the axis of translation of the head within the fronto-parallel plane was chosen such that image motion would be directed along the preferred-null axis of each recorded neuron. For example, if an MT neuron preferred image motion upward and to the right on the display, the cylinder would be reoriented by rotating it counter-clockwise around the line of sight such that the long axis of the cylinder extended from the top-left quadrant to the bottom-right quadrant. Thus, the cylinders onto which our random-dot patches were projected changed orientation with the direction of head motion, such that all of the dots in a neuron’s receptive field would have the same depth defined by motion parallax25.
Several distinct stimulus conditions were presented to control the cues that were available to disambiguate the motion parallax stimuli described above. In all conditions, visual stimuli were presented monocularly to the animal.
Motion Parallax condition
At stimulus onset, animals experienced passive whole-body translation which followed a modified sinusoidal trajectory in the frontoparallel plane24, 25. Each movement involved one cycle of a 0.5 Hz sinusoid that was windowed26 to prevent rapid accelerations at stimulus onset and offset. The resulting retinal velocity profiles for stimuli at different depths are shown by the gray curves in Fig. 2. On half of the trials, platform movement started toward the neuron’s preferred direction. On the remaining half, the motion started toward the neuron’s null direction. The animal was required to move his eyes to maintain visual fixation on a world-fixed target. Along with the physical translation of the head, we moved the OpenGL camera such that the camera followed the trajectory of the animals’ actual eye position. This ensures that the animals experience optical stimulation consistent with self-motion through a stationary 3D virtual environment. In this condition, smooth pursuit eye movement command signals are available to disambiguate depth sign, as demonstrated previously24, 25.
Retinal Motion condition
The retinal image motion of the random-dot patch was the same as in the Motion Parallax condition, but this condition lacks physical head translation and the corresponding counteractive eye movements. In this condition, the OpenGL camera was translated and counter-rotated such that the camera was always aimed at the fixation target, thus effectively simulating eye movements in the Motion Parallax condition. Thus, the Retinal Motion condition reproduces the visual stimulus that would be experienced in the Motion Parallax condition (assuming that animals pursued the fixation target accurately in the Motion Parallax condition).
Dynamic Perspective condition
The motion of the random-dot patch over the receptive field was identical to that in the Retinal Motion condition and the Motion Parallax condition (assuming accurate pursuit), but the scene also contained additional dots (size 0.22cm × 0.22cm) that formed a 3D background. The motion of these background dots provided robust dynamic perspective cues regarding changes in eye orientation relative to the scene (Fig. 1b, magenta triangles; see also Suppl. Movie 4). Background dots were randomly positioned in a volume that spanned a range of depths of ±20cm around the fixation target, and the dot density was 0.01 dots/cm3. Background dots were masked within a circular region that was centered on the receptive field (and the small random-dot patch), and the masked region was typically 2 to 3 times larger than the diameter of the receptive field of each neuron (see Suppl. Fig. 2 for details). The annular mask area included the fixation target in most cases (85/103). The mask ensured that the movement of background dots did not encroach upon the classical receptive field of the neuron under study.
Dynamic Perspective condition without size cues (DPsize)
Since the background dots in the Dynamic Perspective condition have a fixed physical size in the virtual environment, near dots are larger on the display than far dots due to perspective projection. Thus, it is possible that the direction of observer translation could be inferred from the motion of the larger dots. To assess the contribution of this cue, the DPsize condition eliminates the size cue by rendering dots with a fixed retinal size (0.39deg) independent of depth. Otherwise, this condition is identical to the Dynamic Perspective condition.
Dynamic Perspective condition with balanced motion (DPbalanced)
Dots in the Dynamic Perspective condition were distributed in a rectangular volume centered on the fixation target. In this geometry, the speed of near dots is faster, on average, than the speed of far dots. To equate the distributions of speeds of near and far dots and ensure that motion energy in the background stimulus was balanced, we included a condition (DPbalanced) in which background dots are distributed in a volume defined by two cylinders corresponding to equivalent disparities of ±2deg. Dots were distributed uniformly within this volume in terms of equivalent disparity (deg), not uniformly in Cartesian distance (cm). This design makes the speed distributions of near and far dots identical, on average, at each location in the visual field. In addition, this condition employed dots of a fixed retinal size. Thus, the DPbalanced condition provides the “purest” form of dynamic perspective cues; otherwise, stimulus parameters are the same as in the Dynamic Perspective condition.
Combined Motion Parallax and Dynamic Perspective condition (MP+DP)
This condition is identical to the Motion Parallax condition in terms of observer translation and eye movement requirements, but also includes a volume of background dots as in the Dynamic Perspective condition. Thus, this condition provides both eye movement signals and dynamic perspective cues for disambiguating depth sign, allowing us to examine how these cues may combine.
Experimental protocol
Preliminary measurements
After isolating the action potential of a single neuron, the receptive field and tuning properties were explored using a manually-controlled patch of random dots. The direction, speed, position, and horizontal disparity of the random-dot patch were manipulated using a mouse, and instantaneous firing rates were plotted on graphical displays of visual space and velocity space. This procedure allowed us to center stimuli on the receptive field and to obtain initial estimates of tuning parameters.
After these initial qualitative tests, we measured the direction, speed, horizontal disparity, and size tuning of each neuron using random-dot stimuli, as described in detail previously54. Each of these measurements was performed in a separate block of trials, and each stimulus was typically repeated three to five times. Direction tuning was measured with random dots that drifted coherently in eight different directions separated by 45 deg. Speed tuning was measured with random dots moving in the optimal direction at 0, 0.5, 1, 2, 4, 8, 16, and 32 deg/s. If a neuron showed very little response (< 5 spikes/s) to all speeds below ~6 deg/s, the neuron was not studied further because it would not respond sufficiently to the motion parallax stimuli used in the current study. Horizontal disparity tuning was then measured with random-dot stereograms (drifting at the preferred direction and speed) that were presented at binocular disparities ranging from −2 deg to +2 deg in steps of 0.5 deg. Size tuning was measured with random-dot patches having diameters of 0.5, 1, 2, 4, 8, 16, 32 deg. Finally, the spatial profile of the receptive field was measured using a small patch of random dots roughly one-fourth of the estimated receptive field size. This patch was presented at all locations on a 4 × 4 grid that was roughly twice as large as the receptive field. Responses were fitted by a 2D Gaussian function to estimate the center and size of the receptive field.
Depth Tuning Measurement
Depth tuning from motion parallax was measured using random dot stimuli presented monocularly. The patch of random dots was chosen to be ~25% larger than the classical receptive field, and the dot patch was presented at nine distinct depths (corresponding to equivalent disparities ranging from −2deg to +2deg in steps of 0.5 deg). For all neurons, the Motion Parallax, Retinal Motion, and Dynamic Perspective conditions (described above) were randomly interleaved in a single block of trials. For a subset of neurons, the DPsize, DPbalanced, and MP+DP conditions were also interleaved as controls. Each unique depth stimulus was repeated 6–10 times. Animals were required to maintain visual fixation on a world-fixed target in all conditions (the fixation target was presented to both eyes to aid stable vergence). To allow pursuit eye movements to be initiated for the conditions in which they were necessary (Motion Parallax and MP+DP), the visual fixation window had an initial size of 3–4 deg and then shrunk to 70% of that size after 250ms had elapsed.
Data analysis
Neural response quantification
Because our stimuli contained one cycle of sinusoidal motion at 0.5Hz, MT neurons generally showed phasic response profiles, being active during the portions of a trial in which dots moved in their preferred direction and inactive during the other portions. The phase of neural responses was opposite for the two possible phases of observer translation tested (e.g., Fig. 2a). To quantify neural responses, the response profile for one stimulus phase was subtracted from the other phase, resulting in a net response profile (e.g., Fig. 2a, right column). The amplitude of this response profile at the fundamental frequency of the stimulus (0.5Hz) was then computed by Fourier transform.
We quantified the selectivity of MT neurons for depth sign (i.e., a preference for near or far) by computing a Depth-Sign Discrimination Index (DSDI)24, 25 as follows:
| (1) |
For each pair of depths symmetric around zero (e.g. ±1 degree), we calculated the difference in response amplitude between far (Rfar) and near (Rnear) depths, and normalized this relative to response variability (σavg, the average standard deviation of the two responses). We then averaged this metric across the four matched pairs of depths to obtain the DSDI measure, which ranges from −1 to 1. DSDI takes into account trial-to-trial variations in response while quantifying the magnitude of response differences between near and far. Neurons that respond more strongly to near stimuli will have negative DSDI values, and neurons that respond better to far stimuli will have positive DSDI values. DSDI values were calculated separately for each of the stimulus conditions described above.
To assess whether depth-sign selectivity in the Dynamic Perspective condition is related to surround suppression in MT neurons56, 57, we used data from size tuning measurements to quantify surround suppression. As described previously54, we fitted size tuning curves with a difference of error functions and computed the percentage of surround suppression as:
| (2) |
where Ropt is the peak response of fitted tuning curve, Rlargest is the response to the largest stimulus, and S is the spontaneous activity level.
Quantifying dynamic perspective cues in the visual stimulus
To relate the depth-sign selectivity of MT neurons to the dynamic perspective cues available within the receptive field, we developed a method to quantify the dynamic perspective cues within a region of the stimulus. We start from equations that describe the instantaneous retinal velocity of a point in 3D space. When an observer undergoes both translation and rotation, the image velocity of a static object is given by9, 58, 59:
| (3) |
Here, for our viewing geometry, the spatial location of a point is represented by Cartesian coordinates (X, Y, Z) in which X corresponds to the axis of lateral translation (preferred-null axis of each neuron), Y is the orthogonal axis in the frontoparallel plane, and Z is the axis in depth. The variables (Rx, Ry, Rz) and (Tx, Ty, and Tz) describe the rotation and translation of the observer around/along these axes, and (x, y) represents the image projection of the point, given by x= −X/Z and y = −Y/Z. In our experiment, translation occurs along the x axis and rotation only occurs around the y axis, such that Tz = 0, Ty = 0, Rx = 0, and Rz = 0. As a result, Equation (2) simplifies to:
| (4) |
While vx depends on both translation velocity and distance to the point of interest (Z), vy has a very simple relationship with eye rotation relative to the scene (Ry) as well as the (x,y) location of the point in the image. In principle, eye rotation (Ry) could be estimated from vy at a particular image location (x, y). However, uncertainty in vy due to unknown components of self-translation, object movement in the scene, and visual noise make this an unreliable strategy. Akin to the problem of estimating viewing distance from the gradient of vertical disparity37, 60, 61, it is likely that the visual system estimates the gradient of vy over a substantial region of the visual field to obtain a reliable estimate of Ry. The reliability of dynamic perspective cues for estimating Ry will grow with the size of the pooling region and with (x, y) locations that yield larger values of vy. Thus, a reasonable but simple proxy for the amount of dynamic perspective information in a region of the display is the sum of |xy| across that region. We therefore designed a simple metric of dynamic perspective information (DPI) as:
| (5) |
The display region was divided into a grid of small bins, and |xy| was summed across all bins within the region. We show (Suppl. Fig. 4) that the depth-sign selectivity of MT neurons in the Retinal Motion condition is moderately well predicted by this measure.
Statistics
DSDI values were classified as significantly different from zero using a permutation test25. Specifically, the differential responses between movement phases were randomly shuffled across depths, and a permuted DSDI value was computed. We repeated this process 1000 times to obtain a distribution of permuted DSDI values. Significance was defined as the probability that the permuted DSDI values were greater than the measured DSDI (when measured DSDI > 0), or less than the measured DSDI (when DSDI < 0). When 0/1000 permutations exceed the measured DSDI value, we report the probability as P<0.001.
To test whether the incidence of significant depth-sign tuning in the Retinal Motion condition was greater than chance (Fig. 4a), we performed a permutation test. For each neuron, permuted DSDI values were generated as described above. We chose one permuted data set for each neuron and tested the significance of the corresponding DSDI value. Then we counted the number of neurons with permuted DSDI values significantly different from zero. We repeated this process 1000 times to obtain a probability distribution of the number of neurons with significant tuning that would be expected by chance. Significance was then given by the probability that the number of permuted data sets with significant tuning was greater than the observed number of neurons with significant tuning.
Analyses of population data were performed using appropriate non-parametric statistical tests (as described in the main text), including Spearman rank correlations and partial rank correlations, Wilcoxon signed rank tests, and the two-sample Kolmogorov-Smirnov test.
No statistical methods were used to pre-determine sample sizes for the neural recordings, but our sample size is comparable to those generally employed in similar studies in the field. Experimenters were not blind to the purposes of the study, but all data collection was automated by computer. All stimulus conditions in the main experimental test were randomly interleaved.
A methods checklist is available with the supplementary materials.
Supplementary Material
Acknowledgements
This work was supported by NIH grant EY013644 (to GCD) and a CORE grant (EY001319) from the National Eye Institute.
Footnotes
Author contributions: HRK, DEA, and GCD designed the research; HRK performed the recording experiments and data analyses; HRK, DEA, and GCD wrote the manuscript; GCD supervised the project
References
- 1.Rogers B, Graham M. Motion parallax as an independent cue for depth perception. Perception. 1979;8:125–134. doi: 10.1068/p080125. [DOI] [PubMed] [Google Scholar]
- 2.Koenderink JJ, van Doorn AJ. Local structure of movement parallax of the plane. J Opt Soc Am A. 1976;66:717–713. [Google Scholar]
- 3.Wallach H. Perceiving a stable environment when one moves. Annu Rev Psychol. 1987;38:1–27. doi: 10.1146/annurev.ps.38.020187.000245. [DOI] [PubMed] [Google Scholar]
- 4.von Holst E. Relations between the central Nervous System and the peripheral organs. The British Journal of Animal Behaviour. 1954;2:89–94. [Google Scholar]
- 5.Welchman AE, Harris JM, Brenner E. Extra-retinal signals support the estimation of 3D motion. Vision Res. 2009;49:782–789. doi: 10.1016/j.visres.2009.02.014. [DOI] [PubMed] [Google Scholar]
- 6.Royden CS, Banks MS, Crowell JA. The perception of heading during eye movements. Nature. 1992;360:583–585. doi: 10.1038/360583a0. [DOI] [PubMed] [Google Scholar]
- 7.Banks MS, Ehrlich SM, Backus BT, Crowell JA. Estimating heading during real and simulated eye movements. Vision Res. 1996;36:431–443. doi: 10.1016/0042-6989(95)00122-0. [DOI] [PubMed] [Google Scholar]
- 8.Helmholtz Hv, Southall JPC. Helmholtz's treatise on physiological optics. Rochester, N.Y.: The Optical Society of America; 1924. [Google Scholar]
- 9.Longuet-Higgins HC, Prazdny K. The interpretation of a moving retinal image. Proc R Soc Lond B Biol Sci. 1980;208:385–397. doi: 10.1098/rspb.1980.0057. [DOI] [PubMed] [Google Scholar]
- 10.Rieger JH, Lawton DT. Processing differential image motion. J Opt Soc Am A. 1985;2:354–360. doi: 10.1364/josaa.2.000354. [DOI] [PubMed] [Google Scholar]
- 11.Rieger JH, Toet L. Human visual navigation in the presence of 3-D rotations. Biol Cybern. 1985;52:377–381. doi: 10.1007/BF00449594. [DOI] [PubMed] [Google Scholar]
- 12.Warren WH, Hannon DJ. Direction of self-motion is perceived from optical flow. Nature. 1988;336:162–163. [Google Scholar]
- 13.van den Berg AV. Robustness of perception of heading from optic flow. Vision Res. 1992;32:1285–1296. doi: 10.1016/0042-6989(92)90223-6. [DOI] [PubMed] [Google Scholar]
- 14.Rushton SK, Warren PA. Moving observers, relative retinal motion and the detection of object movement. Curr Biol. 2005;15:R542–R543. doi: 10.1016/j.cub.2005.07.020. [DOI] [PubMed] [Google Scholar]
- 15.Warren PA, Rushton SK. Optic flow processing for the assessment of object movement during ego movement. Curr Biol. 2009;19:1555–1560. doi: 10.1016/j.cub.2009.07.057. [DOI] [PubMed] [Google Scholar]
- 16.Braunstein ML, Payne JW. Perspective and the rotating trapezoid. J Opt Soc Am. 1968;58:399–403. doi: 10.1364/josa.58.000399. [DOI] [PubMed] [Google Scholar]
- 17.Rogers S, Rogers BJ. Visual and nonvisual information disambiguate surfaces specified by motion parallax. Percept Psychophys. 1992;52:446–452. doi: 10.3758/bf03206704. [DOI] [PubMed] [Google Scholar]
- 18.Hayashibe K. Reversals of visual depth caused by motion parallax. Perception. 1991;20:17–28. doi: 10.1068/p200017. [DOI] [PubMed] [Google Scholar]
- 19.Nawrot M. Eye movements provide the extra-retinal signal required for the perception of depth from motion parallax. Vision Res. 2003;43:1553–1562. doi: 10.1016/s0042-6989(03)00144-5. [DOI] [PubMed] [Google Scholar]
- 20.Nawrot M, Stroyan K. The motion/pursuit law for visual depth perception from motion parallax. Vision Res. 2009;49:1969–1978. doi: 10.1016/j.visres.2009.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nawrot M, Joyce L. The pursuit theory of motion parallax. Vision Res. 2006;46:4709–4725. doi: 10.1016/j.visres.2006.07.006. [DOI] [PubMed] [Google Scholar]
- 22.Nawrot M. Depth from motion parallax scales with eye movement gain. J Vis. 2003;3:841–851. doi: 10.1167/3.11.17. [DOI] [PubMed] [Google Scholar]
- 23.Naji JJ, Freeman TC. Perceiving depth order during pursuit eye movement. Vision Res. 2004;44:3025–3034. doi: 10.1016/j.visres.2004.07.007. [DOI] [PubMed] [Google Scholar]
- 24.Nadler JW, Nawrot M, Angelaki DE, DeAngelis GC. MT neurons combine visual motion with a smooth eye movement signal to code depth-sign from motion parallax. Neuron. 2009;63:523–532. doi: 10.1016/j.neuron.2009.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nadler JW, Angelaki DE, DeAngelis GC. A neural representation of depth from motion parallax in macaque visual cortex. Nature. 2008;452:642–645. doi: 10.1038/nature06814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nadler JW, et al. Joint Representation of Depth from Motion Parallax and Binocular Disparity Cues in Macaque Area MT. J Neurosci. 2013;33:14061–14074. doi: 10.1523/JNEUROSCI.0251-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Maunsell JH, Van Essen DC. Functional properties of neurons in middle temporal visual area of the macaque monkey. II. Binocular interactions and sensitivity to binocular disparity. J Neurophysiol. 1983;49:1148–1167. doi: 10.1152/jn.1983.49.5.1148. [DOI] [PubMed] [Google Scholar]
- 28.DeAngelis GC, Newsome WT. Organization of disparity-selective neurons in macaque area MT. J Neurosci. 1999;19:1398–1415. doi: 10.1523/JNEUROSCI.19-04-01398.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Britten KH, Shadlen MN, Newsome WT, Movshon JA. The analysis of visual motion: a comparison of neuronal and psychophysical performance. J Neurosci. 1992;12:4745–4765. doi: 10.1523/JNEUROSCI.12-12-04745.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Warren WH, Jr, Hannon DJ. Eye movements and optical flow. J Opt Soc Am A. 1990;7:160–169. doi: 10.1364/josaa.7.000160. [DOI] [PubMed] [Google Scholar]
- 31.Crowell JA, Banks MS, Shenoy KV, Andersen RA. Visual self-motion perception during head turns. Nat Neurosci. 1998;1:732–737. doi: 10.1038/3732. [DOI] [PubMed] [Google Scholar]
- 32.Mahar M, DeAngelis GC, Nawrot M. Roles of perspective and pursuit cues in the disambiguation of depth from motion parallax. Journal of Vision. 13:969. [Google Scholar]
- 33.Page WK, Duffy CJ. MST neuronal responses to heading direction during pursuit eye movements. J Neurophysiol. 1999;81:596–610. doi: 10.1152/jn.1999.81.2.596. [DOI] [PubMed] [Google Scholar]
- 34.Bradley DC, Maxwell M, Andersen RA, Banks MS, Shenoy KV. Mechanisms of heading perception in primate visual cortex. Science. 1996;273:1544–1547. doi: 10.1126/science.273.5281.1544. [DOI] [PubMed] [Google Scholar]
- 35.Shenoy KV, Bradley DC, Andersen RA. Influence of gaze rotation on the visual response of primate MSTd neurons. J Neurophysiol. 1999;81:2764–2786. doi: 10.1152/jn.1999.81.6.2764. [DOI] [PubMed] [Google Scholar]
- 36.Zhang T, Heuer HW, Britten KH. Parietal area VIP neuronal responses to heading stimuli are encoded in head-centered coordinates. Neuron. 2004;42:993–1001. doi: 10.1016/j.neuron.2004.06.008. [DOI] [PubMed] [Google Scholar]
- 37.Kaneko H, Howard IP. Spatial properties of shear disparity processing. Vision Res. 1997;37:315–323. doi: 10.1016/s0042-6989(96)00165-4. [DOI] [PubMed] [Google Scholar]
- 38.Chowdhury SA, DeAngelis GC. Fine discrimination training alters the causal contribution of macaque area MT to depth perception. Neuron. 2008;60:367–377. doi: 10.1016/j.neuron.2008.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tsutsui K, Sakata H, Naganuma T, Taira M. Neural correlates for perception of 3D surface orientation from texture gradient. Science. 2002;298:409–412. doi: 10.1126/science.1074128. [DOI] [PubMed] [Google Scholar]
- 40.Colby CL, Duhamel JR, Goldberg ME. Ventral intraparietal area of the macaque: anatomic location and visual response properties. J Neurophysiol. 1993;69:902–914. doi: 10.1152/jn.1993.69.3.902. [DOI] [PubMed] [Google Scholar]
- 41.Bremmer F, Duhamel JR, Ben Hamed S, Graf W. Heading encoding in the macaque ventral intraparietal area (VIP) Eur J Neurosci. 2002;16:1554–1568. doi: 10.1046/j.1460-9568.2002.02207.x. [DOI] [PubMed] [Google Scholar]
- 42.Saito H, et al. Integration of direction signals of image motion in the superior temporal sulcus of the macaque monkey. J Neurosci. 1986;6:145–157. doi: 10.1523/JNEUROSCI.06-01-00145.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tanaka K, Saito H. Analysis of motion of the visual field by direction, expansion/contraction, and rotation cells clustered in the dorsal part of the medial superior temporal area of the macaque monkey. J Neurophysiol. 1989;62:626–641. doi: 10.1152/jn.1989.62.3.626. [DOI] [PubMed] [Google Scholar]
- 44.Duffy CJ, Wurtz RH. Sensitivity of MST neurons to optic flow stimuli. I. A continuum of response selectivity to large-field stimuli. J Neurophysiol. 1991;65:1329–1345. doi: 10.1152/jn.1991.65.6.1329. [DOI] [PubMed] [Google Scholar]
- 45.Maunsell JH, van Essen DC. The connections of the middle temporal visual area (MT) and their relationship to a cortical hierarchy in the macaque monkey. J Neurosci. 1983;3:2563–2586. doi: 10.1523/JNEUROSCI.03-12-02563.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Newsome WT, Wurtz RH, Komatsu H. Relation of cortical areas MT and MST to pursuit eye movements. II. Differentiation of retinal from extraretinal inputs. J Neurophysiol. 1988;60:604–620. doi: 10.1152/jn.1988.60.2.604. [DOI] [PubMed] [Google Scholar]
- 47.Ono S, Mustari MJ. Extraretinal signals in MSTd neurons related to volitional smooth pursuit. J Neurophysiol. 2006;96:2819–2825. doi: 10.1152/jn.00538.2006. [DOI] [PubMed] [Google Scholar]
- 48.Stanton GB, Bruce CJ, Goldberg ME. Topography of projections to posterior cortical areas from the macaque frontal eye fields. J Comp Neurol. 1995;353:291–305. doi: 10.1002/cne.903530210. [DOI] [PubMed] [Google Scholar]
- 49.Schall JD, Morel A, King DJ, Bullier J. Topography of visual cortex connections with frontal eye field in macaque: convergence and segregation of processing streams. J Neurosci. 1995;15:4464–4487. doi: 10.1523/JNEUROSCI.15-06-04464.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.MacAvoy MG, Gottlieb JP, Bruce CJ. Smooth-pursuit eye movement representation in the primate frontal eye field. Cereb Cortex. 1991;1:95–102. doi: 10.1093/cercor/1.1.95. [DOI] [PubMed] [Google Scholar]
- 51.Gu Y, Watkins PV, Angelaki DE, DeAngelis GC. Visual and nonvisual contributions to three-dimensional heading selectivity in the medial superior temporal area. J Neurosci. 2006;26:73–85. doi: 10.1523/JNEUROSCI.2356-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Van Essen DC, et al. An integrated software suite for surface-based analyses of cerebral cortex. J Am Med Inform Assoc. 2001;8:443–459. doi: 10.1136/jamia.2001.0080443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Komatsu H, Wurtz RH. Relation of cortical areas MT and MST to pursuit eye movements. I. Localization and visual properties of neurons. J Neurophysiol. 1988;60:580–603. doi: 10.1152/jn.1988.60.2.580. [DOI] [PubMed] [Google Scholar]
- 54.DeAngelis GC, Uka T. Coding of horizontal disparity and velocity by MT neurons in the alert macaque. J Neurophysiol. 2003;89:1094–1111. doi: 10.1152/jn.00717.2002. [DOI] [PubMed] [Google Scholar]
- 55.Albright TD, Desimone R, Gross CG. Columnar organization of directionally selective cells in visual area MT of the macaque. J Neurophysiol. 1984;51:16–31. doi: 10.1152/jn.1984.51.1.16. [DOI] [PubMed] [Google Scholar]
- 56.Allman J, Miezin F, McGuinness E. Direction- and velocity-specific responses from beyond the classical receptive field in the middle temporal visual area (MT) Perception. 1985;14:105–126. doi: 10.1068/p140105. [DOI] [PubMed] [Google Scholar]
- 57.Bradley DC, Andersen RA. Center-surround antagonism based on disparity in primate area MT. J Neurosci. 1998;18:7552–7565. doi: 10.1523/JNEUROSCI.18-18-07552.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Koenderink JJ, van Doorn AJ. Facts on optic flow. Biol Cybern. 1987;56:247–254. doi: 10.1007/BF00365219. [DOI] [PubMed] [Google Scholar]
- 59.Royden CS, Crowell JA, Banks MS. Estimating heading during eye movements. Vision Res. 1994;34:3197–3214. doi: 10.1016/0042-6989(94)90084-1. [DOI] [PubMed] [Google Scholar]
- 60.Howard IP, Rogers BJ. Binocular vision and stereopsis. New York: Oxford University Press; 1995. [Google Scholar]
- 61.Kaneko H, Howard IP. Spatial limitation of vertical-size disparity processing. Vision Res. 1997;37:2871–2878. doi: 10.1016/s0042-6989(97)00099-0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.