Wave-CAIPI for Highly Accelerated 3D Imaging

Abstract

Purpose

To introduce the Wave-CAIPI (Controlled Aliasing in Parallel Imaging) acquisition and reconstruction technique for highly accelerated 3D imaging with negligible g-factor and artifact penalties.

Methods

The Wave-CAIPI 3D acquisition involves playing sinusoidal g_y and g_z gradients during the readout of each k_x encoding line, while modifying the 3D phase encoding strategy to incur inter-slice shifts as in 2D-CAIPI acquisitions. The resulting acquisition spreads the aliasing evenly in all spatial directions, thereby taking full advantage of 3D coil sensitivity distribution. By expressing the voxel spreading effect as a convolution in image space, an efficient reconstruction scheme that does not require data gridding is proposed. Rapid acquisition and high quality image reconstruction with Wave-CAIPI is demonstrated for high-resolution magnitude and phase imaging and Quantitative Susceptibility Mapping (QSM).

Results

Wave-CAIPI enables full-brain gradient echo (GRE) acquisition at 1 mm isotropic voxel size and R=3×3 acceleration with maximum g-factors of 1.08 at 3T, and 1.05 at 7T. Relative to the other advanced Cartesian encoding strategies 2D-CAIPI and Bunched Phase Encoding, Wave-CAIPI yields up to 2-fold reduction in maximum g-factor for 9-fold acceleration at both field strengths.

Conclusion

Wave-CAIPI allows highly accelerated 3D acquisitions with low artifact and negligible g-factor penalties, and may facilitate clinical application of high-resolution volumetric imaging.

Introduction

Over the last decade, parallel imaging acquisitions (1–3) through multiple receiver coils have been ubiquitously utilized to accelerate various MRI sequences. A number of modifications have also been proposed to improve the conditioning of parallel imaging acquisitions to enable higher accelerations. Simultaneous multislice (SMS) acquisition involves simultaneous excitation of multiple slices, and offers substantial reduction in 2D imaging scan time (4–6) as it directly reduces the amount of time needed to acquire a fixed number of slices. CAIPIRINHA (Controlled Aliasing in Parallel Imaging Results in Higher Acceleration) (7) further improves reconstruction quality for multislice acquisitions by modulating the phase of the simultaneously excited slices. This modification incurs inter-slice shifts in the phase encoding direction between aliasing image slices, thereby increasing the variation in the coil sensitivity profiles across the slices to improve slice dealiasing. SMS imaging with CAIPIRINHA has been recently demonstrated in accelerated Turbo Spin Echo (TSE) (8,9) and Steady State Free Precession (SSFP) imaging (10). The CAIPIRINHA strategy has also been successfully applied to echo-planar trajectories (11), which allow rapid, high-resolution functional and diffusion weighted imaging (12), Arterial Spin Labeling (ASL) (13,14), and Dynamic Susceptibility Contrast imaging (15).

Application of interslice shifts to 3D imaging forms the basis of 2D-CAIPIRINHA (16), wherein the phase (k_y) and partition (k_z) encoding strategy is modified to shift the spatial aliasing pattern to reduce aliasing and better exploit the coil sensitivity variation. The staggered sampling pattern in 3D k-space is shown to be equivalent to SMS imaging with inter-slice shifts in (17). This connection between slice-shifted 2D and 3D acquisitions was further explored in (18) to facilitate the reconstruction of non-Cartesian SMS trajectories. Alternative approaches for accelerated volumetric imaging include Bunched Phase Encoding (BPE) (19), where a g_y gradient is applied during the readout of each phase encoding line to create a zigzag trajectory that can be reconstructed using Papoulis’s generalized sampling theory to give an alias-free image. Bunch encoding has also been combined with parallel imaging (20–22) to take advantage of the coil sensitivity variation in the readout direction to improve the reconstruction.

An emerging strategy for improved parallel imaging quality is to impose a sparsity-inducing prior on the reconstructed image. In addition to the encoding power of the receive coil profiles, these methods employ pseudo-random (rectilinear) sampling strategies that yield incoherent aliasing artifacts that can be mitigated via sparsity priors (23–26). Among k-space based methods, DESIGN (24) regularizes the GRAPPA (3) result under wavelet transform, while L1-SPIRiT (23) seeks sparse coil images in the wavelet domain that match the calibration and acquired data. Similar to SENSE (2), the general problem of reconstructing multi-channel data can also be formulated as a forward model involving coil sensitivities and a k-space sampling operator, and regularized with Total Variation penalty (25,26). A common feature of these multi-channel Compressed Sensing (CS) algorithms is that the k-space sampling pattern is designed to satisfy CS incoherence requirements, while 2D-CAIPI and BPE modify the k-space trajectory to better exploit the coil sensitivity distribution by shaping the aliasing pattern.

Development and proliferation of multi-channel receive coil arrays have resulted in a ubiquitous use of high channel count systems such as the 32-channel head coil on commercially available scanners. Since the coil elements in close proximity have similar sensitivity profiles, the information provided by the elements is not orthogonal, thereby limiting the actual degrees of freedom available. Conventional parallel imaging cannot fully utilize this limited degree of freedom and fails to achieve high acceleration factors. In particular, such techniques do not utilize the coil sensitivity information present in the fully-sampled readout dimension (x) in a 3D Cartesian acquisition, and this further limits the use of spatial encoding power of the coil sensitivities to two dimensions out of the three. To address these issues, we introduce Wave-CAIPI, which combines and extends the BPE and 2D-CAIPI strategies by playing sinusoidal g_y and g_z gradients simultaneously (with a π/2 phase shift between the two waveforms) during the readout of each k-space line, thus creating inter-slice shifts by modifying the k-space phase and partition encoding strategy. This results in a highly efficient k-space sampling pattern that spreads the aliasing evenly in all spatial dimensions (x, y, and z). Since this scheme takes full advantage of the spatial variation in the 3D coil sensitivity profiles, it enables highly accelerated volumetric imaging with low artifact and negligible signal-to-noise ratio (SNR) penalties.

Herein, we extend our initial proposal reported in abstract form (27) by increasing the spatial resolution 8-fold (from 2 mm to 1 mm isotropic voxel size), demonstrating feasibility at ultra high field strength (7T), employing efficient iterative reconstruction to decrease the computation time 25-fold, rapidly characterizing the Wave gradients to account for the mismatch between theoretical and experimental gradient trajectories, and demonstrate phase and quantitative susceptibility maps derived from a highly accelerated 3D gradient echo (GRE) acquisition.

The main contributions of this work include:

1. Voxel spreading effects of the Wave gradients and the coil sensitivity information are captured in a forward model, which divides the reconstruction problem into small, decoupled linear systems that are solved rapidly. By employing inverse Fourier transform as a pre-conditioner to the generalized SENSE model (28), the proposed formulation explains the effect of Wave gradients as additional phase imparted in image domain, rather than displacement in k-space trajectory. This forward model is also amenable to parallel processing for rapid reconstruction.

2. Wave-CAIPI is demonstrated to provide substantial improvement in image quality and g-factor performance relative to the SENSE, BPE and 2D-CAIPI methods. Because of its efficient utilization of the variation in the sensitivity profiles in all spatial axes, Wave-CAIPI yields g-factor maps close to unity even with 9-fold acceleration at 3T and 7T.

3. Wave-CAIPI is deployed to accelerate high-resolution volumetric GRE acquisition, which is an essential tool for phase imaging (29) and related Susceptibility Weighted Imaging (SWI) (30,31) and Quantitative Susceptibility Mapping (QSM) (32–34) applications. Such acquisitions are inherently long since they need a relatively long echo time to build up contrast. As the proposed method is applicable to any 3D acquisition, dramatic reduction in scan time is warranted for structural imaging protocols (e.g. MPRAGE (35)) as well.

4. Raw phase data obtained from Wave reconstruction are filtered with rapid phase processing algorithms (33,36,37). Starting from the resulting tissue phase, a fast susceptibility dipole inversion algorithm (38) is employed to solve for the underlying susceptibility distribution χ.

5. Example Matlab code that demonstrates Wave reconstruction with data acquired at 7T is offered as supplementary material, and will be also available at: http://martinos.org/~berkin/software.html

Theory

Effect of Wave Gradients on the Acquired Signal

Ignoring relaxation, the received baseband MRI signal s(t) can be written in terms of the underlying magnetization m(r) and the applied time-varying gradients g(t) as,

$$\mathrm{s}(t)={\int }_{\mathit{r}}\mathrm{m}(\mathit{r})\text{exp}(-i\gamma {\int }_0^t\mathbf{g}(\tau )·\mathit{r}d\tau )d\mathit{r}$$ (1)

For rectilinear 3D imaging with phase and partition encoding, the received signal can be expressed using the k-space notation at fixed k_y and k_z as

$$\mathrm{s}(t)={\int }_{x,y,z}\mathrm{m}(x,y,z){\mathrm{e}}^{-i2\pi (k_x(t)x+k_{y}y+k_{z}z)}dxdydz$$ (2)

where the coordinate system is defined with respect to the excitation box. When additional sinusoidal Wave gradients g_y and g_z are played during each readout line in y and z axes (Fig.1), the signal equation can be modified to yield

$$\mathrm{s}(t)={\int }_{x,y,z}\mathrm{m}(x,y,z){\mathrm{e}}^{-i2\pi (k_x(t)x+k_{y}y+k_{z}z)}\text{exp}(-i\gamma {\int }_0^t({\mathrm{g}}_y(\tau )y+{\mathrm{g}}_z(\tau )z)d\tau )dxdydz$$ (3)

Defining $\frac{\gamma }{2\pi }{\int }_0^t{\mathrm{g}}_y(\tau )d\tau ={\mathrm{P}}_y(t)$ and $\frac{\gamma }{2\pi }{\int }_0^t{\mathrm{g}}_z(\tau )d\tau ={\mathrm{P}}_z(t)$, a simpler expression is obtained,

$$\mathrm{s}(t)={\int }_{x,y,z}\mathrm{m}(x,y,z){\mathrm{e}}^{-i2\pi (k_x(t)x+k_{y}y+k_{z}z+{\mathrm{P}}_y(t)y+{\mathrm{P}}_z(t)z)}dxdydz$$ (4)

Now taking the inverse Fourier transform over k_y and k_z, we switch to the hybrid space such that the acquired readout line at a fixed (y, z) location is expressed as

$$\mathrm{s}(t,y,z)={\mathrm{e}}^{-i2\pi ({\mathrm{P}}_y(t)y+{\mathrm{P}}_z(t)z)}{\int }_x\mathrm{m}(x,y,z){\mathrm{e}}^{-i2\pi k_x(t)x}dx$$ (5)

Discretizing this expression and noting that each time point index corresponds to a k-space index yields

$$\mathrm{s}[k,y,z]={\mathrm{e}}^{-i2\pi ({\mathrm{P}}_y[k]y+{\mathrm{P}}_z[k]z)}{\sum }_x\mathrm{m}[x,y,z]{\mathrm{e}}^{-i2\pi kx/N}$$ (6)

where k represents the k-space index that enumerates the data points acquired per readout line and N stands for the matrix size in this axis. Finally, taking the inverse Discrete Fourier transform (DFT) gives

$$\text{wave}[x,y,z]={\sum }_k{\mathrm{e}}^{i2\pi kx/N}({\mathrm{e}}^{-i2\pi ({\mathrm{P}}_y[k]y+{\mathrm{P}}_z[k]z)}\sum _x\mathrm{m}[x,y,z]{\mathrm{e}}^{-i2\pi kx/N})$$ (7)

This expression relates the image acquired with the Wave gradients, wave[x, y, z], to the underlying magnetization m[x, y, z], and suggests a simple explanation for the effect of the Wave gradients:

Each readout line in the underlying image m[x, y, z], is convolved with a point spread function (PSF) that depends on the spatial location (y, z) to yield the acquired wave image.

This observation can be written more succinctly as,

$$\text{wave}[x,y,z]={\mathbf{F}}_x^{-1}·\text{Psf}[k,y,z]·({\mathbf{F}}_x·\mathrm{m}[x,y,z])$$ (8)

Where F_x represents the DFT operator in the x axis, and Psf[k, y, z] = e^{−2π(P_y[k]y+P_z[k]Z)} is the PSF that explains the effect of the Wave gradients. Viewed from this perspective, the forward model for Wave-CAIPI is a simple multiplication in k-space, or a convolution in image space. Note that this property is not generalizable to any arbitrary trajectory (e.g. spiral), but is applicable to cases where the phase and partition encoding trajectories can be represented as summations of rectilinear and non-Cartesian components, so that using inverse DFT allows switching to the hybrid space where the PSF formalism can be utilized.

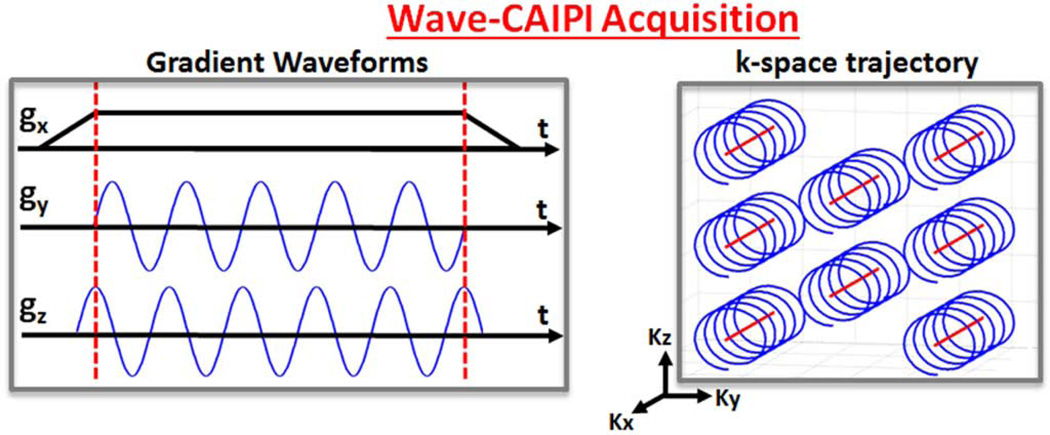
Fig. 1.

Gradient waveforms and k-space trajectory for Wave-CAIPI imaging. Sinusoidal g_y and g_z gradients with a π/2 phase shift between the waveforms incur a corkscrew trajectory in k-space. The corkscrews are also staggered due to the 2D-CAIPI sampling strategy to create inter-slice shifts.

In addition to the Wave gradients, the proposed method employs 2D-CAIPI sampling scheme (16) that staggers the sampling positions in the k_y-k_z plane, e.g., shifting the readouts to lie on a hexagonal grid, in order to create inter-slice shifts across the aliasing slices. The combined effect of sinusoidal Wave gradients and staggered sampling strategy leads to the corkscrew trajectory depicted in Fig.1. While the acquired k-space samples do not fall onto a Cartesian grid, expressing the acquisition as convolution with a PSF allows us to explain the effect of the Wave trajectory as a simple multiplication in Cartesian k-space via Eq.8.

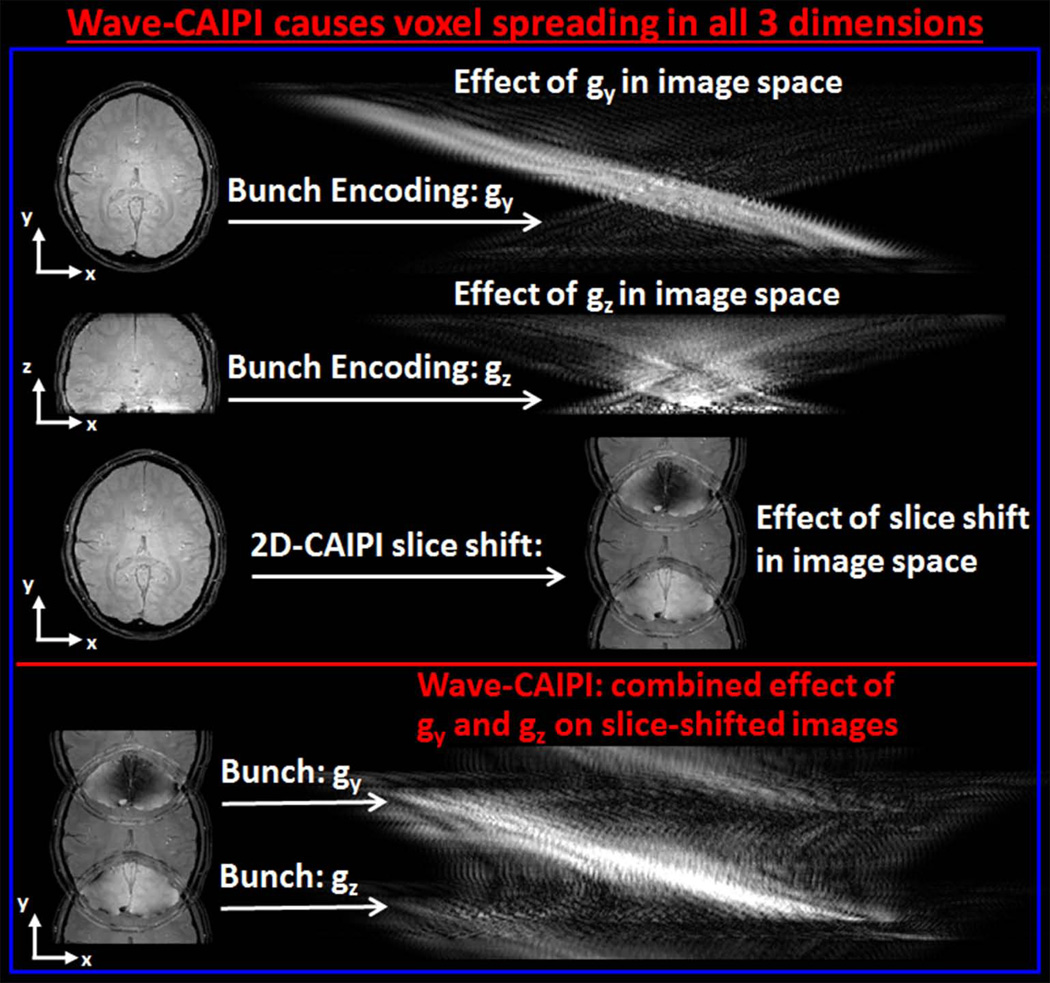
Since the underlying image is convolved with a spatially varying PSF, the amount of voxel spreading is a function of (y, z) coordinates. Note that the Wave gradients g_y and g_z do not cause voxel spreading in the y and z directions, but the only spreading effect is along the x (readout) axis. This effect is demonstrated in Fig.2, where the Wave gradients along y and z axes combined with inter-slice shifts give rise to spreading in all spatial directions.

Fig. 2.

Bunch encoding gradient waveforms g_y and g_z incur voxel spreading in the readout dimension (x-axis). The amount of this spreading is a function of y and z positions, respectively. 2D-CAIPI strategy creates inter-slice shifts in the phase encoding dimension (y-axis). Wave-CAIPI combines the effect of g_y and g_z gradients with slice shifting, and spreads out voxels in all three spatial dimensions.

Forward Model for Parallel Imaging with Wave-CAIPI

In the presence of R-fold acceleration in phase and partition encoding, rows of image readout lines from R spatial positions collapse on each other, which can be unfolded using knowledge of the spatial encoding provided by coil sensitivity profiles. This approach can be extended to the aliasing induced by the Wave sampling pattern. For simplicity, in this example, we consider 2-fold accelerated Wave-CAIPI in phase encoding (k_y) direction only. In this case, two image locations that are half of a field of view (FOV_y) apart will collapse on each other. We denote the measured signal at these locations succinctly as wave[y₁] and wave[y₂], and drop the x and z indices. These rows of image readout lines are related to the underlying magnetization m[y₁] and m[y₂] via the convolution operations wave[y₁] = F⁻¹Psf[y₁]F · m[y₁] and wave [y₂] = F⁻¹Psf[y₂]F · m[y₂]. The forward model that relates the acquired data to the unknown magnetization is then

$$[{\mathbf{F}}^{-1}\text{Psf}[y_1]\mathbf{F}{\mathbf{F}}^{-1}\text{Psf}[y_2]\mathbf{F}]\left[\begin{array}{c}\mathrm{m}[y_1]\\ \mathrm{m}[y_2]\end{array}\right]=\text{wave}$$ (9)

wave = wave[y₁] + wave[y₂] is the collapsed Wave image due to undersampling. With the additional encoding information from n receive coil channels with sensitivity profiles C_i, this system becomes

$$\left[\begin{array}{cc}{\mathbf{F}}^{-1}\text{Psf}[y_1]\mathbf{F}{\mathrm{C}}_1[y_1]& {\mathbf{F}}^{-1}\text{Psf}[y_2]\mathbf{F}{\mathrm{C}}_1[y_2]\\ ⋮& ⋮\\ {\mathbf{F}}^{-1}\text{Psf}[y_1]\mathbf{F}{\mathrm{C}}_n[y_1]& {\mathbf{F}}^{-1}\text{Psf}[y_2]\mathbf{F}{\mathrm{C}}_n[y_2]\end{array}\right]\left[\begin{array}{c}\mathrm{m}[y_1]\\ \mathrm{m}[y_2]\end{array}\right]=\left[\begin{array}{c}{\text{wave}}_1\\ ⋮\\ {\text{wave}}_n\end{array}\right]$$ (10)

Solution of Eq.10 recovers the underlying image rows from the reduced-FOV coil images wave_i . In the more general case of R-fold accelerated Wave imaging with undersampling in phase and partition encoding, the linear system in Eq.10 is modified to solve for the set of R collapsed image rows.

Another way to view the Wave acquisition is through a direct SENSE model that relates the acquired non-Cartesian k-space data to the underlying image via the relation E · i = k. Here, k is the vector of k-space data, E is the encoding matrix that includes coil sensitivities and undersampled non-Cartesian Fourier operator, and i is the vector of the 3D image data. In this relation, the encoding matrix E is dense, and its application will require 3D non-uniform Fast Fourier Transform (NUFFT) (39). However, when inverse DFT is applied to this dense matrix without accounting for how the Wave gradients modify the k-space trajectory, the resulting encoding becomes identical to the PSF formulation of Eq.10. As such, the proposed formulation in Eq.10 employs the inverse DFT as a preconditioner to sparsify the dense encoding, so that the 3D reconstruction problem is decoupled into small problems that are solved independently for each set of R collapsed rows.

The role of 2D-CAIPI shifting, when applied in addition to the Wave gradients, is to modify the rows that will be collapsed on each other. As such, the PSFs and coil profiles are also shifted during reconstruction to account for the interslice shifts across the aliasing slices. Since a separate linear system is formed for each set of R collapsed readout lines, the reconstruction of the whole 3D volume is highly separable and amenable to parallel processing.

The voxel spreading effect of the Wave gradients increases the average distance across aliasing image rows, thereby improving the variation in the coil sensitivity profiles of these collapsed voxels. This effect facilitates the parallel imaging reconstruction, and is further explained in Fig.3. Due to the voxel spreading effect of Wave gradients in the readout direction, the data are 6-fold oversampled in k_x . This extends the readout field of view and entirely captures the spread-out Wave images.

Fig. 3.

Ry=2-fold acceleration causes voxels that are FOVy/2 apart to collapse on each other. Since Wave-CAIPI spreads out the voxels in x-axis, the aliasing voxels are further apart from each other. This increases the variation in coil sensitivity profiles, and improves parallel imaging.

Methods

Characterizing the k-space Trajectory Traversed by Wave Gradients

As system imperfections can cause the physical Wave PSFs to differ from the theoretical ones, characterizing the actual k-space trajectory accurately leads to improved image reconstruction. To this end, the physical y and z trajectories P_y[k] and P_z[k] are estimated using simple and fast calibration scans. This involves taking single-slice projection data (40), in the x-y plane to characterize the P_y-Wave and in the x-z plane to characterize the P_z-Wave. Each projection data is acquired twice: with and without the Wave gradient of interest. The image phase differences for each of the single-slice projections, with and without the Wave gradient, are then computed. This difference is deposited by the Wave gradients, and is proportional to spatial y and z positions. The trajectory estimation is performed for P_y and P_z separately, where the computed phase differences 2πP_y[k]y and 2πP_z[k]z are further refined by phase unwrapping and linear regression with respect to y and z position, respectively. Since these differences, 2πP_y[k]y and 2πP_z[k]z, are linear functions of position indices y and z, we estimate the k-space trajectories P_y[k] and P_z[k] by linear regression. In more detail, we solve the least squares problem

$$\left[\begin{array}{cc}{y}_1& 1\\ ⋮& ⋮\\ y_n& 1\end{array}\right]·[\widehat{{\mathrm{P}}_y}C]=\left[\begin{array}{c}{\mathrm{P}}_y·y_1\\ ⋮\\ {\mathrm{P}}_y·y_n\end{array}\right]$$ (11)

where y₁, …, y_n are the y-positions in image space, P_y ∙ y₁ are the computed phase differences from the calibration data, $\widehat{{\mathrm{P}}_y}$ is the fitted trajectory, and C is a term independent of position that accounts for factors such as phase drift. Similar computation is performed to estimate $\widehat{{\mathrm{P}}_z}$. The fitted trajectories $\widehat{{\mathrm{P}}_y}$ and $\widehat{{\mathrm{P}}_z}$ are combined multiplicatively to yield the PSF estimate $\widehat{\text{Psf}}[x,y,z]={\mathrm{e}}^{-i2\pi (\widehat{{\mathrm{P}}_y}[k]y+\widehat{{\mathrm{P}}_z}[k]z)}$. As the PSFs depend only on the particular gradient system and not the subject that is being scanned, gradient characterization can also be performed on a phantom, independently of the in vivo acquisition. While Fig.1 depicts the gradient waveforms during the readout, the g_x gradient is also pre-phased so that during the readout, the k-space is traversed from −k_x,max to + k_x,max.

Iterative parallel imaging reconstruction for Wave-CAIPI

The estimated PSFs are used in the generalized SENSE model (Eq.10) to unfold the undersampled data acquired with Wave gradients. Coil sensitivity profiles are computed by fitting 7^th order polynomials to low-resolution head array coil images normalized by the body coil algorithm (41), and up-sampled with cubic interpolation to a higher resolution to match the high-resolution of the accelerated acquisition.

In order to avoid forming the encoding matrices in Eq.10 explicitly, the linear system is formulated as a least-squares problem, and solved iteratively with Matlab’s lsqr function (The MathWorks Inc., Natick MA). This involves simple point-wise operations for multiplication with coil sensitivities and PSFs, and allows utilization of the Fast Fourier Transform (FFT). The iterative lsqr algorithm minimizes ${\Vert \mathrm{A}·m-w\Vert }_2^2$, where A represents the encoding matrix in Eq.10, while m and w stand for the unknown image rows and the Wave coil data in this equation. This formulation does not involve any regularization during reconstruction.

Data Acquisition and Reconstruction

Acquisition parameters for the in vivo experiments are summarized in Table 1, and detailed below.

Table 1.

Acquisition parameters for the in vivo experiments

	Resolution (mm3)	Field Strength	TR/TE (ms)	Acceleration	Acquisition Time	Related Figure
Dataset 1	1×1×2	3T	26/13.3	3×3 Retrospective	38 sec	Fig.4 left
Dataset 2	1×1×2	7T	27/10.9	3×3 Retrospective	40 sec	Fig.4 right
Dataset 3	1×1×1	3T	40/17	3×3 Prospective	2.3 min	Figs.5&7
Dataset 4	1×1×1	7T	40/20	3×3 Prospective	2.3 min	Figs.6&8

1. Comparing Wave-CAIPI with Conventional GRE on retrospectively undersampled acquisitions

Wave-CAIPI was implemented on the Siemens IDEA environment (Erlangen, Germany) for whole-brain, 3D GRE sequence. A healthy volunteer was scanned at 3T Tim Trio and 7T Magnetom scanners, and fully-sampled Wave-CAIPI and conventional GRE data were acquired to serve as ground truth. The parameters common to both datasets were, FOV=224×224×120 mm³, 1×1×2 mm³ voxel size, 32 receive coils (42), maximum Wave gradient amplitude=6 mT/m, maximum slew rate=50 mT/m, using 7 sinusoidal Wave cycles/readout. At 3T, scan time for fully-sampled data was 5.7 min with TR/TE=26/13.3 ms and bandwidth=70 Hz/pixel. At 7T, the scan time was 6 min with TR/TE=27/10.9 ms and bandwidth=80 Hz/pixel. The fully-sampled Wave-CAIPI and conventional GRE data were retrospectively undersampled in software environment to achieve a reduction factor of R=3×3. Undersampled Wave-CAIPI data were reconstructed with the proposed parallel imaging technique, while the uniformly-undersampled normal GRE acquisition was reconstructed with the SENSE algorithm (2). Using the fully-sampled data as ground truth, reconstruction artifact levels were quantified with the normalized root-mean-square error (RMSE) metric. G-factor maps were calculated to quantify the noise amplification incurred by Wave-CAIPI and conventional GRE. The reciprocal maps, 1/g-factor, were also plotted to report the retained SNR.

2. Comparing Wave-CAIPI with 2D-CAIPI and BPE on prospectively undersampled acquisitions

To assess the improvement in parallel imaging capability relative to existing parallel imaging techniques, Wave-CAIPI was compared to 2D-CAIPI (16) and BPE (19–22). Two healthy subjects were scanned at 3T and 7T with parameters FOV=240×240×120 mm³, 1 mm³ isotropic voxel size, TR=40 ms, BW=70 Hz/pixel, 32 receive coils, maximum Wave gradient amplitude=6 mT/m, maximum slew rate=50 mT/m, using 7 sinusoidal Wave cycles/readout. The echo times were 17 ms at 3T and 20 ms at 7T. At each field strength, R=3×3 prospectively accelerated GRE data were acquired using Wave-CAIPI, 2D-CAIPI and BPE sampling, where each acquisition took 2.3 min. Additionally, low-resolution (3 mm isotropic) GRE data at TR=12 ms were acquired with body and head coils to estimate coil sensitivity profiles.

3. Processing of GRE phase images and Quantitative Susceptibility Mapping

Raw phase images produced by Wave-CAIPI, 2D-CAIPI and BPE at 1mm³ resolution and R=3×3 acceleration were processed by BET brain masking (43), Laplacian phase unwrapping (36) and V-SHARP (Variable kernel Sophisticated Harmonic Artifact Reduction for Phase data) filtering for background phase removal (33,36,37). V-SHARP employed kernels of increasing diameters (3 to 15 voxels) with a truncation threshold of 0.25 to yield the tissue phase ϕ. The tissue susceptibility χ is related to the phase ϕ via the linear relation Dℱχ = ℱϕ, where ℱ is the 3D DFT operator and $\mathbf{D}=1/3-k_z^2/k^2$ is the susceptibility kernel in k-space (32,44). This kernel effectively undersamples the frequency content of the susceptibility map on the conical surface $3k_z^2=k^2$, which makes the inversion of the relation ill-conditioned (32–34,45,46). Herein, regularized reconstruction with gradient smoothness prior is utilized for susceptibility mapping. This entails the solution of the optimization problem $min{\Vert \mathbf{D}ℱ\chi -ℱ\varphi \Vert }_2^2+\lambda {\Vert \mathbf{M}G\chi \Vert }_2^2$, where M is a binary mask derived from the magnitude image that prevents smoothing across edges, and G is the spatial gradient operator. This objective is minimized using a fast preconditioned conjugate gradient solver (38,47) with λ=0.03.

4. Effect of Wave Gradients within a Single Voxel

In the Wideband acquisition (48), applying an additional g_z encoding gradient during the k_x data readout causes undesirable voxel blurring/tilting artifact. The Wave-CAIPI acquisition aims to avoid this artifact by utilizing sinusoidal g_y and g_z waveforms, which do not result in accrual of gradient moments and avoids large intra-voxel phase variations. Nonetheless, there are some intra-voxel phase variations during the Wave-CAIPI acquisition and potential intra-voxel blurring artifact must be characterized. This potential blurring was characterized for the in vivo acquisition setting (max Wave gradient=6 mT/m, max slew=50 mT/m, 7 Wave cycles/readout) to investigate the degree of voxel blurring incurred by Wave-CAIPI. To this end, the image-space PSF acting on the voxel was computed, and integrated across the voxel to quantify the intra-voxel spreading.

Results

1. Comparing Wave-CAIPI with Conventional GRE on retrospectively undersampled acquisitions

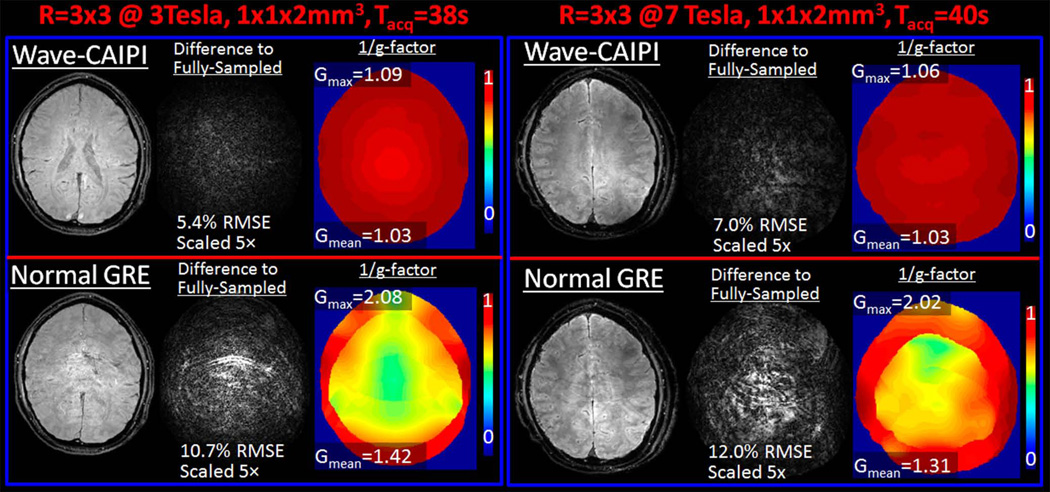
At 3T, 9-fold accelerated Wave-CAIPI yielded 5.4% RMSE relative to the fully-sampled data, whereas the error was 10.7% for conventional GRE with uniform undersampling (Fig.4 left). From g-factor analysis, g_max for Wave vs. normal GRE was found to be 1.09 vs. 2.08 and g_mean was 1.03 vs. 1.42. At 7T, Wave vs. normal GRE reconstruction errors were 7.0% and 12.0% respectively (Fig.4 right). g_max and g_mean for Wave vs. normal GRE were 1.06 vs. 2.02 and 1.03 vs. 1.31, respectively. At both field strengths, Wave-CAIPI yields a 2-fold reduction in maximum g-factor and image artifact levels. For Wave-CAIPI, the difference images at both 3T and 7T are mostly spatially unstructured or “noise-like”, while, for conventional accelerated acquisition, structured aliasing artifacts are observed, particularly in the high g-factor regions.

Fig. 4.

R=3×3-fold retrospectively accelerated acquisitions. Wave-CAIPI and conventional gradient echo (GRE) reconstructions are compared at 3T (left) and 7T (right). Wave-CAIPI offers 2-fold improvement in artifact power and maximum g-factor at both field strengths.

2. Comparing Wave-CAIPI with 2D-CAIPI and BPE on prospectively undersampled acquisitions

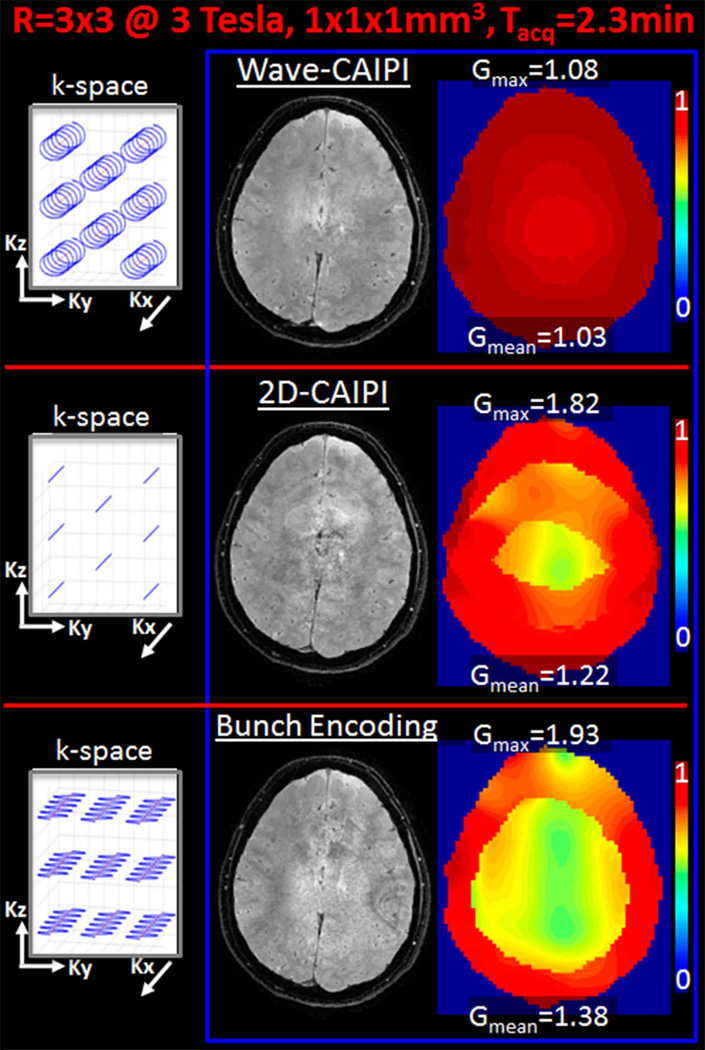
At 3T, Fig.5 depicts the corresponding k-space trajectories, reconstructions and 1/g-factor maps for the three acquisition/reconstruction methods, Wave-CAIPI, 2D-CAIPI and BPE. From g-factor analysis, maximum g-factor g_max for Wave, 2D-CAIPI and BPE were found to be 1.08, 1.82, and 1.93, while the average g-factors g_mean were 1.03, 1.22, and 1.38.

Fig. 5.

R=3×3-fold prospectively accelerated imaging at 3T. Wave-CAIPI, 2D-CAIPI and Bunched Phase Encoding reconstructions, 1/g-factor maps and their respective k-space sampling patterns are demonstrated.

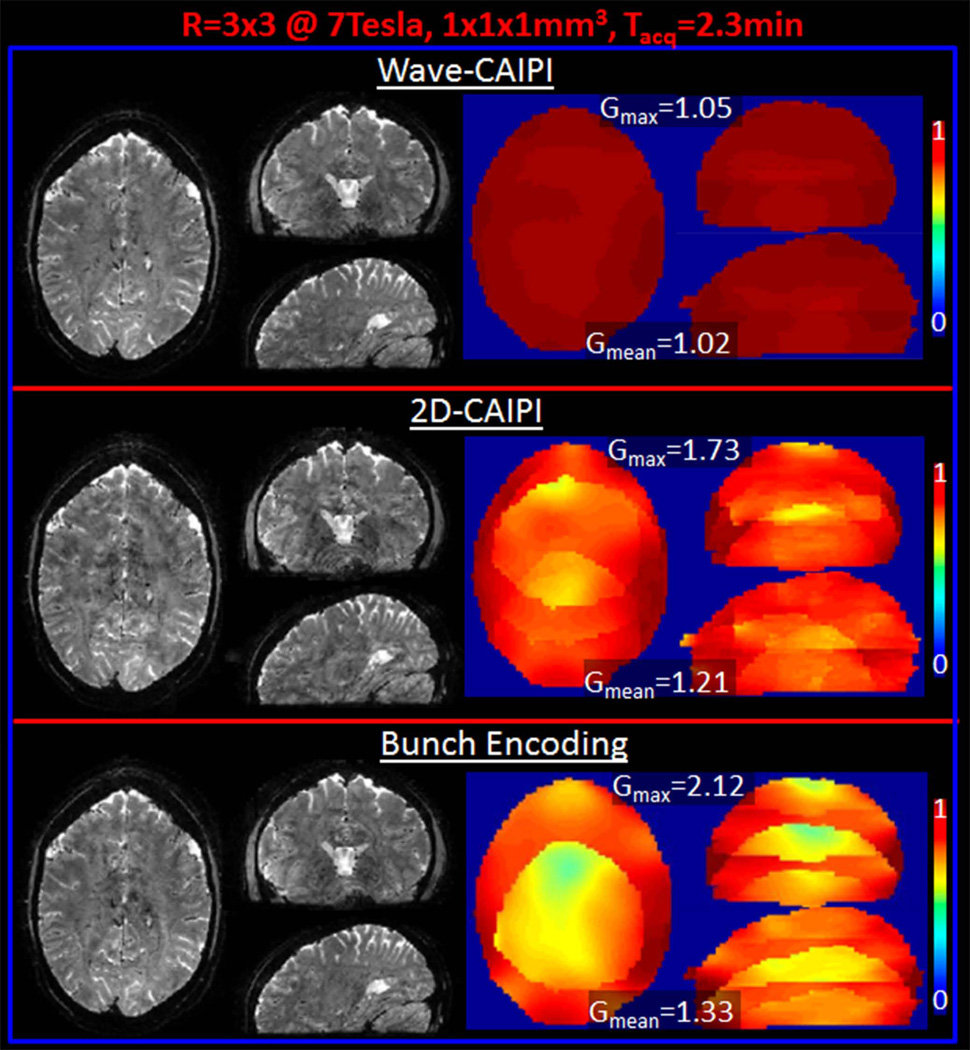
At 7T, g_max for Wave, 2D-CAIPI and BPE were, 1.05, 1.73 and 2.12, and g_mean were 1.02, 1.21 and 1.33 (Fig.6). At both field strengths, Wave-CAIPI yields nearly 2-fold reduction in maximum g-factor relative to other methods tested.

Fig. 6.

R=3×3-fold prospectively accelerated imaging at 7T. Wave-CAIPI, 2D-CAIPI and Bunched Phase Encoding reconstructions and 1/g-factor maps are compared.

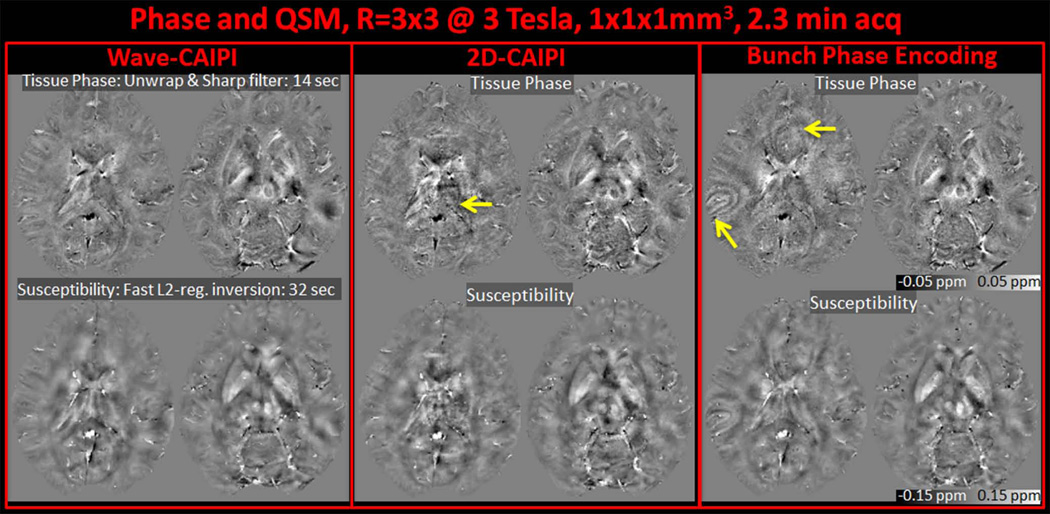
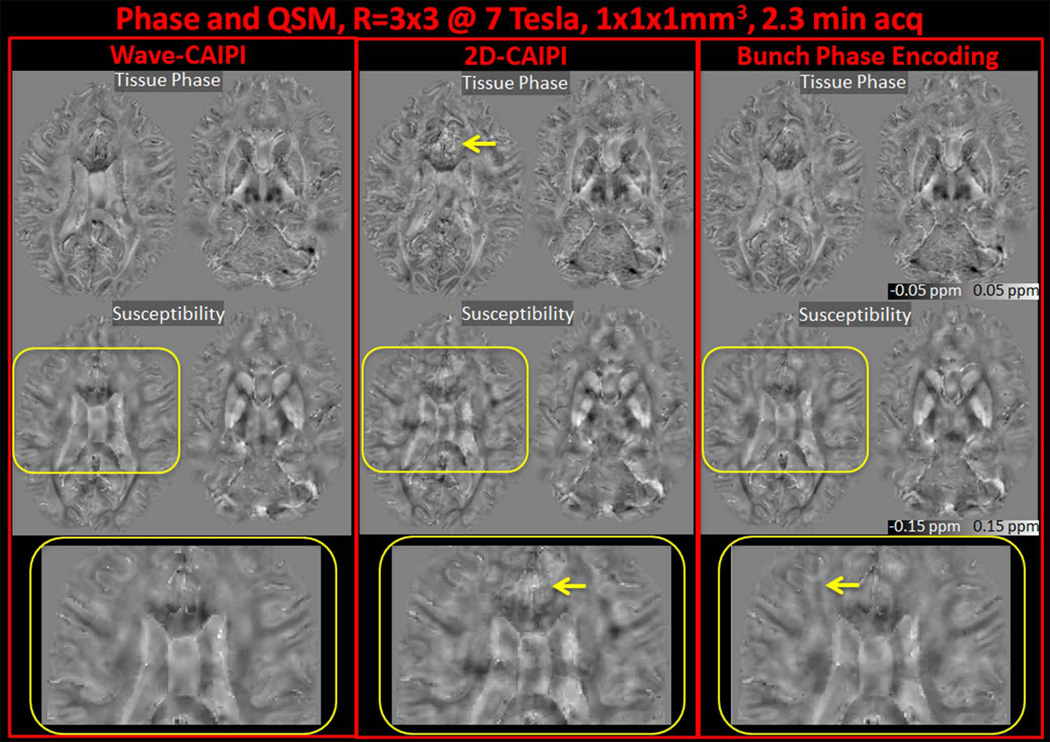
3. Accelerated phase imaging and Quantitative Susceptibility Mapping

Tissue phase images and susceptibility map solutions with R=3×3 fold acceleration and 1 mm³ isotropic resolution from Wave-CAIPI, 2D-CAIPI and BPE reconstructions are presented in Fig.7 for 3T, and Fig.8 for 7T acquisition. The combination of Laplacian unwrapping and V-SHARP filtering took 14 seconds for phase processing, while regularized QSM solution was completed in 32 seconds for the 3D volume.

Fig. 7.

Tissue phase and quantitative susceptibility maps derived from Wave-CAIPI, 2D-CAIPI and Bunched Phase Encoding at 3T and 1 mm3 isotropic resolution are compared. Note the artifacts indicated by the arrows stemming from imperfect parallel imaging reconstruction.

Fig. 8.

Tissue phase and susceptibility maps from Wave-CAIPI, 2D-CAIPI and Bunched Phase Encoding reconstructions at 7T and 1 mm³ isotropic resolution. Note the artifacts indicated by the arrows in the susceptibility map detail.

4. Effect of Wave Gradients within a Single Voxel

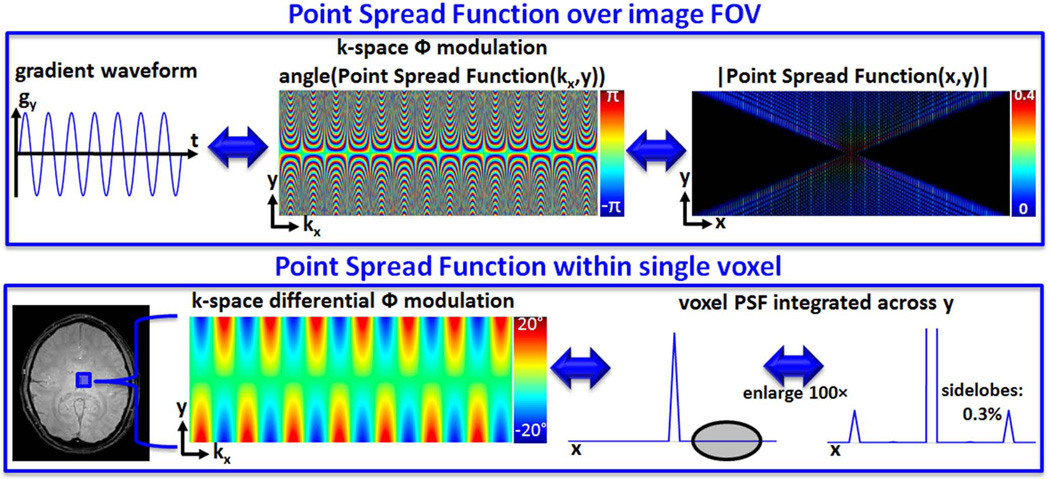
Based on Wave gradient simulation inside a single voxel with 1 mm isotropic size, the image-space PSF acting on the voxel was found to have 0.3% sidelobe amplitude relative to the main lobe (Fig.9). As such, the intra-voxel spreading effect due to Wave gradients is at a negligible level.

Fig. 9.

The non-Cartesian k-space trajectory traversed by the Wave gradient can be explained as additional phase deposited on the Cartesian space. This leads to the point spread function (PSF) formalism that characterizes the voxel spreading effect over the whole FOV. Within each voxel itself, the Wave gradient also causes a differential phase modulation. The sidelobes of the intra-voxel PSF is 0.3% of the main lobe, thus incurring negligible spreading within each voxel.

Discussion

This contribution introduces Wave-CAIPI, which combines and expands 2D-CAIPI and BPE strategies by playing sinusoidal g_y and g_z gradients during the readout of each phase encoding line. This results in an acquisition strategy that spreads the aliasing evenly in all spatial dimensions, including the fully-sampled readout direction. Wave-CAIPI takes full advantage of the variation in the 3D coil sensitivity profiles, and enables highly accelerated volumetric imaging with low artifact and negligible g-factor penalties.

Comparison to conventional parallel imaging reveals that Wave-CAIPI offers 2-fold improvement in image artifact level and maximum g-factor relative to normal GRE with uniform undersampling (Fig.4). At both 3T and 7T field strengths with 9-fold acceleration, Wave-CAIPI yields close to perfect SNR retention (g_mean and g_max almost unity), however the error images relative to fully-sampled data demonstrate 5–7% RMSE. This can be explained by the intrinsic $\sqrt{\mathrm{R}}$ penalty to SNR that is common to all parallel imaging algorithms due to reduction in the data averaging time.

Compared to the advanced parallel imaging strategies 2D-CAIPI and BPE, Wave-CAIPI offers 1.7 and 1.8-fold improvement in maximum g-factor at 3T (Fig.5). Residual aliasing artifacts are visible for 2D-CAIPI and BPE, while Wave-CAIPI produces a high-quality, clean image. Reconstruction artifacts in 2D-CAIPI and BPE are also present in the tissue phase and susceptibility maps (indicated by the arrows in Fig.7), and noise amplification especially hampers the phase images from BPE. In contrast, Wave-CAIPI produces high-quality phase and susceptibility maps.

At 7T, Wave-CAIPI offers 1.6 and 2-fold reduction in maximum g-factor compared to 2D-CAIPI and BPE (Fig.6). The residual aliasing artifacts are visible for 2D-CAIPI and BPE reconstructions, and these propagate to the phase and susceptibility images as pointed by the arrows in Fig.8.

The parallel imaging performance of all three algorithms is improved at 7T compared to 3T, as seen in the g-factor maps and higher quality of the magnitude images (Fig.5 vs. Fig.6). This can be explained by the close proximity of the tight-fitting custom 7T coil (42) to the head, and the increased orthogonality across coils sensitivity profiles due to reduced wavelength at ultra high field. Based on these factors, the artifacts in 2D-CAIPI and BPE phase and susceptibility images appear more subtle (enlarged detail in Fig.8) relative to those in the reconstructions at 3T.

As seen in 2D-CAIPI and BPE results at 3T (Fig.5), 9-fold accelerated images have inadequate SNR due to high g-factor penalty involved in the reconstruction. This has been mitigated by the Wave-CAIPI technique that retains close to unity g-factor penalty. With the benefit of increased field strength, SNR of all three methods have largely improved at 7 Tesla. As such, even higher acceleration factors (e.g. R=4×4) should be achievable with Wave-CAIPI at this field strength for 1 mm resolution. Additionally, using a later echo time than the ones employed in the current study (TE=17 ms at 3T and 20 ms at 7T) would improve the phase SNR of all three methods due to longer phase evolution, as well as enhancing tissue contrast.

Although Wave-CAIPI follows a non-Cartesian corkscrew trajectory in k-space (Fig.1), our proposed reconstruction technique represents this trajectory as additional phase deposited in Cartesian k-space. In this way, Wave-CAIPI reconstruction does not involve data gridding, and requires simple FFT and point-wise multiplication operations. This is made possible by using the FFT as a preconditioner in the forward encoding model (Eq.8), which also allows separable image reconstruction. In Wave-CAIPI, each group of collapsed image rows are unaliased separately by iteratively solving a small linear system, thereby making the reconstruction amenable to parallel processing. Using Matlab running on a workstation with 128 GB memory, Wave-CAIPI reconstruction for whole-brain volume at 1 mm³ resolution requires 30 min of processing. Since this initial implementation considers each collapsed group sequentially, substantial speed-up is expected if parallel processing is enabled.

As shown in the top panel of Fig.9, the voxel spreading effect of the g_y gradient can be explained as additional phase imparted in k-space. The amount of phase modulation is dependent on the y position, which gives rise to convolution kernels that spread the voxels in the readout direction by an amount proportional to their y position. As the Wave gradients are continuous across space, the differential phase modulation inside the voxel leads to an intra-voxel spreading effect. This is characterized in the bottom panel of Fig.9, where the PSF is seen to have negligible sidelobes (0.3% relative to main lobe). As such, the intra-voxels spreading effect of Wave-CAIPI is negligible.

Since Wave-CAIPI achieves high acceleration factors with low artifact and noise amplification penalties, it may substantially facilitate research and clinical applications of modalities derived from GRE data, e.g., anatomical imaging, SWI, QSM, Susceptibility Tensor Imaging (STI) (36,49) and T₂^* mapping. In particular, it has the potential to render STI a clinical examination, which has been used strictly in research studies to date because it requires multiple phase acquisitions at different object orientations relative to B₀. Wave-CAIPI with 9-fold acceleration permits whole-brain GRE imaging at 1 mm isotropic resolution in just 2.3 minutes. Fast phase processing and QSM inversion algorithms employed in this study allow reconstruction of susceptibility maps for the 3D volume in less than a minute. As such, the combination of highly accelerated imaging through Wave-CAIPI and rapid phase and susceptibility mapping may facilitate clinical application of SWI and QSM. Because the proposed acquisition/reconstruction scheme is generalizable to any sequence with 3D encoding, it is warranted to accelerate important protocols such as MPRAGE (35), 3D RARE (fast spin echo, turbo spin echo), attenuated inversion recovery (FLAIR) (50), 3D EPI (51) and 3D GRASE (52). Additionally, to provide faster acquisition with limited FOV, Wave-CAIPI can be combined with inner volume (53) or ZOOM (54) techniques. For such experiments with asymmetric FOV, it is advisable to adjust the 2D-CAIPI shift pattern of the Wave acquisition for optimum g-factor improvement.

A further refinement to image reconstruction may come from including an off-resonance map in the forward model. The voxel shift due to B₀ inhomogeneity and eddy currents for Wave-CAIPI is in the readout direction, and not more than a normal acquisition without the Wave gradients. Accounting for the off-resonance will further improve the image quality of Wave-CAIPI by pairing the collapsed voxels with PSFs at accurate locations. The actual PSFs estimation can also be improved using the slice-selection method proposed by Duyn et al. (40). While this is similar to current estimation scheme, it is very fast and enjoys higher SNR, which is critical for ultra high-resolution acquisitions.

Drawbacks and Limitations of Wave-CAIPI

Wave-CAIPI requires gradient characterization for the estimation of PSFs that are included in the forward model for parallel imaging reconstruction. This requires additional data acquisitions, thereby increasing the total scan time. The current PSF estimation scheme uses rapid, single-slice projections along the y and z axes. This scheme does not depend on the image contrast since it relies on the ratio of two images with and without the Wave gradients. As such, the shortest TR can be selected to further accelerate these calibration scans. The trajectory mapping depends on the particular gradient system being used, which is independent of the subject being scanned. Therefore, the calibration data can also be acquired using a test phantom following the in vivo examination.

Another limitation of Wave-CAIPI is the image reconstruction computation time (30 minutes in Matlab), which is an order of magnitude longer than conventional SENSE reconstruction. This can be mitigated by importing the software to the faster C++ platform for online computation, where parallel processing can be enabled to exploit the separable structure of Wave-CAIPI reconstruction for additional speed-up.

Finally, relative sensitivity of Wave-CAIPI to motion artifacts and other factors in neuroscientific or clinical settings need to be evaluated.

Conclusion

Proposed Wave-CAIPI acquisition/reconstruction technique involves playing sinusoidal g_y and g_z gradient waveforms during the readout of each k-space line, and modifies the phase encoding pattern to incur inter-slice shifts across collapsing slices. This strategy spreads the aliasing in all three dimensions to allow full utilization of coil sensitivity profiles, and enables highly accelerated 3D imaging with low image artifact and negligible noise amplification penalties. Compared to existing parallel imaging techniques of SENSE, 2D-CAIPI and Bunched Phase Encoding, Wave-CAIPI demonstrates up to 2-fold reduction in maximum g-factor at both 3T and 7T. Upon 9-fold acceleration with Wave-CAIPI, 3D GRE imaging achieves 1 mm isotropic voxel size in just 2.3 minutes with whole-brain coverage and close to perfect accelerated SNR retention. Combined with state-of-the-art phase and susceptibility processing algorithms, Wave-CAIPI may enable high-resolution phase imaging, SWI and QSM. Its extension to increasing the resolution in important 3D protocols such as MPRAGE, volumetric RARE, EPI, GRASE and FLAIR may facilitate their clinical application.