Abstract
Sample size modifications in the interim analyses of an adaptive design can inflate the type 1 error rate, if test statistics and critical boundaries are used in the final analysis as if no modification had been made. While this is already true for designs with an overall change of the sample size in a balanced treatment-control comparison, the inflation can be much larger if in addition a modification of allocation ratios is allowed as well. In this paper, we investigate adaptive designs with several treatment arms compared to a single common control group. Regarding modifications, we consider treatment arm selection as well as modifications of overall sample size and allocation ratios. The inflation is quantified for two approaches: a naive procedure that ignores not only all modifications, but also the multiplicity issue arising from the many-to-one comparison, and a Dunnett procedure that ignores modifications, but adjusts for the initially started multiple treatments. The maximum inflation of the type 1 error rate for such types of design can be calculated by searching for the “worst case” scenarios, that are sample size adaptation rules in the interim analysis that lead to the largest conditional type 1 error rate in any point of the sample space. To show the most extreme inflation, we initially assume unconstrained second stage sample size modifications leading to a large inflation of the type 1 error rate. Furthermore, we investigate the inflation when putting constraints on the second stage sample sizes. It turns out that, for example fixing the sample size of the control group, leads to designs controlling the type 1 error rate.
Keywords: Conditional error function, Interim analysis, Maximum type 1 error, Sample size reassessment, Treatment selection
1 Introduction
In the last decade, adaptivity in clinical trials with design modifications such as sample size reassessment or treatment selection at an interim analysis has gained increasing attention. One may argue that there have always been modifications when performing clinical trials, for example simply covered by amendments to the study protocols. However, it has been shown that if, after design modifications, the critical boundaries and test statistics for the corresponding fixed sample size design are used, then the type 1 error rate is inflated. For the comparison of the means of a normally distributed outcome with known variance between a single treatment and a control in parallel groups and balanced sample sizes, that is equal sample size in the treatment and control group, Proschan and Hunsberger (1995) derived the maximum possible type 1 error rate inflation. They assumed that the experimenter, for any interim outcome, would choose the second stage sample sizes in such a way that the conditional type 1 error rate is maximized (“worst case scenario”). This strategy will also maximize the overall type 1 error rate. They showed that the type 1 error rate can be inflated from 0.05 to 0.11. Graf and Bauer (2011) extended these worst case arguments to the case of unbalanced sample size reassessment showing that the maximum type 1 error rate increases to 0.19 when the allocation ratio is allowed to change at interim. However, in this unbalanced case the maximum of the conditional type 1 error rate can only occur if the experimenter knows the value of the nuisance parameter, the common mean under the null hypothesis. This may at least approximately apply for the control treatment if a large number of data from previous experiments is available.
Many methods for type 1 error control in adaptive designs are available for testing a single hypothesis (Bauer, 1989; Bauer and Koehne, 1994; Proschan and Hunsberger, 1995; Lehmacher and Wassmer, 1999; Mueller and Schaefer, 2001; Brannath et al., 2002; Mueller and Schaefer, 2004; Gao et al., 2013) and have been applied in clinical trials. Multiarmed selection designs have been proposed (e.g. Thall et al., 1988, 1988) and have been extended to allowing for adaptive design modifications (Bauer and Kieser, 1999; Koenig et al., 2008; Bretz et al., 2009; Bebu et al., 2013; Sugitani et al., 2013). With the rise of adaptive methods in clinical trials, the main emphasis has been on strict control of the type 1 error rate to maintain the strictly confirmatory nature (EMA, 2007; FDA, 2010; Wang et al., 2013).
However, there are complaints that the adaptive machinery has become too complicated with “tests that resort to nonstandard adjustments and weightings appear mysterious to all but the specialist in adaptive design” (Metha and Pocock, 2012). From an operational perspective, adaptations put a burden on data analysts who have to clean data for interim decision making and on drug supply managers who have to deal with the possibility that doses may be added to or removed from the trial. Uncertainty at the planning stage about the total funds needed for the trial can also be a concern. From a statistical perspective, it has been argued by some experts that adaptive designs offer little advantage over more conventional group-sequential designs (Tsiatis and Metha, 2003; Jennison and Turnbull, 2006; Levin et al., 2013) and that they use test statistics that might violate desirable principles like sufficiency (Burman and Sonesson, 2006). However, these criticisms of adaptive designs are not uncontroversial themselves (Brannath et al., 2006). In any case, such additional burden may prevent experimenters from using adaptive design methodology and resort to either ignoring the issue or using seemingly simple adjustments like Bonferroni or Dunnett corrections. It is therefore desirable to investigate the maximum type 1 error inflation arising from such strategies. Regarding specific clinical trials, the precise quantification of the inflation can also be a guide to decide whether the implementation of the adaptive test machinery is really necessary, or whether a simpler adjustment might suffice, possibly after additional restrictions of the interim decision options, like upper and lower limits on the allowed sample size modifications.
In this work, we investigate the maximum type 1 error rate when k test treatments are compared to a single common control and when treatment selection is allowed at interim either with or without flexible sample size reassessment. Designs of multiarmed clinical trials with interim treatment selection have attracted a lot of research in the last decade (Zeymer et al., 2001; Gaydos et al., 2009; Barnes et al., 2010). Nevertheless, the number of conducted or started trials seems to be rather limited (Elsaesser et al., 2014; Morgen et al., 2014).
In Section 2011, we give a motivating example of a clinical trial where the experimenters decided to use the conservative Bonferroni procedure instead of an adaptive approach. In Section 2004, we introduce the hypothesis tests and the type of interim adaptations investigated to calculate the maximum type 1 error rate. In Section 2001, we consider the situation when the treatment with the largest observed interim effect is always selected for the second stage. Furthermore, we investigate the maximum type 1 error rate when second stage sample sizes are restricted to range within a prefixed interval. In Section 5, we mainly focus on the case of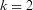 
treatment arms, always proceeding with both treatments and the control to the second stage. In Section 6, we discuss our findings in the context of the motivating example and give some practical considerations. This is followed by concluding remarks in Section 7.
2 Motivating example
Barnes et al. (2010) give a recent case study for a two-stage clinical trial on the drug indacaterol to treat chronic obstructive pulmonary disease (COPD). This study comprised a first stage for dose-finding with dose selection after 14 days of treatment, and a second stage evaluating efficacy and safety during 26 weeks of treatment. The dose-finding stage included seven randomized treatment arms, four doses of the study drug, placebo and two further treatment groups with active comparators. At an interim analysis after the first stage the indacaterol doses were selected using preset efficacy and safety data (Lawrence et al., 2014). A multiplicity correction using a Bonferroni adjustment with 
was applied, despite the fact that in the final efficacy analysis only the two selected indacaterol doses should have been compared individually against placebo based on the pooled data of both stages with prefixed sample sizes. This approach controls the type 1 error rate if the sample size, as in the given example, is prefixed. However, due to the overcorrection, this approach is conservative. The authors themselves acknowledge that the approach “is statistically somewhat conservative, but it has the merit of simplicity”. The question arises whether for such a design sample size reassessment strategies would have been possible without inflating the type 1 error rate.
3 Trial design
In the following, we assume that a clinical trial is designed for k treatment and one control arm where a two-stage design should be applied. In a first stage the observed outcome measures 
from patients 
, randomized to one of 
groups, that is to the control, denoted by index 
, or to one of the treatment groups, 
are investigated. The outcome is assumed to be normally distributed with common known variance, 
. Without loss of generality we set 
. Having obtained at the end of the first stage 
observations in the control and 
, 
observations in the treatment groups, the sample means 
for 
are calculated. The 
denote the prefixed first-stage-allocation-ratios between treatment group i and control. The experimenter may set the second stage sample sizes to 
in the treatment groups and to 
in the control group with the second-to-first-stage-ratios 
, 
based on the interim sample means.
In the final analysis, after the second stage, we test the hypotheses
 |
using the standardized mean difference 
pooling the data of both stages and comparing it to the critical boundary 
as used for the fixed sample size design. This means that adaptivity is not accounted for, neither in the test statistics nor in the critical boundary. The test statistics is defined as:
 |
for 
with 
, 
denoting the second stage sample means.
We obtain the worst case scenarios for each possible interim outcome by searching for the second-to-first-stage ratios maximizing the conditional type 1 error rate, 
. Generalizing the formula in Koenig et al. (2008) the conditional type 1 error rate for rejecting at least one treatment-control comparison in the final analysis, given the observed interim data is (see Appendix A1):
 |
1 |
where α is the preplanned level for the type 1 error rate and 
the critical boundary of the preplanned final tests (see Remark 3.1). The 
, 
, 
are defined as the standardized differences between the sample mean and the common true mean μ under the global null hypothesis of stage 
(at interim) and 
, respectively (without loss of generality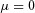 
). The cumulative distribution function and density of the standard normal distribution are denoted by Φ and ϕ, respectively. Note that 
follow independent standard normal distributions.
When second stage sample sizes are not constrained, the maximum type 1 error rate is given by
 |
2 |
where
 |
Whereas 
is a function of 
, 
is a function of 
, the second-to-first-stage-ratios leading to the maximum 
. The 
are determined for a given interim outcome 
and are therefore a function of the 
. Thus, 
does not depend on 
.
In the following we use a quasi Newton method provided by the R-function optim for numerical optimization and for numerical integration we used the R-function integrate (R Development Core Team, 2012). R-programs to calculate the maximum type 1 error rate are available as Supplementary Information.
Remark 3.1 —
The critical boundary
of the preplanned test may be defined in different ways: (i) as the
-quantile of the standard normal distribution,
, if no correction at all for multiplicity is applied or (ii) as a Dunnett critical boundary (Dunnett, 1955) based on the preplanned first-stage-allocation-ratios
,
to adjust for multiplicity due to the treatment-control comparisons. Even strategy (ii) may not guarantee type 1 error control if additional sample size reassessment is performed at interim. Moreover, in case of sample size reassessment (and/or treatment selection) the Dunnett critical boundary would not be fixed a priori when calculated for the actual sample sizes in the final analysis. For simplicity, we will apply the pre-fixed Dunnett boundary,
, based on the preplanned first-stage-allocation-ratios
between treatment and control in the following. Remarks 4.1 and 4.2 discuss how results change if instead critical boundaries are based on actual (reassessed) total sample sizes in the final analysis.
Remark 3.2 —
For
we calculate the maximum type 1 error rate under the global null hypothesis
. A proof that the maximum type 1 error is attained under the global null hypothesis is given in Appendix A2.
Remark 3.3 —
For
, Graf and Bauer (2011) showed, by numerical evaluation, that the maximum type 1 error in the case of balanced first stage sample size between treatments before the interim analysis (
,
) is an upper bound. For
we will likewise set
, since it is the most common scenario applied in practice. Note that for many-to-one comparisons, the scenario with
leads to the smallest required sample size for a given power and significance level. Therefore we will also give some numerical results for this allocation ratio.
4 Selection of the most promising treatment at interim
We first consider that in the interim analysis the treatment group m with the largest observed interim effect 
is selected for the second stage, setting 
for 
. The second-to-first-stage-ratios 
, 
may be set based on the interim results, 
. In the final analysis, only the selected treatment group m is compared to the control group (using data of both stages). The corresponding null hypothesis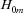 
is rejected, if the final test statistic 
exceeds the critical value 
. Note that the maximum type 1 error rate for the case of always selecting the best treatment is an upper bound for the maximum type 1 error rate when in a particular trial another single treatment is selected, for example the treatment with the second largest observed effect at interim because of potential safety issues for the most effective treatment. Clearly, under the global null hypothesis and for balanced first stage sample sizes over the k treatments, selecting a treatment with an interim effect smaller than the largest observed interim effect will reduce the maximum type 1 error rate. Following the lines of Graf and Bauer (2011), the conditional type 1 error rate 1994 for this scenario simplifies to
 |
3 |
Note that if the treatment with the largest observed interim effect is selected, m is random and therefore also 
is a random variable. In the following we set 
so that 
is no longer a random variable and the maximum type 1 error rate can be evaluated by
 |
4 |
where
 |
5 |
and 
is the probability density function of the maximum of independent standard normal distributions.
4.1 Equal second-to-first-stage-ratios
Let 
with 
, that means only allowing for equal second-to-first-stage ratios, and let furthermore 
indicating balanced first stage sample sizes for the treatment and the control groups. After the second stage, the selected treatment group is compared to the control group (using data of both stages) applying the critical value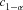 
of the pre-planned test. Note that for this scenario the final test is balanced between both groups. In a slight modification of Proschan and Hunsberger (1995), the conditional type 1 error rate 2013 of the final treatment-control comparison for 
and 
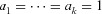reduces to
 |
For notational convenience, the first stage test statistics 
is used. The conditional type 1 error rate does not depend on the unknown nuisance parameter μ.
Calculation of 
in this balanced case follows the lines of Proschan and Hunsberger (1995). The essential difference is that the density of the maximum of k independent standard normal distributions has to be used in the integration. The subspaces of the interim sample space to perform separate optimizations remain the same (see Appendix A3).
The black lines in Fig.1 show that if no correction for multiplicity is done (Fig.1A), the type 1 error is highly inflated and increases with k. Using Dunnett boundaries for k treatment-control comparisons, that means adjusting for all initially planned comparisons (Fig.1B), the overall type 1 error decreases with k, that means correcting for multiplicity of all possible individual treatment-control comparisons leads to a smaller inflation of the overall type 1 error as compared to 
. For increasing k, the correction is done for an increasing number of 
hypotheses not tested in the final analysis. Correcting for all possible individual treatment-control comparisons would be a conservative approach if the second stage sample size would be fixed independently of the data, for example in the planning phase. Here the inflation of the maximum type 1 error rate is caused by the worst case sample size reassessment rule.
Figure 1.
Maximum type 1 error rate 
when always selecting the treatment with the maximum effect at interim for an increasing number of treatment groups k. Results are given when using the uncorrected critical boundary 
(A) or the fixed Dunnett critical boundary 
(B) for equal (black lines) and flexible (gray lines) second-to-first-stage ratios. Nominal one-sided α was set to 0.01 (solid lines), 0.025 (dashed lines), and 0.05 (dotted lines).
For a direct comparison with the case of no treatment selection discussed later (see Section 5), the columns “equal” in Table1 show the maximum overall type 1 error rate for 
with and without correction for multiplicity as well as for the case of 
(Proschan and Hunsberger, 1995).
Table 1.
Maximum type 1 error rate for 
with and without treatment selection, with or without adjustment for multiplicity and with equal or flexible second-to-first stage ratios as compared to the case 
| nominal α |  |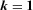
 |
||||
|---|---|---|---|---|---|---|
 |
 |
 |
||||
| treatment selection of most promising treatment | ||||||
| equal (Proschan and Hunsberger, 1995) | flexible (Graf and Bauer, 2011) | equal (Section 4.1) | flexible (Section 4.2) | equal (Section 4.1) | flexible (Section 4.2) | |
| 0.01 | 0.0267 | 0.0491 | 0.0398 | 0.0697 | 0.0224 | 0.0407 |
| 0.025 | 0.0616 | 0.1064 | 0.0887 | 0.1466 | 0.0518 | 0.0892 |
| 0.05 | 0.1146 | 0.1867 | 0.1594 | 0.2496 | 0.0968 | 0.1588 |
| without treatment selection | ||||||
| equal (Proschan and Hunsberger, 1995) | flexible (Graf and Bauer, 2011) | equal (Section 5.1) | flexible (Section 5.2) | equal (Section 5.1) | flexible (Section 5.2) | |
| 0.01 | 0.0267 | 0.0491 | 0.0478 | 0.0800 | 0.0263 | 0.0473 |
| 0.025 | 0.0616 | 0.1064 | 0.1058 | 0.1701 | 0.0610 | 0.1037 |
| 0.05 | 0.1146 | 0.1867 | 0.1897 | 0.2885 | 0.1138 | 0.1842 |
If the first-stage-allocation-ratios are set to 
, 
, a smaller maximum type 1 error rate was found. When using the Dunnett critical boundary, for 
the values are 
for 
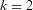and 
and 0.0340 for 
and 4, respectively. For comparison, setting 
, the values are 
(see Table1 and Fig.1), 0.0482 and 0.0463 (see Fig.1) for 
, 3, and 4, respectively. Similar results can be found for 
and 
.
Remark 4.1 —
To give an impression of how results may change if the actual final adapted sample sizes are used in the calculation of the critical Dunnett boundaries (see Remark 3.1) for
, the values would become only slightly smaller than in Table1: 0.0221, 0.0507, and 0.0948 for
, 0.025, and 0.05, respectively.
4.2 Flexible second-to-first-stage-ratios
“Flexible” second-to-first-stage ratios allow different sample size reassessments for the selected treatment and the control, for example a sample size decrease for the control, but a sample size increase for the selected treatment group. For each interim outcome, the worst case 
and 
may differ. The sample size of the final treatment-control comparison may then be unbalanced between treatment arms. If we again assume balanced first stage sample sizes, the conditional type 1 error rate is now calculated by (3) setting 
. We use the independence of 
and 
to get rid of the nuisance parameter μ. The conditional type 1 error rate cannot be written as a function of the test statistic 
as in Section 4.1. As in Graf and Bauer (2011), the calculation of 
can be separated into several parts of the interim subspace using 
instead of 
. To evaluate the maximum type 1 error rate we partition the interim subspace in a way analogous to Graf and Bauer (2011) (see Section 2009 in the Supplemental Materials).
The gray lines in Figs.1A and B show that allowing for flexible second-to-first-stage ratios substantially increases the possible maximum type 1 error rate. Using 
(Fig.1B) in all scenarios leads to a nonmonotonous behavior with respect to the number of treatments k. An explanation for this is that the fixed boundaries are correct for the worst case scenarios, where the overall sample size is balanced between treatment and control, whereas for the unbalanced worst case scenarios they lead to smaller critical boundaries as compared to the boundaries using the actual total sample sizes. For larger k this difference in the correlation matrices is extended to all the 
dropped treatments at interim, so that the differences between unbalanced and balanced critical boundaries tend to increase with increasing k which in the end leads to an increase in the maximum type 1 error rate. Again, to allow a direct comparison to the other discussed scenarios, the columns “flexible” in Table1 show the values for 
for both choices of the critical boundary as well as 
(Graf and Bauer, 2011).
If 
, 
, as in the case of equal second-to-first stage ratios, a smaller maximum type 1 error was found. When using the Dunnett critical boundary, for 
the values are 
, 0.0792, and 0.0753 for 
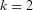, 3, and 4, respectively. For comparison, setting 
, the values are 
(see Table1 and Fig.1), 0.0846, and 0.0830 (see Fig.1) for 
, 3, and 4, respectively. Similar results can be found for 
or 
.
Remark 4.2 —
When using Dunnett critical boundaries as in Remark 4.1, the maximum type 1 error rate up to
(data not shown) is smaller than for Dunnett critical boundaries based on balanced sample sizes. The maximum type 1 error rate is decreasing in k and hence also differences between the two approaches increase with k.
4.3 Constrained second stage sample size
Unconstrained sample size reassessment of course will hardly be used in practice. We therefore put constraints on the second-to-first-stage-ratios 
, 
, 
. The ranges for the maximization in formula 2002 are therefore changed to 
and 
. Figure2 shows the maximum type 1 error rate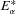 
, 
for different constraints on sample size reassessment using the Dunnett critical boundary 
:
I
, 
, 
: Setting the lower boundary to 0 means that we allow for early rejection at interim. The solid lines in Fig.2 show that 
is increasing with increasing upper boundary, flattening off for larger values. Allowing for flexible second-to-first-stage-ratios (solid lines in Fig.2B), the increase with the upper boundary is even steeper than for equal ratios (Fig.2A). However, the results for 
are very similar.-
II
, 
, 
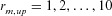: In this scenario, the second stage sample size has to be at least as large as the first stage sample size for the selected treatment and the control. The dashed lines in Fig.2A. show that for equal ratios and 
, the maximum type 1 error is always below the nominal 
. Calculations including numerical integration of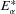 
for 
and 
give a value of 0.02509. Therefore, for 
selecting always only one treatment and the control, such type of constraints may be safely applied in practice without inflating the type 1 error rate. The reason is that there is a tradeoff (i) between the overcorrection from using Dunnett boundaries adjusting for treatment-control comparisons that are not carried over to the final test and (ii) the inflation due to data-dependent choice of the final sample size of the selected treatment (equal ratios, total sample size per selected treatment at least twice the first stage sample size per group). The smaller the prefixed range for the second stage sample sizes the smaller the impact of the latter effect.Similar results can be found for a nominal α of 0.05 and 0.01. For
and 
the values are 
and 
. Note that in the scenario for 
without any interim sample size reassessment, for example: 
, the selection of one treatment and the control would happen quite late in the trial in terms of total sample over all groups (at a fraction of 5/7).Allowing for flexible second-to-first-stage-ratios (Fig.2B) only for smaller windows (smaller
and 
) 
does not exceed α. For example for 
and 
, the number of treatments has to be larger than 3 so that 
will always be below 0.025. III
, 
, 
: In this case, the second-to-first-stage-ratios are allowed to be flexible by definition, the only option for sample size adaptation is the choice of a second stage sample size for the selected treatment to be at least as large as in the first stage and not to exceed 
(see dotted lines in Fig.2B). Such an adaptation may arise from a rare adverse event in the selected treatment group requiring additional information. It is interesting to note that for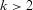 
the maximum type 1 error rate 
will never exceed the nominal level, even if the upper boundary is set to ∞. For 
no inflation occurs with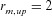 
. Similar results can be found for a nominal α of 0.05 and 0.01. Note that Fig.2B shows that the type 1 error rate is not inflated when Dunnett critical boundaries are used in case of an allocation ratio to control of 
between treatment(s) and control in both stages, that is 
.
Figure 2.
Maximum type 1 error rate 
as a function of the upper boundary 
for the second-to-first-stage-ratio when always selecting the treatment with the maximum effect at interim for constrained second stage sample size for equal (A) and flexible (B) second-to-first-stage-ratios using Dunnett corrected critical boundaries. Solid lines: 
, 
, dashed lines: 
, 
and dotted lines: 
, 
. Nominal one-sided α was set to 0.025.
5 No treatment selection at interim
Since selecting only the treatment with the largest interim effect is a natural strategy often discussed in the literature (Cohen and Sackrowitz, 1989; Bowden and Glimm, 2008; Friede and Stallard, 2008; Stallard et al., 2008; Bauer et al., 2010), we first elaborated on this in Section 2001. However, if all initially planned treatment arms are further investigated in the second stage, under the global null hypothesis, the maximum type 1 error rate is larger than for any other case with treatment selection. The reason is that dropping treatments at the interim analysis can be viewed as a constrained sample size reestimation problem (with 
or 
as the only options for treatment i), and this cannot produce a larger maximum of the conditional type 1 error rate than the unconstrained optimization problem.
For 
we were not able to find a general closed solution for the maximum type 1 error rate (even if a single constant 
is used as a critical boundary for all the k standardized treatment vs. control test statistics). To put the above optimization problem into a manageable framework, we illustrate the calculation for the case of two experimental treatment arms (
) in the following. For the less complex scenario of equal second-to-first-stage ratios, numerical results are reported for 
.
5.1 Equal second-to-first-stage-ratios
As an extension to Proschan and Hunsberger (1995) we first investigate the case of equal second-to-first-stage-ratios setting 
. Assuming furthermore that the first stage sample sizes are balanced, that is setting 
(and therefore also that the final stage sample sizes are balanced between treatment arms), for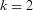 
formula 1994 simplifies to
 |
As in Section 4.1, for notational convenience, the first stage test statistics 
for comparing treatment i to the control are used. The conditional type 1 error rate does not depend on the nuisance parameter μ. The cumulative distribution function of the multivariate normal distribution with two-dimensional mean zero-vector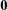 
and covariance-matrix Σ with elements 
and covariance 
is denoted by 
. To calculate the worst case conditional type 1 error rate we have to partition the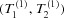 
-plane.
I If
and 
the largest conditional type 1 error rate is obtained by setting 
, 
denoting the worst case second-to-first-stage ratio. The second stage is now overruling the negative interim effect and therefore yielding a 
that is equal to α if 
. Since 
for the bivariate normal distribution with 
(see e.g. Kotz et al., 2000), the contribution of this subspace to the overall maximum type 1 error rate 
is 
.II If
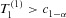or 
the largest conditional type 1 error rate 
(applying early rejection at interim and setting 
) is obtained. This leads to a contribution to 
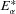of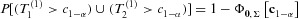 
that is equal to α if 
.
In the remaining interim subspace we were not able to find a closed solution for 
. Therefore, we used numerical optimization of the single parameter r. The “equal”-columns of Table1 show the results for the overall 
for the case of 
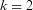, with and without correction for multiplicity. As is to be expected, applying the naive unadjusted critical boundary 
may result in a further considerable type 1 error rate inflation as compared to 
. An interesting finding is that when using the Dunnett critical value, 
are close to the results for 
.
For 
and using Dunnett critical boundaries for 
the maximum type 1 error rate is still inflated up to 0.0545, but interestingly the inflation is smaller compared to 
. For 
treatments, 
is flattening off at an inflated level of 0.0543. For 
and 0.05 the same tendencies can be found.
5.2 Flexible second-to-first-stage-ratios
If we allow for flexible second-to-first-stage-ratios, we again have to use the independent 
(instead of the test statistics 
) to get rid of the nuisance parameter μ. If we assume balanced first stage sample size, the conditional type 1 error rate is now calculated by 1994 setting 
and 
. To explain the worst case scenarios in more detail, we will focus on the subspaces in terms of the interim outcome of the control group 
.
A Subspace (
): 
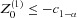is obtained by setting either 
or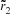 
to ∞ and 
. The contribution of this subspace to 
therefore is 
.- B Subspace (
): The worst case choice is setting 
in the final analysis, getting two independent tests against the asymptotically fixed mean 
. Hence the conditional type 1 error rate reduces to
independent of
. A detailed explanation for the calculation of the maximum type 1 error rate for this subspace B is given in Section 2011 in the Supplemental Materials. Summing up the results for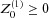 
, the contribution to the overall maximum type 1 error rate can be calculated by 
C Subspace (
): In this region the worst case conditional type 1 error rate depends on all three interim values of control and treatment groups, respectively. If either 
or 
is larger than 
again a conditional type 1 error rate of 1 can be achieved. For the remaining regions we used numerical point-wise optimization and integration for calculating the contribution to the overall type 1 error rate 
.
The columns “flexible” for 
of Table1 show the total 
for flexible second-to-first-stage-ratios applying critical boundaries 
or 
. Without any correction for multiplicity (
), the maximum type 1 error is clearly increased as compared to the case 
. Interestingly, as for the results of equal second-to-first-stage ratios (see Section 5.15.1), when using the pre-specified Dunnett critical boundary, 
is close to the results for 
.
Due to the numerical burden we did not calculate the maximum type 1 error rate for 
. However, we expect similar findings as for the case of equal second-to-first-stage ratios at least for 
and 4, that is the maximum type 1 error rate sightly decreasing when using a Dunnett adjusted critical boundary.
6 Practical recommendations
The results presented for the case of selecting the most promising hypothesis at interim are of great practical interest, because they demonstrate that, given certain restrictions on the second stage sample size, naive strategies may even lead to an adequate control of the type 1 error rate. For example, if the sample size per treatment group in the second stage is at least as large as in the first stage and we only allow for equal second-to-first-stage-ratios, no inflation of the type 1 error rate occurs for the number of treatments 
when simply using the Dunnett critical boundaries. For 
, no inflation occurs when restricting the second-stage sample size to be at maximum 4 times the first-stage sample size (see Fig. A). If we fix the overall sample size in the control group, allowing for any choice of the overall sample size in the selected treatment group that increases its first stage sample size more than twofold does not lead to an inflation of α for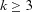 
(see Fig. 2B). Therefore, if in the case study of Barnes et al. (2010) (see Section 2011) only the selection of a single treatment group and control had been pre-specified, the experimenter would have been permitted to do any balanced increase of the sample size, even when using the conventional test statistic and the less conservative Dunnett critical boundary (instead of the applied Bonferroni adjustment) for final testing. If a flexible sample size reassessment for the second stage would have been allowed for (as in Section 4.2), no type 1 error inflation would have occurred if the second stage sample size would have been constrained to be between the first-stage and twice the first stage sample size. However, it has to be noted that for realistic scenarios (as e.g. an upper bound of twice the first stage sample size) and a larger k, the obtained maximum type 1 error rate may be much smaller than α so that even using the Dunnett critical boundaries would lead to conservative procedures. Note that these results only apply when using prespecified-binding constraints on the selection rules.
Allowing for early rejection at interim, the maximum type 1 error rate will always be inflated. In such scenarios, if the use of conventional test statistics is preferred, one may adjust the critical boundary so that the maximum type 1 error rate is controlled. As an example, assume that we only allow for equal second-to-first-stage ratios setting the upper bound of the second-stage-sample size of the selected treatment and control to be twice the first stage sample size. For 
an adjusted level of 0.013 (instead of 0.025) has to be used to control the maximum type 1 error rate. In more detail, if we assume for both treatments an effect size of 0.5 times the standard deviation, a sample size of 
per group would be needed to achieve 80% power. Compared to a fixed sample size test with Dunnett adjusted critical boundaries, this would be a 20.4% increase of the per-group sample size. For increasing k, this is only slightly decreasing: for 
an increase of 18.8% and for 
an increase of 17.0% of the per-group sample size is needed to control the maximum type 1 error rate when additionally allowing for the given sample size reassessment. To achieve a power of 90%, a slightly smaller increase in the per-group sample size is needed, that means an increase of 16.4%, 16.7%, and 15.6% would be needed for 
, 3, and 4, respectively. All these examples show that adjusting for the worst case would be a rather conservative strategy and adaptive tests should be implemented instead (Koenig et al., 2008; Bretz et al., 2009).
7 Discussion
In this paper, we have investigated the maximum type 1 error rate arising from the application of a nonadaptive test used by experimenters who freely adapt their ongoing trials. This problem has been addressed by Proschan and Hunsberger (1995) for the comparison of one treatment with a control and balanced sample sizes before and after the adaptive interim analysis. They considered a restricted rule incorporating a stopping for futility criterion. This leads to procedures where the effect of adjusting the adaptation of the sample size is no longer dramatic. Graf and Bauer (2011) have extended the worst case calculations allowing for unbalanced sample sizes. In this paper, a further level of complexity has been added by considering multiple comparisons of k treatments with a single control. For the case without selection of a treatment arm at interim, we calculate the maximum type 1 error rate for 
in the case of equal and flexible second-to-first-stage-ratios (assuming balanced first stage sample sizes). Not surprisingly, when applying uncorrected level α treatment-control comparisons, the worst case type 1 error is dramatically inflated. By using Dunnett-adjusted critical boundaries, the worst case inflation is still large. Interestingly, the inflation is very similar to the case of comparing 
treatment to a control (Graf and Bauer, 2011). This means that when adjusting for the number of treatments for 
, no noticeable further maximum inflation of the type 1 error rate occurs as compared to 
.
The case of equal and flexible second-to-first-stage ratios was investigated for scenarios where only a single treatment and the control are selected at the interim analysis. In this scenario, there is a trade-off between inflation due to sample size reassessment and the overcorrection for the 
treatments finally not selected and not tested in the statistical analysis. For equal ratios, the maximum type 1 error is monotonically decreasing with k with a finite limit noticeably larger than the nominal level α. As expected, the impact of flexible ratios is more severe, the maximum inflation of the actual level α, though decreasing for small k, is increasing with larger k.
There are several caveats to be mentioned here. First, for the case of flexible ratios the conditional error can only be calculated when the nuisance parameter, the common mean under the global null hypothesis, is known. Secondly, the maximum type 1 error only occurs if the experimenters apply the worst case sample size reassessment rule (maximizing the conditional type 1 error rate) at any point in the interim sample space. Thirdly, in some interim subspace, the maximum is assumed if some of the second stage sample sizes go to infinity. Although theoretically interesting, this of course means that these maximum type 1 error rates can never be reached in real clinical trials. Adjusting for these “unrestricted worst cases” would be an extremely conservative strategy and cannot be recommended for use in practice. Therefore, we also investigated maximum type 1 error rates that arise when the second stage sample sizes are constrained by upper and lower limits. Some of these results are practically interesting, because they demonstrate that in certain cases, when putting restrictions on the second-stage-sample sizes, naive strategies can control the type 1 error rate. Such calculations under constraints could replace simulations of the type 1 error rate in designs with adaptive selection rules, the latter being considered problematic by some researchers (Posch et al., 2011).
Open research problems are at present the unconstrained optimization for 
, which imposes a burden of numerical integration and optimization. For the unconstrained scenario of 
, the optimization lasts up to one half second for one grid point on an Intel(R)Core(TM)i5 CPU M540 processor with 2.53GHz and it is therefore still a time consuming numerical challenge to derive a sufficiently narrow grid over the three dimensional interim subspaces with sufficiently accurate values of the maximum conditional error functions to be integrated. Also scenarios where the selection of s, 
out of k treatment groups and the control are prespecified are of high interest.
As a conclusion, we do not recommend the use of unrestricted “worst case” adjustments since they will be far too conservative for serious consideration. If limits on sample size modifications can be imposed, it is still important to compare the operating characteristics of adaptive designs with the maximum-type-1-error-based adjustments discussed here. Only then we can decide whether sample size limits can or should be imposed and how tight they might be.
Acknowledgments
The work of Alexandra Graf was supported by the Austrian Science Fund (FWF), Project No.: J3344-N26. Part of her work was undertaken during a research stay at the University of Bremen. She is grateful to Werner Brannath for hospitality at the Competence Center for Clinical Trials as well as for helpful comments. Peter Bauer's and Franz Koenig's research has received funding from the European Union Seventh Framework Programme [FP7 2007–2013] under grant agreement No.: 602552. Furthermore, we thank the unknown reviewers, the associate editor and editor Lutz Edler for helpful suggestions as well as Byron Jones for critical proofreading of the paper, which have improved the paper substantially.
Appendix
A.1. Calculation of the conditional type 1 error rate
In the following we assume that the global null hypothesis applies (
for 
). The conditional type 1 error for rejecting at least one treatment-control comparison in the final analysis, given the interim data, can be calculated as follows
In the final analysis after the second stage each test (comparing treatment i to the control group) is based on the following global test statistic:
 |
where 
, 
, 
, have independent standard normal distributions. If the overall test statistic 
is larger than the critical boundary 
we get a false positive decision, which leads to the following inequality:
 |
leading to
 |
Since 
and 
have independent standard normal distributions for every set of values 
, r0, 
, 
and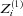 
(and hence are independent of these quantities), the conditional error can be written as in formula (1).
A.2. The maximum type 1 error rate is attained under the global null hypothesis
For 
the maximum type 1 error rate is attained under the global null hypothesis 
. To see this, assume (without loss of generality) that the null hypothesis is not true for H01. Then the conditional error for rejecting at least one true hypothesis is calculated in the same way as 
from formula 1994, but the product going from 2 to k rather than 1 to k, further on denoted by 
. Obviously, for given 
, 
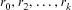. This statement is true since the integrated term in formula 1994, for given 
, is the same for 
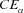and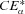 
but r1 does not appear in 
. Since the integrated function in 1994 is at every point larger (or equal) in 
, the whole integral must be larger (or equal) for 
as compared to 
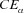for every given constellation of 
.
Let now denote 
the second-two-first-stage-ratios leading to the maximum 
. Due to the above arguments
 |
for all r1. The ratios 
may not be the ratios maximizing 
, but finding the ratios leading to 
can only increase the conditional type 1 error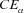 
and thus
 |
This domination also holds for the integral for the type 1 error 
in formula 1999, showing that the global null indeed gives the parameter constellation leading to the largest type 1 error inflation.
A.3. Maximum conditional type 1 error rate when selecting the most promising treatment for the scenario of equal second-to-first-stage-ratios
Following the lines of Proschan and Hunsberger (1995) the maximum conditional type 1 error rate when selecting the treatment with the largest observed interim effect for the scenario of equal second-to-first-stage-ratios (refer to Section 4.1) can be calculated by dividing the interim sample space into three subspaces:
I If
(equivalently 
) the worst case arises from setting 
so that the second stage overrules the first stage adverse effect leading to 
This results in a contribution to 
of 
since 
, 
here denoting the k-dimensional zero vector and Σ the k-dimensional covariance matrix with 
and 
for 
.II Within the subspace
(or equivalently 
), Proschan and Hunsberger (1995) showed that 
is leading to a worst case conditional type 1 error rate 
. We found no simplification of the two-dimensional integration in this subspace.III If
(or equivalently 
) the test can be rejected already at interim (
with 
) leading to a contribution of this subspace of 
where 
is a k-dimensional vector with values 
which is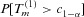 
and reduces to α when using the multiplicity corrected Dunnett critical boundary 
.
Conflict of interest
The authors have declared no conflict of interest.
Supporting Information
Additional supporting information may be found in the online version of this article at the publisher's web-site
References
- Barnes PJ, Pocock SJ, Magnussen H, Iqbal A, Kramer B, Higgins M, Lawrence D. Integrating indacaterol dose selection in a clinical study in COPD using an adaptive seamless design. Pulmonary Pharmacology and Therapeutics. 2010;23:165–171. doi: 10.1016/j.pupt.2010.01.003. [DOI] [PubMed] [Google Scholar]
- Bauer P. Multistage testing with adaptive designs. Biometrie und Informatik in Medizin und Biologie. 1989;20:130–148. [Google Scholar]
- Bauer P, Koehne K. Evaluations of experiments with adaptive interim analysis. Biometrics. 1994;50:1029–1041. [PubMed] [Google Scholar]
- Bauer P, Kieser M. Combining different phases in the development of medical treatments within a single trial. Statistics in Medicine. 1999;18:1833–1848. doi: 10.1002/(sici)1097-0258(19990730)18:14<1833::aid-sim221>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Bauer P, Koenig F, Brannath W, Posch M. Selection and bias - Two hostile brothers. Statistics in Medicine. 2010;29:1–13. doi: 10.1002/sim.3716. [DOI] [PubMed] [Google Scholar]
- Bebu I, Dragalin V, Luta G. Confidence intervals for confirmatory adaptive two-stage designs with treatment selection. Biometrical Journal. 2013;55:294–309. doi: 10.1002/bimj.201200053. [DOI] [PubMed] [Google Scholar]
- Bowden J, Glimm E. Unbiased estimation of selected treatment means in two-stage trials. Biometrical Journal. 2008;50:515–527. doi: 10.1002/bimj.200810442. [DOI] [PubMed] [Google Scholar]
- Brannath W, Posch M, Bauer P. Recursive combination tests. JASA. 2002;97:236–244. [Google Scholar]
- Brannath W, Bauer P, Posch M. On the efficiency of adaptive designs for flexible interim decisions in clinical trials. Journal of Statistical Planning and Inference. 2006;136:1956–1961. [Google Scholar]
- Bretz F, Koenig F, Brannath W, Glimm E, Posch M. Adaptive designs for confirmatory clinical trials. Statistics in Medicine. 2009;28:1181–1217. doi: 10.1002/sim.3538. [DOI] [PubMed] [Google Scholar]
- Burman CF, Sonesson C. Are flexible designs sound? Biometrics. 2006;62:664–669. doi: 10.1111/j.1541-0420.2006.00626.x. [DOI] [PubMed] [Google Scholar]
- Cohen A, Sackrowitz H. Two stage conditionally unbiased estimators of the selected mean. Statistics and Probability Letters. 1989;8:273–278. [Google Scholar]
- Dunnett CW. A multiple comparison procedure for comparing several treatments with a control. JASA. 1955;50:1096–1121. [Google Scholar]
- Elsaesser A, Regnstroem J, Vetter T, Koenig F, Hemmings R, Greco M, Papaluca-Amati M, Posch M. Adaptive designs in European Marketing Authorisation—. A survey of advice letters at the European Medicines Agency. 2014. submitted. [DOI] [PMC free article] [PubMed]
- EMA. Reflection paper on methodological issues in confirmatory clinical trials planned with an adaptive design.Doc. 2007. Ref. CHMP/EWP/2459/02 Available at: http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500003616.pdf.
- FDA Draft Guidance. Adaptive Design Clinical Trials for Drugs and Biologics. 2010. Available at: http://www.fda.gov/downloads/Drugs/…/Guidances/ucm201790.pdf.
- Friede T, Stallard N. A comparison of methods for adaptive treatment selection. Biometrical Journal. 2008;50:767–781. doi: 10.1002/bimj.200710453. [DOI] [PubMed] [Google Scholar]
- Gao P, Liu L, Mehta C. Adaptive designs for noninferiority trials. Biometrical Journal. 2013;55:310–321. doi: 10.1002/bimj.201200034. [DOI] [PubMed] [Google Scholar]
- Gaydos B. EMA/EFPIA 2nd Workshop: Adaptive Design in Confirmatory Trials. UK: EMA Headquaters; 2009. Phase 2/3 adaptive design utilizing a Bayesian decision analytic approach to dose selection. , Available at: http://www.ema.europa.eu/docs/en_GB/document_library/Minutes/2010/04/WC500089206.pdf. [Google Scholar]
- Graf AC, Bauer P. Maximum inflation of the type 1 error rate when sample size and allocation rate are adapted in a pre-planned interim look. Statistics in Medicine. 2011;30:1637–1647. doi: 10.1002/sim.4230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jennison C, Turnbull BW. Adaptive and non-adaptive group sequential tests. Biometrika. 2006;93:1–21. [Google Scholar]
- Koenig F, Brannath W, Bretz F, Posch M. Adaptive Dunnett tests for treatment selection. Statistics in Medicine. 2008;27:1612–1625. doi: 10.1002/sim.3048. [DOI] [PubMed] [Google Scholar]
- Kotz S, Balakrishnan N, Johnson NL. Continuous Multivariate Distributions. John Wiley and Sons, New York, NY; 2000. [Google Scholar]
- Lawrence D, Bretz F, Pocock S. INHANCE: an adaptive confirmatory study with dose selection at interim In: In: Trifilieff A, editor. Indacaterol: The First Once-daily Long-acting Beta2 Agonist for COPD, Milestones in Drug Therapy. Basel, CH: Springer; 2014. pp. 77–92. [Google Scholar]
- Lehmacher W, Wassmer G. Adaptive sample size calcualtions in group sequential trials. Biometrics. 1999;55:1286–1290. doi: 10.1111/j.0006-341x.1999.01286.x. [DOI] [PubMed] [Google Scholar]
- Levin GP, Emerson SC, Emerson SS. Adaptive clinical trial designs with pre-specified rules for modifying the ample size: understanding efficient types of adaptation. Statistics in Medicine. 2013;32:1259–1275. doi: 10.1002/sim.5662. [DOI] [PubMed] [Google Scholar]
- Mehta C, Pocock S. Authors' reply. Statistics in Medicine. 2012;31:99–100. [Google Scholar]
- Morgan CC, Huyck S, Jenkins M, Chen L, Bedding A, Coffey CS, Gaydos B, Wathen JK. Adaptive design: results of 2012 survey on perception and use. Therapeutic Innovation and Regulatory Science. 2014. doi: 10.1177/2168479014522468. [DOI] [PubMed]
- Mueller HH, Schaefer H. Adaptive group sequential designs for clinical trials: combining the advantages of adaptive and of classical group sequential approaches. Biometrics. 2001;95:886–891. doi: 10.1111/j.0006-341x.2001.00886.x. [DOI] [PubMed] [Google Scholar]
- Mueller HH, Schaefer H. A general statistical principle for changing a design any time during the course of a trial. Statistics in Medicine. 2004;23:2497–2508. doi: 10.1002/sim.1852. [DOI] [PubMed] [Google Scholar]
- Posch M, Maurer W, Bretz F. Type 1 error rate control in adaptive designs for confirmatory clinical trials with treatment selection at interim. Pharmaceutical Statistics. 2011;10:96–104. doi: 10.1002/pst.413. [DOI] [PubMed] [Google Scholar]
- Proschan MA, Hunsberger SA. Designed extension of Studies based on conditional power. Biometrics. 1995;51:1315–1324. [PubMed] [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2012. Available at: http://www.R-project.org ISBN 3-900051-07-0. [Google Scholar]
- Stallard N, Todd S, Whitehead J. Estimation following selection of the largest of two normal means. Journal of Statistical Planning and Inference. 2008;138:1629–1638. [Google Scholar]
- Sugitani T, Hamasaki T, Hamada C. Partition testing in confirmatory adaptive designs with structured objectives. Biometrical Journal. 2013;55:341–359. doi: 10.1002/bimj.201200218. [DOI] [PubMed] [Google Scholar]
- Thall PF, Simon R, Ellenberg SS. Two-stage selection and testing designs for comparative clinical trials. Biometrika. 1988;75:303–310. [Google Scholar]
- Thall PF, Simon R, Ellenberg SS. A two-stage design for choosing among several experimental treatments and control in clinical trials. Biometrics. 1988;45:537–547. [PubMed] [Google Scholar]
- Tsiatis AA, Metha CR. On the inefficiency of the adaptive design for monitoring clinical trials. Biometrika. 2003;90:367–378. [Google Scholar]
- Wang SJ, Bretz F, Dmitrienko A, Hsu J, Hung HM, Huque M, Koch G. Panel forum on multiple comparison procedures: a commentary from a complex trial design and analysis plan. Biometrical Journal. 2013;55:275–293. doi: 10.1002/bimj.201200047. [DOI] [PubMed] [Google Scholar]
-
Zeymer U, Suryapranata H, Monassier JP, Opolski G, Davies J, Rasmanis G, Linssen G, Tebbe U, Schroder R, Tiemann R, Machnig T, Neuhaus KL. The
exchange inhibitor Eniporide as an adjunct to early reperfusion therapy for acute myocardial infarction. Journal of the American College of Cardiology. 2001;38:1664–1651. doi: 10.1016/s0735-1097(01)01608-4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional supporting information may be found in the online version of this article at the publisher's web-site