The R-factor gap in macromolecular crystallography: an untapped potential for insights on accurate structures

Abstract

In macromolecular crystallography, the agreement between observed and predicted structure factors (R_cryst and R_free) is seldom better than 20%. This is much larger than the estimate of experimental error (R_merge). The difference between R_cryst and R_merge is the R-factor gap. There is no such gap in small-molecule crystallography, for which calculated structure factors are generally considered more accurate than the experimental measurements. Perhaps the true noise level of macromolecular data is higher than expected? Or is the gap caused by inaccurate phases that trap refined models in local minima? By generating simulated diffraction patterns using the program MLFSOM, and including every conceivable source of experimental error, we show that neither is the case. Processing our simulated data yielded values that were indistinguishable from those of real data for all crystallographic statistics except the final R_cryst and R_free. These values decreased to 3.8% and 5.5% for simulated data, suggesting that the reason for high R-factors in macromolecular crystallography is neither experimental error nor phase bias, but rather an underlying inadequacy in the models used to explain our observations. The present inability to accurately represent the entire macromolecule with both its flexibility and its protein-solvent interface may be improved by synergies between small-angle X-ray scattering, computational chemistry and crystallography. The exciting implication of our finding is that macromolecular data contain substantial hidden and untapped potential to resolve ambiguities in the true nature of the nanoscale, a task that the second century of crystallography promises to fulfill.

Database

Coordinates and structure factors for the real data have been submitted to the Protein Data Bank under accession 4tws.

Introduction

Realistic simulation of X-ray diffraction experiments requires a return to first principles. Currently, there are so many scale factors and corrections that any connection between the final coordinate model and the value of a given pixel on the detector is easily lost, but, in the early days of X-ray crystallography, this relationship was at the forefront of research. Not long after the discovery of X-rays by Röntgen in 1895, he was awarded the first ever Nobel Prize (in 1901), but the properties of this new kind of ‘ray’ were still not well understood. Indeed, Rutherford had only just divided nuclear radiations into three categories (alpha, beta and gamma), and it was by no means clear that Thomson's ‘cathode rays’ (1887) and Rutherford's ‘beta rays’ were both electrons, or that naturally produced gamma rays and machine-produced X-rays were both electromagnetic radiation. Indeed, at that time, it was still debated whether ordinary visible light was a particle or a wave, let alone the newly discovered ‘X-rays’. It was not even clear that crystals were regular arrays of atoms, and the internal structure of the atom itself was still a mystery.

Despite this apparent chaos and confusion, precise measurements were being made. Although W.L. Bragg is now famously known for formulating the first equation relating the position of spots to distances inside the crystal, his father W.H. Bragg is perhaps less well known for his work on X-ray detectors. Röntgen found that X-rays darken photographic film, but, especially in those days, this process was far from quantifiable or linear. Building on the work of Perrin ¹ and Barkla ², Bragg and son used what today is called an ion chamber as the detector for their famous work on rock salt ³. The ion chamber is an amazing linear device that directly converts the intensity of an X-ray beam into an electric current. Even in those days, electric currents could be measured extremely reliably, the basis of the ammeter having been discovered nearly a century earlier by Schweigger and Ampère ^4,5.

It was such precise measurements with this very device ⁶ that enabled Charles G. Darwin (not to be confused with his famous grandfather Charles R. Darwin, author of the 1859 book On the Origin of Species) to extend Maxwell's dynamical theory of electromagnetism to X-rays ⁷. Incidentally, Darwin's lab partner, Henry Moseley, also obtained the first experimental evidence that the atomic numbers proposed by Mendeleev (1869) had any physical significance. They corresponded beautifully to the wavelength of X-rays emitted by chemical elements when bombarded with high-energy radiations ⁸. Until this discovery, acceptance of the periodic table had been slow because it could not explain the systematic discrepancies between atomic number and atomic mass. The neutron was unknown at that time, as it was discovered by Chadwick 19 years later ⁹.

Although the dynamical theory of X-ray diffraction came first, Darwin spent the following nine years revising it to account for imperfect crystals, largely because the dynamical theory was not consistent with Moseley's observations of diffracted intensities. The crystals available at that time were just not perfect enough for dynamical theory to work, much like the protein crystals of today. Darwin's follow-up work was the first to define a variable called f to represent the effect of the structure contained within the unit cell ⁷. Hartree clarified the significance of this concept ¹⁰, much to the delight of W.L. Bragg, who expounded on its usefulness ¹¹. Interestingly, the concept of a structure factor had first been proposed almost a decade previously by Debye and Scherrer ¹², but the idea did not make its way into the English literature until well after the end of World War I. Indeed, the field of crystallography began to make tremendous leaps forward as soon as scientists from both sides of that conflict finally began to communicate.

It is Darwin's master formula predicting the number of photons in a fully recorded spot given the intensity of the incident beam, camera parameters, a few physical constants, and the all-important ‘structure factor’ that enabled the present work. A modernized version of Darwin's formula has been described by Blundell and Johnson ¹³, and has been instructively re-derived by Woolfson ¹⁴.

Specifically, the formula used here is identical to that given by Holton and Frankel ¹⁵:

(1)

where I is the integrated spot intensity (in photons/spot), I_beam is the intensity of the incident beam (photons·s⁻¹·m⁻²), r_e is the classical electron radius (2.818 × 10⁻¹⁵ m), V_xtal is the volume of the crystal (in m³), V_cell is the volume of the crystal unit cell (in m³), λ is the X-ray wavelength (in m), ω is the angular velocity of the crystal (radians·s⁻¹), L is the Lorentz factor (speed/speed), P is the polarization factor (photons/photons), A is the X-ray transmittance of the path through the crystal to the spot (photons/photons), and F is the structure factor (electron equivalents).

Previously we explained how this formula gives intensities on an absolute scale ¹⁵. In the present work, we are concerned with the error associated with this intensity, and the above formula is a useful guide to this error propagation. Any relative error in any of the terms in Eqn 1 propagates directly into a relative error in the spot intensity. For example, if V_xtal is 5% off, then so will I be. If I_beam fluctuates by 5%, that error too propagates into I, as would a 5% fluctuation in the speed of the motor driving the spindle. Uncertainties in the attenuation factor A due to the odd shape of the crystal and vitrified solution around it also propagate into the data as absorption errors, and even a slight mis-alignment of the spindle with the beam may cause a very large change in the Lorentz factor.

Many of these sources of error may be removed by scaling, because, as long as the incident beam intensity, for example, is always 10% lower than expected, all of the spot intensities will be off by exactly the same amount. This means that no inaccuracy is propagated into the final electron density map, which may be placed on an absolute scale by comparing it to the calculated map ¹⁶. However, if the incident beam intensity changes during the course of data collection, then the scale factor must be made to follow it exactly, or the error in the scale factor itself will propagate into the data. In general, scaling may be used to remove sources of error with low frequencies, such as the variation in illuminated volume as the crystal rotates, but cannot remove errors with high frequencies, such as the variation in illuminated volume as the crystal vibrates in the cryo stream ¹⁷.

Because of the complex ways that data processing may suppress certain sources of error and not others, the only way to definitively evaluate the influence of all sources of error is to simulate the diffraction experiment and calibrate the magnitude and frequency of all sources of error on a real-world instrument. To this end, we developed MLFSOM, a program for generating simulated diffraction images given a set of structure factors and a parameterized list of experimental variables. A detailed description of the implementation of this program is provided as Doc S1. The name MLFSOM was chosen because it performs the reverse operation of data-processing programs such as MOSFLM ¹⁸, but the simulation is based on first principles and is not specific to MOSFLM, HKL2000 ¹⁹ or XDS ²⁰. Unlike previous diffraction image simulators ^21–23, implementation of MLFSOM has focused on putting both signal and noise on an absolute scale, enabling direct, side-by-side comparison with real data.

In performing this exercise, we followed in the footsteps of those early pioneers who were also devising models that could quantitatively predict experimental data. However, detector technology has come a long way since the seminal rock salt experiment by Bragg and son, and thus the information needed to create a simulator spans nearly 100 years of literature. In addition, each source of noise implemented in MLFSOM was calibrated by independent experimental measurements. For example, correct estimation of the photon-counting error requires that the data be placed on an absolute scale because this is the only scale on which the error in the count is the square root of the intensity. For counting devices such as multi-wire or pixel array detectors, the pile-up correction and its appropriateness to the time structure of the incoming signal is also a source of error ²⁴, but as we are only concerned here with a CCD detector, this source of error was not implemented. Sources of error such as shutter jitter, beam flicker and irregular spot shape are proportional to the signal, and therefore independent of scale, while errors such as CCD readout noise and dark current are completely independent of the intensity, and therefore must also be put on an absolute scale before they can be meaningfully combined with other errors.

Results

The R-factor gap affects even the highest-quality structures in the Protein Data Bank, so here we elected to simulate one of the most well-understood protein structures, Gallus gallus lysozyme in its tetragonal form, and collected data at the most widely available wavelength, the selenium edge (0.9795 Å). As a selenomethionine analog of this protein was not available, we selected a derivative with the same f″ value of Se at its edge, gadolinium, which also avoids complications of simulating anomalous signal near an absorption edge.

The Gd ligand had to be modeled carefully so that the high electron density of the Gd ion did not dominate the F_obs − F_calc differences. With the simulated data, the position, occupancy and B factor of the ligand atoms were known exactly, and were readily recovered during refinement, so ligand error was negligible. If the ligand was not accurately derived from the real data, a noticeable drop in R_cryst and R_free values was expected for the multi-conformer simulated data relative to the real data. This was not observed, indicating that the Gd ligand contributed little to the R-factor gap in this case.

Data reduction statistics from real and simulated data are very similar

Real and simulated lysozyme diffraction images (Fig.1) were prepared as described in the Experimental procedures, and processed using both MOSFLM and XDS in order to compare and contrast the anomalous signal and other statistical indicators of data quality (Table 1). The mosaic spread reported by MOSFLM for the real dataset was 0.50, and, using a simulated mosaic spread of 0.4 in combination with 0.3% unit cell dispersion as suggested by Nave ²⁵, resulted in a mosaic spread of 0.49 as reported by MOSFLM. XDS uses a different approach for estimating mosaic spread ²⁰, resulting in values of 0.158 for the real data and 0.159 for the simulated data. The similar mosaic spread reported by the two programs is encouraging, and indicates that our representation of mosaicity in the simulation is realistic.

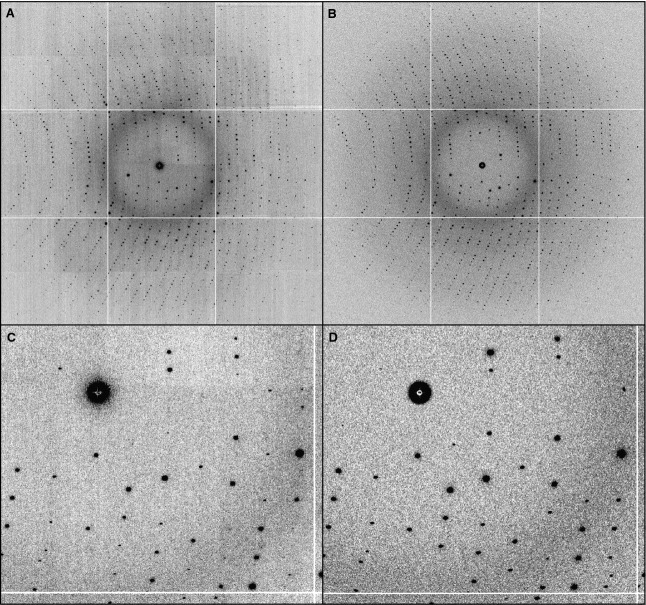
Fig 1.

Example diffraction images for (A) real data collected from Gd-containing lysozyme at Advanced Light Source beamline 8.3.1, and (B) simulated diffraction generated using MLFSOM. (C,D) Magnifications of parts of (A) and (B), respectively.

Table 1.

Data reduction statistics. The simulated data were from the multi-conformer model. Space group, P4₃2₁2; X-ray wavelength, 0.97934 Å, which is far from the Gd edge having a theoretical f ′ = −0.92, f ′′ = 6.7 electrons from Gd. Completeness and unique observations were calculated from the final merged reflection file using MTZDUMP ²⁶. Total observation counts taken from XSCALE ²⁰ or SCALA ²⁶. Friedel mates were treated as symmetry-equivalent in scaling. Values in parentheses are for the outer resolution bin.

	Real	Simulated	Real	Simulated
Data processing program	XDS	XDS	MOSFLM	MOSFLM
Cell dimensions a = b, c (Å)	77.1, 38.7	77.2, 38.8	77.2, 38.8	77.2, 38.8
Resolution (high-resolution bin) (Å)	50–1.45 (1.54–1.45)	50–1.45 (1.54–1.45)	50–1.45 (1.53–1.45)	50–1.45 (1.53–1.45)
I/σ(I) (high-resolution bin)	18.0 (1.99)	15.0 (1.15)	16.6 (2.6)	15.2 (1.2)
R-factor or Rmerge (%)	4.5 (26.8)	5.7 (55.5)	6.0 (28.2)	6.6 (67.5)
Rmeas (%)	5.3 (35.4)	6.7 (72.8)	6.9 (37.3)	7.6 (89.6)
CCa [26a]	99.8 (86.0)	99.8 (65.5)	99.7 (88.8)	99.8 (60.2)
Anomalous CC (%)	69 (–)	62 (–)	46.7 (–)	52.4 (–)
Completeness	96.7 (86.7)	96.4 (85.5)	92.8 (62.3)	92.7 (61.7)
Number of unique observations	19 728	19 731	18 426	19 864
Total number of observations	119 744	120 037	117 173	117 945
Redundancy	6.1 (2.1)	6.1 (2.2)	6.0 (2.2)	5.9 (2.1)
Wilson B factor	18.3	18.8	14.1	14.4

The simulated crystal volume was also adjusted such that the real and simulated data had the same scale when combined with SCALA ²⁶. The scale of the real data changed with phi rotation, and the crystal was bigger than the beam, so a change in the illuminated volume over the course of data collection was expected. These scale factors may also be equally well explained by a variation in incident beam intensity, but this magnitude of drift over such a short experiment was considered highly unlikely with this instrument.

In order to match the low-angle R_merge to that of the real data (3.9%), the detector calibration error was set to 5.4%, which is much larger than the manufacturer's specified value of 0.2%. We confirmed the 0.2% reproducibility of flood fields, so this extra error must have had some other source. Beam flicker, shutter jitter and sample self-absorption may all be excluded because these were calibrated independently, and including all of them in a MLFSOM simulation leads to a low-angle R_merge of 0.5%. Diederichs reported similar unrealistically low values for R_meas in the lowest-angle bin using data simulated with SIM_MX, and postulated that this was primarily due to an unknown and unmodeled systematic error ²³.

Here we implemented this extra error in the form of detector calibration, but other possible candidates are sample vibration ¹⁷, non-isomorphism between parts of the crystal rotating in and out of the beam, and perhaps others. Understanding and reducing these errors is of considerable interest, but they are difficult to distinguish using low-multiplicity datasets such as the one considered here. Thorough discussion of all these phenomena is beyond the scope of the present work, and neither vibration nor self-isomorphism are implemented in the current version of MLFSOM. For this study, we simply require that the combination of all systematic errors result in R_merge = 3.9%, an effect that we simulated by adjusting detector calibration error alone.

The overall <I/σ(I)> at 1.45 Å resolution for the real data was 17.6 (XDS) and 16.6 (MOSFLM), and processing the simulated images resulted in values of 14.7 (XDS) and 15.0 (MOSFLM). The asymptotic ISa ²⁷ from XDS reached 19.2 for the real data and 21.2 with the simulated data. Without the extra systematic error introduced to match R_merge, unrealistically high <I/σ(I)> values were observed, both overall and in the low-angle bin, similar to the results seen with SIM_MX ²³. Overall the results from processing of our real and simulated data were encouraging, and showed that we had developed a simulation that is able to reproduce the expected errors in macromolecule diffraction data.

The sum of all errors is comparable to R_merge

Having generated and processed a realistically noisy simulated dataset, we compared the final, merged structure factors (F_sim) to the structure factors that were initially fed into the MLFSOM simulation (F_start). Although F_sim appears in the data-processing output file as ‘F_obs’, we use F_sim to clarify that it is derived from a simulation and is not an experimental observation. Also, as this is a simulation, F_start may be defined to be the error-free ‘true’ structure factor. This definition allowed us to measure how much error the simulate-and-process-back procedure introduced into the ‘true’ structure factor, and therefore extrapolate the magnitude of the total experimental error in F_obs. This was done by inputting F_start and F_sim into the CCP4 ²⁶ program SCALEIT as though they were merged native and derivative datasets. After least-squares refining and applying a scale and B factor to F_sim, the R-factor (R_diff) between F_start and F_sim was 6.6% overall at 1.45 Å and 2.8% in the low-resolution bin for XDS-processed data. For MOSFLM/SCALA-processed data, these values were 6.9% overall, and 1.6% in the low-angle bin. These low residuals are quite remarkable considering how many sources of error were included in the MLFSOM simulation. The total error in the data (R_diff) was comparable to the self-consistency of the data (R_merge or R_meas), implying that the accuracy of real data is similarly indicated by its precision. Specifically, the root mean square (RMS) value of σ(F_sim) assigned by data-processing programs was found to be lower than the RMS difference between F_start and F_sim by a factor 0.71 for XDS and 0.64 for MOSFLM/SCALA, i.e. the data are slightly less accurate than they are precise.

Overall, the total error in the data was only a few per cent, comparable to the magnitude of R_merge, and thus cannot explain the typically observed macromolecular R_cryst/R_free values of 20–30%. We therefore conclude that the high values of R_cryst/R_free are not a direct manifestation of any of the sources of experimental error implemented in MLFSOM.

Models refined against simulated data have unusually low refinement R values

Given the similarity between F_start and F_sim, it is perhaps not surprising that simply dropping the coordinate model that was used to calculate F_start into refinement against F_sim yields remarkably low values of R_cryst and R_free. Specifically, we obtained starting R_cryst/R_free values of 7.37%/7.16%, which evolve to 6.75%/8.06% after 100 cycles in REFMAC ²⁸. R_merge is an intensity statistic, and therefore represents twice the relative error in F, complicating direct comparison to R_cryst and R_free. Weak data also inflate refinement R-factors significantly above the relative error in σ(F). For these reasons, small-molecule structures are evaluated using R1, for which data with I < 4xσ(I) are omitted, and R_sigma = <σ(I)>/<I>. The validation criterion is R1 < 2*R_sigma, and no structure in the Protein Data Bank passes this test. In our case, both F_sim and F_obs have R_sigma = 4%, and after refining the ‘right answer’ coordinate model against F_sim, we obtained R1 = 4.3%, easily passed this small-molecule quality standard. However, as R1 and R_sigma are rarely used in macromolecular crystallography, we compare R_merge to R_cryst and R_free using data cut to 2 Å resolution (last column of Table 2 and Fig. 3). Refining the ‘right answer’ coordinate model against F_sim data truncated to 2.0 Å yields R_cryst/R_free = 3.92%/5.59%, comparable to R1.

Table 2.

Data refinement statistics.

	Real	Real	Simulated multi-conformer	Simulated single-conformer	Simulated single-conformer
Model	Hand-built	Autobuild	Autobuild	Autobuild	Build-back
Resolution (Å)	1.45	1.45	1.45	1.45	2.0
Rwork	0.1463	0.1910	0.1664	0.1530	0.038
Rfree	0.1733	0.2091	0.1830	0.1624	0.055
Number of atoms	1375	1199	1177	1173	1269
Non-solvent	1165	988	968	945	1012
Solvent	210	211	209	228	271
Wilson B factor	11.27	11.64	12.53	12.71	12.71
RMSD bond lengths (Å)	0.015	0.007	0.008	0.007	0.016
RMSD bond angles (°)	1.60	1.20	1.15	1.06	1.60
Ramachandran favored (%)	98.51	97.60	96.75	95.83	98.43
Ramachandran outliers (%)	0.00	0.80	0.00	0.83	0.00
All-atom clash score 27a	17.27	10.42	7.43	3.27	2.9

Fig 3.

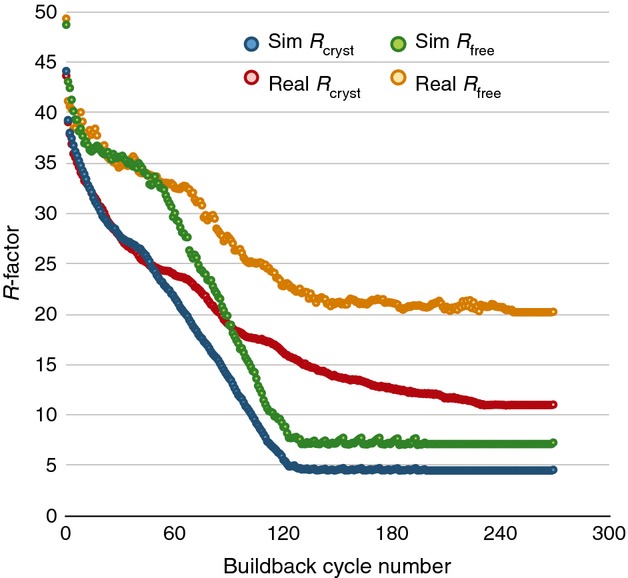
Reduction in R-factors as individual atoms are automatically built into difference maps. The starting coordinate model used to compute Fstart for the simulated data (blue and green) was a single-conformer model of 100% occupied atoms with isotropic B factors. In both cases, the processed data were provided to phenix.autobuild with anomalous differences, the sequence of lysozyme and no other sources of phase information. The resulting model was trimmed of all water atoms and subjected to a simple five-step rebuilding procedure using data truncated to 2.0 Å: (1) refine in REFMAC for 500 cycles, or until atoms and B factors stop moving, (2) add dummy atoms to the five highest peaks in the difference map, (3) assign new atoms the proper atom name if they are within 0.5 Å of an atom in the reference model, (4) remove atoms with B > 100 Ų or that fall on negative difference features < −6σ, and (5) repeat until convergence. Models built into the simulated data converge to very low R_free values (R_cryst = 4.57% and R_free = 7.27%), roughly the same magnitude as the R_merge from the XDS/MOSFLM-processed data, whereas the R_free for the real data never goes below 20%.

However, refining this same model and data in phenix.refine ²⁹, gives significantly higher values, i.e. R_cryst/R_free = 7.38%/9.88% to 2 Å resolution, which do not pass the R1 versus R_sigma test. The main reason for this discrepancy is because implementation of the bulk solvent correction differs between these two refinement programs and the bulk solvent mask from REFMAC was used to compute F_start. REFMAC uses two different solvent probe radii to model ionic and Van der Waals interactions with bulk solvent, whereas phenix.refine uses the same probe radius for all coordinate atoms. Even when phenix.refine was set to optimize_mask = True, the R_cryst/R_free values were 7.19%/9.94% and the F_sim − F_calc difference map only contained features far from atomic positions. Neither of these programs can reproduce the bulk solvent mask of the other in their current implementations. Indeed, after refining the same model against F_obs using each program, R_diff calculated as described above with SCALEIT between the calculated total structure factors ‘FC_ALL_LS’ from REFMAC and ‘F-model’ from phenix.refine yielded an R_diff value of 11.2%. This relatively large difference coming from the bulk solvent, which is ‘invisible’ in normally contoured electron density maps, highlights how sensitive R-factors are to features that fall below traditional map contour levels ¹⁶. However, as it would take three independent sources of 11.2% error to add in quadrature to 20%, and seven sources to reach 30%, this 11.2% is still significantly smaller than the R-factor gap, some other source of systematic error must be involved.

Building atomic models with low R-factors does not require phase information

The uncharacteristically low R_cryst/R_free achieved when refining against simulated data with realistic noise suggests that R_cryst/R_free values obtained with real data may in theory be just as low, provided the ‘true’ state of the electron density in the unit cell is accurately represented by the model. It is unclear what inadequacies in the model are responsible for this. Do mistakes in model building accumulate by becoming ‘locked in’ by phase bias? Or is it simply not possible to represent the ‘true’ electron density of real unit cells using existing coordinate-and-bulk-solvent models?

To address this question, we generated a new set of F_start values from a single-conformer model of lysozyme, and repeated the full MLFSOM simulation and XDS processing followed by phenix.autobuild with anomalous data (Fig.2), and then implemented a simplistic F_sim − F_calc guided build-back procedure (see Experimental procedures). The results are shown in Fig.3, together with those for exactly the same rebuilding algorithm performed on real data. Despite the virtually identical data-processing statistics, the simulated data rapidly converge to small molecule-like R_cryst/R_free values of 3.8%/5.5%, but the real data do not. In fact, the final R_cryst/R_free using F_sim is essentially identical to the values of 3.92%/5.59% obtained by dropping the ‘right answer’ coordinate model directly into the refinement. This result implies that, provided the ‘right answer’ is a single-conformer structure with unit occupancy, good geometry and flat bulk solvent, then simply building into F_obs − F_calc difference features may be expected to rapidly and easily converge to the ‘right answer’. The noise in the data and the lack of any external phase information are simply not enough to trap the building and refinement into a local minimum. We therefore conclude that the reason why building and refinement with F_obs does not converge to small molecule-like R_cryst/R_free values is because the content of the real unit cell cannot be accurately represented by current coordinate models. Otherwise, building into F_obs − F_calc difference features would converge.

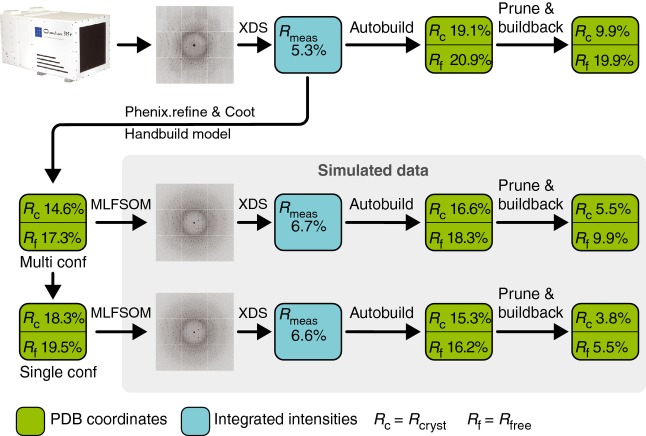
Fig 2.

Schematic representation of the workflow, showing the process used to generate both simulated and real diffraction images, and then process, solve and refine the data. The refinement statistics for the models are detailed in Table 2.

Relative contributions of sources of error

Whenever possible, published values are used for these parameters. For example, detector performance was taken from manufacturer's specifications. Where no published values are available (such as the jitter in the shutter), parameters were measured experimentally at Advanced Light Source beamlines 8.3.1 ³⁰ and 12.3.1 ³¹ (Table 3), but it is a simple matter to input the characteristics of a different beamline if they are known. A general result of testing MLFSOM is that only one of the many sources of noise in the diffraction experiment typically dominates a given dataset. For example, the noise introduced by background scattering limits the signal-to-noise ratio of faint, high-resolution spots, and detector readout noise is only important in cases where the background is very low.

Table 3.

Sources of random error.

Source of error	Values used for simulated data
Photon counting noise	σN = √N
Readout noise	RMS 11.5 electrons/pixel
Shutter jitter	RMS 0.57 ms
Beam flicker	0.15%/√Hz
Dark current	0.036 RMS ADU/pixel/s

Conversely, X-ray background and readout noise have almost no effect on anomalous data. This may be demonstrated by turning off background and readout noise in the simulator or by adding additional readout noise to real images and examining the resulting anomalous signal. Anomalous differences are so small that they may only be measured with thousands of photons per spot, where the relative error due to photon counting is less than a few per cent. Because of this, small relative errors, like the ones that propagate through Darwin's formula, dominate the errors in anomalous difference measurements. However, MLFSOM simulations using realistic levels of shutter jitter, beam flicker and sample self-absorption produced low-angle R_merge values of less than 0.5% and <I/σ(I)> values > 100, which is clearly unrealistic. It was only after including detector calibration error that realistic statistics were obtained, indicating that a truly ‘perfect’ detector would enable S-SAD phasing with Bijvoet ratios less than 0.5%. Unfortunately, no current detectors give R_merge or R_meas values less than 1%.

Discussion

Realistic simulation of diffraction images using MLFSOM, and subsequent processing with commonly used data-reduction programs reproduced essentially all relevant data quality metrics, but still did not change the structure factors by more than a few per cent, indicating that modern data-reduction packages accurately capture structure factor amplitudes. Furthermore, applying a standard SAD phasing pipeline followed by careful rebuilding without phase restraints consistently recovered the ‘right answer’ model with remarkably low R_cryst/R_free values (Fig.3). This tells us that not only are refinement programs stable to realistic noise, but conventional difference map-guided model building should converge to ‘small molecule’ precision. Why is this not possible with real data? There are two places that the residual systematic error may reside: in either the protein or the solvent.

There have been many attempts over the decades to apply multi-conformer models ^32–36, but the reductions in R_free have never been more than approximately 4%. This is consistent with the quadrature summation of errors if half the errors arise from the multi-conformer protein and half from solvent. For example, if 20% error is coming from hidden conformers in the protein region, and another 20% from the unflatness of the solvent region, then the total error will be 28%. If we assume no correlation between the solvent errors and the model errors, then eliminating all errors in either region entirely will still lead to R_free ‘hanging up’ at approximately 20%, not 14% as one would expect if two errors added algebraically to 28%.

Unfortunately, refinement tends to spread errors evenly across the map, which means that the non-flatness of the solvent must be explained if we are to ever achieve noise levels in electron density maps on a par with experimental noise. For example, if there was no noise at all and the model refined down to an R-factor near zero, then removing any single atom would produce an enormous F_obs − F_calc peak. During our automated build-back procedure, the peak height of the next difference feature of the simulated data steadily increased with building cycle, a behavior that is not observed with real macromolecular data (Fig.4). With the simulated data, this is because the phases are steadily improving, the occupancy of all the atoms are unity, the bulk solvent is flat, and each atom has a perfectly Gaussian-shaped Debye–Waller factor. In the case of real data, the model has these same characteristics, and apparently the errors that arise from this assumption accumulate faster than the new difference features rise. However, if the coordinate model were more realistic and the building strategy more intelligent, there would be every reason to expect that the difference features will become increasingly more obvious all the way down to ‘small molecule’-like R-factors. Specifically, if the error in the map arises from experimental noise only, it would generally be less than 5%, and as carbon contains six electrons, single-electron changes are approximately 18%. This is independent of diffracted resolution, implying that data with sufficient overall signal-to-noise are capable of distinguishing single-electron changes. However, as long as the model–data difference remains above 20%, these subtle features remain indiscernible.

Fig 4.

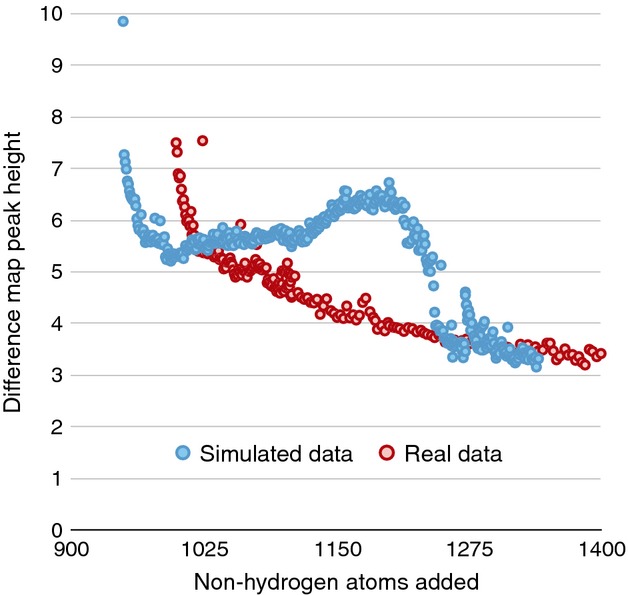
Maximum residual peak height in the difference maps at each step in the autobuild procedure. The peak height of the next difference feature of the simulated data steadily increases with building cycle, behavior that is not seen with real macromolecular data.

Although the bulk solvent itself may at first seem uninteresting, the ‘littoral zone’ between the protein and solvent channels is after all the interface between the molecule of interest and the rest of the world. Substrates, ligands and even other proteins must pass through this region for biochemical reactions to occur, so its structure and the forces involved in it are key to understanding function. A better understanding of solvent density will also have cross-over benefits in other scattering techniques, in much the same way that previous work on crystallographic water ^37–39 led to better water models for small-angle X-ray scattering analyses ⁴⁰. Developments in other fields, such as the ability to distinguish between conformational switching and bona fide disorder in small-angle X-ray scattering analysis ⁴¹, may also help build better crystallographic models. The microscopic behavior of water is still an active field of research ^42–44, and our understanding of it continues to improve. Recently, a molecular dynamics (MD) simulation of a protein crystal revealed details in the solvent density beyond what was originally built into electron density maps ⁴⁵, suggesting that a synergy between MX and MD more fully describing multiple protein conformations and the protein-solvent interface may finally be underway.

An exciting possibility is that realization of such untapped information in the almost 78 000 macromolecular datasets in the Protein Data Bank ⁴⁶ will spark a wave of new methodological developments and functional insights ⁴⁷. It is clear now that model building and refinement are held back neither by noise nor phases but instead by the appropriateness of the modeling framework currently used to represent macromolecules and their environment – both protein and solvent. Better models will inevitably provide better descriptions of the dynamic nature of macromolecules that is so critical for their function. Once such models are built, we expect the wealth of structural data accumulated during the high-throughput structural genomics era to stimulate insights into comprehensive protein dynamics and the key protein–water interface. The resulting enhanced knowledge of flexibility and the solvent interface will propel us towards more accurate crystal structures that will support improvements in computational methods and better link structure to activity and biology.

Experimental procedures

Reference lysozyme dataset

A reference dataset was collected at Advanced Light Source beamline 8.3.1 from a lysozyme crystal measuring 0.12 × 0.21 × 0.3 mm grown with Gd-HPD03A [a neutral gadolinium complex with 10- (2-hydroxypropyl)-1,4,7,10-tetra-azacyclododecane-1,4,7-triacetic acid) as previously described ^48,49. The detector was a model Quantum 315r (Area Detector Systems Corporation, Poway, CA) operating in hardware binning mode with the data collection parameters shown in Table 4. The Gd/lysozyme crystals were chosen because they combine the well-understood nature of lysozyme and the Se-like f″ value of Gd at the Se edge.

Table 4.

Sources of systematic error.

Source of error	Values used for simulated data
Air absorption	Attenuation depth = 3220 mm
Sample self-absorption	100 μm thick × 340 μm wide loop; attenuation depth = 1538 μm
Detector front window	12.7 μm thick; attenuation depth = 610 μm
Detector phosphor	40 μm thick; attenuation depth = 10.9 μm; energy absorption depth = 11.1 μm; visible light self-absorption depth = 100 μm
Detector gain	1.8 ADU/photon
Detector point spread function	g(r2 + g2)−3/2 with g = 30–60 μm (center to corner)
Detector sensitivity spatial variation	5.4% RMS with spatial frequency five pixels
Detector vignette effect	100% center to 40% at corner
Detector ‘window pane’	Three pixel separation between nine modules
Detector size	3096 × 3096 pixels; pixel size = 0.102539 mm
Spindle miss-alignment	−0.1° about vertical
Detector miss-alignment	0.366° tilt; 0.115° twist; −0.141° omega
Crystal mis-setting angles	147.188° about spindle; 34.5869° about vertical; 144.977° about the X-ray beam
Spot splitting threshold	Two pixels or 1°
Maximum sub-spots	10 000
Mosaic spread	0.4°
Unit cell dispersion	0.3% Δd/d
Spectral dispersion	0.014% Δλ/λ
Beam divergence	2.0 × 0.3 mrad
Kahn polarization factor	0.9
Wavelength	0.97934 Å
Exposure time	0.1 s
Flux	7.7 × 1010 photons·s−1
Beam size	100 μm
Crystal size/thickness	120–200 μm, varying with rotation

Simulated lysozyme datasets

Two simulated datasets were generated by MLFSOM using the same parameters as the real data, some of which were refined values from processing of the reference dataset. Other parameters, such as flux, detector calibration error, and the magnitude of all sources of error were each calibrated from independent experiments (Tables 2 and 3). The first simulated dataset (multi-conformer simulated) was generated from a coordinate model containing alternate conformation side chains and Gd ligand positions refined against the real data collected here. This model was generated starting with Protein Data Bank ID 1h87, refining alternately using phenix.refine ²⁹ and REFMAC ²⁸, with periodic rounds of manual rebuilding using Coot ^50,51. After a final refinement using REFMAC, the calculated bulk solvent contribution was extracted using the MSKOUT feature, and these structure factors were added to those of the coordinate atoms before calculating anomalous differences using ano_sfall.com. The resulting values of F⁺ and F^- were then input in to the mlfsom.com script to generate the simulated diffraction images. The second simulated dataset (single-conformer simulated) was generated from a simplified version of this model containing only single conformer side chains and two Gd sites, refined against the real data with the X-ray weight reduced so that the right answer had excellent geometry.

Random errors

The simulated sources of random error included beam flicker, shutter jitter, detector readout noise, dark current, and X-ray shot noise from both Bragg-scattered photons and background. The beam flicker was taken to be the RMS variation of the direct beam intensity on a photodiode placed at the sample position at Advanced Light Source beamline 8.3.1, which was 0.15% at 5 Hz or 0.067%/√Hz if it follows a canonical 1/frequency power spectrum, but, to be safe, the value 0.15%/√Hz was used in the simulation. The shutter jitter was apparent in the variation of the PHIZ camera parameter refined by MOSFLM (Doc. S1), and dominated by the 2 ms update rate of the PMAC motor controller (DeltaTau Inc., Los Angeles, CA). This generates a sawtooth distribution of timing errors with an RMS of 0.577 ms. The readout noise of the detector was taken from blank images as RMS 4.1 pixel level (ADU) variation, with additional noise from the dark current accumulating at 0.036 RMS ADU/s. The shot noise (photon-counting error) was taken as the square root of the expectation value of photons that were absorbed in the phosphor layer of the detector.

Systematic errors

Attenuation of X-rays in the sample, the air and the detector are all sources of systematic error. These were calculated using Beer's law ^52–54 and the tabulated cross-sections from the National Institute of Standards and Technology XCOM database ⁵⁵. The shape of the sample was represented using a facet/planes model, by which the surface of the sample was approximated as a collection of planes defining each facet. As the simulated crystal rotated, the intersection point between the incident X-ray beam and the facet currently in its path was computed. The distance from this point to the center of the sample was taken as the first segment of the X-ray attenuation path, with the second segment similarly calculated for the diffracted beam exiting toward each pixel.

The energy deposited into the phosphor was also computed from Beer's law using its mass energy absorption cross-section ⁵⁶. It is this dose that leads to the visible light that is eventually detected by the CCD. The vignette effect, which makes transmission 40% less efficient at the corners of each fiberoptic taper than at the center, was simulated by scaling down the absorbed photons before calculating the shot noise error, and then scaling back up to simulate the flood-field correction.

The point spread function was implemented as described previously ⁵⁷, with the width varying twofold from the center to corner of each module to simulate the corner correction effect. Another effect of the point spread function varying across the face of the detector is that it limits the applicability of the flood field correction to sharp features such as spots. Together with other sources of systematic error, this calibration error effect must have resulted in the observed R_merge = 3.9% in the lowest-angle bin. Although detector calibration was probably not the only source of systematic error at work, for this low-multiplicity dataset, the total error was implemented as a fixed mask of scale factors varying by RMS 5.4% from unity with a spatial frequency of five pixels. This mask was multiplied by the spot intensities on every image, and the resulting R_merge and ISa were equal to those of the real data.

The simulated spindle was misaligned 0.1° from ideal to induce realistic errors in the Lorentz factor. The illuminated crystal volume was made to vary in thickness from 120 to 200 μm as the crystal rotated, matching the scale factors of the real dataset. Global radiation damage was modeled as an exponential decay with resolution and dose, reaching half the undamaged spot intensity at 10 MGy/Å as described previously ¹⁵. Specific damage may be modeled by a similar dose-dependent conversion of the zero-dose set of pristine structure factors to those of a heavily damaged structure using radiation-induced non-isomorphism of 1% for every MGy of dose ⁵⁸. However, as the total dose to the sample in the real dataset was less than 40 kGy, the effect of radiation damage was negligible for the simulations reported here.

Background scattering from air, water and Paratone-N oil (Hampton Research, Aliso Viejo, CA, USA) was calibrated from constant-resolution pixel average of the diffraction pattern from reference materials of known thickness. Diffuse scatter from disorder in the crystal lattice and Compton scattering from the whole sample were modeled as described in Doc. S1. The sum of all these sources of background reproduced the background level in the reference experiment very well (Fig.1). It should be noted that, by definition, diffuse scatter is ‘flat’ underneath the Bragg peaks, as the act of integrating a background-subtracted spot in reciprocal space is mathematically equivalent to averaging the electron density over a patch of unit cells equal to the reciprocal dimension of the spot size. This is usually a few hundred nanometers, so deviations from the cell repeat must be correlated for many dozens of unit cells in a row for it to contribute more to the integration area than it does outside of it.

Spot shapes were represented as the sum of a collection of Gaussian peaks. Each spot-broadening parameter (beam divergence, spectral dispersion and mosaic spread) was evaluated individually. If sweeping any one of these over its entire range moved a spot by more than two pixels, then the parameter was split into sub-beams or sub-crystals. A separate parameter splitting was performed for every spot. For example, if the beam divergence was wide enough to spread a spot over six pixels, then the beam was divided into three sub-beams, each with one-third of the divergence of the overall beam, but with slightly different directions.

The width of the rocking curve due to each effect was evaluated using the Greenhough–Helliwell equation ⁵⁹, and the effect was split again if it broadened the spot by more than 1°. Each diffraction spot produced by each sub-beam from each sub-crystal was then treated separately when computing spot width, height and tilt on the detector face by partial numerical differentiation of spot position with respect to divergence, dispersion and mosaic rotation about the beam. These widths were then convoluted together to form a single 2D anisotropic Gaussian peak on the detector surface. This shape was then convoluted with the Gaussian series expansion of the point spread function ⁵⁷. The partiality of each sub-spot was computed by applying the rocking width given by the Greenhough–Helliwell equation to the rocking curve of a disk-shaped reciprocal lattice point passing through the Ewald sphere described by Winkler et al. ⁶⁰. MLFSOM also supports Gaussian, Lorentzian, arctan, ‘top hat’ or square rocking curve functions, but the disk function was empirically found to best match the spot shapes of the real data.

Current limitations of MLFSOM

Every effort was made to include all effects postulated to have a significant impact on data quality into the MLFSOM simulation, but the ‘realism’ is by no means perfect. For example, the crystal size was described by a single length parameter, as was the X-ray beam, and both are considered to be square. There is no allowance for non-uniform radiation damage as the crystal rotates ⁶¹. Beam shape and mosaic spread are both presumed to have simple ‘top hat’ shapes with no internal structure. Photon counts have a Poisson distribution, but all other sources of error such as beam flicker, shutter jitter and readout noise were taken from a normal distribution. The spatial, flood and dark corrections normally used with CCD detectors ⁶² are not currently implemented explicitly, nor is electron-counting noise as this becomes significant only for very long exposures.

Processing real and simulated lysozyme data

For both real and simulated lysozyme data, the images were reduced to mtz format reflection files using either MOSFLM ¹⁸, SCALA and TRUNCATE ²⁶ or XDS, XSCALE and XDSCONV ²⁰ as pipelines. In both cases, a 5% R_free set was assigned, and the same R_free flags were used for the real and simulated data. For side-by-side comparisons, both the real and simulated data were input to phenix.autosol as SAD datasets. Statistics are shown in Table 1.

Build-back routine

For the rebuilding test shown in Fig.3, a model of lysozyme was generated to include only a single conformer for every atom, with all occupancies set to 1.0. This model was refined to convergence against the real data using REFMAC with the X-ray weight turned down, so that the resulting model had excellent geometry. A new value of F_start was calculated from this coordinate model and the best-fit bulk solvent mask from the last cycle of REFMAC. This F_start value was used to simulate a new set of images with the same camera and noise parameters described above, and processed back to F_sim using XDS.

The F⁺ and F⁻ data from processing the real, multi-conformer simulated and single-conformer simulated images were input to phenix.autosol and phenix.autobuild, together with the sequence of lysozyme and instructions to find two Gd sites. The final R_cryst/R_free values of these runs are shown in Table 2. The water molecules, side chains and ligands from these models were then removed, and the remaining protein main chain was refined to convergence against F_obs or F_sim (no anomalous) using up to 500 cycles in REFMAC. Then dummy atoms (DUM in REFMAC) were added to the highest five peaks in the F_obs − F_calc or F_sim − F_calc difference map. To simulate ideal chemical intuition on each building cycle, each peak found to be within 0.5 Å of an atom in the ‘right answer’ model was assigned the proper atom name, but the xyz coordinates remained those of the initial picked peak. Each newly added atom was assigned the median B factor of the current model. After each build cycle, another 500 cycles of refinement were performed, and again dummy atoms were added at the top five positive difference peak positions. For each build cycle, if the largest difference peak was negative, any atom found within 0.5 Å of that negative peak was eliminated. Atoms with B factors that increased to more than ten times the median absolute deviation from the median B factor were also discarded. The R_cryst/R_free history of this building and refinement procedure is shown in Fig.3. Exactly the same procedure was applied to the real data, and the results are also shown in Fig.3.

The images for all datasets are available from http://bl831.als.lbl.gov/example_data_sets/mlfsom/. Coordinates and structure factors for the real data have been deposited in the Protein Data Bank under accession number 4tws.

Glossary

ADU

analog-to-digital unit, or integer pixel increment

ALS

advanced light source at Lawrence Berkeley National Laboratory

CC_1/2

Karplus-Diederichs internal correlation between half-datasets

CC

correlation coefficient

CCD

charge coupled device

MCS

multi-conformer simulated

MD

molecular dynamics

MX

macromolecular crystallography

PDB

Protein Data Bank

RMSD

root-mean-square deviation

RMS

root-mean-square

SAD

single-wavelength anomalous diffraction

SCS

single-conformer simulated

S-SAD

sulfur SAD

Author contributions

J.H. conceived of MLFSOM, wrote the program and performed the experiments. K.F. worked on mathematical testing and verification. S.C. developed and tested the program and analyzed the data. J.T. contributed funding and ideas. All authors wrote the paper.

Supporting Information

Additional supporting information may be found in the online version of this article at the publisher's website:

Doc S1

Supplementary methods.