Benchmarking of dynamic simulation predictions in two software platforms using an upper limb musculoskeletal model

Abstract

Several opensource or commercially available software platforms are widely used to develop dynamic simulations of movement. While computational approaches are conceptually similar across platforms, technical differences in implementation may influence output. We present a new upper limb dynamic model as a tool to evaluate potential differences in predictive behavior between platforms. We evaluated to what extent differences in technical implementations in popular simulation software environments result in differences in kinematic predictions for single and multijoint movements using EMG- and optimization-based approaches for deriving control signals. We illustrate the benchmarking comparison using SIMM-Dynamics Pipeline-SD/Fast and OpenSim platforms. The most substantial divergence results from differences in muscle model and actuator paths. This model is a valuable resource and is available for download by other researchers. The model, data, and simulation results presented here can be used by future researchers to benchmark other software platforms and software upgrades for these two platforms.

1. Introduction

Computational musculoskeletal simulations are widely used to evaluate the roles of muscles during movement and to investigate the effects of changes to the musculoskeletal system or neural control associated with age, gender, injury, disease, or clinical interventions. Because of the complex and multijoint arrangements of many muscles, and the often large numbers of muscles coordinated during a movement, it can be difficult or impossible to assess the roles of individual muscles experimentally (Zajac & Gordon 1989). By integrating anatomical information about the size and arrangement of muscles and segments in a system with information about the pattern of activation of muscles during movement, computational simulation studies enable scientists to interrogate the database of quantitative anatomy embodied in biomechanical models to identify contributions of individual muscles to a movement of interest.

Because several approaches and software platforms have emerged for the biomechanical simulation of movement, there is a critical need to establish robustness and repeatability of conclusions derived from a simulation approach across platforms. Specifically, dynamic simulations of movement have been developed and implemented in several software platforms, including SIMM-Dynamics Pipeline-SD/Fast (Delp et al. 1990, Piazza & Delp 1996), OpenSim (Delp et al. 2007), MSMS (Davoodi & Loeb 2011), and Anybody (AnybodyTechnology, Aalborg, Denmark) (Damsgaard et al. 2006), among others. Computational approaches to deriving inputs and calculating the dynamic behavior of a musculoskeletal system are conceptually similar across platforms, and include common modeling and simulation components such as descriptions of joint kinematics and range of motion, damping, passive and active force generators, dynamics engines to solve the equations of motion, and numerical integrators. Despite the conceptual similarities, technical differences in the implementation of computational algorithms can influence simulation output (Wagner et al. 2013). In addition, direct replication of published simulation results remains a challenge for our community for a number of reasons. First, replicating the simulation work of others may require access to both the specific model that was implemented and the software platform that was used. This can be difficult, as some models and platforms are not publicly available, and instead are proprietary to the investigating research group. Next, even when models and platforms are available, there is often a financial expense associated with acquiring multiple different platforms. While transferring published models and control signal inputs from one platform to another may eliminate this financial burden, it also incurs the technical expense of gaining the expertise needed to run complex simulations in multiple systems (Wagner et al. 2013).

Given these issues, which have until recently precluded replication of results across different platforms, the development of benchmarking simulations to evaluate existing and new implementations of computational platforms and simulation predictions would be a valuable resource for the field. A practical benchmarking application should evaluate the most common simulation approaches, specifically the two most common approaches to identifying muscle activation inputs for dynamic simulation: 1) measuring EMG signals experimentally (Buchanan et al. 2004, Lloyd & Besier 2003, Manal et al. 2002, Shao et al. 2009, Winby et al. 2009) or 2) estimating simulation inputs computationally, based on optimal control strategies (Thelen & Anderson 2006, Thelen et al. 2003, Zajac et al. 2003). A benchmarking application for comparison of simulation results across platforms should evaluate both types of approaches for deriving inputs because excitations derived from optimization approaches inherently depend on the dynamic system that is being controlled, while experimentally-derived control signals are independent of the computational platform and model.

The goal of this work was to evaluate to what extent differences in technical implementations result in differences in kinematic predictions for single joint and multijoint movements using EMG- and optimization-based approaches for deriving the control signals. We specifically illustrate the benchmarking comparison using the SIMM-Dynamics Pipeline-SD/Fast and OpenSim platforms, which are the most widely used platforms in the clinical and basic science musculoskeletal modeling community, and have parallel structures for model description and simulation implementation. We present a new dynamic model of the upper limb, described here and implemented in both platforms, as a tool to evaluate the potential differences in predictive behavior between the platforms. We propose that this model can be used by future researchers to benchmark other software platforms, as well as software upgrades for these two platforms, against the simulation results presented here. Control inputs, simulation results, and the model itself will be publically available via simtk.org (https://simtk.org/home/upexdyn/).

2. Methods

We evaluated the differences in simulation outputs between two conceptually similar software platforms for musculoskeletal simulation for two common types of muscle activation inputs: EMG-derived and optimization-derived. First, we describe the methods by which we developed a new dynamic model of the shoulder, elbow, forearm, and wrist to be used in this study as a standard tool to investigate the implications of differences in computational implementation. Next, we implemented this model for simulation in both the SIMM-Dynamics Pipeline-SD/Fast (hereafter referred to as SIMM-SD/Fast; SIMM version 4.2.1, Dynamics Pipeline, version 3.3, Musculographics Inc., Santa Rosa, CA; SD/Fast version B.2.8, PTC, Needham, MA) and OpenSim (version 2.4, Stanford University, Stanford, CA) environments. We then describe simulations of isolated wrist, elbow, and shoulder movements and a multijoint reach using several approaches to evaluate the influence of specific known differences between platforms. In all simulations, identical control sets were used to drive the complementary forward simulations in both platforms to evaluate the effect of the computations themselves under various conditions.

2.1. Dynamic model development

The new dynamic model was designed to represent the anthropometry and muscle force-generating characteristics of a 50^th percentile adult male and was implemented in both software platforms. Given technical differences between the platforms, small modifications to a few parameters were required to enable dynamic simulation in both environments; detailed explanations are provided below.

2.1.1. Joint descriptions

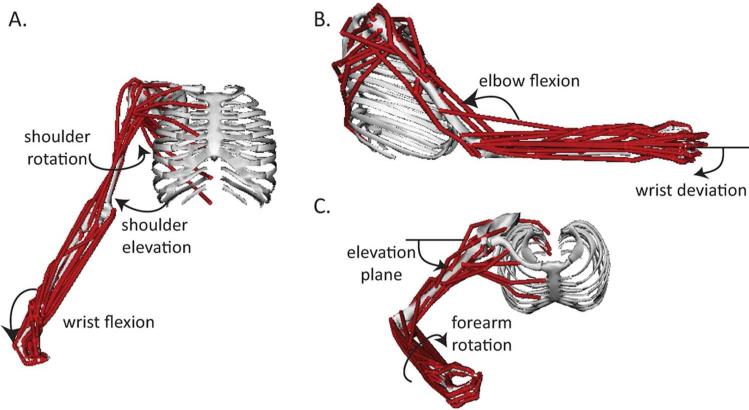
The kinematic foundation (Holzbaur et al. 2005) for the dynamic model included 15 degrees of freedom at the glenohumeral joint (including movement of the clavicle and scapula (de Groot & Brand 2001)), elbow, forearm, wrist, thumb and index finger, with conventions as recommended by the International Society of Biomechanics (Wu et al. 2005). For these dynamic simulations, we reduced the degrees of freedom to 7 in both platforms; 8 degrees of freedom were eliminated by positioning the hand in a grip posture and fixing the degrees of freedom at the index finger and thumb (Fig. 1).

Figure 1.

Musculoskeletal model of the upper limb. Musculoskeletal model of the upper limb. The dynamic model incorporates 7 degrees of freedom, including A) shoulder rotation and elevation (thoracohumeral angle) and wrist flexion, B) wrist deviation and elbow flexion, and C) elevation plane of the shoulder and forearm rotation. 50 musculotendon actuators spanning these joints are also included.

Joint kinematics were defined identically in both platforms with the exception of wrist flexion. As indicated by experimental data (Ruby et al. 1988), wrist flexion in both models is distributed evenly across the proximal and distal rows of carpal bones. In OpenSim, the generalized coordinate wrist flexion directly specifies the rotation of both carpal rows, (e.g., 1° of wrist flexion specifies a 0.5° rotation about the proximal row and a 0.5° rotation about the distal row). In SIMM-SD/Fast, a coordinate transformation was needed because SD/Fast requires a 1:1 correspondence between the generalized coordinate and the imposed rotation. Thus, the generalized coordinate proximal flexion is used, where,

$$ProximalFlexion=0.5\ast \left(WristFlexion\right)$$ (1)

such that 1° of proximal flexion specifies a 1° rotation about the proximal row and a 1° rotation about the distal row, and is identical to 2° of wrist flexion. Despite the coordinate transformation, both platforms have equivalent wrist kinematics. Given (1), the magnitude of proximal flexion moment is equal to twice the magnitude of the corresponding wrist flexion moment. For consistency, we have transformed proximal flexion to wrist flexion for presentation of results throughout the study.

In this study, we added inertial parameter definitions for the segments in the model. Inertial properties were defined for the hand, radius, ulna, and humerus based on previously published descriptions for these segments (McConville et al. 1980, Reich & Daunicht 2000). The masses of the clavicle and scapula were each obtained from (Blana et al. 2008), as derived from (Clauser et al. 1969). We determined the mass center and inertia tensor for clavicle and scapula from the geometric properties of polygonal bone descriptions in the model, with the anthropometry of a 50^th percentile male (Gordon et al. 1989) (SolidWorks Professional, Dassault Systèmes SolidWorks Corp., Waltham, Massachusetts). Inertial properties were implemented identically in both platforms (Table 1).

Table 1.

Inertial parameters for each segment.¹

segment	mass (kg)	Center of mass (m)			Inertia (kg m2)
		Rx	Ry	Rz	Ixx	Ixy	Ixz	Iyy	Iyz	Izz
clavicle	0.15600	−0.011096	0.00637	0.05417	0.00024	−0.00002	−0.00007	0.00026	0.00005	0.00004
scapula	0.70396	−0.054694	−0.03503	−0.04373	0.00124	0.00045	0.00041	0.00115	0.00024	0.00137
humerus	1.99757	0.01806	−0.14014	−0.01275	0.01228	−0.00035	−0.00023	0.00255	0.00123	0.01258
ulna	1.10530	0.00972	−0.09595	0.02429	0.00541	0.00032	−0.00008	0.00115	0.00109	0.00494
radius	0.23359	0.03363	−0.18156	0.01560	0.00044	0.00003	0.00000	0.00009	0.00006	0.00040
proximal _ row	0.00010	0.00000	0.00000	0.00000	0.00001	0.00000	0.00000	0.00001	0.00000	0.00001
hand	0.58190	−0.00301	−0.04250	−0.00112	0.00011	0.00000	0.00000	0.00006	0.00001	0.00015

¹The origins for the segments are as previously defined, with xyz conventions for the segments in the neutral position aligned as follows: x: anterior, y: superior, z: lateral for the right arm (Holzbaur et al. 2005).

2.1.2. Joint restraints

Joint restraint functions are forces or torques applied to the generalized coordinates to enforce joint limits. In the current model, we implemented restraint torques based on elastic torques at the shoulder (Rankin et al. 2010), elbow (Rankin et al. 2010), and wrist (Velisar & Murray 2005) as previously described in the SIMM-SD/Fast environment, with a damping factor of 0.1 Nm*sec/radian (0.001745 Nm*sec/°), which is also consistent with previous work (Rankin et al. 2010).

In both environments, we used the platform-specific commands to define elastic and velocity-dependent (i.e., damping) joint restraint torques. Parameterization of the torques and damping differs in the two platforms. In SIMM-SD/Fast, (i) cubic splines relating the value of the generalized coordinate to the elastic torque are specified at each joint to limit the range of motion, (ii) joint damping is implemented throughout the range of motion, and (iii) damping is defined for all generalized coordinates in the model by a single constant (in Nm*sec/radian). In version 2.4, OpenSim provides a force set called CoordinateLimitForce (CLF) to restrain joint motion. CLF calculates the overall joint restraint torque applied at the joint of interest because of the elastic joint stiffness and damping based on the current value of the generalized coordinate and 6 parameters that define (i) the desired peak elastic stiffness (2 parameters define distinct peak stiffness in Nm/deg for the upper and lower bounds of the range of motion), (ii) the desired peak damping (in Nm*sec/deg), (iii) the values of the generalized coordinate at which the CLF function begins applying the elastic stiffness and damping (2 distinct values for each bound), and (iv) the range (in units of the generalized coordinate) over which the elastic stiffness and damping transition from zero to the desired peak. After reaching the desired peak, the elastic stiffness and damping are maintained at the peak value for any generalized coordinate beyond the bounded region. In OpenSim, the CLF parameters associated with the elastic joint stiffness were chosen mathematically to optimally fit the derivatives of the elastic joint restraint torque curves described previously (Rankin et al. 2010, Velisar & Murray 2005) (Table 2). Then, the joint torques associated with the OpenSim CLF joint stiffness curves were calculated. Cubic splines of the CLF torques were fit and defined in SIMM-SD/Fast, allowing us to apply restraint functions that were identical in both the platforms for benchmarking purposes. To apply constant damping to a joint throughout its range of motion in OpenSim, a second CLF was defined in OpenSim for each generalized coordinate (Table 2). Each of these CLFs has the lower bound set above the upper limit of the generalized coordinate and very small transition region (1 deg), so constant damping equivalent to 0.1 Nm*sec/radian (Rankin et al. 2010, Velisar & Murray 2005) is applied throughout the range of motion.

Table 2.

Coordinate limit force parameters for OpenSim.

Restraint torque CLF
Coordinate	upper limit (°)	upper stifness (Nm/°)	lower _limit (°)	lower _stiffness (Nm/°)	transition (°)	damping (Nm*sec/°)
shoulder elevation	150	100	30	100	542.8423	0
elevation plane	100	100	−60	100	545.4471	0
shoulder rotation	−10	100	−60	100	485.4660	0
elbow flexion	85	0.3037	14	100	139.5813	0
forearm rotation	60	50	−60	50	430.1186	0
wrist flexion	20	52.5961	−6	487.1760	39.1586	0
wrist deviation	60	200	−60	135.3232	92.9160	0
Damping CLF
Coordinate ^	upper _limit (°)	upper stifness (Nm/°)	lower _limit (°)	lower _stiffness (Nm/°)	transition (°)	damping (Nm*sec/°)
shoulder elevation	190	0.00000001	190	0.00000001	1	0.001745
elevation plane	190	0.00000001	190	0.00000001	1	0.001745
shoulder rotation	190	0.00000001	190	0.00000001	1	0.001745
elbow flexion	190	0.00000001	190	0.00000001	1	0.001745
forearm rotation	190	0.00000001	190	0.00000001	1	0.001745
wrist flexion	190	0.00000001	190	0.00000001	1	0.001745
wrist deviation	190	0.00000001	190	0.00000001	1	0.0004363

2.1.3. Muscle descriptions

Fifty Hill-type muscle-tendon actuators representing the 32 muscles and muscle compartments crossing the shoulder, elbow, forearm, and wrist were included. Force-generating characteristics (Table 3) were defined for each muscle-tendon actuator using the dynamic muscle model described by Schutte (1992) as implemented by the developers in each platform. The OpenSim version of this model calculates fiber velocity using the same equations as Dynamics Pipeline muscle model 4 (as implemented in calc_fiber_velocity() in gmc.c). We defined the user-specified damping for the muscle model as 0.017 N/m/s, the default value provided for this model in both platforms based on Schutte (1992). To maintain consistency with our kinematic upper limb model, the normalized isometric force-length curve for active muscle force and the normalized force-strain curve for tendon were set to the default normalized curves defined by SIMM (Delp et al. 1990). Similarly, for consistency with previous work, the normalized force-length relationship for passive muscle was altered in both platforms such that passive force in a muscle-tendon actuator is produced when the muscle is stretched past 1.15 times the optimal fiber length (Gonzalez et al. 1997).

Table 3.

Muscle architectural parameters.

Muscle	Abbreviation	Optimal fiber lengtha (cm)	Peak forceb (N)	Tendon slack length (cm) OpenSimc	Tendon slack length (cm) SIMMc	Pennation angle (°)a,f
Shoulder
Deltoid
Anteriore	DELT1	9.8	1218.9	9.7	9.3	22
Middle	DELT2	10.8	1103.5	11.0	11.0	15
Posterior	DELT3	13.7	201.6	3.8	3.8	18
Supraspinatus	SUPRA	6.8	499.2	4.0	4.0	7
Infraspinatus	INFRA	7.6	1075.8	3.1	3.1	19
Subscapularis	SUBSCAP	8.7	1306.9	3.3	3.3	20
Teres minor	TMIN	7.4	269.5	7.1	7.1	24
Teres major	TMAJ	16.2	144.0	2.0	2.0	16
Pectoralis major
Clavicular	PMAJ1	14.4	444.3	0.3	0.3	17
Sternal	PMAJ2	13.8	658.3	8.9	8.9	26
Ribs	PMAJ3	13.8	498.1	13.2	13.2	25
Latissimus dorsi
Thoracic	LAT1	25.4	290.5	12.0	12.0	25
Lumbar	LAT2	23.2	317.5	17.7	17.7	19
Iliac	LAT3	27.9	189.0	14.0	14.0	21
Coracobrachialis	CORB	9.3	208.2	9.7	9.7	27
Elbow
Triceps
Long	TRIlong	13.4	771.8	14.3	14.3	12
Lateral	TRIlat	11.4	717.5	9.8	9.8	9
Medial	TRImed	11.4	717.5	9.1	9.1	9
Anconeus	ANC	2.7	283.2	1.8	1.8	0
Supinator	SUP	3.3	379.6	2.8	2.8	0
Bicepse
Long	BIClong	11.6	525.1	27.8	27.2	0
Short	BICshort	13.2	316.8	20.0	19.2	0
Brachialis	BRA	8.6	1177.4	5.4	5.4	0
Brachioradialis	BRD	17.3	276.0	13.3	13.3	0
Major wrist or forearm
Extensor carpi radialis longus	ECRL	8.1	337.3	24.4	24.4	0
Extensor carpi radialis brevis	ECRB	5.9	252.5	22.2	22.2	9
Extensor carpi ulnaris	ECU	6.2	192.9	22.9	22.9	4
Flexor carpi radialis	FCR	6.3	407.9	24.4	24.4	3
Flexor carpi ulnaris	FCU	5.1	479.8	26.5	26.5	12
Palmaris longus	PL	6.4	101.0	26.9	26.9	4
Pronator terese	PT	4.9	557.2	9.9	9.8	10
Pronator quadratus	PQ	2.8	284.7	0.5	0.5	10
Wrist/hand muscles
Flexor digitorum superficialis
Digit 5	FDSL	5.2	75.3	33.9	33.9	5
Digit 4	FDSR	7.4	171.2	32.8	32.8	4
Digit 3	FDSM	7.5	258.8	29.5	29.5	7
Digit 2	FDSI	8.4	162.5	27.5	27.5	6
Flexor digitorum profundus e
Digit 5	FDPL	7.5	236.8	28.2	28.2	8
Digit 4	FDPR	8.0	172.9	29.2	29.2	7
Digit 3	FDPM	8.4	212.4	30.3	30.3	6
Digit 2	FDPI	7.5	197.3	30.2	30.2	7
Extensor digitorum communise
Digit 5	EDCL	6.5	39.4	33.5	33.5	2
Digit 4	EDCR	6.3	109.2	36.5	36.5	3
Digit 3	EDCM	7.2	94.4	36.5	36.5	3
Digit 2	EDCI	7.0	48.8	36.5	36.5	3
Extensor digiti minimie	EDM	6.8	72.4	33.5	33.5	3
Extensor indicis propiuse	EIP	5.9	47.3	21.0	21.0	6
Extensor pollicis longuse	EPL	5.4	88.3	23.1	23.1	6
Extensor pollicis brevise	EPB	6.8	46.0	11.6	11.6	7
Flexor pollicis longuse	FPL	5.5	201.0	19.7	19.7	7
Abductor pollicis longuse	APL	7.1	116.7	13.0	13.0	8

^aFiber lengths and pennation angles were defined from experimental literature as described in Holzbaur et al. (2005) and were equivalent between the software platforms.

^bPeak forces reflect measured muscle volumes (Holzbaur et al. 2007b) and isometric strength (Holzbaur et al. 2007a) from 5 adult males as described in the Methods, and were equivalent between the software platforms.

^cTendon slack lengths were as defined in Holzbaur et al. ( 2005) and equivalent between software platforms, except as noted. ^dTendon slack lengths accommodate grip hand posture as described in the Methods, and equivalent between software platforms.

^eTendon slack lengths altered in OpenSim to preserve operating range as described in the Methods.

^fPennation angles expressed in radians in OpenSim.

The parameters we explicitly defined to scale the normalized model to represent individual muscle-tendon actuators included optimal fiber length, peak isometric force, pennation angle, and tendon slack length (Zajac 1989). Parameter values for peak muscle forces, optimal fiber lengths, and pennation angles were identical between the two platforms. Optimal fiber lengths and pennation angles were as described by Holzbaur et al. (Holzbaur et al. 2005). However, we implemented new parameters for peak isometric force, determined from published muscle volume and isometric joint strength data described for these muscles and joints in healthy young adults (Holzbaur, Delp, et al. 2007, Holzbaur, Murray, et al. 2007). The peak isometric muscle forces were determined by calculating the best fit for specific tension (50.8 N/cm²) required to transform the volumes for the same 32 muscles in 5 healthy young males (Holzbaur, Murray, et al. 2007) into joint moments measured at the shoulder, elbow, and wrist in the same 5 individuals (Holzbaur, Delp, et al. 2007), using optimal fiber lengths, moment arms in the experimental joint postures, and muscle lengths in the experimental joint postures.

Muscle pathways were defined by static points, moving points, and three dimensional surfaces representing the origin and insertion points of the muscle and its anatomical path, including constraints from underlying bones and muscles. As previously described (Holzbaur et al. 2005), these paths were defined such that the moment arms estimated using the partial velocity method implemented in SIMM (Delp et al. 1990) replicate experimentally measured moment arms for each joint that a muscle crosses. Two conditions required the paths and/or tendon slack lengths of a subset of muscles to be altered relative to the values reported in the kinematic model. First, we re-oriented the hand segments to replicate a grip posture. As a result, the paths of 14 extrinsic finger muscles were adjusted in order to prevent muscles from penetrating the finger bones in this new posture; tendon slack lengths were adjusted correspondingly to preserve each muscle's operating range at the proximal joints it crosses and to account for the influence of finger posture on wrist joint passive properties (Table 3). The paths and tendon slack lengths for these 14 muscles were implemented identically in both platforms. Second, SIMM and OpenSim handle moving muscle points differently, which causes differences in moment arm calculations for 12 muscles (3 heads of PEC, 3 heads of LAT, DELT2, BIC long and short heads, PT, FPL and APL) (Sherman et al. 2013). In addition, OpenSim does not enable moving points defined to exist only within a specified range of motion; BIC had a single point of this type in the original model. Because of these technical differences between platforms, it was not possible to implement the muscle-tendon paths defined in (Holzbaur et al. 2005) in OpenSim for these 12 muscles. To minimize the differences between the SIMM implementation of these 12 muscle-tendon paths (identical to Holzbaur (2005)) and the OpenSim implementation, adjustments were made in OpenSim only, using experimental muscle moment arms as a guide. For 8 of the 12 affected muscles, the changes to muscle-tendon pathways were minimal and were the only adjustments needed. For the remaining 4 muscles, the changes in muscle-tendon path implemented in OpenSim influenced muscle-tendon length enough to warrant also adjusting tendon slack lengths to preserve the operating ranges of the muscle fibers (Table 3). Overall, the muscle-tendon paths adjusted in OpenSim predicted moment arms that fell within the variability in experimental measurements of muscle moment arms. However, the resulting moment arms and muscle-tendon lengths for these 12 muscles are not identical to those predicted by the implementation in SIMM.

2.2. EMG-driven forward dynamic simulations

To evaluate the difference in simulation output between two different platforms when using experimentally-derived control signals that are independent of the computational platform, we performed a series of EMG-driven forward dynamic simulations. To derive the control signals for this comparison, a single male subject (1.8 m, 79.4 kg) performed 5 trials each of isolated wrist flexion, elbow flexion, and shoulder abduction movements. The subject's anthropometry was similar to the nominal height and weight (1.77m, 75kg) defining the model inertial properties. The experimental protocol was approved by the Wake Forest School of Medicine Institutional Review Board in accordance with the ethical standards of the Helsinki Declaration of 1975, as revised in 2000. EMG was obtained simultaneously from muscles crossing the shoulder (deltoid, pectoralis major, latissimus dorsi), elbow (biceps brachii, brachioradialis, lateral head of the triceps brachii), and wrist (extensor carpi radialis, extensor carpi ulnaris, flexor carpi radialis, flexor carpi ulnaris) using 1 cm surface electrodes (Biopac Systems Inc., Goleta, CA). The measured EMG recordings were filtered with 39^th order Hamming-window linear phase high pass filter (0.2Hz cutoff frequency), rectified, and normalized to the recorded maximum voluntary contraction (MVC) for each muscle. Processed EMG data for muscles with primary action at the joint of interest (as categorized above) were applied as excitations in the model to the muscle from which the signal was recorded and to an appropriate set of synergistic muscles (Table 4), defining the control signals necessary to drive the forward dynamic simulations. For each simulation, excitations for all other muscles were defined to be zero and all joints except for the joint of interest were locked. Separate simulations for each of the 5 recorded trials were performed in OpenSim, and compared to the motion of the joint of interest recorded during EMG data collection. For each joint, a single simulation with the smallest RMS error relative to the measured motion at the joint of interest was selected, and the simulation was replicated in the SIMM-SD/Fast platforms. The simulated single-joint motions were compared between platforms; all simulations were run using the default parameters in each platform.

Table 4.

Summary of control inputs for EMG-driven forward dynamic simulations

Simulation	Muscles with non- zero control inputs	Muscle from which control input was experimentally derived
Shoulder abduction
	DELT2	Deltoid
	PMAJ1	Pectoralis Major
	PMAJ2	Pectoralis Major
	LAT1	Latissimus Dorsi
	LAT2	Latissimus Dorsi
Elbow flexion
	BIClong	Biceps brachii
	BICshort	Biceps brachii
	BRA	Brachialis
	BRD	Brachioradialis
	TRIlong	Long head of triceps brachii
	TRIlat	Lateral head of triceps brachii
	TRImed	Medial head of triceps brachii
Wrist flexion
	ECRL	Extensor carpi radialis
	ECRB	Extensor carpi radialis
	ECU	Extensor carpi ulnaris
	FCR	Flexor carpi radialis
	FCU	Flexor carpi ulnaris

2.3. CMC-driven forward reach

To evaluate the influence of the choice of platform on simulation output when controls are derived from an optimization approach, we performed a CMC analysis of a multijoint forward reach using the OpenSim environment, and used the resulting controls to drive a forward dynamic analysis in both software platforms. The CMC-driven simulation approach has been described in detail previously (Thelen & Anderson 2006, Thelen et al. 2003). In our implementation, the same male subject as above performed five trials of a forward reaching movement with the dominant (right) arm. The reaching movement performed by the subject began with the shoulder near neutral abduction, the elbow flexed 90°-100°, a neutral forearm, and the wrist braced in neutral. The arm was extended forward in the sagittal plane until the elbow was flexed approximately 10°; the participant then returned to the starting position. For comparison across trials, the start of the motion was defined as 0.1 seconds before the movement began, 50% of the motion when the elbow was in its most extended position, and 100% when the arm reached its initial posture or 0.1 seconds after the arm stopped moving. The OpenSim inverse kinematics tool was used to identify the joint postures used by the subject during the reach from the recorded marker locations.

The OpenSim CMC tool was used to calculate the set of muscle excitations that permitted the upper limb model to most accurately replicate the reaching kinematics. These excitations defined the control inputs that would drive a forward dynamic simulation of the forward reach. Wrist degrees of freedom were fixed to reflect the braced experimental conditions and the torso was fixed at 10° relative to gravity to account for the position of the experimental subject's torso. Five forward dynamic simulations of forward reach were developed in OpenSim using the specific CMC-derived control inputs for each of the 5 reaching trials. A single simulation with smallest RMS error relative to the measured reaching motion was selected, and the simulation was replicated in the SIMM-SD/Fast platform.

2.4. Gravity-driven simulations

To examine and compare the effects of non-muscular dynamic components including joint restraint functions and damping on simulation results, we performed a series of gravity-driven forward dynamic simulations of isolated wrist flexion, elbow extension, and shoulder adduction in both SIMM-SD/Fast and OpenSim with all muscles removed. In SIMM, any reference frames and joints used to define moving muscle points that were not associated with limb kinematics were also removed. For each simulation, all joints except for the joint of interest were locked to isolate the effects of the prescribed joint limits and damping coefficients at the individual joint. To isolate the effects of different implementations of muscle model and muscle-tendon pathways on actuator output, we repeated the gravity-driven simulations described above with the addition of the 50 passive muscle-tendon actuators.

All gravity- and EMG-driven simulations in OpenSim and in SIMM/SD-Fast were performed on a 2.66 GHz Intel Core i7 with 12.00 GB of RAM. The CMC-driven simulations were performed on a 2.10 GHz Intel Core i7 with 16.00 GB of RAM.

3. Results

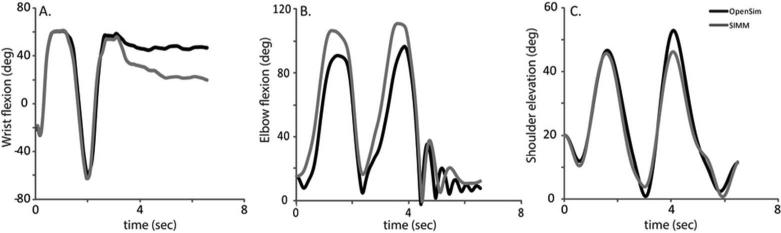
EMG-driven forward dynamic simulations indicate that our dynamic model of the upper limb predicts similar, although not identical, kinematic motion for single joint movements when the same EMG data are used in two popular modeling platforms (Fig. 2). When surface EMG data from the major wrist flexors and extensors served as inputs, the simulated wrist kinematics resulting from SIMM-SD/Fast and OpenSim were comparable (c.f., Fig. 2A; RMSE=15.8°). Similar results were observed at the elbow (Fig. 2B; RMSE=14.8°) and shoulder (Fig. 2C; RMSE=3.1°). The largest differences between software platforms occurred around the second elbow flexion peak (max difference=30.7°) and at the end of the wrist movement, when muscles were minimally active (c.f., Fig. 2A, shaded region; max difference=27.2°; RMSE=7.4° when active vs. 22.7° when resting).

Figure 2.

Joint kinematics for a single trial of EMG-driven forward dynamic simulation at the A) wrist, B) elbow, and C) shoulder. Trials were selected as the trial with minimum RMSE between the simulation and experimental kinematics. OpenSim (black) simulations match well with simulations in the SIMM-SD/Fast (dark grey) platform.

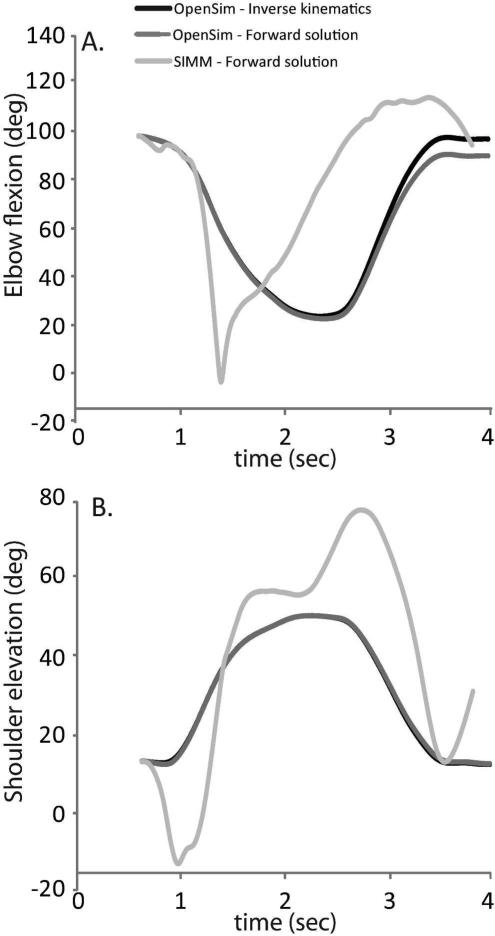
When the optimal control signals derived for a single trial using the CMC algorithm in OpenSim were used to drive forward simulations in both OpenSim and SIMM-SD/Fast, errors between the kinematic motions predicted in the two systems were also observed (Fig. 3). The RMS error for shoulder elevation and elbow flexion were 19.2° and 36.74°, respectively. In particular, within SIMM-SD/Fast the kinematics spanned a larger range of motion for the same controls.

Figure 3.

Forward dynamic simulation kinematics driven using CMC-derived controls in OpenSim (dark grey) and SIMM-SD/Fast (light grey) compared to CMC-derived joint kinematics as calculated in OpenSim (black). The movement began at 0.63 sec in this trial as defined in the text, and was simulated from this point. The CMC-driven forward dynamic simulation in OpenSim tracks the CMC kinematics closely (thus the curves overlay in this figure), while the same controls in SIMM-SD/Fast result in a movement that is substantially altered from the desired kinematics, due to the different mechanical properties of the underlying model implementation.

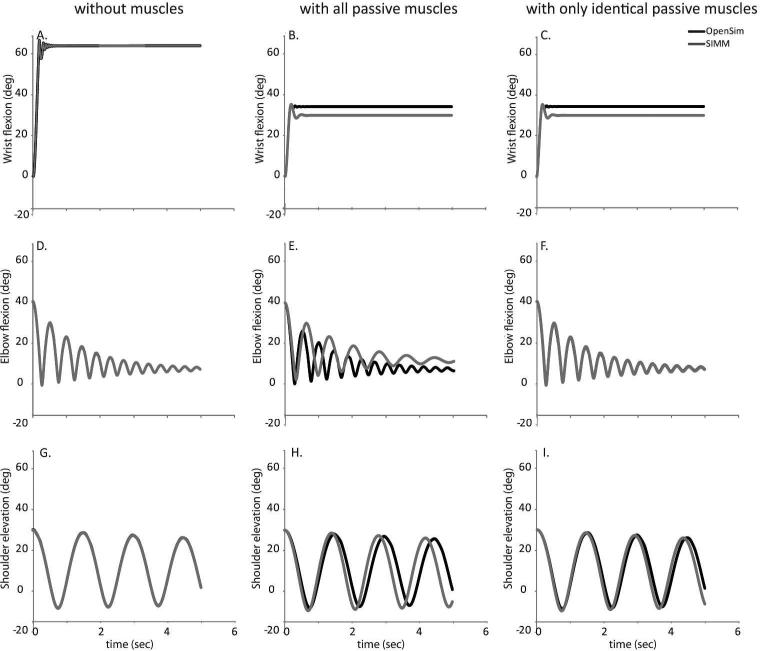
Results from the gravity-driven simulations highlighted differences in the technical implementation of muscle model across platforms as a critical feature that influenced the simulated kinematics. In the absence of muscle forces, the gravity-driven simulations of the wrist (RMSE=0.07°), elbow (RMSE=0.14°), and shoulder (RMSE=0.18°) were virtually identical between platforms (Fig. 4A,D,G). When the gravity-driven simulations include passive muscle forces, differences can be seen between the platforms at all three joints (Fig. 4B,E,H). To distinguish whether these differences were due to the subset of muscles that had different tendon slack lengths or modeled muscle-tendon paths across the platforms, we removed only these muscles and repeated the simulations. When the models with only identical muscles were considered, differences in kinematics were reduced at the elbow and shoulder (Fig. 4F,I), suggesting differences in muscle paths crossing the shoulder and elbow do subtly influence the passive mechanics of the limb for these joints. There was no improvement at the wrist (Fig. 4C); the altered muscles (APL and FPL) did not generate passive force in the simulated movement, suggesting the implementation of the dynamic muscle model may be the primary influence.

Figure 4.

Gravity-driven forward dynamic simulation without muscles (left column), with passive muscles (center column), and with a subset of muscles implemented identically between platforms (right column) at the A-C) wrist, D-F) elbow, and G-I) shoulder. OpenSim (black) simulations and SIMM-SD/Fast (dark grey) simulations perform nearly identically when muscles are absent and only kinematics, inertial properties, damping, and joint restraint torques are present. At the elbow and wrist, average postures toward the end of the simulations differ between the simulations in the presence of all muscles. At the elbow and shoulder, when muscle actuators are eliminated that were not able to be implemented identically, differences between platforms are reduced.

The combined effects of the muscle path and model implementations led to differences in the resting postures of the wrist (Fig. 4B) and the elbow (Fig. 4E) when all passive muscles were included. The final posture estimated using SIMM-SD/FAST was 4.3° more extended than in OpenSim (cf., Fig. 4B, C). For the elbow, the average postures for the final 1 second of simulation when all passive muscle forces were included differed between platforms (cf. Fig. 4E; OpenSim: 7.5°, SIMM-SD/FAST: 11.7°). In contrast, average postures for the final 1 second of simulation at the shoulder were similar between platforms when all muscles were included (cf. Fig. 4H OpenSim: 14.6°, SIMM-SD/FAST: 11.3°). Compared to the wrist, the oscillations observed in the gravity-driven simulations were pronounced and long-lasting at the elbow and shoulder in both platforms, whether passive muscle forces were excluded (Fig. 4, left column) or included (Fig. 4, center and right columns).

All simulations took substantially longer (an order of magnitude) to complete in SIMM-SD/Fast than in OpenSim (Table 5). The time to complete the CMC simulations averaged 4.4h (1.3 h/s of simulation).

Table 5.

Sample computation times for the simulations.

Simulation type	OpenSim (hr:min:sec)	SIMM-SD/Fast (hr:min:sec)
EMG Driven
wrist	0:03:46	2:11:11
elbow	0:09:06	2:55:30
shoulder	0:43:00	20:37:34
Gravity-driven without muscles
wrist	0:00:04	0:03:11
elbow	0:00:06	0:03:11
shoulder	0:00:04	0:04:56
Gravity-driven with muscles
wrist	0:00:43	0:50:54
elbow	0:01:36	2:02:07
shoulder	0:01:23	2:02:30
CMC in OpenSim	Average Time1 (hr:min:sec)	Average Time/simulation (hr:min:sec/sec)
2.1 GHz Intel i7 with 16.00 GB of RAM	4:24:00	1:18:36

¹Average time refers to the average simulation time over the 5 CMC trials.

4. Discussion

This work benchmarks kinematic predictions for single joint and multijoint upper limb movements when using EMG- and optimization-based approaches for deriving the control signals. The insights that can be inferred from simulation predictions are dependent on our understanding of which features of a prediction derive from the dynamic system and which derive from the platform implementation. Further, as computational simulation becomes accessible to the wider biomechanics and clinical communities, including those who are not computer developers and may not be familiar with the technical implications of the various software platforms, benchmarking is particularly valuable. Such methodology enables new users to confirm that simulations are performing as expected and can also convey the impact of different technical implementations on simulation results, including documentation of the impact of software upgrades or user-defined model adaptations (e.g., choosing a different muscle model, or simplifying a muscle-tendon path) within a single platform.

Our simulation results demonstrate that technical differences between the SIMM-SD/Fast and OpenSim platforms do influence simulation outcomes. The most substantial divergence in simulation results arose from different implementations of muscle paths and force-generation in the two software platforms, whether the simulations were driven by gravity, EMG signals, or optimization-based controls. This study has general and important implications for any musculoskeletal simulations performed in any platform, and suggests the importance of critical evaluation of muscle model perfomance (e.g., Millard et al. 2013), as well as further attention to descriptions of the muscle model implemented in different simulations and environments.

This study also makes available a new dynamic model of the upper limb, implemented in two computational platforms. There have been a number of excellent kinematic and dynamic applications (Buchanan et al. 1998, Chadwick et al. 2009, Davoodi & Loeb 2011, Garner & Pandy 2001, Lemay & Crago 1996, Manal et al. 2002, Rankin et al. 2010, Rankin et al. 2011, van der Helm 1994) of modeling and simulation of upper limb movement; however, none have been explicitly cross-checked across software platforms. The model we describe here differs from a previous kinematic model from our group (Holzbaur et al. 2005) in a number of important ways. First, the dynamic model incorporates inertial properties for the relevant segments, including new descriptions of scapula and clavicle inertia derived from the polygonal surface descriptions of these bones. Also, the parameters describing the peak forces for each of the 50 muscles now reflect data describing both muscle volume and moment-generating capacity from 5 healthy young adult male subjects (Holzbaur, Delp, et al. 2007, Holzbaur, Murray, et al. 2007). The hand has been reoriented into a grip posture and the tendon slack lengths updated to preserve the operating ranges of muscles crossing the wrist. Finally, this model has been newly implemented in OpenSim and its kinematic and dynamic behavior verified for consistency between the SIMM/SDFast and OpenSim platforms, including, where necessary, making the appropriate alterations to moving muscle points and tendon slack length as described in the methods. The implementations of the dynamic upper limb model in both platforms, along with the input controls and simulation results, are available for download.

As discussed by Wagner and colleagues (Wagner et al. 2013), the ability to derive consistent results from generic musculoskeletal models implemented by different researchers in different platforms is a critical need for the advancement of our field. Across new platforms, we expect that the benchmarking simulations provided here will help future users evaluate the consistency of their results in the context of our original implementation of the model. To this end, the simulations we provide span a hierarchy of model parameters and were designed to enable the identification of parameters that contribute to differing output. Understanding such differences across software packages enables opportunities for further technical advancement, scientific discussion, and validation of the features of simulation software that are limiting repeatability across platforms. In addition, it can help an individual researcher more carefully interpret their simulation results, ultimately improving the conclusions derived from simulation studies.

Generic biomechanical models are frequently adapted from their published form when applied to investigate specific research problems. For example, several studies (e.g., Crouch et al. 2011, Crouch et al. 2013, Hu et al. 2011, Mogk et al. 2011, Rankin et al. 2010, Rankin et al. 2011) have all altered our previous, kinematic upper limb model (Holzbaur et al. 2005), enabling advancement of a broad range of research questions. The simulations provided here will provide future researchers the opportunity to identify how the need to change specific model parameters to better address their research questions influences both the active and passive properties of the upper limb. Because the simulation results differed between SIMM/SDFast and OpenSim, we advise making such evaluations within in the software package being used for the new study. As a best practice, we also advocate clearly specifying the adaptations made to the provided upper limb model to create new simulations. Doing so enables the replication of results across different simulation studies and contributes to advancement of our understanding of the biomechanics and control of the upper limb.

Passive restraint torques and damping have been introduced into the model, and are intended to reflect restraint torques and damping previously implemented (Rankin et al. 2010, Velisar & Murray 2005) for dynamic simulation of the upper limb. Although different implementation methods for damping and joint restraint torques exist between platforms, their effects on the dynamics of the model are minimal, given our efforts to define the joint torques that result from the platform-specific functions to be identical. It should be noted that because we used the CLF function provided in OpenSim 2.4 as the mechanism to fit the previously defined joint restraint torques, the parameterization that results is only a mathematical fit, and does not result in physiologically meaningful coefficients. The effects of modeled passive joint properties can be seen most explicitly in the gravity-driven simulations when simulations were performed with muscles removed and only damping and restraint torques present. The results from the simulations we provide here (Fig. 4A,D,G) will provide researchers a means to assess how implementations of different passive properties alter the fundamental dynamic system to be controlled.

In the gravity-driven simulations, oscillations were larger in amplitude and persisted longer at the elbow and shoulder than at the wrist. Within SIMM-SD/Fast, damping is, by default, defined by a single parameter for the entire model. While it is possible to define damping uniquely for each degree of freedom within OpenSim (and in SIMM-SD/Fast via more involved computer coding), we defined damping as a constant for all joints in the model because this is the general approach currently adopted by researchers using SIMM-SD/Fast, and it allowed us to maintain consistency between platforms. However, the same damping parameter for all joints in a multijoint limb with different segment masses is likely not appropriate. The choice of damping parameter could easily be optimized on a joint-by-joint basis. Experimental data to guide the selection of damping for each joint is needed, and would be useful for improved simulation outcomes.

We observed a difference in the posture approached at the end of the simulation between the platforms during the gravity-driven simulations with passive muscles at the elbow and wrist. There are several possible contributors one might consider, including the different muscle models and paths, the implementations of the wrist kinematics, and damping and restraint torques. Our simulation results in which the muscles are removed and only the effects of damping, restraint torques, and joint kinematics influence the outcomes suggest that these factors do not lead to observable differences between platforms. The algorithm for calculating muscle force given the muscle model described by Schutte (Schutte 1992) differs between platforms and could influence the muscle force estimated for a given set of inputs. The OpenSim muscle model outputs active fiber force as tendon force minus passive fiber force, instead of using the fiber's current length and velocity to calculate force directly. The latter method is implemented in Dynamics Pipeline, the dynamic simulation software that connects SIMM and SD/Fast. OpenSim and Dynamics Pipeline also use different integrators, so even with identical muscle models (including the normalized curves), the two platforms can calculate slightly different states when resolving fiber and tendon velocities. We have confirmed through additional simulations that the differences in muscle forces that result from the muscle models during dynamic simulation, while subtle (the mean±standard deviation difference in muscle forces is 0.63±0.16N across all wrist extensors being stretched), account for the 4.3° difference in resting position of the wrist. Similarly, the passive moment generated at the elbow differs between platforms, but, in this case the technical differences in implementation of the biceps muscle path have an additional influence on the passive force output, resulting in the 4.2° offset at the elbow in the gravity-driven simulations.

While the importance of passive muscle forces are obvious for gravity-driven simulations with no active muscle forces, there were also observable effects in the EMG-driven simulations. In particular, at the elbow (c.f. Fig. 2B), the differences in passive elbow joint moment resulted in slightly larger flexion torques in SIMM-SD/Fast in the initial posture, which caused immediate elbow flexion at time 0 in SIMMSD/Fast, while the elbow initially extended in OpenSim. Thus, differences in passive muscle forces contribute to the first elbow flexion peak being lower in OpenSim than in SIMM-SD/Fast. Further, just after 2 sec when the elbow extends toward the neutral posture, the OpenSim simulation is able to extend further. Therefore, computational differences affecting passive muscle forces are important even in simulations with active muscles. In addition to these passive differences, the technical differences in implementation of the biceps muscle path likely also lead to subtle differences in active forces from this muscle during the modeled movement.

The simulations driven using optimization-derived controls derived from CMC differed more between platforms than those driven by experimentally-derived controls collected without regard to a given computing platform. We chose to use identical controls in both platforms to isolate the effects of computational implementation on simulation output. In a multijoint movement, the segments influence each other, and we expect that some of the increased error relative to the EMG-driven single joint movements can be attributed to the more complex factors involved in multisegment dynamics. However, it is important to note that the controls derived from an optimization algorithm are predicated on both the movement of interest and the properties of the entire mechanical system, including the damping and joint restraint behavior and the muscle model implementations. When used to drive a simulation in SIMM-SD/Fast, we believe the different implementations of the muscle model primarily affected the movement outcome for these simulations as we expect the implementation differences across platforms affects active as well as passive muscle forces.

When considering the CMC-driven results, we note that while the kinematics differed substantially in SIMM-SD/Fast, the CMC algorithm accurately tracked all of the joint angles with only small deviations from the experimental kinematics in the 5 OpenSim trials; the RMS tracking error for shoulder elevation and elbow flexion were 0.41° and 0.38°, respectively across the five trials, with a maximum error of 2.3° when compared to the experimental kinematics. These results are similar to those found by Thelen and Anderson (Thelen & Anderson 2006) for the lower limb, in which CMC tracked a walking motion within one degree of accuracy. Although the controls implemented in SIMM-SD/Fast did not track the desired motion well, they did create a reaching motion. We expect that implementation of the CMC algorithm in the SIMMSD/Fast environment (e.g. Thelen et al. 2003) would yield a simulated movement that tracked equally well as the CMC implemented in OpenSim, with subtle differences in control signals to account for the different muscle model outputs.

Control signals that accurately track 1 second of upper limb reaching movement were calculated using the CMC algorithm in OpenSim in an average of 1.3 hrs in our study. Other investigators report that a timeframe of approximately 20 minutes was needed to solve the CMC algorithm for a 1 sec simulation of gait in OpenSim (Thelen & Anderson 2006). The longer timeframe required for our simulations may result from the added complexity in the upper limb model relative to the lower limb model. For example, the upper limb model described here includes muscle paths that incorporate multiple moving points and wrapping surfaces, as well as joint descriptions at the shoulder and wrist that incorporate constraints. In addition, we performed simulations in both platforms from the graphical user interface rather than the command prompt, which added computational cost associated with rendering the graphical model and movement during the simulation.

By understanding the differences in performance between platforms, individual users may be able to alter the environments to suit their needs and improve performance. For example, differences in computation times between SIMM-SD/Fast and OpenSim relate in part to the differences in implementing moving muscle points in the two platforms. OpenSim uses a defined class of muscle points whose movement can be described by functions dependent on joint posture. In contrast, in SIMM-SD/Fast, each moving muscle point requires application of constraints to define its path, which greatly increases computation time. One alternative method to perform faster simulations in SIMM-SD/Fast is to generate and use a look-up table describing the musculoskeletal geometry as a function of posture. This approach has been successfully implemented for the upper limb in a forward dynamic simulation of wheelchair propulsion in the SIMM-SD/Fast environment (Rankin et al. 2010, Rankin et al. 2011). Similarly, in OpenSim, users could use the plug-in capability of the software platform to develop new actuator classes; this would be one approach to changing the way in which joint movement is restrained and damping is applied. In such instances, the benchmarking simulations we provide here would enable assessment of how the alternative methods imposed by the user influence the simulation output, both in terms of kinematic results and computational speed.

In this study, we illustrated that differences in implementation in two software platforms widely used by the biomechanics community for the simulation of movement can affect simulation predictions. We demonstrated these effects using popular methods for deriving control signals, for single and multijoint movements, provide a new model of the upper limb with dynamic properties, and present both our control signals and simulation results as a benchmarking tool for the community. Our results suggest that technical details that may seem secondary when developing complex musculoskeletal simulations of multi-joint movements can prove influential to simulation outcomes, highlighting the importance of accessible benchmarking data. In particular, the differences in implementation of muscle model may be of particular importance in the low inertia, low force regime of movement or for optimization-driven simulations with multijoint behavior near joint limits. Simulation times in SIMM-SD/Fast exceed those for OpenSim by an order of magnitude, which supports the development of alternate methods to improve simulation times in this platform. These results provide a foundation for the future development of benchmarking simulations in these and other computational platforms and are a valuable resource for replication of simulation results within the musculoskeletal modeling community.