Trabecular Plates and Rods Determine Elastic Modulus and Yield Strength of Human Trabecular Bone

Abstract

The microstructure of trabecular bone is usually perceived as a collection of plate-like and rod-like trabeculae, which can be determined from the emerging high-resolution skeletal imaging modalities such as micro computed tomography (μCT) or clinical high-resolution peripheral quantitative CT (HR-pQCT) using the individual trabecula segmentation (ITS) technique. It has been shown that the ITS-based plate and rod parameters are highly correlated with elastic modulus and yield strength of human trabecular bone. In the current study, plate-rod (PR) finite element (FE) models were constructed completely based on ITS-identified individual trabecular plates and rods. We hypothesized that PR FE can accurately and efficiently predict elastic modulus and yield strength of human trabecular bone. Human trabecular bone cores from proximal tibia (PT), femoral neck (FN) and greater trochanter (GT) were scanned by micro computed tomography (μCT). Specimen-specific ITS-based PR FE models were generated for each μCT image and corresponding voxel-based FE models were also generated in comparison. Both types of specimen-specific models were subjected to nonlinear FE analysis to predict the apparent elastic modulus and yield strength using the same trabecular bone tissue properties. Then, mechanical tests were performed to experimentally measure the apparent modulus and yield strength. Strong linear correlations for both elastic modulus (r²=0.97) and yield strength (r²=0.96) were found between the PR FE model predictions and experimental measures, suggesting that trabecular plates and rods morphology adequately captures three-dimensional (3D) microarchitecture of human trabecular bone. In addition, the PR FE model predictions in both elastic modulus and yield strength were highly correlated with the voxel-based FE models (r²=0.99, r²=0.98, respectively), resulted from the original 3D images without the PR segmentation. In conclusion, the ITS-based PR models predicted accurately both elastic modulus and yield strength determined experimentally across three distinct anatomic sites. Trabecular plates and rods accurately determine elastic modulus and yield strength of human trabecular bone.

Introduction

Osteoporosis is a common disease that occurs with age, in which reduced bone mass and strength leads to increased risk of fracture. Millions of fragility fractures occur directly because of osteoporosis, often at trabecular-dominant bone sites. Indeed, the trabecular bone plays an important role in load transmission and energy absorption in major joints such as the knee, hip, and spine [1-3]. For example, the trabecular bone carries more than 75% of the load in a vertebral body [4]. It is believed that, in addition to the bone volume fraction (the ratio of the volume of bone tissue to the overall bulk volume), the detailed microarchitecture, including trabecular orientation and connectivity, is important in governing the mechanical properties of trabecular bone [5-8]. Moreover, two major types of trabeculae – namely the trabecular plate and rod – play critical and distinct roles in determining the apparent strength and failure behavior of trabecular bone. Recently, an individual trabecula segmentation (ITS) analysis technique has been developed to decompose the entire trabecular bone network into a collection of individual plates and rods. The ITS technique was further used to assess trabecular plate and rod morphology of both micro computed tomography (μCT) and high resolution peripheral quantitative computed tomography (HR-pQCT) images of human trabecular bone [9]. Studies using this ITS technology demonstrated that trabecular microarchitecture changed from platelike to rod-like in osteoporosis and other metabolic bone diseases, and suggested that a conversion from plate-like to rod-like trabecular bone was an important etiologic factor in age-and osteoporosis-related bone fragility [10-13]. The ITS technique has also demonstrated the importance of trabecular plates and axial trabeculae in supporting mechanical loads imposed on human vertebrae [6]. Furthermore, ITS-based morphological analysis can detect microstructural abnormalities in postmenopausal women with fragility fractures independent of areal bone mineral density (aBMD) [14] and reveal dramatic differences in trabecular microarchitecture between different ethnicities [15, 16].

We have demonstrated that the ITS-based morphological parameters such as plate bone volume fraction (pBV/TV) and axial bone volume fraction (aBV/TV) are highly correlated with experimentally and computationally determined elastic modulus and yield strength of human trabecular bone [17, 18]. To further examine the biomechanical roles of trabecular plates and rods, we developed an ITS-based, specimen specific, plate-rod (PR) micro finite element (μFE) modeling strategy. These PR μFE models are constructed exclusively by ITS plate and rod segmentations, maintaining essentially all the plate and rod microarchitecture: number, shape, volume of trabecular plates and rods, and orientation and connectivity between trabecular plates-plates, plates-rods, and rods-rods. Alternatively, specimen specific, voxel-based μFE models do not make any assumption regarding trabecular types but fully represent the original 3D trabecular microarchitecture. Recently, we examined the accuracy and efficiency of the PR modeling strategy in an idealized, synthetic trabecular bone structure model, and demonstrated that the Young's modulus that was predicted by the ITS-based PR model correlated strongly with those by the voxel-based model at various voxel sizes [19]. Additionally, conversion from the voxel model to the PR model resulted in a 47-fold reduction in the number of elements [20]. Independently, Vanderoost et al. developed specimen-specific skeleton based beam-shell μFE models for simulating trabecular bone elastic modulus [36]. However, from a biomechanical perspective, it is not clear whether the simplified trabecular plate and rod morphology alone sufficiently represents the 3D microarchitecture of human trabecular bone. To determine whether the simplified PR model can accurately predict the mechanical properties of the complex human trabecular bone architecture, a thorough validation of the PR model against the “gold standard” mechanical testing is required.

The purpose of this study was to compare the predictions in elastic modulus and yield strength of the μCT PR model, which was based completely and explicitly on ITS plate and rod segmentations and reconstructions, with those determined by mechanical testing as well as by μCT-image-based voxel model, the computational “gold standard” measurements. In addition, we aimed to demonstrate that the ITS-based PR FE model provides a highly efficient and alternative method to predict both linear and nonlinear mechanical properties of human trabecular bone. We hypothesized that the plate and rod morphology are the most critical determinants of the mechanical properties of human trabecular bone; thus, the simplified PR FE model that consists of only plate and rod elements can accurately predict the Young's modulus and yield strength of human trabecular bone.

Materials and Methods

Specimen preparation and μCT scanning

Fifteen sets of freshly frozen human cadaveric tibiae (11 male/4 female, age: 71 ± 9 years, ranged from 55 to 84 years old) and fifteen sets of proximal femurs (8 male/7 female, age 73 ± 14 years, ranged from 40 to 91 years old) were obtained from the International Institute for the Advancement of Medicine (Scranton, PA) with no history of bone related metabolic diseases. Contact X-ray radiography was performed to verify that there was no fracture in the specimens. Cylindrical trabecular bone cores with a diameter of ∼8.5 mm were prepared from proximal tibiae and femurs along the main trabecular orientation [21]. In total, 22 proximal tibia (PT), 20 femoral neck (FN) and 20 greater trochanter (GT) trabecular bone cores were prepared. Specimens were kept in sealed plastic bags at -20°C and wrapped with wet gauze between preparations. These specimens were also described in our previous work [16]. The specimens were scanned along the cylindrical axis using a μCT scanner (VivaCT 40, Scanco Medical AG, Basserdorf, Switzerland) at 15 μm voxel size with 55 kVp energy and 200 ms integration time. The middle 13 mm trabecular bone of the cylinder was scanned to assure that the 8 mm strain gage region in mechanical testing was included in the μCT image. The grayscale images corresponding to the 8 mm strain measurement region were then down sampled to 30 μm voxel size and thresholded for further processing.

Mechanical testing

After μCT scanning, the bone marrow near the two ends of the bone cores was cleaned out with a water jet. The specimens were then glued into customized brass cylindrical end caps with the inner diameter the same as the diameter of trabecular bone cores. The specimens were pushed to the bottom of the end cap to eliminate movement during mechanical testing and to reduce end-artifacts [22]. A uniaxial compression test was performed on each core to measure the mechanical properties (MTS 810, Eden Prairie, MN) at room temperature, while keeping the specimen hydrated. An 8 mm strain gage (MTS, 632.26F-20) was attached to the middle of the specimen to measure strain. To ensure uniform deformations between the end caps and no yielding at the endcap-bone interface, a 25 mm extensometer (MTS 634.11F-24) was attached to the end caps. The specimen was preconditioned by 3 cycles with a 0.05% strain per second loading speed and a final ramp beyond the yield point. The elastic modulus was calculated by the linear curve fit within a 0-0.2% strain range. The yield strength and the yield strain were calculated using a 0.2% offset technique [22].

Voxel-based μFE models

The down sampled and thresholded μCT images of trabecular bone were converted to μFE models by converting each voxel to 8-node brick element. It should be noted that voxel μFE models were based on the original μCT images of trabecular bone. A uniaxial compression test was simulated through μFE analysis (μFEA), and fixed boundary conditions were assigned to the nodes at the two ends of the model. The bone tissue constitutive law was prescribed based on the elasto-plastic material model that incorporates geometric large deformations and material non-linearity [23, 24]. Poisson's ratio was defined as 0.3, and a 15 GPa tissue modulus was applied. The tissue-level yield strains were assumed to be 0.81% of strain in tension and compression [25]. The post-yield tissue modulus was 5% of its initial value. An implicit parallel finite element framework, Olympus [26], was used to solve the nonlinear μFE models on a Sun Constellation Linux Cluster at the Texas Advanced Computing Center. For each model, we calculated the apparent modulus from the slope of the linear curve fit of the stress-strain curve. The yield strength and yield strain were determined using the 0.2% offset technique [22].

PR μFE models

PR μFE models were constructed from the ITS segmented and reconstructed μCT image of each trabecular bone specimen (Fig. 1). Through the PR modeling procedure, individual trabecular plates and rods were meshed into shell and beam elements, respectively. First, the μCT image of trabecular microarchitecture (Fig. 1A) underwent an iterative thinning process and generated the skeleton image, consisting of the central axes of trabecular rods and the medial surfaces of trabecular plates (Fig. 1B) [27, 28]. Then, the entire skeleton was decomposed into individual plate and rod skeletons with every voxel uniquely classified as inner plate, plate edge, inner rod, rod end and junction points based on digital topological analysis (DTA) and ITS (Fig. 1B) [29, 30]. Using ITS segmentation, both curve and surface skeletons were segmented into individual pieces (Fig. 1C) and recovered to their full bone volume with individual trabecular plates and rods (Fig. 1D). The skeleton and reconstructed ITS images of trabecular bone were further processed for generation of PR μFE model based exclusively on the plate and rod assumption (Fig. 1E, F). Plate-plate junction, rod-rod junction, plate-rod junction, rod end and plate edge junction points were used as connection nodes in the PR model. In addition, the key turning points on plate edges and rod curves were identified as shape-refining nodes in the PR model. Each trabecular rod was meshed into a beam element with two nodes connecting this rod to its neighboring trabeculae. A curvy rod was further divided into segments by the key turning points on the rod curve, so the curvature of trabecular rods could be preserved in the PR model (Fig. 2). Each trabecular plate was meshed into multiple triangular shell elements through Delaunay Triangulation using the node set of plate-plate junction, plate-rod junction, plate edge junction and turning points on the plate edges (Fig. 3). Delaunay triangulation algorithm follows the “empty circle” principle that the circumcircle of each triangle does not contain any of the other nodes, therefore avoids thin triangles [31]. By incorporating both connection nodes and shape-refining nodes, the connectivity and shape of each individual trabecular plates and rods were fully preserved in the PR model. The segmented trabecular plate and rod skeleton was recovered layer by layer to the original volume of trabecular bone microarchitecture. Each voxel was determined as part of a trabecular plate or rod. Thickness of a trabecular plate was calculated from its volume divided by the sum of area of the triangular shell elements associated with this plate. Thickness of a trabecular rod, namely diameter of its corresponding cylindrical beam elements, was calculated from the rod volume and the sum of length of the beam elements. Therefore, the shell and beam elements in the PR model maintained the original volume of each trabecular plates and rods. It should be noted that the thickness of shell and beam elements was not shown in the model.

Figure 1.

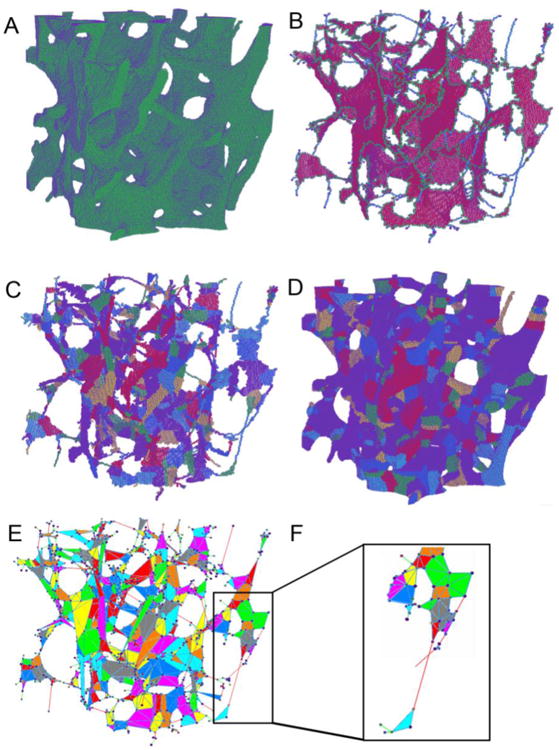
Illustration of ITS-based PR modeling on a cubical trabecular bone specimen. (A) the original 3D volume of the trabecular bone. (B) Microstructural skeleton with the trabecular type labeled for each voxel. Plate skeleton voxels are shown in red, surface edge voxels in green, rod skeleton voxels in blue. (C) Segmented microstructural skeleton with individual trabeculae labeled by color for each skeleton voxel. (D) Recovered trabecular bone with individual trabeculae labeled by color for each voxel. (E) PR model with shell and beam elements and color indicating different trabeculae. (F) Details of the beam-shell connection.

Figure 2.

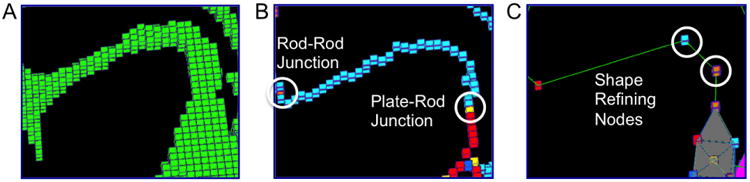
Meshing trabecular rods into beam elements. (A) Original microarchitecture of a trabecular rod; (B) Rod-rod junction or plate-rod junction at both ends of the trabecular rod skeleton; (C) Shape refining nodes divide the rod into three beam elements.

Figure 3.

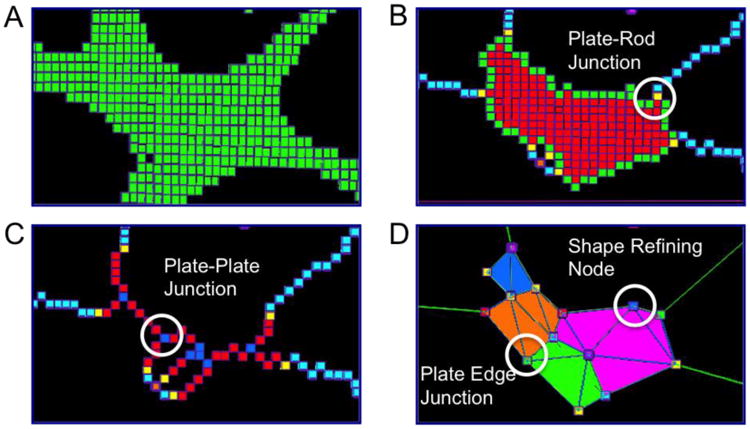
Meshing trabecular plates into shell elements. (A) Original microarchitecture of the trabecular plate; (B) Plate-rod junctions connecting plate and rod skeletons; (C) Plate-plate junctions connecting plate-arc skeletons; (D) Plate edge junctions and shape refining nodes are added to construct triangular shell elements.

We used ABAQUS 6.10 (Dassault Sytemes USA, Waltham, MA) software to perform finite element analysis on the PR model. Shell and beam elements were defined as STRI3 and B31 elements in the ABAQUS library, respectively. Trabecular bone tissue was assumed to have elastic modulus of 15 GPa and Poisson's ratio equal to 0.3, the same as the voxel model. In the PR model, trabecular bone tissue was assumed to yield at 0.81% strain with a post-yield modulus equal to 5% of the elastic modulus. A compression test along the longitudinal axis of trabecular bone core was simulated up to 1% apparent strain. Elastic modulus of the PR model was determined as the slope of the linear curve fit for the stress-strain curve in elastic range. The yield strength and yield strain were determined using the 0.2% offset method [22]. PR models were compared with those by voxel models for the trabecular bone specimens from PT, FN and GT, as shown in Fig. 4.

Figure 4.

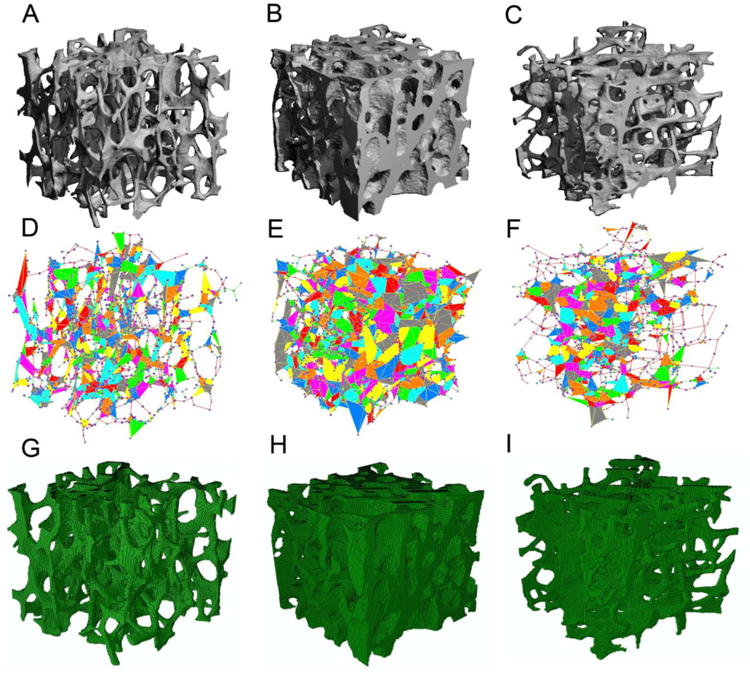
μCT image of human trabecular bone from (A) PT, (B) FN, and (C) GT; PR models for (D) PT, (E) FN, and (F) GT; corresponding voxel models for (G) PT, (H) FN, and (I) GT.

Predictions of anisotropic mechanical properties by PR μFE model

In order to test the ability of the PR μFE model in characterizing and quantifying 3D anisotropic trabecular bone microarchitecture, we extracted a 5.1×5.1×5.1mm³ cubical sub-volume from each μCT image of a randomly select subgroup of specimens, including 10 FN specimens, 10 PT specimens, and 10 GT specimens. The z axis was aligned with the longitudinal axis of the bone core, and x, y axes were orthogonal in the transverse plane. Voxel models and PR models were generated for the cubical sub-volumes, as described before. Three uniaxial compression tests were performed along x, y and z axes, respectively. Elastic modulus (E_x, E_y, E_z) and yield strength (σ_x, σ_y, σ_z) along x, y and z axes were predicted by both PR μFE model and voxel model.

PR model of distal tibia and distal radius

The accuracy of PR models was further tested on a separate and independent set of μCT images of trabecular bone from the distal tibia (n=15) and distal radius (n=15), which corresponded to the scan region under clinical HR-pQCT protocol. Cylindrical sub-volume (8.5 mm diameter, 8 mm length) was extracted from the μCT images at 37 μm voxel size. PR model and voxel model were generated and subjected to nonlinear FE analysis. The elastic moduli and yield strengths predicted by PR models were compared with those by corresponding voxel models.

Statistical analyses

Statistical analyses were performed using NCSS software (NCSS 2007, NCSS Statistical Software, Kaysville, Utah). Descriptive data were presented in the form of mean ± standard deviation (SD). Elastic modulus and yield strength predicted by PR models were correlated with those derived from voxel models and measured directly from mechanical testing experiments. Paired T-test was applied to examine the difference among PR model predictions, voxel model predictions and experimental measurements. Two-sided p values <0.05 were considered to indicate statistical significance. Bland-Altman plots were shown to present the agreement of the PR model relative to mechanical testing experiment and voxel model. The relative difference between two methods (difference/average) was plotted versus their average.

Results

Both PR and voxel μFE models predicted the stress-strain behavior of human trabecular bone as measured experimentally (Fig. 5). The elastic modulus and yield strength predicted by the PR μFE model were not different from those experimentally measured by mechanical testing (p>0.15) across different anatomic sites (Table 1). Strong correlations were found between the PR model predictions and those measured experimentally (Young's modulus: R² = 0.97; Yield strength: R² = 0.96, Fig. 6A and 6C). With reference to experimental measurements, the PR model had an average error of 0.00 (-0.24∼0.24, 95% agreement limit) in predicting elastic modulus and error of 0.02 (-0.32∼0.37) in predicting yield strength (Fig. 7A and 7C). In addition, PR model predictions in elastic modulus and yield strength strongly correlated with those of voxel models, which were based on original μCT trabecular bone microarchitecture (R² = 0.99 and 0.98, respectively), as shown in Fig. 6B and 6D. Excellent agreement was found between PR model and voxel model in predicting elastic modulus with a relative error of 0.02 (-0.14∼0.20), whereas PR model underestimated yield strength that was determined by voxel model by around 21% (error: -0.44∼0.01, p<0.001, Fig. 7B and 7D). We also noted that voxel model overestimated yield strength relative to mechanical testing measurements by around 23% (error: -0.04∼0.50, p<0.001). Table 2 showed comparison between the original trabecular microarchitecture as assessed by ITS analysis and the simplified PR μFE model. Plate and rod bone volume fraction (pBV/TV and rBV/TV) were maintained in the PR μFE models. The number of trabeculae in ITS and the number of elements in the PR model suggested that each trabecular plate was modeled by 6 shell elements, on average, and each trabecular rod was modeled by 1.06 beam elements. It should also be noted that one of the benefits of the PR μFE models is a drastic reduction in model size and computation time. Overall, conversion from voxel model to PR model resulted in 83-fold reduction in model size and 324-fold reduction in nonlinear FEA computation time (Table S1). If taking account the model generation time, PR model-based FEA led to 215-fold reduction in total computation time compared with voxel model.

Figure 5.

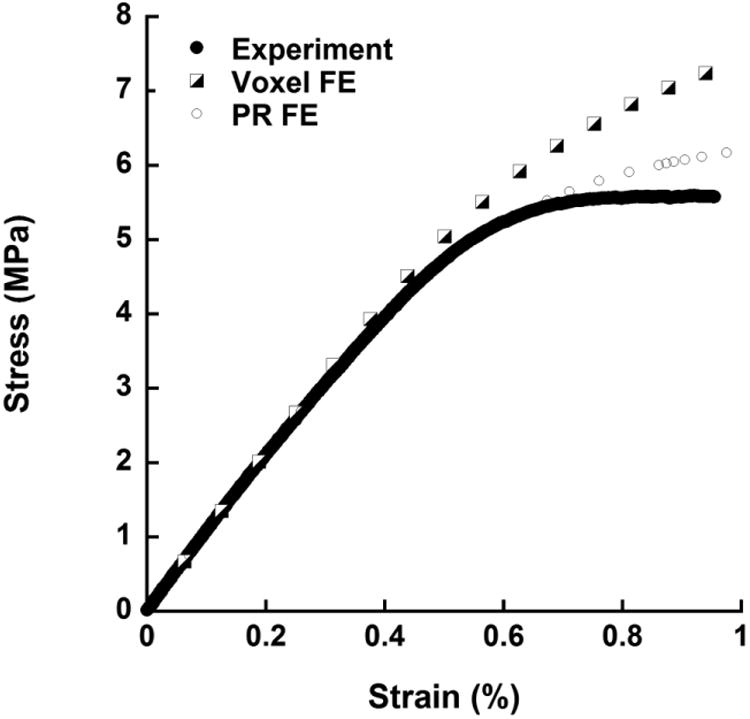
A randomly chosen typical set of strain-stress curves acquired from the mechanical testing experiment, voxel model FEA and PR model FEA.

Table 1.

Elastic modulus and yield strength measured by mechanical testing experiment and predicted by FE analysis using voxel model and PR model. Data is shown as Mean ± SD.

	Elastic modulus (MPa)			Yield strength (MPa)
	PR model	Experiment	Voxel model	PR model	Experiment	Voxel model
PT	757 ± 383	785 ± 407c	739 ± 387c	3.98 ± 2.11b	4.09 ± 2.32c	5.12 ± 2.72b,c
FN	3,239 ± 1,518	3,132 ± 1,466	3,155 ± 1,447	18.68 ± 8.83b	18.72 ± 8.88c	23.50 ± 11.61b,c
GT	491 ± 329	498 ± 349	489 ± 339	2.66 ± 1.82b	2.44 ± 1.65c	3.29 ± 2.33b,c
Pooled	1,452 ± 1,515	1,430 ± 1,457	1,419 ± 1,466	8.25 ± 8.91b	8.16 ± 8.92c	10.08 ± 11.14b,c

^aPR model predictions different from experimental measurements;

^bPR model predictions different from voxel model predictions;

^cvoxel model predictions different from experimental measurements, p<0.05.

Figure 6.

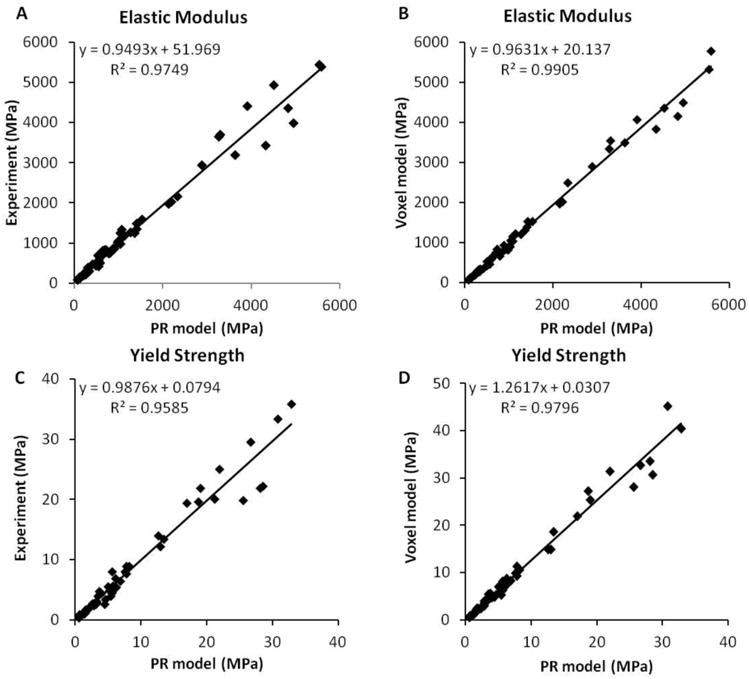
Linear regressions of the elastic modulus (A, C) and yield strength (B, D) between PR model prediction and voxel model prediction and experimental measurements (data pooled from three sites).

Figure 7.

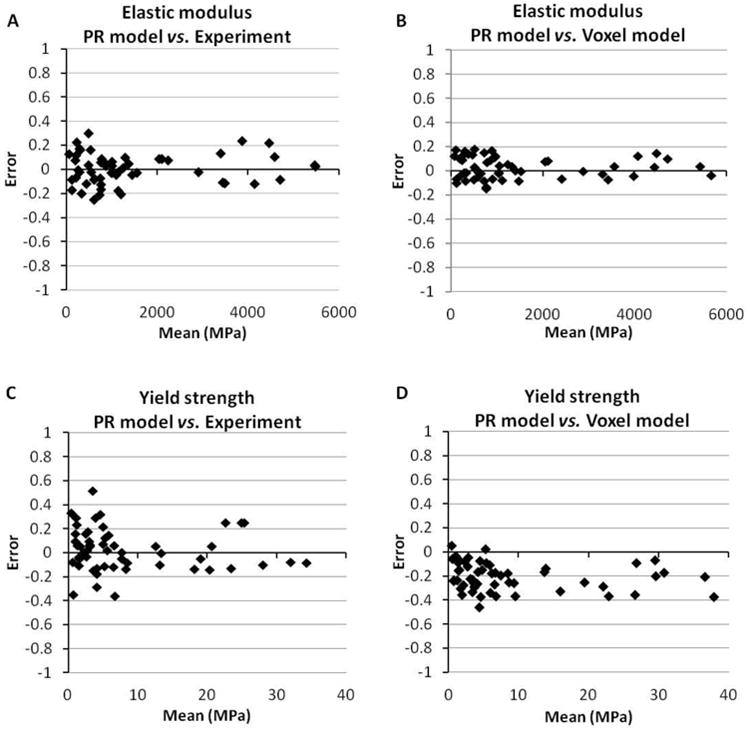
Bland-Altman plots of the prediction error of PR model compared to voxel model and mechanical testing experiment. Error = (PR model - voxel model or experiment) / mean.

Table 2.

ITS evaluation of the original trabecular microarchitecture and assessment of the recreated microarchitecture in the PR model.

	PT (n=22)	FN (n=20)	GT (n=20)	Pooled (n=62)
ITS parameters
BV/TV	0.106 ± 0.031	0.293 ± 0.104	0.111 ± 0.070	0.162 ± 0.110
pBV/TV	0.094 ± 0.031	0.281 ± 0.101	0.083 ± 0.036	0.149 ± 0.110
rBV/TV	0.014 ± 0.004	0.012 ± 0.004	0.013± 0.004	0.013 ± 0.004
Number of plates	4,163 ± 1,060	8,033 ± 2,524	4,028 ± 1,744	5,237 ± 2,548
Number of rods	1,751 ± 439	2,056 ± 808	1,719 ± 670	1,828 ± 655
PR model parameters
BV/TV	0.106 ± 0.031	0.293 ± 0.104	0.111 ± 0.070	0.162 ± 0.110
pBV/TV	0.094 ± 0.031	0.281 ± 0.101	0.083 ± 0.036	0.149 ± 0.110
rBV/TV	0.014 ± 0.004	0.012 ± 0.004	0.013± 0.004	0.013 ± 0.004
Number of shell elements	23,973 ± 6,553	48,951 ± 16,117	22,836 ± 10,460	30,803 ± 16,220
Number of beam elements	1,868 ± 461	2,163 ± 842	1,820 ± 714	1,936 ± 688

BV/TV is also highly correlated with the experimental measurements of elastic modulus and yield strength in these on-axis specimens. However, whereas BV/TV predicted anisotropic mechanical properties of human trabecular bone poorly, the PR μFE models accurately predicted the anisotropic mechanical properties of trabecular bone. As shown in Fig. 8 and 9, BV/TV was highly correlated with the on-axis E_z and σ_z (R²=0.98, 0.98), but only moderately correlated with off-axis E_x, Ey_, σ_x and σ_y (R²=0.65∼0.77). Yet, the PR μFE models were able to predict both elastic modulus and yield strength along all directions, x, y and z-axes, respectively, in comparisons to voxel models (R²=0.96∼0.99).

Figure 8.

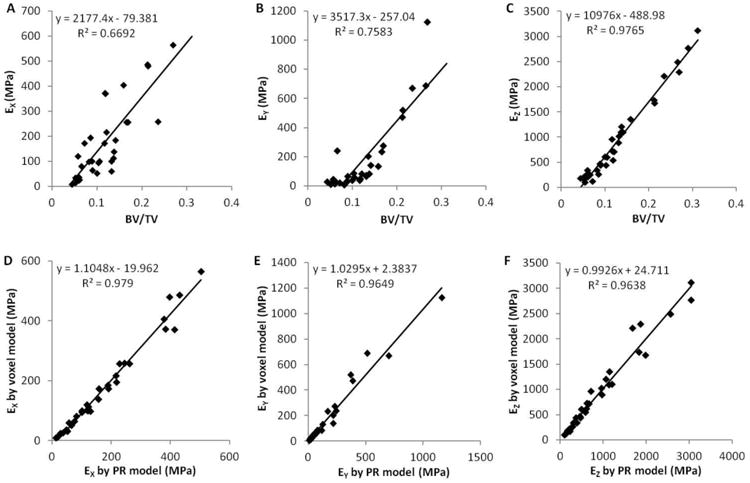
(A∼C) Linear regressions between bone volume fraction and the elastic modulus along x, y and z axes determined by voxel models; (D∼F) linear regressions between the elastic modulus along x, y and z axes predicted by PR models and voxel models.

Figure 9.

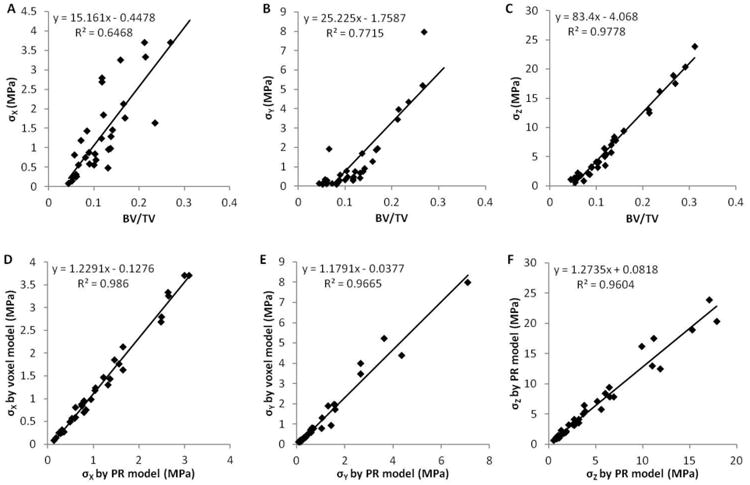
(A∼C) Linear regressions between bone volume fraction and the yield strength along x, y and z axes determined by voxel models; (D∼F) linear regressions between the yield strength along x, y and z axes predicted by PR models and voxel models.

We observed similar accuracy of PR model predictions for a separate and independent set of distal tibia and distal radius trabecular bone specimens (Figure 10). PR model predictions of elastic modulus and yield strength highly correlated with voxel model predictions (R²=0.98, 0.97), with a relative error of 0.08 (-0.07∼0.20) and -0.22 (-0.40∼0.01), respectively.

Figure 10.

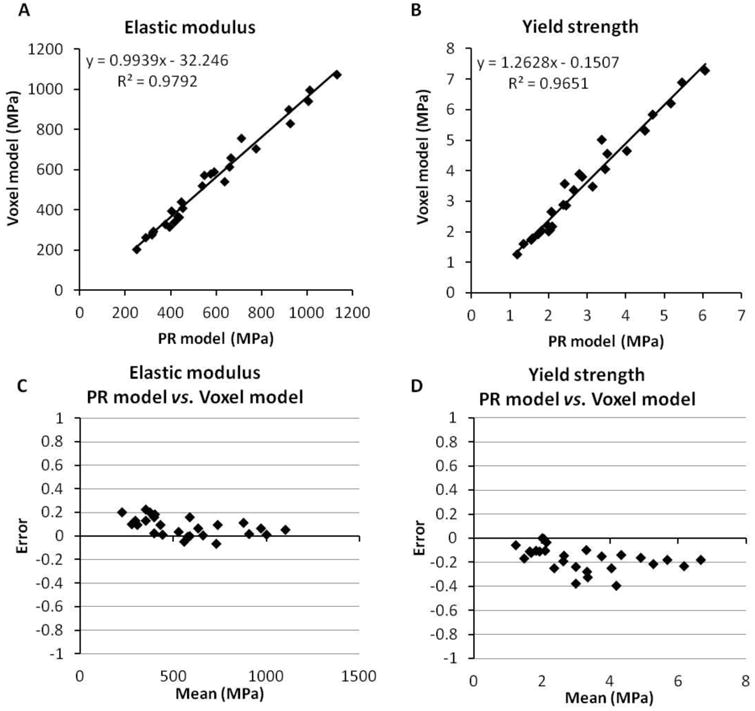
Comparison between PR model and voxel model for the test set of trabecular bone specimens at distal tibia and distal radius.

Discussion

Human trabecular bone consists mainly of a collection of trabecular plates and rods connected to form an anisotropic network. It has been demonstrated that there is an apparent transition from plate-like to rod-like microarchitecture in osteoporotic trabecular bone by either the Structure Model Index (SMI) or more advanced ITS based measures [10, 32, 33]. From both computational and experimental studies, it has been shown that trabecular plates play a more dominant role in mechanical integrity of human trabecular bone [17, 34, 35]. It is not clear how adequate is the plate-rod assumption of trabecular bone microarchitecture in quantifying mechanical properties of human trabecular bone. In this study, we constructed μFE models based explicitly on the ITS plate and rod segmentations and tested their ability in predicting elastic modulus and yield strength measured experimentally and computed by voxel based μFE models.

The reconstructed PR μFE models based on ITS preserve the 3D trabecular bone microarchitecture, including trabecular types and their bone tissue volume, trabecular orientation, and trabecular connectivity. The results indicate that these reconstructed PR μFE models predict accurately the elastic modulus and yield strength determined by the gold standard mechanical testing and voxel based μFE models. Furthermore, these PR μFE models also adequately describe the anisotropic elastic and yield properties of human trabecular bone. Therefore, our results suggest that trabecular plates and rods adequately determine elastic modulus and yield strength of human trabecular bone. In addition, these PR μFE models provided 83-fold reduction in model size and 324-fold reduction in nonlinear FEA computational time to determine yield strength of trabecular bone. In Vanderoost et al., they achieved a 7-fold reduction in the number of elements, and a 33-fold reduction in the central processing unit (CPU) time in linear analyses for estimating elastic modulus [36]. One of their pilot nonlinear analyses indicated a 45-fold reduction in CPU time. However, both models of Vanderoost and our early work significantly underestimated apparent elastic modulus and strength in comparison to those by voxel models or experiments. The refined PR modeling strategy we proposed in this study demonstrated accurate prediction of both elastic modulus and yield strength by nonlinear FE analysis, and achieved more significant reduction in model size and computational time.

There are several limitations of this study. We only used uniform and isotropic material properties for trabecular bone tissue, which are certainly inhomogeneous and anisotropic. Although, it is interesting that PR μFE models using this single constant material property of trabecular bone tissue predicted well the on-axis mechanical properties of human trabecular bone from several anatomic sites, it remains to be seen how inhomogeneous and anisotropic trabecular bone tissue properties affect apparent, anisotropic properties of human trabecular bone. Second, we assumed symmetric tissue-level strengths under compression and tension in predicting the yield strength of trabecular bone. Using the same material property, PR μFE models predicted yield strengths that did not differ from experimental measurements, whereas voxel μFE models overestimated yield strengths as measured in experiments. It was shown that voxel μFE models with tissue strength asymmetry taken into account could accurately predict yield strengths measured experimentally [37]. It remains to be tested whether tissue strength asymmetry would influence yield strength prediction by the PR μFE models. Furthermore, both the voxel and the PR μFE models used the elasto-plastic material law, which has a significant limitation in post-yield behaviors of bone such as unloading. Although, this limitation will not affect the conclusions of the current study regarding elastic modulus and yield strength of human trabecular bone, a better constitutive law for bone tissue, in general, for both voxel and PR μFE models is needed for post-yield behaviors such as unloading or ultimate strength.

The feasibility of our PR μFE modeling approach has been quantified in idealized plate and rod microstructural models, which were made of either a combination of two plates and four rods or purely eight interconnected rods in a unit cell [38]. Excellent agreement was found between the mechanical properties calculated from PR models and the corresponding voxel models, such as elastic modulus and yield strength. This idealized study provided fundamental assessment of PR μFE models in predicting mechanical properties of trabecular bone, independent of biological variations among human bone specimens and image noises existing in the imaging process. We have also applied PR μFE models on clinical HRpQCT images and demonstrated the ability of HRpQCT-based μFE PR models to predict bone strength and discriminate postmenopausal women with and without vertebral fractures [20]. Elastic modulus and yield strength predicted by HRpQCT-based PR models were strongly correlated with those by voxel models. Furthermore, HRpQCT-based PR model revealed marked mechanical deficiency in postmenopausal women with vertebral fracture compared with nonfracture controls. Therefore, the ITS based PR μFE models also provide a highly efficient and alternative approach for clinical prediction of mechanical integrity in patients.

In summary, we used ITS based trabecular plate and rod segmentation to create PR μFE models, which maintain only plate-rod microarchitecture of human trabecular bone. By comparing the prediction in elastic modulus and yield strength to those determined by experiments and voxel based computations, we concluded that trabecular plate and rod microarchitecture sufficiently determine mechanical properties of human trabecular bone. The study also provides the validation of the PR μFE approach in quantifying mechanical properties of trabecular bone in both basic science and clinical studies.

Highlights.

• We develop a plate-rod finite element model based on trabecular microarchitecture.

• The plate-rod model can accurately predict the elastic modulus and yield strength.

• We compare the plate-rod model with voxel model and mechanical testing.

• The plate-rod model predictions strongly correlate with reference methods.

• The plate-rod model achieves a major reduction in model size and computation time.