Control and Plasticity of the Presynaptic Action Potential Waveform at Small CNS Nerve Terminals

SUMMARY

The steep dependence of exocytosis on Ca²⁺ entry at nerve terminals implies that voltage control of both Ca²⁺ channel opening and the driving force for Ca²⁺ entry are powerful levers in sculpting synaptic efficacy. Using fast, genetically encoded voltage indicators in dissociated primary neurons, we show that at small nerve terminals K⁺ channels constrain the peak voltage of the presynaptic action potential (AP_SYN) to values much lower than those at cell somas. This key AP_SYN property additionally shows adaptive plasticity: manipulations that increase presynaptic Ca²⁺ channel abundance and release probability result in a commensurate lowering of the AP_SYN peak and narrowing of the waveform, while manipulations that decrease presynaptic Ca²⁺ channel abundance do the opposite. This modulation is eliminated upon blockade of Kv3.1 and Kv1 channels. Our studies thus reveal that adaptive plasticity in the AP_SYN waveform serves as an important regulator of synaptic function.

INTRODUCTION

The flow of information in neural circuits is primarily regulated by modulation of synaptic efficacy. Exocytosis of chemical neuro-transmitters is triggered by elevation of intracellular Ca²⁺ in the vicinity of the exocytosis machinery (Pumplin et al., 1981). This process is highly nonlinear, typically showing a 3^rd–5^th power-law relationship between Ca²⁺ influx and exocytosis (Ariel and Ryan, 2010; Augustine et al., 1985; Borst and Sakmann, 1998; Dodge and Rahamimoff, 1967; Mintz et al., 1995; Schneggen-burger and Neher, 2000; Scimemi and Diamond, 2012). The time course and magnitude of Ca²⁺ influx through voltage-gated calcium channels (VGCCs) is therefore poised to have enormous influence on chemical neurotransmission. At typical CNS synapses, presynaptic Ca²⁺ influx is mediated by Ca_V2.1 and Ca_V2.2 VGCCs (Ariel et al., 2012; Takahashi and Momiyama, 1993; Wheeler et al., 1994), so-called high-voltage-activated channels that require large membrane depolarizations to drive them to the open state. The presynaptic action potential(AP_SYN) controls the fraction of Ca²⁺ channels that open and the temporal envelope of the driving force for Ca²⁺ entry by rapid coordination of Na⁺ and K⁺ channel opening (Na_V and K_V, respectively) (Hille, 2001; Hodgkin and Huxley, 1952). The highly nonlinear influence of Ca²⁺ on exocytosis thus dictates that modest changes in AP properties have a large influence on synapse function.

Details of the action potential waveform have largely been deduced from cell somas and certain giant nerve terminals (Bean, 2007). Measurements of the AP peak in these experimental conditions recorded values (~40 mV) approaching the reversal potential for Na⁺ ions (Bean, 2007). As expected, blockade of K_Vs does not impact the AP peak mainly because it is dominated by Na⁺ flux (Alle et al., 2009). Given the typical voltage activation of VGCCs, such membrane potentials would likely drive virtually 100% of channels to an open state, leading to an all-or-none type calcium influx at synapses. Quantitative determinations of AP_SYN magnitude have largely been carried out in electrically accessible nerve terminals (Boudkkazi et al., 2011; Taschenberger and von Gersdorff, 2000), many of which have specialized architectures that carry out high-fidelity relay operations (Forsythe and Barnes-Davies, 1993). However, much less is known about the amplitude and kinetics of the AP at more typical small en passant CNS boutons. Recent optical measurements found that the somatic AP and AP_SYN at distal boutons have different shapes in cortical neurons and are differentially influenced by K_V channels (Foust et al., 2011; Rowan et al., 2014).

Here we made use of recent developments in fast (400 μs) genetically encoded fluorescent voltage indicators (Kralj et al., 2012, Maclaurin et al., 2013) to carry out measurements at single en passant boutons in dissociated hippocampal neurons where somatic AP waveforms are known to operate in the 1.5–2.5 ms regime (Abdul-Ghani et al., 1996; Gong et al., 2008; Kralj et al., 2012; Mitterdorfer and Bean, 2002). We show that unlike at the cell soma, the AP_SYN peak is heavily influenced by K_V function. Use of ionophore-based calibration allowed us to estimate this peak AP_SYN membrane potential at ~+7 mV, placing it in a regime that would enable very efficient modulatory control of Ca²⁺ currents through changes in K_V function. We go on to show that such control is manifest in adaptive plasticity, where changes in nerve terminal VGCC abundance result in changes in AP_SYN wave-form that in turn serve to maintain release properties in a useful operating range.

RESULTS

Archaerhodopsin-Based Recordings of Action Potentials at Single Nerve Terminals

Although optical recordings of membrane voltage using electro-chromic dyes have been successfully used, their utility has been restricted. Labeling cells by injection techniques or the eventual internalization of extracellular membrane dyes by their nature limits the complexity and length of experiments (Bradley et al., 2009; Foust et al., 2011; Popovic et al., 2011; Sabatini and Regehr, 1997). Genetically encoded optical membrane potential indicators in principle circumvent these technical barriers. It was recently discovered that Archaerhodopsin (Arch) emits fluorescence that is linearly proportional to membrane potential with rapid response kinetics (Maclaurin et al., 2013). This opens the door to detailed measurements of action potential (AP) waveforms in subcellular regions that are not amenable to electrode-based recordings (Peterka et al., 2011). When expressed in dissociated primary hippocampal neurons, Arch-GFP localizes to all regions of the cell (Figure 1A), including dendrites, fine axonal arbors, and presynaptic boutons. Although the quantum yield for Arch fluorescence when excited at 640 nm is low, its far-red fluorescence emission and excellent voltage sensitivity makes it feasible to image this probe even at synaptic boutons (Figure 1A inset). When imaged at high-time resolution (2 kHz), the bouton fluorescence showed distinct time-locked spikes when a train of APs were triggered using field stimulation (Figure 1B). Measurements from single boutons showed that the signal-to-noise ratio associated with detecting individual spikes was ~4:1, and averaging over several hundred trials resulted in very-high-fidelity recordings of the apparent AP waveform (Figure 1C). To confirm that these presynaptic voltage spikes were indeed APs, we varied the strength of the field stimulus and found that the spikes appeared in an expected all-or-none fashion as one presumably crosses a minimal threshold for AP initiation (Figures S1A and S1B, available online). Furthermore, these signals were dependent on Na⁺ channel function as the spikes were eliminated in the presence of Tetrodotoxin (TTX) (Figure 1C), revealing a small direct field-stimulus impact on the local membrane potential. The presence of the direct-field stimulus-driven membrane potential change suggests that the recorded spike waveform is the superposition of the propagating AP with the direct field stimulus-driven change in membrane potential. Although in principle these two components could sum nonlinearly, we reasoned that the direct field stimulus contribution is sufficiently small that a linear approximation would hold, allowing one to recover the AP waveform from the recorded spike by subtracting the signal obtained in the presence of TTX (Figure 1D). We tested the validity of this assumption by comparing AP waveforms generated by opposite polarity field stimuli at the same boutons (Figure S1C). These experiments showed that provided the field stimulus-driven membrane potential change was less than 10% of the AP peak, its polarity did not influence the shape of the extracted AP waveform (Figures S1C and S1D), and thus the linear superposition assumption was valid (Figure S1E). All subsequent analysis was restricted to recordings that satisfied this criterion. As one can improve the signal to noise by averaging over many trials, it is important to determine if this impacts the ability to accurately extract AP parameters. Previous use of electrochromic dye indicators to follow neuronal activity suffered from considerable phototoxicity, so we examined the stability of the signals across trials under our recording conditions. These experiments demonstrated that Arch appears to have remarkable photostability, as the spike amplitude is stable over the entire imaging period (~100,000 frames, 400 trials) (Figures 1E and 1F). A second concern is whether any temporal jitter associated with each trial might lead to significant broadening of the averaged signal. We chose a subset of experiments with the highest signal to noise for single trial spikes (>9:1) and used spline fitting (Figure S1F) to determine the AP width from each trial and compared the average spline fit value of the full width at half maximum (FWHM) across 400 trials with the FWHM of the average trace (Figure 1G). Similar analysis across a population of boutons showed that the FWHMs calculated using these two approaches were statistically indistinguishable (1.4% ± 4.6%, n = 6). For a more accurate estimate of both peak ΔF/F values and the FWHM during an action potential, we also corrected the traces for the low-pass filtering imposed by the time resolution of Arch’s response to V_m changes, which could lead to underestimation of AP peak and overestimation of FWHM values (Figure S1G, see Experimental Procedures). Using these approaches, we characterized the AP_SYN from a collection of boutons. On average, AP_SYN reached a peak fluorescence over baseline of 0.45 ± 0.03 ΔF/F and had a FWHM of 2.27 ± 0.26 ms (n = 24).

Figure 1. Optical Measurements of Action Potential Waveforms.

(A) Montage of several fields (GFP fluorescence) from a dissociated hippocampal neuron expressing Arch-GFP. Red arrow represents a typical region of measurements of presynaptic waveforms. Scale bar, 10 μm. Inset image showing the Arch fluorescence of two en passant boutons; scale bar, 2 μm.

(B) Arch fluorescence intensity of the boutons shown in (A) stimulated with single stimuli at 8 Hz. Red arrow indicates stimulation.

(C) Average AP recorded from the boutons shown in (A) with (red) and without (black) the addition of TTX.

(D) Action potential after subtraction of direct field effect (black minus red as shown in B).

(E) Individual single bouton peak ΔF/F for 390 consecutive trials shows no apparent rundown.

(F) Representative consecutive 8 Hz 50-trial averages of the presynaptic AP waveform spaced for clarity.

(G) FWHM extracted from each of 400 single trials at a single bouton with spline fitting (see Experimental Procedures and Figure S1F) compared to the the FWHM of the trial averaged AP waveform (dashed line).

Presynaptic Bouton AP Is Controlled by K_V1 and K_V3.1 Potassium Channels

In general, the value of the AP peak and the speed of repolarization are dictated by the abundance and kinetics of Na⁺ and K⁺ channels in different cellular regions. In order to determine which K⁺ channels control the AP waveform, we used a combination of pharmacology and shRNA-based knockdown. Previous reports indicate that APs in axons mainly rely on a combination of Shaker (K_V1) and Shaw (K_V3) family K⁺ channels as well as calcium-activated K⁺ channels (BKCa) under some conditions (Alle et al., 2011; Boudkkazi et al., 2011; Debanne et al., 2011; Deng et al., 2013; Foust et al., 2011; Johnston et al., 2010; Kole et al., 2007). We found that AP_SYN was completely insensitive to the BKCa channel blocker iberiotoxin (IBX, 100 nM; Figures 2A and 2B) or to removal of external calcium (data not shown). In contrast, application of 1 mM tetraethylammonium (TEA), an inhibitor of K_V3 and K_V1 channels (Gutman et al., 2005), led to increases in the peak AP_SYN (109% ± 8%) as well as the FWHM (2.99 ± 0.58 ms) (Figures 2A and 2B). Similarly, application of dendrotoxin-K (DTX, 100 nM), a blocker of K_V1.1, K_V1.2, and K_V1.6 family K⁺ channels, also led to an increase in the AP_SYN peak (113% ± 8%) and FWHM (3.84 ± 0.60 ms; Figures 2A and 2B). Both toxins also eliminated the after-hyperpolarization. Simultaneous addition of both toxins led to roughly additive effects on the peak AP_SYN (133% ± 9%) as well as the FWHM (4.51 ± 0.60 ms; Figures 2A and 2B). In contrast, dual application of DTX and TEA impacted the FWHM (increase of 48% ± 18%; Figure 2C), but not the amplitude (Figure 2D) of the somatic AP waveform. These findings were consistent with previous measurements using patch-clamp recordings at the cell body (Kole et al., 2007; Mitterdorfer and Bean, 2002; Storm, 1987). None of these K_V toxins significantly altered the resting baseline fluorescence of Arch (p = 0.89, n = 7 pre- and post-TEA and DTX application; data not shown), indicating that resting membrane potential was unaltered by blockade of these K_Vs.

Figure 2. K⁺ Channel Modulation of Presynaptic Action Potential Waveform.

(A) Population average AP waveforms from synaptic boutons in control (black; n = 24) in the presence of iberiotoxin (Iberia, 100 nM, magenta; n = 6), tetraethylammonium chloride (TEA, 1 mM, red; n = 9), dendrotoxin-K (DTX, 100 nM, blue; n = 13), and a combination of TEA and DTX (green; n = 10). Somatic APs are shown under control conditions (gray) and in the presence of a combination of TEA and DTX (teal; n = 6). Peaks are normalized to control waveforms for boutons and soma, respectively; all dashed lines display SE of AP peak measurements.

(B) Average FWHM of the action potential waveforms shown in (A).

(C) Percent change in FWHM after application of TEA and DTX at the bouton (92% ± 31%) and soma (48% ± 18%).

(D) Average percent change in peak amplitude of the action potential waveforms after application of TEA and DTX at the bouton and soma. All error bars shown are mean ± SEM; *p < 0.05 and **p < 0.01 using ANOVA comparison with Turkey’s post hoc comparisons to determine significance.

In order to verify the conclusions based on pharmacological blockade, we made use of shRNA-mediated knockdown of K_V3 and K_V1 channels. As previous studies demonstrated that K_V3.1b is preferentially trafficked to axons (Xu et al., 2007), we chose this isoform for shRNA targeting. We recorded the AP_SYN waveform in neurons simultaneously transfected with Arch and shRNA directed to K_V3.1b and then examined the impact of TEA application on waveform characteristics (Figure 3A). These experiments demonstrated that K_V3.1b KD increased AP_SYN amplitude (116% ± 10%) to values similar to those of control amplitude after treatment with TEA. Moreover, the addition of TEA no longer impacted the AP_SYN waveform in K_V3.1b knock-down (KD) neurons (Figures 3A–3C). A number of K_V1 family members have been reported to be potentially present in axons, in particular K_V1.1 (Smart et al., 1998). Next, we recorded AP_SYN in neurons expressing shRNA-targeting Kv1.1 before and after DTX treatment. Loss of K_V1.1 led to AP_SYN peak values (120% ± 5%) that were similar to controls treated with DTX, although we found that the resulting AP_SYN retained some sensitivity to further DTX application (Figures 3D and 3E) and maintained a FWHM similar to controls (2.81 ± 0.26 ms for Kv1.1 KD without DTX). Quantitative immunofluorescence staining against K_V1.1 demonstrated that shRNA transfection led to >90% depletion of this protein (Figure S2). Thus, it seems likely that the remaining DTX sensitivity might arise from K_V1 heterotetramers assembling from alternate subfamily members (for example K_V1.2, K_V1.3, K_V1.6, etc.). Taken together, these results strongly indicate that K_V3 and K_V1 both serve to control the AP_SYN waveform.

Figure 3. K_V3.1b and K_V1 Control the Presynaptic AP.

(A) Population average AP_SYN recordings in control (left, n = 9) and shRNA targeting K_V3.1b-expressing (right, n = 7) neurons. Population average APs for these two groups are shown in black and overplayed with APs recorded in the presence of TEA (red) for comparison. AP waveforms were also measured in the presence of a K_V1 blocker (DTX) in both control and shRNA Kv3.1b cells in the absence (blue) and in the presence (green) of TEA.

(B) Ratio of peak AP waveform amplitude after addition of TEA for control and shRNA-targeted knockdown of Kv3.1b (shKv3.1b) normalized to pretreatment.

(C) FWHM measurements of the AP waveforms for control and shRNA K_V3.1b neurons before and after inclusion of TEA.

(D) Ratio of peak AP waveform amplitude after addition of DTX for control and shRNA-targeted knockdown of Kv1.1 (shKv1.1) normalized to pretreatment (n = 13).

(E) FWHM measurements of the AP waveforms for control and shRNA Kv1.1 neurons before and after inclusion of DTX. All bar graphs shown are mean ± SEM. *p < 0.05.

The most striking feature of these experiments was the differential impact of K_V blockade on the amplitude of AP_SYN compared to the somatic waveform. Indeed, if the action potentials both had amplitudes closer to the Na⁺ reversal potential, it is difficult to imagine how the Arch signal could rise 33% without exceeding it. To address this question, we attempted to locally calibrate Arch to estimate AP amplitudes in terms of voltage in different cellular regions.

Calibration of Arch Fluorescence Signals

Meaningful comparison of Arch responses in different regions cannot be made in the absence of local calibration. This is because only Arch fluorescence arising from copies of the indicator in the plasma membrane reflect V_m, but the total fluorescence reflects contrbutions from both the plasma membrane and intracellular compartments. To correct for variations in the surface fraction of Arch in different cellular regions, we developed an iononophore-based approach based on previous studies (Maric et al., 1998). We recorded AP waveforms subcellulary (soma or axon) and subsequently applied gramicidin, a cation-selective pore, to collapse the membrane potential (V_m) to 0 mV (Meunier, 1984; Podleski and Changeux, 1969) while monitoring the fluorescence change in the same subcellular regions (Figures 4A and 4B). This approach necessarily ignores possible differences in resting V_m in different regions, and given that the PNa/PK of gramicidin is ~3.5 (Hille, 2001) it may not fully bring V_m to 0. However, with these caveats in mind one can then compare the gramicidin response to the magnitude of the AP waveform at the subcellular level in a region-specific fashion. The mean ΔF/F response of gramicidin at boutons was 41.4% ± 2.8% (n = 6) and at somas was 15.6% ± 4% (n = 6). This difference likely reflects greater contributions in total fluorescence from intracellular compartments in the soma compared to the bouton. Comparison of the somatic AP peak amplitude with the somatic gramicidin response indicated that the somatic AP response was always ~50% larger than the latter (Figure 4C), while AP_SYN reached an amplitude that was roughly equivalent to the peak of the gramicidin response (Figure 4C). With the assumption that V_REST = −65 mV (see Experimental Procedures) and that gramicidin collapses V_m to 0 in both regions, these data provide a local calibration for Arch (ΔF/FmV⁻¹). The somatic calibration factor was 0.24% ± 0.09% ΔF/FmV⁻¹, while the bouton calibration factor was 0.63% ± 0.03% ΔF/FmV⁻¹. Using these calibration factors, we estimated the somatic AP peak at 37.6 ± 8.1 mV (Figures 4D and 4E), in close agreement with most electrophysiological measurements (Bean, 2007). In contrast, using the same approach at boutons we estimate that the AP_SYN reaches a peak of 6.8 ± 4.9 mV (Figures 4D and 4E).

Figure 4. Subcellular Calibration of Archaerhodopsin Fluorescence.

(A and B) Example action potential waveform recorded from en passant boutons (A) and a soma (B) with corresponding traces of Arch fluorescence during extracellular application of gramicidin bringing resting membrane potential (V_REST) to ~0 mV (V₀). Gramicidin trace has been filtered (5 Hz) for clarity from a 1 kHz recording.

(C) Average AP peak height normalized to corresponding gramicidin traces for individual boutons (1.03 ± 0.07; n = 6) and somas (1.53 ± 0.17; n = 6).

(D) Average paired recordings from the same neurons at the bouton and soma (n = 9) converted from fluorescence to mV based on this calibration.

(E) Average AP peak voltage of APs shown in (D). All bar graphs shown are mean ± SEM. *p < 0.05.

It is possible that either the presence of Arch or possible proton pumping by Arch might lead to underestimates of the AP_SYN peak. We tested for this possibility in three ways. First, we coexpressed WT Arch (fused to a nonfluorescent GFP, Arch_DARK) with VAMP-mOr2 to mark synaptic boutons and loaded the transfected and adjacent untransfected boutons with Fluo5F (Figure S3A). Overlays of single AP-driven Ca²⁺ and Arch signals showed that the Ca²⁺ signal began to rise with minimal delay after the start of the AP reaching 55% ± 6% (n = 9) of the Ca²⁺ signal peak by the peak of the AP, almost identical to values previously obtained at similar recording temperatures (30°C; Sabatini and Regehr, 1996). Comparisons of the peak single AP-driven Ca²⁺ influx in Arch-transfected and untransfected boutons had identical amplitudes (0.73 ± 0.15 versus 0.71 ± 0.19, n = 9 and 11 cells, respectively; Figure S3B), indicating that expression of Arch did not impair Ca²⁺ influx and by extension did not alter the AP waveform. Second, we measured the efficacy of AP-driven exocytosis in boutons coexpressing Arch_DARK and vGlut-pHluorin in the presence and absence of 640 nm illumination (Figures S3C–S3F). These experiments showed that the imaging conditions used to measure Arch fluorescence do not impact synaptic efficacy. Third, we compared the ratio of AP and gramicidin responses at somas and boutons using a non-pumping, but somewhat slower (~4-fold slower time resolution), variant of Arch (Arch EEQ; Gong et al., 2013). Using this mutant, we found that both somatic and bouton APs normalized to their gramicidin responses were lower than what we obtained with WT Arch (Figures S3G and S3H). We suspect that this discrepancy arises from the slower time resolution of this variant. Nonetheless, the ratio of the two gramicidin-normalized responses was ~1.33, similar to the 1.50 value obtained with WT Arch. These results indicate that complications from light-induced proton pumping under the conditions used here are likely minimal. The significant impact of K_V blockade on AP_SYN, but not the somatic AP peak, taken together with our gramicidin-based calibration estimates indicate that the presynaptic action potential in these small boutons likely reaches a significantly lower V_m at its peak than that at cell somas.

Superlinear Control of Presynaptic Calcium Entry by KV3 and KV1

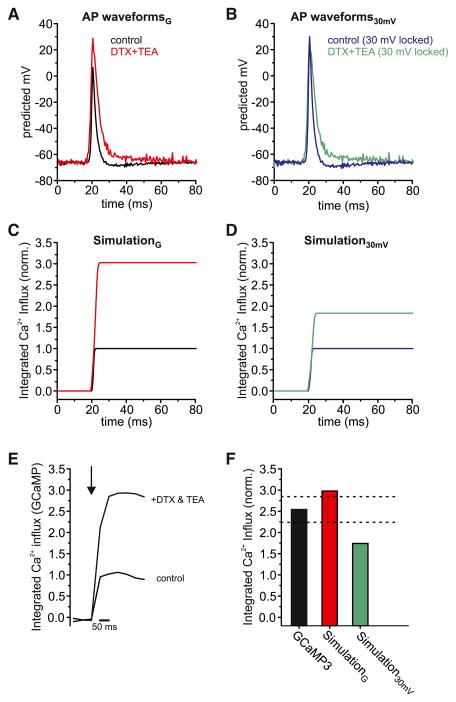
Voltage-gated Ca²⁺ channels open through a series of voltage-dependent transitions from the closed states (Li et al., 2007). Therefore, the rate of depolarization, the peak amplitude, and the FWHM can all have strong influences on AP-driven Ca²⁺ influx (Bischofberger et al., 2002; Borst and Sakmann, 1999; Sabatini and Regehr, 1997). The lower-amplitude AP_SYN waveform is well poised to allow significant nonlinear modulation of Ca²⁺ influx since it would tend to drive fewer VGCCs to the open state. In order to estimate how changes in AP_SYN waveforms might be expected to impact Ca²⁺ influx, we used previous measurements of the voltage-dependent gating properties of VGCCs (Li et al., 2007) to calculate the impact on integrated Ca²⁺ influx under K_V blockade (see Experimental Procedures). We compared two different scenarios: in the first scenario we utilized waveforms with and without K_V1 and K_V3 blockade based on our gramicidin calibration (AP waveforms_G with peak amplitudes of 28.7 ± 6.1 mV and 6.8 ± 3.8 mV, respectively; Figure 5A); in the second scenario we utilized AP_SYN with fixed 30 mV amplitudes and only varied the time courses (AP waveforms_30mV; Figure 5B), more similar to what one would expect at cell somas. These two simulations predicted dramatically different estimates on the impact of Kv blockade on total Ca²⁺ influx: our gramicidin-based simulations predicted a ~3-fold increase in Ca²⁺ influx, while the fixed 30 mV amplitude simulation predicted only a ~1.7-fold increase after toxin blockade (Figures 5C and 5D). We tested these predictions by measuring Ca²⁺ influx before and after Kv blockade using a genetically encoded calcium sensor (GCaMP3) that naturally integrates [Ca²⁺] over short time scales (Figure 5E). We measured a 2.54 ± 0.29-fold (n = 9) increase in Ca²⁺ influx after application of K_V-blocking toxins (Figure 5F). These value most closely match our numerical estimates of calcium influx using the gramicidin-calibrated AP waveforms (Figure 5F). Thus, the large changes in Ca²⁺ influx we observe are most accurately predicted if the starting AP waveform peaks at a much lower V_m than typically observed at cell somas.

Figure 5. Presynaptic Ca²⁺ Entry Controlled by K_V3 and K_V1.

(A) Peak-aligned gramicidin-calibrated AP_SYN waveforms (AP waveforms_G) for control (black) and after DTX/TEA treatment (red).

(B) Peak-aligned waveforms from (A) normalized to maintain a constant peak (30 mV; AP waveforms_30mV) before (blue) and after DTX/TEA treatment (green).

(C) Corresponding numerical estimates of the impact of DTX/TEA-driven changes in waveform on integrated Ca²⁺ influx based on known VGCC gating properties for our gramicidin-based AP_SYN (Simulation_G).

(D) Corresponding numerical estimates of the impact of DTX/TEA-driven changes in waveform on integrated Ca²⁺ influx based on known VGCC gating properties for 30 mV locked amplitude (Simuation_30mV).

(E) Representative measured (GCaMP3) single AP-driven presynaptic Ca²⁺ influx averaged for six trials (spaced at 30 s intervals) from boutons under control conditions and with the combination of TEA and DTX.

(F) Average single AP-driven bouton Ca²⁺ influx normalized to control conditions from n = 9 cells after application of DTX and TEA (black); dashed line represents measured SE. Red and green bars are the numerical estimates for the impact of DTX/TEA blockade on Ca²⁺ influx using our gramicidin-calibrated (Simulation_G; red) or 30 mV amplitude (Simulation_30mV; green) waveforms.

Modulation of Presynaptic Calcium Channel Abundance Leads to Adaptive Changes in the Presynaptic AP Waveform

The potent control of K_v channels on the AP_SYN peak opens the possibility for AP_SYN to serve as a substrate for modulation that could impact Ca²⁺ influx and release probability (Pr). Such control could work synergistically with direct modulation of VGCC function or abundance in controlling synaptic transmission. We previously showed that the abundance of presynaptic VGCCs is determined in a rate-limiting fashion by the availability of the VGCC subunit α2δ (Hoppa et al., 2012). α2δ’s are a family of GPI-anchored proteins whose expression drives presynaptic VGCCs accumulation and increased release probability (Pr), while removal leads to loss of presynaptic VGCCs and decreased Pr. We demonstated that part of the increase arose from changing the proximity of VGCCs to release sites (Hoppa et al., 2012), which could be expected from an increased density of channels at active zones. However, we expected that changing the number of active zone VGCCs would also increase total Ca²⁺ influx, which could also drive increases in Pr. Instead, we found that this increase in Pr was accompanied by lower AP-driven presynaptic Ca²⁺ influx as if the system had partially compensated for the closer coupling of VGCCs to release sites. We speculate that this could result from changes in AP_SYN confounding simple correlations of AP-driven Ca²⁺ influx and active zone VGCC abundance. We therefore compared AP_SYN measurements in control conditions with those where we coexpressed Arch with either overexpression of α2δ-1 (+α2δ-1) or an shRNA targeting α2δ-1. These experiments revealed that expression of α2δ strongly influenced the AP_SYN waveform: increasing α2δ expression lowered the AP_SYN peak amplitude and narrowed the FWHM, whereas the loss of α2δ did the opposite (Figures 6A–6C). Comparison of the α2δ overexpression with the shRNA knockdown across a population of neurons showed that genetic manipulation of VGCC abundance leads to an ~11 mV modulation (based on our gramicidin calibrations) in the AP_SYN peak amplitude and an ~800 μsec change in the FWHM. Thus, the AP_SYN waveform shows strong adaptive plasticity associated with changes in VGCC abundance. This modulation appears to be specific to the AP_SYN waveform, as direct comparisons of the somatic AP waveform between control and overexpression of α2δ showed no difference (Figures S4A–S4C).

Figure 6. Adaptive Plasticity of Action Potential Waveforms Mediated by K_V3/K_V1.

(A) Population average AP_SYN waveforms from control (black, n = 24), α2δ-1-overexpressing (red, n = 15), and α2δ-1-shRNA-expressing (blue, n = 11) neurons.

(B and C) Average peak (6.8 ± 3.8, 1.22 ± 2.6, and 13.95 ± 3.3 mV) and FWHM measurements (2.27 ± 0.26, 1.77 ± 0.11, and 2.72 ± 0.18 ms) of the associated AP waveforms shown in (A) for control, α2δ and shRNA α2δ conditions, respectively.

(D) Population average AP_SYN in the presence of DTX and TEA from control (black, n = 10), α2δ-1-overexpressing (red, n = 9), and α2δ-1-shRNA-expressing (blue, n = 9) neurons.

(E) Average peak voltage (28.7 ± 6.1, 24.8 ± 7.3, 27.0 ± 4.8) measurements of the AP waveforms shown in (D) (for control, α2δ, and shRNA α2δ conditions, respectively).

(F) FWHM (4.51 ± 0.56, 4.38 ± 0.62, and 4.98 ± 0.57 ms) measurements of the AP waveforms shown in (D) (for control, α2δ, and shRNA α2δ conditions, respectively).

These changes in AP_SYN suggest that the α2δ-induced regulation potentially acts through one of the K_V channels primarily responsible for sculpting this waveform. If so, blocking these K⁺ channels should eliminate modulation imparted by α2δ. To test this hypothesis, we examined AP_SYN in the presence of the K_V1 and K_V3 channel blockers TEA and DTX for control, +α2δ-1, and shRNA targeting α2δ-1 neurons (Figure 6D). These experiments demonstrated that the modulation of AP_SYN conferred by α2δ was eliminated after K_V3 and K_V1 blockade: under K_V blockade, both the peak and FWHM of AP_SYN are statistically identical for control, +α2δ-1, and shRNA targeting α2δ-1 neurons (Figures 6E and 6F).

Since blockade of both K_V3 and K_V1 eliminates the associated changes in AP_SYN driven by α2δ manipulation, one can use these same conditions to examine how α2δ manipulation impacts Ca²⁺ influx disentangled from any impact on AP_SYN. We measured Ca²⁺ influx using GCaMP3 in the presence of TEA + DTX and compared this for neurons cotransfected with either α2δ-1 or α2δ-1 shRNA. These experiments showed that overexpressing α2δ-1 led to a 33% increase, while depleting α2δ-1 led to a 40% decrease in Ca²⁺ influx (Figure 7A). Assuming that α2δ-1 does not alter VGCC gating properties, this predicts that overexpression or depletion of α2δ-1 led to a net gain of 1.31 ± 0.10 or a net decrease of 0.59 ± 0.09 in synaptic plasma membrane VGCC abundance, respectively (Figure 7B). We showed that changes in presynaptic Ca²⁺ influx imparted by Kv blockade were in excellent numerical agreement with the quantitative model of VGCC gating driven by our measured AP_SYN waveforms (Figure 5). We sought to determine if the changes in AP_SYN driven by α2δ manipulations would also lead to predictable changes in Ca²⁺ influx, taking into account the above predicted impact on VGCC surface abundance. GCaMP3-based measurements showed that α2δ-1 overexpression or shRNA-based α2δ-1 depletion resulted in a 40% or 20% decrease of presynaptic Ca²⁺ influx, respectively (Figure 7C). These measures were in excellent quantitative agreement with numerical estimates of integrated Ca²⁺ influx simulation based on VGCC gating (Figure 7C) driven by our measured AP_SYN under these conditions (Figure 6A), corrected for the separate changes in VGCC plasma membrane abundance driven by α2δ (Figure 7B). These data demonstrate that control of AP_SYN can dramatically alter Ca²⁺ influx, even lowering the influx despite increases in VGCC abundance.

Figure 7. Adaptive Plasticity in AP_SYN Compensates for Changes in Ca²⁺ Channel Density to Control Ca²⁺ Influx.

(A) Average integrated AP-driven Ca²⁺ influx measured from synaptic boutons in the presence of DTX and TEA from control (black, n = 9), α2δ-1-overexpressing (red, n = 8), and α2δ-1-shRNA-expressing (blue, n = 9) neurons. Bar graphs shown are mean ± SEM. *p < 0.05 using ANOVA comparison with Turkey’s post hoc comparisons to determine significance.

(B) Extrapolated relative density of presynaptic Ca_ve channels normalized to control (black) for α2δ overexpression (red) and targeted knockdown with shRNA (blue). Bar graphs shown are mean ± SEM

(C) Average integrated Ca²⁺ influx measured from synaptic boutons stimulated with one action potential for α2δ overexpression (red) and targeted knockdown with shRNA (blue) as measured by GCaMP3 (solid bars with SEM shown by dashed lines) normalized to control for clarity. Corresponding numerical estimates predicting the integrated I_ce for the gramicidin-calibrated waveforms (Simulation) corrected for changes in presynaptic VGCC abundance (striped bar graphs) are shown adjacently for comparison.

Adaptive changes in presynaptic function have previously been documented at the Drosophila neuromuscular junction, where the system responds rapidly to acute changes in the efficacy of neurotransmission (Müller and Davis, 2012). We wondered if the phenomena uncovered here might reflect a similar homeostatic response to modifications in neurotransmitter release. To test this idea, we examined the AP_SYN waveform at nerve terminals in which exocytosis, and hence neurotransmission, had been eliminated by chronic expression of tetanus toxin light chain (TeTx LC) that cleaves VAMP-2 (Schiavo et al., 1992). One might expect this manipulation to trigger increases in AP_SYN FWHM and peak similar to that obtained by removal of α2δ. In contrast, these experiments revealed that TeTx LC expression did not change AP waveform, indicating that the adaptive plasticity sculpting AP_SYN is not driven by changes in exocytosis (Figure S5). Rather, the adaptive plasticity controlling AP_SYN appears to be directly related to changes in VGCC abundance.

DISCUSSION

The AP waveform encodes parameters that transduce electrical information into a chemical signal via VGCCs. The relative Na_v and K_v channel abundance and their biophysical properties are critical in determining the AP shape and amplitude. Relatively little is known about how the Na_v/K_v balance is achieved, maintained, or potentially exploited for modulatory purposes. This is particularly true of small en passant presynaptic boutons where standard electrophysiological approaches are not easily applied. To examine the characteristics of the AP at small CNS en passant boutons, we made use of the discovery that the light-sensing protein Arch can be excited to generate fluorescence emission whose intensity is linearly proportional to V_m. Although this protein has typically been exploited to drive hyperpolarizing proton currents with light, we think this is unlikely to be playing a significant role in our experiments for several reasons: first, the red excitation used here is much less efficient than the optimum proton-pumping yellow wavelengths; second, the long time scales of exposure (10 s prior to recordings and recordings that last ~50 s) are known to typically inactivate proton pumping; third, we found that these same imaging conditions had no impact on action potential-driven exocytosis; fourth, we found good agreement with a non-proton-pumping mutant of Arch when comparing the gramicidin normalized ΔF/F AP amplitudes in somas versus boutons. The nonpumping variant of Arch, however, has an ~4-fold slower time resolution (Gong et al., 2013) and was not used for further experiments.

Kv Channels Play an Important Role in Controlling AP Amplitude at Synapses

To understand how AP_SYN might be controlled quantitatively, we devised an ionophore-based calibration scheme allowing approximate subcellular calibration. The absolute accuracy of this approach relies upon the assumption that the resting V_m is uniform throughout the cell. To our knowledge, there is no simple method to examine this question; however, potential differences could not account for the observed differences in the AP peak/gramicidin ratio in the two cell compartments we measured. The closeness of the AP_SYN peak with the gramicidin response clearly indicates that the peak cannot reach voltages significantly greater than 0 mV, while at cell somas the AP peak clearly significantly exceeds 0 mV. We cannot directly measure if gramicidin brings V_m to 0 mV at boutons as previously reported at neuronal soma (Maric et al., 1998); however, the slight bias in gramicidin selectivity for K⁺ ions would likely lead to an overestimate of the magnitude of the response and therefore not alter our conclusions. Furthermore if the resting V_m in nerve terminals was significantly lower than that at cell somas, it would imply that the absolute magnitude of AP_SYN is undersestimated but not alter our conclusion that the peak does not significantly exceed 0 mV. Our observations that K_V1/K_V3 channel blockade leads to a significant increase in peak height (>30%) strongly implies that the AP_SYN peak must normally lie well below the Na⁺ reversal potential at synaptic boutons. Finally, numerical estimates of how these waveforms would influence VGCC gating shows that our independent measurements of synaptic Ca²⁺ were best explained by lower-amplitude AP_SYN waveforms (Figures 5F and 7C).

Our findings that the AP peak at en passant synapses (7 mV) lies far below optimal value for maximum open probability of Ca²⁺ channels (~40 mV) stands in contrast to classic studies in the squid stellate ganglion, a giant nerve terminal that carries out a flight response. Measurements of Ca²⁺ influx and presynaptic AP waveforms in the squid giant synapse demonstrated that at its peak AP_SYN reaches a value that will open virtually all available synaptic VGCC, albeit with a low driving force for Ca²⁺ influx, thus driving large Ca²⁺ currents during the falling phase of the AP (Augustine et al., 1985; Katz and Miledi, 1967; Llinás et al., 1981). We speculate that the main difference may simply be due to a lower relative Na⁺ channel density in the en passant boutons studied here. Indeed, at other giant synapses where AP_SYN reaches high positive values, the AP appears to be boosted by specific preterminal Na⁺ enrichments (Leão et al., 2005; Engel and Jonas, 2005; Hu and Jonas, 2014). Interestingly, these latter synapses share a common feature with squid stellate ganglion: they contain multiple active zones and usually discharge a large quantity of vesicles upon activation. Under these conditions, the influence of K_V channels on Ca²⁺ influx is more modest, since it only controls the duration that VGCCs are open, in agreement with computational estimates based on detailed kinetic models of calcium channel opening (Bischofberger et al., 2002). Thus, action potentials that are dominated by Na_V are very reliable transducers of electrical signaling but at the expense of modulation of the waveform and, in turn, Ca²⁺ influx. Our measurements were made in dissociated cultures of hippocampal neurons that lose the inherent circuit architecture found in vivo. Such conditions may therefore make comparisons with recordings in more intact systems difficult. However, recordings of somatic AP waveforms in acute hippocampal slices report AP shapes very similar to the values we report here (Meeks et al., 2005).

Functional Consequences of Low-Voltage Action Potentials

We speculate that many neurons in the brain with small en passant synapses and single active zones that dominate the hippocampus and cortex are optimized for much greater modulation of Ca²⁺ influx by relying on a predominance of K_V channels and the resulting lower-amplitude APs. Interestingly, we found two conditions impacted the peak of AP_SYN that were accompanied by changes in Ca²⁺ influx, consistent with our low-voltage AP model. In the first case, blockade of K_V3.1 and K_V1.1 led to an ~30% increase in AP_SYN amplitude and an ~300% increase in Ca²⁺ influx. This increase was in excellent agreement with independent numerical simulations of Ca²⁺ influx with waveforms whose amplitudes change from +7 to + 28 mV in addition to the observed changes in FWHM. In the second case, overexpression of α2δ led to decreases in AP_SYN amplitude and FWHM that led to ~45% decreases in Ca²⁺ influx, despite the ~30% increase in presynaptic VGCC abundance (see below). We found that the two dominant channels that dictate AP waveform in the synapse were the fast-activating K_V1 and K_V3 channels. These channels are classically low- and high-voltage activated, respectively, and it is therefore surprinsing that both seem to constrain the AP_SYN peak. This suggests that the activation threshold for Kv3 channels in the axon may be lower than that reported from recordings in cell somas or nonneuronal cells.

Adaptive Plasticity in the AP_SYN Waveform

Modifications in AP_SYN upon α2δ manipulation may represent a way to maintain Pr in a useful operating range when VGCC numbers are altered. We previously found that α2δ expression resulted in closer coupling of VGCCs to release sites, which alone would have driven increases in Pr. Our experiments show that such changes also drive compensatory changes in AP_SYN, resulting in higher Pr with less total Ca²⁺ influx. These changes in AP_SYN are entirely eliminated by K_V3.1/K_V1.1 blockade. We further used the K_V3.1/K_V1.1 blockade to measure Ca²⁺ entry since this separates changes associated with different APs. We conclude that although overexpression of α2δ can almost triple the total abundance of Ca_V2.1, it likely only leads to an ~30% increase in surface VGCCs, while suppression of α2δ expression leads to an ~40% decrease (assuming no significant impact of these conditions on VGCC gating). These studies imply that the ability to increase the surface abundance of VGCCs is limited. The molecules and mechanisms that set this limit are currently unknown, but the experimental paradigm introduced here should prove useful in future molecular investigations.

The availability of robust optical tools allowed us to investigate unique features or the presynaptic AP waveform that revealed several consequential principles: (1) the presynaptic AP peak amplitude is much smaller than that measured at the soma; (2) this amplitude allows a wider range of modulation of the waveform and AP-driven Ca²⁺ entry; and (3) the presynaptic waveform displays adaptive plasticity in response to changes in VGCC abundance. We expect that the approaches developed here to investigate the control of presynaptic action potentials will prove indispensable for further molecular dissection of Ca²⁺ channel function in the presynaptic milieu.

EXPERIMENTAL PROCEDURES

Cell Culture

Hippocampal CA1–CA3 regions were dissected with dentate gyrus removed from ~36 hr-old Sprague-Dawley rats, dissociated (bovine pancreas trypsin; 5 min at room temperature [RT]), and plated onto polyornithine-coated cover-slips inside a 6-mm diameter cloning cylinder as previously described (Hoppa et al., 2012). Calcium phosphate-mediated gene transfer was used to transfect 7-day-old cultures with the described plasmids (below) as previously described (Ariel and Ryan, 2010). Sprague-Dawley rats met with the approval of Weill Cornell Institutional Review.

Plasmids

Arch-GFP was acquired from Addgene (Plasmid 22217: FCK-Arch-GFP) and cotransfected at a 5:4 ratio with other cDNA. “Dark-Arch,” which contains a TYG-to-GGG mutation in the eGFP chromophore that reduces the quantum yield, was kindly provided by A. Cohen (Harvard University). The vGlut-pHluorin construct is as previously described (Balaji and Ryan, 2007). Physin-GCaMP3 was kindly provided by Loren Looger. GFP-Archaerhodopsin-3 (Arch) Plasmid and Arch-EEQ mutant were acquired from Addgene. The TeTx LC sequence was PCR amplified from a plasmid kindly provided by M. Dong (Harvard Medical School) and inserted into a pcDNA3 vector. shRNAs for rat K_V1.1 and K_V3.1b were based on the following sequences: rat K_V1.1, TAGTTCTCCTAACTTAGCCTCTGACAGTG; rat K_V3.1b, ACCTTC GAGTTCCTCATGCGTGTTGTCTT. These sequences were provided in host vectors from OriGene USA.

Live-Cell Imaging and Stimulation Conditions

All experiments were performed at 30°C using a custom-built objective heater. Coverslips were mounted in a rapid-switching, laminar-flow perfusion and stimulation chamber on the stage of a custom-built laser-scanning confocal microscope. The total volume of the chamber was ~75 μl and was perfused at a rate of 400 μl/min. During imaging, cells were continuously perfused in a standard saline solution containing the following in mM: 119 NaCl, 2.5 KCl, 2 CaCl₂, 2 MgCl₂, 25 HEPES (buffered to pH 7.4), 30 glucose, 10 μM 6-cyano-7-nitroquinoxaline-2,3-dione (Research Biochemicals), and 50 μM D,L-2-amino-5-phosphonovaleric acid (Research Biochemicals). TTX was used at a concentration of 300 nM (Alomone Labs). Iberiotoxin (IBX), Tetrodotoxin (TTX), Conotoxin MVIIC (Cono), and Dendrotoxin-K (DTX) were supplied by Alomone Labs. All toxins were kept as 1000× stock solutions in water for no more than 30 days stored at −20°C before use. Tetraethylammonium chloride (TEA) was procured from Sigma and stored at RT. Working concentrations were as follows: 100 nM for IBX, 300 nM for TTX, 3 μM for Cono, 100 nM for DTX, and 1 mM for TEA. All toxins were applied for 2 min (except iberiotoxin, which was applied for 5 min) before any measurements in live-cell experiments. Chemicals were purchased from Sigma, except where noted.

Timing between TTX application and washout experiments was ~8 min. For all measurements of AP_SYN, we used a three-part selection criteria to select region of interest (ROI) for AP_SYN measurement. First, all our measured boutons were >300 μm from the soma and included distinct tiny swellings (<2 μm diameter) indicative of en passant boutons. Second, we engaged in three rounds of trial averaging before, during, and after application of TTX. We only proceeded in our measurements if there was TTX sensitivity as well as a full recovery of spike firing after TTX washout to validate the measured spikes at action potential waveforms. As a third criteria, we also assayed shape and stability of the axon over these trials with termination of experiments if there was any swelling or large movement of the axon over the recording period.

Stimulus Control

Action potentials were evoked by passing 1 ms current pulses, yielding fields of ~12 V/cm (unless otherwise noted) through the chamber via Platinum/Iridium electrodes. For averaging across many trials in Arch recordings, the stimulus was locked to defined frame number intervals using a custom-built 14-bit hardware counter. Unless otherwise noted, trial averaging of AP waveforms were derived from 390 stimuli delivered at ~8 Hz. For lower time resolution experiments (vGlut-pHluorin, GCamP3) stimuli were controlled through software counting via a USB-DAQ (Texas Instruments; NI-DAQ mx 6501) programmed in Labview.

Wide-Field Imaging

Specimens of Archaerhodopsin-transfected neurons were illuminated by a 637 nm laser 140 mW (Coherent OBIS Laser) with HQ620/60× and 660LP dichroic (Chroma) through a 40× 1.3 NA Zeiss Fluar Objective and a custom beam expander to provide an ~25 μm diameter spot with a final power density of ~2,250 W/cm². Archaerhodopsin fluorescent emission was collected through a HQ700/75 m filter (Chroma) and captured with an IXON3 897 camera (Andor) in a cropped sensor mode (10 MHz readout, 500 ns pixel shift speed) to achieve 2 kHz frame rate imaging (exposure time of 485 μs) over an 85 × 27 pixel area with the use of an intermediate image plane mask (Optomask, Cairn Research) to prevent light exposure of nonrelevant pixels. Light was collected through an HQ700/75 m filter (Chroma). Measurements using vGlut-pHluorin were measured as previously described (Ariel and Ryan, 2010). For combined measurements of pHluorin and Arch, we used a custom set of optical filters made by Chroma, with a zet488/640 dichroic and dual-band excitation filter 500/60 and 620/60×. Solid-state diode pumped 488 or 561 nm lasers (both 100 mW; Coherent Sapphire) that were shuttered using acousto-optic tunable filters. Light was collected through a zet405/488/640 m filter (Chroma). For all combined pHluorin and Arch experiments, an additional 514/30 emission filter was inserted into the optical pathway to block any possible light contamination from strong 640 nm illumination. For these experiments, fluorescent emission was captured at 1 kHz for increased field of view. Optical measurements of Ca²⁺ using linearization of GCaMP3 and measurements of exocytosis using vGlut-pHluorin were achieved as previously described (Hoppa et al., 2012). Briefly, GCaMP3 fluorescence was collected with an exposure time of 49.72 ms and images acquired at 20 Hz, while pHluorin fluorescence was collected with an exposure time of 18.72 ms acquired at 50 Hz. Combined measurements of Arch_DARK and Fluo5F were acquired at 1 kHz using identical filter sets as described for vGpH and Arch above. After finding a responsive axonal branch expressing VAMP-mOrange2 with boutons for firing action potentials, the dish was loaded with Fluo5F-AM dye (1 μg/ml) for 10 min at 30°C and then washed with perfusion with standard Tyrodes saline as described above for 20 min. Ca²⁺ Influx and AP waveform were then measured using time-locked stimulation.

Local Calibration of Arch Fluorescence

Local calibration of Arch was achieved by measuring the change in fluorescence (ΔF/F) of cell somas or presynaptic boutons in response to application of gramicidin (G5002, Sigma). Gramicidin stock solution was prepared by dissolving in MeOH (10 mg/ml) stored at 4°C. Stock was added to a saline solution containing (in mM) 156 NaCl, 2 KCl, 10 HEPES (pH 7.1), 10 glucose, 10 μM CNQX, 50 μM AP-5, with a final gramicidin concentration of 200 μg/ml. In order to increase measurement accuracy, we increased the imaging area to 100 × 40 pixels and an exposure time of 975.6 μs (1 kHz acquisition). The response was determined from the average fluorescence over 3 s of data in the plateau region of the response. As gramicidin is permeant to monovalent cations, this should collapse V_m to 0 mV. To obtain an approximate calibration, we assumed the resting potential prior to gramicidin application was −65 mV, which is in agreement with most measurements and is expected from the Goldman Hodgkin Katz equation $V_m=RT/Fln((pK{[K]}_o^{+}+\mathit{pNa}{[Na]}_o^{+}+\mathit{pCl}{[Cl]}_i^{-})/(pK{[K]}_i^{+}+\mathit{pNa}{[Na]}_i^{+}+\mathit{pCl}{[Cl]}_o^{-}))$ with intracellular concentrations of the following (in mM): 140 K⁺, 20 Na⁺, 18 Cl⁻; with associated permeabilities (p) of 1.0:0.05:0.45 for pK⁺:pNa⁺:pCl⁻, respectively. These data indicate that at boutons the effective sensitivity of Arch provides a change in fluorescence (ΔF/F) corresponding to 0.63%/mV, while at cell somas it was 0.24%/mV.

Image and Data Analysis

Images were analyzed in ImageJ (http://rsb.info.nih.gov/ij) by using custom-written plugins (http://rsb.info.nih.gov/ij/plugins/time-series.html). Stimulation with 300 nM TTX was used to isolate the field stimulation from AP signal and was subtracted from our AP recordings at the soma and bouton. ΔF/F values of the AP were calculated after background subtraction. Measurements of background were measured using a square 10 × 10 pixel ROI. Finally, AP waveforms were corrected for the temporal resolution of Arch by deconvolution using an FFT-based algorithm in Origin Pro 8 with a normalized 500 μs exponential response function. Automated peak and FWHM analyses were carried out using Origin Pro 8’s peak-fitting algorithm. To determine the FWHM of AP waveforms in individual trials, spline fitting (Matlab, Mathworks) using a cubic smoothing B-spline to interpolate between frames at an over-sampled time resolution of 10 μs was used.

Immunofluorescence and Quantification

To quantify the efficiency of shRNA-mediated KD, neurons were fixed for 10 min with 1% paraformaldehyde and blocked with TBS containing 4% nonfat dry milk and 0.3% Triton X-100 for 30 min and incubated with the primary antibody at 1:1,000 in TBS with 4% nonfat dry milk at 4°C overnight. Alexa 488-, Alexa 546-, and Alexa 647-conjugated secondary antibodies were applied in primary antibody incubated samples with different color combinations as needed. Immunofluorescence images of fixed cells were acquired using an epifluorescence microscope with an EMCCD camera. Expression levels of K_V1 were measured using an anti-K_V1.1 antibody (NeuroMab, UC Davis/NIH) at cell bodies corrected for background in surrounding regions to avoid possible spatial overlap with other cells. This was compared to the fluorescence intensity in nontransfected (GFP-negative) cell bodies.

Numerical Simulation of Calcium Influx for Different AP Waveforms

The multistate model of the closed and open states of VGCCs at nerve terminals (states S_n, where n = 0–4 are closed states and n = 5 is an open state) (Li et al., 2007) as described by the following: for n = 0, dS_n(t)/dt = −k⁺_n(V)^*S_n + k⁻_n+1(V)^*S_n+1(t); for n = 1–3, dS_n(t)/dt = k⁺_n−1(V)^*S_n−1(t) − k⁻_n(V)^*S_n(t) −k⁺_n(V)^*S_n + k⁻_n+1(V)^*S_n+1(t); for n = 4, dS_n(t)/dt = k⁺_n−1(V)^*S_n−1(t) − k⁻_n(V)^*S_n(t) − k⁺_n^*S_n + k⁻_n+1^*S_n+1(t); for n = 5 (open state), dO(t)/dt = k⁺₄^*S₄(t)−k⁻_o^*O(t); where for n = 0–3, k⁺_n(V) = α_ne^(V(t)/Vn); for n = 4, k⁺₄ = α₄; for n = 1–4, k⁻_n(V) = β_ne^(−V(t)/Vn); and for n = 5, k⁻₅ = β₅.

These differential equations were integrated numerically with a fourth-order Runge-Kutta method in Berkeley Madonna with V(t) defined by the different AP waveforms as described. The results are plotted as the integrated value of Ca influx, where Ca(t) = (55 mv − V(t))^* (0.8^*O_Cav2.2(t) + 0.2^*O_Cav2.1(t)).

The different channel contributions were taken as 80% N-type (Cav2.2) and 20% P-type (Cav2.1) using the gating parameters as determined in Li et al. (2007), and an effective reversal potential of 55 mV was assumed. We adjusted the rate constants determined in Li et al. (2007) for the fact that our measurements are carried out at 30°C while the gating measurements were carried out at 23°C. A temperature factor of two was therefore used in all rate constants.