Heteronuclear transverse and longitudinal relaxation in AX₄ spin systems: Application to ¹⁵N relaxations in ¹⁵NH₄⁺

Highlights

• •Group theory is used to simplify the calculations of nuclear spin relaxation rates.
• •Transverse and longitudinal ¹⁵N nuclear relaxation rates in ¹⁵NH₄ ⁺ are derived.
• •An ammonium ion bound to a protein domain rotates rapidly within its binding site.

Abstract

The equations that describe the time-evolution of transverse and longitudinal ¹⁵N magnetisations in tetrahedral ammonium ions, ¹⁵NH₄⁺, are derived from the Bloch-Wangsness-Redfield density operator relaxation theory. It is assumed that the relaxation of the spin-states is dominated by (1) the intra-molecular ¹⁵N–¹H and ¹H–¹H dipole–dipole interactions and (2) interactions of the ammonium protons with remote spins, which also include the contribution to the relaxations that arise from the exchange of the ammonium protons with the bulk solvent. The dipole–dipole cross-correlated relaxation mechanisms between each of the ¹⁵N–¹H and ¹H–¹H interactions are explicitly taken into account in the derivations. An application to ¹⁵N-ammonium bound to a 41 kDa domain of the protein DnaK is presented, where a comparison between experiments and simulations show that the ammonium ion rotates rapidly within its binding site with a local correlation time shorter than approximately 1 ns. The theoretical framework provided here forms the basis for further investigations of dynamics of AX₄ spin systems, with ammonium ions in solution and bound to proteins of particular interest.

1. Introduction

The transverse and longitudinal nuclear spin-relaxation rates, which can be obtained from NMR spectra, are accurate reporters on the interactions and dynamics of molecules ranging from small organic molecules and ions [1], [2], [3], [4] to large macromolecular complexes [5], [6], [7], [8]. The observed relaxation rates can be modulated when the nuclei in question exchange between different magnetic environments, which has stimulated the development of theory [9] and solution-state NMR pulse sequences [10], [11], [12] to probe chemical exchange from nuclear relaxation rates and also methods to separate the contributions from exchange and internal dynamics [13], [14].

Under physiological conditions, the chemical exchange of the ¹⁵NH₄ ⁺ protons with the bulk solvent is so fast that these protons are barely observed in even simple one-dimensional ¹H NMR spectra. Moreover, the exchange rate of the ammonium protons with the bulk solvent is often much faster than the ¹⁵N–¹H scalar coupling [15] thus hindering the acquisition of two-dimensional ¹⁵N–¹H correlation spectra. However, under certain conditions, including acidic aqueous solutions and when the ammonium ion is bound to proteins [16] or nucleic acid complexes [17], [18], [19], the exchange rate of the ammonium protons becomes sufficiently slow to allow for both detection of the ammonium protons and acquisition of ¹⁵N–¹H correlation spectra. The feasibility of obtaining such ¹⁵N–¹H correlation maps provides a promising tool for characterising the dynamics of the ammonium ion and for correlating the dynamics with the environments.

The ionic radius of the ammonium ion (1.44 Å) is similar to the radius of the potassium ion (1.33 Å), so that ammonium can be used as a proxy for potassium to probe potassium binding sites [16], [17], [18], [19] in proteins and nucleic acids. As was shown recently [16], ¹⁵NH₄ ⁺ can be observed even when bound to proteins with molecular weights in excess of 40 kDa, but it is currently not clear whether it is fast reorientation of the ammonium ion within the binding site or favourable cross-correlated relaxation mechanisms that allow for such measurements.

Given the development of techniques to probe ammonium ions in proteins and nucleic acids and also considering the interest in probing the regulations of enzymes by monovalent cations in general, it is of interest to derive equations that describe the transverse and longitudinal relaxations of ammonium ions under various conditions. A derivation of the ¹⁵N relaxation rates of ammonium ions is presented here, which is based on Bloch-Wangsness-Redfield relaxation theory as well as group theory. An application to ¹⁵N-ammonium bound to a 41 kDa domain of the protein DnaK is presented, illustrating the utility of the derived equations.

2. Theory and results

The longitudinal and transverse relaxation rates of the various spin-states of the ¹⁵N-ammonium AX₄ spin-system are calculated using the Bloch-Wangsness-Redfield theory [20], [21], [22], [23]. We assume here that the geometric structure of the AX₄ spin-system is that of a tetrahedron, which for ammonium means that the ¹⁵N nucleus is in the centre, with each of the four protons located at the corners of the tetrahedron (see below). Thus, the symmetry-adapted elements of an irreducible basis representation have symmetries that fall within the irreducible representations of the T_d point group [24], that is, A ₁, A ₂, E, T ₁, T ₂. The total spin density operator that completely describes the spin-state of ¹⁵NH₄ ⁺ can be written as a direct product of spin density operators describing the ¹⁵N and proton spin-states. The ¹⁵N and proton spin density operators can in turn be expressed as linear combinations of a set of basis operators. Here we derive ¹⁵N relaxation rates in terms of two sets of proton spin density basis operators: (1) Proton spin density operators that are the projection operators of the eigenfunctions to the proton Zeeman Hamiltonian. These energy eigenfunctions are denote by |m ₁ m ₂ m ₃ m ₄〉, where m_i (i  = 1, 2, 3, 4) is the eigenvalue of the Zeeman Hamiltonian (α  ≡ 1/2, β  ≡ −1/2). The corresponding projection operator, which is the relevant density operator element, is denoted by |m ₁ m ₂ m ₃ m ₄〉〈m ₁ m ₂ m ₃ m ₄|. (2) Proton spin density operators from the basis of Cartesian/shift operator basis, where each basis operator represents a combination of longitudinal and zero-quantum magnetisations of the four protons, that is, {H _z1, H _z2, … ,  H _z1 H _z2, … ,  H ₊₁ H ₋₂, … ,  H _z1 H _z2 H _z3 H _z4}, where H _{z i} is the longitudinal product operator of proton i, and H _{+ i} and H _{− i} are the corresponding shift (raising and lowering) operators. As shown below, we use group theory to derive symmetry-adapted proton spin eigenfunctions, thereby simplifying the calculation of the relaxation rates.

2.1. Constructing symmetry-adapted basis functions

Symmetry-adapted basis functions for the spin wavefunctions in tetrahedral T _d symmetry can be conveniently constructed with the basic tools of group theory. The major strength of using the symmetry-adapted basis functions, as opposed to non-symmetry adapted functions, is that time-evolutions are simpler since total-symmetric Hamiltonians (A ₁ in the T _d point group) cannot mix functions with different symmetry. In the context of NMR spectroscopic investigations of AX₄ spin-systems, this means that the time-evolution of the spin-system and the observed relaxation rates are more intuitive. Below we briefly outline how the symmetry-adapted basis functions, which are also eigenfunctions of the proton Zeeman Hamiltonian, ${\widehat{\mathcal{H}}}_Z$, are constructed.

For the four X spins of the AX₄ spin system, for example the four protons of the ammonium ion, the Zeeman basis consists of 16 elements, which we denote as {|αααα〉, |αααβ〉, |ααβα〉, ... , |ββββ〉}, and which satisfy the following eigenvalue equation:

$${\widehat{\mathcal{H}}}_Z|m_1{m}_2{m}_3{m}_4\rangle =(m_1+m_2+m_3+m_4)\hslash {\omega }_{\text{H}}|m_1{m}_2{m}_3{m}_4\rangle$$ (1)

The symmetry-operations within the T _d point group are those of one E (identity operator), eight C ₃ axes (proper rotations), three C ₂ axes (proper rotations), six S ₄ axes (improper rotations), and six σ _d planes (dihedral symmetry planes) [24]. Thus, the order of the T _d group, h, is 24, and the T _d point-group is isomorphic to the S ₄ symmetric group of permutations of four elements.

It is noted that the 24 symmetry operations cannot mix states with different eigenvalues to the Zeeman Hamiltonian; that is, the matrix representations of the symmetry elements are block-diagonal. The function |αααα〉 is the only function with eigenvalue $+2\hslash {\omega }_{\text{H}}$ and since this function is total-symmetric it is already an irreducible representation with symmetry A ₁. The four functions {|αααβ〉, |ααβα〉, |αβαα〉, |βααα〉} are the only functions with eigenvalue of $+\hslash {\omega }_{\text{H}}$ and these functions are therefore considered separately. The number of symmetry-adapted basis functions within each of the irreducible representations of the T_d group is determined using Schur’s orthogonality theorems [24], [25] that leads to

$$a_l=\frac{1}{h}{\displaystyle \sum _c}g(c){\chi }^{(l)}{(c)}^{\ast }\chi (c)$$ (2)

where a_l is the number of functions with representation l, the sum is over the classes c of symmetry operations, g(c) is the number of operations within the class, and ${\chi }^{(l)}(c)$ and $\chi (c)$ are the characters of the representation l and of the set of functions in question, respectively. The characters ${\chi }^{(l)}(c)$ are available from standard character-tables while $\chi (c)$ is simply the number of basis functions that do not change under the given symmetry operation. Thus,

$$a_{A1}=\frac{1}{24}(1\times 1\times 4+8\times 1\times 1+3\times 1\times 0+6\times 1\times 0+6\times 1\times 2)=1$$ (3)

$$a_{A2}=\frac{1}{24}(1\times 1\times 4+8\times 1\times 1+3\times 1\times 0+6\times (-1)\times 0+6\times (-1)\times 2)=0$$ (4)

$$a_E=a_{T1}=0$$ (5)

$$a_{T2}=\frac{1}{24}(1\times 3\times 4+8\times 0\times 1+3\times (-1)\times 0+6\times (-1)\times 0+6\times 1\times 2)=1$$ (6)

The four basis functions, {|αααβ〉, |ααβα〉, |αβαα〉, |βααα〉}, therefore span one function with A ₁ symmetry and three functions with T ₂ symmetry (the order of the T ₂ symmetry is three). The full set of symmetry-adapted functions are now generated from the original set by applying the 24 symmetry operations and multiplying by the character of the symmetry operation in question as detailed elsewhere [24], [25]. Thus, generation from |αααβ〉 gives,

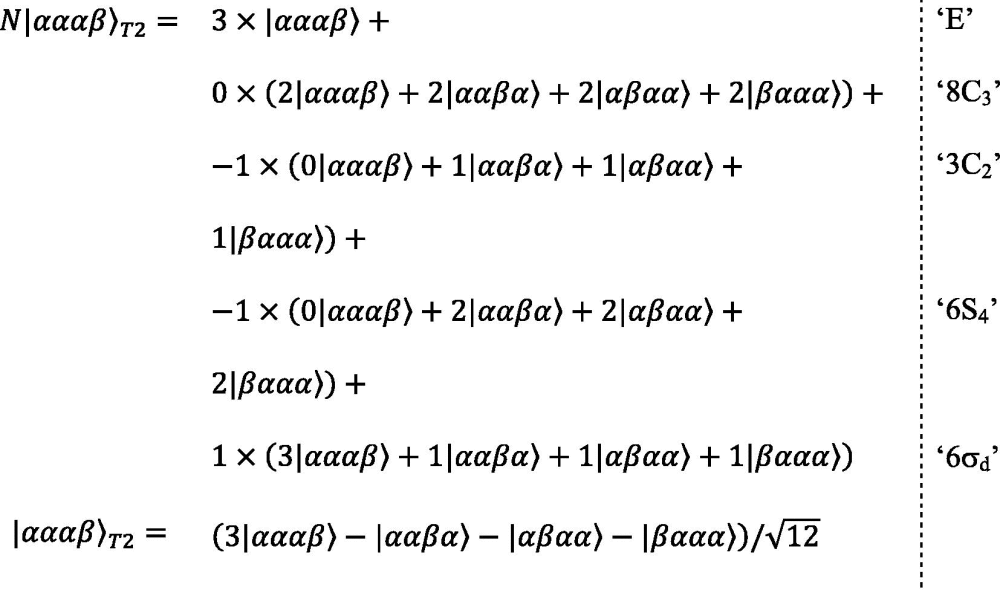(7)

Three additional functions with T ₂ symmetry can be constructed in a similar manner by applying the procedure detailed in Eq. (7) to the other three functions that have an eigenvalue of $+\hslash {\omega }_{\text{H}}$, that is |ααβα〉, |αβαα〉 and |βααα〉. Finally, a basis set of functions with T ₂ symmetry, which consists of three orthonormal functions, can be constructed from linear combinations of the four functions generated above. Although the exact form of such a basis set can vary, we chose here to use the three functions that are also eigenfunctions to the C ₂ operators as basis functions; these functions are given in Fig. 1 . The linear combination with A ₁ symmetry can be generated following a strategy similar to the one given above, yielding:

$${|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\rangle }_{A1}=(|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\rangle +|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\mathrm{\alpha }\rangle +|\mathrm{\alpha }\mathrm{\beta }\mathrm{\alpha }\mathrm{\alpha }\rangle +|\mathrm{\beta }\mathrm{\alpha }\mathrm{\alpha }\mathrm{\alpha }\rangle )/2$$ (8)

Fig. 1.

Energy level diagram and nitrogen transitions within the Zeeman basis for the AX₄ spin-system, exemplified by the ¹⁵NH₄⁺ ammonium ion that forms the basis for the theoretical framework and relaxation rate calculations presented here. Shown from the top-left are a spin-2 manifold with A₁ symmetry, three degenerate spin-1 manifolds with T₂ symmetry and two degenerate spin-0 manifolds (singlet) with E symmetry. The ¹⁵N single-quantum transitions are marked with arrows and numbered.

Following the method outlined above in Eqs. (1), (2), (3), (4), (5), (6), the six basis functions with eigenvalue of 0 to the proton Zeeman Hamiltonian, {|ααββ〉, ... , |ββαα〉}, can be shown to span one function with A ₁ symmetry, three functions with T ₂ symmetry and two functions with E symmetry. The function with A ₁ symmetry is trivially given by the sum of the six elements:

$${|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\mathrm{\beta }\rangle }_{A1}=(|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\mathrm{\beta }\rangle +|\mathrm{\alpha }\mathrm{\beta }\mathrm{\alpha }\mathrm{\beta }\rangle +|\mathrm{\alpha }\mathrm{\beta }\mathrm{\beta }\mathrm{\alpha }\rangle +|\mathrm{\beta }\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\rangle +|\mathrm{\beta }\mathrm{\alpha }\mathrm{\beta }\mathrm{\alpha }\rangle +|\mathrm{\beta }\mathrm{\beta }\mathrm{\alpha }\mathrm{\alpha }\rangle )/\sqrt{6}$$ (9)

The functions with T ₂ symmetry and E symmetry can be generated using the basis function |ααββ〉 for generation and the method outlined in Eq. (7), which gives:

$${|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\mathrm{\beta }\rangle }_{T2}=(|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\mathrm{\beta }\rangle -|\mathrm{\beta }\mathrm{\beta }\mathrm{\alpha }\mathrm{\alpha }\rangle )/\sqrt{2}$$ (10)

$${|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\mathrm{\beta }\rangle }_E=(2|\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\mathrm{\beta }\rangle -|\mathrm{\alpha }\mathrm{\beta }\mathrm{\alpha }\mathrm{\beta }\rangle -|\mathrm{\alpha }\mathrm{\beta }\mathrm{\beta }\mathrm{\alpha }\rangle -|\mathrm{\beta }\mathrm{\alpha }\mathrm{\alpha }\mathrm{\beta }\rangle -|\mathrm{\beta }\mathrm{\alpha }\mathrm{\beta }\mathrm{\alpha }\rangle +2|\mathrm{\beta }\mathrm{\beta }\mathrm{\alpha }\mathrm{\alpha }\rangle )/2\sqrt{3}$$ (11)

The function given in Eq. (10), along with the other functions with T ₂ symmetry that are directly generated following the method described above, are already eigenfunctions to the C ₂ operators. The full set of three orthonormal basis functions is given in Fig. 1. Moreover, the function given in Eq. (11) with E symmetry is also already an eigenfunction to the C ₂ operators. Finally, the symmetry-adapted functions, |αβββ〉_A1, |αβββ〉_T2, |ββββ〉_A1, are obtained by exchanging α for β and β for α in the functions obtained above, i.e., |αααβ〉_A1, |αααβ〉_T2, |αααα〉_A1. The resulting energy level diagram and the orthonormal basis functions are shown in Fig. 1, which also shows the nitrogen transitions coupled to the Zeeman symmetry-adapted basis set of proton spin-states.

2.2. Transitions and heteronuclear transverse relaxation within the AX₄ spin-system

Fig. 1 shows the symmetry-adapted basis functions for the Zeeman Hamiltonian in the tetrahedral ammonium ion. An important consequence of the tetrahedral symmetry of the ammonium ion is that a total-symmetric Hamiltonian, which is invariant under the symmetry operations of the molecule, can only mix states with the same symmetry. Therefore, the five eigenfunctions with A ₁ symmetry, {|αααα〉_A1, |αααβ〉_A1, |ααββ〉_A1, |αβββ〉_A1, |ββββ〉_A1}, form a separate spin-2 manifold; the functions with T ₂ symmetry form a degenerate set of three spin-1 manifolds, while the functions with E symmetry form two spin-0 manifolds (singlets).

The angular frequencies of the nine nitrogen transitions shown in Fig. 1 depend both on the total Zeeman Hamiltonian, ${\widehat{\mathcal{H}}}_Z=(H_{z1}+H_{z2}+H_{z3}+H_{z4}){\omega }_{\text{H}}+N_z{\omega }_{\text{N}}$ and the ¹⁵N–¹H scalar-coupling Hamiltonian, ${\widehat{\mathcal{H}}}_J=\pi J_{\text{NH}}(2H_{z1}{N}_z+2H_{z2}{N}_z+2H_{z3}{N}_z+2H_{z4}{N}_z)$. The transitions ν₁  =  N ₊(|ββββ〉〈ββββ|_A1) and ν₅  =  N ₊(|αααα〉〈αααα|_A1) therefore form the two outer-most lines of the AX₄ quintet, the central line is formed from ν₃, ν₇ and ν₉ and {ν₂, ν₆} and {ν₄, ν₈} form the remaining two lines. Here the transitions associated with a degenerate set of manifolds are constructed as normalised sums, as described previously [26], for example, ν₆  =  N ₊(|αβββ〉〈αβββ|_T2,1  + |αβββ〉〈αβββ|_T2,2  + |αβββ〉〈αβββ|_T2,3)$/\sqrt{3}$, where |αβββ〉〈αβββ|_T2,i symbolise the population operators of the three degenerate levels (i  = 1, 2, 3) within the T ₂ symmetry.

When transverse ¹⁵N magnetisation of the ammonium ion is created in a standard NMR experiment the spin-state is conveniently described using the product operator formalism [27]. Here, the equilibrium density operator, σ _eq, of the spin system can be written: σ _eq  ∝  γ _H (H _z1  +  H _z2  +  H _z3  +  H _z4) +  γ _N N _z, where γ _H and γ _N are the gyromagnetic ratios of the proton and the nitrogen, respectively, and H _z1, … ,  H _z4 and N _z are the canonical Cartesian product operator density elements describing the longitudinal magnetisations of the four protons and the nitrogen spin, respectively. The equilibrium density operator, σ _eq, contains the sum of the longitudinal magnetisation of all the protons and the symmetry of σ _eq is therefore totally-symmetric A ₁ representation. Density operators created by evolving the ¹H–¹⁵N scalar coupling Hamiltonian will therefore also be of A ₁ symmetry. For example, the first INEPT of a standard ¹H–¹⁵N correlation experiment, 90_x(¹H) − 1/4J _NH  − 180_x(¹H,¹⁵N) − 1/4J _NH  − 90_y(¹H), will lead to a density operator proportional to 2N _z(H _z1  +  H _z2  +  H _z3  +  H _z4), which we denote 2N _z H _z. For calculations of time-evolutions of the AX₄ spin-system it is therefore also often convenient to consider the basis constructed from the Cartesian operators; Table 1 provides the relationship between the two basis sets in the context of transverse ¹⁵N magnetisation for the ammonium ion.

Table 1.

Relationship between the elements of the Cartesian longitudinal product operator basis and the transitions of the Zeeman basis.

Cartesian basisa	Zeeman basis
N+	${\nu }_1+{\nu }_2+{\nu }_3+{\nu }_4+{\nu }_5+\sqrt{3}{\nu }_6+\sqrt{3}{\nu }_7+\sqrt{3}{\nu }_8+\sqrt{2}{\nu }_9$
2N+Hz	$4{\nu }_1+2{\nu }_2+0{\nu }_3-2{\nu }_4-4{\nu }_5+2\sqrt{3}{\nu }_6+0{\nu }_7-2\sqrt{3}{\nu }_8+0{\nu }_9$
4N+HzHz	$6{\nu }_1+0{\nu }_2-2{\nu }_3+0{\nu }_4+6{\nu }_5-0{\nu }_6-2\sqrt{3}{\nu }_7+0{\nu }_8+2\sqrt{2}{\nu }_9$
8N+HzHzHz	$4{\nu }_1-2{\nu }_2+0{\nu }_3+2{\nu }_4-4{\nu }_5-2\sqrt{3}{\nu }_6+0{\nu }_7+2\sqrt{3}{\nu }_8+0{\nu }_9$
16N+HzHzHzHz	${\nu }_1-{\nu }_2+{\nu }_3-{\nu }_4+{\nu }_5-\sqrt{3}{\nu }_6+\sqrt{3}{\nu }_7-\sqrt{3}{\nu }_8+\sqrt{2}{\nu }_9$
N+H+H−	$0{\nu }_1+3{\nu }_2+4{\nu }_3+3{\nu }_4+0{\nu }_5-\sqrt{3}{\nu }_6+0{\nu }_7-\sqrt{3}{\nu }_8-2\sqrt{2}{\nu }_9$
2N+H+H−Hz	$0{\nu }_1+6{\nu }_2+0{\nu }_3-6{\nu }_4+0{\nu }_5-2\sqrt{3}{\nu }_6+0{\nu }_7+2\sqrt{3}{\nu }_8+0{\nu }_9$
4N+H+H−HzHz	$0{\nu }_1+3{\nu }_2-4{\nu }_3+3{\nu }_4+0{\nu }_5-\sqrt{3}{\nu }_6+0{\nu }_7-\sqrt{3}{\nu }_8+2\sqrt{2}{\nu }_9$
N+H+H−H+H−	$0{\nu }_1+0{\nu }_2+4{\nu }_3+0{\nu }_4+0{\nu }_5+0{\nu }_6-4\sqrt{3}{\nu }_7-0{\nu }_8+4\sqrt{2}{\nu }_9$

^aThe following notation has been used: H_z = H_z1 + H_z2 + H_z3 + H_z4; H_zH_z = H_z1H_z2 + H_z1H_z3 + H_z1H_z4 + H_z2H_z3 + H_z2H_z4 + H_z3H_z4; H_zH_zH_z = H_z1H_z2H_z3 + H_z1H_z2H_z4 + H_z1H_z3H_z4 + H_z2H_z3H_z4; H_zH_zH_zH_z = H_z1H_z2H_z3H_z4; H₊H₋ = ${\sum }_{i\ne j}{H}_{+\text{,}i}{H}_{-\text{,}j}$; H₊H₋H_z = ${\sum }_{i\ne j\ne k}{H}_{+\text{,}i}{H}_{-\text{,}j}{H}_{z\text{,}k}$; H₊H₋H_zH_z = ${\sum }_{i\ne j\ne k\ne l}{H}_{+\text{,}i}{H}_{-\text{,}j}{H}_{z\text{,}k}{H}_{z\text{,}l}$; H₊H₋H₊H₋ = ${\sum }_{i\ne j\ne k\ne l}{H}_{+\text{,}i}{H}_{-\text{,}j}{H}_{+\text{,}k}{H}_{-\text{,}l}$.

2.3. Time-evolution of the spin-system

Following the Bloch-Wangsness-Redfield theory [20], [21], [22], [23], the evolution of the spin-system is given by the Liouville-von Neumann equation,

$$\frac{d\sigma (t)}{\mathit{dt}}=-i[{\widehat{\mathcal{H}}}_0\text{,}\sigma (t)]-\widehat{\Gamma }(\sigma (t)-{\sigma }_{\text{eq}})$$ (12)

where ${\widehat{\mathcal{H}}}_0$ is the time-independent part of the Hamiltonian, σ _eq is the equilibrium density operator, and $\widehat{\Gamma }$ is the relaxation super-operator, which is derived from the stochastic time-dependent Hamiltonian, ${\widehat{\mathcal{H}}}_1(t)$. The Hamiltonian ${\widehat{\mathcal{H}}}_1(t)$ can be factored into second-rank tensor spin operators and functions that depend on the spatial variables,

$${\widehat{\mathcal{H}}}_1(t)={\displaystyle \sum _m}{\displaystyle \sum _{q=-2}^2}{F}_{m2}^q(t){\mathbf{A}}_{m2}^q$$ (13)

where the index m is over the various interactions, for example, the ¹⁵N–¹H₁ or ¹H₁–¹H₂ dipole interactions. The time-dependent Hamiltonian can be factorised, such that the functions $F_{\mathit{mk}}^q(t)$, which give the spatial part, are proportional to the spherical harmonic functions, $F_{\mathit{mk}}^q(t)\propto Y_k^q({\Omega }_m^{\text{lab}}(t))$, and the tensor spin operators, ${\mathbf{A}}_{m2}^q$, are given by the traditional set, as discussed elsewhere [20], [21], [22]. The spherical angle ${\Omega }_m^{\text{lab}}(t)$ is the angle of the interaction-vector of m in the laboratory-frame; for the ¹⁵N–¹H₁ interaction this interaction-vector is the ¹⁵N–¹H internuclear vector. We will here relate the angle ${\Omega }_m^{\text{lab}}(t)$, of the interaction-vector in the laboratory-frame via a molecular coordinate-frame for the ammonium ion. By doing so, each interaction m will then relate to the laboratory frame by a time-independent rotation to the molecular frame, ${\Omega }_m^{\text{mol}}$, followed by a time-dependent interaction–independent rotation into the laboratory frame. The molecular coordinate frame used here for these rotations for the ammonium ion is shown in Fig. 2 .

Fig. 2.

A schematic representation of the molecular coordinate frame used here to calculate the nitrogen relaxation rates. The nitrogen atom (blue) is placed at the origin, the proton H₁ at $(r_{\text{NH}}/\sqrt{3})${1, 1, 1}, H₂ at $(r_{\text{NH}}/\sqrt{3})${−1, −1, 1}, H₃ at $(r_{\text{NH}}/\sqrt{3})${1, −1, −1}, and H₄ at $(r_{\text{NH}}/\sqrt{3})${−1, 1, −1}. The spherical coordinates of the interaction vectors were calculated based on the positions shown above, for example, for the ¹⁵N–¹H₁ interaction the spherical coordinates $({\Omega }_{\text{N}''–''\text{H}1}^{\text{mol}})$ are $\theta ={\cos }^{-1}\frac{1}{\sqrt{3}}\text{,}\varphi =\pi /4$.

Since the functions $F_{\mathit{mk}}^q(t)$ are proportional to the spherical harmonics, $Y_2^q$, their rotations are governed by the Wigner rotation matrices [28], [29]. The stochastic Hamiltonian can therefore be expressed as:

$${\widehat{\mathcal{H}}}_1(t)={\displaystyle \sum _m}{\displaystyle \sum _{q=-2}^2}{\displaystyle \sum _{q^{\prime }=-2}^2}{D}_{q\text{,}{q}^{\prime }}^{(2)}({\Omega }_m^{\text{mol}})F_{\mathit{Mol}\text{,}2}^{q^{\prime }}(t){\mathbf{A}}_{m2}^q$$ (14)

where $F_{\mathit{Mol}\text{,}2}^{q^{\prime }}$ are the random functions that describe the spatial coordinates of the molecular coordinate frame; these functions are independent of the interaction m. The relaxation super-operator then becomes:

$$\widehat{\Gamma }=\frac{1}{5}{\displaystyle \sum _{m\text{,}n\text{,}p\text{,}q}}{j}_{m\text{,}n}^q({\omega }_p)[{\mathbf{A}}_{m2p}^{-q}\text{,}[{\mathbf{A}}_{n2p}^q\text{,}]]$$ (15)

where ${\mathbf{A}}_{m2p}^q$ is the q component of the second-rank tensor spin operator for the interaction m, with frequency ω_p, and $j_{m\text{,}n}^q({\omega }_p)$ is the q component of the spectral density function arising from the m and n interactions, which is calculated from the random functions of spatial variables:

$$j_{m\text{,}n}^q(\omega )=\frac{5}{2}\text{Re}\left[{\int }_{-\infty }^{\infty }d\tau 〈{\displaystyle \sum _{q^{\prime }}}{D}_{q\text{,}{q}^{\prime }}^{(2)}({\Omega }_m^{\text{mol}})F_{\mathit{Mol}\text{,}2}^{q^{\prime }}(t){\displaystyle \sum _{q^{″}}}{D}_{-q\text{,}{q}^{″}}^{(2)}({\Omega }_n^{\text{mol}})F_{\mathit{Mol}\text{,}2}^{q^{″}}(t+\tau )〉\exp (-i\omega \tau )\right]$$ (16)

Finally, the matrix representation of $\widehat{\Gamma }$ in a basis set $\mathcal{B}$ is given by:

$${\widehat{\Gamma }}_{\mathit{rs}}=\langle {\mathcal{B}}_r|\widehat{\Gamma }|{\mathcal{B}}_s\rangle =\frac{1}{5}{\displaystyle \sum _{m\text{,}n\text{,}p\text{,}q}}{j}_{m\text{,}n}^q({\omega }_p)\left.〈{\mathcal{B}}_r\left|[{\mathbf{A}}_{m2p}^{-q}\text{,}[{\mathbf{A}}_{n2p}^q\text{,}{\mathcal{B}}_s]]\right.〉/\langle {\mathcal{B}}_r|{\mathcal{B}}_r\rangle \right)$$ (17)

For the dipolar I–S interaction we have $F_{\mathit{Mol}\text{,}2}^q(t)=-\sqrt{6}{d}_{\mathit{IS}}{Y}_2^q({\Omega }^{\text{lab}}(t))$, where $d_{\mathit{IS}}=(\frac{{\mu }_0}{4\pi })\hslash {\gamma }_I{\gamma }_S{r}_{\mathit{IS}}^{-3}$ and ${\Omega }^{\text{lab}}(t)$ is the orientation of the molecular coordinate-frame relative to the laboratory frame. Assuming isotropic tumbling for the symmetric AX₄ molecule gives [21], [22]:

$$\text{Re}\left[{\int }_{-\infty }^{\infty }d\tau \langle F_{\mathit{Mol}\text{,}2}^{q^{\prime }}(t)F_{\mathit{Mol}\text{,}2}^{q^{″}}(t+\tau )\rangle \exp (-i\omega \tau )\right]={\delta }_{q^{\prime }\text{,}{q}^{″}}{\left(-1\right)}^{q^{\prime }}\frac{2}{5}\frac{{\tau }_c}{1+{\omega }^2{\tau }_c^2}$$ (18)

where τ_c is the rotational correlation time of the molecule.

Table 2 summarises the angular frequencies and transverse relaxation rates of spin A for the AX₄ spin system in the basis set consisting of the transitions between Zeeman levels, exemplified by the relaxation rates of the ammonium ion. The calculations of the relaxation rates include the four ¹⁵N–¹H dipolar interactions and the six ¹H–¹H dipolar interactions. The chemical shift anisotropy of the ¹⁵N nucleus is not included here because the chemical shift tensor will be isotropic due to the tetrahedral geometry. For a distorted tetrahedral geometry, for example for an ammonium ion in an anisotropic environment, contributions from chemical shift anisotropy can occur.

Table 2.

Angular frequencies and transverse heteronuclear relaxation^a rates of ¹⁵N in ammonium ions for the symmetry-adapted Zeeman basis (Fig. 1):

Time evolution	$\frac{d\overline{\mathit{\nu }}}{\mathit{dt}}=(-\widehat{\mathit{R}}+i{\mathit{\omega }}_Z)\overline{\mathit{\nu }}$
Angular frequencies	ω11 = ωN − 4πJNH
	ω22 = ω66 = ωN − 2πJNH
	ω33 = ω77 = ω99 = ωN
	ω44 = ω88 = ωN + 2πJNH
	ω55 = ωN + 4πJNH
	ωij = 0 for i ≠ j
Relaxation rates	${\widehat{\mathit{R}}}_{1\text{,}1}=\frac{1}{5}{d}_{\text{NH}}^2(3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{1}{20}{d}_{\text{HH}}^2(27J({\omega }_{\text{H}})+72J(2{\omega }_{\text{H}}))+2\lambda$
	${\widehat{\mathit{R}}}_{2\text{,}2}=\frac{1}{10}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{40}{d}_{\text{HH}}^2(9J(0)+7J({\omega }_{\text{H}})+6J(2{\omega }_{\text{H}}))+\frac{5}{4}\lambda +\frac{3}{2}\theta$
	${\widehat{\mathit{R}}}_{3\text{,}3}=\frac{1}{15}{d}_{\text{NH}}^2(8J(0)+3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+12J({\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{20}{d}_{\text{HH}}^2(2J(0)+9J({\omega }_{\text{H}}))+\lambda +2\theta$
	${\widehat{\mathit{R}}}_{4\text{,}4}={\widehat{\mathit{R}}}_{2\text{,}2}$
	${\widehat{\mathit{R}}}_{5\text{,}5}={\widehat{\mathit{R}}}_{1\text{,}1}$
	${\widehat{\mathit{R}}}_{66}=\frac{1}{30}{d}_{\text{NH}}^2(20J(0)+21J({\omega }_{\text{H}})+7J({\omega }_{\text{H}}-{\omega }_{\text{N}})+18J({\omega }_{\text{N}})+42J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{40}{d}_{\text{HH}}^2(9J(0)+25J({\omega }_H)+26J(2{\omega }_H))+\frac{7}{4}\lambda +\frac{1}{2}\theta$
	${\widehat{\mathit{R}}}_{77}=\frac{1}{15}{d}_{\text{NH}}^2(8J(0)+9J({\omega }_{\text{H}})+3J({\omega }_{\text{H}}-{\omega }_{\text{N}})+12J({\omega }_{\text{N}})+18J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{20}{d}_{\text{HH}}^2(13J({\omega }_{\text{H}})+12J(2{\omega }_{\text{H}}))+\lambda +2\theta$
	${\widehat{\mathit{R}}}_{88}={\widehat{\mathit{R}}}_{66}$
	${\widehat{\mathit{R}}}_{99}=\frac{4}{15}{d}_{\text{NH}}^2(2J(0)+3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+3J({\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{20}{d}_{\text{HH}}^2(J(0)+2J({\omega }_{\text{H}})+2J(2{\omega }_{\text{H}}))+\lambda +2\theta$
	${\widehat{\mathit{R}}}_{1\text{,}2}=-\frac{1}{2}\lambda$
	${\widehat{\mathit{R}}}_{1\text{,}3}=0$
	${\widehat{\mathit{R}}}_{1\text{,}4}=0$
	${\widehat{\mathit{R}}}_{1\text{,}5}=0$
	${\widehat{\mathit{R}}}_{1\text{,}6}=\frac{\sqrt{3}}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\frac{9\sqrt{3}}{20}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})-\frac{\sqrt{3}}{2}\lambda$
	${\widehat{\mathit{R}}}_{1\text{,}7}=-\frac{9\sqrt{3}}{10}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{1\text{,}8}=0$
	${\widehat{\mathit{R}}}_{1\text{,}9}=-\frac{9}{10\sqrt{2}}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{2\text{,}3}=-\frac{3}{4}\lambda$
	${\widehat{\mathit{R}}}_{2\text{,}4}=0$
	${\widehat{\mathit{R}}}_{2\text{,}5}=0$
	${\widehat{\mathit{R}}}_{2\text{,}6}=\frac{2}{5\sqrt{3}}{d}_{\text{NH}}^{2}J(0)-\frac{27\sqrt{3}}{40}{d}_{\text{HH}}^{2}J(0)+\frac{\sqrt{3}}{4}\lambda -\frac{\sqrt{3}}{2}\theta$
	${\widehat{\mathit{R}}}_{2\text{,}7}=\frac{\sqrt{3}}{10}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\frac{9\sqrt{3}}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})-\frac{\sqrt{3}}{4}\lambda$
	${\widehat{\mathit{R}}}_{2\text{,}8}=-\frac{9\sqrt{3}}{20}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{2\text{,}9}=-\frac{9}{10\sqrt{2}}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{3\text{,}4}=-\frac{3}{4}\lambda$
	${\widehat{\mathit{R}}}_{3\text{,}5}=0$
	${\widehat{\mathit{R}}}_{3\text{,}6}=\frac{1}{10\sqrt{3}}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\frac{27\sqrt{3}}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})-\frac{1}{4\sqrt{3}}\lambda$
	${\widehat{\mathit{R}}}_{3\text{,}7}=\frac{8}{15\sqrt{3}}{d}_{\text{NH}}^{2}J(0)+\frac{1}{\sqrt{3}}\lambda -\frac{2}{\sqrt{3}}\theta$
	${\widehat{\mathit{R}}}_{3\text{,}8}=\frac{1}{10\sqrt{3}}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\frac{27\sqrt{3}}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})-\frac{1}{4\sqrt{3}}\lambda$
	${\widehat{\mathit{R}}}_{3\text{,}9}=-\frac{9}{10\sqrt{2}}{d}_{\text{HH}}^{2}J(0)$
	${\widehat{\mathit{R}}}_{4\text{,}5}=-\frac{1}{2}\lambda$
	${\widehat{\mathit{R}}}_{4\text{,}6}=-\frac{9\sqrt{3}}{20}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{4\text{,}7}=\frac{\sqrt{3}}{10}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\frac{9\sqrt{3}}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})-\frac{\sqrt{3}}{4}\lambda$
	${\widehat{\mathit{R}}}_{4\text{,}8}=\frac{2}{5\sqrt{3}}{d}_{\text{NH}}^{2}J(0)-\frac{27\sqrt{3}}{40}{d}_{\text{HH}}^{2}J(0)+\frac{\sqrt{3}}{4}\lambda -\frac{\sqrt{3}}{2}\theta$
	${\widehat{\mathit{R}}}_{4\text{,}9}=-\frac{9}{10\sqrt{2}}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{5\text{,}6}=0$
	${\widehat{\mathit{R}}}_{5\text{,}7}=-\frac{9\sqrt{3}}{10}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{5\text{,}8}=\frac{\sqrt{3}}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\frac{9\sqrt{3}}{20}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})-\frac{\sqrt{3}}{2}\lambda$
	${\widehat{\mathit{R}}}_{5\text{,}9}=-\frac{9}{10\sqrt{2}}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{6\text{,}7}=\frac{1}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\frac{3}{4}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})-\frac{3}{4}\lambda$
	${\widehat{\mathit{R}}}_{6\text{,}8}=-\frac{3}{2}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{6\text{,}9}=\frac{2}{5}\sqrt{\frac{2}{3}}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\sqrt{\frac{2}{3}}\lambda$
	${\widehat{\mathit{R}}}_{7\text{,}8}=\frac{1}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\frac{3}{4}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})-\frac{3}{4}\lambda$
	${\widehat{\mathit{R}}}_{7\text{,}9}=\frac{8}{15}\sqrt{\frac{2}{3}}{d}_{\text{NH}}^{2}J(0)+\sqrt{\frac{2}{3}}\lambda -2\sqrt{\frac{2}{3}}\theta$
	${\widehat{\mathit{R}}}_{8\text{,}9}=\frac{2}{5}\sqrt{\frac{2}{3}}{d}_{\text{NH}}^{2}J({\omega }_{\text{H}})-\sqrt{\frac{2}{3}}\lambda$
	${\widehat{\mathit{R}}}_{i\text{,}j}={\widehat{\mathit{R}}}_{j\text{,}i}\mathit{for}i>j$

^a$J(\omega )={\tau }_c/(1+{\omega }^2{\tau }_c^2)\text{,}$d_HH and d_NH are defined in the text, and λ and θ are the selective longitudinal and transverse relaxation rates, respectively, of the ammonium protons caused by external spins and chemical exchange.

In the spin-1 manifolds with T ₂ symmetry, Fig. 1, there are three degenerate states for each eigenvalue of the proton Zeeman Hamiltonian and in the spin-0 singlet manifolds with E symmetry there are two degenerate states. Since relaxation is not able to lift these degeneracies, as is also the case for the symmetric states of a rapidly rotating methyl group [30], it is sufficient to calculate the relaxation rates for just one of the degenerate states within each set. For example, the three transitions {N ₊|αβββ〉〈αβββ|_T2,1, N ₊|αβββ〉〈αβββ|_T2,2, N ₊|αβββ〉〈αβββ|_T2,3} between the three T ₂ symmetry-adapted energy states are combined into one transition ν₆  =  N ₊(|αβββ〉〈αβββ|_T2,1  + |αβββ〉〈αβββ|_T2,2  + |αβββ〉〈αβββ|_T2,3)/$\sqrt{3}$, which is considered for the calculation of relaxation rates.

In the study of macromolecules and large macromolecular complexes it is often of interest to identify spin-states with slow transverse relaxation rates, as for example are explained in the ¹⁵N–¹H TROSY [31] or the ¹³CH₃ methyl-TROSY [32], [33] techniques. For the AX₄ spin-system, the two outermost lines, N ₊|αααα〉〈αααα|_A1 and N ₊|ββββ〉〈ββββ|_A1, are potential candidates, since their transverse relaxation rates do not depend on the spectral density at zero frequency, J(0). This situation arises here because the matrix-representation of the dipolar Hamiltonian is traceless and the four protons, here all with the same spin quantum number, are placed in a symmetric tetrahedron around the nitrogen thus leading to cancellations of the dipolar field at the position of the nitrogen. The cancellation of the dipolar interactions means that the outer ¹⁵N NMR lines of slow-tumbling ammonium ions can appear significantly sharper than would be expected from only considering the auto-relaxation of the nitrogen nucleus by the four protons. As detailed below, it should be noted that the two outermost lines also relax due to interactions with external spins and chemical exchange with the bulk solvent, thus leading to line-broadening.

It is often convenient to consider the evolution of the spin-system using the basis of Cartesian density spin-operators, for example because the effect of interactions with external spins is diagonal to first approximation [32]. Moreover, those spin operators with A ₁ symmetry are of special interest here because these can easily be generated from the equilibrium spin-density operator of the spin-system. Table 3 summarises the angular frequencies and transverse relaxation rates of the Cartesian density spin-operators.

Table 3.

Angular frequencies and transverse heteronuclear relaxation rates of ¹⁵N for the spin-operators of the Cartesian basis:

Time evolution	$\frac{d}{\mathit{dt}}\left(\begin{array}{c}\hfill N_{+}\hfill \\ \hfill 2N_{+}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 4N_{+}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 8N_{+}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 16N_{+}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill N_{+}{\mathit{H}}_{+}{\mathit{H}}_{-}\hfill \\ \hfill 2N_{+}{\mathit{H}}_{+}{\mathit{H}}_{-}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 4N_{+}{\mathit{H}}_{+}{\mathit{H}}_{-}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill N_{+}{\mathit{H}}_{+}{\mathit{H}}_{-}{\mathit{H}}_{+}{\mathit{H}}_{-}\hfill \end{array}\right)=\left(-{\widehat{\mathit{R}}}_{\text{C}}+i{\widehat{\mathit{\omega }}}_{\text{C}}+{\widehat{\mathit{\lambda }}}_{\text{ext}}+{\widehat{\theta }}_{\text{ext}}\right)\left(\begin{array}{c}\hfill N_{+}\hfill \\ \hfill 2N_{+}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 4N_{+}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 8N_{+}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 16N_{+}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill N_{+}{\mathit{H}}_{+}{\mathit{H}}_{-}\hfill \\ \hfill 2N_{+}{\mathit{H}}_{+}{\mathit{H}}_{-}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 4N_{+}{\mathit{H}}_{+}{\mathit{H}}_{-}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill N_{+}{\mathit{H}}_{+}{\mathit{H}}_{-}{\mathit{H}}_{+}{\mathit{H}}_{-}\hfill \end{array}\right)$
Angular frequencies	${\hat{\mathit{\omega }}}_{\text{C}}=\pi J_{\mathit{NH}}\left(\begin{array}{ccccccccc}0\hfill & 4\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 1\hfill & 0\hfill & 3\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 4\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right)+{\omega }_N\hat{\mathbf{1}}$
Transverse relaxation rates	${\widehat{\mathit{R}}}_{\text{C,}11}=\frac{1}{5}{d}_{\text{NH}}^2(4J(0)+6J({\omega }_{\text{H}})+3J({\omega }_{\text{N}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))$
	${\widehat{\mathit{R}}}_{\text{C,}21}=0$
	${\widehat{\mathit{R}}}_{\text{C,}31}=-\frac{1}{30}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{N}}))$
	${\widehat{\mathit{R}}}_{\text{C,}41}=0$
	${\widehat{\mathit{R}}}_{\text{C,}51}=0$
	${\widehat{\mathit{R}}}_{\text{C,}61}=-\frac{1}{30}{d}_{\text{NH}}^2(6J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_H+{\omega }_N))$
	${\widehat{\mathit{R}}}_{\text{C,}71}=0$
	${\widehat{\mathit{R}}}_{\text{C,}81}=0$
	${\widehat{\mathit{R}}}_{\text{C,}91}=0$
	${\widehat{\mathit{R}}}_{\text{C,}12}=0$
	${\widehat{\mathit{R}}}_{\text{C,}22}\frac{1}{10}{d}_{\text{NH}}^2(4J(0)+9J({\omega }_{\text{H}})+2J({\omega }_{\text{H}}-{\omega }_{\text{N}})+3J({\omega }_{\text{N}})+12J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{1}{10}{d}_{\text{HH}}^2(9J({\omega }_{\text{H}})+36J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}32}=0$
	${\widehat{\mathit{R}}}_{\text{C,}42}=-\frac{1}{10}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{N}}))-\frac{9}{40}{d}_{\text{HH}}^2(J({\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}52}=0$
	${\widehat{\mathit{R}}}_{\text{C,}62}=0$
	${\widehat{\mathit{R}}}_{\text{C,}72}=-\frac{1}{30}{d}_{\text{NH}}^2(6J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{20}{d}_{\text{HH}}^2(J({\omega }_{\text{H}})-2J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}82}=0$
	${\widehat{\mathit{R}}}_{\text{C,}92}=0$
	${\widehat{R}}_{\text{C,}13}=-\frac{1}{5}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{N}}))$
	${\widehat{\mathit{R}}}_{\text{C,}23}=0$
	${\widehat{\mathit{R}}}_{\text{C,}33}=\frac{1}{15}{d}_{\text{NH}}^2(4J(0)+9J({\omega }_{\text{H}})+3J({\omega }_{\text{H}}-{\omega }_{\text{N}})+3J({\omega }_{\text{N}})+18J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{10}{d}_{\text{HH}}^2(5J({\omega }_{\text{H}})+16J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}43}=0$
	${\widehat{\mathit{R}}}_{\text{C,}53}=-\frac{1}{5}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{N}}))-\frac{9}{10}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{\text{C,}63}=\frac{1}{30}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))-\frac{3}{20}{d}_{\text{HH}}^2(J({\omega }_{\text{H}})-4J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}73}=0$
	${\widehat{\mathit{R}}}_{\text{C,}83}=-\frac{1}{30}{d}_{\text{NH}}^2(6J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{10}{d}_{\text{HH}}^2(3J({\omega }_{\text{H}})-2J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}93}=\frac{6}{5}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{\text{C,}14}=0$
	${\widehat{\mathit{R}}}_{\text{C,}24}=-\frac{1}{10}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{N}}))-\frac{9}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{\text{C,}34}=0$
	${\widehat{\mathit{R}}}_{\text{C,}44}=\frac{1}{10}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{H}})+2J({\omega }_{\text{H}}-{\omega }_{\text{N}})+3J({\omega }_{\text{N}})+12J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{20}{d}_{\text{HH}}^2(5J({\omega }_{\text{H}})+8J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}54}=0$
	${\widehat{\mathit{R}}}_{\text{C,}64}=0$
	${\widehat{\mathit{R}}}_{\text{C,}74}=\frac{1}{30}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{10}{d}_{\text{HH}}^2(J({\omega }_{\text{H}})+J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}84}=0$
	${\widehat{\mathit{R}}}_{\text{C,}94}=0$
	${\widehat{\mathit{R}}}_{\text{C,}15}=0$
	${\widehat{\mathit{R}}}_{\text{C,}25}=0$
	${\widehat{\mathit{R}}}_{\text{C,}35}=-\frac{1}{30}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{N}}))-\frac{3}{20}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{\text{C,}45}=0$
	${\widehat{\mathit{R}}}_{\text{C,}55}=\frac{1}{5}{d}_{\text{NH}}^2(4J(0)+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+3J({\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{18}{5}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{\text{C,}65}=\frac{3}{5}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{\text{C,}75}=0$
	${\widehat{\mathit{R}}}_{\text{C,}85}=\frac{1}{30}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))-\frac{9}{20}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{\text{C,}95}=0$
	${\widehat{\mathit{R}}}_{\text{C,}16}=-\frac{1}{10}{d}_{\text{NH}}^2(6J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))$
	${\widehat{\mathit{R}}}_{\text{C,}26}=0$
	${\widehat{\mathit{R}}}_{\text{C,}36}=\frac{1}{60}{d}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))-\frac{3}{40}{d}_{\text{HH}}^2(J({\omega }_{\text{H}})-4J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}46}=0$
	${\widehat{\mathit{R}}}_{\text{C,}56}=\frac{9}{5}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{\text{C,}66}=\frac{1}{30}{d}_{\text{NH}}^2(12J(0)+15J({\omega }_{\text{H}})+4J({\omega }_{\text{H}}-{\omega }_{\text{N}})+21J({\omega }_{\text{N}})+24J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{40}{d}_{\text{HH}}^2(27J(0)+46J({\omega }_{\text{H}})+14J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}76}=0$
	${\widehat{\mathit{R}}}_{\text{C,}86}=-\frac{1}{30}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{N}}))+\frac{3}{40}{d}_{\text{HH}}^2(9J(0)-9J({\omega }_{\text{H}})+10J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}96}=-\frac{1}{30}{d}_{\text{NH}}^2(6J({\omega }_H)+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{20}{d}_{\text{HH}}^2(3J({\omega }_{\text{H}})-J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}17}=0$
	${\widehat{\mathit{R}}}_{\text{C,}27}=-\frac{1}{20}{d}_{\text{NH}}^2(6J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{40}{d}_{\text{HH}}^2(J({\omega }_{\text{H}})-2J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}37}=0$
	${\widehat{\mathit{R}}}_{\text{C,}47}=\frac{1}{20}{d}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{20}{d}_{\text{HH}}^2(J({\omega }_{\text{H}})+J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}57}=0$
	${\widehat{\mathit{R}}}_{\text{C,}67}=0$
	${\widehat{\mathit{R}}}_{\text{C,}77}=\frac{1}{15}{d}_{\text{NH}}^2(4J(0)+6J({\omega }_{\text{H}})+2J({\omega }_{\text{H}}-{\omega }_{\text{N}})+9J({\omega }_{\text{N}})+12J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{20}{d}_{\text{HH}}^2(18J(0)+11J({\omega }_{\text{H}})+8J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{\text{C,}87}=0$
	${\widehat{\mathit{R}}}_{\text{C,}97}=0$
	${\widehat{\mathit{R}}}_{\text{C,}18}=0$
${\widehat{\mathit{R}}}_{\text{C,}28}=0$
${\widehat{\mathit{R}}}_{\text{C,}38}=-\frac{1}{60}{d}_{\text{NH}}^2(6J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{20}{d}_{\text{HH}}^2(3J({\omega }_{\text{H}})-2J(2{\omega }_{\text{H}}))$
${\widehat{\mathit{R}}}_{\text{C,}48}=0$
${\widehat{\mathit{R}}}_{\text{C,}58}=\frac{1}{10}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))-\frac{27}{20}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{\text{C,}68}-\frac{1}{30}{d}_{\text{NH}}^2(4J(0)+3J({\omega }_{\text{N}}))+\frac{3}{40}{d}_{\text{HH}}^2(9J(0)-9J({\omega }_{\text{H}})+10J(2{\omega }_{\text{H}}))$
${\widehat{\mathit{R}}}_{\text{C,}78}=0$
${\widehat{\mathit{R}}}_{\text{C,}88}=\frac{1}{30}{d}_{\text{NH}}^2(12J(0)+9J({\omega }_{\text{H}})+4J({\omega }_{\text{H}}-{\omega }_{\text{N}})+21J({\omega }_{\text{N}})+24J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{40}{d}_{\text{HH}}^2(27J(0)+16J({\omega }_{\text{H}})+14J(2{\omega }_{\text{H}}))$
${\widehat{\mathit{R}}}_{\text{C,}98}=\frac{1}{30}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))-\frac{3}{20}{d}_{\text{HH}}^2(4J({\omega }_{\text{H}})-J(2{\omega }_{\text{H}}))$
${\widehat{\mathit{R}}}_{\text{C,}19}=0$
${\widehat{\mathit{R}}}_{\text{C,}29}=0$
${\widehat{\mathit{R}}}_{\text{C,}39}=\frac{6}{5}{d}_{\text{HH}}^{2}J(2{\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{\text{C,}49}=0$
${\widehat{\mathit{R}}}_{\text{C,}59}=0$
${\widehat{\mathit{R}}}_{\text{C,}69}=-\frac{1}{15}{d}_{\text{NH}}^2(6J({\omega }_H)+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{10}{d}_{\text{HH}}^2(3J({\omega }_{\text{H}})-J(2{\omega }_{\text{H}}))$
${\widehat{\mathit{R}}}_{\text{C,}79}=0$
${\widehat{\mathit{R}}}_{\text{C,}89}=\frac{1}{15}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))-\frac{3}{10}{d}_{\text{HH}}^2(4J({\omega }_{\text{H}})-J(2{\omega }_{\text{H}}))$
${\widehat{\mathit{R}}}_{\text{C,}99}=\frac{1}{5}{d}_{\text{NH}}^2(3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+4J({\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{20}{d}_{\text{HH}}^2(13J({\omega }_{\text{H}})+8J(2{\omega }_{\text{H}}))$
Relaxation by external spins	${\hat{\mathit{\lambda }}}_{\text{ext}}=-\lambda \mathit{diag}(0\text{,}1\text{,}2\text{,}3\text{,}4\text{,}0\text{,}1\text{,}2\text{,}0)$
	${\hat{\mathit{\theta }}}_{\text{ext}}=-\theta \mathit{diag}(0\text{,}0\text{,}0\text{,}0\text{,}0\text{,}2\text{,}2\text{,}2\text{,}4)$

^a $J(\omega )={\tau }_c/(1+{\omega }^2{\tau }_c^2)$, d_HH and d_NH are defined in the text and $\hat{\mathbf{1}}$ is the 9 × 9 identity matrix.

2.4. Relaxation caused by external sources

Nuclear spins external to the AX₄ spin system can cause relaxation of the AX₄ spin-states in a similar manner to the relaxation of spin-states in the –CH₃ spin-system by ‘external’ nuclear spins [32], [34]. For the ammonium ion, such relaxations could be caused by protons in the vicinity of the protein-bound ammonium ion or by chemical exchange of the ammonium protons with the bulk solvent. We consider here the scenario where only the proton spins of the ammonium ion are relaxed by external spins, which in the Cartesian basis is described by two diagonal matrix operators [34], [35] (see Table 3), one matrix operator for longitudinal relaxation, ${\hat{\mathit{\lambda }}}_{\text{ext}}$, and one for transverse relaxation, ${\hat{\mathit{\theta }}}_{\text{ext}}$:

$${\hat{\mathit{\lambda }}}_{\text{ext}}=\lambda \mathit{diag}(0\text{,}1\text{,}2\text{,}3\text{,}4\text{,}0\text{,}1\text{,}2\text{,}0)$$ (19a)

$${\hat{\mathit{\theta }}}_{\text{ext}}=\theta \mathit{diag}(0\text{,}0\text{,}0\text{,}0\text{,}0\text{,}2\text{,}2\text{,}2\text{,}4)$$ (19b)

In the Zeeman-derived basis of spin operators, the action of the external spins can be calculated by a basis transformation of Eq. (19a), (19b) into the Zeeman-derived basis using the relations of Table 1, and these are denoted by λ and θ in Table 2. As seen in Table 2, the effect of the interaction of the ammonium protons with external spins is to transfer magnetisation between adjacent transitions of the Zeeman basis. In the NMR spectrum of the AX₄ spin-system, the relaxation caused by the external protons is thus manifested as a transfer of magnetisation between adjacent lines of the coupled spectrum, for example between the outermost ${\omega }_{\text{N}}+4\pi J_{\text{NH}}$ line and the ${\omega }_{\text{N}}+2\pi J_{\text{NH}}$ line.

2.5. Longitudinal relaxation within the AX₄ spin-system

When probing molecular motions and dynamics from nuclear spin-relaxation rates a, combination of transverse and longitudinal relaxation rates often provide a more accurate picture of the molecular dynamics than either one of the rates alone [36], [37]. We have calculated the longitudinal relaxation rates for the longitudinal operators in the product operator basis, which comprise ten operators, denoted by: {E/2, H _z, 2H _z H _z, 4H _z H _z H _z, 8H _z H _z H _z H _z, N_z, 2N_zH _z, 4N_zH _z H _z, 8N_zH _z H _z H _z, 16N_zH _z H _z H _z H _z}, where E is the identity operator. For simplicity we have ignored the zero-quantum proton coherences since these are only generated via cross-correlated relaxation mechanisms and are normally not populated at the start of the NMR experiment. As for the calculation of the transverse relaxation rates, the four ¹⁵N–¹H dipolar interactions and the six ¹H–¹H dipolar interactions were all included for the calculations of the longitudinal relaxation rates. The obtained rates are given in Table 4 .

Table 4.

Longitudinal relaxation rates of the basis operators in the Cartesian basis:

Time evolution	$\frac{d}{\mathit{dt}}\left(\begin{array}{c}\hfill E/2\hfill \\ \hfill {\mathit{H}}_{\text{z}}\hfill \\ \hfill 2{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 4{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 8{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill N_z\hfill \\ \hfill 2N_z{\mathit{H}}_{\text{z}}\hfill \\ \hfill 4N_z{\mathit{H}}_{\text{z}}{H}_{\text{z}}\hfill \\ \hfill 8N_z{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 16N_z{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \end{array}\right)=-\left(\widehat{\mathit{R}}+{\widehat{\mathit{\lambda }}}_{\text{ext}}\right)\left(\begin{array}{c}\hfill E/2\hfill \\ \hfill {\mathit{H}}_{\text{z}}\hfill \\ \hfill 2{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 4{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 8{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill N_z\hfill \\ \hfill 2N_z{\mathit{H}}_{\text{z}}\hfill \\ \hfill 4N_z{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 8N_z{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \\ \hfill 16N_z{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\hfill \end{array}\right)$
Longitudinal relaxation rates	${\widehat{\mathit{R}}}_{1\text{,}i}=0\text{for}i=1\text{,}2\text{,}\dots \text{,}10$
	${\widehat{\mathit{R}}}_{2\text{,}1}=-2({\widehat{\mathit{R}}}_{2\text{,}2}+{\gamma }_N/{\gamma }_H{\widehat{\mathit{R}}}_{2\text{,}6})$
	${\widehat{\mathit{R}}}_{3\text{,}1}=0$
	${\widehat{\mathit{R}}}_{4\text{,}1}=-2({\widehat{\mathit{R}}}_{4\text{,}2}+{\gamma }_N/{\gamma }_H{\widehat{\mathit{R}}}_{4\text{,}6})$
	${\widehat{\mathit{R}}}_{5\text{,}1}=0$
	${\widehat{\mathit{R}}}_{6\text{,}1}=-2({\widehat{\mathit{R}}}_{6\text{,}2}+{\gamma }_N/{\gamma }_H{\widehat{\mathit{R}}}_{6\text{,}6})$
	${\widehat{\mathit{R}}}_{7\text{,}1}=0$
	${\widehat{\mathit{R}}}_{8\text{,}1}=-2({\widehat{\mathit{R}}}_{8\text{,}2}+{\gamma }_N/{\gamma }_H{\widehat{\mathit{R}}}_{8\text{,}6})$
	${\widehat{\mathit{R}}}_{9\text{,}1}=0$
	${\widehat{\mathit{R}}}_{10\text{,}1}=-2({\widehat{\mathit{R}}}_{10\text{,}2}+{\gamma }_N/{\gamma }_H{\widehat{\mathit{R}}}_{10\text{,}6})$
	${\widehat{\mathit{R}}}_{2\text{,}2}=\frac{1}{10}{d}_{\text{NH}}^2(3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{10}{d}_{\text{HH}}^2(J({\omega }_{\text{H}})+4J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{3\text{,}2}=0$
	${\widehat{\mathit{R}}}_{4\text{,}2}=-\frac{9}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{5\text{,}2}=0$
	${\widehat{\mathit{R}}}_{6\text{,}2}=-\frac{2}{5}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})-6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))$
	${\widehat{\mathit{R}}}_{7\text{,}2}=0$
	${\widehat{\mathit{R}}}_{8\text{,}2}=\frac{3}{5}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{9\text{,}2}=0$
	${\widehat{\mathit{R}}}_{10\text{,}2}=0$
	${\widehat{\mathit{R}}}_{2\text{,}3}=0$
	${\widehat{\mathit{R}}}_{3\text{,}3}=\frac{1}{5}{d}_{\text{NH}}^2(3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{10}{d}_{\text{HH}}^2(5J({\omega }_{\text{H}})+16J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{4\text{,}3}=0$
	${\widehat{\mathit{R}}}_{5\text{,}3}=-\frac{9}{10}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{6\text{,}3}=0$
	${\widehat{\mathit{R}}}_{7\text{,}3}=-\frac{3}{10}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})-6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{10}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{8\text{,}3}=0$
	${\widehat{\mathit{R}}}_{9\text{,}3}=\frac{9}{5}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{10\text{,}3}=0$
	${\widehat{\mathit{R}}}_{2\text{,}4}=-\frac{9}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{3\text{,}4}=0$
	${\widehat{\mathit{R}}}_{4\text{,}4}=\frac{3}{10}{d}_{\text{NH}}^2(3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{20}{d}_{\text{HH}}^2(5J({\omega }_{\text{H}})+8J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{5\text{,}4}=0$
	${\widehat{\mathit{R}}}_{6\text{,}4}=0$
	${\widehat{\mathit{R}}}_{7\text{,}4}=0$
	${\widehat{\mathit{R}}}_{8\text{,}4}=-\frac{1}{5}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})-6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{6}{5}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{9\text{,}4}=0$
	${\widehat{\mathit{R}}}_{10\text{,}4}=\frac{18}{5}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{2\text{,}5}=0$
	${\widehat{\mathit{R}}}_{3\text{,}5}=-\frac{3}{20}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{5\text{,}5}=\frac{2}{5}{d}_{\text{NH}}^2(3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{18}{5}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{6\text{,}5}=0$
	${\widehat{\mathit{R}}}_{7\text{,}5}=0$
	${\widehat{\mathit{R}}}_{8\text{,}5}=0$
	${\widehat{\mathit{R}}}_{9\text{,}5}=-\frac{1}{10}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})-6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{10}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{10\text{,}5}=0$
	${\widehat{\mathit{R}}}_{2\text{,}6}=-\frac{1}{10}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})-6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))$
	${\widehat{\mathit{R}}}_{3\text{,}6}=0$
	${\widehat{\mathit{R}}}_{4\text{,}6}=0$
	${\widehat{\mathit{R}}}_{5\text{,}6}=0$
	${\widehat{\mathit{R}}}_{6\text{,}6}=\frac{2}{5}{d}_{\text{NH}}^2(3J({\omega }_{\text{N}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))$
	${\widehat{\mathit{R}}}_{7\text{,}6}=0$
	${\widehat{\mathit{R}}}_{8\text{,}6}=-\frac{1}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{N}})$
	${\widehat{\mathit{R}}}_{9\text{,}6}=0$
	${\widehat{\mathit{R}}}_{10\text{,}6}=0$
	${\widehat{\mathit{R}}}_{2\text{,}7}=0$
	${\widehat{\mathit{R}}}_{3\text{,}7}=-\frac{1}{5}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})-6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{5}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{4\text{,}7}=0$
	${\widehat{\mathit{R}}}_{5\text{,}7}=0$
	${\widehat{\mathit{R}}}_{6\text{,}7}=0$
	${\widehat{\mathit{R}}}_{7\text{,}7}=\frac{3}{10}{d}_{\text{NH}}^2(J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+2J({\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{10}{d}_{\text{HH}}^2(J({\omega }_{\text{H}})+4J(2{\omega }_{\text{H}}))$
	${\widehat{\mathit{R}}}_{8\text{,}7}=0$
	${\widehat{\mathit{R}}}_{9\text{,}7}=-\frac{3}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{N}})-\frac{9}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
	${\widehat{\mathit{R}}}_{10\text{,}7}=0$
	${\widehat{\mathit{R}}}_{2\text{,}8}=\frac{9}{10}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{3\text{,}8}=0$
${\widehat{\mathit{R}}}_{4\text{,}8}=-\frac{3}{10}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})-6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{5}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{5\text{,}8}=0$
${\widehat{\mathit{R}}}_{6\text{,}8}=-\frac{6}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{N}})$
${\widehat{\mathit{R}}}_{7\text{,}8}=0$
${\widehat{\mathit{R}}}_{8\text{,}8}=\frac{1}{5}{d}_{\text{NH}}^2(3J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+2J({\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{3}{10}{d}_{\text{HH}}^2(5J({\omega }_{\text{H}})+16J(2{\omega }_{\text{H}}))$
${\widehat{\mathit{R}}}_{9\text{,}8}=0$
${\widehat{\mathit{R}}}_{10\text{,}8}=-\frac{6}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{N}})-\frac{9}{10}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{2\text{,}9}=0$
${\widehat{\mathit{R}}}_{3\text{,}9}=\frac{6}{5}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{4\text{,}9}=0$
${\widehat{\mathit{R}}}_{5\text{,}9}=-\frac{2}{5}{d}_{\text{NH}}^2(J({\omega }_{\text{H}}-{\omega }_{\text{N}})-6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{18}{5}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{6\text{,}9}=0$
${\widehat{\mathit{R}}}_{7\text{,}9}=-\frac{3}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{N}})-\frac{9}{40}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{8\text{,}9}=0$
${\widehat{\mathit{R}}}_{9\text{,}9}=\frac{1}{10}{d}_{\text{NH}}^2(9J({\omega }_{\text{H}})+J({\omega }_{\text{H}}-{\omega }_{\text{N}})+6J({\omega }_{\text{N}})+6J({\omega }_{\text{H}}+{\omega }_{\text{N}}))+\frac{9}{20}{d}_{\text{HH}}^2(5J({\omega }_{\text{H}})+8J(2{\omega }_{\text{H}}))$
${\widehat{\mathit{R}}}_{10\text{,}9}=0$
${\widehat{\mathit{R}}}_{2\text{,}10}=0$
${\widehat{\mathit{R}}}_{3\text{,}10}=0$
${\widehat{\mathit{R}}}_{4\text{,}10}=\frac{9}{10}{d}_{\text{HH}}{d}_{\text{NH}}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{5\text{,}10}=0$
${\widehat{\mathit{R}}}_{6\text{,}10}=0$
${\widehat{\mathit{R}}}_{7\text{,}10}=0$
${\widehat{\mathit{R}}}_{8\text{,}10}=-\frac{1}{5}{d}_{\text{NH}}^{2}J({\omega }_{\text{N}})-\frac{3}{20}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
${\widehat{\mathit{R}}}_{9\text{,}10}=0$
${\widehat{\mathit{R}}}_{10\text{,}10}=\frac{6}{5}{d}_{\text{NH}}^2(J({\omega }_{\text{H}})+J({\omega }_{\text{N}}))+\frac{18}{5}{d}_{\text{HH}}^{2}J({\omega }_{\text{H}})$
Relaxation by external spins	${\hat{\mathit{\lambda }}}_{\text{ext}}=\lambda \mathit{diag}(0\text{,}1\text{,}2\text{,}3\text{,}4\text{,}0\text{,}1\text{,}2\text{,}3\text{,}4)$

2.6. Coupled ¹⁵N spectra of ¹⁵NH₄⁺

When the density spin-operator N ₊ evolves under the free-precession Hamiltonian and N ₊ is directly detected, then a canonical quintet (1:4:6:4:1) reflecting the number and degeneracies of the Zeeman eigenstates (Fig. 1) is observed. When an antiphase coherence is evolved and/or detected, the angular frequencies of the five transitions remain unchanged, but the relative intensities of the NMR lines within the quintet are altered. For example, evolution of the anti-phase coherence 2N ₊ H _z, and detection of N ₊ gives a spectrum with relative peak intensities within the quintet of 1:2:0:−2:−1, which can be derived from:

$$\mathit{FID}(t)=\langle \exp (-i{\widehat{\mathcal{H}}}_{0}t)2N_{+}{\mathit{H}}_z\exp (i{\widehat{\mathcal{H}}}_{0}t)|N_{+}\rangle$$ (20)

where we have ignored relaxation for the moment. The central line (ν₃, ν₇, ν₉) is not observed since the antiphase coherence 2N ₊ H _z does not include these transitions (Table 1).

Evolving anti-phase coherences of AX_n spin systems lead to coupling patterns and multiplet structures of the A-spin NMR spectrum that can be intuitively derived from a modified Pascal’s triangle. In the modified Pascal’s triangle presented here, each X spin that is scalar coupled to A and whose spin-state is described with the identity operator splits the NMR line into two lines with equal intensity, while each X spin whose state is described by the longitudinal density element, X _z, splits the NMR line into two lines with opposite intensity (Fig. 3 ). For the 2N ₊ H _z coherence considered above, the NMR line is therefore first split into two lines with opposite intensity by one X _z operator and subsequently split by three identity operators, which leads to the 1:2:0:−2:−1 multiplet structure. The Appendix A gives a detailed description of using the modified Pascal’s triangle to describe the ¹⁵N antiphase spectra of ¹⁵NH₄ ⁺ and Table 5 gives a complete list of expected relative intensities for the possible evolutions and detections of antiphase coherences.

Fig. 3.

A modified Pascal’s triangle depicting the intuitive derivation of the multiplet structure obtained by evolving/detecting the 2N₊H_z coherence. The single longitudinal proton density element splits the NMR line in two lines with opposite intensity, while each of the remaining scalar coupled protons splits the NMR line in two lines with equal intensity.

Table 5.

Expected relative intensity ratios for evolution and detection of density spin-operators of the Cartesian basis.^a

σEvolve	σDetect
	N+	2N+Hz	4N+HzHz	8N+HzHzHz	16N+HzHzHzHz
N+	1:4:6:4:1	1:2:0:−2:−1	1:0:−2:0:1	1:−2:0:2:−1	1:−4:6:−4:1
2N+Hz	1:2:0:−2:−1	1:1:0:1:1	1:0:0:0:−1	1:−1:0:−1:1	1:−2:0:2:−1
4N+HzHz	1:0:−2:0:1	1:0:0:0:−1	3:0:2:0:3	1:0:0:0:−1	1:0:−2:0:1
8N+HzHzHz	1:−2:0:2:−1	1:−1:0:−1:1	1:0:0:0:−1	1:1:0:1:1	1:2:0:−2:−1
16N+HzHzHzHz	1:−4:6:−4:1	1:−2:0:2:−1	1:0:−2:0:1	1:2:0:−2:−1	1:4:6:4:1

^aRelative intensity ratios are calculated according to $\langle \exp (-i{\widehat{\mathcal{H}}}_{0}t){\sigma }_{\text{Evolve}}\exp (i{\widehat{\mathcal{H}}}_{0}t)|{\sigma }_{\text{Detect}}\rangle$ followed by a separation of terms according to frequency. See Appendix A for a simple derivation based on the modified Pascal’s triangle.

It is often the case that antiphase coherences are either detected or evolved during the indirect evolution time of a 2D or 3D correlation spectrum. For example, the simplest ¹⁵N–¹H HSQC correlation spectrum usually corresponds to the evolution of and indirect ‘detection’ of the singly anti-phase coherence 2N _x H _z as described below. The operator that is indirectly detected is the operator that is transferred back to directly-detectable magnetisations, which in turn depends on the pulse sequence.

2.7. Application to ¹⁵N-ammonium bound to a protein – the 41 kDa ATP binding domain of DnaK

The equations derived above provide the basis to characterise the local dynamics and chemical exchange properties of ammonium ions in various environments. While variations of the correlation time of ammonium ions in different solvents have been measured and correlated with ammonium:solvent interactions [3], little is known about how specific monovalent cation binding sites in proteins affect the correlation time of the bound ammonium ion.

The activity of the bacterial Hsp70 homologue DnaK, an ATP-hydrolysing enzyme that functions as a molecular chaperone in the cell, relies on the binding of two potassium ions. It was shown, however, that potassium can be substituted by ammonium with the enzyme retaining more than half of its activity [38], [39]. Such enzyme-bound ¹⁵N ammonium ions can be observed in ¹⁵N edited NMR spectra in favourable cases [16], when the protein environment decreases the rate of exchange of the ammonium protons with the bulk solvent to less than ∼J _NH. For the DnaK enzyme, very weak ammonium proton signals are observed in 1D ¹H NMR spectra in the absence of nucleotide, while the addition of ADP and phosphate creates an environment that protects the ammonium ion from the bulk solvent and makes it observable in ¹⁵N-edited NMR spectra. The observation of ammonium NMR signals provides an opportunity for probing the properties of K⁺/NH₄ ⁺ binding sites, as was shown in a previous study of the regulation of the human histone deacetylase 8 (HDAC8) by monovalent cations [16], [40]. Here we will illustrate the utility of the derived equations, taking the characterisation of K⁺/NH₄ ⁺ sites a step further by probing the local correlation time of DnaK-bound ammonium from 2D ¹⁵N–¹H correlation spectra.

Fig. 4a shows the ¹H-coupled ¹⁵N–¹H correlation spectrum of the 41 kDa ¹⁴N-ATP-binding domain of DnaK in 150 mM ¹⁵NH₄Cl. Briefly, transverse antiphase 2N₊H_z coherence is generated via an initial INEPT step, which is followed by indirect ¹⁵N chemical shift evolution without decoupling of the ¹H–¹⁵N scalar coupling. Finally, the transverse nitrogen magnetisation is transferred back to transverse proton magnetisation via a reversed INEPT step followed by direct proton detection with ¹⁵N decoupling. Details are given in Section 4. Fig. 4a shows four lines corresponding to the four transitions, ν₁, {ν₂, ν₆}, {ν₄, ν₈,}, ν₅ (Fig. 1) with a relative intensity ratio of approximately 1:1:0:1:1, as is expected from Table 5. Also as expected, the central line is not observed because the central transitions ν₃, ν₇, ν₉ are not included in the 2N ₊ H _z density product operator (Table 1). The linewidths, which are directly proportional to the transverse relaxation rates, of the four transitions appear to be very similar and comparison with the simulated spectra in Fig. 4b shows that the local correlation time, τ_c, of the DnaK-bound ammonium is shorter than approximately 1 ns.

Fig. 4.

Application to ¹⁵N-ammonium bound to the nucleotide-binding domain of the protein DnaK. (A) ¹⁵N–¹H HSQC (¹H-coupled) correlation spectrum of ¹⁴N-DnaK in 150 mM ¹⁵NH₄Cl (see Section 4 for full conditions). The two sets of peaks, with distinct proton chemical shifts, report individually on the two potassium binding sites of DnaK. A 1D ¹⁵N trace is shown for the downfield ammonium peak highlighting the relative intensities of the four observed lines at −4πJ_NH, −2πJ_NH, 2πJ_NH, and 4πJ_NH, corresponding to the transitions ν₁, {ν₂, ν₆}, {ν₄, ν₈}, and ν₅, respectively (inset). The crystal structure of the ATPase domain of Hsp70 (PDB: 1HPM [38]) with the two potassium ions in the active site shown as purple spheres. (B) Comparison of the experimental 1D trace of (A) with 1D ¹⁵N traces obtained from simulations using the equations derived above. The spectral parameters used to generate the simulated spectra are identical to those used for the experimental spectrum. λ = θ = 15 s⁻¹ was assumed in the simulations, although the specific values of λ and θ do not alter the relative intensity ratio. The comparison of the experimental spectrum with a nearly 1:1:0:1:1 relative intensity ratio with the simulated spectra indicates that the local correlation time is shorter than ∼1 ns. The simulated spectra show that for slow tumbling ammonium ions, the outermost lines are significantly sharper than the inner lines due to the symmetric dipolar field created by the four protons with the same spin-state (see main text). The other ammonium signal, with a proton frequency of ∼6.8 ppm, shows the same pattern as discussed above.

3. Conclusions

In summary, we have developed the theoretical framework for calculating the ¹⁵N relaxation rates of ¹⁵N-ammonium. It was assumed that the geometric structure of the ammonium ion is that of a tetrahedron, which in turn means that symmetries of the energy eigenstates fall within the symmetries of the T_d point group. We presented the equations that describe the transverse nitrogen relaxations of the ammonium ion in two basis sets, the Zeeman-derived basis and the Cartesian basis, as well as the relaxation rates of the longitudinal spin-density operators in the Cartesian basis. All dipole–dipole, auto- and cross-correlated relaxation mechanisms within the ammonium ion were explicitly included in the calculations and it was also shown how the relaxation of the ammonium protons caused by external spins can be taken into account.

An application of the derived equations to the study of the dynamics of enzyme-bound ammonium ions was described, where it was concluded that the local correlation time of ammonium bound to the 41 kDa domain of DnaK is less than ∼1 ns. Thus, the ammonium ion is rotating rapidly within the cation-binding site of DnaK, since the protein itself is expected to have a rotational correlation time of approximately 25 ns at 298 K. The narrow ¹⁵N NMR signals that were observed previously for protein-bound ammonium ions [16] can therefore be a consequence of two effects, (i) fast rotation of the ion within the protein binding sites as observed here for the enzyme DnaK or (ii) contributions from cross-correlated relaxation mechanisms originating from the high symmetry of the molecule as outlined in the previous sections.

The theoretical framework presented here provides an avenue for further investigations of free and enzyme-bound ammonium ions to elucidate the kinetic and dynamic aspects of monovalent cation binding. Combination of the derived equations with modifications of currently available NMR pulse sequences and experiments will thus shed more light on the local dynamics of ammonium ions in the binding sites of enzymes, thereby allowing more detailed characterisations of monovalent cation:enzyme interactions.

4. Materials and methods

4.1. Calculation of relaxation rates

The relaxation rates were calculated using an in-house Mathematica (Wolfram Research) script based on a strategy developed previously [41]. This script evaluates the Wigner matrix rotations and the commutator-relations involved and is available directly from the authors upon request.

4.2. Protein sample preparations

The NMR sample of the ATP binding domain of DnaK from Thermus thermophilus was prepared as explained previously [16]. The protein concentration was ∼50 μM in 100% H₂O containing 150 mM ¹⁵NH₄Cl, 0.5 mM ADP, 50 mM (NH₄)H₂PO₄, 5 mM MgCl₂, 1 mM DTT, 1 mM NaN₃ and 75 mM Tris pH 7.5.

4.3. NMR experiments

The NMR experiment shown in Fig. 4 is a ¹H-coupled ¹⁵N–¹H HSQC, obtained from a standard ¹⁵H–¹H HSQC by removing the 180° proton decoupling pulse during the indirect nitrogen evolution. The experiment was performed on a Bruker Avance III 500 MHz (11.7 T) spectrometer using an HCN inverse RT probe. The spectrum was recorded with 48 complex points in the indirect dimension, a sweep-width of 1000 Hz, and was processed using nmrPipe [42].

Appendix A

The strategy of using the modified Pascal’s triangle to calculate the observed multiplet structure for ¹⁵N coherences of the ¹⁵NH₄ ⁺ group is described below. Fig. 5 a shows the traditional schematic representation of the Pascal’s triangle used to calculate the relative intensities of the multiplet structure of the in-phase ¹⁵N spectrum of ¹⁵NH₄ ⁺. Briefly, each proton that is scalar-coupled to the ¹⁵N nucleus splits the NMR line into two lines with equal intensity and separated by the ¹⁵N–¹H scalar coupling constant, J _NH, resulting in the canonical 1:4:6:4:1 quintet structure. The intensities observed for the individual NMR lines, i.e. the population differences associated with the underlying transitions, when evolving the 2N ₊ H _z coherence (and observing N ₊) are derived in Fig. 3. For the 2N ₊ H _z coherence, the density element of one of the scalar coupled protons is described by 2H _z  = (|α〉〈α| −|β〉〈β|), while the density elements of the three remaining protons are those of the identity operator E  = (|α〉〈α| +|β〉〈β|). For the modified Pascal’s triangle, we incorporate the 2H _z density element by splitting the NMR line into two lines with opposite intensity (+) and (−). Subsequent application of three identity operators gives the relative intensities of the NMR lines obtained by evolving 2N ₊ H _z and observing N ₊, which are 1:2:0:−2:−1 (Table 5). The relative intensities of the NMR lines and the multiplet structures that are obtained by evolving 4N ₊ H _z H _z, 8N ₊ H _z H _z H _z, and 16N ₊ H _z H _z H _z are derived in Fig. 5b–d.

Fig. 5.

Multiplet structures of the ¹⁵N NMR spectrum of ¹⁵NH₄⁺ calculated using the modified Pascal’s triangle described above. (A) The typical Pascal’s triangle coupling-pattern corresponding to evolution and detection of N₊ resulting in a multiplet structure with relative intensities of 1:4:6:4:1. (B) A modified Pascal’s triangle depicting the situation where the 4N₊H_zH_z coherence is evolved and N₊ is detected, which mathematically corresponds to calculating the elements $\langle \exp (-i{\widehat{\mathcal{H}}}_{0}t)4N_{+}{\mathit{H}}_{\text{z}}{\mathit{H}}_{\text{z}}\exp (i{\widehat{\mathcal{H}}}_{0}t)|N_{+}\rangle$ and separating terms according to frequency. (C and D) Show the modified Pascal’s triangles for the evolution of 8N₊H_zH_zH_z and 16N₊H_zH_zH_zH_z with detection on N₊, respectively.

Using the strategy described above, it can also be seen that evolving N ₊ followed by indirect ‘detection’ of 2N ₊ H _z, e.g. in an HSQC correlation experiment, results in a multiplet with intensity ratios of 1:2:0:−2:−1, since $\langle \exp (-i{\widehat{\mathcal{H}}}_{0}t){\sigma }_{\text{B}}\exp (i{\widehat{\mathcal{H}}}_{0}t)|{\sigma }_{\text{A}}\rangle =\langle \exp (i{\widehat{\mathcal{H}}}_{0}t){\sigma }_{\text{A}}\exp (-i{\widehat{\mathcal{H}}}_{0}t)|{\sigma }_{\text{B}}\rangle$. More generally, ‘detecting’ 2N ₊ H _z can in the schematic picture described here be calculated by multiplying the populations of the five lines with 1:1/2:0:−1/2:−1, which is obtained from the overlap between N ₊ and 2N ₊ H _z for the individual transitions: that is, 1/1:2/4:0/6:−2/4:−1/1 = 1:1/2:0:−1/2:−1. Similarly, the multiplet structure obtained by indirect detection of 4N ₊ H _z H _z is calculated by multiplying the populations with 1:0:−1/3:0:1, detection of 8N ₊ H _z H _z H _z by multiplying by 1:−1/2:0:1/2:−1, and detection of 16N ₊ H _z H _z H _z H _z by multiplication of 1:−1:1:−1:1. For example, evolving 4N ₊ H _z H _z followed by indirect detection of 2N ₊ H _z is calculated as 1*1:0*1/2:−2*0:0*−1/2:1*−1 = 1:0:0:0:−1. The strategy outlined above is general and can also be applied to calculate AX_n multiplet structures, such as AX₃, AX₂, and AX.