Optimal Tests of Treatment Effects for the Overall Population and Two Subpopulations in Randomized Trials, using Sparse Linear Programming

Abstract

We propose new, optimal methods for analyzing randomized trials, when it is suspected that treatment effects may differ in two predefined subpopulations. Such subpopulations could be defined by a biomarker or risk factor measured at baseline. The goal is to simultaneously learn which subpopulations benefit from an experimental treatment, while providing strong control of the familywise Type I error rate. We formalize this as a multiple testing problem and show it is computationally infeasible to solve using existing techniques. Our solution involves a novel approach, in which we first transform the original multiple testing problem into a large, sparse linear program. We then solve this problem using advanced optimization techniques. This general method can solve a variety of multiple testing problems and decision theory problems related to optimal trial design, for which no solution was previously available. In particular, we construct new multiple testing procedures that satisfy minimax and Bayes optimality criteria. For a given optimality criterion, our new approach yields the optimal tradeoff between power to detect an effect in the overall population versus power to detect effects in subpopulations. We demonstrate our approach in examples motivated by two randomized trials of new treatments for HIV.

1 Introduction

An important goal of health research is determining which populations, if any, benefit from new treatments. Randomized trials are generally considered the gold standard for producing evidence of treatment effects. Most randomized trials aim to determine how a treatment compares to control, on average, for a given population. This results in trials that may fail to detect important differences in benefits and harms for subpopulations, such as those with a certain biomarker or risk factor. This problem affects trials in virtually all disease areas.

Consider planning a randomized trial of an experimental treatment versus control, where there is prior evidence that treatment effects may differ for two, predefined subpopulations. Such evidence could be from past trials or observational studies, or from medical knowledge of how the treatment is conjectured to work. Our goal is to construct a multiple testing procedure with optimal power to detect treatment effects for the overall population and for each subpopulation. We consider both Bayes and minimax optimality criteria. Existing multiple testing procedures in general do not satisfy either of these criteria.

It is a challenging problem to construct optimal multiple testing procedures. According to Romano et al. (2011), “there are very few results on optimality in the multiple testing literature. ” The problems we consider are especially challenging since we require strong 2 control of the familywise Type I error rate, also called the studywide Type I error rate, as defined by Hochberg and Tamhane (1987). That is, we require that under any data generating distribution, the probability of rejecting one or more true null hypotheses is at most a given level α. We incorporate these constraints because control of the studywide Type I error rate is generally required by regulatory agencies such as the U.S. Food and Drug Administration and the European Medicines Agency for confirmatory randomized trials involving multiple hypotheses (FDA and EMEA, 1998).

Strong control of the familywise Type I error rate implies infinitely many constraints, i.e., one for every possible data generating distribution. The crux of our problem is constructing multiple testing procedures satisfying all these constraints and optimizing power at a given set of alternatives. In the simpler problem of testing only the null hypothesis for the overall population, the issue of infinitely many constraints can be sidestepped; this is because for most reasonable tests, strong control of the Type I error is implied by control of the Type I error at the global null hypothesis of zero average treatment effect. In contrast, when dealing with multiple populations, procedures that control the familywise Type I error at the global null hypothesis can have quite large Type I error at distributions corresponding to a positive effect for one subpopulation and a nonpositive effect for another. For this reason, optimization methods designed for a single null hypothesis, such as those of Jennison (1987); Eales and Jennison (1992); Banerjee and Tsiatis (2006); and Hampson and Jennison (2013), do not directly apply to our problem. Though in principle these methods could be extended to handle more Type I error constraints, such extensions are computationally infeasible in our problems, as we discuss in Section 7.

Our solution hinges on a novel method for transforming a fine discretization of the original multiple testing problem into a large, sparse linear program. The resulting linear program typically has over a million variables and constraints. We tailor advanced optimization tools 3 to solve the linear program. To the best of our knowledge, this is the first computationally feasible method for constructing Bayes or minimax optimal tests of treatment effects for subpopulations and the overall population, while maintaining strong control of the familywise Type I error rate.

We apply our approach to answer the following open questions: What is the maximum power that can be gained to detect treatment effects in subpopulations if one is willing to sacrifice x% power for detecting an effect in the overall population? What is the minimum additional sample size required to increase power for detecting treatment effects in subpopulations by x%, while maintaining a desired power for the overall population?

A motivating data example is given in Section 2. We define our problem in Section 3, present our method for solving it in Section 4, and demonstrate this method in Section 5. We explain how we overcome computational challenges in our problem in Sections 6 and 7. Section 8 extends our method to decision theory problems. The sparse linear programming algorithm we use is given in Section 9. We conclude with a discussion of limitations of our approach and future directions for research in Section 10.

2 Example: Randomized Trials of New Antiretroviral Treatments for HIV

We demonstrate our approach in scenarios motivated by two recently completed randomized trials of maraviroc, an antiretroviral medication for treatment-experienced, HIV positive individuals (Fätkenheuer et al., 2008). There is suggestive evidence from these trials that the treatment benefit may differ depending on the suppressive effect of an individual’s background therapy, as measured by the phenotypic sensitivity score (PSS) at baseline. The estimated average treatment benefit of maraviroc among individuals with PSS less than 3 was larger than that among individuals with PSS 3 or more. This pattern has been observed for other antiretroviral medications, e.g., in randomized trials of etravirine (Katlama et al.,2009). We refer to those with PSS less than 3 as subpopulation 1, and those with PSS 3 or more as subpopulation 2. In the combined maraviroc trials, 63% of participants are in subpopulation 1.

In planning a trial of a new antiretroviral medication, it may be of interest to determine the average treatment effect for the overall population and for each of these subpopulations. We construct multiple testing procedures that maximize power for detecting treatment benefits in each subpopulation, subject to constraints on the familywise Type I error rate and on power for the overall population.

3 Multiple Testing Problem

3.1 Null Hypotheses and Test Statistics

Consider a randomized trial comparing a new treatment (a=1) to control (a=0), in which there are two prespecified subpopulations that partition the overall population. Denote the fraction of the overall population in subpopulation k ∈ {1, 2} by p_k. We assume each patient is randomized to the new treatment or control with probability 1/2, independent of the patient’s subpopulation. Below, for clarity of presentation, we focus on normally distributed outcomes with known variances. In Section A of the Supplementary Materials, we describe asymptotic extensions allowing a variety of outcome types, and where the variances are unknown and must be estimated.

For each subpopulation k ∈ {1, 2} and study arm a ∈ {0, 1}, assume the corresponding patient outcomes are independent and distributed as $Y_{ka,i}~N({\mu }_{ka},{\sigma }_{ka}^2)$, for each patient i = 1, 2, … n_ka. For each subpopulation k ∈ {1, 2}, define the population average treatment effect as Δ_k = µ_k1 − µ_k0. For each k ∈ {1, 2}, define H_0k to be the null hypothesis Δ_k ≤ 0, i.e., that treatment is no more effective than control, on average, for subpopulation k; define H_0C to be the null hypothesis p₁Δ₁+p₂Δ₂ ≤ 0, i.e., that treatment is no more effective than 5 control, on average, for the combined population.

Let n denote the total sample size in the trial. For each k ∈ {1, 2} and a ∈ {0, 1}, we assume the corresponding sample size n_ka = p_kn/2; that is, the proportion of the sample in each subpopulation equals the corresponding population proportion p_k, and exactly half of the participants in each subpopulation are assigned to each study arm. This latter property can be approximately achieved by block randomization within each subpopulation.

We assume the subpopulation fractions p_k and the variances ${\sigma }_{ka}^2$ are known. This implies the following z-statistics are sufficient statistics for (Δ₁,Δ₂):

$$\text{for each subpopulation}k\in \{1,2\},Z_k=(\frac{1}{n_{k1}}\sum _{i=1}^{n_{k1}}{Y}_{k1,i}-\frac{1}{n_{k0}}\sum _{i=1}^{n_{k0}}){\upsilon }_k^{-1/2},$$

for ${\upsilon }_k={\sigma }_{k1}^2/n_{k1}+{\sigma }_{k0}^2/n_{k0}$.

We also consider the pooled z-statistic for the combined population,

$$Z_C=\sum _{k=1}^2{p}_k(\frac{1}{n_{k1}}\sum _{i=1}^{n_{k1}}{Y}_{k1,i}-\frac{1}{n_{k0}}\sum _{i=1}^{n_{k0}}{Y}_{k0,i}){(p_1^2{\upsilon }_1+p_2^2{\upsilon }_2)}^{-1/2}.$$

We then have Z_C = ρ₁Z₁ + ρ₂Z₂, for ${\rho }_k={[{\rho }_k^2{\upsilon }_k/(p_1^2{\upsilon }_1+{\rho }_2^2{\upsilon }_2)]}^{1/2}$, which is the covariance of Z_k and Z_C. The vector of sufficient statistics (Z₁,Z₂) is bivariate normal with mean $({\delta }_1,{\delta }_2)=({\mathrm{\Delta }}_1/\sqrt{{\upsilon }_1},{\mathrm{\Delta }}_2/\sqrt{{\upsilon }_2})$ and covariance matrix the identity matrix. We call (δ₁, δ₂) the non-centrality parameters of (Z₁,Z₂). For Δ^min > 0 the minimum, clinically meaningful treatment effect, let ${\delta }_1^{\text{min}}$ and ${\delta }_2^{\text{min}}$ be the non-centrality parameters that correspond to Δ₁ = Δ^min and Δ₂ = Δ^min, respectively.

Define δ_C = EZ_C = ρ₁δ₁ + ρ₂δ₂. We use the following equivalent representation of the null hypotheses above:

$$H_{01}:{\delta }_1\le 0;H_{02}:{\delta }_2\le 0;H_{0C}:{\rho }_1{\delta }_1+{\rho }_2{\delta }_2\le 0.$$ (1)

For any (δ₁, δ₂), denote the corresponding set of true null hypotheses in the family ℋ = {H₀₁,H₀₂,H_0C} by ℋ_TRUE(δ₁,δ₂); for each k ∈ {1, 2}, this set contains H_0k if and only if δ_k ≤ 0, and contains H_0C if and only if ρ₁δ₁ + ρ₂δ₂ ≤ 0.

3.2 Multiple Testing Procedures and Optimization Problem

The multiple testing problem is to determine which subset of ℋ to reject, on observing a single realization of (Z₁,Z₂). The pair (Z₁,Z₂) is drawn from the distribution P_δ1,_δ2, defined to be the bivariate normal distribution with mean vector (δ₁,δ₂) and covariance matrix the 2 × 2 identity matrix.

Let 𝒮 denote an ordered list of all subsets of the null hypotheses ℋ. Consider multiple testing procedures for the family ℋ, i.e., maps from each possible realization of (Z₁,Z₂) to an element of 𝒮, representing the null hypotheses rejected upon observing (Z₁,Z₂). It will be useful to consider the class ℳ of randomized multiple testing procedures, defined as the maps M from each possible realization of (Z₁,Z₂) to a random variable taking values in 𝒮. Formally, a randomized multiple testing procedure is a measurable map M = M(Z₁,Z₂, U) that depends on (Z₁,Z₂) but also may depend on an independent random variable U that has a uniform distribution on [0, 1]. Define the class of deterministic multiple testing procedures ℳ_det to be all M ∈ ℳ such that for any (z₁, z₂) ∈ ℝ² and u, u′ ∈ [0, 1], we have M(z₁, z₂, u) = M(z₁, z₂, u′); for such procedures, we let M(z₁, z₂) denote the value of M(z₁, z₂, u), which does not depend on u.

The reason we use randomized procedures, rather than restricting to deterministic procedures, is computational. We show in Section 4 that the discretized version of our optimization problem reduces to a linear program, when we optimize over a class of randomized procedures. In contrast, if we restrict to deterministic procedures, the optimization problem reduces to an integer program. Linear programs are generally much easier to solve than integer programs. This computational advantage is especially important in our context where we have a large number of variables and constraints. Though we optimize over randomized procedures, it turns out that each optimal solution in the examples in Section 5.1 is a deterministic procedure, as we discuss in Section 10. For conciseness, we write “multiple testing procedure” instead of “randomized multiple testing procedure,” with the understanding that unless otherwise stated, we deal with the latter throughout.

Let L denote a bounded loss function, where L(s; δ₁,δ₂) represents the loss if precisely the subset s ⊆ ℋ is rejected when the true non-centrality parameters are (δ₁, δ₂). An example is the loss function that imposes a penalty of 1 unit for failing to reject the null hypothesis for each subpopulation when the average treatment effect is at least the minimum, clinically meaningful level in that subpopulation. This loss function can be written as $\mathrm{L̃}(s;{\delta }_1,{\delta }_2)={\sum }_{k=1}^{2}1[{\delta }_k\ge {\delta }_k^{\text{min}},H_{0k}\notin s]$, where 1[C] is the indicator function taking value 1 if C is true and 0 otherwise. In Section D of the Supplementary Materials, we consider modifications of L̃ where the penalty is proportional to the corresponding treatment benefit, up to a given maximum penalty. Our general method can be applied to any bounded loss function that can be numerically integrated with respect to δ₁, δ₂ by standard software with high precision. In particular, we allow L to be non-convex in (δ₁, δ₂), which is the case in all our examples.

We next state the Bayes version of our general optimization problem. Let Λ denote a prior distribution on the set of possible pairs of non-centrality parameters (δ₁, δ₂). We assume Λ is a distribution with compact support on (ℝ², ℬ), for ℬ a σ-algebra over ℝ².

Constrained Bayes Optimization Problem

For given α > 0, β > 0, ${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$, L, and Λ, find the multiple testing procedure M ∈ ℳ minimizing

$$\int E_{{\delta }_1,{\delta }_2}\{L(M(Z_1,Z_2,U);{\delta }_1,{\delta }_2)\}d\mathrm{\Lambda }({\delta }_1,{\delta }_2),$$ (2)

under the familywise Type I error constraints: for any (δ₁, δ₂) ∈ ℝ²,

$$P_{{\delta }_1,{\delta }_2}\{M\text{rejects any null hypotheses in}{\mathscr{H}}_{\text{TRUE}}({\delta }_1,{\delta }_2)\}\le \alpha ,$$ (3)

and the power constraint for the combined population:

$$P_{{\delta }_1^{\text{min}},{\delta }_2^{\text{min}}}\{M\text{rejects}{H}_{0C}\}\ge 1-\beta .$$ (4)

The objective function (2) encodes the expected loss incurred by the testing procedure M, averaged over the prior distribution Λ. The constraints (3) enforce strong control of the familywise Type I error rate.

The corresponding minimax optimization problem replaces the objective function (2) by

$$\underset{({\delta }_1,{\delta }_2)\in \wp }{\text{sup}}{E}_{{\delta }_1,{\delta }_2}L(M(Z_1,Z_2,U);{\delta }_1,{\delta }_2),$$ (5)

for ℘ a subset of ℝ² representing the alternatives of interest.

4 Solution to Constrained Bayes Optimization Problem

The above constrained Bayes optimization problem is either very difficult or impossible to solve analytically, due to the continuum of Type I error constraints that must be satisfied. Our approach involves discretizing the constrained Bayes optimization problem. We approximate the infinite set of constraints (3) by a finite set of constraints, and restrict to multiple testing procedures that are constant over small rectangles. This transforms the constrained Bayes optimization problem, which is non-convex, into a large, sparse linear program that we solve using advanced optimization tools. In Section 6, we bound the approximation error in the discretization using the dual linear program; we apply this to show the approximation error is very small in our examples.

We first restrict to the class of multiple testing procedures ℳ_B ⊂ ℳ that reject no hypotheses outside the region B = [−b, b] × [−b, b] for a fixed integer b > 0. Intuitively, if we select b large enough that (Z₁,Z₂) ∈ B with high probability under the prior Λ, we may expect the Bayes risk of the optimal solution among procedures in ℳ_B to be within a small value ∈ of the optimal solution over ℳ. For the examples in Section 5.1, we verify that it is sufficient to set b = 5 to achieve this at ε = 0.005, as shown in Section 6. In Section B of the Supplementary Materials, we show how to augment the structure of an approximately optimal procedure among ℳ_B to allow rejection of null hypotheses outside of B.

We next restrict to a finite subset of the familywise Type I error constraints (3). These will be selected from points in G = {(δ₁, δ₂) : δ₁ = 0 or δ₂ = 0 or ρ₁δ₁ + ρ₂δ₂ = 0}, which represents the pairs of non-centrality parameters at which the first subpopulation has zero average benefit, the second subpopulation has zero average benefit, or the combined population has zero average benefit. Our restricting to G is motivated by the conjecture that the worst-case, familywise Type I error occurs on the union of the boundaries of the null spaces for H₀₁,H₀₂,H_0C. We verified this holds for each example in Section 5.1. We also prove in Section 5.2 that for a class of multiple testing procedures with certain intuitively appealing properties, the worst-case, familywise Type I error always occurs at some (δ₁, δ₂) ∈ G. Let G′ denote a finite subset of G; e.g., for some τ₁, τ₂ > 0, we could set G′ to be

$$G_{\tau ,b}=[\{(k{\tau }_1,0):k\in \mathbb{Z}\}\cup \{(0,k{\tau }_2):k\in \mathbb{Z}\}\cup \{({\rho }_{2}k{\tau }_1,-{\rho }_{1}k{\tau }_1):k\in \mathbb{Z}\}]\cap B.$$

In Section 6, we discuss why certain carefully selected, finite subsets G′ of G lead to solutions that are very close to optimal for the original problem, and that satisfy all constraints of the original problem.

The next step is to define a subclass of multiple testing procedures that are constant over small rectangles. For fixed τ = (τ₁, τ₂), for each k, k′ ∈ ℤ, define the rectangle R_k,k′ = [kτ₁, (k+1)τ₁)×[k′τ₂, (k′+1)τ₂). Let ℛ denote the set of such rectangles in the bounded region B, i.e., ℛ = {R_k,k′ : k, k′ ∈ ℤ,R_k,k′ ⊂ B}. Define ℳ_ℛ to be the subclass of multiple testing procedures M ∈ ℳ_B that, for any u ∈ [0, 1] and rectangle r ∈ ℛ, satisfy $M(z_1,z_2,u)=M(z_1^{\prime },z_2^{\prime },u)$ whenever (z₁, z₂) and ($z_1^{\prime },z_2^{\prime }$) are both in r. For any procedure M ∈ ℳ_ℛ, its behavior is completely characterized by the finite set of values m = {m_rs}_{r∈ℛ,s∈𝒮}, where

$$m_{rs}=P[M(Z_1,Z_2,U)\text{rejects precisely the subset of null hypotheses}s|(Z_1,Z_2)\in r].$$ (6)

For any r ∈ ℛ, it follows that

$$\sum _{s\in 𝒮}{m}_{rs}=1,\text{and}{m}_{rs}\ge 0\text{for any}s\in 𝒮.$$ (7)

Also, for any set of real values {m_rs}_{r∈ℛ,s∈𝒮} satisfying (7), there is a multiple testing procedure M ∈ ℳ_ℛ satisfying (6), i.e., the procedure M that rejects precisely the subset of null hypotheses s with probability m_rs when (Z₁,Z₂) ∈ r.

The advantage of the above discretization is that if we restrict to procedures in ℳ_ℛ, the objective function (2) and constraints (3)–(4) in the constrained Bayes optimization problem are each linear functions of the variables m. This holds even when the loss function L is non-convex. To show (2) is linear in m, first consider the term inside the integral in (2):

$$E_{{\delta }_1,{\delta }_2}L(M(Z_1,Z_2,U);{\delta }_1,{\delta }_2)$$ (8)

$$=\sum _{r\in \Re ,s\in 𝒮}{E}_{{\delta }_1,{\delta }_2}[L(M(Z_1,Z_2,U);{\delta }_1,{\delta }_2)|M(Z_1,Z_2,U)=s,(Z_1,Z_2)\in r]\times P_{{\delta }_1,{\delta }_2}[M(Z_1,Z_2,U)=s|(Z_1,Z_2)\in r]P_{{\delta }_1{\delta }_2}[(Z_1,Z_2)\in r]=\sum _{r\in \Re ,s\in 𝒮}L(s;{\delta }_1,{\delta }_2)P_{{\delta }_1,{\delta }_2}[(Z_1,Z_2)\in r]m_{rs}.$$ (9)

The objective function (2) is the integral over Λof (8), which by the above argument equals

$$\sum _{r\in \Re ,s\in 𝒮}\{\int L(s;{\delta }_1,{\delta }_2)P_{{\delta }_1,{\delta }_2}[(Z_1,Z_2)\in r]d\mathrm{\Lambda }({\delta }_1,{\delta }_2)\}{m}_{rs}.$$ (10)

The constraints (3) and (4) can be similarly represented as linear functions of m, as we show in Section C of the Supplementary Materials.

Define the discretized problem to be the constrained Bayes optimization problem restricted to procedures in ℳ_ℛ, and replacing the familywise Type I error constraints (3) by those corresponding to (δ₁, δ₂) ∈ G′. The discretized problem can be expressed as:

Sparse Linear Program Representing Discretization of Original Problem (2)–(4)

For given α > 0, β > 0, ${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$, τ, b, G′, L, and Λ, find the set of real values m = {m_rs}_{r∈ℛ,s∈𝒮} minimizing (10) under the constraints:

$$\text{for all}({\delta }_1,{\delta }_2)\in G\prime ,\sum _{r\in \Re }\sum _{s\in 𝒮:s\cap {\mathscr{H}}_{\text{TRUE}}({\delta }_1,{\delta }_2)\ne \varnothing }{P}_{{\delta }_1,{\delta }_2}[(Z_1,Z_2)\in r]m_{rs}\le \alpha ;$$ (11)

$$\sum _{r\in \Re }\sum _{s\in 𝒮:H_{0C}\in s}{P}_{{\delta }_1^{\text{min}},{\delta }_2^{\text{min}}}[(Z_1,Z_2)\in r]m_{rs}\ge 1-\beta ;$$ (12)

$$\text{for all}r\in \Re ,\sum _{s\in 𝒮}{m}_{rs}=1;$$ (13)

$$\text{for all}r\in \Re ,s\in 𝒮,m_{rs}\ge 0.$$ (14)

The constraints (11) represent the familywise Type I error constraints (3) restricted to (δ₁, δ₂) ∈ G′ and M ∈ ℳ_ℛ; (12) represents the power constraint (4) restricted to ℳ_ℛ. We refer to the value of the Bayes objective function (10) evaluated at m as the Bayes risk of m. Denote the optimal solution to the above problem as ${\mathbf{m}}^{*}={\{m_{rs}^{*}\}}_{r\in ℛ,s\in 𝒮}$, which through (6) characterizes the corresponding multiple testing procedure which we denote by M* ∈ ℳ_ℛ.

The constraint matrix for the above linear program is quite sparse, that is, a large fraction of its elements are 0. This is because for any r ∈ ℛ the constraint (13) has only |𝒮| nonzero elements, and for any r ∈ ℛ, s ∈ 𝒮, the constraint (14) has only 1 nonzero element. The power constraint (12) and the familywise Type I error rate constraints (11) generally have many nonzero elements, but there are relatively few of these constraints compared to (13) and (14).

The coefficients in (11) and (12) can be computed by evaluating the bivariate normal probabilities P_δ1,δ2 [(Z₁,Z₂) ∈ r]. This can be done with high precision, essentially instantaneously, by standard statistical software such as the pmvnorm function in the R package mvtnorm. For each r ∈ ℛ, s ∈ 𝒮, the term in curly braces in the objective function (10) can be computed by numerical integration over (δ₁, δ₂) ∈ ℝ² with respect to the prior distribution Λ. We give R code implementing this in the Supplementary Materials. The minimax version (5) of the optimization problem from Section 3.2 can be similarly represented as a large, sparse linear program, as described in Section J of the Supplementary Materials. We show in Section 9 how to efficiently solve the resulting discretized problems using advanced optimization tools.

5 Application to HIV Example in Section 2

5.1 Solution to Optimization Problem in Four Special Cases

We illustrate our method by solving special cases of the constrained Bayes optimization problem. We use the loss function L̃ defined in Section 3.2. The risk corresponding to L̃ has an interpretation in terms of power to reject subpopulation null hypotheses. We define the power of a procedure to reject a null hypothesis H ∈ ℋ as the probability it rejects at least H (and possibly other null hypotheses). For any non-centrality parameters ${\delta }_1\ge {\delta }_1^{\text{min}},{\delta }_2<{\delta }_2^{\text{min}}$ and any M ∈ ℳ_ℛ, the risk E_δ1,δ2 L̃ (M(Z₁,Z₂, U); δ₁, δ₂) equals one minus the power of M to reject H₀₁ under (δ₁, δ₂); an analogous statement holds for subpopulation 2. For ${\delta }_1\ge {\delta }_1^{\text{min}},{\delta }_2<{\delta }_2^{\text{min}}$, the risk equals the sum of one minus the power to reject each subpopulation null hypothesis.

We specify the following prior on the non-centrality parameters $({\delta }_1,{\delta }_2):\mathrm{\Lambda }={\sum }_{j=1}^4{w}_j{\lambda }_j$, where w = (w₁,w₂,w₃,w₄) is a vector of weights. Let λ₁, λ₂, λ₃, λ₄ be point masses at $(0,0),({\delta }_1^{\text{min}},0),(0,{\delta }_2^{\text{min}})$, and (${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$) respectively. We consider two cases below. In the first, called the symmetric case, we set the subpopulation proportions p₁ = p₂ = 1/2 and use the symmetric prior Λ₁ defined by weights w⁽¹⁾ = (0.25, 0.25, 0.25, 0.25). In the second, called the asymmetric case, we set p₁ = 0.63 and use the prior Λ₂ defined by weights w⁽²⁾ = (0.2, 0.35, 0.1, 0.35); this case is motivated by the example in Section 2, where subpopulation 1 is 63% of the total population and is believed to have a greater likelihood of benefiting from treatment than subpopulation 2. In Section D of the Supplementary Materials, we give examples using a continuous prior distribution on ℝ².

For each case, we solved the corresponding linear program using the algorithm in Section 9. The dimensions of the rectangles in the discretization are set at τ = (0.02, 0.02), and we set b = 5. We describe how G′ is determined in Section 6.2. Each discretized linear program has approximately 1.5 million variables and 1.8 million constraints; all but a couple hundred constraints are sparse. We give the precise structure of this linear program in Section 9.

We set α = 0.05 and set each variance ${\sigma }_{ka}^2$ to be a common value σ². Let $M_{H_{0C}}^{\mathrm{U}\mathrm{M}\mathrm{P}}$ denote the uniformly most powerful test of the single null hypothesis H_0C at level α, which rejects H_0C if (Z₁,Z₂) is in the region R_UMP = {(z₁, z₂) : ρ₁z₁ + ρ₂z₂ > Φ⁻¹(1 − α)}, for Φ the standard normal cumulative distribution function. To allow a direct comparison with $M_{H_{0C}}^{\mathrm{U}\mathrm{M}\mathrm{P}}$, we set the total sample size n equal to n_min, defined to be the minimum sample size such that $M_{H_{0C}}^{\mathrm{U}\mathrm{M}\mathrm{P}}$ has 90% power to reject H_0C when the treatment benefit in both populations equals Δ^min. We round all results to two decimal places.

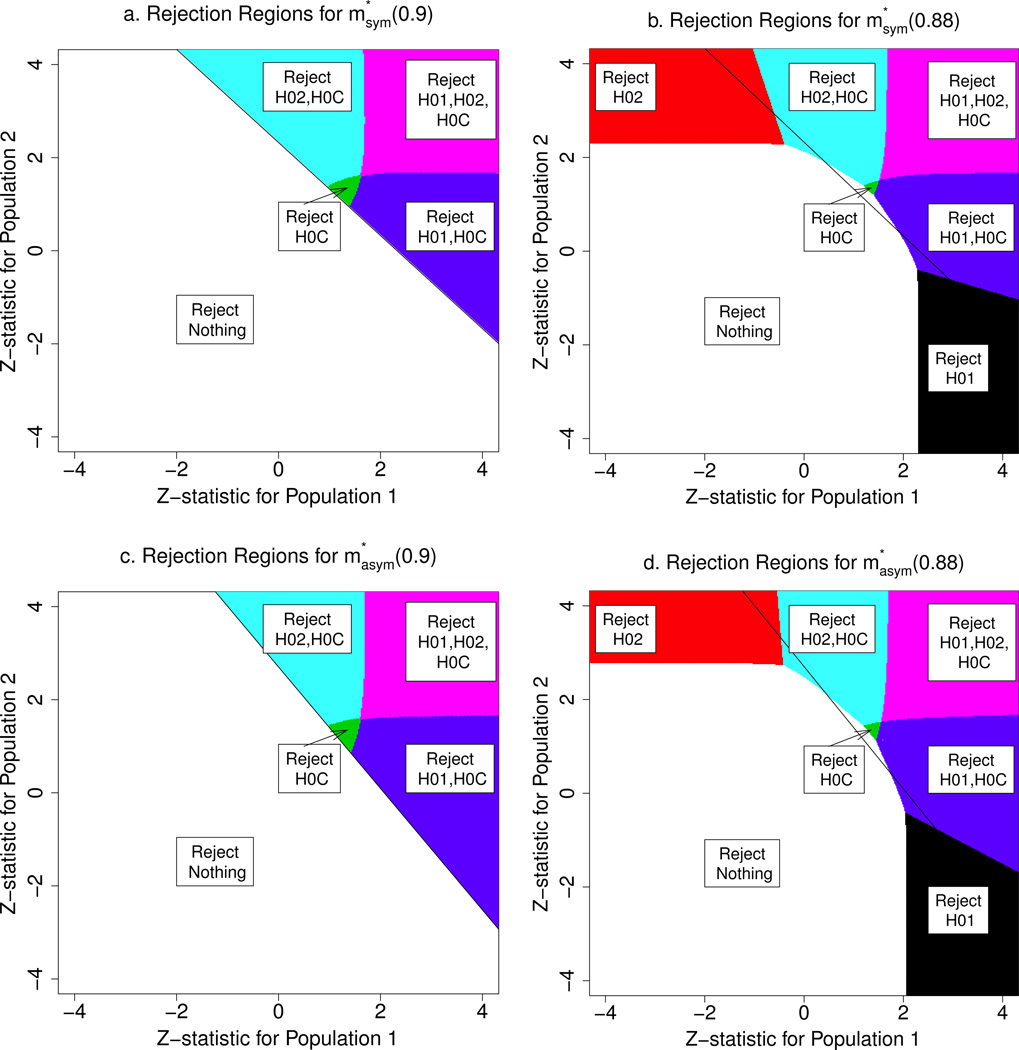
Consider the symmetric case. Let ${\mathbf{m}}_{\text{sym}}^{*}(1-\beta )$ denote the solution to the discretized problem at H_0C power constraint 1 − β. For 1 − β = 0.9, any multiple testing procedure that satisfies the power constraint (4) and the familywise Type I error constraint (3) at the global null hypothesis (δ₁, δ₂) = (0, 0) must reject H_0C whenever (Z₁,Z₂) ∈ R_UMP and cannot reject any null hypothesis when (Z₁,Z₂) ∉R_UMP, except possibly on a set of Lebesgue measure zero; this follows from Theorem 3.2.1 of Lehmann and Romano (2005). Since this must hold for the optimal procedure ${\mathbf{m}}_{\text{sym}}^{*}(0,9)$ what remains to be determined is what regions in R_UMP correspond to ${\mathbf{m}}_{\text{sym}}^{*}(0,9)$ rejecting H₀₁,H₀₂, both, or neither. The rejection regions for ${\mathbf{m}}_{\text{sym}}^{*}(0,9)$, computed using our method, are depicted in Figure 1a. For each s ∈ 𝒮, the region where ${\mathbf{m}}_{\text{sym}}^{*}(0,9)$ rejects precisely s is shown in a different color.

Figure 1.

Optimal multiple testing procedures, for the symmetric case (a) and (b), and for the asymmetric case (c) and (d). In each plot, the black line is the boundary of RUMP for the corresponding case.

Consider weakening the H_0C power constraint from 1 − β = 0.9 to 0.88. The optimal solution ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$ is shown in Figure 1b. Unlike ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$, the procedure ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$ has substantial regions outside R_UMP where it rejects a single subpopulation null hypothesis. However, there is a small region in R_UMP where ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$ does not reject any null hypothesis. Also, in some parts of R_UMP corresponding to one z-statistic being large and positive while the other is negative, ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$ only rejects the null hypothesis corresponding to the large z-statistic, while ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$ rejects both this and H_0C.

The optimal solutions ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$ and ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$ illustrate a tradeoff between power for H_0C and for H₀₁,H₀₂, as shown in the first two columns of Table 1. For each procedure, the first row gives one minus the Bayes risk, which is a weighted sum of power under the three alternatives (${\delta }_1^{\text{min}},0),(0,{\delta }_2^{\text{min}}$), and (${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$); these alternatives correspond to the treatment only benefiting subpopulation 1, only benefiting subpopulation 2, and benefiting both subpopulations, respectively, at the minimum, clinically meaningful level. The contributions from each of these are given in rows 2–4 of Table 1. There is no contribution from the alternative (0, 0) since the loss function L̃ is identically zero there.

Table 1.

Bayes risk and power for optimal multiple testing procedures in symmetric and asymmetric cases, at 1 − β = 0.9 and 1 − β = 0.88.

	Symmetric Case		Asymmetric Case
	${\mathbf{m}}_{\text{sym}}^{*}(0.9)$	${\mathbf{m}}_{\text{sym}}^{*}(0.88)$	${\mathbf{m}}_{\text{asym}}^{*}(0.9)$	${\mathbf{m}}_{\text{asym}}^{*}(0.88)$
One Minus Bayes Risk	0.52	0.58	0.67	0.71
Power for H01 at $({\delta }_1^{\text{min}},0)$	0.39	0.51	0.55	0.67
Power for H02 at $(0,{\delta }_2^{\text{min}})$	0.39	0.51	0.25	0.30
[Power H01 at $({\delta }_1^{\text{min}},{\delta }_2^{\text{min}})$ + Power H02 at $({\delta }_1^{\text{min}},{\delta }_2^{\text{min}})$]/2	0.65	0.66	0.64	0.64
Power for H0C at $({\delta }_1^{\text{min}},{\delta }_2^{\text{min}})$	0.90	0.88	0.90	0.88

The upshot is that using the procedure ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$ in place of ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$ involves sacrificing 2% power for H_0C at (${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$), but gaining 11% power to reject H₀₁ at $({\delta }_1^{\text{min}},0)$ plus an identical increase in power to reject H₀₂ at $(0,{\delta }_2^{\text{min}})$. We further discuss this tradeoff over a range of β values in Section 5.3.

Next consider the asymmetric case, corresponding to p₁ = 0.63 and prior Λ₂. Let ${\mathbf{m}}_{\text{asym}}^{*}(1-\beta )$ denote the solution to the corresponding discretized problem at 1 − β. Figures 1c and 1d show the optimal solutions ${\mathbf{m}}_{\text{asym}}^{*}(0.9)$ and ${\mathbf{m}}_{\text{asym}}^{*}(0.88)$. The main difference between these and the solutions for the symmetric case is that ${\mathbf{m}}_{\text{asym}}^{*}(0.9)$ and ${\mathbf{m}}_{\text{asym}}^{*}(0.88)$ have larger rejection regions for H₀₁ and smaller rejection regions for H₀₂. The power tradeoff between ${\mathbf{m}}_{\text{asym}}^{*}(0.9)$ and ${\mathbf{m}}_{\text{asym}}^{*}(0.88)$ is given in the last two columns of Table 1. Sacrificing 2% power for H_0C at (${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$) leads to an increase in 12% power to reject H₀₁ at $({\delta }_1^{\text{min}},0)$, and an increase in 5% power to reject H₀₂ at $(0,{\delta }_2^{\text{min}})$.

5.2 Monotonicity Properties and Approach for Verifying (3)

Let ℳ* denote the set $\{{\mathbf{m}}_{\text{sym}}^{*}(0.9),{\mathbf{m}}_{\text{asym}}^{*}(0.9),{\mathbf{m}}_{\text{sym}}^{*}(0.88),{\mathbf{m}}_{\text{asym}}^{*}(0.88)\}$. Each procesdure M* ∈ ℳ* satisfies properties that we define next. For any M ∈ ℳ_det and any R ⊆ ℝ², define the following monotonicity properties with respect to R: for any (z₁, z₂) ∈ R,

1. if H₀₁ ∈ M(z₁, z₂), then $H_{01}\in M(z_1^{\prime },z_2)$ for any $(z_1^{\prime },z_2)\in R$ for which $z_1^{\prime }\ge z_1$;

2. if H₀₂ ∈ M(z₁, z₂), then $H_{01}\in M(z_1,z_2^{\prime })$ for any $(z_1,z_2^{\prime })\in R$ for which $z_1^{\prime }\ge z_1,z_2^{\prime }\ge z_2$;

3. if H_0C ∈ M (z₁, z₂), then $H_{0C}\in M(z_1^{\prime },z_2^{\prime })$ for any $(z_1^{\prime },z_2^{\prime })$ for which $z_1^{\prime }\ge z_1,z_2^{\prime }\ge z_2$;

4. if M(z₁, z₂) ≠ ∅, then M(z₁+x, z₂+x) ≠ ∅ for any x > 0 such that (z₁+x, z₂+x) ∈ R.

We verified that each procedure M* ∈ ℳ* satisfies all of these monotonicity properties with respect to the region R = B. These properties are intuitively appealing. Also, they simplify the process of verifying all the familywise Type I error constraints (3) of the original problem; below, we give an overview of the main steps involved in verifying this for the procedures ℳ*. The full argument is given in Section H of the Supplementary Materials, including the proof of the following theorem:

Theorem 1: (a.) For any M ∈ ℳ_det ∩ ℳ_B that satisfies (a)–(d) with respect to R = B,

$$\underset{({\delta }_1,{\delta }_2)\in {ℝ}^2}{\text{sup}}{P}_{{\delta }_1,{\delta }_2}[M(Z_1,Z_2)\cap {\mathscr{H}}_{\mathit{\text{TRUE}}}({\delta }_1,{\delta }_2)\ne \varnothing ]=\underset{({\delta }_1,{\delta }_2)\in {ℝ}^2}{\text{sup}}{P}_{{\delta }_1,{\delta }_2}[M(Z_1,Z_2)\cap {\mathscr{H}}_{\mathit{\text{TRUE}}}({\delta }_1,{\delta }_2)\ne \varnothing ].$$ (15)

(b.) For any M ∈ ℳ_det that satisfies (a)–(d) with respect to R = ℝ², (15) holds.

By part (a) of Theorem 1, to verify the familywise Type I error constraints (3) of the original problem for all (δ₁, δ₂) ∈ ℝ², it suffices to check the constraints for all (δ₁, δ₂) ∈ G. We check these latter constraints by first partitioning G into multiple regions. For each region that is sufficiently far from B, we directly prove (3) holds over that region, using that ℳ* ⊆ ℳ_B. Each of the remaining regions is discretized, and we compute the familywise Type I error at each point in the discretization; we combine this with an analytic bound on the maximum possible discrepancy between the familywise Type I error rate at any point in that region, and the familywise Type I error rate at the nearest point in the discretization.

To upper bound (15) by 0.05 using this approach, it was necessary to solve the discretized problems at α = 0.05 − 10⁻⁴. This reduction from 0.05 had a negligible effect on the Bayes risk of the resulting procedures, as described in Section H of the Supplementary Materials.

5.3 Optimal Power Tradeoff for Combined Population versus Subpopulations

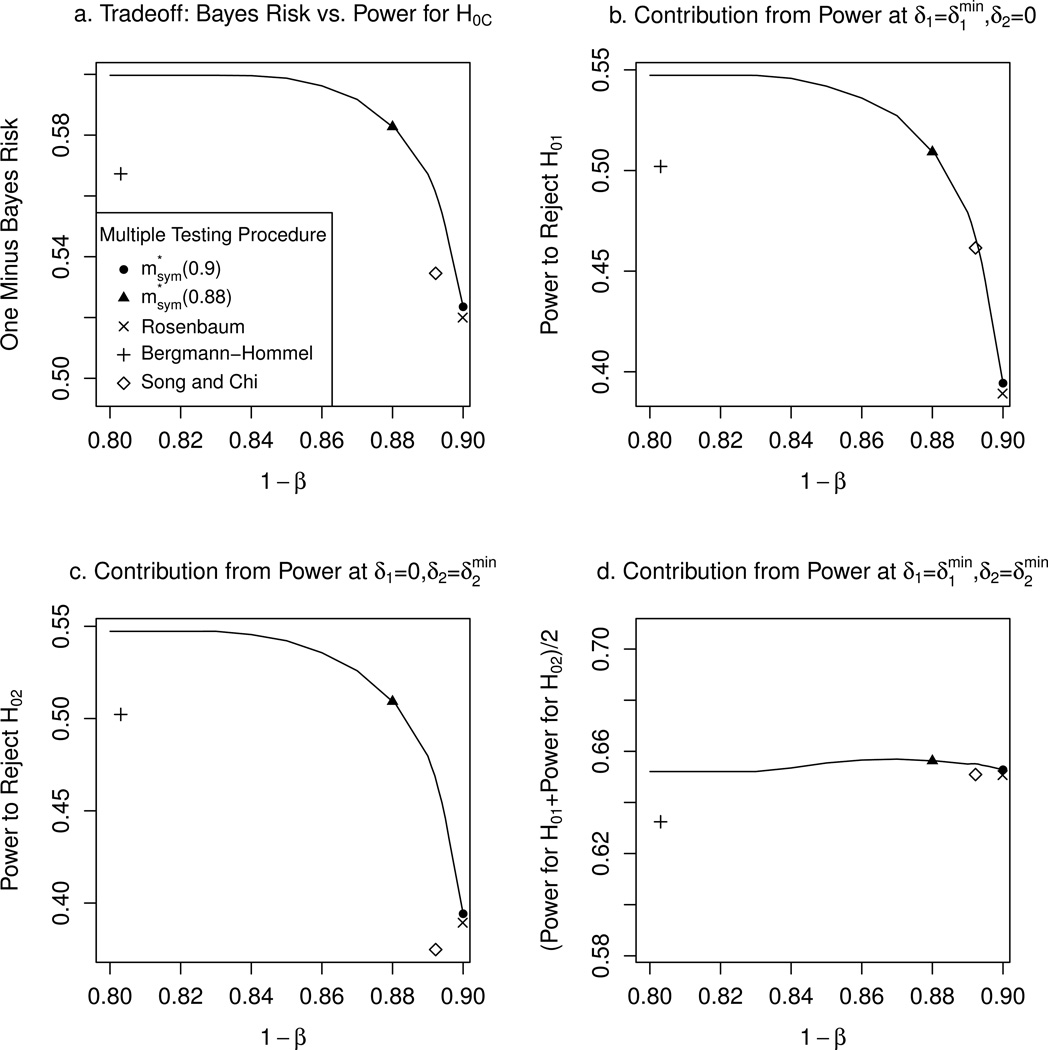
We explore the tradeoffs in power for rejecting a subpopulation null hypothesis when the treatment only benefits one subpopulation, versus power for rejecting the combined population null hypothesis when the treatment benefits both subpopulations. Figure 2 shows the Bayes risk and its components for the optimal procedure ${\mathbf{m}}_{\text{sym}}^{*}(1-\beta )$, for each value of 1 − β in a grid of points on the interval [0.8, 0.9], for the symmetric case. The solid curve in Figure 2a gives the optimal tradeoff between the Bayes risk and the constraint 1 − β on the power to reject H_0C at (${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$). Figures 2b–d show the contribution to the Bayes risk from power under the three alternatives $({\delta }_1^{\text{min}},0)$, $(0,{\delta }_2^{\text{min}})$, and (${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$).

Figure 2.

Optimal tradeoff between Bayes risk and power constraint 1 − β on H_0C, for symmetric case, i.e., p₁ = p₂ = 1/2 and prior Λ₁. In (a), we give one minus the Bayes risk on the vertical axis, so that in all four plots above, larger values represent better performance.

In each plot, we included points corresponding to ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$ and ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$, as well as three existing multiple testing procedures. The first is a procedure of Rosenbaum (2008) that rejects H_0C when $M_{H_{0C}}^{\mathrm{U}\mathrm{M}\mathrm{P}}$ does, and if so, additionally rejects each subpopulation null hypothesis H_0k for which Z_k > Φ⁻¹(1 − α). The second existing method is an improvement on the Bonferroni and Holm procedures by Bergmann and Hommel (1988) for families of hypotheses that are logically related, as is the case here. The third is a special case of the method of Song and Chi (2007) that trades off power for H_0C to increase power for H₀₁, we augmented their procedure to additionally reject H₀₂ in some cases. The details of the latter two procedures are given in Section E of the Supplementary Materials. Each of the three existing procedures strongly controls the familywise Type I error rate at level α.

The procedure of Rosenbaum (2008) is quite close to the optimal threshold at 1 − β = 0.9, being suboptimal compared to ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$ by only 0.4% in terms of the Bayes risk; the corresponding rejection regions are very similar to those of ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$. The procedure of Bergmann and Hommel (1988) is suboptimal by 5% in power for rejecting H₀₁ at $({\delta }_1^{\text{min}},0)$ and for rejecting H₀₂ at $(0,{\delta }_2^{\text{min}})$. The procedure of Song and Chi (2007) is close to optimal for rejecting H₀₁ at $({\delta }_1^{\text{min}},0)$, but is 9% suboptimal for H₀₂ at $(0,{\delta }_2^{\text{min}})$. This is not surprising since their procedure was designed with a focus on the null hypothesis for a single subpopulation, rather than for both a subpopulation and its complement.

The tradeoff curves are steep near 1 − β = 0.9, indicating that a small sacrifice in power to reject H_0C at (${\delta }_1^{\text{min}},{\delta }_2^{\text{min}}$) leads to a relatively large gain in power to detect subpopulation treatment effects when the treatment benefits only one subpopulation. The first two columns of Table 1, which compare ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$ versus ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$, are an example of this tradeoff. Diminishing returns set in for 1 − β less than 0.84, in that there is negligible improvement in the Bayes risk or any of its components if one further relaxes the power constraint for H_0C.

Consider the impact of increasing the total sample size n above n_min, holding Δ^min and the variances ${\sigma }_{sa}^2$ fixed. Define the multiple testing procedure ${\mathbf{m}}_{SS}^{*}(n)$ to be the solution to the discretized optimization problem in the symmetric case at 1 − β = 0.9 and sample size n, for n ≥ n_min. As n increases from n_min, the rejection regions of ${\mathbf{m}}_{SS}^{*}(n)$ progress from ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$ as in Figure 1a to rejection regions qualitatively similar to ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$ as in Figure 1b; these regions are given in Section F of the Supplementary Materials. Increasing sample size from n = n_min to n = 1.06n_min, the power of ${\mathbf{m}}_{SS}^{*}(n)$ to reject H₀₁ at $({\delta }_1^{\text{min}},0)$ increases from 42% to 52%; there is an identical increase in power to reject H₀₂ at $(0,{\delta }_2^{\text{min}})$.

To give a sense of the value of increasing power from 42% to 52%, consider testing the single null hypothesis H₀₁ based on Z₁, using the uniformly most powerful test of H₀₁ at level α′. Consider the sample size for which the power of this test is 42% at a fixed alternative ${\mathrm{\Delta }}_1={\mathrm{\Delta }}_1^{\text{min}}>0\text{and}{\sigma }_{10}^2>0,{\sigma }_{11}^2>0$. To increase power to 52%, one needs to increase the sample size by 38%, 31%, or 28%, for α′ equal to 0.05, 0.05/2 or 0.05/3, respectively. In light of this, the above 10% gains in power for detecting subpopulation treatment effects at the cost of only a 6% increase in sample size (and while maintaining 90% power for H_0C), as ${\mathbf{m}}_{SS}^{*}(n)$ does, is a relatively good bargain.

The tradeoff curve in Figure 2a is optimal, i.e., no multiple testing procedure satisfying the familywise Type I error constraints (3) can have Bayes risk and power for H_0C corresponding to a point that exceeds this curve. The Bayes risk is a weighted combination of power at the three alternatives given above, as shown in Figures 2b–d. It follows that no multiple testing procedure satisfying (3) can simultaneously exceed all three power curves in Figures 2b–d. However, there do exist procedures that have power greater than one or two of these curves but that fall short on the other(s). By solving the constrained Bayes optimization problem using different priors Λ, one can produce examples of such procedures.

A similar pattern as in Figure 2 holds for the asymmetric case. The main difference is that power to reject H₀₁ at $({\delta }_1^{\text{min}},0)$ is larger than power to reject H₀₂ at $(0,{\delta }_2^{\text{min}})$. In Section F of the Supplementary Materials, we answer the question posed in Section 1 of what minimum additional sample size is required to achieve a given power for detecting treatment effects in each subpopulation, while maintaining 90% power for H_0C and strongly controlling the familywise Type I error rate. We do this for p₁ = p₂, but the general method can be applied to any subpopulation proportions.

6 Using the Dual of the Discretized Problem to Bound the Bayes Risk of the Original Problem

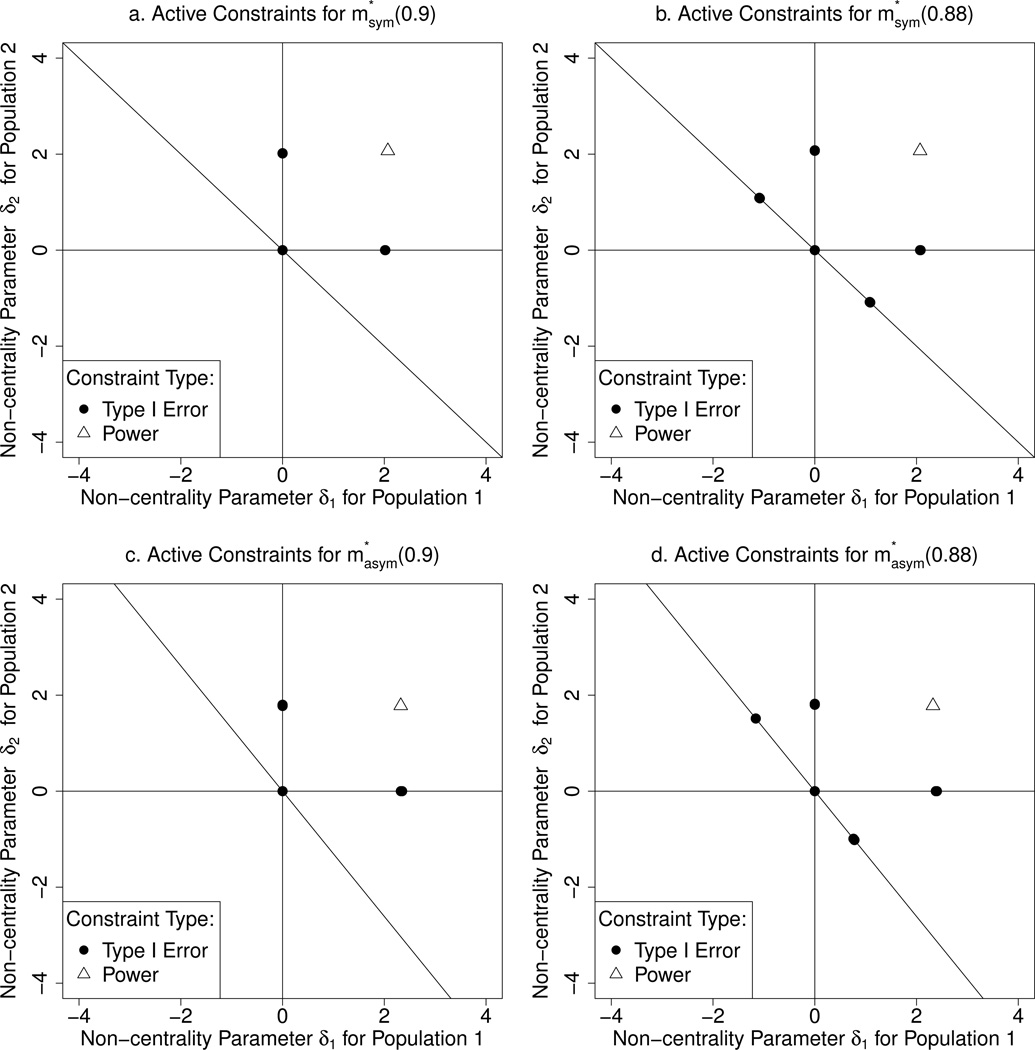
6.1 Active Constraints in the Dual Solution of the Discretized Problem

For each optimal procedure from Section 5.1, Figure 3 shows the constraints among (11) and (12) that are active, i.e., for which the corresponding inequalities hold with equality. In all cases, the global null hypothesis (δ₁, δ₂) = (0, 0), the power constraint (12), and one constraint on the boundary of the null space for each of H₀₁ and H₀₂, are active. In addition, each of the optimal procedures at 1 − β = 0.88 has two active constraints on the boundary of the null space for H_0C. The active familywise Type I error constraints correspond to the least-favorable distributions for a given procedure.

Figure 3.

Active constraints for optimal procedures ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$, ${\mathbf{m}}_{\text{sym}}^{*}(0.88)$, ${\mathbf{m}}_{\text{sym}}^{*}(0.9)$; and ${\mathbf{m}}_{\text{asym}}^{*}(0.88)$. Lines indicate boundaries of null spaces for H₀₁,H₀₂,H_0C.

To illustrate the importance of all these constraints, consider what would happen if we only imposed the familywise Type I error constraint (3) at the global null hypothesis and the power constraint (4) at 1− β = 0.88. The optimal solution to the corresponding constrained Bayes optimization problem in the symmetric case has familywise Type I error 0.54 at non-centrality parameters $({\delta }_1^{\text{min}},0)$ and $(0,{\delta }_2^{\text{min}})$; in the asymmetric case, the familywise Type I error at each of these alternatives is 0.39 and 0.69, respectively. The rejection regions are given in Section G of the Supplementary Materials. This demonstrates the importance of the additional familywise Type I error constraints.

As described in Section 5.2, the optimal solutions to the discretized problems in Section 5.1 satisfy all constraints (3); this holds despite our not having imposed the constraints (3) for (δ₁, δ₂) ∈ G \ B. Intuitively, this is because the optimal solutions are driven by the active constraints, all of which are contained in B for the value b = 5 used in defining our discretized problem.

6.2 Improving Accuracy by More Closely Approximating the Active Constraints

For each example in Section 5.1, we first solved the discretized problem at an initial, relatively coarse discretization, where we set b = 5, τ₁ = τ₂ = 0.1, and G′ = Gτ,b. The locations of active constraints in the resulting solution were then used to construct a new, more focused set $G_{\mathit{\text{new}}}^{\prime }\subset G$ of constraints (3). Specifically, for each active familywise Type I error constraint (δ₁, δ₂) from the solution at the initial discretization, we included in $G_{\mathit{\text{new}}}^{\prime }$ a high concentration of points along a small line segment in G containing (δ₁, δ₂); we did not include any other points. The motivation was to simultaneously obtain closer approximations to the active constraints of the original problem, and to reduce the total number of constraints. We then solved the discretized problem at the finer discretization b = 5, τ₁ = τ₂ = 0.02, using familywise Type I error constraints $G\prime =G_{\mathit{\text{new}}}^{\prime }$. The set $G_{\mathit{\text{new}}}^{\prime }$ for each example from Section 5.1 is given in Section K of the Supplementary Materials. As one example, the number of constraints in $G_{\mathit{\text{new}}}^{\prime }$ is 106 for the symmetric case at 1 − β = 0.88.

6.3 Bounding the Bayes Risk of the Optimal Solution to the Original Problem

The optimal multiple testing procedures shown in Figure 1 are the solutions to versions of the discretized problem (10)–(14), which is an approximation to the constrained Bayes optimization problem (2)–(4). We refer to the latter as the original problem. A natural question is how the optimal Bayes risk for the discretized problem compares to the optimal Bayes risk achievable in the original problem.

We use the optimal solution ν* to the dual of the discretized problem to obtain a lower bound on optimal Bayes risk of the original problem. For a given discretized problem and optimal dual solution ν*, let C_FWER denote the set of indices of active familywise Type I error constraints among (11); these are the indices j of the pairs (δ_1,j, δ_2,j) ∈ G′ corresponding to the nonzero components ${\nu }_j^{*}$ of ν*. Let ${\nu }_p^{*}$ denote the value of the dual variable corresponding to the power constraint (12). Let ℳ_c denote the subclass of multiple testing procedures in ℳ that satisfy all the constraints (3) and (4) of the original problem. Then we have the following lower bound on the objective function (2) of the original problem:

$$\underset{M\in {ℳ}_c}{\text{inf}}\int E_{{\delta }_1,{\delta }_2}L(M(Z_1,Z_2,U);{\delta }_1,{\delta }_2)d\mathrm{\Lambda }({\delta }_1,{\delta }_2)$$ (16)

$$\ge \underset{M\in ℳ}{\text{inf}}[\int E_{{\delta }_1,{\delta }_2}L(M(Z_1,Z_2,U);{\delta }_1,{\delta }_2)d\mathrm{\Lambda }({\delta }_1,{\delta }_2)+{\nu }_p^{*}\{1-\beta -P_{{\delta }_1^{\text{min}},{\delta }_2^{\text{min}}}(M\text{rejects}{H}_{0C})\}+\sum _{j\in C_{\mathrm{F}\mathrm{W}\mathrm{E}\mathrm{R}}}{\nu }_j^{*}\{P_{{\delta }_{1,j},{\delta }_{2,j}}(M\text{rejects any null hypothesis in}{\mathscr{H}}_{\text{TRUE}}({\delta }_{1,j},{\delta }_{2,j}))-\alpha \}],$$ (17)

which follows since all components of ν* are nonnegative, by definition. The minimization problem (17) is straightforward to solve since it is unconstrained. We give the solution in Section I of the Supplementary Materials, which is computed by numerical integration. We then computed the absolute value of the difference between this lower bound and the Bayes risk of the optimal solution to the discretized problems in Section 5.1, which is at most 0.005 in each case. This shows the Bayes risk for the optimal solution to each discretized problem is within 0.005 of the optimum achievable in the original problem, so little is lost by restricting to the discretized procedures at the level of discretization we used.

7 Computational Challenge and Our Approach to Solving It

Previous methods, such as those of Jennison (1987); Eales and Jennison (1992); and Banerjee and Tsiatis (2006) are designed to test a null hypothesis for a single population. These methods require specifying one or two constraints that include the active constraints for a given problem. This can be done for a single population since often the global null hypothesis of zero treatment effect and a single power constraint suffice. However, as shown in the previous section, in our problem there can be 6 active constraints in cases of interest. Especially in the asymmetric case shown in Figure 3d, it would be difficult to a priori guess this set of constraints or to do an exhaustive search over all subsets of 6 constraints in G′. Even if the set of active constraints C_FWER for our problems from Section 5.1 were somehow known or correctly guessed, the problems could still be challenging to solve using standard optimization methods such as Lagrange multipliers. We discuss this in Section L of the Supplementary Materials.

Our approach overcomes the above computational obstacles by transforming a fine discretization of the original problem to a sparse linear program that contains many constraints; we then leverage the machinery of linear program solvers, which are expressly designed to optimize under many constraints simultaneously. The sparsity of the constraint matrix of the discretized linear program is crucial to the computational feasibility of our approach. This sparsity results from being able to a priori specify a subset G′ of the familywise Type I error constraints that contains close approximations to the active constraints, where G′ is not so large as to make the resulting linear program computationally intractable. The size of G′ in the examples from Section 5.1 and in the examples in the Supplementary Materials was never more than 344. More generally our method is computationally feasible with G′ having up to a thousand constraints.

8 Application to Decision Theory Framework

A drawback of the hypothesis testing framework when considering subpopulations is that it does not directly translate into clear treatment recommendations. For example, if the null hypotheses H_0C and H₀₁ are rejected, it is not clear whether to recommend the treatment to subpopulation 2. We propose a decision theory framework that formalizes the goal of recommending treatments to precisely the subpopulations who benefit at a clinically meaningful level. The framework allows one to explore tradeoffs in prioritizing different types of errors in treatment recommendations to different subpopulations. The resulting optimization problems, which were not solvable previously, are solved using our general approach.

We use the definitions in Section 3.1. Our goal is to construct a decision procedure D, i.e., a measurable map from any possible realization of (Z₁,Z₂) to a set of subpopulations (∅, {1}, {2}, or {1, 2}) to recommend the new treatment to. We consider randomized decision procedures, i.e., we allow D to additionally depend on a random variable U that is independent of Z₁,Z₂ and that has uniform distribution on [0, 1].

We next define a class of loss functions. For each subpopulation k ∈{1, 2}, let l_k,FP be a user-defined penalty for recommending the treatment to subpopulation k when ${\delta }_k<{\delta }_k^{\text{min}}$ (a False Positive); let l_k,FN be the penalty for failing to recommend the treatment to subpopulation k when ${\delta }_k\ge {\delta }_k^{\text{min}}$ (a False Negative). Define the loss function L_D (d; δ₁, δ₂) = L_D,₁(d; δ₁, δ₂) + L_D,₂(d; δ₁, δ₂), where for each d ⊆ {1, 2} and k ∈{1, 2},$L_{D,k}(d;{\delta }_1,{\delta }_2)=l_{k,FP}1[{\delta }_k<{\delta }_k^{\text{min}},k\in d]+l_{k,FN}1[{\delta }_k\ge {\delta }_k^{\text{min}},k\notin d]$. For illustration, we consider two loss functions. The first, $L_D^{(1)}$, is defined by l_k,FN = 1 and l_k,FP = 2 for each k; the second, $L_D^{(2)}$, is defined by l_k,FN = 2 and l_k,FP = 1 for each k.

We minimize the Bayes criterion ∫ E_δ1,δ2 {L(D(Z₁,Z₂, U); δ₁, δ₂)} dΛ(δ₁, δ₂), over all decision procedures D as defined above, under the constraints that for any (δ₁, δ₂) ∈ ℝ², P_δ1,δ2 {∑_{k∈D(Z1,Z2,U)} p_kΔ_k ≤ 0} ≤ α} These constraints impose a bound of α on the probability of recommending the new treatment to an aggregate population (defined as the corresponding single subpopulation if D = {1} or {2}, or the combined population if D = {1, 2}) having no average treatment benefit.

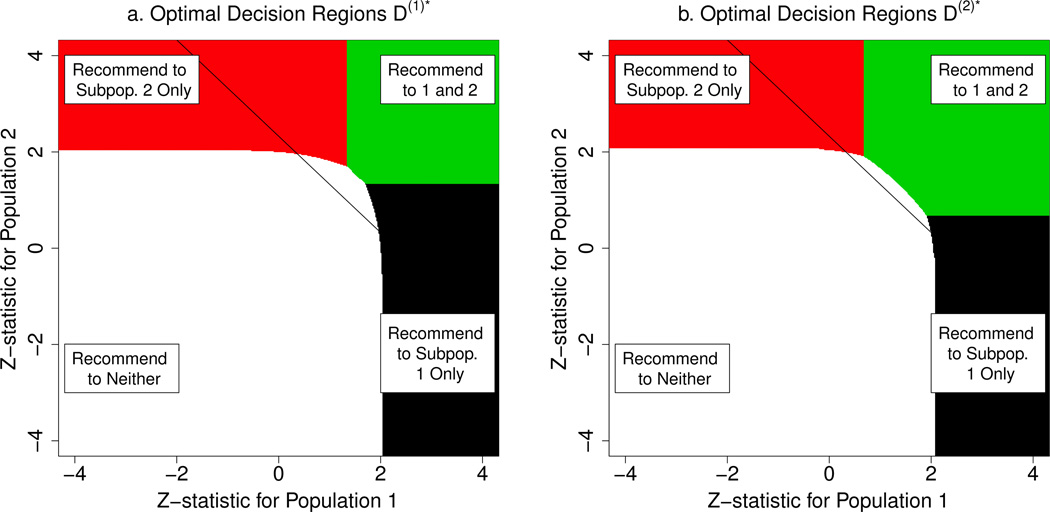
We consider the symmetric case from Section 5.1. The optimal decision regions are given in Figure 4. The optimal decision rule under $L_D^{(1)}$, denoted by D^(1)*, is more conservative in recommending the treatment than the optimal rule under $L_D^{(2)}$, denoted by D^(2)*. This is because the former loss function penalizes more for false positive recommendations. Table 2 contrasts D^(1)* and D^(2)*. When $({\delta }_1,{\delta }_2)=({\delta }_1^{\text{min}},{\delta }_2^{\text{min}})$, the conservative rule D^(1)* recommends treatment to both subpopulations 21% less often compared to D^(2)*. However, when the treatment only benefits one subpopulation, the conservative rule D^(1)* has 11% greater accuracy in recommending it to just that subpopulation.

Figure 4.

Optimal decision regions for symmetric case (p₁ = 1/2, Λ = Λ₁), for oss functions (a) $L_D^{(1)}$ and (b) $L_D^{(1)}$. For comparability to Figure 1, we included the solid line representing the boundary of the rejection region for $M_{H_{0C}}^{\mathrm{U}\mathrm{M}\mathrm{P}}$.

Table 2.

Probabilities of Different Recommendations by Optimal Decision Procedures D⁽¹⁾* and D⁽²⁾*, at three alternatives (Alt). The optimal recommendation (Rec.) at each alternative is in bold type.

Alt:	$({\delta }_1,{\delta }_2)=({\delta }_1^{\text{min}},0)$				$({\delta }_1,{\delta }_2)=({\delta }_1^{\text{min}},{\delta }_2^{\text{min}})$				(δ1, δ2) = (0, 0)
Rec.:	∅	{1}	{2}	{1, 2}	∅	{1}	{2}	{1, 2}	∅	{1}	{2}	{1, 2}
D(1)*	0.45	0.48	0.01	0.06	0.16	0.14	0.14	0.57	0.95	0.02	0.02	0.01
D(2)*	0.46	0.37	0	0.17	0.13	0.4	0.4	0.78	0.95	0.01	0.01	0.02

One may prefer to strengthen the constraints above to require for any (δ₁, δ₂) ∈ ℝ², P_δ1,δ2 [D(Z₁,Z₂, U) ∩ {k : δ_k ≤ 0} ≠ ∅] ≤ α, that is, to require probability at most α of recommending the new treatment to any subpopulation having no average treatment benefit. Our framework allows computation of the tradeoff between optimal procedures under these different sets of constraints, which is an area of future research.

9 Algorithm to Solve Our Large, Sparse Linear Programs

The discretized problem from Section 4 can be represented as a large-scale linear programming problem. To show this, define the following ordering of subsets of ℋ:

$$𝒮\prime =(s_0,\dots ,s_6)=(\varnothing ,\{H_{01}\},\{H_{02}\},\{H_{0C}\},\{H_{01},H_{0C}\},\{H_{02},H_{0C}\},\{H_{01},H_{02},H_{0C}\}).$$

We leave out the subset {H₀₁,H₀₂}, since by the results of Sonnemann and Finner (1988) it suffices to consider only coherent multiple testing procedures, which in our context are those that reject H_0C whenever {H₀₁,H₀₂} is rejected. For a given ordering r₁, r₂, … of the rectangles ℛ, define x = (m_r1s1, …,m_r1s6,m_r2s1, …, m_r2s6,m_r3s1 …), which has n_υ = |ℛ|(|𝒮′| − 1) components. We do not include the variables m_ris0 in x, since by (13) these variables are functions of variables already in x; in particular, $m_{r_i{s}_0}=1-{\sum }_{j=1}^6{m}_{r_i{s}_j}$.

The discretized problem from Section 4 can be expressed in the canonical form:

$$\underset{x\in {ℝ}^{n_{\upsilon }}}{\text{max}}{\mathbf{c}}^{\mathbf{T}}\mathbf{x}\mathrm{s}.\mathrm{t}.\mathbf{A}\mathbf{x}\le \mathbf{b}.$$ (18)

The objective function c^Tx represents the Bayes objective function (10). We set the first n_d = |G′| + 1 rows of A to comprise the dense constraints, which include the familywise Type I error constraints (11) and the H_0C power constraint (12). The remaining ns rows of A comprise the sparse constraints (13) and (14). Since |ℛ| = (2b/τ +1)², for the symmetric case at 1− β = 0.88 in Section 5.1 with b = 5, τ = τ₁ = τ₂ = 0.02, and |𝒮′| − 1 = 6, we have n_υ = |ℛ|(|𝒮′| − 1) = 1,506,006, n_d = |G′|+1 =106 (where $G\prime =G_{\mathit{\text{new}}}^{\prime }$ defined in Section 6.2), and n_s = |ℛ| + n_υ = 1,757,007. Then A is a 1,757,113 × 1,506,006 matrix with structure:

$$\mathbf{A}=\left[\frac{\frac{n_d=106\text{rows in which most elements are non-zero}}{|\Re |=251,001\text{rows of the form}:\{\begin{array}{c}111111000000000000000000000000\dots \hfill \\ 000000111111000000000000000000\dots \hfill \\ 000000000000111111000000000000\dots \hfill \\ ⋮\hfill \end{array}}}{-{\mathbf{I}}_{1,506,006},\text{that is},\text{the negative}{n}_{\upsilon }\times n_{\upsilon }\text{identify matrix}}\right],$$

b is a vector with n_d + n_s = 1, 757, 113 components (comp.) as follows:

$${\mathbf{b}}^T=\left(\begin{array}{cccc}\hfill |G\prime |=105\text{comp}.\hfill & \hfill 1\text{comp}.\hfill & \hfill |\Re |=251,001\text{comp}.\hfill & \hfill n_{\upsilon }=1,506,006\text{comp}.\hfill \\ \hfill \alpha ,\alpha ,\dots ,\alpha ,\hfill & \hfill -(-1-\beta ),\hfill & \hfill 1,1,\dots ,1\hfill & \hfill 0,0,\dots ,0\hfill \end{array}\right),$$

and c is a vector with n_υ = 1,506,006 components.

The problem scale of (18) is quite large. In particular, the constraint matrix A has ≈ 2.6 × 10¹² entries. However, we can solve (18) by exploiting the sparsity structure of A. We use a projected subgradient descent method, which consists of a subgradient descent step and a projection step, where the solution at iteration k + 1 is x^(k+1) = P_s (x^(k) − δ_kg^(k)), where P_s(.) means projection onto the feasible region determined by the sparse constraints, δ_k is a step size, and g^(k) is the subgradient of x_k, defined as

$${\mathbf{g}}^{(k)}=\{\begin{array}{cc}\hfill \mathbf{c},\hfill & \hfill \text{if for all}i=1,\dots ,n_d,{\mathbf{a}}_i^T{\mathbf{x}}^{(k)}\le b_i,\hfill \\ \hfill -{\mathbf{a}}_{i\prime },\hfill & \hfill \text{otherwise},\text{where}i\prime \text{is a randomly selected index in}\{i:{\mathbf{a}}_i^T{\mathbf{x}}^{(k)}>b_i\}.\hfill \end{array}$$

The projection operator P_s(.) can be applied in 𝒪(n_υ) oating point operations (ops) by computing the projection in |ℛ| independent subsystems, each with |𝒮′| − 1 variables. Checking violations of n_d dense constraints together with the projection costs at most 𝒪(n_υ(n_d+1)) flops per iteration. The projected subgradient descent method above is guaranteed to converge to the optimum of (18) (Boyd et al., 2004). However, it may take a large number of iterations to achieve a high precision solution. In our implementation, we continue until an iteration k′ is reached where the proportion improvement in the objective function value is smaller than 10⁻³; we then use x^(k′) as the initial point in a parametric simplex solver (Vanderbei, 2010). Though each iteration of a parametric simplex solver runs in superlinear time, for our problem it only requires a few iterations to move from x^(k′) to a very precise optimal solution. Our solutions all had duality gap at most 10⁻⁸ showing they are within 10⁻⁸ of the true optimal solution to the discretized problem.

10 Discussion

An area of future research is to consider a variety of optimization criteria, and to find a multiple testing procedure (if one exists) that simultaneously has good performance under each criterion. For example, one may specify a finite set of pairs of loss functions and priors, with each pair determining an objective function of the form (2). Our general method can be adapted to minimize the maximum of these objective functions, under the constraints (3) and (4), as described in Section J of the Supplementary Materials.

Though the discretized problem involved optimizing over the class of randomized multiple testing procedures ℳ_ℛ, the optimal solutions in all our examples were in ℳ_det. This is interesting, since there is no a priori guarantee that there exists an optimal solution that is deterministic, since the problem involves the large class of constraints (11). If the optimal solution to a problem is not deterministic, it might be possible to learn from its structure to find a close approximation that is deterministic; this is an area for future research.

An important question posed by a reviewer is what to do if, for given L and Λ, the optimal solution to the constrained Bayes optimization problem does not have monotonicity properties (a)–(d). Then Theorem 1 would not apply, and the active constraints would not be guaranteed to be in G. How to handle this situation is an area for future research, but we briey describe two approaches that could be tried. The first approach is to augment G′ to additionally include points (δ₁, δ₂) outside of G. For example, one could include a grid of points on the subset of B where at least one null hypothesis is true. Intuitively, if each active constraint in the original problem is closely approximated by a constraint in the discretized problem, one may expect the solution to the discretized problem to be approximately feasible and optimal. A limitation is that the more constraints one adds, the more computationally difficult the discretized problem becomes.

A second way to handle the above situation is to restrict attention to the subclass of procedures that satisfy monotonicity properties (a)–(d). In Section M of the Supplementary Materials, we generalize the definitions of the these properties to randomized multiple testing procedures, and denote the subclass satisfying these properties by ℳ_mon ⊂ ℳ. We show our general method can be adapted to solve the constrained Bayes optimization problem restricted to procedures in ℳ_mon, by encoding each monotonicity property as a set of sparse constraints in the discretized problem. A limitation is that the optimal solution restricted to procedures ℳ_mon may have worse performance compared to the optimal solution over ℳ.

An additional area of future research is to apply our methods to construct optimal testing procedures for trials comparing more than two treatments. Other potential applications include optimizing seamless Phase II/Phase III designs and adaptive enrichment designs.

Though we focused on two subpopulations, it may be possible to extend our approach to three or four subpopulations. This is an area for future research. However, with more than this many populations, our approach will likely be computationally infeasible. This is because the number of variables in the discretized linear program grows with the fineness of the discretization as well as the number of components in the sufficient statistic for the problem. One strategy for reducing the computational burden in larger problems is to start by solving the problem at a relatively coarse discretization; one can then use the structure of the resulting solution to inform where to set constraints when solving the problem at a finer discretization. An example of this strategy was used in Section 6.2.