New York State TrueAllele® Casework Validation Study

Abstract

DNA evidence can pose interpretation challenges, particularly with low-level or mixed samples. It would be desirable to make full use of the quantitative data, consider every genotype possibility, and objectively produce accurate and reproducible DNA match results. Probabilistic genotype computing is designed to achieve these goals. This validation study assessed TrueAllele® probabilistic computer interpretation on 368 evidence items in 41 test cases and compared the results with human review of the same data. Whenever there was a human result, the computer's genotype was concordant. Further, the computer produced a match statistic on 81 mixture items (for 87 inferred matching genotypes) in the test cases, while human review reported a statistic on 25 of these items (30.9%). Using match statistics to quantify information, probabilistic genotyping was shown to be sensitive, specific, and reproducible. These results demonstrate that objective probabilistic genotyping of biological evidence can reliably preserve DNA identification information.

DNA evidence resides at the center of modern criminal justice ¹ and is used to help apprehend, convict, and exonerate suspects ². An ideal DNA system would provide identification information with thoroughness, accuracy, and objectivity. These desirable features are already found in the data generation process, in which a largely automated DNA laboratory transforms biological specimens into quantitative computer signals. However, the subsequent data interpretation process may not possess these ideal attributes.

Rule-based human or computer ³ review can work well with pristine DNA data, such as reference samples. Casework evidence is usually not pristine, however. DNA evidence extracted under real-world conditions is often mixed (having multiple contributors), damaged (by heat or bacteria), or low template (thus hard to discern with certainty).

The DNA data pattern that results from such evidence may suggest multiple genotype possibilities, thereby reducing identification information. Human review of ambiguous DNA can be a time-consuming process that considers only some genotype possibilities, and does not fully elicit all the information that the data contain ⁴. Moreover, human comparison of DNA evidence and suspect genotypes may not be entirely objective ^5–8.

Computer interpretation of DNA evidence overcomes these issues. Specifically, quantitative computer modeling is:

• Thorough, with parallel computers considering virtually every genotype possibility;

• Accurate, able to employ mathematical models that more fully preserve the identification information residing in the DNA data; and

• Objective, interpreting evidence without knowledge of any suspect's genotype.

Such computer processing can effectively handle the mixed, damaged, and low-level DNA evidence that currently consumes much of the human review effort.

Computers can thoroughly examine every genotype possibility through statistical Markov chain Monte Carlo (MCMC) computing ^9,10 on probability models ^11,12. Probabilistic genotypes have been recognized by regulatory bodies such as SWGDAM ¹³ and standards organizations such as ANSI/NIST ¹⁴ as a valid approach to DNA interpretation and reporting. Genotype probability has a long scientific tradition in genetics ^15–17 and human identification ^18–20, with statistical computer solutions for DNA mixtures ^4,21. Human review simplifies DNA data and considers only some genotype possibilities ²². The well-established laws of probability ^23,24 and scientific inference ^25,26 permit a more complete interpretation.

This study examined Cybergenetics TrueAllele® Casework, a probabilistic genotyping computer system that interprets DNA evidence using a statistical model. We analyzed 368 items of anonymized, adjudicated evidence from the New York State Police (NYSP) Forensic Investigation Center (FIC). We studied 81 mixture items, focusing on contributors with mixture weights between 5% and 95%; these contributors yielded 87 inferred genotypes that matched a known suspect. We measured the sensitivity, specificity, and reproducibility of these genotypes using match information. We compared computer results with those from human review.

This study was submitted to the DNA Subcommittee of the New York State Commission on Forensic Science as part of the technology approval process mandated for NYS public DNA laboratories. The DNA Subcommittee made a unanimous binding recommendation for TrueAllele approval on May 20, 2011, which was ratified by the Commission on June 27, 2011.

In this paper, we first discuss computer methods for interpreting quantitative DNA mixture data and information-based validation metrics. We then describe the case materials used in the study and how we classified items. Finally, we present validation results that quantify the sensitivity, specificity, and reproducibility of computer interpretation on this mixture data set.

Methods and Materials

Interpreting Uncertain DNA Evidence

A definite genotype can be determined when a person's DNA produces clean data. However, when the data signals are less definitive or when there are multiple contributors to the evidence, uncertainty arises. This uncertainty is expressed in the resulting genotype, which may describe different genetic identity possibilities. Such genotype uncertainty may translate into reduced identification information when a comparison is made with a suspect.

The DNA identification task can thus be understood as a two-step process ²⁷:

• Objectively inferring genotypes from evidence data, accounting for allele pair uncertainty using probability, and

• Subsequently matching genotypes, comparing evidence with a suspect relative to a population, to express the strength of association using probability.

The match strength is reported as a single number, the likelihood ratio (LR), which quantifies the gain in identification information produced by having examined the DNA evidence ^28–30.

The TrueAllele Casework system is a MATLAB® (The MathWorks, Natick, MA) computer implementation of this two-step DNA identification inference approach. The computer objectively infers genotypes from DNA data through statistical modeling ^31,32, without reference to any suspect. To preserve the identification information present in the data, the system represents genotype uncertainty using probability ³³. These probabilistic genotypes are stored on a PostgreSQL relational database ³⁴ for persistent and secure storage ³⁵. Subsequent comparison with suspects provides investigative and evidentiary identification information. A user visually asks interpretation questions of DNA case data, reviews the computer's answers, and generates a report on the match statistics found.

Identification Information

This study uses identification information ³⁶ to quantify the sensitivity, specificity, and reproducibility of DNA interpretation methods and for making comparisons between methods ³⁷. The LR logarithm (powers of ten or “order of magnitude”) provides an additive measure of match information ^38,39 called the “weight of evidence.”

With a strong DNA match between evidence and suspect, relative to a population, the LR is typically more than a million (log(LR) > 6). The LR can be in the quintillions (log(LR) > 18) when using 13 or more short tandem repeat (STR) loci on unambiguous DNA data. A mismatch will have a small LR under 1, often less than a trillionth (log(LR) < −12). The LR thus quantifies the extent of match, based on DNA data ^40,41. A numerical presentation of scientific support is more precise than qualitative words like “inclusion” or “exclusion” ⁴², which are binary decisions perhaps best left to a trier of fact.

The weight of DNA evidence is used as an information metric throughout this study (Results). For method sensitivity, log(LR) measures the identification information inferred from DNA data. Interpretation specificity is measured by a negative log(LR) value between evidence and a nonmatching individual. We quantify reproducibility through information variation within a case. The productivity of DNA processing can be assessed by how often an informative sample produces a reportable match statistic.

Genotype Probability

Uncertainty in DNA evidence translates into genotype uncertainty. All mixture interpretation methods report out a list of allele pair possibilities and assign a probability to each pair ⁴³. Prior to examining DNA data, our belief is that an evidence genotype has an allele pair probability distribution based on allele frequency in a human population. Observing data at a genetic locus can change this belief, because some contributor genotype possibilities become more likely than others, based on how well they explain the data. Combining likelihood and prior will form a new genotype, whose posterior probability distribution ⁴⁴ typically eliminates hundreds of allele pairs and concentrates on just a few probable ones.

DNA mixture interpretation methods differ by the likelihood function they employ to explain the data. The most informative methods have a likelihood function that uses all the quantitative peak height data and other available information ⁴⁵; these include statistical computer modeling systems ^21,46 such as TrueAllele ⁴⁷. Human interpretation often simplifies the observed peak heights into qualitative all-or-none allele events to form a list of allele pairs ²⁷. Such threshold-based binary likelihood functions can lose identification information, as they do not use all of the available data ⁴⁵. Combined likelihood ratio (CLR) qualitative interpretation considers known (e.g., victim) contributor genotypes, whereas combined probability of inclusion (CPI) does not ²².

Mixture Weight Probability

Individuals contribute their DNA to a mixture item in a certain proportion, or “mixture weight.” Analysts can infer this mixture weight (mean and variance) for the DNA template from quantitative peak height data and assumed contributor genotypes. This human approximation uses only those genetic loci where every allele peak can be unambiguously assigned to some contributor. Computers can instead use all of the loci to infer the mixture weight of the DNA template ³², achieving greater precision.

Mixture weight is an auxiliary variable that can help assess the complexity of a mixture item (Results). A small mixture weight can produce a lower quantity of contributor DNA, which may reduce match information through stochastic effects. In a 50:50 mixture interpreted without assuming a victim reference, more allele pair combinations are possible, and this genotype uncertainty can decrease DNA match information.

Evidence Items

We reanalyzed 41 cases (39 adjudicated and two proficiency tests) that had been previously analyzed by competent DNA analysts at the NYSP FIC. These 41 cases covered many interpretation situations commonly encountered in forensic casework. The cases contained 32 sexual assaults (some having a victim reference) and homicides involving up to 30 evidence items with multiple victims (Table 1A).

Table 1.

Case items. Subtotals organized by (A) type of crime, (B) source of biological sample, and (C) mixture classification

(A) Type
Sexual assault	32
Homicide	3
Assault	4
Miscellaneous	2
	41

(B) Source
Vaginal swab	17
Anal swab	7
Penile swab	1
Semen stain	39
Clothing item	10
Bedding item	3
Weapon	11
Cigarette butt	2
Condom	1
Dried secretion	8
Hair	3
Bite mark	2
Fingernail	9
Blood stain	69
Miscellaneous	24
	206
(C) Category
Simple	39
Intermediate	18
Complex	24
	81

The 368 study items were derived from 206 distinct biological source samples. These samples included diverse evidence sources, such as vaginal swabs, anal swabs, oral swabs, penile swabs, dried secretions, blood stains, semen stains, weapons, cigarette butts, condoms, human hair, bite marks, and fingernail scrapings (Table 1B).

The NYSP laboratory processed the items using Applied Biosystems (AB; Foster City, CA) ProfilerPlus® and Cofiler® STR kits and generated electronic data .fsa files on an AB 3100-series genetic analyzer. Cybergenetics uploaded these files to the TrueAllele system for probabilistic genotyping. The data and results were then available for a retrospective comparison with the corresponding case reports.

The TrueAllele-inferred mixture weights of these evidence items were broadly distributed (Fig.1). Our goal was to study actual mixtures, rather than background contamination or single-source samples. We therefore focused on the 87 inferred evidence genotypes from the 81 matching items that had a mixture weight between 5% and 95%. Different mixture interpretation methods may define a match in different ways (e.g., by item, contributor, or genotype). In this multimethod study, a match is always between a genotype of an evidence contributor and a known reference genotype.

Fig 1.

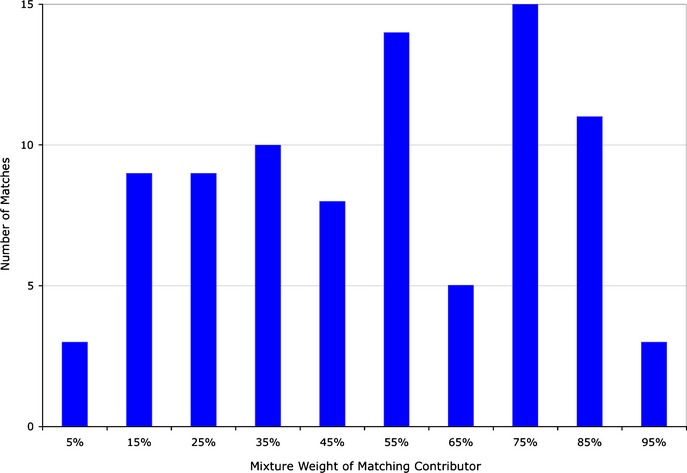
Study mixture weights. The distribution of mixture weight over the case items' matched contributors is shown as a histogram. The x-axis is the TrueAllele-determined mixture weight of the matching contributor, binned in groups of 10% (i.e., 0–10%, 11–20%, etc.). The y-axis is the number of matches that fall within each mixture weight bin. The total number of counts (87) is the number of reported computer matches.

Mixture Classification

Prior to computer analysis, mixture evidence items were classified as simple, intermediate, or complex and assessed by an experienced DNA analyst. About half of the items were in the simple category, with the remainder divided between the intermediate and complex categories (Table 1C). The number and nature of the contributors to the items were tabulated, as shown (Table 2). Other mixture classifications ^48,49 have been tailored to manual mixture review protocols having limited sensitivity and are not relevant to the study of data information content or statistical computer interpretation.

Table 2.

Item complexity. The rows are organized into three groups, based on our simple, intermediate, and complex mixture classification. In the left half of the table, the number of contributors is shown, arranged by total, known, and unknown contributor columns. The right half shows the number of inferred genotypes, giving the number having a TrueAllele match statistic, how many of those were reported by the human review laboratory with an associated match statistic, and the corresponding fraction of human to computer reporting (the computer always generated a match statistic when human review produced a statistic)

Complexity	Contributors			Matches
	Total Number in DNA Item	Number of Knowns	Number of Unknowns	Number Reported by TA with LR Statistic	Number Reported by Laboratory with DNA Statistic	Fraction Reported by Laboratory with DNA Statistic
Simple	2	1	1	32	17	0.531
	2	0	2	4	0	0.000
	3	1	2	4	0	0.000
				40	17	0.425
Intermediate	2	1	1	8	2	0.250
	2	0	2	7	2	0.286
	3	1	2	4	0	0.000
	3	0	3	1	0	0.000
				20	4	0.200
Complex	2	1	1	7	2	0.286
	2	0	2	15	0	0.000
	3	1	2	5	2	0.400
				27	4	0.148
				87	25	0.288

LR, likelihood ratio.

Most of the simple mixture case items had two contributors (Table 2, simple) and came from sexual assault differential extractions. Usually one contributor was known, and the task was to infer the unknown second contributor. The DNA quantity was adequate, and the data showed clear major and minor contributors.

The intermediate mixture items were more challenging for people to interpret. Some were derived from low-template DNA sources, while others contained contributors in approximately equal 50:50 mixture weights. They had two or three contributors, with multiple unknown contributors appearing in most of the items (Table 2, intermediate).

Complex mixture items had two or three contributors, usually with multiple unknown contributors (Table 2, complex). The STR data often showed peak height imbalance or equally weighted contributors. There were low-template DNA items, and several cases had multiple suspect or victim references.

Results

The study examined 4958 alleles in 202 single-source profiles across the 41 cases. The genotypes inferred by the TrueAllele statistical computing system were in complete concordance with human review of the same data. With single-source concordance established, the remainder of the paper focuses on validating DNA mixture interpretation.

Opinions vary about what genotype should be inferred from DNA mixture data ⁴⁵. Regardless of interpretation method, the log(LR_method) of any inferred genotype, relative to a known suspect and reference population, provides a measure of identification information in a single number. Human (e.g., CPI, CLR) and computer (e.g., TrueAllele) mixture interpretation methods thus share a common information vocabulary, so we can quantitatively assess and compare DNA interpretation methods through their match statistics.

Sensitivity

Identification information measures sensitivity, quantifying how well an interpretation method preserves the log(LR) weight of DNA evidence. We examined TrueAllele sensitivity on a set of 87 matches, comparing inferred genotype information from simple, intermediate, and complex cases (Fig.2). These histograms show that the computer preserved considerable identification information. Simple cases (blue) had an average log(LR) of 14.92, intermediate cases (green) averaged 12.05, and the complex case (orange) average was 10.47 (Table 3, θ = 1%). These log(LR) averages correspond to match statistics at the quadrillion, trillion, and billion levels, respectively.

Fig 2.

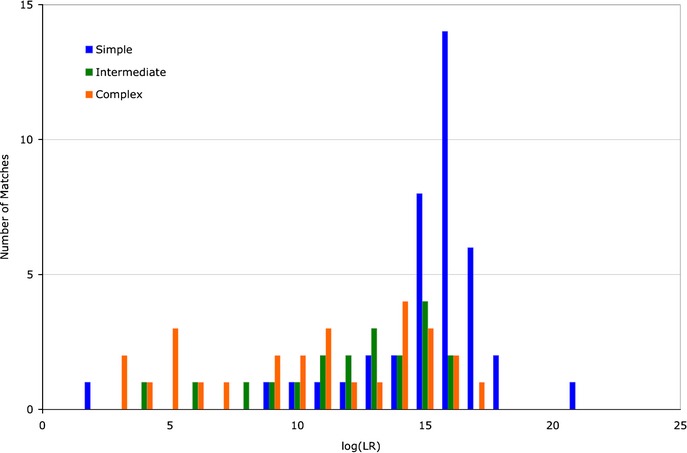
Genotype information sensitivity. The distribution of genotype match information (as inferred by TrueAllele) is shown as a log(LR) histogram of counts for each complexity category, with theta at 1%. The simple items (blue) are distributed more to the right than the intermediate items (green). The leftmost distribution is for the complex items (orange), which tend to be less informative.

Table 3.

Sensitivity and reproducibility. The rows organize the evidence genotypes by their mixture item classification as simple, intermediate, or complex. The middle columns give the DNA match information (mean and within-group standard deviation) in each category on a log(LR) scale. To account for co-ancestry, theta values of both 0% and 1% were used. The mixture weight distribution is presented for each category in the rightmost columns

Mixture Category	N	log(LR) Information				Mixture Weight
		θ = 0%		θ = 1%		Mean (%)	SD (%)
		Mean	SD	Mean	SD
Simple	40	15.78	0.117	14.92	0.125	54.9	23.2
Intermediate	20	12.99	0.232	12.05	0.249	48.9	25.2
Complex	27	11.41	0.584	10.47	0.519	50.1	30.0

With current manual mixture interpretation methods, not all items of evidence will yield a reportable match statistic. Prior to SWGDAM's 2010 mixture interpretation guidelines, a DNA analyst might have reported an item using qualitative “consistent with,” “cannot be excluded,” or “insufficient” language, without attaching a match number. Now, under current SWGDAM guidelines, a laboratory's newly elevated peak threshold may result in no statistic ⁵⁰.

The TrueAllele computer, however, has no choice but to infer a genotype that can be used later on in a statistical match comparison. The computer is programmed to report a LR value at every locus in a genotype comparison, unlike human review ⁵. If the data are uninformative, that fact is reflected in a diffuse genotype distribution and a low LR score.

The weight of DNA evidence in this study ranged from a log(LR) of 2.02 (hundred) to 21.35 (sextillion), with a median value of 14.50 (quadrillion). On mixtures found in forensic practice, TrueAllele can produce match statistics comparable to single-source DNA random match probabilities. This occurs when there is clear genotype separation of the component contributors.

Specificity

When two genotypes are dissimilar, their match information can be negative. The greater the dissimilarity, the greater the magnitude of the negative log(LR) value. Equivalently ³⁰, when a person did not contribute their DNA to the biological evidence, the support in the STR data for their having contributed is generally far less than the alternative view that some else contributed, that is,

so that log(LR) is negative. The degree of negativity can be used to quantify how specifically an interpretation method discriminates between nonmatching genotypes.

We compared each of the 87 matched mixture evidence genotypes with the (<87) reference genotypes from the other 40 cases. Each of these 7298 comparisons should generate a mismatch between the unrelated genotypes from different cases and hence a negative log(LR) value. A genotype inference method having good specificity should exhibit mismatch information values that are negative in the same way that true matches are positive.

The (empirical) distribution functions of information are shown in Fig.3 for the simple, intermediate, and complex items on a log(LR) scale with theta at 1%. The average weight of evidence was −22.65 for the simple genotypes, with a maximum of −6.55 (Table 4). Restated linearly, the average statistic of a mismatching simple item was under one in sextillion and never exceeded one in a million. The information distribution of intermediate items moved to the right, having a mean of −20.46 and a maximum of −4.70. Complex items shifted further, averaging −19.56, but not exceeding −3.67. While less definite genotypes gave less definitive mismatch statistics, the log(LR) was always less than zero and was well separated from the positive values of matching genotypes.

Fig 3.

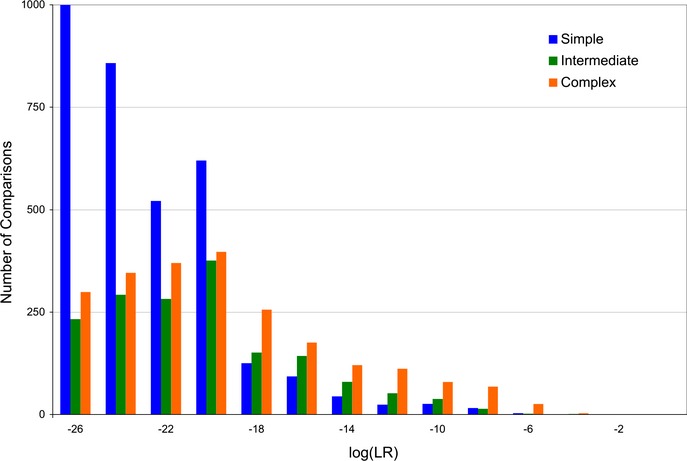
Genotype information specificity. The distribution of genotype mismatch comparison information (as inferred by TrueAllele) is shown as a log(LR) histogram of counts for each complexity category, with theta at 1%. The simple items are most specific (blue), distributed more to the left than the intermediate items (green). The rightmost distribution is for the complex items (orange), which are the least specific.

Table 4.

Specificity. The rows organize the evidence genotypes by their mixture item classification as simple, intermediate, or complex. The columns give the DNA match information (mean, standard deviation and maximum) in each category, on a log(LR) scale with theta at 1%

Mixture Category	N	log(LR) Information
		Mean	SD	Maximum
Simple	3380	−22.65	3.300	−6.55
Intermediate	1664	−20.46	4.111	−4.70
Complex	2254	−19.56	4.964	−3.67

Reproducibility

We measured interpretation reproducibility by examining the information variation of duplicate computer runs on the same evidence item. These log(LR) variations can be combined across many case items in the same category to compute a within-group standard deviation ⁴. The computer lends itself to reproducible solutions—it is far easier to rerun a program on the same data than have people arduously rework the same problem manually.

We had previously observed that one unknown mixture problems are more reproducible than two unknown problems ⁴. Across the spectrum of the 87 inferred matching genotypes from mixture items in this study, we again see that more informative results tend be more reproducible (Fig.4). In this figure, the two replicate TrueAllele runs (blue, green) are shown sorted by descending information, with a median log(LR) of 14.50. As identification information decreases (from left to right), we see increasing divergence between an item's two inferred log(LR) values (red line).

Fig 4.

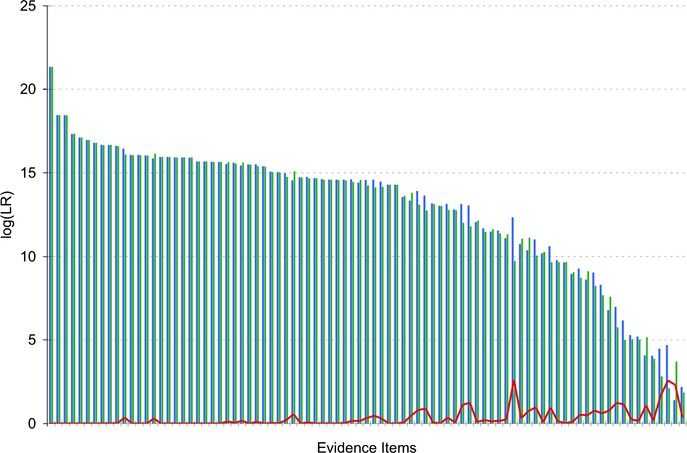
Replicate genotype information. The inferred genotypes are sorted by descending match information, with theta at 1%. For each matched genotype, the first (blue bar) and second (green bar) independent TrueAllele computer runs' match statistics are shown on a log(LR) scale. The information difference between the two genotype replicates is shown (red line).

This information divergence is a natural consequence of statistical sampling and is independent of any particular mathematical model or data interpretation method. Lower DNA quantity increases a data peak's coefficient of variation, which in turn diffuses genotype probability. Because less probable allele pairs are sampled by the computer less frequently, they exhibit greater match statistic fluctuation. TrueAllele's information variation is relatively small (Table 3).

Categorizing items by their complexity confirms that more informative data produce (on average) more reproducible interpretation (Table 3, θ = 1%). The simple items had a within-group log(LR) standard deviation of 0.125. The intermediate samples doubled that variation to 0.249, while complex ones more-than-doubled the spread yet again to 0.519. The observed with-in group standard deviations (Table 3) were all less than the match statistic variation due to population sampling, typically one power of ten with standard population databases having over a hundred individuals ⁵¹. TrueAllele mixture interpretation was thus reproducible in all the data situations examined.

Case Reporting

A DNA match statistic should be reproducible. When reporting a case, Cybergenetics will process an item in (at least) two independent TrueAllele computer runs. When duplicate runs yield match statistics that differ by more than two log units, one of the Markov chain solutions may have failed to properly sample from the posterior distribution.

This difference is resolved by rerunning the same request a third time for genotype consensus. Such resolvent computer runs attained concordance in every case, identifying the aberrant run and providing greater reproducibility in the reported results. Triplicate computer interpretation for the six cases having log(LR) values under 5 (Fig.4, extreme right) confirmed the previous solution in two cases, slightly increased the statistic in three cases, and, in one case, eliminated the equivocal match.

Human Comparison

Human review may not always produce a numerical match value. For the 40 computer-matched genotypes inferred from simple items, human review in this study yielded a statistic (e.g., CPI, CLR) 42.5% of the time (Table 2, fraction reported by laboratory with DNA statistic). The human yield was less on the 20 intermediate items, with people generating a statistic for just 20% of the inferred genotypes. On the 27 computer-inferred genotypes from complex items, only 14.8% resulted in a statistic upon human review. Overall, the laboratory's human review reported a numerical DNA match statistic for 25 of the 87 computer genotype matches (28.8%), or 25 statistics produced for the 81 evidence items (30.9%).

We can represent the relative information yield for these mixtures in a chart that shows the amount of preserved identification information, along with the mixture interpretation method (Fig.5). The TrueAllele weight of evidence (blue) is shown in the background and sorted in descending log(LR) order for the 87 computer-inferred genotype matches. For the 24 recorded human interpretation numerical scores, a LR equivalent match result is shown, with bars for the 4 single-source conditional match probability (gray), 8 mixture CLR (green), and 12 mixture CPI (orange) results. Overall, we see less human-derived match information, both in the number of reported match statistics and in the statistic's value.

Fig 5.

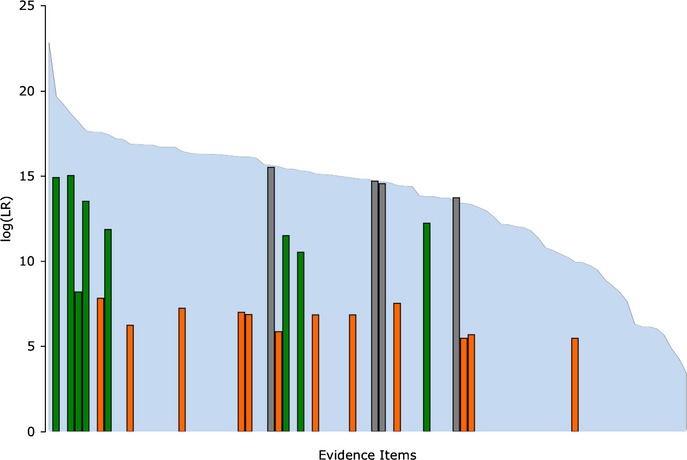
Computer versus human match information. The blue background shows the computer-inferred match information for each genotype, as in Fig.4. The foreground bars show logarithms of human match statistics obtained on the same DNA mixture genotypes. The human review methods used were conditional match probability (CMP) (gray), combined likelihood ratio (CLR) (green), and combined probability of inclusion (CPI) (orange). The TrueAllele LRs were calculated with theta at 0% for CLR and CPI and at theta = 3% for CMP, to correspond to the reported laboratory results.

The human inferred log(CLR) statistic of 8.20 (Fig.5, third green bar from left) was appreciably lower than its CLR neighbors, which had statistics of 15.03 and 13.52 (the corresponding computer log(LR) values were all around 18). This match statistic reduction occurred because the human interpretation reported on just 8 of the 13 STR loci in this case. At the other five loci, the unknown 60% major contributor shared its alleles with the victim. Many laboratories do not report victim genotypes, which can reduce the match score. The computer is not restricted in this way and, instead, infers and reports contributor genotypes at every locus.

Productivity

TrueAllele interpretation produced a match statistic for every item. With human review, however, three mixture items were examined for each match statistic that was produced (Table 2). People may restrict their interpretation to those biological specimens that yield simple DNA results, thus forcing the laboratory to process more evidence items to identify such specimens. A probabilistic computer interprets every item (regardless of complexity) and so can find a DNA match statistic sooner. Reducing the number of examined DNA samples could accelerate turnaround time, consume fewer reagents, and reduce human effort ⁵².

Mixture Weight

For comparison purposes, we manually computed the mixture weights on Excel spreadsheets for 45 two person mixtures, considering only those loci where the contributor allele sets did not overlap. At each locus, the contributor peak height sum was divided by the allele peak height total to estimate mixture weight. Examining the differences between TrueAllele-computed mixture weight (using all loci in a probability model computation) and these less exact human spreadsheet estimates, we found good agreement between the computer and human solutions (Fig.6).

Fig 6.

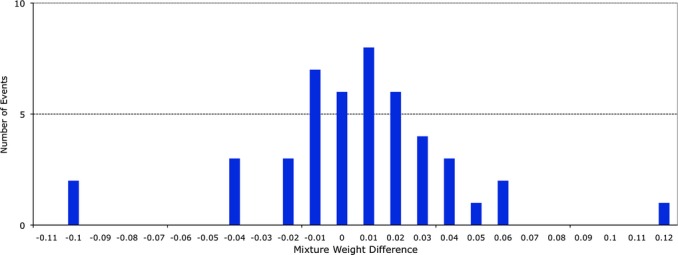
Mixture weight comparison. The mixture weights of items having two contributors were determined by two different quantitative allele peak methods. TrueAllele used all of the peak height data at all loci in a Markov chain computation. Human calculation was made on a spreadsheet that used peak heights from alleles that could be separated by assumed contributor. A histogram of the differences is shown, with the x-axis showing the difference in inferred mixture weight between human and computer and the y-axis showing the number of such occurrences.

For each of the three classifications, we paired each DNA match's log(LR) (θ = 1%) together with its mixture weight. These scatter plots show how greater item complexity is associated with reduced match information and somewhat lower mixture weight (Fig.7). On average (Table 3), the simple mixture contributor genotypes (Fig.7A) had more information (log(LR) of 14.92) and a higher mixture weight (54.9%). Intermediate genotypes (Fig.7B) showed less identification information (12.05) and somewhat lower mixture weights (48.9%). The complex items (Fig.7C) had the least information (10.47) and about the same mixture weights (50.1%).

Fig 7.

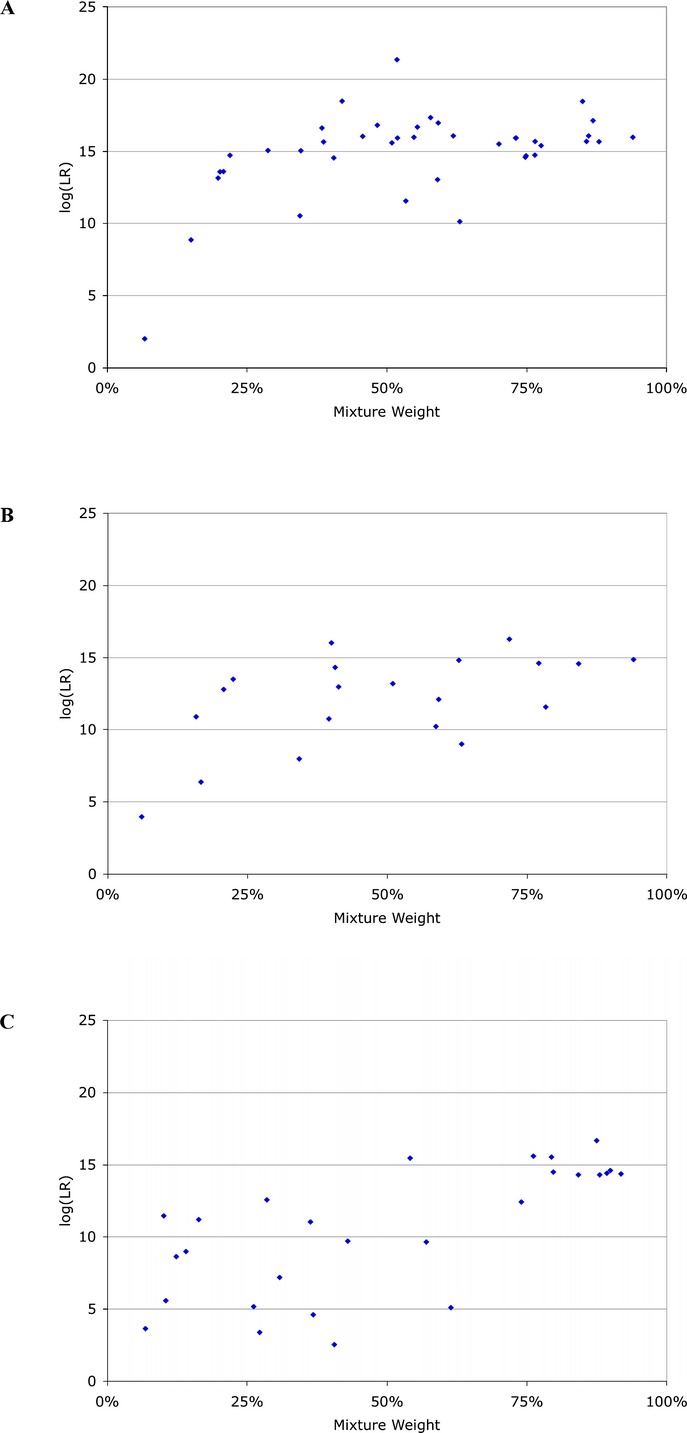
Mixture weight versus information. For each category, a scatter plot is shown of information versus mixture weight for all genotypes in that category. The (A) simple items tend to have more identification information and higher mixture weights than other items. The (B) intermediate items have less information and lower mixture weights, while the (C) complex items have the least information, on average. The likelihood ratio values were calculated with theta at 1%.

There is an apparent simple category outlier in the bottom left corner of the scatter plot (Fig.7A), having a mixture weight of 7% and a log(LR) of 2.02 (see also Fig.2, leftmost blue bar). The item had two contributors, each with its own matched genotype. The item classification was based on the (easier to interpret) major contributor genotype, rather than on the minor contributor genotype involved in the match shown. Human review examines unseparated item data peaks, whereas a probabilistic computer infers and compares a mathematically separated contributor genotype with a reference genotype.

Conclusions

In today's forensic laboratory, a greater range of biological evidence undergoes DNA analysis (e.g., property crimes, touch DNA), with ever more challenging items submitted (e.g., low-template mixtures). Many laboratories have responded by introducing automation into their workflow. This greater analytical capacity, in turn, has created bottlenecks in data interpretation and technical review. To overcome these bottlenecks ⁵³, we tested how Cybergenetics TrueAllele Casework statistical modeling system could provide automated DNA data interpretation.

The study reanalyzed 41 previously reviewed cases spanning diverse interpretation situations commonly encountered in forensic casework. There were 368 evidence items across many categories of evidence, including 81 mixture items that yielded 87 genotype matches. We found genotype concordance in all the items, verifying the computer's ability to accurately separate genotypes across a wide range of mixture weights and complexities.

A thorough mixture interpretation considers all genotype possibilities, whether or not they are immediately evident from the peak height data. Thorough statistical review also determines allele peak uncertainty directly from the observed data ⁵⁴, obviating the need for a less precise threshold approach to addressing stochastic variation. Such thoroughness is needed for robust probability inference ⁴⁴. Computers can achieve this thorough examination through statistical sampling ^9,10, whereas a person might take many years to explore one mixture problem's vast variable space.

The interpretation of STR DNA data by TrueAllele probability modeling provides objectivity, eliminating examiner bias in forensic DNA casework ⁸. The evidence genotypes are inferred from the data without any knowledge of a suspect genotype ⁴. Using this system, a genetic testing laboratory could design their workflow to ensure that analysts complete their evidence examination and record inferred genotypes, before they see a suspect's genotype ⁷.

The TrueAllele system achieves greater genotype accuracy in probabilistic inference from mixture data than does current manual review ^13,22. The system preserves more of the identification information present in the evidence by making better use of the data ⁴⁵. When human review does report a match statistic, the computer's positive log(LR) can provide greater sensitivity. When the data do not support a match, the computer quantifies its specificity through a negative log(LR). With inconclusive human review on informative data, the computer will typically produce a match statistic ^55,56.

The study showed that TrueAllele's statistical processing was reproducible across independent replicated computer runs ⁴. This reproducibility, coupled with greater accuracy, establishes the validated system's reliability for forensic casework and experimental science ⁵⁷.

A reproducible DNA interpretation method permits standardization of mixture reporting in the laboratory. Current human review approaches can lead to very different match statistics on the same DNA data ^45,58,59. Trained TrueAllele analysts, however, can produce statistically similar results when interpreting the same data.

In summary, we have shown that TrueAllele Casework is a reliable way to interpret mixed and single-source DNA evidence. The system provides a forensic DNA laboratory with a standardized interpretation approach that thoroughly examines data, eliminates examiner bias, accurately preserves identification information, quantifies match strength (whether positive and negative), and yields reproducible results.