Measurement of Foot Placement and its Variability with Inertial Sensors

Abstract

Gait parameters such as stride length, width, and period, as well as their respective variabilities, are widely used as indicators of mobility and walking function. Foot placement and its variability have thus been applied in areas such as aging, fall risk, spinal cord injury, diabetic neuropathy, and neurological conditions. But a drawback is that these measures are presently best obtained with specialized laboratory equipment such as motion capture systems and instrumented walkways, which may not be available in many clinics and certainly not during daily activities. One alternative is to fix Inertial Measurement Units (IMUs) to the feet or body to gather motion data. However, few existing methods measure foot placement directly, due to drift associated with inertial data. We developed a method to measure stride-to-stride foot placement in unconstrained environments, and tested whether it can accurately quantify gait parameters over long walking distances. The method uses ground contact conditions to correct for drift, and state estimation algorithms to improve estimation of angular orientation. We tested the method with healthy adults walking over-ground, averaging 93 steps per trial, using a mobile motion capture system to provide reference data. We found IMU estimates of mean stride length and duration within 1% of motion capture, and standard deviations of length and width within 4% of motion capture. Step width cannot be directly estimated by IMUs, although lateral stride variability can. Inertial sensors measure walks over arbitrary distances, yielding estimates with good statistical confidence. Gait can thus be measured in a variety of environments, and even applied to long-term monitoring of everyday walking.

1. Introduction

Human walking exhibits variability from step to step. This may reflect variations in the sensory, neural, and biomechanical systems that produce gait. Gait parameters such as step length, width, and period and their respective variabilities can therefore serve as indicators of mobility or function in a variety of populations [1, 2]. Changes in such parameters have been observed with aging [3] or development [4]. They may be associated with risk or fear of falling [5, 6], cognitive or attentional capacity [7, 8], and brain activity [9]. Step parameters also vary with conditions such as spinal cord injury [10], Parkinson’s disease [11], traumatic brain injury [12], cerebellar ataxia [13], and multiple sclerosis [14]. But a difficulty is that the measurement of foot placement typically requires specialized equipment such as motion capture systems, thereby limiting measurements to the laboratory. Technological developments in miniature inertial measurement units (IMUs: accelerometers and gyroscopes) offer the potential to measure strides outside the laboratory. However, accelerometers measure translational accelerations and gyroscopes measure angular velocities in a body-fixed reference frame, and these imperfect measurements must somehow be transformed into foot placement in an absolute frame. If that transformation could be achieved with accuracy comparable to laboratory equipment, it would enable evaluation of strides and stride variability in the field, using only foot-mounted sensors.

One approach for using foot-mounted sensors exploits empirical or kinematic associations between inertial measurements and step parameters. Human walking is quite systematic, so that speed and step parameters are correlated with each other [4] and with inertial measurements. These correlations, derived from previous gait data, allow step parameters to be estimated from IMUs mounted on the body [15, 2, 16]. Estimation accuracy can be improved by calibrating trends for specific individuals [17] rather than a population. This approach is, however, less applicable to gait pathologies or other cases where locomotion may vary considerably from previous calibration data. An alternative is to use a kinematic leg model to associate data from inertial sensors on the leg with step parameters [18, 19]. This also requires kinematic model parameters, which may themselves require calibration for a subject.

Another approach is to integrate inertial measurement data over time to yield positions in space. The principal challenge of integration is drift, referring to errors in position and orientation that accumulate over time due to imperfect data. Drift in orientation may be reduced with a state estimator or Kalman Filter [20], which models the IMU motion in space to predict accelerations and angular velocities, and uses the mismatch with actual measurements to reduce orientation errors. Position drift can be reduced by resetting the foot’s velocity to zero at each footfall. This model assumption is imperfect, but does not rely on subject-specific calibration or normative correlation data. A combination of such drift correction methods can be used to localize the foot in the sagittal plane [21] or in space [22, 23, 24, 25]. Similar assumptions may be applied to waist-mounted IMUs for estimating stride parameters [26]. These methods require minimal assumptions regarding the subject’s gait, mainly that the foot is periodically stationary on the ground.

These drift reduction methods may facilitate measurement of foot placement variability over long distances of over-ground walking. Variability is best measured over many strides [27], which is often challenging to capture in absolute space. But stride variability only requires the foot’s displacement relative to the preceding footfall, for which drift error can be stabilized using the methods above (e.g., [22]). In the present study, we propose an algorithm, using no skeleton or correlation model, for estimating foot placement and its variability from inertial data. We then test the algorithm against reference data obtained from a mobile motion capture system [28], during long walking bouts.

2. Inertial Sensor Processing

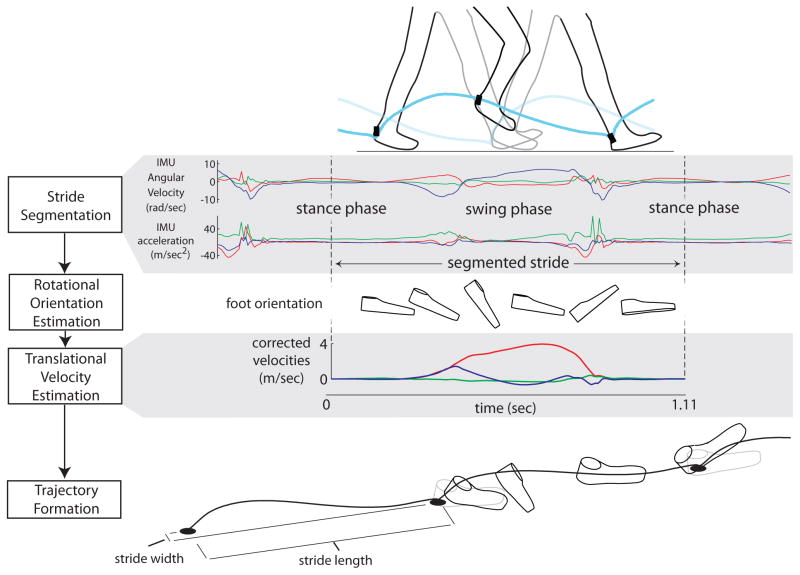
We assemble an algorithm to integrate foot-mounted IMU data and yield drift-reduced stride displacements. We divide the processing into four steps (Figure 1): (1) stride segmentation, (2) rotational orientation estimation, (3) translational velocity estimation, and (4) trajectory formation. Stride segmentation uses raw sensor measurements to detect zero velocity instants when the foot is stationary on the ground. We estimate orientation by integrating the gyroscope data and correcting for tilt drift with a Kalman Filter. We estimate translational velocity by integrating accelerometer data, then adjusting the velocities to be compatible with each zero velocity instant. Finally, the foot trajectory is formed by integrating the corrected velocities, oriented with respect to a local walking heading. That trajectory directly yields foot placement, from which stride parameters are calculated.

Figure 1.

Overview of IMU processesing steps (shown at left), with representative data trajectories (plotted at right). Stride segmentation uses accelerometer and gyroscope readings to determine periods when the foot is stationary on the ground. Orientation estimation uses a Kalman Filter to correct for drift in tilt and yield orientation of the foot in space. Velocity estimation is performed by integrating tilt-corrected accelerometer signals, subject to a zero velocity correction. Finally, trajectory formation is performed by integrating corrected velocities to yield foot trajectories in space.

Stride Segmentation

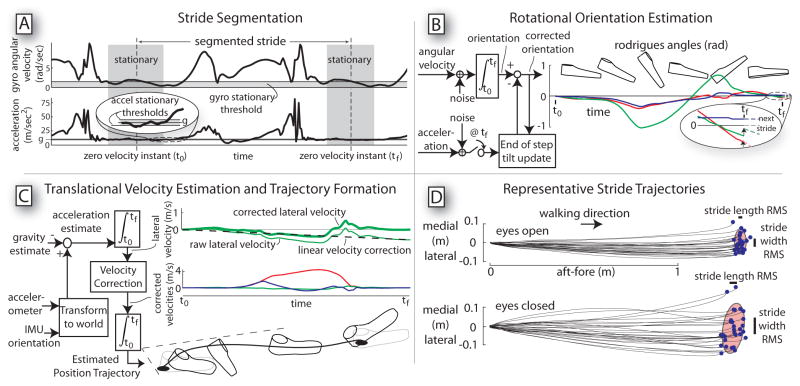
We identify zero velocity instants based on raw IMU data (Figure 2 A). We use thresholds on the magnitude of the gyroscope and accelerometer signals to identify these times. Assuming solid ground and no foot slip, the foot velocity and acceleration will be near zero during part of each stance phase. We identify stationary phases as periods when the gyroscope output magnitude is small and the accelerometer output magnitude is close to gravitational (g). The midpoint of each stationary interval defines a zero velocity instant, demarcating strides. In the present study, we used magnitude thresholds of 1.7 radian·s⁻¹ and 0.8 m·s⁻² (relative to g). We also exclude erroneously detected phases caused by short periods of constant velocity and low angular velocity during swing, as well as quick foot slips during stance. These are detected as unusually short stationary or swing periods. We have found minimum period thresholds of 0.133s for stationary and 0.2s for swing to perform well.

Figure 2.

A: Stride segmentation to determine stationary foot instants. Thresholds on the magnitudes of the gyroscope (top) and accelerometer (bottom) signals are used to determine foot stationary phases. A minimum stationary phase duration is also used to reduce the effect of noise. The midpoint of each stationary phase defines a zero velocity instant, which demarcates strides. B: Orientation estimation algorithm. Orientation of the foot in space is estimated by integrating angular velocities from foot-mounted gyroscopes. At each zero velocity instant during stance (t = t_f), the accelerometer provides an estimate of gravity, which is used to perform a discrete Kalman update of the orientation estimate. The orientation trajectories (plotted as Rodrigues angles at right) are corrected impulsively at the end of each stride (inset). C: Velocity estimation and trajectory formation. Translational velocity in space is found by integrating the transformed and gravity compensated accelerometer readings during the stride. A zero velocity correction is then applied, where a linear trend is subtracted from the cumulative velocity between stationary instants. Finally, the trajectory of the foot in space is found by integrating the velocity over each stride. Stride parameters are then calculated from the foot trajectories. D: Foot trajectories and stride measurements obtained from IMU data. Overhead view is shown of representative IMU trajectories for the right foot of one subject, for an eyes open (top) and eyes closed (bottom) walking trial. The trajectories are aligned to a common origin, defined as the beginning of each stride. Stride length and width are defined by a local heading determined from three successive strides. Stride variability is defined as the root-mean-square (RMS) variability of length and width.

This simple algorithm identifies zero velocity instants during normal walking using few parameters. It is not optimized for estimating stance and swing durations nor for detecting events such as footfall or toe-off.

Rotational Orientation estimation

Orientation of each IMU in space is determined by integrating gyroscope signals with a discrete Kalman Filter (Figure 2 B). Gyroscope-derived orientations are subject to drift, but the estimated vertical direction, referred to as tilt, can be corrected based on the accelerometer’s reading of gravity. We integrate the gyroscope signals over time to estimate the 3d angular orientation of the IMU [22]. Then a discrete tilt correction is applied at the detected zero velocity instant at the end of each stride. The accelerometers are used as an inclinometer to produce a discrete Kalman update, which stabilizes tilt drift over arbitrarily long durations. The Kalman Filter requires relative values of the measurement and process noise to integrate the sensors. The gyroscope variance describes the gyroscope noise, the accelerometer variance describes the accelerometer noise and the zero velocity assumption noise. The process variance describes the constant angular velocity assumption noise. We found modest gains sufficient for tilt correction, with the Kalman updates correcting about 2.6 · 10⁻³ tilt radians per footfall.

The integration yields a time-varying representation of the IMU’s orientation. This is expressed relative to the IMU’s initial orientation, which is an arbitrary home orientation reference. (The IMU can be attached to the foot in any orientation.) The gravity vector in the initial orientation defines vertical. The output of these calculations is therefore a tilt-corrected IMU orientation in space. This algorithm does not correct for drift in heading about vertical, which can potentially be reduced using other sensors such as magnetometers [25].

Translational Velocity estimation

Foot velocity can be estimated from accelerometer signals (Figure 2 C). We first use the IMU orientation to transform accelerometer readings into absolute space. Acceleration in space is found by subtracting the estimated gravity vector. The result is integrated forward in time, starting at one detected zero velocity instant and ending at the next. This yields a velocity estimate which is subject to drift during each stride. To correct for drift, we constrain foot velocity to zero at the zero velocity instant at the end of each stride. Rather than an impulsive correction [22], we distribute the correction over the stride assuming that error grows linearly with time, to yield a smooth correction.

Trajectory formation

The foot’s trajectory in space is obtained by integrating the corrected velocities (Figure 2 C). This is also subject to unbounded drift in absolute space, but stride measurement only requires displacement relative to the preceding footfall. Foot placement therefore only drifts over the relatively short duration of a single stride, and can be estimated with reasonable accuracy. It is obtained by integrating foot velocity between successive zero velocity instants. Having corrected for drift in tilt and foot placement, the resulting trajectory is mostly only subject to growing drift in heading about vertical. Since subjects may also vary heading anyway, we do not rely on the global heading estimate over long durations.

To measure stride displacements, we define a local heading from foot trajectories. We define the forward walking direction from a linear fit of three successive footfalls locations. The forward direction and gravity vector together define the local lateral direction. Each foot trajectory is then examined with respect to the local frame (Figure 2 D).

Finally, we compute stride parameters (Figure 2 D). Stride parameters, such as stride length and width, are calculated from the foot trajectories between successive footfalls in their local frames. Stride variability is computed from the root-mean-square variations about the average stride length and width. Stride duration is calculated based on the difference between successive peak times of filtered estimated speed. All integrations are performed using the trapezoidal method.

3. Experiment

We tested IMU-based stride measurements against motion capture performed during over-ground walking. We measured 9 healthy young subjects walking normally with eyes open, and induced greater variability by collecting trials with eyes closed. This is intended to test the sensitivity of stride measurements to changes that might occur with a gait pathology. We used a cart-mounted motion capture system to collect simultaneous reference data (Figure 3). We quantified both the statistical agreement between the IMU and motion capture estimates, and the sensitivity of the IMU and motion capture estimates to different walking conditions. Subjects provided informed consent according to Institutional Review Board procedures.

Figure 3.

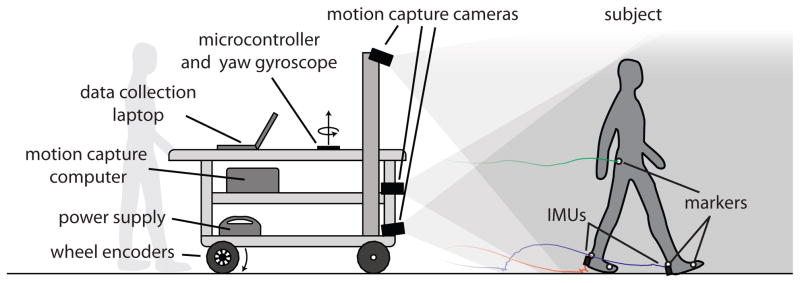
Experimental setup for testing foot placement measurement. Subjects walked down a hallway while wearing foot-mounted IMUs and motion capture markers. To collect reference data, an experimenter pushed a mobile motion capture cart behind the subject. The cart was instrumented to use dead reckoning to calculate the motion of the subject in a world frame, yielding a comparison between motion capture and IMU results.

Each subject performed multiple straight walking trials down a hallway. An average of 93 steps were recorded per trial, and a total of 90 trials were collected of both conditions. An IMU was attached to the heel of each shoe (Memsense, Rapid City, South Dakota, nIMUs, gyroscope range: 1200deg · s⁻¹, accelerometer range: 10g, sampled at 150 Hz). To provide a laboratory-based measurement of foot kinematics, a motion capture system (PhaseSpace, Inc. San Leandro, California) with six cameras was mounted on a mobile cart. The cart was equipped with a vertical axis gyroscope and two wheel encoders to localize the cart using dead reckoning [28]. The subject stood motionless for 20 seconds prior to each trial to yield baseline inertial sensor data. A total of 22 trials were excluded due to hardware failures or protocol deviations. Within each trial, the first and last 6 steps were excluded to focus on steady walking. During eyes closed trials, two experimenters walked beside the subject and provided audible cues to keep the subject near the centerline of the hallway.

We examined the agreement between the IMU and motion capture stride estimates. To test the performance of the IMU estimation, we compared the IMU-based stride estimates against motion capture. This was performed for eyes open and eyes closed conditions to test sensititivity to changes in gait. Because neither measurement is perfectly accurate, we compared motion capture and IMU stride estimates using intraclass correlation (ICC), which summarizes the agreement between methods and quantifies unexplained variance in the data ([29]; A-1 method). We summarized gait variability for stride length, width, and duration by calculating root mean squares (RMS) for each walk, and averaging across walks for each condition for each subject. To compare the sensitivity of IMU estimates to motion capture estimates, we performed a paired t-test between eyes closed and eyes open estimates.

4. Results

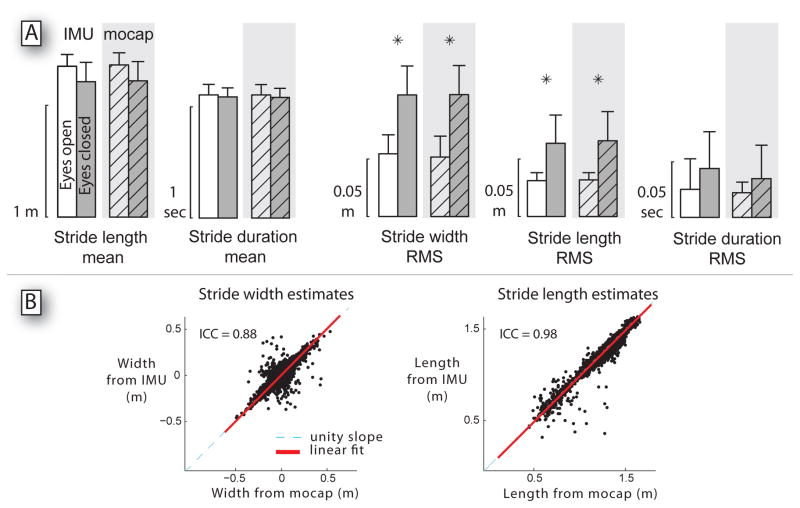
We found the IMU estimates of gait parameters to agree reasonably well with motion capture data (Figure 4 A). Estimates of mean stride parameters agreed to within 1%, and estimates of RMS variability of stride width and length agreed to within 4%. (Estimates of stride duration variability agreed less well; we believe this is due to poor motion capture estimates.) As an indicator of the ability to detect relatively subtle changes to gait, both methods revealed significant increases in stride width and length variability for walking with eyes closed. No significant difference was observed in other measures for eyes closed walking, using either measurement method. We summarize the overall correspondence between IMU and motion capture in two ways. First, the RMS difference between the IMU and motion capture estimates of all stride lengths is 3.2% of the mean stride length. Second, we quantify the fraction of data variation shared by the two instruments using the intra-class correlation coefficient (ICC). We observed ICC values of 0.88 for stride width, and 0.98 for stride length (Figure 4 B), indicating good agreement.

Figure 4.

A: Comparison of stride parameters as measured with IMU and motion capture. Shown are mean stride length and duration, and RMS variability of stride width, length and duration, for eyes open and eyes closed conditions. Error bars represent standard deviation across subjects. Asterisks denote significant differences detected between eyes open and closed conditions (paired t-test, p < 0.05). B: Correlation between stride measurements using IMU and motion capture. Individual stride width and length estimates are shown for all subjects and conditions (5538 strides). IMU estimates are plotted against motion capture estimates, along with intra-class correlation (ICC) and the corresponding linear fit. Perfect agreement would yield a line of unity slope.

5. Discussion

We sought to determine whether foot-mounted IMUs can estimate stride measures from over-ground walking. We devised an algorithm that calculates stride parameters that are drift-stabilized, meaning that errors do not grow unbounded with time. Results show that stride measures are comparable between IMU and motion capture methods (Figure 4 A), agreeing to within a few percent. Both methods also agree on increased stride variability resulting from walking with eyes closed, indicating sufficient sensitivity to detect relatively small changes in gait [1]. Having quantified IMU performance relative to motion capture, we next consider the limitations and provide recommendations for use.

The main sensitivity of this algorithm is to stride segmentation. Stride segmentation errors, when a stationary instant fails to be detected, or when one is detected during the swing phase, significantly degrade the algorithm’s performance. Such errors are normally not an issue except during extremely slow or unsteady walking. Stride segmentation may be facilitated through good sensor placement. Here we used the back of the shoe to accommodate comparison with motion capture, but we prefer the top of the shoe above the instep, which yields longer stationarity durations. The segmentation algorithm can also be improved by applying additional constraints. If both feet are instrumented with time-synchronized IMUs, the swing of one foot can indicate stationarity of the other. This can reduce segmentation errors substantially, albeit only for walking and not running gaits. The algorithm presented here is simple and uses few parameters; it can easily be replaced by alternative methods as appropriate.

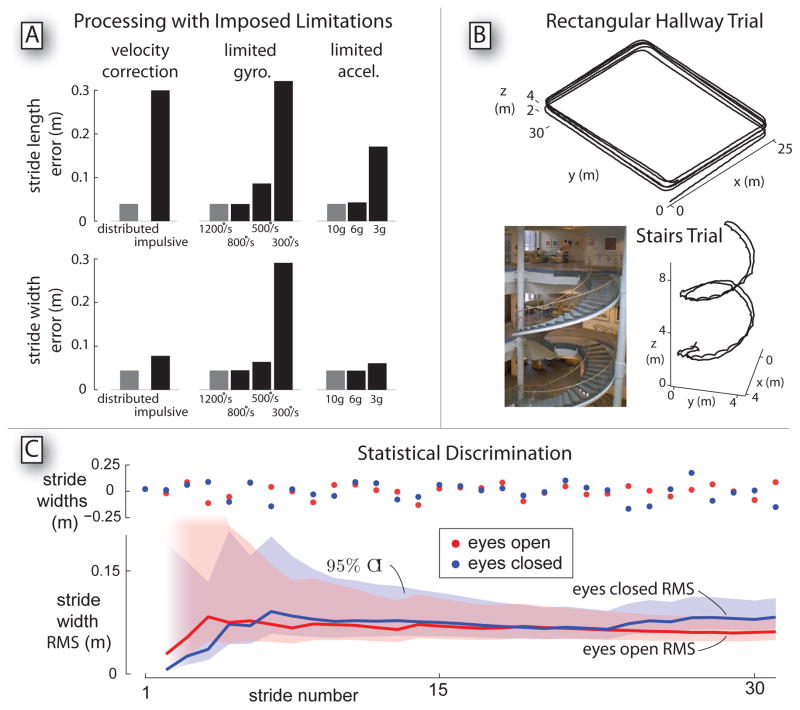
There are a few assumptions under which the proposed algorithm performs best. One is that drift in translational velocity occurs continuously over time. We distribute each stride’s velocity correction (Figure 2 C) linearly over the entire time interval between stationary instants. Alternately, the velocity could be corrected impulsively, for example at each stationary instant [22]. This may be appropriate if the errors occur at that time, such as with gyroscopes that are sensitive to the impulsive accelerations of heelstrike. Another assumption is that foot motions are within the IMU’s range and bandwidth. To estimate the consequences of these assumptions, we reprocessed our data with impulsive velocity corrections, and separately with artificially reduced sensor ranges (Figure 5 A). We found the distributed velocity correction to yield considerably lower errors (with respect to motion capture) compared with impulsive correction. We also found a sharp performance degradation when limiting IMU ranges. Decreasing the gyroscope range resulted in stride length estimate outliers similar to the strides with uncharacteristically low length estimates from the IMU (Figure 4 B). Therefore a likely cause for these outliers is momentary gyroscope saturation. Our algorithm appears to work best with distributed zero correction, and with IMUs with sufficient ranges and bandwidth.

Figure 5.

A: IMU estimation errors with imposed limitations. Stride length (top) and width (bottom) errors are shown (relative to motion capture), using the proposed algorithm with a distributed vs. impulsive zero velocity correction. Also compared are calculations made with artificially limited ranges for gyroscopes (between $1200\frac{\mathit{deg}}{s}$ and $300\frac{\mathit{deg}}{s}$) and accelerometers (between 10g and 3g). Errors are summarized as standard deviation of difference between IMU and motion capture estimate. B: Demonstration of IMU processing applied to walking in non-laboratory environments. (Top:) Walking around a rectangular hallway circuit of approximately 110 meters, completed five times. (Bottom:) Walking up and down a set of spiral staircases (illustrated by photograph). Representative data from one subject show relatively low drift in absolute positions. C: Estimation of stride width variability as a function of number of strides. As individual stride widths are measured (top) from a representative subject, the estimate of stride width variability (bottom) improves in confidence (shaded areas for 95% confidence intervals).

Although not the focus of this study, integration methods such as ours are also applicable to position estimation in space. Previous studies based on integration of inertial data have measured relatively short walking bouts [22, 25]. Our methods can also track an IMU reasonably well in space for distances on the order of 100 m (Figure 5 B). Most integration methods rely on the principal assumption of a zero velocity instant within each stride, reducing but not eliminating drift. Further drift reduction is possible using additional assumptions. For example, if the walking surface is assumed level, altitude drift can be reduced. If the heading is constant [30], or measurable with magnetometers or GPS [25], its drift can also be reduced. Position, velocity, and sensor calibrations can be incorporated into the Kalman Filter in addition to the proposed Kalman filtering scheme, allowing zero velocity updates to correct angular orientation estimates [25]. A spline based velocity correction can also be used to correct foot velocity, which works well in certain circumstances with sensors of limited range [23]. Of course, such variations require additional assumptions, which can lead to amplified errors if violated. For general applicability, we have presented a near-minimal set of assumptions here.

Integration methods complement other gait measurement methods. These include IMU approaches using a kinematic body model or a correlation model from walking data. These may be accurate under particular conditions, but may become inaccurate when the models do not apply. In contrast, integration methods assume nothing of the human’s geometry or motion other than the existence of zero velocity instants. They also apply to relatively unconstrained, over-ground locomotion in varied environments. This contrasts with laboratory measurements using motion capture or sensor-embedded walkways. These can yield accurate drift-free measurements, but usually for a limited number of steps in a confined space. An advantage of IMU integration is that a large number of strides may be measured with good accuracy. This can enhance stride parameter estimation (e.g., [27]). An example is the effect of walking with eyes open vs. closed, which is best discriminated with a relatively large number of strides (Figure 5 C), which are otherwise difficult to capture accurately during over-ground walking. Given accurate inertial sensors, we believe integration methods are especially well suited for the estimation of stride parameters and their variabilities.