Abstract
Background and Aims Plant growth, the increase of organ dimensions over time, and development, the change in plant structure, are often studied as two separate processes. However, there is structural and functional evidence that these two processes are strongly related. The aim of this study was to investigate the co-ordination between growth and development using mango trees, which have well-defined developmental stages.
Methods Developmental stages, determined in an expert way, and organ sizes, determined from objective measurements, were collected during the vegetative growth and flowering phases of two cultivars of mango, Mangifera indica. For a given cultivar and growth unit type (either vegetative or flowering), a multistage model based on absolute growth rate sequences deduced from the measurements was first built, and then growth stages deduced from the model were compared with developmental stages.
Key Results Strong matches were obtained between growth stages and developmental stages, leading to a consistent definition of integrative developmental growth stages. The growth stages highlighted growth asynchronisms between two topologically connected organs, namely the vegetative axis and its leaves.
Conclusions Integrative developmental growth stages emphasize that developmental stages are closely related to organ growth rates. The results are discussed in terms of the possible physiological processes underlying these stages, including plant hydraulics, biomechanics and carbohydrate partitioning.
Keywords: Absolute growth rate, AGR, developmental stage, growth asynchronism, growth unit, growth stage, inflorescence, hidden semi-Markov chain, Mangifera indica, mango, plant growth, plant development, segmentation model, thermal time
INTRODUCTION
Development is the sum of events that contribute to the progressive elaboration of the body of an organism (Steeves and Sussex, 1989). Plant development is defined as a series of identifiable events resulting in a qualitative (germination, flowering, etc.) or quantitative (number of leaves, number of flowers, etc.) change in plant structure (Gatsuk, 1980; Bonhomme, 2000). Usually, when studying the development of a whole plant, a distinction is made between vegetative and reproductive developments (Fehr et al., 1971; Schneiter and Miller, 1981). A developmental (or phenological) stage characterizes a period during which the plant or organ shows a precise combination of morphological traits. It is generally based on a visible discontinuity in the development process. Developmental stages may be used for several purposes. In climatology, they are used as indicators of the impact of climate change on plant development (Legave et al., 2009; Olesen, 2011). In agronomy, they are used to determine optimal timing for plant treatment against pests (Meier et al., 2009). They are also used to predict flowering and harvest dates (Normand and Léchaudel, 2006). Developmental stages are identified by expert examination, but the transition between two successive developmental stages may not always be obvious (e.g. change in leaf colour), and this is a source of uncertainty when identifying a succession of developmental stages.
Growth is defined as an irreversible increase in plant or organ dimensions over time, e.g. length, width, diameter, area, volume and mass. Plant growth patterns are often characterized by the cumulative increment of a dimension over time, modelled by a sigmoidal curve composed of three successive phases: an early accelerating phase where growth is exponential, a linear phase, and a plateau (Goudriaan and Van Laar, 1994) where growth tends toward zero as the final size is reached. Conventional methods of growth analysis are often based on growth parameters at specific time points in an organ’s growth (e.g. relative growth rate during the initial exponential growth, or maximum absolute growth rate at the inflection point, see Cookson et al., 2005).
Growth and development are often studied separately. However, these two processes are strongly related. For instance, the partitioning of carbohydrates between organs during plant growth as well as growth rates depend on organ type, organ developmental stage and environmental conditions (Pantin et al., 2011; Dechaine et al., 2014). We thus propose an integrative approach for studying the co-ordination between growth and development of plant organs. Previous studies considered growth and development together by quantifying developmental stages, for example by calculating a mean developmental stage over a population in relation to mean shoot dry mass (Kalu and Fick, 1981; Borreani et al., 2003). Boyes et al. (2001) also used quantitative measurements (e.g. total leaf area and rosette dry mass) to quantify the phenotypes of consecutive developmental stages. However, since these studies used pre-defined developmental stages simply as triggers for the collection of growth data, they did not consider the co-ordination between growth and development. The BBCH scale describes the growth stages of development for many mono- and dicotyledonous plant species (Meier et al., 2009). However, this scale uses cumulative dimensions over time (e.g. leaf area or axis length) to characterize growth. At a specific stage, it cumulates the effects of all the previous stages, and thus does not constitute information specific to the stage being quantified.
Cumulative dimensions over time take the form of a trend (i.e. a slowly varying component), while the absolute growth rates (dimension increment per time unit) for successive time periods obtained by first-order differencing can be seen as a rapidly varying component that highlights local fluctuations with respect to cumulative dimensions [see Chatfield (2003) for introductory notions of time series analysis]. In this way, the information extracted from growth is compatible with the developmental stages which change rapidly. Our aim was thus to determine ‘developmental growth stages’ that integrate both developmental stages identified by an expert examination and growth stages deduced from the measurements of cumulative dimensions over time. To determine growth stages, we hypothesized that it is possible to split the growth of an organ into successive stages that may be determined by changes in absolute growth rate (based on the assumption that absolute growth rate changes less within stages than between stages) and we used segmentation models designed to highlight ‘stage changes’ during the growth process (Guédon et al., 2007).
In our study, the mango tree was chosen because of its well-defined developmental stages. We considered the growth and development of three organ types: the vegetative axis; its attached leaves; and the inflorescence. We considered three leaf positions along the vegetative axis to investigate possible growth asynchronisms between them. We designed our study to address the following questions. (1) Can growth stages of vegetative and reproductive organs be identified independently of developmental stages? (2) Can we identify integrative ‘developmental growth stages’ that account for both developmental traits and growth characteristics? (3) Can growth stages be used to investigate asynchronisms between concomitant and topologically connected organs (the vegetative axis and its leaves)?
MATERIALS AND METHODS
Field sites and plant material
Our study was conducted in Réunion Island (21°10′S; 55°50′E) in 2010. Two cultivars of mango, Mangifera indica, Cogshall and José, characterized by their contrasting origins and growth habits were chosen for the study. Cogshall is a Floridian cultivar and José is a local cultivar. Mango vegetative growth is characterized by the production of growth units (GUs) defined as the portions of shoot developed during an uninterrupted period of growth. These GUs are composed of an axis bearing several leaves that show simultaneous growth (Hallé and Martin, 1968). In Réunion Island, mango vegetative growth occurs from August to May and flowering occurs during the cool dry season from July to October after a vegetative rest in June. Inflorescences are modified GUs in which leaves are aborted and axillary buds develop into secondary and higher order axes that bear flowers (Bell, 1991; Davenport, 2009). By convention, GU will hereafter refer only to the vegetative GU.
In order to consider some variability in the duration of developmental stages, we studied the development of mango organs under contrasting temperature conditions. Vegetative organs were studied from February to April 2010 and from September to November 2010. Mango inflorescences were studied from July to November 2010. The study of each cultivar was conducted at three sites located at different elevations. For Cogshall, the sites were located at 65, 150 and 300 m above sea level (m a.s.l.). For José, the sites were located at 65, 300 and 450 m a.s.l. The selected sites corresponded to orchards with similar agronomic practices, i.e. tree training, irrigation, fertilization and phytosanitary treatments. An automatic temperature recorder sheltered from direct sun recorded air temperature every 15 min at each site [see fig. 1 of Dambreville et al. (2013) for the temperature variability across sites and seasons].
Data collection
Vegetative and reproductive organs were selected at budburst on pest- and disease-free GUs at the periphery of the canopy. The GU datasets comprised 72 individuals for Cogshall, corresponding to a total of 1059 measurement occasions (between 11 and 20 occasions per individual), and 54 individuals for José, corresponding to a total of 907 measurement occasions (between 11 and 23 occasions per individual). By convention, the initial measurement occasion is not counted because of the side effect of the differentiation to compute absolute growth rates (AGRs) from organ dimensions over time. Inflorescence datasets comprised 43 individuals for Cogshall, corresponding to a total of 1545 measurement occasions (between 18 and 48 occasions per individual), and 47 individuals for José, corresponding to a total of 1699 measurement occasions (between 17 and 53 occasions per individual). The effects of leaf position on growth and developmental patterns were evaluated by studying three leaves per GU, the ‘first distal leaf’ (the most apical leaf at the top of the GU), the ‘sub-distal leaf’ (just below the first distal leaf) and the ‘proximal leaf’ (the most proximal leaf at the base of the GU). These leaves were chosen based on a preliminary study for their contrasting sizes, the proximal leaf being larger than the sub-distal and the first distal leaves. Fruits were absent at the time of flowering and did not interfere with inflorescence development. For GU development, young fruits were present on the trees during the September–November measurement period, but were absent during the February–April measurement period. We considered that the traits measured for GU development mainly depend on the local growth context.
The developmental stages used in our study (Figs 1 and 2) were adapted by F. Normand from Aubert and Lossois (1972). To study the development of inflorescences, we split flowering into two stages: stage F, from opening of the first flower of the inflorescence to opening of the apical flower on the main axis; and stage PF, from opening of the apical flower on the main axis to the last flower still open on the inflorescence. The developmental stage of the studied organs was recorded at the same time of day on each consecutive day from budburst to the end of organ growth (approx. 10–25 d for complete growth of a GU or an inflorescence). The day on which the organ reached its mature stage was also noted (stages H and G for GUs and inflorescences, respectively; Figs 1 and 2). At the same time, the length of GU axes (from base to apical bud), the length and maximum width of foliar lamina and the length of the inflorescence main axis (from base to apical flower bud) were measured. Initial measurements were made as soon as the organs reached sufficient size to avoid damage.
Fig. 1.
Developmental stages of mango growth unit (axis and leaves) (adapted by F. Normand from Aubert and Lossois, 1972). Images: F. Normand.
Fig. 2.
Developmental stages of mango inflorescence (adapted by F. Normand from Aubert and Lossois, 1972). Images: F. Normand.
Growth is defined as an increase in dimension over time. The axis was considered to be a 1-D structure where the increase in axis biomass is assumed to be roughly proportional to the increase in axis length (since secondary growth does not occur in the young axis). The leaf was considered to be a 2-D structure where the increase in leaf biomass is assumed to be roughly proportional to the increase in leaf area (changes in leaf thickness were assumed to be negligible over the measurement period). Leaf area was estimated non-destructively using the following relationships calibrated in preliminary experiments: leaf area = 0·74 × leaf length × leaf maximum width (n = 60, R2 = 0·992, P < 0·001) for Cogshall; and leaf area = 0·72 × leaf length × leaf maximum width (n = 60, R2 = 0·998, P < 0·001) for José. Since the young leaves are folded at the central vein, only their length was measured, and leaf area was estimated using the following equation: leaf area = 0·164 × leaf length2 (n = 15, R2 = 0·936, P < 0·001) for both cultivars.
Identification of growth stages
We used thermal time to take account of the effect of temperature on growth and development (see Supplementary Data Appendix S1 for the definition of thermal time models and the computation of base temperatures). We built multistage models for each cultivar on the basis of AGR sequences which were multivariate for GUs (axis and three leaves) and univariate for inflorescences (axis). In a preliminary study, we compared the use of relative growth rate (RGR) sequences instead of AGR sequences to build multistage models. The RGR can be seen as a non-linear transform with respect to AGR that in particular down-scales drastically the growth rate variations at the end of growth of an organ. We found this to be a definitive defect to highlight abrupt changes of growth rate corresponding to the growth arrest of an organ.
Segmentation models
Segmentation models were built to identify growth stages on the basis of AGR sequences. These two-scale models are hidden semi-Markov chains (HSMCs), which are formally defined in the Supplementary Data Appendix S2. In our context, the succession and duration of growth stages (coarse scale) are represented by a non-observable semi-Markov chain, while the AGRs of leaves, GU or inflorescence axes within a growth stage (fine scale) are represented by observation distributions attached to each state of the semi-Markov chain. Hence, each state of the semi-Markov chain represents a growth stage. A semi-Markov chain is defined by three sub-sets of parameters, as follows.
(1) Initial probabilities to model which is the first stage occurring in the sequence measured for a GU or an inflorescence,
(2) Transition probabilities to model the succession of stages during the growth of a GU or an inflorescence,
(3) Occupancy distributions attached to non-absorbing states (a state is said to be absorbing if, after entering this state, it is impossible to leave it) to model the stage duration in number of successive measurements. As possible parametric state occupancy distributions we used binomial distributions B(d, n, p), Poisson distributions P(d, λ) and negative binomial distributions NB(d, r, p) with an additional shift parameter d ≥ 1.
An HSMC adds a fourth sub-set of parameters to the three sub-sets of parameters of the underlying semi-Markov chain.
(4) Observation distributions to model AGRs of axes or leaves within a growth stage. The AGRs were computed from measurements of organ length (for GU and inflorescence axes) or area (for leaves). These AGRs took the form of semi-continuous data that were either continuous or equal to zero. After investigating the direct modelling of these AGRs using semi-continuous distributions (see Supplementary Data Appendix S3), we chose to use unimodal discrete parametric distributions – chosen among binomial distributions B(d, n, p), Poisson distributions P(d, λ) and negative binomial distributions NB(d, r, p) with an additional shift parameter d ≥ 0 – that can degenerate as a probability mass at zero and thus discretize AGRs. The AGR units were chosen such as to render discretization errors negligible. The AGRs for GU and inflorescence axes were in 0·1 mm (°Cd)–1, while those for leaves were in mm2 (°Cd)–1.
Since the index parameter of sequences was measurement occasion rather than thermal time (which is unevenly spaced with long intervals between successive thermal times), the estimated state occupancy distributions were not directly interpretable in the thermal time scale. Nevertheless, the fact that the estimated state occupancy distributions were always bell-shaped with small relative dispersions (i.e. μj > σj for each state j where μj and σj are the mean and standard deviation of the estimated state j occupancy distribution) indicates that stage durations were rather homogeneous for the different individuals in a given sample. Therefore, the estimated HSMCs should be considered as a tool to segment the AGR sequences in successive stages.
‘Left–right’ HSMCs composed of successive transient states followed by a final absorbing state were estimated on the basis of each dataset. A state is said to be transient if, after leaving this state, it is impossible to return to it. In a ‘left–right’ model, the states are thus ordered and each state can be visited at most once. As the last measurement was arbitrary with regard to GU or inflorescence development, the length of the last stage was assumed to be systematically truncated (or ‘right-censored’) and could not be modelled. Each estimated model was used to compute the most probable state sequence for each observed sequence (Guédon, 2003). The restored state sequence can be viewed as the optimal segmentation of the corresponding observed sequence into sub-sequences, each corresponding to a given growth stage.
Selecting the number of states of the underlying semi-Markov chain
In a first exploratory analysis, we examined AGR sequence segmentation using the developmental stages determined in an expert way. It was then obvious that some consecutive developmental stages either at the beginning (e.g. B1 and B2 for GUs; Fig. 1) or at the end of development could not be distinguished on the basis of growth data. We then set a maximum number of states of the underlying semi-Markov chain (fewer than the number of developmental stages) and evaluated the possible number of states (e.g. five, six and seven states for GUs) just below this maximum by applying the practical approach discussed in Guédon et al. (2007).
Assessing the robustness of the segmentation in growth stages
We also computed growth stages on the basis of calendar time AGR sequences. For the discretization of calendar time AGRs, we chose units (mm d–1 for GU axes, 10 mm2 d–1 for leaves and 0·5 mm d–1 for inflorescence axes) that make the ranges of calendar time AGRs the closest to the ranges of thermal time AGRs. In this way, the discretization errors were similar. We applied the methodology previously described for thermal time AGR sequences to build segmentation models for Cogshall and José GUs and inflorescences on the basis of calendar time AGR sequences. We then compared the growth stages obtained using calendar time and thermal time AGRs, the objective being to characterize the modulation of the ontogeny by the temperature.
RESULTS
A ‘left–right’ six-state HSMC was built for each dataset (Cogshall and José GUs and inflorescences). These models were then used to segment the thermal time AGR sequences into successive growth stages. We first assessed the assumption of segmentation into growth stages. In particular, we checked that the AGR distributions for consecutive stages were well separated and that the segmentation ambiguity was low (since the growth stages are not directly observable but are obtained using HSMCs); see details in Supplementary Data Appendix S4.
Growth stages
Growth units.
For both cultivars, six growth stages were identified for GUs using HSMCs (Table 1).
Table 1.
Estimated mean AGR of the growth unit axis, proximal, sub-distal and first distal leaves for the six vegetative growth stages in two mango cultivars, Cogshall and José
| Cogshall |
José |
|||||||
|---|---|---|---|---|---|---|---|---|
| Axis 0·1 mm (°Cd)–1 | Proximal leaf mm2 (°Cd)–1 | Sub-distal mm2 (°Cd)–1 | First distal mm2 (°Cd)–1 | Axis 0·1 mm (°Cd)–1 | Proximal leaf mm2 (°Cd)–1 | Sub-distal mm2 (°Cd)–1 | First distal mm2 (°Cd)–1 | |
| Stage 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Stage 1 | 15·21 | 5·03 | 0·11 | 0·33 | 14·56 | 5·96 | 0·50 | 0·59 |
| Stage 2 | 17·92 | 26·10 | 10·81 | 5·93 | 16·07 | 25·37 | 9·76 | 6·64 |
| Stage 3 | 4·64 | 64·78 | 40·47 | 27·54 | 11·49 | 46·80 | 26·69 | 20·04 |
| Stage 4 | 0·25 | 2·77 | 5·26 | 5·09 | 1·71 | 1·85 | 3·76 | 3·41 |
| Stage 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Stage 0: no growth occurred for the axis or leaves.
Stage 1: the axis grew with an AGR just below its maximum. Axis AGR was almost the same for Cogshall and José. The leaves began to grow, with a higher AGR for proximal than distal leaves. These marked differences between leaf AGRs meant an earlier beginning of growth for proximal than for distal leaves, especially for Cogshall. Leaf AGRs were slightly higher for José than for Cogshall.
Stage 2: axis AGR was maximal. It was higher for Cogshall than for José. Leaf AGR was higher for the proximal leaf, intermediate for the sub-distal leaf, and lower for the first distal leaf. There was almost no difference between leaf AGRs in Cogshall and José.
Stage 3: axis AGRs were lower than in the previous stage, especially for Cogshall compared with José. Leaf AGRs were maximal at each leaf position. However, AGRs were higher for the proximal leaf, intermediate for the sub-distal leaf and lower for the first distal leaf, like in stage 2. Leaf AGRs were higher for Cogshall than for José.
Stage 4: almost no growth of the axis occurred, with a higher AGR for José than for Cogshall. Leaf AGR was far lower than in stage 3. It was higher for sub-distal and first distal leaves than for proximal leaves, expressing an earlier decrease in growth for proximal leaves. Leaf AGR was higher for Cogshall than for José.
Stage 5: no growth occurred for axis or leaves.
The comparison of growth stages of GUs computed on the basis of calendar time and thermal time AGR sequences gave a 97 % match for Cogshall (35 differences in assignment of growth stages among 1059 measurement occasions) and 94 % for José (55 differences among 907 measurement occasions). Therefore, the variations of temperature (a maximum of 4·1 °C for GUs during the measurement period) and between the experimental orchards (maximum of 9·2 °C) only slightly modulated the definition of growth stages.
Inflorescences
There was a degenerate estimated state occupancy distribution (the only possibility was to stay one time instant in this state) and high AGRs for the first stage where the growth was effective (stage 1). We interpreted these parameters estimated for stage 1 as a side effect of the minimal axis size required to measure the inflorescences. The real stage corresponding to the beginning of inflorescence growth extended before the measurement occasion identified with the occurrence of stage 1, and the corresponding AGR was indeed far lower. In the remainder of this analysis, we will consider stages 0 and 1 as a single macro-stage. We checked that this side effect, while detectable, was of rather low amplitude for the GU axes and undetectable for the leaves.
For both cultivars, we identified five growth stages for the inflorescence axis (Table 2).
Table 2.
Estimated mean AGR [0·1 mm (°Cd)–1] of the inflorescence axis for the five reproductive growth stages in two mango cultivars, Cogshall and José
| Cogshall | José | |
|---|---|---|
| Stage 0 + 1 | 6·37 | 3·00 |
| Stage 2 | 7·32 | 6·58 |
| Stage 3 | 15·17 | 14·79 |
| Stage 4 | 3·93 | 3·59 |
| Stage 5 | 0 | 0 |
Stage 0 + 1: no growth occurred, followed by beginning of growth.
Stage 2: for both cultivars, AGRs were higher than in the previous stage.
Stage 3: AGRs were maximal for both cultivars.
Stage 4: for both cultivars, AGRs were lower than in the previous stage.
Stage 5: no growth occurred.
For stages 2–4, AGRs were slightly higher for Cogshall than for José. The comparison of inflorescence growth stages computed on the basis of calendar time and thermal time AGR sequences gave a 91 % match for Cogshall (133 differences in assignment of growth stages among 1545 measurement occasions) and 88 % for José (197 differences among 1699 measurement occasions). The less rich information provided by a single variable in the case of inflorescences compared with four variables (axis and three leaves) in the case of GUs and the slightly higher variations of temperature (a maximum of 5 °C for inflorescences during the measurement period instead of 4·1 °C for GUs) probably explains the lower match rate for inflorescences.
Leaf–axis asynchronism during growth of the GU
We examined the relationships between relative axis length and relative leaf area to illustrate further the asynchronism between axis and leaf growths (Figs 3A, B for scatterplots and Fig. 3C for local polynomial regression fitting). Axis length for both cultivars increased first, followed by an increase in leaf area. This analysis showed more marked asynchronism between axis length and leaf area for Cogshall than for José, probably due to the fact that the axis stopped growing earlier in Cogshall than in José (stage 3 axis AGR was 26 % of stage 2 maximum AGR in Cogshall whereas it was 71 % of maximum AGR in José; see Table 1). For both cultivars, the proximal leaf grew before the other two leaves, and the first distal leaf grew after the proximal and sub-distal leaves.
Fig. 3.
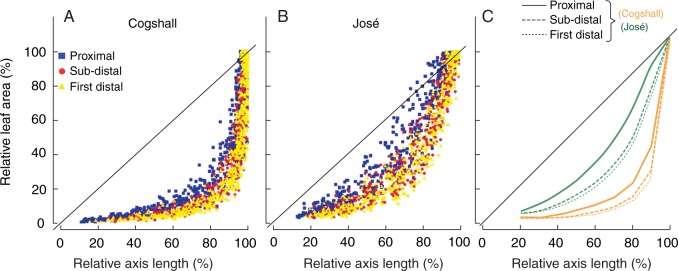
Relative leaf area in relation to relative axis length during growth of the growth unit in two mango cultivars, Cogshall (A) and José (B). Colours and symbols represent leaf positions: proximal (blue square), sub-distal (red circle) and first distal (yellow triangle). (C) Loess (non-parametric regression method) smoothing of the relationship between relative leaf area and relative axis length for Cogshall (orange) and José (green). Line types represent leaf position: proximal (solid), sub-distal (dashed) and first distal (dotted). Percentages are calculated as the length of the growth unit axis and leaf area divided by the final length of the growth unit axis and the final leaf area, respectively. The black bold line on each graph represents x = y.
Correspondence between growth stages and developmental stages
The next step in the study was to explore the relationships between growth stages and developmental stages. Six growth stages have been identified for GUs, and five for inflorescences. We hypothesized that there were correspondences between growth stages and developmental stages, combining succession constraints (i.e. preserving stage order) and higher counts for the matching between a given developmental stage and a given growth stage (Table 3). The match rate between growth stages and developmental stages was about 75 % for Cogshall and José GUs and inflorescences.
Table 3.
Confusion matrices between growth stages obtained using segmentation models and developmental stages determined from morphological observations in an expert way for growth units (axis and leaves) and inflorescences of two mango cultivars, Cogshall and José
| (a) Growth units | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Developmental stage | Cogshall |
José |
||||||||||||
| Growth stage |
Growth stage |
|||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | Total | 0 | 1 | 2 | 3 | 4 | 5 | Total | |
| B1 | 12 | 0 | 0 | 0 | 0 | 0 | 12 | 6 | 0 | 0 | 0 | 0 | 0 | 6 |
| B2 | 67 | 0 | 0 | 0 | 0 | 0 | 67 | 63 | 1 | 0 | 0 | 0 | 0 | 64 |
| C | 33 | 13 | 0 | 0 | 0 | 0 | 46 | 47 | 31 | 0 | 0 | 0 | 0 | 78 |
| D | 0 | 139 | 33 | 0 | 0 | 0 | 172 | 0 | 99 | 9 | 0 | 0 | 0 | 108 |
| E | 0 | 6 | 162 | 78 | 0 | 0 | 246 | 0 | 16 | 160 | 44 | 0 | 0 | 220 |
| F | 0 | 0 | 3 | 213 | 33 | 1 | 250 | 0 | 0 | 4 | 162 | 33 | 1 | 200 |
| G | 0 | 0 | 0 | 7 | 121 | 66 | 194 | 0 | 0 | 0 | 11 | 113 | 54 | 178 |
| H | 0 | 0 | 0 | 0 | 2 | 70 | 72 | 0 | 0 | 0 | 0 | 2 | 51 | 53 |
| Total | 112 | 158 | 198 | 298 | 156 | 137 | 1059 | 116 | 147 | 173 | 217 | 148 | 106 | 907 |
| Match: | 77 % | Match: | 77 % | |||||||||||
| Mismatch: | 23 % | Mismatch: | 23 % | |||||||||||
| (b) Inflorescences | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Developmental stage | Cogshall |
José |
||||||||||||
| Growth stage |
Growth stage |
|||||||||||||
| 0 + 1 | 2 | 3 | 4 | 5 | Total | 0 + 1 | 2 | 3 | 4 | 5 | Total | |||
| B1 | 25 | 0 | 0 | 0 | 0 | 25 | 18 | 0 | 0 | 0 | 0 | 18 | ||
| B2 | 90 | 0 | 0 | 1 | 0 | 91 | 145 | 0 | 0 | 0 | 0 | 145 | ||
| C | 83 | 10 | 1 | 1 | 0 | 95 | 160 | 17 | 0 | 1 | 0 | 178 | ||
| D1 | 19 | 74 | 7 | 0 | 0 | 100 | 21 | 123 | 5 | 0 | 0 | 149 | ||
| D2 | 0 | 36 | 32 | 1 | 0 | 69 | 0 | 51 | 16 | 2 | 0 | 69 | ||
| E | 0 | 30 | 344 | 57 | 0 | 431 | 0 | 120 | 305 | 27 | 0 | 452 | ||
| F | 0 | 1 | 128 | 435 | 90 | 654 | 0 | 44 | 100 | 357 | 103 | 604 | ||
| PF | 0 | 0 | 0 | 0 | 43 | 43 | 0 | 0 | 0 | 3 | 42 | 45 | ||
| G | 0 | 0 | 0 | 0 | 37 | 37 | 0 | 0 | 0 | 0 | 39 | 39 | ||
| Total | 217 | 151 | 512 | 495 | 170 | 1545 | 344 | 355 | 426 | 390 | 184 | 1699 | ||
| Match: | 76 % | Match: | 73 % | |||||||||||
| Mismatch: | 24 % | Mismatch: | 27 % | |||||||||||
The hypothesized correspondences are shown in bold.
Growth units
Developmental stages B1, B2 (bud swelling) and C (bud opening) corresponded to growth stage 0, where no growth occurred (Table 3). Developmental stage D (axis apparent and leaves folded at their central vein) corresponded to growth stage 1, where axis AGR was almost maximal and the leaves began to grow. Developmental stage E corresponded to growth stage 2, where axis AGR was maximal. Developmental stage F (petioles oriented 135 ° and dangling leaves) corresponded to growth stage 3, where leaf AGR was maximal. Developmental stage G (hardening, move up and darkening of the leaves) corresponded to growth stage 4, where organ growth began to stop. Developmental stage H (mature shoot) corresponded to growth stage 5, where growth ceased.
Inflorescences
Developmental stages B1, B2 (bud swelling) and C (bud opening) corresponded to growth macro-stage 0 + 1 (Table 3). Developmental stages D1 (secondary axes close to the main axis of the inflorescence) and D2 (beginning of the opening of the secondary axes) corresponded to growth stage 2, where the axis began to grow. Developmental stage E (no open flower, growth of all the primary and secondary axes) corresponded to growth stage 3, where AGR was maximal. Developmental stage F (from opening of the first flower to opening of the apical flower on the main axis) corresponded to growth stage 4, where AGR decreased. Developmental stages PF (from opening of the apical flower on the main axis to the last open flower) and G (no more open flowers) were grouped together into growth stage 5, where inflorescence axis growth ceased.
Time to the first occurrence of growth stages and developmental stages
In our case of GU and inflorescence follow-up data, the limit between two growth stages could not be identified precisely on the thermal time scale. Rather, these limits were located somewhere within an interval between two thermal time points corresponding to consecutive measurement dates. This effect of interval censoring on stage durations was rather strong in our case since the average number of measurement occasions per growth stage was small (e.g. between 1·5 and 4·2 for GU axis). This effect was smaller on the time to the first occurrence of a stage, which cumulates successive stage durations, except for the very first stages.
Figures 4 and 5 showed the correspondence between times to the first occurrence of developmental stages and growth stages. We have shown only those stages where growth occurred. Thermal times to the first occurrence of vegetative stages were longer in José than in Cogshall (Fig. 4). The growth stages and developmental stages in both cultivars were initially fairly synchronous, became more desynchronized at growth stage 3, and resynchronized at the end of growth (Fig. 4). Thermal times to the first occurrence of reproductive stages were longer in José than in Cogshall (Fig. 5). For both cultivars, growth stage 4 and developmental stage F were less synchronous than the previous stages.
Fig. 4.
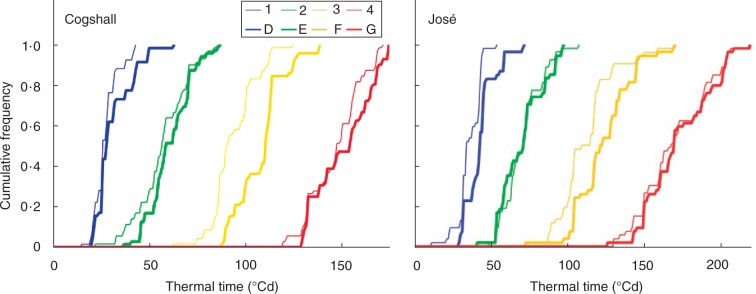
Cumulative relative frequencies of thermal time (in °Cd) to the first occurrence of growth unit stages, either growth stages obtained using segmentation models (numbers) or developmental stages determined from morphological observations in an expert way (letters), for two mango cultivars, Cogshall and José.
Fig. 5.

Cumulative relative frequencies of thermal time (in °Cd) to the first occurrence of inflorescence stages, either growth stages obtained using segmentation models (numbers) or developmental stages determined from morphological observations in an expert way (letters), for two mango cultivars, Cogshall and José.
DISCUSSION
Co-ordination between growth stages and developmental stages
We chose to use thermal time AGRs to take account of the effect of temperature on plant growth and development. The thermal time can be viewed as a non-linear transform of the calendar time that plays the role of an implicit time-varying temperature explanatory variable that modulates organ growth with reference to regression models. In our study, the difference in temperature between the different experimental orchards (whose altitudes vary between 65 and 450 m a.s.l.) and the variations of temperature during the growing period only slightly modulated the definition of growth stages, which were thus very robustly determined by ontogeny (as illustrated by the strong matches between calendar time and thermal time growth stages). Nevertheless, thermal time constitutes a convenient way to relate growth patterns, expressed in an appropriate unit, to physiological processes.
The small variability remaining in the time to the first occurrence of a growth stage or developmental stage (Figs 4 and 5) was probably due to the fact that temperature was not the only factor affecting the growth and development of mango GUs and inflorescences. This variability might be explained by other environmental factors such as light or humidity (Arnold, 1959; Brisson and Delécolle, 1991; Bonhomme, 2000). It could also be due to endogenous factors such as the position of the GU, i.e. apical or lateral, which affects the final size of the organs (Normand et al., 2009).
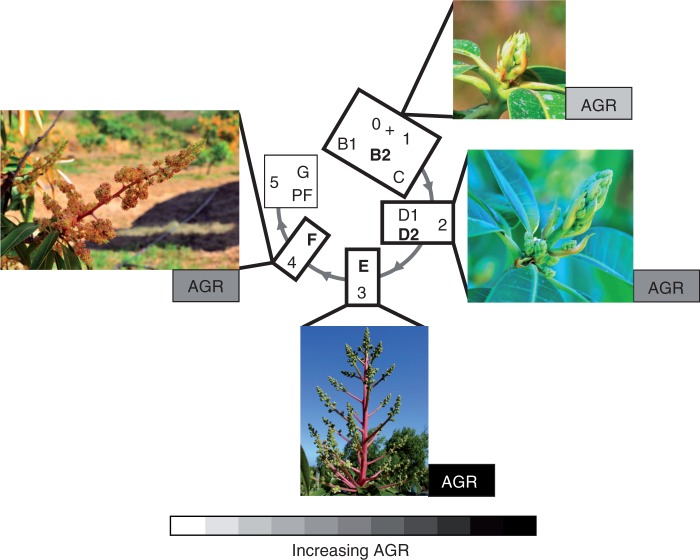
We obtained strong matches between growth stages and developmental stages (about 75 %; Table 3). This showed that the developmental stages determined on the basis of selected morphological discontinuities (changes in colour, shape, angle or texture) were closely related to changes in the growth dynamics. Based on these results, we defined ‘developmental growth stages’ by integrating growth and developmental traits. These stages showed that maximal leaf AGR occurred when the leaf was limp and hung down (Fig. 6). This is consistent with the positive relationship between cellular expansion, decreasing leaf dry matter content, increasing water content per cell and increasing leaf limpness as shown in mango (Taylor, 1970). Leaf growth can occur only when lignification of the cell wall is low and its elasticity is high (Taylor, 1971; Dale, 1988). This is consistent with our results which showed that the arrest of leaf growth corresponded to an increase in lamina rigidity and an upswing of the lamina (stage G, Fig. 6).
Fig. 6.
Correspondences between developmental stages determined from morphological observations in an expert way (inside the central circle, Fig. 1) and growth stages obtained using segmentation models (outside the circle, Table 1) for vegetative organs. Main developmental stages in bold are illustrated by the photographs. Variations in AGR for axis and leaves are illustrated using a white (0 % of organ maximal AGR) to black (100 % of organ maximal AGR) scale. AGRs are shown for the growth unit axis, proximal leaf, sub-distal leaf and first distal leaf (upwards).
Our results showed that maximal leaf AGR occurred when the angle of the petiole was 135 ° downward on the axis (Fig. 6). Previous studies showed that a steep leaf angle reduces exposure to excessive radiation in the middle of the day (Falster and Westoby, 2003). Excessive light interception increases leaf temperature, which may be a disadvantage as it increases the respiration rate more than the photosynthetic rate, and decreases water-use efficiency (Falster and Westoby, 2003). In mango, the 135° angle may protect the leaf from excessive radiation at an important period of leaf growth, when AGR is maximal. Changes in petiole angle may also be related to variations in petiole biomechanics properties since leaves with downward inclined angles require lower biomass investments in petioles (Niinemets, 1998). The putative lower investment in petioles suggests that lamina growth is being promoted, which is consistent with the maximal AGR observed at this stage.
For inflorescences, maximal axis AGR occurred before flower opening (Fig. 7). AGR decreased at the beginning of flowering, possibly due to competition for resources between flowers growth and axis growth. Growth arrest corresponded partially to stage PF, after opening of the apical flower on the inflorescence main axis. This determinate growth illustrated the close relationship between developmental traits (opening of the apical flower) and growth traits (growth arrest). However, our study could not distinguish whether opening of the apical flower stopped the growth of the axis, or whether axis growth arrest caused opening of the apical flower.
Fig. 7.
Correspondences between developmental stages determined from morphological observations in an expert way (inside the central circle, Fig. 2) and growth stages obtained using segmentation models (outside the circle, Table 2) for inflorescences of mango. Main developmental stages in bold are illustrated by the photographs. Variations in AGR for the inflorescence main axis are illustrated using a white (0 % of organ maximal AGR) to black (100 % of organ maximal AGR) scale.
The BBCH scale (Meier et al., 2009) is a system used to identify and code the developmental stages of mono- and dicotyledonous plant species, including mango (Hernandez Delgado et al., 2011). It divides the entire developmental cycle of plants into ten main stages, each one being split into ten secondary stages, which themselves may be divided into ten tertiary stages. This scale put milestones on the continuous development of organs, defined as the percentage of the final organ size attained. Consequently, these stages mix organ development and growth. For instance, stage 312 corresponds to the time at which shoots are about 20 % of their final length. However, these stages, since they refer to final length, are identifiable only a posteriori, not during organ growth. Moreover, a large variability is often observed within and between plants in organ final size. It could then be difficult to parameterize this scale. The BBCH scale thus does not define integrative stages describing both the growth and development of the growing organ. Our ‘developmental growth stages’ go beyond this basic morphological description of development as they open up the possibility to deduce growth dynamics from developmental observations at any time in GU and inflorescence development.
Growth asynchronisms between the axis and leaves within a GU
Few studies have considered within-GU asynchronisms. Here, by identifying intrinsic growth stages using HSMCs, we propose a method that can be used to study asynchronisms between organs belonging to the same GU. In our study, asynchronisms were first detected between the axis and the leaves: from a morphological, i.e. macroscopic, point of view, maximal axis AGR preceded maximal leaf AGR. These results are in agreement with Parisot (1988) who noted that maximum axis growth occurred before that of the leaves. Two hypotheses may be put forward to explain the earlier growth of the axis compared with the leaves. First, a structural hypothesis: since leaf performance depends on the hydraulic and biomechanical support provided by the parent axis (Preston and Ackerly, 2004), the axis must grow first before it can support the growth of the leaves. Secondly, a metabolic hypothesis: at the beginning of GU growth, the leaves are still small, and in a distal position. They probably attracted fewer carbohydrates than the growing axis. Both phenomena probably act together. Our results showed that even though adult GUs allocate more biomass to the leaves than to the axis (Normand et al., 2008), axis growth was promoted during the first part of GU build-up. The axialization process, i.e. the predominance of the axis component over the foliar component, has been shown to determine the vegetative status of the shoot in apple (Lauri and Kelner, 2001), cherry (Lauri, 1992) and some tropical species (Lauri and Térouanne, 1991) including mango (Normand et al., 2009). We showed here that axialization dynamics changed during GU establishment (Fig. 3) and also differed between the two mango cultivars, with a longer axis growth period for José than for Cogshall (Table 1). This is consistent with the cultivar growth habits since José has an open canopy and long GUs with narrow leaves, and Cogshall has a dense, compact canopy with smaller GUs and larger leaves (Dambreville et al., 2013).
Segmentation models also highlighted asynchronisms between the growth of the proximal and distal leaves, with higher time lags for the beginning of growth than for growth arrest (Table 1; Fig. 3). Earlier growth of proximal leaves would lead to earlier access to resources compared with distal leaves. This could reduce the availability of the resources needed for the growth of distal leaves and thus explain both their lower AGR and their smaller final size compared with proximal leaves (Dambreville et al., 2013). In contrast to the beginning of growth, the growth arrest was more synchronous between the axis and the leaves (Table 1, stage 4). Hallé and Martin (1968) suggested that the growth arrest of the apical meristem was due to an extensive use of carbohydrates by the leaf growth.
Comparisons between growth stages of GUs and inflorescences
Despite the common ontogenetic origin of GUs and inflorescences, our results showed that the first occurrence of the growth stage where the AGR was maximal began at a higher thermal time sum for the inflorescence axis compared with the GU axis (Figs 4 and 5; mean values of 75 °Cd and 113 °Cd for the inflorescence axes of Cogshall and José, respectively, compared with 57 °Cd and 71 °Cd for the GU axes of Cogshall and José, respectively). Similarly, the time to the first occurrence of growth stage 4, where growth decreased, occurred at a higher thermal time sum for the inflorescence axis compared with the GU axis (Figs 4 and 5; mean values of 172 °Cd and 210 °Cd for the inflorescence axes of Cogshall and José, respectively, compared with 148 °Cd and 172 °Cd for the GU axes of Cogshall and José, respectively). These differences may be explained by the trophic status of the organs since the faster growth of the GU is likely to be related to the transition from the heterotrophic to autotrophic status of the leaves (Turgeon, 1989), whereas the slower growth of the inflorescence may be related to the increasing heterotrophy from budburst to the end of the flowering and fruit-set.
Conclusions
Multivariate sequences were used to determine GU growth stages (AGR of the axis and three selected leaves), whereas univariate sequences were used to determine inflorescence growth stages (main axis AGR only). A perspective for our study would be to consider the growth of the secondary axes of the inflorescences. Inflorescence growth stages could then be computed on the basis of a multivariate sequence (AGR of main axis and selected secondary axes) in order to study asynchronisms between inflorescence components. Since inflorescences and GUs are homologous structures (Bell, 1991), it would be interesting to compare within-GU and within-inflorescence asynchronisms.
Our study has built a bridge between developmental stages, defined from a set of morphological traits observable during organ development, and growth stages, defined here by segmentation models applied to AGRs. We have shown that all morphological traits included in developmental stages, such as leaf limpness, petiole angle or opening of the apical flower of the inflorescence, are related to contrasting organ growth dynamics. With the development of plant phenotyping platforms and the increase in the throughput of development and growth data, there is a real challenge in identifying how developmental and growth processes can be studied and related to each other. At the plant scale, this approach involves well-known processes such as carbohydrate assimilation and allocation, cell division and expansion, and hydraulics. From an applied point of view, the knowledge of the growth characteristics associated with the developmental stages is also crucial to better understand, and possibly act upon, the interactions between plant development and pests and diseases.
SUPPLEMENTARY DATA
Suppelementary data are available online at www.aob.oxfordjournals.org and consist of the following. Appendix S1: thermal time models and base temperatures. Appendix S2: definition of hidden semi-Markov chains and associated statistical methods. Appendix S3: direct modelling of absolute growth rates using semi-continuous distributions. Appendix S4: validation of the assumption of segmentation in growth stages. Table S1: GU models – Sup-norm distances between observation distributions for consecutive states. Table S2: segmentation uncertainty
ACKNOWLEDGEMENTS
We thank Doralice Jessu and Emilie Serin for their contributions to field work, Alexandre Law-Yat and Raoul Zitte for hosting our experiments on their mango orchards, Christine Granier for fruitful and supportive discussions, and a referee for helpful comments that led to an improvement in the presentation of this article. This work was funded by CIRAD, the French government, the Regional Council of Réunion Island and the European Agricultural Fund for Rural Development (EAFRD, No. 111.34).
LITERATURE CITED
- Arnold CY. 1959. The determination and significance of the base temperature in a linear heat unit system. Proceedings of the American Society for Horticultural Science 74: 430–445. [Google Scholar]
- Aubert B, Lossois P. 1972. Considérations sur la phénologie des espèces fruitières arbustives. Fruits 27: 269–286. [Google Scholar]
- Bell AD. 1991. Plant form: an illustrated guide to flowering plant morphology. New York: Oxford University Press. [Google Scholar]
- Bonhomme R. 2000. Bases and limits to using ‘degree.day’ units. European Journal of Agronomy 13: 1–10. [Google Scholar]
- Borreani G, Roggero PP, Sulas L, Valente ME. 2003. Quantifying morphological stage to predict the nutritive value in sulla (Hedysarum coronarium L.). Agronomy Journal 95: 1608–1617. [Google Scholar]
- Boyes DC, Zayed AM, Ascenzi R, et al. 2001. Growth stage-based phenotypic analysis of Arabidopsis. A model for high throughput functional genomics in plants. The Plant Cell 13: 1499–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brisson N, Delécolle R. 1991. Développement et modèles de simulation de cultures. Agronomie 12: 253–263. [Google Scholar]
- Chatfield C. 2003. The analysis of time series: an introduction, 6th edn Boca Raton, FL: Chapman & Hall/CRC Press. [Google Scholar]
- Cookson SJ, Van Lijsebettens M, Granier C. 2005. Correlation between leaf growth variables suggest intrinsic and early controls of leaf size in Arabidopsis thaliana. Plant, Cell and Environment 28: 1355–1366. [Google Scholar]
- Dale JE. 1988. The control of leaf expansion. Annual Review of Plant Physiology and Plant Molecular Biology 39: 267–295. [Google Scholar]
- Dambreville A, Normand F, Lauri P-É. 2013. Plant growth co-ordination in natura: a unique temperature-controlled law among vegetative and reproductive organs in mango. Functional Plant Biology 40: 280–291. [DOI] [PubMed] [Google Scholar]
- Davenport TL. 2009. Reproductive physiology. In: Litz RE, ed. The mango: botany, production and uses, 2nd edn Wallingford, UK: CABI, 97–169. [Google Scholar]
- Dechaine JM, Brock MT, Iniguez-Luy FL, Weinig C. 2014. Quantitative trait loci × environment interactions for plant morphology vary over ontogeny in Brassica rapa. New Phytologist 201:657–669. [DOI] [PubMed] [Google Scholar]
- Falster DS, Westoby M. 2003. Leaf size and angle vary widely across species: what consequences for light interception? New Phytologist 158: 509–525. [DOI] [PubMed] [Google Scholar]
- Fehr WR, Caviness CE, Burmood DT, Pennington JS. 1971. Stage of development descriptions for soybeans, Glycine max (L.) Merrill. Crop Science 11: 929–931. [Google Scholar]
- Gatsuk LE, Smirnova OV, Vorontzova LI, Zaugolnova LB, Zhukova LA. 1980. Age states of plants of various growth forms: a review. Journal of Ecology 68: 675–696. [Google Scholar]
- Goudriaan J, Van Laar HH. 1994. Modelling potential crop growth processes. Dordrecht, The Netherlands: Springer. [Google Scholar]
- Guédon Y. 2003. Estimating hidden semi-Markov chains from discrete sequences. Journal of Computational and Graphical Statistics 12: 604–639. [Google Scholar]
- Guédon Y, Caraglio Y, Heuret P, Lebarbier E, Meredieu C. 2007. Analyzing growth components in trees. Journal of Theoretical Biology 248: 418–447. [DOI] [PubMed] [Google Scholar]
- Hallé F, Martin R. 1968. Étude de la croissance rythmique chez l’Hévéa (Hevea brasiliensis Müll. -Arg., Euphorbiacées, Crotonoïdées). Adansonia 8: 475–503. [Google Scholar]
- Hernández Delgado PM, Aranguren M, Reig C, et al. 2011. Phenological growth stages of mango (Mangifera indica L.) according to the BBCH scale. Scientia Horticulturae 130: 536–540. [Google Scholar]
- Kalu BA, Fick GW. 1981. Quantifying morphological development of alfalfa for studies of herbage quality. Crop Science 21: 267–271. [Google Scholar]
- Lauri P-É. 1992. Données sur le contexte végétatif lié à la floraison chez le cerisier (Prunus avium). Canadian Journal of Botany 70: 1848–1859. [Google Scholar]
- Lauri P-É, Kelner J-J. 2001. Shoot type demography and dry matter partitioning: a morphometric approach in apple (Malus domestica). Canadian Journal of Botany 79: 1270–1273. [Google Scholar]
- Lauri P-É, Terouanne É. 1991. Eléments pour une approche morphométrique de la croissance végétale et de la floraison: le cas d’espèces tropicales du modèle de Leeuwenberg. Canadian Journal of Botany 69: 2095–2112. [Google Scholar]
- Legave JM, Christen D, Giovannini D, Oger R. 2009. Global warming in Europe and its impacts on floral bud phenology in fruit species. Acta Horticulturae 838: 21–26. [Google Scholar]
- Meier U, Bleiholder H, Buhr L, et al. 2009. The BBCH system to coding the phenological growth stages of plants: history and publications. Nachrichtenblatt des Deutschen Pflanzenschutzdienstes 61: 41–52. [Google Scholar]
- Niinemets Ü. 1998. Adjustment of foliage structure and function to a canopy light gradient in two co-existing deciduous trees. Variability in leaf inclination angles in relation to petiole morphology. Trees – Structure and Function 12: 446–451. [Google Scholar]
- Normand F, Bissery C, Damour G, Lauri P-É. 2008. Hydraulic and mechanical stem properties affect leaf-stem allometry in mango cultivars. New Phytologist 178: 590–602. [DOI] [PubMed] [Google Scholar]
- Normand F, Léchaudel M. 2006. Toward a better interpretation and use of thermal time models. Acta Horticulturae 707: 159–165. [Google Scholar]
- Normand F, Pambo Bello AK, Trottier C, Lauri P-É. 2009. Is axis position within tree architecture a determinant of axis morphology, branching, flowering and fruiting? An essay in mango. Annals of Botany 103: 1325–1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olesen T. 2011. Late 20th century warming in a coastal horticultural region and its effects on tree phenology. New Zealand Journal of Crop and Horticultural Science 39: 119–129. [Google Scholar]
- Pantin F, Simonneau T, Rolland G, Dauzat M, Muller B. 2011. Control of leaf expansion: a developmental switch from metabolics to hydraulics. Plant Physiology 156: 803–815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisot E. 1988. Etude de la croissance rythmique chez de jeunes manguiers (Mangifera indica L.). III: Croissance et développement de jeunes manguiers. Fruits 43: 235–247. [Google Scholar]
- Preston KA, Ackerly DD. 2004. The evolution of allometry in modular organisms. In: Pigliucci M, Preston KA, eds. Phenotypic integration: studying the ecology and evolution of complex phenotypes. Oxford: Oxford University Press, 80–106. [Google Scholar]
- Schneiter AA, Miller JF. 1981. Description of sunflower growth stages. Crop Science 21: 901–903. [Google Scholar]
- Steeves TA, Sussex IM. 1989. Patterns in plant development. Cambridge: Cambridge University Press. [Google Scholar]
- Taylor FJ. 1970. Some aspects of the development of mango (Mangifera indica L.) leaves. I. Leaf area, dry weight and water content. New Phytologist 69: 377–394. [Google Scholar]
- Taylor FJ. 1971. Some aspects of the development of mango (Mangifera indica L.) leaves. III. A mechanical analysis. New Phytologist 70: 911–922. [Google Scholar]
- Turgeon R. 1989. The sink–source transition in leaves. Annual Review of Plant Physiology and Plant Molecular Biology 40: 119–138. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.