Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2004 Jun 7;101(24):8848–8851. doi: 10.1073/pnas.0401428101

Preferential states in soil moisture and climate dynamics

Paolo D'Odorico †,‡, Amilcare Porporato §
PMCID: PMC428435  PMID: 15184676

Abstract

Summer precipitation in continental midlatitude regions is significantly contributed by local recycling, i.e., by moisture returning to the atmosphere through evapotranspiration from the same region. On the other hand, reduced soil moisture availability may limit evapotranspiration rates with effects on the planetary boundary layer dynamics through the partitioning between sensible and latent heat fluxes. Thus, a dependence may exist between precipitation and antecedent soil moisture conditions. Here we provide theoretical and experimental evidence in support of the hypothesis that in continental regions summer soil moisture anomalies affect the probability of occurrence of subsequent precipitation. Owing to these feedbacks, two preferential states may arise in summer soil moisture dynamics, which thus tend to remain locked either in a “dry” or a “wet” state, whereas intermediate conditions have low probability of occurrence. In this manner, such land–atmosphere interactions would explain the possible persistence of summer droughts sustained by positive feedbacks in response to initial (spring) surface moisture anomalies.

The understanding of the water cycle in midlatitude continental regions is still controversial, because of the difficulty of assessing land–atmosphere interactions and their effect on summer precipitation. A number of studies have provided evidence either in support of (1–5) or against (6–8) the hypothesis of a positive feedback between summer soil moisture and subsequent precipitation in such regions. General Circulation Model (GCM) simulations have shown that anomalies in spring/early-summer soil moisture can affect the regime of summer precipitation in North America (2, 9). Depending on the occurrence of wet (dry) spring anomalies, the system remains locked for the rest of the warm season in a state with above (below) average precipitation. The positive feedback between soil moisture and rainfall can be sustained also by changes in large-scale circulation caused by initial soil moisture anomalies (10, 11). GCM analyses have shown (i) the ability of land–atmosphere interactions to enhance and sustain droughts (or floods) (2); (ii) the dependence between the magnitude and timing of an initial anomaly and the intensity and duration of its effects (i.e., droughts or floods) (12); and (iii) how the initial anomaly may arise from natural climatic variability (9).

Reanalysis data and back-trajectory algorithms (13, 14) aimed at determining the moisture sources in central North America found that summer precipitation over the Mississippi basin is contributed up to 30–40% by local evapotranspiration, depending on whether the summer is dry or wet. Other estimates (15) have confirmed the importance of precipitation recycling to the regional water cycle in continental regions. More recently, ref. 5 used GCMs to provide evidence that the persistence observed in patterns of warm-season precipitation is associated with the land–atmosphere feedback. Ref. 1 analyzed both precipitation and soil moisture records and found a significant correlation between precipitation and previous soil moisture conditions, suggesting the existence of a feedback mechanism between soil water content and subsequent precipitation. In a subsequent study (16, 17) the same authors used a simplified one-dimensional model of atmospheric boundary layer to show how, depending on the early-morning atmospheric conditions, soil moisture may indeed trigger deep convection in some midlatitude continental regions. These results suggest that the soil moisture–precipitation feedback acts mainly through rainfall-triggering mechanisms. Similar conclusions were also reached in ref. 18. As a consequence, soil moisture is expected to affect more the frequencies of rainfall occurrences than the amount of rainfall yielded by each storm.

Link Between Rainfall Frequency and Soil Moisture

Here we show that daily rainfall occurrences are significantly dependent on previous soil moisture conditions and we relate this soil moisture–precipitation feedback to the emergence of preferential states in the dynamics of summer soil moisture. We use data available for the central part of North America to analyze the dependence existing between regional soil water content and subsequent daily rainfall occurrences. A direct assessment of this dependence is possible for the state of Illinois, where a unique network of soil moisture stations provides biweekly measurements for the period 1981 to the present (19, 20). This region has been argued to be affected by local recycling and soil moisture–rainfall feedbacks (1, 2, 13–17).

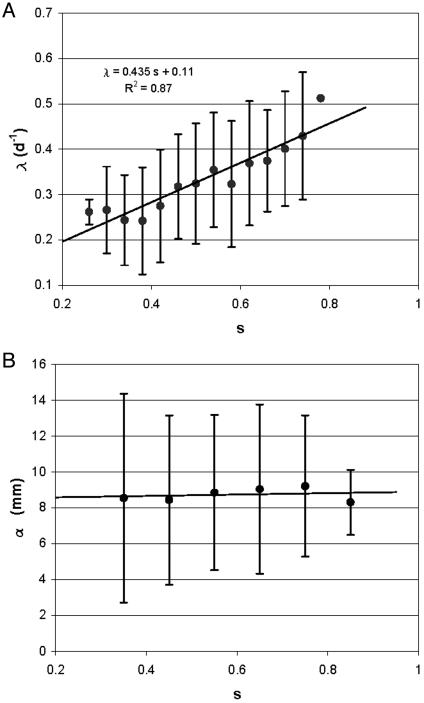
Fig. 1A shows a plot of average storm frequency, λ, as a function of statewide average soil moisture for a station centrally located in the region of interest. The biweekly soil moisture observations were interpolated in time and then averaged across Illinois to provide daily estimates of statewide average soil water content in the top 50 cm. For each summer day (i.e., May 1 to September 30 between 1980 and 2002) the rainfall frequency in the subsequent 21 days was calculated and related to the regional average soil moisture. Daily rainfall data (National Oceanic and Atmospheric Administration/National Climatic Data Center) were taken from the station of Peoria, IL. Different soil depths and lengths of the temporal intervals used for the storm frequency estimation provided weaker rainfall–soil moisture dependence. A similar analysis was carried out for the average storm depth, α (Fig. 1B). Interestingly, the results show the existence of a relatively strong dependence (r2 = 0.87) between frequency of rainstorm occurrences and antecedent soil moisture conditions (Fig. 1 A), whereas almost no correlation (r2 ≈ 0) exists between soil water content and subsequent storm depths (Fig. 1B).

Fig. 1.

Fig. 1.

Open in a new tab

Relationship between relative soil moisture, s (averaged over a depth of 50 cm and across the state of Illinois), and precipitation regime at Peoria. (A) Average storm frequency, λ, calculated for different soil moisture classes (i.e., in intervals of width 0.04). The solid line represents a linear fit(r2 = 0.87). (B) Average storm depth, α, as a function of soil moisture. α appears to be independent of s (α = 8.8 mm). In both figures the error bars represent ± standard deviation.

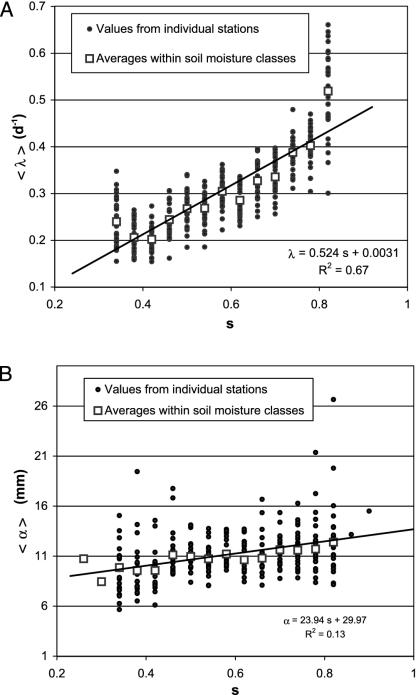
To further support the previous finding, we repeated the same analysis with rainfall records from 27 precipitation stations uniformly distributed across the state of Illinois: three stations were selected within each of the nine climate divisions defined by the National Climatic Data Center (www.ncdc.noaa.gov/oa/documentlibrary/normals/usmap.pdf). The dependence between the statewide average soil moisture (in the top 50 cm of soil) and the average frequency, λ, and depth, α, of precipitation in the subsequent 21 days was investigated. It was found that in all these stations λ was significantly dependent on precedent soil moisture conditions, whereas the average storm depth had a weaker correlation with the soil water content in the previous days. These results are shown in Fig. 2, where data from all of the 27 stations are reported as a function of soil moisture, and a linear fit provides a regional assessment of the dependence of storm frequency and depth on antecedent soil moisture conditions.

Fig. 2.

Fig. 2.

Open in a new tab

Link between relative soil moisture (averaged over a depth of 50 cm and across the state of Illinois) and precipitation regime in 27 rainfall stations in Illinois. (A) Average storm frequency, λ, calculated for different soil moisture classes (i.e., in intervals of width 0.04). The solid line represents a linear fit (r2 = 0.67). (B) Average storm depth, α, as a function of soil moisture. α appears to be only weakly dependent on s (r2 = 0.13). In both plots the small solid points represent average values (taken within soil moisture classes) from each station, whereas the open squares represent averages over the 27 stations.

The previous results seem to indicate that the soil moisture–rainfall feedback acts through an enhancement of the likelihood of rainfall occurrence, rather than through an increase in the amount of rain yielded by each storm. This feature of the land–atmosphere feedbacks supports the theoretical results of refs. 16, 18, 21, and 22, and it could have important implications for the interpretation of the impact of land–atmosphere interactions on the dynamics of the terrestrial water cycle. It should be noticed, however, that the observed link between soil moisture dynamics and frequency of rainfall events is only a necessary but not a sufficient condition for the existence of causality relations between soil moisture and subsequent rain. Thus, the hypothesis that other factors may be responsible for the observed correlation (i.e., Figs. 1 and 2) cannot be ruled out. Yet, in what follows we will show that our hypothesis of soil–atmosphere interaction is consistent with the observed persistence in daily soil moisture data when interpreted in the light of a theoretical model that explicitly incorporates a soil moisture dependence of rainfall events.

Preferential States in Soil Moisture Dynamics

Although much effort has been spent in understanding the physical mechanisms linking precipitation to previous soil moisture conditions (16, 17, 23), the implications for the soil moisture dynamics have been less investigated. Refs. 24 and 25 developed a simplified model of soil water balance at the annual time scale that explicitly accounts for rainfall recycling. Such a model provided a theoretical underpinning to the fact that the soil– atmosphere system can exhibit two preferential states corresponding to a dry and wet mode of the annual soil moisture probability density function. However, no observational evidence of the existence of such preferential states, or of the functional dependence existing between precipitation and regional soil water content, has been provided up to now.

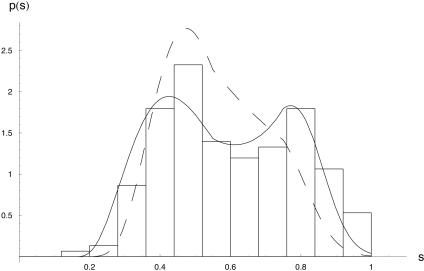
Using the soil moisture statistics obtained for Peoria, here we provide experimental evidence of the existence of preferential states in the summer dynamics of soil moisture. As shown in Fig. 3, a well defined bimodality is present in the frequency distribution of soil moisture observations, indicating a relatively high likelihood for the summer soil moisture dynamics to be either in a dry state or in a wet state, in the same region where evidence of soil moisture–rainfall feedback was found (e.g., Figs. 1 A and 2 A). The bimodality in the distribution is also consistent with the nonparametric test of ref. 26, which allows us to reject the hypothesis that the available soil moisture measurements are sampled from a unimodal distribution. This finding is robust with respect to changing soil moisture station (at least 12 of 18 stations showed clear bimodality) and depth (top 10, 30, and 50 cm). Moreover, to rule out the possibility that soil moisture–precipitation feedbacks and the bimodality were induced by the seasonality of soil moisture and precipitation, the same analysis was repeated with summer seasons of different length (May–September and June–August). In both cases we consistently found the existence of soil moisture–precipitation dependence and multimodality in the soil moisture distribution. The fact that in this region the late growing season can be considered to be practically under statistically steady conditions is also confirmed by the analyses of ref. 27.

Fig. 3.

Fig. 3.

Open in a new tab

Probability distribution of soil moisture. The histograms show the soil moisture distribution estimated from the data of the Illinois soil moisture network (25, 26). Depth-average (top 50 cm) soil moisture values are taken from Peoria for the May–September seasons in the years 1980–2002. Similar behavior is found for soil moisture at different depths in at least two-thirds of the stations. The figure shows also the probability distribution of regional soil moisture calculated by the model with λ expressed as a linear function of s (solid line) and as a constant (λ = 0.35, dashed line). The λ = λ(s) function was the same as determined from data fitting (Fig. 1 A).

A Simple Theoretical Interpretation

A simplified mathematical description of the stochastic soil water balance, valid at the daily time scale and explicitly accounting for the soil moisture dependence of storm frequency (see Appendix and also ref. 28), can be used to corroborate the hypothesis that the bimodality in soil moisture dynamics is a direct consequence of the soil moisture dependence of rainstorm frequency due to soil–atmosphere feedback (Fig. 1 A). The analytical solution of the steady-state probability density function of the stochastic model with a linear dependence of storm frequency on soil moisture is shown in Fig. 3 (solid line). The bimodal shape favorably compares with the frequency distribution directly determined from the data (Fig. 3, histograms). Moreover, the bimodality emerges only if λ is a function of soil moisture (Fig. 1 A), whereas it disappears when λ is assumed to be constant, i.e., independent of soil moisture (Fig. 3, dashed line).

Thus, a state-dependence in the timing of the forcing of the terrestrial water balance is found to be able to generate bimodality in the probability distribution of soil water content, suggesting that the positive feedback between soil moisture and the timing of precipitation may lead to the observed emergence of two preferential states in summer soil moisture dynamics.

Conclusions

This study advances the understanding of important features of the water cycle and of summer hydroclimatic dynamics at the midlatitudes. Experimental and theoretical evidence has been provided in support of the hypothesis that a soil moisture–precipitation feedback exists in the course of the warm season. An empirical functional dependence has been determined between soil moisture and frequency of subsequent storm events. The analysis of extensive soil moisture records has also been used to assess the emergence of two preferential states in the summer soil water balance.

Using the analytical results of a stochastic soil moisture model valid at the daily time scale, we showed these preferential states to be consistent with a soil moisture-dependence of rainfall frequency. These results show not only that land–atmosphere feedbacks may sustain and enhance the effect of initial moisture anomalies occurring at the beginning of the warm season, but also that, because of such feedbacks, summer soil moisture dynamics evolve toward either a dry or a wet state in which the system may remain locked for the rest of the warm season.

Appendix

Following the approach proposed in ref. 28, a suitable soil-moisture dependence of the frequency of rainfall events may be included in the stochastic soil moisture model of refs. 29 and 30 to obtain a more realistic description of the role of soil moisture–precipitation feedbacks. In this manner, compared with the analysis of refs. 24 and 25, the stochastic soil moisture model allows us to account for the distinction between frequency and amount of rainfall events in soil–atmosphere interaction, providing an efficient yet parsimonious description of the soil water balance valid at the daily time scale.

Briefly, the water balance at the daily time scale for a surface soil layer of thickness, Z is expressed as

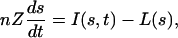graphic file with name M1.gif [1]

where s is relative soil moisture (0 ≤ s ≤ 1, with s = 1 at saturation), n is the soil porosity, I(s, t) is the rate of rainfall infiltration, and L(s) are losses due to evapotranspiration and deep infiltration. I(s, t) is modeled as a nonhomogeneous Poisson process (28) of storm occurrences with rate λ(s) (i.e., average storm frequency). Each storm has a depth, r, modeled as an exponentially distributed random variable of mean α (29, 30). To account for mechanisms of soil saturation, at each storm occurrence, rainfall infiltration is equal to either the storm depth, r, or to the soil storage capacity, nZ(1 – s), whichever is less. Losses due to evapotranspiration and deep infiltration are modeled as a deterministic function of s (30)

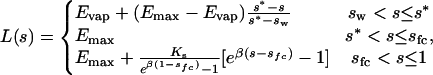graphic file with name M2.gif

where sfc is soil moisture at field capacity, Ks is the saturated hydraulic conductivity, β is a parameter of the moisture retention curve (30), Emax is the rate of (unstressed) evapotranspiration, Evap the rate of evaporation from the ground, s* is the soil water content in conditions of incipient water stress, and sw is the soil moisture at the so-called wilting point. For s < sw, L(s) linearly decreases, reaching a zero value at s = sh (hygroscopic point).

The analytical integration of Eq. 1 provides the steady-state probability density function of soil moisture (28, 30). Full details on the rationale of the model and the methods of solution are provided by refs. 28 and 30. In particular, in ref. 28 we show that the stochastic differential equation (Eq. 1) with state-dependent Poisson noise may show interesting phase transitions, which could be the underlying mechanisms for the emergence of spatial and temporal patterns of hydroclimatic states due to soil–atmosphere interaction.

In Fig. 3 the loss function parameters are (27) Emax = 0.33 cm/d; Ks = 2.0 cm/d; sh = 0.14; sfc = 0.55; and s* = 0.75. This choice of the soil parameters is consistent also with the soil type at Peoria (20, 31). The other soil parameters are sw = 0.18, n = 0.445 (31), and active soil depth, Z = 50 cm (27). Evap is equal to 0.02 cm/d. Summertime average storm depth at Peoria is α = 8.8 mm (Fig. 1B).

This paper was submitted directly (Track II) to the PNAS office.

References

  • 1.Findell, K. L. & Eltahir, E. A. B. (1997) Water Resourc. Res. 33, 725–735. [Google Scholar]
  • 2.Oglesby, R. J. & Erickson, D. J., (1989) J. Climate 2, 1362–1380. [Google Scholar]
  • 3.Jensen, J. C. (1935) Bull. Am. Meteorol. Soc. 16, 142–145. [Google Scholar]
  • 4.McNish, A. G. (1936) EOS Trans. AGU 1, 124–129. [Google Scholar]
  • 5.Koster, R. D., Suarez, M. J., Higgins, R. W. & Van den Dool, H. M. (March 12, 2003) Geophys. Res. Lett. 30, 1241, 10.1029/2002GL016571 [Google Scholar]
  • 6.Holzman, B. (1937) Sources of Moisture for Precipitation in the United States (U.S. Dept. of Agriculture, Washington, DC), Tech. Bull. 589.
  • 7.Georgakakos, K. P., Bae, D.-H. & Cayan, D. R. (1995) Water Resourc. Res. 31, 655–675. [Google Scholar]
  • 8.Salvucci, G. D., Saleem, J. A. & Kaufmann, R. (2002) Adv. Water Resourc. 25, 1305–1312. [Google Scholar]
  • 9.Oglesby, R. J. (1991) J. Climate 4, 890–897. [Google Scholar]
  • 10.Namias, J. (1959) in Rossby Memorial Volume, ed. Bolin, B. (Oxford Univ. Press, Oxford), pp. 240–248.
  • 11.Namias, J. (1978) Mon. Weather Rev. 106, 1557–1567. [Google Scholar]
  • 12.Oglesby, R. J., Marshall, S., Erickson, D. J., Roads, J. O. & Robertson, F. R. (July 31, 2002) J. Geophys. Res. 107, 4224, 10.1029/2001JD001045. [Google Scholar]
  • 13.Dirmeyer, P. A. & Brubaker, K. L. (1999) J. Geophys Res. 107, 19383–19397. [Google Scholar]
  • 14.Brubaker, K. L., Dirmeyer, P. A., Sudradjat, A. & Levy, B. S. (2001) J. Hydrometeorol. 2, 537–557. [Google Scholar]
  • 15.Eltahir, E. A. B. & Bras, R. L. (1996) Rev. Geophys. 34, 367–378. [Google Scholar]
  • 16.Findell, K. L. & Eltahir, E. A. B. (2003) J. Hydrometeorol. 4, 552–569. [Google Scholar]
  • 17.Findell, K. L. & Eltahir, E. A. B. (2003) J. Hydrometeorol. 4, 570–583. [Google Scholar]
  • 18.Eltahir, E. A. B. & Pal, J. S. (1996) J. Geophys. Res. 101, 26237–26245. [Google Scholar]
  • 19.Robock, A., Vinnikov, K. Y., Srinivasan, G., Entin, J. K., Hollinger, S. E., Speranskaya, N. A., Liu, S. & Namkhai, A. (2000) Bull. Am. Meteorol. Soc. 81, 1281–1299. [Google Scholar]
  • 20.Hollinger, S. E. & Isard, S. A. (1994) J. Climate 7, 822–833. [Google Scholar]
  • 21.Emanuel, K. A. & Bister, M. (1996) J. Atmos. Sci. 53, 3276–3285. [Google Scholar]
  • 22.Zeng, N., Shuttleworth, J. W. & Gash, J. H. C. (2000) J. Hydrol. (Amsterdam) 228, 228–241. [Google Scholar]
  • 23.Eltahir, E. A. B. (1998) Water Resourc. Res. 34, 765–776. [Google Scholar]
  • 24.Rodriguez-Iturbe, I., Entekhabi, D. & Bras, R. L. (1991) Water Resourc. Res. 27, 1899–1906. [Google Scholar]
  • 25.Entekhabi, D., Rodriguez-Iturbe, I. & Bras, R. L. (1992) J. Climate 5, 798–813. [Google Scholar]
  • 26.Silverman, B. W. (1986) Density Estimation for Statistics and Data Analysis (Chapman & Hall, London).
  • 27.Salvucci, G. D. (2001) Water Resourc. Res. 37, 1357–1365. [Google Scholar]
  • 28.Porporato, A. & D'Odorico, P. (2004) Phys. Rev. Lett. 92, 1106011-1. [DOI] [PubMed] [Google Scholar]
  • 29.Rodriguez-Iturbe, I., Porporato, A., Ridolfi, L., Cox, D. & Isham, V. (1999) Proc. R. Soc. London Ser. A 455, 3789–3805. [Google Scholar]
  • 30.Laio, F., Porporato, A., Ridolfi, L. & Rodriguez-Iturbe, I. (2001) Adv. Water Resourc. 24, 707–723. [Google Scholar]
  • 31.Hollinger, S. E., Reinke, B. C. & Peppler, R. A. (1994) Illinois Climate Network: Site Descriptions, Instrumentation, and Data Management (Illinois State Water Survey, Champaign), Circular 178.

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES