Kinetic isotope effects in Ras-catalyzed GTP hydrolysis: Evidence for a loose transition state

Abstract

A remote labeling method has been developed to determine ¹⁸O kinetic isotope effects (KIEs) in Ras-catalyzed GTP hydrolysis. Substrate mixtures consist of ¹³C-depleted GTP and [¹⁸O,¹³C]GTP that contains ¹⁸O at phosphoryl positions of mechanistic interest and ¹³C at all carbon positions of the guanosine moiety. Isotope ratios of the nonvolatile substrates and products are measured by using a chemical reaction interface/isotope ratio mass spectrometer. The isotope effects are 1.0012 (0.0026) in the γ nonbridge oxygens, 1.0194 (0.0025) in the leaving group oxygens (the β–γ oxygen and the two β nonbridge oxygens), and 1.0105 (0.0016) in the two β nonbridge oxygens. The KIE in the β–γ bridge oxygen was computed to be 1.0116 or 1.0088 by two different methods. The significant KIE in the leaving group reveals that chemistry is largely rate-limiting whereas the KIEs in the γ nonbridge oxygens and the leaving group indicate a loose transition state that approaches a metaphosphate. The KIE in the two β nonbridge oxygens is roughly equal to that in the β–γ bridge oxygen. This indicates that, in the transition state, Ras shifts one-half of the negative charge that arises from P_γ–O_β–γ fission from the β–γ bridge oxygen to the two β nonbridge oxygens. The KIE effects, interpreted in light of structural and spectroscopic data, suggest that Ras promotes a loose transition state by stabilizing negative charge in the β–γ bridge and β nonbridge oxygens of GTP.

Ras is the prototypical member of the family of small G proteins, which along with Gα subunits of heterotrimeric G proteins, constitute a class of GTP hydrolases that regulate diverse signaling pathways in eukaryotes (1). Ras orchestrates multiple signaling pathways and regulates cell differentiation, proliferation, and apoptosis (2–4). The GTP-bound forms of G proteins are functionally active: that is, they bind to “effector” molecules and regulate their activities or location within the cell. Hydrolysis of GTP results in deactivation and effector release (5). In the absence of other factors, the duration of the active signaling state depends on the intrinsic hydrolytic rate of the G protein, which is typically very slow. However, Ras and other G proteins are subject to specific regulation by GTPase-activating proteins (GAPs), which accelerate intrinsic hydrolytic rates by factors ranging from 10 to 10⁵. In particular, RasGAP increases the GTPase rate of Ras by a factor of 10⁵, from 10^–4 s^–1 to 10 s^–1 (6). Mutations that impair either intrinsic or GAP-facilitated GTPase activity leave Ras in a prolonged state of activation, which is responsible for its role in oncogenic diseases (7).

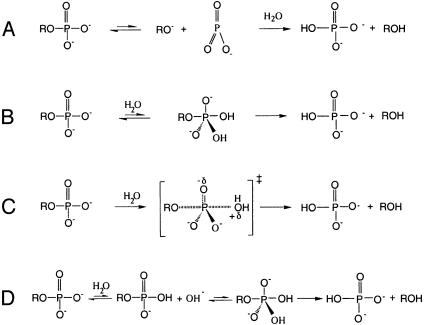
Ras catalyzes the in-line attack of water on the γ phosphate of GTP with inversion of configuration (8). However, the nature of the transition state and the rate-limiting step of Ras-catalyzed GTP hydrolysis remain unclear (9–16). A phosphoryl transfer reaction may either proceed through a metaphosphate or a phosphorane intermediate, or by a concerted pathway (Fig. 1) (17, 18). A metaphosphate intermediate is characterized by complete bond cleavage to the leaving group, absence of bond formation to the incoming nucleophile, and an increase in bond order of the nonbridge oxygens (Fig. 1 A). In contrast, for a phosphorane intermediate, there is no bond cleavage to the leaving group, complete bond formation with the incoming nucleophile, and a decrease in bond order of the nonbridge oxygens (Fig. 1B). The two extreme mechanisms are further distinguished by charge distribution. Negative charge accumulates on the leaving group upon formation of a metaphosphate intermediate, whereas, in a phosphorane intermediate, charge on the nonbridge oxygens increases if it is not neutralized by protonation (Fig. 1B). True metaphosphate intermediates probably do not exist in aqueous solution or at enzyme active sites (18). Typically, a phosphoryl transfer reaction is concerted with a transition state that is intermediate in structure between metaphosphate and phosphorane extremes (Fig. 1C). Transition states with largely metaphosphate or phosphorane characteristics are referred to as “loose” or “tight,” respectively.

Fig. 1.

Mechanisms for hydrolysis of phosphomonoesters. Dissociative (A) and associative (B) mechanistic extremes, the concerted pathway (C), and the substrate-assisted mechanism (D) are shown.

It has been proposed that Ras-catalyzed GTP hydrolysis proceeds through a metaphosphate-like transition state (9). A wealth of physical organic data are consistent with loose transition states for both nonenzymatic and enzymatic hydrolysis of phosphate monoesters (17–19). Analysis of linear free-energy relationships indicates that the transition state for nonenzymatic hydrolysis of phosphoanhydrides, of which GTP is one example, is metaphosphate-like (10). An alternative, substrate-assisted general base catalysis mechanism (Fig. 1D) has been proposed for Ras (12–14) and has been extended to the hydrolysis of other phosphate esters (15, 16, 20). In this mechanism, GTP abstracts a proton from the attacking water as a preequilibrium step, in contrast with the conventional scheme in which water directly attacks the γ phosphorus of GTP (8, 9). The transition state of the reaction was proposed to be phosphorane-like in this mechanism, although this is not fundamentally required by the proton transfer.

Also in question is the rate-limiting step for Ras-catalyzed GTP hydrolysis. The active site of Ras is not fully formed in crystal structures of complexes with nonhydrolyzable GTP analogs (21, 22). In contrast, RasGAP stabilizes a catalytically competent active site conformation as observed in the crystal structure of the Ras·RasGAP complex in which Ras is bound to the transition state analog GDP·Mg²⁺·AlF₃ (23). Mutational studies show that RasGAP stimulates the GTPase activity of Ras not only by providing a catalytic residue, the “arginine finger” at position 789, but also by stabilizing the catalytically competent conformation of Ras, as is evident from the diminished, but substantial GAP activity of RasGAP in which the arginine finger is mutated (6). On the basis of an empirical bond valence computer simulation study, the active site conformation as observed in the Ras·GDP·AlF₃·RasGAP complex is proposed to be more conducive to catalysis than Ras in the basal, GTP-bound state (24). These experimental and computational results suggest that conformational change is required to confer catalytic competence upon Ras. However, it is not clear whether this conformational step is rate-limiting for hydrolysis. Kinetic studies using fluorescently labeled GTP analogues have been carried out to determine the nature of the rate-limiting step of Ras-catalyzed GTP hydrolysis, but the interpretation of these are inconclusive (25–27).

Knowledge of the transition state and rate-limiting steps of an enzyme-catalyzed reaction is critical to understanding the catalytic roles of the chemical groups in the active site of the enzyme. In the Ras mechanism, interactions between Arg-789 of RasGAP and Gln-61 of Ras with AlF₃ (which mimics the pentacoordinate γ phosphate of GTP in the transition state) are taken as evidence for a tight transition state, in which charge is expected to accumulate on the nonbridge oxygen atoms of the γ phosphate (23). On the other hand, electrostatic interactions with the β nonbridge oxygens and with the β–γ bridge oxygen, which are also observed in the structure, are consistent with a loose transition state. In Ras and other members of the G protein family, chemical steps are closely linked to conformational changes. The mechanistic relationship between these cannot be understood if the actual events associated with the kinetic barriers are unknown.

For enzyme mechanisms in which bond-breaking and bond-making events are partially or fully rate-limiting, measurements of kinetic isotope effects (KIEs) resulting from the use of isotopically labeled substrates can be used to deduce the structure of the transition state. In particular, KIE studies have contributed greatly to knowledge of the transition states for nonenzymatic and enzyme-catalyzed hydrolysis of phosphate monoesters, diesters, and triesters (19, 28, 29). A KIE is defined as the rate at which a light substrate is converted to product, divided by the corresponding rate for a substrate labeled with a heavy isotope. Isotope effects arise from the effect of isotopic substitution on the zero point energy levels of the vibrational modes of the reactant as it proceeds from the ground state to the transition state. Changes in stretching modes, which are directly related to changes in bond order, make the dominant contribution to the primary KIE, although changes in other normal modes may have significant effects on secondary KIEs. A decrease in bond order at the transition state results in a normal isotope effect (>1), whereas an increase causes an inverse isotope effect (<1). The magnitude of the KIE in an enzymatic reaction also depends on the extent to which the chemical step that gives rise to bond order changes is rate-limiting (30). If the chemical step is completely rate-limiting, the observed KIE is equal to the intrinsic KIE associated with the chemical step. However, the intrinsic KIE may be masked if binding or conformational steps are completely rate-limiting.

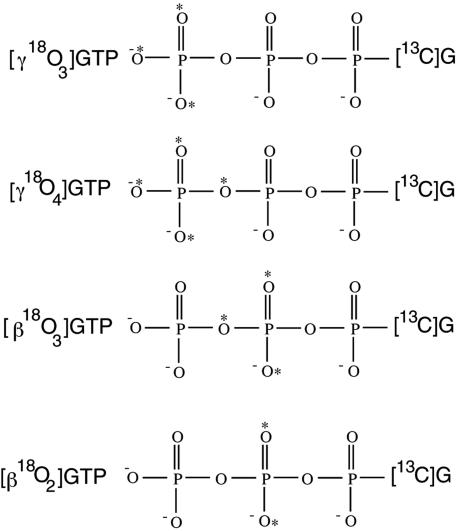
Here, we report the use of ¹⁸O KIEs to deduce the structure of the transition state for Ras-catalyzed GTP hydrolysis conducted in the absence of RasGAP. The experimental scheme inherits the concepts of internal competition, remote labeling and the use of isotope ratio mass spectrometry (IRMS), which were critical to the success of earlier studies on phosphoryl transfer reactions (31, 32). In the internal competition method, unlabeled and labeled substrates undergo the reaction in the same tube and the change in their relative abundance is used to calculate the KIE. We used mixtures of ¹³C-depleted GTP ([¹²C]GTP) and ¹⁸O-,¹³C-labeled GTP substrates that contain ¹⁸O labels at phosphoryl positions of mechanistic interest and ¹³C labels at all carbon positions. The change in the ¹⁸O/¹⁶O ratio at the ¹⁸O-labeled sites of reactant and product is therefore directly proportional to the change in the carbon isotope ratio of these species. To determine the carbon isotope ratios, a reactant or product mixture is delivered by high-pressure liquid chromatography (HPLC) to a chemical reaction interface (CRI), where it is converted by pyrolysis to CO₂, and injected into the IRMS. This analytical system is ideally suited to measure isotope ratios in nonvolatile samples (33–35). We have used these techniques, along with a suite of specifically labeled ¹⁸O-labeled GTP substrates (Fig. 2), to determine the KIEs for Ras-catalyzed hydrolysis of GTP labeled at β and γ nonbridge oxygen atoms, and the β–γ bridge oxygen. Analysis of these data provides direct insight into the structure of the transition state of this reaction.

Fig. 2.

¹⁸O-,¹³C-labeled nucleotides used in this study.

Materials and Methods

Reagents. ¹⁸O-,¹³C-labeled nucleotides were synthesized by using chemical or enzymatic reactions that enable the addition of either P_i or [¹⁸O₄]P_i to the terminal phosphate group of ¹³C-labeled guanine nucleotides. Synthesis of [γ¹⁸O₄]GTP and [γ¹⁸O₃]GTP were performed by using established procedures (36–38). Synthesis and purification protocols for these and for [β¹⁸O₃]GTP and [β¹⁸O₂]GTP are described in Supporting Text and Table 2, which are published as supporting information on the PNAS web site.

Preparation of Substrate Mixtures. High precision in the measurement of isotope ratios on an isotope ratio mass spectrometer can only be achieved when the isotope ratio of the sample is close to natural abundance. Accordingly, substrate mixtures are prepared by mixing [¹⁸O,¹³C]GTP and [¹²C]GTP in a ratio of 0.0118:1 to reconstitute natural abundance of carbon. It was realized later that the carbon isotope ratios of our reaction mixtures were typically 20% higher than the natural abundance, which was attributed to the residual ¹³C level in the ¹³C-depleted GTP. However, the slight enrichment of the sample in ¹³C was not found to compromise the precision with which isotope ratios were measured by HPLC/CRI/IRMS.

Protein Expression and Purification. The cDNA construct encoding residues 1–166 of H-Ras was obtained from Sung-Hou Kim (University of California, Berkeley) and recloned into the pET28a vector (Invitrogen). Overexpressed protein was purified by Ni-affinity and Q Sepharose (Amersham Pharmacia) chromatography. The guanine nucleotide exchange factor used in these studies consists of CDC25^Mm, the C-terminal 285-residue catalytic fragment of mouse CDC25 (39) fused at its N terminus with GST. The plasmid encoding pGEX-2T-CDC25^Mm was obtained from Alfred Wittinghofer (Max Planck Institute, Munich). GST-CDC25^Mm was purified with a glutathione affinity column and chromatography on Q Sepharose.

Preparation of Ras in Complex with [¹⁸O, ¹³C]GTP and [¹²C]GTP. Ras copurifies with bound GDP because of the high affinity of GDP for Ras. It is desirable to remove this endogenous GDP so that the GDP generated from the hydrolysis of the substrate mixture can be used for KIE analysis. For this purpose, Ras is first stripped of GDP and reloaded with a caged GTP analog, hydroxyphenacyl GTP (HPA-GTP), which can be readily displaced with isotopically labeled substrate (37) as described in Supporting Text. The Ras complex with isotopically labeled substrates is used immediately for KIE experiments.

Steady-State Ras-Catalyzed GTP Hydrolysis. A typical reaction mixture consists of 1 mM GTP (0.5 mg/ml), 25 μM Ras (0.5 mg/ml), and 4 μM GST-CDC25^Mm (0.25 mg/ml) in 1 mM MgCl₂/50 mM Tris·HCl, pH 7.5 in a 1-ml volume. GST-CDC25^Mm is included to increase the rate of GTP release from Ras·GTP, which can be as slow as 10^–5 s^–1. The rate of GTP release under the reaction condition is typically ≈10^–2 s^–1, which is much greater than the rate of GTP hydrolysis by Ras and thereby is not expected to affect the observed KIEs. Typically, reactions were carried out for 24 h at 37°C. Substantial conversion of GTP into GDP occurs, whereas spontaneous hydrolysis of GTP is negligible over this period. Reactions were stopped by heating the reaction mixture at 65°C for 10 min.

Sample Preparation for IRMS Measurements. Ion exchange chromatography was carried out by using a 1-ml HiTrap Q column on an AKTA FPLC system (Amersham Pharmacia). A gradient of ammonium acetate from 0 to 1 M in 50 ml was used to separate the reactant (GTP) from the product (GDP). The fractional extent of the reaction was calculated from the peak areas of GTP and GDP. Fractions containing GTP and GDP were collected and ammonium acetate was removed by lyophilization. GTP and GDP were converted to guanosine for IRMS measurement. For this purpose, the nucleotide was redissolved in 100 μl of 20 mM K₂HPO₄ and 1 mM MgCl₂, and 1 μl of alkaline phosphatase (Sigma P5521) was added to the solution. The conversion of GTP or GDP to guanosine was normally complete overnight.

Measurement of Isotope Ratios. Isotope ratio measurements were conducted on a HPLC/CRI/IRMS system, which was described in detail by Abramson et al. (33–35). Guanosine samples were introduced into the HPLC/CRI/IRMS system through a Supelcosil-LC-18 column with an isocratic flow of 5% acetonitrile in water. We determined the isotope ratios for I_p, I₀, and I_s in the same chromatographic run so that instrument drift is canceled out when ratios among these are taken (see Data Analysis). The use of this continuous flow apparatus eliminates the need for offline procedures to convert substrate and product to gas as required by a standard isotope ratio mass spectrometer, thereby reducing the sample requirement for each experiment. Each injection typically contains ≈30 μg of guanosine.

Data Analysis. KIEs were calculated with Eqs. 1, 2, or 3 where R_s and R_p are the relative abundances of the doubly labeled substrate and the ¹³C-depleted substrate in the substrate mixture (R_s) or the product mixture (R_p) and f stands for fractional reaction extent.

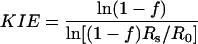[1]

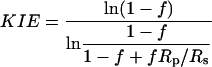[2]

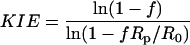[3]

R₀ is the relative abundance at the beginning of the reaction. The isotope ratios (I_s, I_p, and I₀) in the guanosine samples derived from corresponding substrate or product were corrected for the residual ¹³C level in the ¹³C-depleted GTP (I_r) to compute the changes in the relative abundances (R_s/R₀, R_p/R_s, and R_p/R₀). Specifically, R_s/R₀, R_p/R_s, or R_p/R₀ is given by (I_s – I_r)/(I₀ – I_r), (I_p – I_r)/(I_s – I_r), or (I_p – I_r)/(I₀ – I_r), respectively.

Results and Discussion

Measurement and Analysis of KIE Data. Internal competition methods measure the isotope effect on (V/K), which represents the ratio of V_max and K_m (30). We follow standard notation and report KIE as ¹⁸(V/K) in Table 1. The values for individual determinations are available in Supporting Text. Control experiments were carried out by using a nucleotide that is ¹³Cbut not ¹⁸O-labeled. For each experiment, five replicate measurements were taken of I_s, I_p, and I₀. Each triplet of I_s, I_p, and I₀, yielded two KIE values computed either from the ratio R_s/R₀ by equation (1) or the ratio R_p/R₀ by equation (3). ¹⁸(V/K) values obtained by Eq. 1 were averaged separately from those obtained by using Eq. 3. In most experiments, the value calculated by Eq. 1 agrees within one standard deviation with that obtained by using Eq. 3. In the several cases where ¹⁸(V/K) computed by Eqs. 1 and 3 do not agree, the values by Eq. 2 agree with other independent experiments and are included. For experiments in which steady-state reactions were initiated with Ras bound to endogenous GDP, ¹⁸(V/K) values were calculated by Eq. 1 only. The unweighted average of all individual determinations of each isotope effect and its standard deviation are presented in Table 1. The isotope effects in the right hand-most column were corrected for incomplete ¹⁸O labeling by the formula ¹⁸(V/K)_cor = [¹⁸(V/K) – 1]/[1 – ¹⁸(V/K) + ¹⁸(V/K)y], where y is the isotopic purity of ¹⁸O labeling (32).

Table 1. KIEs in Ras-catalyzed GTP hydrolysis.

Isotopomer	No. of determinations	18(V/K) (average)	18(V/K)*
Control†	8	1.0026 (0.0028)	1.0026
[γ18O3]GTP	10	1.0012 (0.0026)	1.0013
[γ18O4]GTP	9	1.0121 (0.0019)	1.0129
[β18O3]GTP	8	1.0186 (0.0025)	1.0194
[β18O2]GTP	6	1.0099 (0.0016)	1.0105
β-γ bridge‡			1.0116
β-γ bridge§			1.0088

^*Corrected for incomplete ¹⁸O labeling.

^†Substrate consists of ¹³C-depleted GTP and GTP containing ¹³C but not ¹⁸O labels.

^‡Calculated as the ratio of ¹⁸(V/K)s in [γ¹⁸O₄]GTP and [γ¹⁸O₃]GTP.

^§Calculated as the ratio of ¹⁸(V/K)s in [β¹⁸O₃]GTP and [β¹⁸O₂]GTP.

The standard deviation among independent determinations is ≈0.2% for all experiments. The observed isotope effect for the control nucleotide, for which no KIE is expected, is 1.0026, with a standard deviation of 0.0028. The isotope effects for the labeled nucleotides are not corrected by this value because the deviation of KIE from unity for the control is not statistically significant. The observed isotope effects in [γ¹⁸O₄]GTP, [β¹⁸O₃]GTP, and [β¹⁸O₂]GTP are highly significant, ranging from 6.5 to 7.7 times their standard error of measurement. The isotope effect in the β–γ oxygen was calculated by the ratio of the isotope effects in [γ¹⁸O₄]GTP and [γ¹⁸O₃]GTP or by that of [β¹⁸O₃]GTP and [β¹⁸O₂]GTP. The respective values of 1.0116 and 1.0088 agree with each other within experimental errors.

Nature of the Rate-Limiting Step for Ras-Catalyzed GTP Hydrolysis. The ¹⁸O kinetic isotope effects observed for Ras-catalyzed GTP hydrolysis depend not only on the structure of the transition state but also on the rate constants of the steps on the reaction pathway (30). This reaction can be described by equation (4), where Ras* refers to a conformational state of the enzyme that is competent to catalyze GTP hydrolysis. The observed KIE is given by Eq. 5, where ¹⁸(V/K)_i is the intrinsic isotopic effect in the chemical step and c_f is the forward commitment of the reaction.

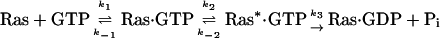[4]

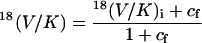[5]

Forward commitment is defined by the ratio of the rate constant of the chemical step (k₃) to the net rate of substrate release from the Ras*·GTP complex. If substrate release from Ras·GTP is slow (small k_–1) or the conformational change from Ras·GTP to Ras*·GTP is rate-limiting (k_–2 is small compared to k₃), forward commitment is significant and KIEs are suppressed. To facilitate the observation of KIEs, we included a guanine nucleotide exchange factor, GST-CDC25^Mm (39) in our reaction mixture to increase k_–1 so that the contribution of slow substrate release to forward commitment was minimized. However, the potential contribution of the conformational step (Ras → Ras*) to the forward commitment remains. The determination of ¹⁸(V/K)_i and c_f can be made only in special cases (40, 41). Here, we are able to arrive at an upper bound for the forward commitment, given the maximum expected value for ¹⁸(V/K)_i in the leaving group as determined from KIE studies of similar enzyme-catalyzed reactions.

It is important to point out that the isotope effect in the β–γ bridge oxygen underestimates the extent of P_γ–O_β–γ bond cleavage at the transition state. The charge that is deposited on the β–γ bridge oxygen due to P_γ–O_β–γ bond cleavage can be delocalized into the two nonbridge oxygens. Accordingly, the P_β–O_β–γ bond order increases, whereas the bond orders of the two P_β–O_nonbridge bonds decrease by the same amount. This point is illustrated in the case of a metaphosphate intermediate when the P_γ–O_β–γ bond is fully cleaved. The β–γ bridge oxygen undergoes a loss of bond order of 2/3 (2 to 4/3), instead of 1. The remaining one-third of the loss in P_γ–O_β–γ bond order is realized in the change in the bond order of the two β nonbridge oxygens (3 to 8/3). Therefore, the isotope effect in [β¹⁸O₃]GTP, in which the β–γ bridge oxygen and the two β nonbridge oxygens are labeled, truly reflects the extent of P_γ–O_β–γ bond cleavage and is hereafter referred to as the isotope effect in the leaving group.

The isotope effect of 1.0194 in the leaving group is significant, when compared with the KIE of 1.03 observed for the enzymatic hydrolysis of p-nitrophenyl phosphate by mutants of protein tyrosine phosphatase (42–45). If the latter is taken as a reference value for ¹⁸(V/K)_i, then we can conclude that the forward commitment for Ras is ≈0.5 and the isotope effects observed in other oxygen positions are also at least 60% of their intrinsic values. It is also possible that ¹⁸(V/K)_i is in fact ≈1.02 and the forward commitment is close to zero. A small forward commitment indicates that chemistry is largely, if not completely, rate-limiting and suggests that the catalytically competent conformation of Ras is in rapid equilibrium with the noncompetent conformations (basal state) before hydrolysis occurs. This result does not contradict the notion that the conformational step contributes significantly to the rate of GTP hydrolysis. The free energy of Ras*·GTP, which dictates the population of this activated species, can still be a significant, even dominant, component of the apparent activation free energy of the overall hydrolysis reaction.

The Transition State of Ras-Catalyzed GTP Hydrolysis. The transition state of Ras appears to have significant metaphosphate character. KIEs for the leaving group (1.0194) and the γ nonbridge oxygens (1.0012) (Table 1) are similar to the corresponding primary and secondary isotope effects for the nonenzymatic and enzymatic hydrolysis of phosphate monoesters, which have loose, metaphosphate-like transition states (17, 18). Isotope effects for the leaving group are ≈1.02 in nonenzymatic (46) and protein phosphatase-catalyzed hydrolysis of p-nitrophenyl phosphate (42–45). If the general acid that protonates the leaving oxygen atom is mutated, the isotope effects increase to 1.03 in several of the protein phosphatases (42–45). The secondary isotope effect in the γ nonbridge oxygens of GTP reflects the change in bond order of these atoms in the transition state relative to the ground state. Secondary isotope effects observed for the hydrolysis reactions of phosphate monoesters range from slightly inverse (0.994) to slightly normal (1.003) (42, 43, 45, 46). The agreement between the KIEs observed for Ras and the corresponding KIEs for hydrolysis of phosphate monoesters provides strong evidence that Ras-catalyzed GTP hydrolysis follows a hydrolytic pathway typical of dianionic phosphate monoesters. The transition state is loose, featuring extensive bond cleavage to the leaving group but little change in the bond order of the γ nonbridge oxygen atoms.

It has been pointed out that a secondary isotope effect near unity, which is observed in the hydrolysis of phosphate monoesters and is reported for Ras-catalyzed GTP hydrolysis here (Table 1), is consistent with both a concerted mechanism with a loose transition state and a substrate-assisted mechanism (16). A large and inverse secondary isotope effect is expected if a metaphosphate has a bond order of 5 as depicted in Fig. 1 A. The discrepancy with the observed values was rationalized by a resonance structure of metaphosphate that has a bond order of 4 (47, 48) and by the loss of O_γnonbridge–P_γ–O_β–γ bending mode in the transition state (28). The secondary isotopic effect of unity is not consistent with the substrate-assisted mechanism as shown in Fig. 1D. However, it could result from two compensating isotope effects in a modified substrate-assisted mechanism, in which the attack of the hydroxide on the monoanionic γ-phosphoryl group is concerted with respect to cleavage of the bond to the leaving group. The proton transfer step is expected to show an inverse equilibrium isotope effect of 0.984 (49), which can be counterbalanced by a normal isotope effect of 1.016 (1.000/0.984) due to the weakening of P_γ–O_nonbridge bond resulting from nucleophilic attack by water. Therefore, the KIE in [γ¹⁸O₃]GTP cannot be used to distinguish between the two mechanisms. However, the large KIE in [β¹⁸O₃]GTP that indicates substantial bond cleavage to the leaving group is strong evidence for a loose transition state, but is not typical for a tight transition state (50).

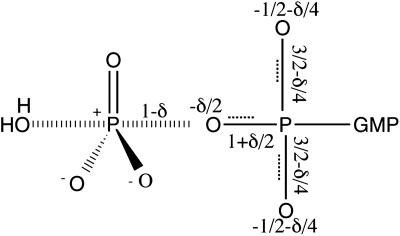
Ras Redistributes Charge in the Transition State. The charge distribution on the β–γ bridge oxygen and the two β nonbridge oxygens can be inferred from the isotope effects in these atoms. The charge that is displaced by the cleavage of the P_γ–O_β–γ bond depends on the value of the intrinsic isotope effects (Fig. 3). Part of this charge is delocalized into the two β nonbridge oxygen atoms, which gives rise to the KIE in [β¹⁸O₂]GTP. As discussed above, the total change in the bond order of the two P_β–O_nonbridge bonds is expected to be equal to one-half of the change in the bond order of the β–γ bridge oxygen (1/3 versus 2/3 in the case of a metaphosphate intermediate) for uncatalyzed GTP hydrolysis. However, the observed isotope effect of 1.0105 in [β¹⁸O₂]GTP (Table 1) is roughly equal to the isotope effect in the β–γ bridge oxygen (1.009 or 1.012 by two independent determinations in Table 1). The disproportionate KIE effect in [β¹⁸O₂]GTP cannot be explained by the loss of the O_β-nonbridge–P_β–O_β–γ-P_γ torsion mode, which would add to the dominant contribution from the decrease in bond order. The KIE in the β–γ bridge oxygen also includes contributions from the loss of O_β–γ–P_γ–O_γ-nonbridge bending modes and the reaction coordinate as well. Although it is difficult to determine the magnitudes of these contributions, it is safe to say that the effect from the loss of a bending mode is larger than that of a torsional mode. Instead, the equality of the two isotope effects probably reflects a disproportionate reduction in the bond orders of the two β nonbridge oxygen atoms as suggested above. That is, half of the change in P_γ–O_β–γ bond order is realized in the two P_β–O_nonbridge bonds. Correspondingly, one-half, rather than one-third, of the charge deposited on the β–γ bridge oxygen is transferred to the two β nonbridge positions. Thus, although Ras does not fundamentally change the transition state structure with respect to the bond order of the γ nonbridge oxygens, it does change the distribution of charge among the β–γ bridge oxygen and the two β nonbridge oxygens. The transition state structure that is consistent with the KIEs for Ras-catalyzed GTP hydrolysis is depicted in Fig. 3.

Fig. 3.

Transition state structure for Ras-catalyzed GTP hydrolysis as revealed by observed isotope effects. A charge δ (due to partial or full cleavage of the O_β–γ–P_γ bond) is delocalized into the β phosphorus system. δ lies between –1 and –0.67 (0.02/0.03 = 0.67), which corresponds to an intrinsic KIE of 1.03, the maximum value observed for hydrolysis of phosphate monoesters, or of 1.02, the observed KIE, respectively.

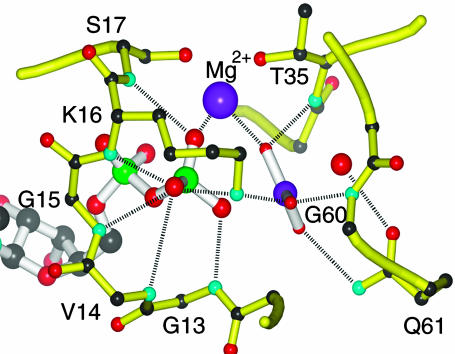
Stabilization of a Metaphosphate-Like Transition State by Ras. Elucidation of the transition state structure affords a better understanding of the mechanism by which Ras catalyzes GTP hydrolysis. Upon approaching the transition state as depicted in Fig. 3, the negative charge on the β–γ bridge oxygen and the two β nonbridge oxygens increases. Interactions of Ras with these three oxygen atoms thereby become stronger and afford preferential stabilization of the transition state. As shown in Fig. 4, Ras interacts extensively with the β–γ bridge oxygen and the two β nonbridge oxygens in the crystal structure of both the ground state Ras·GppNHp (21) and the Ras·GDP·AlF₃·RasGAP (23), which is proposed to mimic a transition state complex. The majority of these interactions involve residues 13–17 in the P-loop, a glycine-rich motif that is conserved in most nucleotide-binding proteins (51, 52). On the other hand, the KIE data indicate that the charge on the γ nonbridge oxygen atoms is not substantially altered in the transition state. For the modified substrate-assisted mechanism, this charge is even expected to decrease, because the positive charge of the proton can be only partially offset by the negative charge displaced by P_γ–O_nonbridge bond cleavage. Therefore, protein interactions with γ nonbridge oxygens are not expected to promote catalysis. In fact, fewer interactions are observed of Ras with the γ nonbridge oxygens of GTP analogs or with AlF₃ than with the β phosphate oxygen atoms. We propose that the residues interacting with γ phosphoryl group, including Gln-61, which is particularly important for catalysis, serve to position the γ phosphoryl group with respect to the protein and the attacking water (23).

Fig. 4.

Interactions of Ras with the transition state analog, GDP·AlF₃, from the crystal structure of Ras·GDP·AlF₃·RasGAP (PDB ID 1WQ1). The functional groups of Ras that contribute to interactions with the pro-S β nonbridge oxygen include the main chain NH groups of Val-14, Gly-15, and Lys-16, as well as the Nζ of Lys-16. The main chain NH of Ser-17 and Mg²⁺ interact with pro-R oxygen. The amide hydrogen of Gly-13 forms a strong hydrogen bond with the β–γ bridge oxygen. Interactions between Ras and γ nonbridge oxygens include Mg²⁺, the main chain NH of Thr-35 and Gly-60, the side chain of Gln-61, and the side chain of Lys-16.

Spectroscopic and computational studies also suggest that Ras promotes a loose transition state for GTP hydrolysis. Fourier transform IR experiments show that the asymmetric stretch of 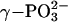of Ras-bound GTP shifts to higher wave number, whereas the asymmetric stretch of 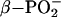shifts down 14 cm^–1 relative to the absorption of free GTP in solution (37, 53, 54). The frequency shifts reveal that the interactions of Ras with GTP decrease the bond order of 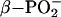and increase the bond order of 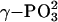. Valence bond calculations (24) indicate that the interactions between the Ras active site and the γ nonbridge oxygens are anticatalytic, and that the catalytic effect of Ras comes mainly from the stabilization of negative charge at the β phosphate by the positive electrostatic potential of the protein. Computed activation free energies indicate that Ras and Ras-GAP more efficiently stabilize a metaphosphate-like than a phosphorane-like transition state (24).

Conclusions

Isotope effects afford a detailed description of the transition state of Ras-catalyzed GTP hydrolysis. An isotope effect of 1.0194 in leaving group reveals that chemistry is largely, if not completely, rate-limiting. The isotope effects in γ nonbridge oxygens (1.0013) and leaving group (1.0194) also agree well with the corresponding isotope effects in uncatalyzed and enzymatic hydrolysis reactions of dianionic phosphate monoesters, providing strong evidence that Ras-catalyzed GTP hydrolysis has a similar transition state. The isotope effect in the two β nonbridge oxygens reveals that Ras changes the distribution of the charge at the transition state between β–γ bridge oxygen and the two β nonbridge oxygens. The two β nonbridge oxygens receive half, instead of one third, of the charge as expected for an uncatalyzed reaction. We propose that Ras catalyzes GTP hydrolysis by electrostatically stabilizing the charge on β–γ bridge oxygen and the two β nonbridge oxygens in the transition state. The interactions between Ras and the γ phosphoryl group likely serve to position γ phosphoryl group with respect to protein and the attacking water.

The work described here serves as a starting point for more extensive exploration of catalytic mechanisms in regulatory GTPases, particularly GAP activation and the role of the endogenous “arginine finger” present in the active sites of heterotrimeric G protein α subunits. The use of specifically ¹⁸O-labeled nucleotide triphosphates as described here, coupled with modern sensitive isotope detection methods, sets the stage for mechanistic analysis of nucleotide triphosphate hydrolases, many of which play important roles in biological regulation and chemo–mechanical energy transduction.