Significance
Total internal reflection microscopy is a low noise, minimally invasive, near surface particle-tracking technique widely used in physics and biology for the precise investigation of surface forces and interactions and fluorescent imaging of live cells and single molecules. In total internal reflection microscopy (TIRM), a particle is tracked, with nanometer precision, by the intensity of light it scatters from the evanescent field of a totally internally reflected beam of light. The present work introduces the first to our knowledge in situ, absolute position calibration method for TIRM (and total internal reflection fluorescence microscopy), which has the potential to greatly expand its measurement capabilities and bring quantitative results to studies using this technique.
Keywords: TIRM, TIRFM, optical tweezer, particle tracking, calibration
Abstract
A noninvasive, in situ calibration method for total internal reflection microscopy (TIRM) based on optical tweezing is presented, which greatly expands the capabilities of this technique. We show that by making only simple modifications to the basic TIRM sensing setup and procedure, a probe particle’s absolute position relative to a dielectric interface may be known with better than 10 nm precision out to a distance greater than 1 μm from the surface. This represents an approximate 10× improvement in error and 3× improvement in measurement range over conventional TIRM methods. The technique’s advantage is in the direct measurement of the probe particle’s scattering intensity vs. height profile in situ, rather than relying on assumptions, inexact system analogs, or detailed knowledge of system parameters for calibration. To demonstrate the improved versatility of the TIRM method in terms of tunability, precision, and range, we show our results for the hindered near-wall diffusion coefficient for a spherical dielectric particle.
Total internal reflection microscopy (TIRM) is a near-field optical imaging (1, 2) and particle-tracking (3) technique with nanometer resolution in the vertical dimension that allows for the detection of surface forces down to the subpiconewton regime. In TIRM, a particle is tracked by the intensity of light it scatters from the evanescent field of a totally internally reflected beam. Because the intensity of an evanescent field drops off exponentially with distance from the interface, z, that is,
| [1] |
with typically 100 nm or less, the excitation region is thin and selective, and the signal-to-noise ratio inherently high, so sensing can be done with very low laser powers (∼1 mW) noninvasively and nondestructively. As such, TIRM is widely practiced in the biological sciences (2, 4–10) and a popular method for imaging and particle tracking in rapidly growing fields such as protein-folding measurements (11), single-molecule studies (12–14), and investigations of the secretion mechanisms of cells (15–18).
TIRM’s attraction for physical scientists lies mainly in its resolution. It is among the most sensitive methods for tracking motion perpendicular to a surface. By measuring the object’s height probability density function in thermal equilibrium and inverting the Boltzmann distribution, the potential energy profile can easily be obtained (3). In this way, TIRM has been used with good success in photonic force microscopes (19–22) to measure electrostatic double layer, van der Waals, optical, and critical Casimir forces acting on micrometer-sized particles (23–27).
Most of these measurements, in biology and in physics, stand to benefit greatly from quantification of a tracked particle’s absolute position, but currently proceed uncalibrated out of necessity. The intensity of the light scattered by the probe particle as a function of height is essentially unknown and assumed to follow the exponential profile in Eq. 1 with the decay length calculated from the geometry of the setup. In this article, we make the majority of our comparisons against this class of experiments.
Significant past efforts in calibrating the evanescent scattering intensity profile have gone in two main directions. The first replaces the dynamical experimental system with a carefully fabricated, static calibration standard that mimics experimental parameters but has known height values (28–31). The accuracy of this calibration depends on the faithfulness of the reproduction. More promising is the category of in situ calibration methods. However, there are limited means for the precise and noninvasive positioning of micrometer-sized probes (11). Meanwhile, diffusive dynamics of colloids have been exploited successfully to provide an independent height reference used to calibrate scattering intensity (32–35). However, this approach not only presupposes the availability of large amounts of time-resolved data, but also demands precise knowledge of several difficult experimental parameters such as local temperature, viscosity of the fluid, and size and geometry of the particle.
Without an accurate, accessible, in situ calibration available, the TIRM method has so far found limited use beyond the simplest, most well-approximated systems (5). For example, in measurements over a large range of distances from the surface, requiring accurate knowledge of absolute positions, involving inhomogeneous media, nonspherical particles, or highly reflective materials such as metals, the potential of the technique has not been fully realized (36–38).
We propose an optical tweezer (39)-based calibration that directly measures the intensity–height profile for a given scatterer and TIRM configuration and can be performed quickly and in situ. The optical tweezer, or single-beam gradient optical trap, holds the scatterer in three dimensions at a fixed position relative to the beam focus (40). By shifting the focus, the particle can be made to approach the surface in precisely measured steps. The scattering intensity is monitored until further steps produce no change in the signal, indicating that the bead has reached the surface.
In Experiment, we discuss the experiment in detail, including the setup. A few straightforward changes made to the usual TIRM setup enable our in situ calibration. First, the collection objective is replaced by a high numerical aperture (NA) water-immersion objective capable of 3D optical tweezing of a micrometer-sized dielectric particle. Second, the micrometer vertical stage on which the objective is mounted is fitted with closed-loop piezo controls for finely calibrated focus adjustment. And finally, the top surface of the glass sample slide is coated with a quarter-wavelength thick layer of evaporated glass to cancel the optical tweezer reflected beam. By opening and closing an iris located in the back focal plane of the objective, we adjust trap laser power and the NA and can quickly switch between 3D optical tweezing (calibration) and 2D optical trapping (measurement) modes of operation.
In Data, we discuss the data-taking procedure and detailed considerations that make this calibration possible. Because the correspondence of piezo step size to particle displacement is an important prerequisite in our experiment, we take steps to measure and eliminate distortions in the particle’s trapping potential energy profile due to reflections or the presence of a thick electrical double layer. Data are presented that demonstrate the necessity and effectiveness of an antireflection coating as well as the addition of salt into the suspending fluid.
In Results, we demonstrate the effectiveness of the proposed calibration method for absolute position TIRM with two main results. The first experiment measures intensity–height calibration curves for several evanescent field penetration depths ranging from 90 nm to 270 nm taken with the same probe particle. The error on β determined in this way does not diverge as the angle of incidence approaches the critical angle as with traditional methods, but rather remains below 1% in all fits. A key and yet unexplored feature of TIRM sensing techniques is the ability to freely tune (even in real time) the length-scale parameter β to optimize for precision or range. Our demonstrated ability to measure, accurately and in situ, the β parameter should therefore greatly improve the versatility and applicability of the TIRM technique.
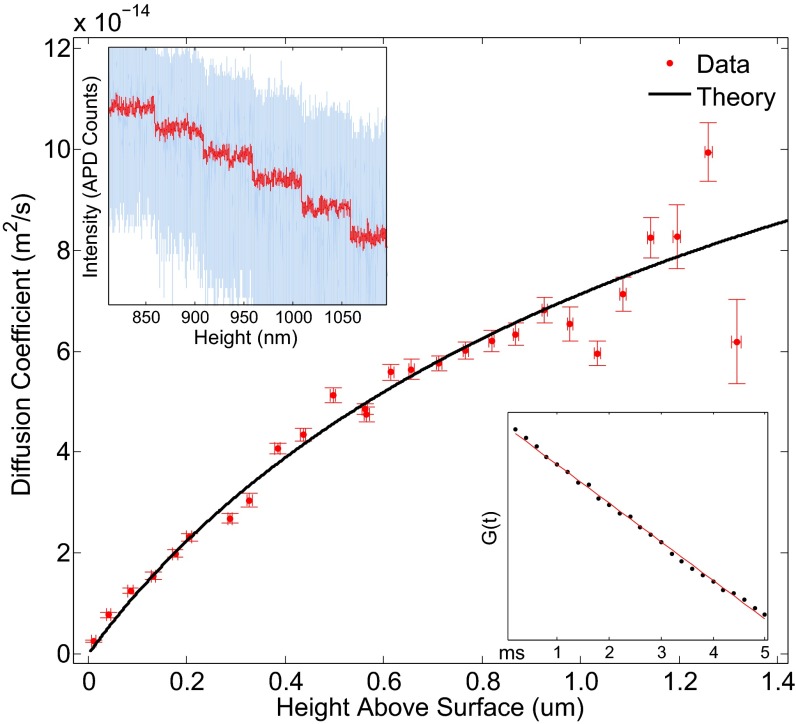
To prove this extended versatility, along with the calibration’s accuracy, we also perform experiments in which we fix the angle of incidence such that the penetration depth is about 300 nm and measure the hindered perpendicular diffusion coefficient of a 3-μm glass bead in steps of 50 nm out to a distance of about 1.2 μm. Our results agree with hydrodynamic theory throughout, and are, to our knowledge, the longest-range and most accurate measurement of hindered near-wall diffusion using TIRM.
Experiment
Setup.
In our experiment we use plain glass spheres with a density of 2.0 g/cm3 and a nominal diameter of 3 μm (Corpuscular; C-SIOs-3.0). The beads come suspended in deionized water and are diluted by a factor of 100 and allowed to equilibrate at room temperature before being loaded into the sample chamber. The chambers have thicknesses of 15–20 μm for use with a short working-distance objective and are fabricated by pressing two strips of sealing film (Solaronix Meltonix 1170-25) between a no. 1.7 coverslip and a glass slide and heating to 120 °C for 3–4 h in an oven. The chambers are open on two sides so that the samples may be loaded by capillary action of the fluid.
The antireflection (AR) coating, when it is applied, is deposited onto the top surface of the glass slide via plasma enhanced chemical vapor deposition (PECVD). It consists of a quarter-wavelength thick layer of evaporated SiO2, with index 1.45, which closely approximates the geometric mean of n = 1.42 for glass (n = 1.52) and water (n = 1.33).
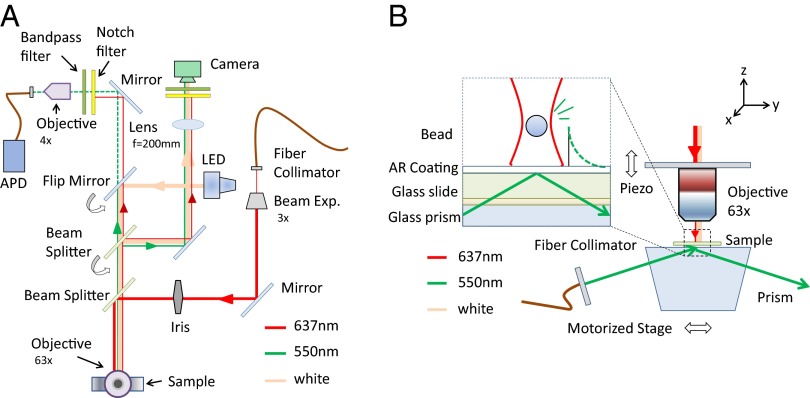
Fig. 1 shows the optical setup; a top–down view and a side view are provided. Three light sources illuminate our sample. The collimated output from a 637-nm diode laser (Thorlabs LP637-SF70) serves as our single-beam optical trap. It is expanded and then focused through an objective onto the sample surface. The evanescent wave used for positional sensing is generated by total internal reflection of a 550-nm laser source (NKT Photonics SuperK) at the lower water–glass boundary of the sample chamber. A polarizer and a half-wave plate are used to control the polarization of the 550-nm source. p polarization (or transverse-magnetic polarization) was chosen for our experiments (41) and the scattered light was detected without a polarizer. Finally, for visualization and positioning, a white light-emitting diode provides bright-field illumination of the sample surface over our 50-μm field of view.
Fig. 1.
(A) Top–down view of the total internal reflection microscopy (TIRM) setup with the trap, scattered, and illumination paths denoted with red, green, and yellow lines, respectively. A 45° mirror above the 63× objective used to direct the beam downward onto the sample surface is not shown. (B) Side view of the TIRM setup. Inset shows zoom in of a measured bead with the optical trap (red) and evanescent field profile (green) superimposed.
During the experiment, our sample slides rest on a 60° prism made of BK7 glass with index-matching fluid in between. The prism is mounted on a two-axis motorized translation stage (Thorlabs LNR50S) that controls lateral positioning of the sample with micrometer precision. A vertical translation stage (Thorlabs MAX301) with closed-loop piezo electronics positions the objective with better than 5 nm precision. The vertical travel range is 4 mm manually and 20 μm by piezo.
We use a water immersion objective (Leica 63× NA 1.25) to avoid the detrimental effects of spherical aberration introduced by the immersion oil and aqueous suspension fluid index mismatch (42). This also ensures that a vertical step in the piezo motor corresponds to an equal magnitude displacement of the optical trap focus in our sample fluid.
The same objective collects the photons scattered by a single glass bead from the evanescent sensing field. The scattered light, after traversing bandpass filters, is focused by a 4× objective onto a multimode optical fiber and fed into a photon counter [Micro Photon Devices PDM avalanche photodiode (APD)]. The photon-counting interval can be set with a function generator in combination with a pulse counter (National Instrument PCI-6602) and in this experiment ranges from 200 μs to 1 ms. The diameter of the multimode fiber core is 100 μm, which sets the size of the collection area on the sample surface, measured with a stuck bead, to be about 6 μm in diameter. Outside this area, the extinction is nearly complete, with counts at background levels. Alignment is performed before each experiment to center the optical trap in the collection region.
Data.
We observe that the single-beam gradient optical trap (39) was sufficient to lift a 3-μm diameter glass bead in water at powers as low as 20 mW behind the objective. Because in this experiment gravitational and radiation pressure forces act in the same direction, the bead, as expected, is trapped axially slightly below the focus of the beam (40). The 550-nm laser source, used to generate the evanescent field for sensing near the glass–water interface, is kept at relatively low power (less than 1 mW at a spot size of 300 μm) to prevent perturbation of the optical field and optical forces acting on the bead. Background counts, taken with the bead held far (at least 2 μm) from the glass–water interface, are mostly due to scattering of the evanescent field by impurities on the glass slide and contribute ∼15–20 photon counts per millisecond, resulting in a signal-to-noise ratio typically better than 100 for our experiments.
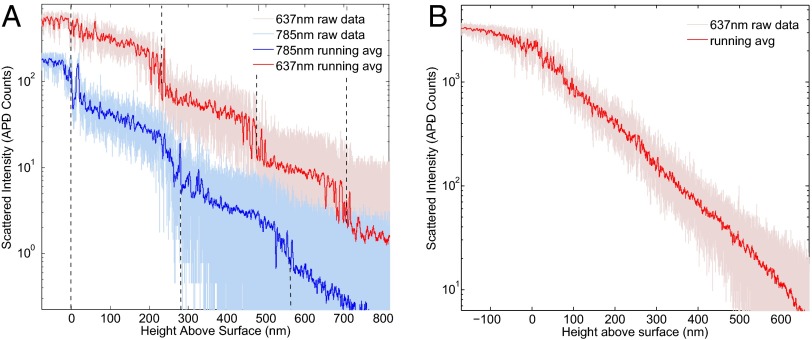
The particle absolute position as a function of scattering intensity is determined as follows: The background measurement is taken, and then the bead is lowered in precisely measured steps toward the surface and the scattered intensity is monitored until contact of the bead with the surface is made. Two abrupt changes in the collected signal are observed at the bead–surface contact point (Fig. 2). First, the intensity becomes constant with further piezo steps, and second, the variance in measured counts decreases and approaches Poisson statistics. This decrease in variance is due to the fact that the bead is no longer diffusing because it is in contact with the surface. We use these features to find the location of the surface and therefore the absolute position of the bead. Because the ability of the bead to approach the surface is limited by the presence of a strong electrical double-layer force (23, 43), NaCl is introduced into the sample fluid at a minimum concentration of 0.01 M in a typical calibration scan. The effects of salt concentration on the measured intensity profile are further discussed below.
Fig. 2.
Plots of measured scattered light intensity vs. height for a 3-μm bead above the surface of a glass microscope slide. Red: Using a 637-nm wavelength optical tweezer. Blue: Using a 785-nm wavelength optical tweezer. (A) No AR coating: The step-like behavior is due to formation of a standing-wave component in the optical trap due to reflection from the glass–water interface. The plots are shifted vertically for clarity. (B) AR coated: The reflection is eliminated and the bead is able to step smoothly toward the surface.
AR Coating.
Optical tweezing near a dielectric boundary suffers from a known complication due to interference caused by a weakly reflected backward-traveling wave (36, 44). Therefore, even as the focus of the optical tweezer shifts, the interference fringes remain fixed relative to the location of the surface, resulting in step-like behavior of the trapped particle at regular intervals (45). The effect of the standing-wave modulation of our optical trap, despite the relatively low index contrast and reflectivity (∼0.4%) at the water–glass interface, can be observed in our data (Fig. 2A). We further confirm the effect is optical by changing the wavelength of the trapping laser from 637 nm to 785 nm. The spacing of the fringes is measured to increase 21 ± 2%, which agrees with the theoretical prediction of 23%.
To overcome this complication we use the previously described AR coating made of a quarter-wave layer (110 nm thickness) of SiO2, which reduces by more than a factor of 10 the standing-wave modulation of the optical tweezer while still maintaining the glass surface’s chemical and electrical properties.
The intensity vs. height profile measured for a 3-μm glass sphere above an AR-coated glass surface is shown in Fig. 2B.
Salt Concentration.
Plain glass beads in deionized water above a glass substrate exhibit strong electrical double-layer repulsion because both surfaces acquire a negative charge upon contact with the fluid. This electrostatic repulsion is partially screened by a mobile layer of positively charged counter ions whose thickness (characterized by the Debye length) depends upon the concentration of dissolved electrolytes and can be hundreds of nanometers in extent in low-molarity aqueous solutions (46). In the case where the Debye length and separation (z) are small compared with the radius of the particle, the potential profile of the electrical double-layer interaction is well approximated by a decaying exponential (47)
| [2] |
where A is a constant that depends on the surface potentials and geometries of the interacting bodies (23, 48) and can be quite large in the case of glass in water, and the Debye length
| [3] |
is determined by the permittivity of the fluid and the concentration of electrolyte species in with valency , where is the Avogadro constant.
As we lower the glass bead held in our optical tweezer in steps toward the glass surface, interaction of their double layers can not only disturb the equilibrium position of the sphere relative to the optical tweezer focus, but also in some cases altogether prevent the sphere from coming into contact with the surface.
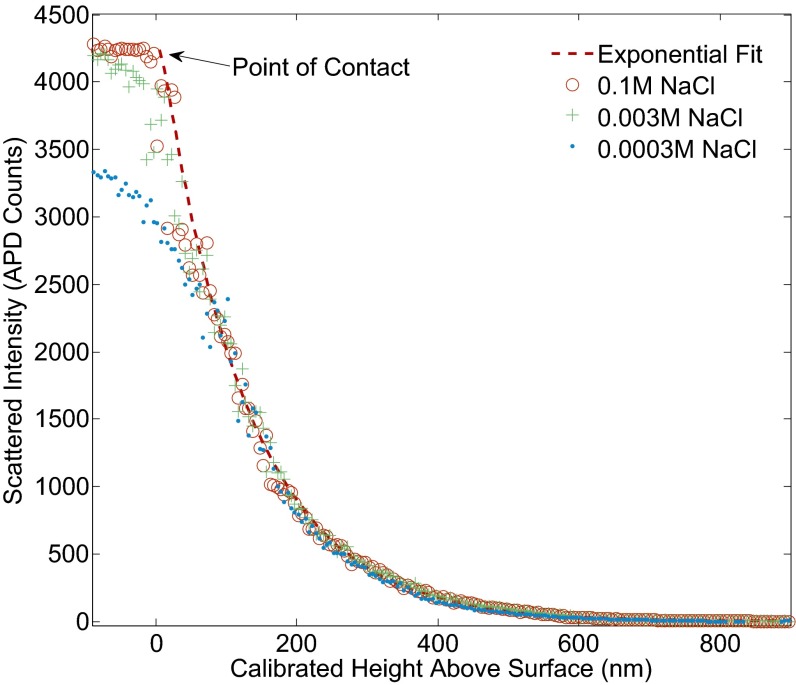
Fig. 3 illustrates this effect. In the presence of a strong double layer, as the trapping beam focus moves toward the surface, the bead does not follow. In the data, this manifests as lower than expected APD counts. However, by increasing electrolyte concentration, by the addition of NaCl to the colloidal mixture, the double layer is thinned and its influence diminished until the resulting intensity–height curve is similar to what one would expect from a hard-wall potential. By examining the shape of the curves as a function of ion concentration, we determined 0.01 M to be a reasonable lower bound on the required salt concentration for an accurate calibration. As our piezo has precision better than 5 nm, we estimate that the contact point determined in this way has an uncertainty less than 10 nm.
Fig. 3.
Intensity–height curves obtained for the a 3-um diameter bead in water for various NaCl concentrations (corresponding Debye lengths: 1 nm, 5 nm, and 20 nm). The blue curve shows a condition of insufficient screening: Despite the optical tweezer focus moving beneath the surface of the glass, the negatively charged bead is repelled electrostatically at close separations and unable to actually approach the negatively charged surface. Green and red curves: Additional salt brings calibration curves closer to the ideal exponential behavior.
Results
To demonstrate the utility of our calibration method we present two results, obtained with 3-μm diameter glass beads optically trapped in water above a glass surface. The first result (Fig. 4) shows our method’s sensitivity to changes in angle of incidence of the totally internally reflected (550 nm) beam. The second result (Fig. 5) demonstrates simultaneous calibration as well as high spatial and temporal resolution particle tracking via a highly accurate, long-range measurement of the hindered near-wall diffusion coefficient.
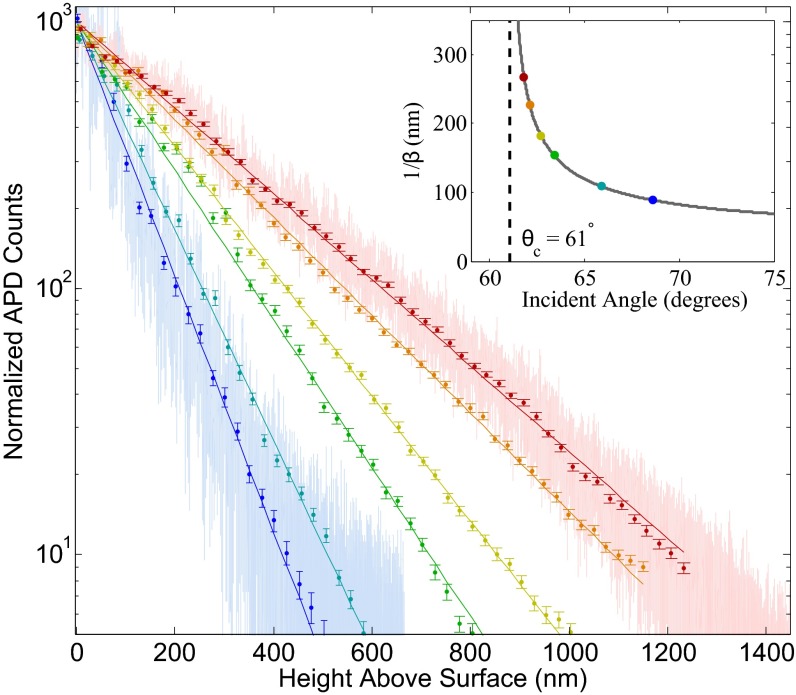
Fig. 4.
Normalized scattered intensity profiles as a function of height for a 3-μm diameter SiO2 bead in water as angle of incidence of probe beam is varied. Fitted decay lengths of the evanescent field intensity are 90.8 nm, 110.6 nm, 115.6 nm, 159.9 nm, 185.2 nm, 236.4 nm, and 268.9 nm, corresponding to angles of 68.6°, 65.9°, 63.4°, 63.3°, 62.7°, 62.1°, and 61.8°, respectively. The error on all fits is less than 1%. The critical angle is 61.0° for the system. For clarity, raw data are shown for the longest and shortest decay length measurements. Inset plots color-coded decay lengths (as measured) on the curve .
Fig. 5.
Measured diffusion coefficient as a function of height for motion in the normal direction. Temperature is assumed to be room temperature (22 °C). Fitted particle radius is (1.26 ± 0.02) μm. Top Left Inset shows raw scattered intensity data (blue) and its moving average (red), showing 50-nm piezo steps. Bottom Right Inset shows example autocorrelation function (black circles) and linear fit (red line) in the intermediate time (diffusive) regime.
It should be noted that even in a system involving only the low-index contrast materials glass and water, multiple reflections coupled with the bead’s anisotropic scattering of light may still result in small distortions of the intensity–height profile from exponential (29). Although our in situ calibration technique is capable of measuring and quantifying these distortions, in our case, they are muted by the presence of the AR coating, which, although designed for the trap wavelength of 637 nm, still works to reduce normal incidence reflectivity at the probe wavelength of 550 nm by more than fivefold. Considering this, we fitted our results in this model system to pure exponentials.
Calibrated Evanescent Field Profile.
The decay-length of the evanescent field used for positional sensing depends upon the angle of the incident beam and diverges as the angle approaches the critical angle (49). The functional form of β vs. angle of incidence is
| [4] |
As it is difficult, in typical TIRM experiments, to determine the angle of incidence with precision better than 0.5° (16, 28, 50), uncalibrated TIRM measurements, even in systems with well-behaved exponential intensity–distance relations, suffer from growing uncertainty in the β parameter. For example, assuming the typical quoted index of refraction for glass slides of 1.52 ± 0.01 and a 0.5° uncertainty in angle, at of 150 nm, the uncertainty in β is ∼13%. For a bead at a nominal height of 400 nm from the surface, this translates into an uncertainty of about 50 nm from the determination of β alone. As this error is systematic to the measurement, it cannot be reduced by increasing integration or data collection time. At of 250 nm, the uncertainty becomes even more dramatic (∼35%), corresponding to an uncertainty of 140 nm at a bead height of 400 nm.
As we mentioned in the Introduction, one major advantage of the TIRM technique over other high-precision positional sensing techniques is the experimenter’s ability to tune desired sensitivity against desired range by changing the parameter. This ability is lost in a typical uncalibrated TIRM experiment, where evanescent-field decay lengths are usually kept to around 100 nm or below to ensure a correct estimation of the β parameter.
Fig. 4 demonstrates precise and accessible tuning of the decay-length parameter to values between 90 and 270 nm, spanning the range from that of a typical TIRM experiment to the upper limit of the validity of the exponential–intensity profile (41). The scans took approximately 2 min each and are fitted to pure exponentials according to the least-squares method. The error on the β parameters does not exceed 1% on any fit and can be further improved with increased integration time.
Wall Effects on Diffusion Coefficients.
A sphere in fluid diffusing close to a planar surface will experience increased viscous drag compared with its motion in the bulk. This increased drag force manifests in the Brownian dynamics of the particle as reduced diffusion. In particular, the parallel and perpendicular diffusion coefficients of a sphere of radius R at height z above a substrate calculated using hydrodynamic theory are (51, 52)
| [5] |
| [6] |
where and .
The exact dependence of the diffusion coefficients on z has been validated by experimenters with varying methods but overall success (53–56). As such measurements require very high temporal and positional resolution, for motion perpendicular to the planar surface, TIRM has more than once been the particle-tracking technique of choice (36, 50, 57–59). In these measurements, however, TIRM has historically fallen short of the holographic, interferometric methods of particle tracking. Without a reliable calibration scheme, errors in absolute position are large and the measurement range is limited. Existing diffusion coefficient measurements based on TIRM do not extend beyond several hundred nanometers from the surface and either are sparse or systematically disagree with hydrodynamic theory.
Here, we perform a simultaneous calibration and particle-tracking experiment where a 3-μm diameter glass sphere held by an optical tweezer is lowered in steps of 50 nm toward the glass surface in an evanescent field with a decay length of about 300 nm. At each piezo position, the scattered field intensity is monitored for 20 s with a temporal resolution of 200 μs. The average intensity at each point is used to build the intensity–position calibration curve, and the full time series, converted to positions, is used to generate the autocorrelation function.
The position autocorrelation function for a particle undergoing damped Brownian motion in a harmonic oscillator potential (formed by the optical trap) can be derived, for instance, via a simple Langevin equation (60, 61). For overdamped systems (such as ours) where the particle is weakly trapped in a viscous fluid, the autocorrelation function takes on a simple analytical form (60)
| [7] |
where t is the time delay between two measurements of particle position, is the resonant frequency of the trap, , and is the Stokes drag coefficient divided by mass. In the limit of very small t, that is, at times shorter than the momentum relaxation time for the sphere (in our case around 1 μs), the motion of the particle is ballistic and the autocorrelation function is quadratic. In the limit of large t, at t > 20 ms, the autocorrelation function reflects that of an overdamped harmonic oscillator and is a decaying exponential. At intermediate timescales, the motion resembles that of a freely diffusing particle, and the autocorrelation can be approximated by a linear function,
| [8] |
whose slope is the diffusion coefficient . This dependence is shown in Fig. 5, Inset, which allows us to extract via a linear fit of the particle’s autocorrelation function at t between 200 μs and 5 ms. For a more detailed description of the data analysis see SI Appendix.
Fig. 5 shows the diffusion coefficient as a function of height obtained in this manner, which agrees well with predictions from hydrodynamic theory. The measurement that produced these data took a total of 20 min and spans the distance range from a few nanometers to 1.2 μm above the glass surface.
As the trapping power was measured to be 40 mW behind the objective, we assume negligible heating of the fluid and particle (62). The fitted radius of the bead assuming the measured room temperature of 22 °C is 1.26 ± 0.02 μm.
Precise Measurement of Bead Radius.
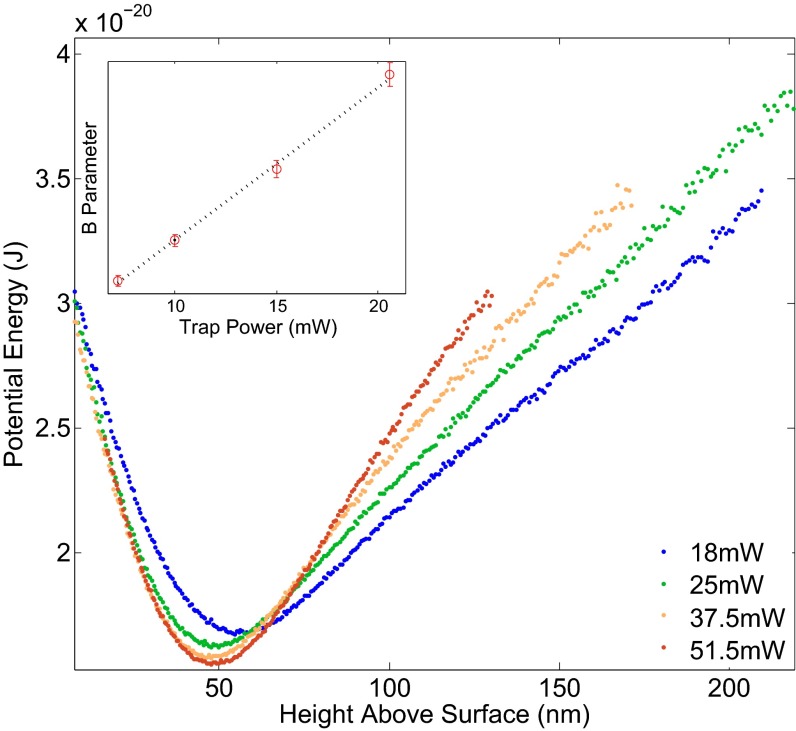
To confirm the accuracy of the fit result, we implement an independent method of determining bead radius, whereby we measure the change in effective bead mass as a function of trap radiation pressure and extract the bead mass intercept (at zero radiation power) via a linear regression.
The potential energy profile for a glass bead above a glass surface is expected to be, combining the double-layer repulsion discussed previously and the gravitational and radiation pressure effects (23, 25, 43),
| [9] |
where , and are the densities of glass and water, V the volume of the bead, g is the gravitational acceleration, and ϕ is the force due to radiation pressure. We reduce the NA of the trapping beam by closing the iris in the back focal plane of the objective, largely removing axial confinement of the particle, and obtain the parameter B by fitting the potential for several different trapping powers. Assuming that radiation pressure scales linearly with laser power (P) for a given bead and trap configuration, i.e., , a linear fit of B vs. P yields from the intercept the bead mass and therefore radius.
Fig. 6 shows potential energy profiles obtained for the glass sphere whose diffusion coefficient we measured in Wall Effects on Diffusion Coefficients. The optical trap NA was reduced to less than 0.2 and the trap power varied between 18 mW and 51 mW. The bead radius we obtain by fitting the potential energy profiles, assuming room temperature, is 1.27 ± 0.05 μm, which is in good agreement with the 1.26 ± 0.02-μm result in Wall Effects on Diffusion Coefficients.
Fig. 6.
Potential energy profiles measured for four different powers of the low numerical aperture trapping beam. Curves are shifted horizontally to better visualize change in the B parameter (as defined in Eq. 9) or the slope of the linear portion of the potential. Inset shows B parameter vs. trapping power and the linear fit used to calculate the particle’s radius.
Conclusions
We have developed a scheme for high-resolution absolute position particle tracking, using the TIRM scattering method. As the TIRM technique is itself highly sensitive and highly tunable, our main innovation is the introduction of to our knowledge the first in situ calibration that does not rely on explicit knowledge of additional experimental system parameters. By direct measurement of the essential experimental parameters under exact experimental conditions, we eliminate errors associated with their usual estimation or calculation.
Compared with typical TIRM experiments, we demonstrate a more than 10× error reduction in determining the decay-length parameter that sets the measurement range of a TIRM experiment. We show free and ready tuning of this parameter, a valuable experimental degree of freedom rarely before exploited due to prohibitively large errors. We are able to locate the point of contact, with better than 10 nm precision, yielding absolute instead of relative positional values. To show the extended versatility of the TIRM technique we repeated an experiment requiring high sensitivity, long range, and absolute positions that has previously proved challenging for this sensing method. Our results exceed in range that of previous experiments by a factor of 3 and show good agreement with hydrodynamic theory throughout. In the future, we imagine precise measurements in inhomogeneous media, amid more complex geometries, above metal surfaces, and more, to access novel forces in previously unexplored systems.
Supplementary Material
Acknowledgments
We thank the Evelyn Hu and David Weitz groups at Harvard University for shared equipment and helpful discussions. This work is supported by National Science Foundation Graduate Research Fellowships Program Grant DGE1144152.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1422178112/-/DCSupplemental.
References
- 1.Ambrose EJ. A surface contact microscope for the study of cell movements. Nature. 1956;178(4543):1194. doi: 10.1038/1781194a0. [DOI] [PubMed] [Google Scholar]
- 2.Axelrod D. Cell-substrate contacts illuminated by total internal reflection fluorescence. J Cell Biol. 1981;89(1):141–145. doi: 10.1083/jcb.89.1.141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Prieve DC. Measurement of colloidal forces with tirm. Adv Colloid Interface Sci. 1999;82:93–125. [Google Scholar]
- 4.Liebert RB, Prieve DC. Species-specific long range interactions between receptor/ligand pairs. Biophys J. 1995;69(1):66–73. doi: 10.1016/S0006-3495(95)79876-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Axelrod D. Total internal reflection fluorescence microscopy in cell biology. Traffic. 2001;2(11):764–774. doi: 10.1034/j.1600-0854.2001.21104.x. [DOI] [PubMed] [Google Scholar]
- 6.Amann KJ, Pollard TD. Direct real-time observation of actin filament branching mediated by Arp2/3 complex using total internal reflection fluorescence microscopy. Proc Natl Acad Sci USA. 2001;98(26):15009–15013. doi: 10.1073/pnas.211556398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hern JA, et al. Formation and dissociation of M1 muscarinic receptor dimers seen by total internal reflection fluorescence imaging of single molecules. Proc Natl Acad Sci USA. 2010;107(6):2693–2698. doi: 10.1073/pnas.0907915107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Serulle Y, Sugimori M, Llinás RR. Imaging synaptosomal calcium concentration microdomains and vesicle fusion by using total internal reflection fluorescent microscopy. Proc Natl Acad Sci USA. 2007;104(5):1697–1702. doi: 10.1073/pnas.0610741104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bowser DN, Khakh BS. Two forms of single-vesicle astrocyte exocytosis imaged with total internal reflection fluorescence microscopy. Proc Natl Acad Sci USA. 2007;104(10):4212–4217. doi: 10.1073/pnas.0607625104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sako Y, Minoghchi S, Yanagida T. Single-molecule imaging of EGFR signalling on the surface of living cells. Nat Cell Biol. 2000;2(3):168–172. doi: 10.1038/35004044. [DOI] [PubMed] [Google Scholar]
- 11.Sarkar A, Robertson RB, Fernandez JM. Simultaneous atomic force microscope and fluorescence measurements of protein unfolding using a calibrated evanescent wave. Proc Natl Acad Sci USA. 2004;101(35):12882–12886. doi: 10.1073/pnas.0403534101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stephens DJ, Allan VJ. Light microscopy techniques for live cell imaging. Science. 2003;300(5616):82–86. doi: 10.1126/science.1082160. [DOI] [PubMed] [Google Scholar]
- 13.Moerner WE. New directions in single-molecule imaging and analysis. Proc Natl Acad Sci USA. 2007;104(31):12596–12602. doi: 10.1073/pnas.0610081104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ha T. Single-molecule fluorescence resonance energy transfer. Methods. 2001;25(1):78–86. doi: 10.1006/meth.2001.1217. [DOI] [PubMed] [Google Scholar]
- 15.Allersma MW, Bittner MA, Axelrod D, Holz RW. Motion matters: Secretory granule motion adjacent to the plasma membrane and exocytosis. Mol Biol Cell. 2006;17(5):2424–2438. doi: 10.1091/mbc.E05-10-0938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Allersma MW, Wang L, Axelrod D, Holz RW. Visualization of regulated exocytosis with a granule-membrane probe using total internal reflection microscopy. Mol Biol Cell. 2004;15(10):4658–4668. doi: 10.1091/mbc.E04-02-0149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Burchfield JG, Lopez JA, Mele K, Vallotton P, Hughes WE. Exocytotic vesicle behaviour assessed by total internal reflection fluorescence microscopy. Traffic. 2010;11(4):429–439. doi: 10.1111/j.1600-0854.2010.01039.x. [DOI] [PubMed] [Google Scholar]
- 18.Wang X, et al. Imaging of dynamic secretory vesicles in living pollen tubes of Picea meyeri using evanescent wave microscopy. Plant Physiol. 2006;141(4):1591–1603. doi: 10.1104/pp.106.080168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Neuman KC, Nagy A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat Methods. 2008;5(6):491–505. doi: 10.1038/nmeth.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Maragò OM, Jones PH, Gucciardi PG, Volpe G, Ferrari AC. Optical trapping and manipulation of nanostructures. Nat Nanotechnol. 2013;8(11):807–819. doi: 10.1038/nnano.2013.208. [DOI] [PubMed] [Google Scholar]
- 21.Taylor MA, et al. Subdiffraction-limited quantum imaging within a living cell. Phys Rev X. 2014;4:011017. [Google Scholar]
- 22.Phillips D, et al. Shape-induced force fields in optical trapping. Nat Photonics. 2014;8:400–405. [Google Scholar]
- 23.Prieve DC, Frej NA. Total internal reflection microscopy: A quantitative tool for the measurement of colloidal forces. Langmuir. 1990;6:396–403. [Google Scholar]
- 24.Bevan MA, Prieve DC. Direct measurement of retarded van der waals attraction. Langmuir. 1999;15:7925–7936. [Google Scholar]
- 25.Flicker SG, Bike SG. Measuring double layer repulsion using total internal reflection microscopy. Langmuir. 1993;9:257–262. [Google Scholar]
- 26.Walz JY, Prieve DC. Prediction and measurement of the optical trapping forces on a microscopic dielectric sphere. Langmuir. 1992;8:3073–3082. [Google Scholar]
- 27.Hertlein C, Helden L, Gambassi A, Dietrich S, Bechinger C. Direct measurement of critical Casimir forces. Nature. 2008;451(7175):172–175. doi: 10.1038/nature06443. [DOI] [PubMed] [Google Scholar]
- 28.Prieve DC, Walz JY. Scattering of an evanescent surface wave by a microscopic dielectric sphere. Appl Opt. 1993;32(9):1629–1641. doi: 10.1364/AO.32.001629. [DOI] [PubMed] [Google Scholar]
- 29.Mattheyses AL, Axelrod D. Direct measurement of the evanescent field profile produced by objective-based total internal reflection fluorescence. J Biomed Opt. 2006;11(1):014006. doi: 10.1117/1.2161018. [DOI] [PubMed] [Google Scholar]
- 30.Gell C, Berndt M, Enderlein J, Diez S. TIRF microscopy evanescent field calibration using tilted fluorescent microtubules. J Microsc. 2009;234(1):38–46. doi: 10.1111/j.1365-2818.2009.03147.x. [DOI] [PubMed] [Google Scholar]
- 31.McKee CT, Clark SC, Walz JY, Ducker WA. Relationship between scattered intensity and separation for particles in an evanescent field. Langmuir. 2005;21(13):5783–5789. doi: 10.1021/la046856p. [DOI] [PubMed] [Google Scholar]
- 32.Behrens SH, Plewa J, Grier DG. Measuring a colloidal particle’s interaction with a flat surface under nonequilibrium conditions. Euro Phys J E Soft Matter Biol Phys. 2003;10:115–121. doi: 10.1140/epje/e2003-00013-2. [DOI] [PubMed] [Google Scholar]
- 33.Volpe G, Brettschneider T, Helden L, Bechinger C. Novel perspectives for the application of total internal reflection microscopy. Opt Express. 2009;17(26):23975–23985. doi: 10.1364/OE.17.023975. [DOI] [PubMed] [Google Scholar]
- 34.Harlepp S, Robert J, Darnton N, Chatenay D. Subnanometric measurements of evanescent wave penetration depth using total internal reflection microscopy combined with fluorescent correlation spectroscopy. Appl Phys Lett. 2004;85:3917–3919. [Google Scholar]
- 35.Prieve DC, Bike SG, Frej NA. Brownian motion of a single microscopic sphere in a colloidal force field. Faraday Discuss Chem Soc. 1990;90:209–222. [Google Scholar]
- 36.Clapp AR, Dickinson RB. Direct measurement of static and dynamic forces between a colloidal particle and a flat surface using a single-beam gradient optical trap and evanescent wave light scattering. Langmuir. 2001;17:2182–2191. [Google Scholar]
- 37.Banerjee A, Kihm KD. Experimental verification of near-wall hindered diffusion for the Brownian motion of nanoparticles using evanescent wave microscopy. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72(4 Pt 1):042101. doi: 10.1103/PhysRevE.72.042101. [DOI] [PubMed] [Google Scholar]
- 38.Volpe G, Quidant R, Badenes G, Petrov D. Surface plasmon radiation forces. Phys Rev Lett. 2006;96(23):238101. doi: 10.1103/PhysRevLett.96.238101. [DOI] [PubMed] [Google Scholar]
- 39.Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt Lett. 1986;11(5):288–290. doi: 10.1364/ol.11.000288. [DOI] [PubMed] [Google Scholar]
- 40.Ashkin A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys J. 1992;61(2):569–582. doi: 10.1016/S0006-3495(92)81860-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Helden L, et al. Single-particle evanescent light scattering simulations for total internal reflection microscopy. Appl Opt. 2006;45(28):7299–7308. doi: 10.1364/ao.45.007299. [DOI] [PubMed] [Google Scholar]
- 42.Rohrbach A, Stelzer EH. Trapping forces, force constants, and potential depths for dielectric spheres in the presence of spherical aberrations. Appl Opt. 2002;41(13):2494–2507. doi: 10.1364/ao.41.002494. [DOI] [PubMed] [Google Scholar]
- 43.Ducker WA, Senden TJ, Pashley RM. Direct measurement of colloidal forces using an atomic force microscope. Nature. 1991;353:239–241. [Google Scholar]
- 44.Jonáss A, Zemánek P, Florin E-L. Single-beam trapping in front of reflective surfaces. Opt Lett. 2001;26(19):1466–1468. doi: 10.1364/ol.26.001466. [DOI] [PubMed] [Google Scholar]
- 45.Jákl P, et al. Behaviour of an optically trapped probe approaching a dielectric interface. J Mod Opt. 2003;50:1615–1625. [Google Scholar]
- 46.Israelachvili JN. 1991. Intermolecular and Surface Forces (Academic, London), 2nd Ed.
- 47.Derjaguin B. On the repulsive forces between charged colloid particles and on the theory of slow coagulation and stability of lyophobe sols. Trans Faraday Soc. 1940;35:203–215. [Google Scholar]
- 48.Verwey E, Overbeek JTG. Theory of the stability of lyophobic colloids. J Colloid Sci. 1955;10:224–225. doi: 10.1021/j150453a001. [DOI] [PubMed] [Google Scholar]
- 49.Born M, Wolf E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Cambridge University Press; Cambridge, UK: 1999. [Google Scholar]
- 50.Kihm K, Banerjee A, Choi C, Takagi T. Near-wall hindered brownian diffusion of nanoparticles examined by three-dimensional ratiometric total internal reflection fluorescence microscopy (3-d r-tirfm) Exp Fluids. 2004;37:811–824. [Google Scholar]
- 51.Brenner H. The slow motion of a sphere through a viscous fluid towards a plane surface. Chem Eng Sci. 1961;16:242–251. [Google Scholar]
- 52.Goldman A, Cox RG, Brenner H. Slow viscous motion of a sphere parallel to a plane walli motion through a quiescent fluid. Chem Eng Sci. 1967;22:637–651. [Google Scholar]
- 53.Schäffer E, Nørrelykke SF, Howard J. Surface forces and drag coefficients of microspheres near a plane surface measured with optical tweezers. Langmuir. 2007;23(7):3654–3665. doi: 10.1021/la0622368. [DOI] [PubMed] [Google Scholar]
- 54.Carbajal-Tinoco MD, Lopez-Fernandez R, Arauz-Lara JL. Asymmetry in colloidal diffusion near a rigid wall. Phys Rev Lett. 2007;99(13):138303. doi: 10.1103/PhysRevLett.99.138303. [DOI] [PubMed] [Google Scholar]
- 55.Faucheux LP, Libchaber AJ. Confined Brownian motion. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1994;49(6):5158–5163. doi: 10.1103/physreve.49.5158. [DOI] [PubMed] [Google Scholar]
- 56.Pralle A, Florin E-L, Stelzer E, Hörber J. Local viscosity probed by photonic force microscopy. Appl Phys A Mater Sci Process. 1998;66:S71–S73. [Google Scholar]
- 57.Bevan MA, Prieve DC. Hindered diffusion of colloidal particles very near to a wall: Revisited. J Chem Phys. 2000;113:1228–1236. [Google Scholar]
- 58.Frej NA, Prieve DC. Hindered diffusion of a single sphere very near a wall in a nonuniform force field. J Chem Phys. 1993;98:7552–7564. [Google Scholar]
- 59.Pagac E, Tilton R, Prieve D. Hindered mobility of a rigid sphere near a wall. Chem Eng Commun. 1996;148:105–122. [Google Scholar]
- 60.Uhlenbeck GE, Ornstein LS. On the theory of the brownian motion. Phys Rev. 1930;36:823. [Google Scholar]
- 61.Wang MC, Uhlenbeck GE. On the theory of the brownian motion ii. Rev Mod Phys. 1945;17:323–342. [Google Scholar]
- 62.Peterman EJ, Gittes F, Schmidt CF. Laser-induced heating in optical traps. Biophys J. 2003;84(2 Pt 1):1308–1316. doi: 10.1016/S0006-3495(03)74946-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.